Abstract
Grinding robots are widely used in the automotive, mechanical processing, aerospace industries, among others, due to their strong adaptability, high safety and intelligence. The grinding process parameters are the main factors that affect the quality and efficiency of grinding robots. However, it is difficult to obtain the optimal combination of the grinding process parameters only by manual experience. This study proposes an artificial intelligence-based method for optimizing the process parameters of a grinding robot using neural networks and a genetic algorithm, with the aim to reduce the workpiece surface roughness and shorten the grinding time. Specifically, this is the first study utilizing a multi-objective optimization approach to optimize the process parameters of a grinding robot. Based on the experimental data of the grinding robot ROKAE XB7, the long short-term memory (LSTM) and multilayer perceptron (MLP) neural networks were trained to fit the quantitative relationships between the process parameters of the grinding robot, such as feed rate, spindle pressure and pneumatic motor pressure, and the result of grinding surface roughness and grinding time. After that, the non-dominated sorting genetic algorithm II (NSGA-II) was used to calculate the Pareto optimal process parameter combinations using the trained LSTM and MPL model as the objective function. Compared with the method based on manual experience, the process parameters optimized with this method achieved a reduction in surface roughness of at least 13.62% and a reduction in the whole grinding process time of 28%. The excellent grinding results obtained for grinding time and surface roughness validated the feasibility and efficiency of the proposed multi-objective method for the optimization of grinding robots’ process parameters in practical manufacturing applications.
1. Introduction
Grinding robots (GR), characterized by flexibility, intelligence, and low cost, can effectively improve the surface quality of workpieces when combined with professional grinding tools for machining. They are widely applied in the manufacturing process of mechanical parts [1]. The intelligence of GR is highlighted by their strong compatibility with artificial intelligence methods, making them ideally suited for use in machining processes with complex process features. Robotic grinding is an extremely complex process, and the grinding quality is affected by multiple process parameters of grinding robots (PPGR), as well as by multifactorial interactions. During the robotic grinding process, the instability of the grinding force can affect the material removal rate (MRR), thereby affecting the quality of robotic grinding [2]. Therefore, researchers have focused on improving the grinding quality by enhancing the control performance of GR and increasing the grinding force control accuracy [3,4]. In fact, the grinding force is also affected by grinding depth, grinding speed and tool feed rate [1]. The grinding quality not only depends on the grinding force but also is affected by variant process parameters such as contact stress, spindle speed and feed speed [5].
In addition to improving the quality of grinding, increasing the economic productivity of the grinding process by increasing the grinding speed and shortening the grinding time is one of the main objectives of industrial production applications using GR [6]. However, a high grinding speed can lead to an increased wear of the grinding tool, resulting in a lower grinding quality. Moreover, the setting of the PPGR heavily relies on human expertise, which poses a challenge for synchronously optimizing grinding time and grinding quality.
Based on the complex relationships between PPGR, it is necessary to clarify the quantitative relationship between PPGR and grinding quality, to predict the grinding quality under the current process parameters and then to optimize the parameters. In order to obviate the current reliance on manual empirical judgement and to quantify more accurately the influence of PPGR on grinding quality, researchers have proposed to use artificial intelligence reinforcement learning to predict the grinding quality [7]. Based on the prediction model of grinding quality based on the grinding parameters, the grey target decision-making method [8], the response surface methodology [9] and other methods have been used to optimize the process parameters in order to improve the grinding quality. Xie et al. [10] optimized the polishing parameters of the polishing process for mold steel by using the response surface methodology to optimize the polishing pressure, feed speed and rotating speed of the tool, aiming to reduce the surface roughness of the workpiece. The above research methods only focus on optimizing the process parameters with the objective of improving the grinding quality. However, in actual production, a multi-objective optimization method that considers both quality and grinding time needs to be considered.
The state-of-the-art research on multi-objective optimization methods for grinding process parameters mainly focuses on the optimization of the process parameters of traditional grinding equipment such as grinding machines, polishing machines, sanding machines, etc. Zhang et al. [11] proposed a hybrid particle swarm optimization (HPSO) algorithm that considered grinding wheel speed, feed rate, grinding depth and dressing lead as the process parameters to be optimized and conducted a multi-objective optimization with production cost, production rate and surface roughness as the objectives. Numerous studies used mathematical models [12] and artificial intelligence methods such as neural networks (NN) [13], genetic algorithms (GA) [14], particle swarm optimization (PSO) [15] for the optimization of the process parameters of the grinding process [16]. Khalilpourazari et al. [17] aimed to optimize the grinding process considering a tri-objective mathematical model to simultaneously optimize the final surface quality, the grinding cost and the total process time using the multi-objective dragonfly algorithm (MODA).
However, there is a lack of research on multi-objective optimization methods for PPGR in recently published papers. Comprehensive research on the optimization of traditional grinding process parameters showed that the use of multi-objective optimization algorithms to optimize the grinding process parameters is an effective method to improve the quality and efficiency of grinding. GR primarily use a series-parallel hinge structure with flexible motion space, and their grinding methods are different from those of traditional grinding equipment. The grinding methods of GR are mainly two: one consists in grasping the workpiece and placing it in contact with a fixed grinding tool, and the other uses an end effector installation grinding tool to grind the fixed workpiece. The PPGR are also not entirely the same as those of traditional polishing equipment. In practice, workers are required to set the PPGR based on their experience and debug them on site. The debugging process will consume a lot of material and time. At the same time, the manual empirical method can only adjust the PPGR according to the expected grinding quality as a single goal. It is difficult to set the optimal grinding robot process parameters according to both grinding quality and time. Hence, there is an urgent need for a multi-objective optimization method for PPGR considering both grinding quality and grinding time, in order to obviate the reliance on manual experience.
The goal of this paper was to propose an intelligent approach to simultaneously optimize the robot grinding quality (average surface roughness Ra) and grinding time using historical grinding data and to demonstrate the effectiveness of the proposed method by a grinding trial. For this purpose, a multi-objective optimization of the PPGR based on the non-dominated sorting genetic algorithm II (NSGA-II) was utilized. In addition, long short-term memory (LSTM) and multilayer perceptron (MLP) were used to predict the grinding Ra and grinding time of the robot by considering the effects of burr wear and the robot motion characteristics, respectively, so to predict the grinding results more precisely. The superiority of the proposed method was verified by comparing the grinding results of the Pareto optimal process parameter combinations calculated by the method proposed in this paper with those obtained with the manually determined, empirical parameters. This study provides a strong support for improving the selection of PPGR, which, in the current practical applications, seriously relies on manual experience and on-site debugging and thus is not efficient in determining the optimal process parameter combinations.
2. Methodology
2.1. Mathematical Model of Surface Roughness
The non-linear relationship between processing parameters and Ra for a GR is explained by a mathematical description. The grinding robot grips the workpiece with an end effector and contacts the radially compliant material removal tools (RCMRT) fitted with rotary burrs to grind the workpiece, as shown in Figure 1.
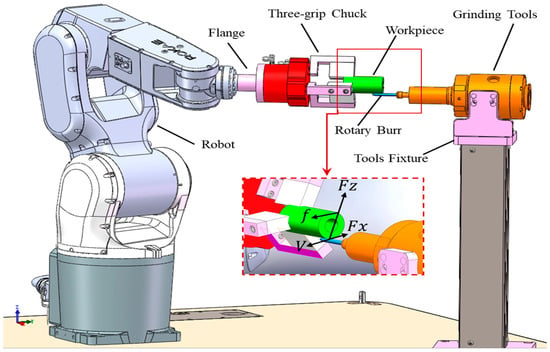
Figure 1.
The model of the robotic grinding system.
Rotary burrs resembles cylindrical milling cutters in CNC machining, and their grinding mechanism is comparable to that of a machine tool for surface milling. Hence, the multiple regressions in the form of an exponential function [18] to depict the in-process surface roughness during the grinding process, as shown below:
where Ra is the average surface roughness, V is the spindle speed, f is the feed rate, d is the depth of cut, D is the burrs’ diameter, is the dynamic grinding force ratio, in which Fx is the component of the grinding force in the tangential direction at the contact point, and Fz is the component of the grinding force in the normal direction at the contact point, α, m, n, k, β and C are the regression coefficients of the model. In the actual grinding process, the material of the workpiece, the processing size and the processing craft determine d and D, while the PPGR V, f, Fx and Fz are set by engineers according to the site conditions. In Figure 1, f is determined by the linear velocity by which the GR grips the workpiece, which can be set directly in the controller of the robot. The cutting force Fz is the radial floating force output from the rotary burrs. The RCMRT contains an air-suspended bearing and, by adjusting the air pressure of the bearing, can control the spindle output to stabilize the volume of the radial floating sanding force. The linear relationship between the air pressure and the floating force of the RCMRT is shown in Figure 2.
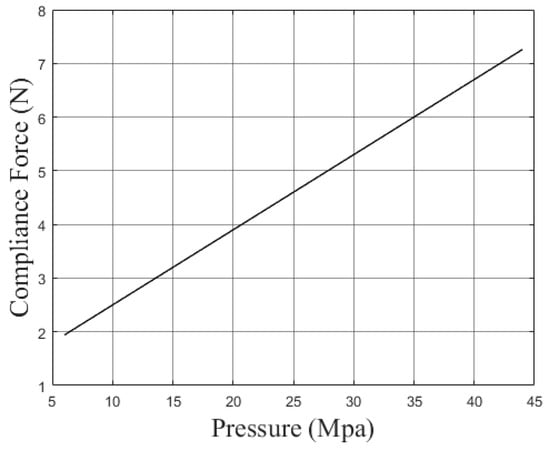
Figure 2.
Compliance force and pressure.
The conversion to a quantitative relationship can be obtained with Equation (2)
where Pz is the input pneumatic motor pressure, Kz is the scale factor. The cutting force Fx is the tangential force at the point of contact between the rotary burrs and the workpiece, and both Fx and V, expressed in Equations (3) and (4), are determined by the torque and speed provided by the air motor of the spindle in the RCMRT:
where Vg is the capacity of the pneumatic motor, Pr is the spindle pressure, η is the volumetric efficiency, qv is the flow rate. According to the Bernoulli equation in fluid dynamics, qv can be expressed by the following equation
where ST is the cross-sectional area of the pipes, is the density of air. Substituting Equations (2) to (5) into (1) yields:
The constant term in the formula obtained by integrating the substitutions is integrated as Co in Equation (7), and the static variable representing the structural property is integrated as Qo in Equation (8). The simplified surface roughness Equation (6) is obtained by combining the constant Co and the structural property term Qo, obtaining a mathematical model for the relationship between the PPGR and the quality of Ra.
2.2. Algorithm for Multi-Objective Optimization
Equation (6) shows that the grinding average surface roughness Ra of the robot is subject to the interaction of feed rate f, spindle pressure Pr and pneumatic motor pressure Pz and suggests that it is difficult to use a mathematical model to accurately optimize the grinding results under different process parameters. Therefore, this paper considered the burr wear in the grinding process and the motion characteristics of the GR and used the LSTM and MLP neural network algorithms to fit the quantitative relationship between the grinding surface roughness and the time for different PPGR and predict the grinding results. The constructed LSTM model and MLP model were used as the objective function of the multi-objective optimization algorithm NSGA-II, and the Pareto front was calculated to obtain the optimal sets of PPGR.
2.2.1. LSTM Model for Fitting the Surface Roughness
The long short-term memory (LSTM) neural network is a special type of recurrent neural network. Unlike general artificial neural networks (ANN), it can handle data with temporal relationships [19]. In the GR grinding process, it is known, from Equation (6), that the burrs’ size D also affects Ra. The grinding burrs will be worn as grinding is carried out, resulting in a change in the size of the burrs, i.e., in the surface state, which affects the grinding surface quality [17]. The wear of the rotary burrs is affected by the PPGR. When predicting the surface quality of the grinding, it is necessary to consider the impact of the rotary burrs’ wear caused by the grinding of the previous workpiece on the grinding of the next workpiece. Therefore, this paper proposes to train the LSTM neural network for predicting the surface quality for certain PPGR settings, considering the effect of rotary burrs’ wear on the grinding quality.
LSTM has the ability to remember past input data. Its network structure is shown in Figure 3 and includes a cell state, a forget gate, a memory gate and an output gate. The LSTM has two inputs at each moment, which are the input process parameters at the current moment and the predicted values of Ra at the output of the previous moment. The two inputs are integrated into a single vector by the forget gate, which compresses the input vector to the (0, 1) interval through a sigmoid neural layer and compares it with the pre-sequence input features stored in the cell state, forgetting part of the features. The memory gate extracts the process parameter features of the current input using the tanh function and controls the weight of saving the current parameter features in the cell state using the sigmoid function. The output gate processes the current input PPGR, the Ra from the previous time step and the parameters stored in the cell state and outputs the predicted Ra for the current time step.
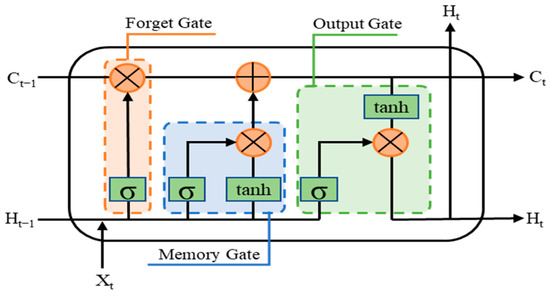
Figure 3.
Structure of the LSTM network.
The cell state in the LSTM remembers the grinding burrs’ wear state features included in the surface quality at the previous moment, affects the predicted value of the grinding surface quality in the output gate and is transmitted to the cell state at the next moment to affect the predicted value of the surface roughness at the next moment.
2.2.2. MLP Model for Fitting the Grinding Time
Usually, the optimization of GR efficiency mainly focuses on improving the MRR and surface quality, without considering the influence of a robot motion characteristics on the grinding time. The grinding time in actual industrial production comprises two elements, which are the execution time of the robot’s movement when the workpiece is not in contact with the grinding burrs and the duration of the subsequent grinding process. Based on the required grinding quality, the GR feed speed during the grinding process is stable, while the speed before contact with the workpiece is flexibly decided by engineers based on the production environment and requirements. The motion rate of the GR is usually set to the maximum to boost productivity. However, the robot motion comprises acceleration and deceleration stages, which require a certain space for the acceleration- and deceleration-linked motions. Figure 4 is reproduced from [20] and shows the time taken to cover the same distance with different robot speed parameters. When the robot motion distance is insufficient, setting the motion speed too high will not reduce the actual motion time of the robot.
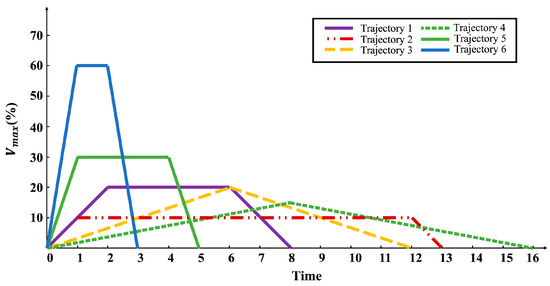
Figure 4.
Velocity–time curves for different velocity parameters of the robot.
In practical applications, GR use an S-shaped or a trapezoidal acceleration and deceleration control, and changes in the speed parameters will affect the robot trajectory execution time. The relationship between execution time and speed changes is nonlinear. Neural networks are widely used in regression fitting non-linear relationships between system parameters to predict the output of the system [21]. In order to accurately predict the grinding time, this paper used a Multi-Layer Perception (MLP) neural network to adjust the relationship between the speed parameter of the GR and the final grinding time. To ensure the homology of the data, the input parameters of the MLP were the same as those of the LSTM, which were three-dimensional vectors containing the robot speed f, the spindle pressure Pr and the pressure of the pneumatic motor Pz. The MLP includes an input layer, a hidden layer and an output layer. The transfer weight between the neurons in the input layer and those in the hidden layer is used to extract the features of the input data. The quantitative relationship between the input and the output of the neural network was fitted by the full connection between the neurons in the hidden layer and the activation function to achieve the accurate prediction of the grinding time.
2.2.3. NSGA-II for Multi-Objective Optimization
The genetic algorithm (GA) is an effective tool for optimizing nonlinear and complex problems based on natural selection processes in biological systems. Traditional GA algorithms are computationally inefficient and only suitable for single-objective optimization. In this paper, the non-dominated sorting genetic algorithm-II (NSGA-II) was used to find the combination of RRGR that minimized Ra and grinding time, as described above. The NSGA-II algorithm incorporates an elitist strategy to prevent the loss of superior individuals and obtains the Pareto front by performing non-dominated sorting on all parent and offspring individuals that are mixed. The result on the Pareto front is a series of bounded solutions calculated according to the optimization objective, none of which dominates the other. However, it is possible to obtain the optimal result for the scenario in exam depending on the application and the constraints of the optimization problem.
From the analysis in Section 2.1, it is evident that an increase in the GR speed f would lead to a higher grinding surface roughness and would reduce the grinding time. Therefore, the surface quality and grinding time during the robot grinding process are two conflicting optimization objectives. The optimal Pareto front according to the optimization objective can be computed using the NSGA-II. The multi-objective optimization algorithm based on NSGA-II used in this paper is shown in Figure 5. Firstly, a randomly generated initialized population P0 of size N was generated, and using the tournament selection algorithm, crossover and mutation were performed to obtain the offspring Q0, which was combined into a population R0. Then, iteration through all the solutions in the population R0 was carried out, the number of dominated sets was computed for each solution for a fast non-dominated sorting, and the fitness values of each level of non-dominated solutions in the sorted Z1, Z2, Z3 were assigned according to their frontier levels. In this case, the solutions in the first level of the non-dominated frontier Z1 were the best solutions, and all the solutions in this level were retained in the new-generation population P1 according to the elitism strategy. If the number of Z1 is less than N, the next level of non-dominated solutions in level Z2 is selected to complement them, until the number of remaining solutions in the P1 population is not sufficient to merge all solutions within a complete non-dominated frontier level. The solutions in the last set of nondominated solutions that cannot be merged into the P1 population are sorted by crowded distance. The sorted top solution were selected to complement the remaining P1 population to reach N. P1 was selected with a crowded comparison operator through the tournament selection algorithm, and Q1 was generated using the traditional GA algorithm with crossover and mutation. P1 and Q1 were combined for the R1 population, and the operation of the fast nondominated sorting was repeated until the number of iteration generations was reached.
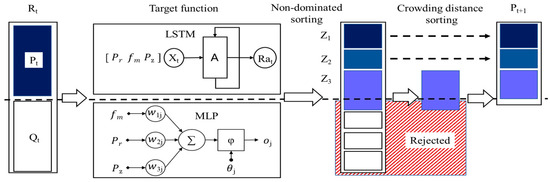
Figure 5.
Structure of the LSTM-MLP-NSGAII model.
The predicted surface quality and grinding time from the LSTM and MLP models, which were built and trained, were then input. The predicted results were quickly non-dominatedly sorted, and the parent population Pt+1 of the new generation was obtained by calculating the crowding distance. The new offspring population Qt+1 was obtained using the genetic algorithm based on the elitist strategy, and the above steps were repeated. After continuous selection, mutation, crossover and iteration to reach the number of generations set by the algorithm, the optimal Pareto front was obtained.
3. Experiment and Method Implementation
3.1. Experiment Platform
To the purpose of studying the influence of the PPGR on machining quality and grinding time, it was necessary to control the air pressure of the RCMRT and the speed of robot motion during the grinding process. Therefore, a GR platform with the RCMRT was established, as in Figure 6. The GR platform mainly consisted of three main parts: a storage table with the aluminum tubes (STAT), the industrial robot and the RCMRT. The STAT contained 6061 aluminum panels with three plastic pins for mounting the grinding workpieces. The model of the industrial robot was ROKAE XB7 with a 7 kg load. The maximum linear velocity at the end of the robot is 300 mm/s. The RCMRT was installed in the working range of the GR and fixed in the worktable of the industrial robot platform by steel brackets. The RCMRT is a pneumatic tool consisting of a support pressure providing a constant grinding force and a pneumatic motor providing high-speed rotation of the grinding shaft. The RCMRT can provide a compliance force ranging from 0.89 N to 6.7 N, corresponding to a spindle pressure Pr from 0.034 MPa to 0.45 MPa. The RCMRT has two air circuits used to drive the pneumatic motor and the compliance force, which are controlled by the force and the rotating pneumatic valve. On the spindle of the RCMRT, tungsten carbide rotary burrs with a double cut, a 1/8″ diameter, a 9/16″ length and a 1/8″ shank were installed to remove the oxide layer from a cylindrical tube of 6061 aluminum alloy. The MarSurf PS 10 handheld roughness measuring instrument was used to measure Ra after grinding. In practical production, due to GR structural rigidity, the grinding trajectory, the product materials and other factors, the requested grinding surface quality Ra is in the range of 0.2–3.2. In this study on tubes with a 6061 aluminum cylindrical surface, the requested grinding surface quality Ra was 0.8–1.6.
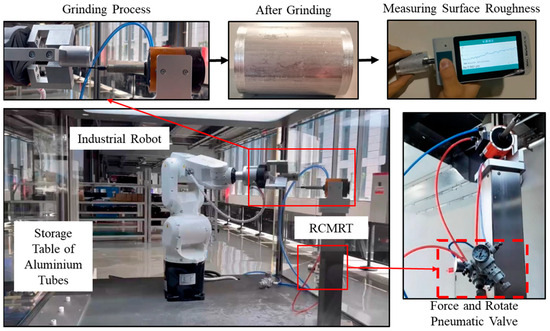
Figure 6.
Experimental platform of robotic grinding.
3.2. Experiment Dataset
The aluminum alloy workpiece to be ground was stored in the STAT, and the GR gripped the workpiece and moved it over the RCMRT. The pneumatic valve opened to drive the rotation of the spindle of the RCMRT and maintain the grinding compliance force. Then, the GR placed the workpiece in contact with the rotary burrs rotating at high speed and rotated the workpiece by 360 degrees to complete the grinding of the cylindrical surface of the aluminum tube. Throughout the grinding process, the speed of the robot moving the workpiece to the top of the RCMRT and the feed rate f of the workpiece were controlled by setting the linear velocity in the robot controller. The ROKAE controller has three modes for setting the motion speed, i.e., the joint velocity percentage (PER), the tool central point (TCP) speed and the orientation velocity (ORI). In this experiment, the TCP speed range was set from 25 mm/s to 300 mm/s, with a step of 25 mm/s, as the feed rate f in the PPGR.
In order to validate the proposed optimization method for the PPGR, grinding experiments were first conducted according to the PPGR shown in Table 1, and the model training dataset was compiled. The experiments were divided into four groups. We used 12 rotary burrs, for a total of 300 grinding experiments, with 25 grinding operations performed for each rotary burr. In each group of experiments, f and Pz were combined non-repetitively from the minimum to the maximum value in stepwise crossover and with a specific Pr, obtaining a unique PPGR combination for each group. After four grinding operations for each rotary burr, a group of specific PPGR combinations was evaluated for burr wear estimation.

Table 1.
The experimental process parameters dataset of robotic grinding.
After grinding the surface of the cylindrical workpiece at an interval of 120 degrees, we selected three measurement points, measured and recorded the value of Ra, and then determined the average of the results. The grinding results are shown in Figure 7. The 300 sets of experimental results and their PPGR constituted the basic training dataset for the multi-objective optimization method proposed in this paper. The red line in Figure 7a indicates that the grinding time did not decrease linearly with the increase in robot speed. After the speed reached a certain value, the decrease in grinding time slowed down. Figure 7b shows the test data for the wear of the rotary burrs and the fluctuation of Ra in the testing groups during the grinding process. This result showed that the wear of a rotary burr over the course of 25 grinding passes was very complex and difficult to extrapolate from empirical formulas. Therefore, the use of neural networks to fit the grinding time and grinding quality results was necessary to accurately predict the performance of the PPGR.
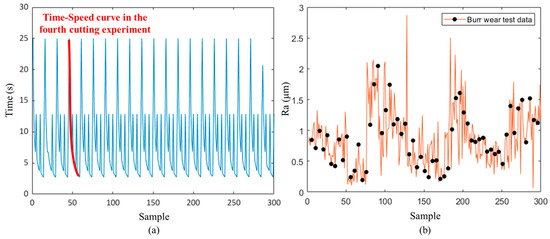
Figure 7.
Experimental grinding results. (a) Grinding time; (b) grinding surface roughness.
3.3. LSTM and MLP Neural Network Training
The intelligent algorithms mentioned in this paper were run on a computer with a CPU of i5-11400 @ 2.6GHz and 16 GB of RAM. The construction of the neural network was implemented in a Python 3.8 environment based on the Sklearn, Tensorflow algorithm package. The LSTM and MLP neural network models were trained using the experimental dataset obtained in Section 3.2, and the model parameters are shown in Table 2. Prior to model training, the experimental dataset was normalized to the range of 0.1 to 0.9 in each column to speed up model convergence and was divided into a validation set containing 10% of the data and a training set with 90% of the data. The width of the rolling window for the network training data was set to 25, and 0 padding was applied at the beginning to each burr’s data. When the first grinding data of the burrs were input, the first 24 rows of the input matrix and the label vector were set to zero to indicate that the current grinding sequence was the first. The model was initialized with the parameters shown in Table 2, and the training of the model was started with the validation and testing datasets. The training results are shown in Figure 8. Figure 8a shows that the LSTM model achieved an mean squared error (MSE) of less than 0.01 after being trained for 200 iterations using the training and validation sets. Based on the MLP model, the training results for the grinding time are shown in Figure 8b, with an MSE of less than 0.0086 achieved after model training, indicating that the model had converged, and the training was complete.

Table 2.
Parameters of the LSTM and MLP neural networks.
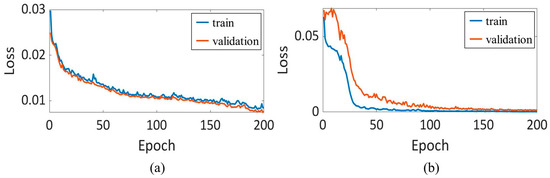
Figure 8.
Experimental training results. (a) Loss of the LSTM network; (b) lLoss of the MLP network.
3.4. Surface Roughness and Grinding Time Prediction
To validate the prediction accuracy of the trained LSTM and MLP models for Ra and grinding time, a set of experimental parameters was randomly selected from the experimental parameter groups and recombined for the grinding experiments. The recombined PPGR were inputted into the LSTM surface roughness model and the MLP grinding time model according to the grinding sequence to form a matrix. The predicted results of the models were compared with the actual results, as shown in Figure 9. As the surface roughness is significantly affected by the environment, the model prediction of Ra has a certain error compared with the real value. The grinding time is mainly affected by the speed and trajectory of the GR, and the acceleration and deceleration characteristics of the GR lead to a certain error when the speed changes.
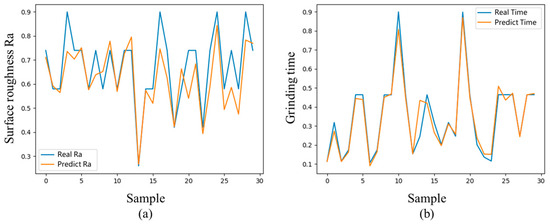
Figure 9.
Experimental prediction results. (a) Average surface roughness Ra prediction results; (b) grinding time prediction results.
The mean absolute percentage error (MAPE) is commonly used in the evaluation of neural network prediction results. The MAPE was used to evaluate the prediction results of the trained models. The MAPE of the LSTM model for predicting Ra was 0.0576, and the MAPE of the MLP model for predicting the grinding time was 0.0079, and both were within the acceptable error range.
4. Optimization and Validation of the Process Parameters
To validate the effectiveness of the multi-objective optimization method proposed in this paper for the PPGR, two similar burrs with similar wear conditions that had been used with the same process parameters and for the same grinding times were prepared for the experiment. The two burrs were used for the grinding trials in the optimization group and the manual experience group. Each burr was utilized for six consecutive grinding tasks on the aluminum tubes. The grinding trials with the PPGR obtained from the multi-objective optimization method proposed in this paper were considered the optimization group. The grinding trials conducted by on-site workers based on their experience while debugging the parameters were considered the manual experience group. The historical PPGR and grinding results of the burrs were input as a sequence into the multi-objective optimization algorithm, with the minimum Ra and grinding time as the optimization objectives, to calculate the Pareto front of the optimal PPGR combination for the subsequent six grinding operations. The surface quality results of the grinding aluminum tube cylindrical surface for the optimization group and the manual experience group are shown in Figure 10. The workpieces 21 to 26 represent the grinding group with optimized parameters, while the workpieces 45 to 50 represent the manual experience group. It can be seen in Figure 10 that the surface finish of the optimization group was better than that of the manual experience group.

Figure 10.
Comparison of the trials with the optimization group and the manual experience group.
The surface roughness of the ground workpiece was measured, and the PPGR and grinding times were recorded, as shown in Table 3. The numbers marked in black pencil on the aluminum tubes in Figure 10 correspond to the values in the No. column of the table.

Table 3.
Results of the comparison between the multi-objective optimization and manual experience methods.
In terms of grinding quality, the aluminum tubes from No. 21 to No. 26 were subjected to parameter-optimized grinding and corresponded to those from No. 45 to No. 50 that were subjected to grinding with manually determined parameters. Therefore, the grinding of the tubes No. 21 and No. 45 corresponded to the 21st grinding for the two groups, using tools with same grinding parameters and used the same number of times. The final grinding results showed that the minimum value of Ra for the optimized group was 0.135 μm for No. 25, and the maximum value was 0.506 μm for No. 22, while the minimum value of Ra for the manual experience group was 0.345 μm for No. 48, and the maximum value was 1.721 μm for No. 49. The Ra value of the optimized group was lower by a maximum of 92.16% than that of the manual experience group. The mean value of Ra for the optimized group was 0.283 μm with a variance of 0.0183, while the mean value for the manual experience group was 0.751 μm with a variance of 0.2592. The quality of the grinding in the optimized group was generally improved, and the fluctuation of Ra was smaller. Compared with the optimized group, the grinding quality of the manual empirical group was much worse and fluctuated greatly, mainly because the manual empirical method could not accurately predict the relationship between grinding parameters and grinding quality. At the same time, workers can only rely on their visual and empirical judgement when evaluating tool wear, which is very inaccurate; so, the setting of the grinding parameters and the final grinding quality are uncertain and require extensive debugging and testing to obtain the final parameters that can be applies.
In terms of grinding time, the optimized group showed a maximum reduction of 53.83% compared to the manual experience group, with the shortest grinding time of 2.699 s for the optimized group and of 2.711 s for the manual experience group. Although the grinding time of the aluminum tube No. 24 was 54.01% longer than that of the aluminum tube No. 48. in the same grinding sequence, the surface roughness Ra value was 13.62% smaller. After excluding the loading and unloading time, the optimized group required a total of 25.375 s to grind the six groups of workpieces, and the manual experience group requires 35.242 s; the total grinding time of the optimized group was 28% shorter than that of the manual experience group. Comprehensively comparing grinding quality and time of the optimization group and the manual experience group, after grinding six groups, the optimization group finally obtained a stable parameter range, while the manual experience group was still in the debugging stage, with large parameter variations. Therefore, it is evident that the optimized group could obtain the best combination of parameters in terms of grinding quality and time more quickly than the manual experience group.
From the results and comparisons, it can be concluded that the proposed multi-objective optimization of the PPGR based on LSTM-MLP-NSGAII could achieve a better performance than the PPGR adjustment method relying on the experience of workers.
5. Discussion and Conclusions
To allow the simultaneous optimization of grinding time and quality, which is difficult when evaluating the PPGR manually, this paper proposes a multi-objective optimization method for the PPGR. The efforts made and the conclusions reached are summarized as follows:
- Based on the mechanism of the rotary burrs and the driving characteristics of the RCMRT, a model for the qualitative relationship between surface quality of a robotic pneumatic grinding system, robot speed, radial compliance force and spindle air pressure was presented.
- The proposed LSTM-MLP-NSGAII model considers the effects of burr wear and robot kinematics on grinding quality and time in an integrated approach compared to traditional methods that rely on manual experience.
- A multi-objective optimization method for the PPGR is proposed, taking surface roughness and grinding time into account for the first time.
- Compared with the manual empirical method, the Ra achieved was at least 13.62% better than that obtained with the manual empirical method, and the grinding time was reduced by 28%.
The proposed multi-objective optimization method utilizes artificial intelligence algorithms instead of complex mathematical models, not only realizing the optimization of the PPGR, but also extending the scope of the optimization application of GR. However, in this paper only the optimization for grinding quality and time was studied, and the optimized parameters were limited. Future research will extend the range of the process parameters and the grinding process optimization objectives of the current neural networks for the multi-mode grinding optimization of grinding robots and promote the intelligent development of grinding robots.
Author Contributions
Conceptualization, R.L. and J.Y.; methodology, R.L.; software, R.L.; validation, R.L. and Z.W.; formal analysis, R.L.; investigation, R.L.; resources, J.Y.; data curation, R.L.; writing—original draft preparation, R.L.; writing—review and editing, J.Y.; visualization, Z.W.; supervision, Z.W.; project administration, J.Y.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundations of China, grant number 52275482.
Data Availability Statement
Not applicable.
Acknowledgments
The authors wish to thank Mingyang Zhang for providing technical support during the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, T.; Yuan, C.; Zou, Y. Online Optimization Method of Controller Parameters for Robot Constant Force Grinding Based on Deep Reinforcement Learning Rainbow. J. Intell. Robot. Syst. 2022, 105, 85. [Google Scholar] [CrossRef]
- Zhao, X.; Lu, H.; Yu, W.; Tao, B.; Ding, H. Robotic Grinding Process Monitoring by Vibration Signal Based on LSTM Method. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar] [CrossRef]
- Song, Y.; Liang, W.; Yang, Y. A Method for Grinding Removal Control of a Robot Belt Grinding System. J. Intell. Manuf. 2012, 23, 1903–1913. [Google Scholar] [CrossRef]
- Nogi, Y.; Sakaino, S.; Tsuji, T. Force Control of Grinding Process Based on Frequency Analysis. IEEE Robot. Autom. Lett. 2022, 7, 3250–3256. [Google Scholar] [CrossRef]
- Zhang, H.; Li, L.; Zhao, J.; Zhao, J.; Gong, Y. Theoretical Investigation and Implementation of Nonlinear Material Removal Depth Strategy for Robot Automatic Grinding Aviation Blade. J. Manuf. Process. 2022, 74, 441–455. [Google Scholar] [CrossRef]
- Sauter, E.; Sarikaya, E.; Winter, M.; Wegener, K. In-Process Detection of Grinding Burn Using Machine Learning. Int. J. Adv. Manuf. Technol. 2021, 115, 2281–2297. [Google Scholar] [CrossRef]
- Pandiyan, V.; Murugan, P.; Tjahjowidodo, T.; Caesarendra, W.; Manyar, O.M.; Then, D.J.H. In-Process Virtual Verification of Weld Seam Removal in Robotic Abrasive Belt Grinding Process Using Deep Learning. Robot. Comput.-Integr. Manuf. 2019, 57, 477–487. [Google Scholar] [CrossRef]
- Zheng, P.; Liu, D.; Guo, J.; Zhi, Z. A New Method for Optimizing Process Parameters of Active Measurement Grinding Based on Grey Target Decision Making. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 4645–4658. [Google Scholar] [CrossRef]
- Kahraman, M.F.; Öztürk, S. Experimental Study of Newly Structural Design Grinding Wheel Considering Response Surface Optimization and Monte Carlo Simulation. Measurement 2019, 147, 106825. [Google Scholar] [CrossRef]
- Xie, Y.; Chang, G.; Yang, J.; Zhao, M.; Li, J. Process Optimization of Robotic Polishing for Mold Steel Based on Response Surface Method. Machines 2022, 10, 283. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, M.; Li, J.; Ming, W.; Shao, X.; Huang, Y. Multi-Objective Optimization for Surface Grinding Process Using a Hybrid Particle Swarm Optimization Algorithm. Int. J. Adv. Manuf. Technol. 2014, 71, 1861–1872. [Google Scholar] [CrossRef]
- Wen, X.M.; Tay, A.A.O.; Nee, A.Y.C. Micro-Computer-Based Optimization of the Surface Grinding Process. J. Mater. Process. Technol. 1992, 29, 75–90. [Google Scholar] [CrossRef]
- Kruszyński, B.W.; Lajmert, P. An Intelligent Supervision System for Cylindrical Traverse Grinding. CIRP Ann. 2005, 54, 305–308. [Google Scholar] [CrossRef]
- Venu Gopal, A.; Venkateswara Rao, P. Selection of Optimum Conditions for Maximum Material Removal Rate with Surface Finish and Damage as Constraints in SiC Grinding. Int. J. Mach. Tools Manuf. 2003, 43, 1327–1336. [Google Scholar] [CrossRef]
- Pawar, P.J.; Rao, R.V.; Davim, J.P. Multiobjective Optimization of Grinding Process Parameters Using Particle Swarm Optimization Algorithm. Mater. Manuf. Process. 2010, 25, 424–431. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Y.; Gao, Z.; Peng, F.; Tang, X.; Yan, R.; Zhang, Y. Intelligent Learning Model-Based Skill Learning and Strategy Optimization in Robot Grinding and Polishing. Sci. China Technol. Sci. 2022, 65, 1957–1974. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Khalilpourazary, S. Optimization of Time, Cost and Surface Roughness in Grinding Process Using a Robust Multi-Objective Dragonfly Algorithm. Neural Comput. Applic. 2020, 32, 3987–3998. [Google Scholar] [CrossRef]
- Tangjitsitcharoen, S.; Thesniyom, P.; Ratanakuakangwan, S. Prediction of Surface Roughness in Ball-End Milling Process by Utilizing Dynamic Cutting Force Ratio. J. Intell. Manuf. 2017, 28, 13–21. [Google Scholar] [CrossRef]
- Peng, Y.; Yamaguchi, H.; Funabora, Y.; Doki, S. Modeling Fabric-Type Actuator Using Point Clouds by Deep Learning. IEEE Access 2022, 10, 94363–94375. [Google Scholar] [CrossRef]
- Zhang, M.; Yan, J. A Data-Driven Method for Optimizing the Energy Consumption of Industrial Robots. J. Clean. Prod. 2021, 285, 124862. [Google Scholar] [CrossRef]
- Mao, Z.; Peng, Y.; Hu, C.; Ding, R.; Yamada, Y.; Maeda, S. Soft Computing-Based Predictive Modeling of Flexible Electrohydrodynamic Pumps. Biomim. Intell. Robot. 2023, 3, 100114. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).