Abstract
This paper presents a solution aimed at enhancing the accuracy of abrasive waterjet cutting (AWJC) for the processing of carbon-fiber-reinforced polymers (CFRP). Processing CFRP with high accuracy and good surface quality in a short processing time is a difficult task. One crucial problem is the occurrence of shape errors, overcuts, at the cut-in and cut-out point during the cutting process. Shape errors have the potential to create mechanical stress concentrators, which can result in structural failures and compromise the integrity and reliability of components. The primary objective of this study was to gain a comprehensive understanding of the formation mechanism underlying the shape error. The observed shape error is closely associated with both the lead-in/lead-out strategies employed and the process parameters selected. The experimental investigation focused on two commonly used strategies for CFRP cutting: lead-in/lead-out in arc and lead-in/lead-out in line. In order to minimize shape errors, this study proposed a correction method that offers a set of recommendations for selecting the appropriate lead-in/out strategy and a suitable combination of process parameters. Additionally, a mathematical model has been developed to determine the depth of the shape error. The conclusions drawn from this study have been successfully validated through industrial applications.
1. Introduction
In industries characterized by high standards and demands, such as the aerospace, automotive, and medicine industries, the utilization of advanced materials with exceptional properties is imperative [1,2]. Carbon-fiber-reinforced polymer/plastics (CFRP) are essential in high-end industries due to their exceptional properties. CFRP offers a high strength-to-weight ratio, making it strong and lightweight. Its excellent fatigue resistance ensures durability under repeated loading [1]. CFRP’s stiffness and corrosion resistance make it stable and low-maintenance [2]. It maintains mechanical properties in extreme temperatures and provides design flexibility [3]. CFRP’s biocompatibility is ideal for medical implants, and its impact resistance ensures safety in critical situations [4]. These properties have led to widespread adoption in various applications.
CFRPs have numerous aerospace applications due to their exceptional properties. CFRPs are extensively used in aircraft structures (fuselage sections, wings, tail sections), engine components (fan blades, spinner cones, nacelles, and exhaust component), interior components (seat frames, interior panels), helicopter rotor blades, spacecraft, satellites, and unmanned aerial vehicles (UAVs) [3,5,6].
The processing of advanced composite material with high accuracy and good surface quality in a short processing time is a difficult task [3,6]. The abrasive waterjet (AWJ) process is a suitable tool for cutting [7], turning [8], drilling [6], milling [9], cleaning [10], or surface preparation [11]. The AWJ processing principle involves the utilization of a high-pressure waterjet combined with abrasive particles to remove material, as is presented in Figure 1 [6,12]. The main AWJ parameters are waterjet pressure, abrasive mass flow, traverse speed or feed rate, standoff distance, and material thickness [12,13,14]. The kerf characteristics in abrasive waterjet (AWJ) cutting include several factors, including the kerf width, taper, top radius, and surface quality and integrity (as depicted in Figure 1b) [14,15,16].

Figure 1.
The AWJ process: (a) AWJ system and (b) kerf geometry.
Abrasive waterjet cutting (AWJC) uses a fluid tool suitable for machining all types of materials and it has several distinctive advantages such as low mechanical stress, complex shape-processing capabilities, an absence of heat-affected zones (HAZ) and thermal stress, and environmental-friendliness [9,12,13]. AWJC is also highly effective in cutting modern composite materials, whether they are produced using 3D printing technology from plastics or metals [17].
Defects such as delamination, fiber pull-out, abrasive embedment [6,15], dimensional deviation [7], or low surface quality [18] can occur during the processing of CFRP using AWJC technology. One of the most critical defects that can occur when machining CFRP with AWJ is delamination of the layers. The integrity and functionality of the part are compromised when this defect occurs [6,15,19,20]. According to Shanmugam et al. [20], delamination arises as a result of the shock wave generated when the waterjet impacts the material. Delamination typically occurs during the initial piercing phase rather than during the subsequent cutting process. To avoid delamination in CFRP during AWJC, several techniques can be employed: optimizing the cutting parameters, pre-drilling pilot holes, suitable nozzle configuration [6], or proper piercing methods [19]. The acoustical emission monitoring technique is employed to detect defects in CFRP, such as delamination, crack propagation, and fiber breakage [21,22].
The surface quality and integrity of CFRP after AWJC can significantly impact its overall performance and reliability [18,23]. Those directly affect its structural integrity. Any defects, delamination, or surface irregularities introduced during AWJC can weaken the material and compromise its load-bearing capacity. High-quality surfaces with minimal defects ensure a better structural stability and reliability [22]. CFRP materials are commonly used in applications where fatigue resistance is critical, such as in aerospace and automotive components. Poor surface quality, including micro-cracks and roughness, can act as stress concentrators, reducing the material’s fatigue life and leading to premature failure [18,22]. In applications where aerodynamics or hydrodynamics are critical, such as in aerospace or marine structures, surface roughness and shape errors can lead to drag, turbulence, and performance inefficiencies. A smooth and clean-cut surface is desired to minimize post-processing requirements and maintain the structural integrity of the material. Achieving a good surface quality depends on factors like the cutting parameters, abrasive characteristics, cutting system, and material composition [18,22].
The characteristics of the kerf are investigated during the cutting process for CFRP [15]. The main geometrical kerf characteristics are width, taper, and top radius [14,15]. These geometrical characteristics directly impact the accuracy and overall quality of the cut parts. Proper selection and optimization of the process parameters is crucial for achieving high-quality cut surfaces and superior dimensional accuracy. The response surface methodology (RSM) is a suitable approach that can be employed for the optimization of AWJC [6,24].
Tolerances for CFRP parts can range from a few micrometers to a few millimeters, depending on the complexity of the part and the criticality of its function. The typical quality requirements in the case of the AWJC of composite materials used in aircraft structures are as follows: the surface roughness should not exceed Ra = 10 µm, the minimum accuracy required is about 0.25 mm, and the edge quality should have no adverse effects such as delamination [25]. For machining large aircraft structures such as wings or the fuselage, hybrid composite machining centers (combining AWJC and mechanical cutting processes) are utilized. These centers allow machining of parts up to 50 m in length with high accuracy [25].
An important aspect of the CFRP cutting process is the introduction of shape errors at the cut-in/cut-out point of the material. This shape error is in correlation with the lead-in/out strategy [7,26]. The lead-in/out strategy refers to a technique used to initiate and terminate the cutting process, as is shown in Figure 2. In this technique, specific strategies are employed to smoothly transition the AWJ into and out of the material being cut. The lead-in refers to the starting point (cut-in) of the waterjet on the material’s surface, while the lead-out denotes the point where the AWJ exits the material.
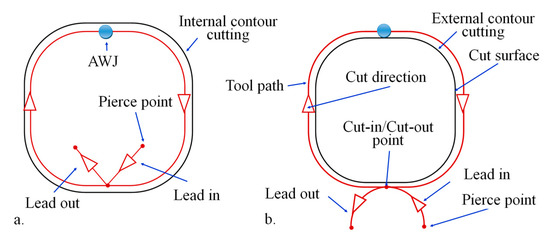
Figure 2.
The principle of the lead-in/out strategy: (a) lead-in/out in a straight line and (b) lead-in/out in an arc.
The first recommendation is to work with outside corners, and it is usually preferable to extend the corner into a lead [27]. When processing an internal or external contour without outside corners (Figure 2), it is essential to employ the proper lead-in/lead-out strategies. There are various lead-in/lead-out strategies employed in AWJC:
- Lead-in/out in a straight line (Figure 2a): This strategy involves a linear or straight-line path for the waterjet during the cut-in and cut-out phases [26,27]. This strategy, also known as the “V” shape lead, is commonly preferred for general AWJC applications [27].
- Lead-in/out in an arc (Figure 2b): In this approach, the AWJ follows a curved or arc path during the cut-in and cut-out phases [27,28].
The choice of lead-in and lead-out strategies in AWJC can have a notable impact on the overall process time, especially in the context of industrial applications. A well-designed lead-in/out strategy can minimize the time spent on these movements, reducing the overall process time, and increasing productivity. Efficient lead-in/out strategies can optimize material utilization by minimizing waste.
When cutting CFRP with AWJ at the cut-in and cut-out points, there is a possibility of shape errors occurring, specifically overcutting [26]. These shape errors are also called witness marks [28]. AWJ is not a rigid tool as in the case of a milling cutter; it is a “soft knife” [7]. It moves to one side or the other of the tool path or stays behind the cutting head, generating a cutting lag [29]. The effects introduced by the AWJ are compensated for by the lead strategy and the acceleration and deceleration [26,27,28]. Ming Chen et al. conducted a study on shape errors occurring in the cut-in/cut-out region during the AWJC of Aluminum alloy 6061. It was concluded that the use of a very low feed rate during the lead-in/lead-out in line strategy contributed to the occurrence of shape errors. Although the errors were reduced, they were not completely eliminated [7,26].
Figure 3 illustrates an example of a shape error that occurred while cutting an internal contour in a 6 mm thick CFRP part. In Figure 3b, an overcut is observed at the cut-in and cut-out points. The overcut has a length of 2.2 mm and a depth of 1.3 mm.

Figure 3.
A shape error example appeared the cut-in and cut-out point. (a) A 6 mm CFRP part cut with AWJ. (b) The shape error (overcut) appeared during internal contour cutting.
Shape errors that result in mechanical stress concentrators can indeed lead to structural failures and compromise the integrity and reliability of components. These areas experience higher stress levels compared to the surrounding material, leading to potential weaknesses or failure points [23]. It is crucial to avoid the presence of mechanical stress concentrators to ensure the structural robustness of a design. By minimizing or eliminating stress concentrators, it can improve the overall strength, durability, and performance of the components, reducing the risk of failure and ensuring their long-term reliability [23,30]. Mechanical stress concentrators in aerospace CFRP components can have significant implications for their structural integrity and performance [30]. Franco et al. found that stress concentration around the drilled holes for fastening purposes in aluminum-composite hybrid joints used in aircraft structures could potentially lead to failure during flight due to fatigue loading [31]. Kant et al. conducted a comprehensive study of stresses in composite laminate structures, identifying significant stress concentrations at free edges and hole/cut-out/notch edges as potential factors driving failure, including the possibility of delamination [32]. Makki et al. conducted an evaluation of stress concentration factors for composite materials with varying hole diameters. Their experimental findings demonstrated an increase in gross stress concentration with an increase in hole diameter [33]. Ryo Naito et al. investigated the effects of stress concentration on CFRP behavior using a high-speed camera. Their study revealed that crack growth and shear failure occur from stress concentrator areas due to high stress concentration during the loading process just before final fracture [34].
When advanced composite materials such as CFRP are machined using AWJC, minimizing or eliminating the stress concentrators introduced by the cutting process becomes an important requirement.
The paper proposes a study aimed at solving the shape error problem introduced by AWJ during CFRP cutting. However, there is a research gap in understanding the specific influence of process parameters on shape errors at the cut-in and cut-out points in AWJC of CFRP. An experimental study was conducted to evaluate and understand the phenomenon. Two lead-in/lead-out strategies, lead-in/out in arc and lead-in/out in line, were investigated. The study aimed to determine the proper combination of strategy and process parameters. Based on the findings, a recommended strategy and set of process parameters were proposed.
2. Materials and Methods
2.1. Design of Experiments
In this experimental investigation, two different strategies, lead-in/out in arc and lead-in/out in line, were analyzed. To efficiently design the experiment and explore the effects of the variables, a factorial design was employed. Factorial designs allow for the simultaneous examination of multiple factors and their interactions [35]. Rammohan et al. employed a factorial design of experiments technique to predict AWJC parameters [36].
In Figure 4, the graphical representation of the analyzed strategies and the main geometrical parameters is presented.
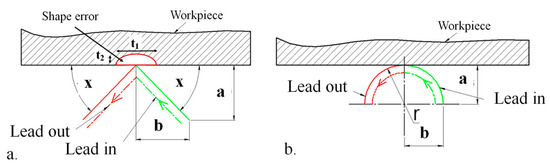
Figure 4.
The graphical representation of the analyzed strategies: (a) lead-in/out in line and (b) lead -in/out in arc.
For the first strategy, which involves lead-in and lead-out in a straight line, the input variable selected was the lead angle (Figure 4a). The following values were chosen for the lead angle: 5, 35, 65, and 85°. Each lead line had a length of 3 mm. If the lead-in line is long enough, the influence of this parameter on the shape error is minimal [26].
In the case of lead-in and lead-out in an arc, the arc radius was varied with the following values: 1, 3, 5, and 7 mm (Figure 4b).
The nozzle traversing speed or feed rate, denoted as V, plays a key role in the AWJ process [15,22,36,37,38] and was varied throughout the experiment to assess its impact on the outcomes. In this study, the feed rate was calculated by using the Zeng mathematical model, Equation (1) [26,38].
where V—feed rate (mm/min), Nm—machinability, P—waterjet pressure (MPa), mw—water flow rate (L/min), m—abrasive flow rate (kg/s), Cs—measurement system constant, Q—surface quality, H—cutting thickness (mm), and D—internal focusing tube diameter (mm) [26,38].
This mathematical model is considered one of the most comprehensive and accurate models available. It has been widely adopted by commercial AWJ equipment manufacturers, such as Omax and Flow, who have integrated it into their software for calculating cutting parameters. The developed model includes a parameter called surface quality (Q), which is categorized into five classes (Q1–Q5) [39]. Figure 5 illustrates the quality characteristics of the cut surface.

Figure 5.
The quality characteristics of the cut surface.
The feed rate was calculated for three different cutting qualities: V = 4572 mm/min—Q1 separation quality, V = 4136 mm/min—Q3 medium quality, and V = 2299 mm/min—Q5 finishing quality. The constant process parameters were Nm = 500 (for CFRP), P = 345 MPa, m = 0.0075 kg/s, Cs = 788 (metric), H = 3 mm, and D = 0.76 mm.
During the experiment, a total of 72 trials were conducted. The experimental design followed a 4 × 3 full factorial design, resulting in 12 unique combinations of treatments [35]. Each treatment combination corresponds to a different combination of lead angle/arc and feed rate. To minimize processing and measurement errors, every experimental trial was repeated three times, ensuring reliable and accurate outcomes.
In Table 1, the input parameters of the AWJC process which were varied during the experiments are shown.

Table 1.
The AWJC process input parameters, varied during the experiments.
The output parameters analyzed in this study are the dimensions of shape error, specifically the depth (t2) and width (t1).
2.2. Experimental Setup
The experimental setup involved the use of an industrial AWJ machine, specifically the Omax 2626 model (Figure 6a). Omax machines are widely used in industries globally and share similarities with other brands like Flow, WJS, or Wardjet. The machine was equipped with a standard cutting head. The reason for selecting this machine is that the results obtained from this study can be easily implemented in industry, and the experiments can be replicated using commonly available equipment. A high-pressure pump was utilized to generate water pressure of up to a maximum of 400 MPa. To control the abrasive flow, an Alffi abrasive supply system was employed, allowing for variation in the abrasive mass flow within the range of 0 to 600 g/min.

Figure 6.
The experiment setup: (a) the Omax 2626 AWJ equipment, (b) the designed clamping system, and (c) the CFRP workpiece.
A newly designed clamping device was developed to ensure the secure and rigid fixation of CFRP specimens during the cutting process. This clamping device is shown in Figure 6b. The CFRP specimens were machined using the AWJC process, resulting in final dimensions of 100 × 30 × 3 mm, as shown in Figure 6c.
Table 2 presents the primary experimental parameters employed in this study. The cutting parameters were calculated for CFRP material cut with a thickness of 3 mm. To minimize the machining errors caused by the wear of the cutting system, a novel cutting system (focus tube and orifice) was installed.

Table 2.
Experimental parameters.
2.3. Materials
For this study, a 3 mm thick CFRP sheet manufactured by ECOTECH was used. The CFRP workpiece used in the study was produced using unidirectional prepreg carbon fiber (CE 8201-200-45) arranged at an angle of 0°/90°, combined with a 364 g/m² epoxy resin. The mechanical properties of the material were 230–294 GPa Young’s modulus and 3530–5490 MPa tensile strength [40]. The production process involved hot pressing. The dimensions of the CFRP workpiece were 350 × 150 mm.
The abrasive grains used in the experimental trials were Barton garnet, a mineral material. Garnet is the most commonly used abrasive material in AWJC. The characteristics of the abrasive were as follows: a grain size of 260 µm, hardness of 7.5–8.0 Mohs, and specific density of 3.9–4.1 g/cm3 [41].
2.4. Experimental Results
The shape error was measured optically using the PG 2000 Cutting Tool Inspection System, manufactured by Guhring. Figure 7a illustrates the setup of the microscope used for the measurement. This measuring microscope was well-suited for the size and shape of the samples. The measurements were taken from a perpendicular direction to the top surface of the specimen. With a 10× optical magnification, the measuring accuracy was approximately 2 µm. The shape error was evaluated by measuring two dimensions: t2 depth of the shape error and t1 length of the shape error (Figure 7b). A few machined samples are shown in Figure 7c,d.
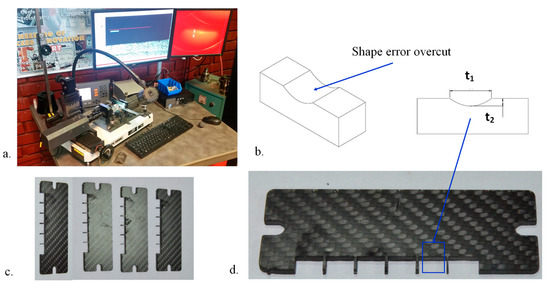
Figure 7.
A process CFRP sample.
The experimental results obtained from the study are presented in Table 3, showcasing the outcomes and findings derived from the conducted experiments. The experimental trial was repeated three times, and the average of these values along with the standard deviation was calculated.

Table 3.
The experimental results.
3. Results and Discussions
The experimental data were analyzed to investigate the occurrence of shape errors at the cut-in and cut-out points during the cutting process. The depth of the shape error is a critical dimensional parameter that needs to be considered when evaluating the mechanical stress concentrator point.
3.1. Morphology of the Cut Surfaces
The cut surfaces of the CFRP specimens were examined using a microscope to study the behavior of the material during the AWJC process. This morphology analysis aimed to identify characteristics such as delamination, cracks, uncut fibers, fiber pull-out, or particle embedment [12,22,42,43]. The AWJ cut surfaces were examined and categorized into three zones: the initial damage zone (IDZ), the smooth cutting zone (SCZ), and the rough cutting zone (RCZ) [16].
In Figure 8a, microscopic images of a specimen obtained during this experiment are shown, highlighting the general shape error obtained (t2 bottom = 0.203 mm in depth/t1 bottom = 1.92 mm). In this experimental run, the following parameters were used: lead-in/lead-out in line strategy (lead angle 65°), V = 4136 mm/min, P = 350 MPa, SOD = 1 mm, and ma = 0.45 kg/min.

Figure 8.
Microscopic image of the cut CFRP specimens.
In the microscopic image from Figure 8b, a smooth surface quality is observed without any signs of matrix smearing, abrasive embedment, or a high percentage of pull-out fibers.
Surface roughness was measured using the Nano Focus 3D microscope μsurf expert, and a Gaussian filter with a 0.8 mm cutoff wavelength was applied. The dimensions of the scanned surface were 1.6 × 1.6 mm. The surface roughness was Ra =1.97 µm (Sa = 2.84 µm) on the IDZ, Ra =2.86 µm (Sa = 4.42 µm) on the SCZ, and for the RCZ, Ra =3.08 µm (Sa = 4.69 µm). Upon examining the topography and roughness profiles of the surfaces, it was noted that the valleys, peaks, and craters displayed an asymmetric and non-uniform pattern of variation. The surfaces display a wavy texture, characterized by the varying widths and heights of the peaks and valleys observed along their length. These peaks and valleys are aligned in the direction of the AWJ flow. Mardi et al. also observed similar surface topography characteristics on the surface cut with AWJ [43]. The maximum depth of the valleys is 6 μm, while the maximum height of the peaks is 5 μm. Additionally, a rounded edge (rk = 0.12 mm) was observed on the IDZ.
The observations involved examining the cut surface at various magnifications to identify the CFRP damage (Figure 9). In 2 out of the 72 runs, delamination of the fiber layers was observed on the bottom part of the cut surface. In Figure 9b, a specimen is presented with delamination that occurred during a run utilizing the lead-in/lead-out in line strategy, with a lead angle of 5° and a feed rate of 4136 mm/min. In this case, the delamination measures 1.4 × 5 mm and is observed in the same area as the cut-in/cut-out point. Figure 9c showcases a different specimen with delamination. This delamination, measuring 0.8 × 3 mm, occurred in an experimental run employing the lead-in/lead-out in arc strategy with a lead radius of 3 mm and a cutting speed of 2299 mm/min. Notably, the cut-in/cut-out point of this run is in a different area compared to where the delamination occurred.

Figure 9.
Morphological defects appear during experiments.
Uncut fibers appear in just one experimental run, in the rough cutting zone, shown in Figure 9d. It was obtained during a trial with the lead-in/lead-out in line strategy (lead angle 45°) and a feed rate of 2299 mm/min.
The defects, such as delamination of the fiber layers and uncut fibers, observed during the experimentation could potentially be attributed to defects in the CFRP material. However, after analysis, no specific correlation with process parameters or other factors was found. Further investigation is needed to better understand and address these issues.
This indicates that the cutting process was successful in preserving the structural integrity of the CFRP material without causing significant damage or defects.
3.2. Investigation on the Shape Error Generated by Using the Lead-In/Lead-Out in Line Strategy
Figure 10 illustrates the correlation between the shape error dimensions (depth t2 and width t1) and the process parameters (lead angle and feed rate) in the case of the lead-in/lead-out in line strategy. The shape error dimensions were evaluated for different values of lead angle (x: 5, 35, 65, 85°) and feed rate (V: 2299, 4136, 4572 mm/min).
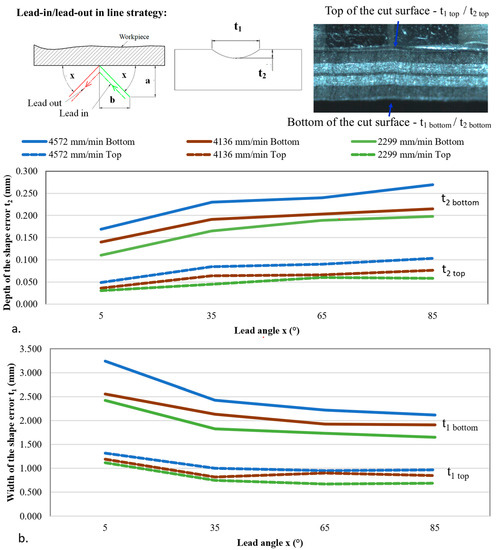
Figure 10.
Influence of the lead angle on the shape error dimensions in the case of the lead-in/lead-out in line strategy: (a) the depth of the shape error t2 and (b) the width of the shape error t1.
In the case of the lead-in/lead-out in line strategy, the minimum dimensions of the shape error are, at the bottom, t2 bottom = 0.11 mm in depth/t1 bottom = 3.240 mm in width, and for the top of the cut surface, t2 top = 0.03 mm in depth and t1 top = 1.12 mm in width. This result was obtained during an experimental trial using the following parameters: lead angle x = 5°, V = 4572 mm/min, P = 350 MPa, SOD = 1 mm, and ma = 0.45 kg/min. In the search to minimize the depth of the shape error, significant reductions were achieved, with a minimum depth of 0.11 mm being attained. However, complete elimination was not attained, as evidenced by the experimental findings.
As depicted in Figure 10a, it is evident that increasing the lead angle from 5° to 85° results in an increase in the depth of the shape error for both the top and bottom of the cut surface. Conversely, the width of the shape error decreases with an increase in the lead angle (Figure 10b).
When analyzing the effect of feed rate variation (2299–4572 mm/min), it was observed that decreasing the feed rate resulted in a decrease in the depth and width of the shape error (as shown in Figure 10).
The variation in shape error dimensions was analyzed in the case of the lead-in/lead-out in line strategy. The depth of the shape error was found to decrease with a decreasing feed rate and increase with an increasing lead angle. The width of the shape error decreases as the lead angle increases and increases with higher feed rates.
3.3. Investigation on the Shape Error Generated by Using the Lead-In/Lead-Out in Arc Strategy
Figure 11 presents the relationship between the shape error dimensions (depth t2 and width t1) and the process parameters (lead radius and feed rate) in the context of the lead-in/lead-out in arc strategy. The shape error dimensions were examined across various lead radius values (r: 1, 3, 5, 7 mm) and feed rate values (V: 2299, 4136, 4572 mm/min).

Figure 11.
Influence of the lead radius on the shape error dimensions in the case of the lead-in/lead-out in arc strategy: (a) the depth of the shape error t2 and (b) the width of the shape error t1.
For lead-in/lead-out in arc strategies, the minimum dimensions of the shape error are, at the bottom, t2 bottom = 0.049 mm in depth/t1 bottom = 1.736 mm in width, and for the top of the cut surface, t2 top = 0.038 mm in depth and t1 top = 0.4 mm in width. It was obtained during an experimental trial using the following parameters: lead radius of 7 mm, V = 2299 mm/min, P = 350 MPa, SOD = 1 mm, and ma = 0.45 kg/min. The selection criteria focused on minimizing the depth of the shape error. Although the depth of the shape error was reduced to below 0.05 mm, it was not completely eliminated.
Figure 11a demonstrates that increasing the lead arc radius from 1 to 7 mm results in a reduction in the depth of the shape error at both the bottom and top of the cut surface. Furthermore, Figure 11b indicates that as the lead arc radius increases, the width of the shape error decreases.
A decrease in the feed rate, ranging from 2299 to 4572 mm/min, resulted in a corresponding decrease in the depth and width of the shape error, as illustrated in Figure 10b. This consistent trend was observed for both the top and bottom of the cut surface.
In conclusion, for the lead-in/lead-out in arc strategy, to minimize the depth of the shape error, it is recommended to decrease the feed rate and increase the lead arc radius.
3.4. Discussions and Mathematical Modelling
To minimize or eliminate the stress concentrators that arise during the cutting process due to the lead-in/lead-out process, it is essential to gain a comprehensive understanding of the formation mechanism of the shape error.
The first observation indicates that the shape error (overcut) occurring at the cut-in and cut-out point AWJC of CFRP is significantly reduced but not completely eliminated. In lead-in/lead-out in arc strategies, the minimum dimensions of the shape error are observed at t2 = 0.049 mm in depth and t1 = 1.736 mm in width. On the other hand, in the case of the lead-in/lead-out in line strategy, the minimum dimensions are t2 = 0.11 mm in depth and t1 = 3.240 mm in width. When comparing these strategies based on the criterion of minimizing the depth of the shape error, it can be concluded that the lead-in/lead-out in arc strategies are significantly more accurate than the lead-in/lead-out in line strategy.
The shape error is in close correlation with the lead-in/lead-out geometry. CNC machines adapt the feed rate at direction changes by implementing advanced control algorithms and motion planning strategies. When a direction change occurs, the machine controller adjusts the feed rate to ensure a smooth and accurate motion [44].
The formation mechanism of the shape error is attributed to the deceleration of the machine during the lead-in and lead-out movements, which causes the AWJ to remove additional material from the workpiece. The decrease in the feed rate results in the generation of shape errors.
This theory is supported by experimental evidence. Increasing the lead arc radius from 1 to 7 mm generates a decrease in the depth of the shape error. Additionally, selecting a higher value for the lead arc radius (over 3 mm) ensures smoother jet movement without significant decelerations.
For lead-in/lead-out in line, as the lead angle increases from 5° to 85°, there is an increase in the reduction of the feed rate. To achieve a smooth and constant movement, it is recommended to decrease the lead angle, which also leads to a decrease in the depth of the shape error.
In conclusion, to minimize the depth of the shape error, it is recommended to select the lead-in/lead-out in arc strategy with a high value of lead arc radius (over 3 mm). This approach will result in smoother jet movement without significant decelerations.
A decrease in the feed rate, ranging from 4572 to 2299 mm/min, led to a reduction in the depth and width of the shape error. This trend was observed for both lead-in/lead-out strategies. By reducing the feed rate, the shape error is decreased due to a lower percentage of deceleration during the lead-in/lead-out process. This reduction in the feed rate not only leads to a smoother and more accurate motion but also results in a reduced variation of the feed rate along the cutting tool path.
It was seen that reducing the feed rate resulted in improved surface roughness and accuracy. Additionally, it was found that the kerf taper decreased as the feed rate decreased. The observation made by Popan et al. aligns with the findings of this study [22].
Multiple models were trained using the experimental data to predict the depth of the shape error in AWJC. The experimental results obtained in the AWJC process are suitable for statistical analysis using ANOVA (analysis of variance) [6,45]. It is a powerful statistical tool that helps us understand the relationship between variations in the dependent variable (the depth of the shape error) and different independent variables (feed rate and lead radius).
In this study, several models were tested to predict the shape error depth during the AWJC process. These models included cubic, two-factor interaction, quadratic, and linear models. The fit test was conducted to evaluate how well each model fits the experimental data. Among all the models tested, the linear model showed a statistically significant relationship with the data (p < 0.05, p = 0.0004). This means that the linear model provides a strong and meaningful representation of the relationship between the process parameters and the shape error depth. The significance level of p = 0.0004 indicates that the relationship is highly unlikely to occur by chance, further confirming the validity of the linear model in explaining the observed data.
The statistical analysis, presented in Table 2, demonstrated that the linear model provides a good fit to the data, with an adjusted R-squared value of 0.9081. This high R-squared value indicates that approximately 91% of the variability in the dependent variable can be explained by the linear model, making it a reliable predictor for the given data.
In this model, the lead radius is a significant predictor (p = 0.0004) of the depth of the shape error (Table 4). The regression model equation derived from the analysis is as follows:
where t2—depth of shape error (mm), r—lead radius (mm), and V—feed rate (mm/min).
t2 = 0.0748 − 0.0056 × r + 2.95 × 10−6 × V

Table 4.
Linear regression model statistics.
The model was completed by incorporating the feed rate calculation model developed by Zeng (Equation (1)). By integrating Zeng’s model into the framework, the depth of the shape error can be calculated, considering important parameters such as water pressure, material thickness, abrasive mass flow, and cutting quality. This results in the formulation of a new model, represented by Equation (3), which enables the estimation of the depth of the shape error based on the process parameters.
where t2—depth of shape error (mm), r—lead radius (mm), Nm—machinability (500 for CFRP), P—waterjet pressure (MPa), mw is the water flowrate (L/min), ma—abrasive flow rate (kg/s), Cs—measurement system constant (for metric is 788), Q—surface quality (Q1 separation, Q3 medium, Q5 finishing), H—cutting depth (mm), and D—internal diameter of the focusing tube (mm) [26,38].
The model was experimentally validated through thirty trials using composite material (CFRP) with thicknesses of 2, 4, and 6 mm. The results demonstrated a satisfactory level of agreement between the experimental values and the calculated values, with a maximum difference of 14%.
3.5. Shape Error Correction Method
The shape error correction method involves a set of recommendations for selecting the appropriate lead-in/out strategy and a suitable combination of process parameters. To minimize the depth of the shape error at the cut-in and cut-out points during the abrasive waterjet cutting of composite materials like CFRP, the following recommendations are advised:
- The lead-in/lead-out in arc strategy should be chosen, as it facilitates smooth AWJ movement and helps to maintain a constant feed rate. It is recommended to increase the lead arc radius to a value greater than 3 mm.
- To minimize the depth of the shape error, it is essential to find the optimal combination of process parameters. One key parameter is the feed rate or traverse speed. It is recommended to decrease the feed rate, as this helps decrease the depth of the shape error. The feed rate can be determined using the Zeng model, which takes into account the key parameters of the AWJC process (Equation (1)). In this application, the finishing cutting quality Q5 is recommended.
- The model that was formulated (Equation (3)) can be employed to estimate the depth of the shape error.
3.6. Method Validation
The proposed methodology was implemented in an industrial company for the cutting of 120 parts made of CFRP with a thickness of 5 mm. The external contour (225 × 72 mm) and five holes with a diameter of 20 ± 0.05 mm were machined, as shown in Figure 12.

Figure 12.
The CFRP industrial part processed with the proposed method.
The cutting tests were conducted using an AWJC CNC machine, CMS Tecnocut 1740, which was equipped with a 60 HP hydraulic pump capable of generating pressures up to 400 MPa. The machine’s movements were controlled by a TechnoCAM CNC controller, which operates in three axes.
Based on the shape error correction method, the lead-in/lead-out strategy was selected. Lead-in/lead-out in arc strategies were implemented with a 5 mm arc radius value. To minimize the depth of the shape error, it is recommended to increase the lead arc radius to a value greater than 3 mm. However, this value should not be increased too much as it could lead to a longer tool path and increased machining time. An optimal value must be selected. The feed rate value, V = 2050 mm/min, was calculated using Equation (1) to achieve a finishing cutting quality (Q5). The cutting parameters utilized were as follows: P = 340 MPa, V = 2050 mm/min, SOD = 1 mm, and ma = 0.45 kg/min. The holes were initially pierced using low pressure (P = 100 MPa) with the abrasive waterjet (AWJ) to prevent material delamination.
The part was successfully cut without any delamination issues, meeting the required quality standards. The dimensions of the shape error were measured using an optical microscope, following the same procedure as the previous experiment. The measurements revealed a depth of 0.04 mm and a width of 1.9 mm at the bottom of the cut surface. For the top of the cut surface, the depth was measured to be 0.055 mm (0.052 mm calculated value with the developed model) and the width was 0.6 mm. The depth of the shape error was reduced to 0.055 mm from its initial value of 0.3 mm before the implementation of the proposed methodology. The implementation of the new method resulted in a significant reduction in the shape error by 81%. The machining time for the part using the newly implemented method was 1.8 min, while the previous method resulted in a machining time of 1.85 min. A reduction in time was obtained, 0.05 min, suggesting that the implementation of the new method has influenced the machining time. The machining time is strongly influenced by the length of the lead-in/out tool path, and in this validation test, those lengths were similar.
4. Conclusions
This paper presents an investigation focused on reducing the shape errors that occur at the cut-in and cut-out points during abrasive waterjet cutting of CFRP. Shape errors that create areas of concentrated mechanical stress have the potential to cause structural failures and compromise the integrity and reliability of CFRP components. Therefore, it is crucial to minimize or eliminate stress concentrators that are introduced during the cutting process. The research yielded the following conclusions:
- The shape error observed during the cutting process is caused by the decrease in the feed rate at the cut-in and cut-out points. This is attributed to the machine deceleration during lead-in and lead-out movements, resulting in the removal of extra material from the workpiece.
- Although the shape error could be significantly reduced, it was not completely eliminated. In the case of lead-in/lead-out in arc strategy, the minimum dimensions of the shape error were found to be 0.049 mm in depth and 1.736 mm in width. Conversely, for lead-in/lead-out in line strategy, the minimum dimensions were 0.11 mm in depth and 3.240 mm in width. Based on the criterion of minimizing the depth of the shape error, the lead-in/lead-out in arc strategy was found to be more suitable for CFRP cutting.
- A shape error correction method was proposed, providing a set of recommendations for selecting the appropriate lead-in/out strategy and a suitable combination of process parameters. This approach offers several benefits, including minimizing the shape error (up to 80%), improving overall cutting accuracy (up to ±0.05 mm), and reducing the machining time.
- The proposed method has been successfully validated and implemented in industrial applications, demonstrating its effectiveness in improving the accuracy of CFRP cutting and reducing the machining time. This research contributes to the advancement of AWJC technology and provides valuable insights for practical applications in the manufacturing industry.
- A mathematical model was formulated to estimate the depth of the shape error, considering the main process parameters of AWJC. This model provides a predictive tool with over 85% accuracy, enabling the estimation of the shape error depth and optimization of the cutting process.
- Future investigations could explore new composite materials (reinforced with fiberglass, kevlar, wood, metal), optimize the jet trajectory by involving multi-axis AWJC machines, or design new geometries for lead-in/lead-out tool paths, such as spline curves.
Author Contributions
Conceptualization, methodology, investigation, I.A.P., A.I.P., and C.C.; validation, I.A.P. and A.I.P.; supervision, N.B. and D.F.; writing—original draft, I.A.P., C.C., and N.P.; research funding, N.B. and D.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by HORIZON 2020—DiCoMI Project, “Directional Composites through Manufacturing Innovation”, GA Nr. 778068.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ding, J.; Cheng, L.; Chen, X.; Chen, C.; Liu, K. A Review on Ultra-High Cycle Fatigue of CFRP. Compos. Struct. 2021, 256, 113058. [Google Scholar] [CrossRef]
- Al-Lami, A.; Hilmer, P.; Sinapius, M. Eco-Efficiency Assessment of Manufacturing Carbon Fiber Reinforced Polymers (CFRP) in Aerospace Industry. Aerosp. Sci. Technol. 2018, 79, 669–678. [Google Scholar] [CrossRef]
- Poór, D.I.; Geier, N.; Pereszlai, C.; Xu, J. A Critical Review of the Drilling of CFRP Composites: Burr Formation, Characterisation and Challenges. Compos. Part B Eng. 2021, 223, 109155. [Google Scholar] [CrossRef]
- Chua, C.Y.X.; Liu, H.-C.; Di Trani, N.; Susnjar, A.; Ho, J.; Scorrano, G.; Rhudy, J.; Sizovs, A.; Lolli, G.; Hernandez, N.; et al. Carbon Fiber Reinforced Polymers for Implantable Medical Devices. Biomaterials 2021, 271, 120719. [Google Scholar] [CrossRef]
- Guo, F.; Xiao, Q.; Xiao, S.; Wang, Z. Assembly Technology for Aeronautical CFRP Structures under the Collaborative Constrains of Geometric Shape, Physical Performance and Service Stability. Compos. Struct. 2023, 318, 117071. [Google Scholar] [CrossRef]
- Popan, I.A.; Balc, N.; Popan, A.I. Avoiding Carbon Fibre Reinforced Polymer Delamination during Abrasive Water Jet Piercing: A New Piercing Method. Int. J. Adv. Manuf. Technol. 2022, 119, 1139–1152. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, S.; Zeng, J.; Chen, B.; Xue, J.; Ji, L. Correcting Shape Error on External Corners Caused by the Cut-in/Cut-out Process in Abrasive Water Jet Cutting. Int. J. Adv. Manuf. Technol. 2019, 103, 849–859. [Google Scholar] [CrossRef]
- Hutyrová, Z.; Ščučka, J.; Hloch, S.; Hlaváček, P.; Zeleňák, M. Turning of Wood Plastic Composites by Water Jet and Abrasive Water Jet. Int. J. Adv. Manuf. Technol. 2015, 84, 1615–1623. [Google Scholar] [CrossRef]
- Dekster, L.; Karkalos, N.E.; Karmiris-Obratański, P.; Markopoulos, A.P. Evaluation of the Machinability of Ti-6Al-4V Titanium Alloy by AWJM Using a Multipass Strategy. Appl. Sci. 2023, 13, 3774. [Google Scholar] [CrossRef]
- Hardy, M.C.; Herbert, C.R.J.; Kwong, J.; Li, W.; Axinte, D.A.; Sharman, A.R.C.; Encinas-Oropesa, A.; Withers, P.J. Characterising the Integrity of Machined Surfaces in a Powder Nickel Alloy Used in Aircraft Engines. Procedia CIRP 2014, 13, 411–416. [Google Scholar] [CrossRef]
- Nag, A.; Srivastava, M.; Petrů, J.; Váňová, P.; Srivastava, A.K.; Hloch, S. Comparison of Continuous and Pulsating Water Jet during Piercing of Ductile Material. Materials 2023, 16, 3558. [Google Scholar] [CrossRef] [PubMed]
- Srinivasu, D.S.; Axinte, D.A. Surface Integrity Analysis of Plain Waterjet Milled Advanced Engineering Composite Materials. Procedia CIRP 2014, 13, 371–376. [Google Scholar] [CrossRef]
- Zou, X.; Fu, L.; Wu, L.; Zuo, W. Research on Multiphase Flow and Nozzle Wear in a High-Pressure Abrasive Water Jet Cutting Head. Machines 2023, 11, 614. [Google Scholar] [CrossRef]
- Basarman, A.-P.; Lobonțiu, M. Kerf Variation Analysing for Abrasive Water Jet Cutting of a Steel Square Part. MATEC Web Conf. 2017, 112, 03002. [Google Scholar] [CrossRef]
- Dhanawade, A.; Kumar, S. Experimental Study of Delamination and Kerf Geometry of Carbon Epoxy Composite Machined by Abrasive Water Jet. J. Compos. Mater. 2017, 51, 3373–3390. [Google Scholar] [CrossRef]
- Popan, I.A.; Contiu, G.; Campbell, I. Investigation on Standoff Distance Influence on Kerf Characteristics in Abrasive Water Jet Cutting of Composite Materials. MATEC Web Conf. 2017, 137, 01009. [Google Scholar] [CrossRef]
- Szatkiewicz, T.; Perec, A.; Radomska-Zalas, A.; Banaszek, K.; Balasz, B. Preliminary Studies into Cutting of a Novel Two Component 3D-Printed Stainless Steel–Polymer Composite Material by Abrasive Water Jet. Materials 2023, 16, 1170. [Google Scholar] [CrossRef]
- Bañon, F.; Sambruno, A.; Batista, M.; Simonet, B.; Salguero, J. Study of the Surface Quality of Carbon Fiber–Reinforced Thermoplastic Matrix Composite (CFRTP) Machined by Abrasive Water Jet (AWJM). Int. J. Adv. Manuf. Technol. 2020, 107, 3299–3313. [Google Scholar] [CrossRef]
- Kim, G.; Denos, B.R.; Sterkenburg, R. Influence of Different Piercing Methods of Abrasive Waterjet on Delamination of Fiber Reinforced Composite Laminate. Compos. Struct. 2020, 240, 112065. [Google Scholar] [CrossRef]
- Shanmugam, D.K.; Nguyen, T.; Wang, J. A Study of Delamination on Graphite/Epoxy Composites in Abrasive Waterjet Machining. Compos. Part A Appl. Sci. Manuf. 2008, 39, 923–929. [Google Scholar] [CrossRef]
- Lissek, F.; Haeger, A.; Knoblauch, V.; Hloch, S.; Pude, F.; Kaufeld, M. Acoustic Emission for Interlaminar Toughness Testing of CFRP: Evaluation of the Crack Growth Due to Burst Analysis. Compos. Part B Eng. 2018, 136, 55–62. [Google Scholar] [CrossRef]
- Popan, I.A.; Bocanet, V.; Balc, N.; Popan, A.I. Investigation on Feed Rate Influence on Surface Quality in Abrasive Water Jet Cutting of Composite Materials, Monitoring Acoustic Emissions. In Advances in Manufacturing Engineering and Materials; Lecture Notes in Mechanical, Engineering; Hloch, S., Klichová, D., Krolczyk, G.M., Chattopadhyaya, S., Ruppenthalová, L., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 105–113. ISBN 978-3-319-99352-2. [Google Scholar]
- Yamamoto, G.; Onodera, M.; Koizumi, K.; Watanabe, J.; Okuda, H.; Tanaka, F.; Okabe, T. Considering the Stress Concentration of Fiber Surfaces in the Prediction of the Tensile Strength of Unidirectional Carbon Fiber-Reinforced Plastic Composites. Compos. Part A Appl. Sci. Manuf. 2019, 121, 499–509. [Google Scholar] [CrossRef]
- Perec, A.; Fajdek-Bieda, A.; Pude, F.; Radomska-Zalas, A. Process optimization by applying the response surface methodology (RSM) to the abrasive suspension water jet cutting of phenolic composites. Facta Univ. 2022, 20, 1–16. [Google Scholar] [CrossRef]
- Mohamed, H. Trimming of CFRP Aircraft Components. In Proceedings of the WJTA-IMCA Conference and Expo, Houston, TX, USA, 9–11 September 2013. [Google Scholar]
- Chen, M.; Zhang, S.; Zeng, J.; Chen, B. Correcting Shape Error Located in Cut-in/Cut-out Region in Abrasive Water Jet Cutting Process. Int. J. Adv. Manuf. Technol. 2019, 102, 1165–1178. [Google Scholar] [CrossRef]
- Omax “Precision Practices: Lead-Ins and Lead-Outs”. 2023. Available online: https://www.Omax.Com/En/Us/Media-Center/Tips/Precision-Practices-Lead-Ins-and-Lead-Outs (accessed on 1 June 2023).
- WARDJet Reducing Lead-in/Lead-out Witness Marks. 2023. Available online: https://my.wardjet.com/Waterjet/University/Precision-Quality (accessed on 1 June 2023).
- Hlaváč, L.M. Revised Model of Abrasive Water Jet Cutting for Industrial Use. Materials 2021, 14, 4032. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.A.; Rajesh, R.; Pugazhendhi, S. A Review of Stress Concentration Studies on Fibre Composite Panels with Holes/Cutouts. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 1461–1472. [Google Scholar] [CrossRef]
- Di Franco, G.; Zuccarello, B. Analysis and Optimization of Hybrid Double Lap Aluminum-GFRP Joints. Compos. Struct. 2014, 116, 682–693. [Google Scholar] [CrossRef]
- Kant, T.; Swaminathan, K. Estimation of Transverse/Interlaminar Stresses in Laminated Composites—A Selective Review and Survey of Current Developments. Compos. Struct. 2000, 49, 65–75. [Google Scholar] [CrossRef]
- Mohamed Makki, M.; Chokri, B. Experimental, Analytical, and Finite Element Study of Stress Concentration Factors for Composite Materials. J. Compos. Mater. 2017, 51, 1583–1594. [Google Scholar] [CrossRef]
- Ryo, N.; Mitsuhiro, O.; Daisuke, F. Effects of Stress Concentration on the Mechanical Properties of Carbon Fiber Reinforced Plastic. Int. J. Smart Mater. Mechatron. 2015, 2, 136–139. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 10th ed.; Wiley: Hoboken, NJ, USA, 2020; ISBN 978-1-119-49247-4. [Google Scholar]
- Rammohan, S.; Kumaran, S.T.; Uthayakumar, M.; Korniejenko, K.; Nykiel, M.; Velayutham, A. Prediction of Abrasive Waterjet Machining Parameters of Military-Grade Armor Steel by Semi-Empirical and Regression Models. Materials 2022, 15, 4368. [Google Scholar] [CrossRef] [PubMed]
- Jankovic, P.; Igic, T.; Nikodijevic, D. Process Parameters Effect on Material Removal Mechanism and Cut Quality of Abrasive Water Jet Machining. Theor. Appl. Mech. 2013, 40, 277–291. [Google Scholar] [CrossRef]
- Zeng, J.; Kim, T.J. Development of an Abrasive Waterjet Kerf Cutting Model for Brittle Materials. In Jet Cutting Technology; Springer: Berlin/Heidelberg, Germany, 1992; pp. 483–501. [Google Scholar]
- Valleyknife. Available online: http://www.valleyknife.com/waterjet_services.html (accessed on 1 June 2023).
- ECOTECH—CFRP Manufacturer. Available online: https://www.r-g.de/en/index.html (accessed on 26 May 2023).
- Nag, A.; Ščučka, J.; Hlavacek, P.; Klichová, D.; Srivastava, A.K.; Hloch, S.; Dixit, A.R.; Foldyna, J.; Zelenak, M. Hybrid Aluminium Matrix Composite AWJ Turning Using Olivine and Barton Garnet. Int. J. Adv. Manuf. Technol. 2018, 94, 2293–2300. [Google Scholar] [CrossRef]
- Thongkaew, K.; Wang, J.; Li, W. An Investigation of the Hole Machining Processes on Woven Carbon-Fiber Reinforced Polymers (CFRPs) Using Abrasive Waterjets. Mach. Sci. Technol. 2019, 23, 19–38. [Google Scholar] [CrossRef]
- Mardi, K.B.; Dixit, A.R.; Pramanik, A.; Hvizdos, P.; Mallick, A.; Nag, A.; Hloch, S. Surface Topography Analysis of Mg-Based Composites with Different Nanoparticle Contents Disintegrated Using Abrasive Water Jet. Materials 2021, 14, 5471. [Google Scholar] [CrossRef]
- Yang, M.; Yang, J.; Zhu, L.; Yu, X. A Novel Curvature Circle Iterative Algorithm for Contour Error Control of Multi-Axis CNC Machine Tools. Precis. Eng. 2020, 65, 23–31. [Google Scholar] [CrossRef]
- Mohankumar, V.; Kanthababu, M.; Velayudham, A. Abrasive Waterjet Cutting of Boron Carbide Particles Reinforced Al 6063 MMCs—A Semi Empirical Modeling Approach in the Prediction of Kerf Angle. Measurement 2021, 181, 109492. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).