Influence of the Slot Fillet and Vane Root Fillet on the Turbine Vane Endwall Cooling Performance
Abstract
1. Introduction
2. Computational Method and Validation
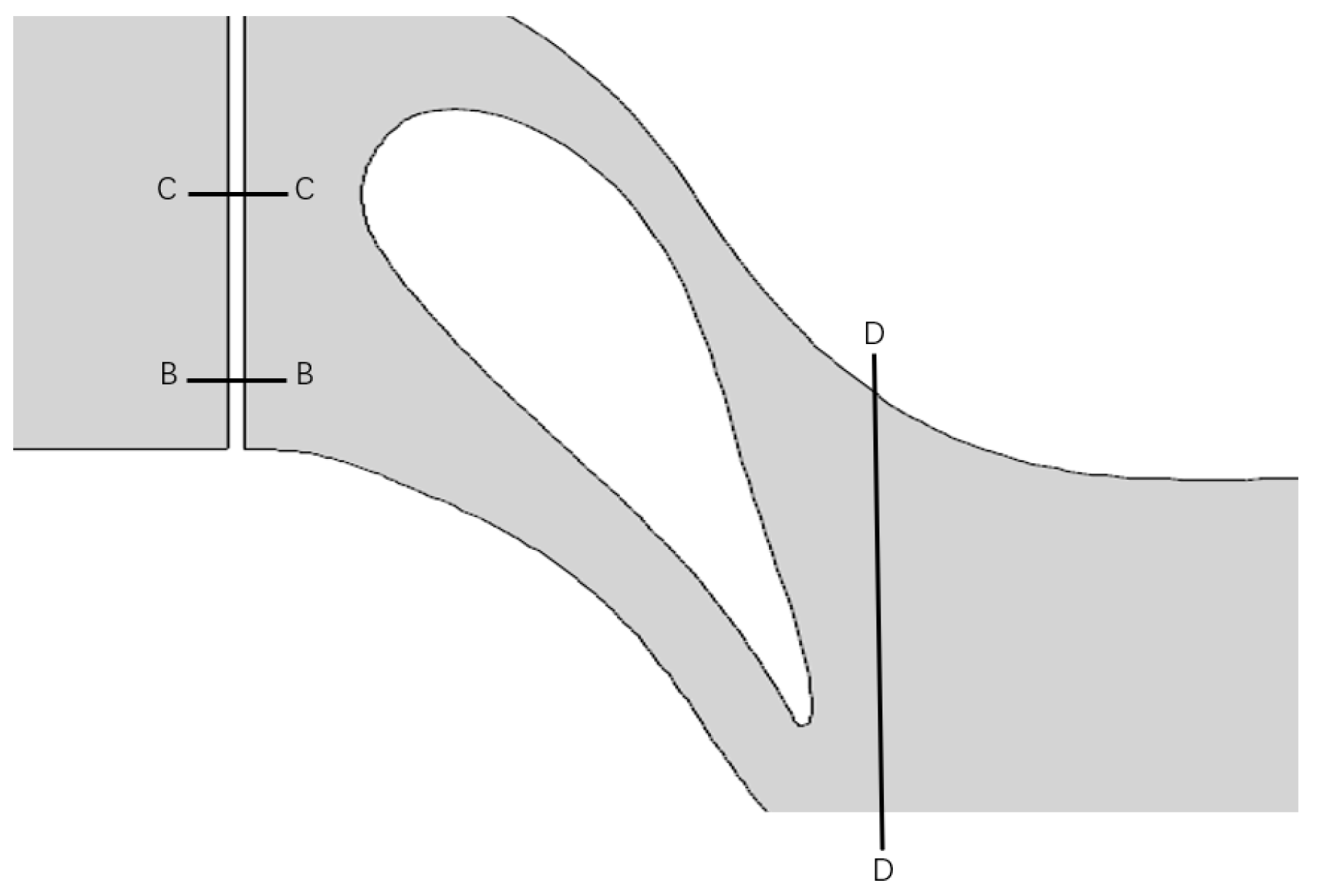
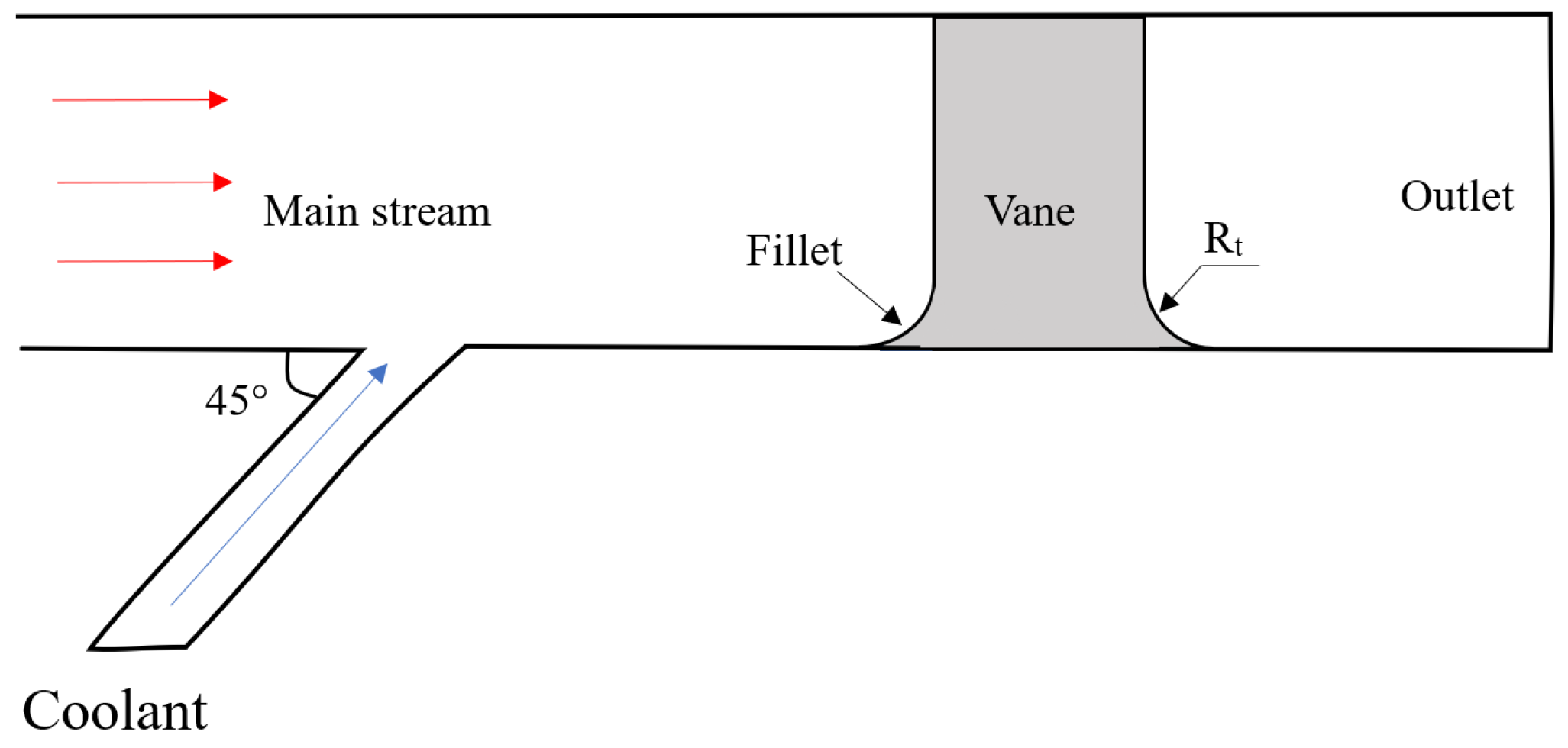
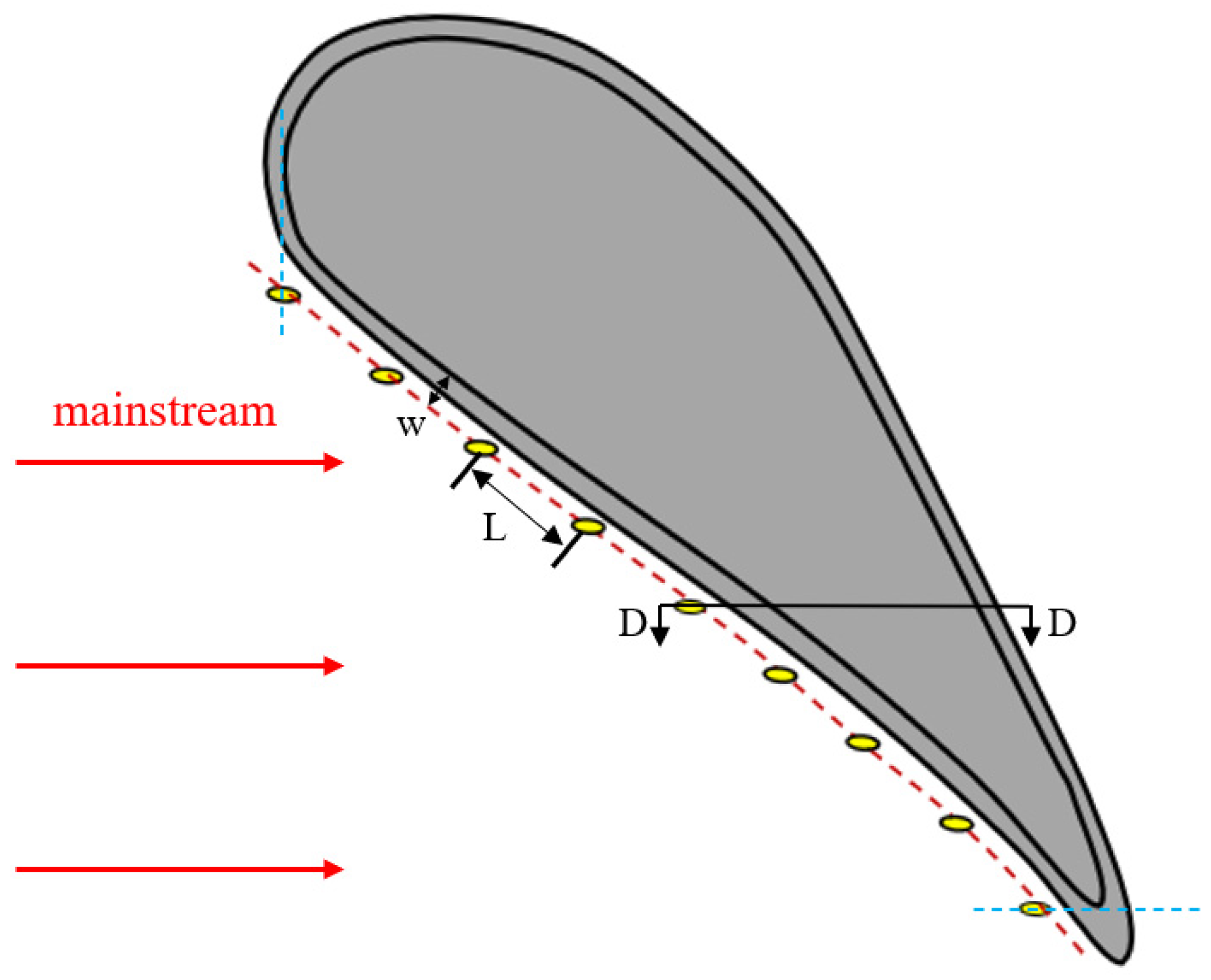
2.1. Geometrical Model
2.2. Numerical Method
2.3. Turbulence Model
2.4. Grid Independence
3. Results
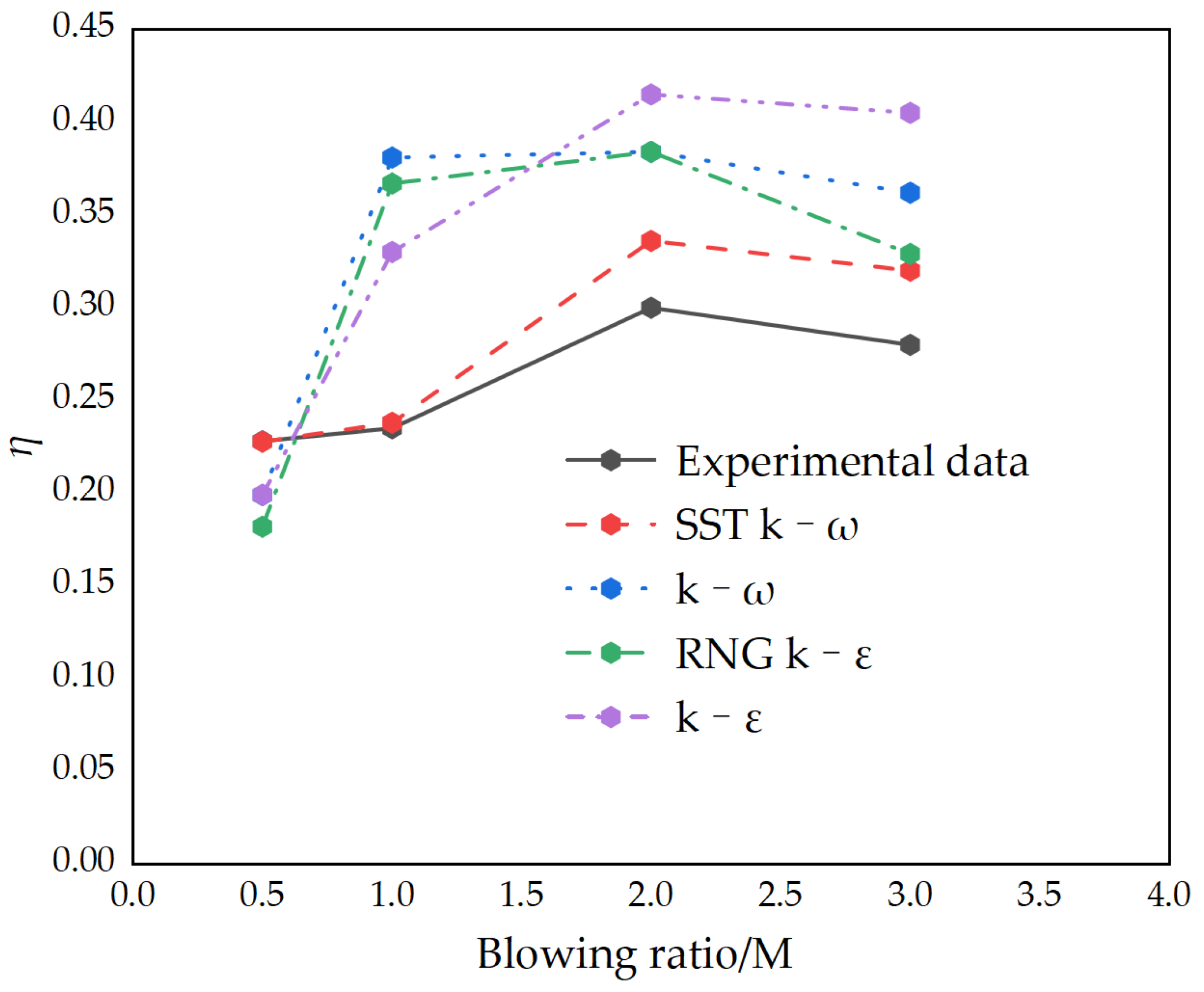
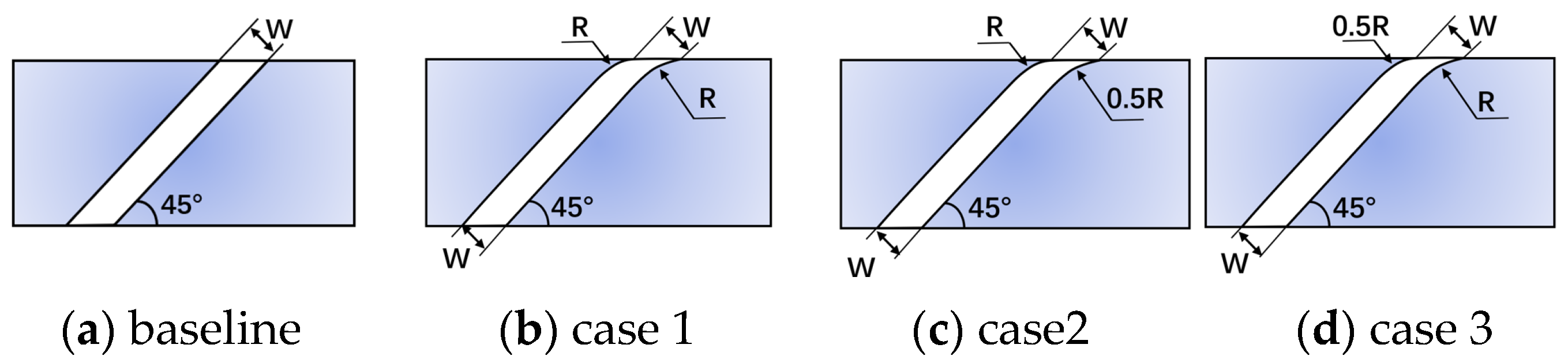
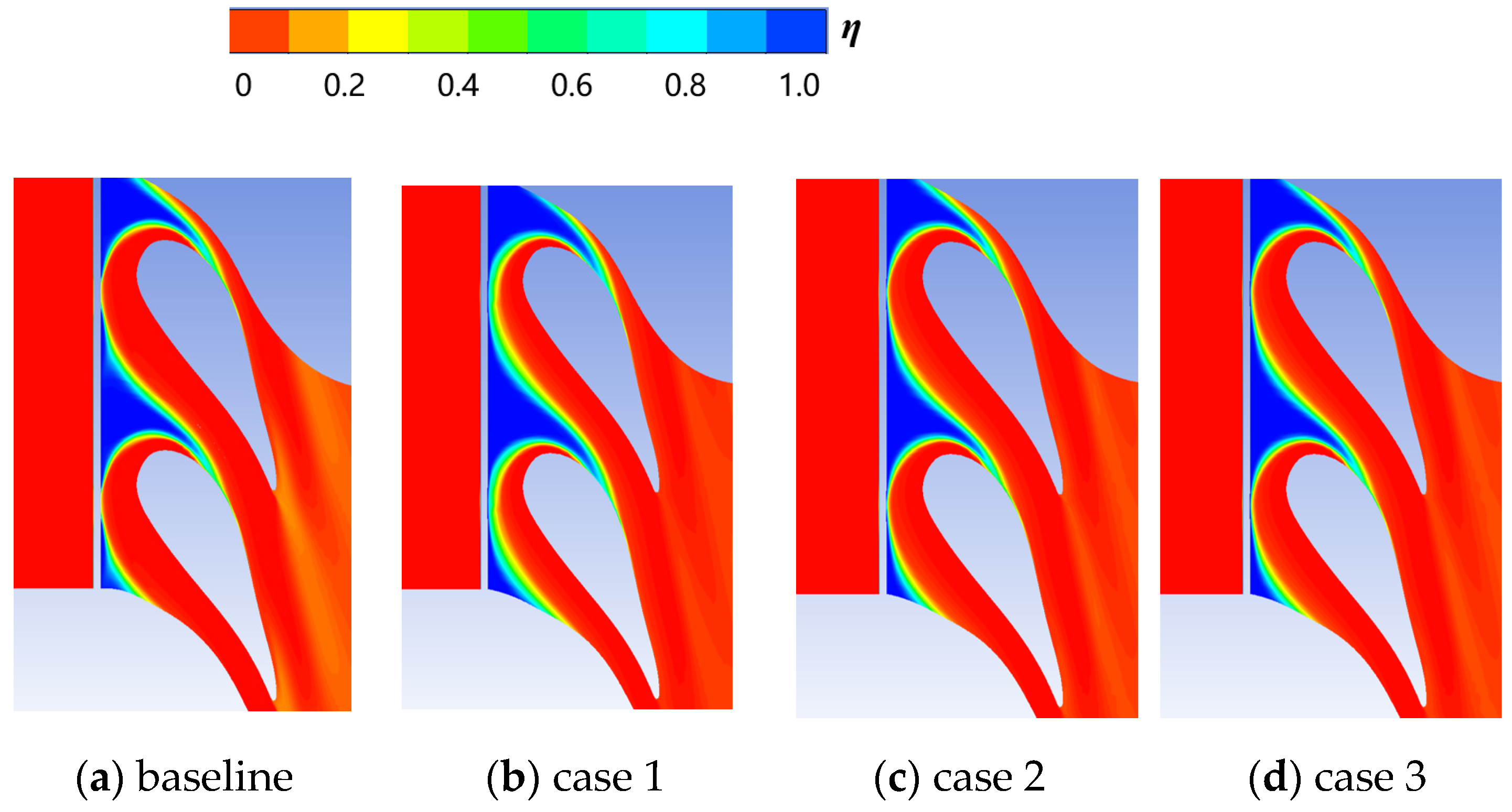
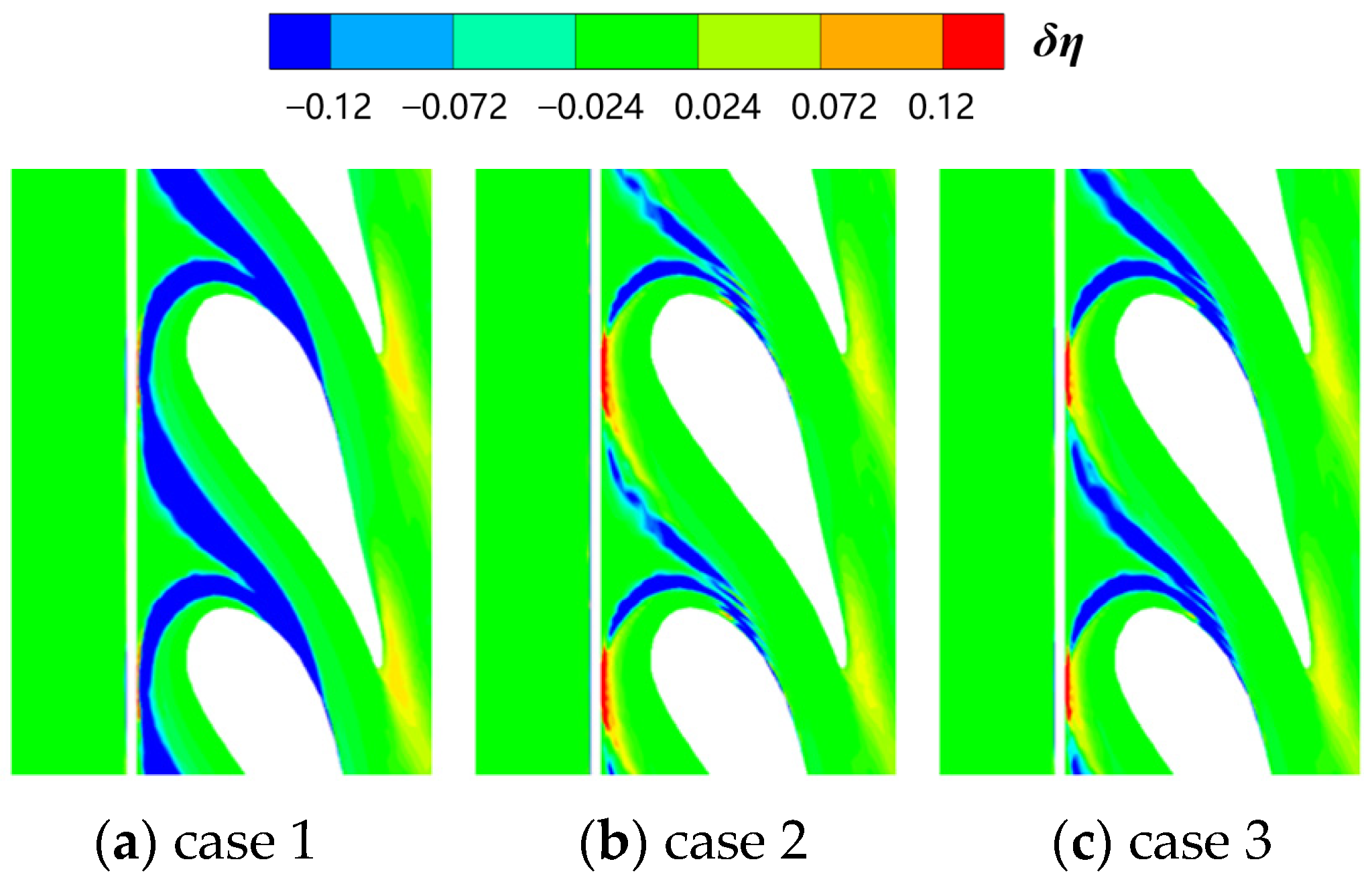
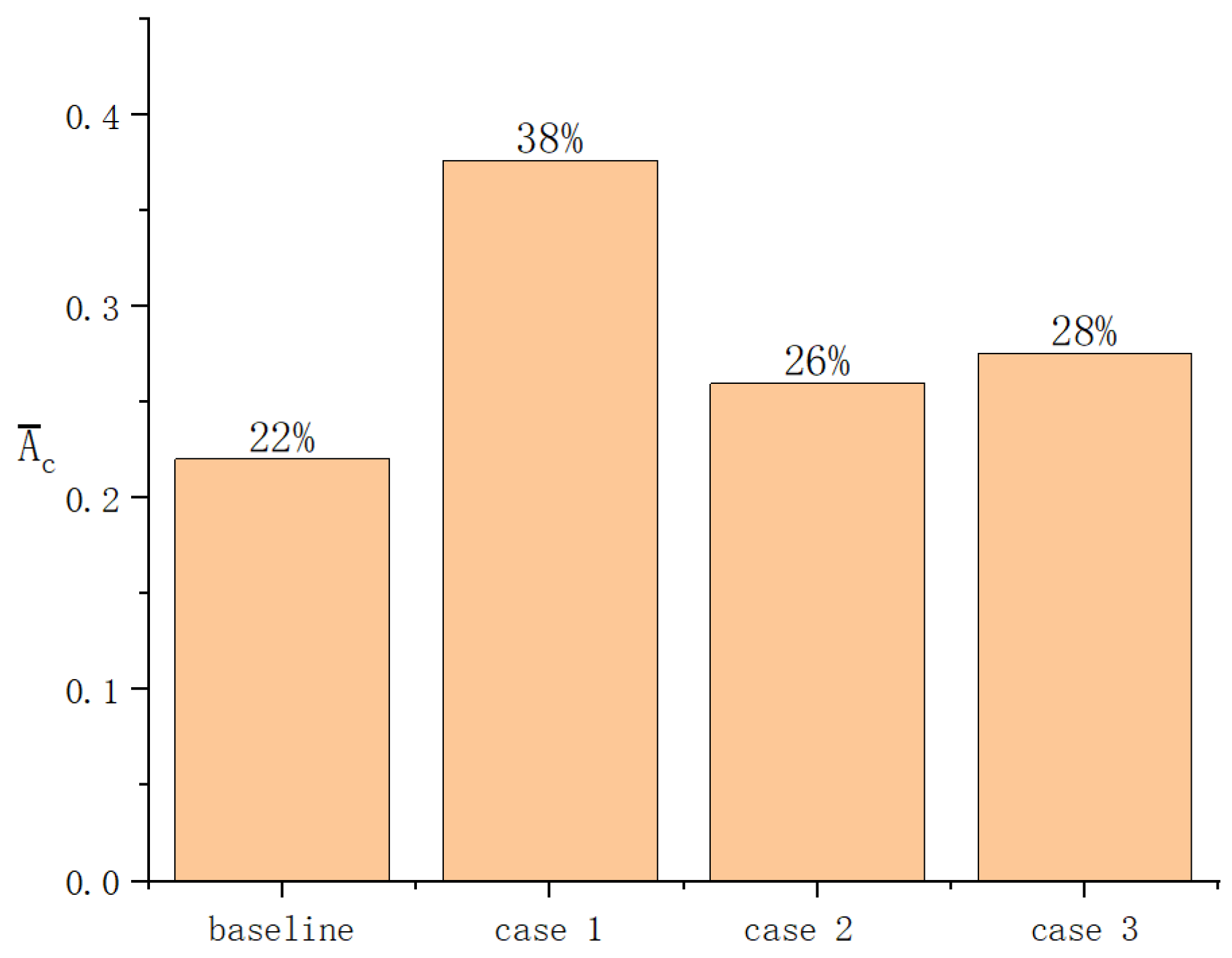
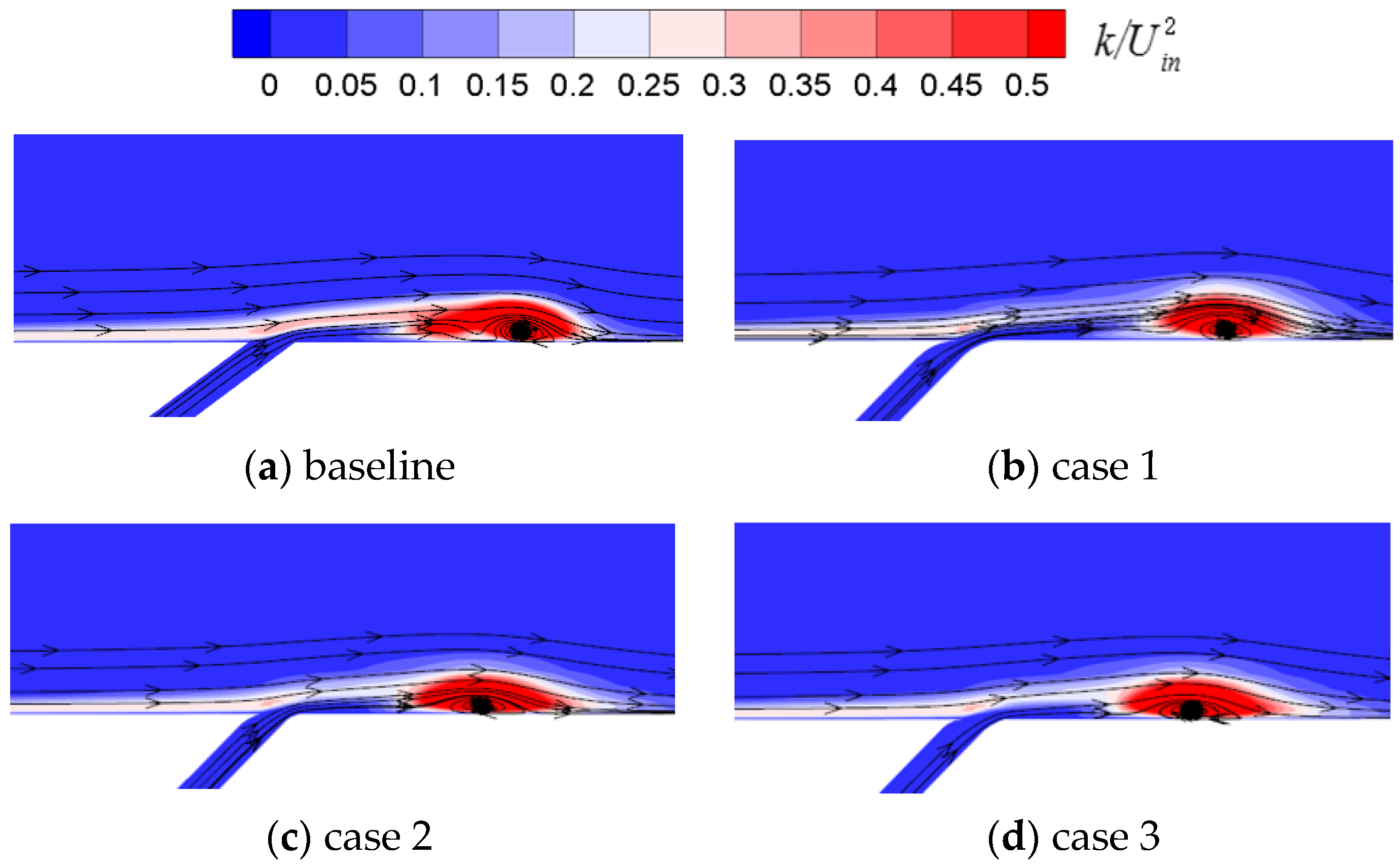
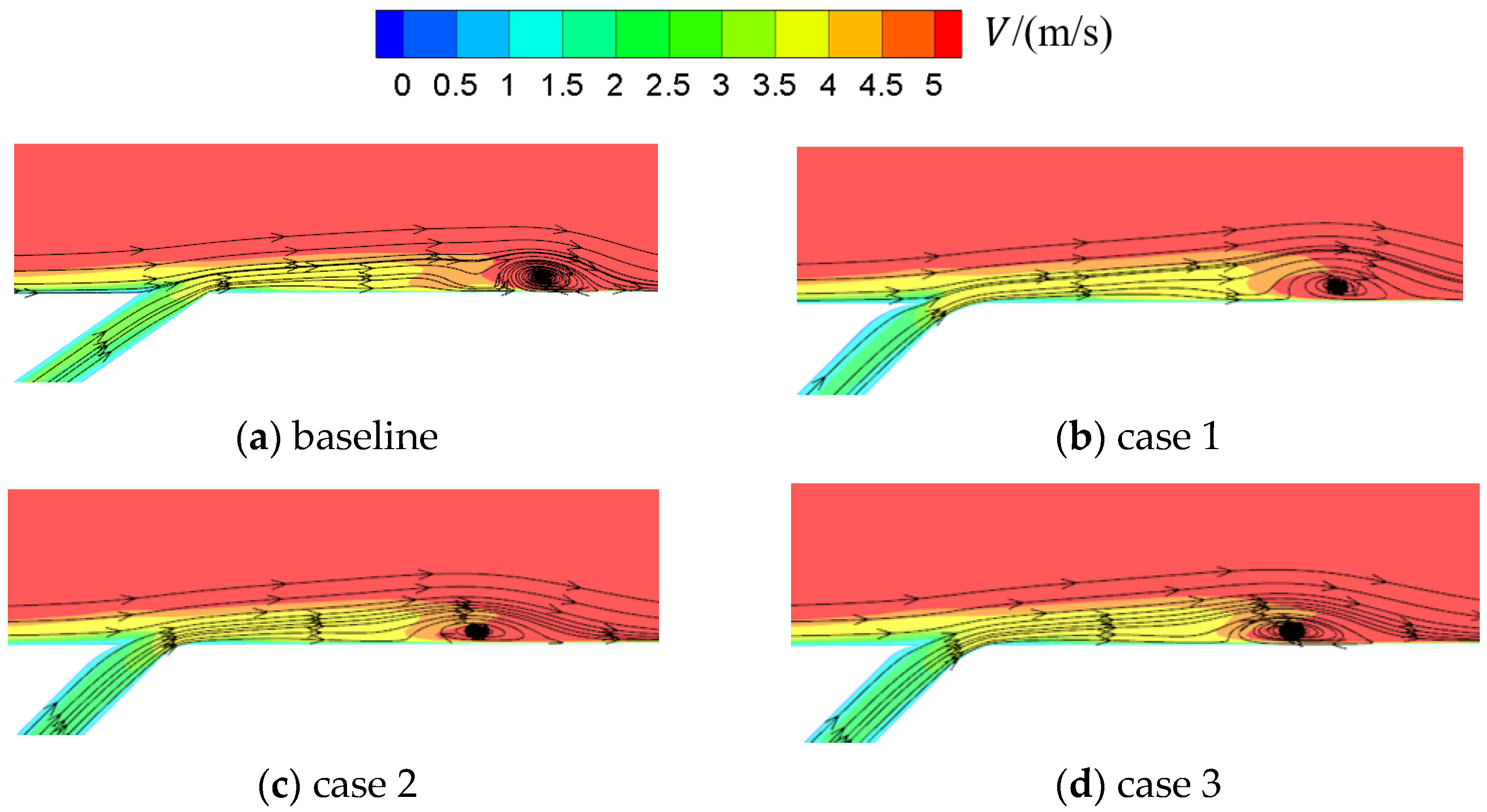
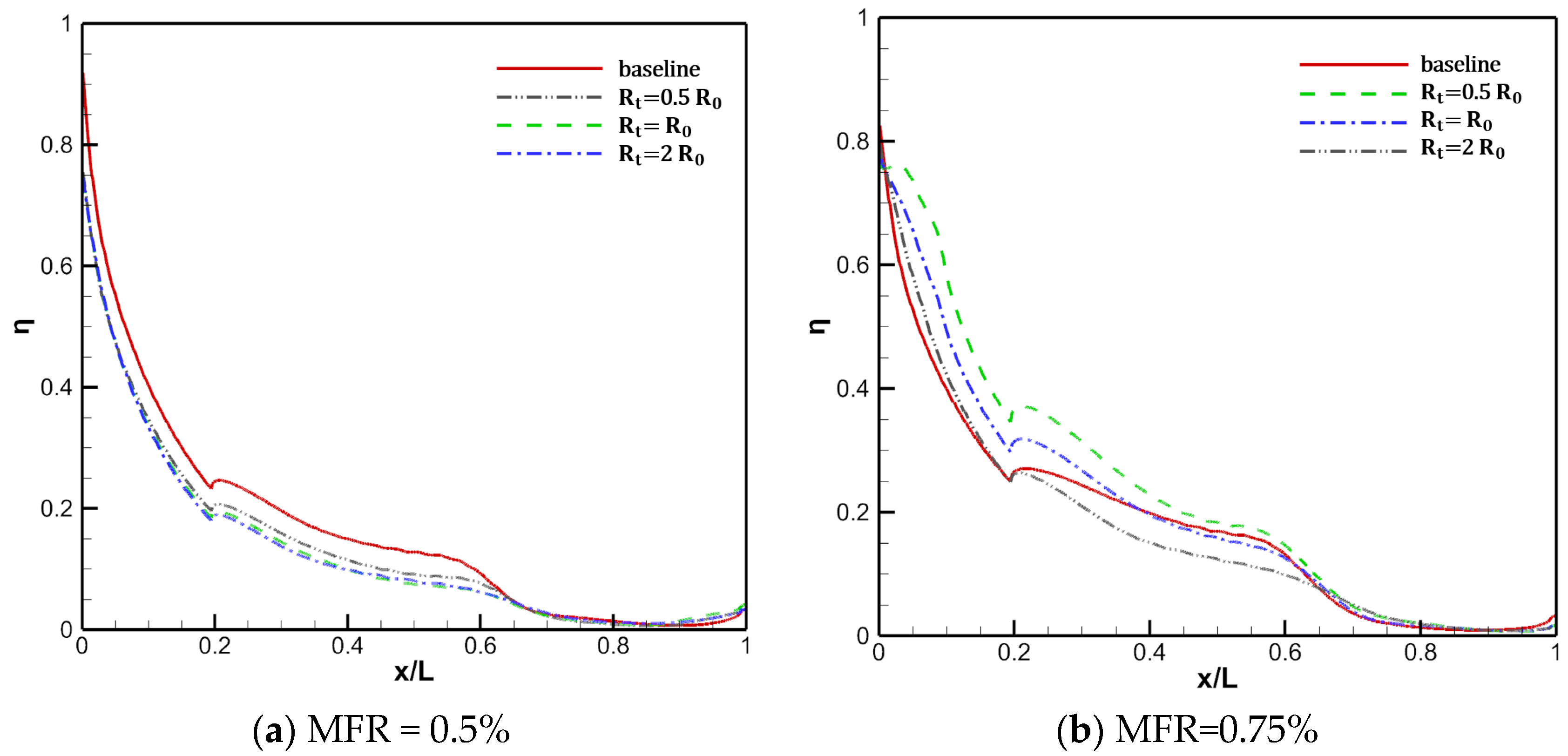
3.1. Influence of Slot Fillet
3.2. Influence of Slot Fillet
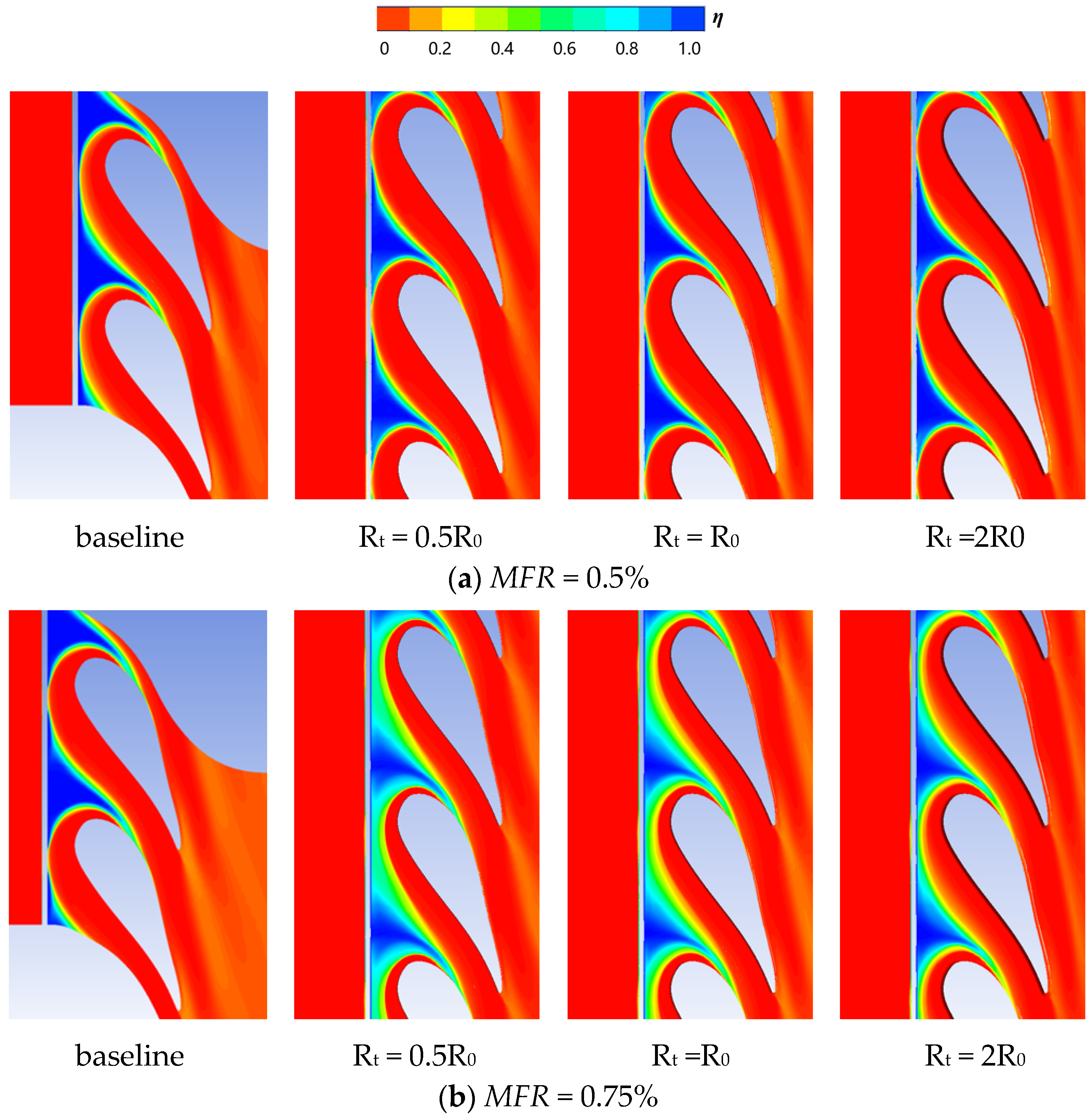
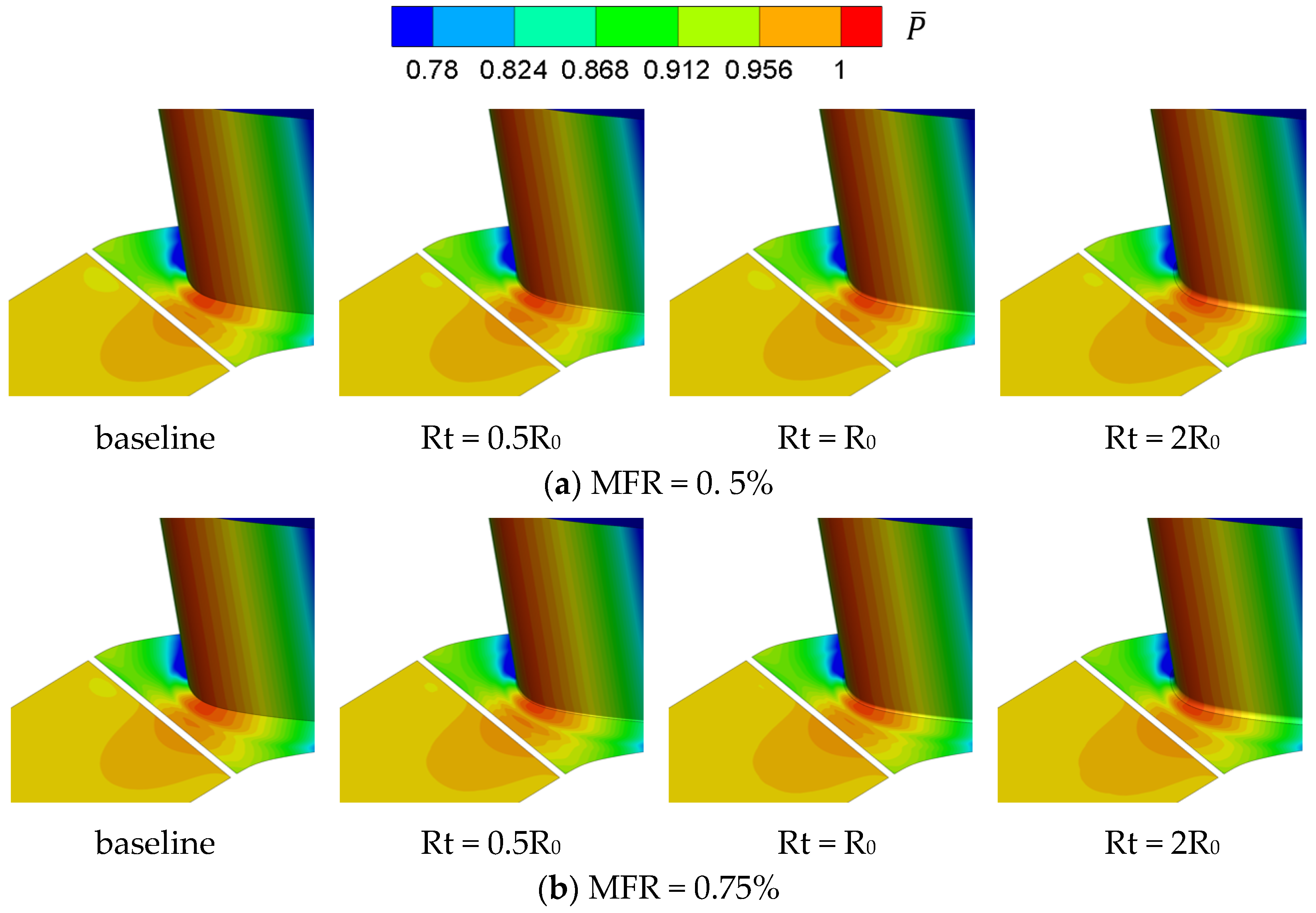
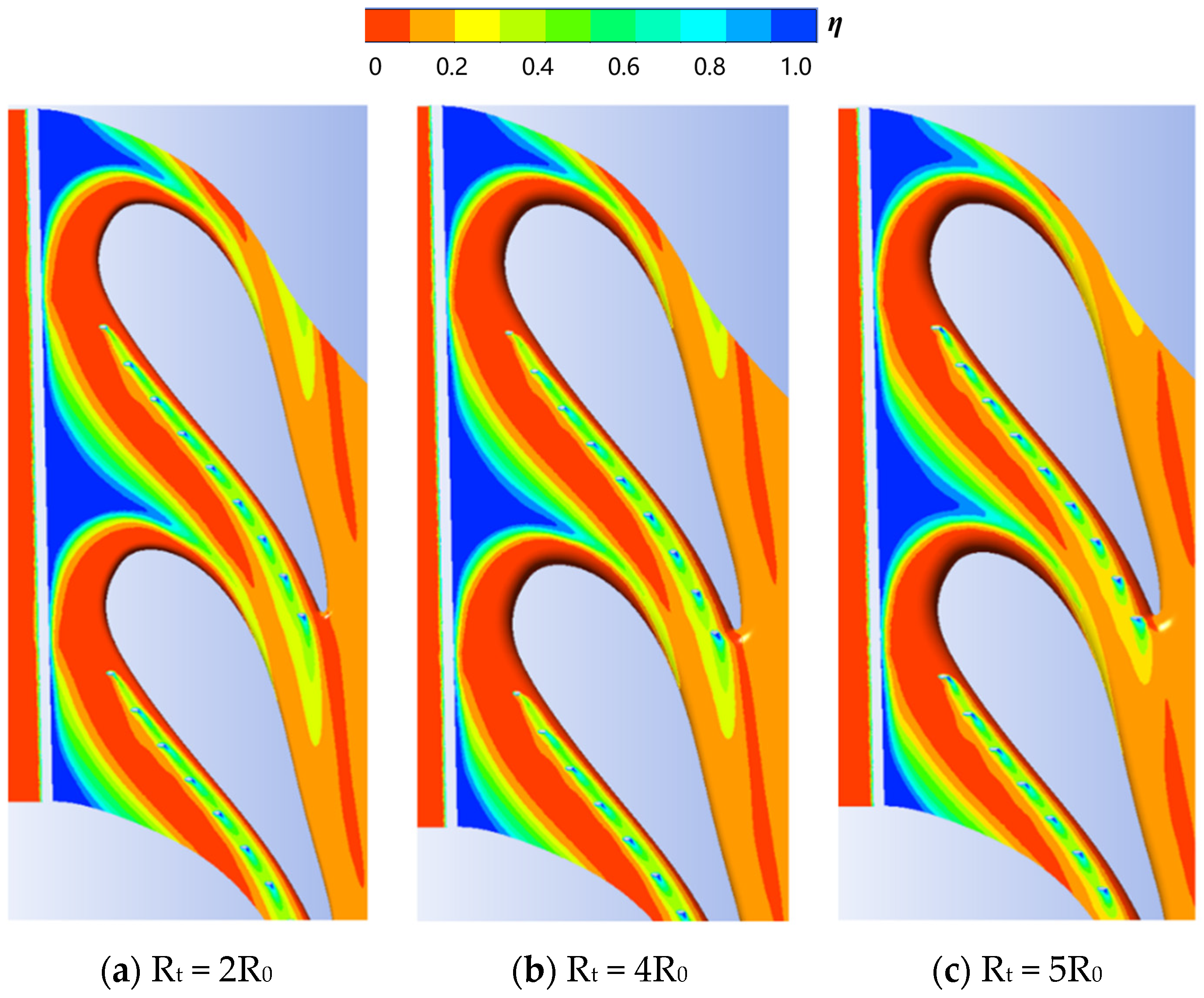
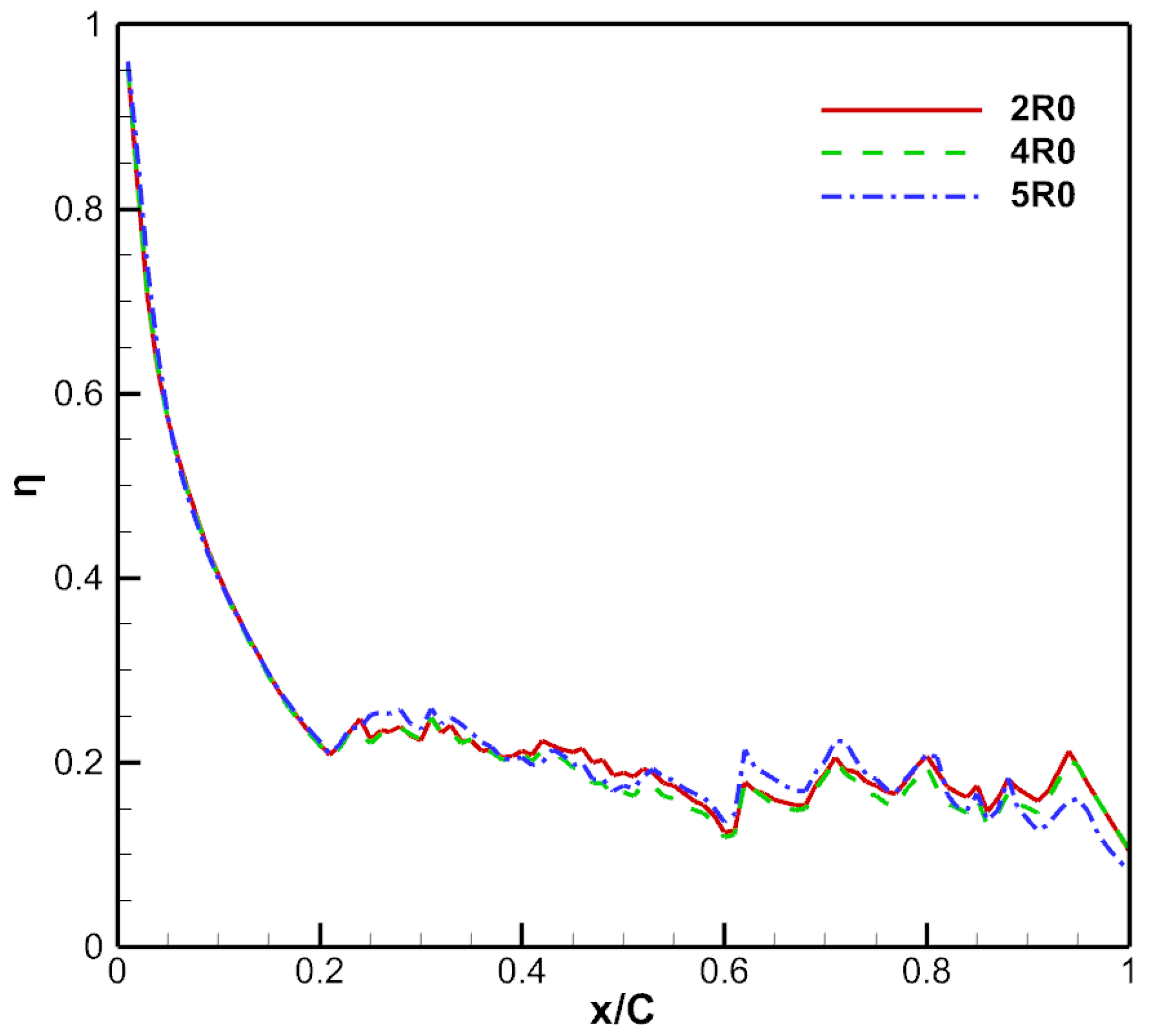
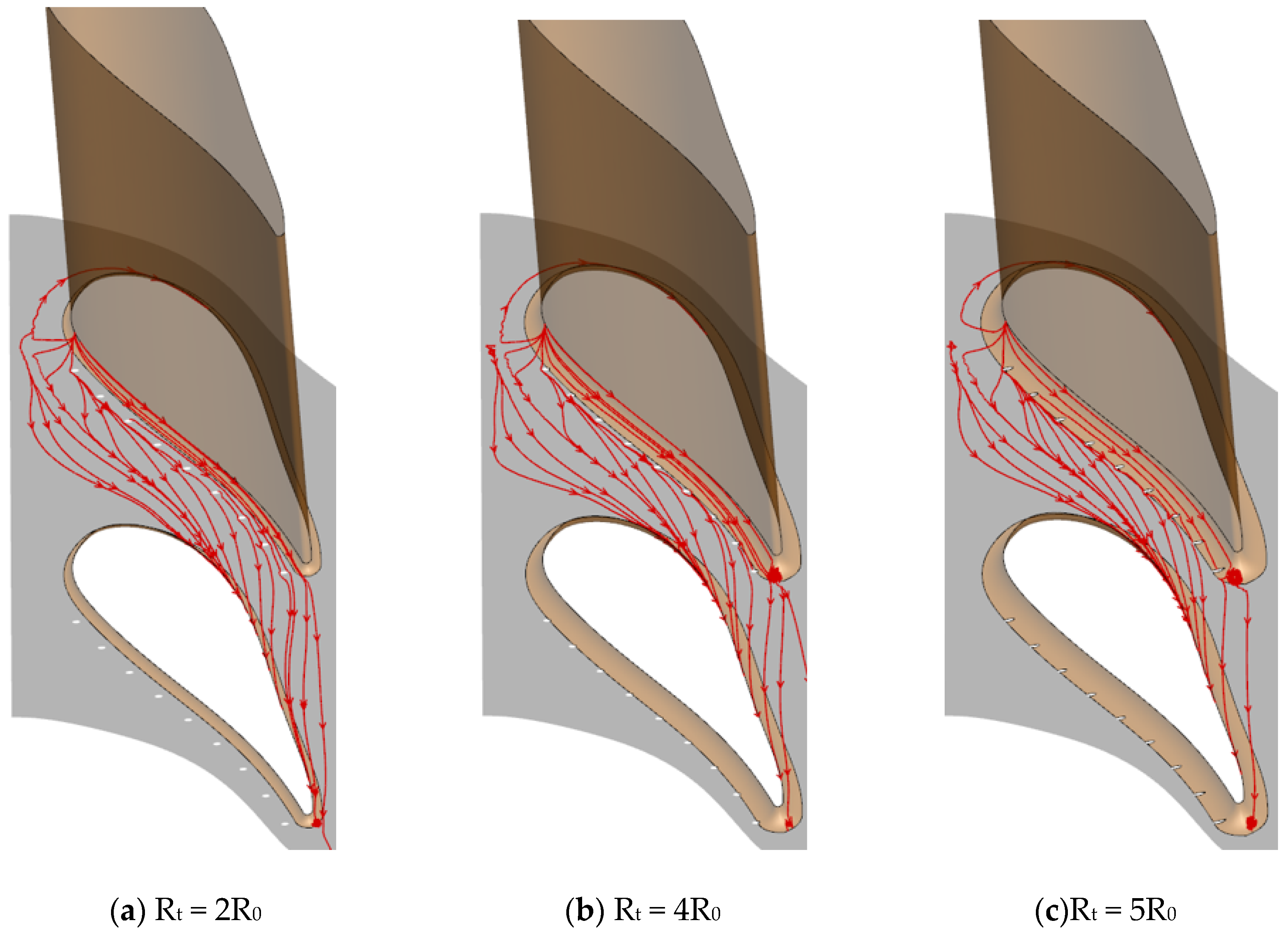
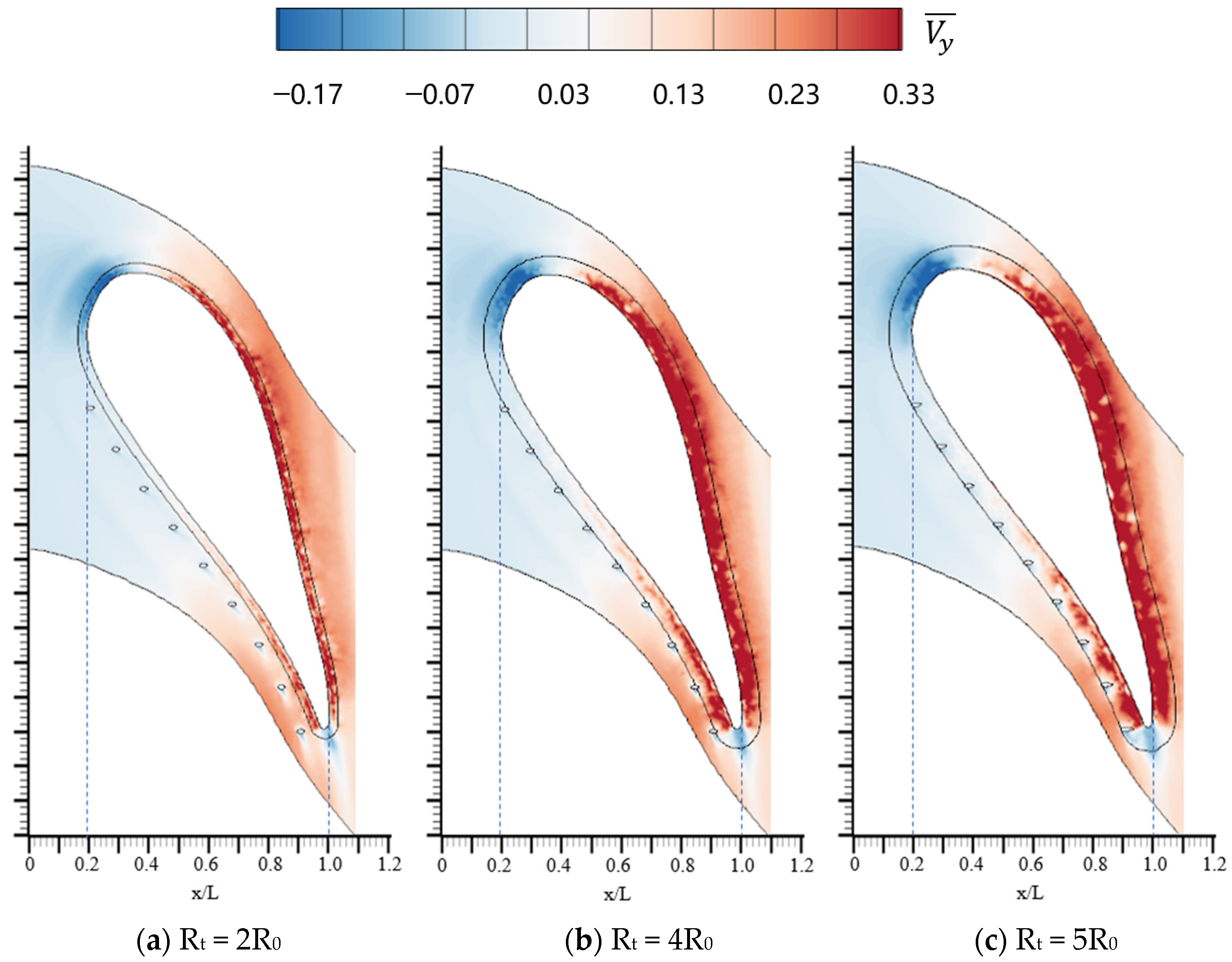
3.3. Influence of Vane Fillet
4. Conclusions
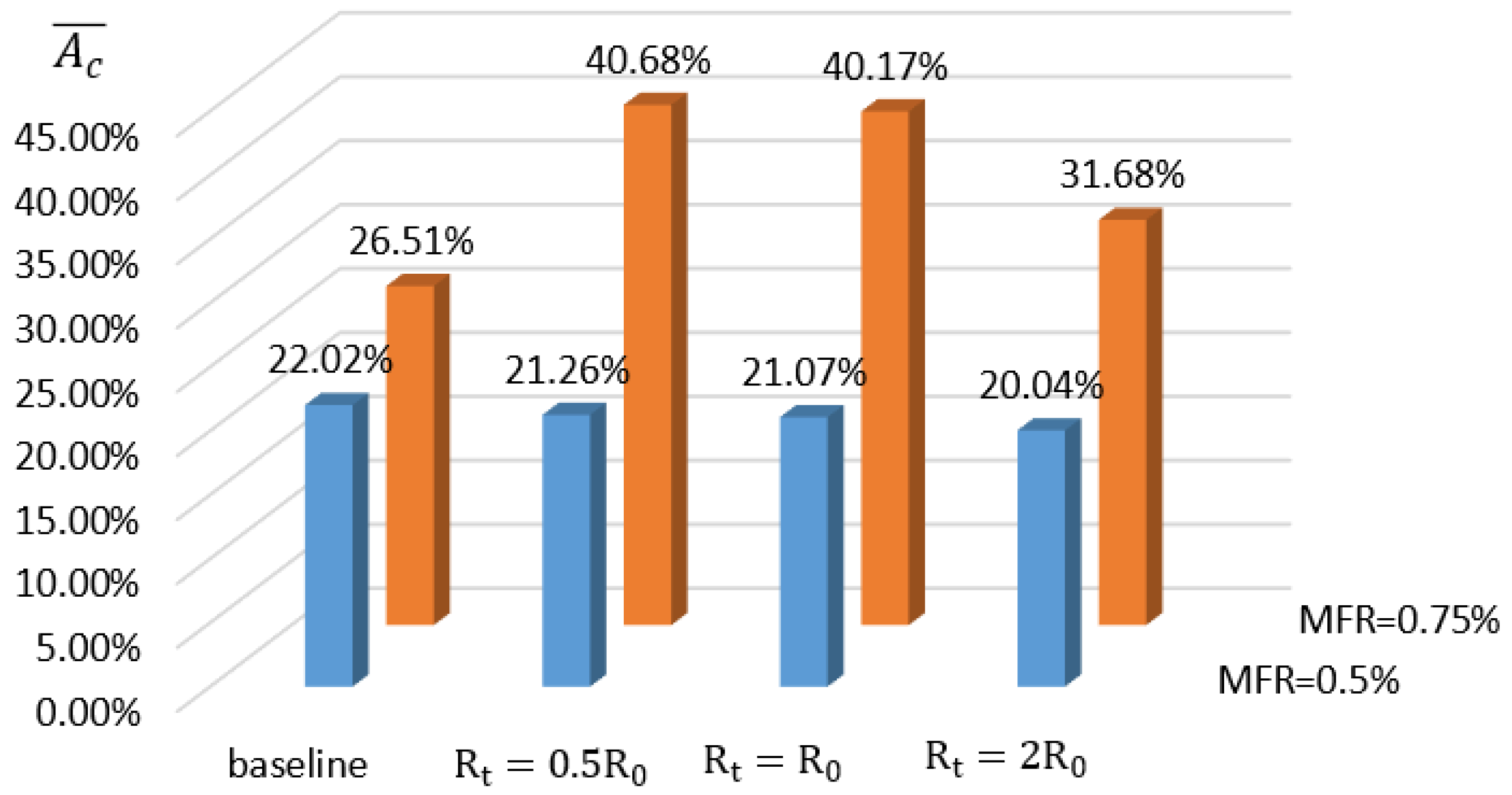
- The altered coolant momentum caused by the slot fillet influences the interaction of the coolant and the mainstream in the boundary layer. In case 1, the slot fillets change the speed direction of the coolant near slot outlet, making the direction of the coolant more consistent with the mainstream. The coolant performance is greatly improved by introducing the slot fillets, with an increase of 42% in effective cooling area compared to the baseline.
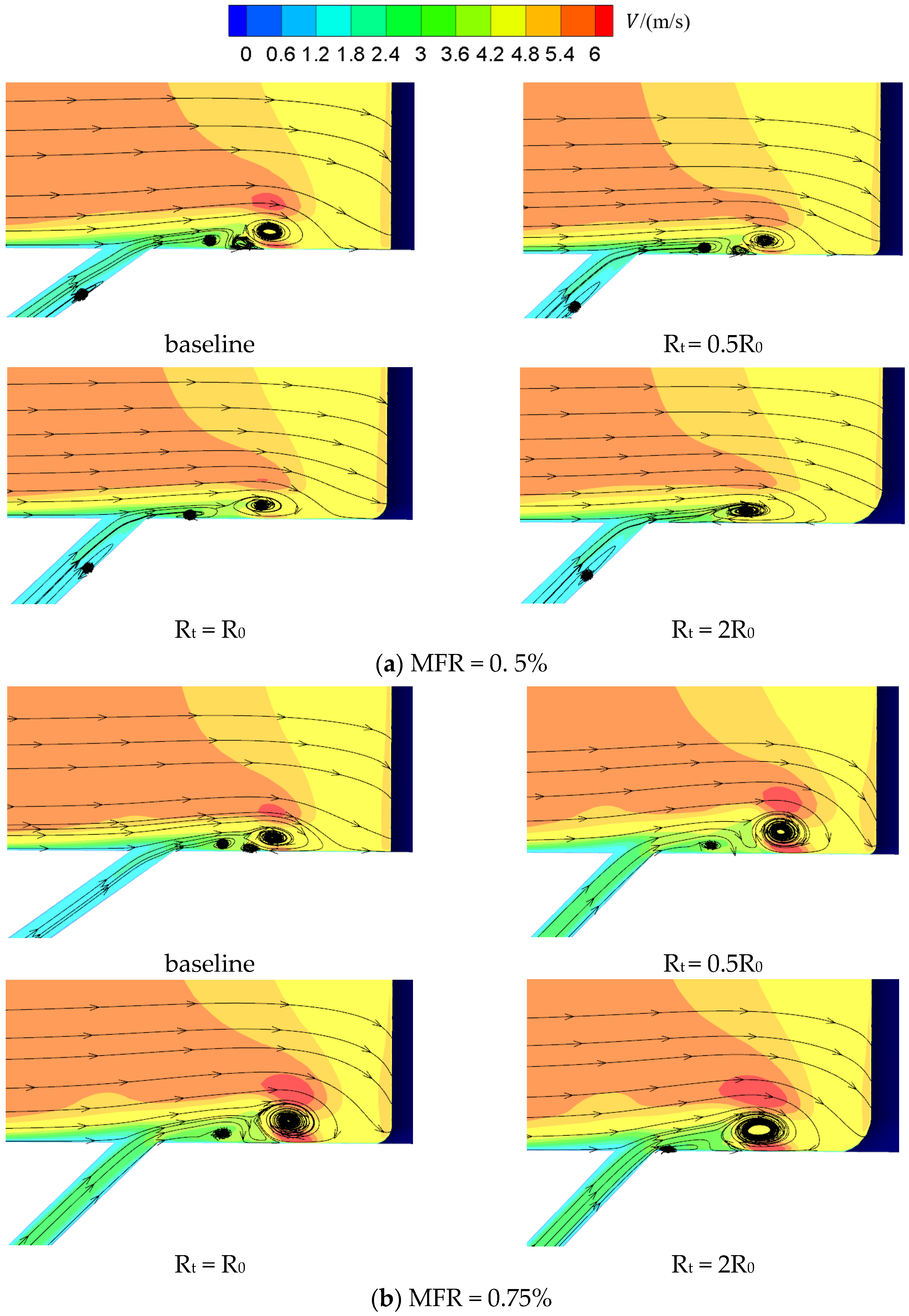
- The vane fillet with a small radius delays the separation of the boundary layer flow. It is attributed to the fact that the fillet with a small radius produces a pressure gradient opposed to the horseshoe vortex driving pressure gradient. Therefore, the horseshoe vortex is weakened by the introduction of the vane fillet. However, the fillet with a large radius makes the entire boundary layer flow separate early. The fillet with a large radius decreases the cooling performance.
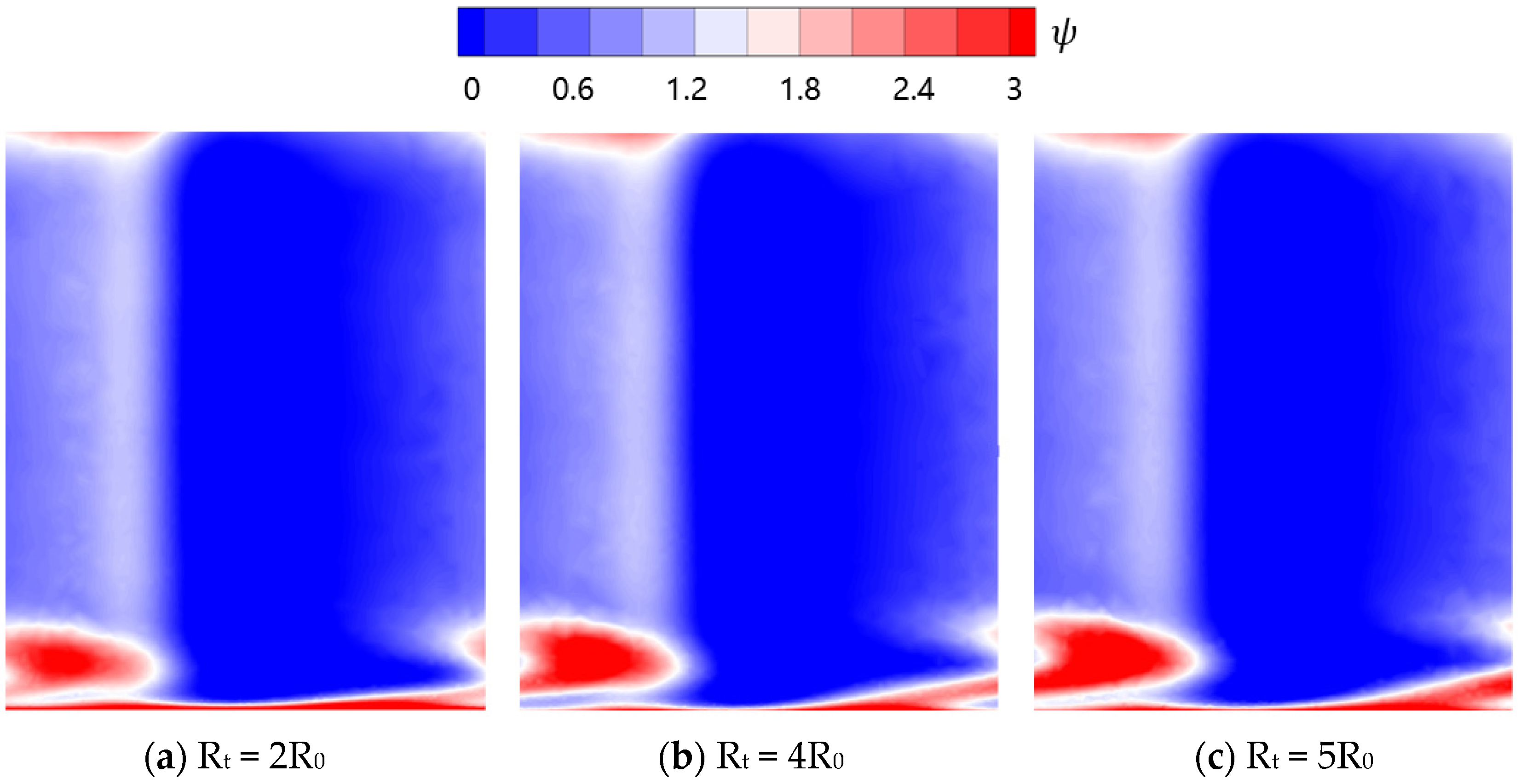
- The cooling performance of the film hole coolant is significantly influenced by the relative positions of the vane root fillet and the film holes. The increase of the fillet radius greatly improves the lateral component of the airflow close to the endwall. This is attributed to the fact that the airflow turns into stagnation as it approaches the fillet, increasing the local static pressure. As a result, the coolant avoids the fillet, increasing the lateral velocity component. The increase of the vane fillet radius improves the adiabatic cooling effectiveness, but aggravates the thermal loss coefficient.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | η0 | baseline adiabatic cooling effectiveness | |
| T∞ | ρ | density | |
| Taw | η | adiabatic film cooling effectiveness | |
| A | area (m2) | laterally averaged adiabatic film cooling effectiveness | |
| P* | total pressure (Pa) | area-averaged adiabatic film cooling effectiveness | |
| M | blowing ratio | ψ | thermal loss coefficient |
| v | velocity (m·s–1) | Subscripts | |
| P | pressure (Pa) | aw | adiabatic wall |
| T | temperature (K) | c | coolant |
| P | pressure coefficient | ∞ | mainstream |
| y+ | dimensionless wall—normal height of the first cell at wall | out | outlet |
| Greek | t | vane root fillet | |
| δη | adiabatic cooling effectiveness difference | Acronyms | |
| ηs | wall adiabatic cooling effectiveness | MFR | ratio of the film coolant mass flow rate to the mainstream flow |
References
- Hada, S.; Thole, K.A. Computational study of a midpassage gap and upstream slot on vane endwall film-cooling. Heat Transf. Parts A B 2011, 133, 011024. [Google Scholar] [CrossRef]
- Wang, H.P.; Olson, S.J.; Goldstein, R.J.; Eckert, E.R.G. Flow Visualization in a Linear Turbine Cascade of High Performance Turbine Blades. ASME J. Turbomach. 1997, 119, 1–8. [Google Scholar] [CrossRef]
- Langston, L.S.; Nice, M.L.; Hooper, R.M. Three-Dimensional Flow Within a Turbine Cascade Passage. ASME J. Turbomach. 1977, 99, 21–28. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Spores, R.A. Turbulent Transport on the Endwall in the Region Between Adjacent Turbine Blades. ASME J. Turbomach. 1988, 110, 862–869. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, W.; Wang, Z.; Tong, Z. Conjugate Heat Transfer Simulation of Overall Cooling Performance for Cratered Film Cooling Holes. Machines 2022, 10, 395. [Google Scholar] [CrossRef]
- Chowdhury, N.H.; Shiau, C.C.; Han, J.C.; Zhang, L.; Moon, H.K. Turbine vane endwall film cooling with slashface leakage and discrete hole configuration. ASME J. Turbomach. 2017, 139, 061003. [Google Scholar] [CrossRef]
- Gao, H.; Li, X.; Ren, J.; Jiang, H. Effect of leakage flow on the endwall cooling performance in high subsonic turbine cascade. Int. J. Therm. Sci. 2021, 170, 107140. [Google Scholar] [CrossRef]
- Tao, Z.; Yao, Y.; Zhu, P.; Song, L.; Li, J. Experimental and numerical study on film cooling effectiveness of an annular cascade endwall with different slot configuration. Int. J. Therm. Sci. 2020, 158, 106517. [Google Scholar] [CrossRef]
- Du, K.; Li, Z.G.; Li, J.; Sunden, B. Influence of the upstream slot geometry on the endwall cooling and phantom cooling of vane suction side surface. Appl. Therm. Eng. 2017, 121, 688–700. [Google Scholar] [CrossRef]
- Kim, J.; Sohn, H.-S.; Choi, S.; Hsu, W.-T.; Uedab, O.; Cho, H.H. Effect of misalignment at 2nd vane endwall on heat transfer with purge flow. Int. J. Heat Mass Transf. 2021, 170, 121034. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, X. Turbine Endwall Film Cooling With Combustor-Turbine Interface Gap Leak-age Flow: Effect of Incidence Angle. J. Therm. Sci. 2013, 22, 135–144. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, Z.; Zhang, X.; Peng, J.; Zhang, F.; Wu, X. Improving cooling performance and robustness of NGV endwall film cooling design using micro-scale ribs considering incidence effects. Energy 2022, 253, 124203. [Google Scholar] [CrossRef]
- Sharma, O.P.; Butler, T.L. Predictions of Endwall Losses and Secondary Flows in Axial Flow Turbine Cascades. ASME J. Turbomach. 1987, 109, 229–236. [Google Scholar] [CrossRef]
- Miao, X.; Zhang, Q.; Atkin, C.; Sun, Z.; Li, Y.S. Improving purge air cooling effectiveness by engineered end-wall surface structures- Part I: Duct flow. J. Turbomach. 2018, 140, 091001. [Google Scholar] [CrossRef]
- Rose, M.G. Non-axisymmetric end wall profiling in the HP NGVs of an axial flow gas turbine. In Proceedings of the ASME 1994 International Gas Turbine and Aeroengine Congress and Exposition, Hague, The Netherlands, 13–16 June 1994. [Google Scholar]
- Babu, S.; Kiran, K.N.; Tom, J.K.; Anish, S. Numerical Investigation on Effects of Profiled Endwall Over Purge Flow in Linear Turbine Cascade. In Proceedings of the 7th Asian Joint Workshop on Thermophysics and Fluid Science, Trivandrum, India, 24 November 2018. [Google Scholar]
- Mensch, A.; Thole, K.A. Overall Effectiveness and Flowfield Measurements for an Endwall with Non-axisymmetric Contouring. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Sauer, H.; Müller, R.; Vogeler, K. Reduction of secondary flow losses in turbine cascades by leading edge modifications at the endwall. J. Turbomach. 2001, 123, 207–213. [Google Scholar] [CrossRef]
- Shih, T.I.P.; Lin, Y.L. Controlling secondary-flow structure by leading-edge airfoil fillet and inlet swirl to reduce aerodynamic loss and surface heat transfer. J. Turbomach. 2003, 125, 48–56. [Google Scholar] [CrossRef]
- Blair, M.F. An experimental study of heat transfer and film cooling on large-scale turbine endwalls. Am. Soc. Mech. Eng. 1974, 79788, V01AT01A033. [Google Scholar] [CrossRef]
- Du, K.; Li, J. Numerical study on the effects of slot injection configuration and endwall alignment mode on the film cooling performance of vane endwall. Int. J. Heat Mass Transf. 2016, 98, 768–777. [Google Scholar] [CrossRef]

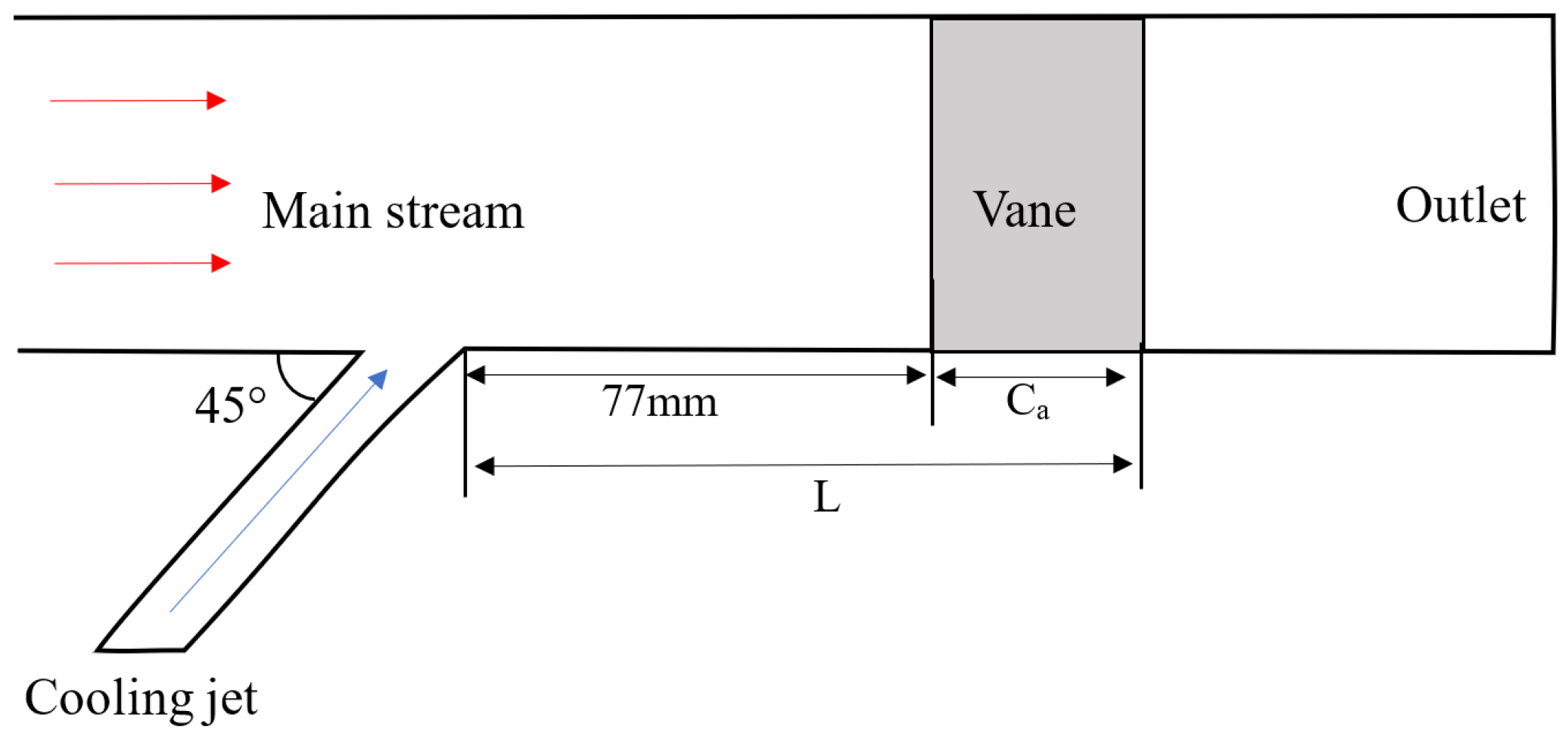
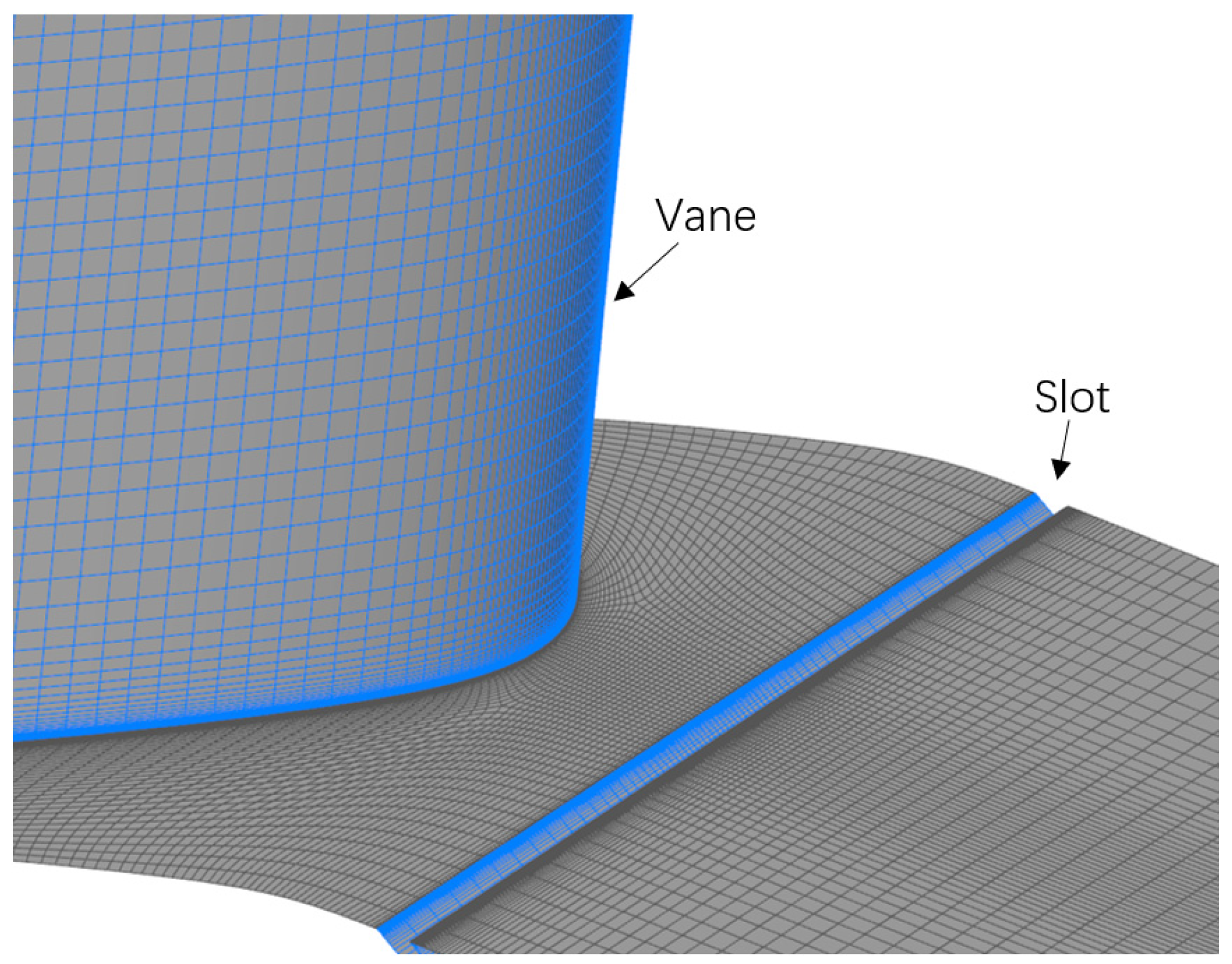



| Parameters | Value |
|---|---|
| Chord length of blade C (mm) | 594 |
| Axial chord of blade Ca (mm) | 293 |
| Pitch/chord (P/C) | 0.77 |
| Inlet total temperature (K) | 333.19 |
| Inlet total pressure (kPa) | 107.64 |
| Outlet static pressure (kPa) | 107 |
| Inlet turbulence intensity | 1.0% |
| Inlet angle (°) | 0 |
| Outlet angle (°) | 72 |
| Coolant inlet total temperature (K) | 293.15 |
| Grid Numbers | |
|---|---|
| 4.5 × 106 | 0.2625 |
| 7.0 × 106 | 0.2726 |
| 9.0 × 106 | 0.2742 |
| 1.1 × 107 | 0.2746 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, K.; Pei, X.; Shan, X.; Zhao, Z.; Liu, C. Influence of the Slot Fillet and Vane Root Fillet on the Turbine Vane Endwall Cooling Performance. Machines 2023, 11, 729. https://doi.org/10.3390/machines11070729
Du K, Pei X, Shan X, Zhao Z, Liu C. Influence of the Slot Fillet and Vane Root Fillet on the Turbine Vane Endwall Cooling Performance. Machines. 2023; 11(7):729. https://doi.org/10.3390/machines11070729
Chicago/Turabian StyleDu, Kun, Xiangpeng Pei, Xiaoming Shan, Zunsheng Zhao, and Cunliang Liu. 2023. "Influence of the Slot Fillet and Vane Root Fillet on the Turbine Vane Endwall Cooling Performance" Machines 11, no. 7: 729. https://doi.org/10.3390/machines11070729
APA StyleDu, K., Pei, X., Shan, X., Zhao, Z., & Liu, C. (2023). Influence of the Slot Fillet and Vane Root Fillet on the Turbine Vane Endwall Cooling Performance. Machines, 11(7), 729. https://doi.org/10.3390/machines11070729







