Abstract
Electrothermal actuation is widely employed in MEMS systems, and the electrothermal V-shaped actuator (referred to as EVA) has garnered attention due to its stable output force. However, current EVAs in MEMS face the challenge of limited driving displacement. To investigate the impact of metal coating on the driving displacement of silicon EVAs, a mechanical model is established, and a formula for calculating the maximum displacement is derived. The theoretical analysis results are compared between cases with and without metal coating. To validate the formula’s accuracy, the COMSOL simulation platform is utilized, employing the finite element method to model and simulate actuators with various metal coatings. The analysis demonstrates that the calculated results have a maximum error of 10% compared to the simulation results. The metal coating enhances the displacement of silicon EVAs to different degrees, with a more pronounced effect observed for metal coatings with lower resistivity. Notably, a copper metal coating doubles the displacement of silicon EVAs at a voltage of 4 V. In other words, under the same displacement, a silicon EVA with a metal coating requires a lower input voltage compared to the group without a metal coating, resulting in a significant voltage reduction of 33.75%.
1. Introduction
Microactuators are essential components of microelectromechanical systems (MEMS), serving as the driving or actuating units of the system. They are responsible for energy conversion, motion and force transmission, as well as responding to system information. Generally, microactuators can be categorized into several types: electrostatic actuators, electromagnetic actuators, piezoelectric actuators, and electrothermal actuators. Electrostatic actuators [1,2] offer fast response speeds, but they require high driving voltages, making them incompatible with integrated circuits. Electromagnetic actuators [3] rely on special magnetic materials, which complicates their fabrication process. Piezoelectric actuators [4] involve complex manufacturing techniques and generate small displacements. Electrothermal actuators [5], based on the Joule heating effect, can produce stable and controllable displacements and driving forces. Compared to other actuators, they exhibit greater actuation forces. Consequently, electrothermal actuators find extensive applications in various micro-devices and systems, such as linear motors designed by Maloney et al. [6], nanomaterial testing devices developed by Espinosa et al. [7], micro grippers designed by Andersen et al. [8], and safety thermal devices designed by Hu et al. [9]. Additionally, with the advancement of the semiconductor industry, electrothermal actuators can be manufactured using mature integrated circuit fabrication processes, making them an integral part of MEMS devices.
However, the output displacement of electrothermal actuators is small, which is difficult to meet the needs of practical applications. In recent years, research on electrothermal actuators is mainly on the improvement of their structure and new materials. Wang Z. et al. [10] designed a U-shaped electrothermal actuator capable of producing circular motion, with a maximum jaw deflection of 9.1 um at a voltage of 14 V for the microgripper. Zhang Z. et al. [11] designed a Z-shaped electrothermal actuator similar to a V-beam in terms of symmetrical structure and linear motion output but less rigid than a V-beam. P. Shivhare et al. [12] proposed an electrothermally driven microgripper with a two-finger structure, where the gripping finger is driven via a V-shaped electrothermal actuator that produces a displacement of nearly 14 um at 1.2 V. Chu J. K. et al. [13] designed a symmetrical structure of microgripper based on V-shaped electrothermal actuators to achieve a simple gripping operation of microcells with relatively small moving displacement. Zhuo Zhang et al. [14] used copper and SU-8 photoresist to prepare V-shaped electrothermal microactuators, and the combination of the two materials provided a large motion drive and much flexibility for the integration and design of micro-robotic grippers. Li-Nuan Tsai et al. [15] prepared nickel and diamond nanocomposites for electrothermal microactuators, and the nanocomposites can save about 73% of power compared to microactuators made of pure nickel. K. Ochiai et al. [16] obtained larger displacements with a trapezoidal gold-plated MEMS thermal microactuator prepared using the SOI-MUMPS technique. Nguyen et al. [17] performed platinum coating on a silicon electrothermal V-shaped actuator, and, at the same displacement, the driving voltage was reduced by 40% for specimens with platinum coating compared to specimens without coating. H. Hussein et al. [18] investigated the influence of actuator size and material properties on its performance and successfully validated the theoretical model via finite element simulation. Fan Q. et al. [19] fabricated flexible double-layer ETAs by bonding graphite paper and a PI film, enabling significant deformation of the “U”-shaped electrothermal actuator under low constraint conditions. Zhang D. et al. [20] proposed a V-shaped electrothermal MEMS actuator model that considers human error factors using a cascaded ANSYS simulation model and fuzzy mathematical calculation model. Nouha Alcheikh et al. [21] studied the dynamics model of an electrothermal-driven MEMS V-shaped microbeam resonator using experimental, analytical, and numerical approaches.
Through the analysis of the aforementioned research, it is found that among various types of electrothermal actuators, V-shaped actuators offer a simpler structure and provide larger displacement in MEMS systems compared to other micro-actuators. This paper is based on the metal coating of silicon EVA and establishes theoretical models for silicon EVA with and without metal coating. The theoretical models validate that the metal coating effectively enhances the driving displacement of silicon EVA. This study identifies the resistivity of the metal coating as a key parameter influencing the driving displacement of the V-shaped actuator. Additionally, COMSOL simulation software is utilized for simulation, and the theoretical results are compared with the simulation results to verify the accuracy of the theoretical findings.
2. Theoretical Analysis
The mechanical model of the silicon EVA can be converted into a rigid structure subjected to an external load [22], as shown in Figure 1.
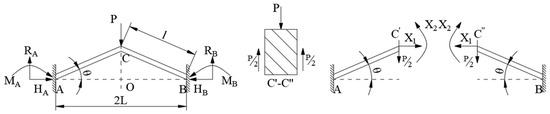
Figure 1.
Simplified mechanical model of silicon EVA.
After converting to external loads subjected to forces, the simplified mechanical model can be studied as a three-time super-stationary problem. Since the structural model is a symmetric structure, it is not difficult to analyze the section to obtain the same shear force at section as , but the axial force and axial force are unknown, so the mechanical model can be reduced to a quadratic super-stationary problem for analysis. Assuming that the left anchor area in Figure 1 is a static base, the deformation coordination condition of the static base can be obtained as the horizontal displacement and the turning angle at the back section of the cantilever beam subjected to free elongation via thermal expansion are zero.
In the above equation, , represents the thermal expansion coefficient of the material, and represents the temperature variation of the actuator.
According to Castigliano’s theorem [23], the horizontal displacement and angle at section can be calculated.
From the above equation, is the rotational inertia of the cantilever beam, is Young’s modulus of the material, is the bending moment, and is the tensile stress.
- In , the bending moment at section can be calculated.
The tensile stress at section can be calculated as follows:
From Equations (2), (4), and (5), can be deduced.
From the above equation, is the cross-sectional area of the cantilever beam in the above equation.
- 2.
- In , the bending moment at section can be calculated.
The tensile stress at section can be calculated as follows:
Bringing the results of Equations (7) and (8) into Equation (3), can be calculated as follows:
Bring the results of Equations (6) and (9) into Equation (1), the force and moment on section can be calculated.
Since the bending moment and external load at section are known, the displacement at section can be obtained in a V-shaped cantilever beam of symmetrical structure.
It is assumed that there are two displacement variables in and directions at section , as shown in Figure 2.
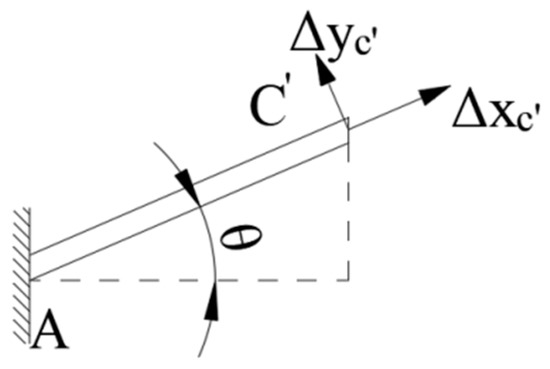
Figure 2.
Simple diagram of unilateral displacement change in silicon EVA.
The values of and have been calculated in Equations (10) and (11), and the values of and can be found by bringing the results into Equations (13) and (14). Therefore, the maximum displacement at the top of the cantilever beam in Equation (12) can be calculated, as shown in Figure 3.
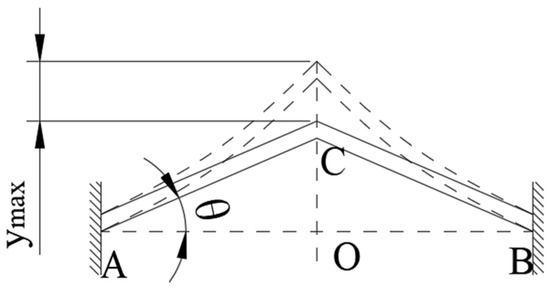
Figure 3.
Simplified model of silicon EVA displacement.
2.1. Silicon EVA Heat Transfer Model without Metal Coating
The silicon EVA with a certain resistance value will produce the maximum displacement at the apex of the V-shaped beam under no load when a constant voltage is applied. It is assumed that the resistance can convert all the electrical energy into thermal energy in a certain time , neglecting the heat loss of the silicon EVA conducted through the air gap [24,25], as shown in Figure 4, according to the law of conservation of energy [26].
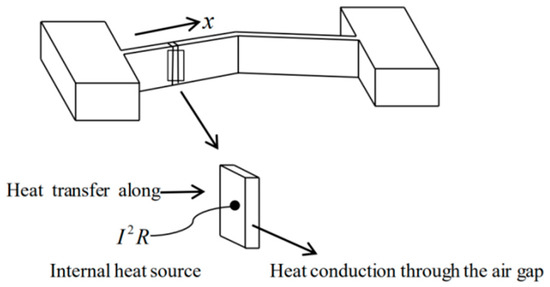
Figure 4.
Silicon EVA heat transfer model without metal coating.
From the equation above, is the mass of the cantilever beam, is the specific heat capacity of the cantilever beam, and is the resistance value of the cantilever beam.
According to Equation (16), can be calculated.
From Equations (15) and (17), the maximum output displacement of the silicon EVA can be obtained.
2.2. Heat Transfer Model of Silicon EVA with Metal Coating
In the silicon EVA heat transfer system, there are various parameters that affect the actuation displacement, such as cantilever beam angle , cantilever beam length , cantilever beam mass , cantilever beam cross-sectional area , etc. The silicon EVA resistance with metallic coating can be calculated by ensuring that the simulation model with metallic coating and the without metal coating group have the same dimensional parameters as shown in Figure 5 [26].
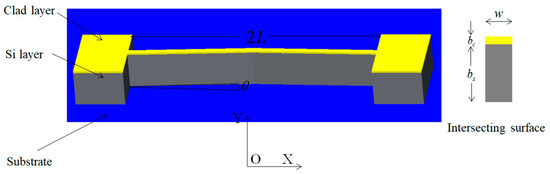
Figure 5.
Silicon EVA model with metal coating.
The metal coating resistance can be calculated.
From the equation above, is the metal coating resistivity, and is the cross-sectional area of the metal coating.
The resistance of the silicon layer can be calculated as follows:
From the equation above, is silicon layer resistivity, and is the cross-sectional area of the silicon layer.
From Equations (19) and (20), the total resistance of the silicon EVA with metal coating can be calculated.
For the silicon EVA with a metal coating, the resistance is equivalent to connecting metal and silicon in parallel [26], resulting in , while the smaller the metal resistivity of the coating, the smaller the total resistance . The silicon EVA heat transfer model with metal coating has a coupled silicon and metal bilayer material heat transfer effect, as shown in Figure 6, with the following two forms of conduction: heat transfer through the air gap and heat transfer inside the beam. The heat conduction inside the beam dominates at the microscale, and the heat conduction through the air gap can be neglected [24,25]. Without considering the heat loss via air gap conduction, the maximum output displacement of the silicon EVA with the metal coating is inversely proportional to the total resistance .
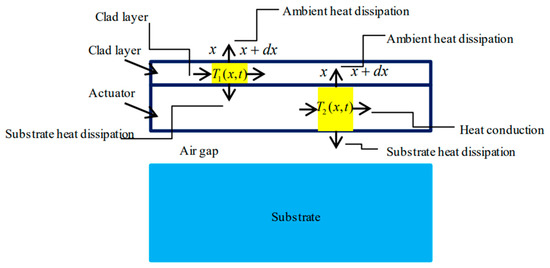
Figure 6.
Silicon EVA heat transfer model with metal coating.
Comparing Equations (18) and (22), it can be found that in the presence of metal coating, the total resistance of the actuator decreases due to the coupling effect of the metal coating with the silicon cantilever beam, which affects the conductivity of the actuator. Therefore, the silicon EVA with metal coating has a larger output displacement when the same size voltage is applied, and the effect of the metal coating on the output displacement of the silicon EVA is further verified using the simulation below.
3. Results and Discussion
3.1. Simulation Parameter Setting
On the premise that the metal coating group and the without metal coating group have the same structural size, the geometric size of the EVA model is set to and , as shown in Figure 7.
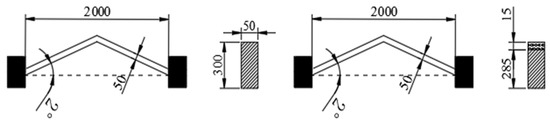
Figure 7.
Structure size of metal coating group and without metal coating group.
During the actuator motion, the multiphysics field dynamic simulation of electrothermal has two energy conversion processes, electrical energy is converted into thermal energy, and thermal energy is converted into mechanical energy. So, the COMSOL software is selected to simulate the actuator properties. The properties of the materials involved are shown in Table 1.

Table 1.
Material parameters.
The actuator is set to be in an environment with a temperature of 293.15 [K], along with fixed constraints on both sides of the V-shaped beam, and thermal expansion is chosen to couple with the electromagnetic thermal multiphysics field. Since actuators generally work at small voltages in microsystems, 1 V, 2 V, 3 V, and 4 V were, therefore, input to the actuator during the simulation to study the characteristics of EVA.
In summary, the displacement equations for the silicon electrothermal actuator were set up using MATLAB’s scripting language, incorporating relevant parameters such as resistivity and thickness associated with the metal coating and silicon electrothermal actuator. The equations were effectively solved using the MATLAB solver. The results were then compared and analyzed alongside the simulation data from COMSOL to gain a comprehensive understanding of the influence of various metal coatings on the actuator’s displacement.
3.2. Calculation and Simulation Results
Figure 8 shows the relationship between the input voltage and the maximum temperature of EVA. From the figure, it can be seen that with the input voltage increasing, the actuator temperature shows exponential growth, with the actuator temperature rising slowly between 0 V and 1 V and rising faster between 3 V and 4 V. Among them, the growth rate of the group with the metal coating is larger than that of the without metal coating group, and the temperature change curves of the actuators with Ag and Cu coating basically match, and the temperature difference between the group with metal coating and the group without metal coating is the largest at the input voltage of 4 V (deviation of 22,700 K). The metal coating affected the maximum temperature of silicon EVA at different input voltages of .
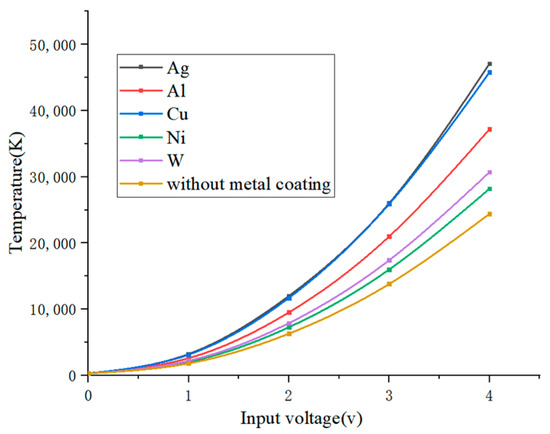
Figure 8.
EVA input voltage–temperature characteristics.
Figure 9 shows the displacement changes of EVA at different positions under different input voltages. It can be found that EVA has a bell-shaped distribution of position and displacement changes in the range of 0~2000 um, and the output displacement of EVA is the largest at the position of 1000 um. In the four voltages (1 V, 2 V, 3 V, and 4 V), the influence of the metal coating on the silicon EVA displacement is , which is basically the same as the metal coating affecting the maximum temperature of silicon EVA. The only difference is that the silicon EVA displacement change with Cu coating is slightly larger than with Ag coating; the reason may be that at the same temperature, Cu has a better expansion effect than Ag.
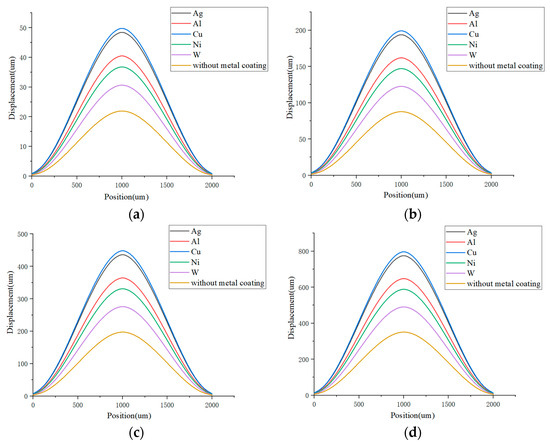
Figure 9.
Characteristics of output displacement at different positions of EVA (a) at a voltage of 1 v, (b) at a voltage of 2 v, (c) at a voltage of 3 v, and (d) at a voltage of 4 v.
The graph of EVA input voltage versus maximum displacement is given in Figure 10. It can be found that the maximum displacement of EVA increases exponentially with the increase in input voltage from 0 to 4 V. At the input voltage of 4 V, the maximum deviation of displacement between the group with metal coating and the without metal coating is 445.5 um (i.e., about twice as much as the without metal coating group). According to this figure, it can also be found that for the same size of output displacement, the input voltage required for the group with the metal coating will be less than that of the group without the metal coating. If the displacement reaches up to 351 um, this corresponds to an input voltage of 2.65 V and 4 V for the group with metal coating and the without metal coating, respectively, saving about 1.35 V (i.e., about 33.75%).
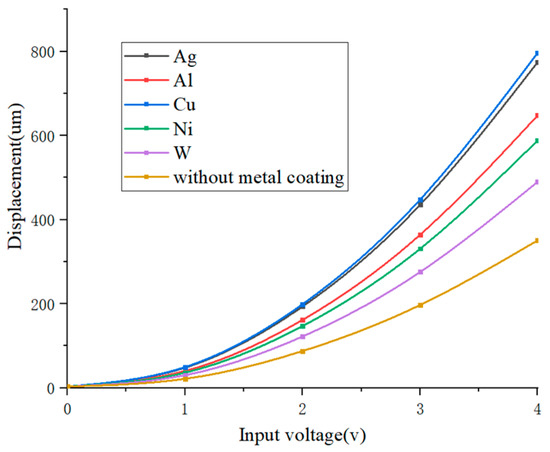
Figure 10.
EVA input voltage–maximum displacement characteristics.
It can be found from the graphical comparison of the calculated and simulated results, as shown in Figure 11, that the deviation of the displacement between the calculated and simulated results increases gradually as the input voltage increases. The comparison between calculated and simulated results for silicon EVA without metal coating, as shown in Figure 11a, shows that the deviation in displacement between calculated and simulated results are small in the voltage range from 0 V to 1 V. Beyond this range, the deviation increases, reaching 30.93 um at a voltage of 4 V (relative error of about 9.85%). In the group with a metal coating, the error between the simulated and simulated results of silicon EVA for Al coating is larger at 37.52 (relative error is about 4.84%) at an input voltage of 4 V, as shown in Figure 11c. The error analysis shows that the deviation of the displacement is within 10% for the silicon EVA in different cases, and it can be seen that the numerical simulation results and the theoretical analysis basically match, which further verifies the correctness of the theoretical derivation.
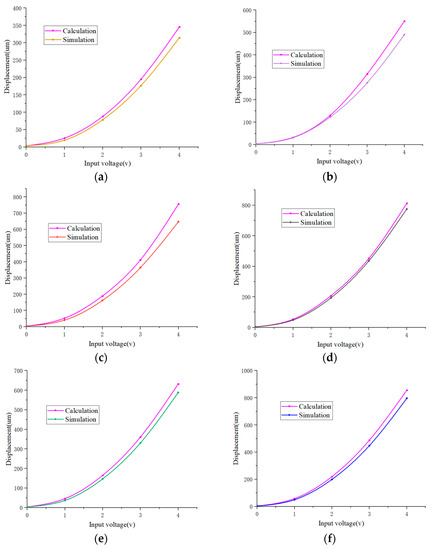
Figure 11.
Comparison of EVA calculation and simulation results: (a) without metal coating; (b) metal Ag coating; (c) metal Al coating; (d) metal Cu coating; (e) metal Ni coating; (f) metal W coating.
4. Conclusions
This study performed calculations and simulations on the displacement of silicon EVA with and without metal coating, comparing different resistivities of the metal coatings. The results demonstrate that silicon EVA with a metal coating can achieve larger displacements, providing approximately twice the displacement of the group without a metal coating at 4 V. In other words, under the same displacement, the silicon EVA with a metal coating requires a lower input voltage compared to the group without a metal coating, resulting in a significant voltage reduction of 33.75%. Moreover, the maximum deviation between the calculated and simulated displacements is within 10%, indicating the validity of the results.
Furthermore, it is also evident that the lower the resistivity of the metal material, the greater the impact on the output displacement of silicon EVA. The metal coating reduces the overall resistance of the system and enhances the conductivity of silicon EVA, thereby influencing the output displacement. Hence, the metal coating not only decreases the resistivity of silicon EVA but also improves the operational quality and efficiency of the actuator (due to lower driving voltage).
This study has investigated the influence of different metal coatings on the driving displacement of silicon EVA. Future work will involve experimental research to validate the theoretical models and simulation results. Additionally, further exploration will be conducted to investigate different coating thicknesses and determine the optimal thickness that maximizes displacement improvement. This will contribute to improving the performance and expanding the application of silicon EVA in MEMS systems.
Author Contributions
Conceptualization, F.D. and S.L.; methodology, S.L.; formal analysis, F.D.; resources, Y.H.; writing—original draft preparation, F.D.; writing—review and editing, S.L.; visualization, S.L.; supervision, Y.H.; project administration, F.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Guangxuan Program Funding Project of Shenyang Ligong University and Liaoning Provincial Department of Education (LJKMZ20220601).
Data Availability Statement
The authors confirm that the data supporting the findings of this survey paper are available within the related research papers cited in this article.
Acknowledgments
This research was supported by the Guangxuan Program Funding Project of Shenyang Ligong University and Liaoning Provincial Department of Education (LJKMZ20220601), the authors would like to express our appreciation to them.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Afrang, S.; Nematkhah, N. A new MEMS based variable capacitor using electrostatic vertical comb drive actuator and auxiliary cantilever beams. Microsyst. Technol. 2019, 25, 3317–3327. [Google Scholar] [CrossRef]
- Gupta, S.; Pahwa, T.; Narwal, R.; Prasad, B.; Kumar, D. Optimiz ing the performance of MEMS electrostatic comb drive actuator with different flexure springs. In Proceedings of the 2012 COMSOL Conference, Bangalore, India, 1–2 November 2012. [Google Scholar]
- Takanami, S.; Kitagawa, W.; Takeshita, T. Design for improvement of torque-thrust characteristic in simultaneous drive in two-degree-of-freedom electromagnetic actuator. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–6. [Google Scholar]
- Moussa, R.; Grossard, M.; Boukallel, M.; Hubert, A.; Chaillet, N. Modeling and control of a piezoelectric microactuator with pro prioceptive sensing capabilities. Measurement 2014, 24, 590–604. [Google Scholar]
- Sarkar, N.; Ellis, M.; Skidmore, G.D. Electrothermal properties and modeling of polysilicon microthermal actuators. J. Microelectromech. Syst. 2003, 12, 513–523. [Google Scholar]
- Maloney, J.M.; Schreiber, D.S.; Devoe, D.L. Large-force electrothermal linear micromotors. J. Micromech. Microeng. 2004, 14, 226–234. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Zhu, Y.; Moldovan, N. Design and operation of a MEMS-based material testing system for nanomechanical characterization. J. Microelectromech. Syst. 2007, 16, 1219–1231. [Google Scholar] [CrossRef]
- Andersen, K.N.; Carlson, K.; Petersen, D.H.; Molhave, K.; Eichhorn, V.; Fatikow, S.; Bøggild, P. Electrothermal microgrippers for pick-and-place operations. Microelectron. Eng. 2008, 85, 1128–1130. [Google Scholar] [CrossRef]
- Hu, T.; Zhao, Y.; Li, X.; Zhao, Y.; Bai, Y. Integration design of MEMS electro-thermal safety-and-arming devices. Microsyst. Technol. 2017, 23, 953–958. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, X.; Chen, X. Design, modeling, and characteriza tion of a MEMS electrothermal microgripper. Microsyst. Technol. 2015, 21, 2307–2314. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, Y.; Liu, X.; Zhang, X. A Comparison model of V- and Z-shaped electrothermal microactuators. In Proceedings of the 2015 IEEE International Conference on Mechatronics and Automation, Beijing, China, 2–5 August 2015. [Google Scholar]
- Shivhare, P.; Uma, G.; Umapathy, M. Design enhancement of a chevron electrothermally actuated microgripper for improved gripping performance. Microsyst. Technol. 2016, 22, 2623–2631. [Google Scholar] [CrossRef]
- Chu, J.K.; Zhang, R.; Chen, Z.P. A novel SU-8 electrothermal microgripper based on the type synthesis of the kinematic chain method and the stiffness matrix method. J. Micromech. Microeng. 2011, 21, 054030. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, Y.; Zhang, X. Experimental Study on the Life and Nonlinear Actuation Behaviors of V-shaped SU-8 Electrothermal Microactuators. In Proceedings of the 2018 IEEE 14th International Conference on Control and Automation (ICCA), Anchorage, AK, USA, 12–15 June 2018; pp. 1052–1057. [Google Scholar]
- Tsai, L.N.; Shen, G.R.; Cheng, Y.T.; Hsu, W. Performance improvement of an electrothermal microactuator fabricated using Ni-diamond nanocomposite. J. Microelectromech. Syst. 2006, 15, 149–158. [Google Scholar] [CrossRef]
- Ochiai, K.; Osada, T.; Muro, H. Study on MEMS Thermal Microactuators with Pedestal-Type Beam Shape and Au Electrocoating. IEE J. Trans. SM 2012, 133, 100–104. [Google Scholar]
- Nguyen, D.T.; Hoang, K.T.; Pham, P.H. Larger displacement of silicon electrothermal V-shaped actuator using surface sputtering process. Microsyst. Technol. 2021, 27, 1985–1991. [Google Scholar] [CrossRef]
- Hussein, H.; Younis, M.I.; Fariborzi, H. Task feasibility of V shape electrothermal actuators. Eng. Res. Exp. 2020, 2, 035035. [Google Scholar] [CrossRef]
- Fan, Q.; Miao, J.; Tian, M. Low-voltage Driven Flexible Double-layer Electrothermal Actuator for Smart Human-machine Interactions. Sens. Actuators Phys. 2020, 315, 112352. [Google Scholar] [CrossRef]
- Zhang, D.; Cai, A.; Zhao, Y.; Hu, T. Macro Modeling of V-Shaped Electro-Thermal MEMS Actuator with Human Error Factor. Micromachines 2021, 12, 622. [Google Scholar] [CrossRef] [PubMed]
- Alcheikh, N.; Ouakad, H.M.; Younis, M.I. Dynamics of V-Shaped Electrothermal MEMS-Based Resonators. J. Microelectromech. Syst. 2020, 29, 1372–1381. [Google Scholar] [CrossRef]
- Zhang, X. Research on New Electrothermal Microdrives. Ph.D. Thesis, Shanghai Jiaotong University, Shanghai, China, 2010. [Google Scholar]
- Liu, H.W. Mechanics of Materials; Machinery Industry Press: Beijing, China, 1993; pp. 56–60. [Google Scholar]
- Kolahdoozan, M.; Rouhani Esfahani, A.; Hassani, M. Experimental and numerical investigation of the arms displacement in a new electrothermal MEMS actuator. J. Adv. Des. Manuf. Technol. 2017, 10, 71–81. [Google Scholar]
- Chen, R.S.; Kung, C.; Lee, G.B. Analysis of the optimal dimension on the electrothermal microactuator. J. Micromech. Microeng. 2002, 12, 291. [Google Scholar] [CrossRef]
- Liu, C. Foundations of MEMS; Prentice Hall: Hoboken, NJ, USA, 2011; Chapter 6; pp. 101–102. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).