Numerical Simulations of the Driving Process of a Wheeled Machine Tire on a Snow-Covered Road

Abstract

Wheeled machines, such as agricultural tractors, snowplows, and wheeled mobile robots, usually work on icy or snow-covered roads. Therefore, it is very important to study the driving and slip resistance of the tires of these machines. In this paper, we investigate the driving behavior of tires on snow-covered terrain by means of numerical simulations. A high-fidelity snow-covered road model is established, and smoothed particle hydrodynamics (SPH) and the finite element method (FEM) are employed to account for the behaviors of the snow layers and the pavement, respectively. We use the node-to-surface algorithm for the contact interactions between the snow and the pavement. The SPH parameters for the snow are calibrated by means of a triaxial compression experiment. A simplified tire model is established as well, using the FEM, and the effectiveness of the model is demonstrated via comparisons with the experimental data in terms of stiffness. Finally, the tire driving performance on the snow-covered road is simulated, and the influence of the tire surface configuration, external load, inflation pressure, and snowpack compression on the tire traction behaviors is systematically investigated.

1. Introduction

Machines such as agricultural tractors [1,2], snowmaking machines, snowplows [3], wheeled mobile robots [4], and even airplanes often travel along snow-covered roads. Thus, in the operating process of such wheeled machinery, operational or driving security is a critical issue. Slippery, snow-covered surfaces are one of the main causes of operational failures. Research indicates that when a wheeled machine spins on snowy ground, the snow tends to stick to the front of the mechanism. Furthermore, traveling on snow-covered ground can reduce the friction coefficient of the tires with respect to the road [5,6] and make them more likely to slide.

The tire is the only part of a wheeled machine that transfers power to the ground. The running of a wheeled machine depends on the quality of the tire tread and the materials that interact with the tire, for example, water, snow, and ice [7,8]. Series researchers have studied the running behavior of tires on snow-covered roads by means of numerical computation. Among the methods employed, the FEM has always been applied in the description of tire mechanics and dynamical response, whereas for snow-covered roads, researchers have two main options including the mesh-based method and the particle-based method. The mesh-based method consists of the Lagrange and Euler method [9], whereas the particle-based method consists of the discrete element method (DEM for short) and smoothed particle hydrodynamics [10]. The following section addresses the application of these methods to snow-covered roads and the simulation of the tire driving performance on snow-covered roads using these methods.

In the Lagrange-based FEM, due to the element nodes in keeping with the materials during the computation process, the simulated error is much higher than that allowed by the method [9]. In the process of tire driving on snow-covered roads, both a rubber tire and non-elastic snow may undergo large deformations; therefore, Lagrange’s method was only used for snow description in previous studies, and very few researchers have adopted it recently. According to Euler’s method, which is usually applied to fluids, there is no movement of the FEM mesh along with the deformation of the material [11]. For the accurate description of large deformations in snow, Euler’s method was adopted to subdivide snow-covered roads. For instance, Seta et al. [12] used a Lagrange mesh and a Euler mesh for tires and snow, respectively, in an FEM model, and correctly forecasted the tire and snow interaction based on the model calculation. Choi et al. [13] employed a Lagrange-based FEM and the finite volume method (abbreviated as FVM) to simulate the interaction between tires and snow, and obtained simulation results that were consistent with the experimental results. However, the rolling resistance was not considered in the model; thus, Lee et al. [14] improved the model by using the Gaussian great likelihood method to determine the mechanical properties of snow in addition to considering the snow depth and friction coefficients to achieve good results.

Due to its merits in handling large, deformed, mobile, and bulky materials, particle-based methods were widely used in numerical calculations for large-scale deformation problems. Recently, they were used instead of the conventional FEM to describe soft materials, including snow and soil. As we know, among the particle-based methods, the DEM is often used to model granular materials [15,16,17,18], while SPH is suitable for simulating the mechanical properties of continuous materials [19,20,21,22]. In the DEM, the internal forces between particles are calculated through linear or nonlinear contact models, such as tied and failed models [17], linear spring models [23,24], and cohesive element models, before the connections between the particles fail. In the case of a failed interaction between the DEs, the relative displacement and the radii of two DE particles can be used to determine the contact force between them. Hence, the calculation of the transformation from tied or cohesive interaction to contact, as well as the failure criterion, for snow grains is an important issue in the description of the mechanical behavior of snow when using the DEM. The Mohr–Coulomb failure criterion is often used to determine the transformation of road surfaces from continuous to granular states [25,26]. For instance, in [16], the authors utilized the DEM to model a multi-component road surface composed of gas, water droplets, and ice particles. Then, they predicted the mechanical response of snow under compression testing. The authors of [17] proposed a novel model in which DEs were interconnected through elastic and damping bonds. The strain between two DEs was then calculated based on their relative displacement, while the stress was approximated via a sawtooth-shaped constitutive relationship. Once the stress reached a cohesive strength, the bonding or cohesive element failed, leading to the release of stress. To account for the contact forces between DEs, a collision model was incorporated into the analysis. Notably, the method involved important parameters, including the temperature, density, and strain rate, and the results demonstrated a high accuracy in describing the mechanical behavior of snow under various strain rates. Independently, the authors of [27] described a novel approach for the simulation of snow. They investigated the formation of snow particles and proposed a discrete element model, along with a calculation model similar to a bonding failure algorithm, to simulate the bonding and separation between DEs. A parallel bond model [28] was subsequently utilized to account for the contact forces between particles. With these tools, the authors were able to accurately model complex, nonlinear, and fluid-like snow surfaces. Similarly, in [15], the authors developed a new model for snow based on an open source. Specifically, they simulated discrete snow particles by randomly distributing elastic–brittle bonds, mimicking a bonding failure algorithm. Consequently, when the stress between particles exceeded the bonding strength, the bonds failed, and loose particles formed subsequently. Moreover, in [29], the authors employed the FEM to model tires and a DEM to model snow. By means of a novel FEM/XDEM coupled algorithm, they were able to calculate the interaction between tires and snow and simulate the tire tracks on a snow-covered road.

SPH is a kind of Lagrange formula without mesh. In the method, the mass is allocated proportionally to the volume, and the density is computed by adding the total number of adjacent particles with weight. Different from the DEM, the interaction among the particles is calculated using the smooth core function and core radius in SPH. This method can accurately model the liquidity and large deformation of continuity medium, making it well-suited to describe the mechanical properties of the snow surface. In [30], based on implicit SPH, a continuous flow model of elastic–plastic was developed to simulate the process of accumulation, deformation, compression, and hardening of snow. Furthermore, the authors built a tire FE model, in which the M-R constitutive equation is used to represent the stress–strain relationship of rubber. In this research [31], the influence of the vertical load, air pressure, traveling velocity, and snow depth on the friction coefficient between the two sides was investigated. In [32,33], a GPU parallel algorithm was developed for the SPH model of snow, which significantly increases the computation efficiency.

Based on the above, we conclude the merits and demerits of these methods, as illustrated in

Table 1. The merits and demerits of snow modeling.

Method		Merits	Demerits
Mesh-based	Lagrange	This method is mature and computationally efficient [34].	The shortcoming of this method is that it cannot be used to describe the large deformation problem, and breaking frequently happens during the computation [10].
	Euler	This approach can be used to model large deformation problems [35].	This method is computationally inefficient [10].
Particle-based	DEM	This method can be used to simulate the mechanical properties of discrete snow and to describe the spray phenomenon [34].	This method is computationally inefficient [34].
	SPH	The SPH method has the advantage of computational accuracy in describing the liquidity and large deformation of snow [10].

.

The SPH method has the advantage of computational accuracy in describing the liquidity and large deformation of the snow compared with the mesh-based FEM, and at the same time, it has the advantage of computational efficiency compared with the same meshless DEM; thus, we adopt the SPH method to model snow particles and use FE to disperse the tires to systematically study the driving performance of tires on snow-covered roads. The structure of this paper is as follows: Section 2 introduces the tire FE model, including the processes of establishing the FE model for the tires, setting the parameters in the model, and verifying the validity of the tire FE model using tire stiffness experiments. In Section 3, we obtain the snow road model using SPH, and then calibrate the corresponding parameters using a three-axis compression experiment. In Section 4, numerical simulations of the tire driving on snow-covered roads are implemented, and the effects of the tire tread type, tire load, tire inflation pressure, and snowpack compression on the tire traction performance are analyzed. In the end, we draw the conclusions in Section 5.

2. FE Model of Tire

The design of a tire determines its mechanical performance. The overall performance of a wheel machine is greatly influenced by tires with varying mechanical properties. As is common knowledge, a precise FE model is crucial for simulating mechanical performance. In this section, we offer a thorough FE model and use experiments with radial and vertical stiffness to confirm its viability.

2.1. Process of Establishing Tire FE Model

The majority of snow tire designs include a radial architecture. A radial tire is one whose tire cords are positioned radially and are securely fastened to the tire with a cushion that is placed around the circumference or close to the periphery. The tread, body, side wall, and other components of the tire make up its intricate construction. In this paper, the tire is represented by a straightforward FE model. The particular modeling method is best explained as follows:

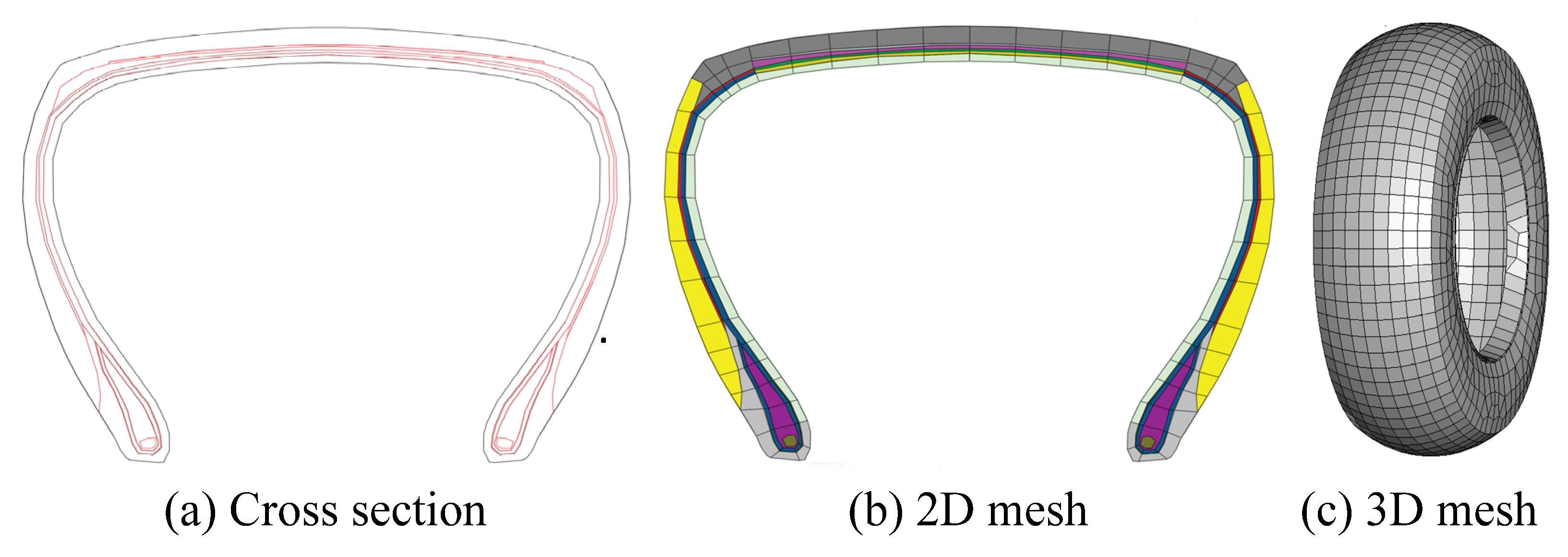
• Draw the tire’s cross-section, leaving out the tread, and then perform geometric cleaning. The tire’s cleaned cross-section is depicted in Figure 1a.
• Divide the FE mesh on the cross-sectional view of the tire in Figure 1a, as shown in Figure 1b in 2D. It is noted that the mesh size has a significant impact on the model’s computing time. A very small grid will increase the computation time and reduce the effectiveness of the computer. Therefore, we must choose a suitable mesh to shorten the computation times and improve the computing efficiency in order to ensure the model’s accuracy.
• On the two-dimensional mesh, we obtain the complete three-dimensional FE mesh model of the smooth tire by rotating it 360° and stitching the corresponding nodes, as shown in Figure 1c.
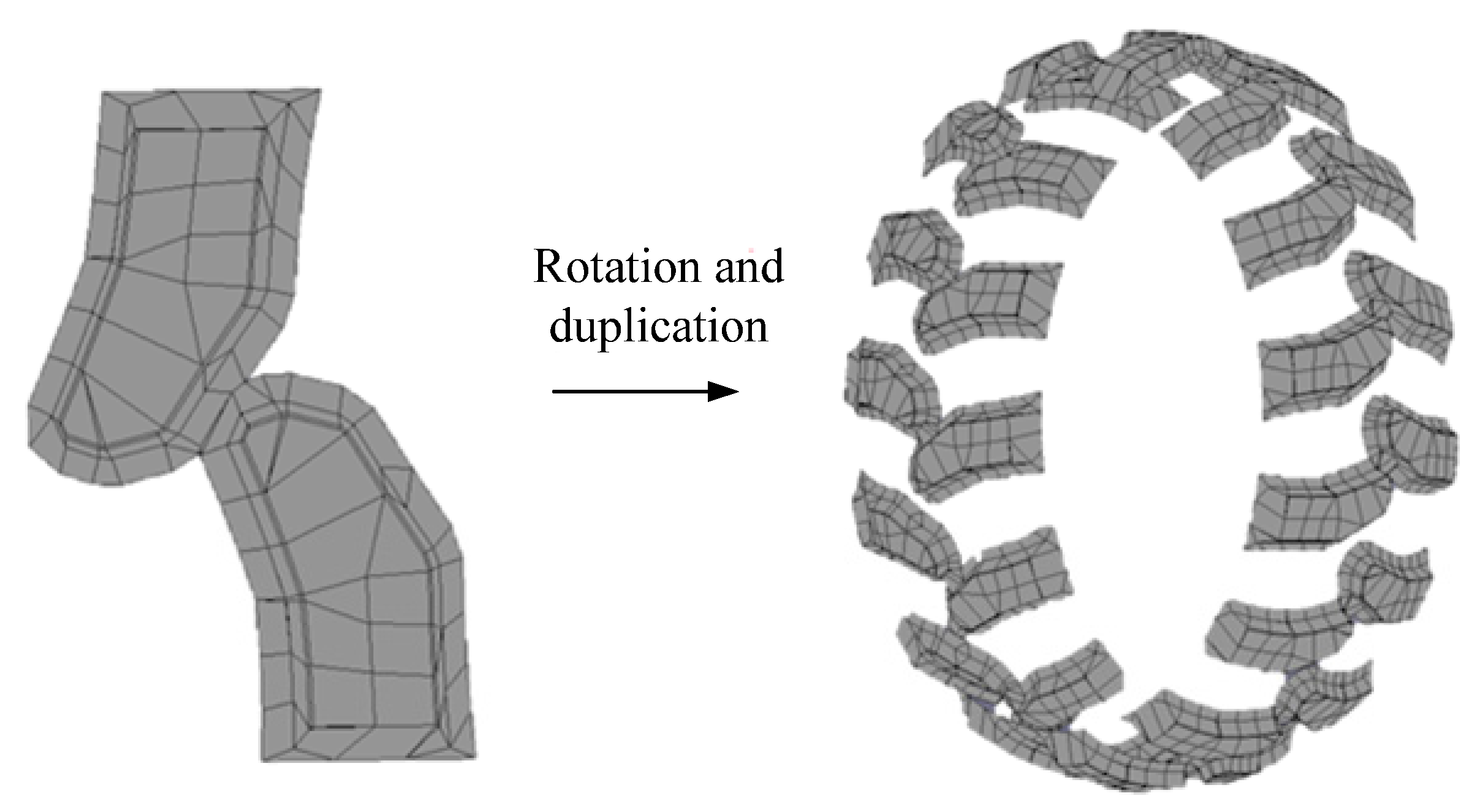
• Due to the periodicity of the pattern, we first establish a geometric model of the tread in a cycle, and then rotate the tread mesh for one revolution to obtain the final finite element mesh model of the tire tread using the rotation function. Figure 2 demonstrates the final FE model of the tire tread.
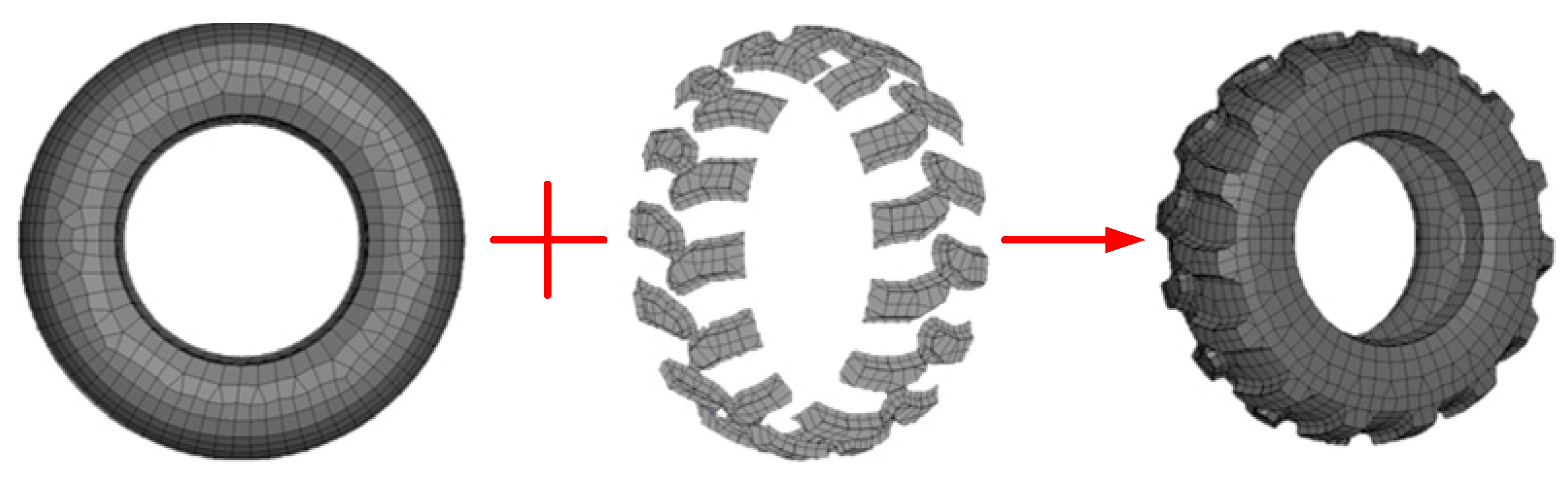
• Once the FE model of the tire body and tire tread are established, both the two components need to be adhered by means of a tied algorithm. Note that the nodes on the external surface of the tire body are set as the master surface, while the faces that match it on the tire tread are the slave surface, and the nodes on the slave surface are slave nodes, naturally. The resulting FE model of the tire is shown in Figure 3.

2.2. Model Parameters

In a radial tire, a high nonlinear rubber is used for the side wall as well as the tread [36]. So, it is very suitable to model the material behavior using the hyperelastic Yeoh constitutive equation. Referring to our previous work in [37], the material parameters of the rubber are set as shown in

Table 2. Material parameters of rubber from [37].

Rubber Material Component	Density, kg∙m3	Yeoh Strain Energy Potential Constants
		C10	C20	C30	Di (i = 1,2,3)
Tread rubber	1.13 × 103	2.37	−9.87	43.66	0
Belt rubber	7.53 × 103	5.65	−35.12	145.76	0
Carcass rubber	3.85 × 103	3.67	−14.73	77.87	0
Inner liner rubber	1.14 × 103	2.13	−14.91	67.67	0
Sidewall rubber	1.08 × 103	2.26	−10.00	45.30	0
Apex rubber	1.15 × 103	2.15	−7.84	33.91	0
Bead filler rubber	1.17 × 103	4.76	−12.97	65.78	0
Bead rubber	1.23 × 103	4.55	−39.05	179.76	0

. In Table 2, C_ij is a material shear property, which indicates the shear properties of the material. It is necessary to obtain these parameters by means of appropriate mechanical experiments. The complex structure composed of the cord layer, belt layer, and bead bundle can be regarded as an anisotropic material based on the matrix of the rubber. Therefore, this part is described using a typical anisotropic material model, also referred to in [37,38], and the specific parameter values of the anisotropic material are shown in

Table 3. Parameters of anisotropic material [37,38].

Parameter, Unit	Belt Layer	Cord Ply Layer	Bead
Density, kg∙m−3	4.99 × 103	1.14 × 103	7.80 × 103
Young’s modulus, MPa
Ea	80,641.06	22,002.34	149,403.06
Eb	57.49	24.27	281.65
Ec	57.49	24.27	281.65
Poisson’s ratio
Vba	2.67 × 10−4	4.49 × 10−4	6.26 × 10−4
Vca	2.67 × 10−4	4.49 × 10−4	6.26 × 10−4
Vcb	0.49	0.49	0.49
Shear modulus, MPa
Gab	13.99	6.01	64.96
Gbc	19.29	8.14	94.51
Gca	13.99	6.01	64.96

.

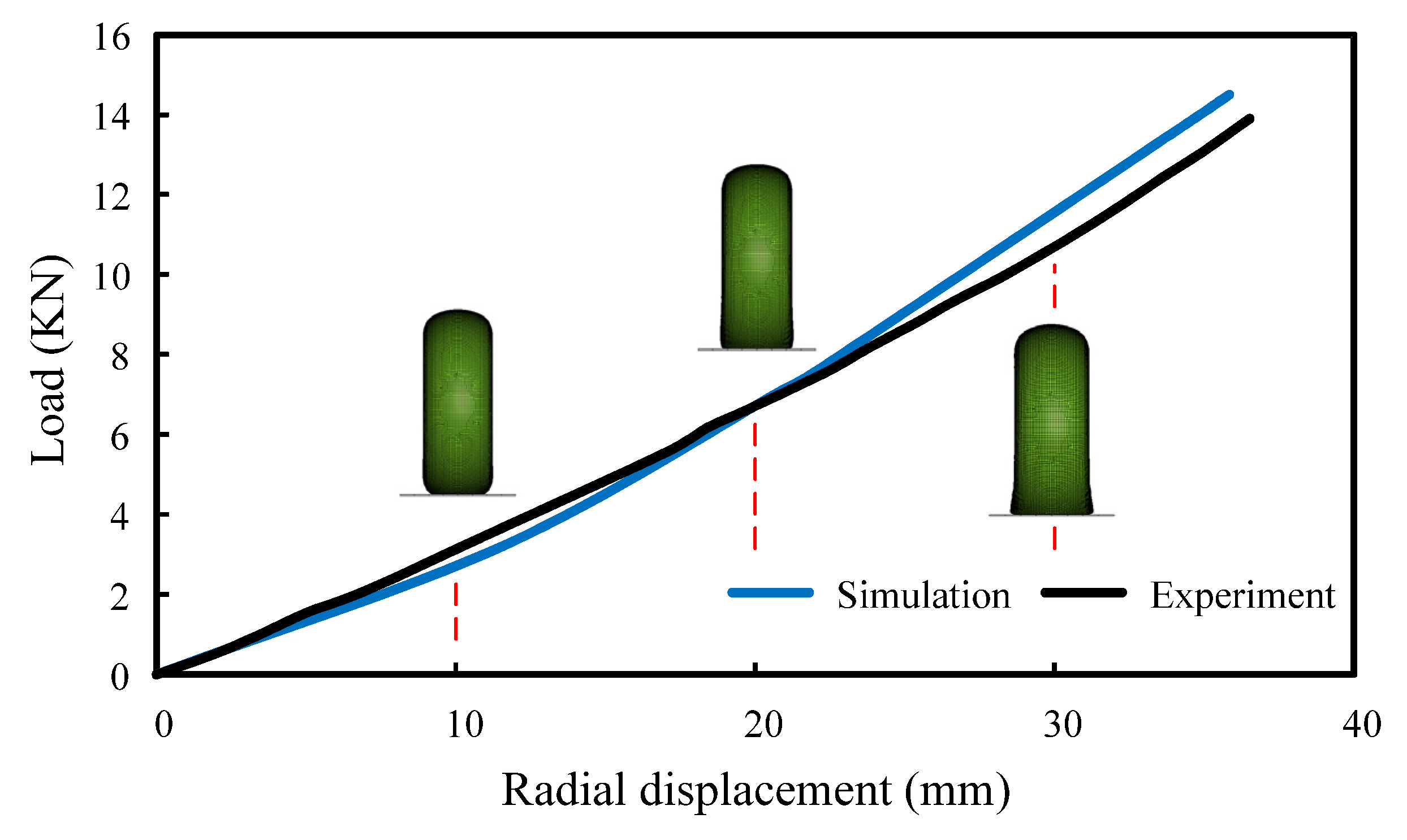
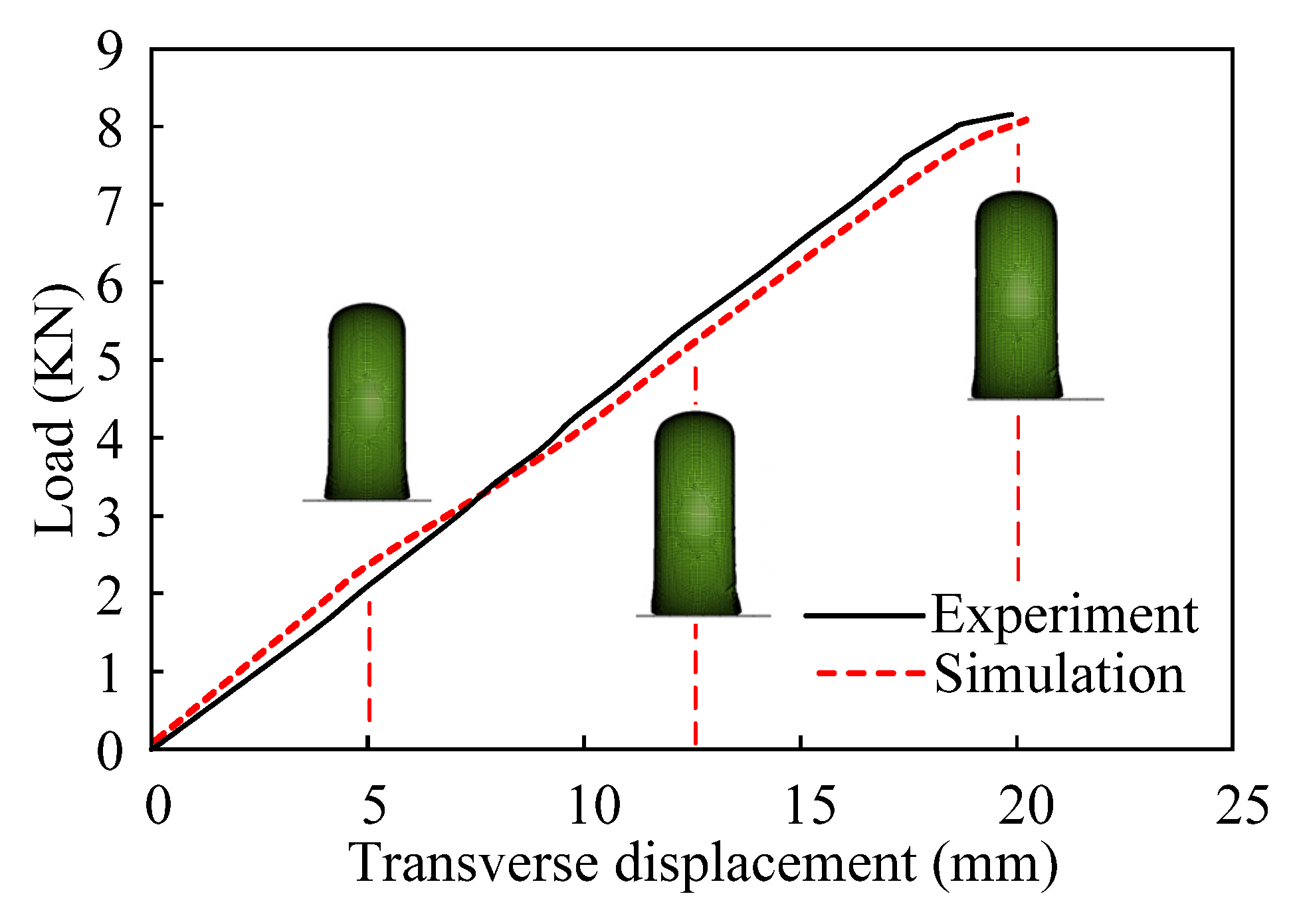
2.3. Verification of Tire FE Model using Stiffness Experiments

In [39], it is indicated that the tire tread size has little influence on the total rigidity, which can be neglected. We take the existing tire rigidity experiments as the simulated object, and model it by using the tire’s FE model established in Section 2.1. Note that, in the experiment, we use a skidding tire obtained from the type 175/65R14 tire by wear. We compare the simulation results with the experimental data to demonstrate its efficiency. The experimental procedure is as follows: the tire pressure remains constant, and the wheel rim is fixed; then, the radial forces of the tire are applied via a vertical upward displacement on the pavement. Likewise, with a constant tire pressure and a fixed six degree of freedom of the wheel rim, the tire is subjected to radial compression by means of a vertical displacement, and then the transverse force is exerted on the tire using an applied axial displacement. The experimental system and the FE model are shown in Figure 4. The road can be reduced to a rigid wall and can be divided by shell elements. The internal side of a tire is applied to a homogeneous surface load, which can be used to simulate the tire pressure. The tire-to-pavement contact is set to a surface-to-surface contact. Figure 5 and Figure 6 show the load displacement curves for the radial and lateral tire rigidity tests, respectively. It is shown from these two figures that the simulated and experimental data are in good agreement with each other in terms of the radial and transverse rigidity, which shows that the FE model can be used as a substitute for the real tire.

3. Model of Snow-Covered Road

A snow-covered road is formed by many scattered snowflakes that are characterized by noncontinuity. By taking into account that when tires roll on snowy ground, they move irregularly when snowflakes are compressed and struck with each other, we adopt the SPH method to simulate dispersed snowflakes, and adopt the FEM for the foundation pavement. The snow-covered road model presented in this article is illustrated in Figure 7.

3.1. SPH Method

The SPH approach is introduced in order to simulate the movement of celestial objects. With scientific advances, SPH can be applied in the description of a continuous structural rupture, rupture, solid lamination, and brittle fracture. Since there are no mesh restrictions, SPH is often used to treat large deformations. The SPH model is composed of several separate particles. Every single SPH particle may be regarded as a ball whose center is the center of the particle and whose radius is r. Apart from the weight, velocity, and stress, the computation procedure also needs to be stored for every SPH particle, including the DOF, center of mass, volume, and so on [40]. The following SPH motion equation satisfies [41]:

$$\frac{D\rho }{Dt}=-\frac{1}{\rho }\frac{\partial v^x}{\partial x^{\alpha }}$$

(1)

$$\frac{D{v}^x}{Dt}=\frac{1}{\rho }\frac{\partial {\sigma }^{\alpha \beta }}{\partial x^{\beta }}+f^{\alpha }$$

(2)

where α and β represent the Cartesian components x, y, and z, respectively. ρ is the material density of the SPH particle, v is the motion velocity, σ^αβ is the total stress tensor of the SPH model, and f^α is the acceleration component caused by external forces. During calculation, the total stress is decomposed into hydrostatic stress and deviatoric stress. In order to enhance the stability of the numerical simulation, it is necessary to add a kind of artificial viscous term into the control equation in order to decrease the nonphysical vibration. The artificial viscosity in the model is between 0 and 0.01 [41]. Furthermore, the interaction of the SPH particles in the neighboring regions is decided by the smoothing length. Using Equation (3), the smallest smoothing length H_min and the maximal smoothing length H_max are obtained. Here, h₀ is the initial smoothing length, and h(t) is the instantaneous smoothing length:

$$H_{min}\times h_0\le CSLH\times h\left(t\right)\le H_{max}\times h_0$$

(3)

The Drucker–Prager criterion was used to determine the damage among the snow particles SPH, i.e.,

$$\stackrel{-}{\sigma }-ptan\beta -p_d=0$$

(4)

$$p=-\frac{{\sigma }_{kk}}{3}=-\frac{{\sigma }_{ij}{\delta }_{ij}}{3}$$

(5)

In Equation (4), p is the hydrostatic stress, β is the friction angle, and p_d is the interparticle force.

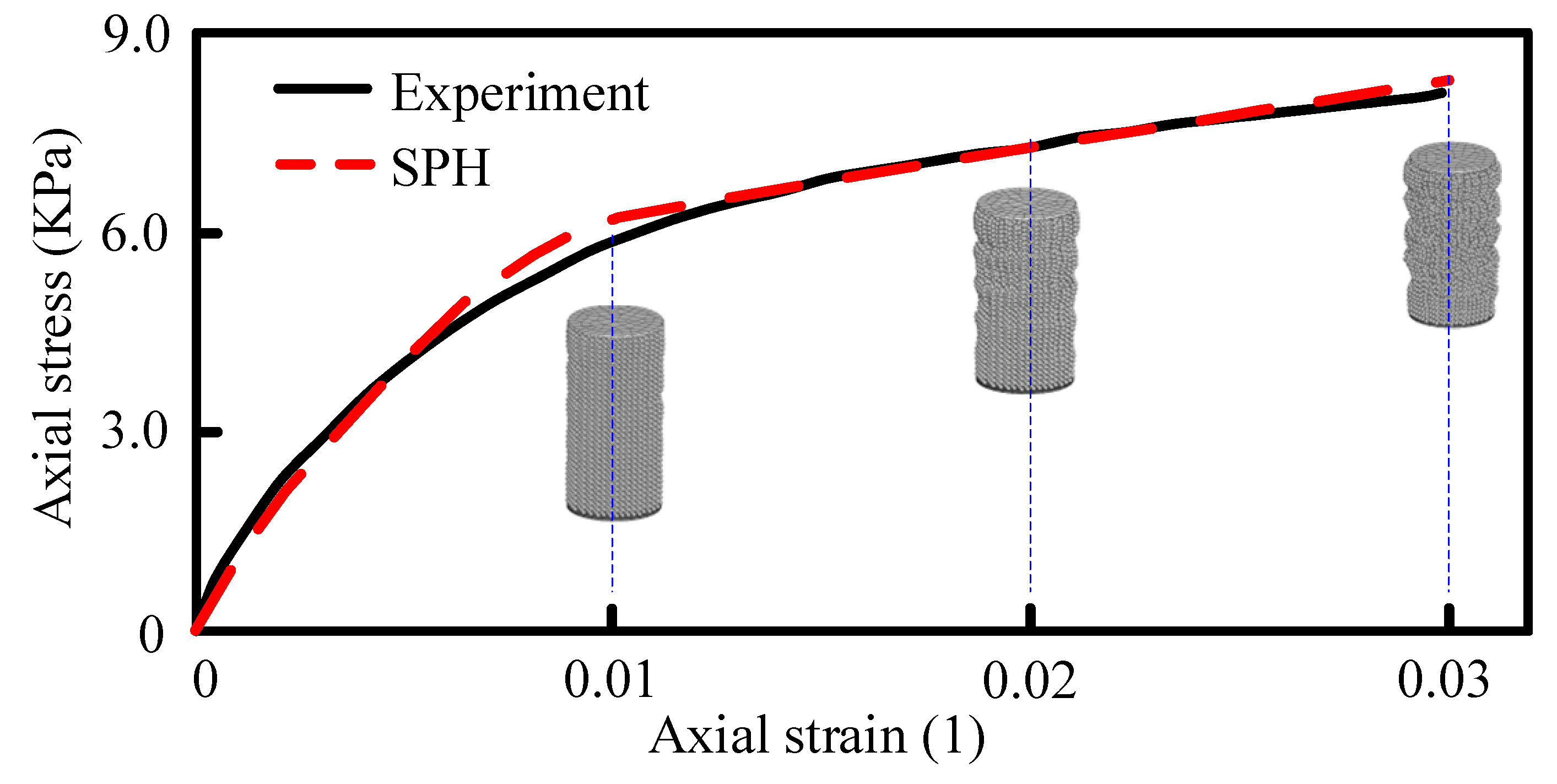
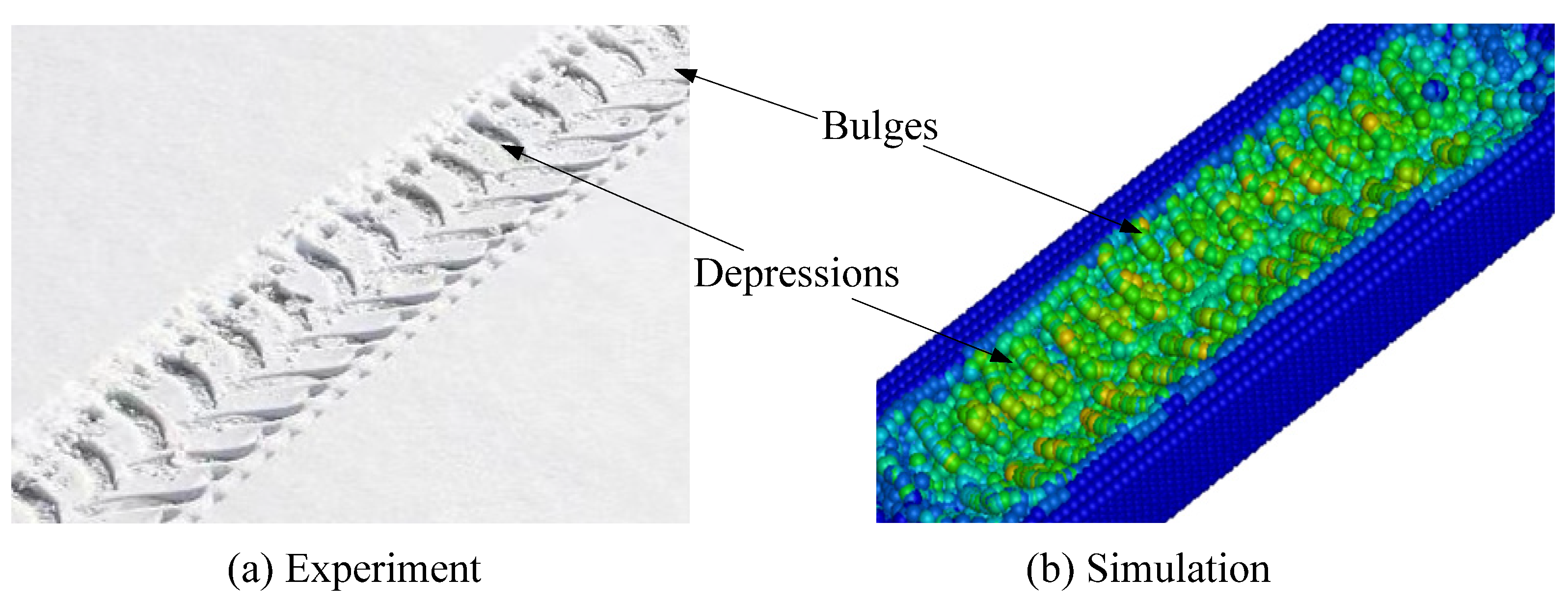
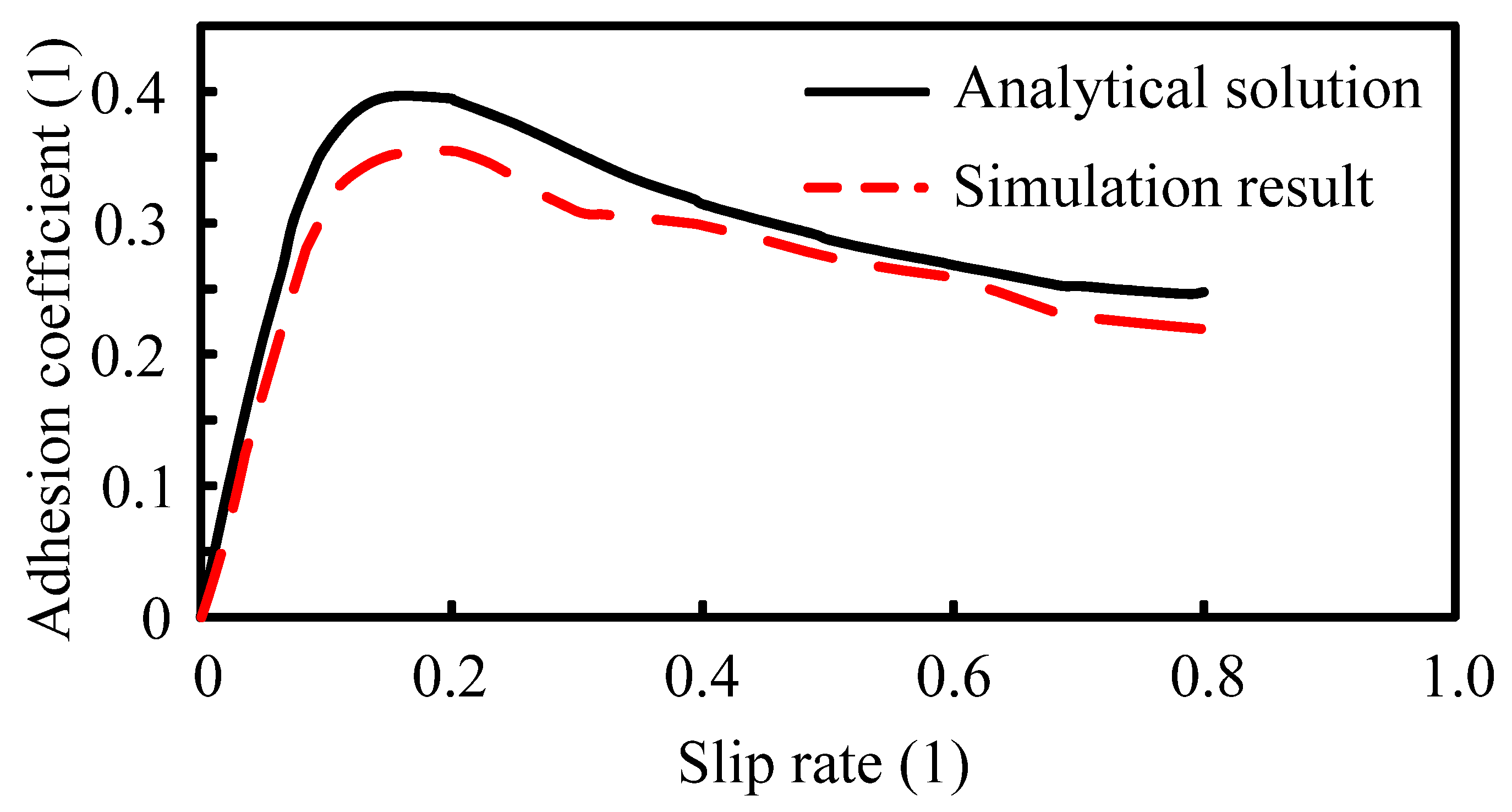
3.2. Parameter Calibration of SPH for Snow

The accurate calibration of the micro parameters of the SPH components is required for a reliable simulation. In our work, a triaxial compressive experiment on compressed snow is used for the calibration of the parameters of SPH for snow. By referring to [42], we developed a numerical model for the simulation of the compressive process in compressed snow samples, as shown in Figure 8. In the model, the SPH particles are employed to represent a cylinder compressed snow sample with a diameter of 29 mm and a height of 126 mm. The upper and lower plates are subdivided by six-node solid elements, and the pressure film around the cylindrical body was discreted by means of shell elements. In this model, the contact forces between the SPH particles and the upper plate, lower plate, and the PVC plastic membrane are calculated using the well-known node-to-surface algorithm [43]. Furthermore, the physical parameters of the model are determined according to

Table 4. Physical parameters for rigid plate and PVC.

Part	Rigid Plate	PVC
Density, g∙mm−3	7.85 × 10−3	1.17 × 10−3
Young’s modulus, Pa	2.1 × 1011
Poisson’s ratio	0.30	0.49

[42].

According to the three-axis compression experiment, the critical parameters of the SPH model are calibrated. Using the parameters calibrated in

Table 5. Micro parameters calibrated for compressed snow.

Parameter	Value
Static friction coefficient (SPH–Road)	0.60
Kinetic friction coefficient (SPH–Road)	0.40
Static friction coefficient (SPH–Tire)	0.30
Kinetic friction coefficient (SPH–Tire)	0.15
Smoothing length	1.20
Scaling factor for smoothing length	0.20

, the axial stress and strain curves of the simulation and experiment are given in Figure 9. From Figure 9, we can find that the simulation results correspond well with the experiment results, which shows that the SPH model is able to describe the exact mechanics properties of the actual compaction.

4. Numerical Simulation of Tire Driving on Snow-Covered Road

In this section, a numerical method is used to investigate the driving behavior of the tires on snow-covered ground. In order to achieve this goal, we construct a calculation model including the tire and the snowy road according to Section 2 and Section 3, and then verify the effectiveness of this model with the help of the theoretical adhesion coefficient–slip curve. Furthermore, in order to obtain some useful information for the tire design, the influence of the tire profile, tire load, tire inflated pressure, and the amount of snowfall on the driving performances are studied.

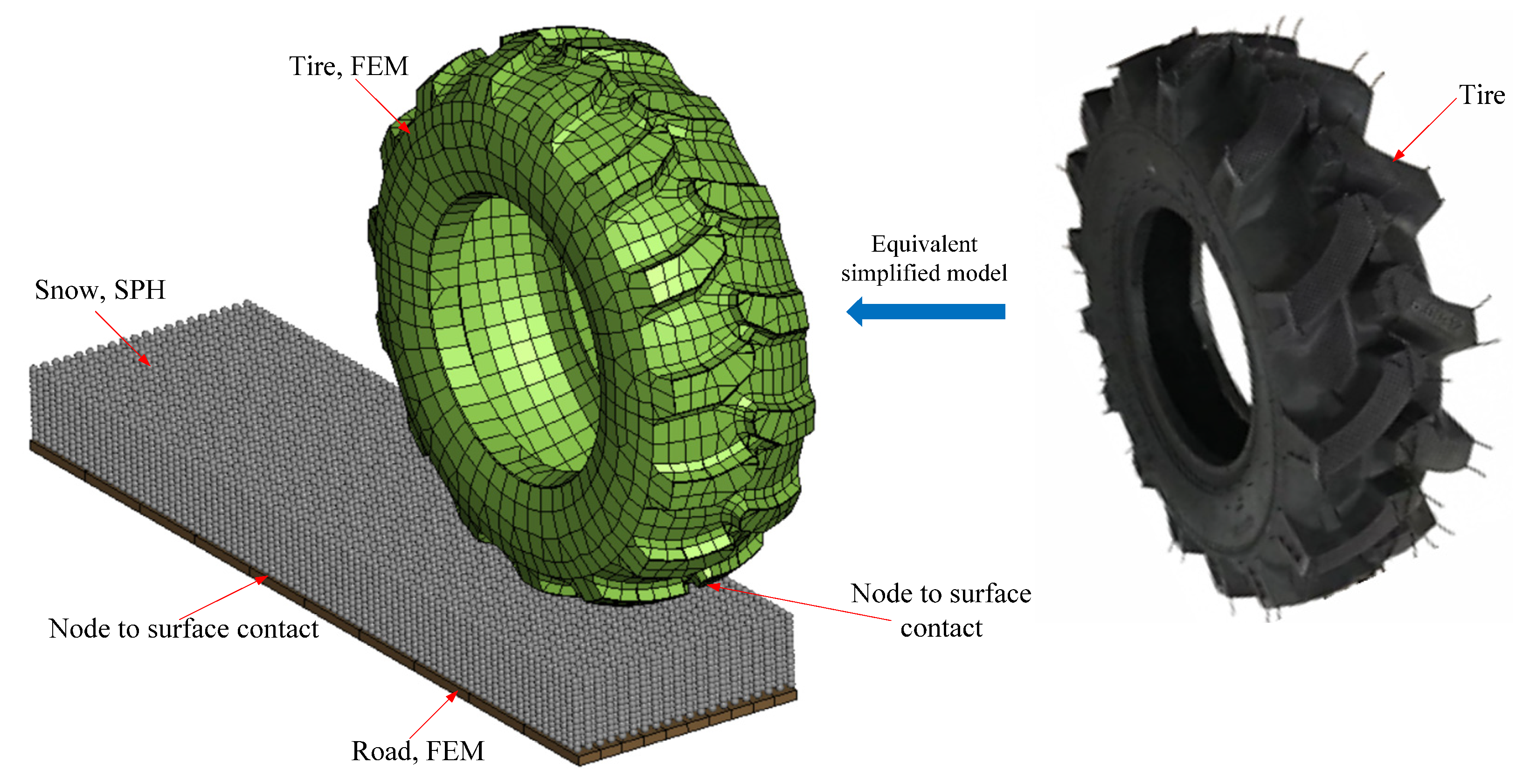
4.1. SPH-FEM Coupled Model

For the purpose of driving the tire on the snow-covered road, we select a model 600-12 radial tire with a width of 150 mm, an outer diameter of 600 mm, and a tooth of 15. The tire is depicted on the right side of Figure 10. The simulation model for driving tires on the snowy road is related to the SPH model and the FEM. Therefore, we call it the SPH-FEM coupled model. We developed a driving model for tires on snowy roads, as depicted in Figure 10. This model is composed of 5727 finite elements and 112,503 SPH particles, and the SPH particles are 0.20 mm in diameter. The contact forces between the tire and snow, the snow and the underlying pavement, and the tire and pavement are calculated using a node-to-surface algorithm, wherein the outer surface of the tire and the surface of the pavement are arranged as master surfaces, and the nodes in the center of the SPH particles are defined as slave nodes. The dynamic and static friction coefficients between the tire and the road are set at 0.5 and 0.8, respectively [43].

In this model, the tire pressure of the model is simulated with the application of a homogeneous surface load. Finally, the tire pressure is maintained at a constant value of 0.25 MPa during the entire simulation. The rigid rim is subjected to a vertical load to simulate the mass of the wheeled mobile machinery. The speed of a tire on a highway is separated into an angle speed and a horizontal speed. The horizontal velocity of the tire is determined to be 8.33 m/s, and the rotational speed of the tire is determined via longitudinal slip S_R. The angular speed is raised to its highest level, and it remains stable throughout the whole process. The gravitational field is applied to all the nodes in the model. Under S_R = 0, the driving process of the tire on the snow-covered road is shown in Figure 11, and the simulation and experimental comparison of the tire’s final trace on the surface of the road are shown in Figure 12.

The course of tire rolling generates crushing and shearing behavior on the snow-covered road, resulting in notable rutting marks on the surfaces where the tire was in contact with the snow. It is observed that when a tire passes by, there is a concave distortion in the surface of the snow particles, and a slight displacement in the surface of the treads. Due to the crushing of the tire body, the snow particles surrounding the tire body have a slight uplift, showing the transformation from continuity to the discreteness of the snow surface during the driving process. Figure 12 shows a comparison between the simulated and experimental tire traces. On the simulation results graph, the displacement of the snow particles relative to the thread bump is negative. The maximum difference in the displacement at the snowy road elevation or depression is less than or approximately equal to the tread height. The result of the simulation coincides with the actual phenomenon, revealing the shifting characteristics of the discreet medium itself during the snow tire driving process. Moreover, the simulation results are highly correlated with the experimental results regarding the driving track mark.

We calculate the tire driving procedure under various slip rates, and the longitudinal adhesion coefficient μ_L is acquired at various slip rates. The simulation result of the μ_L–S_R curve is compared with the theoretical result, which is derived from [44], as shown in Figure 13. As the slip rate reaches 0.2, when the longitudinal adhesion coefficient is at its maximum, the adhesive strength is the greatest, and the braking property is the best. But as the sliding rate goes up, the tire’s shear action on the snow-covered ground becomes weaker, causing the tire’s adhesive coefficient to drop. The simulation adhesion coefficient–slip ratio curve was highly correlated with the theoretical curve, further verifying the correctness of the FEM-SPH model developed in the paper for the tire–snow-covered road. Nevertheless, the longitudinal adhesion coefficient derived from the simulated results is always lower than the theoretical one, because the real snow particles do not have the same dimensions and shapes, and the accumulation of snow particles results in a mutually interlocking effect, which greatly improves the shear resistance of the real snow. On the contrary, the SPH model is made up of uniform ball grains, which cannot completely describe the mechanics characteristics of actual snow particles.

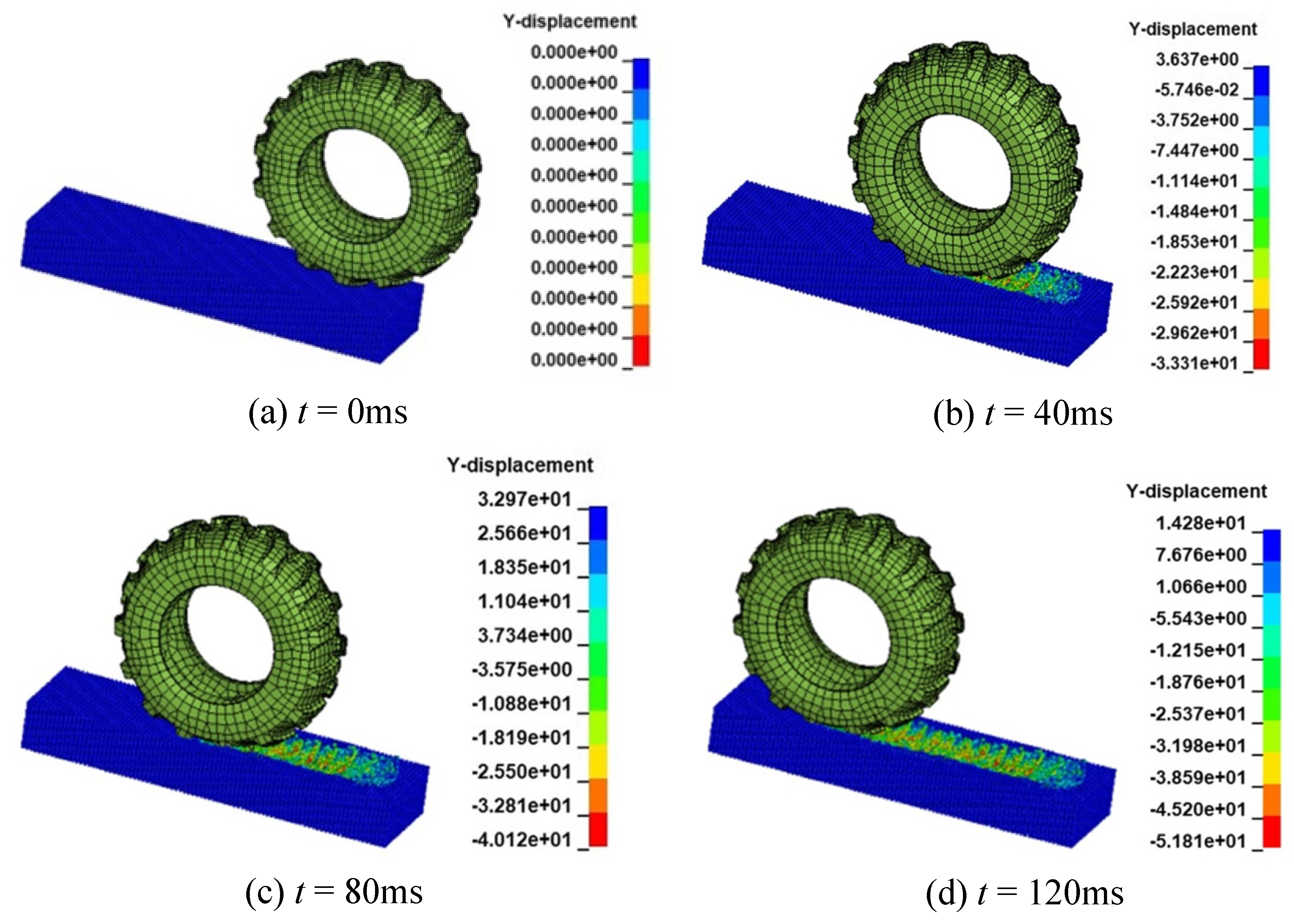
4.2. Numerical Simulation Examples

On the low-adhesion snow-covered road, the tire traction property is one of the most important indexes for evaluating the driving capability. As such, it is very important to study the tire traction performance. In this work, we research the influential factors of tire drag on snow-covered roads, such as the tire profile, tire load, tire inflated pressure, and the amount of snowfall, and so on, so as to give advice on how to drive safely in snow.

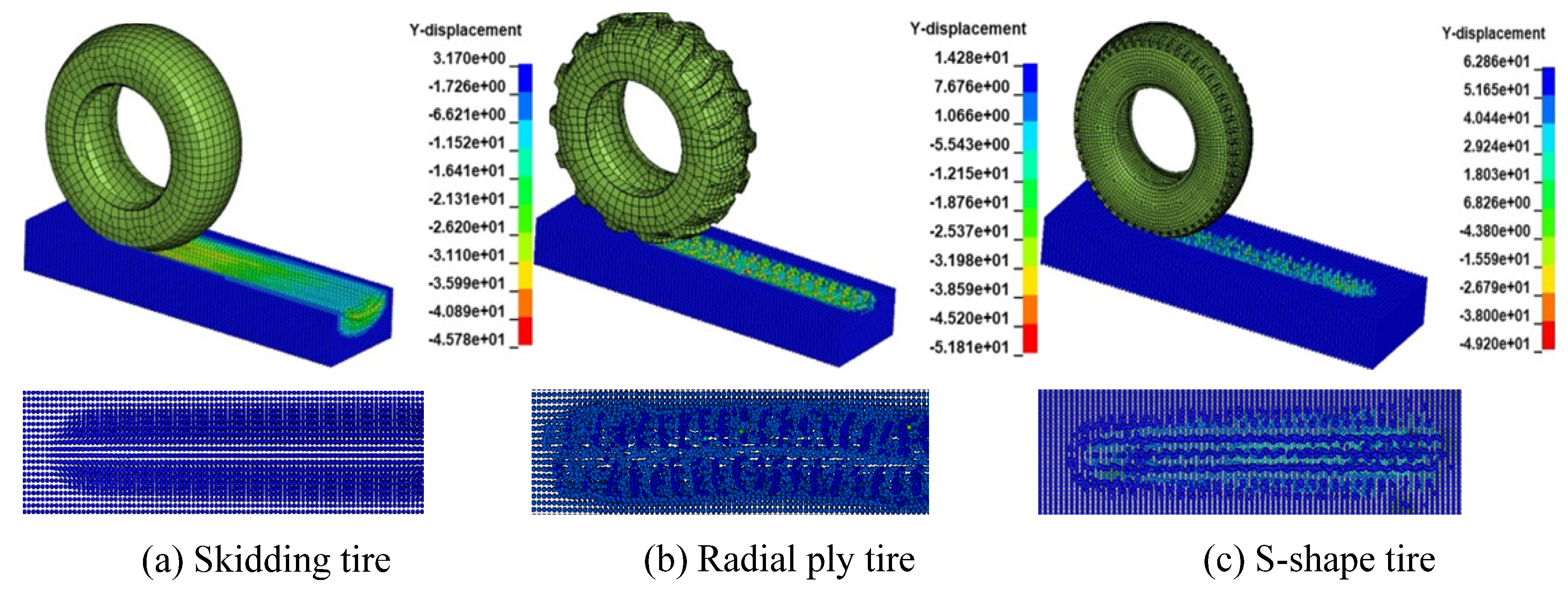
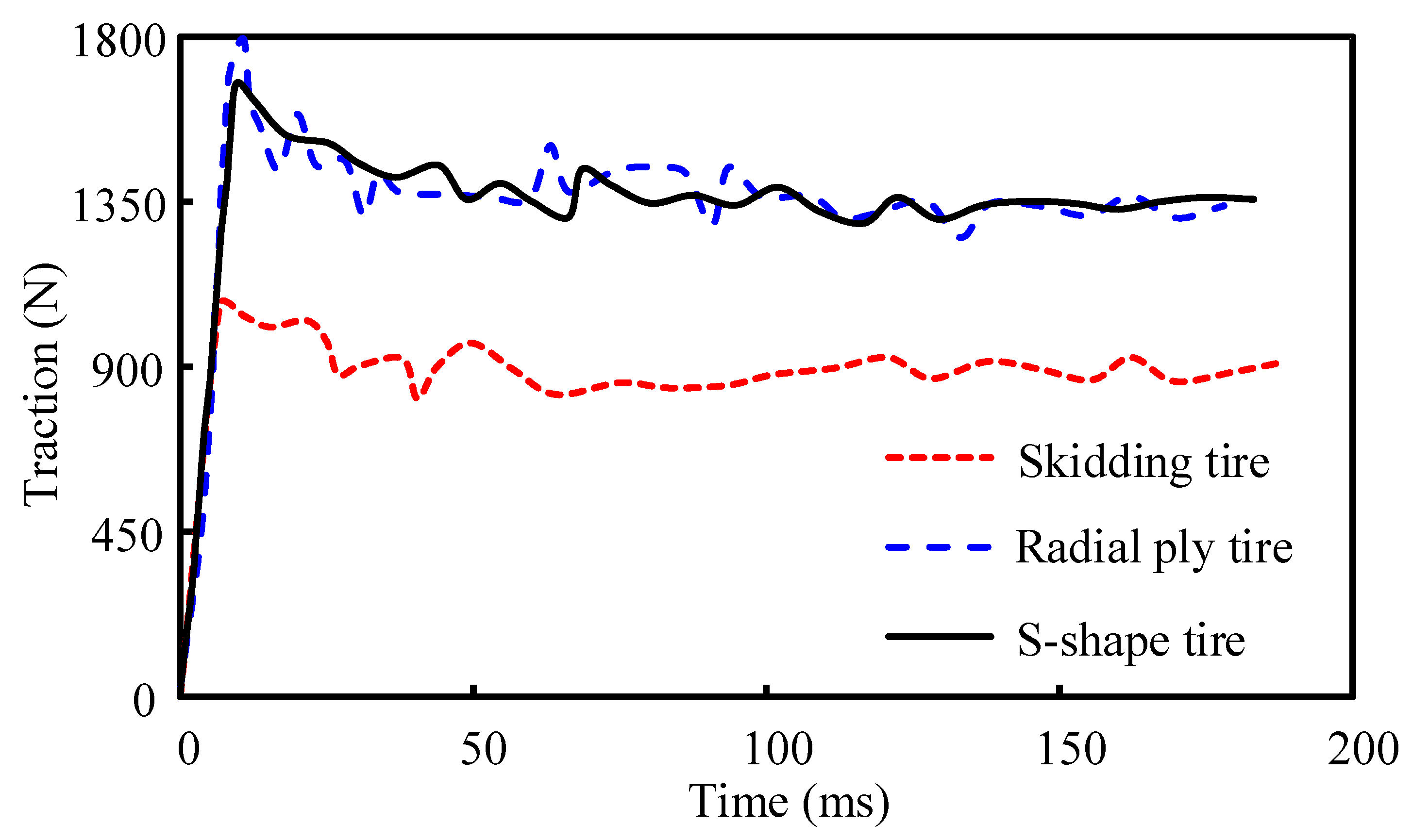
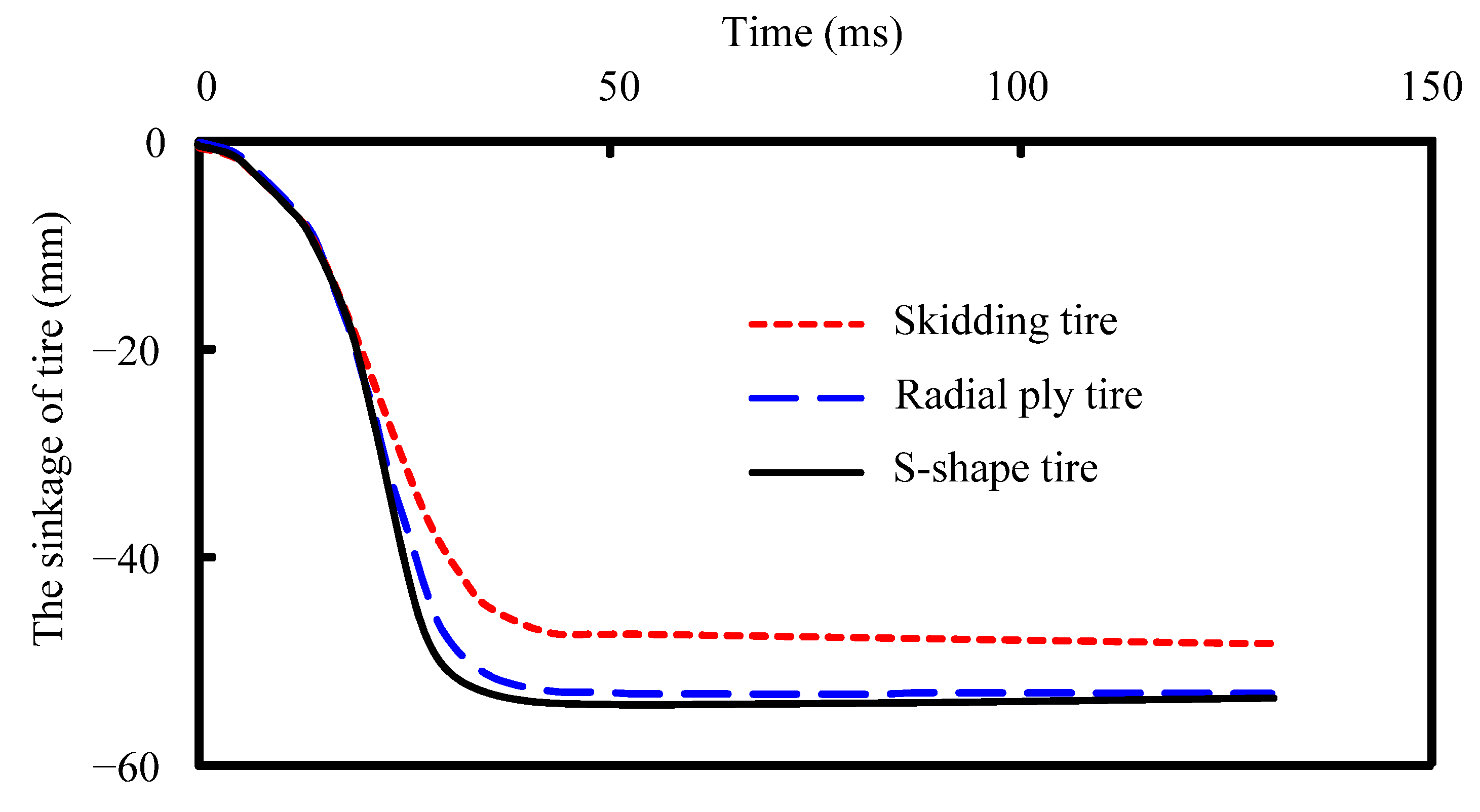
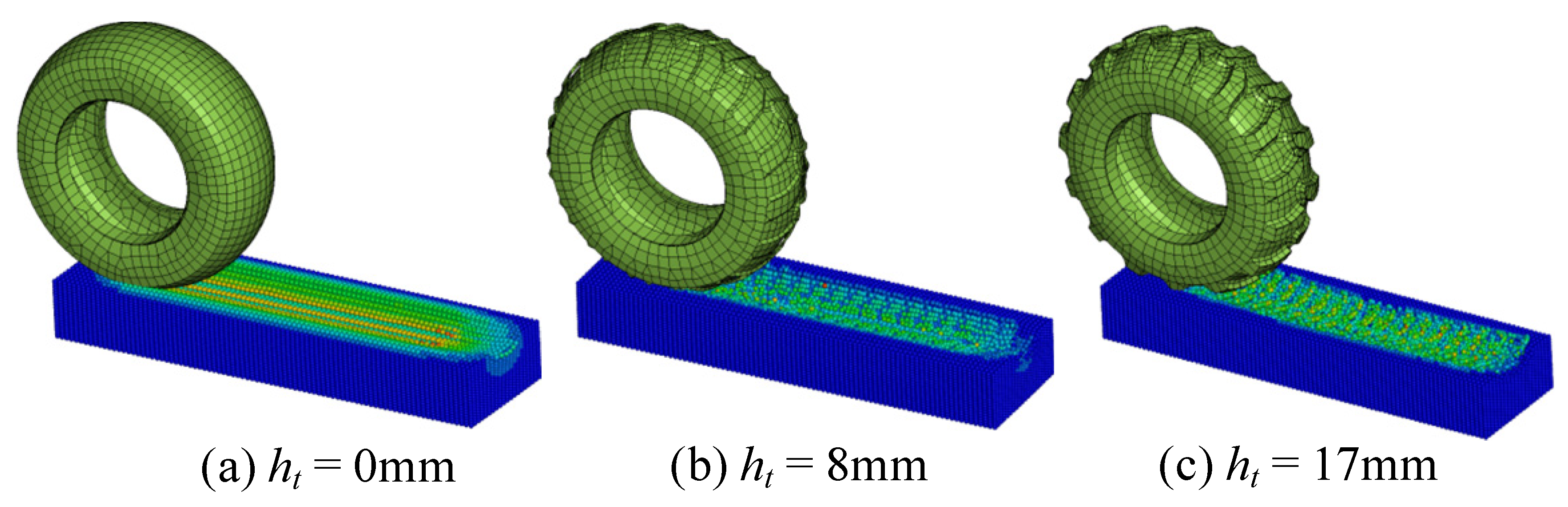
4.2.1. Tire Tread

The tire tread pattern is one of the main factors affecting the tire performance in snow conditions. The groove on the front of the tire can improve the tire’s resistance to the ground grip, which affects the tire’s tractive ability. In this section, we develop three types of tire models, as illustrated in Figure 14. The simulation of the driving behavior of the three types of tires on the snow-covered road is carried out, and the results are obtained for each type of tire. As can be seen from Figure 14, due to the flow characteristics of snow particles, the snowy road is made to be depressed and moves toward the side when the tire goes through, and the snow surrounding the tire rises up due to the pressure of the tire, so that a distinct path is formed. Because of the “chipping” action of the tire on the snow-covered road, the tracks produced by the polished tire are quite shallow, leaving a shallow furrow, whereas the radial ply tire and S-shape tire produce distinct trails resembling their treads.

Figure 15 illustrates the driving traction over time for the three different tire types. From the figure, we can see that the traction force rises rapidly and reaches the highest point when the tire is inserted into the snow and the speed accelerates, regardless of whether the tire has the tread pattern. Since the radial ply tire and the S-shape tire have an apparent angle, the angle generates a greater longitudinal shear force when it comes into contact with the snow, so it has a more significant effect on the driving traction of the tire. Likewise, regardless of the type of tire, when it goes into a smooth-running phase, the traction force essentially becomes steady, with a value fluctuation at about 1360 N for tires with a tread pattern, while the polished tire traction force has a fluctuation at about 907 N; obviously, the traction properties of both tires with a tread pattern are comparable but superior to those of the polished tire. Figure 16 denotes the variation of tire sinkage in the course of driving on the snow-covered road under the condition of polished tires and two types of tires with a tread pattern. From the drawing, we can see that since the beginning of the process is the period of gradual loading, during this period, the tire is embedded into the snow, the amount of tire sinkage is also raised, and when it achieves a certain value, the tire travels at a constant velocity, the sinkage is stabilized, and the curve becomes even. The results indicate that the radial tire is stable around 53 mm, and the polished tire is about 45 mm. Based on the curve, we can find that the sinkage of the patterned tire is much bigger than that of the polished tire. When running, the tires with a tread pattern have a “digging and cutting“ action on the snowy road, so the tire is more likely to be buried by the snow particles, and the sinkage of the radial ply tire and the S-shape tire are comparatively similar to each other.

Apart from the type of the tread, the height of the tread also affects the tensile performance. In fact, for off-road tires, the tread height is usually 17–20 mm. In this paper, we set up three kinds of tread pattern height for the radial ply tire as follows: for the tread pattern height of 0 mm, we call it the polished tire; for the tread pattern height of 8 mm, we call it the half-pattern high tire; and the tread pattern height is 17 mm. We set the same conditions and parameters apart from the tread pattern height of the three tires. Figure 17 and Figure 18 show the driving patterns and traction curves under various tire heights. From these two figures, we find that the tire tread has a large cutting action on the snow particles; the greater the tread pattern height is, the more obvious the rutting marks produced, and therefore, the friction factor is larger, the tire is less likely to slip, and the road is safer. As a result, we suggest that the driver quickly examine the tread of the tires. Once the driver finds out that the tire is old, the tread wear is more serious, and the contour is incomplete, the tire must be changed quickly.

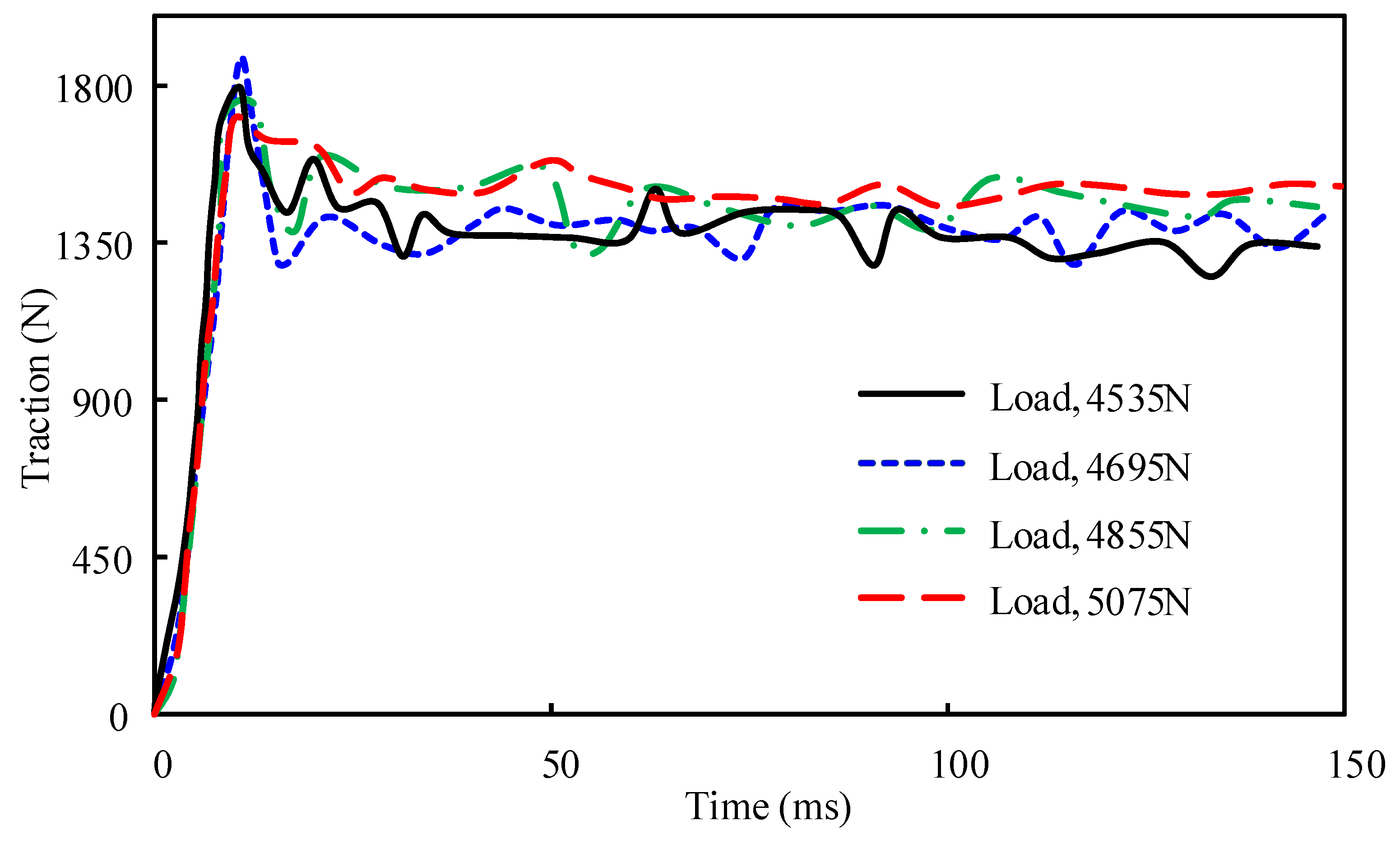
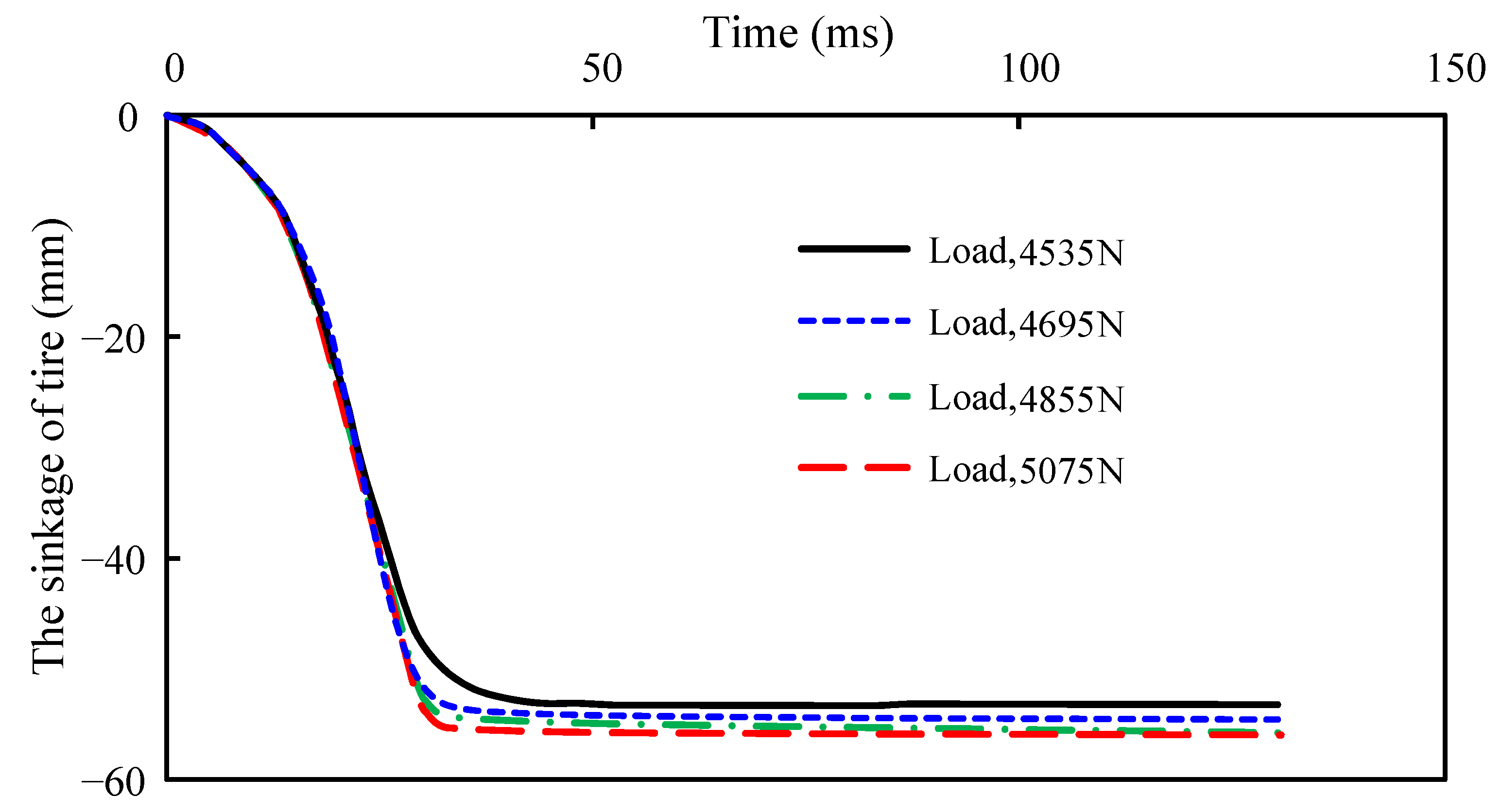
4.2.2. Wheel Load

We study the traction performance of tires with different wheel loads. If a four-wheeler is used as the research object, an unladen weight of 1750 kg and a maximum load of 260 kg are used. Therefore, the wheel load is set at 4535 N, 4695 N, 4855 N, and 5075 N on the snow-covered road. Figure 19 shows the traction curve of the tires driving on snowy roads in different load conditions over time. The mean tractions of these four kinds of loads are 1360 N, 1408 N, 1460 N, and 1480 N, respectively; obviously, their values are not very different, and there is a positive relationship between the traction and the wheel load. Figure 20 illustrates the variation of the rim indentation with the travel time in four types of loads. The results show that the higher the load on the wheel, the greater the indentation and the higher the degree of compaction of the snow. Therefore, it can be seen that when the wheel load rises from 4855 N to 5075 N, the rim drop does not change significantly. Notably, the higher the load on the snow, the more compact the snow will be, and the more difficult it will be for the tire to become embedded into the snow, which will lead to the decrease in the friction coefficient and in the danger of the driving factor.

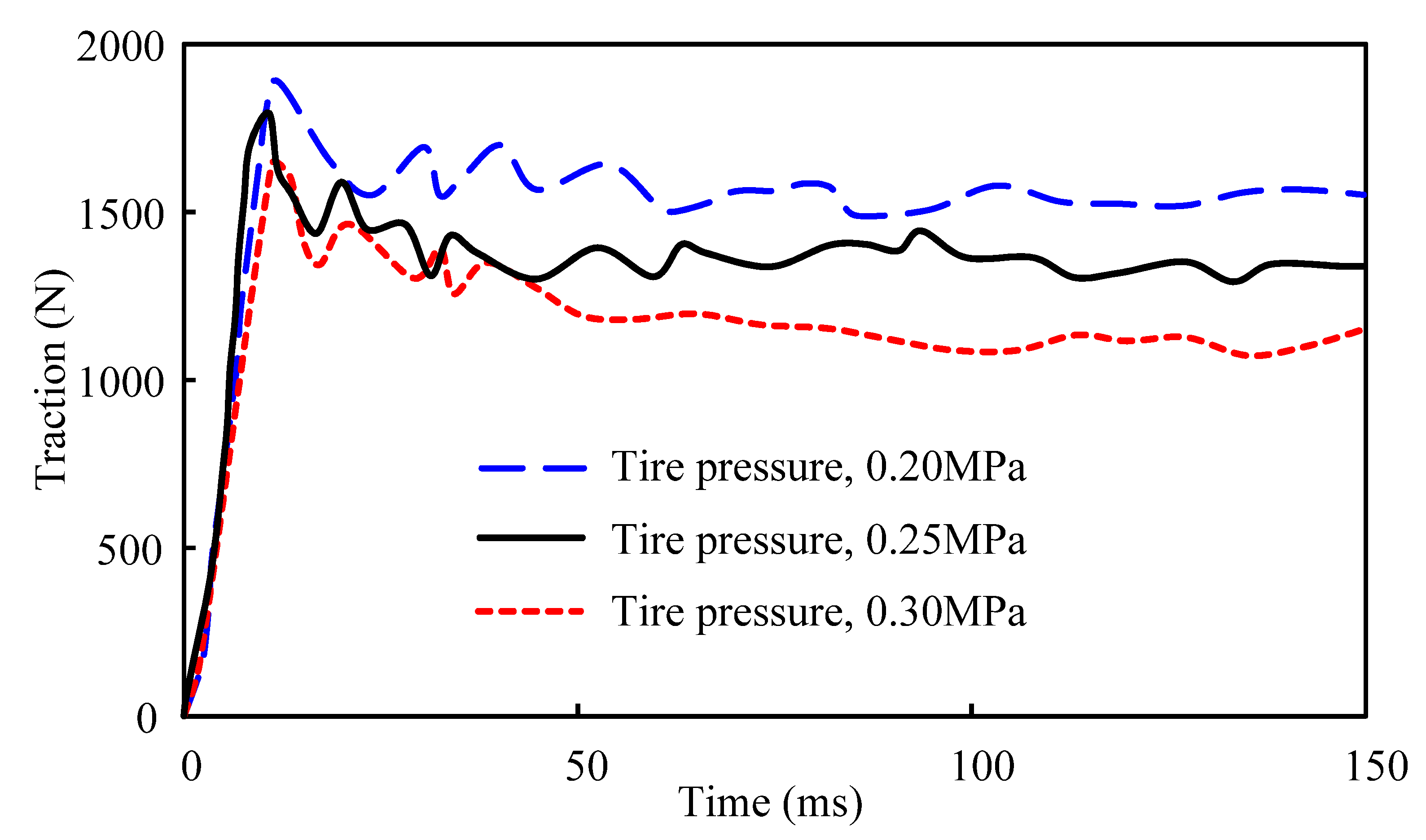
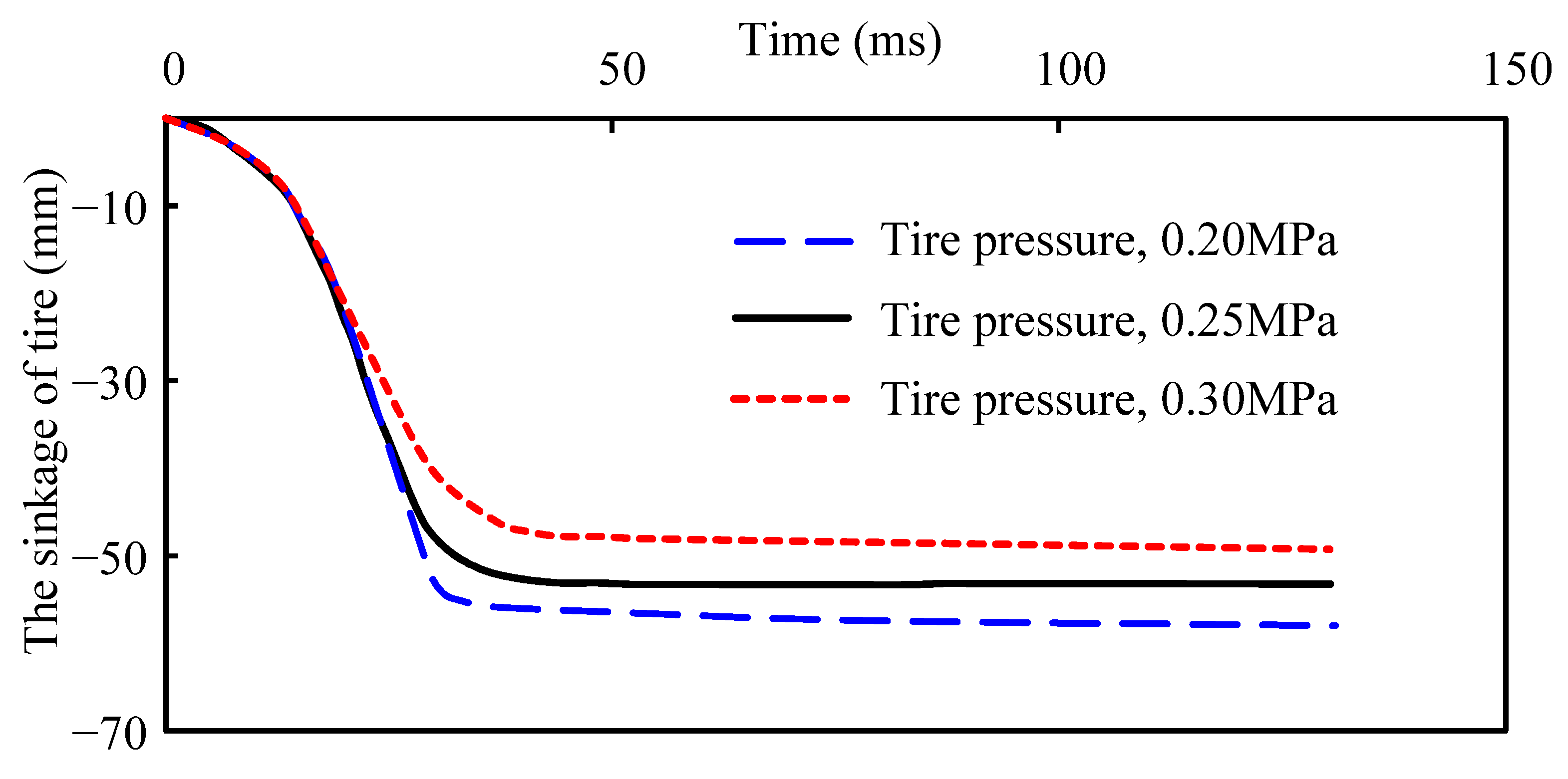
4.2.3. Tire Inflated Pressure

When driving on snowy and icy road in the winter, the friction coefficient between the tire and the road is low, so it is easy to experience a lateral slide. On snow-covered roads, the inflation pressure has a direct influence on the driving performance of the tire [45]. Therefore, it is necessary to improve the adhesion of the tire by means of changing the inflated pressure. The majority of radial car tires in daily life adopt 250 kPa as the standard air pressure. Therefore, we select 0. 20 MPa, 0. 25 MPa, and 0. 30 MPa as the inflated pressure, and then simulate the driving process of a radial ply tire on snow-covered road.

Figure 21 illustrates the change in the traction performance for three types of tire inflation pressure on snowy roads. The results show that the traction decreases with the increase in the inflated pressure. Figure 22 shows the historical tendency of the rim sinkage over time with different inflated pressures. The results show that its value decreases along with the increase in the inflated pressures in the stable driving state of the tire. This is due to the fact that when it drops below the recommended inflation pressures, that is to say, when it has a lower pressure, the tire becomes “fatty” and has more contact area with the snow, which results in a greater adhesion and a greater traction, but also causes more tire wear and oil loss. As the inflated pressure increases, the tire becomes "stiff and high", which translates into less contact with the snowy ground and a lower traction. In conclusion, it is necessary to keep the inflated pressure at an appropriate level so as to ensure that the tire does not get stuck in the snow and does not make the contact area with the snow too small, thereby decreasing the possibility of sideways slipping. An appropriate tire pressure can also provide sufficient horsepower to keep the car running.

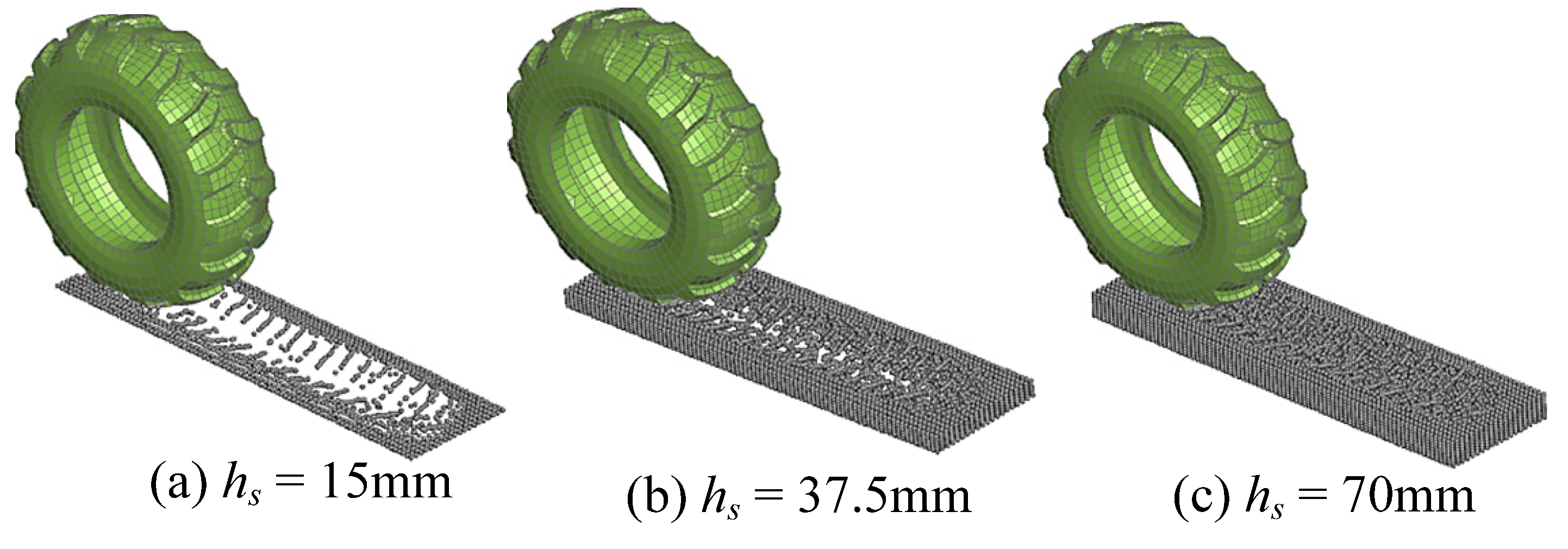
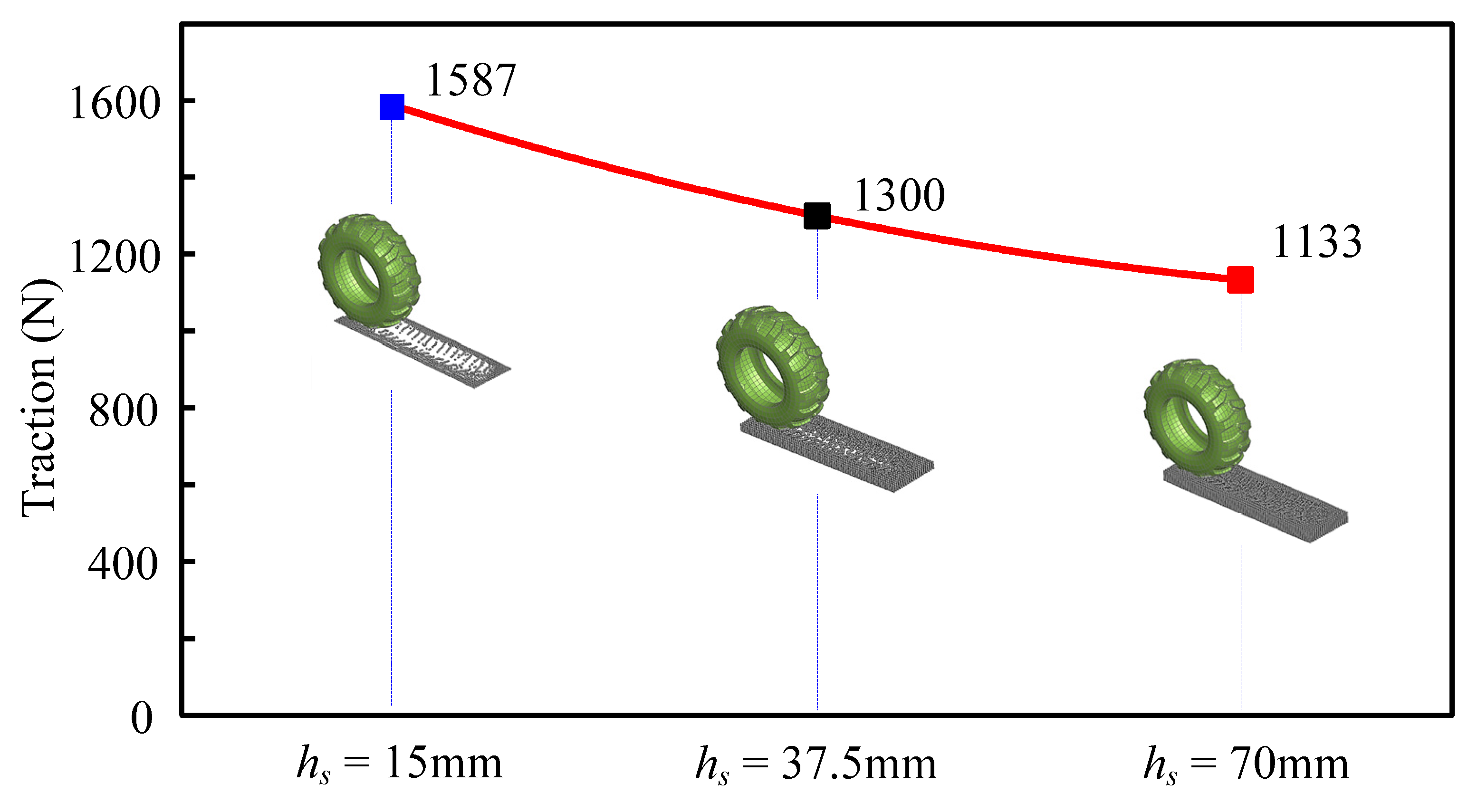
4.2.4. Snowfall

The maneuverability of a mobile mechanism on wheels is influenced by many factors, such as the inflated pressure, wheel load, and type of tread. In addition, the depth of snow cover on the ground is also a very important factor. We investigate the influence of snowfall, which corresponds to the depth of snow, on the tire driving performance. In this work, the FEM-SPH coupled road models were created using three different snow thicknesses of 15 mm, 37.5 mm, and 70 mm. Figure 23 illustrates the driving marks in three different snowfalls, Figure 24 shows the traction property of the tire driving on the road with different snowfalls over time, and Figure 25 is the tendency of the traction performance when traveling on a pavement with varying snowfalls. This research shows that when the pavement has only a comparatively thin layer of snow, the tire is able to make better contact with the ground, which causes a higher friction coefficient and drag force, with an average drag force of 1587 N when running at a constant speed. Conversely, when the snow cover is a little thicker on the pavement, the tire comes into contact with a smaller area of the pavement, and when the snowfall is more than 70 mm, it becomes denser, so there is hardly any contact between the tires and the pavement surface, the friction coefficient and the drag force are lowered, and the mean traction power is only 1133 N.

5. Conclusions

Considering the large deformation and discrete characteristics of snow, we adopted the SPH method to describe snow particles and established an FEM-SPH coupling model to represent the dynamic behavior of tires driving on snow-covered roads. And then, we verified the tire FE model using the radial and transverse stiffness experiments. Finally, the micromechanical parameters of the SPH snow particles were calibrated using a triaxial compression experiment. Based on the above, we performed simulations of the tire traction performance on snowy roads. The major findings are as follows:

• The SPH model provides an accurate description of the fluidity, failure, and discontinuity of snow particles. The established FE model may also reflect the mechanical property of a tire.
• The tire treads model can obviously improve the operating capacity of the tire on the snow-covered road. The deeper the tread, the higher the performance of the tire.
• A positive correlation exists between the traction property and the wheel load. Therefore, a relatively high tire load can improve the tire’s coefficient of friction on the snowy ground, thus improving the tire’s performance on the snowy road.
• A lower inflated pressure will make it easier for the tire to attach to the snow, which will improve the traction of the tire while traveling. Therefore, it is suggested that the inflated pressure should be reduced correctly in order to increase the grip of the tires on the snow-covered road.
• Finally, the depth of snow on the road is a very important driver of road safety. Consequently, when applying anti-lock devices while driving on a snow-covered road, it is possible to effectively increase the coefficient of friction between the tire and the road surface, thereby reducing the risk of operation.