Abstract
In mechanical cutting and machining, self-excited vibration known as “Chatter” often occurs, adversely affecting a product’s quality and tool life. This article proposes a method to identify chatter by applying a machine learning model to classify data, determining whether the machining process is stable or vibrational. Previously, research studies have used detailed surface image data and sound generated during the machining process. To increase the specificity of the research data, we constructed a two-input model that enables the inclusion of both acoustic and visual data into the model. Data for training, testing, and calibration were collected from machining flanges SS400 in the form of thin steel sheets, using electron microscopes for imaging and microphones for sound recording. The study also compares the accuracy of the two-input model with popular models such as a visual geometry group network (VGG16), residual network (Restnet50), dense convolutional network (DenseNet), and Inception network (InceptionNet). The results show that the DenseNet model has the highest accuracy of 98.8%, while the two-input model has a 98% higher accuracy than other models; however, the two-input model is more appreciated due to the generality of the input data of the model. Experimental results show that the recommended model has good results in this work.
1. Introduction
The chatter in turning is the unwanted vibration of the turning tool, lathe, or part being machined. Chatter usually occurs due to causes such as the variable stiffness of the turning system, improper cutting conditions, or unbalanced turning tools. When cutting, there is contact between the workpiece and the tool, causing the cutting force. This cutting force constantly changes, affecting the workpiece, tool, and machine tool system, leading to elastic deformation [1]. This deformation generates self-excited vibration, also known as chatter, which leads to negative consequences, including unsatisfactory surface quality, reduced tool life, and even tool breakage. To control this vibration phenomenon, the use of a stability graph as an analysis method has been proposed. The stability graph includes parameters relating to spindle speed (workpiece speed) and depth of cut [2]. During the machining process, the engineer must determine the technical parameters related to cutting speed and depth of cut within a stable range. Urbikain et al. have documented significant endeavors in the scientific literature aimed at forecasting stability and minimizing chatter, particularly in relation to turning systems [3]. However, this method is limited by an assumption regarding the dependence of the chatter on the cutting speed and depth of cut and not on other factors. This graph cannot wholly model the complexity of the process.
Currently, with high demand for product quality and low cost, it is no longer appropriate to choose the cutting mode so that the machining process is completed in a stable area. Therefore, methods for the detection and removal of chatter are constantly being researched and developed. There are many different methods to eliminate chatter, such as changing the spindle, changing the hardness of the tool holder, or changing the damping parameter to avoid the vibrational area. Methods can be divided into two groups: active methods and passive methods. Dynamic Vibration Control, or active vibration damping, is a technical method used to reduce or eliminate the effects of vibration [3]. The working principle of active vibration damping is based on using sensing, control, and counter-force devices to minimize the impact of vibration [4,5,6]. Passive Vibration Control is a vibration reduction method that actively uses passive devices and materials to absorb and disperse vibrational energy. Unlike active vibration reduction, passive vibration reduction does not need sensors, controls, and dynamic opposing force-generating devices [7,8,9,10].
When comparing two groups of methods, each method has its own respective advantages and disadvantages; therefore, depending on each specific case, technology engineers can choose the method that is more appropriate. Regardless of the method used, detecting the occurrence of chatter is essential to introduce external influences to avoid chatter or to stop the machining process to minimize the number of defective products. As the workpiece hardness parameters change due to the non-uniformity of the material, tool wear and the influence of random factors in the technology system can appear irregularly, resulting in chatter appearing irregularly at any time. In addition, in industrial production, workers’ direct intervention and supervision in the machining process is increasingly limited. The reason for this is that labor costs increase production costs. Therefore, the design and manufacture of an automatic and accurate chatter detection system to limit the number of defective products due to the timely automatic detection of the system is desirable. Therefore, chatter detection is always improved and increasingly explored by researchers and manufacturers. Moreover, it is very important to recognize, minimize, and eliminate vibration because it directly affects the manufactured product’s surface quality and dimensional accuracy. The chatter detection process can be divided into four stages. The first stage is to collect experimental data from sensors such as dynamometers, accelerometers, and microphones. The second stage involves signal processing using theoretical methods such as time, frequency, and time–frequency domains. The third stage is to compute and select different features representing the cutting state. The final step is to make a decision based on either the threshold method or the intelligent recognition algorithm. When classifying according to the data collected in the machining process, several research works are relevant and therefore discussed below.
Chatter detection relies on sensor signals such as force sensors, position sensors, and accelerometers to detect vibrations. Many methods have been proposed to determine the existence of the chatter state in the collected signal [11]. G. Urbikain et al. created a monitoring instrument using Labview code. This tool, constructed from the integration of reconfigurable Input/Output (I/O) structures and Field Programmable Gate Arrays (FPGAs), was implemented in practical sessions on the machine [12]. Wu et al. [13] used analytical methods such as the phase plane method, Poincaré method, spectral analysis, and a Lyapunov index. Dong et al. [14] used sophisticated displacement measurements to detect chatter states based on the nonlinear characteristics of the vibration signal during milling. Yamato et al. [15] used mechanical energy and power factors based on noise observation theory to detect vibration. These methods do not require frequency domain analysis, minimizing the algorithm’s complexity. Based on the Hilbert–Huang transform theory, the vibration signal is decomposed into a series of intrinsic mode functions. The Hilbert spectral analysis method was introduced to identify vibration by analyzing the mode function’s time and frequency domain spectrum [16]. A vibration recognition technique using wavelet transform and machine learning has been proposed. Moreover, studies have used the standard deviation of the wavelet transform and wavelet wave packet energy to generate two-dimensional feature vectors for vibration detection. Then, a pattern classification method using a support vector machine (SVM) was designed based on these feature vectors [17]. In shear force signal processing, an improved moving average algorithm based on local mean decay (LMD) resolves nonlinear forces and enhances vibration detection.
Acoustic signal-based chatter detection involves using acoustic data to monitor and analyze the occurrence of chatter in mechanical machining processes. Vibration detection based on acoustic signals involves the observation of a temporary decrease in the radiated spectral power of the acoustic signals when the shear state transitions from a steady state to a vibrational state [18]. In addition, there is a positive hysteresis feedback relationship between the signals of the acoustic field and vibration [19]. Cao et al. [20] performed a time–frequency analysis on the signals of the acoustic field, which were recorded using microphones for vibration detection. Sallese et al. [21] studied the linearity of the signals of the acoustic field and analyzed the machine vibration and the emitted audio signal to develop a set of features for vibration detection during machining. Features extracted from different process signals have been analyzed to classify and distinguish between vibration and non-vibration.
One approach to determine chatter in the machining process is to rely on visual signals. Chatter detection using visual data requires a different approach than sound-based methods. This method requires specialized equipment, such as a high-resolution camera or machine vision system, to capture images of the machined surface. To obtain a clear and accurate image, the camera must be positioned correctly, focused, and calibrated. The distinction among studies within this group of methods often lies in the feature extraction stage that is derived from the chatter’s feature image. This can be proceeded using various image processing techniques, such as edge detection, texture analysis, or statistical measurements. In recent years, deep learning algorithms such as convolutional neural networks (CNNs) have been used to learn and extract related features automatically. Chaudhary and other researchers have used convolutional neural networks to investigate difficulties surrounding image motions. Nevertheless, they have not considered the impact of weights and hyperparameters on classification performance [22,23]. D. Checa and G. Urbikain have suggested a novel approach that integrates experimental trials, machine-learning modeling, and virtual reality visualization to surpass these restrictions. Initially, tools possessing distinct geometric aspects were evaluated. Following that, the experimental data were processed using various machine-learning methodologies such as regression trees, multilayer perceptrons, bagging, and random forest ensembles [24]. Liu et al. proposed a k-means clustering method to initialize any experienced consequences, which improved the accuracy of the recognition and accelerated the convergence during training [25]. Another alternative for weight initialization is to minimize the classification error by applying a genetic algorithm; however, it may be stuck at a local optimal point and require improvements relating to the convergence. An automatic method of hyperparameter selection has been developed, based on high-performance computation and spatial statistics techniques, to accelerate model selection. Bayesian optimization has also been applied to automatically determine the best hyperparameter configuration for deep convolutional neural networks [26]; moreover, probabilistic models have been used to estimate the test error function. Although the existing optimization algorithms have different characteristics in terms of complexity, optimal efficiency, exploratory power, and evaluation cost, the hyperparameter optimization still requires further study.
Most of the abovementioned studies have applied either visual, acoustic, or force and acceleration data to identify vibration and stability phenomena in turning processes. These data are usually collected separately in the laboratory or through a production process. However, these data are often local to each machining case. The recognition and classification model will not be accurate for other data sets. The problem is that a chatter recognition model is needed based on different data sets: images, sounds, forces, accelerations, etc., are simultaneously fed into the same model. To overcome these limitations, this research study proposes the use of a multi-input model to classify data. The main focus of this research is to recognize chatter from image and audio signals in order to diversify the input data and develop a more generalized chatter detection model compared to single-data models. This means that, to determine whether a machining process is experiencing chatter, the model needs to both “listen” to the sound of the process and incorporate the ability to “observe” the surface quality of the product. This study does not use two sets of input data, namely image and audio, simultaneously during the machining process. Instead, it synchronizes the data after separately collecting them. The model, which collects multiple input data simultaneously, can also be applied similarly in further analyses by the author when high-speed image capturing devices are available. To compare the advantages of the two-input model, the author compared the results with those obtained using currently popular models such as VGG16, RestNet, DenseNet, and InceptionNet. Input data included image, a sound–image combination, and sound. By combining visual and acoustic data, the author used a method that stitches together the surface of the workpiece and the sound frequency spectrum to enable the image to obtain more features related to the vibration phenomenon during the turning process, allowing the detection model to produce more comprehensive and accurate results.
2. Material and Method
2.1. Material
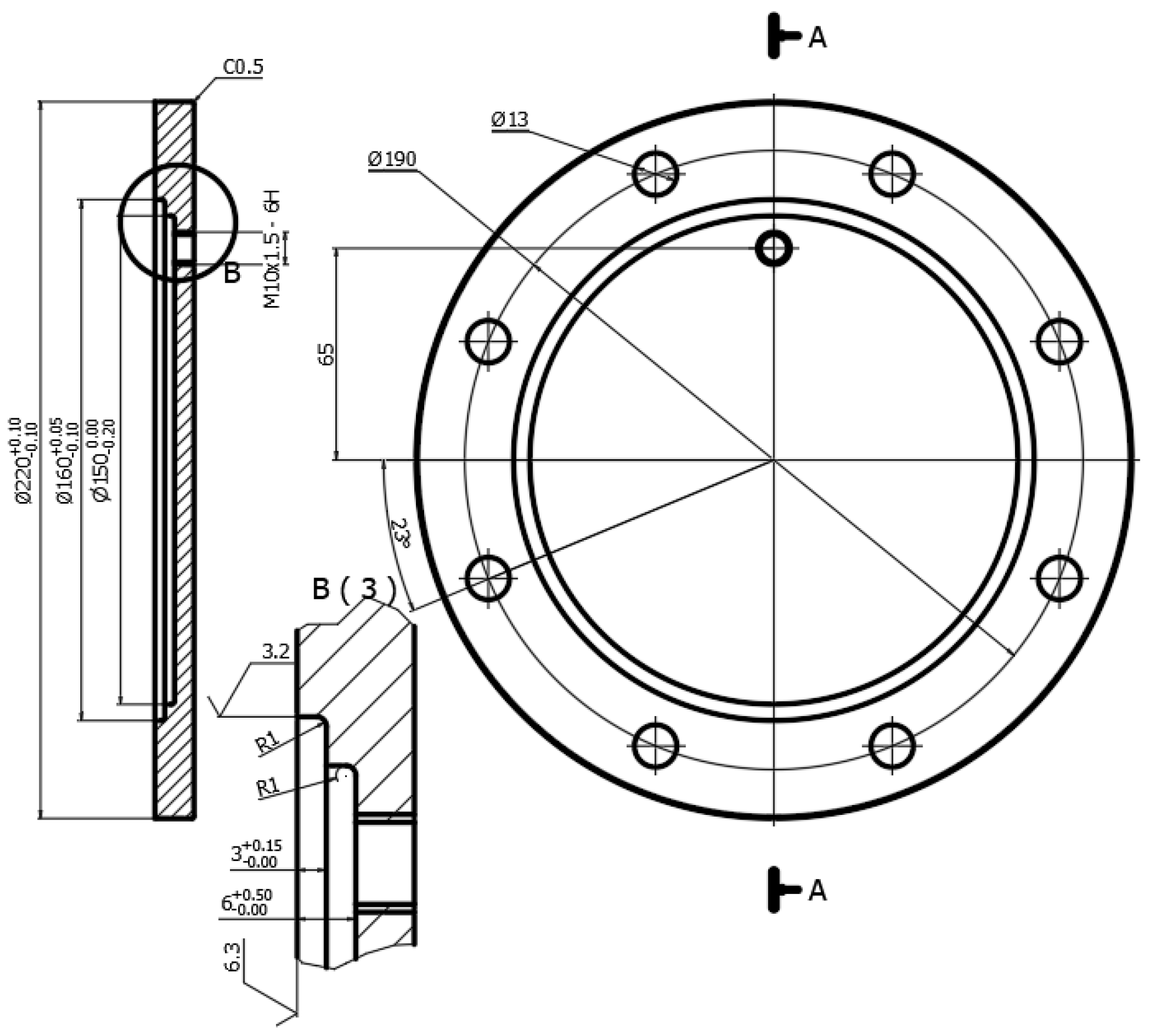
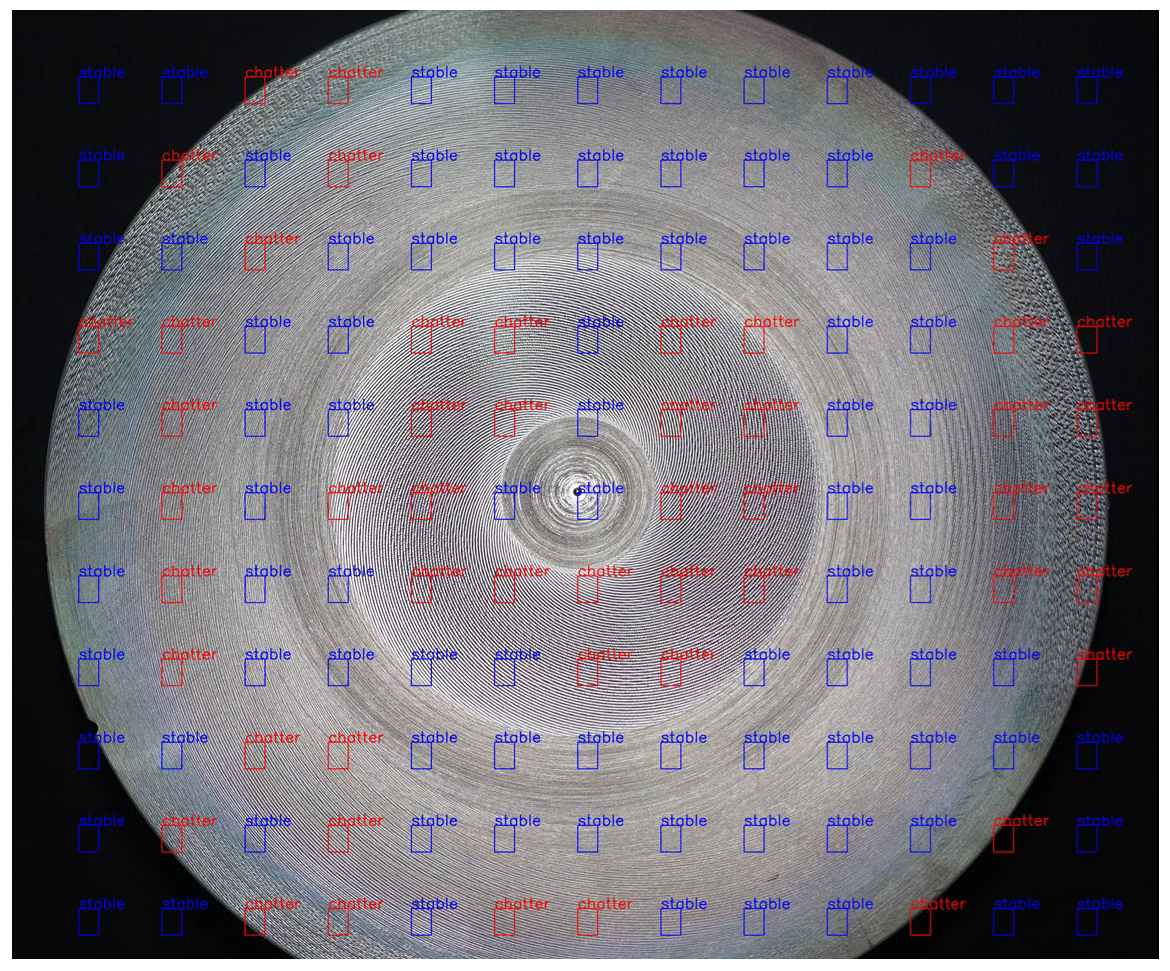
In the turning process, chatter often occurs when the rigidity of the machine, the tool, and the part is not guaranteed, and when the machining mode is not appropriate. Research becomes more difficult when the objective requires the collection of extensive image data relating to the machined surface while simultaneously collecting the sound in the machining of the corresponding surface area. To solve this problem, thin flanges and turn top faces were processed for the following reasons. Firstly, thin sheet parts are very common in machines and equipment. Figure 1 shows the shaft-bearing flange cover of the gantry. Secondly, because a thin plate part has a unique way of turning, when turning in the radial direction, the author chose to maintain a constant speed of the main spindle and a constant feed rate so that the cutting speed would change continuously from the outer diameter to the inner diameter. Moreover, the exit angle of the chip would also change, resulting in an alteration of the cutting conditions and parameters. The thin plate part was externally mounted on a three-pin spoke chuck, and the rigidity of the part changed according to its proximity to the center. All these changes cause the top-face turning of the part of the thin-plate flange to form alternating stable and vibrational areas (Figure 2).
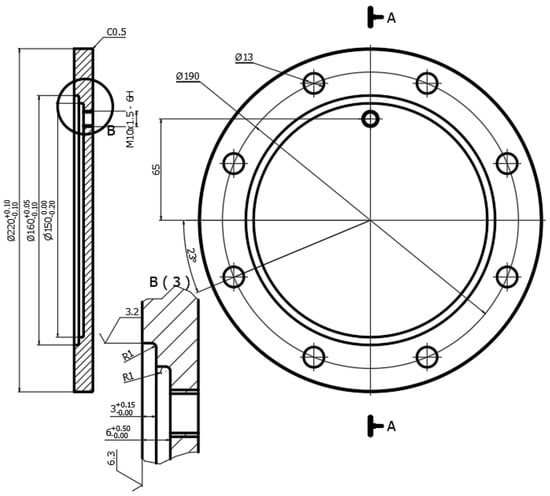
Figure 1.
The drawing of machined flange surface.

Figure 2.
The surface of the product after turning process.
The material of the parts in the study was SS400 steel (according to Japanese standards) with a density of 7.8 g·cm−3. The number of experimental pieces was 50, the diameter of parts was 220 mm, the thickness of parts was 15 mm, and the sample was machined using a Moriseiki SL_20 CNC lathe. The mounting option chosen was to use a three-jaw chuck as a clamp from the outside. Fabrication was carried out using a tungsten carbide lathe WNMG080404. The cutting mode parameters are as follows: cutting depth t = 2 mm, cutting speed n = 800 rpm, and feed rate f = 0.2 mm/rev (Table 1). These parameters were chosen due to the machine’s capabilities and the cutter manufacturer’s recommendations for the respective workpiece material.

Table 1.
The workpiece, tool, and cutting parameters.
2.2. Signal Acquisition and Processing Devices
To the collect surface images of the finished parts at many different locations, the study used a Dino-Lite AM3113 digital microscope with 50 magnification that was connected to a computer. At the same time, the turning sound was recorded using an external Woaichang BM900 microphone near the lathe chuck to collect the sound during the turning process. As a result, the team obtained complete and accurate images and sound data with which to analyze and evaluate the stability or vibration on the surface of the fabricated parts (Figure 3).

Figure 3.
(Left): the microphone for collecting sounds. (Right): the electronic microscope for collecting images.
To determine and classify the machining surface and distinguish which processing stage is stable and which is vibrating, thereby also associating the obtained audio clip with either the stable or vibration machining process, the authors used the surface roughness criterion Ra. This criterion is measured using the Mitutoyo SJ_301 surface roughness measuring device. Classifications were made based on occurring chatter when Ra > 2 μm and stability when Ra < 2 μm. Marking the areas of stability and vibration on the surface of the parts provided a surface image of the components (Figure 4).

Figure 4.
Marking the areas of stability and vibration on the surface of parts.
2.3. Classification Models
Convolutional neural networks (CNNs) are a popular type of neural network for image classification tasks. Compared to traditional neural networks, CNNs can integrate spatial information of input data, resulting in better image processing performance. The basic building block of a CNN is the convolutional layer, which applies a learned set of filters to the input data, producing a set of activation maps corresponding to different input features. These activation maps are then fed into a pooling layer, which reduces the dimensionality of the data by selecting the maximum or average value in a small window of the activation map. The output of the pooling layer is then fed into a fully connected layer, producing the final classification output. The fully connected layer is similar to the output layer in traditional neural networks, except that it retrieves its input from the outcome of the convolutional and pooling layers instead of directly from the input data. One advantage of CNNs is their ability to learn features directly from data instead of relying on handcrafted features. This result is achieved through backpropagation, adjusting the learned parameters of the convolutional filters during training to maximize the classification accuracy of the output. This study used machine learning methods to identify and classify images to detect vibration processes. In particular, the authors used the five most currently popular models, which are VGG16, Restnet50, DenseNet, InceptionNet, and two-input CNN.
VGG16 is based on a series of convolutional and pooling layers, followed by three fully connected layers for classification. The VGG16 model comprises 16 layers, including 13 convolutional layers, 5 max-pooling layers, and 3 fully combined layers. The convolutional layers have a fixed filter size of 3 × 3 and a stride of 1, and the max pooling layers have a fixed pool size of 2 × 2 with a stride of 2. The architecture also includes batch normalization, and Rectified Linear Unit (ReLU) activation functions after each convolutional layer, which improves the training speed and stability. The final three fully connected layers have 4096, 4096, and 1000 neurons, respectively. The last fully connected layer has a softmax activation function for classification into one of 1000 classes [27].
The architecture of DenseNet is based on the idea of densely connecting each layer to every other layer in a feed-forward fashion. The DenseNet model consists of multiple dense blocks, each containing numerous layers. Each layer receives the feature maps from all preceding layers as input within each dense block. The output feature maps from each layer are concatenated together before being fed into the next layer in the thick block. In addition to the dense blocks, the DenseNet architecture also includes transition layers, which reduce the spatial size of the feature maps between the dense blocks. The transition layers consist of a batch normalization layer, a 1 × 1 convolutional layer, and a 2 × 2 average pooling layer. The final layer of the DenseNet model is a global intermediate pooling layer, followed by a fully connected layer with a softmax activation function for classification [28].
ResNet50 is based on residual blocks, which allow for the training of profound neural networks by mitigating the vanishing gradient problem. The residual blocks contain skip connections that bypass one or more layers, allowing gradients to propagate more easily during backpropagation. The ResNet50 model consists of 50 layers and includes four blocks of convolutional layers, each with a different number of filters and a global average pooling layer followed by a fully connected layer for classification. The first convolutional layer uses a large filter size of 7 × 7 with a stride of 2, which helps reduce the input image’s spatial size dimension. After each block of convolutional layers, a downsampling layer is included to reduce the spatial size of the feature maps. The downsampling is achieved using a convolutional layer with a stride of 2, which reduces the width and height of the feature maps by a factor of 2. The architecture also includes batch normalization, and ReLU activation functions after each convolutional layer, which improves the training speed and stability [29].
InceptionNet uses multiple filters with different sizes within a single convolutional layer, rather than a single convolutional layer with a fixed filter size. The InceptionNet model includes multiple inception modules, each of which contains parallel convolutional layers of different filter sizes (1 × 1, 3 × 3, and 5 × 5) and a pooling layer. The output of each of these parallel branches is concatenated before being fed into the next inception module. InceptionNet also includes auxiliary classifiers, which combat the vanishing gradient problem by providing intermediate supervision during training. These classifiers are added after some of the inception modules and include a global average pooling layer followed by a fully connected layer and a softmax activation function. The InceptionNet architecture also includes batch normalization, and ReLU activation functions after each convolutional layer, which improves the training speed and stability [30].
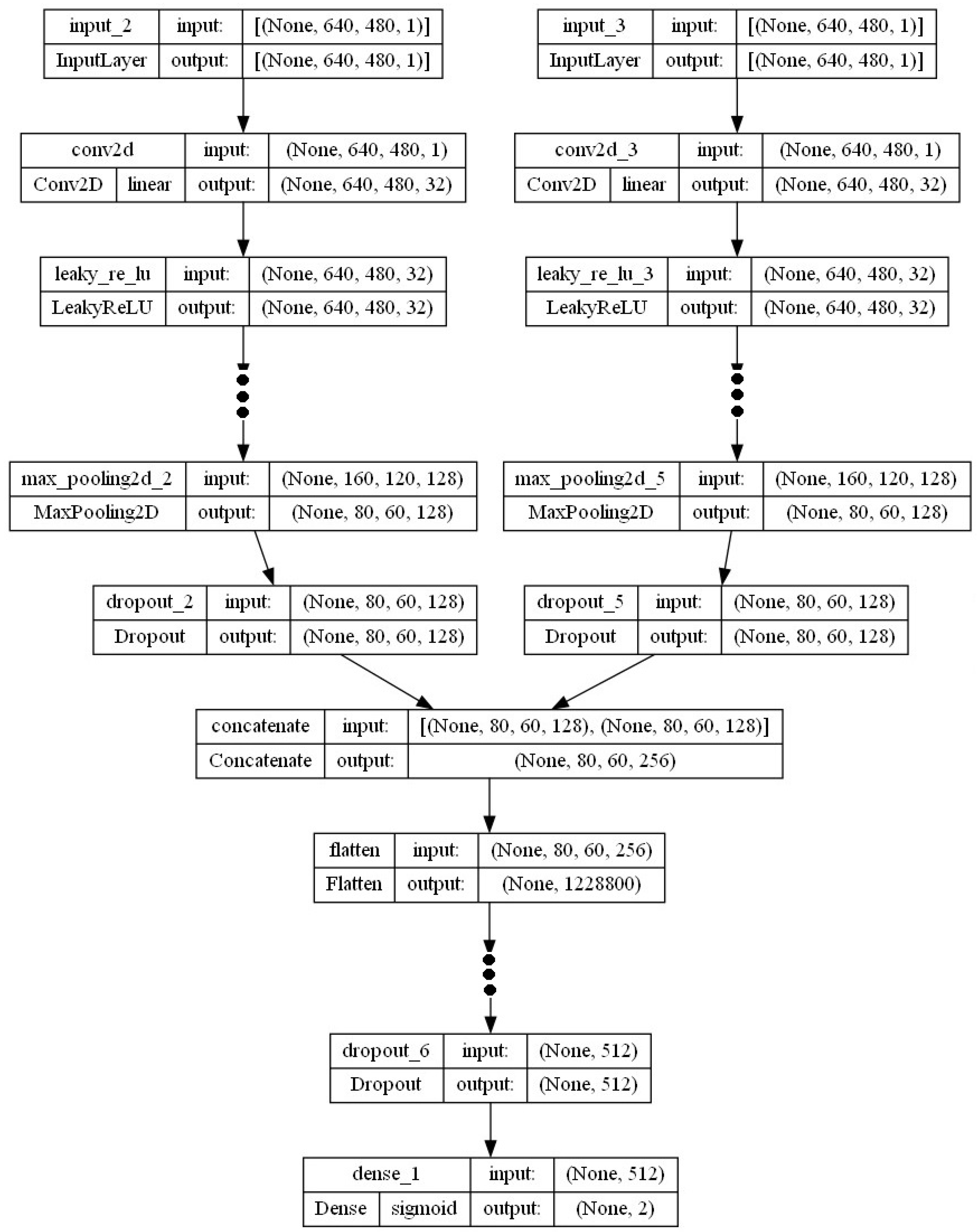
A multi-input CNN is a convolutional neural network (CNN) architecture in which many independent inputs are fed into the network. It allows simultaneous processing and learning from various input data sources, such as images, text, or time series data. These inputs are then combined in the typical layers of the network to learn and generate an ordinary prediction. Multi-input CNNs are often used in applications where combining information from multiple input data sources can improve model accuracy. In this study, visual and acoustic data were used simultaneously to improve the recognition ability of the model compared to models that only use a single type of input data. The study combined two sets of input data; specifically, in one machining area, two data sets were collected simultaneously, and visual data and acoustic data of the workpiece surface were generated during the cutting process. The data were then processed using two methods. Method 1: an image file was created by merging 2 image files, namely, an image of the workpiece surface and a frequency spectrum image file of the sound file. Then put this image file into the CNN model for classification. Method 2: two models were performed for two separate image files and the combined in the CNN model (Figure 5).
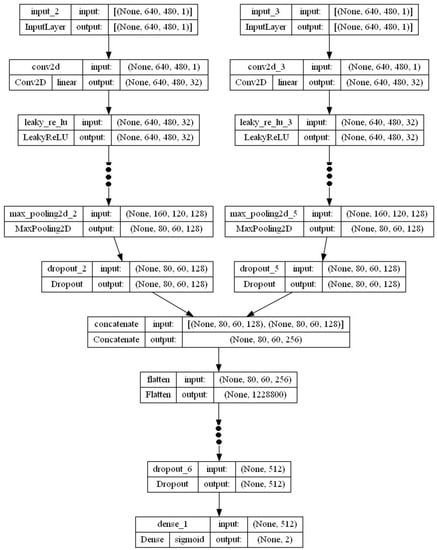
Figure 5.
The architecture of the 2_input model.
For each input, three convolutional layers were used to extract the feature. These layers were composed of the following components (Table 2): The first hidden layer is called Convolution2D, which is a convolutional layer. With 32 filters, a 3 × 3 kernel and a LeakyReLU activation function (a leaky version of the Rectified Linear Unit—ReLU) allow for a slight gradient when the unit is inactive. This layer serves as the input layer. Next, a pooling layer with a method to obtain the maximum value, called MaxPooling2D, is used. This layer is set to a pooled size of 2 × 2, which halves the input size in both spatial dimensions. The next layer is an adjustment layer that uses a dropout method called dropout. It is set to randomly remove 25% of the neurons in the layer to prevent overfitting. The layers mentioned above were duplicated twice, increasing the filter size to 64 and 128 (to accommodate more complex features) and adjusting the dropout ratio to 25% and 40% (to avoid overfitting). The output of the convolutional layers for both inputs passes through the concatenation layer, and the result is then converted by the Flatten layer from a 2D matrix to a vector. This process allows the completely standard connection layers to process the output. Next, a fully connected layer consisting of 512 neurons, using the leaky rectifier activation function, is used. This layer is combined with a dropout layer that randomly removes 50% of the neurons and processes the input from the Flatten layer. Finally, the output layer has 2 neurons corresponding to 2 states and uses the softmax activation function to make probabilistically similar predictions for each layer.

Table 2.
The specifications of a two-input model’s architecture.
This research paper focuses on adjusting the hyperparameters of the model, with particular attention given to the batch size, optimizer, loss function, and normalization operation. Table 3 presents the most favorable outcomes of the comparisons made in this study.

Table 3.
Optimal hyperparameter values.
This study collected data sets consisting of image files obtained during turning. After processing, the image files are divided into several parts and again divided into training, calibration, and testing sets at a ratio of 80:10:10. To speed up training and reduce the model optimization time, a Python program was installed on a Dell server with 16 physical cores, using TensorFlow and Keras libraries. The model was trained using a GTX GPU 1080 Ti graphics card.
There are many methods used to evaluate the effectiveness of a classification model, including an examination of accuracy, accuracy and coverage, error, F1 score, confusion matrix, time, and memory. Accuracy is calculated as the ratio of the number of individuals correctly classified into a given layer to the total number of individuals classified into that layer. On the other hand, coverage is the ratio of individuals correctly classified into a layer to the total number of individuals of that layer. The F1 score is an index that combines the accuracy and coverage of the model and is defined as the harmonic mean of two of these indexes. By using an F1 score, one can better understand the model’s performance compared to using precision or coverage only. This study evaluates the proposed model using accuracy, F1 score, and confusion matrix tests.
3. Results and Discussion
3.1. Data Collection and Processing
This study collected data by machining 50 parts of flanges. During the machining process, the authors collected sounds during the turning process. For each flange part, a sound file with a length of 82.5 s and a machined surface was obtained. Then, using a radial length, the surface was divided into 33 equal segments. Each segment corresponds to a machining area, and each machining area corresponds to an acoustic clip during the machining of the corresponding location. That is, the surface of the workpiece is divided into 33 regions according to the acreage of a square with dimensions of 3.3 mm × 3.3 mm. The soundtrack obtained during machining is divided into 33 segments, each being 2.5 s in length. As a result, 33 image files named and 33 corresponding sound files named were obtained. Therefore, using the files and .
where:
i: the index for the ith part of the flange (i =1 ÷ 50)
k: the index of the machining area on the flange k (k = 1 ÷ 33)
After 50 flange parts were machined during turning, stability and vibration groups were distinguished using a roughness meter. The surface is classified as a stability group if Ra < 2 μm. When Ra > 2 μm, the machined surface was classified as a chatter (Figure 6). The part used a three-pin spoke chuck and a cutting mode of n = 800 rpm as a constant when machining the thin flange; therefore, the cutting speed varied in different diameter positions. The phenomenon of vibration and stability appears and disappears at various locations. Because of this, the research collects many visual and acoustic data areas corresponding to different vibrational and stable states. Through this approach, the cost of the experiment is reduced, and stable and vibrational acoustic and visual data are obtained across various cutting modes and conditions.

Figure 6.
The machined surface after measuring roughness and marking stable and chatter zones.
After determining the stable and vibrational areas, an electron microscope was used to capture the images of the surface parts of the finished product in the marked areas. The regions are labeled as either chatter or stable (Figure 7). Overall, 1650 image files along with 1650 sound files were obtained after using the roughness meter to partition the stability and vibration data. Moreover, 987 image and sound files were collected in a steady state and 663 image and sound files were in a vibrational state.

Figure 7.
(Left): the chatter zone. (Right): the stable location.
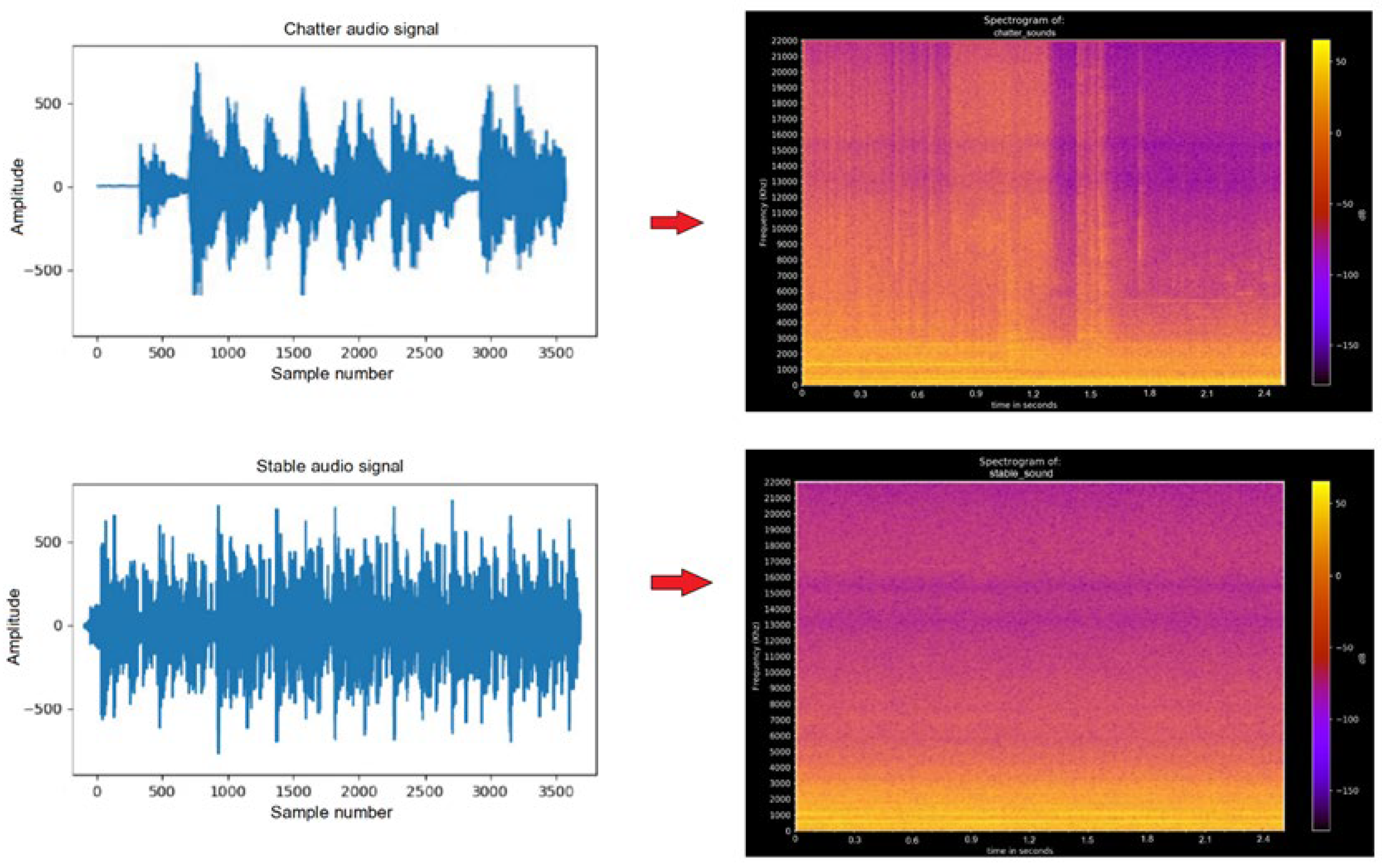
The results of the audio waves were collected using a recording device and recording software. Audio files were cut into audio segments of the same length of time. Then, the audio files were converted to a frequency domain using the Fourier transform. As a result, the transformed image files of the audio segments were obtained. At that time, the study used the convolutional neural network algorithm to classify images. To help neural networks process data more easily, preprocessing techniques including audio sample data were used to separate this complex audio wave into parts, separating the low tones, the upper tones, and the higher tones. Then, the total energy in the frequency bands (from low to high) was calculated and reconnected to create a fingerprint—a unique identification for each audio segment. The technique is possible because of the Fourier transform, which was used to break down complex audio waves into single audio waves. After this, the total energy of each monophonic audio was calculated. The result is a table of numbers representing the energy levels of each frequency range. After the fast Fourier transformation of 1650 sound files, a set of 1650 image files was obtained (Figure 8).
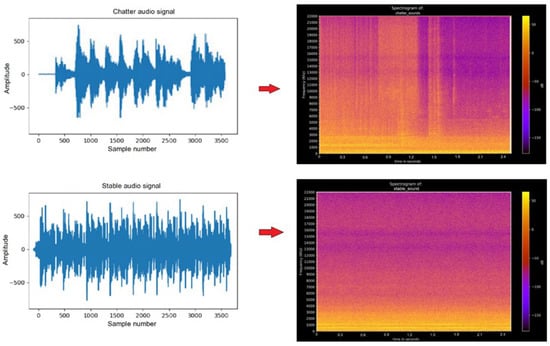
Figure 8.
(Left): the chart of audio signal with chatter and stable. (Right): the spectrogram of chatter and stable.
To create a visual data set that captures both the surface characteristics of the workpiece during turning and the acoustic characteristics of the turning, the image processing technology was used to combine two surface images of the part and sound spectrograms. The study has created 1650 image files that are typical of the chatter turning process (Figure 9) and stable turning process (Figure 10). The distribution of different types of data in the data set is shown in Table 4.

Figure 9.
(Left): a chatter image of the combined surface. (Right): the sound spectrogram.

Figure 10.
(Left): the stable chatter in an image of the combining surface. (Right): the sound spectrogram.

Table 4.
Distribution of different types of data in the data set.
3.2. The Results of Applying CNN Models to Detect Chatter Using Surface Images of Parts during Turning
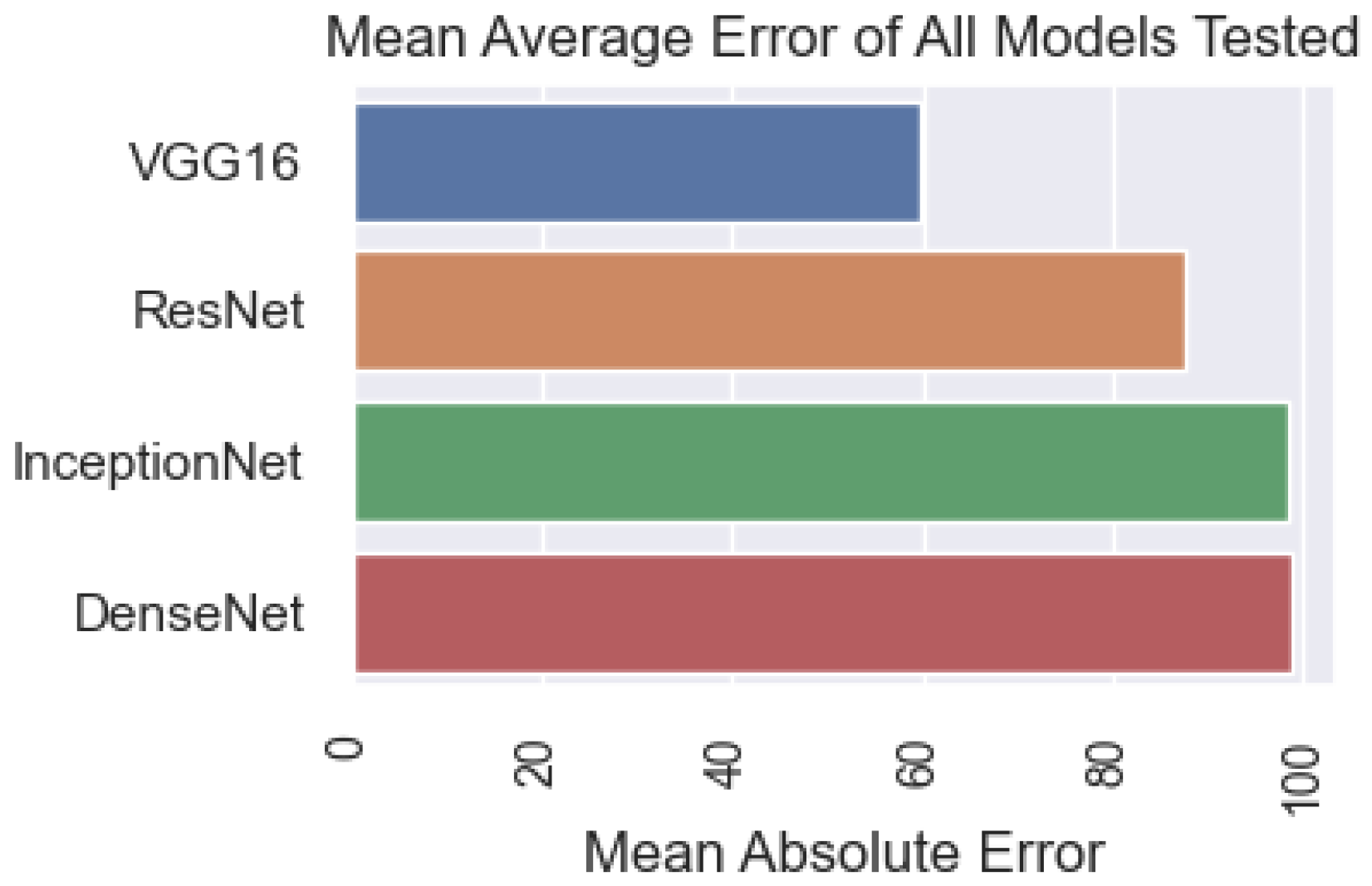
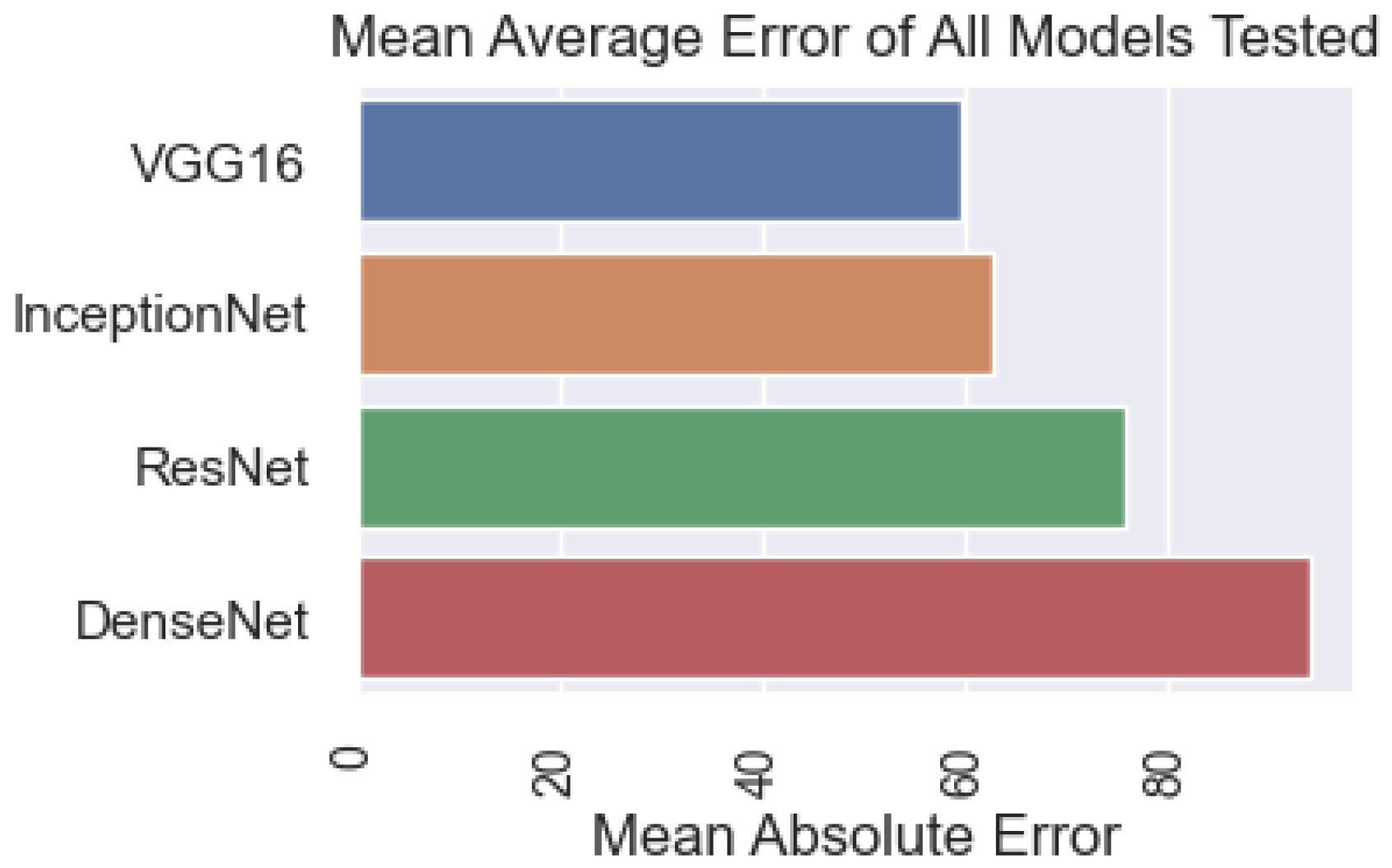
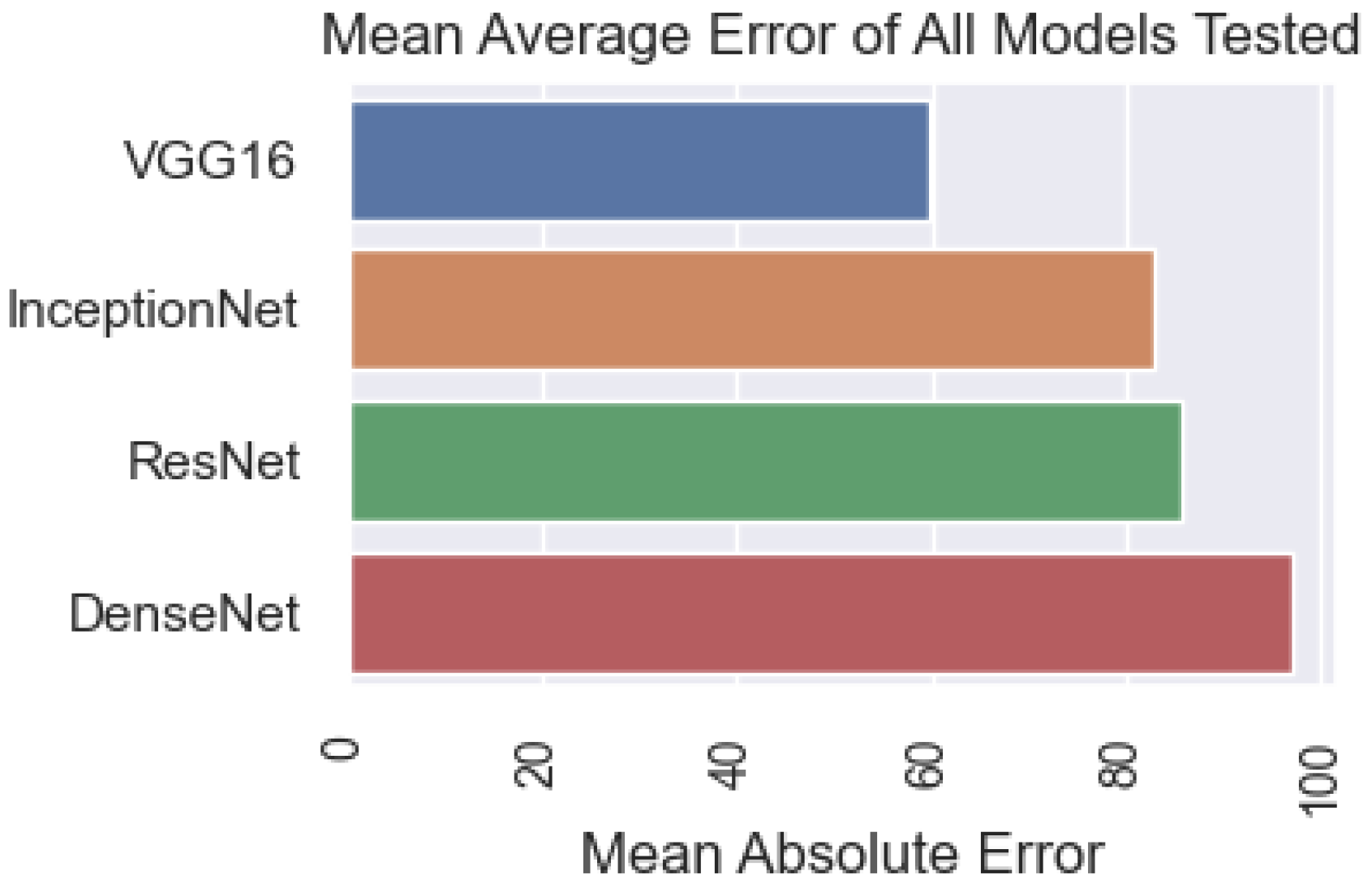
This section presents the results obtained from the recommended method and other models. The accuracy of the models is compared based on the criteria shown in Figure 11. The results show that the DenseNet model has the best results, with 98.8%. Next is InceptionNet, with an accuracy of 98.29%. The ResNet model achieved a result below 87.55% and the VGG16 model achieved 59.84%.
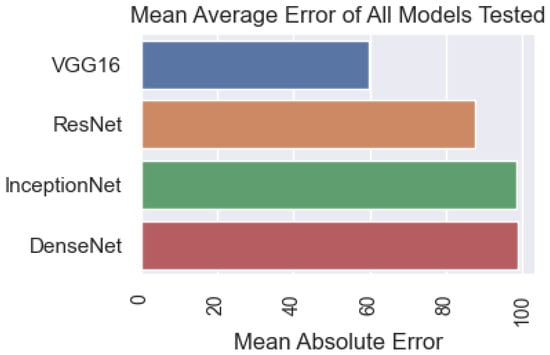
Figure 11.
Comparison of the model’s accuracy with the input data of images.
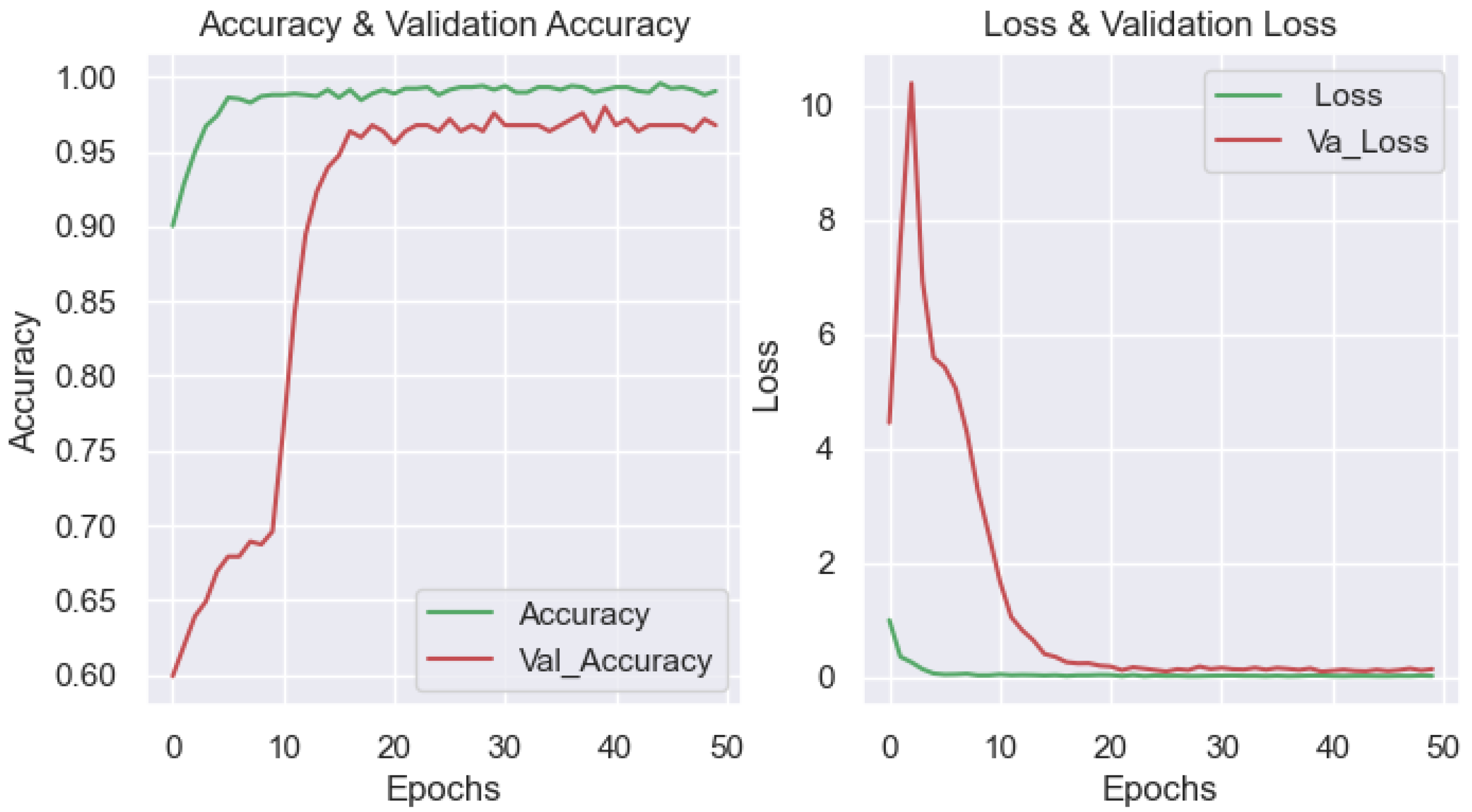
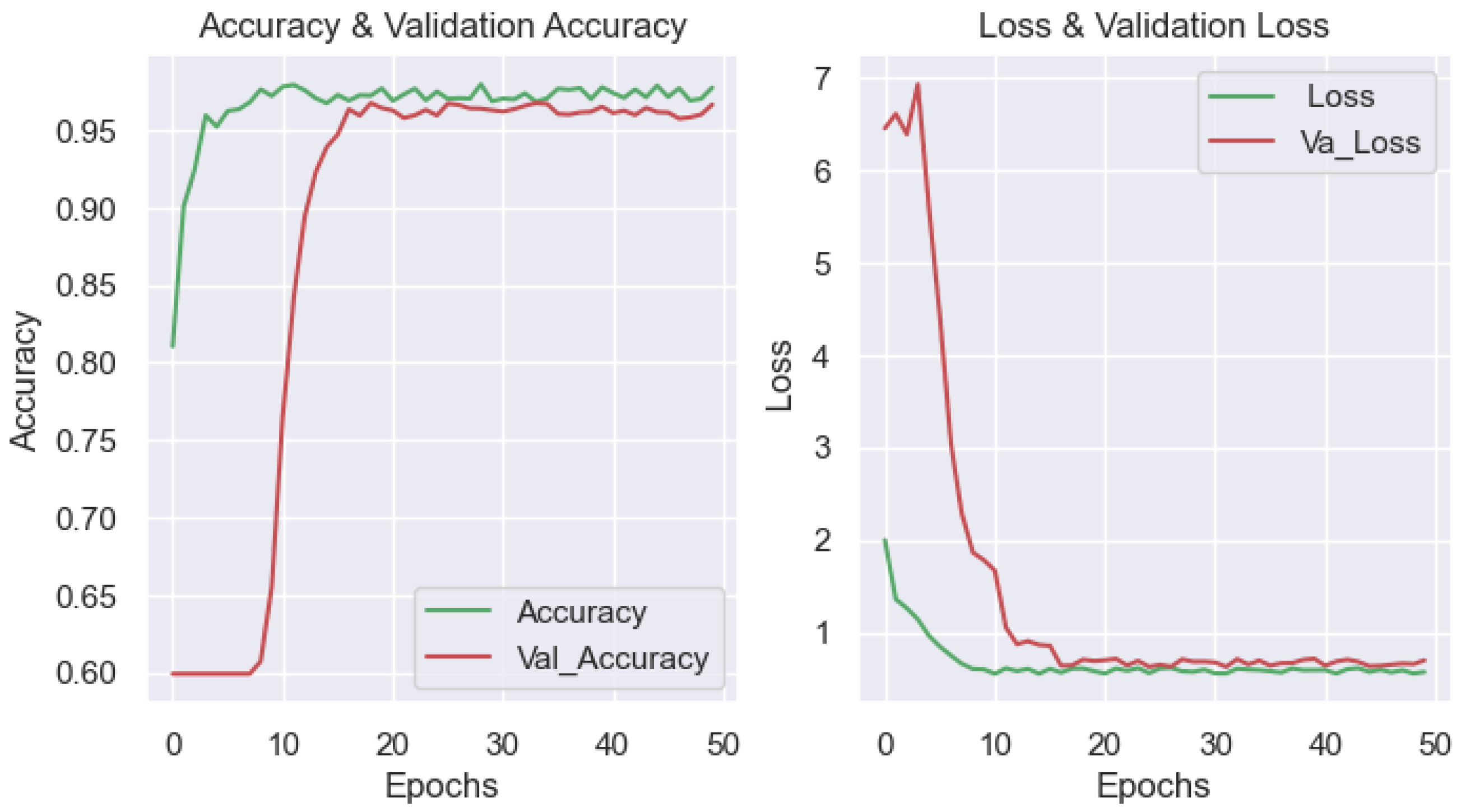
When analyzing the curve graph depicting the accuracy and loss of the visual data set during a training process of 50 epochs for the DenseNet model (Figure 12), the following observations were made: The stability of the training process can be observed from the 20th epoch. The result shows that the model works well because the loss of data decreases during training and testing until it reaches a stable point with a minimal error. However, there is an abnormal appearance of moving points in the loss and accuracy data due to the insufficiently large input data set. Despite this volatility, the model still achieved relatively good results, as shown by the evaluation indicators in Table 5.
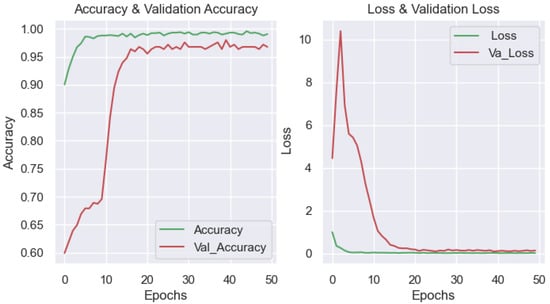
Figure 12.
(Left): training and validation accuracy. (Right): training and validation loss with image input _DenseNet.

Table 5.
Image input DenseNet accuracy values with image input.
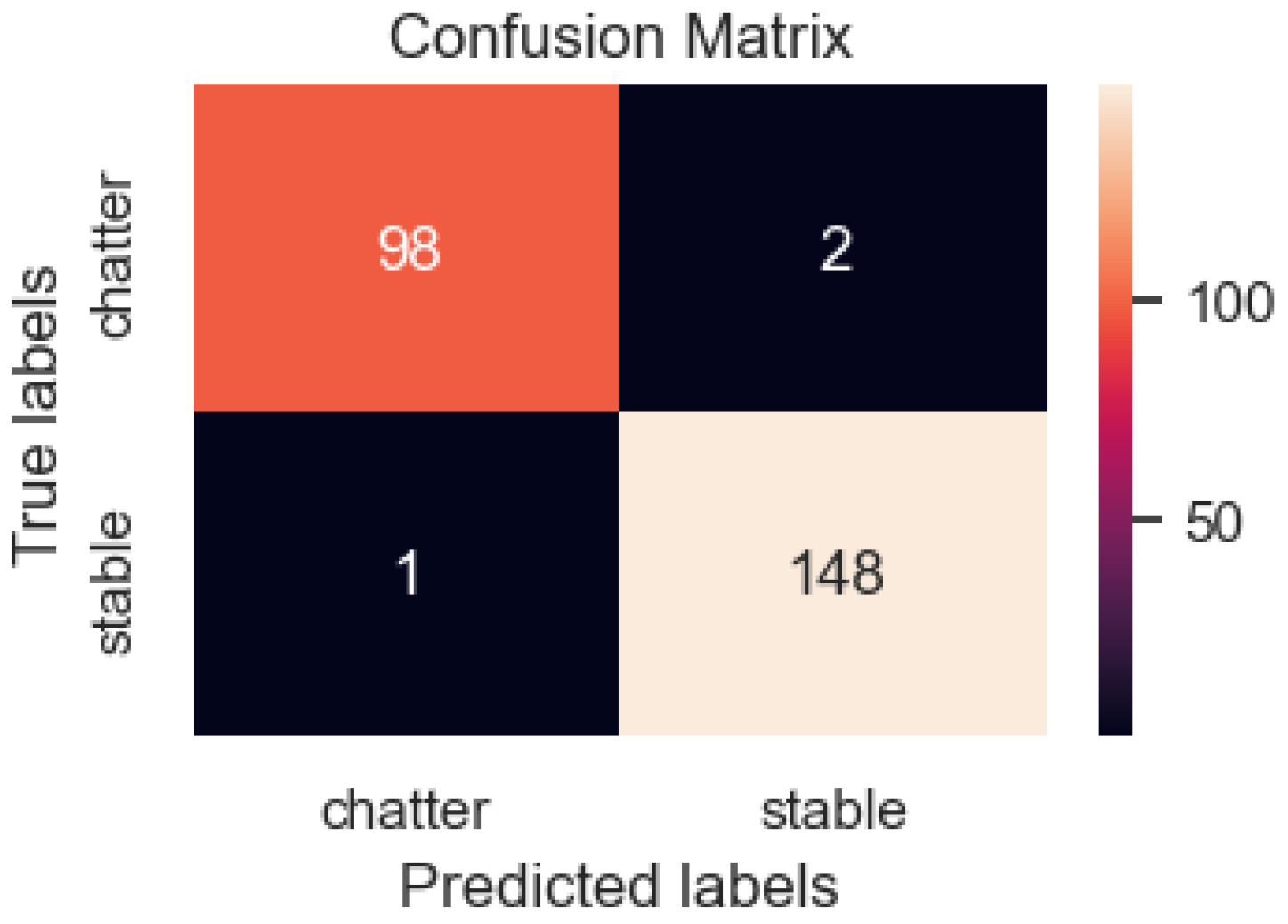
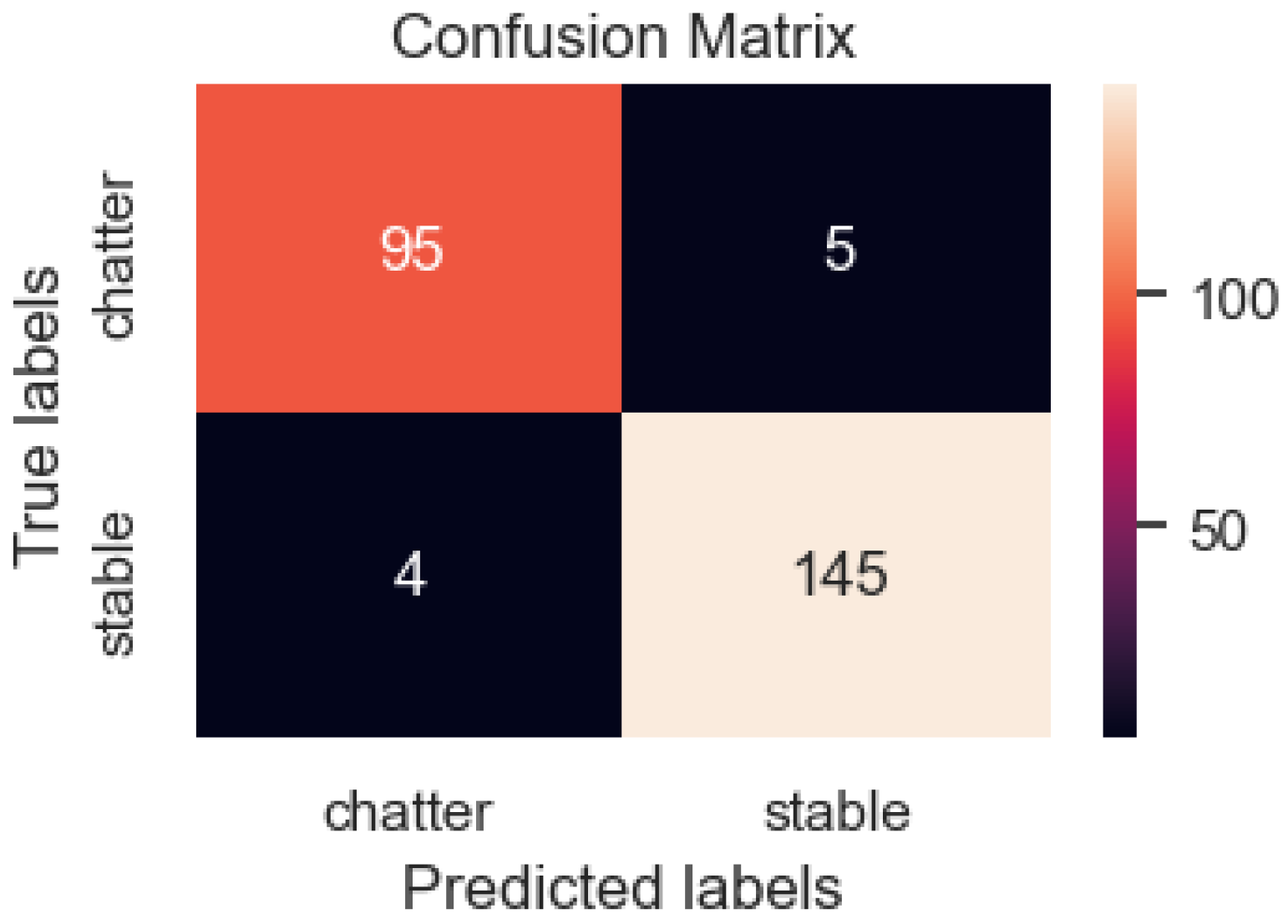
To illustrate the predictive power of the deep learning model, the confusion matrix analysis method was applied. Figure 13 shows the calculation made using the confusion matrix for the testing data set. Each matrix column has one layer that is predicted by the model and one even layer. Typically, the matrix consists of four categories: True Positive (T.P.), which means that the prediction and the real value are both positive; True Negative (T.N.), meaning that the forecast and the actual value are both negative; False Positive (F.P.), meaning the prediction is positive while the real value is negative; False Negative (F.N.), meaning the forecast is negative while the actual value is positive. Of the 249 test data samples, there are 100 chatter samples and 149 stable samples. However, the prediction model provided 98 chatter samples and 2 stable samples; therefore, there were two cases in which model made a wrong prediction. From the 149 images of the stable machining group, one datum was assigned to the chatter group, and the remaining 148 images were correctly classified. After evaluating the wrong data, the model had a prediction error of 1.21%.
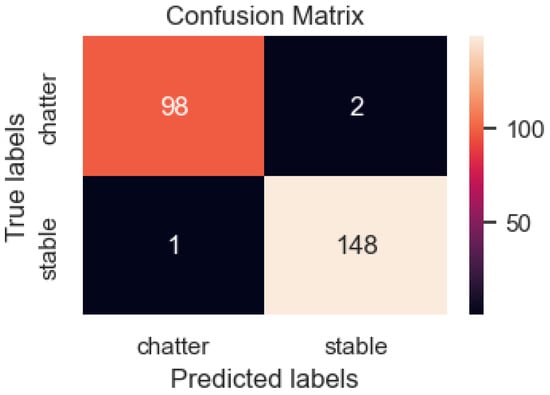
Figure 13.
The confusion matrix of the DenseNet model with images’ input data.
3.3. Results of Applying CNN Models to Detect Chatter by Acoustic Data during Turning
In this section, the results obtained from both the recommended method and other models will be presented. The accuracy of the models is compared based on the established criteria, as shown in Figure 14. The results show that the DenseNet model achieved the best results with an accuracy of 93.57%. Next, the ResNet model achieved an accuracy of 75.84%. InceptionNet and VGG16 achieved 62.91% and 59.79%, respectively. This result shows that the DenseNet model remained the most accurate compared to other models. However, the accuracy of the DenseNet model for the sound data set (93.57%) is lower than that of the DenseNet model that achieved 98.8%.
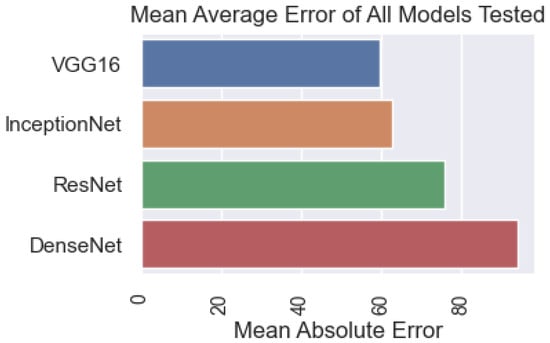
Figure 14.
Comparison of model accuracy with machining sound as input data.
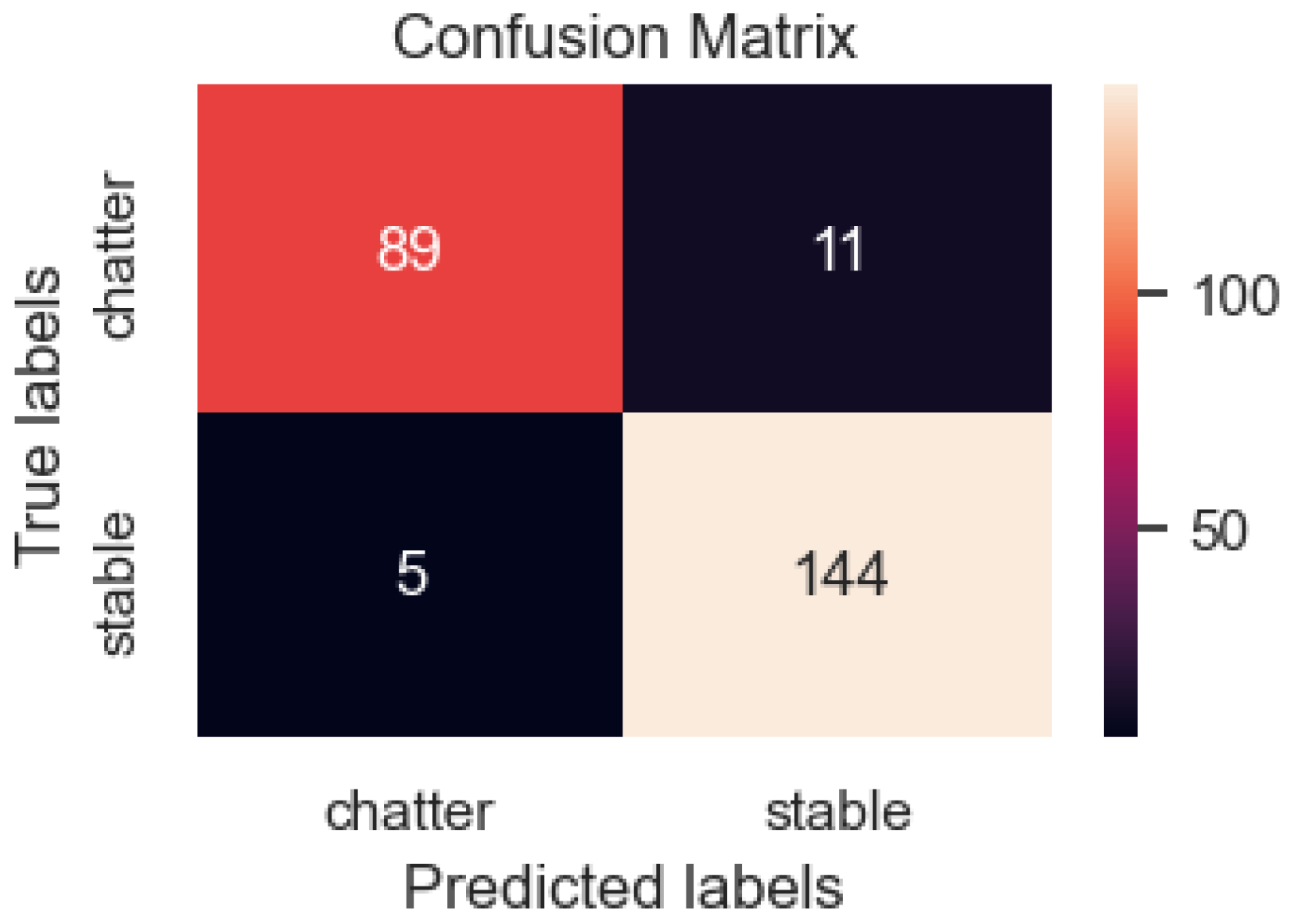
Table 6 shows the evaluation metrics of the DenseNet model, which used turning sounds as the input data for the 249 data samples tested, including 100 samples of chatter and 149 samples of stability. However, the model predicted 89 samples as chatter and 11 samples as stability, indicating a prediction error in 11 samples. Of the 149 sound samples, there are 5 error samples (Figure 15). After evaluating the wrong cases, the model’s accuracy on the test set was 93.5%. This is less accurate than the model that used image data as its input, which achieved 98.8%. This is possibly due to noise factors in data acquisition, possibly during processing, and the abnormal noise of other mechanical mechanisms influencing the prediction results.

Table 6.
Image input DenseNet accuracy values.
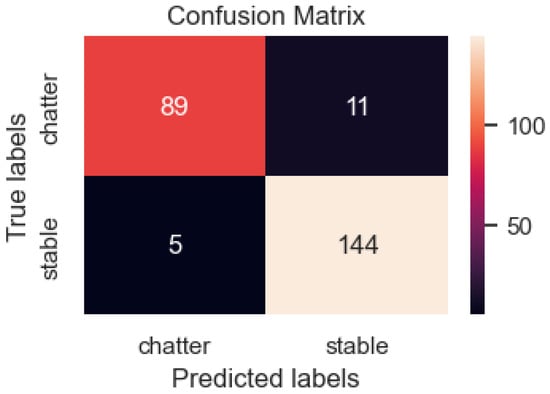
Figure 15.
The DenseNet model confusion matrix with input data of sounds.
3.4. Model Results for Image Files Combined between Image and Sound Files
In this section, the results obtained from the recommended method and different models are presented. Based on the accuracy criteria of the models, the results are shown in Figure 16. The results show that the DenseNet model provided the best results with 96.38%, followed by ResNet, with a model accuracy score of 85.84%. InceptionNet and VGG16 achieved relatively low results (82.91% and 58%, respectively). Compared with the acoustic input data set, the discriminant DenseNet model in this composite data set is more accurate; however, it is still less accurate than when the image data set is used. This issue substantiates the combination of both acoustic and visual elements and enhances the comprehensiveness of the data.
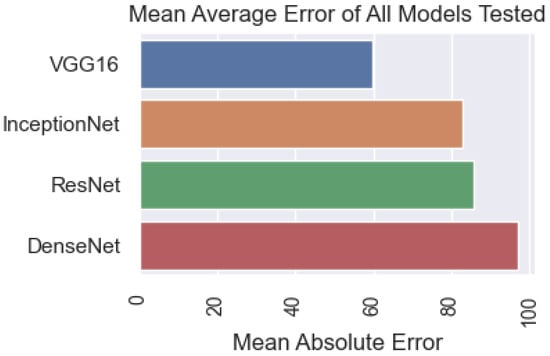
Figure 16.
Comparison of model accuracy when a combination of sound and image data from the machined surface is used as input data.
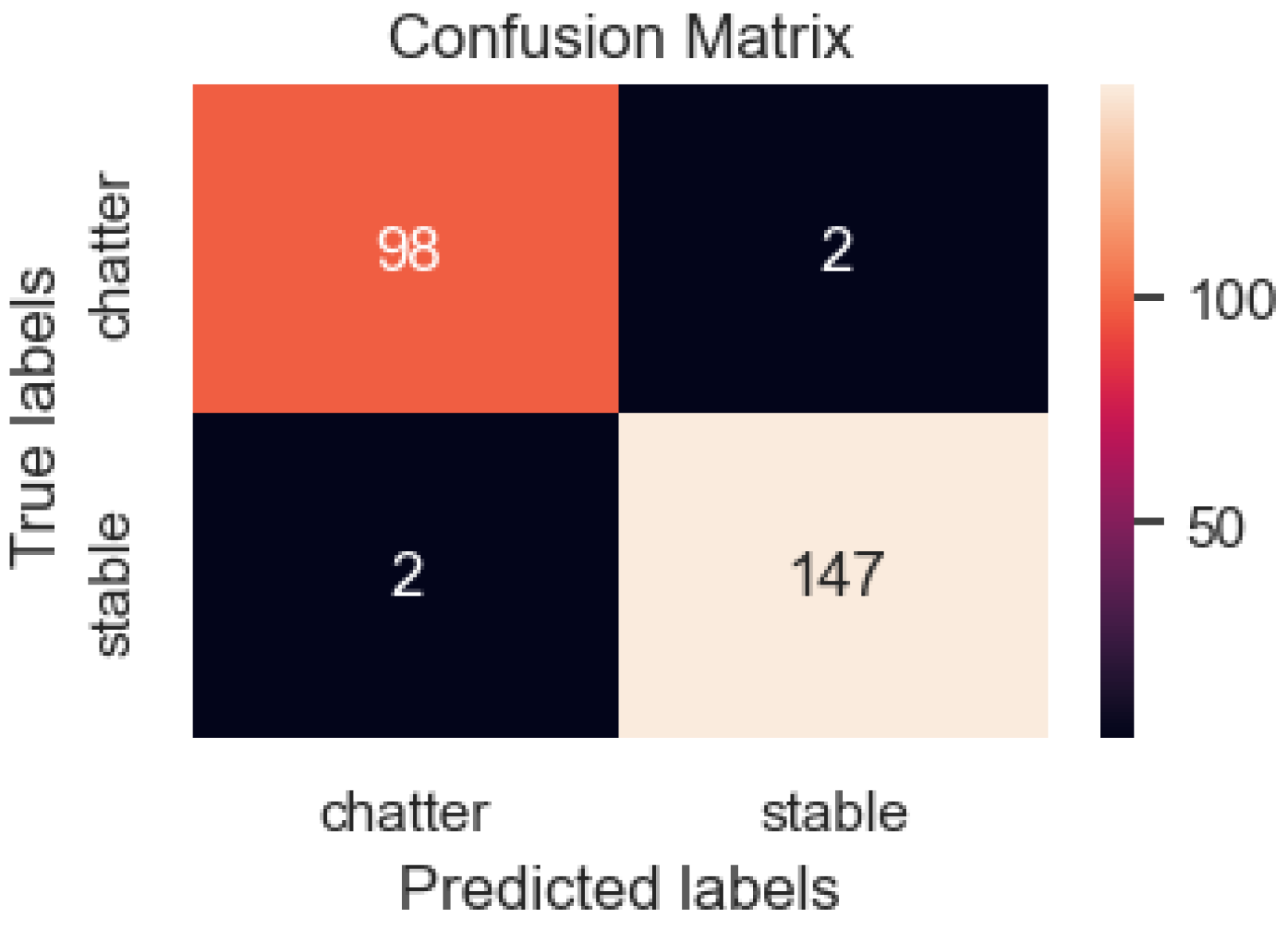
In total, 249 data samples were tested using the DenseNet model, which used combinations of sound and image data from machined surface as input data, including 100 samples of chatter and 149 samples of stability (Figure 17). However, the model predicted 95 samples as chatter and 5 samples as stability, indicating a predicting error in five samples. Of the 149 images in the stable machining group, 4 were assigned to the chatter group, and the remaining 145 images were correctly classified. After evaluating the false cases, the model’s accuracy on the testing set was 96.3%. This is less accurate than the model that used only images as input data (98.8%) but higher than the DenseNet model’s score when using the acoustic data set (93.57%). There is a remarkable improvement in the accuracy of chatter detection with this image-merge data set. Information regarding the accuracy of this case is presented in Table 7.
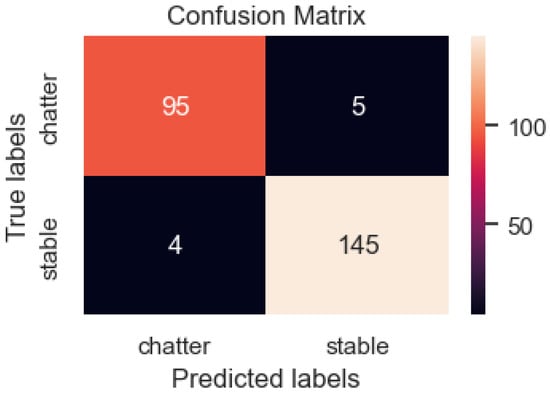
Figure 17.
The DenseNet model confusion matrix when images and sounds are used as input data.

Table 7.
Image and sound input DenseNet accuracy values.
3.5. Model Results with Input Data of the Two-Input Model
In this section, the results obtained from the proposed method are presented. The following graphs illustrate the data set’s accuracy and loss curves, whose features were extracted using the 2_input model. Transfer learning techniques extracted parts from the data set, and the models were trained in 50 epochs. The stability of the training can be observed from the 16th epoch through the curves in Figure 18.
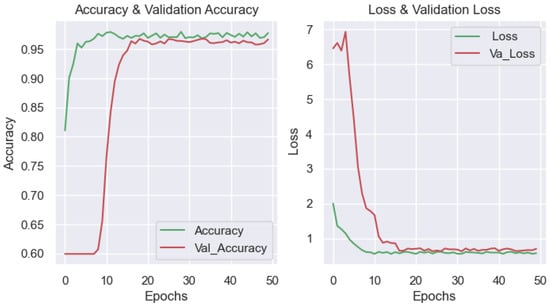
Figure 18.
(Left): training and validation of accuracy. (Right): training and validation of loss for the two_ inputs model.
After 50 epochs, the two-input model achieved an accuracy of 98.7% when generating surface images of the workpiece combined with the corresponding sound captured during the machining process. The model evaluation results are shown in Table 8. To illustrate the predictive power of the deep learning model, we compared the accuracy of its results using the confusion matrix. Out of 249 test data samples, there were 100 machining group chatter samples with vibration; the model predicted two pieces of data incorrectly. Of the 149 images of the vibration-free machining group, two pieces of data were assigned to the chatter group, and the remaining 147 samples were correctly classified. After evaluating the misleading data, the model achieved a prediction accuracy of 98.7%. As observed in Figure 19, the wrong samples are distributed in both data sets.

Table 8.
Two-input model accuracy values.
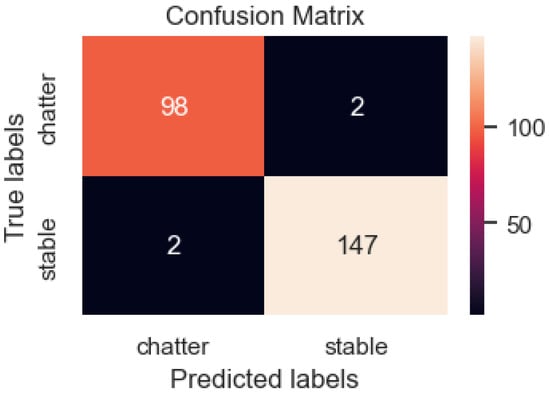
Figure 19.
DenseNet model confusion matrix with two_input data.
When comparing the model performance criteria for the different input data sets (Table 9), the F1_score metric shows that the DenseNet model performed the best on the image data set, with an accuracy of 98%. The second best performing model was the DenseNet model that was trained on a data set consisting of combined audio and image inputs, with an accuracy of 95%. The worst performing model was trained on an audio-only data set, with an accuracy of 92%. This demonstrates that a combination of image and audio inputs results in higher accuracy than when classifying audio files alone. When comparing the accuracy of the two-input model to the other three models, it ranked second, with an accuracy of 97%. This indicates that the two-input model learned better features than the combined image or audio inputs. Although the accuracy of the two-input model was lower than that of the image data set model, the overall quality of the input data set was better, and the data were more diverse.

Table 9.
Comparison of models.
3.6. Discussion
Academically, this research has achieved good results related to building a vibration detection model based on the concept of designing and manufacturing machining equipment, specifically a CNC lathe that can hear and see to detect abnormal problems. Chatter detection during machining is performed when detecting and checking the product after machining a part. At this point, the spindle stops, and the device takes pictures to determine which areas are stable and which are chattered (Figure 20). This means that the device will check the quality of the entire product surface before deciding to process the next part. Then, the shutter speed and image noise factors will be removed. It is essential to eliminate mass product failures.

Figure 20.
Applying the vibrational surface detection model.
However, for the results of this study to apply to the actual production model in the case of both processing and testing (Figure 21), the confounding factors must be minimized. Regarding image acquisition, a high-speed camera is required for continuous shooting so that the image is not blurred. As well as in the machining process, it is necessary to arrange the camera in a position less affected by chips and cooling water. Similarly, acoustic noise factors should also be limited when collecting sound data for training or testing, such as spindle motor sounds, tool change sounds, etc. However, these difficulties will be eliminated when there is specialized equipment and optimal noise filtering algorithms in the future.

Figure 21.
Detection of chatter in online turning.
The recent application of CNN for vibration detection during close turning is very popular. Zhu et al. studied vibration detection in thin material turning based on DCNN. Tran et al. used a dynamometer as a sensor, which achieved a vibration detection accuracy of up to 92.12%. Rahimi et al. applied a neural network and physics-based model to detect vibration during turning. The data collected during machining is converted into a short-term travel frequency spectrum through STFT transformation. Features are mapped to five machining states, such as idle; tool enter cut workpiece, knife out of the workpiece, stable cutting, and vibration cutting. Sener et al. collected spindle rotation speed data in steady state machining and chatter to detect chatter. Kounta et al. used VGG16 and RestNet models to detect chatter through an acoustic signal. The sound is converted into an image through the FFT transformation and has an accuracy of 99.88%. The above studies often achieve high accuracy because the authors usually collect a limited amount of the data in the model training, and the collected signals are often processed under laboratory conditions with little error caused by external confounding factors. When evaluating a model, if the size of the training data is small, the recorded accuracy of the testing set does not represent the model’s advantages. Overcoming these limitations, this study used acoustic and visual data for training.
In our study, in addition to comparing the accuracy of currently popular CNN models to determine the optimal model for vibration detection through input data as images or sounds, our system combined visual and acoustic data, which were then used for training. This approach was carried out in various ways to enhance the generality of the model, achieving a higher level of generality compared to previous studies and thereby improving its applicability. Table 10 highlights our contribution compared to previous achievements in the literature. Although the accuracy is lower, the generality of the system data is better.

Table 10.
Comparison with previous studies.
4. Conclusions
This study designed a turning experimental model based on a thin flange to collect visual and acoustic data while turning. The data set has 987 pairs of visual data of surface parts, acoustic data of stable machining, and 663 pairs of data related to the vibrational state. The research classified data using different machine learning models (VGG16, RestNet, DenseNet, and InceptionNet) and individual visual and acoustic data. Using data from the surface images of machined parts, the Dense-Net model achieved a 98.8% accuracy, followed by InceptionNet (98.29%), RestNet (87.55%), and VGG16 (59.84%). Moreover, when classifying using the acoustic data set, the DenseNet model still had the highest accuracy (93.57%), followed by the ResNet model (75.84%), InceptionNet (62.91%), and VGG16 (59.79%). Similarly, when combining the two data types of images and sounds by merging two images and then performing recognition, the models achieved the following accuracy scores: DenseNet 96.38%, ResNet 85.84%, InceptionNet 82.91%, and VGG16 58%. In conclusion, with the image and sound data set collected in this study, the DenseNet model consistently achieved better accuracy than the other models.
The investigation also built a two-input model to classify data, and the resulting model accuracy was 98.7%. Although the accuracy is lower than that of the single-data model, the data combination model and the two-input data model are more appreciated because they are process-specific.
The analysis also opens a new direction for the monitoring of the machining process by using machine learning tools, which the authors will explore using multi-input data, such as cutting force, acceleration, sound, and image, etc. All these data will be transformed into frequency spectrum images and fed into the CNN model. Then, the data model will be more specific, and the model will make more accurate decisions.
Author Contributions
Conceptualization, Q.N.T.H., T.T.D. and P.S.M.; funding acquisition, Q.N.T.H., T.T.D. and P.S.M.; project administration, Q.N.T.H., T.T.D., V.-T.N., V.T.T.N. and P.S.M.; supervision, Q.N.T.H., T.T.D. and P.S.M.; visualization, Q.N.T.H., T.T.D. and P.S.M.; writing—original draft, Q.N.T.H. and T.T.D.; writing—review and editing, Q.N.T.H., T.T.D., V.-T.N., V.T.T.N. and P.S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work belongs to the project grant No: T2023-129, which is funded by Ho Chi Minh City University of Technology and Education, Vietnam. Additionally, the Machines Editorial Board funded the APC.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
We acknowledge the support from HCMC University of Technology and Education, Ho Chi Minh City, Vietnam (HCMUTE).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bravo, U.; Altuzarra, O.; De Lacalle, L.N.L.; Sánchez, J.A.; Campa, F.J. Stability limits of milling considering the flexibility of the workpiece and the machine. Int. J. Mach. Tools Manuf. 2005, 45, 1669–1680. [Google Scholar] [CrossRef]
- Altintaş, Y.; Budak, E. Analytical Prediction of Stability Lobes in Milling. CIRP Ann. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Urbikain, G.; Olvera, D.; López de Lacalle, L.N.; Beranoagirre, A.; Elías-Zuñiga, A. Prediction Methods and Experimental Techniques for Chatter Avoidance in Turning Systems: A Review. Appl. Sci. 2019, 9, 4718. [Google Scholar] [CrossRef]
- Dumanli, A.; Sencer, B. Active control of high frequency chatter with machine tool feed drives in turning. CIRP Ann. 2021, 70, 309–312. [Google Scholar] [CrossRef]
- Wan, S.; Li, X.; Su, W.; Yuan, J.; Hong, J.; Jin, X. Active damping of milling chatter vibration via a novel spindle system with an integrated electromagnetic actuator. Precis. Eng. 2019, 57, 203–210. [Google Scholar] [CrossRef]
- Fernández-Lucio, P.; Del Val, A.G.; Plaza, S.; Pereira, O.; Fernández-Valdivielso, A.; de Lacalle, L.N.L. Threading holder based on axial metal cylinder pins to reduce tap risk during reversion instant. Alex. Eng. J. 2023, 66, 845–859. [Google Scholar] [CrossRef]
- Rubio, L.; Loya, J.A.; Miguélez, M.H.; Fernández-Sáez, J. Optimization of passive vibration absorbers to reduce chatter in boring. Mech. Syst. Signal. Process. 2013, 41, 691–704. [Google Scholar] [CrossRef]
- Miguélez, M.H.; Rubio, L.; Loya, J.A.; Fernández-Sáez, J. Improvement of chatter stability in boring operations with passive vibration absorbers. Int. J. Mech. Sci. 2010, 52, 1376–1384. [Google Scholar] [CrossRef]
- Pelayo, G.U.; Trejo, D.O. Model-based phase shift optimization of serrated end mills: Minimizing forces and surface location error. Mech. Syst. Signal. Process. 2020, 144, 106860. [Google Scholar] [CrossRef]
- Urbikain, G.; Olvera, D.; de Lacalle, L.N.L.; Elías-Zúñiga, A. Spindle speed variation technique in turning operations: Modeling and real implementation. J. Sound. Vib. 2016, 383, 384–396. [Google Scholar] [CrossRef]
- Pelayo, G.U.; Olvera-Trejo, D.; Budak, E.; Wan, M. Special Issue on Machining systems and signal processing: Advancing machining processes through algorithms, sensors and devices. Mech. Syst. Signal. Process. 2023, 182, 109575. [Google Scholar] [CrossRef]
- Urbikain, G.; de Lacalle, L.N.L. MoniThor: A complete monitoring tool for machining data acquisition based on FPGA programming. SoftwareX 2020, 11, 100387. [Google Scholar] [CrossRef]
- Wu, S.; Li, R.; Liu, X.; Yang, L.; Zhu, M. Experimental study of thin wall milling chatter stability nonlinear criterion. Procedia CIRP 2016, 56, 422–427. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, W. Chatter identification in milling of the thin-walled part based on complexity index. Int. J. Adv. Manuf. Technol. Technol. 2017, 91, 3327–3337. [Google Scholar] [CrossRef]
- Yamato, S.; Hirano, T.; Yamada, Y.; Koike, R.; Kakinuma, Y. Sensor-less online chatter detection in turning process based on phase monitoring using power factor theory. Precis. Eng. 2018, 51, 103–116. [Google Scholar] [CrossRef]
- Peng, C.; Wang, L.; Liao, T.W. A new method for the prediction of chatter stability lobes based on dynamic cutting force simulation model and support vector machine. J. Sound. Vib. 2015, 354, 118–131. [Google Scholar] [CrossRef]
- Grossi, N.; Sallese, L.; Scippa, A.; Campatelli, G. Chatter stability prediction in milling using speed-varying cutting force coefficients. Procedia CIRP 2014, 14, 170–175. [Google Scholar] [CrossRef]
- Filippov, A.V.; Nikonov, A.Y.; Rubtsov, V.E.; Dmitriev, A.I.; Tarasov, S.Y. Vibration and acoustic emission monitoring the stability of peakless tool turning: Experiment and modeling. J. Mater. Process. Technol. 2017, 246, 224–234. [Google Scholar] [CrossRef]
- Potočnik, P.; Thaler, T.; Govekar, E. Multisensory chatter detection in band sawing. Proc. CIRP 2013, 8, 469–474. [Google Scholar] [CrossRef]
- Cao, H.; Yue, Y.; Chen, X.; Zhang, X. Chatter detection in milling process based on synchro squeezing transform of sound signals. Int. J. Adv. Manuf. Technol. 2017, 89, 2747–2755. [Google Scholar] [CrossRef]
- Sallese, L.; Grossi, N.; Scippa, A.; Campatelli, G. Investigation and correction of actual microphone response for chatter detection in milling operations. Meas. Control. 2017, 50, 45–52. [Google Scholar] [CrossRef]
- Chaudhary, S.; Taran, S.; Bajaj, V.; Sengur, A. Convolutional neural network based approach towards motor imagery tasks EEG signals classification. IEEE Sens. J. 2019, 19, 4494–4500. [Google Scholar] [CrossRef]
- Ho, Q.N.T.; Do, T.T.; Minh, P.S. Studying the Factors Affecting Tool Vibration and Surface Quality during Turning through 3D Cutting Simulation and Machine Learning Model. Micromachines 2023, 14, 1025. [Google Scholar] [CrossRef]
- Checa, D.; Urbikain, G.; Beranoagirre, A.; Bustillo, A.; de Lacalle, L.N.L. Using Machine-Learning techniques and Virtual Reality to design cutting tools for energy optimization in milling operations. Int. J. Comput. Integr. Manuf. 2022, 35, 951–971. [Google Scholar] [CrossRef]
- Ma, M.; Liu, L.; Chen, Y.A. KM-Net Model Based on k-Means Weight Initialization for Images Classification. In Proceedings of the 2018 IEEE 20th International Conference on High Performance Computing and Communications, IEEE 16th International Conference on Smart City, IEEE 4th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Exeter, UK, 28–30 June 2018; pp. 1125–1128. [Google Scholar] [CrossRef]
- Zheng, M.; Tang, W.; Zhao, X. Hyperparameter optimization of neural network-driven spatial models accelerated using cyberenabled high-performance computing. Int. J. Geogr. Inf. Sci. 2019, 33, 314–345. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. arXiv 2018, arXiv:1608.06993. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv 2014, arXiv:1409.4842. [Google Scholar] [CrossRef]
- Zhu, W.; Zhuang, J.; Guo, B.; Teng, W.; Wu, F. An optimized convolutional neural network for chatter detection in the milling of thin-walled parts. Int. J. Adv. Manuf. Technol. 2020, 106, 3881–3895. [Google Scholar] [CrossRef]
- Tran, M.-Q.; Liu, M.-K.; Tran, Q.-V. Milling chatter detection using scalogram and deep convolutional neural network. Int. J. Adv. Manuf. Technol. 2020, 107, 1505–1516. [Google Scholar] [CrossRef]
- Rahimi, M.H.; Huynh, H.N.; Altintas, Y. Online chatter detection in milling with hybrid machine learning and physics-based model. CIRP J. Manuf. Sci. Technol. 2021, 35, 25–40. [Google Scholar] [CrossRef]
- Sener, B.; Gudelek, M.U.; Ozbayoglu, A.M.; Unver, H.O. A novel chatter detection method for milling using deep convolution neural networks. Measurement 2021, 182, 109689. [Google Scholar] [CrossRef]
- Kounta, C.A.K.A.; Arnaud, L.; Kamsu-Foguem, B.; Tangara, F. Deep learning for the detection of machining vibration chatter. Adv. Eng. Softw. 2023, 180, 103445. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).