Abstract
Multi-cell hexagonal tubes have been applied in a wide range of industries. The present study investigates strengthening a single regular hexagonal tube under a dynamic axial load with three different geometrical shapes. The results are then compared with crashworthiness indicators from the finite element code LS-DYNA using the simple additive weighting method, and the appropriate section of a multi-cell hexagonal tube under dynamic axial load is selected. An idea is further presented by assuming the thicknesses variable for certain parts of the selected section to improve crashworthiness criteria. Combinations with different variable thicknesses in defined thickness intervals are made into a lattice. Numerical tests are performed based on the lattice nodes using LS-DYNA. The regression models for crashworthiness indicators are created using the Minitab software and optimized to find optimum combinations of thicknesses. The optimization results are tested again by LS-DYNA, and the appropriate answers are determined. The comparison of the results of this method with those of optimization with constant thicknesses demonstrates improvement in the crashworthiness indicators.
1. Introduction
Energy absorbers have widespread industrial applications, such as in automobile chassis, helicopter fuselage, trains, offshore platforms, ships, and military equipment [1,2,3,4,5]. Several structures have been suggested for energy absorption during crashes, and scientists have extensively studied thin-walled structures analytically, numerically, and experimentally. Many researchers have investigated the folding behavior of these structures under axial loads. In addition, scientists are exploring nature-inspired designs to develop energy absorbers with superior performance, with honeycomb structures being one of the best-known examples [6,7]. Conventional and hierarchical honeycomb structures are commonly used as good energy absorbers due to their unique deformation and mechanical properties under dynamic impact loads [6].
Metal thin-walled structures have gained popularity as excellent lightweight structural materials due to their strength and energy absorption capability. The collapse mechanism of energy-absorbing structures is significantly influenced by the material used. Aluminum alloys are generally preferred as energy-absorbing materials due to their superior performance in crushing [8,9,10,11].
Alexander [12] proposed a theoretical model for predicting the mean crushing force and energy absorption of cylindrical tubes by axial loading. Wierzbicki and Abramowicz [13] improved this model with an analytical solution to the axial progressive crushing of a square column with thin walls using their super-folding element method. Chen and Wierzbicki [14] investigated the axial crushing resistance of single-cell, double-cell, and triple-cell hollow tubes undergoing quasi-static axial loading, and demonstrated that multi-cell tubes could increase specific energy absorption (SEA) by approximately 15 percent compared to corresponding hollow tubes. Kim et al. [15] suggested the implementation of modified multi-cell configuration sections consisting of four small square cells at the corners of square columns to enhance the crashworthiness capability of square columns. Zhang et al. [16] found that a single-square cell tube has 50 percent less energy absorption than a multi-cell square tube with nine parts. The experimental results by Zhang and Zhang [17] improved the formula for finding the average crushing force of thin-wall multi-cell structures under quasi-static loading by comparing it to the previous formula.
Honeycomb structures have extensive applications and have been developed with innovative designs to improve their anti-impact performance. Niknejad and Liaghot [18] derived a mathematical formula for the instantaneous folding force in a hexagonal tube under axial load, which they found to agree well with experimental results. Qiu and Gao [19] applied finite element analysis to consider the crashworthiness indicators of different multi-cell hexagonal cross-sectional tubes under axial dynamic loading. They tested a multi-criteria decision-making method for selecting the optimal sectional configuration and studied the optimization of multi-cell hexagonal tubes subjected to axial load. Alavi Nia and Parsapour [20] conducted numerical and experimental studies on the crushing behavior of polygonal multi-cell tubes, finding that multi-cell tubes with octagonal and hexagonal sections absorbed the highest amount of energy per unit mass. Altin and Acar [21] used surrogate-based optimization for honeycomb structures to achieve maximum specific energy absorption.
Hierarchical design can be used as a reinforcement strategy for innovative structures that can be further developed. Researchers have reported that hexagonal structures exhibit excellent behavior and have the largest available area [22]. The response surface method (RSM), a statistical technique that uses quantitative data, can be used to determine a regression model and improve the response influenced by input variables [23].
The present study uses a numerical method to investigate the crashworthiness performance of hexagonal structures with three reinforcement patterns under dynamic axial loading. The simple additive weighting (SAW) method selects the most suitable configuration. It is assumed that all thicknesses of this section of the multi-cell tube are variable. Regression models for crashworthiness criteria are then created based on the results of finite element analysis (FEA) tests in domain sampling. Finally, the regression models are optimized to obtain an efficient approach for determining the optimal thicknesses.
2. Problem Description
2.1. Geometrical Parameters
Honeycomb structures typically feature repeated hexagonal patterns. In this study, a larger regular hexagon with an inner side width of 48 mm was filled with seven smaller regular hexagonal cells, with a side width of 16 mm for the smaller hexagonal tubes. The side of the smaller hexagons that coincides with the side of the larger hexagon (type A in Figure 1) is omitted. Figure 1 shows two reinforcement connections: those between the vertex of an incomplete small hexagon and a larger hexagon (type B) and those between the vertices of adjacent small hexagons (type C). The figure displays three cross-sectional configurations of multi-cell hexagonal tubes (types A, B, and C), all with a length of 180 mm. The thickness of the main hexagonal tube is assumed to be 1.6 mm, and the thickness of all inner edges in different sections is 0.8 mm.
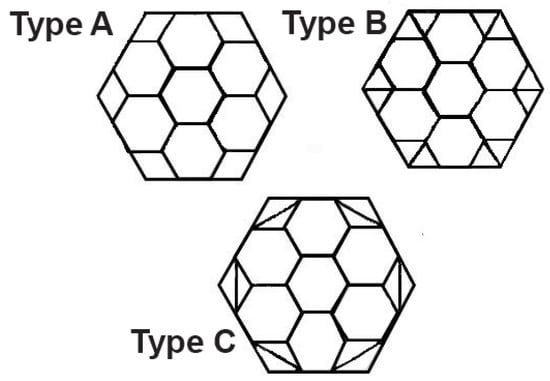
Figure 1.
Schematic of different sections of multi-cell hexagonal tubes.
2.2. Numerical Analysis
The finite element code LS-DYNA was used to solve the axial dynamic compression problem. A striker with an initial mass of 600 kg and velocity of 15 m/s was used to strike the top of the tube. The bottom of the tube was held in place by a rigid base (Figure 2).
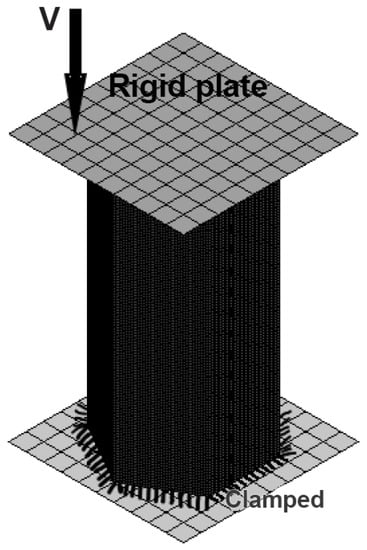
Figure 2.
Finite element model under dynamic axial load.
2.2.1. Model Properties and Verification
The tubes used in this study were made of aluminum 6061, with the following mechanical properties: Young’s modulus = 68 GPa, density = 2700 kg/m, ultimate strength = 130.7 MPa, initial yield strength = 71 MPa, Poisson’s ratio = 0.33, and strain hardening exponent = 0.18.
The aluminum alloy was modeled in LS-DYNA using elastic–plastic material model 123 with piecewise linear plastic hardening. The crash distance was defined as two-thirds of the original tube length, resulting in a crash distance of 120 mm. The equivalent time for this crash distance was 8 milliseconds, obtained from the displacement–time curve.
The Belytschko–Tsay shell element is known for its high accuracy and speed in thin-shell simulations, making it highly recommended for implicit simulations. This study used the Belytschko–Tsay four-node shell elements with five integration points in the thickness direction. The optimal mesh size was set at 1.5 mm because a finer mesh did not cause a significant change in the energy absorption as calculated by numerical tests. The Contact-Automatic-Nodes-to-Surface algorithm was created to examine the contact interactions between a mass block and tube as well as between the tube and a rigid base. Additionally, the Contact-Automatic-Single-Surface algorithm was used to establish contact between the outer walls and the inner ribs of the tube, preventing interpenetration during progressive buckling. The hourglass control was employed to avoid spurious zero deformation modes and volumetric locking based on stiffness. The ratio of the total kinetic energy to the total internal energy was maintained at less than . These methods have been previously documented in [19,24].
The finite element modeling method was verified by comparing the simulation results of the single-wall regular hexagonal tube model under quasi-static and dynamic axial compression load with the analytical solutions of the average force for a single-wall hexagonal tube. The theoretical formula for the average force for a single hexagonal tube under quasi-static load, as proposed by Zhang and Qiu [17,25], can be expressed as follows:
In Equation (2), represents the flow stress, represents the yield stress, and indicates the ultimate stress. The exponent of the power law n is equal to 0.18. Substituting these values into the equation obtains a flow stress () of 88.68 MPa. The parameter B represents the half length of the outer side width of the hexagonal tube, while t represents its wall thickness. In this case, B = 24 mm and t = 1.6 mm. The effective crash distance to the original length ratio (k) is 0.78 for a single wall tube [11].
The above values were placed into Equation (1) to obtain the mean crush force, yielding a value of 13.01 KN for F. A manufactured sample and the DBSL-SJ-30 machine model from Transcell Technology Company were utilized for the experimental quasi-static test. The mechanical properties of the specimen material were previously tested. The axial crush testing was quasi-static, with a 5 mm/min loading speed and a 150 KN capacity. The resulting mean crush force for the single aluminum hexagonal tube was 12.4 KN, consistent with the theoretical formula. Figure 3 shows the dimensions of the hexagonal tube and the quasi-static test. The relative error between the experimental and theoretical results is 5.6%. In the numerical quasi-static test with LS-DYNA software, the average crush force was determined as 11.68 KN, resulting in a relative error of 5.8% compared to the experimental quasi-static test. Tran and Hou [26] have noted that the strain rate has a negligible effect on aluminum alloy and can be disregarded. A dynamic coefficient parameter () was introduced to consider the inertia effect. The range of possible values is between 1.1 and 1.6, and was set as 1.1 in this study [19].

Figure 3.
Hexagonal specimen for axial compression test and experimental test setup.
The theoretical dynamic average response force is denoted by F, and was calculated using Equation (3) as 14.31 KN. In contrast, for the FEM model numerical analysis, the dynamic average force was extracted using LS-DYNA, resulting in F = 12.90 KN. Thus, a relative error of approximately 9.8% was identified between the FEA model and the theoretical solution. When the value obtained from the experimental quasi-static test for the mean crash force with a dynamic coefficient parameter is converted, for a resulting value of F = 13.64 KN. Consequently, the relative error between the quasi-static experimental test using a dynamic coefficient and the dynamic finite element test was 5.4%.
2.2.2. Definition of Crashworthiness Indicators
The crashworthiness criteria of various multi-cell tubes were compared under axial dynamic loading. These criteria include the specific energy absorption (SEA), crushing force efficiency (CFE), and peak crushing force (F). The SEA can be calculated using the following equation:
In the above formula the mass of the multi-cell tube is represented by m, while E denotes the energy absorbed during a crash. The maximum crushing force (F) is a crucial safety indicator for vehicles, as it is related to deceleration and the risk of severe injury to occupants. Therefore, a higher F value is undesirable. The average crush force (F) is obtained by dividing the energy absorption (E) by the effective length of the tube ().
The ratio of the average response force to the peak response force is defined as the crushing force efficiency.
The ideal crushing force efficiency is unity, and when it occurs, F is equal to F.
3. Selecting the Applicable Multi-Cell Tube with the SAW Method Based on the Numerical Results of Different Sections of the Multi-Cell Structure under Axial Dynamic Loading
The LS-DYNA software was used to generate the crushing force–time diagram for each of the three sections (types A, B, and C) of multi-cell hexagonal tubes subjected to dynamic axial loads. These diagrams are presented in Figure 4, with a maximum impact time of 8 ms, corresponding to the point when the striker passes the effective length of the tube (2/3 of the total length). During impact, there is a linear relationship between displacement and time. The energy absorption–time diagrams for all three types of tubes are shown in Figure 5, Figure 6 and Figure 7, illustrating the deformation mode of type A, B, and C multi-cell hexagonal tubes under axial dynamic loads at t = 8 ms.
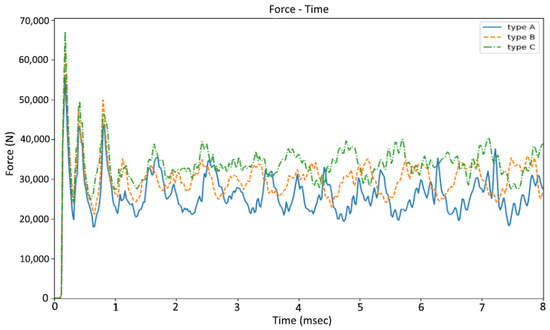
Figure 4.
The responding crushing force–time graph for different sectional configurations of hexagonal multi-cell tubes (type A, type B, and type C).
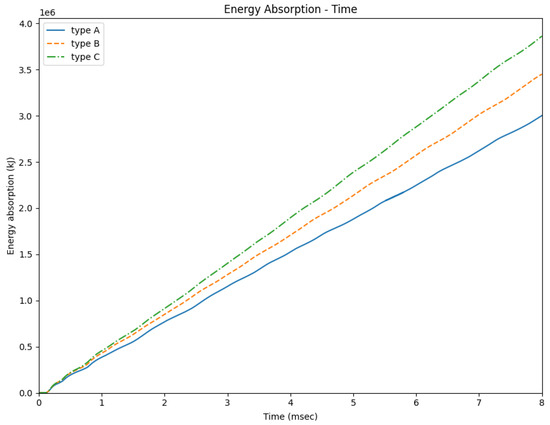
Figure 5.
The energy absorption–time curves for different sectional configurations of hexagonal multi-cell tubes (type A, type B, and type C).
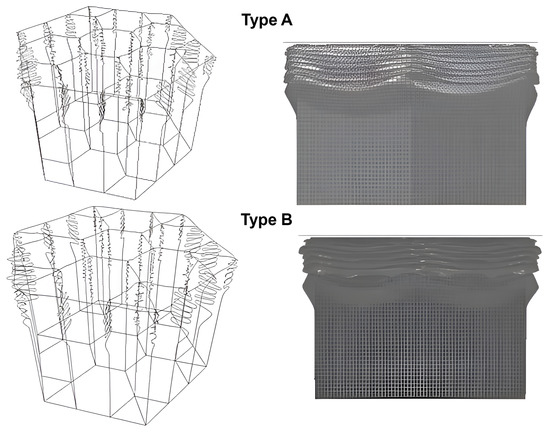
Figure 6.
Different deformation mode (Isometric line and front) views of multicell hexagonal tubes (types A and B) under dynamic axial load at a time equal to 8 ms.
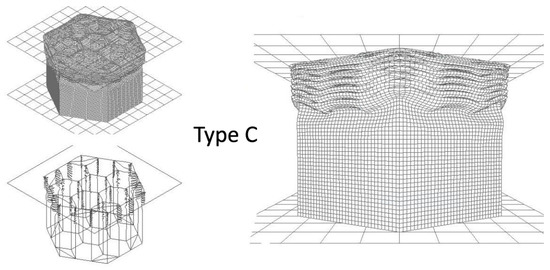
Figure 7.
Deformation view of the multi-cell hexagonal tube (type C) under dynamic axial load (Isometric, Isometric line mode, and front) at a time equal to 8 ms.
The values obtained directly from the FEA tests are shown in Table 1.

Table 1.
Crashworthiness criteria results of different configuration types (A, B, and C) obtained directly from FEA.
The present study used the Simple Additive Weighting (SAW) method to calculate the appropriate cross-sectional shape of the examined tubes. This is a multi-attribute procedure that utilizes the principle of weighted summation. In order to apply SAW, the decision matrix should be normalized to a scale comparable with all existing alternatives. The SAW procedure involves four steps, as outlined in [23].
Step 1. Normalized decision matrix when the criterion has a positive concept:
When the criterion has a negative concept:
Step 2. represents the weight of the criteria, which can be obtained in different ways. In this study, the analytic hierarchy process (AHP) was utilized. Initially, paired comparison matrices were created for the indicators and types based on their respective importance. The complete method is described in the study of Saaty [24].
Step 3. Calculate the preference using the following:
Step 4. The alternatives are ranked from the highest to the lowest value, with larger values of indicating those alternatives that receive a higher rank.
In this study, the SAW method was used to evaluate a decision matrix of 3 × 3 (Table 2), which involved four steps.

Table 2.
Decision matrix.
Step 1. The following process was used to calculate the normalization matrix for the positive concepts (SEA in the first column and CFE in the third) according to Equation (7) and for the negative concept (F in the second column) according to Equation (8).
Step 2. In this scenario, SEA is considered more important than F and CFE is considered less important. Based on the importance of each indicator, the matrices shown below are formed. The sum of the values in each column is calculated and the values of each column are divided by the algebraic sum of that column; then, the average is calculated for each row. Note that the algebraic sum of the weights must be equal to one.
Here, the weights of SEA, F, and CFE were set as 0.540, 0.297, and 0.163, respectively.
Step 3. The numerical values from Steps 1 and 2 are substituted according to Equation (9).
Step 4. Here, = 0.9504 is the highest value of V (i = 1, 2, 3). Accordingly, type C is the best selection of multi-cell cross-sectional hexagonal tubes under dynamic axial load.
4. Optimization of the Selected Section of the Multi-Cell Hexagonal Tube with Variable Thicknesses
4.1. Problem Explanation
The section of the multi-cell hexagonal tube selected for this study was type C, as it exhibited the best performance under axial dynamic loading. Edge thicknesses were then assumed to be variable (Figure 8) and represented by , , , and . Regression equations were created for each criterion using LS-DYNA tests to improve the crashworthiness criteria. The optimum thicknesses within the design intervals were determined through an optimization process to develop a crashworthiness energy absorber that dissipated more energy with less material. For safety reasons, the peak force value (F) was defined as less than or equal to an acceptable level of 70 KN, as suggested in several previous research papers [27,28]. The goal was to achieve the best crushing force efficiency (CFE) by ensuring that the average crushing force (F) was equal to F.
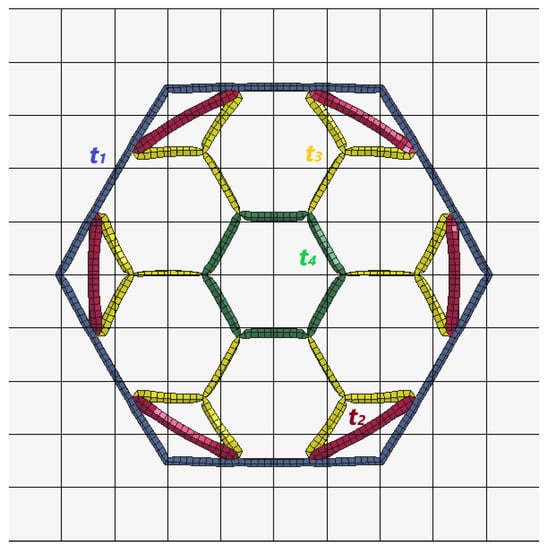
Figure 8.
Regular hexagonal multi-cell tube type C with variable thicknesses ( blue, red, yellow, and green).
4.2. Regression Model
Regression is a statistical method used to establish a relationship between several variables and a single response of a system. The response surface method has been successfully applied in various fields, with regression models constructed based on experimental or finite element analysis (FEA) results. A statistical approach such as regression modeling can be used for optimization purposes. Polynomial functions are commonly employed in constructing regression models. In the multi-cell hexagonal tube section examined in this study, all the edges were thin-wall members and thickness intervals of 0.8 mm ≤ ≤ 2.0 mm and 0.4 mm ≤ , , ≤ 1.0 mm were selected.
This paper utilizes polynomial functions to estimate SEA, F, and CFE. A mesh of sampling points was generated by designing sample points in different domains of each design thickness () with all possible data. The numerical range for was divided into three limits: lower, middle, and upper (0.8 mm, 1.4 mm, and 2.0 mm). The thickness range of the inner edges of , , and was divided into four parts with increasing growth of 0.2 mm (0.4 mm, 0.6 mm, 0.8 mm, and 1.0 mm). It was assumed that the thickness of the main edges of the hexagonal tube should be greater than or equal to each thickness of the inner edges. For instance, the combination of = 0.8 mm, = 1.0 mm, = 0.4 mm, and = 0.8 mm was removed from the numerical tests because > . A total of 156 numerical tests were performed using LS-DYNA software for these thickness combinations, and ten combinations were randomly selected to validate the regression models.
The LS-DYNA software was used to directly extract the results of energy absorption, mass, and peak force. The mean force, specific energy absorption, and crashing force efficiency were calculated using mathematical equations (Equations (4)–(6)). The regression models for SEA, F, and CFE were constructed using Minitab statistical software based on the results of FEA tests. The Pareto chart was initially used to evaluate the effect of different thicknesses. Figure 9 shows the Pareto chart for SEA, illustrating the importance of different thicknesses and powers and their products based on their effect. The goodness-of-fit statistical test was used to measure how well the sample data fit the population distribution as a normal distribution to ensure good accuracy in regressions. The criteria for determining the accuracy of the regressions are explained in the following.
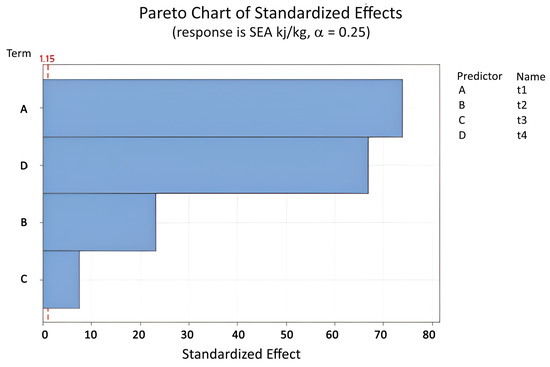
Figure 9.
Pareto chart of standardized effect of variable thicknesses (, , , ) for SEA (Equation (12)).
The relative squared error (R-sq, known as the determination coefficient) is a statistical measurement between observed data in a problem and the fitted regression line, and is defined as the percentage of variation in response. When the fit between the data and the model has higher accuracy, this indicates a greater R-sq value. The formulation of R-sq is as follows:
where N is the number of observations, y is the dependent variable, represents the mean of the y values, and represents the predicted value of the model.
R-sq (adjusted) can decrease when fewer important factors are added, making it a more accurate method than R-sq, which can only increase. R-sq (predicted) is utilized to measure how effectively a model predicts the response of new data; models with higher values are more predictive. It is more useful for comparing models than R-sq (adjusted), as it is derived from observations not included in the model construction.
In the above equation, N represents the number of observations (samples) and p the number of predictors. Linear fitting regression models for the response functions of SEA, F, and CFE were obtained based on the forward selection method using Minitab software (Table 3, Table 4 and Table 5) [22].

Table 3.
Summary statistics of linear SEA regression model.

Table 4.
Summary statistics of F linear regression model.

Table 5.
Summary statistics of CEF linear regression model.
The linear regressions demonstrate moderate accuracy. As shown in Figure 9, all variable thicknesses have a higher standardized effect coefficient than regression. The important influence of these variable thicknesses (, , , ) is shown in Equation (12) and Figure 9. To ensure higher accuracy of the linear regression models, the order of variables was increased to the second order; the pairwise interactions , , , , , and were included, while parameters with less impact were removed based on the defined index. The new regression models are represented by Equations (15)–(17) and in Table 6, Table 7 and Table 8. Figure 10 shows the effect of the different variables on the regression model for SEA.

Table 6.
Summary statistics for SEA quadratic regression model.

Table 7.
Summary statistics for F quadratic regression model.

Table 8.
Summary statistics for CFE quadratic regression model.
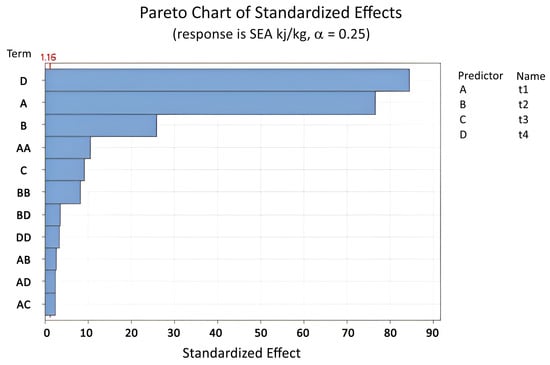
Figure 10.
Pareto chart of standardized effect of variable thicknesses (, , , ) for SEA (Equation (15)).
For higher accuracy of the model, the order of variables was increased to three and interactions were used up to the second order (Equations (18)–(20) and Table 9, Table 10 and Table 11). The effects of the different parameters in Equation (18) are shown in Figure 11.

Table 9.
Summary statistics for SEA regression model.

Table 10.
Summary statistics for F regression model.

Table 11.
Summary statistics for CFE regression model.
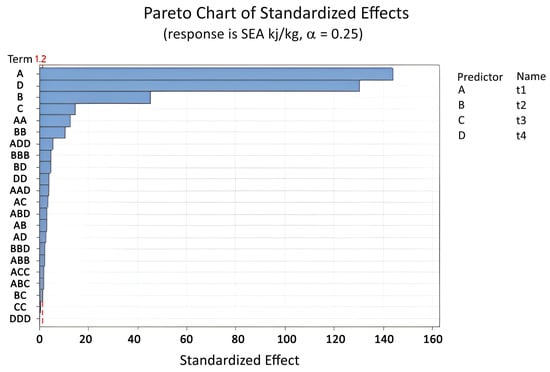
Figure 11.
Pareto chart of standardized effect of variable thicknesses (, , , ) for SEA (Equation (18)).
The results of the regression models agree with those of the LS-DYNA software, even when the striker angle with the horizon is less than three degrees.
4.3. Optimization of Different Variable Thicknesses of Multi-Cell Tube under Dynamic Axial Load
Following the construction of the SEA, F, and CFE functions, two optimization plans are used to find the best design thicknesses that can satisfy the required conditions.
4.3.1. Plan A: Optimization of Variable Thicknesses Aimed at Increasing Specific Energy Absorption and Acceptable Peak Force
The regression model of SEA and the constraint of peak force [29,30] define the optimization problem for a multi-cell hexagonal tube as follows:
The optimal thicknesses are determined using the response optimizer in Minitab software. This method uses a regression model formed for each indicator and optimizes them with appropriate settings. It proposes several sets of suitable thicknesses which FEA tests directly. They are introduced as a group of answers if they confirm the optimization conditions. The optimal results have been further verified by the solver of the genetic algorithm (GA).
Certain thickness optimization results were eliminated, as they did not satisfy the optimization conditions (Equation (21)) after the FEA tests. For example, the solution = 2.000 mm, = 0.745 mm, = 0.400 mm, and = 1.000 mm is obtained with response optimizer F = 70.3 KN, which is greater than the constraint of 70 KN peak force, and as such was omitted.
Finally, five optimal options were confirmed (Table 12), with the best combination of thicknesses being = 2.000 mm, = 0.509 mm, = 0.917 mm, and = 1.000 mm (Figure 12).

Table 12.
Results of the suggested thickness design points for Plan A optimization conditions.
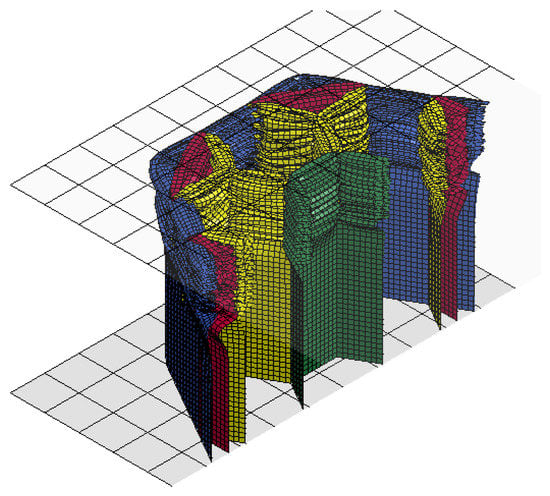
Figure 12.
The cutting part of the isometric view of the optimum multi-cell hexagonal tube under dynamic axial load at time = 8 ms ( blue, red, yellow, and green).
If = 2 mm and = = = , according to the optimization conditions in Equation (21) and re-examining the answers extracted by LS- DYNA, the solution is = 0.741 mm, F = 70 KN, and SEA = 8.9604, which is approximately 7.36% lower than optimal thicknesses. This demonstrates the importance of using different thicknesses for the different inner parts of the multi-cell hexagonal tube in order to improve the crashworthiness indicators.
4.3.2. Plan B: Optimization of Thicknesses Aimed at Crushing Force Efficiency and Acceptable Peak Force
Increasing the crash force efficiency (CFE) while limiting the picking force is defined as follows:
The optimization results for the CFE model were obtained using the response optimizer and tested again with the LS-DYNA software. The optimal results are listed in Table 13. One favorable solution for CFE is the combination of thicknesses with = 2.000 mm, = 0.552 mm, = 0.4 mm, and = 1.0 mm. Here, the CFE value obtained from the regression model is 60.375% and the FEA solution is 61.320%.

Table 13.
Results of the suggested thickness design points for Plan B optimization conditions.
5. Conclusions
This paper explored three configurations (types A, B, and C) of multi-cell hexagonal tubes under dynamic axial loading and used the finite element code LS-DYNA to evaluate their crashworthiness. The study began by selecting the most suitable section of a multi-cell hexagonal tube using the simple additive weighting (SAW) method. The selected section was further analyzed using variable thicknesses (, , , ). A design domain was established to select different combinations of thicknesses, creating a lattice of points for nonlinear numerical tests. Each point in the lattice represented a unique combination of four different thicknesses for different section parts. Finite element analysis (FEA) tests were then conducted on each point to calculate the crashworthiness criteria, including SEA, F, and CFE. The results were recorded and used to create an accurate regression model for these criteria using Minitab software. Polynomial functions were optimized using the response optimizer to improve crashworthiness indicators compared to scenarios in which all edges had the same thickness. The optimization results provided several options for thickness combinations that enhanced the crashworthiness criteria. This method of using variable thicknesses can be applied to improve the design of multi-cell energy absorbers and optimize their crashworthiness.
Author Contributions
The initial plan of this research was formed by R.S., with the management and consultation of M.M.M. The validation of the numerical model was done by R.S. and its testing in the laboratory under the supervision of M.M.M. and Y.M. R.S. used LS-DYNA and Minitab software to create and analyze the results in coordination with M.M.M., the research supervisor and Y.M., the project consultant. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data that support the findings of this study, including the results of experimental and analytical tests, K files, and the results of building regressions and optimizing combinations, are available and can be provided upon request from the corresponding author.
Conflicts of Interest
The authors declare that they have no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SEA | Specific energy absorption |
| F | Average force |
| F | Peak force |
| CEF | Crushing force efficiency |
| Flow stress | |
| Yield stress | |
| Ultimate stress | |
| n | Exponent of the power law |
| S | Standard deviation |
| E | Crash energy absorbed |
| m | Mass of tube |
| B | Outer side width |
| t | Thickness |
| Effective length | |
| K | The ratio of the effective crash distance to the original length |
| Dynamic coefficient | |
| SAWM | Simple additive weighting method |
| R-sq | Relative squared error |
| p | Number of samples |
| N | Number of observations |
| AHPM | Analytic hierarchy process method |
References
- Wei, L.; Zhao, X.; Yu, Q.; Zhu, G. Quasi-static axial compressive properties and energy absorption of star-triangular auxetic honeycomb. Compos. Struct. 2021, 267, 113850. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Li, Z.; Shi, C. On the crashworthiness of bio-inspired hexagonal prismatic tubes under axial compression. Int. J. Mech. Sci. 2020, 186, 105893. [Google Scholar] [CrossRef]
- Jiang, H.; Ren, Y.; Jin, Q.; Zhu, G.; Hu, Y.; Cheng, F. Crashworthiness of novel concentric auxetic reentrant honeycomb with negative Poisson’s ratio biologically inspired by coconut palm. Thin-Walled Struct. 2020, 154, 106911. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Z.; Yang, Z.; Li, X. In-plane dynamic crushing behaviors of a novel auxetic honeycomb with two plateau stress regions. Int. J. Mech. Sci. 2019, 151, 746–759. [Google Scholar] [CrossRef]
- Dong, Z.; Li, Y.; Zhao, T.; Wu, W.; Xiao, D.; Liang, J. Experimental and numerical studies on the compressive mechanical properties of the metallic auxetic reentrant honeycomb. Mater. Des. 2019, 182, 108036. [Google Scholar] [CrossRef]
- Wang, Z. Recent advances in novel metallic honeycomb structure. Compos. Part Eng. 2019, 166, 731–741. [Google Scholar] [CrossRef]
- Mirfendereski, L.; Salimi, M.; Ziaei-Rad, S. Parametric study and numerical analysis of empty and foam-filled thin-walled tubes under static and dynamic loadings. Int. J. Mech. Sci. 2008, 50, 1042–1057. [Google Scholar] [CrossRef]
- Wierzbicki, T. Crushing analysis of metal honeycombs. Int. J. Impact Eng. 1983, 1, 157–174. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 1–510. [Google Scholar] [CrossRef]
- Tran, V.X.; Hong, S.T.; Pan, J.; Tyan, T.; Prasad, P. Crush behaviors of aluminum honeycombs of different cell geometries under compression dominant combined loads. Sae Tech. Pap. 2006, 22, 73–109. [Google Scholar] [CrossRef]
- Kocabas, I.; Yilmaz, H. Crashworthiness Performance of Al6061 Tubes with Stiffened Quatrefoil Sections under Axial and Oblique Impact Conditions. MÜHendis Makina 2021, 63, 23–40. [Google Scholar] [CrossRef]
- Alexander, J.M. An approximate analysis of the collapse of thin cylindrical shells under axial loading. Q. J. Mech. Appl. Math. 1960, 13, 10–15. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Abramowicz, W. On the Crushing Mechanics of Thin-Walled Structures. J. Appl. Mech. 1983, 50, 727–734. [Google Scholar] [CrossRef]
- Chen, W.; Wierzbicki, T. Relative merits of single-cell, multi-cell and foam-filled thin-walled structures in energy absorption. Thin-Walled Struct. 2001, 39, 287–306. [Google Scholar] [CrossRef]
- Kim, H.S. New extruded multi-cell aluminum profile for maximum crash energy absorption and weight efficiency. Thin-Walled Struct. 2002, 40, 311–327. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, G.; Zhang, H. Theoretical prediction and numerical simulation of multi-cell square thin-walled structures. Thin-Walled Struct. 2006, 44, 1185–1191. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H. Numerical and theoretical studies on energy absorption of three-panel angle elements. Int. J. Impact Eng. 2012, 46, 23–40. [Google Scholar] [CrossRef]
- Niknejad, A.; Liaghat, G.H.; Moslemi Naeini, H.; Behravesh, A.H. A theoretical formula for predicting the instantaneous folding force of the first fold in a single cell hexagonal honeycomb under axial loading. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2010, 224, 2308–2315. [Google Scholar] [CrossRef]
- Qiu, N.; Gao, Y.; Fang, J.; Feng, Z.; Sun, G.; Li, Q. Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases. Finite Elem. Anal. Des. 2015, 104, 89–101. [Google Scholar] [CrossRef]
- Alavi Nia, A.; Parsapour, M. Comparative analysis of energy absorption capacity of simple and multi-cell thin-walled tubes with triangular, square, hexagonal and octagonal sections. Thin-Walled Struct. 2014, 74, 155–165. [Google Scholar] [CrossRef]
- Altin, M.; Acar, E.; Güler, M.A. Crashworthiness optimization of hierarchical hexagonal honeycombs under out-of-plane impact. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2021, 235, 963–974. [Google Scholar] [CrossRef]
- Maulud, D.; Abdulazeez, A.M. A Review on Linear Regression Comprehensive in Machine Learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Ibrahim, A.; Surya, R.A. The Implementation of Simple Additive Weighting (SAW) Method in Decision Support System for the Best School Selection in Jambi. In Proceedings of the Journal of Physics: Conference Series, Bandar Lampung, Indonesia, 9–11 August 2019; IOP Publishing: Bristol, UK, 2019; Volume 1338, p. 12054. [Google Scholar] [CrossRef]
- Saaty, R.W. The analytic hierarchy process-what it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Qiu, N.; Gao, Y.; Fang, J.; Sun, G.; Kim, N.H. Topological design of multi-cell hexagonal tubes under axial and lateral loading cases using a modified particle swarm algorithm. Appl. Math. Model. 2018, 53, 567–583. [Google Scholar] [CrossRef]
- Tran, T.; Hou, S.; Han, X.; Chau, M. Crushing analysis and numerical optimization of angle element structures under axial impact loading. Compos. Struct. 2015, 119, 422–435. [Google Scholar] [CrossRef]
- Liu, Y. Crashworthiness design of multi-corner thin-walled columns. Thin-Walled Struct. 2008, 46, 1329–1337. [Google Scholar] [CrossRef]
- Kurtaran, H.; Eskandarian, A.; Marzougui, D.; Bedewi, N.E. Crashworthiness design optimization using successive response surface approximations. Comput. Mech. 2002, 29, 409–421. [Google Scholar] [CrossRef]
- Hou, S.; Li, Q.; Long, S.; Yang, X.; Li, W. Crashworthiness design for foam filled thin-wall structures. Mater. Des. 2009, 30, 2024–2032. [Google Scholar] [CrossRef]
- Qin, R.; Zhou, J.; Chen, B. Crashworthiness Design and Multiobjective Optimization for Hexagon Honeycomb Structure with Functionally Graded Thickness. Adv. Mater. Sci. Eng. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).