Temperature Rise Calculation of the High Speed Magnetic Suspension Motor Based on Bidirectional Electromagnetic–Thermal–Fluid Coupling Analysis
Abstract
1. Introduction
2. Models and Methods
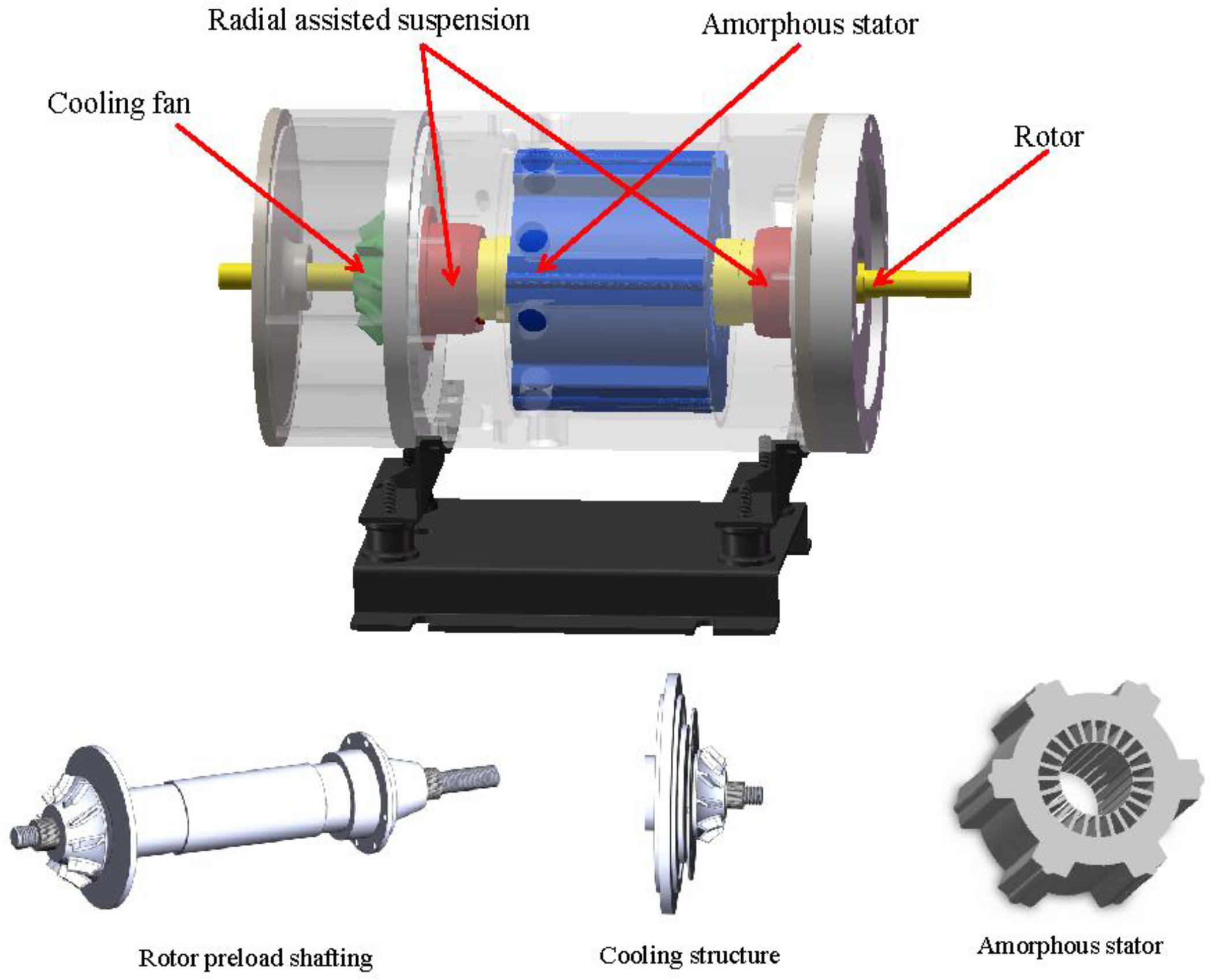
2.1. Physical Model
2.2. Mathematic Model
2.3. Methods
2.3.1. Meshing and Boundary Conditions
- Considering the symmetry and heat transfer characteristics of the motor structure, as well as the requirements of the computer hardware, the 1/12 region of the motor is taken as the research object in order to improve the analysis efficiency.
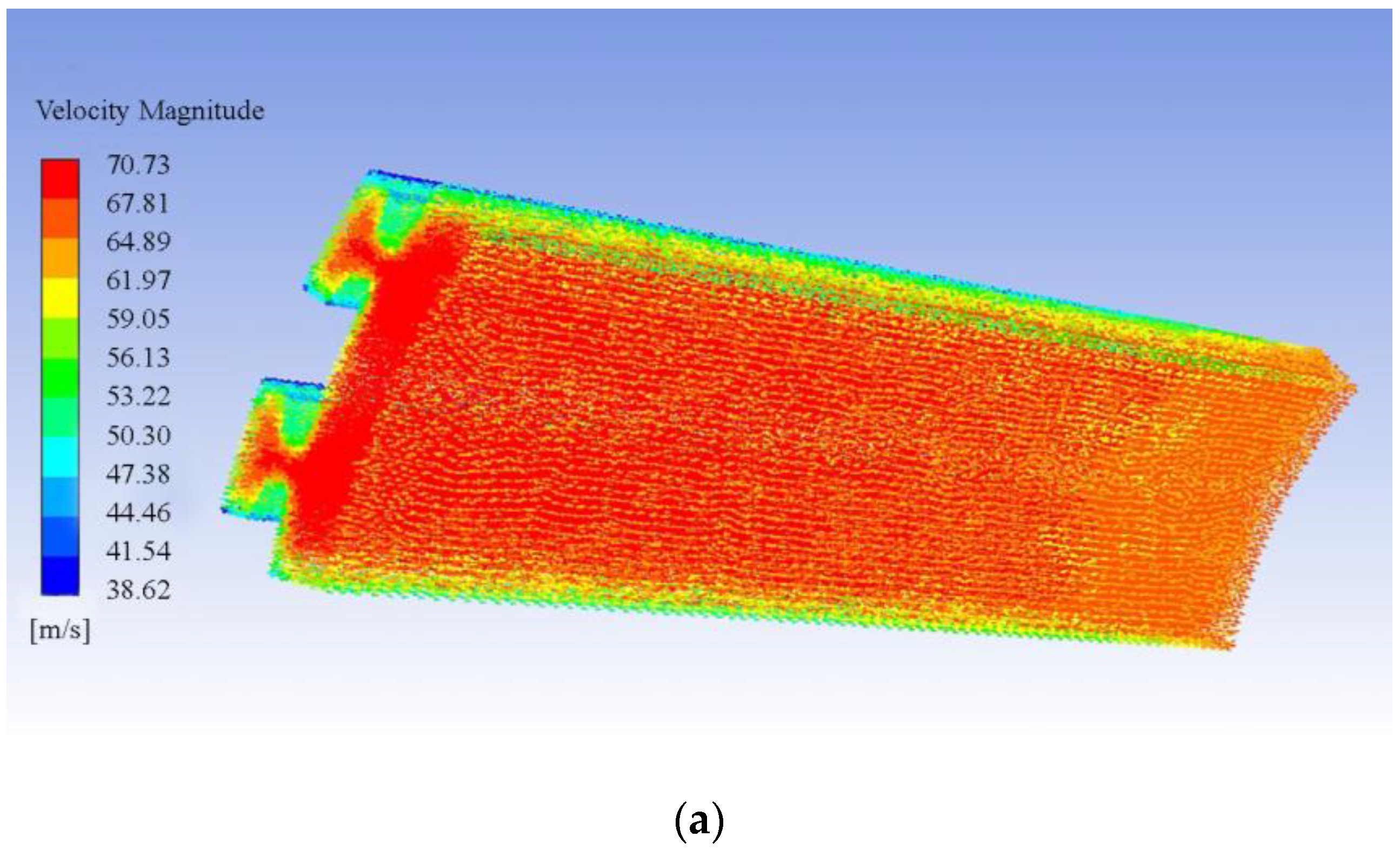
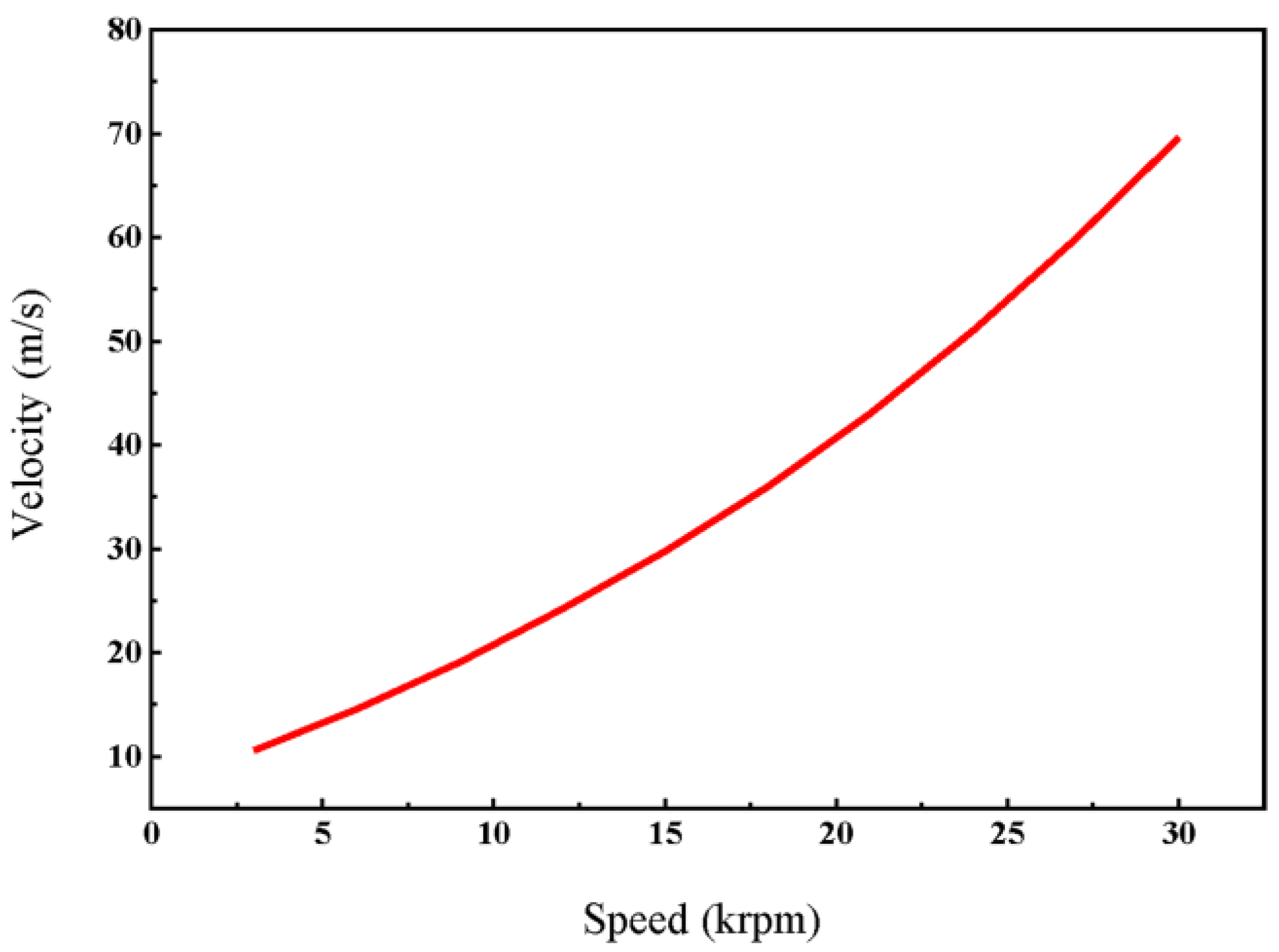
- In the solution domain of the temperature field analysis, the inlet boundary condition is the air speed of the cooling fan, and the cooling air speed varies with the motor speed. At 30 krpm, the inlet air speed is 70 m/s, the outlet is set as the pressure outlet boundary condition, the outlet pressure is 1 standard atmosphere, and the ambient temperature is 26.5 °C.
- When the high speed motor speed becomes larger, the internal air Reynolds number is much higher for turbulent flow. Therefore, the standard k-ε model is used to solve the flow field. The rotor and air gap interface is the moving boundary, and the speed at the interface is set as the rotor speed.
- The amorphous stator core, winding, rotor core, and permanent magnet in the solution domain are all heat sources. Due to the relatively low surface temperature of the external motor housing, the influence of radiation heat transfer is ignored.
- The performance parameters of the materials used in each part of the motor are shown in Table 2. Since Fluent simulation can simulate the actual test environment of the motor, the parameter of convective heat transfer coefficient does not need input. Only parameters such as boundary conditions and material properties of the motor need to be input into the temperature field model.
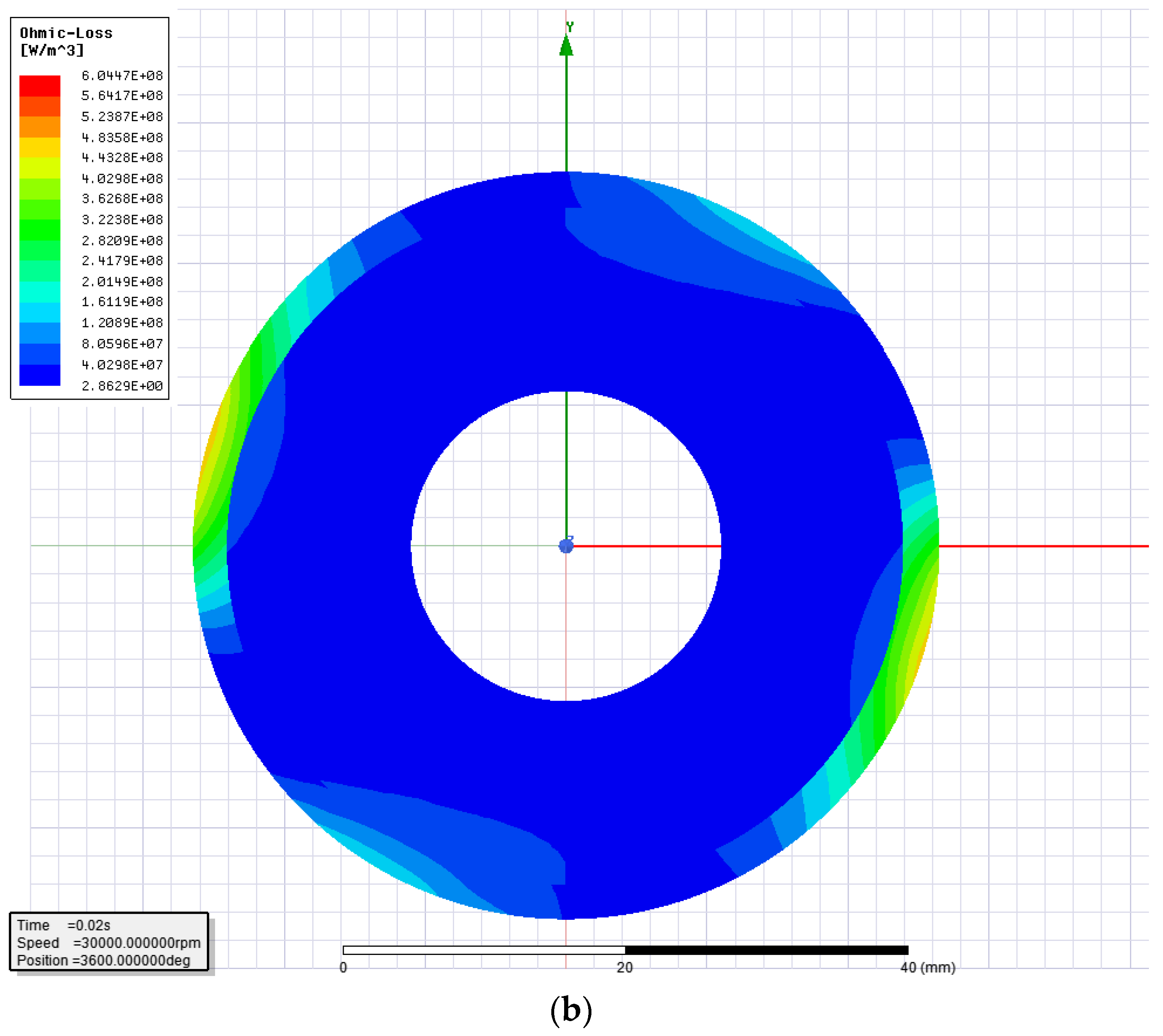
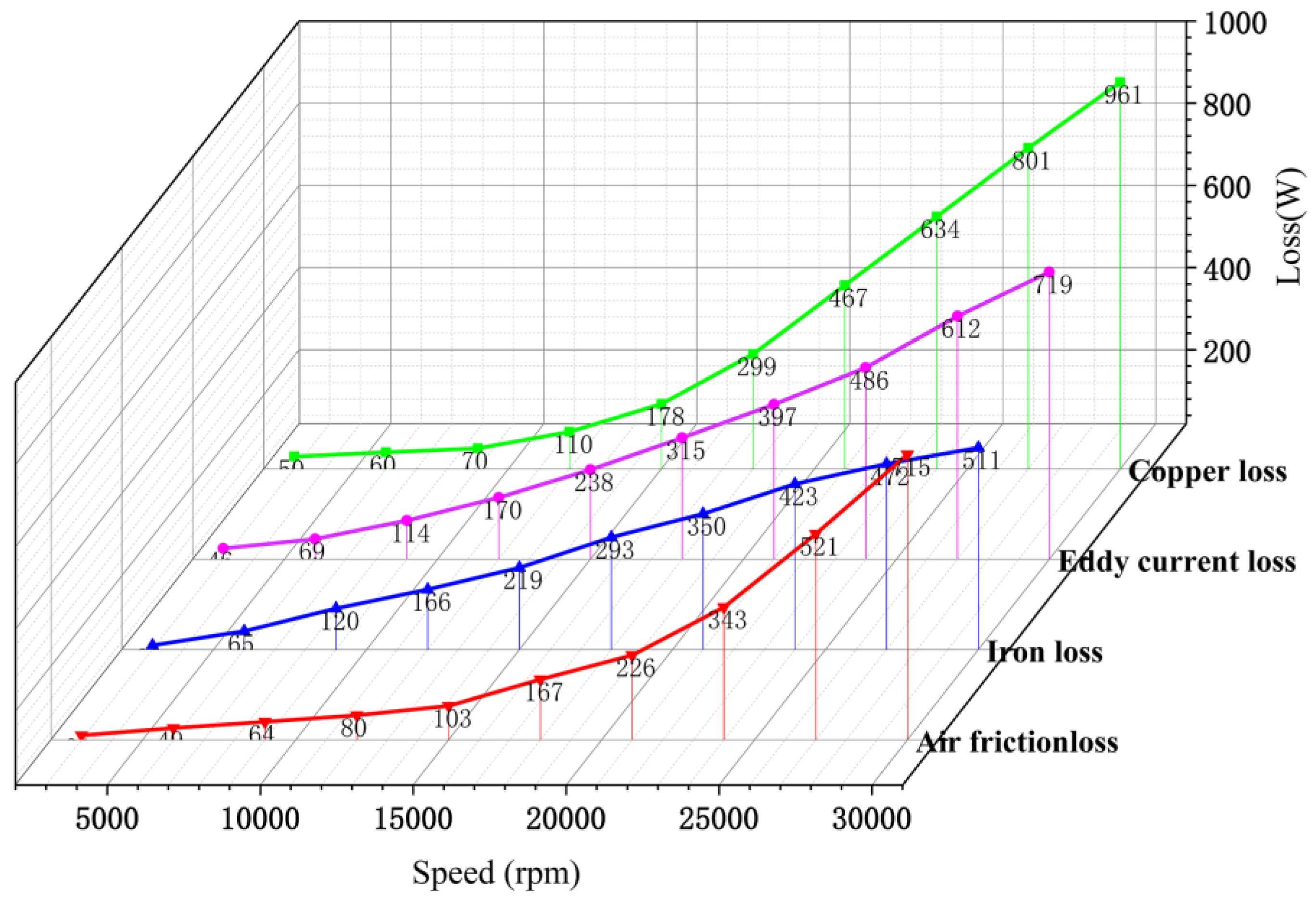
2.3.2. Calculation of the Heat Source of the Electromagnetic Field
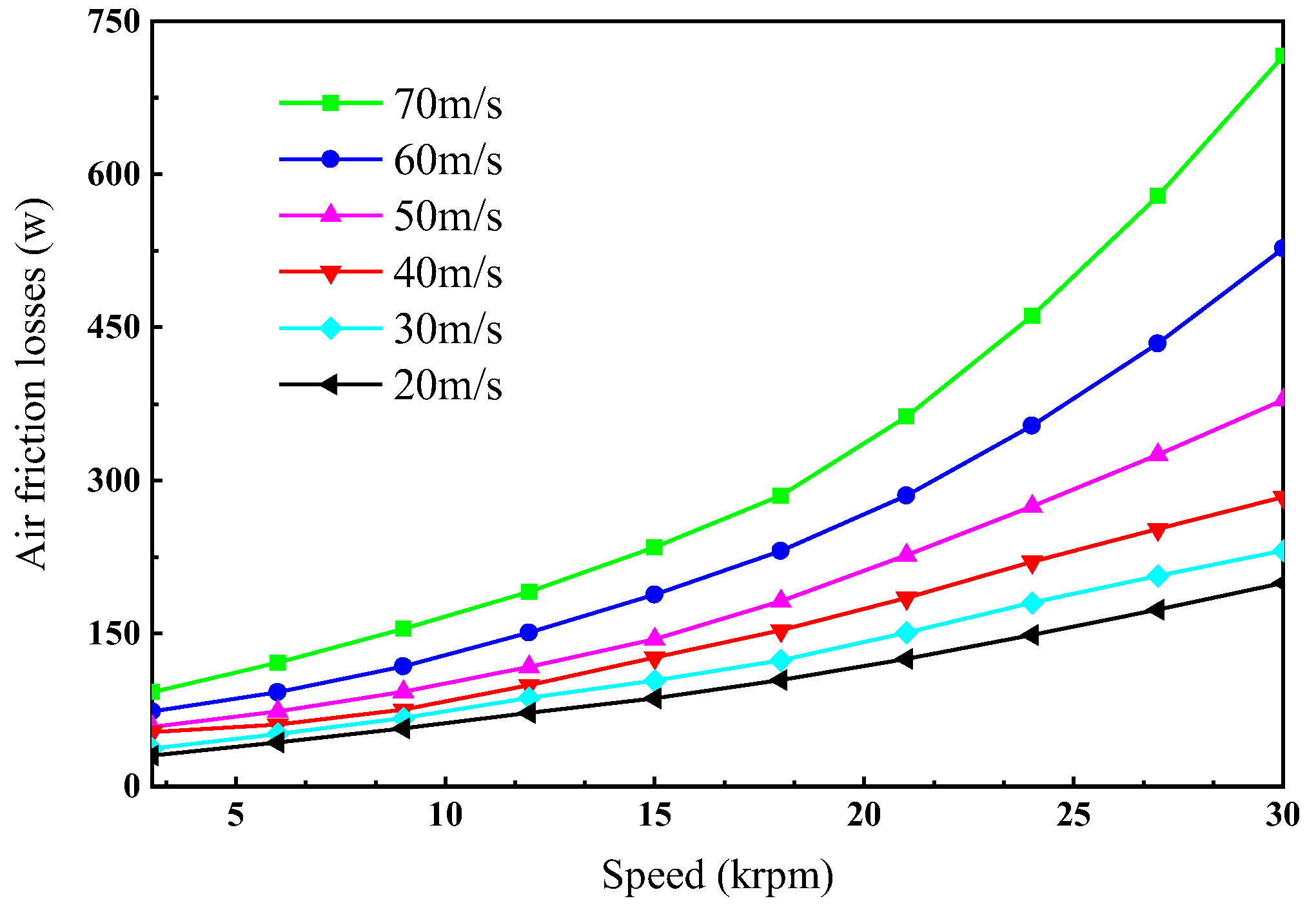
2.3.3. Calculation of Cooling Conditions for the Flow Field
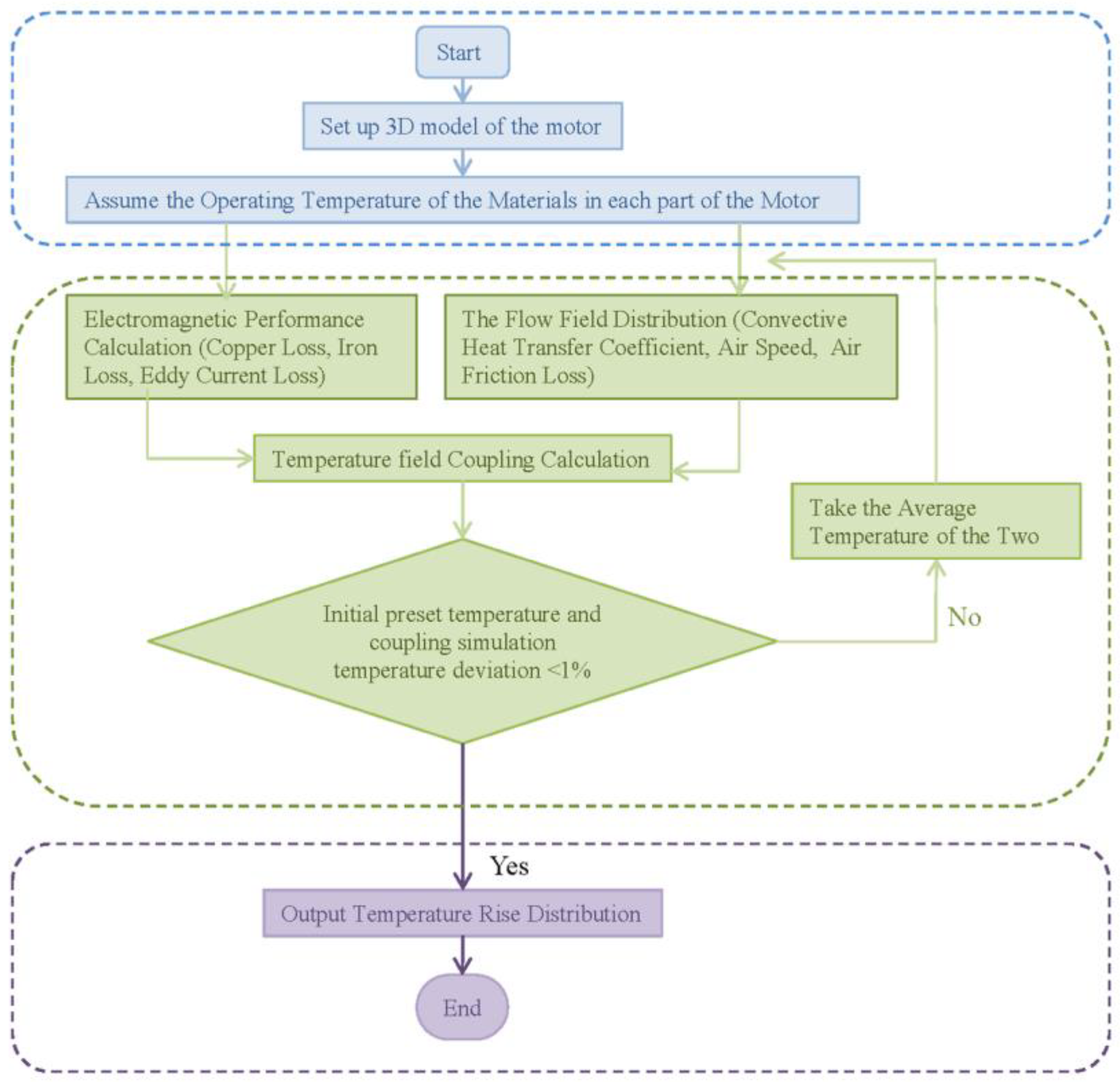
2.3.4. Coupled Iterative Analysis
3. Results
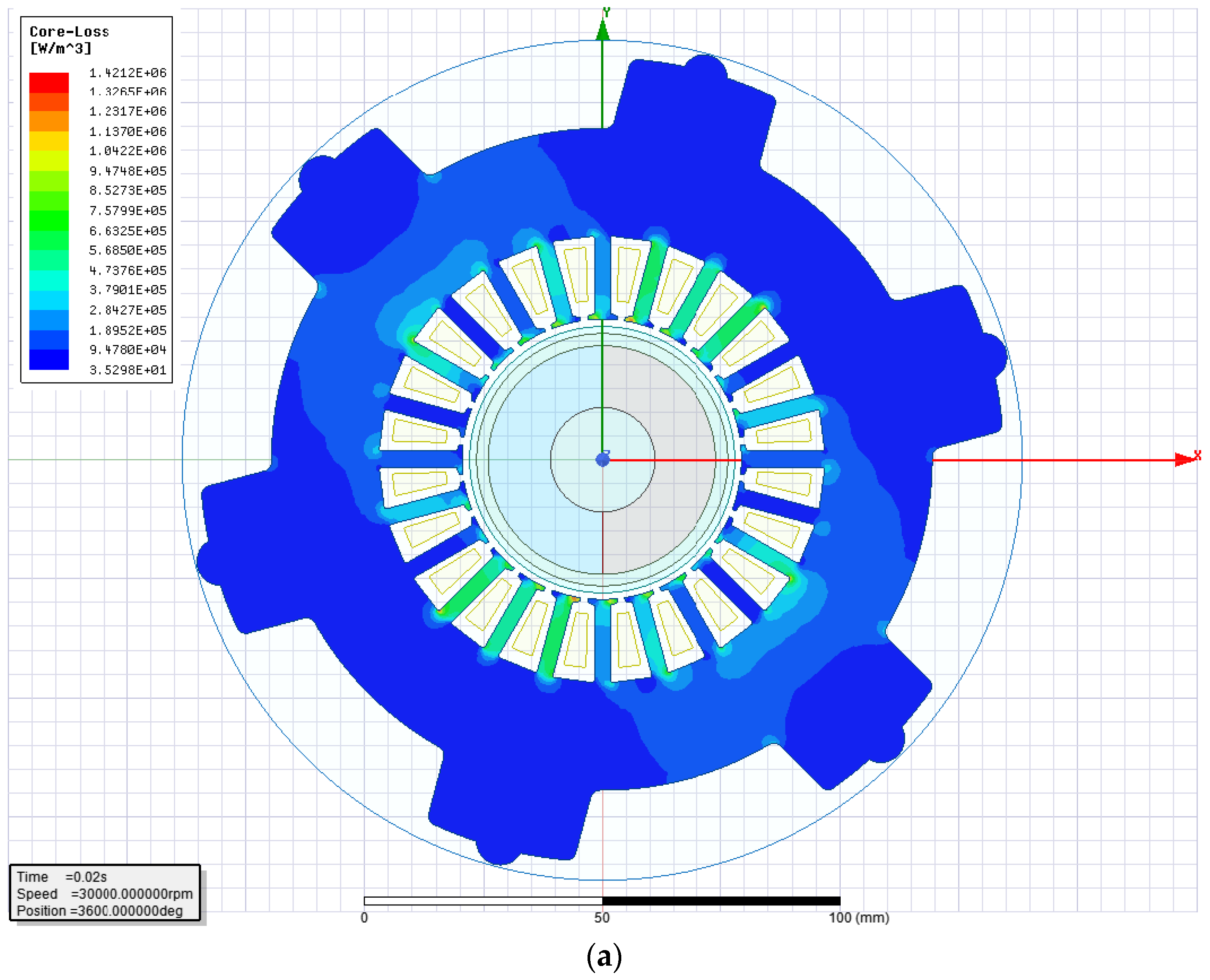
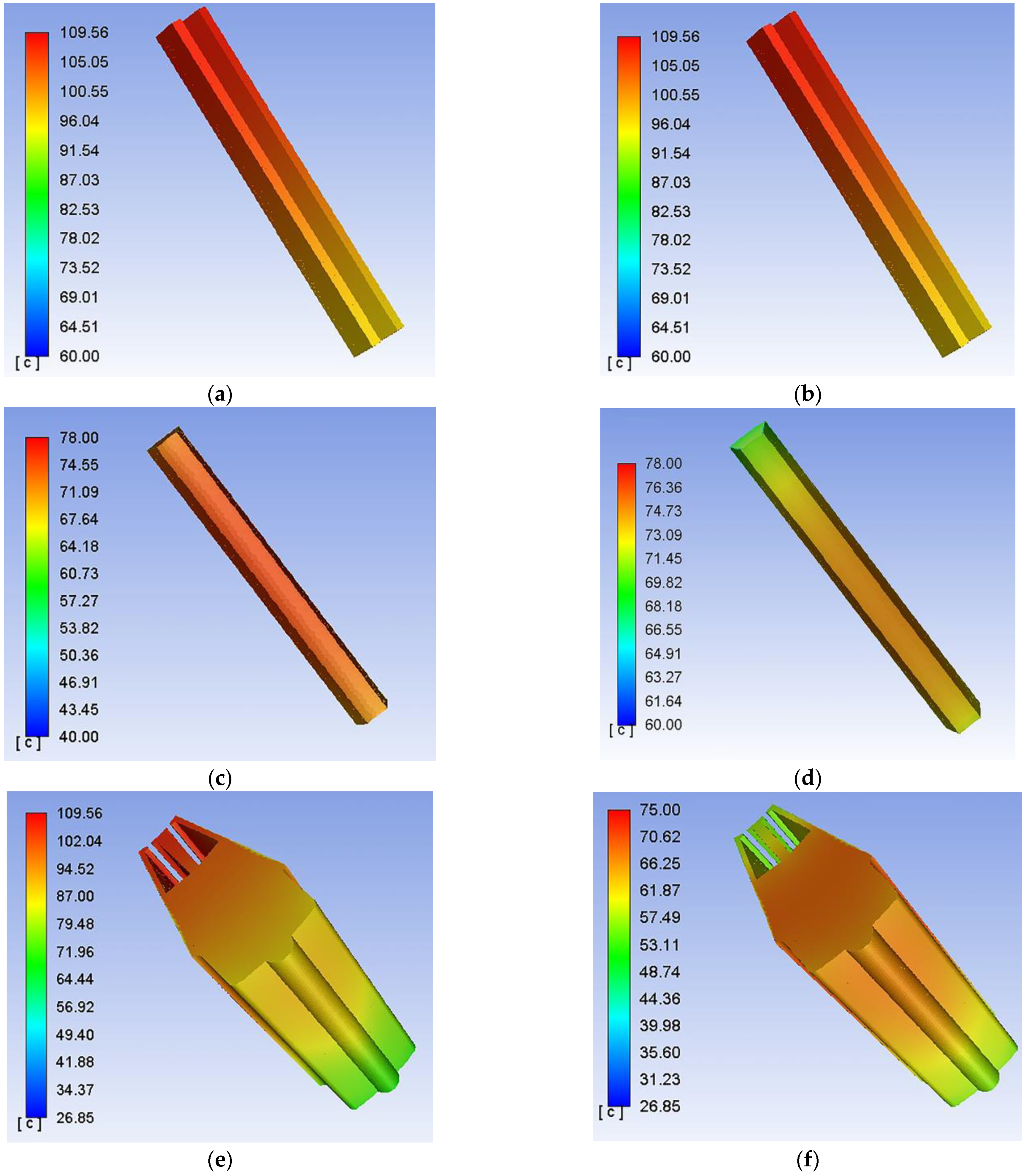
3.1. Comparison with the Traditional Temperature Rise Analysis Method
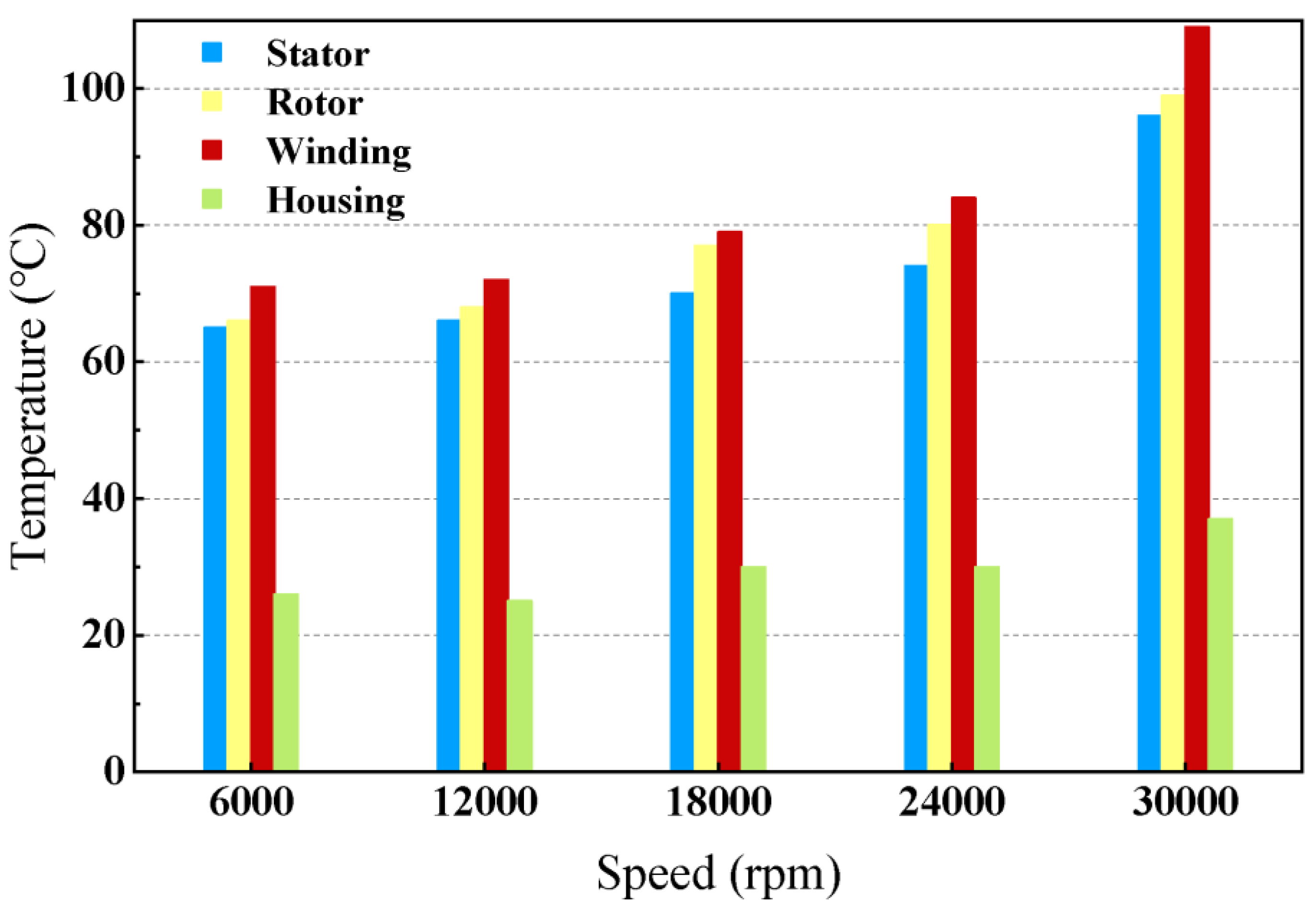
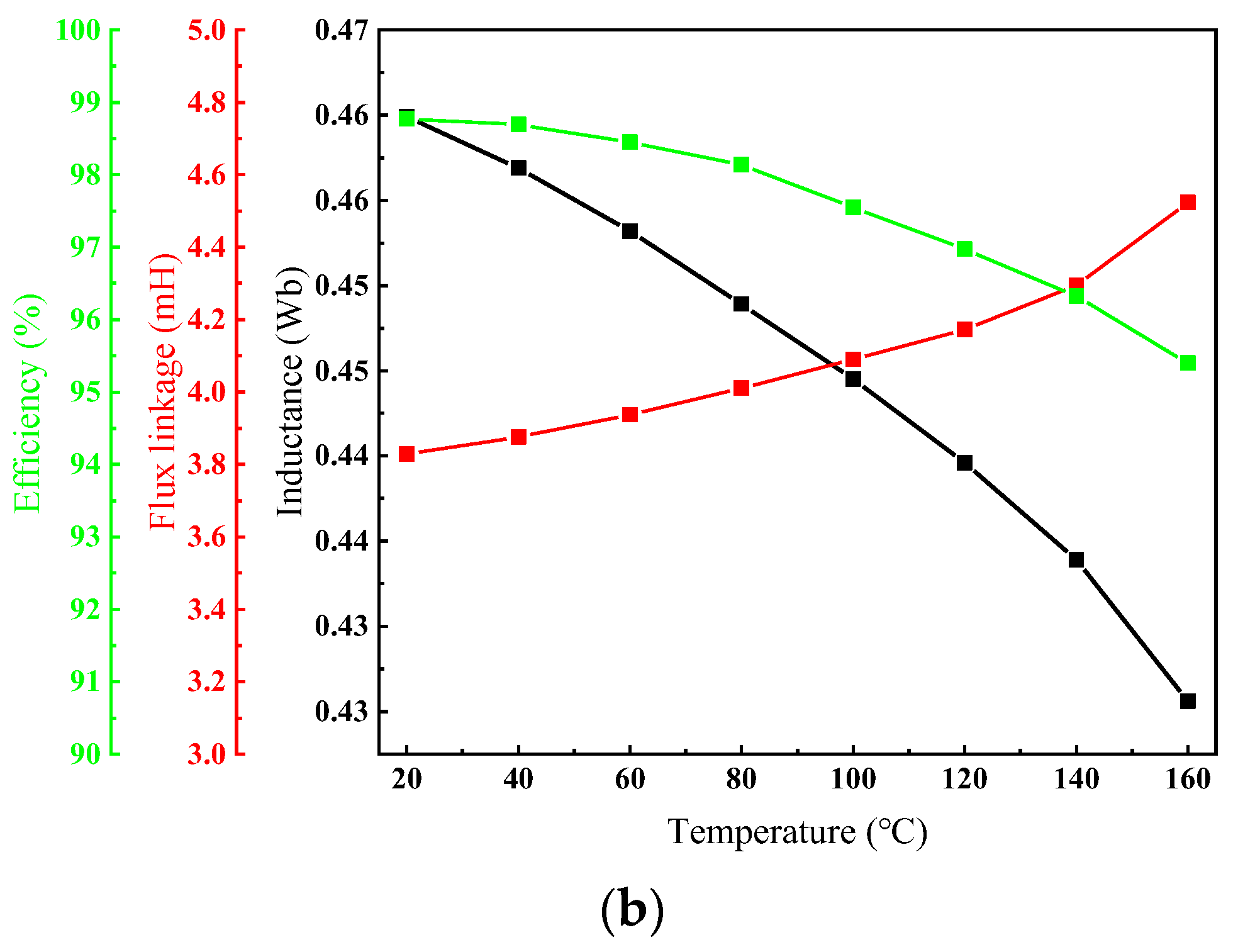
3.2. Temperature Rise Analysis under Different Working Conditions
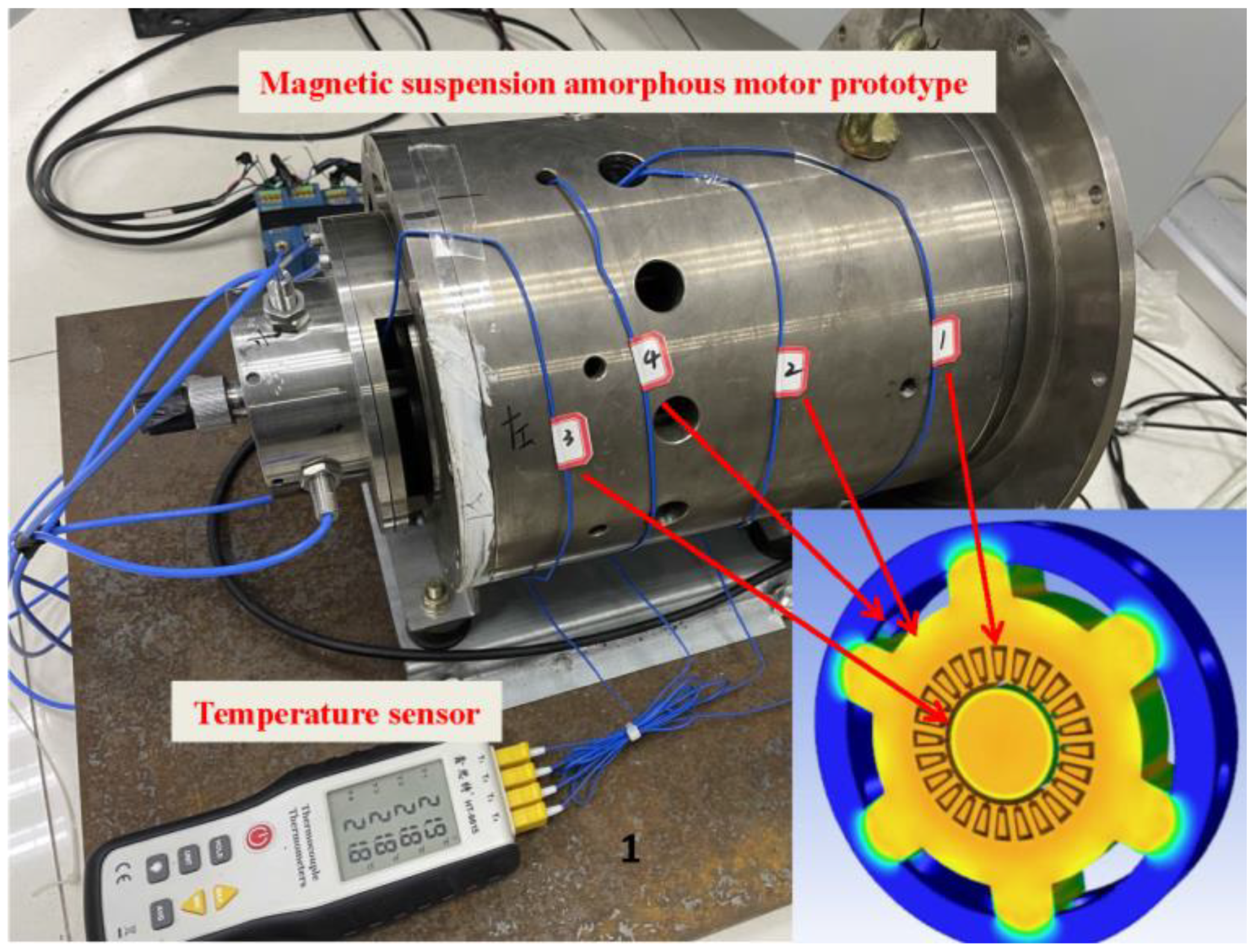
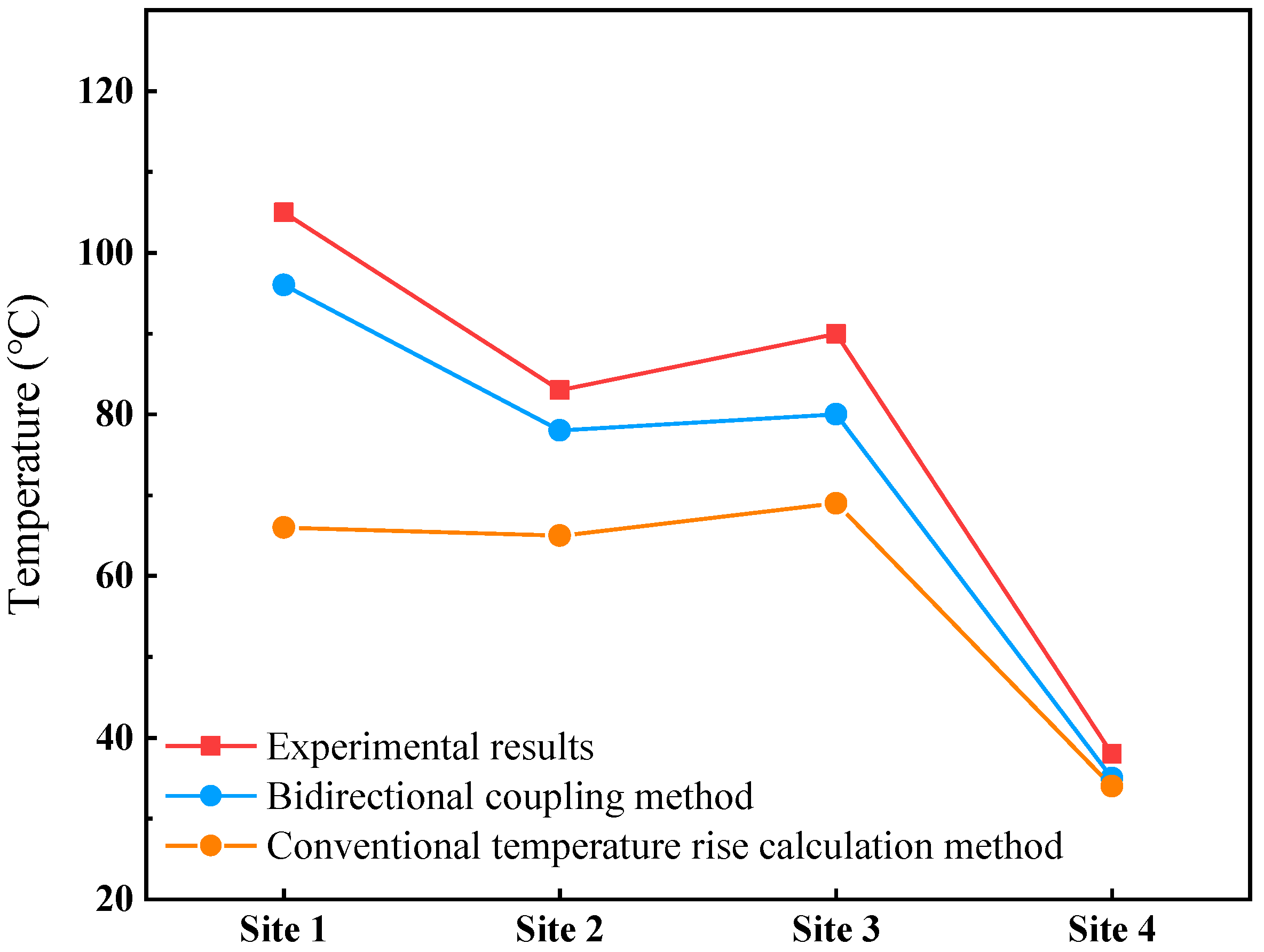
3.3. Experimental Verification
4. Conclusions
- Updating the electromagnetic properties of materials through multiple coupling iterations is the key to improve the precision of motor loss analysis.
- Compared with the traditional thermal analysis method, the coupling method can achieve accurate data transmission, and the analysis results are closer to the actual operation of the motor.
- With the increase in the cooling rate, air friction loss will increase rapidly. However, for the magnetic levitation motor, due to the increase in air gap width, axial cooling air is sufficient, and forced air cooling can effectively cool the motor rotor.
- The temperature rise measurement shows that the coupling temperature analysis results are in good agreement with the test results, and the overall error is less than 10 °C. The analysis results of this paper are of great significance to improve the analysis accuracy of motor loss and temperature rise and to accurately predict the temperature rise in the motor design stage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, X.; Le, Y.; Han, B. System Electromagnetic Loss Analysis and Temperature Field Estimate of a Magnetically Suspended Motor. Prog. Electromagn. Res. M 2017, 55, 51–61. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, J.; Liu, X.; Han, B. Loss Calculation and Thermal Analysis of Rotors Supported by Active Magnetic Bearings for High-Speed Permanent-Magnet Electrical Machines. IEEE Trans. Ind. Electron. 2016, 63, 2027–2035. [Google Scholar] [CrossRef]
- Dong, B.; Wang, K.; Han, B.; Zheng, S. Thermal Analysis and Experimental Validation of a 30 kW 60,000 r/min High-Speed Permanent Magnet Motor with Magnetic Bearings. IEEE Access 2019, 7, 92184–92192. [Google Scholar] [CrossRef]
- Liu, X.; Liu, G.; Han, B. A Loss Separation Method of a High-Speed Magnetic Levitated PMSM Based on Drag System Experiment without Torque Meter. IEEE Trans. Ind. Electron. 2019, 66, 2976–2986. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, B.; Jia, J.; Zhang, X.; Liu, J. Design and Analysis of Cooling System for High Speed PM Synchronous Motor with Magnetic Bearings. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Republic of Korea, 7–10 October 2018; pp. 228–233. [Google Scholar]
- Cai, X.; Cheng, M.; Zhu, S.; Zhang, J. Thermal Modeling of Flux-Switching Permanent-Magnet Machines Considering Anisotropic Conductivity and Thermal Contact Resistance. IEEE Trans. Ind. Electron. 2016, 63, 3355–3365. [Google Scholar] [CrossRef]
- Souhil, S.; Harmand, S.; Laloy, D. Study of the thermal behavior of a synchronous motor with permanent magnets. Int. J. Eng. 2009, 3, 229–256. [Google Scholar]
- Rostami, N.; Feyzi, M. Lumped-Parameter Thermal Model for Axial Flux Permanent Magnet Machines. IEEE Trans. Magn. 2013, 49, 1178–1184. [Google Scholar] [CrossRef]
- Armor, A.; Chari, M. Heat flow in the stator core of large turbine-generators, by the method of three-dimensional finite elements part Ⅱ: Temperature distribution in the stator iron. IEEE Trans. Power Appar. Syst. 1976, 95, 1657–1668. [Google Scholar] [CrossRef]
- Joo, D.; Cho, J.H.; Woo, K.; Kim, B.T.; Kim, D.K. Electromagnetic Field and Thermal Linked Analysis of Interior Permaanent-Magnet Synchronous Motor for Agricultural Electric Vehicle. IEEE Trans. Magn. 2011, 47, 4242–4245. [Google Scholar] [CrossRef]
- Li, G.; Ojeda, J.; Hoang, E.; Gabsi, M.; Lecrivain, M. Thermal–electromagnetic analysis for driving cycles of embedded flux-switching permanent-magnet motors. IEEE Trans. Veh. Technol. 2012, 61, 140–151. [Google Scholar] [CrossRef]
- Tang, H.; Zhang, M.; Dong, Y.; Li, W.; Li, L. Influence of the opening width of stator semiclosed slot and the dimension of the closed slot on the magnetic field distribution and temperature field of the permanent magnet synchronous motor. IET Electr. Power Appl. 2020, 14, 1642–1652. [Google Scholar] [CrossRef]
- Jungreuthmayer, C.; Bäuml, T.; Ganchev, M.; Kapeller, H.; Haumer, A. A Detailed Heat and Fluid Flow Analysis of an Internal Permanent Magnet Synchronous Machine by Means of Computational Fluid Dynamics. IEEE Trans. Ind. Electron. 2012, 59, 4568–4578. [Google Scholar] [CrossRef]
- Li, W.; Qiu, H.; Zhang, X.; Yi, R. Influence of Copper Plating on Electromagnetic and Temperature Fields in a High-Speed Permanent-Magnet Generator. IEEE Trans. Magn. 2012, 48, 2247–2253. [Google Scholar]
- Chen, S.; Zhang, Q.; He, B.; Hui, D.; Huang, S. Thermal Analysis of High Density Permanent Magnet Synchronous Motor Based on Multi Physical Domain Coupling Simulation. J. Electr. Eng. Technol. 2017, 12, 91–99. [Google Scholar] [CrossRef]
- Shafigh, N.; Huang, Z.; Andreas, K.; Oskar, W.; Mats, L. Thermal Modeling of Directly Cooled Electric Machines Using Lumped Parameter and Limited CFD Analysis. IEEE Trans. Energy Convers. 2013, 28, 979–990. [Google Scholar]
- Tong, W.; Dai, S.; Wu, S.; Tang, R. Performance Comparison Between an Amorphous Metal PMSM and a Silicon Steel PMSM. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Shotaro, O.; Nicolas, D.; Yoshiyuki, K.; Masaharu, I.; Keisuke, F. Core Loss Reduction of an Interior Permanent-Magnet Synchronous Motor Using Amorphous Stator Core. IEEE Trans. Magn. 2016, 52, 2261–2268. [Google Scholar]
- Liu, X.; Yu, H.; Shi, Z.; Xia, T.; Hu, M. Electromagnetic-fluid-thermal field calculation and analysis of a permanent magnet linear motor. Appl. Therm. Eng. 2018, 129, 802–811. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, D.; Chen, J.; Zhang, Q.; Xuan, T. Electromagnetic-Thermal-Fluidic Analysis of Permanent Magnet Synchronous Machine by Bidirectional Method. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Wrobel, R.; Staton, D.; Lock, R.; Booker, J.; Drury, D. Winding Design for Minimum Power Loss and Low-Cost Manufacture in Application to Fixed-Speed PM Generator. IEEE Trans. Ind. Appl. 2015, 51, 3773–3782. [Google Scholar] [CrossRef]
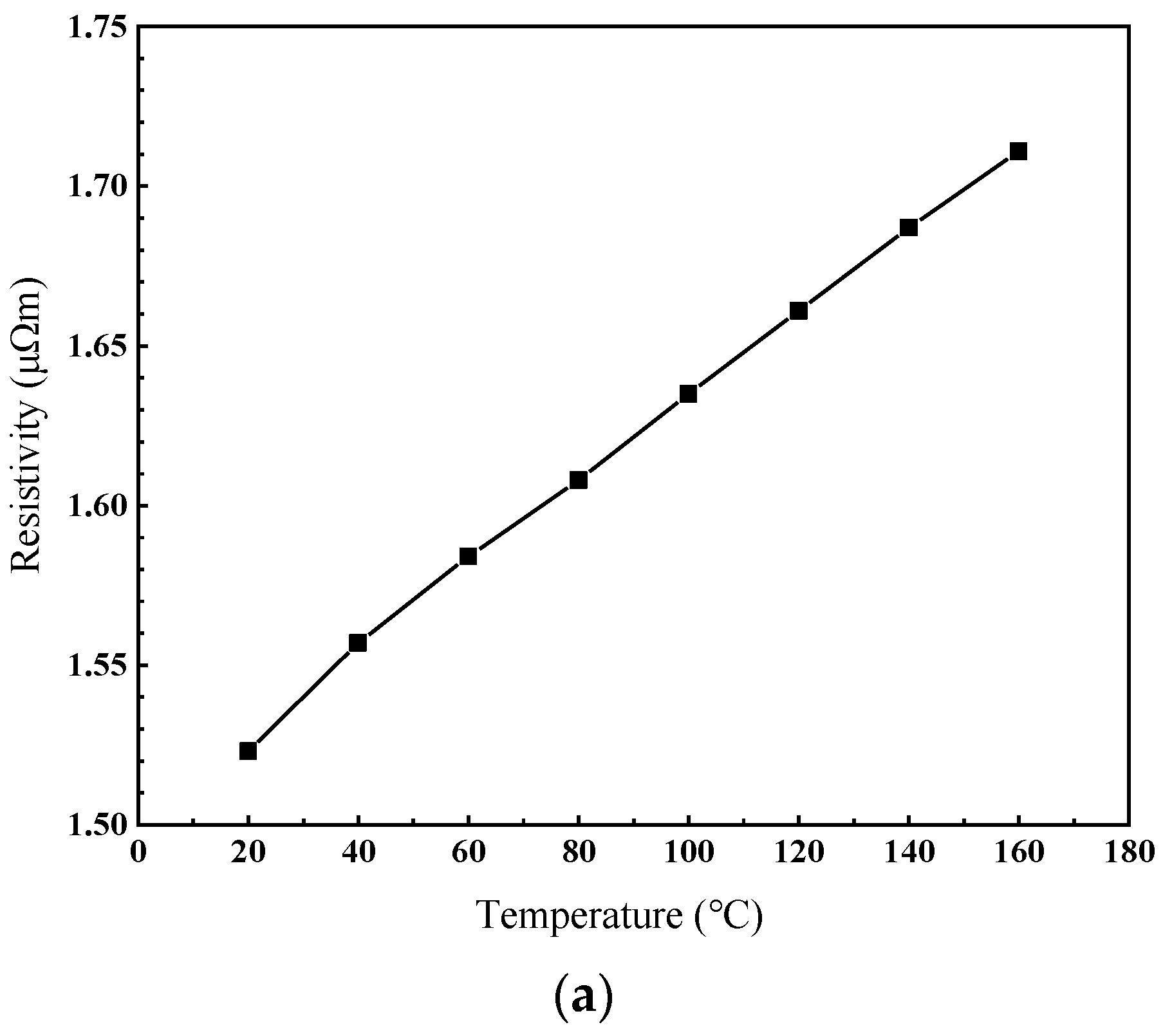
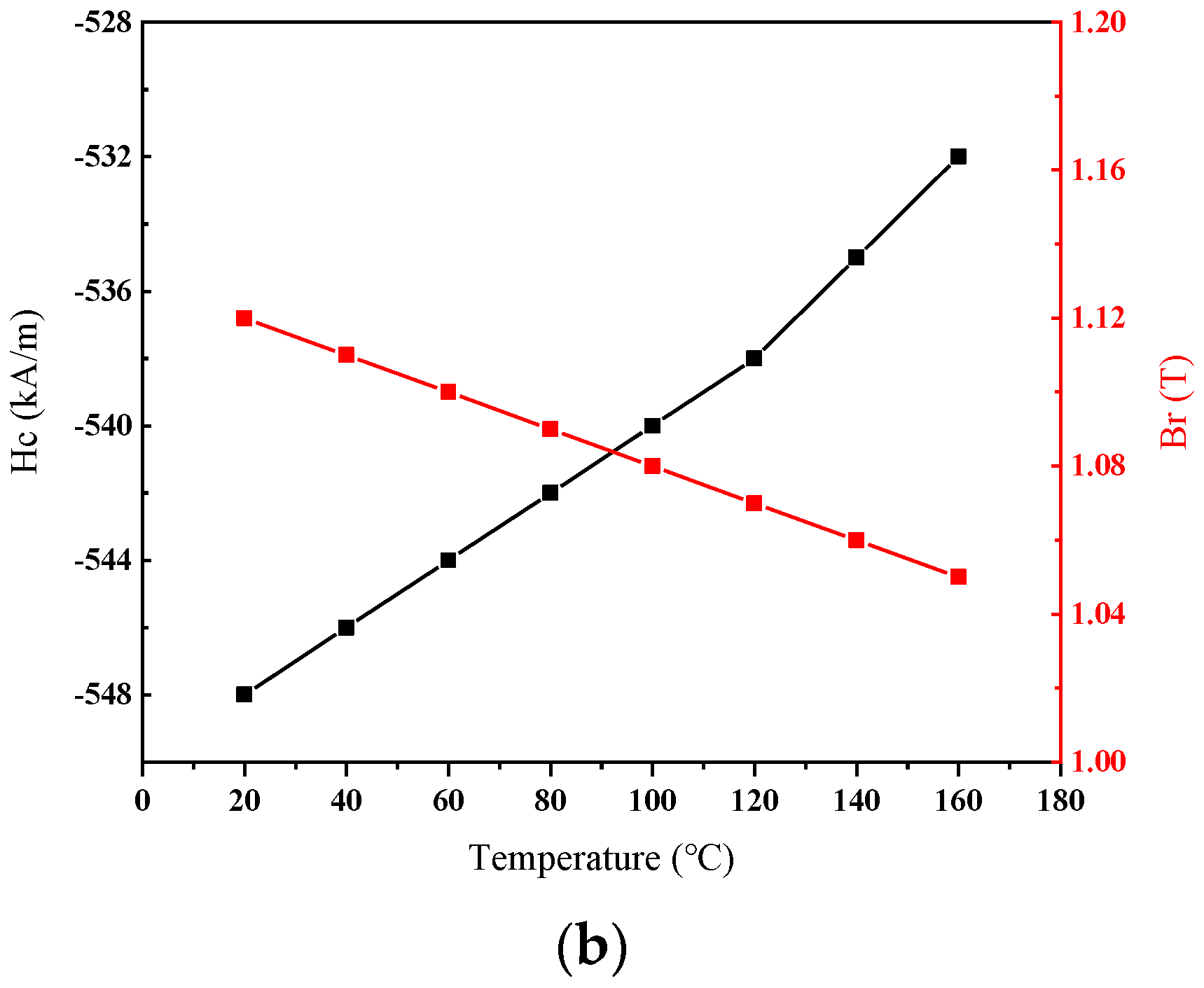
- Yang, M.; Li, Y.; Yang, Q.; Lin, Z.; Yue, S.; Wang, H. Magnetic Properties Measurement and Analysis of High Frequency Core Materials Considering Temperature Effect. IEEE Trans. Appl. Supercond. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Han, T.; Wang, Y.; Shen, J. Analysis and Experiment Method of Influence of Retaining Sleeve Structures and Materials on Rotor Eddy Current Loss in High-Speed PM Motors. IEEE Trans. Ind. Appl. 2020, 56, 4889–4895. [Google Scholar] [CrossRef]




| Parameters | Value |
|---|---|
| Rated power/kW | 37.5 |
| Rated speed/rpm | 30,000 |
| Rated voltage/V | 380 |
| Winding layer | single |
| Slot number | 24 |
| Stator outer diameter mm | 139 |
| Stator inter diameter/mm | 58.85 |
| Rotor outer diameter/mm | 53 |
| Rotor inter diameter/mm | 22 |
| Poles number | 2 |
| Parameters | Materials | Density (kg/m3) | Heat Capacity J/(kg•K) | Specific Thermal Conductivity (W/m/K) |
|---|---|---|---|---|
| Stator | Amorphous | 7180 | 430 | 18 |
| Magnet | Ti-alloy | 4500 | 612 | 8 |
| Rotor sleeve | Sm2Co17 | 8300 | 500 | 23 |
| Winding | Copper | 8930 | 386 | 400 |
| Housing | Steel | 7850 | 500 | 15 |
| Stator | Amorphous | 7180 | 430 | 18 |
| Number of Iterations | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|
| Initial preset temperature | Magnet | 72.7 | 75.5 | 77 | 77.5 |
| Stator | 102.4 | 105.7 | 107.6 | 108.3 | |
| Winding | 102 | 106 | 108 | 109 | |
| Coupling simulation temperature | Magnet | 78.3 | 78.5 | 78 | 78 |
| Stator | 109 | 109.5 | 109 | 108 | |
| Winding | 110 | 110 | 110 | 109 | |
| error | 7.7% | 3.9% | 1.3% | 0.7% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Shi, G.; Lai, Y.; Yu, J.; Wang, L.; Song, Y. Temperature Rise Calculation of the High Speed Magnetic Suspension Motor Based on Bidirectional Electromagnetic–Thermal–Fluid Coupling Analysis. Machines 2023, 11, 364. https://doi.org/10.3390/machines11030364
Hu X, Shi G, Lai Y, Yu J, Wang L, Song Y. Temperature Rise Calculation of the High Speed Magnetic Suspension Motor Based on Bidirectional Electromagnetic–Thermal–Fluid Coupling Analysis. Machines. 2023; 11(3):364. https://doi.org/10.3390/machines11030364
Chicago/Turabian StyleHu, Xiaolu, Guibing Shi, Yifan Lai, Juntao Yu, Li Wang, and Yumei Song. 2023. "Temperature Rise Calculation of the High Speed Magnetic Suspension Motor Based on Bidirectional Electromagnetic–Thermal–Fluid Coupling Analysis" Machines 11, no. 3: 364. https://doi.org/10.3390/machines11030364
APA StyleHu, X., Shi, G., Lai, Y., Yu, J., Wang, L., & Song, Y. (2023). Temperature Rise Calculation of the High Speed Magnetic Suspension Motor Based on Bidirectional Electromagnetic–Thermal–Fluid Coupling Analysis. Machines, 11(3), 364. https://doi.org/10.3390/machines11030364








