Target Oil Pressure Recognition Algorithm for Oil Pressure Following Control of Electronic Assisted Brake System
Abstract
:1. Introduction
- The braking intention parameters mainly include vehicle status, the driver’s behavioral characteristics, and the driver’s braking operation. The vehicle state is fed back in the braking process, as a result of which it has a certain hysteresis. The driver’s behavioral characteristics are difficult to accurately measure and are greatly affected by the driver’s subjective behavior. Therefore, the brake intention is usually identified by the relevant parameters of the brake operation, namely, the force and displacement of the brake pedal [5,6,7,8,9,10,11,12];
- The braking force of the electronic-assisted brake system is determined by the oil pressure of its hydraulic system. Therefore, the control target is the oil pressure, and the control object is the motor, transmission mechanism, and hydraulic system [13,14,15,16,17]. Obviously, the rapid acquisition of target oil pressure is one of the key factors in the design of a control algorithm for the electronic-assisted brake system;
- The solution method depends on an accurate vehicle dynamics model [13,14]. However, the vehicle dynamics model has multiple degrees of freedom with strong nonlinear characteristics, so it struggles to obtain the accurate parameters of the vehicle’s body to build the accurate dynamics model. Moreover, the solution process is time-consuming;
- The look-up table method can quickly obtain the target oil pressure by referring to the vacuum-assisted characteristic curves [15,16,17], and it achieves better real-time performance than the solution method. However, the target oil pressure is usually obtained by a phased interpolation method, which would lead to problems such as uneven oil pressure jump inflection points and interpolation errors;
- The current braking force control algorithms mainly include PID control, sliding mode variable structure control, and the neural network control algorithm [18,19,20,21,22,23]. PID control requires high accuracy in the system model, and it has poor anti-interference abilities. The sliding mode variable structure control algorithm has great anti-interference abilities, but when the system state trajectory reaches the sliding mode surface, it struggles to ensure strict sliding along the sliding mode towards the balance point, such that chattering occurs. The neural network control algorithm is suitable for solving complex and nonlinear control problems, but it requires a large number of training samples and requires high computing power in the controller.
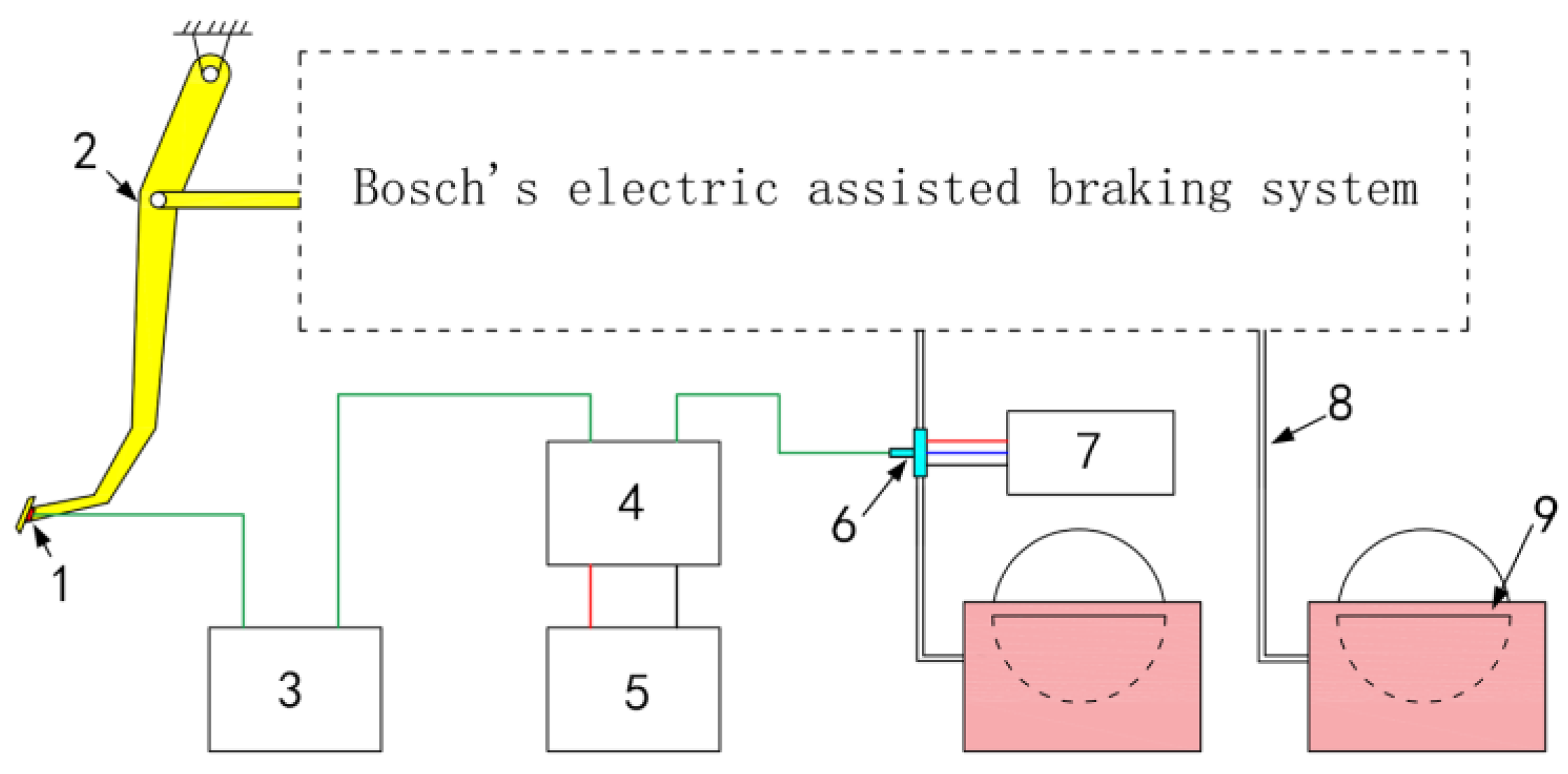
- The target oil pressure recognition algorithm based on the T-S fuzzy neural network model is proposed by referring to the assist characteristics of a mature braking system, used for quickly obtaining accurate target oil pressure, which can shorten the development time and facilitate the rapid deployment of control strategies;
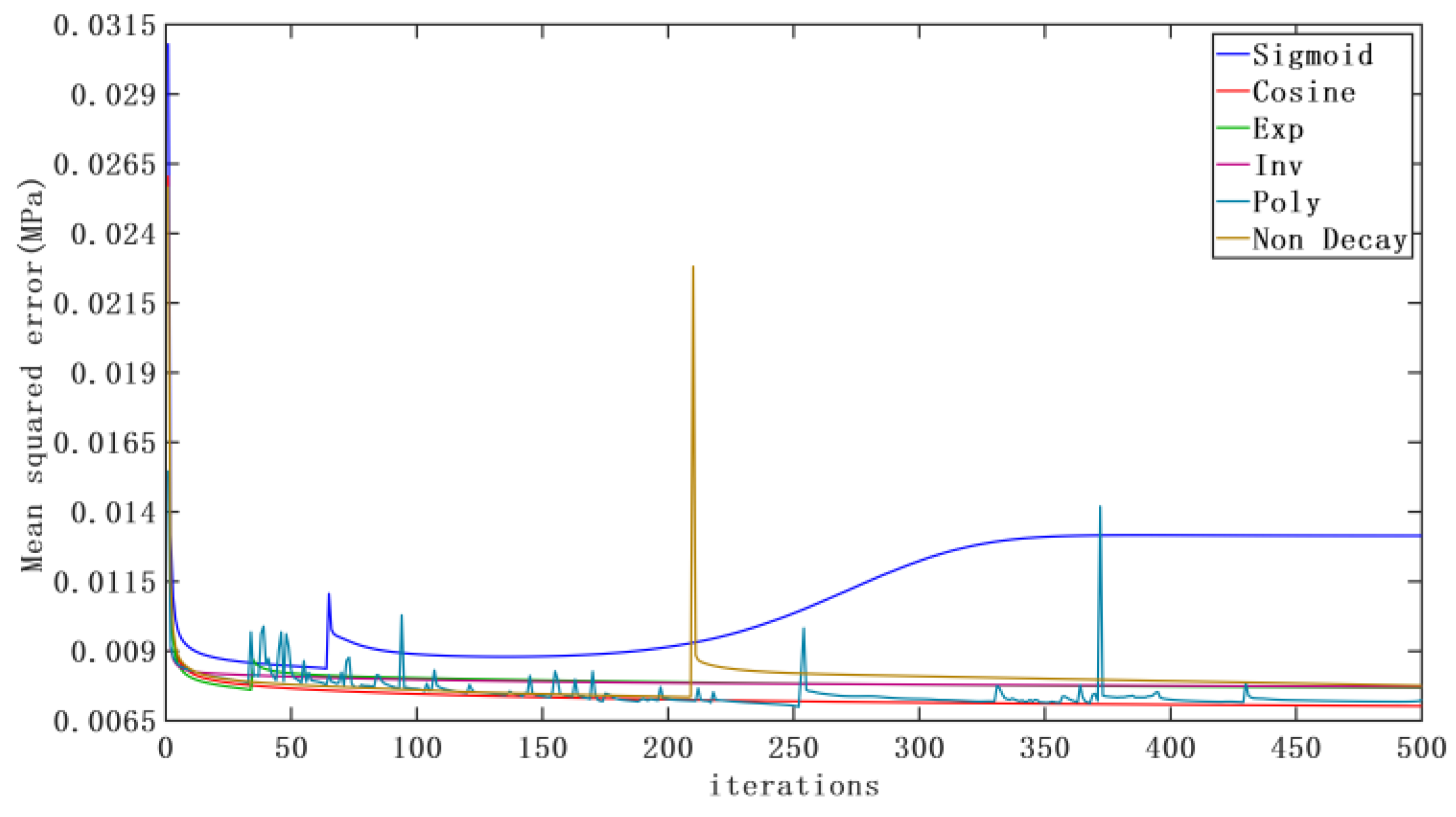
- In the training process of the model, the fuzzy C-means clustering algorithm replaces the random initialization method to identify the antecedent parameters, and the learning rate cosine attenuation strategy is introduced to improve the convergence speed of the model and avoid falling into the local minimum. Meanwhile, the T-S fuzzy neural network parameters are trained separately under different braking conditions, based on the braking conditions classification algorithm, to significantly improve the accuracy of the target oil pressure identification;
- The identified target oil pressure is taken as the input of the oil pressure following the control, and then the target oil pressure following the control method based on the traditional PID and fuzzy PID approaches and the experimental method is determined for verifying the feasibility of the method;
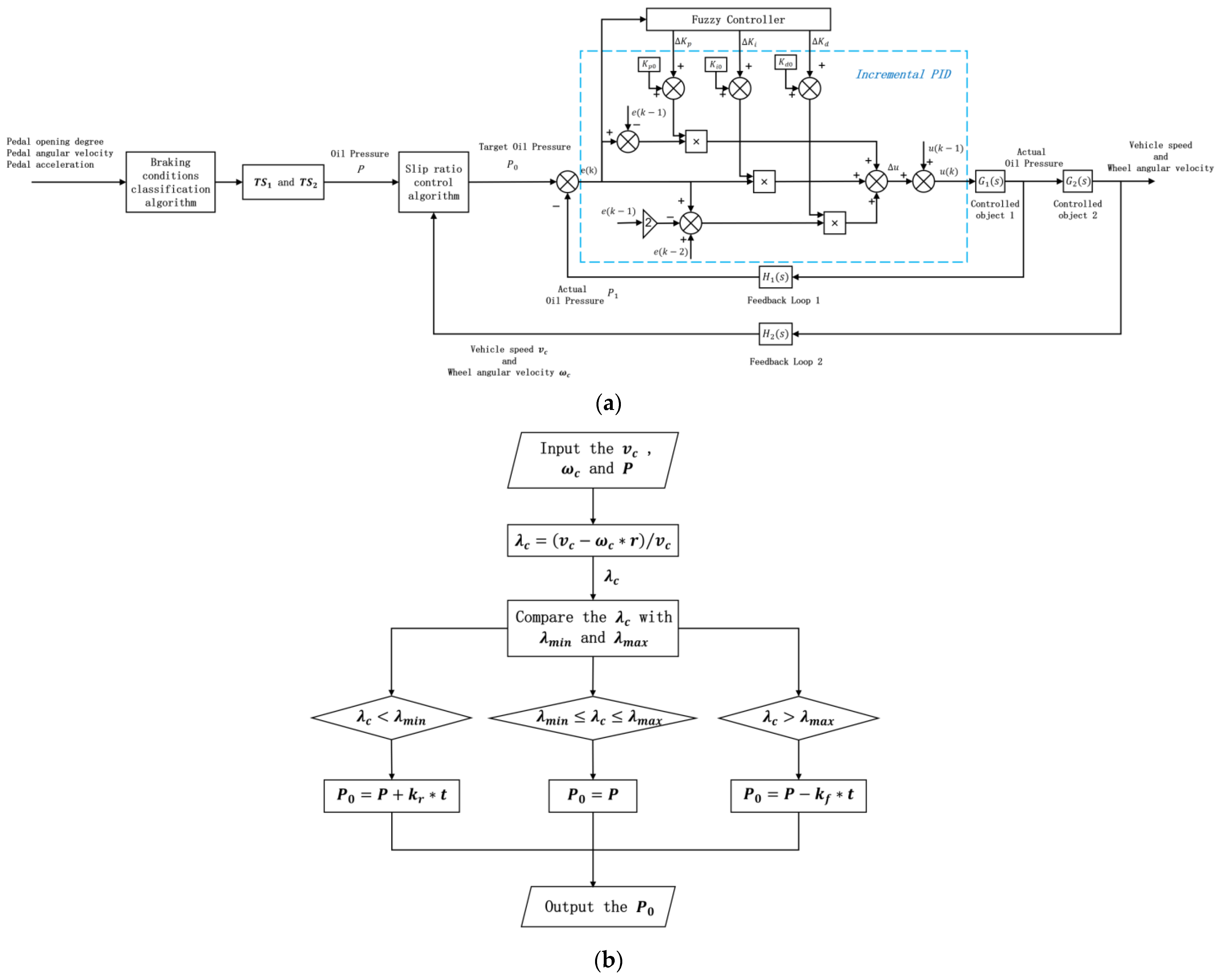
- The correction method of target oil pressure is suggested based on the slip ratio to further improve the accuracy of the target oil pressure.
2. Principles and Modeling
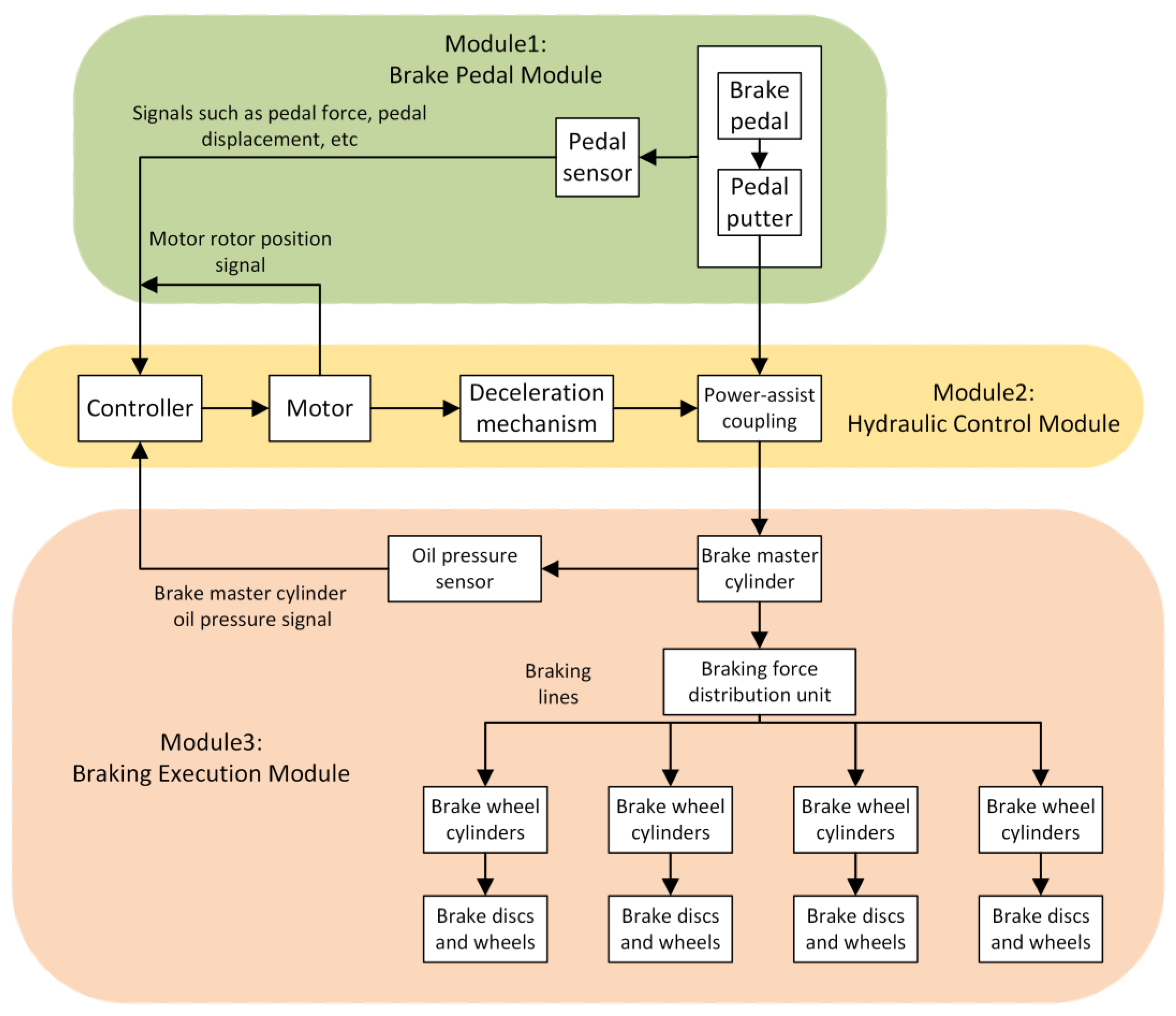
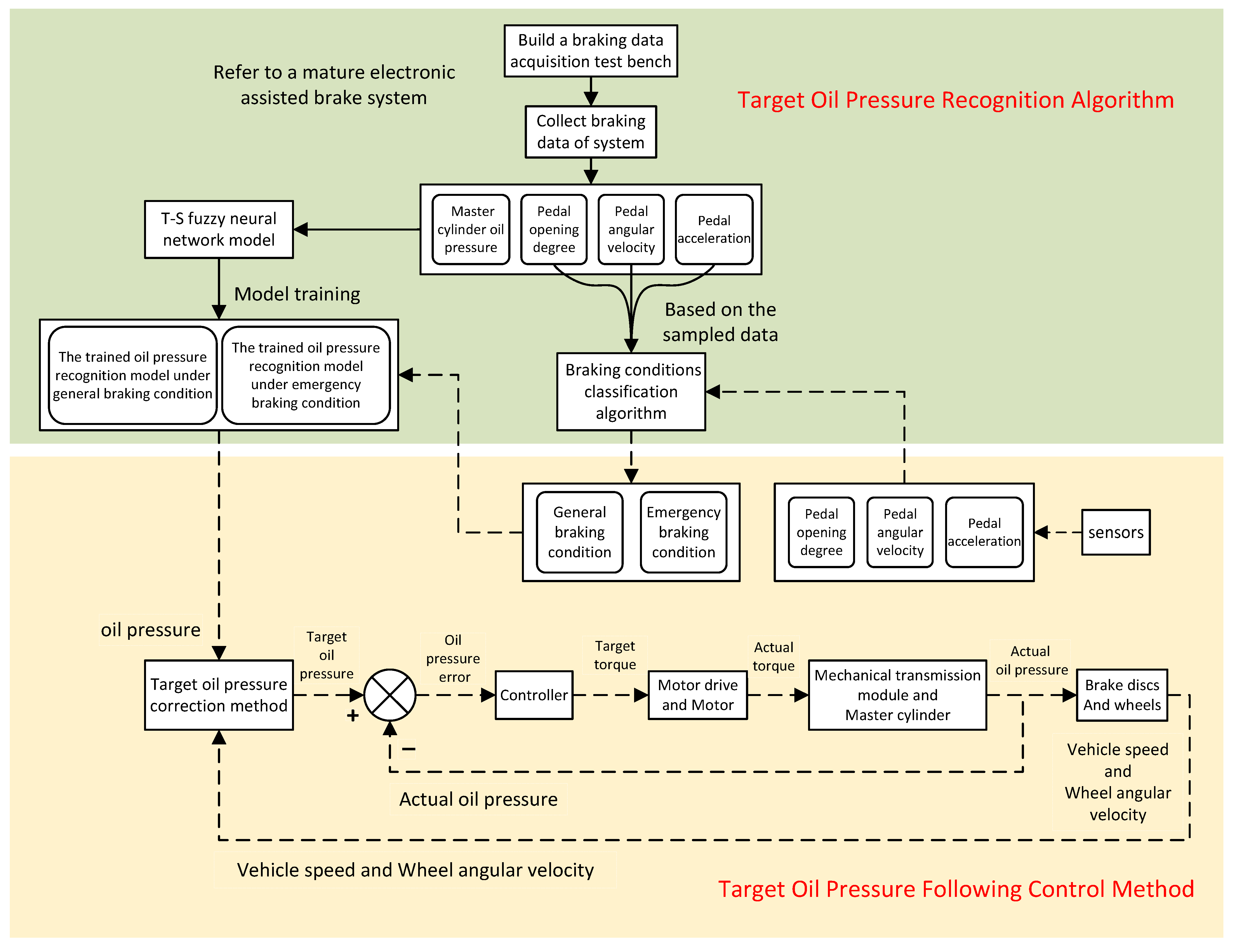
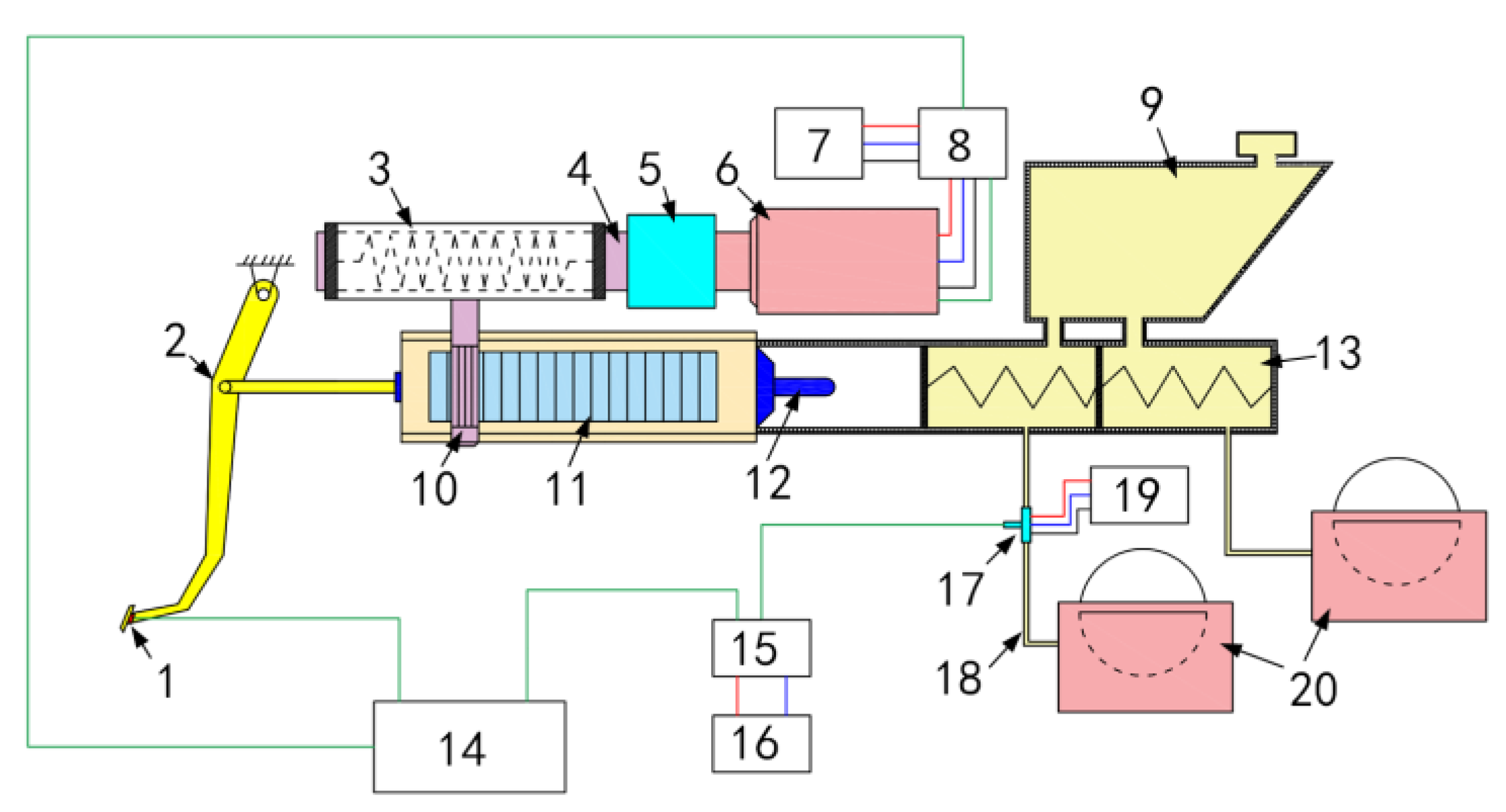
2.1. The Framework of the Research Content
2.2. Target Oil Pressure Recognition Algorithm of Electronic Assisted Brake System
2.2.1. Classification of Braking Conditions
| Algorithm 1 Algorithm flow |
| Step 1: Is true? If true, go to Step 2, otherwise, go to Step 3. |
| Step 2: Does satisfy (1) or (2)? |
| (1) and |
| (2) and |
| If one of them is satisfied, it belongs to . If neither is satisfied, it belongs to . |
| Step 3: true? If true, go to Step 4, otherwise, go to Step 5. |
| Step 4: Is true? If true, it belongs to , otherwise, determine whether satisfies (3) or (4). |
| (3) and |
| (4) and |
| If one of them is satisfied, it belongs to . If neither is satisfied, it belongs to . |
| Step 5: Is true? If true, it belongs to , otherwise, determine whether satisfies (5) or (6). |
| (5) and |
| (6) and |
| If one of them is satisfied, it belongs to . If neither is satisfied, it belongs to . |
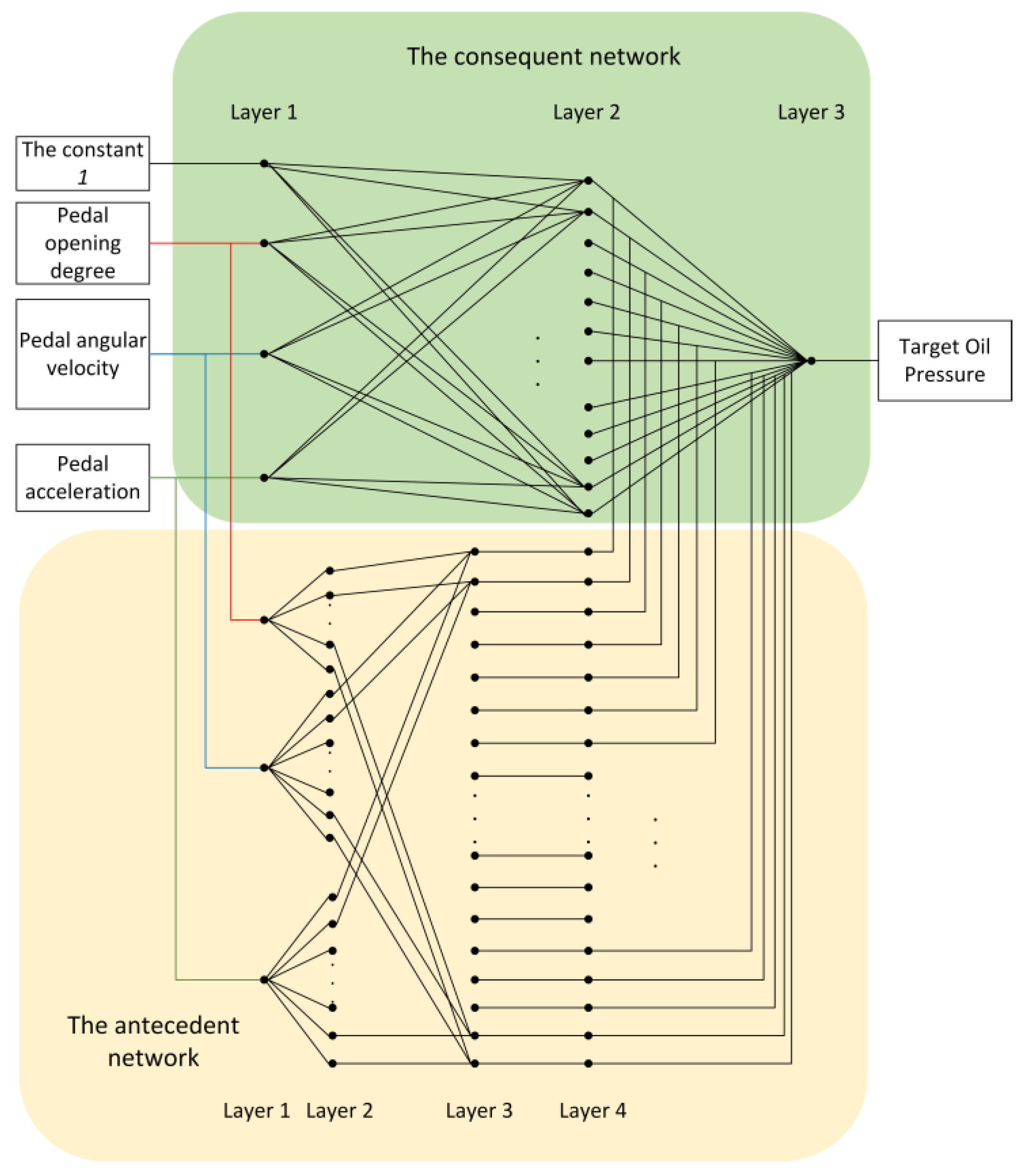
2.2.2. T-S Fuzzy Neural Network Model for Target Oil Pressure Recognition Algorithm
2.3. Parameter Recognition of T-S Fuzzy Neural Network
2.3.1. Recognition of Antecedent Parameters by Fuzzy C-Means Clustering Algorithm
| Algorithm 2 Algorithm flow |
| Step 1: The number of clusters is set to h, the initial cluster center is , the iteration stop threshold is , the iterative counter q = 0, and the value of the fuzzy weighted index m is 2. |
| Step 2: The fuzzy membership matrix is calculated with Equation (18). |
| Step 3: The h cluster centers can be obtained from Equation (17). |
| Step 4: According to Equations (15) and (16), the value of the fuzzy clustering objective function is calculated. If , the algorithm is terminated, and the fuzzy membership matrix and the clustering center matrix V are obtained. Otherwise, let q = q + 1, and go to Step 2. |
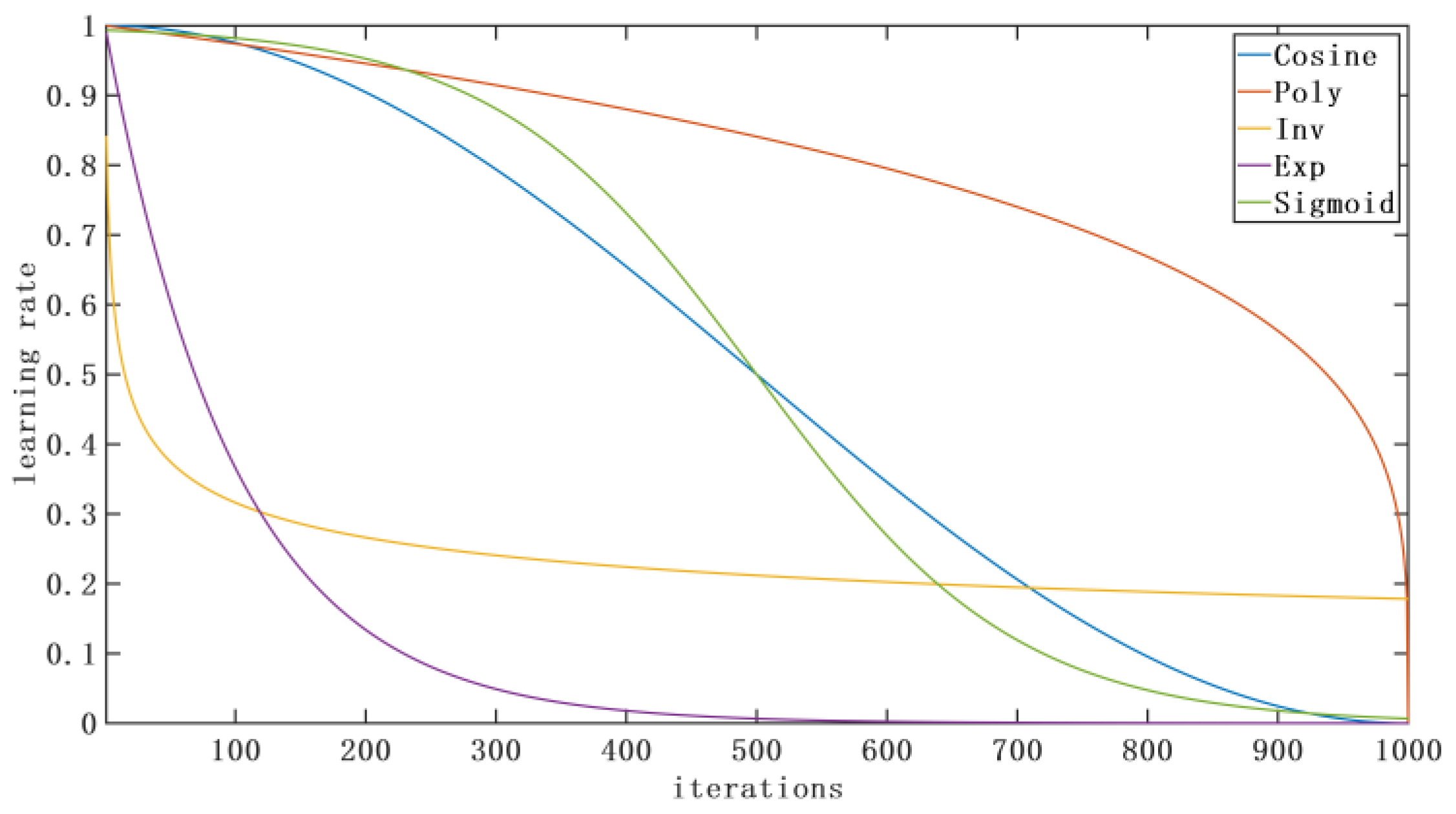
2.3.2. Learning Rate Cosine Attenuation Strategy
2.4. Training Method of Target Oil Pressure Recognition Model
2.5. Target Oil Pressure Following Control Method
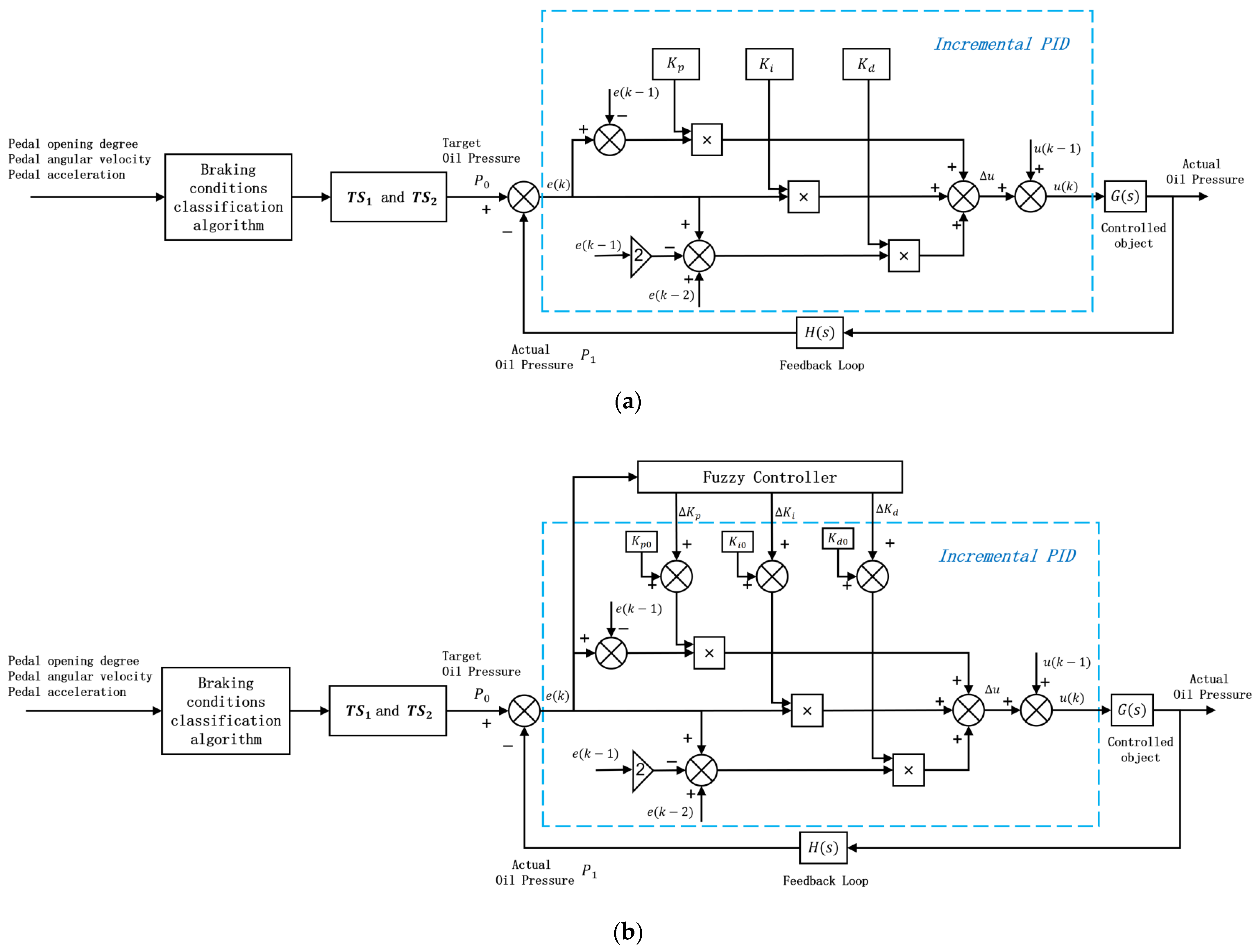
2.5.1. Traditional PID Controller and Fuzzy PID Controller
2.5.2. Correction Method of Target Oil Pressure
3. Model Training and Experiments
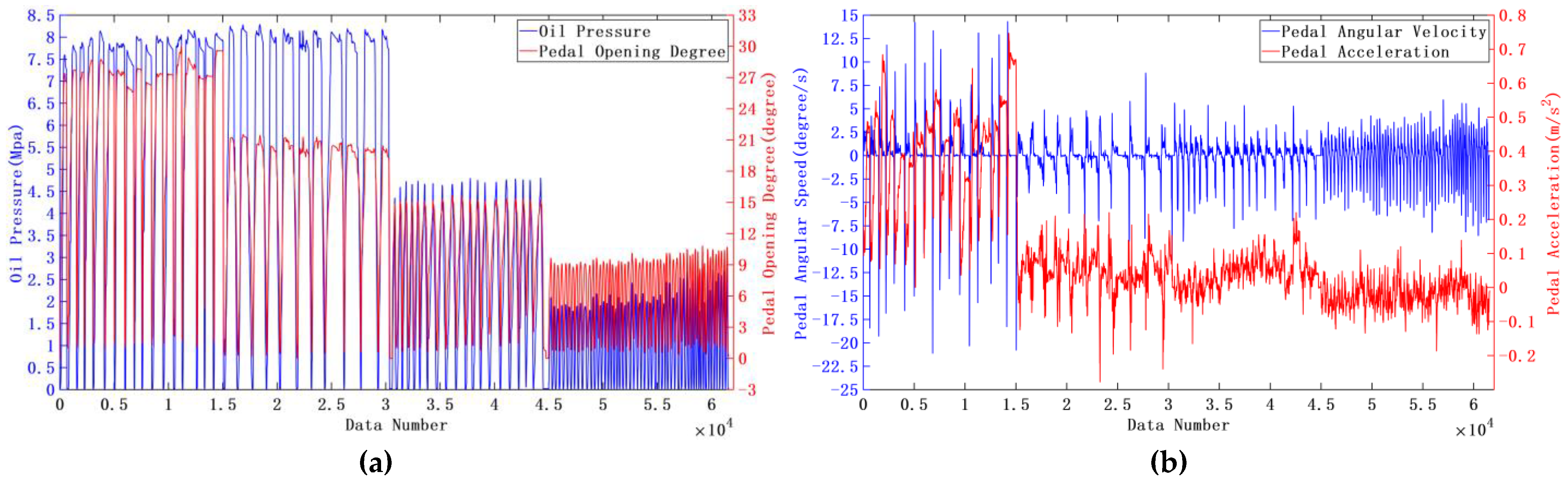
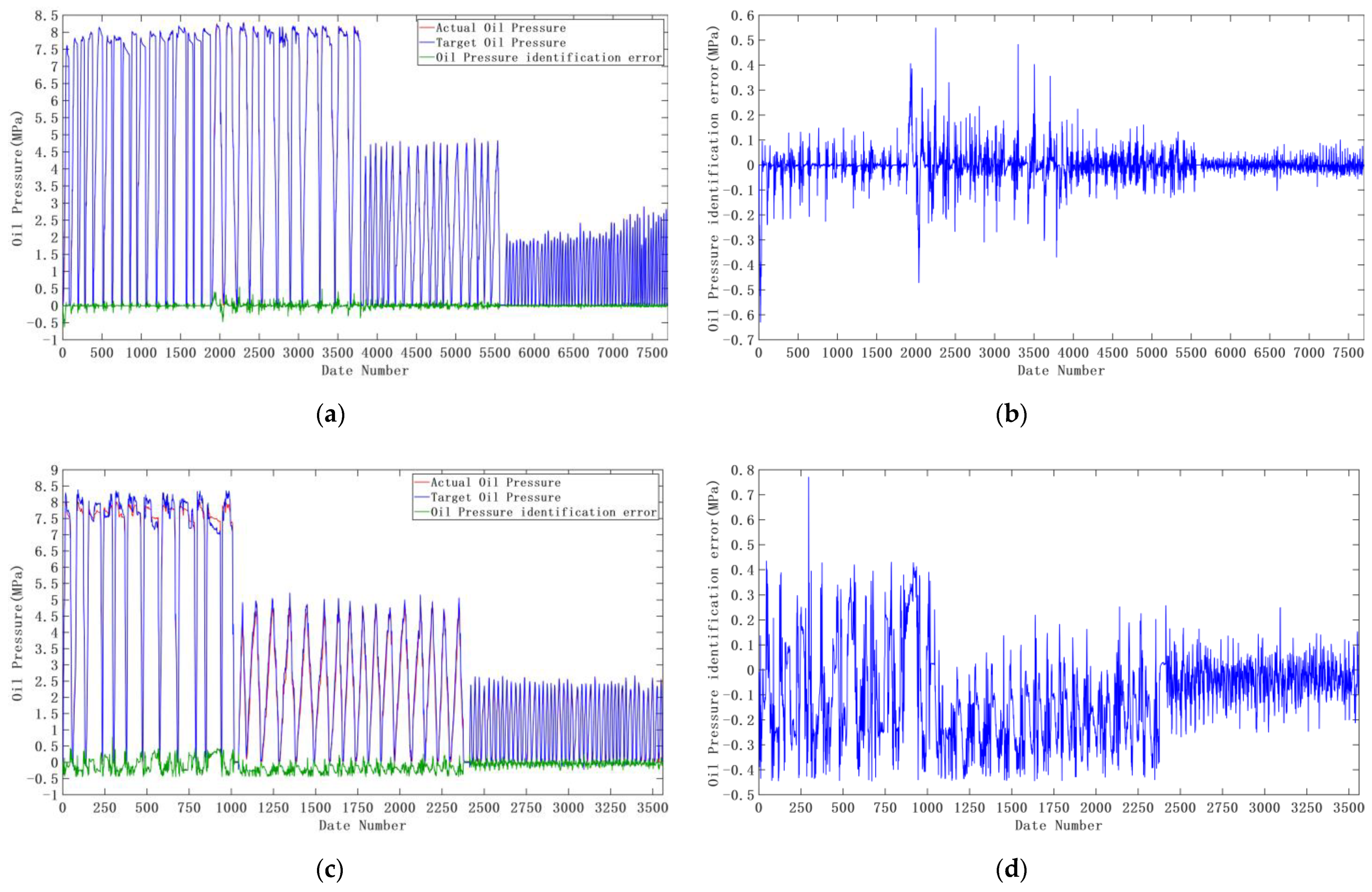
3.1. Training of Target Oil Pressure Recognition Model
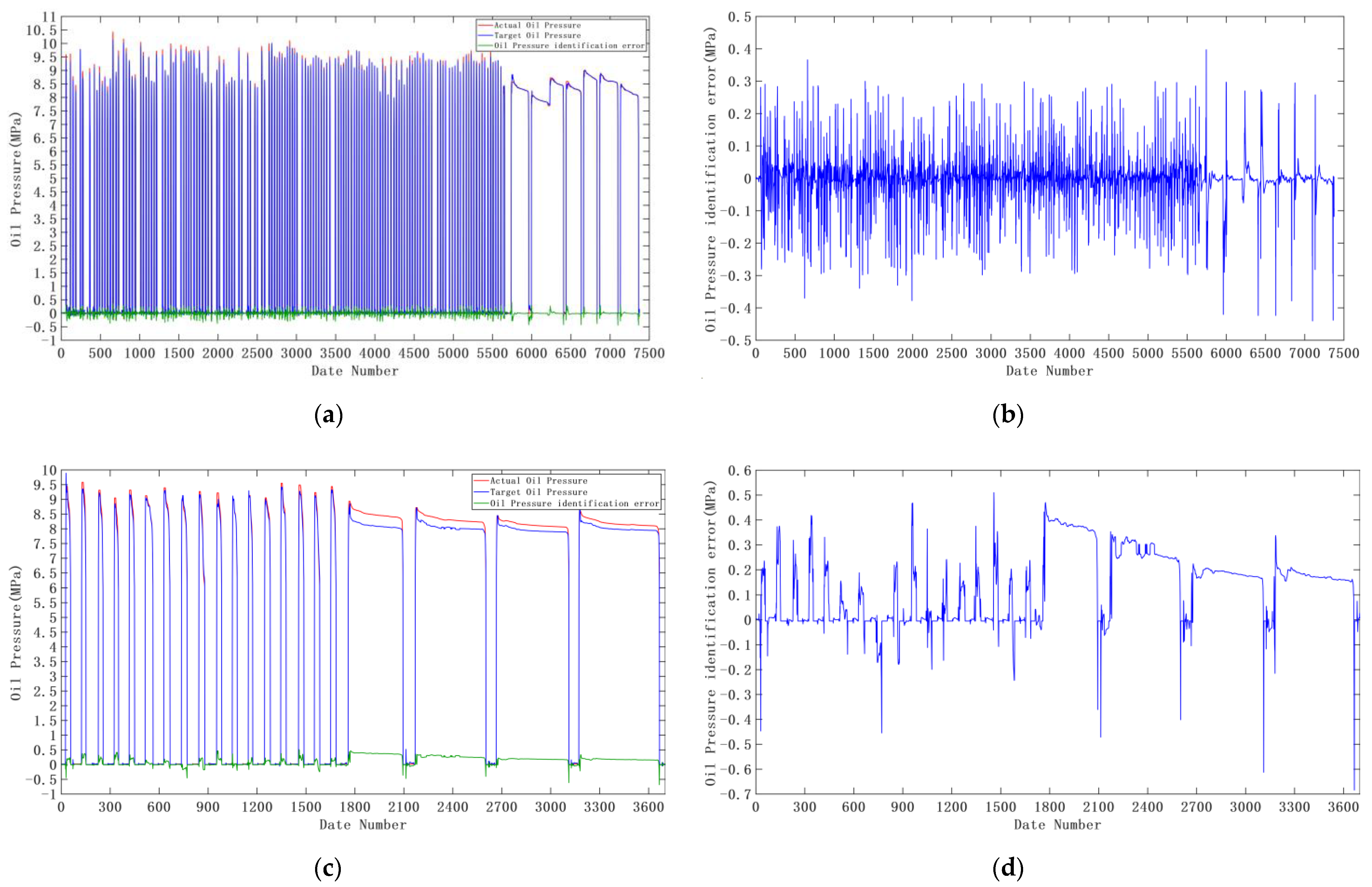
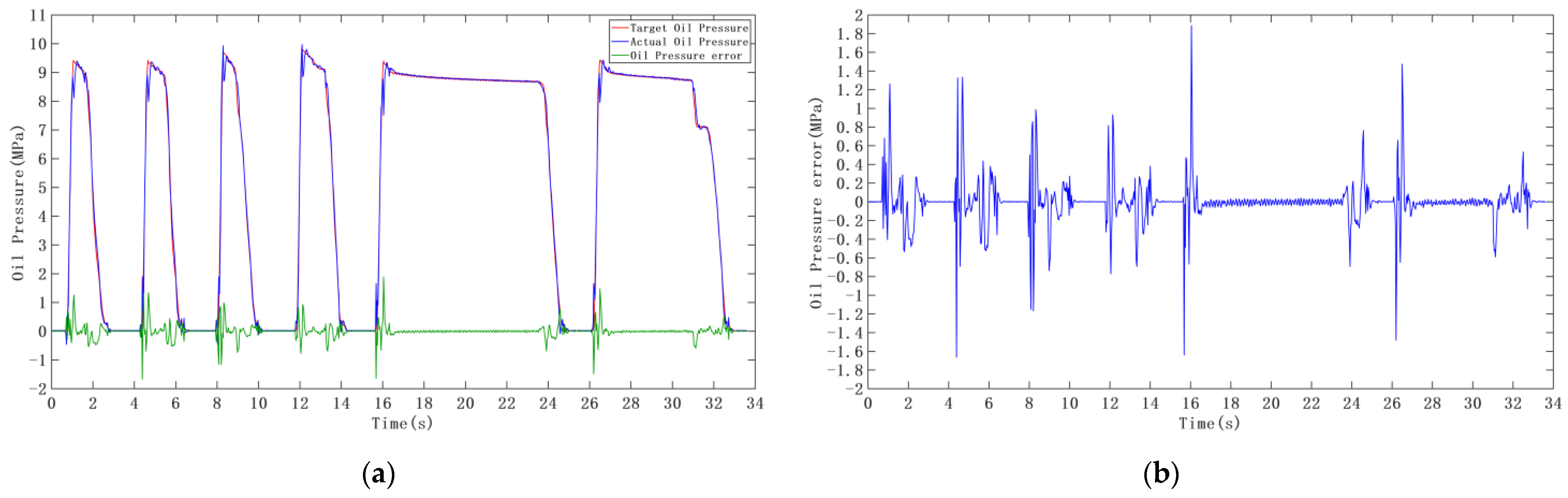
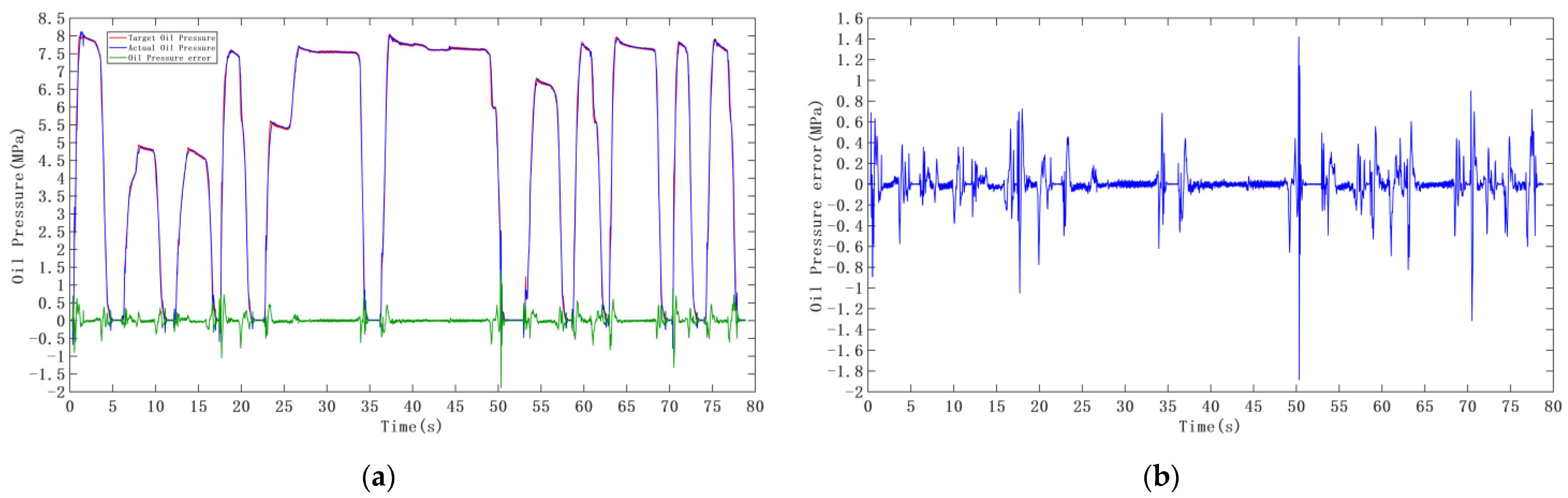
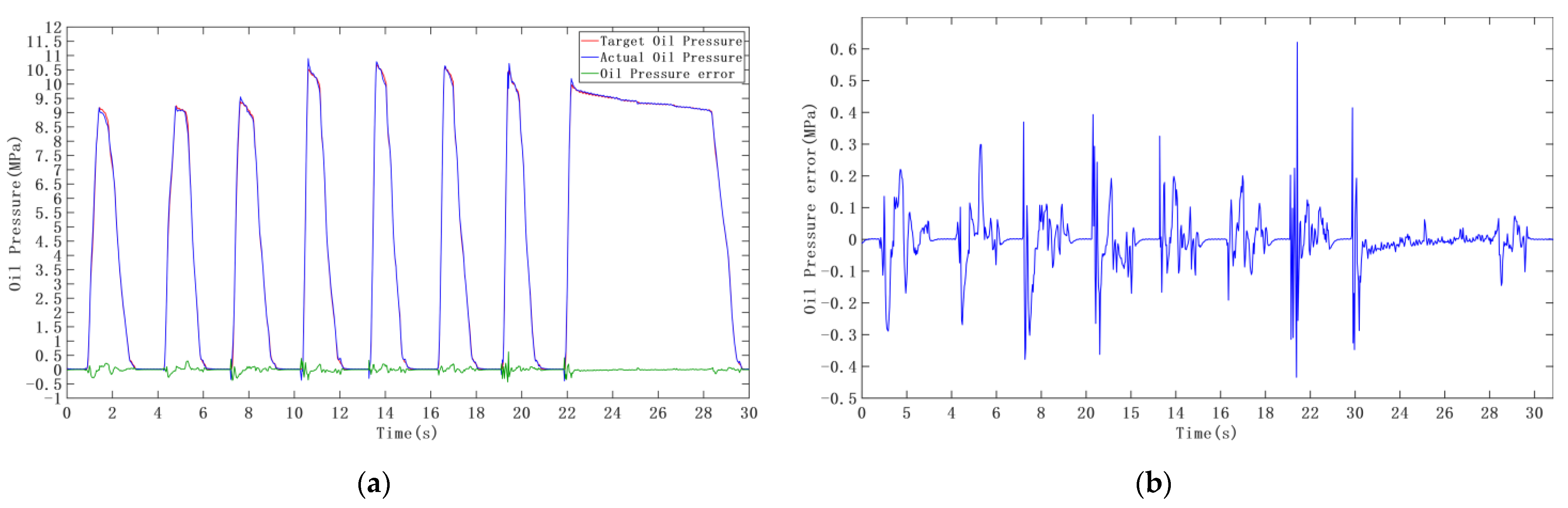
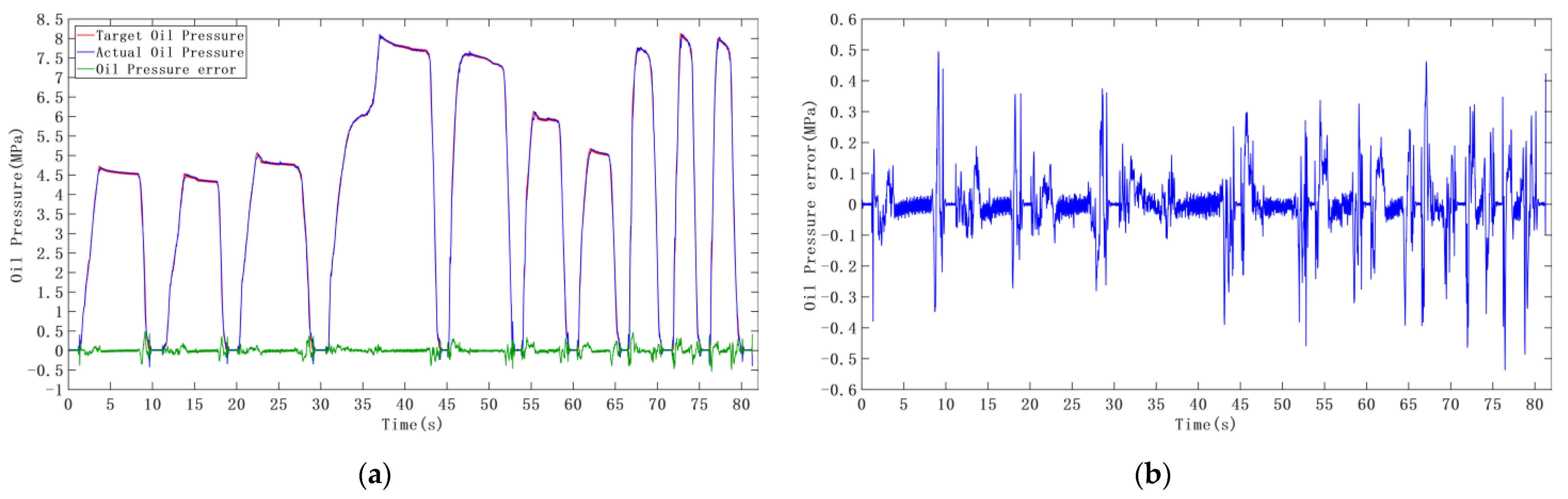
3.2. Experiments of Target Oil Pressure Following Control
4. Conclusions
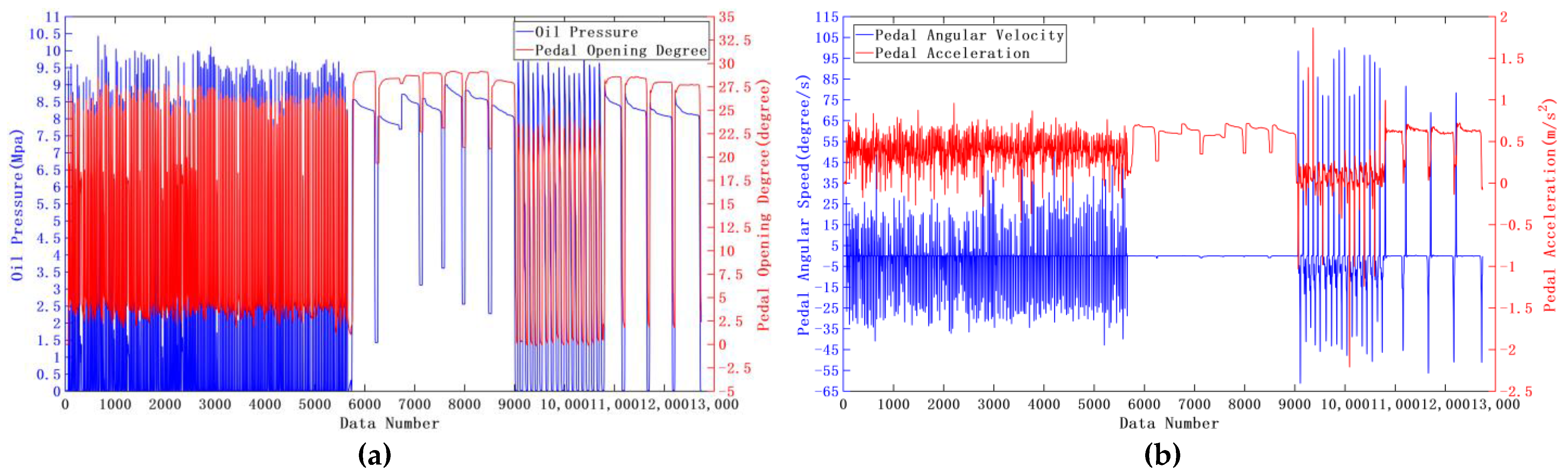
- Pedal opening degree, pedal angular velocity and pedal acceleration can be used as the basis for the classification of braking conditions;
- The sample data of emergency braking conditions and general braking conditions obviously differ in terms of pedal opening change rate and pedal acceleration, and therefore, the two braking conditions need to be distinguished, and the neural network parameters trained respectively under emergency braking and general braking conditions can significantly improve the accuracy of identification;
- The initial values of the T-S fuzzy neural network model parameters , , trained by the fuzzy C-means clustering algorithm are helpful in improving the training accuracy of the model compared with the random initialization of each parameter. Using the learning rate cosine decay strategy is beneficial to speeding up the training rate in the early stage of model training, jumping out of the local minimum, improving the accuracy of the model in the later stage of training, and helping the model converge;
- The fuzzy PID control and incremental PID control algorithm can realize the torque control of the power motor without relying on an accurate model of the electronically assisted brake system, and can also realize the following control of the oil pressure. This method has better control accuracy than the traditional PID controller.
- When using the fuzzy C-means clustering algorithm to calculate the initial values of and , the number of cluster centers is artificially selected, which involves subjective factors, and whether the number of cluster centers is set reasonably will affect the clustering results;
- Due to the limitations of the experimental conditions, the vehicle status information is not involved in the brake data collection and brake control algorithm verification experiments, and the correction method of target oil pressure cannot be verified because of the lack of related test data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Wu, X.; Cheng, S.; Shi, J.; Ping, X.; Yue, W. Design and experiment of control architecture and adaptive dual-loop controller for brake-by-wire system with an electric booster. IEEE Trans. Transp. Electrif. 2020, 6, 1236–1252. [Google Scholar] [CrossRef]
- Yu, Z.; Han, W.; Xu, S.; Xiong, L. Development status of hydraulic pressure control of electronic hydraulic brake system. J. Mech. Eng. 2017, 53, 1–15. [Google Scholar] [CrossRef]
- Chen, Q.; Shao, H.; Liu, Y.; Xiao, Y.; Wang, N.; Shu, Q. Hydraulic-pressure-following control of an electronic hydraulic brake system based on a fuzzy proportional and integral controller. Eng. Appl. Comput. Fluid Mech. 2020, 14, 1228–1236. [Google Scholar] [CrossRef]
- Büchler, R. Future brake systems and Technologies–Mk C1®–Continental’s brake system for future vehicle concepts. In Proceedings of the 7th International Munich Chassis Symposium 2016, 1st ed., 16 August 2016; Springer Vieweg: Wiesbaden, Germany. Available online: https://link.springer.com/chapter/10.1007/978-3-658-14219-3_45 (accessed on 1 November 2022).
- Hua, Y.; Jiang, H.; Tian, H.; Xu, X.; Chen, L. A comparative study of clustering analysis method for driver’s steering intention classification and identification under different typical conditions. Appl. Sci. 2017, 7, 1014. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, X.; Yu, Q.; Yuan, T. Identification of driver braking intention based on long short-term memory (LSTM) network. IEEE Access 2020, 8, 180422–180432. [Google Scholar] [CrossRef]
- Fang, E.; Zhang, D.; Cheng, Z. Research on recognition method and application of passenger car driver’s braking intention. Shanghai Auto 2016, 1, 49–53. [Google Scholar]
- Ju, J.; Bi, L.; Feleke, A.G. Noninvasive neural signal-based detection of soft and emergency braking intentions of drivers. Biomed. Signal Process. Control 2022, 72, 9. [Google Scholar] [CrossRef]
- Zheng, H.; Ma, S.; Fang, L.; Zhao, W.; Zhu, T. Braking intention recognition algorithm based on electronic braking system in commercial vehicles. Int. J. Heavy Veh. Syst. 2019, 26, 268–290. [Google Scholar] [CrossRef]
- Gu, Y.; Xie, J.; Liu, H.; Yang, Y.; Tan, Y.; Chen, L. Evaluation and analysis of comprehensive performance of a brake pedal based on an improved analytic hierarchy process. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2636–2648. [Google Scholar] [CrossRef]
- Meng, D.; Zhang, L.; Yu, Z. A dynamic model for brake pedal feel analysis in passenger cars. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 955–968. [Google Scholar] [CrossRef]
- Pei, X.; Pan, H.; Chen, Z.; Guo, X.; Yang, B. Coordinated control strategy of electro-hydraulic braking for energy regeneration. Control. Eng. Pract. 2020, 96, 104324. [Google Scholar] [CrossRef]
- Tavernini, D.; Vacca, F.; Metzler, M.; Savitski, D.; Ivanov, V.; Gruber, P.; Hartavi, A.E.; Dhaens, M.; Sorniotti, A. An explicit nonlinear model predictive abs controller for electro-hydraulic braking systems. IEEE Trans. Ind. Electron. 2020, 67, 3990–4001. [Google Scholar] [CrossRef]
- Nadeau, J.; Micheau, P.; Boisvert, M. Collaborative control of a dual electro-hydraulic regenerative brake system for a rear-wheel-drive electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 1035–1046. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, H.; He, R.; Chen, R.; Chen, H. A Mechatronic Brake Booster for Electric Vehicles: Design, Control, and Experiment. IEEE Trans. Veh. Technol. 2020, 69, 7040–7053. [Google Scholar] [CrossRef]
- Chu, L.; Xu, Y.; Zhao, D.; Chang, C. Research on pressure control algorithm of regenerative braking system for highly automated driving vehicles. World Electr. Veh. J. 2021, 12, 112. [Google Scholar] [CrossRef]
- Chen, P.; Wu, J.; Zhao, J.; He, R. Design and power assisted braking control of a novel electromechanical brake booster. SAE Int. J. Passeng. Cars-Electron. Electr. Syst. 2018, 11, 171–181. [Google Scholar] [CrossRef]
- Meng, B.; Yang, F.; Liu, J.; Wang, Y. A survey of brake-by-wire system for intelligent connected electric vehicles. IEEE Access 2020, 8, 225424–225436. [Google Scholar] [CrossRef]
- Zhu, F.; Guo, H.; Xu, W.; Liu, J.; Chen, H.; Lv, Y. Modeling of a novel Brake-by-Wire (BBW) system for electric vehicle based on dual Closed—loop PID. In Proceedings of the 31st Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019. [Google Scholar]
- Zhao, X.; Li, L.; Wang, X.; Mei, M.; Liu, C.; Song, J. Braking force decoupling control without pressure sensor for a novel series regenerative brake system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 1750–1766. [Google Scholar] [CrossRef]
- Yang, I.; Choi, K.; Huh, K. Development of an electric booster system using sliding mode control for improved braking performance. Int. J. Automot. 2012, 13, 1005–1011. [Google Scholar] [CrossRef]
- Aksjonov, A.; Vodovozov, V.; Raud, Z. Improving energy recovery in blended antilock braking systems of electric vehicles. In Proceedings of the 16th IEEE International Conference on Industrial Informatics (INDIN), Univ Porto, Fac Engn, Porto, Portugal, 18–20 July 2018. [Google Scholar]
- Zhao, J.; Deng, Z.; Zhu, B.; Chang, T.; Chen, Z. Hydraulic pressure control of electric power braking system based on RBF network sliding mode. J. Mech. Eng. 2020, 56, 106–114. [Google Scholar]
- Chae, H.; Kang, C.; Kim, B.; Kim, J.; Chung, C.; Choi, J. Autonomous braking system via deep reinforcement learning. In Proceedings of the 2017 IEEE 20th International conference on intelligent transportation systems (ITSC), Yokohama, Japan, 16–19 October 2017. [Google Scholar]
- Min, K.; Yeon, K.; Jo, Y.; Sim, G.; Sunwoo, M.; Han, M. Vehicle deceleration prediction based on deep neural network at braking conditions. Int. J. Automot. 2020, 21, 91–102. [Google Scholar] [CrossRef]
- Xia, G.; Li, J.; Tang, X.; Zhao, L.; Sun, B. Layered control of forklift lateral stability based on Takagi-Sugeno fuzzy neural network. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 1767–1780. [Google Scholar] [CrossRef]
- Li, J. Research on robot motion control based on variable structure fuzzy neural network based on T-S model. In Proceedings of the 5th International Conference on Environmental Science and Material Application (ESMA), Xi’an, China, 15–16 December 2019. [Google Scholar]
- Wang, N.; Yao, W.; Zhao, Y.; Chen, X. Bayesian calibration of computer models based on Takagi-Sugeno fuzzy models. Comput. Methods Appl. Mech. Eng. 2021, 378, 113724. [Google Scholar] [CrossRef]
- Lu, M.; Peng, T.; Yue, G.; Ma, B.; Liao, X. Dual-channel hybrid neural network for modulation recognition. IEEE Access 2021, 9, 76260–76269. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Chatterjee, S.; Sen, S.; Sinitca, A.; Kaplun, D.; Sarkar, R. A deep learning model for classifying human facial expressions from infrared thermal images. Sci. Rep. 2021, 11, 1–17. [Google Scholar]
- Nakamura, K.; Derbel, B.; Won, K.; Hong, B. Learning-rate annealing methods for deep neural networks. Electronics 2021, 10, 2029. [Google Scholar] [CrossRef]
- Wang, W.; Lee, C.; Liu, J.; Colakoglu, T.; Peng, W. An empirical study of cyclical learning rate on neural machine translation. Nat. Lang. Eng. 2022, 1–21. [Google Scholar] [CrossRef]
- Vodovozov, V.; Petlenkov, E.; Aksjonov, A.; Raud, Z. Simulation study of electric vehicles at fuzzy PID control of braking torque. In Proceedings of the Informatics in Control, Automation and Robotics: 17th International Conference, ICINCO 2020 Lieusaint, Paris, France, 7–9 July 2020. [Google Scholar]
- Umnitsyn, A.; Bakhmutov, S.V. Intelligent anti-lock braking system of electric vehicle with the possibility of mixed braking using fuzzy logic. J. Phys. Conf. Ser. 2021, 2061, 2021. [Google Scholar] [CrossRef]
- He, Y.; Lu, C.; Shen, J.; Yuan, C. A second-order slip model for constraint backstepping control of antilock braking system based on Burckhardt’s model. Int. J. Model. Simul. 2020, 40, 130–142. [Google Scholar] [CrossRef]
- Cao, K.; Hu, M.; Wang, D.; Qiao, S.; Guo, C.; Fu, C.; Zhou, A. All-Wheel-Drive Torque Distribution Strategy for Electric Vehicle Optimal Efficiency Considering Tire Slip. IEEE Access 2021, 9, 25245–25257. [Google Scholar] [CrossRef]
- Gowda, D.V.; Ramachandra, A.C. Slip ratio control of anti-lock braking system with bang-bang controller. Int. J. Comput. Tech. 2017, 4, 97–104. [Google Scholar]

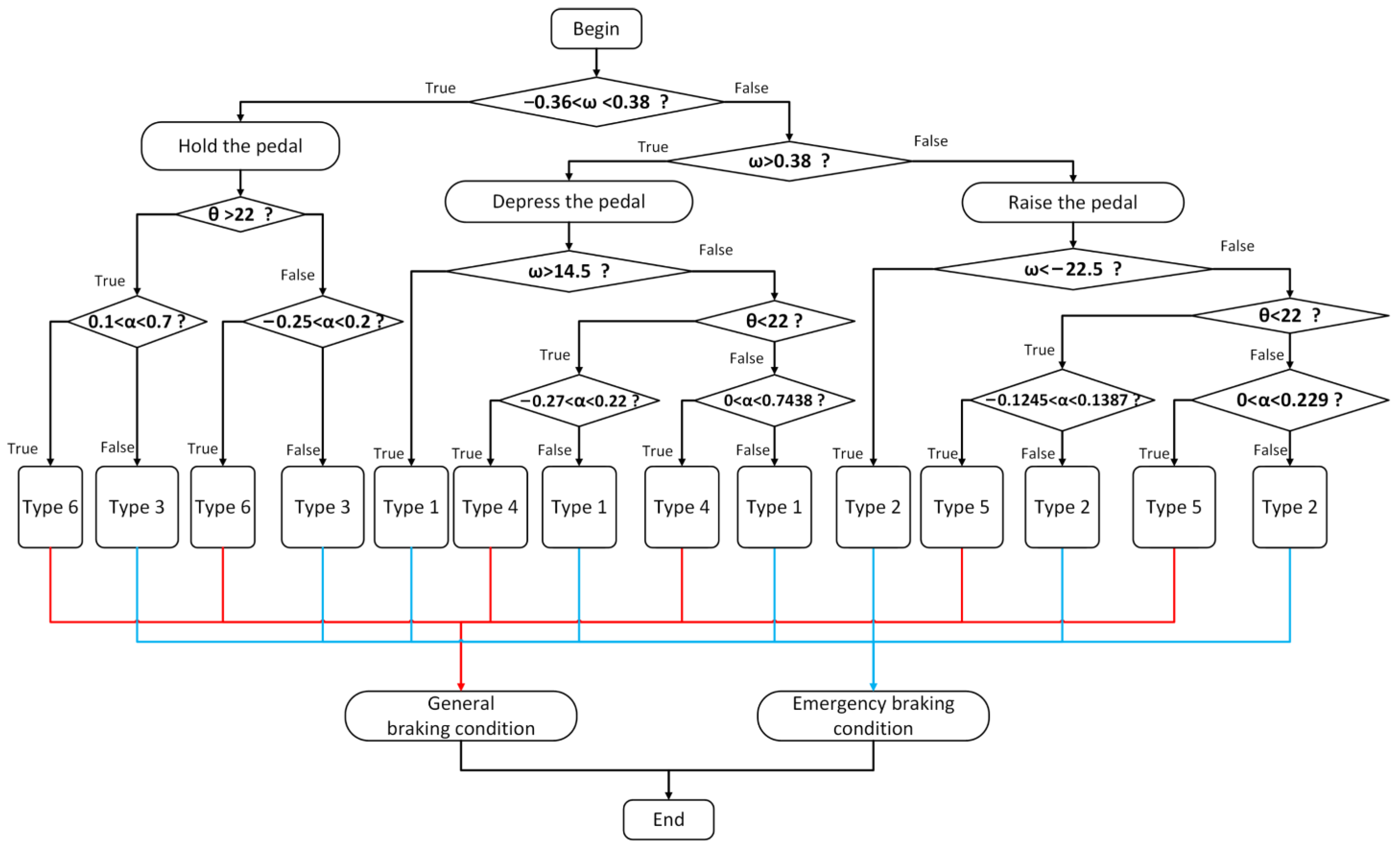




| Braking Conditions | Pedal Parameters | |||
|---|---|---|---|---|
| Emergency braking condition | Depress the pedal | -- | -- | |
| (0.38, 14.5) | ||||
| Hold the pedal | (−0.36, 0.38) | |||
| Raise the pedal | -- | -- | ||
| (−22.5, −0.36) | ||||
| General braking condition | Depress the pedal | (0.38, 14.5) | (0, 0.7438) | |
| (−0.27, 0.22) | ||||
| Hold the pedal | (−0.36, 0.38) | (0.1, 0.7) | ||
| (−0.25, 0.2) | ||||
| Raise the pedal | (−22.5, −0.36) | (0, 0.229) | ||
| (−0.1245, 0.1387) | ||||
| Parameters Setting and Results | Learning Rate Attenuation Strategies | |||||
|---|---|---|---|---|---|---|
| Exp | Cosine | Sigmoid | Poly | Inv | No Attenuation | |
| 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | |
| 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | |
| p | -- | -- | -- | 0.25 | 0.25 | -- |
| 0.99 | -- | -0.01 | -- | -- | -- | |
| MSE (MPa) | 0.007683 | 0.007027 | 0.013144 | 0.007266 | 0.007717 | 0.007761 |
| Control Parameters e(k) | ||||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | ||
| NB | PB | PB | PM | PM | PS | PS | ZO | |
| NM | PB | PM | PM | PS | PS | ZO | NS | |
| NS | PB | PM | PM | PS | ZO | ZO | NS | |
| ZO | PM | PM | PS | ZO | NS | NM | NM | |
| PS | PS | PS | ZO | NS | NS | NM | NB | |
| PM | PS | ZO | NS | NM | NM | NM | NB | |
| PB | ZO | NM | NM | NM | NM | NB | NB | |
| NB | NB | NB | NM | NM | NS | ZO | ZO | |
| NM | NB | NB | NM | NS | NS | ZO | ZO | |
| NS | NM | NM | NS | NS | ZO | PS | PS | |
| ZO | NM | NM | NS | ZO | PS | PS | PM | |
| PS | NM | NS | ZO | PS | PS | PM | PB | |
| PM | ZO | ZO | PS | PS | PM | PM | PB | |
| PB | ZO | ZO | PS | PM | PM | PB | PB | |
| NB | PS | NS | NB | NB | NB | NM | PS | |
| NM | PS | NS | NB | NM | NM | NS | PS | |
| NS | ZO | NS | NM | NM | NS | NS | ZO | |
| ZO | ZO | NS | ZO | NS | ZO | NS | ZO | |
| PS | ZO | ZO | ZO | ZO | ZO | ZO | ZO | |
| PM | PB | NS | PS | PS | PS | PS | PB | |
| PB | PB | PM | PM | PM | PS | PS | PB | |
| Error Evaluation Indexes | Braking Conditions Classification | |||
|---|---|---|---|---|
| Emergency Braking Condition | General Braking Condition | Without Braking Conditions Classification | ||
| Training set | Sample size | 7374 | 7698 | 15136 |
| Maximum error (MPa) | 0.4403 | 0.6295 | 1.2273 | |
| Minimum error (MPa) | ||||
| MSE (MPa) | 0.0049 | 0.0038 | 0.0216 | |
| Testing set | Sample size | 3702 | 3560 | 7262 |
| Maximum error (MPa) | 0.6841 | 0.7705 | 1.2684 | |
| Minimum error (MPa) | ||||
| MSE (MPa) | 0.0351 | 0.0396 | 0.1062 | |
| PID Controller | Error Evaluation Indexes | Braking Conditions Classification | |||||
|---|---|---|---|---|---|---|---|
| Emergency Braking Condition | General Braking Condition | ||||||
| Oil Pressure Rising | Oil Pressure Holding | Oil Pressure Falling | Oil Pressure Rising | Oil Pressure Holding | Oil Pressure Falling | ||
| Traditional PID Controller | Maximum error (MPa) | 1.8480 | 0.2191 | 0.6542 | 0.4424 | 0.1157 | 1.7369 |
| Minimum error (MPa) | |||||||
| MSE (MPa) | 0.3325 | 0.0406 | 0.0778 | 0.0448 | 0.0354 | 0.0654 | |
| Fuzzy PID Controller | Maximum error (MPa) | 0.4789 | 0.2609 | 0.3335 | 0.3022 | 0.0328 | 0.5443 |
| Minimum error (MPa) | |||||||
| MSE (MPa) | 0.1411 | 0.0411 | 0.0610 | 0.0266 | 0.0224 | 0.0266 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Yu, Y.; Luo, J.; Xu, Z. Target Oil Pressure Recognition Algorithm for Oil Pressure Following Control of Electronic Assisted Brake System. Machines 2023, 11, 183. https://doi.org/10.3390/machines11020183
Chen L, Yu Y, Luo J, Xu Z. Target Oil Pressure Recognition Algorithm for Oil Pressure Following Control of Electronic Assisted Brake System. Machines. 2023; 11(2):183. https://doi.org/10.3390/machines11020183
Chicago/Turabian StyleChen, Lei, Yunchen Yu, Jie Luo, and Zhongpeng Xu. 2023. "Target Oil Pressure Recognition Algorithm for Oil Pressure Following Control of Electronic Assisted Brake System" Machines 11, no. 2: 183. https://doi.org/10.3390/machines11020183
APA StyleChen, L., Yu, Y., Luo, J., & Xu, Z. (2023). Target Oil Pressure Recognition Algorithm for Oil Pressure Following Control of Electronic Assisted Brake System. Machines, 11(2), 183. https://doi.org/10.3390/machines11020183






