Posture and Dynamics Analysis of Hydraulic Support with Joint Clearance under Impact Load
Abstract
1. Introduction
2. Materials and Methods
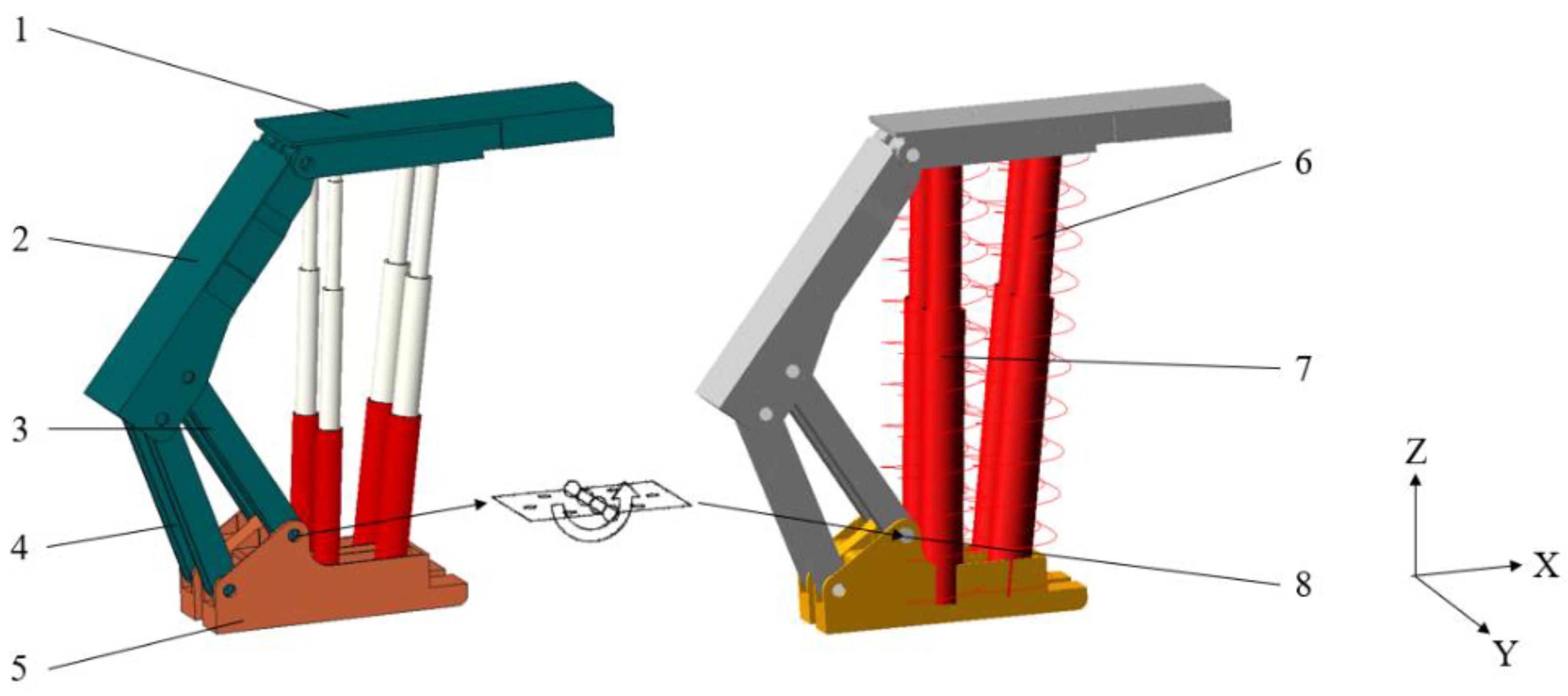
2.1. Ideal Model of Hydraulic Support
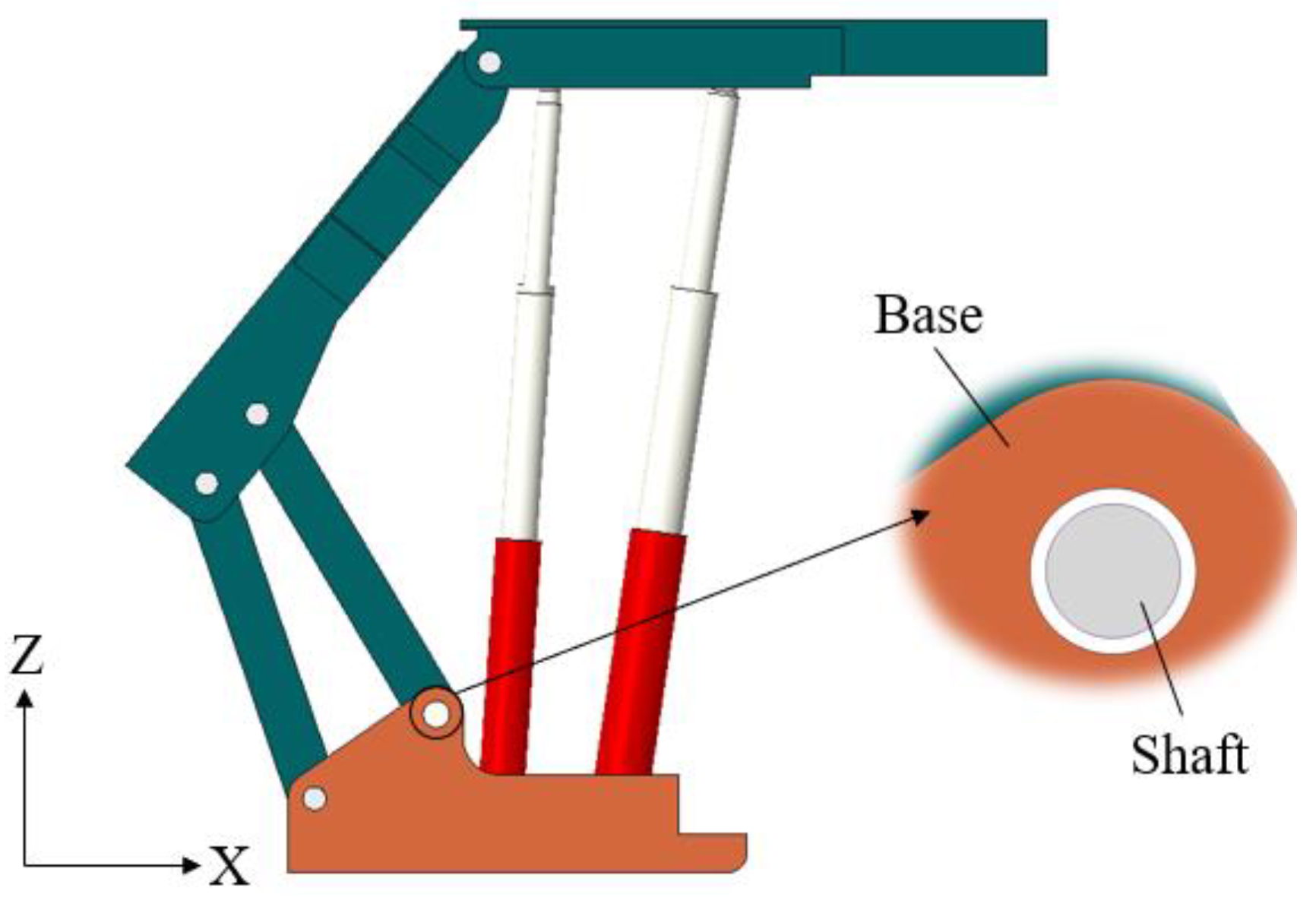
2.2. Hydraulic Support Model with Clearance
2.3. Column Equivalent Model
3. Results
3.1. Action Mode of Impact Load
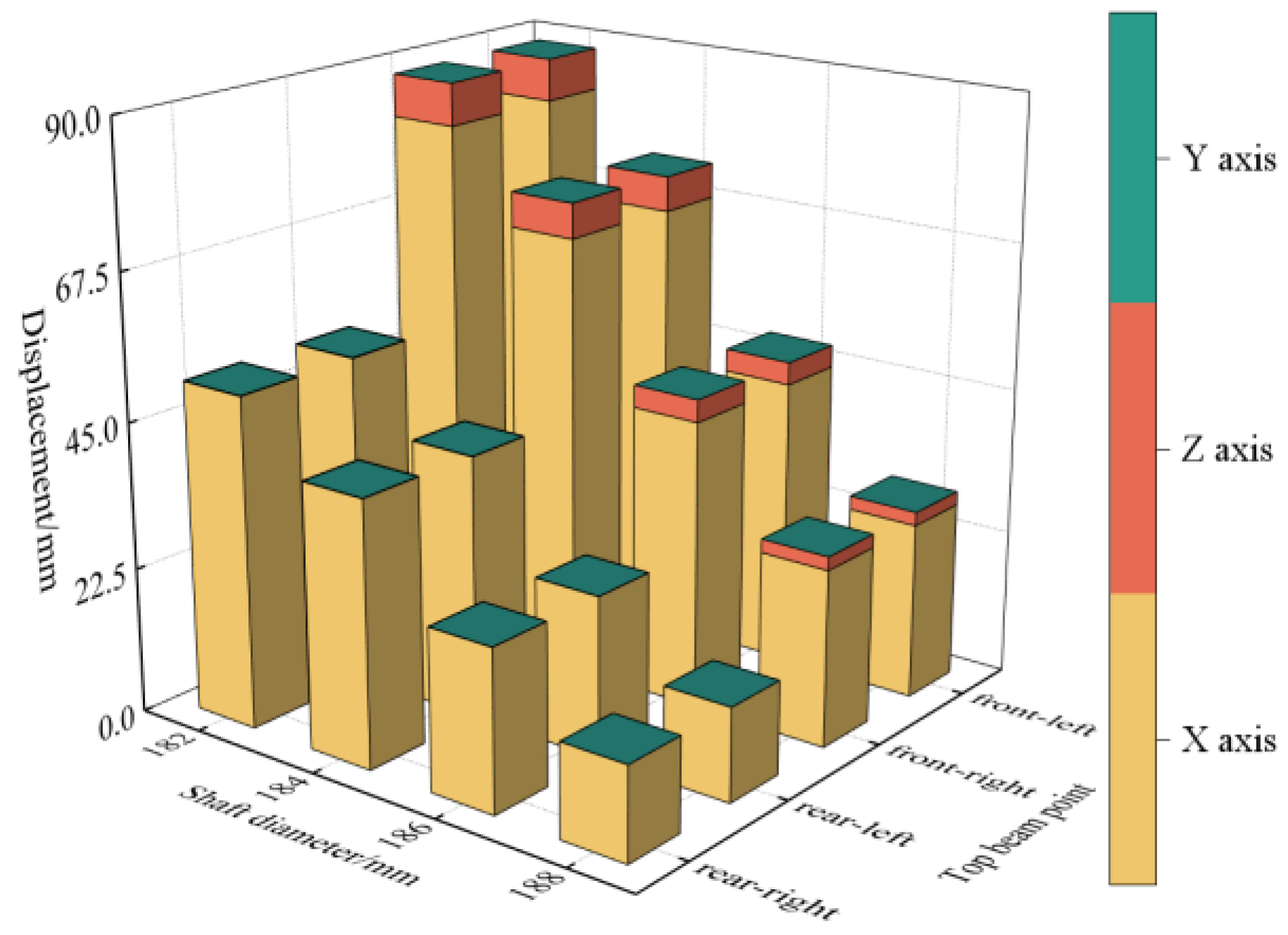
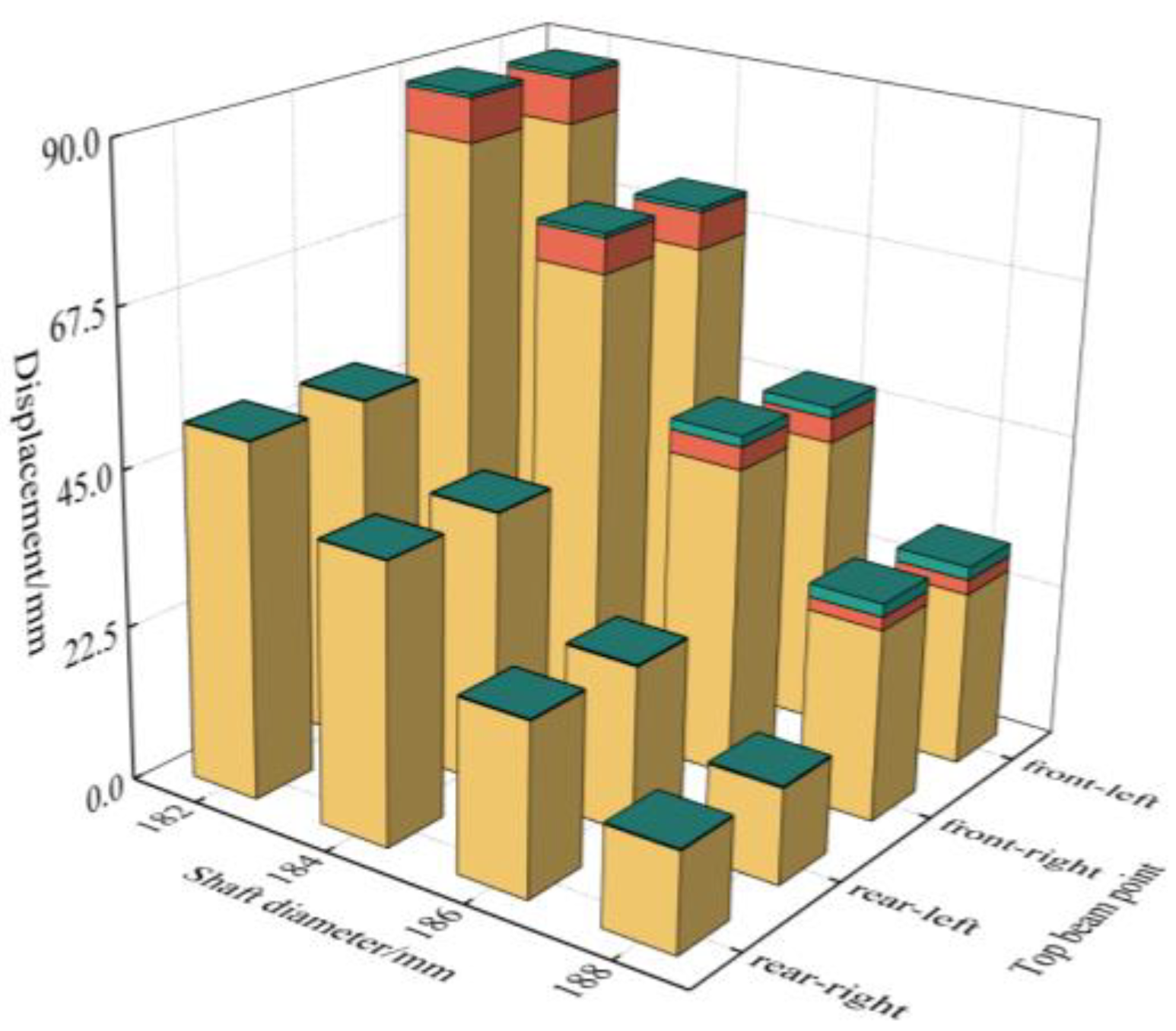
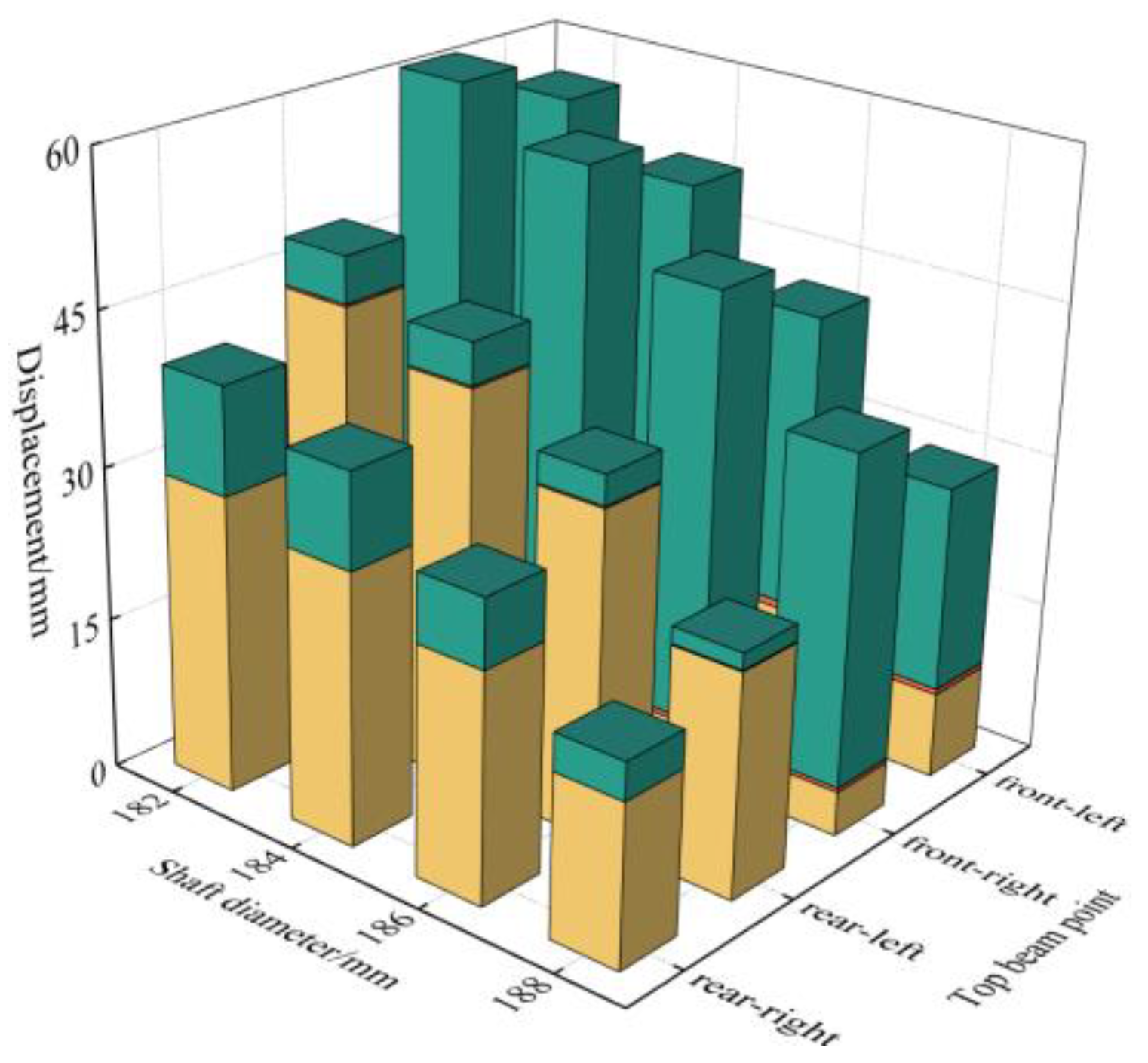
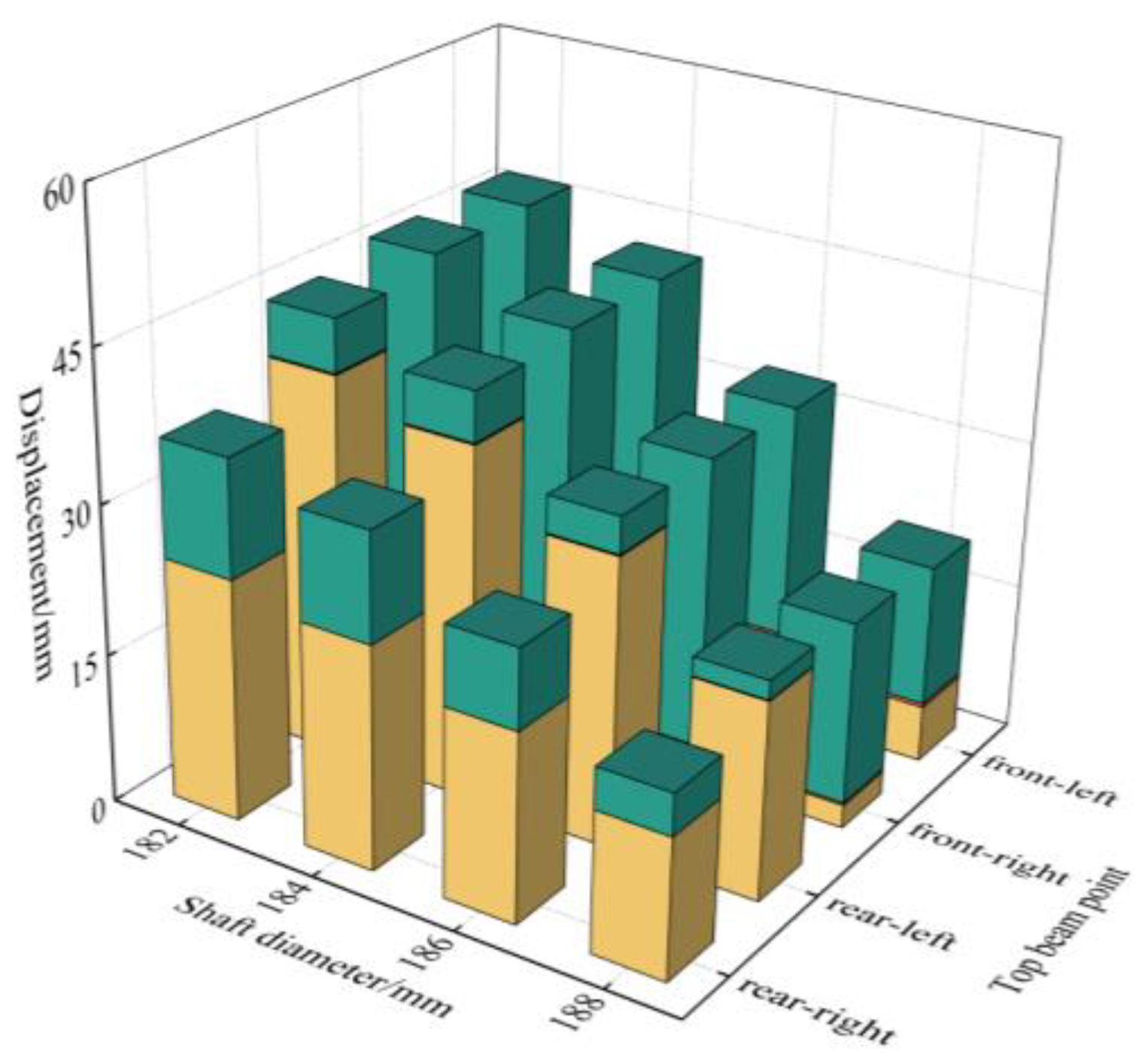
3.2. Posture Analysis of Hydraulic Support under Impact Load
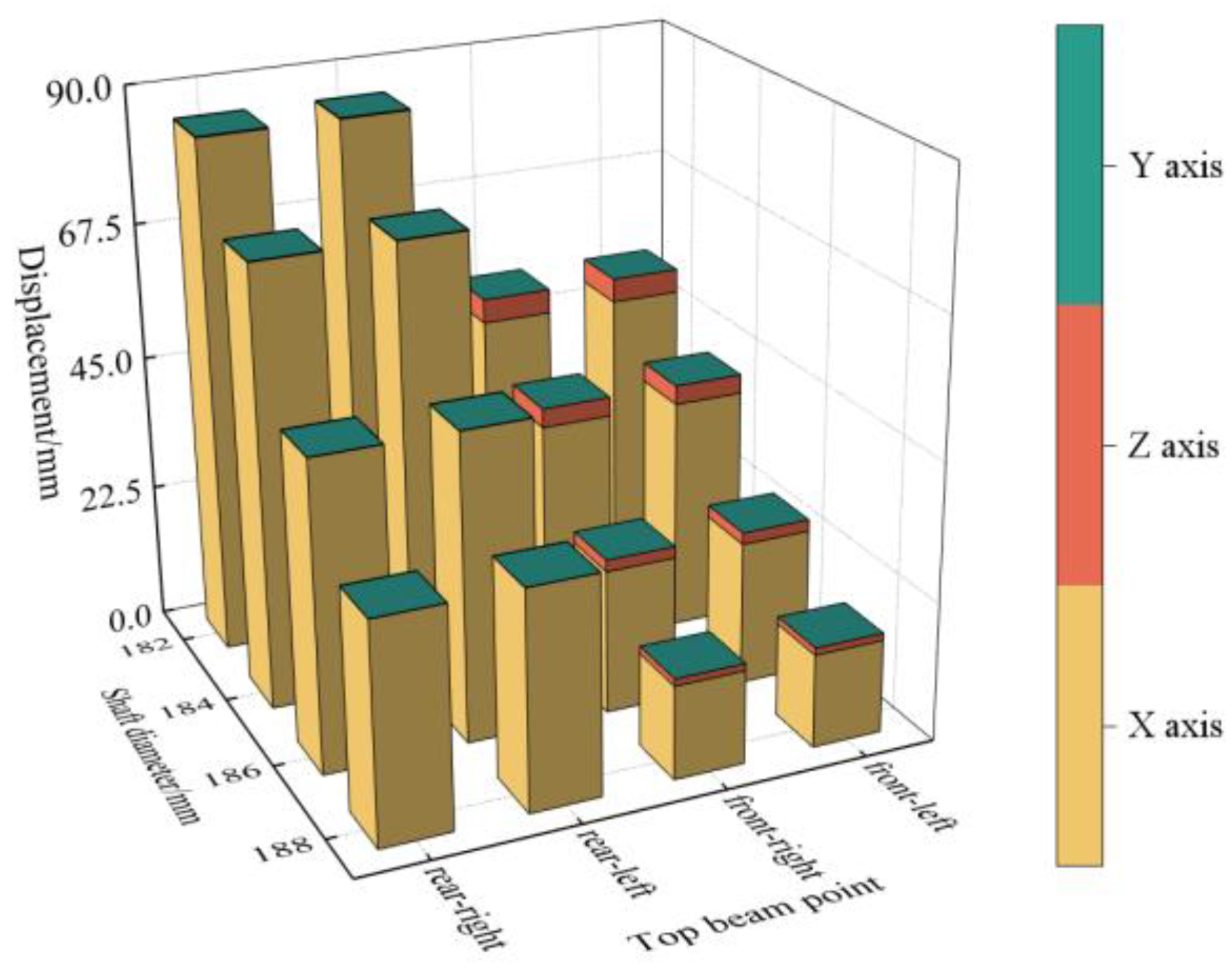
3.2.1. Impact Load Acts on the Front End of Double-Clearance-Support Top Beam
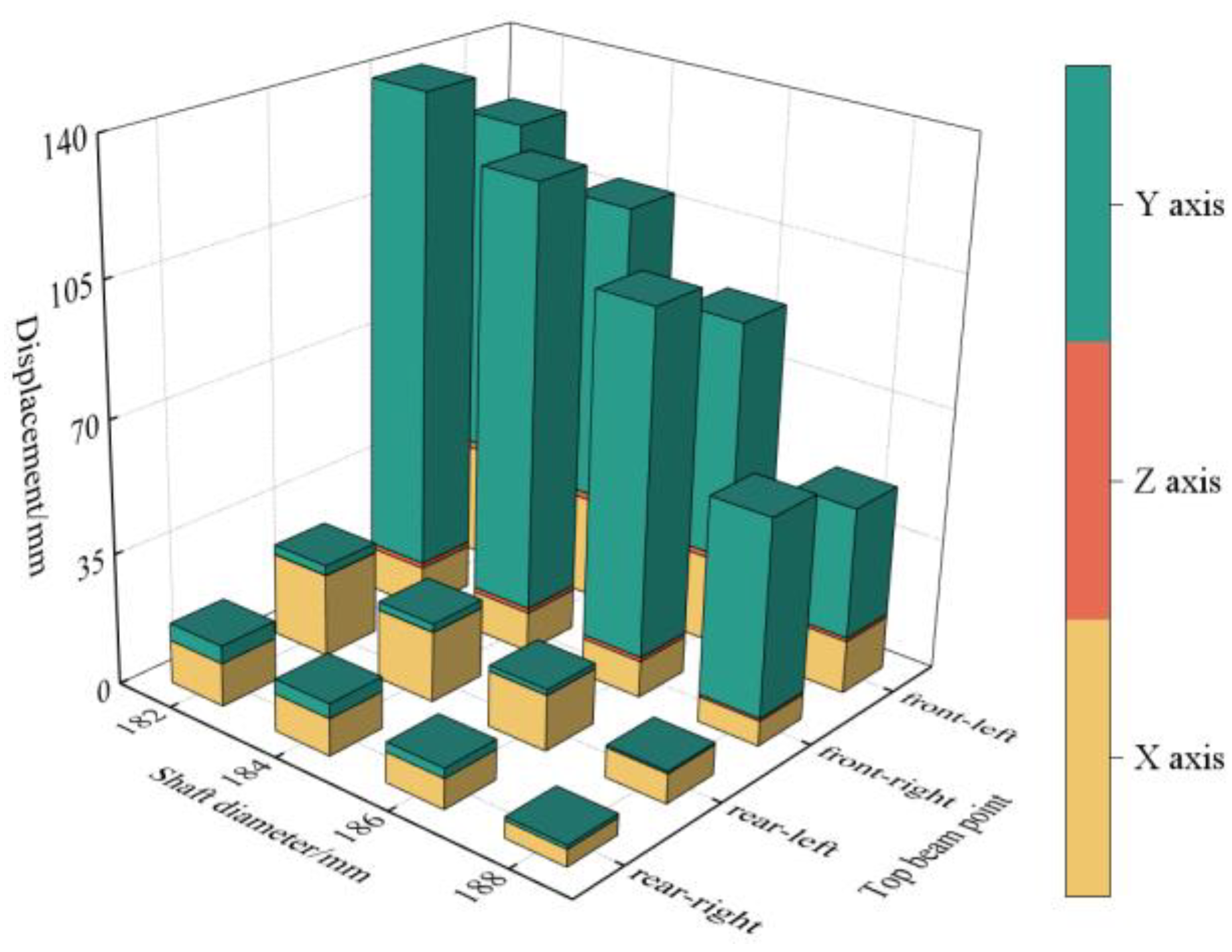
3.2.2. Impact Load Acting on the Tail End of Double-Clearance-Support Top Beam
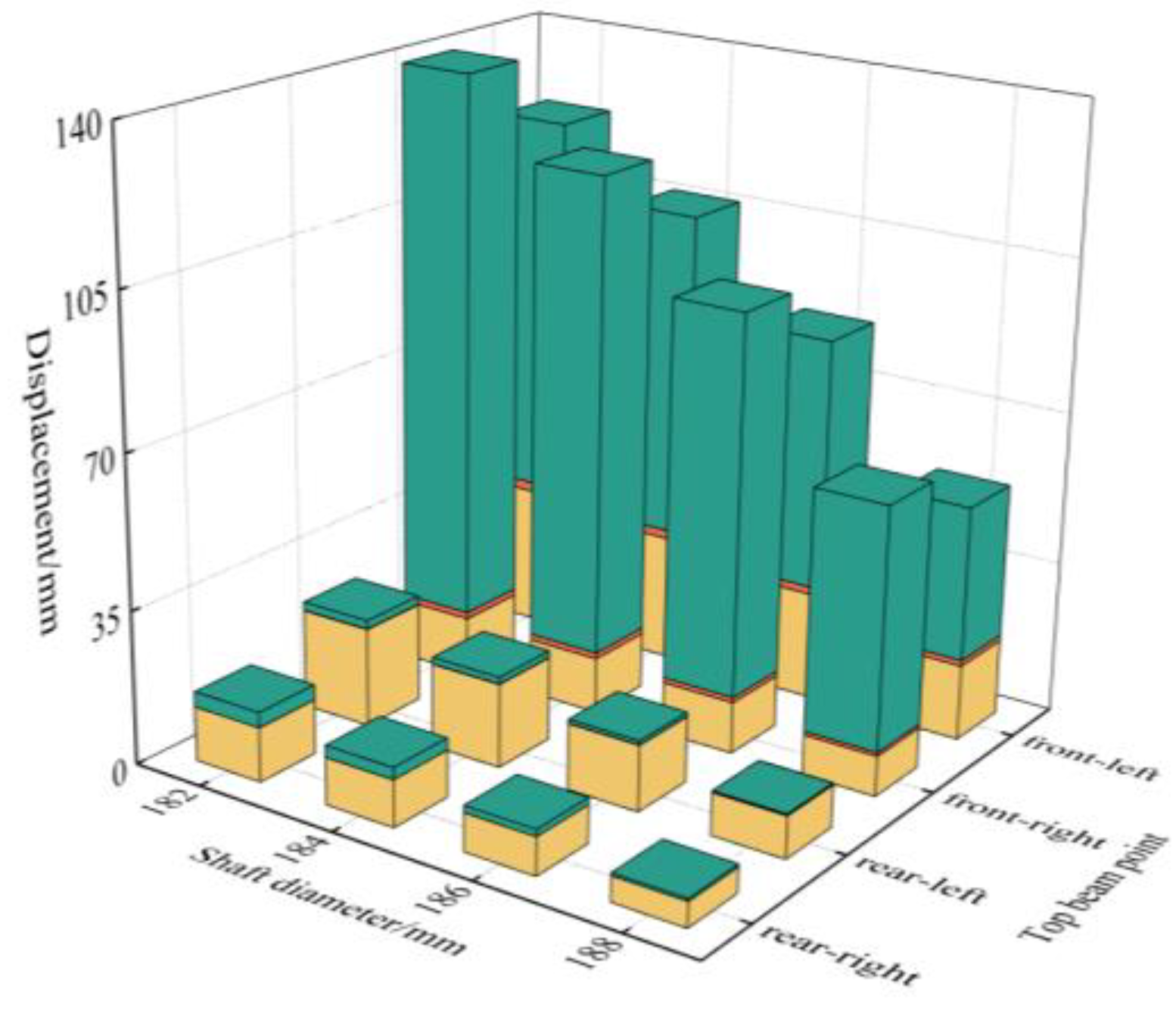
3.2.3. Impact Load Acts on the Front End of Single-Clearance-Support Top Beam
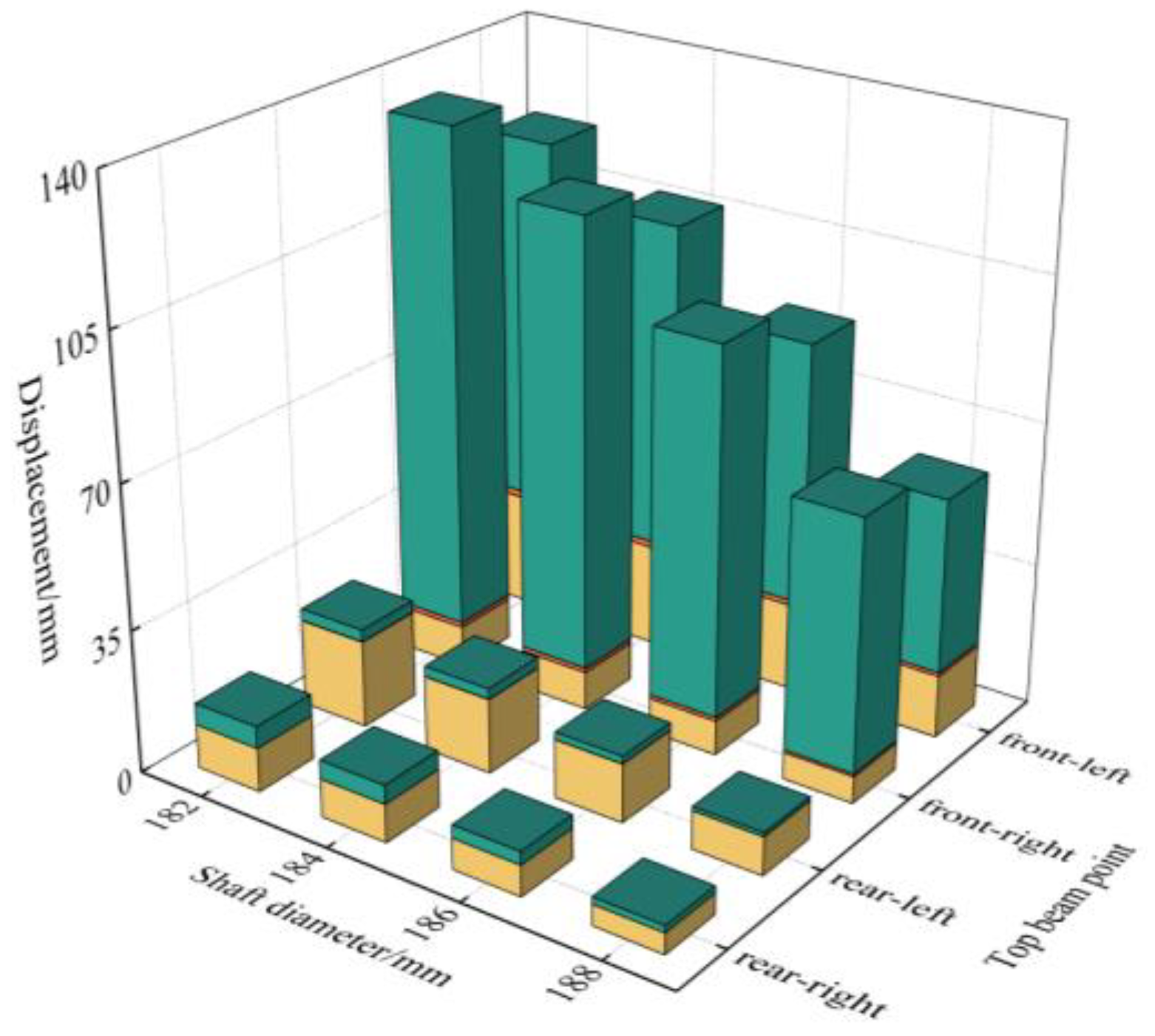
3.2.4. Impact Load Acts on the Tail End of Single-Clearance-Support Top Beam
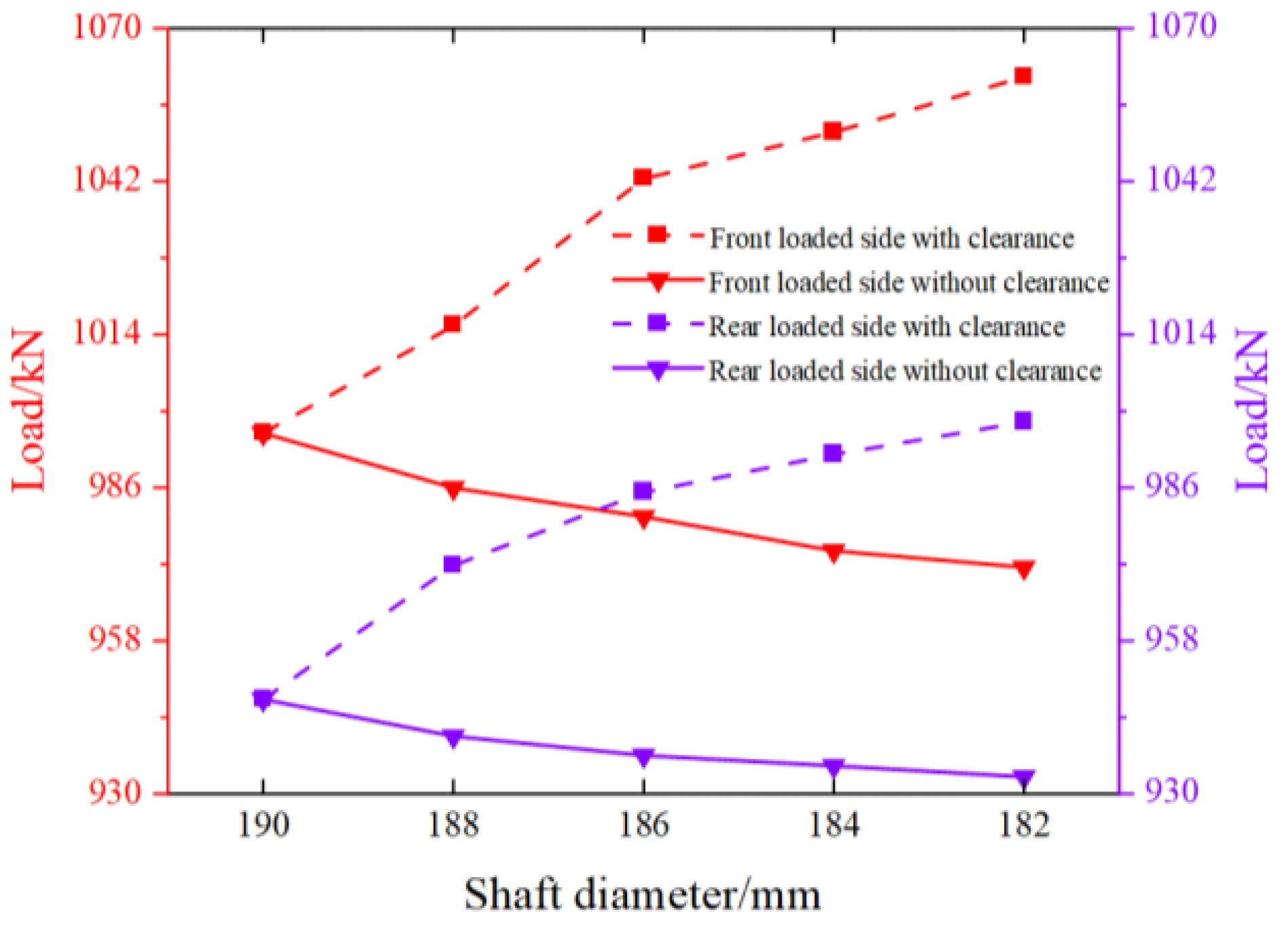
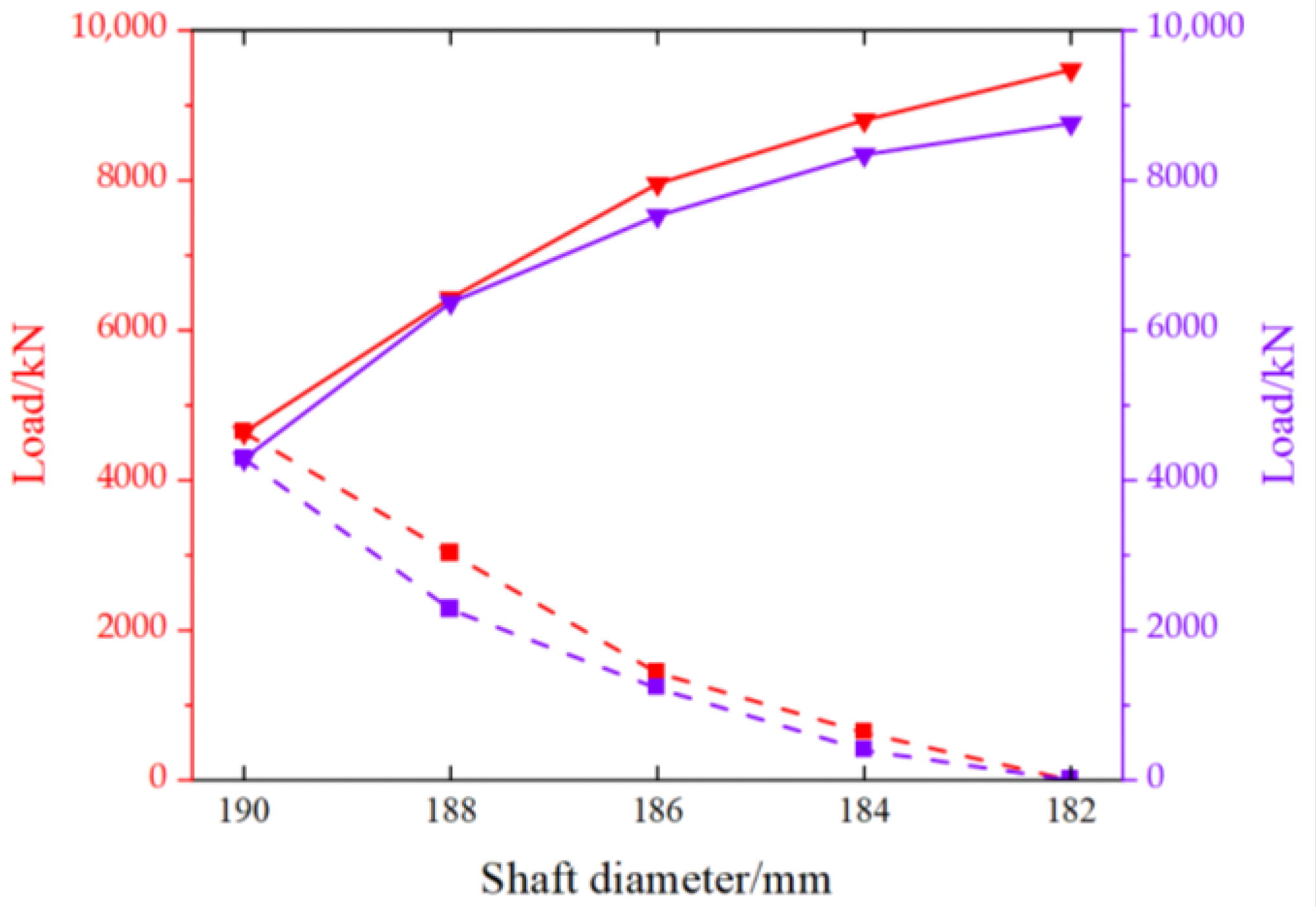
3.3. Dynamic Analysis of Hydraulic Support with Clearance
3.3.1. Mechanical Analysis of the Hinge Point between the Top Beam and Shield Beam
3.3.2. Mechanical Analysis of the Hinge Point between the Base and Front Connecting Rod
3.3.3. Mechanical Analysis of Hinge Point between Base and Rear Connecting Rod
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, Y. Supporting Condition Acquisition and Fuzzy Comprehensive Evaluation Method for Hydraulic Support. J. China Coal Soc. 2017, 42 (Suppl. S1), 260–266. [Google Scholar]
- Kang, H.; Wang, G.; Jiang, P.; Wang, J.; Zhang, N.; Jing, H.; Huang, B.; Yang, B.; Guan, X.; Wang, Z. Conception for Strata Control and Intelligent Mining Technology in Deep Coal Mines with Depth More than 1000 m. J. China Coal Soc. 2018, 43, 1789–1800. [Google Scholar]
- Yan, S.; Xu, G.; Fan, Z. Development Course and Prospect of the 50 Years’ Comprehensive Mechanized Coal Mining in China. Coal Sci. Technol. 2021, 49, 1–9. [Google Scholar]
- Frith, R.C. A Holistic Examination of the Load Rating Design of Longwall Shields after More than Half a Century of Mechanised Longwall Mining. Int. J. Min. Sci. Technol. 2015, 25, 687–706. [Google Scholar] [CrossRef]
- Wang, G.; Pang, Y.; Li, M.; Ma, Y.; Liu, X. Hydraulic Support and Coal Wall Coupling Relationship in Ultra Large Height Mining Face. J. China Coal Soc. 2017, 42, 518–526. [Google Scholar]
- Pan, J.; Qi, Q.; Liu, S.; Wang, S.; Ma, W.; Kang, X. Characteristics, Types and Prevention and Control Technology of Rock Burst in Deep Coal Mining in China. J. China Coal Soc. 2020, 45, 111–121. [Google Scholar]
- Bao, Y. Research on Intelligent Control Key Technology of Fully Mechanized Top Coal Caving Face in Extra Thick Coal Seam. Coal Sci. Technol. 2020, 48, 55–61. [Google Scholar]
- Liang, L.; Tian, J.; Zheng, H.; Jiao, S. A Study on Force Transmission in a Hydraulic Support under Impact Loading on Its Canopy Beam. J. China Coal Soc. 2015, 40, 2522–2527. [Google Scholar]
- Ren, H.; Zhang, D.; Gong, S.; Zhou, K.; Xi, C.; He, M.; Li, T. Dynamic Impact Experiment and Response Characteristics Analysis for 1:2 Reduced-Scale Model of Hydraulic Support. Int. J. Min. Sci. Technol. 2021, 31, 347–356. [Google Scholar] [CrossRef]
- Szurgacz, D.; Brodny, J. Analysis of the Influence of Dynamic Load on the Work Parameters of a Powered Roof Support’s Hydraulic Leg. Sustainability 2019, 11, 2570. [Google Scholar] [CrossRef]
- Szurgacz, D.; Brodny, J. Tests of Geometry of the Powered Roof Support Section. Energies 2019, 12, 3945. [Google Scholar] [CrossRef]
- Guan, E.; Miao, H.; Li, P.; Liu, J.; Zhao, Y. Dynamic Model Analysis of Hydraulic Support. Adv. Mech. Eng. 2019, 11, 1687814018820143. [Google Scholar] [CrossRef]
- Witek, M.; Prusek, S. Numerical Calculations of Shield Support Stress Based on Laboratory Test Results. Comput. Geotech. 2016, 72, 74–88. [Google Scholar] [CrossRef]
- Erkaya, S. Effects of Joint Clearance on the Motion Accuracy of Robotic Manipulators. J. Mech. Eng. 2018, 64, 82–94, 13p. [Google Scholar]
- Chen, X.; Fan, H. Dynamic Modeling and Response Analysis of Spatial Parallel Mechanism Considering Lubrication Clearance of Spherical Joints. Eur. J. Mech. A/Solids 2022, 92, 104458. [Google Scholar] [CrossRef]
- Hou, Y.; Deng, Y.; Zeng, D. Dynamic Modelling and Properties Analysis of 3RSR Parallel Mechanism Considering Spherical Joint Clearance and Wear. J. Cent. South Univ. 2021, 28, 712–727. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, J.; He, F.; Yu, D.; Wen, H. Design of Virtual Simulation Teaching Experiment for the Dynamics Analysis of Reciprocating Mechanism with Joint Clearance. Exp. Technol. Manag. 2022, 39, 162–166. [Google Scholar]
- Matekar, S.B.; Fulambarkar, A.M. Displacement Analysis of Slider in Slider-Crank Mechanism with Joint Clearance. Aust. J. Mech. Eng. 2020, 20, 949–958. [Google Scholar] [CrossRef]
- Feng, B.Z.; Xin, J.; Fei, L.; Jun, Z.J.; Yang, Z. Reducing Undesirable Vibrations of Planar Linkage Mechanism with Joint Clearance. J. Mech. Sci. Technol. 2018, 32, 559–565. [Google Scholar]
- Qingliang, Z.; Yangyang, L.; Yang, Y. Dynamic Analysis of Hydraulic Support with Single Clearance. Stroj. Vestn. J. Mech. Eng. 2021, 67, 53–66. [Google Scholar]
- Wang, X.; Cui, T.; Xie, J.; Shen, H.; Liu, Y.; Wang, B. Virtual Simulation Method of Hydraulic Support Motion Considering Pin Shaft Clearance. Coal Sci. Technol. 2021, 49, 186–193. [Google Scholar]
- Su, Y.; Guo, C.; Chen, W. Applicability Analysis of Internal Cylindrical Contact Model with Micro Clearance in Multibody System. Lubr. Eng. 2020, 45, 106–113. [Google Scholar]
- Jing, Q.; Liu, H. Dynamic Characteristics of Linkage Mechanism Considering Clearance of Cylinder Pair. J. Vib. Shock. 2021, 40, 32–39. [Google Scholar]
- Xu, W. Study on Load Characteristics of Hydraulic Support Column under Impact Load. Coal Mine Mach. 2021, 42, 63–66. [Google Scholar]
- Zeng, Q.L.; Meng, Z.S.; Wan, L.R.; Wang, C.L. Analysis on Force Transmission Characteristics of Two-Legged Shield Support under Impact Loading. Shock. Vib. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Zeng, Q.; Xu, P.; Meng, Z.; Wan, L. Dynamic Response Analysis of Four Column Chock Shield Support under Impact Load. Coal Sci. Technol. Available online: https://kns.cnki.net/kcms/detail/11.2402.TD.20220926.1612.002.html (accessed on 31 December 2022).





| Hydraulic Cylinder | Diameter of Hydraulic Cylinder/mm | Hydraulic Rod Diameter/mm | Effective Liquid Column Length/mm | |
|---|---|---|---|---|
| Front column | First-stage cylinder | 390 | 370 | 1 956 |
| Second-stage cylinder | 290 | 260 | 2 006 | |
| Rear column | First-stage cylinder | 335 | 305 | 2 076 |
| Second-stage cylinder | 230 | 210 | 2 052 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Q.; Xu, P.; Meng, Z.; Ma, C.; Lei, X. Posture and Dynamics Analysis of Hydraulic Support with Joint Clearance under Impact Load. Machines 2023, 11, 159. https://doi.org/10.3390/machines11020159
Zeng Q, Xu P, Meng Z, Ma C, Lei X. Posture and Dynamics Analysis of Hydraulic Support with Joint Clearance under Impact Load. Machines. 2023; 11(2):159. https://doi.org/10.3390/machines11020159
Chicago/Turabian StyleZeng, Qingliang, Penghui Xu, Zhaosheng Meng, Chen Ma, and Xiaowan Lei. 2023. "Posture and Dynamics Analysis of Hydraulic Support with Joint Clearance under Impact Load" Machines 11, no. 2: 159. https://doi.org/10.3390/machines11020159
APA StyleZeng, Q., Xu, P., Meng, Z., Ma, C., & Lei, X. (2023). Posture and Dynamics Analysis of Hydraulic Support with Joint Clearance under Impact Load. Machines, 11(2), 159. https://doi.org/10.3390/machines11020159





