Study on Aerodynamic Drag Reduction by Plasma Jets for 600 km/h Vacuum Tube Train Sets
Abstract
:1. Introduction
2. Numerical Calculation Model
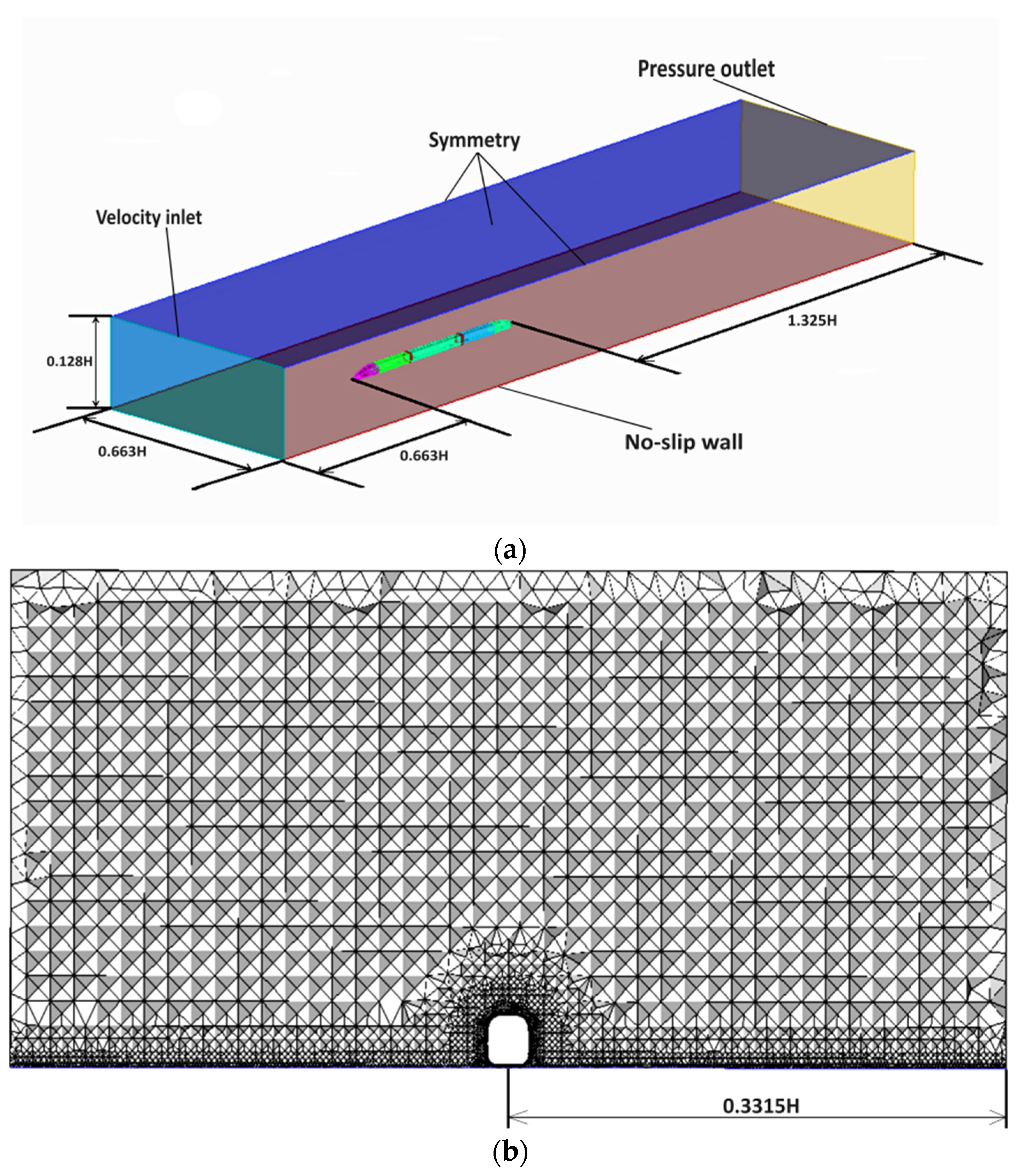
2.1. Geometric Model and Simulation Conditions
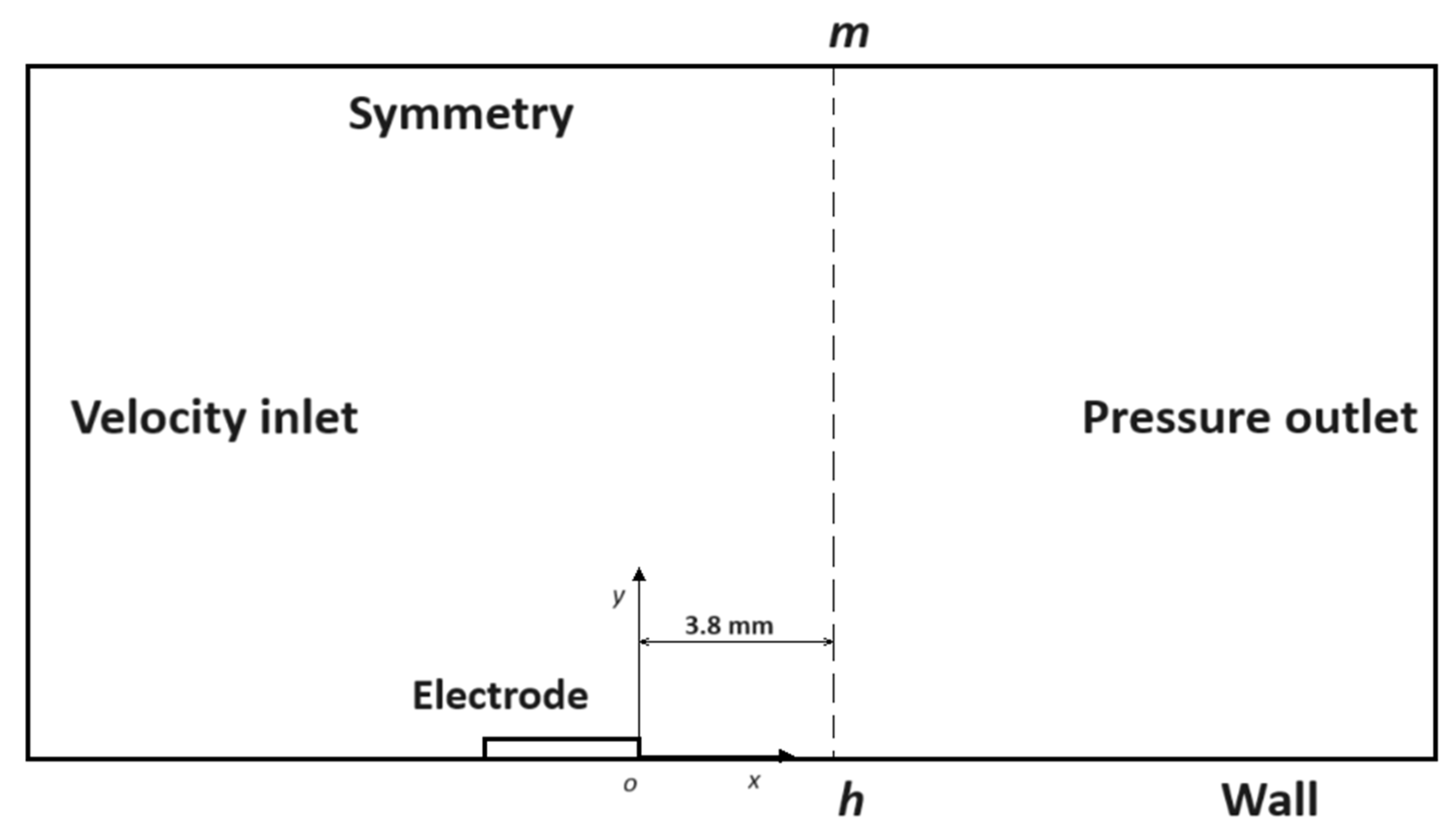
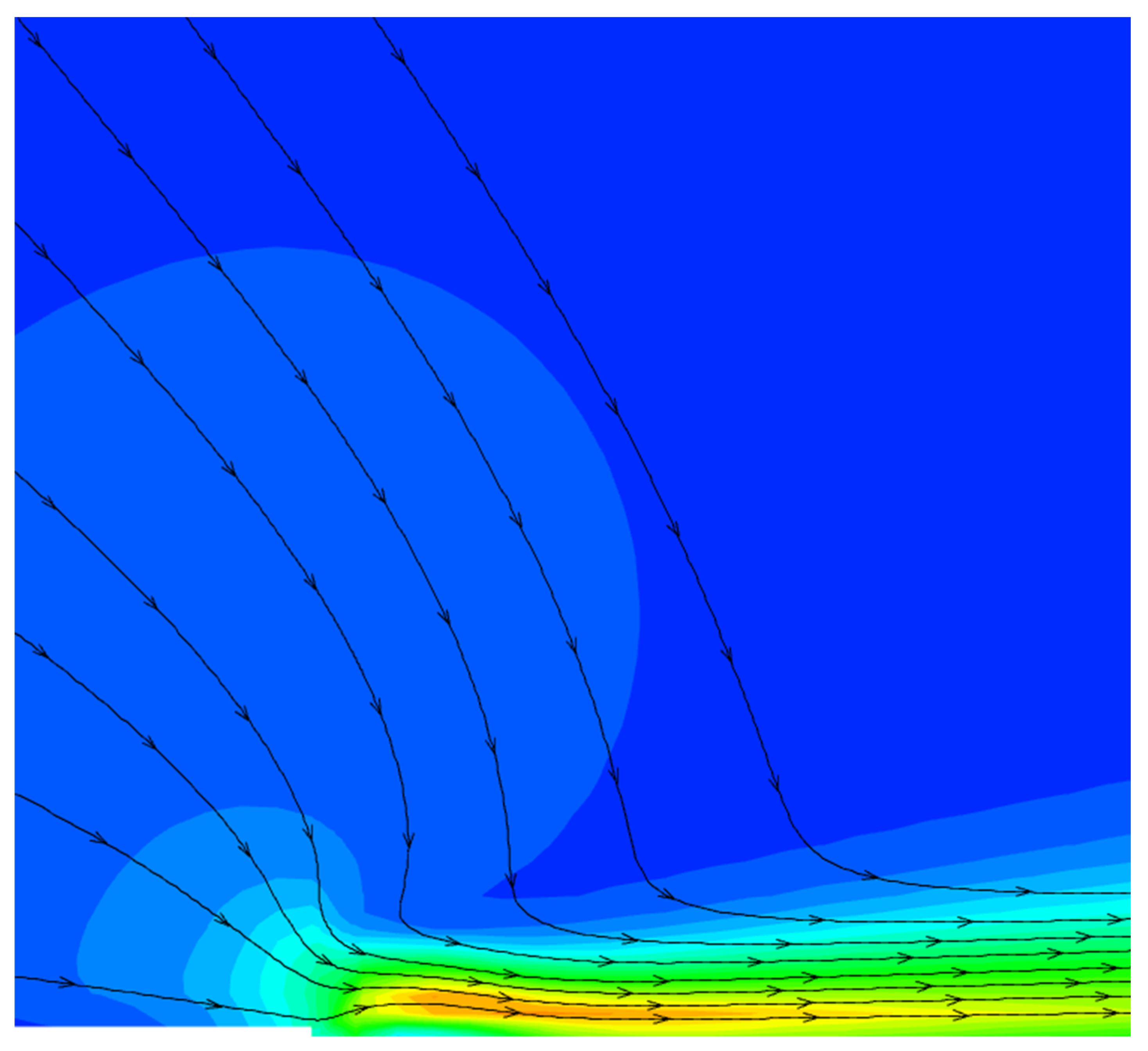
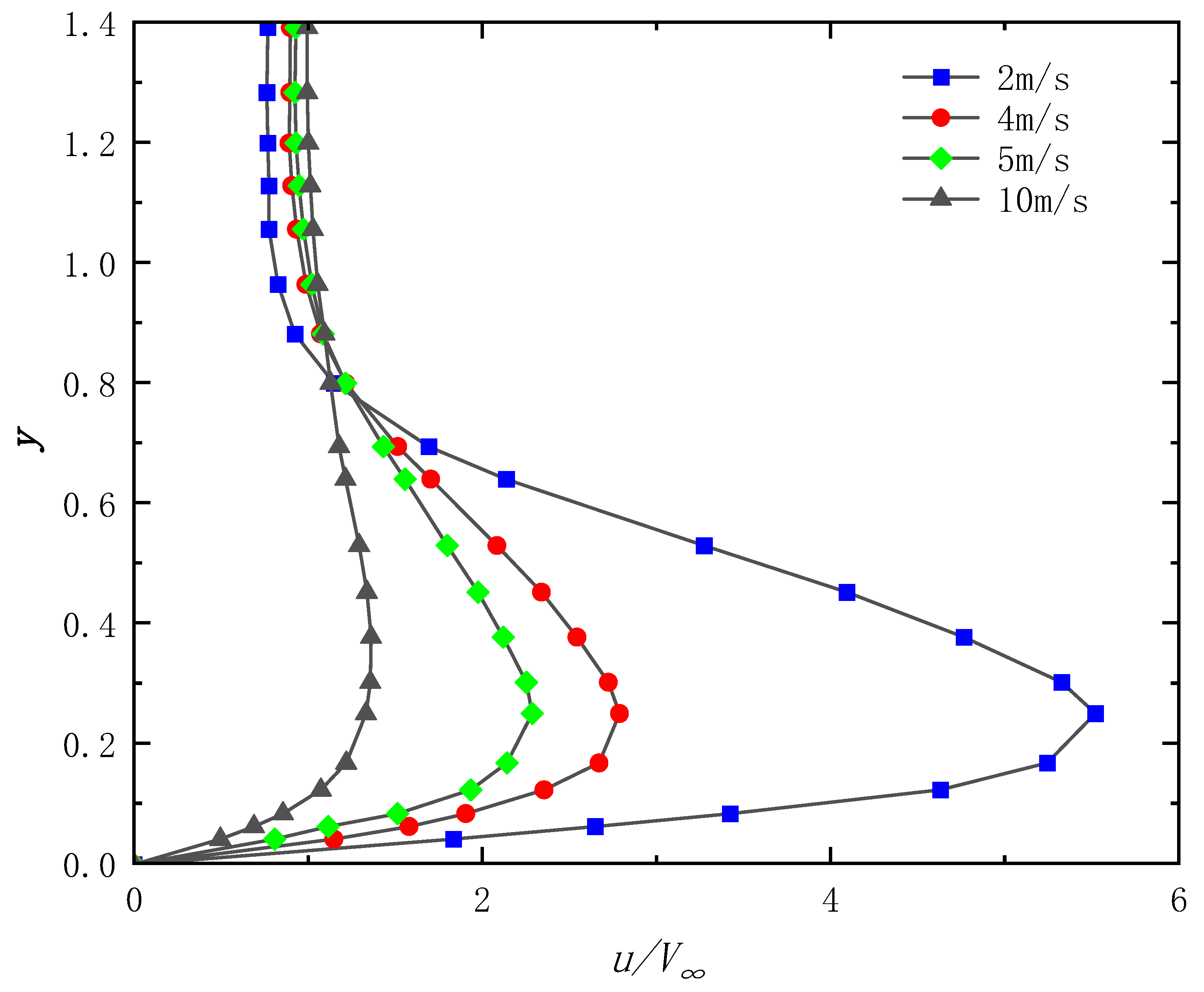
2.2. Validation of Numerical Plasma Simulation
2.3. Knudsen Number
2.4. Dimensionless Coefficients
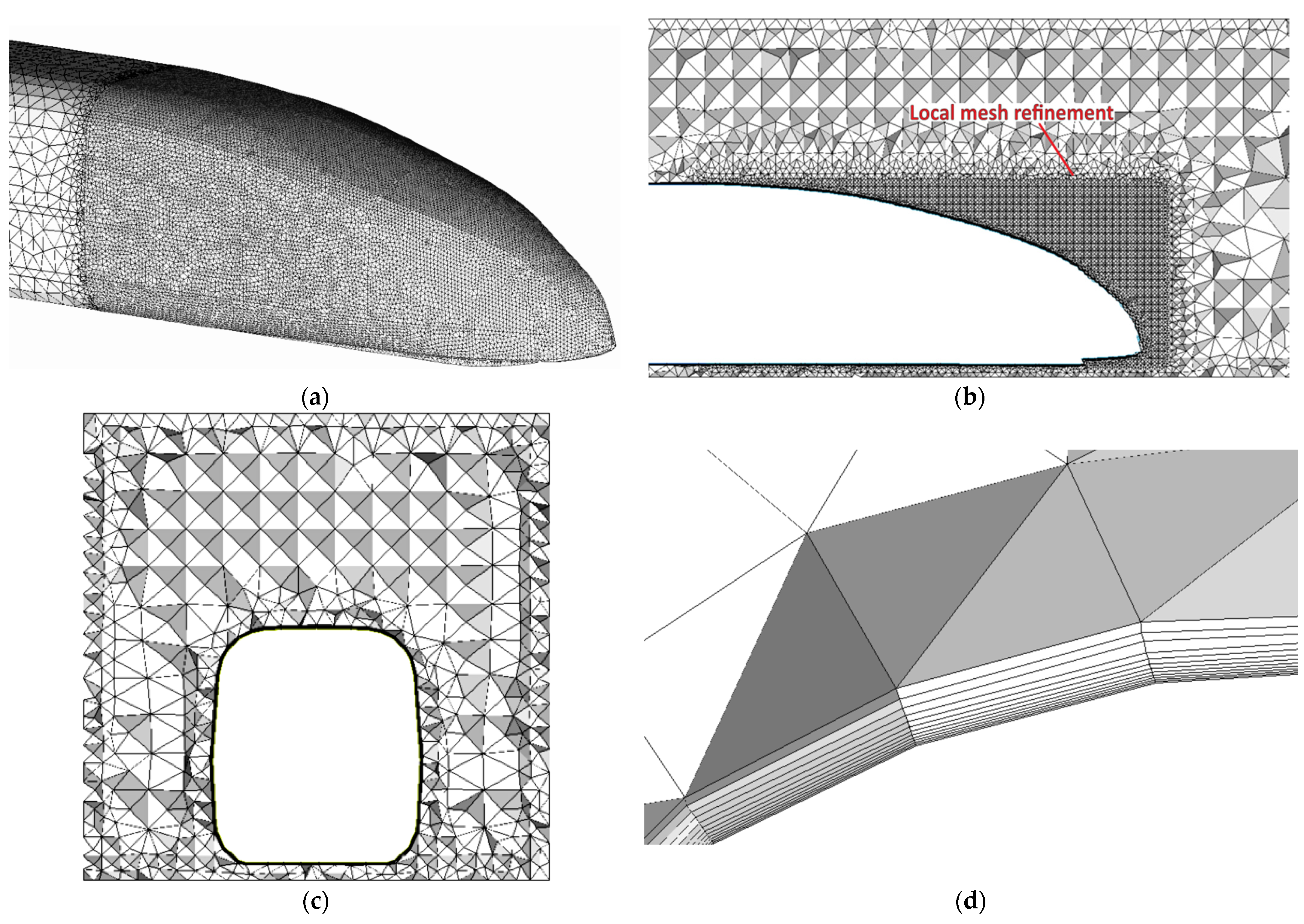
2.5. Reliability Analysis and Mesh Partitioning Strategy
2.6. Validation of Mathematical Techniques
3. Discussion
Determination of SDBD Position at the Rear of the High-Speed Train
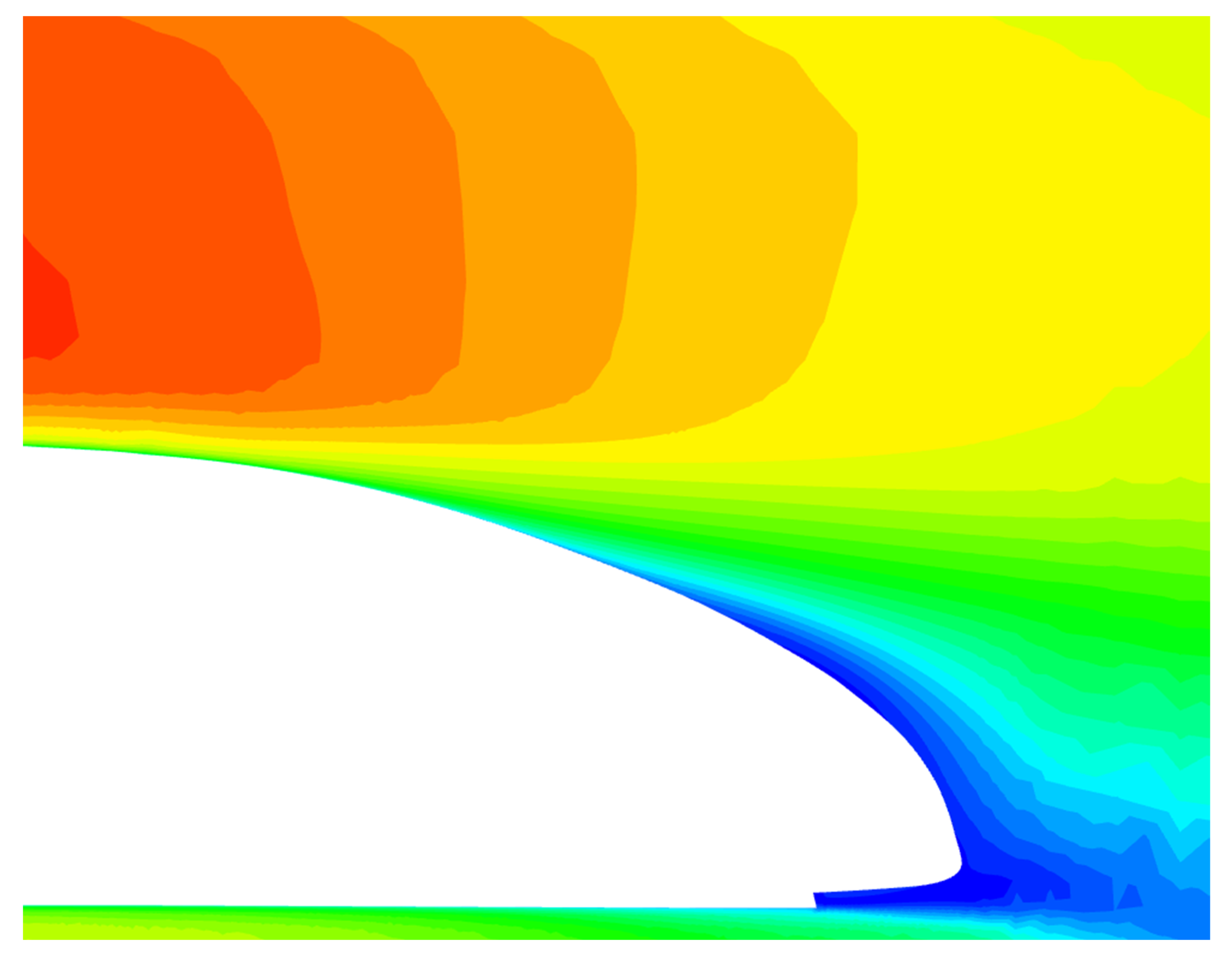
4. Analysis of Results
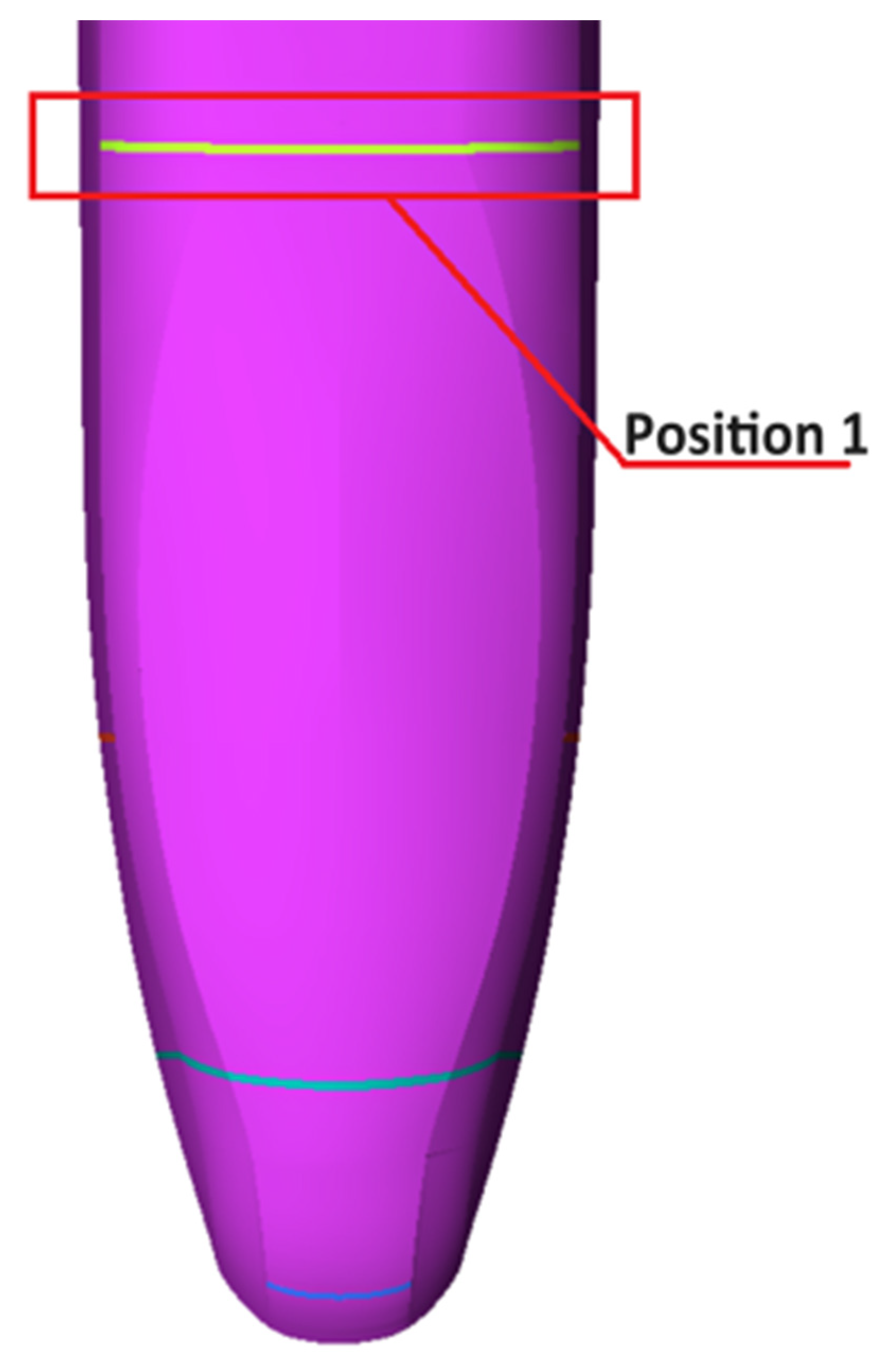
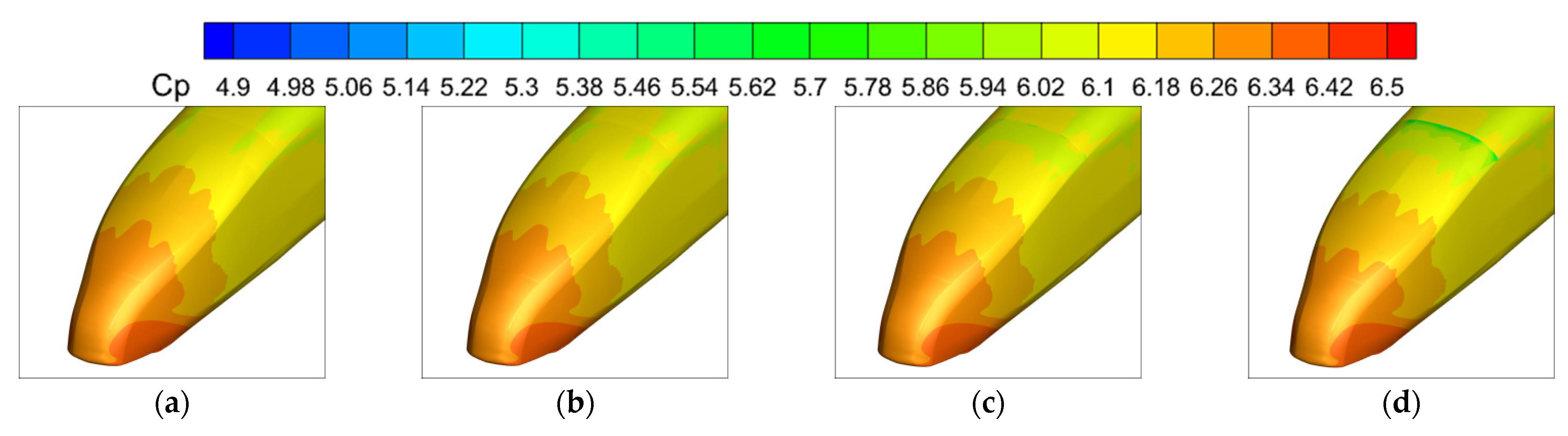
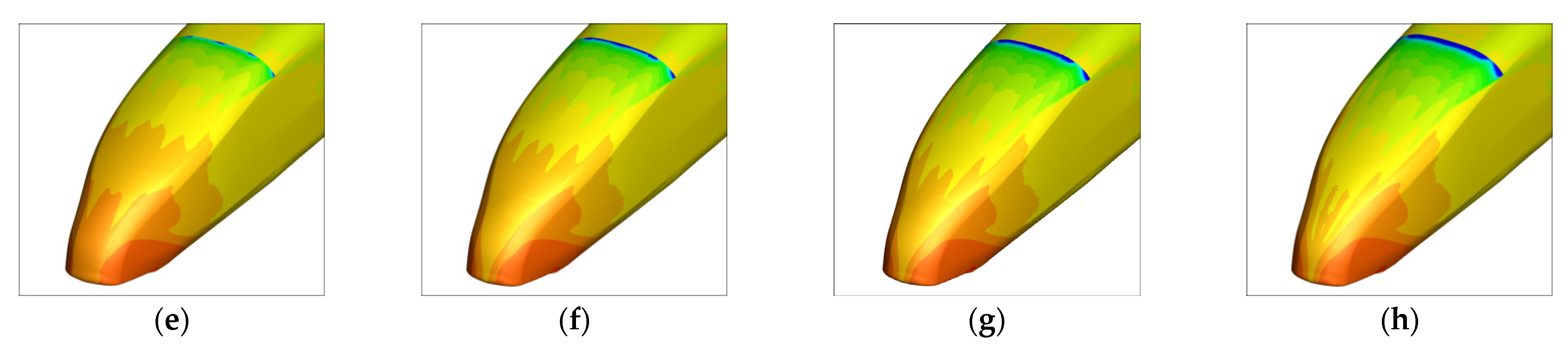
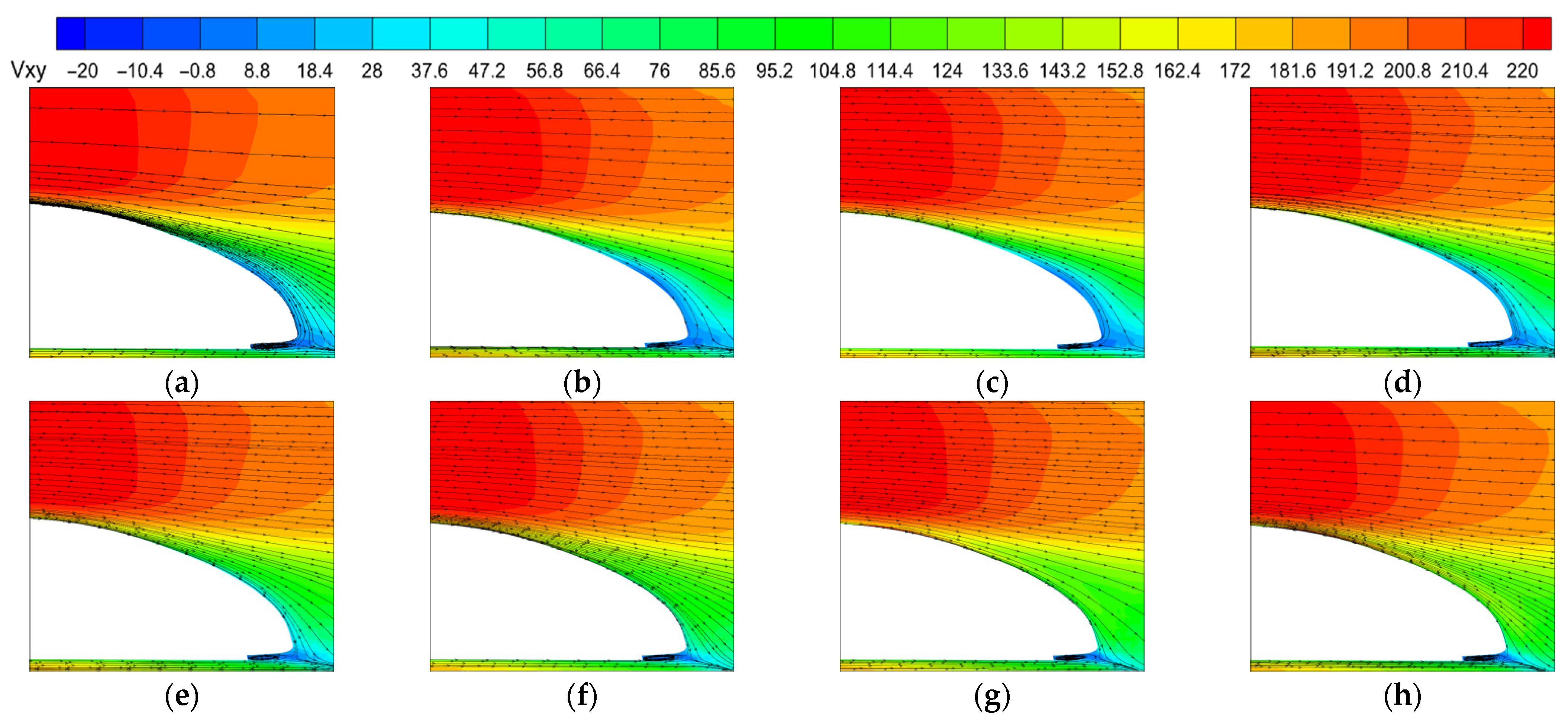
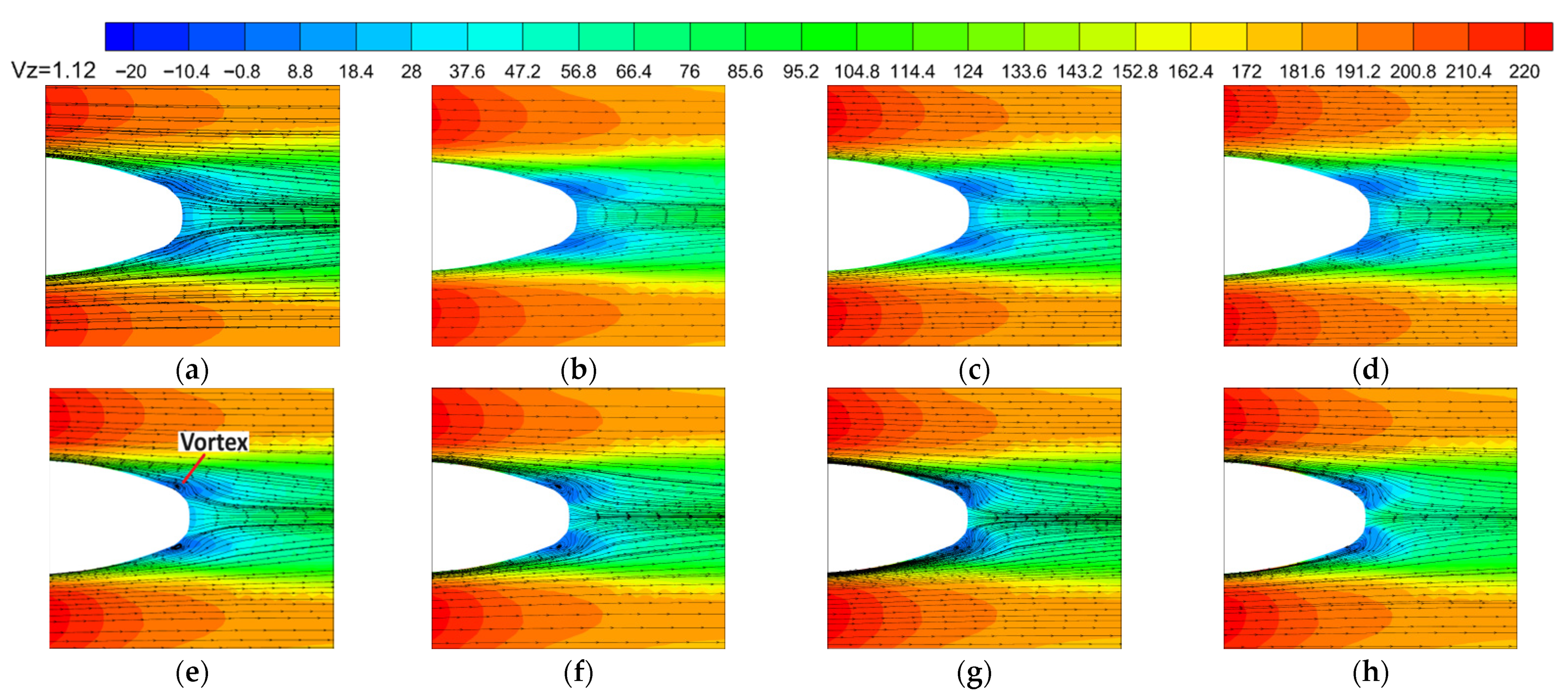
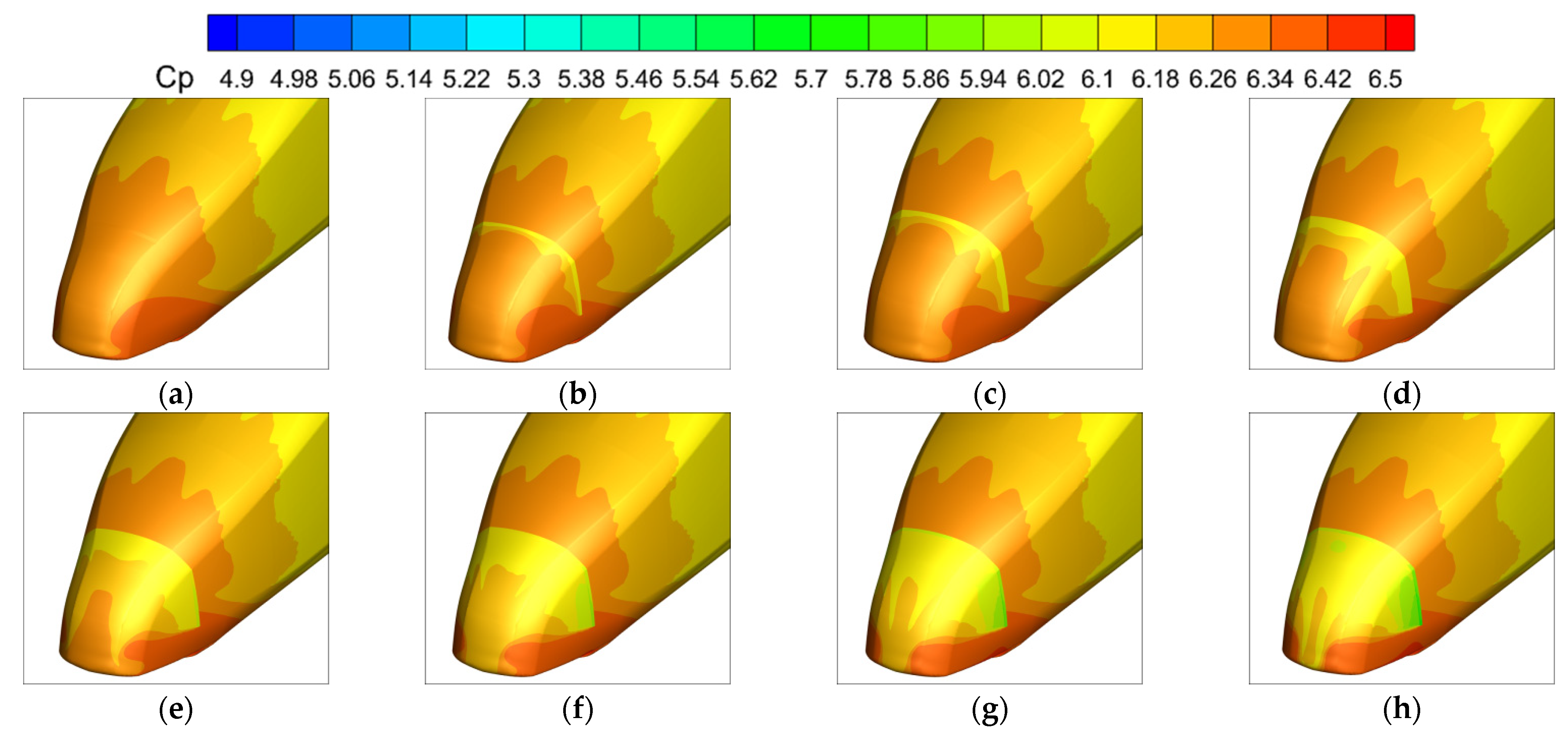
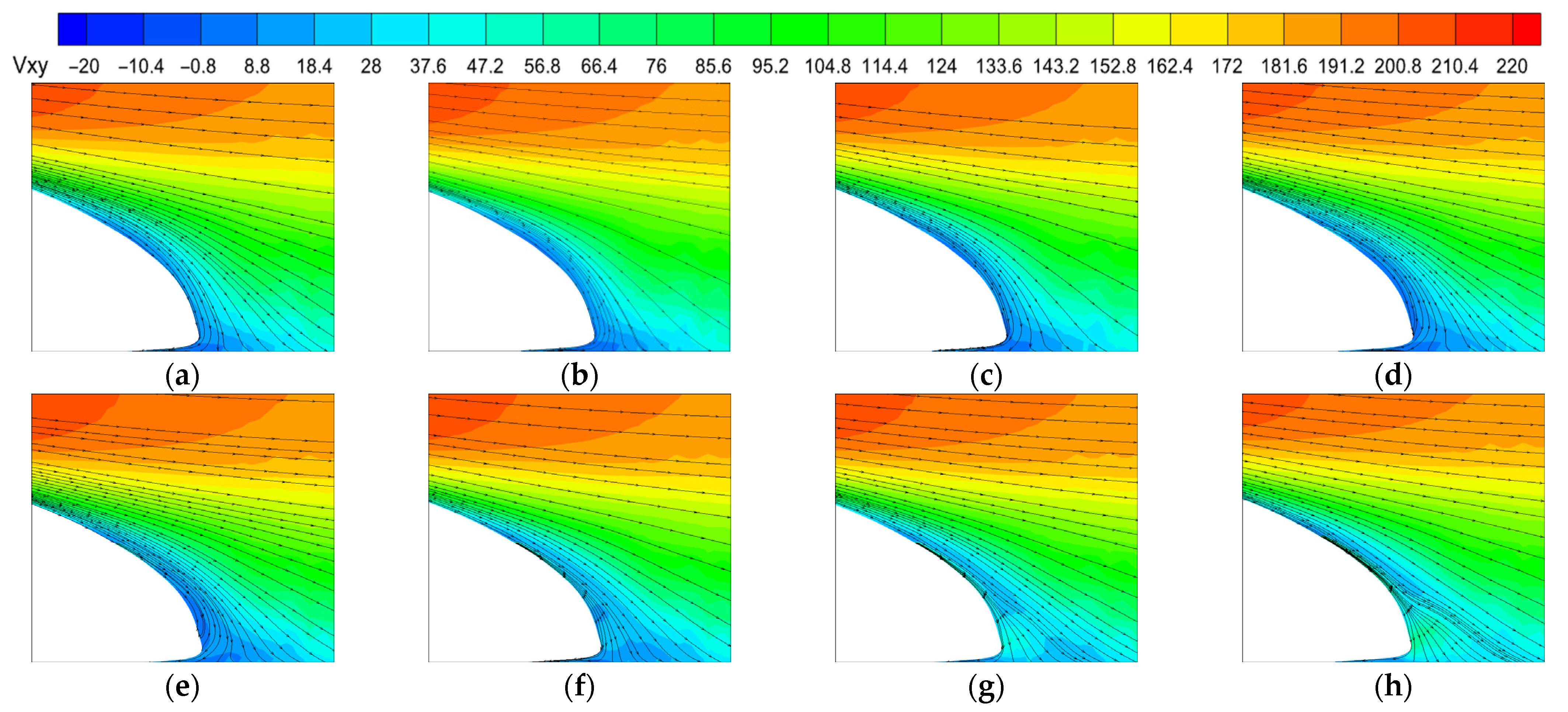
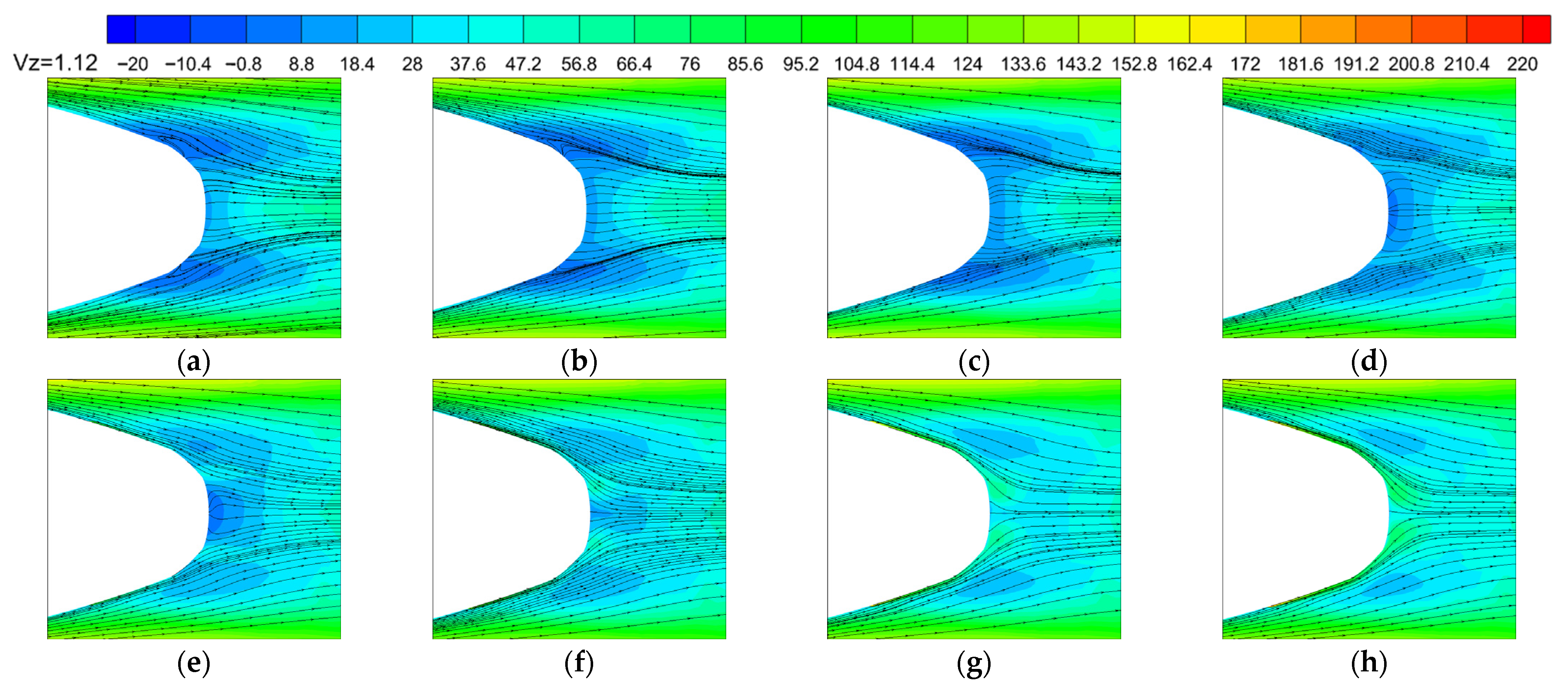
4.1. Position 1
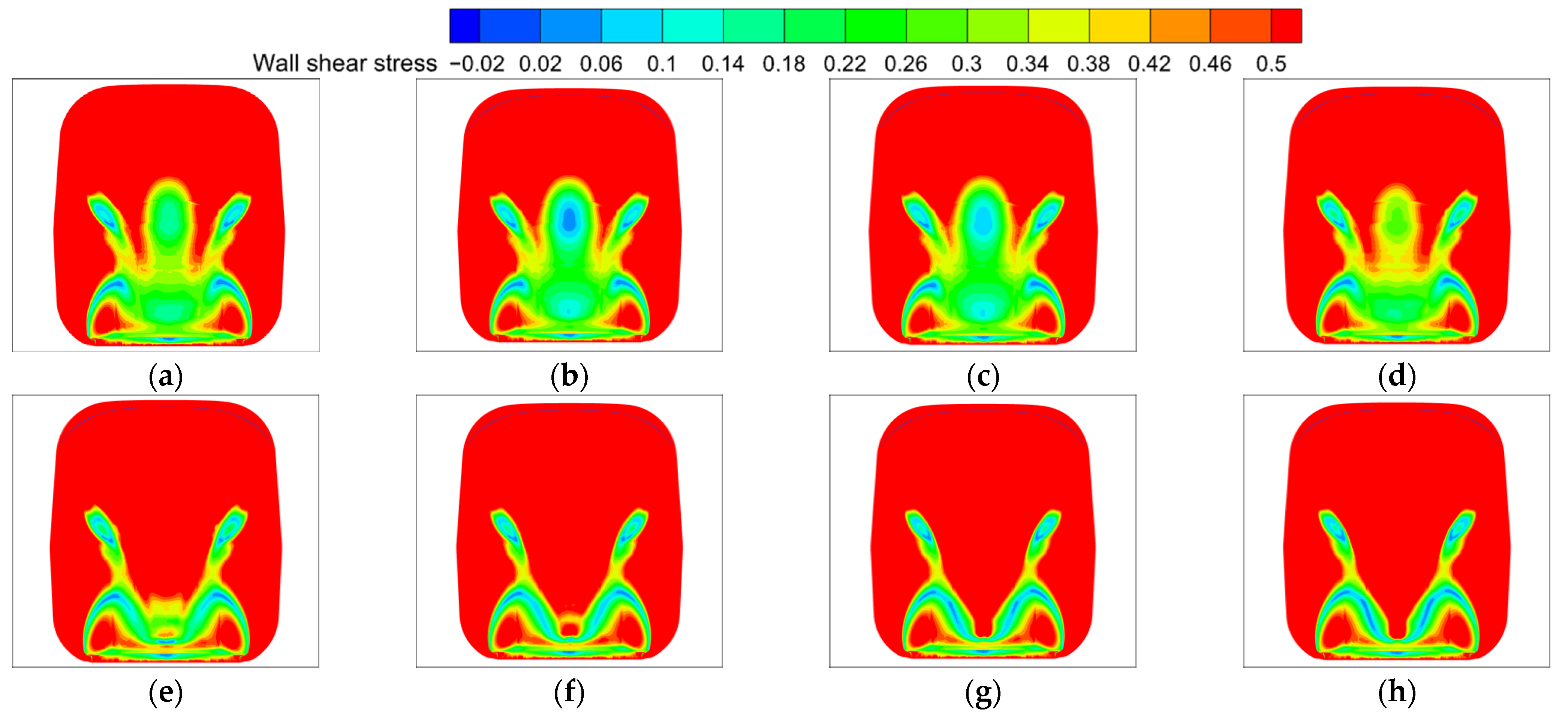
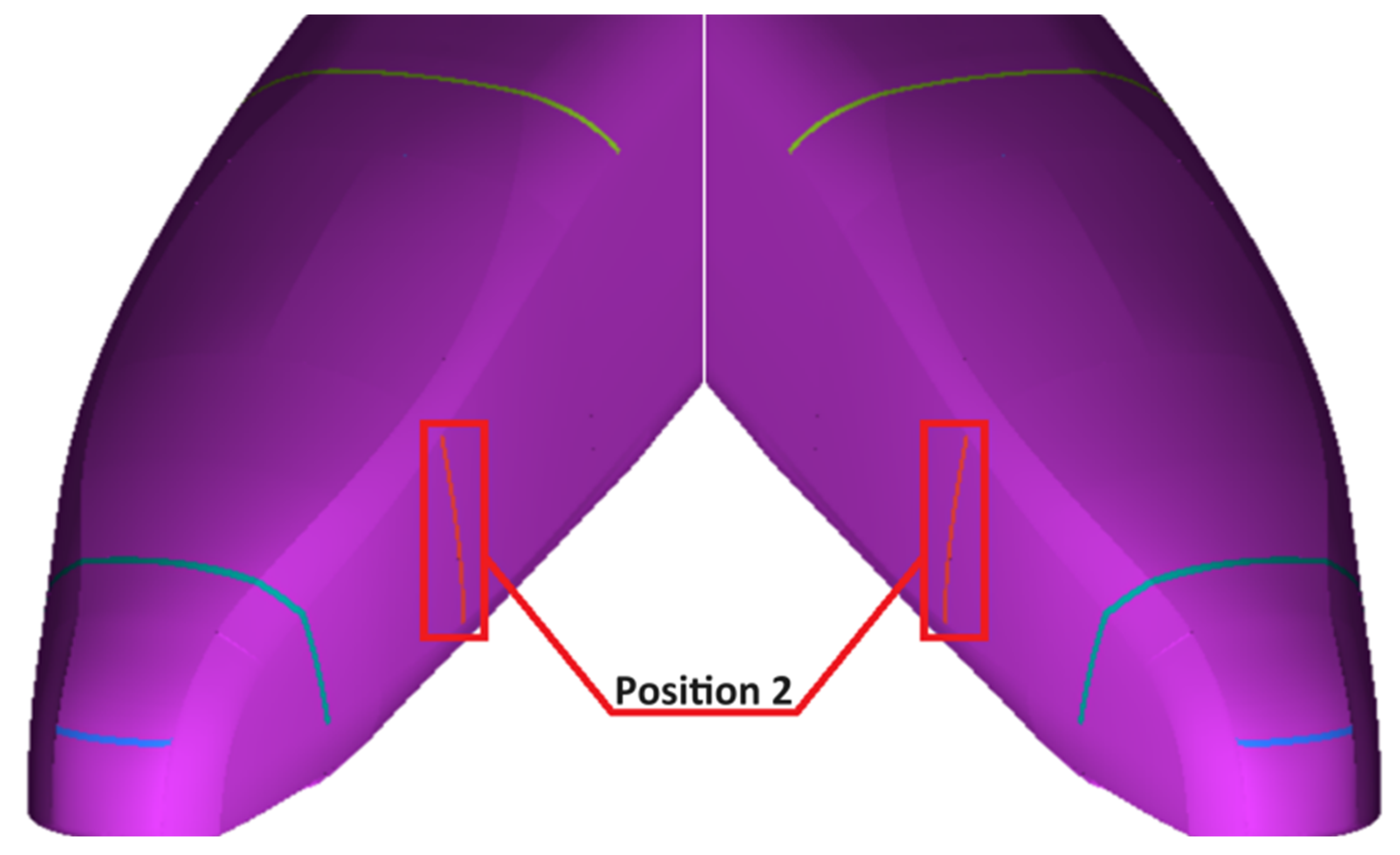
4.2. Position 2
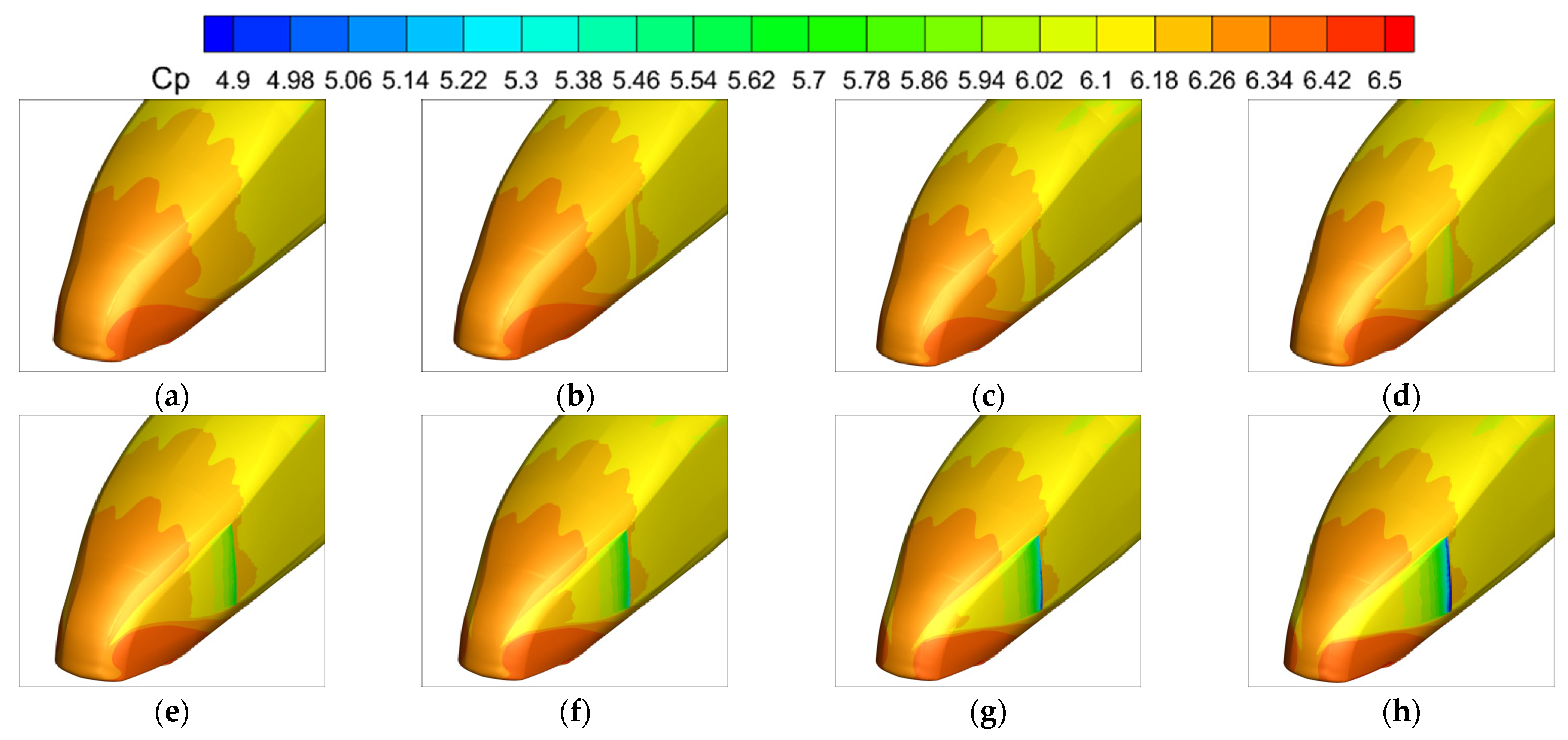
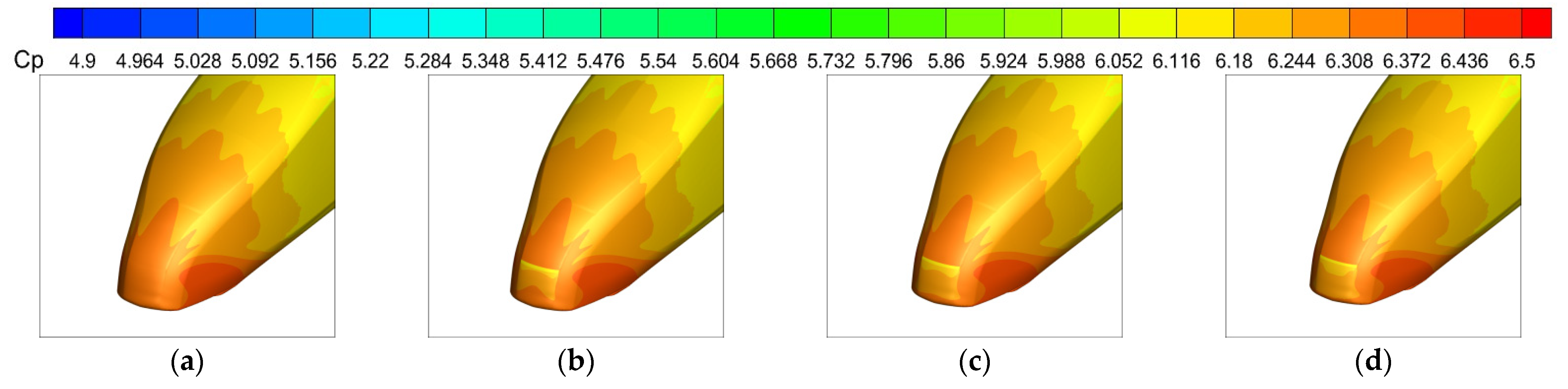
4.3. Position 3
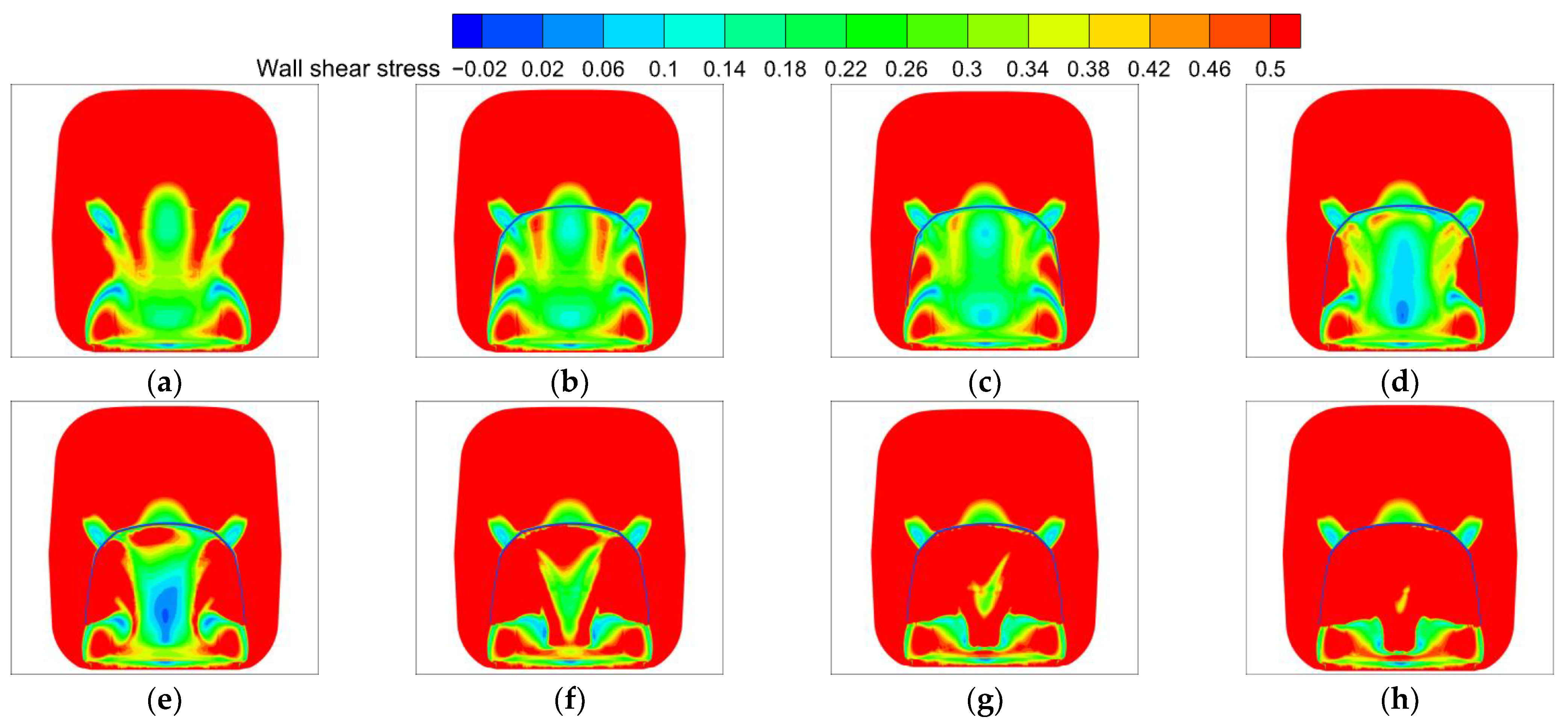
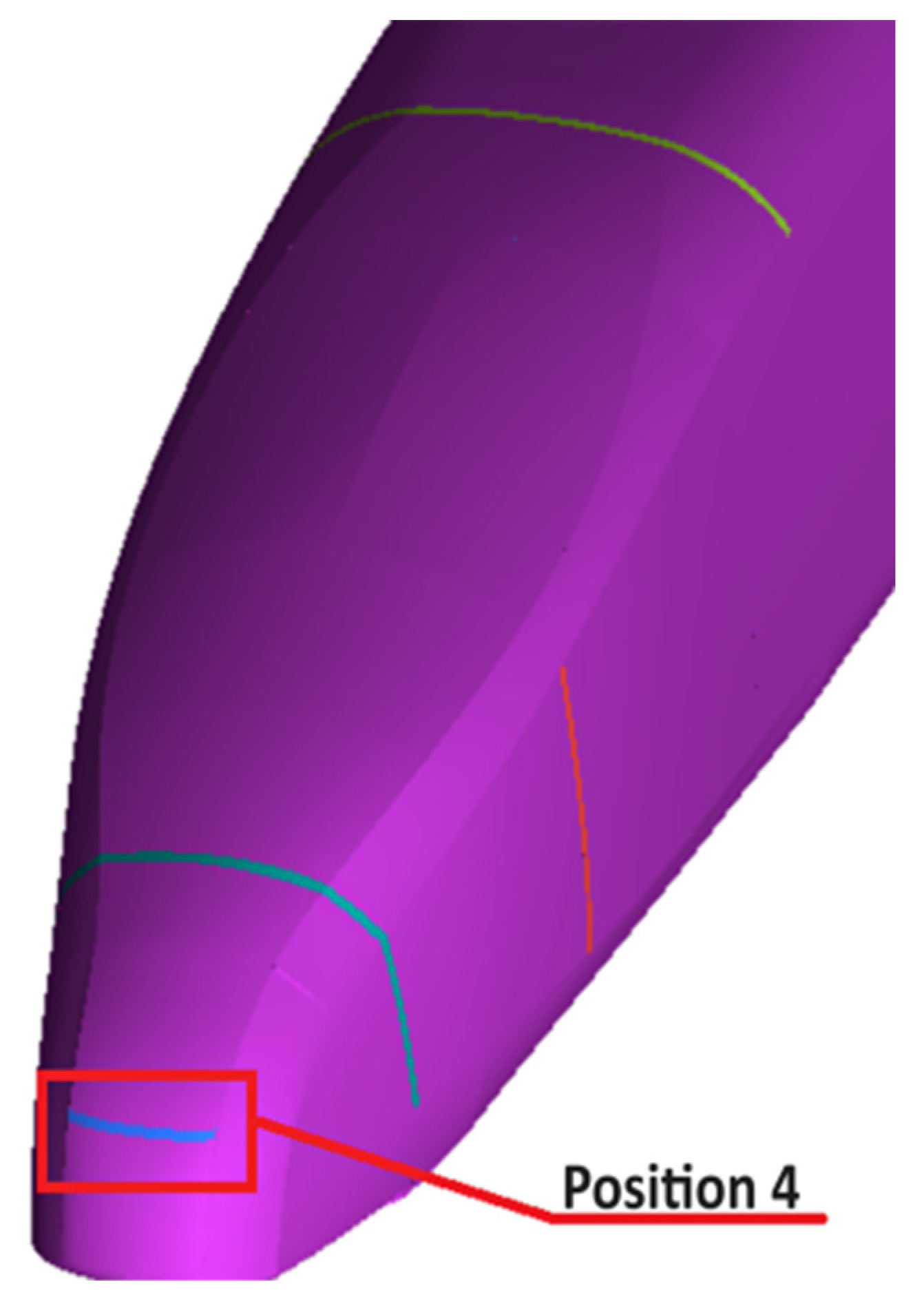
4.4. Position 4
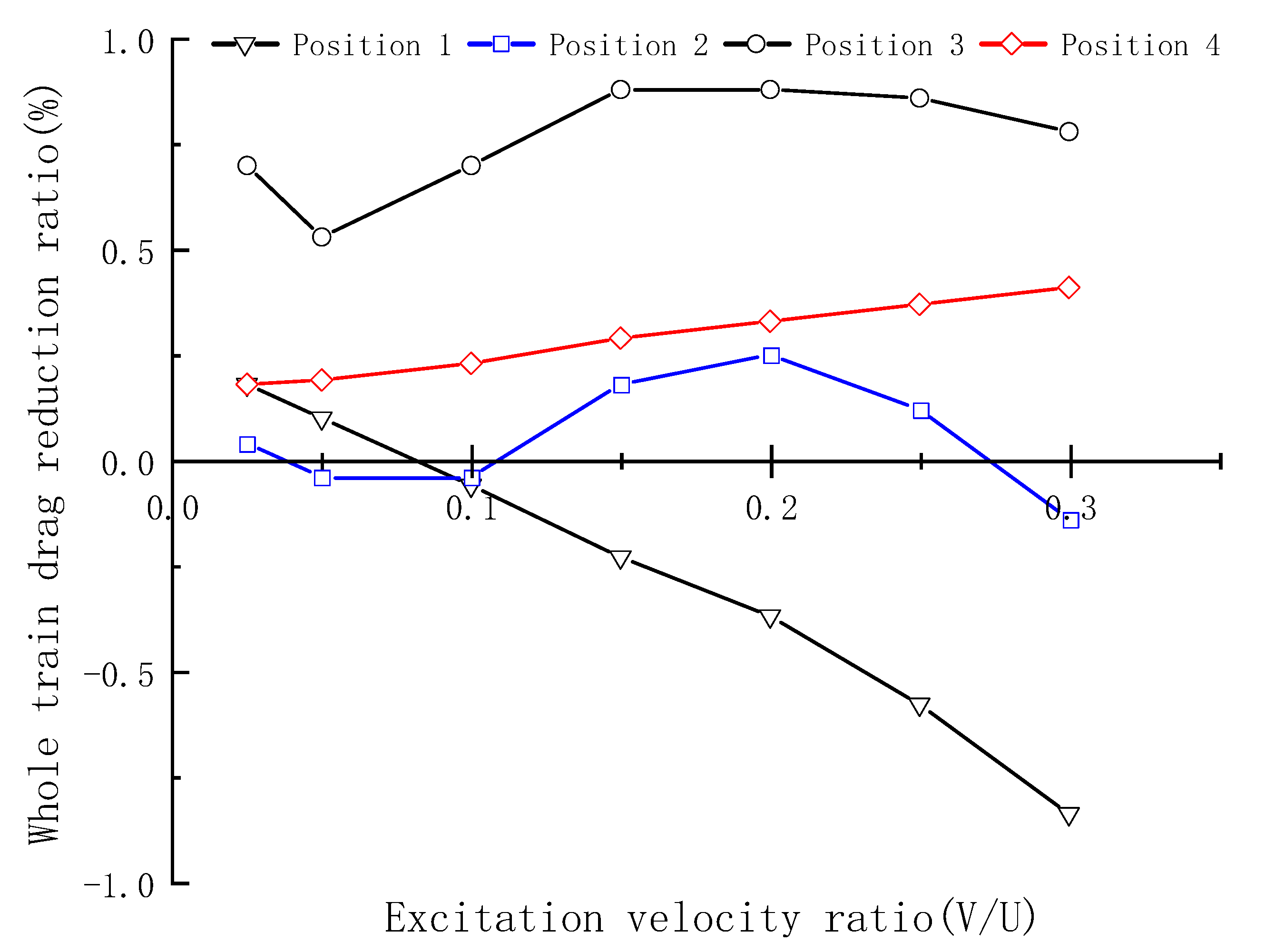
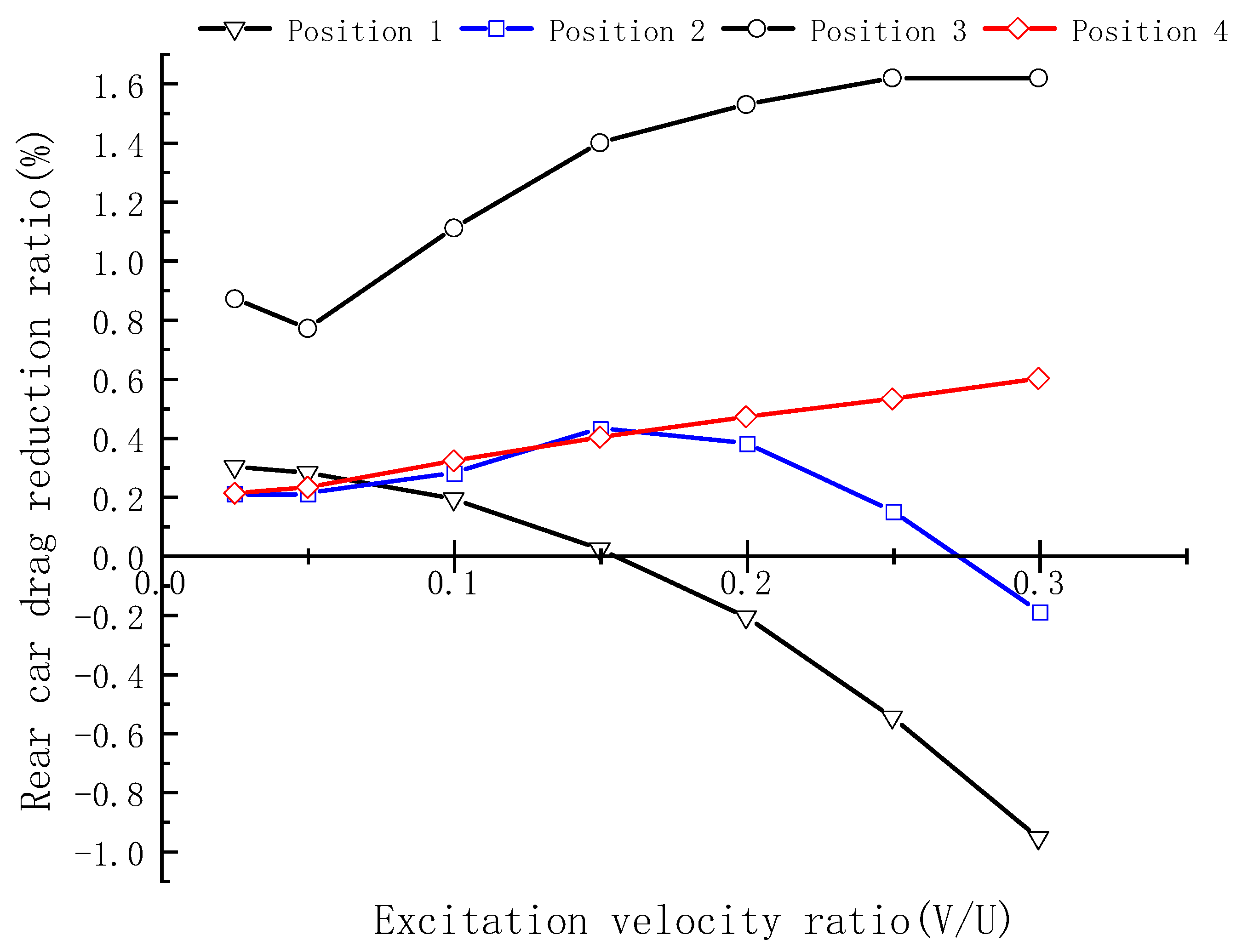
4.5. Comparison of Drag Reduction Effects at Four Positions
5. Conclusions
- (1)
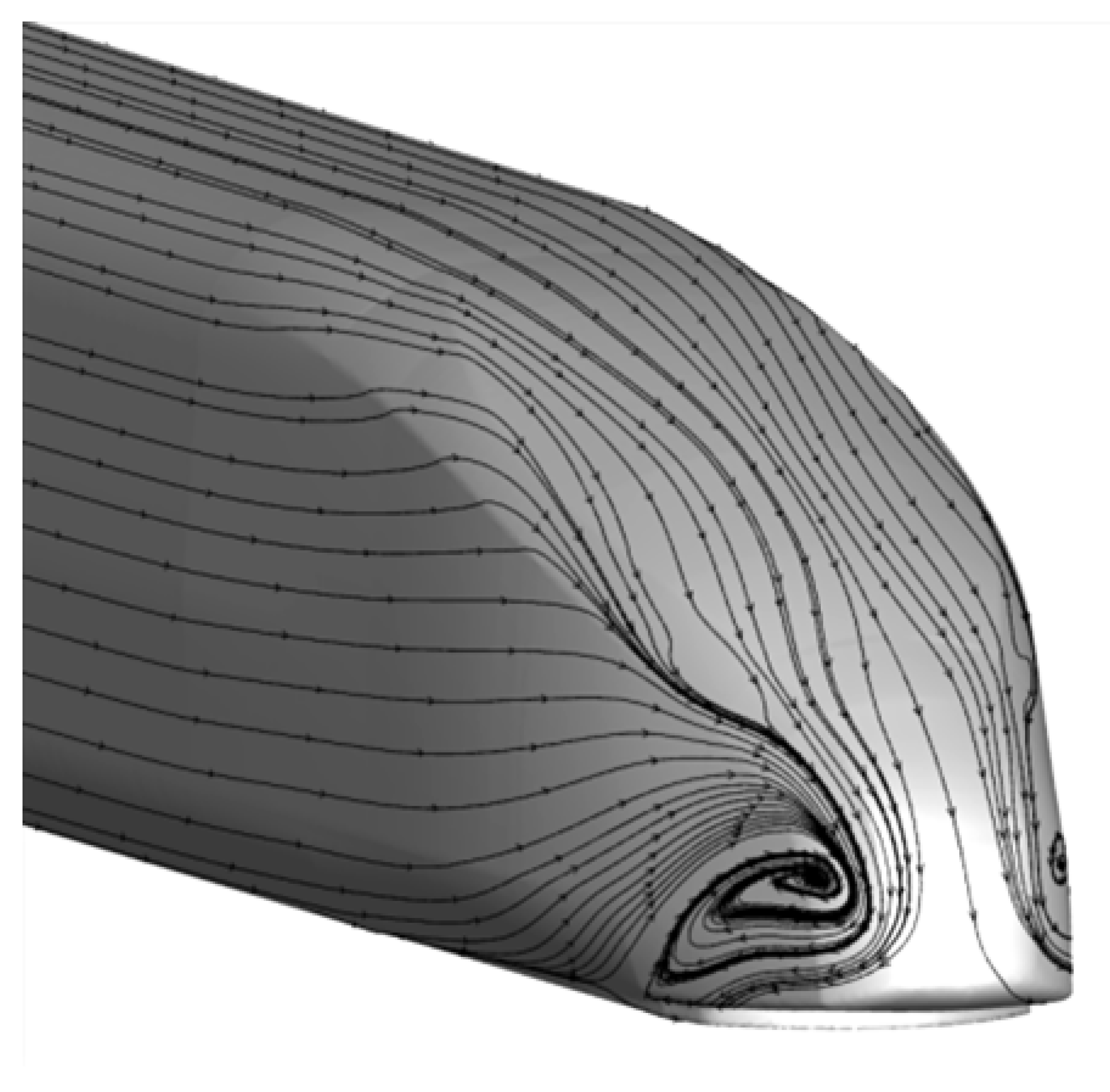
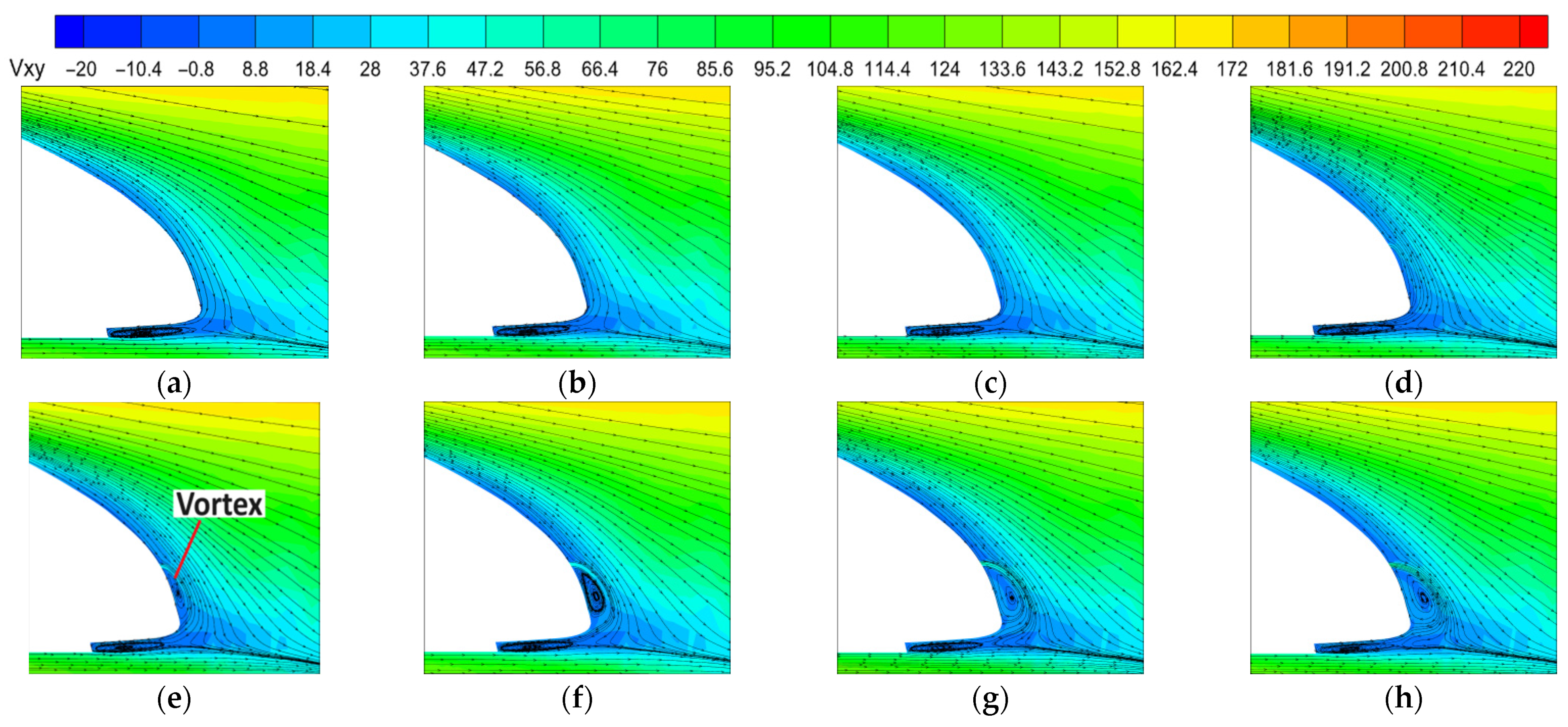
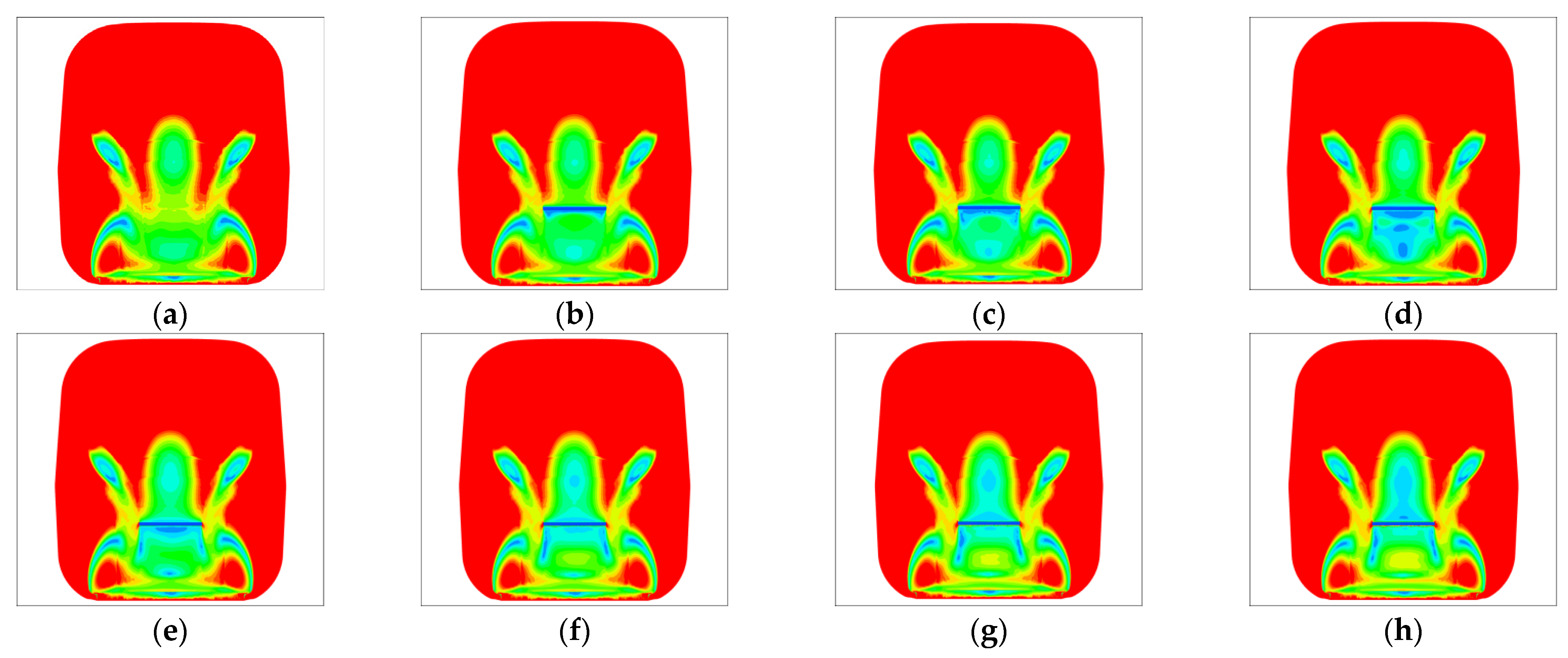
- The flow control mechanism of plasma on rolling stock delays the flow separation by causing directional gas flow close to the wall, moving the flow separation point backward, reducing the size of the negative pressure zone at the end of the train’s body, and reducing the pressure difference drag between the front and rear of the train’s body to reduce the drag coefficient of the entire train.
- (2)
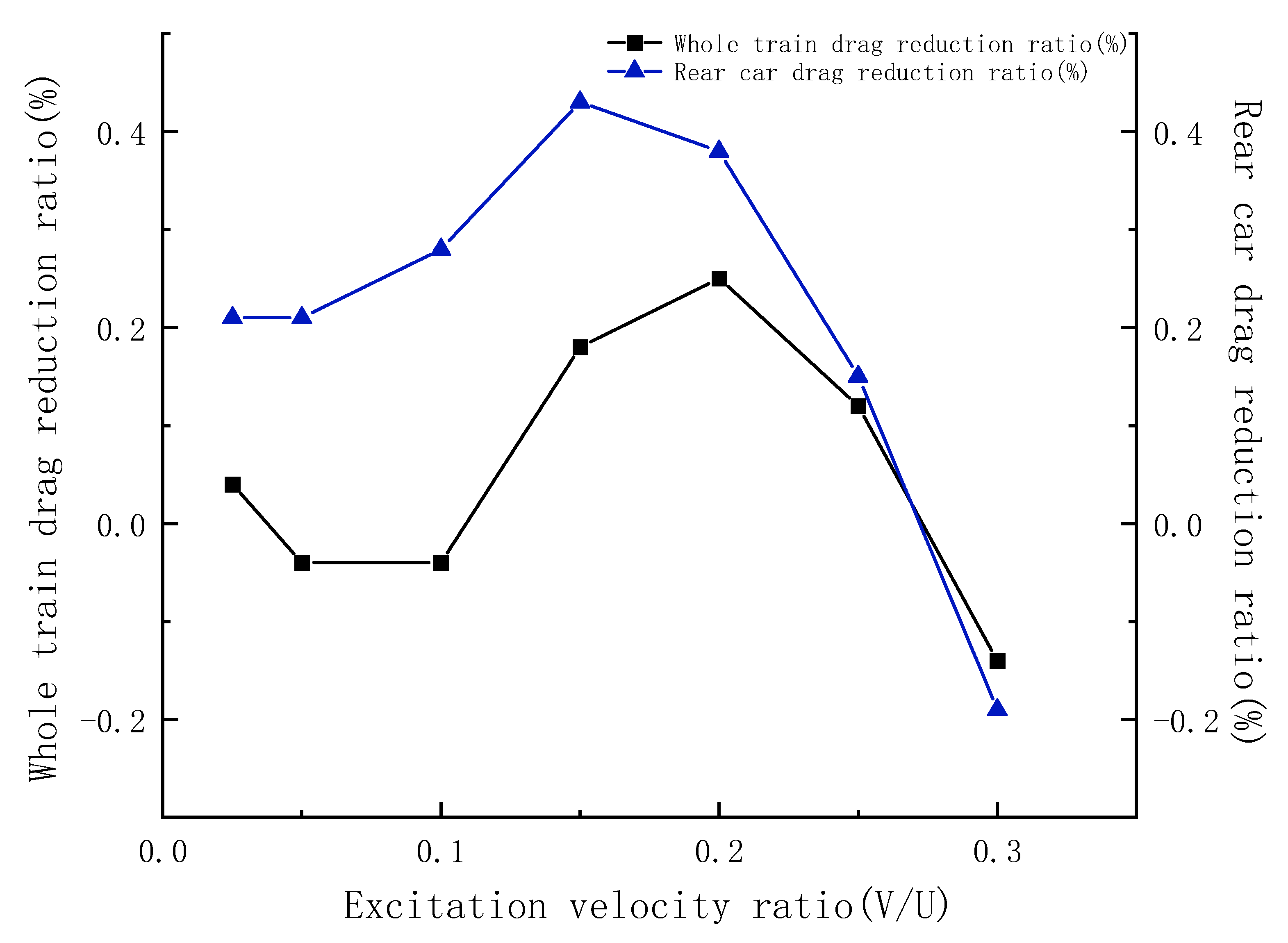
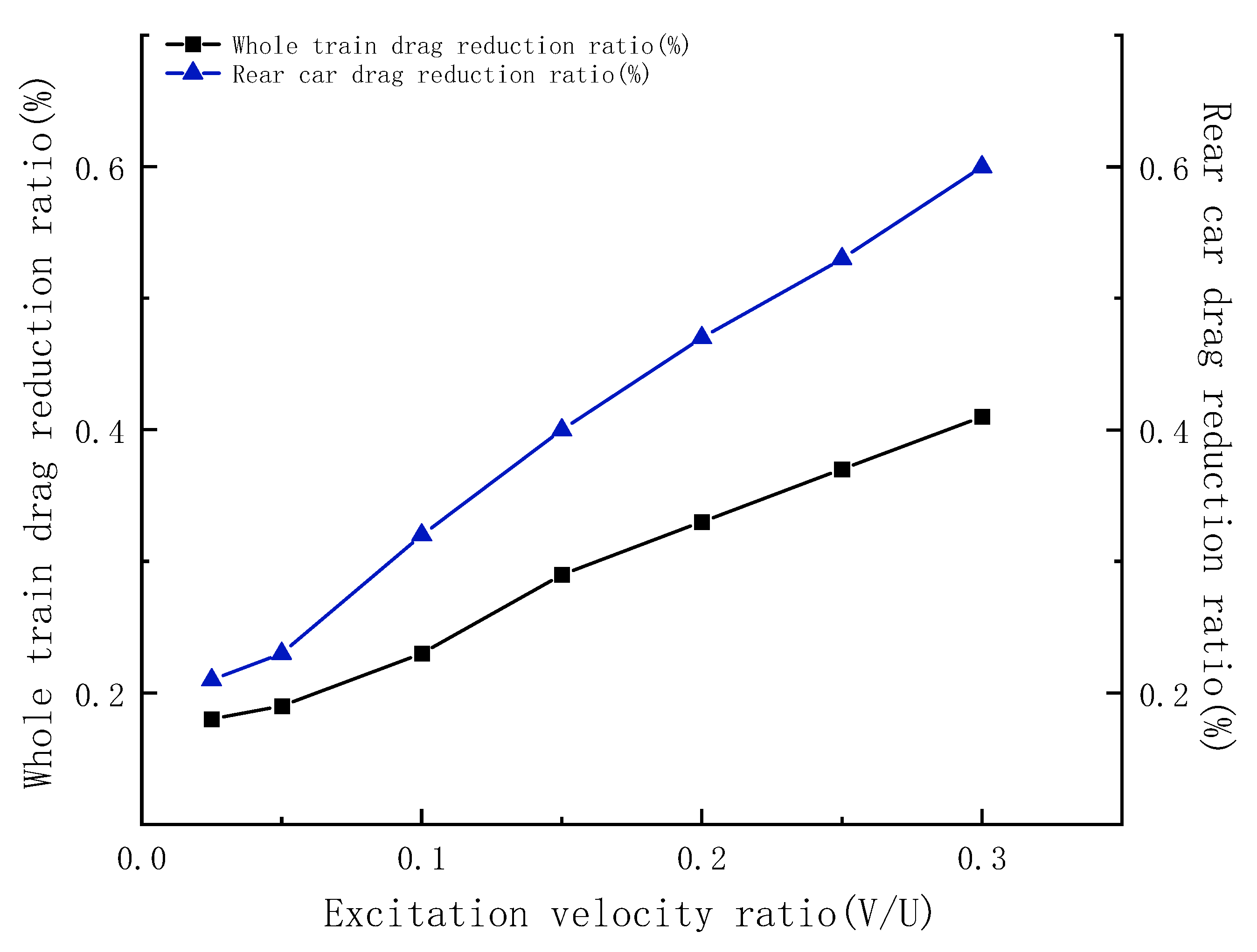
- The best drag reduction scheme can be obtained by studying the most effective way to reduce drag. The SDBD device is installed at the flow separation around the tip of the nose, and the drag reduction effect is maximized close to the excitation velocity ratio of V/U = 0.2, with the drag reduction ratio of about 0.88%; the drag reduction ratio of the rear car reaches the maximum at the excitation velocity ratio of V/U = 0.25, with the drag reduction ratio of 1.62%.
- (3)
- In the four positions of the excitation jet, position 4 produces the excitation jet when the rolling stock rear car wall shear stress reduction amplitude and range are larger than the other three positions to produce the excitation jet, and when the excitation velocity ratio of V/U = 0.1, the area of the low-stress zone at the nose tip of the rear car develops to its maximum, reaching the minimum value of wall shear stress, thereby more effectively reducing the surface friction drag of the train.
- (4)
- Vacuum tube moving train plasma excitation drag reduction is feasible, but the maximum drag reduction ratio is not more than 2%, so the effect is weak. Due to the fact that the vacuum tube belongs to a very narrow space, its internal flow field changes are more intense and variable, so using a simple plasma excitation jet to achieve the purpose of drag reduction effect is very limited.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Z.; Chen, Z.; Ding, W. Optimization Design of Quasi-streamlined EMU Head Shape and Aerodynamic Performance Analysis. J. Fudan Univ. (Nat. Sci.) 2014, 53, 681–688. [Google Scholar]
- Li, X.; Zhao, H.; Deng, W. BFOD: Blockchain-based Privacy Protection and Security Sharing Scheme of Flight Operation Data. IEEE Internet Things J. 2023, 1. [Google Scholar] [CrossRef]
- Yan, S.; Shao, H.; Min, Z.; Peng, J.; Cai, B.; Liu, B. FGDAE: A new machinery anomaly detection method towards complex operating conditions. Reliab. Eng. Syst. Saf. 2023, 236, 109319. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, J.; Chen, H.; Chen, J.; Li, Y.; Xu, J.; Deng, W. Intelligent Diagnosis Using Continuous Wavelet Transform and Gauss Convolutional Deep Belief Network. IEEE Trans. Reliab. 2022, 72, 692–702. [Google Scholar] [CrossRef]
- Yu, M.; Pan, Z.; Jiang, R.; Zhang, J. Multi-objective Optimization Design of the High-speed Train Head Based on the Approximate Model. J. Mech. Eng. 2019, 55, 178–186. [Google Scholar]
- Guo, D.; Wu, E.Q.; Wu, Y.; Zhang, J.; Law, R.; Lin, Y. Flight BERT: Binary Encoding Representation for Flight Trajectory Prediction. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1828–1842. [Google Scholar] [CrossRef]
- Li, M.; Zhang, W.; Hu, B.; Kang, J.; Wang, Y.; Lu, S. Automatic assessment of depression and anxiety through encoding pupil-wave from HCI in VR scenes. ACM Trans. Multimed. Comput. Commun. Appl. 2022, 20, 1–22. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.; Song, J.; Li, Z.; Lu, S. A clinical-oriented non severe depression diagnosis method based on cognitive behavior of emotional conflict. IEEE Trans. Comput. Soc. Syst. 2022, 10, 131–141. [Google Scholar] [CrossRef]
- Liang, Z.; Jiye, Z.; Tian, L.; Zhang, W. Multi-objective Aerodynamic Optimization Design for Head Shape of High-speed Trains. J. Southwest Jiaotong Univ. 2016, 51, 1055–1063. [Google Scholar]
- Duan, Z.; Song, P.; Yang, C.; Deng, L.; Jiang, Y.; Deng, F.; Jiang, X.; Chen, Y.; Yang, G.; Ma, Y.; et al. The impact of hyperglycaemic crisis episodes on long-term outcomes for inpatients presenting with acute organ injury: A prospective, multi-centre follow-up study. Front. Endocrinol. 2022, 13, 1057089. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, H.; Guo, D.; Lin, Y. Improving Airport Arrival Flow Prediction Considering Heterogeneous and Dynamic Network Dependencies. Inf. Fusion 2023, 100, 101924. [Google Scholar] [CrossRef]
- Zhou, X.; Cai, X.; Zhang, H.; Zhang, Z.; Jin, T.; Chen, H.; Deng, W. Multi-strategy competitive-cooperative co-evolutionary algorithm and its application. Inf. Sci. 2023, 635, 328–344. [Google Scholar] [CrossRef]
- Xie, C.; Zhou, L.; Ding, S.; Liu, R.; Zheng, S. Experimental and numerical investigation on self-propulsion performance of polar merchant ship in brash ice channel. Ocean. Eng. 2023, 269, 113424. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y.; Jin, T.; Lei, Z.; Todo, Y.; Gao, S. Maximum Lyapunov exponent-based multiple chaotic slime mold algorithm for real-world optimization. Sci. Rep. 2023, 13, 12744. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Zhou, L.; Ding, S.; Tan, X.; Gao, J.; Zhang, M. Numerical simulation of ship maneuverability in level ice considering ice crushing failure. Ocean. Eng. 2022, 251, 111110. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Y.; Deng, W. An interpretable dynamic inference system based on fuzzy broad learning. IEEE Trans. Instrum. Meas. 2023, 72, 2527412. [Google Scholar] [CrossRef]
- Xiao, Y.; Shao, H.; Feng, M.; Han, T.; Wan, J.; Liu, B. Towards trustworthy rotating machinery fault diagnosis via attention uncertainty in Transformer. J. Manuf. Syst. 2023, 70, 186–201. [Google Scholar] [CrossRef]
- Chen, X.; Shao, H.; Xiao, Y.; Yan, S.; Cai, B.; Liu, B. Collaborative fault diagnosis of rotating machinery via dual adversarial guided unsupervised multi-domain adaptation network. Mech. Syst. Signal Process. 2023, 198, 110427. [Google Scholar] [CrossRef]
- Ren, Z.; Zhen, X.; Jiang, Z.; Gao, Z.; Li, Y.; Shi, W. Underactuated control and analysis of single blade installation using a jackup installation vessel and active tugger line force control. Mar. Struct. 2023, 88, 103338. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Z.; Liu, Z.; Wang, R. A spatial coupling model to study dynamic performance of pantograph-catenary with train-track excitation. Mech. Syst. Signal Process. 2021, 151, 107336. [Google Scholar] [CrossRef]
- Duan, F.; Song, Y.; Gao, S.; Liu, Y.; Chu, W.; Lu, X.; Liu, Z. Study on aerodynamic instability and galloping response of rail overhead contact line based on wind tunnel test. IEEE Trans. Veh. Technol. 2023, 72, 7211–7220. [Google Scholar] [CrossRef]
- Shu, Y.; Jin, T. Stability in measure and asymptotic stability of uncertain nonlinear switched systems with a practical application. Int. J. Control. 2023, 96, 2917–2927. [Google Scholar] [CrossRef]
- Deng, W.; Li, K.P.; Zhao, H.M. A flight arrival time prediction method based on cluster clustering-based modular with deep neural network. IEEE Trans. Intell. Transp. Syst. 2023. [Google Scholar]
- Liu, J.; Zhang, J.; Zhang, W. Analysis of aerodynamic characteristics of high-speed trains in the evacuated tube. J. Mech. Eng. 2013, 49, 137–143. [Google Scholar] [CrossRef]
- Opgenoord, M.M.J.; Caplan, P.C. Aerodynamic design of the hyperloop concept. AIAA J. 2018, 56, 4261–4270. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Z.; Wu, T.; Bao, X. Solving the family traveling salesperson problem in the Adleman–Lipton model based on DNA Computing. IEEE Trans. NanoBiosci. 2022, 21, 75–85. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.M.; Zhang, P.P.; Zhang, R.C.; Yao, R.; Deng, W. A novel performance trend prediction approach using ENBLS with GWO. Meas. Sci. Technol. 2023, 34, 025018. [Google Scholar] [CrossRef]
- Jia, W.; Wang, K.; Cheng, A.; Kong, X.; Cao, X.; Li, Q. Air flow and differential pressure characteristics in the vacuum tube transportation system based on pressure recycle ducts. Vacuum 2018, 150, 58–68. [Google Scholar] [CrossRef]
- Dong, D.; Wenjun, N.; Tao, S. A review on the state of art and future trends of atmospheric pressure low temperature plasma. Trans. China Electrotech. Soc. 2017, 32, 1–9. [Google Scholar]
- Zhang, P.; Wang, J.; Shi, W.; Wu, Z. Experimental study on the separation control by plasma actuator in subsonic flow. J. Exp. Fluid Mech. 2007, 21, 35–39. [Google Scholar]
- Bo, Y.; Min, S.; Mindi, B. Experimental investigation of airfoil flow separation control by dielectric barrier discharge plasma actuator. High Volt. Eng. 2014, 40, 212–218. [Google Scholar]
- Che, X.; Nie, W.; Hou, Z.; He, H. High altitude plasma flow control simulation through ground experiment. Acta Aeronaut. Astronaut. Sin. 2015, 36, 441–448. [Google Scholar]
- Orlov, D.; Apker, T.; He, C.; Othman, H.; Corke, T. Modeling and experiment of leading edge separation control using SDBD plasma actuators. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; p. 877. [Google Scholar]
- Zhou, S. Research on Aerodynamic Drag Reduction of GTS Model Based on Plasma Flow Control. Master’s Thesis, Jilin University, Changchun, China, 2020. [Google Scholar]
- Hui, Z. Research on Train Drag Reduction Based on Plasma Active Flow Control. Ph.D. Thesis, Jilin University, Changchun, China, 2020. [Google Scholar]
- Gao, G.; Yan, X.; Peng, K. Primary research on drag reduction of train based on plasma flow. J. Electrotechnol. 2019, 34, 855–862. [Google Scholar]
- Zhang, Y. Simulation Study on Aerodynamic Characteristics of Magnetic Levitation Transportation System with Low Vacuum Tube. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2019. [Google Scholar]
- Zhang, K.R. Optimization of streamline structure and analysis of aerodynamic characteristics of high-speed train in restricted space. Master’s Thesis, Qingdao University of Science and Technology, Qingdao, China, 2020. [Google Scholar]
- Huang, Z.; Liang, X.; Chang, N. Numerical Analysis of Train Aerodynamic Drag of Vacuum Tube Traffic. J. Mech. Eng. 2019, 55, 165–172. [Google Scholar] [CrossRef]
- Anderson, J.D. Fundamentals of Aerodynamics, 5th ed.; Aviation Industry Press: Beijing, China, 2014. [Google Scholar]
- Shyy, W.; Jayaraman, B.; Andersson, A. Modeling of glow discharge-induced fluid dynamics. J. Appl. Phys. 2002, 92, 6434–6443. [Google Scholar] [CrossRef]
- He, D. Analysis of Drag Reduction Mechanism and Energy Consumption of Vacuum Tube Train Suction System. Master’s Thesis, Hunan University, Changsha, China, 2019. [Google Scholar]
- Zhang, K.Y.; Li, Q.L.; Wang, C.W.; Jia, W.G. Research on aerodynamic noise of vacuum tube high-speed train. J. Vac. Sci. Technol. 2019, 39, 950–957. [Google Scholar]
- Liu, H. Research on Comprehensive Operation Energy Consumption of Vacuum Tube Transportation System. Master’s Thesis, Qingdao University of Science and Technology, Qingdao, China, 2016. [Google Scholar]
- Liu, G.; Zhang, J.; Zhang, W. Aerodynamic drag and system parameter design of vacuum tube high-speed train. J. Vac. Sci. Technol. 2014, 34, 10–15. [Google Scholar]
- Kim, T.K.; Kim, K.H.; Kwon, H.B. Aerodynamic Characteristics of a Tube Train. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 1187–1196. [Google Scholar] [CrossRef]
- Yang, Z.; Mao, M.; Chen, Y. Influence Laws Between Underbody Structure Parameters of High Speed Train and Aerodynamic Drag. J. Tongji Univ. (Nat. Sci. Ed.) 2019, 47, 1055–1064. [Google Scholar]
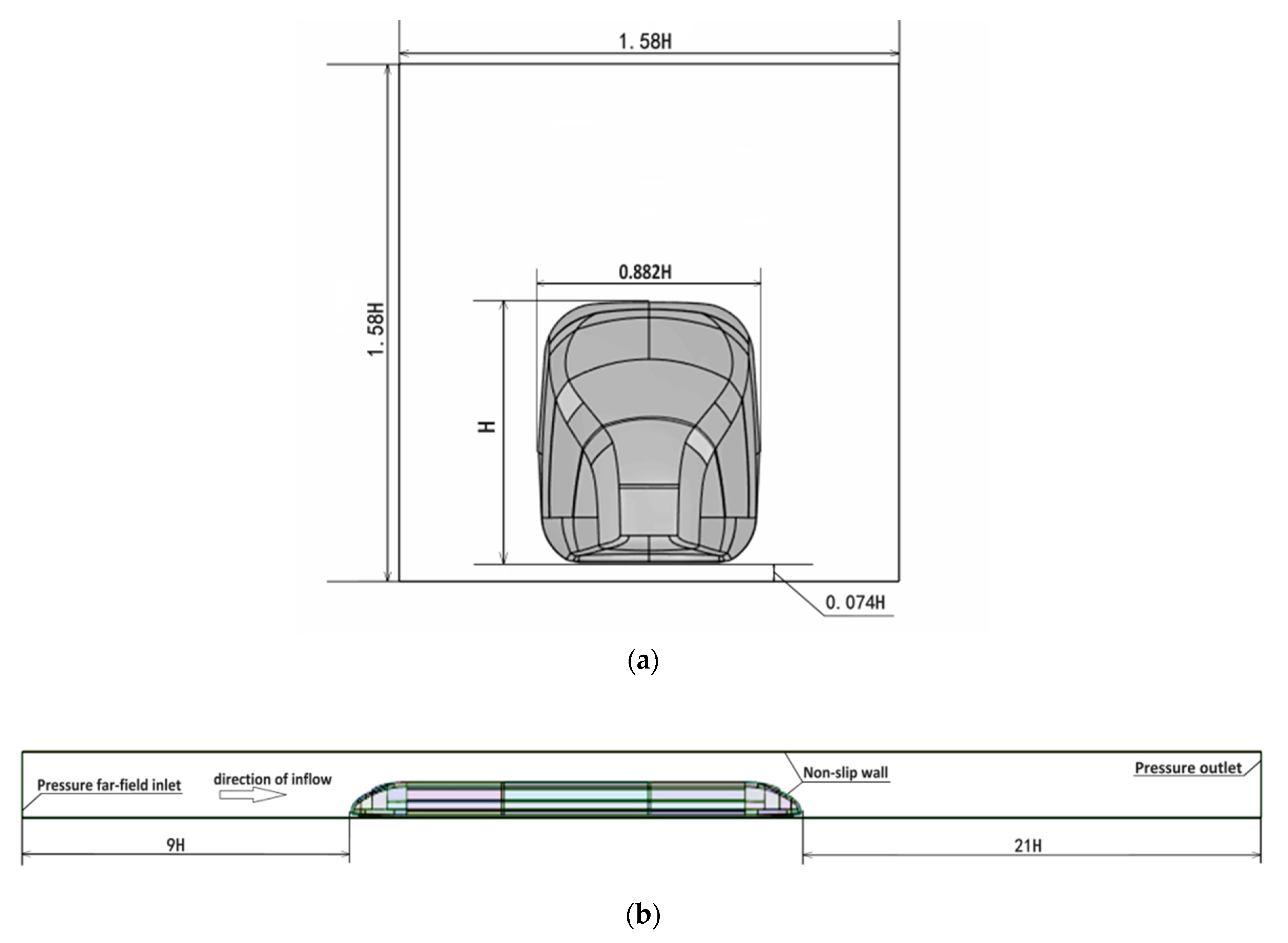









| Computational Domain | Boundary Condition | Calculation Settings |
|---|---|---|
| Tube inlet | Pressure far field | 0.489 Ma |
| Tube outlet | Pressure outlet | 0 |
| Train body | Wall | No-slip |
| Tube | Wall | 167 m/s |
| Computational Domain | Boundary Condition | Calculation Settings |
|---|---|---|
| Inlet | Velocity inlet | 2–10 m/s |
| Outlet | Pressure outlet | 0 |
| Side surface | Wall | symmetry |
| Bottom surface | Wall | Fixed wall |
| Mesh Density | Coarse | Medium | Fine |
|---|---|---|---|
| Mesh density (106) | 14 | 25 | 45 |
| Aerodynamic drag coefficient | 0.5250 | 0.5130 | 0.5129 |
| Grid Density (Million) | 9 | 16 | 28 | 33 | Experimental |
|---|---|---|---|---|---|
| Pneumatic drag coefficient | 0.321 | 0.3 | 0.318 | 0.343 | 0.335 |
| inaccuracies | 4% | 10% | 5% | −2% | - |
| Position Number | Excitation Position |
|---|---|
| Position 1 | Position of flow separation above the front windshield of the rear car, between the equal-section body and streamlined rear portion of a moving train |
| Position 2 | Upstream flow separation on both sides of the tailgate windshield |
| Position 3 | Flow separation around the tip of the nose |
| Position 4 | nasal tip where the rear vortex falls off |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, A.; Cui, H.; Guan, Y.; Deng, J.; Zhang, Y.; Deng, W. Study on Aerodynamic Drag Reduction by Plasma Jets for 600 km/h Vacuum Tube Train Sets. Machines 2023, 11, 1078. https://doi.org/10.3390/machines11121078
Li A, Cui H, Guan Y, Deng J, Zhang Y, Deng W. Study on Aerodynamic Drag Reduction by Plasma Jets for 600 km/h Vacuum Tube Train Sets. Machines. 2023; 11(12):1078. https://doi.org/10.3390/machines11121078
Chicago/Turabian StyleLi, Ang, Hongjiang Cui, Ying Guan, Jichen Deng, Ying Zhang, and Wu Deng. 2023. "Study on Aerodynamic Drag Reduction by Plasma Jets for 600 km/h Vacuum Tube Train Sets" Machines 11, no. 12: 1078. https://doi.org/10.3390/machines11121078
APA StyleLi, A., Cui, H., Guan, Y., Deng, J., Zhang, Y., & Deng, W. (2023). Study on Aerodynamic Drag Reduction by Plasma Jets for 600 km/h Vacuum Tube Train Sets. Machines, 11(12), 1078. https://doi.org/10.3390/machines11121078






