1. Introduction
The precision motion platform, widely applied in the fields of semiconductor manufacturing, ultra-precision testing and machining, etc., is one of the key subsystems for high-end equipment, such as mask aligners, OLED/Micro-LED display printers and chip super-resolution detection manipulators, to achieve large-stroke micron/nanoscale precision positioning. For this kind of platform, a macro–micro structure is generally adopted to realize a multi-stage mechanical drive, which is designed to connect directly or in bridge-type form. Utilizing cooperative control on the above structure can help equipment reach the industrial requirement of micro–nano high-accuracy positioning under large-stroke movement.
Due to the backlash phenomenon that generally exists in mechanical connections, self-excited oscillation may finally occur when its energy accumulates to a certain extent from the relative motion between different mechanisms. In addition, long-term wear in the joints of mechanisms will gradually increase the backlash, then aggravate the self-excited oscillation and eventually cause a state of instability, which greatly deteriorates the positioning-control performance of mechanical systems [
1]. Specifically, in the field of OLED/micro-LED display printing, more special requirements have been raised for the printing process concerning the precision and stability of the above-mentioned macro–micro motion platforms. An OLED/micro-LED display inkjet printer under manufacture working conditions usually needs to work continuously for several months or much longer without readjustment, and it injects huge amount of ink droplets into the designated pixel slots at high speeds without online visual observation feedback. Considering that the impact position of each ink drop always shows randomness within a certain range and film formation defects cannot be repaired after printing, the positioning bias between the print head nozzle and designated pixel slot caused by mechanical backlash, and the random impact position deviation of ink drops, will jointly produce an obvious influence on the printing precision, which directly degrades the quality of wet film forming and also the final product. For example, when printing using the OLED inkjet equipment shown in
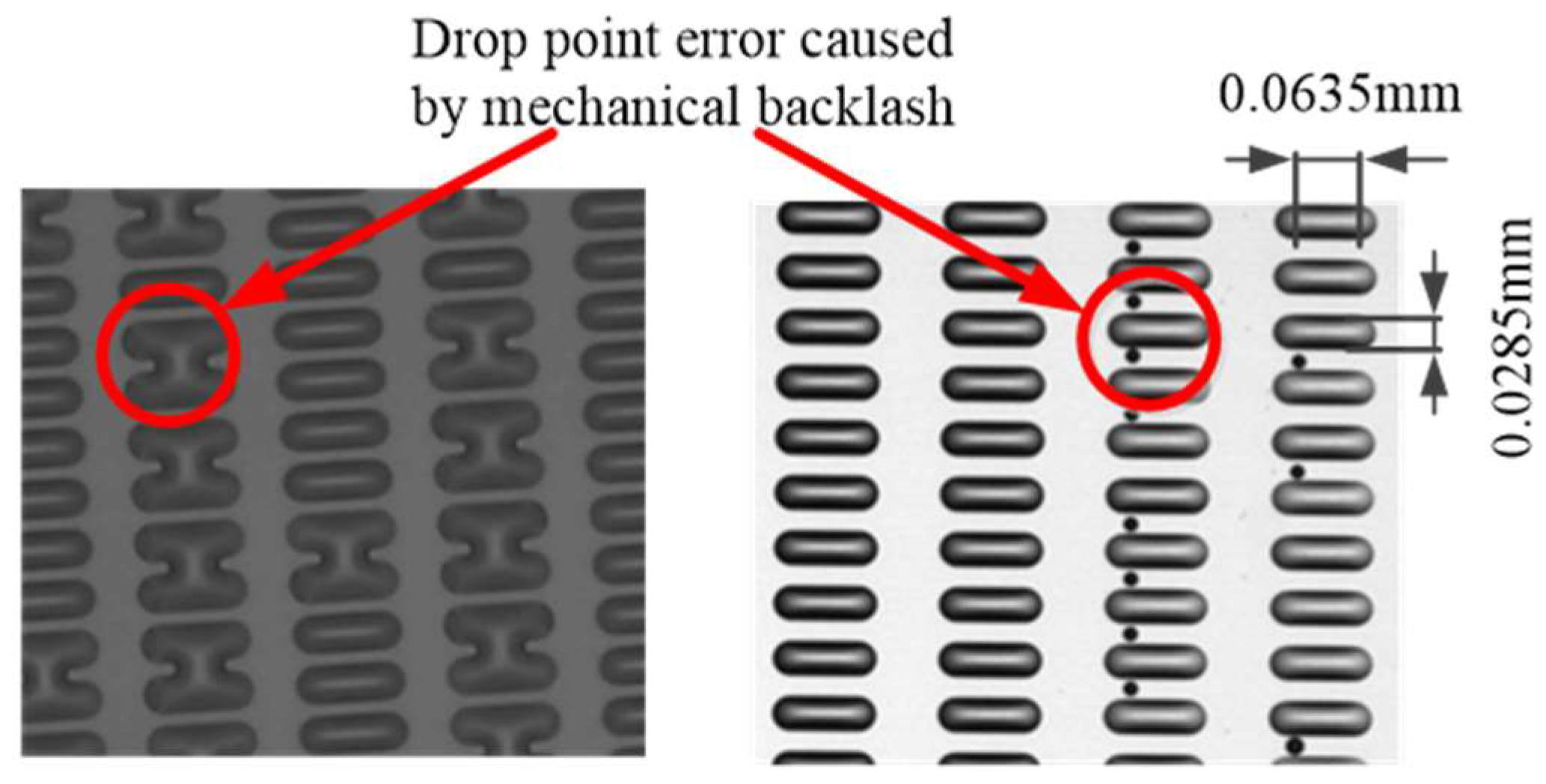
Figure 1, due to the inaccurate positioning influence caused by backlash, several ink drops landed outside of their corresponding pixel slots, forming liquid bridges or scatters (shown in
Figure 2), which will cause the displayer to glow abnormally.
Given that the impact position deviation of ink drop is relatively small compared to the backlash-caused bias, and the backlash generated from initial installation, midway maintenance or component wear is generally inevitable in practice, it may lead to massive disqualification of OLED products and time/financial losses once tiny backlashes can be detected long after manufacture starts. Therefore, it is highly necessary to analyze and compensate for this backlash characteristic in the control design process, as the last defense line for ensuring the equipment’s accuracy, robustness and final production quality. In Ref. [
2], the Nyquist method was applied to analyze under what working conditions the limit-cycle phenomenon will be excited by backlash. In Ref. [
3], a general hysteresis model in the form of a piecewise function was established to represent backlash, and then a multi-step model predictive compensator for discontinuous systems was proposed to suppress its effect. Ref. [
4] focused on analyzing the influence of valve backlash on hydraulic manipulator dynamics and designing a robust compensator via the back-stepping method. Considering the strong coupling between multi-axes, modeling and experimental analysis on the coupling characteristics through backlash in a macro–micro positioning system based on a planar parallel structure has been carried out in Ref. [
5]. Furthermore, taking coupling, backlash effect and uncertain disturbances into account, a global iterative sliding mode control method was proposed to adaptively compensate for the matched unknown dynamics and suppress chattering by varying gains [
6]. In addition, an extended set-membership filter-based observer was designed to estimate the backlash influence for a robotic flexible ureteroscope system [
7]. On the basis of time-delay estimation for observing the comprehensive effect of backlash and external disturbance, a self-tuning robust controller was constructed to enhance the motion performance of robotic manipulators [
8].
In addition to considering the influence of mechanical backlash, a corresponding control strategy based on a macro–micro structure will determine the dynamic performance of the whole system. At present, the commonly used control structure is to employ double closed-loop feedback on the macro/micro parts, respectively, so as to realize overall stability and accurate positioning through the cooperative actions of different parts in a platform [
9,
10]. In terms of control strategy design, the traditional double-loop PID control and its extended methods have been widely used in this kind of motion platform due to its advantages, e.g., no need for modeling, simple design, fewer control parameters and easy adjustment, etc., and it can generally help systems achieve the specified motion accuracy under no-disturbance working conditions [
11,
12,
13]. The control strategies based on frequency-domain analysis could suppress various coupling vibrations by expanding the system bandwidth, which optimizes the dynamic characteristics of platforms [
14,
15,
16]. Nowadays, various modern control strategies, such as predictive control, sliding mode control, internal model control and active disturbance rejection control, have also been gradually applied in such platforms to comprehensively improve both their dynamic performance and positioning accuracy from the angles of convex optimization, nonlinear feedforward and disturbance robustness enhancement [
17,
18,
19,
20]. Moreover, adopting the double-input single-output (DISO) control method can avoid the influence of errors introduced by mechanical assembly or an accuracy gap between sensors, and reflects a certain increase in the motion accuracy [
21,
22,
23].
Based on the above literature review, existing work has already discussed the backlash characteristic in transmission mechanisms and its corresponding compensation methods, providing inspiring research directions. Several high-precision positioning control strategies for macro–micro dual-drive systems have also been proposed, which can effectively promote the system tracking performance from both the control structure and the algorithm levels. However, there is still no suitable identification method for obtaining micro-backlash parameters online that has been applied to the above macro–micro dual-drive motion system so far. Thus, it is unable to analyze the influence of time-varying backlash on the macro–micro coupling state and the positioning accuracy in real time, and it cannot even make accurate compensations. Furthermore, during operation, the platform performance may be affected by several factors, including backlash, the macro–micro coupling effect, environmental disturbance, etc., but current control strategies have not fully considered those factors, nor have they studied a class of macro–micro motion platforms with large stroke (more than 0.6 m). Hence, using existing control strategies is not adequate for such platforms to achieve the required positioning accuracy of OLED/Micro-LED display printing, which may ultimately lead to the disqualification of wet film formation.
In order to achieve a good film-forming quality, aiming at a class of large-stroke macro–micro dual-drive motion platform applied in OLED/Micro-LED display printers, the dynamic model of macro–micro dual-drive motion system, including mechanical micro-backlash, is first established in
Section 2 for analyzing the influence of backlash associated with mechanical coupling. In
Section 3, a stepwise nonlinear identification method is proposed as the basis of accurate backlash compensation, which is designed to estimate the backlash parameters online through state observation. Then, considering the combined influence of backlash, mechanical coupling and external disturbance, a decoupling sliding mode compound control strategy (DSMC) is proposed to realize both strong robustness and micron-precision positioning of a long-stroke macro–micro motion platform (
Section 4). In
Section 5, an illustrative simulation example and overall performance comparison under traditional PID and proposed DSMC control strategies are discussed. Lastly, the corresponding experimental results are provided in
Section 6 for further verification.
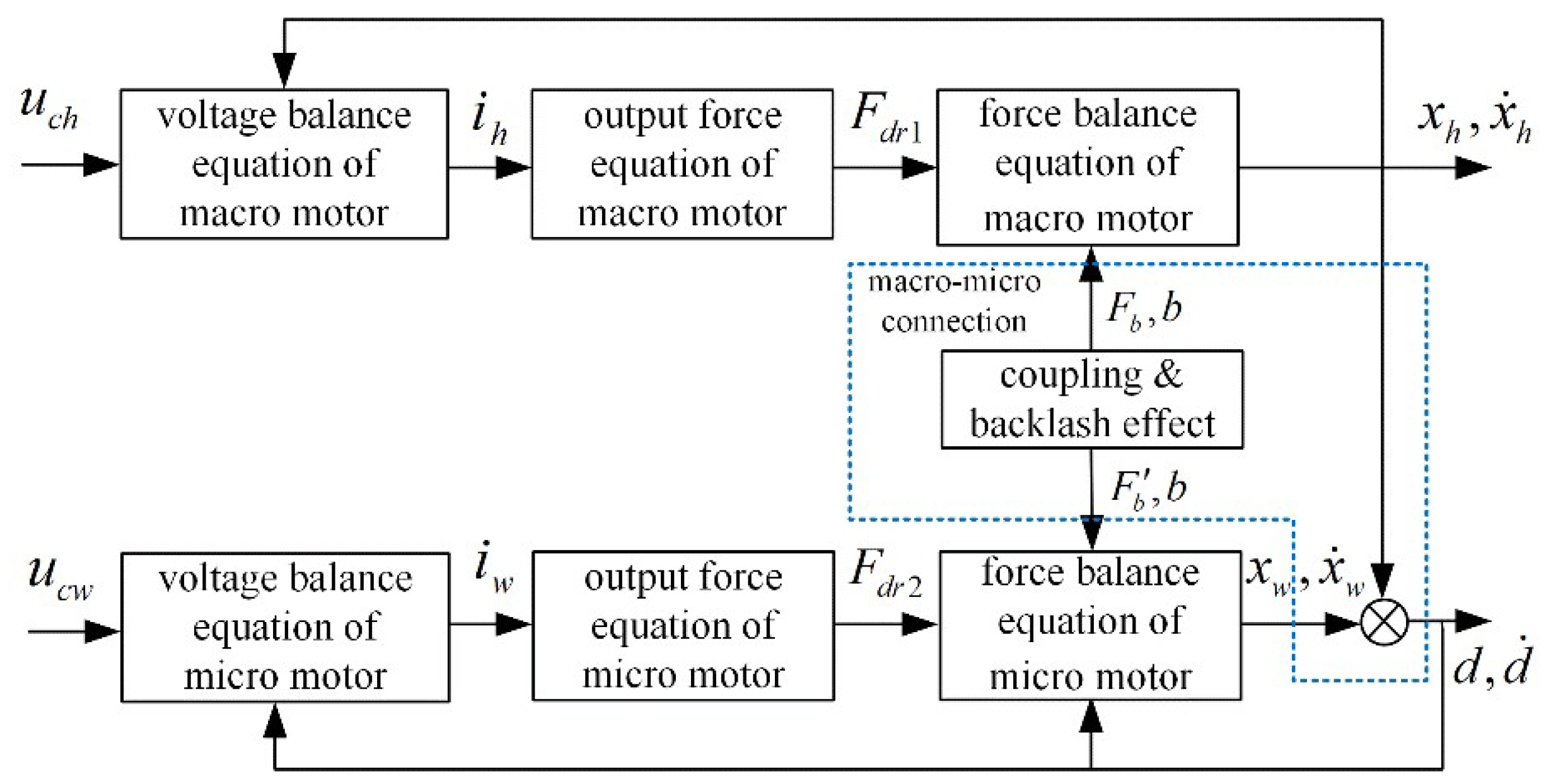
2. Dynamic Modeling of Macro–Micro Dual-Drive Motion Platform and Control Problem Formulation
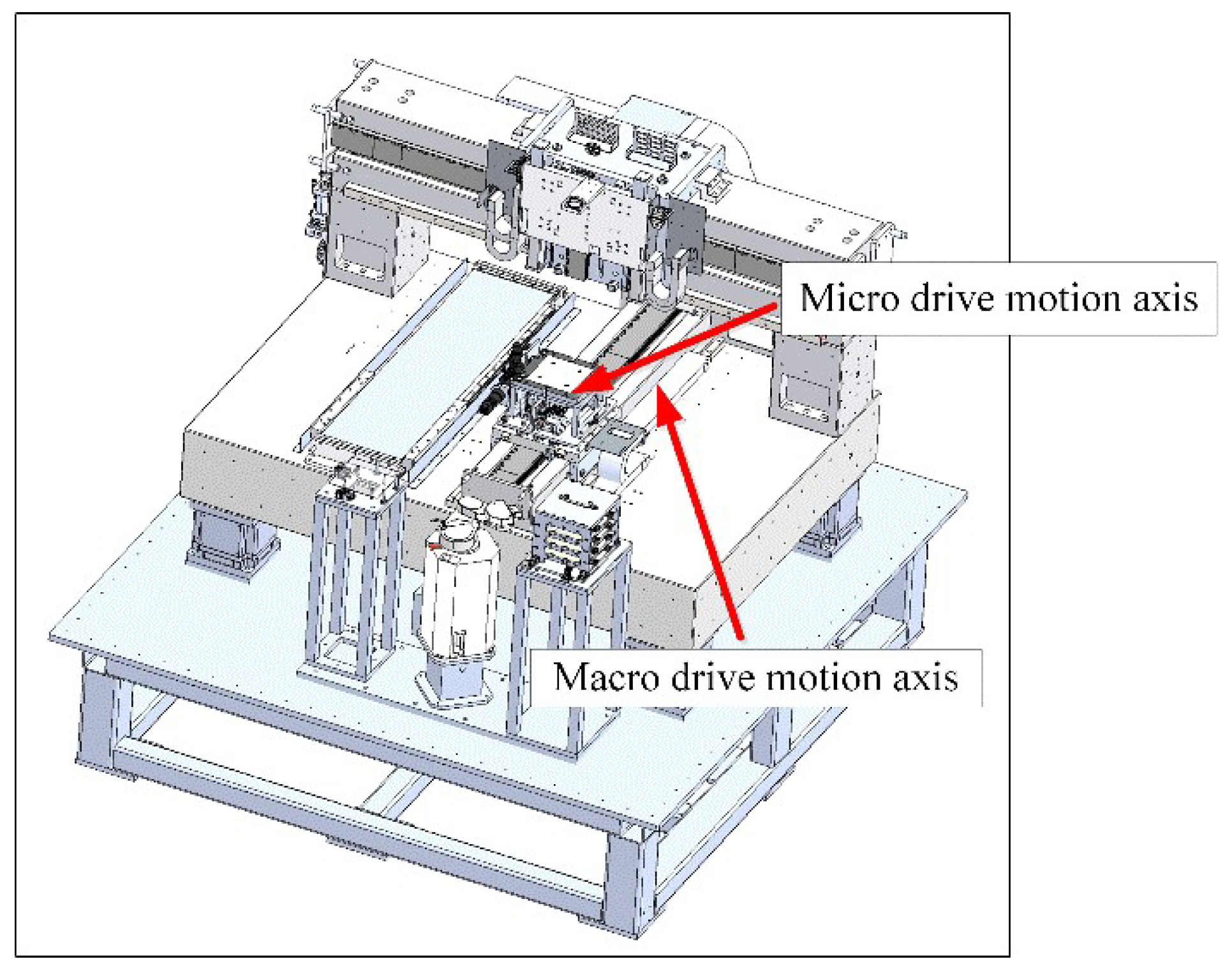
The macro–micro dual-drive motion platform currently applied in OLED/Micro-LED equipment is mainly composed of a macro mechanism series connected with a micro mechanism, where its macro mechanism is designed to ensure the large-stroke motion-positioning accuracy at micron level, and its micro mechanism makes further compensation based on the coarse positioning. The macro and micro mechanisms are actuated by a linear motor and voice coil motor, respectively, and their positions are both measured via laser interferometer. Since the platform adopts the air floating form, friction influence will not be considered.
Figure 3 shows the mechanical structure diagram of the macro–micro dual-drive motion platform.
2.1. Description of Macro–Micro Dual-Drive Motion Platform
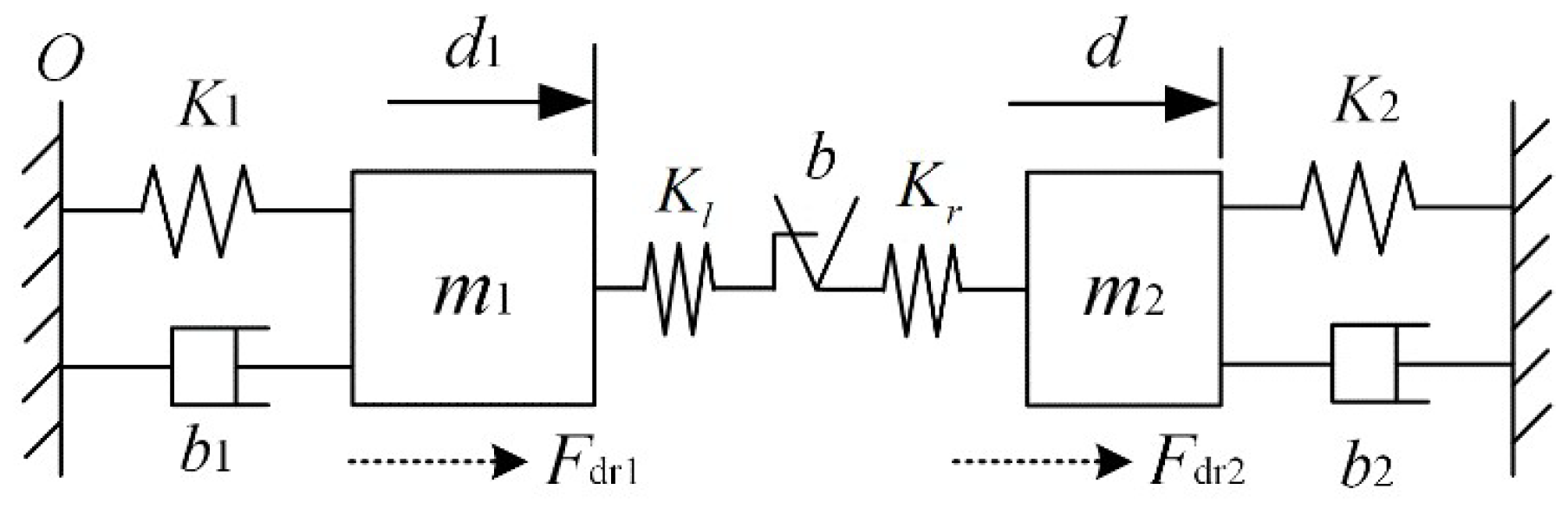
Based on the designed mechanical structure above, the schematic diagram of the macro–micro dual-drive motion platform is shown in
Figure 4.
In
Figure 4,
and
are the equivalent mass of the macro and micro mechanism, respectively;
indicates the backlash between macro and micro mechanisms. The equivalent connection stiffness and damping coefficient between the macro mechanism and the base are expressed by
and
respectively, while the equivalent load stiffness and damping coefficient of the micro mechanism are respectively represented by
and
.
and
are the equivalent elastic coefficients of the connection between the backlash and the macro/micro mechanism, respectively. Here, the macro mechanism and the micro mechanism are series-connected with a backlash inbetween, which constitute the dynamics of a dual-drive motion platform. The electromagnetic driving force generated by macro and micro actuators are defined as
and
, respectively.
and
are, respectively, the macro displacement and the total displacement of the platform (that is, the displacement of the end of the micro mechanism) relative to
point under the above driving forces. Since the absolute displacements of macro and micro mechanisms can be respectively expressed as
and
considering the backlash effect, their corresponding force balance equations can be written as follows
where
and its reaction force
are the actual load forces transmitted from the mechanical backlash acting on the macro and micro mechanism, respectively, relating to the relative displacement, backlash width and the equivalent elastic force between the macro and micro mechanisms. Secondly, given that the voltage balance equation and the output force equation of the macro/micro mechanisms’ driving motors show a similar form, respectively, their general description can be expressed as follows
where
represent the armature voltage (control voltage), equivalent inductance, equivalent resistance, armature current, back EMF coefficient and electromagnetic force coefficient of the corresponding driving motor, respectively. Here, we define the above parameters with subscript
h to describe the macro linear motor, while those parameters with subscript
w are set to describe the micro voice coil motor.
represents the absolute displacement of macro/micro mechanisms, that is,
for the macro mechanism and
for the micro mechanism. Above all, Equations (1)–(4) are the dynamic model of the macro–micro dual-drive motion platform with backlash effect.
It can be observed that the load force terms appear in the macro/micro force balance Equations (1) and (2), respectively, under the influence of backlash. Furthermore, the extra force term in Equation (2) is generated from the combined influence of the macro/micro mechanism coupling effect and also backlash, which shows that the positioning accuracy of the platform will be affected greatly by the above influence. Therefore, modeling and analyzing the coupling and backlash effect precisely is the theoretical basis for the following compensation.
2.2. Description of Backlash Characteristic
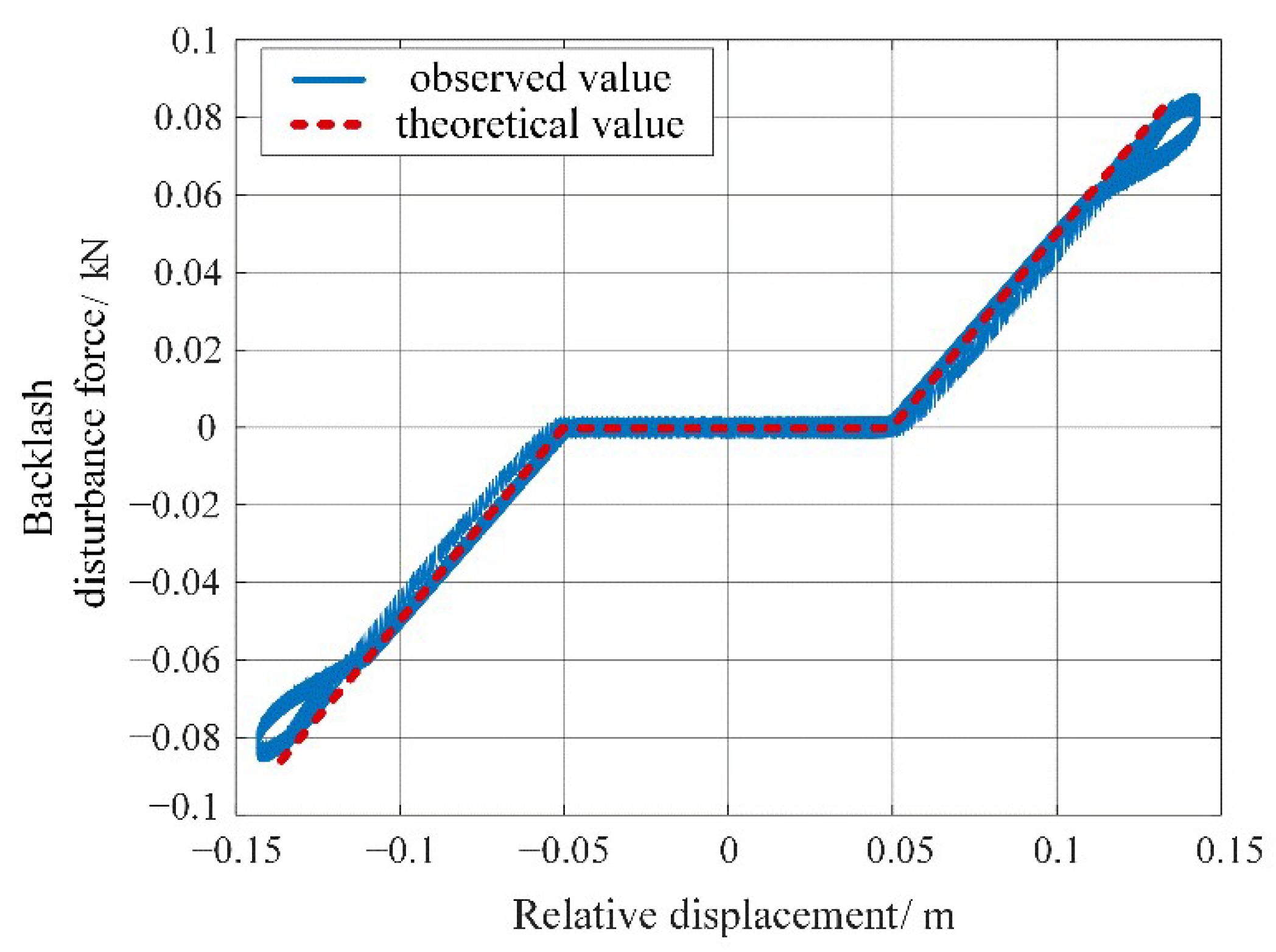
Backlash is essentially a kind of multi-valued discontinuous nonlinear disturbance, caused by insufficient machining accuracy or assembly errors of mechanical components. It will lead to discontinuity and sudden changes of motion and force transmission, and greatly reduce the accuracy and rapidity of such positioning/motion systems. The influence of the backlash effect acting on the transmitted force is shown in
Figure 5.
In
Figure 5, the horizontal axis represents the displacement of the mechanism actuator, and the vertical axis represents the transmitted load force,
indicates the continuous load force curve when without backlash, while
(also in Equation (1)) depicts the actual load force curve transmitted through backlash.
represent the left and right backlash widths, respectively, when the platform is at the initial position; thus, the total backlash width satisfies
. Without loss of generality, we consider that
and
. For discontinuous
, its horizontal segment is defined as I; segments with slope
and
are defined as II and III respectively.
It can be seen from
Figure 5 that backlash causes the original load force curve
to shift to the left or right side according to different motion directions, which can be equivalent to introducing a disturbance force in dead-zone form into the macro and micro mechanisms. It can be described as
where
represents the relative displacement between the macro and micro mechanism.
According to Equations (1), (2) and (5), although the backlash does not directly exist in the mechanisms but between them, the discontinuous jump of both actual load force and the additional disturbance force term caused by it can be transmitted to the entire platform through the relative displacement of macro and micro actuators, resulting in the motion-state fluctuation of each actuator, and also reflecting the backlash influence on the mechanical coupling. In addition, since the actual displacement of the micro mechanism is jointly decided by the displacement reference signal and the backlash size, by combining Equations (3)–(5), it can be seen that the speed state () fluctuation of the micro actuator can reversely cause the control current fluctuation of the micro voice coil motor under the influence of the mechanical coupling disturbance, and then lead to the output driving force () oscillation, which significantly affects the positioning accuracy of the entire platform and may damage the motor further.
In summary, the macro–micro motion platform model, considering backlash (1)–(5), can not only describe the macro and micro motion dynamics’ characteristics in line with the actual working conditions, but also reflect the influence of the backlash on the control performance, which is the basis for designing effective motion control strategies for such kinds of platforms.
2.3. Control Problem Formulation
To realize high-precision positioning for the class of large-stroke macro–micro dual-drive motion platform applied in the OLED/Micro-LED printing field, two main challenges we will deal with in this paper are summarized as follows, based on the above dynamic model (1)–(5):
Mechanical backlash introduces piecewise force into macro and micro mechanisms, which makes it difficult to identify the time-varying width of backlash using common linear methods, and further causes backlash compensation to be less accurate.
Under loading conditions in practice, macro and micro mechanisms are both affected by a discontinuous mechanical coupling effect and external environmental disturbance (e.g., random airflow, base vibration); thus, the high positioning accuracy of the entire motion platform is not easy to achieve.
3. Improved Backlash Model and Nonlinear Identification Method Design
For challenge 1, an improved quasi-linear backlash model is first proposed in this section, which can express the piecewise model (5) in a continuous form. Then, based on the improved model, a corresponding nonlinear identification method is designed to accurately estimate the time-varying backlash characteristic online.
3.1. Quasi-Linear Backlash Model
First, define the backlash state factor as follows
When the decision condition ∗ > 0, the system is in the backlash state, and vice versa. As the signal of the condition changes, the factor outputs 0 or 1, indicating the switch of the system states.
In order to judge the state switch I↔II and I↔III, define the above switch conditions as
and
respectively, then Equation (6) can be rewritten as
By introducing Equation (7) into Equation (5), the backlash disturbance force can be expressed in the following linear form
Equation (8) is the improved quasi-linear backlash model based on the dead zone function. For the convenience of identification method design, the backlash state marker
is separated from its characteristic parameter
thus, Equation (8) can be rewritten as the following form
As can be seen from Equation (9), when the backlash disturbance force is measurable, the backlash parameters can be obtained via linear identification methods. Therefore, the proposed improved quasi-linear model can effectively solve the identification problem caused by the backlash discontinuity.
3.2. Nonlinear Identification Method Design for Backlash Characteristics
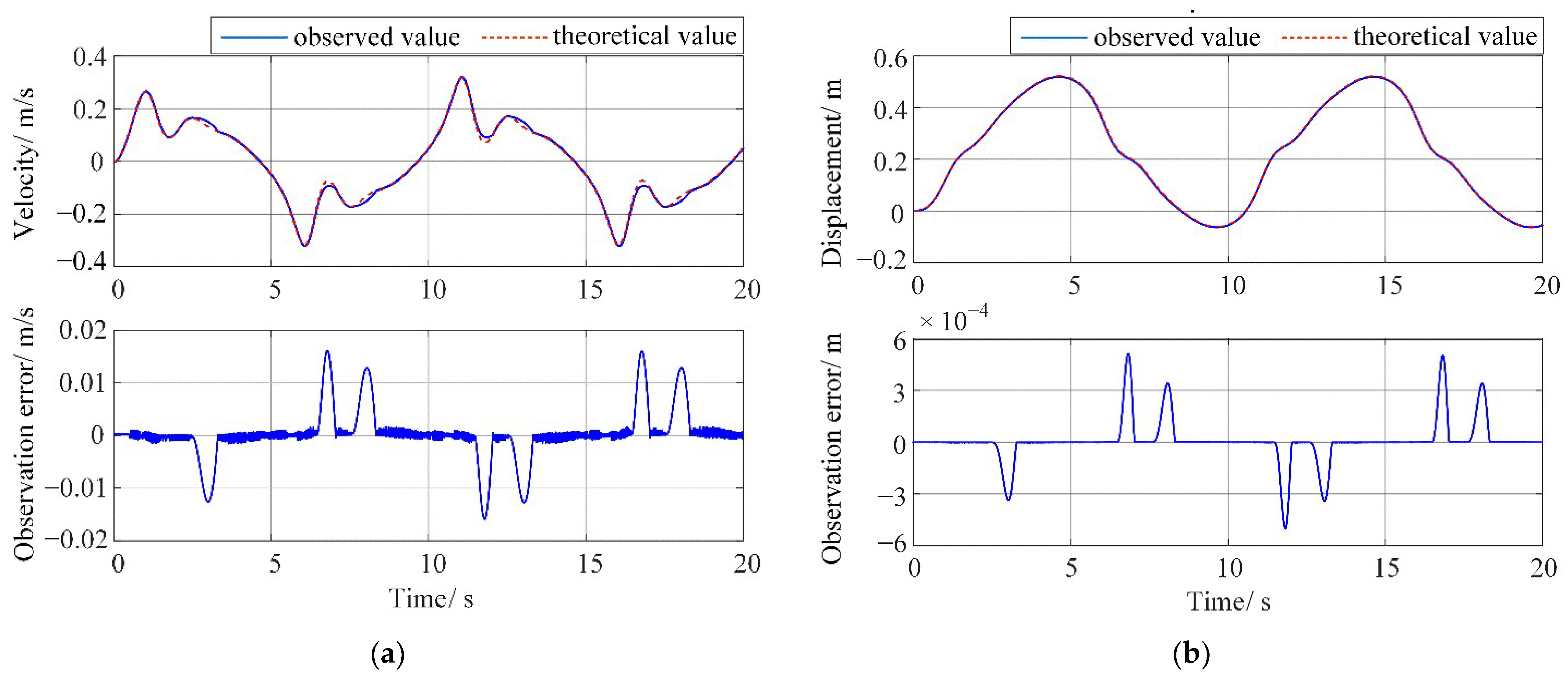
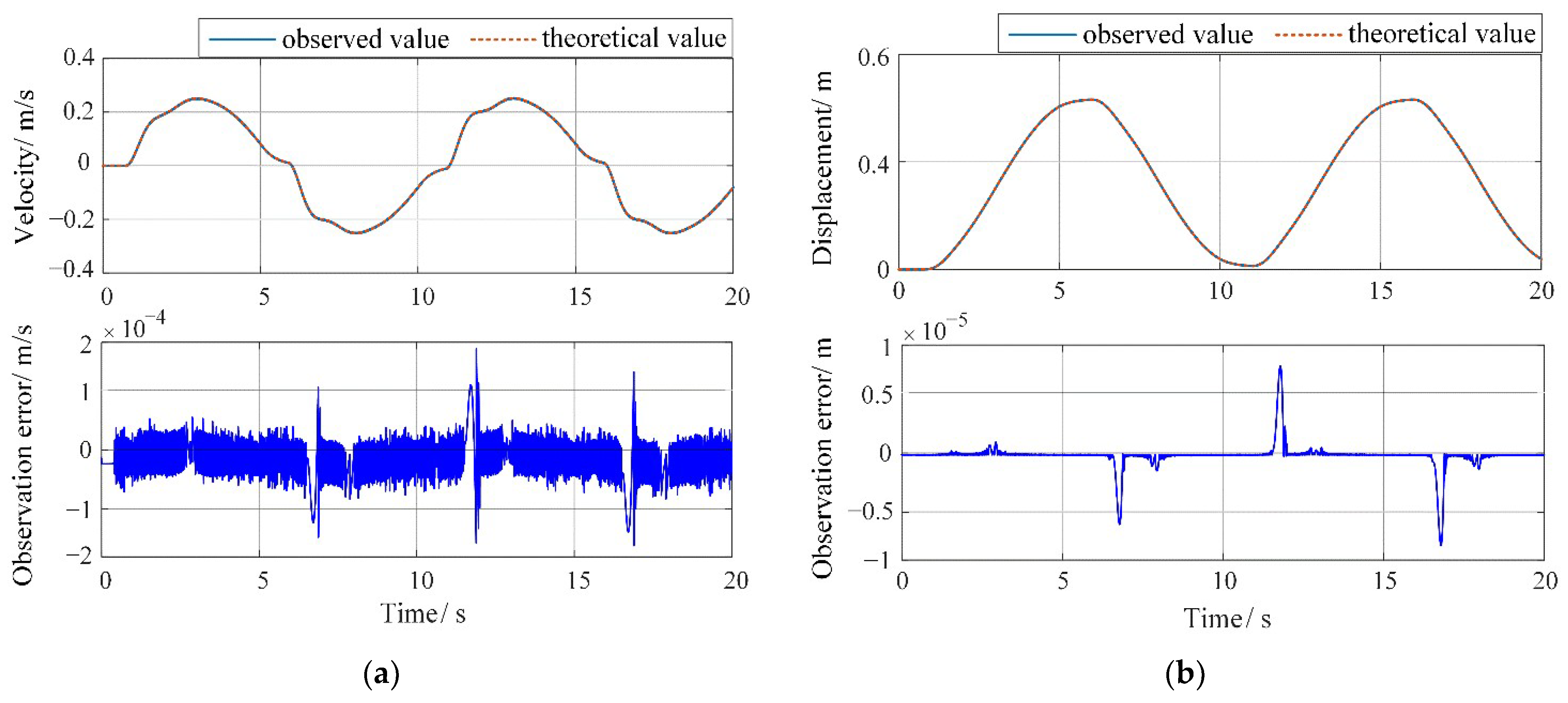
In practice, the disturbance force transmitted through the backlash is usually unknown. Therefore, it is necessary to estimate the value of disturbance force accurately for the further backlash parameter identification. In this section, a stepwise identification method based on nonlinear sliding mode theory is proposed. Firstly, is estimated according to the dynamic model (1)–(5). Then, based on the estimated and quasi-linear model (9), the backlash parameters are identified online.
- A.
Estimation of nonlinear backlash disturbance force
Due to the discontinuity of , a nonlinear observer is designed based on the second-order sliding mode super-twisting theory. It can simultaneously ensure finite-time observation of the displacement and velocity of the macro and micro mechanisms, and then calculate the using the above signals.
The observation is carried out under the following working condition: the macro mechanism is driven to run a micro sine motion, and the micro mechanism is dragged to follow this motion. In this case, the micro mechanism can be regarded as the load of the macro mechanism, and the dynamic equations of the platform under this condition can be written as
where
and
represent the sum of equivalent elastic force and stiffness force of the macro/micro mechanism, respectively, and
is the input driving force of the macro mechanism in the estimation test. Let
Equation (10) can be rewritten in state equation form as follows
According to Equation (11), the nonlinear observer for macro and micro mechanisms based on a second-order sliding mode super-twisting method is designed as follows
where
and
are the observed displacement of the macro/micro mechanism, respectively,
and
are the observed velocity of the macro/micro mechanism, respectively,
represents the corresponding observed error of each state, and
and
are observer parameters to be designed. In addition, the following conditions also must be satisfied
where
,
. Subtracting Equation (11) from Equation (12), we have
where
,
,
,
,
is the observed error term caused by the uncertainty of elastic and stiffness parameters. The expression of
is
Considering that the estimated value of the equivalent elastic force and stiffness force has little error with the true value under the above test conditions, and the observer is also stable and convergent,
in the second equation in Equation (14) can be ignored here. Thus, we have
In the actual system, due to the existence of various noises and unmodeled dynamics, the value of observed states often contains high frequency oscillations, so it is necessary to introduce a low-pass filter for removing its high frequency component. Defining
as filtered
, and combining Equation (15) with Equation (16), we can obtain the actual disturbance force transmitted by backlash as
Equation (17) is essentially a function of nonlinear observation errors from displacement and velocity estimations on the corresponding mechanism.
In addition, the consuming times
required for the macro and micro motion states’ observation using Equation (12) can also be estimated. Their corresponding time upper bounds for the states to converge from the initial value to the small neighborhood of the real value are calculated as follows
where
represent times required for one cycle of the state observation error oscillation of macro and micro mechanisms, respectively. Combining Equations (18) and (19) and the convergence of the above second-order sliding mode super-twisting method, it can be found that the observation error of each state will always converge to a tiny neighborhood of the corresponding state’s real value within a finite time, and the convergence time is determined by the state observer parameters
,
and
.
In summary, the actual disturbance force can be indirectly obtained in a finite time by estimating the real-time motion states of the dual-drive platform based on the sliding mode super-twisting method.
- B.
Identification of backlash characteristics based on the quasi-linear model
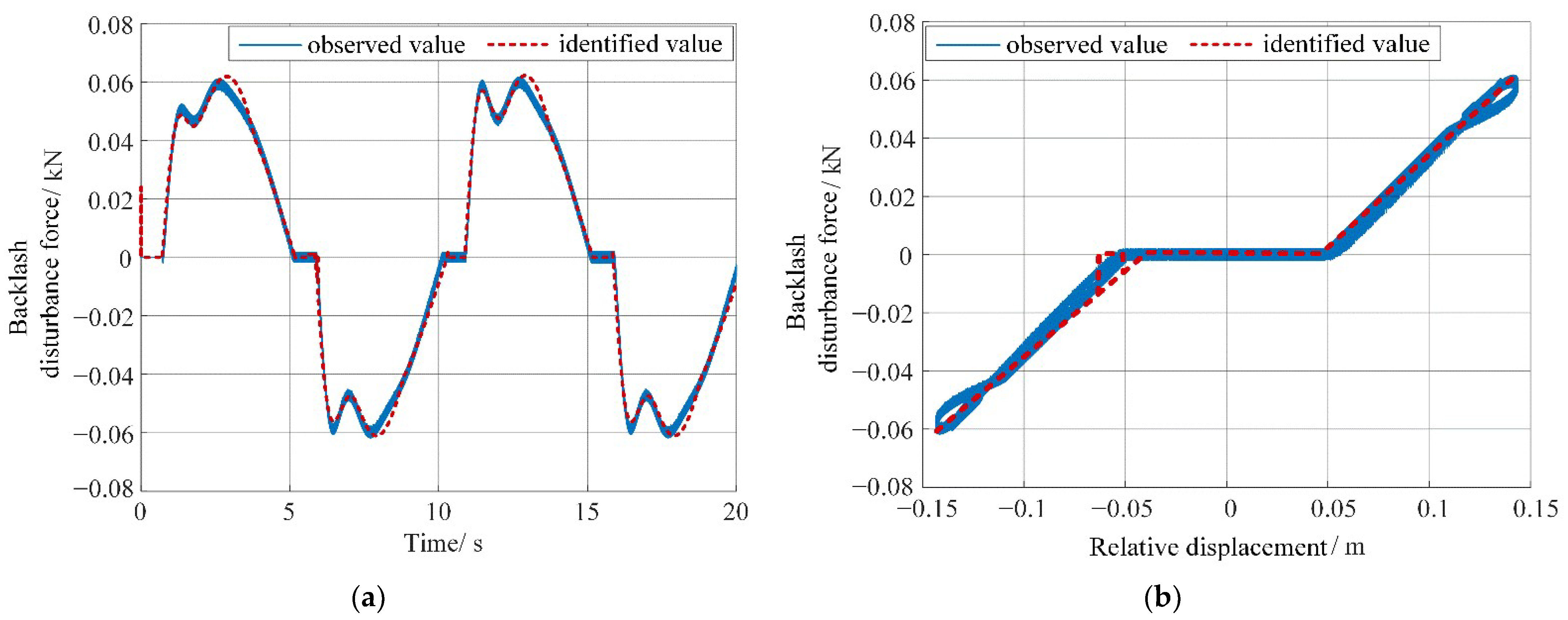
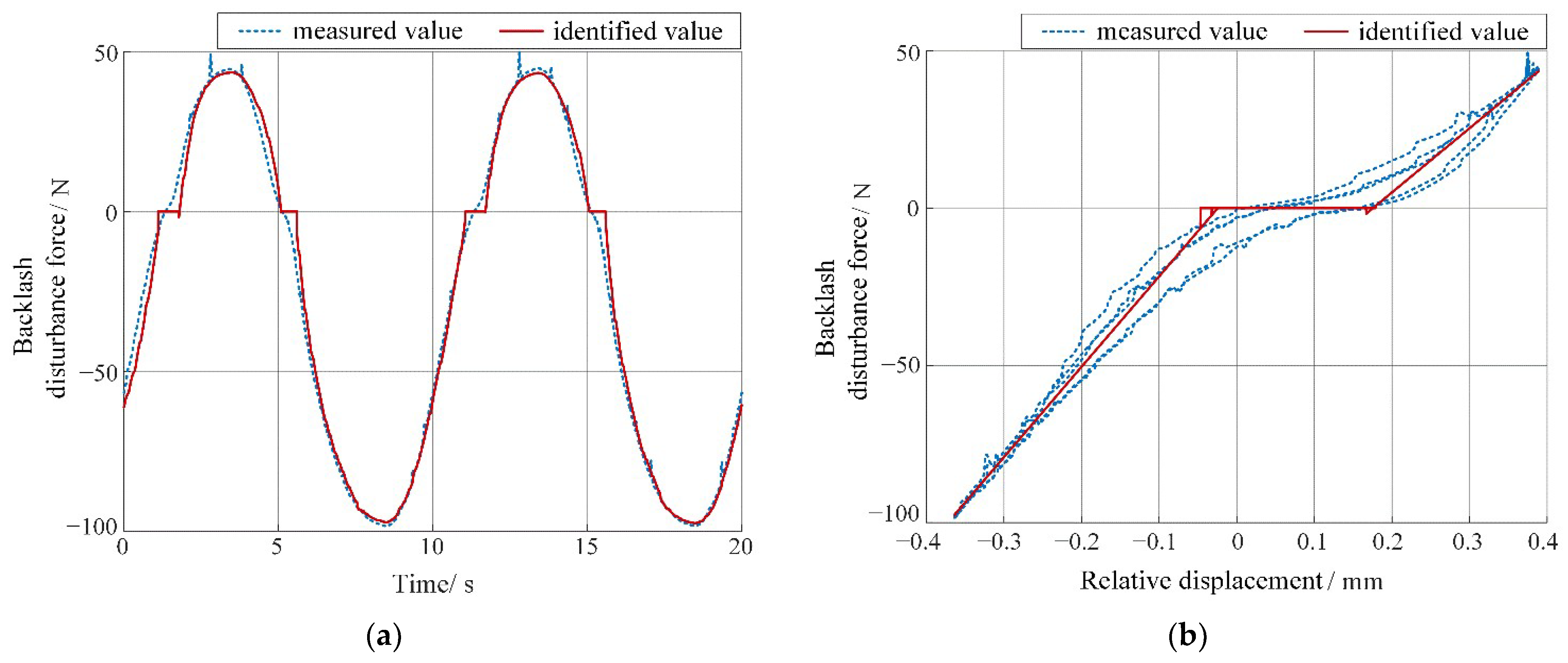
Based on the disturbance force estimated by Equation (17) and the quasi-linear backlash model (9), though discontinuous states still exist, linear identification methods now can be directly applied to identify the backlash characteristics online. Considering the balance between real-time capability and precision requirement, recursive least-squares method (RLS) is selected here to identify the real-time backlash state marker and the characteristic parameter simultaneously.
The RLS identification method based on the quasi-linear backlash model is given as follow
where
is the gain vector and
is the covariance sequence of observation error. Assume that the noise effect has already been eliminated by filtering. Here, the disturbance force sequence
, which is estimated by Step A in real time, is taken as a set of input signals required for RLS identification, that is,
sequence in Equation (20). In addition, according to Equation (9) and measurable signal
(the relative displacement between macro and micro mechanisms), the backlash state marker
can be initially predicted as another set of the input signal for starting identification, which will be updated automatically in each iteration as the identification results converge. Under the persistent excitation of the two above sets of input signal, the iteration process for calculating backlash characteristic parameter
is shown in
Figure 6.
It is noted that the initial value of backlash parameters should be set as a non-zero value for ensuring the next step iterative calculation can continue. Here, and are selected, respectively.
To summarize, the estimated disturbance force and identified backlash widths associated with state marker are the key information needed in the following backlash compensator design.
4. Decoupling Sliding Mode Compound Positioning Control Design
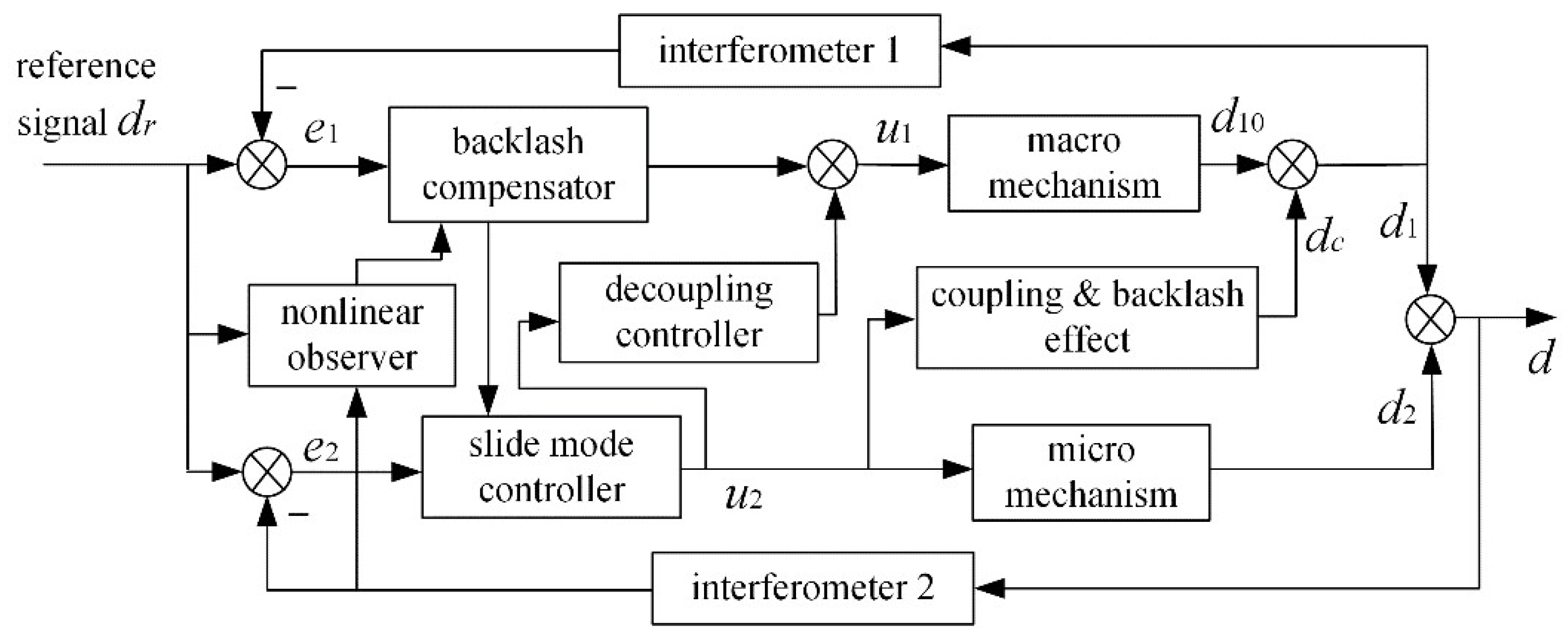
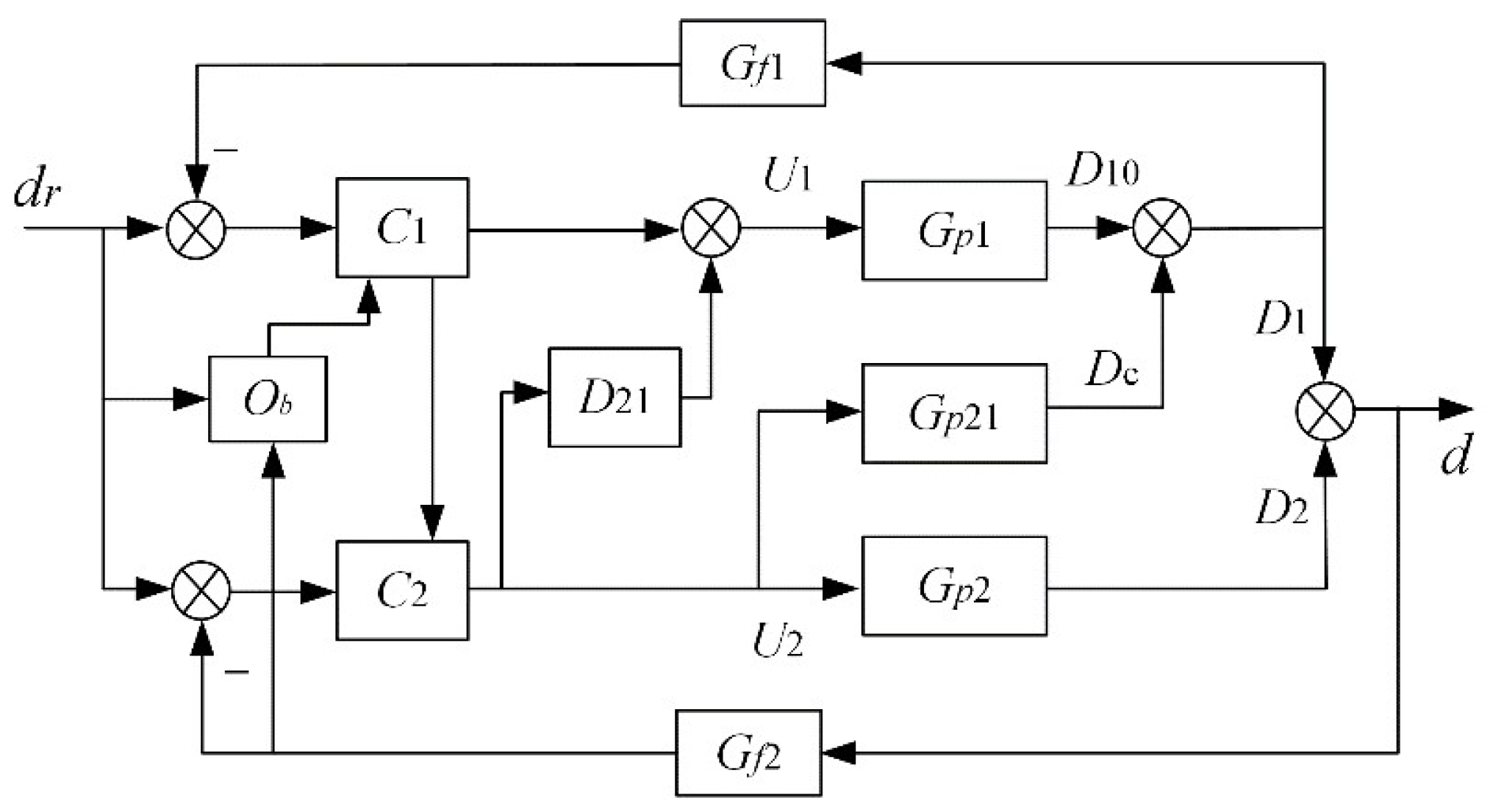
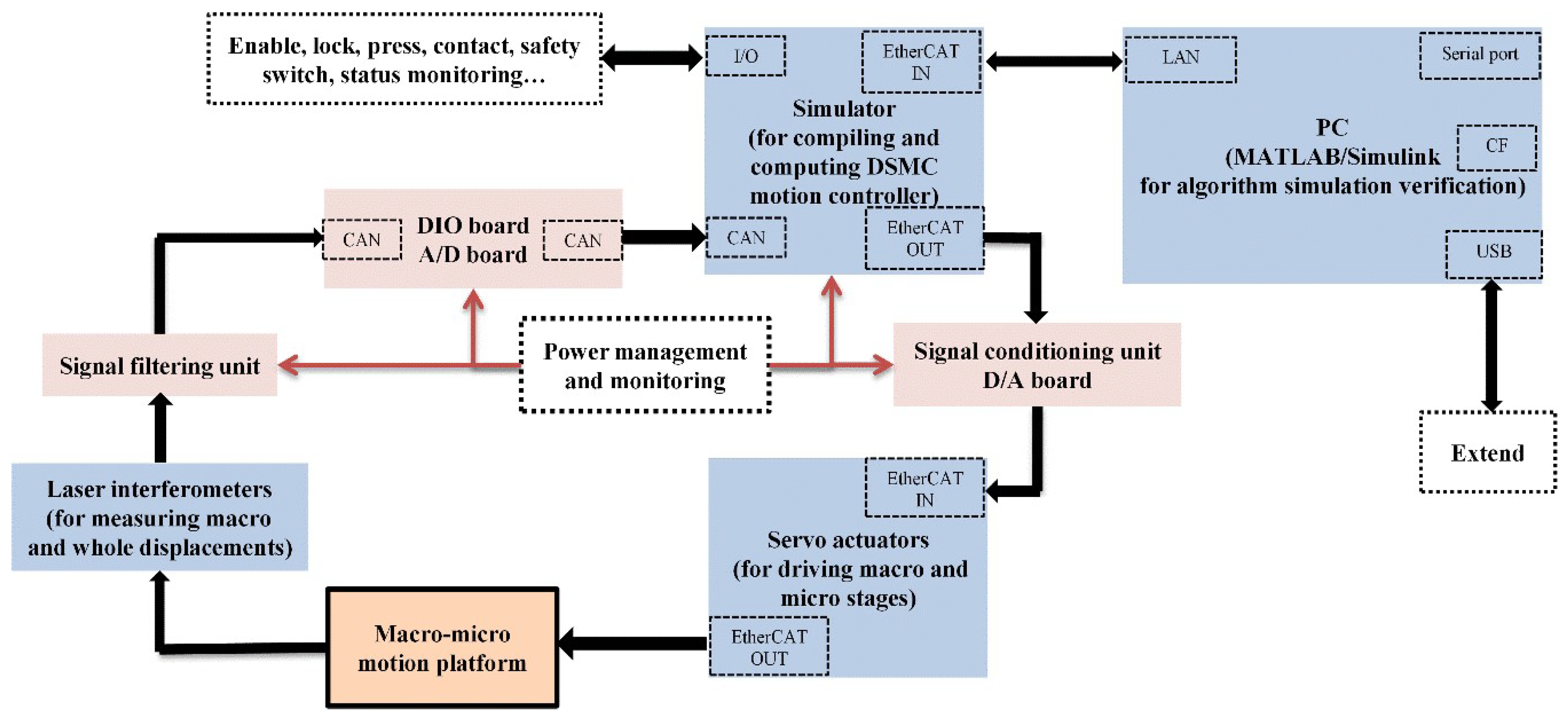
For challenge 2, according to the established model (1)–(5), a decoupling sliding mode control strategy based on backlash compensation is proposed in this section. According to the online identification result, the influence of the backlash disturbance force on macro and micro mechanisms is precisely compensated. Then, a decoupling controller is adopted to eliminate the influence of micro motion acting on the macro mechanism positioning. Next, an adaptive integral sliding mode control method for the micro mechanism is proposed to ensure both strong robustness and high-precision positioning of the end of the platform. The control schematic diagram is shown in
Figure 7.
For the convenience of following the explanation, according to the control strategy shown in
Figure 7, the control block diagram for the platform is given in
Figure 8.
In
Figure 8,
is the displacement reference signal of the platform,
represents the nonlinear velocity observer used to identify backlash parameters.
and
are the backlash compensator (including compensation for both macro/micro motion) and the sliding mode controller to be designed, respectively, and
and
are the corresponding control inputs generated by the above-mentioned controller, respectively.
and
represent the dynamics of the macro/micro mechanisms, respectively, and their corresponding responses are
and
, respectively.
and
represent the dynamics of the interferometer installed at the end of the macro/micro mechanisms, respectively.
represents the coupling and backlash combined dynamics in Equation (2), whose response under controller input
is
.
is the decoupling controller to be designed, which can compensate for the influence of the micro motion reflected on the macro mechanism via the feedforward way.
4.1. Decoupling Control Design for Macro Mechanism Based on Backlash Compensation
Since the micro mechanism is installed at the end of the macro mechanism, the basic order of the platform positioning accuracy is mainly determined by the macro mechanism. In order to improve the overall positioning accuracy, the coupling effect from the micro mechanism acting on the macro positioning must be effectively eliminated.
However, under the backlash effect, the coupling force exists in a discontinuous form as expressed by Equation (5), which makes the system dynamic nonlinear. Thus, the coupling effect can hardly be eliminated by common linear decoupling methods. To overcome this problem, the backlash influence must be accurately compensated for before decoupling, that is, a backlash compensator for macro motion should be provided. Here, combining the nonlinear observer (12) and RLS method (20), the compensator can be given as
where
indicates the time-varying compensation value for the macro mechanism, and the backlash state is determined by the state factor
. Due to the finite-time convergence characteristic of observer (12),
can be obtained timely in each control interval, thus eliminating the backlash discontinuous influence in the corresponding control period.
Then,
and
can be rewritten as their linear form
and
, ensuring that the macro/micro coupling effect can be directly compensated for via a linear decoupling method. In this case, the system dynamics must be satisfied
then we have
According to Equations (1)–(4),
and
can be indicated as
where
are the coefficients of the coupling transfer function, which can be obtained via experimental identification. From Equations (23)–(25), the decoupling controller is designed as
By choosing appropriate control parameters based on the identification result, the stability of the macro positioning control loop can be ensured.
4.2. Adaptive Integral Sliding Mode Positioning Control Design for Micro Mechanism
In this section, an integral sliding mode control method based on backlash compensation is proposed to improve the micro positioning accuracy. By designing a nonlinear sliding mode surface, and estimating the upper bound of residual disturbance adaptively, the controller will ensure the total displacement of the platform’s end converges to the reference signal within the designated tracking error range.
As can be seen from Equation (2), backlash disturbance term
will introduce oscillation and affect micro positioning accuracy. However, if only adopting the sliding mode robust term to suppress oscillation here, the control algorithm will get too conservative; therefore, a feedforward compensation of
for micro motion has to be carried out according to the disturbance observer (17). Then, further considering the influence of external disturbances, the dynamics (2)–(4) for the micro mechanism can be rewritten as
where
, and
is the residual force after backlash compensation, which is generated from the backlash estimation error. Let
be the upper bound of the external disturbance; then we have
. If the upper bound of
is
, then the total disturbance force
for the motion system is also bounded, which can be expressed as
. Thus, the upper bound of the total disturbance can be estimated.
Due to the reason that
is much smaller than other coefficients, the influence of derivative term
can be ignored; then, Equation (28) is simplified as
Define
, then the micro dynamics model (27) and (29) can be rewritten in state equation form as
where
is the estimated backlash size obtained from
Section 3,
are the actuator’s velocity and the acceleration of the macro mechanism estimated via Equation (12).
In order to ensure that the platform tracks the reference displacement signal, the tracking error is defined as
the nonlinear integral sliding mode surface is designed as
where
and
are control parameters to be designed, which satisfy
. In order to further improve the tracking dynamic performance, design
as the following piecewise function form
where
is set as the switch boundary of tracking error. Since the micro mechanism is used to compensate the micro positioning error generated from the macro mechanism, its travel range is much smaller than that of the macro part. Therefore, when the macro positioning error exceeds the designated boundary (
), the micro mechanism does not response; conversely, the compensation for the displacement micro-error starts. At that time, use
to replace the integral term in the traditional sliding mode surface; thus, the small error can be “amplified”, that is, when
, there is
, then the high tracking accuracy for this dual-drive platform can be ensured, and the control strategy can also be switched in time when the required compensation exceeds the range of the micro mechanism.
When the system state reaches stable,
. Choose the first Lyapunov function
as
Substituting Equation (32) and its derivative into
, we have
Since the total disturbance term
is unknown, its upper bound
will be estimated by adaptive control here. Define the estimated upper bound as
, the estimated error is
Choose another Lyapunov function
as
where
. According to Equations (36) and (37), we have
Therefore, according to Equations (35)–(38), the adaptive integral sliding mode controller is designed as
where
and
are the control parameters for adjusting the tracking error convergence boundary. Furthermore, the adaptive law for estimating the upper bound of the total disturbance is designed as
Theorem 1. For the micro mechanism described in Equation (30), the control law (39) and adaptive law (40) are adopted to compensate macro positioning and ensure that the dual-drive platform’s tracking error converges to the designed small neighborhood of the equilibrium point in finite time , and the motion system is also asymptotically stable.
Proof. Substitute Equations (39) and (40) into system (30), we get
When
, it satisfies
It can be seen that the tracking error will converge to the state equilibrium point as
converges to
in a finite time. To determine the convergence range of the tracking error, define the third Lyapunov function as follows:
It can be obtained from Equations (32), (33) and (43)
Therefore, when the tracking error satisfies the following inequality
holds. From Equation (45), by selecting appropriate sliding mode surface and control parameters
, the surface can be ensured to converge in a small, designed neighborhood, and the micro tracking error can also converge to the designed range. □
7. Conclusions
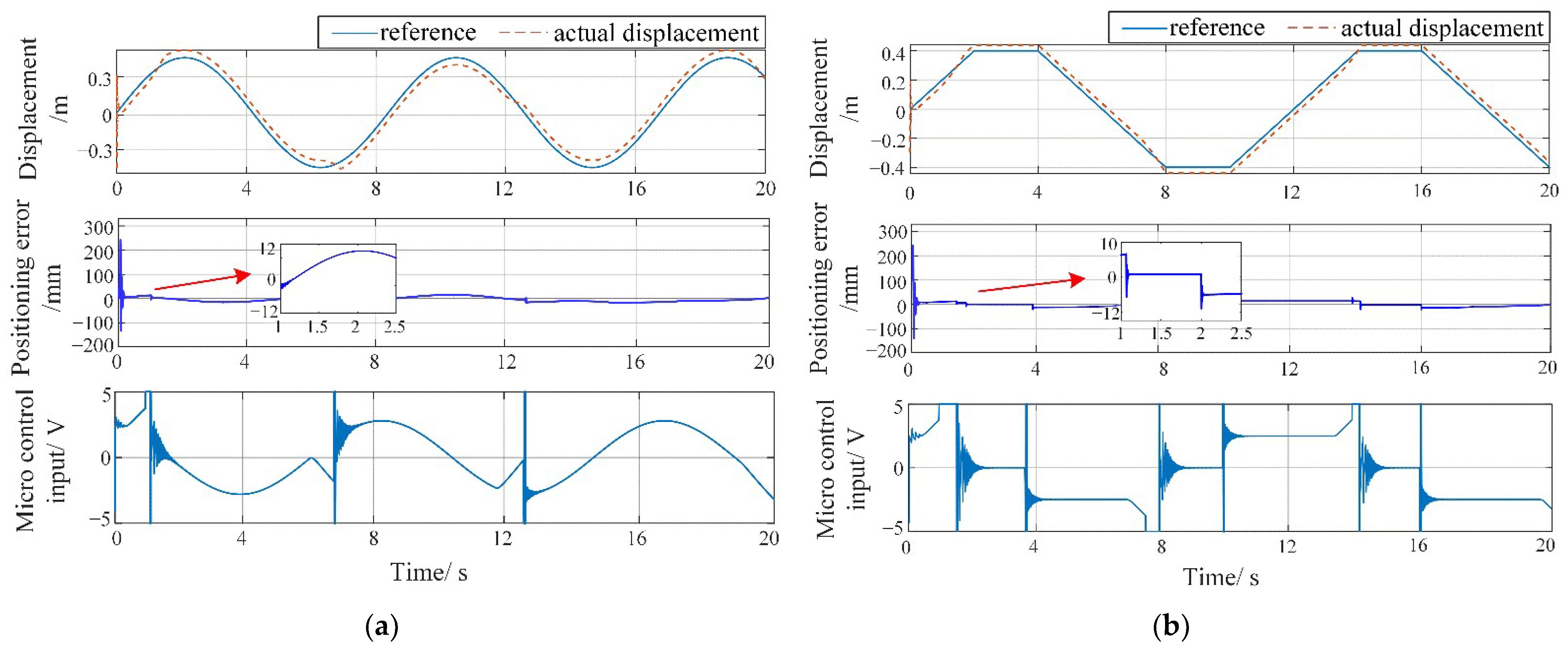
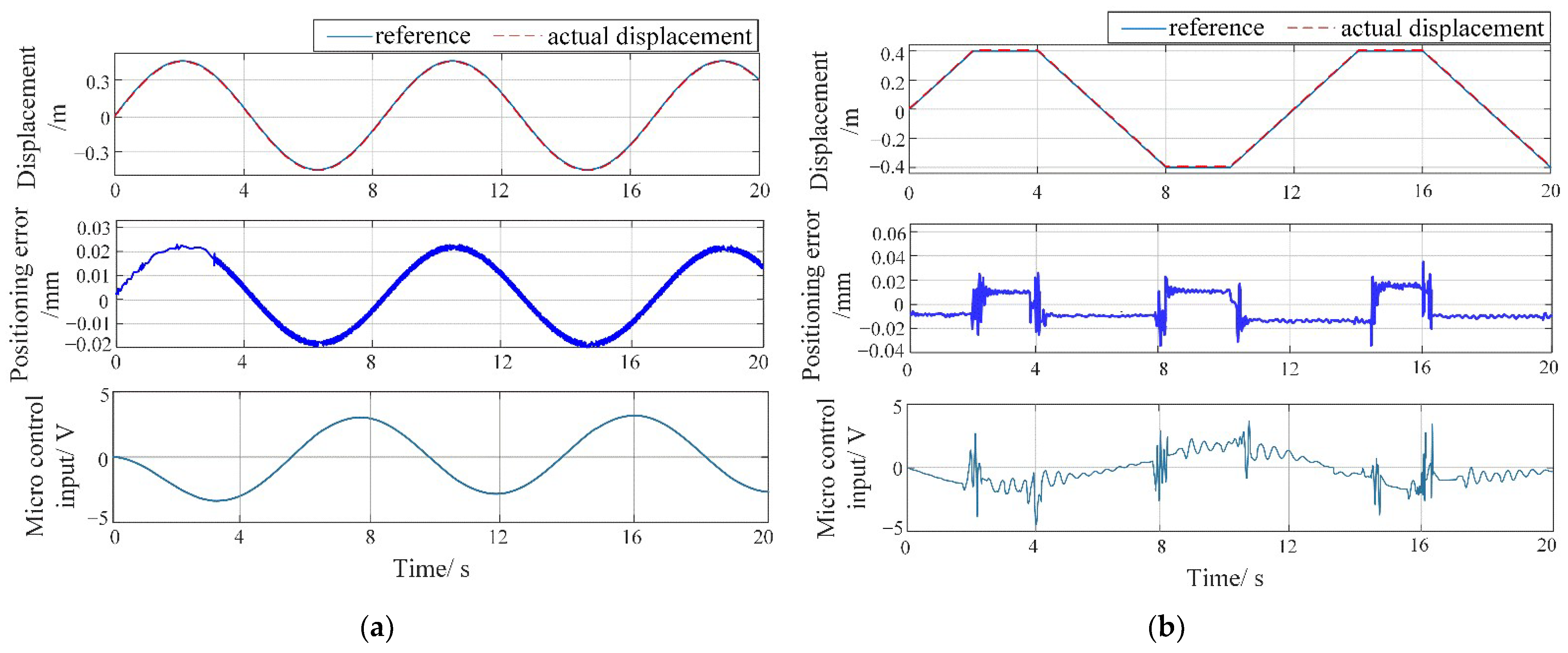
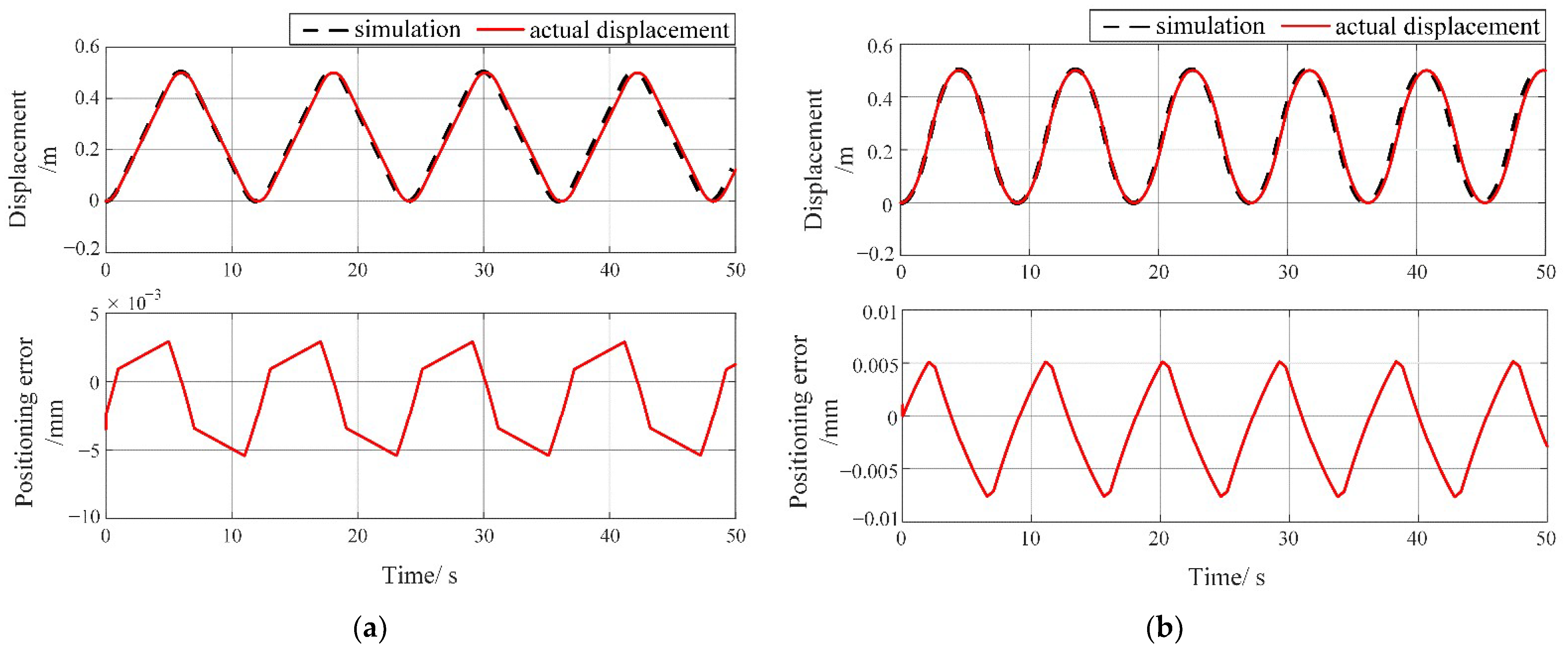
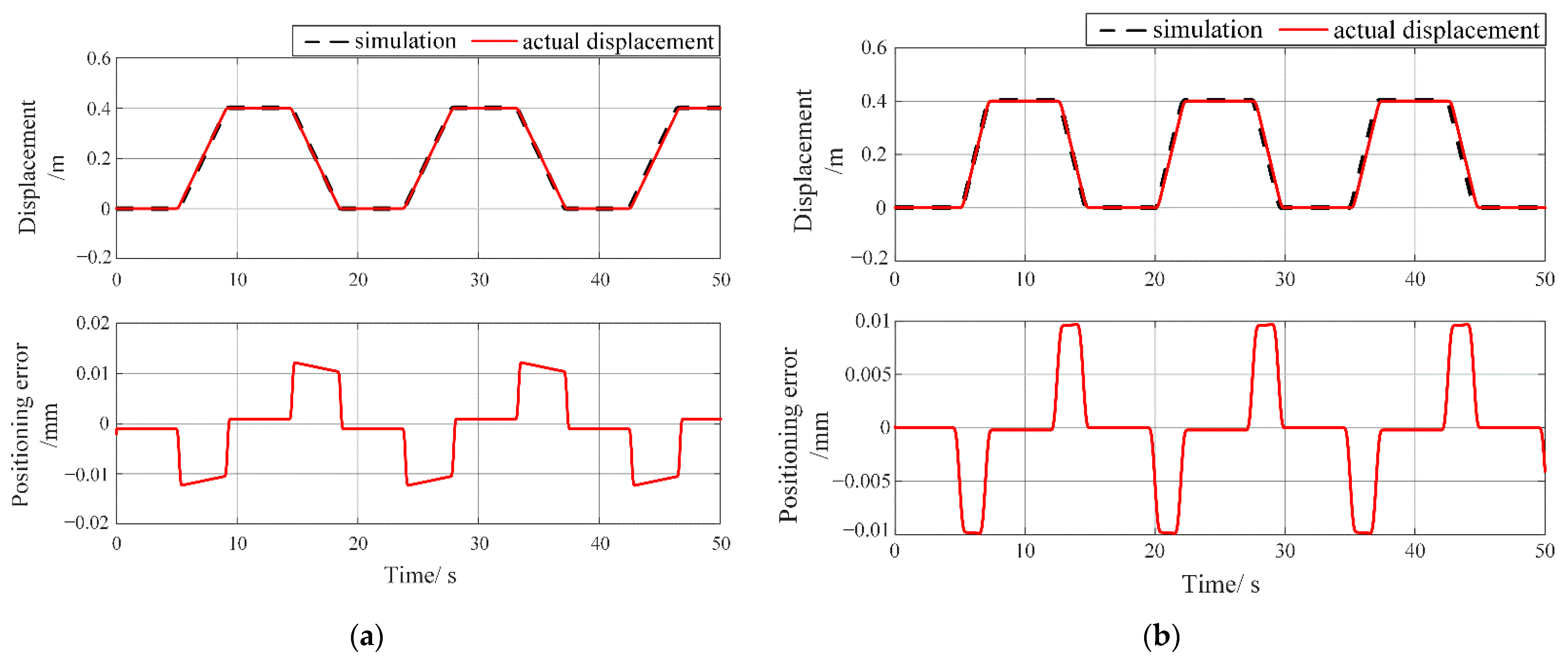
In this paper, a quasi-linear backlash-improved model is first proposed, and the dynamic model of the macro–micro dual-drive motion platform, including the combined effect of the backlash and macro–micro coupling, is also established. Secondly, in order to accurately estimate the backlash effect online for compensation, a stepwise nonlinear identification method based on the quasi-linear model is proposed accordingly. Then, a decoupling adaptive integral sliding mode compound control strategy is designed, associated with online backlash compensation to realize micron-level accuracy for macro–micro cooperative motion under the influence of backlash and coupling. Simulation and experimental results both show that the motion states can converge to a tiny neighborhood of the actual value within 0.2 s during online estimation, and the average identification error of backlash parameters is about 6.3% by adopting the proposed identification method. By combining backlash compensation, simulation results demonstrate that the platform’s positioning accuracy under sinusoidal and trapezoidal reference signals reaches an average 20 μm and 18 μm with a stroke of 1 m and 0.8 m, respectively, and its corresponding average positioning errors have been reduced to 0.015% and 0.018% when utilizing the DSMC strategy, which outperforms the results under the traditional PID method. In summary, the proposed control strategy combined with this identification method can significantly improve the positioning accuracy of this kind of macro–micro dual-drive motion platform under general working conditions.
In further research, our test rig will be upgraded, and validation experiments on the DSMC strategy will still be carried out once test conditions allow. Subsequently, other considerations related to high-precision positioning performance and printing efficiency, such as dismatched environmental disturbance suppression, multi-axis path planning for ultra large-area printing, top-level safety-critical cooperative positioning control design, etc., will be taken into account based on current research results to further enhance both the control performance and industrial practicality of this kind of system applied in large-scale OLED/Micro-LED inkjet printing equipment.