High-Speed Design with Separated Tapering for Reducing Cogging Torque and Torque Ripple of a 3 kW Dry Vacuum Pump Motor for the ETCH Process
Abstract
:1. Introduction
2. Features of Concentrated Winding V-IPMSM for High Speed
3. Separated Tapering Design Process and Principles for ETCH Dry Vacuum Pump Motor
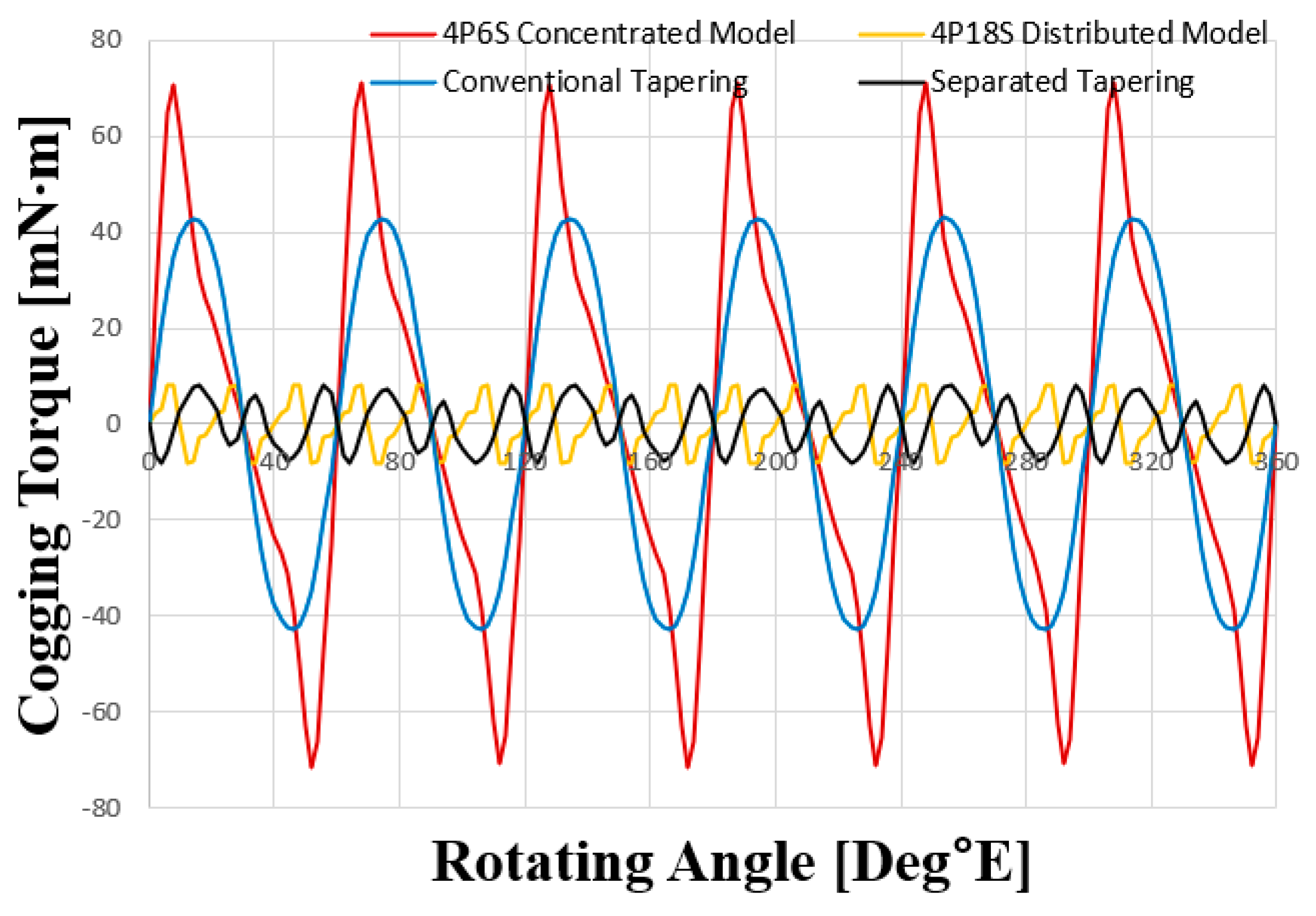
4. Results
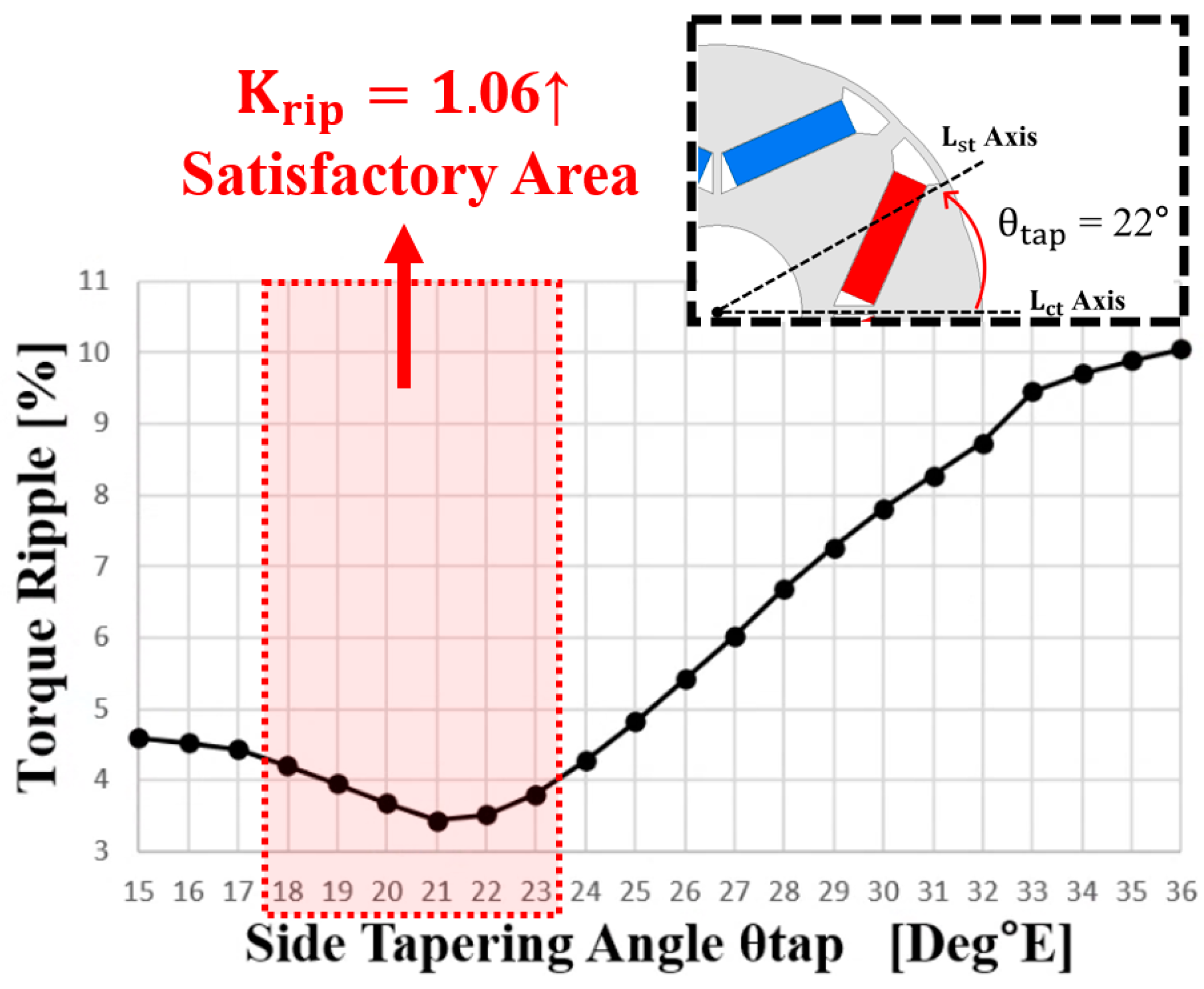
4.1. Data Analysis with Tapering Parameters
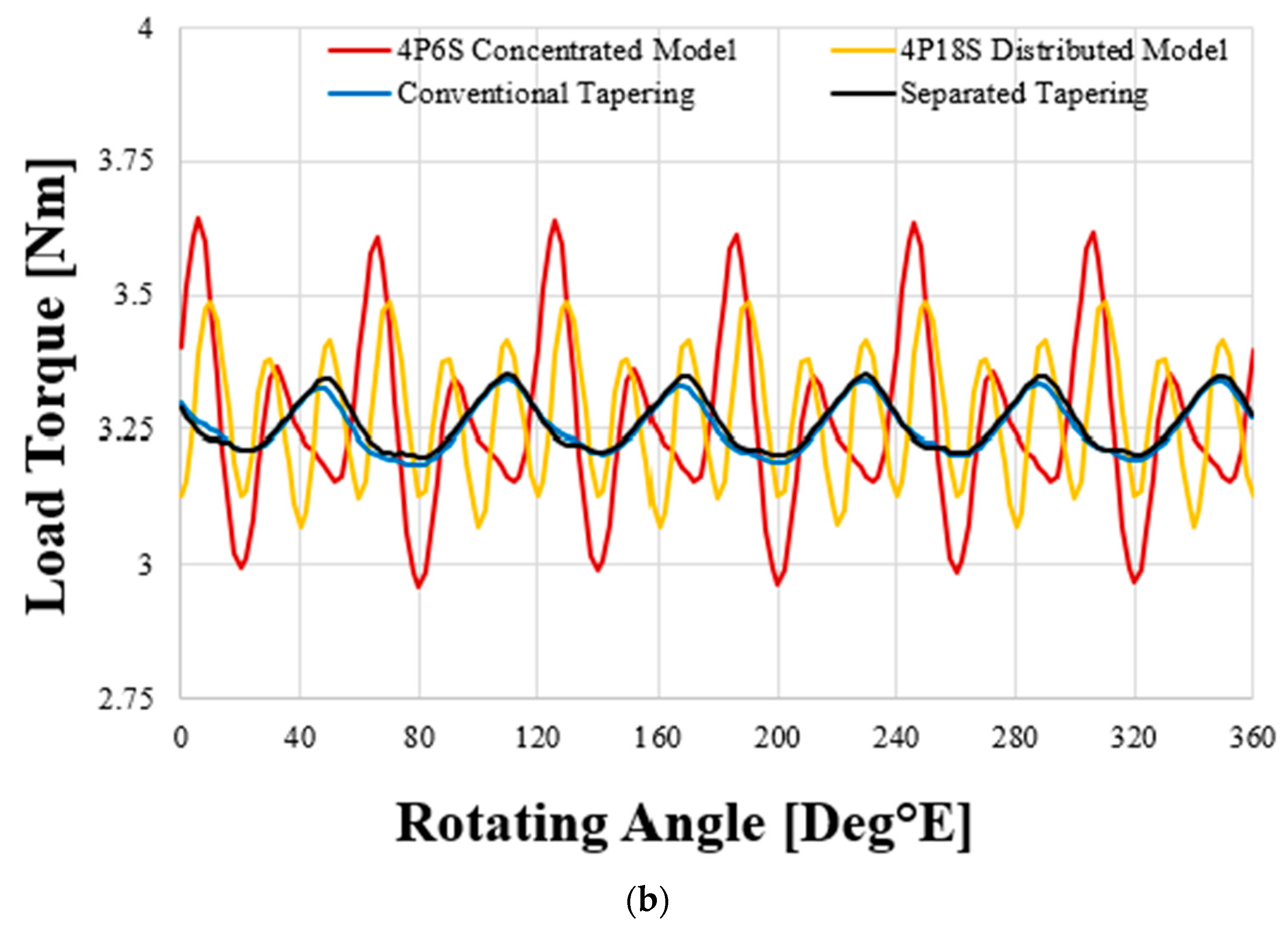
4.2. Comparison of Analysis Data at Two Operation Points of 6600 rpm and 9000 rpm
4.3. Analysis of B Plots, and Demagnetization of Permanent Magnet Check
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, J.; Zhang, L.; Meng, D.; Su, H. Simulation, Verification and Optimization Design of Electromagnetic Vibration and Noise of Permanent Magnet Synchronous Motor for Vehicle. Energies 2022, 15, 5808. [Google Scholar] [CrossRef]
- Alharkan, H. Torque Ripple Minimization of Variable Reluctance Motor Using Reinforcement Dual NNs Learning Architecture. Energies 2023, 16, 4839. [Google Scholar] [CrossRef]
- Lee, M.; Hwang, Y.; Nam, K. Torque Ripple Minimizing of Uniform Slot Machines with Delta Rotor via Subdomain Analysis. Energies 2021, 14, 7390. [Google Scholar] [CrossRef]
- Qu, C.; Guo, Z.; Hu, Y.; Wang, X.; Han, F. Multi-Objective Optimization Design of a New Permanent Magnet Synchronous Motor Based on the Taguchi Method. Energies 2022, 15, 7347. [Google Scholar] [CrossRef]
- Caruso, M.; Di Tommaso, A.O.; Miceli, R.; Viola, F. A Cogging Torque Minimization Procedure for Interior Permanent Magnet Synchronous Motors Based on a Progressive Modification of the Rotor Lamination Geometry. Energies 2022, 15, 4956. [Google Scholar] [CrossRef]
- Tao, X.; Takemoto, M.; Tsunata, R.; Ogasawara, S. Novel Rotor Structure Employing Large Flux Barrier and Disproportional Airgap for Enhancing Efficiency of IPMSM Adopting Concentrated Winding Structure. IEEE Access 2023, 11, 2848–2862. [Google Scholar] [CrossRef]
- Lee, C.-S.; Kim, H.-J. Harmonic Order Analysis of Cogging Torque for Interior Permanent Magnet Synchronous Motor Considering Manufacturing Disturbances. Energies 2022, 15, 2428. [Google Scholar] [CrossRef]
- Akiki, P.; Hassan, M.H.; Bensetti, M.; Dessante, P.; Vannier, J.C.; Prieto, D.; McClelland, M. Multiphysics Design of a V-Shape IPM Motor. IEEE Trans. Energy Convers. 2018, 33, 1141–1153. [Google Scholar] [CrossRef]
- Egorov, D.; Petrov, I.; Pyrhönen, J.J.; Link, J.; Stern, R.; Sergeant, P.; Sarlioglu, B. Hysteresis Loss in NdFeB Permanent Magnets in a Permanent Magnet Synchronous Machine. IEEE Trans. Ind. Electron. 2022, 69, 121–129. [Google Scholar] [CrossRef]
- Hwang, S.-W.; Lim, M.-S.; Hong, J.-P. Hysteresis Torque Estimation Method Based on Iron-Loss Analysis for Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2016, 52, 8204904. [Google Scholar] [CrossRef]
- Liu, G.; Liu, M.; Zhang, Y.; Wang, H.; Gerada, C. High-Speed Permanent Magnet Synchronous Motor Iron Loss Calculation Method Considering Multiphysics Factors. IEEE Trans. Ind. Electron. 2020, 67, 5360–5368. [Google Scholar] [CrossRef]
- Yamazaki, K.; Seto, Y. Iron loss analysis of interior permanent-magnet synchronous motors-variation of main loss factors due to driving condition. IEEE Trans. Ind. Appl. 2006, 42, 1045–1052. [Google Scholar] [CrossRef]
- Yamazaki, K.; Kumagai, M.; Ikemi, T.; Ohki, S. A Novel Rotor Design of Interior Permanent-Magnet Synchronous Motors to Cope with Both Maximum Torque and Iron-Loss Reduction. IEEE Trans. Ind. Appl. 2013, 49, 2478–2486. [Google Scholar] [CrossRef]
- Yamazaki, K.; Ishigami, H. Rotor-Shape Optimization of Interior-Permanent-Magnet Motors to Reduce Harmonic Iron Losses. IEEE Trans. Ind. Electron. 2010, 57, 61–69. [Google Scholar] [CrossRef]
- Kim, K.-C.; Jeon, S.-H. Analysis on Correlation Between Cogging Torque and Torque Ripple by Considering Magnetic Saturation. IEEE Trans. Magn. 2013, 49, 2417–2420. [Google Scholar] [CrossRef]
- Dosiek, L.; Pillay, P. Cogging Torque Reduction in Permanent Magnet Machines. IEEE Trans. Ind. Appl. 2007, 43, 1565–1571. [Google Scholar] [CrossRef]
- Seo, J.H.; Choi, H.S. Cogging Torque Calculation for IPM Having Single Layer Based on Magnetic Circuit Model. IEEE Trans. Magn. 2014, 50, 8102104. [Google Scholar] [CrossRef]
- Hwang, S.M.; Eom, J.B.; Hwang, G.B.; Jeong, W.B.; Jung, Y.H. Cogging torque and acoustic noise reduction in permanent magnet motors by teeth pairing. IEEE Trans. Magn. 2000, 36, 3144–3146. [Google Scholar] [CrossRef]
- Lukaniszyn, M.; Jagiela, M.; Wrobel, R. Optimization of permanent magnet shape for minimum cogging torque using a genetic algorithm. IEEE Trans. Magn. 2004, 40, 1228–1231. [Google Scholar] [CrossRef]
- Abbaszadeh, K.; Alam, F.R.; Teshnehlab, M. Slot opening optimization of surface mounted permanent magnet motor for cogging torque reduction. Energy Convers. Manag. 2012, 55, 108–115. [Google Scholar] [CrossRef]
- Liu, T.; Huang, S.D.; Gao, J.; Lu, K.Y. Cogging torque reduction by slot-opening shift for permanent magnet machines. IEEE Trans. Magn. 2013, 49, 4028–4031. [Google Scholar] [CrossRef]
- Koh, C.S.; Seol, J.S. New cogging-torque reduction method for brushless permanent-magnet motors. IEEE Trans. Magn. 2003, 39, 3503–3506. [Google Scholar]
- Bianchi, N.; Bolognani, S. Design techniques for reducing the cogging torque in surface-mounted PM motors. IEEE Trans. Ind. Appl. 2002, 38, 1259–1265. [Google Scholar] [CrossRef]
- Bianchini, C.; Immovilli, F.; Lorenzani, E.; Bellini, A.; Davoli, M. Review of design solutions for internal permanent-magnet machines cogging torque reduction. IEEE Trans. Magn. 2012, 48, 2685–2693. [Google Scholar] [CrossRef]
- Islam, R.; Husain, I.; Fardoun, A.; McLaughlin, K. Permanent-magnet synchronous motor magnet designs with skewing for torque ripple and cogging torque reduction. IEEE Trans. Ind. Appl. 2009, 45, 152–160. [Google Scholar] [CrossRef]
- Ishikawa, T.; Slemon, G.R. A method of reducing ripple torque in permanent-magnet motors without skewing. IEEE Trans. Magn. 1993, 29, 2028–2031. [Google Scholar] [CrossRef]

















| Parameter | Value | Unit |
|---|---|---|
| Poles/Slots Speed Current | 4/6 | - |
| 6600~9000 | RPM | |
| 11~18.4 | Arms | |
| Rated power Rated torque | 3 | kW |
| 4.45 | N·m | |
| Airgap length | 0.5 | mm |
| Stator diameter (inner, outer) | 25.5, 50 | mm |
| Rotor diameter (inner, outer) | 8, 25 | mm |
| Stack length | 45 | mm |
| Core | 30PNF1600 | |
| Material | Permanent magnet | N42UH |
| Coil | Copper |
| θtap | Load Torque Tavg (Nm) | Tripple | Krip (Torque/Tripple) |
|---|---|---|---|
| 15 | 4.4926 | 4.58977 | 0.978829 |
| 16 | 4.4898 | 4.530269 | 0.991067 |
| 17 | 4.4867 | 4.430873 | 1.012599 |
| 18 | 4.4833 | 4.202262 | 1.066878 |
| 19 | 4.4786 | 3.949895 | 1.133853 |
| 20 | 4.4736 | 3.683834 | 1.214387 |
| 21 | 4.4688 | 3.44164 | 1.298451 |
| 22 | 4.464 | 3.521505 | 1.26764 |
| 23 | 4.4582 | 3.806469 | 1.171217 |
| 24 | 4.451 | 4.279937 | 1.039969 |
| 25 | 4.4463 | 4.819738 | 0.922519 |
| 26 | 4.4402 | 5.420927 | 0.819085 |
| 27 | 4.4328 | 6.030049 | 0.735118 |
| 28 | 4.4263 | 6.68956 | 0.661673 |
| 29 | 4.4208 | 7.270177 | 0.608073 |
| 30 | 4.4139 | 7.816217 | 0.564711 |
| 31 | 4.4066 | 8.267145 | 0.533026 |
| 32 | 4.4011 | 8.727364 | 0.504287 |
| 33 | 4.4193 | 9.456249 | 0.467342 |
| 34 | 4.4141 | 9.700732 | 0.455028 |
| 35 | 4.4086 | 9.882956 | 0.446081 |
| 36 | 4.4049 | 10.04336 | 0.438588 |
| Parameter | Basic Concentrated Winding Model (Model 1) | Distributed Winding Model (Model 2) | Conventional Tapering Model (Model 3) | Final Separated Tapering Model (Model 4) |
|---|---|---|---|---|
| Cogging torque (mNm) | 142.44 | 16.26 | 176.17 | 16.84 |
| Load torque (Nm) | 4.49 | 4.44 | 4.45 | 4.46 |
| Torque ripple (%) | 16.03 | 11.32 | 4.2 | 3.55 |
| Krip | 0.28 | 0.39 | 1.06 | 1.26 |
| L2L + IR (Vmax) | 238.97 | 216.73 | 224.22 | 228.02 |
| Current (A) | 13.4 | 14.2 | 19.5 | 18.4 |
| Current density (A/mm2) | 8.53 | 9.42 | 12.35 | 11.71 |
| Output power (kW) | 3.01 | 3.01 | 3.03 | 3.04 |
| Parameter | Basic Concentrated Winding Model (Model 1) | Distributed Winding Model (Model 2) | Conventional Tapering Model (Model 3) | Final Separated Tapering Model (Model 4) |
|---|---|---|---|---|
| Load torque (Nm) | 3.26 | 3.27 | 3.26 | 3.26 |
| Torque ripple (%) | 21.42 | 12.85 | 4.83 | 4.65 |
| Krip | 0.15 | 0.25 | 0.67 | 0.7 |
| L2L + IR (Vmax) | 277.23 | 257.22 | 252.54 | 263.76 |
| Current (A) | 9.7 | 10.4 | 11.7 | 11 |
| Current density (A/mm2) | 6.17 | 6.9 | 7.45 | 7 |
| Output power (kW) | 2.99 | 3.05 | 3.02 | 3.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, D.-H.; Yang, I.-J.; Hong, M.-K.; Jung, D.-H.; Kim, W.-H. High-Speed Design with Separated Tapering for Reducing Cogging Torque and Torque Ripple of a 3 kW Dry Vacuum Pump Motor for the ETCH Process. Machines 2023, 11, 991. https://doi.org/10.3390/machines11110991
Choi D-H, Yang I-J, Hong M-K, Jung D-H, Kim W-H. High-Speed Design with Separated Tapering for Reducing Cogging Torque and Torque Ripple of a 3 kW Dry Vacuum Pump Motor for the ETCH Process. Machines. 2023; 11(11):991. https://doi.org/10.3390/machines11110991
Chicago/Turabian StyleChoi, Do-Hyeon, In-Jun Yang, Min-Ki Hong, Dong-Hoon Jung, and Won-Ho Kim. 2023. "High-Speed Design with Separated Tapering for Reducing Cogging Torque and Torque Ripple of a 3 kW Dry Vacuum Pump Motor for the ETCH Process" Machines 11, no. 11: 991. https://doi.org/10.3390/machines11110991
APA StyleChoi, D.-H., Yang, I.-J., Hong, M.-K., Jung, D.-H., & Kim, W.-H. (2023). High-Speed Design with Separated Tapering for Reducing Cogging Torque and Torque Ripple of a 3 kW Dry Vacuum Pump Motor for the ETCH Process. Machines, 11(11), 991. https://doi.org/10.3390/machines11110991








