Impact of Grid-Connected Inverter Parameters on the Supraharmonic Emissions in Distributed Power Generation Systems
Abstract
:1. Introduction
- Giving mathematical expressions that present the parameters that affect the SH emissions of GCIs;
- Studying the effect of some of the parameters on the emissions of GCIs mathematically by simulation and by experimental studies;
- Studying the effect of parameters’ symmetry and asymmetry of parallel-connected GCIs on the total emissions to the grid;
- Giving a corner stone for studying the propagations and penetration of SH emissions of GCIs in single-phase installations in addition to filtering them out and preventing them from flowing into the grid.
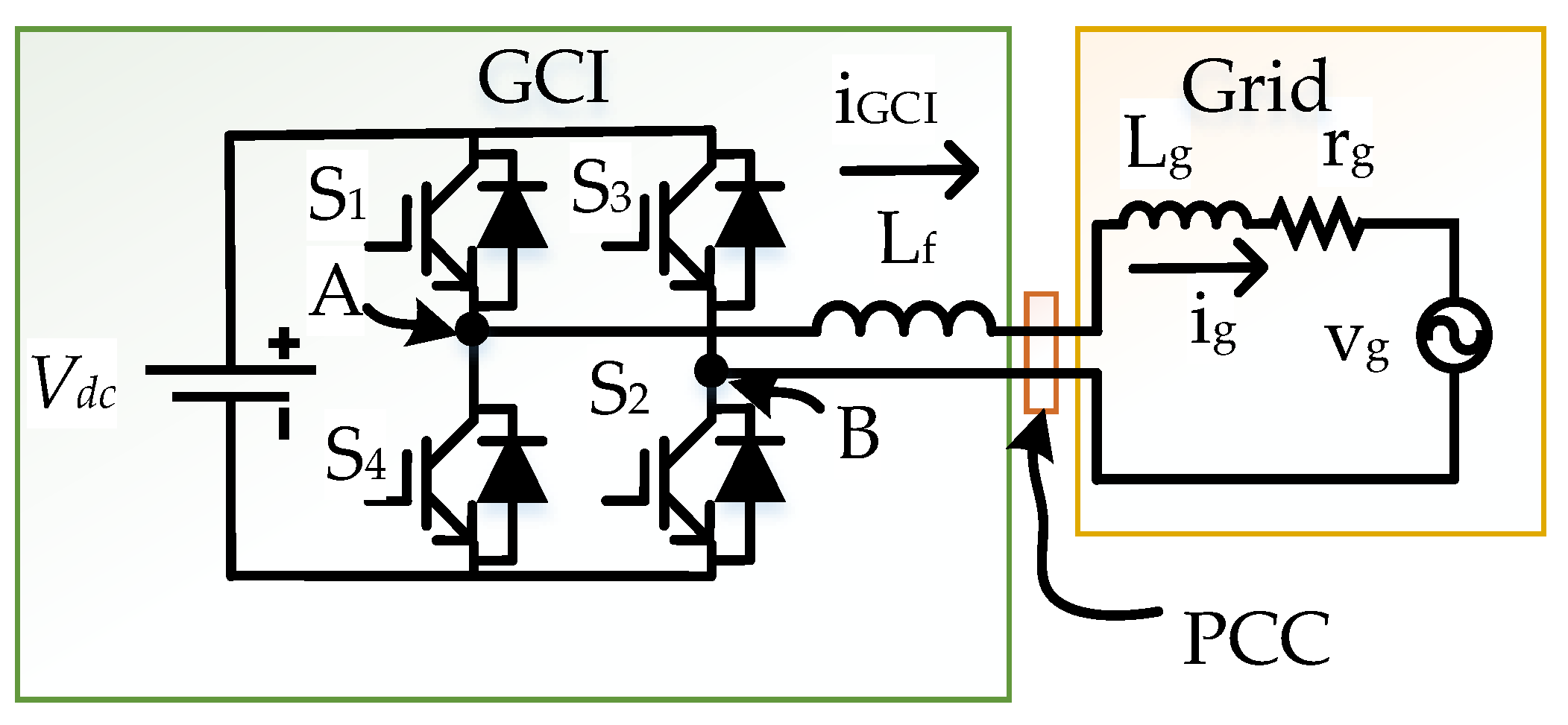
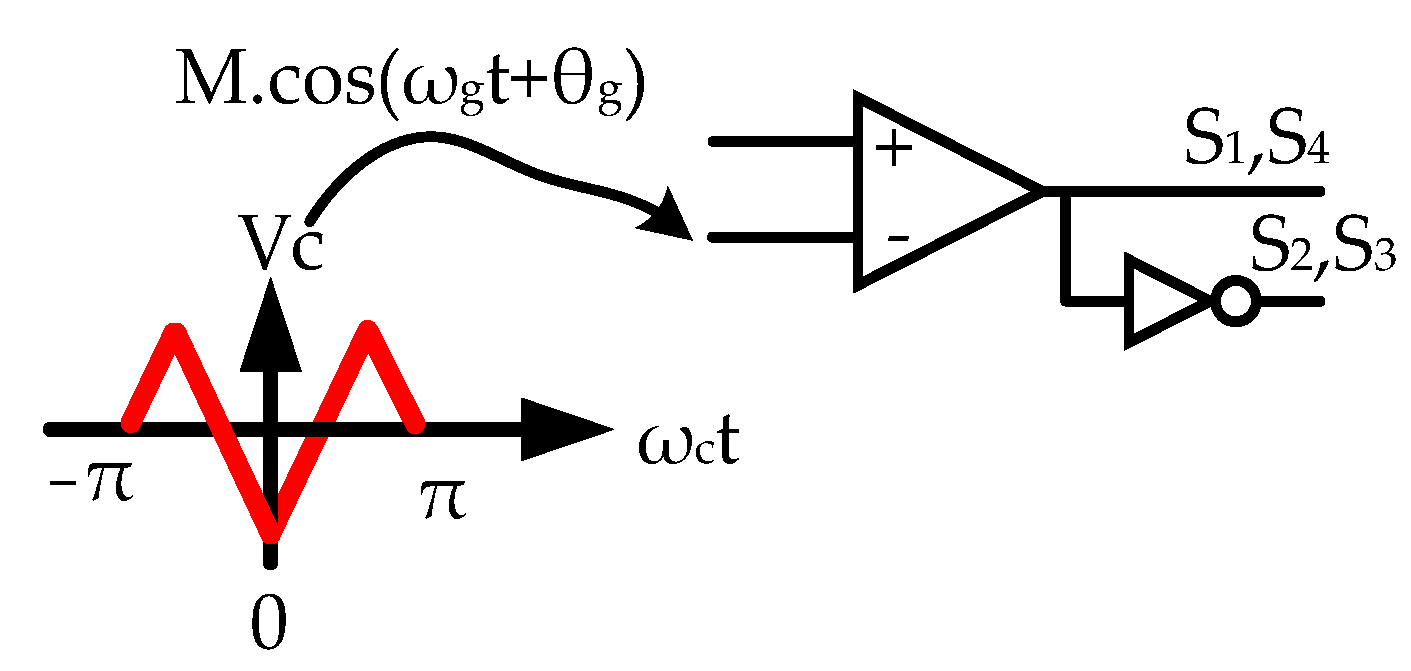
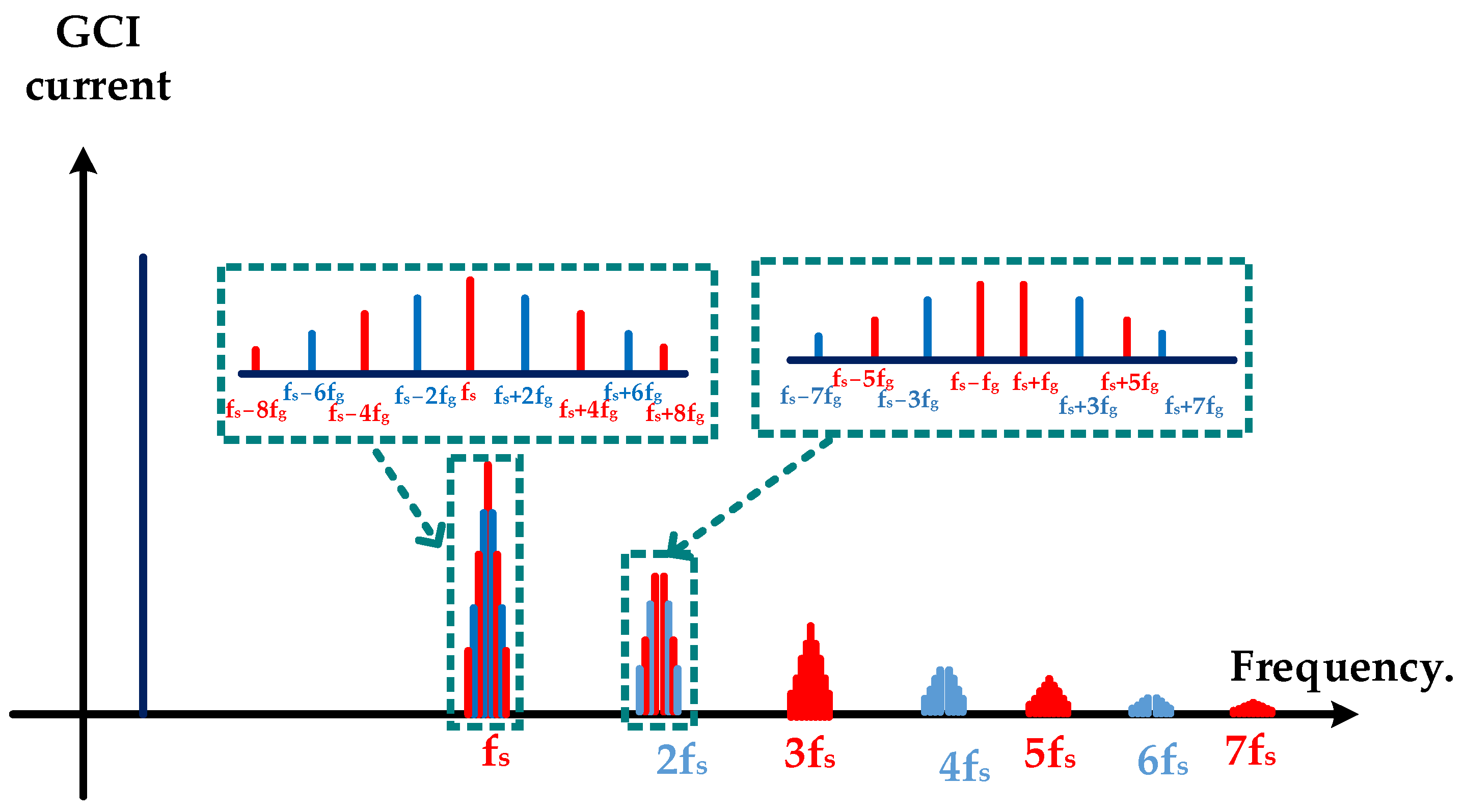
2. SH Emissions of Single-Phase GCI
3. GCI Parameter Effect on the High Frequency Emissions
4. Carrier Phase-Shift Concept to Reduce the Total SH Emissions of Parallel GCIs in DPGSs
5. Simulation Studies
5.1. GCI Model
5.2. Simulation with One GCI
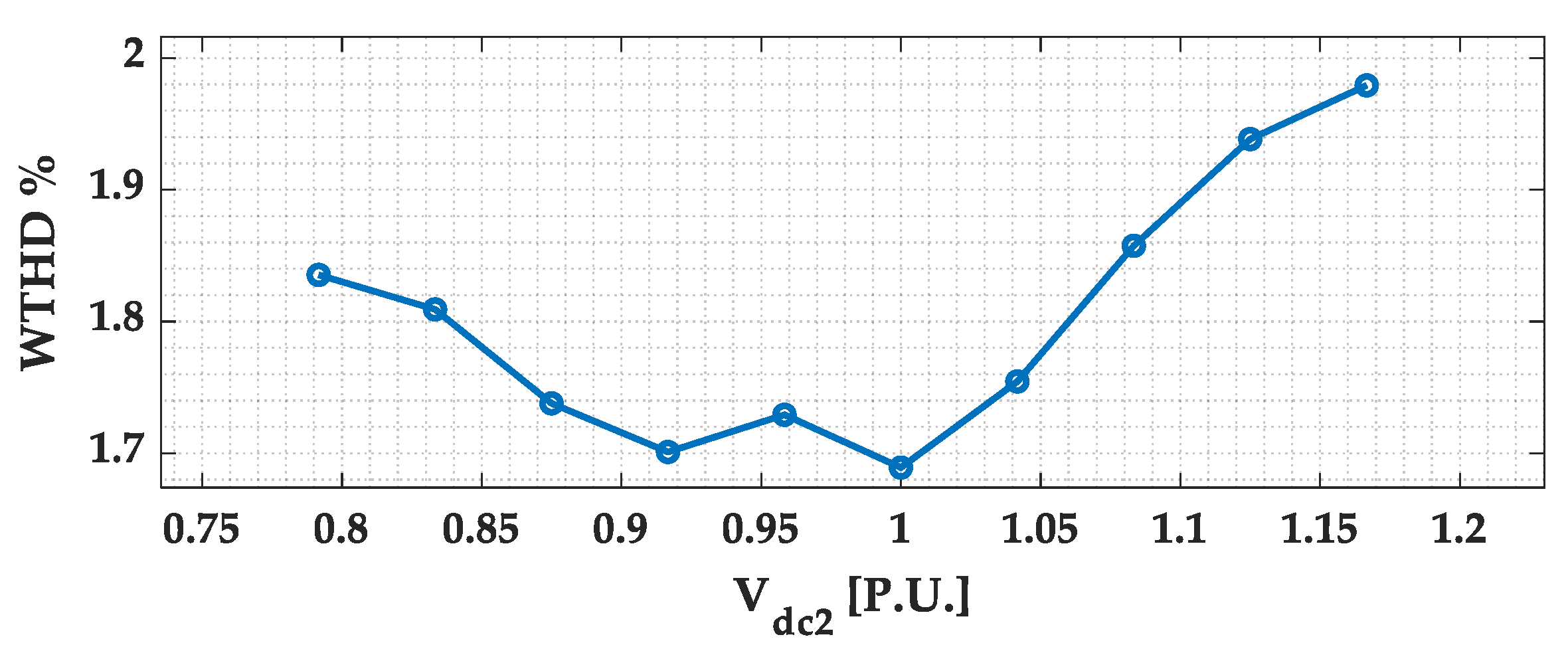
- The amplitude of the SH emissions of single-phase GCIs depends on the DC-link voltage and the coupling filter inductance.
- The relationship between the DC-link voltage and SH emissions amplitudes of GCIs is non-linear.
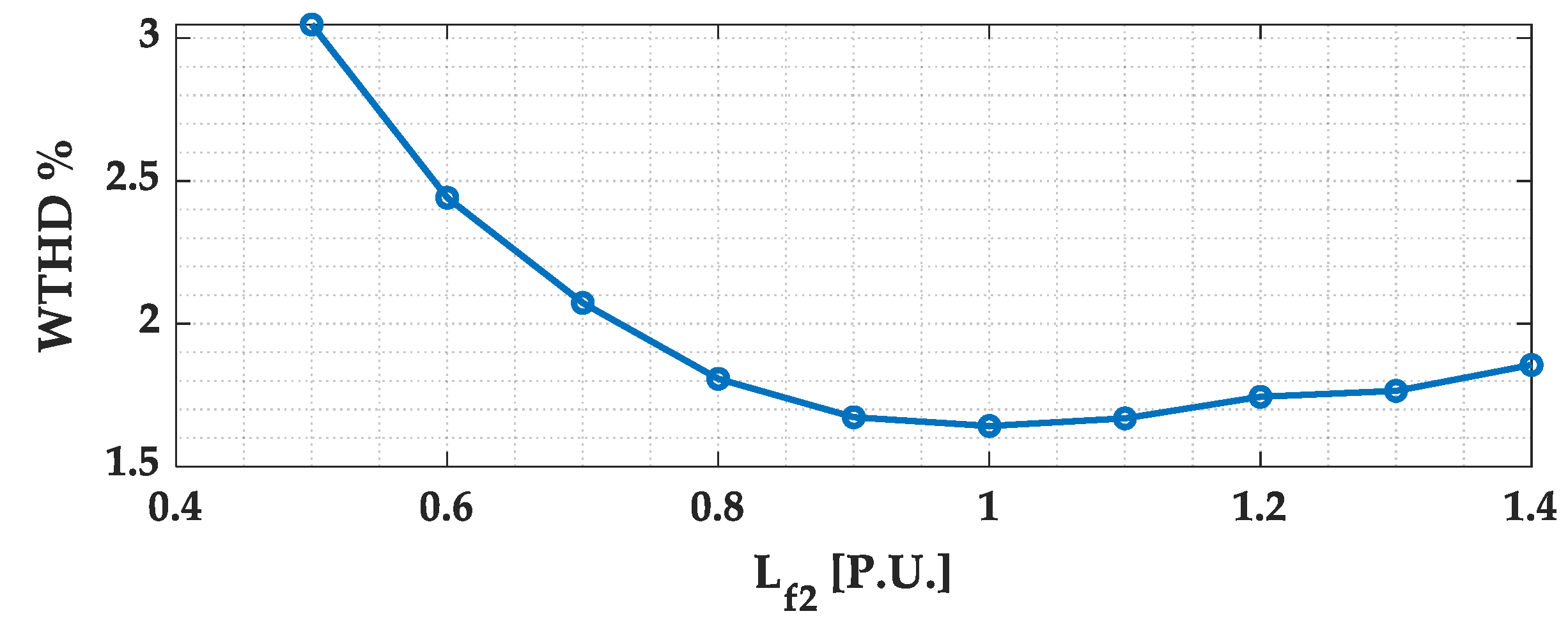
- The amplitudes of the SH emissions of GCIs are in an inverse relationship with the coupling filter inductance.
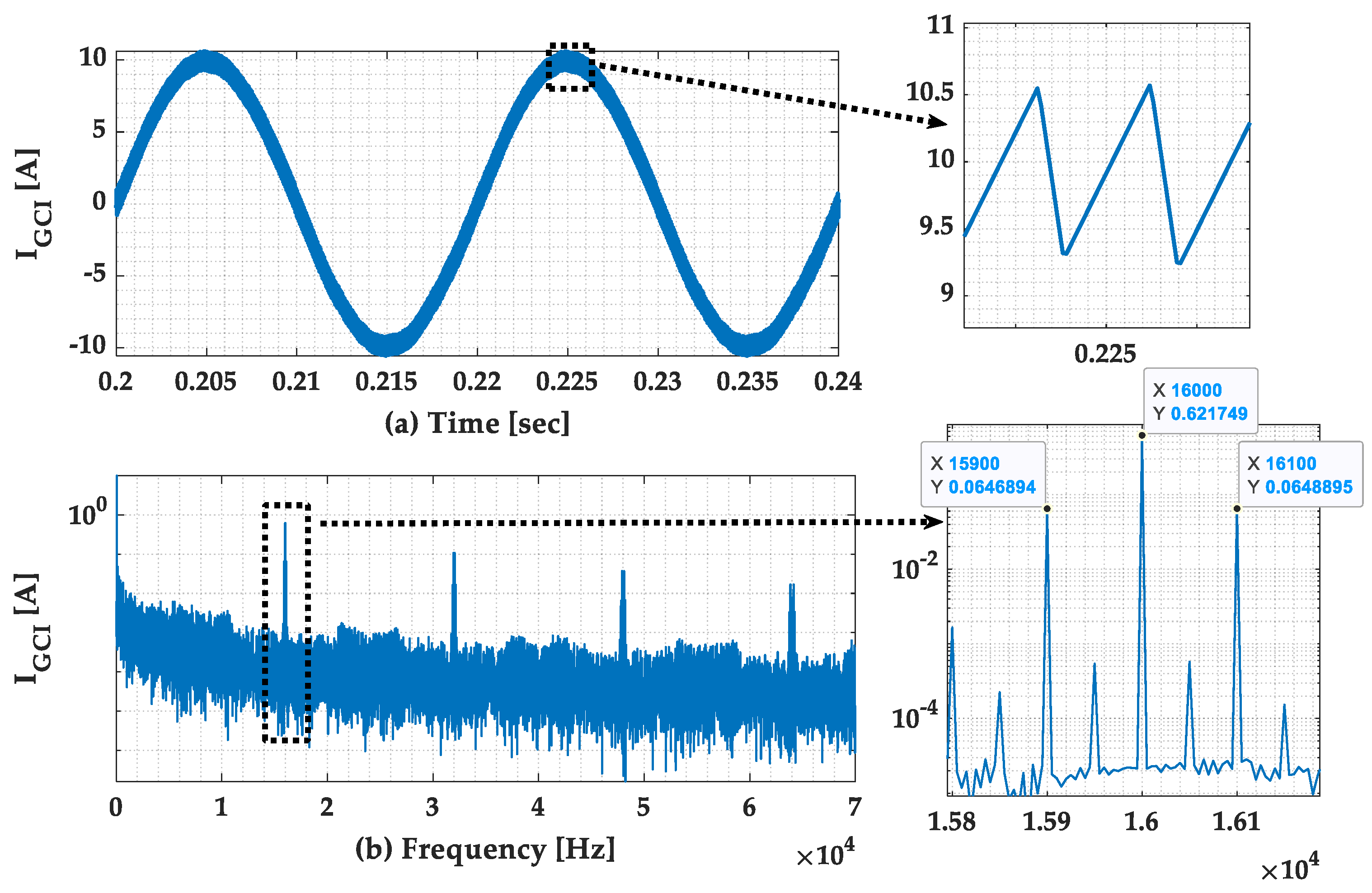
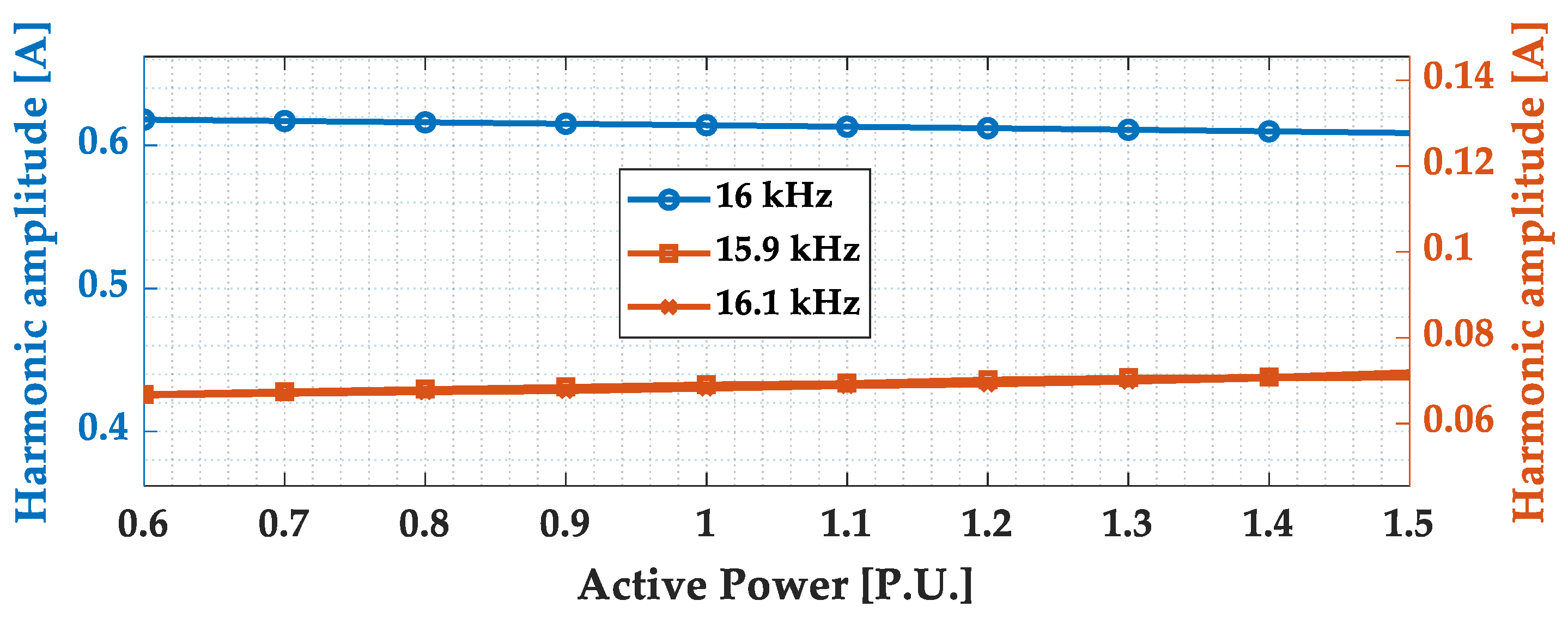
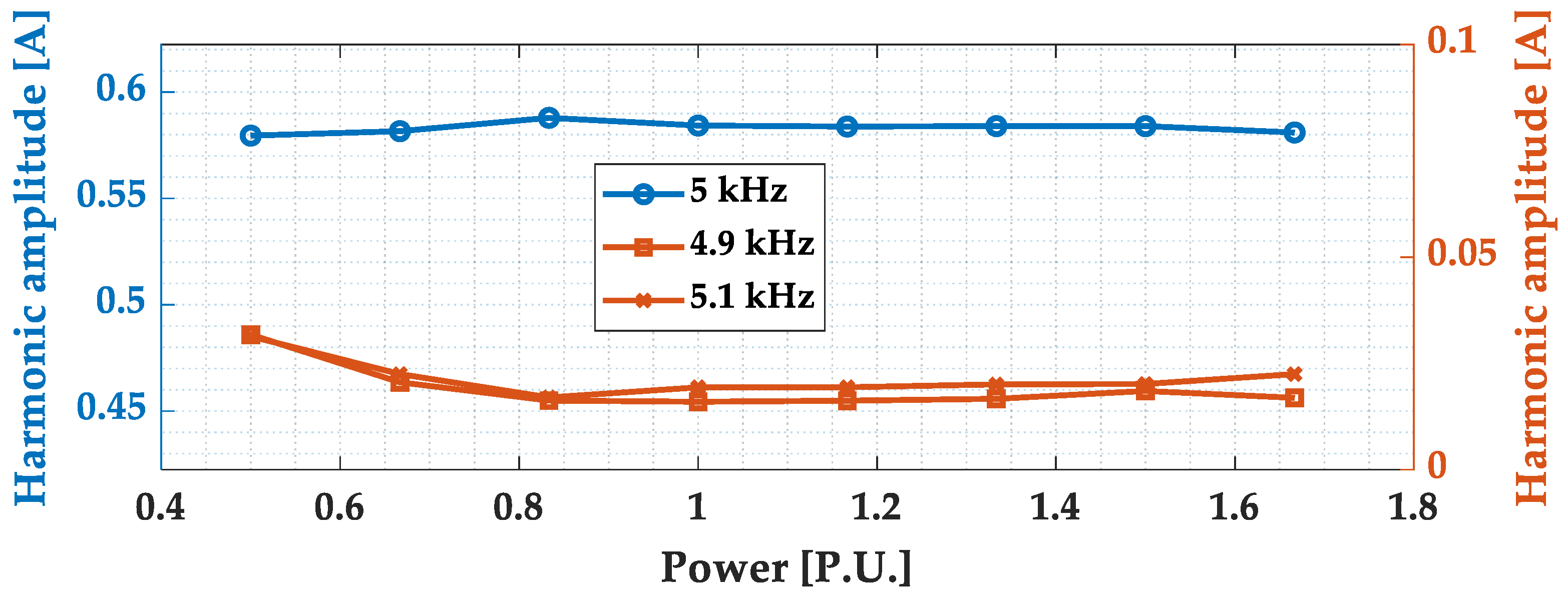
- The amplitude of the SH emissions of single-phase GCIs are independent of the active power variation.
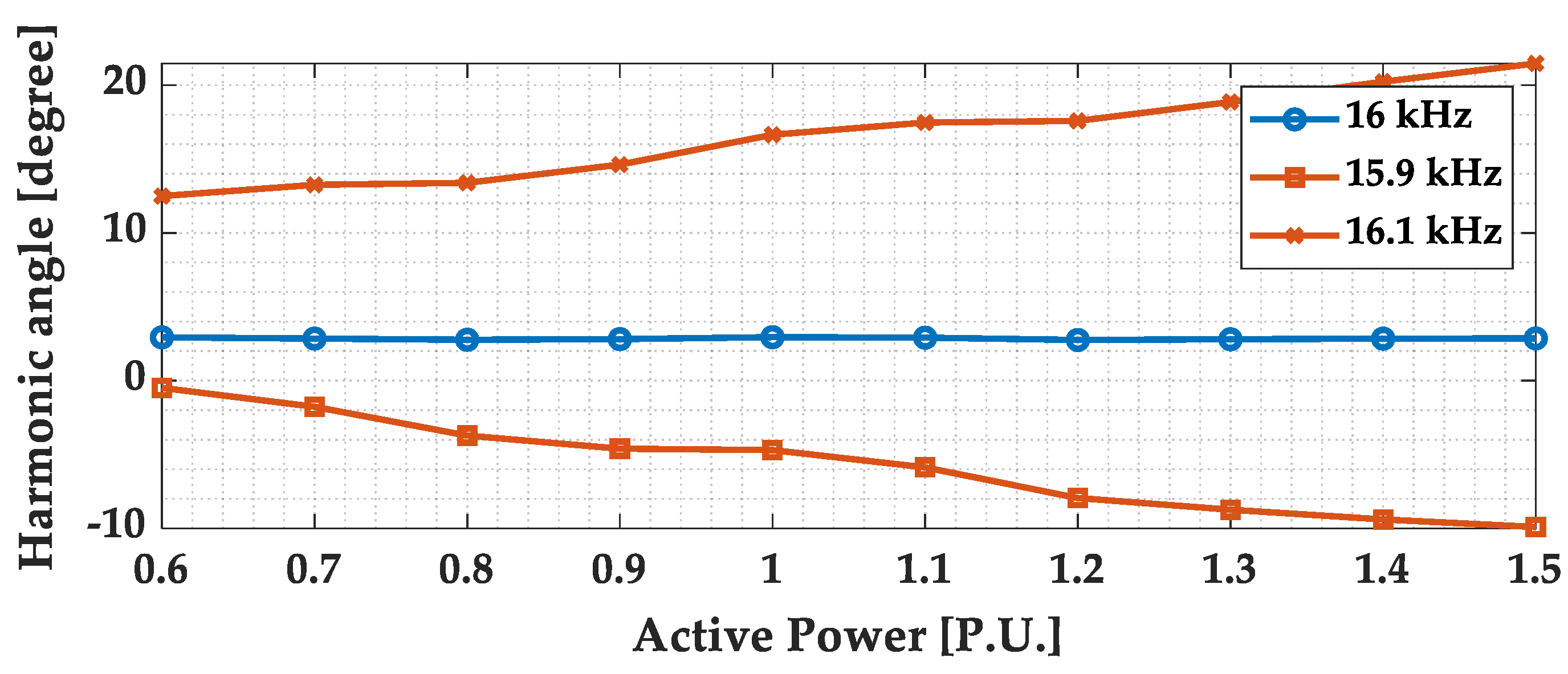
- The phase of the carrier harmonics is independent of the active power variations
- The active power variation affects only the phase of the sideband harmonics.
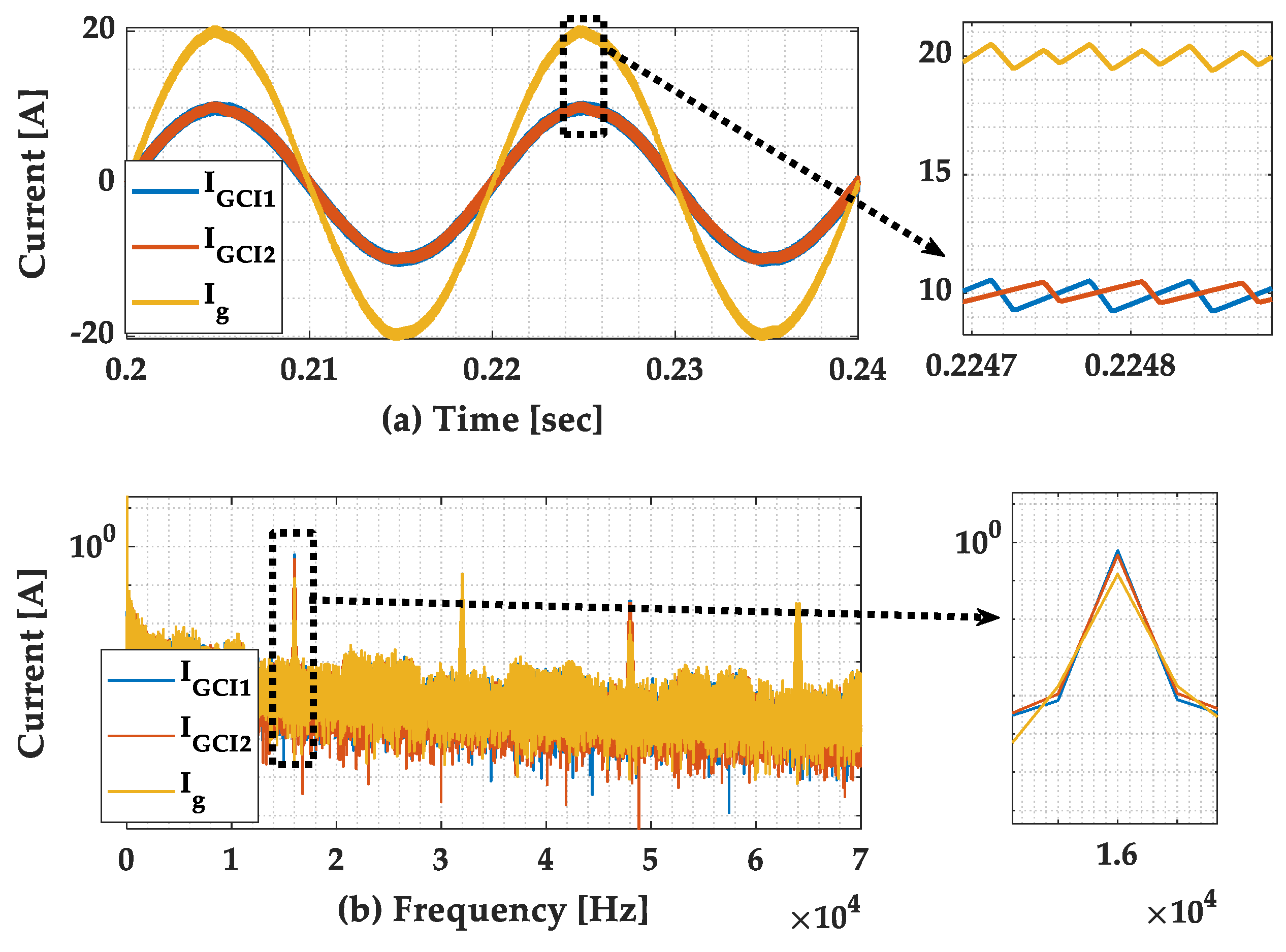
5.3. Simulation with Two Parallel GCIs
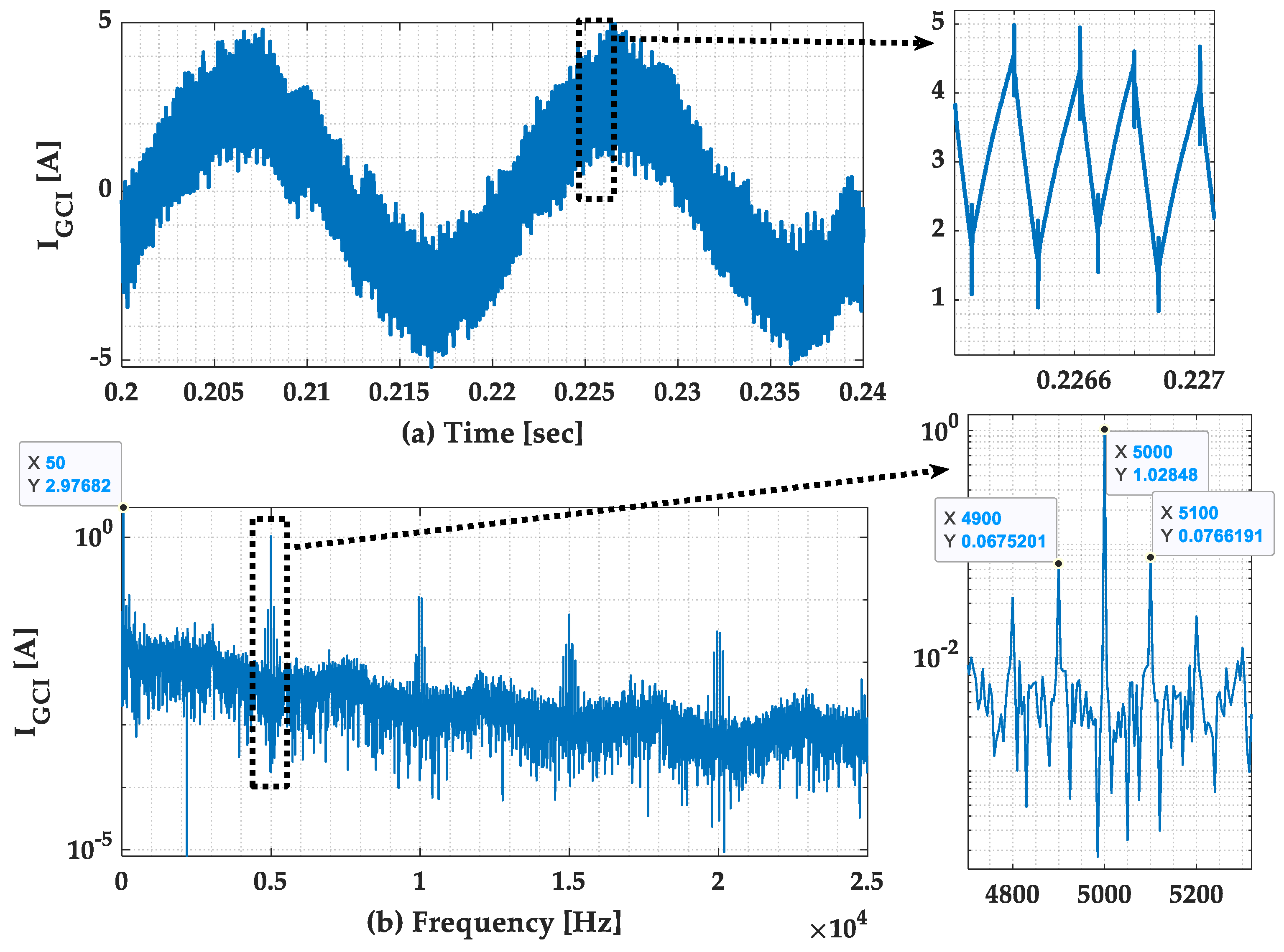
6. Experimental Verifications
6.1. System Description
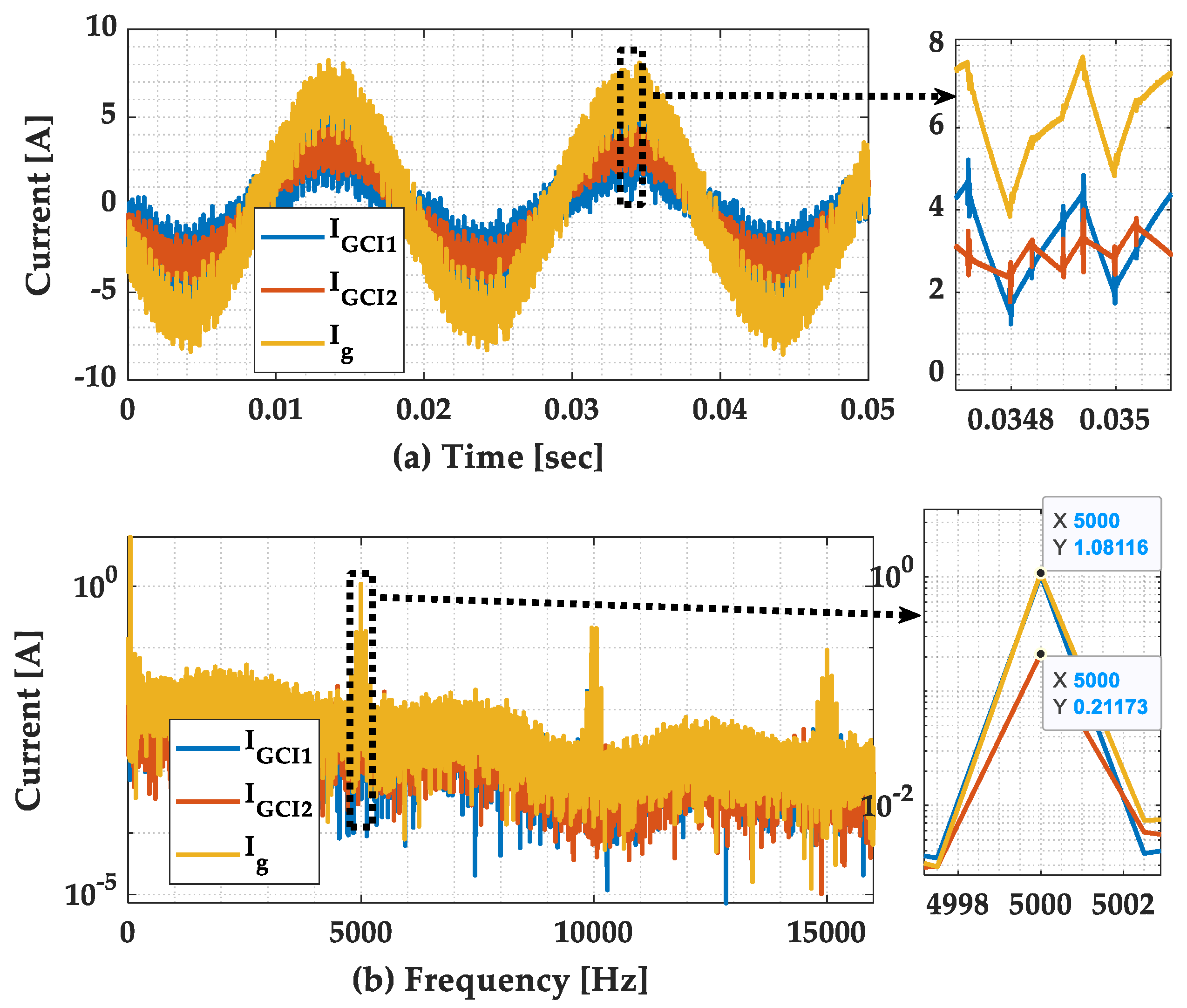
6.2. Study 1: One GCI
6.3. Study 2: Two Parallel GCIs
7. Conclusions and Future Work
- The amplitude of the SH emissions of single-phase GCIs depends on the DC-link voltage and the coupling filter inductance.
- The amplitude of the SH emissions of single-phase GCIs is independent of the active power variation.
- The phase of the carrier harmonics is independent of the active power variations
- The active power variation affects only the phase of the sideband harmonics.
- Studying deeply the propagations and penetrations of SH of single-phase GCIs in low-voltage grids.
- Studying the interference between single-phase GCIs and any other switching converter, such as switched-mode power supplies and LED lamps, at any residential installation.
- Developing active filters to mitigate the emissions of GCIs in the SH range.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DPGS | Distributed power generation system |
| GCI | Grid-connected inverters |
| PCC | Point of common coupling |
| SH | Supraharmonic |
| PV | Photovoltaic |
| PWM | Pulse width modulation |
| HF | High frequency |
| PR | Proportional resonance |
| WTHD | Weighted total harmonic distortion |
Variables
| Inverter output voltage | |
| DC-link voltage | |
| Grid angular frequency—reference signal angular frequency | |
| Grid phase—reference signal phase | |
| Carrier angular frequency | |
| Carrier phase | |
| Modulation index | |
| Bessel function of the first kind | |
| Instantaneous value of the grid voltage | |
| The amplitude of the grid voltage | |
| The load angle | |
| The instantaneous current injected to the grid | |
| The instantaneous fundamental current | |
| The instantaneous carrier switching harmonics | |
| The instantaneous sideband current switching harmonics | |
| The coupling filter inductance | |
| The grid inductance | |
| The coupling filter resistance | |
| The grid resistance | |
| RMS | Root mean square |
| RMS values of fundamental | |
| RMS values of n-order harmonic components |
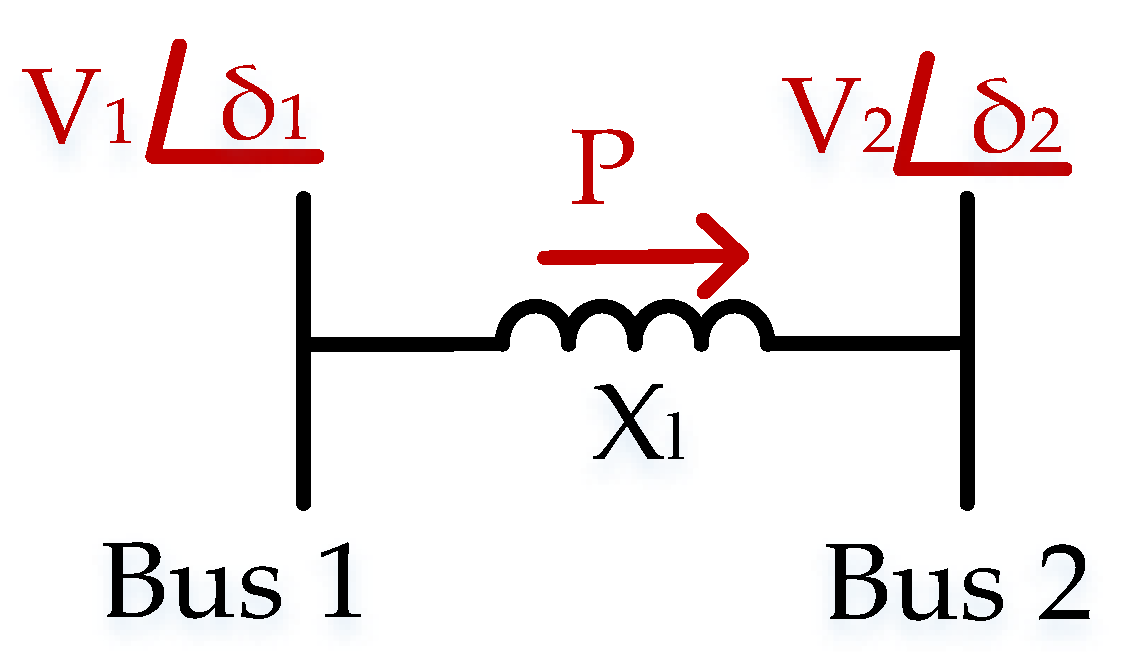
Appendix A. Load Angle Definition in Power Systems
References
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Chen, Z.; Kjaer, S.B. Power electronics as efficient interface in dispersed power generation systems. IEEE Trans. Power Electron. 2004, 19, 1184–1194. [Google Scholar] [CrossRef]
- Meyer, J.; Bollen, M.; Amaris, H.; Blanco, A.M.; de Castro, A.G.; Desmet, J.; Klatt, M.; Kocewiak, Ł.; Rönnberg, S.; Yang, K. Future work on harmonics-some expert opinions Part II-supraharmonics, standards and measurements. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25 May 2014; IEEE: Piscataway, NJ, USA; pp. 909–913. [Google Scholar]
- Alfalahi, S.T.; Alkahtani, A.A.; Al-Shetwi, A.Q.; Al-Ogaili, A.S.; Abbood, A.A.; Mansor, M.B.; Fazea, Y. Supraharmonics in power grid: Identification, standards, and measurement techniques. IEEE Access 2021, 9, 103677–103690. [Google Scholar] [CrossRef]
- CLC/TR 50669:2017; Investigation Results on Electromagnetic Interference in the Frequency Range Below 150 kHz. NSAI Standards, Irish Standard Recommendation, S.R. Gelenec: Dublin, Ireland, 2018.
- CLC/TR 50627; Study Report on Electromagnetic Interference between Electrical Equipment/Systems in the Frequency Range Below 150 kHz. NSAI Standards, Irish Standard Recommendation, S.R. NSAI: Dublin, Ireland, 2013.
- Sakar, S.; Rönnberg, S.; Bollen, M.H. Immunity test of LED lamps based on IEC 61000-4 19 and unexpected consequence. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13 May 2018; IEEE: Piscataway, NJ, USA; pp. 1–6. [Google Scholar]
- IEC 61000-4-19:2014; Part 4-19: Testing and Measurement Techniques—Test for Immunity to Conducted, Differential Mode Disturbances and Signalling in the Frequency Range 2 kHz to 150 kHz at a.c. Power Ports. International Electrotechnical Commission: Geneva, Switzerland, 2014.
- Kirchhoff, J.; Klein, G. Results of the OPTINOS project-deficits and uncertainties in photovoltaic inverter test procedure. In Proceedings of the 24th European Photovoltaic Solar Energy Conference and Exhibition 2009, Hamburg, Germany, 21–25 September 2009. [Google Scholar]
- Sakar, S.; Rönnberg, S.; Bollen, M. Interferences in AC–DC LED drivers exposed to voltage disturbances in the frequency range 2–150 kHz. IEEE Trans. Power Electron. 2019, 34, 11171–11181. [Google Scholar] [CrossRef]
- Sakar, S.; Rönnberg, S.K.; Bollen, M. Interharmonic emission in AC–DC converters exposed to nonsynchronized high-frequency voltage above 2 kHz. IEEE Trans. Power Electron. 2020, 36, 7705–7715. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, D.; Xiao, X. Evaluation of supraharmonic emission levels of multiple grid-connected VSCs. IET Gener. Transm. Distrib. 2019, 13, 5597–5604. [Google Scholar] [CrossRef]
- Darmawardana, D.; Perera, S.; Robinson, D.; Ciufo, P.; Meyer, J.; Klatt, M.; Jayatunga, U. Investigation of high frequency emissions (supraharmonics) from small, grid-tied, photovoltaic inverters of different topologies. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13 May 2018; IEEE: Piscataway, NJ, USA; pp. 1–6. [Google Scholar]
- Espín-Delgado, Á.; Rönnberg, S. Modeling and Analysis of Supraharmonic Propagation for Stochastic Studies. IEEE Trans. Power Deliv. 2022, 37, 4899–4910. [Google Scholar] [CrossRef]
- Menti, A.; Barkas, D.; Kaminaris, S.; Psomopoulos, C.S. Supraharmonic emission from a three-phase PV system connected to the LV grid. Energy Rep. 2021, 7, 527–542. [Google Scholar] [CrossRef]
- Darmawardana, D.; Perera, S.; Robinson, D.; Meyer, J.; Jayatunga, U. Important Considerations in Development of PV Inverter Models for High Frequency Emission (Supraharmonic) Studies. In Proceedings of the 2020 19th International Conference on Harmonics and Quality of Power (ICHQP), Dubai, United Arab Emirates, 6 July 2020; IEEE: Piscataway, NJ, USA; pp. 1–6. [Google Scholar]
- Espín-Delgado, Á.; Busatto, T.; Ravindran, V.; Rönnberg, S.K.; Meyer, J. Evaluation of supraharmonic propagation in LV networks based on the impedance changes created by household devices. In Proceedings of the 2020 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), The Hague, The Netherlands, 26 October 2020; IEEE: Piscataway, NJ, USA; pp. 754–758. [Google Scholar]
- Aboutaleb, A.M.; Roumeliotis, G.G.; Desmet, J.; Knockaert, J. Analysis of transmission line modelling in the MATLAB/Simscape software package. In Proceedings of the 27th International Conference on Electricity Distribution (CIRED 2023), Rome, Italy, 12–15 June 2023; Institution of Engineering and Technology (IET): London, UK, 2023; pp. 4009–4013. [Google Scholar] [CrossRef]
- Rönnberg, S.; Bollen, M. Measurements of primary and secondary emission in the supraharmonic frequency range, 2–150 kHz. In Proceedings of the International Conference and Exhibition on Electricity Distribution, Guangzhou, China, 15–18 June 2015. [Google Scholar]
- Rönnberg, S.K.; Bollen, M.H.J.; Amaris, H.; Chang, G.W.; Gu, I.Y.H.; Kocewiak, Ł.H.; Meyer, J.; Olofsson, M.; Ribeiro, P.F.; Desmet, J. On waveform distortion in the frequency range of 2–150 kHz-Review and research challenges. Electr. Power Syst. Res. 2017, 150, 1–10. [Google Scholar] [CrossRef]
- Solatialkaran, D.; Khajeh, K.G.; Zare, F. A novel filter design method for grid-tied inverters. IEEE Trans. Power Electron. 2020, 36, 5473–5485. [Google Scholar] [CrossRef]
- He, S.; Liu, B. Distributed Carrier Phase Shifting Control Method for Modular Interleaved Parallel Inverters. IEEE Trans. Transp. Electrif. 2022, 9, 2497–2508. [Google Scholar] [CrossRef]
- Poon, J.; Johnson, B.; Dhople, S.V.; Rivas-Davila, J. Decentralized carrier phase shifting for optimal harmonic minimization in asymmetric parallel-connected inverters. IEEE Trans. Power Electron. 2020, 36, 5915–5925. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- IEEE Std 519-2014 (Revision of IEEE Std 519-1992); IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2014; pp. 1–29. [CrossRef]








| Parameter | Value |
|---|---|
| DC-link voltage | 600 V |
| Switching frequency | 16 kHz |
| Coupling filter inductance | , 10 mH |
| Injected active power | 1.6263 kW |
| Grid impedance | |
| Grid voltage and frequency | 230 Vrms, 50 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aboutaleb, A.M.; Desmet, J.; Knockaert, J. Impact of Grid-Connected Inverter Parameters on the Supraharmonic Emissions in Distributed Power Generation Systems. Machines 2023, 11, 1014. https://doi.org/10.3390/machines11111014
Aboutaleb AM, Desmet J, Knockaert J. Impact of Grid-Connected Inverter Parameters on the Supraharmonic Emissions in Distributed Power Generation Systems. Machines. 2023; 11(11):1014. https://doi.org/10.3390/machines11111014
Chicago/Turabian StyleAboutaleb, Abdellatif M., Jan Desmet, and Jos Knockaert. 2023. "Impact of Grid-Connected Inverter Parameters on the Supraharmonic Emissions in Distributed Power Generation Systems" Machines 11, no. 11: 1014. https://doi.org/10.3390/machines11111014
APA StyleAboutaleb, A. M., Desmet, J., & Knockaert, J. (2023). Impact of Grid-Connected Inverter Parameters on the Supraharmonic Emissions in Distributed Power Generation Systems. Machines, 11(11), 1014. https://doi.org/10.3390/machines11111014







