Path Planning Technique for Mobile Robots: A Review
Abstract
:1. Introduction
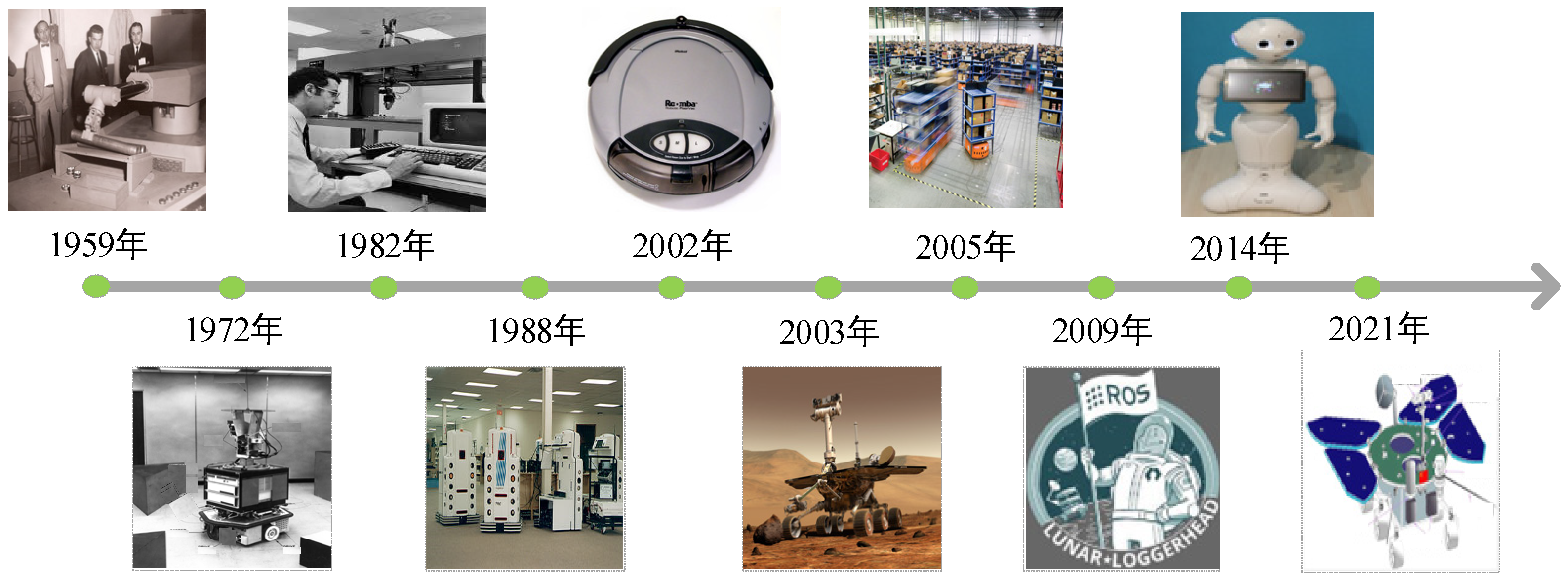
1.1. Evolution of Mobile Robotics
1.2. Contribution of Manuscript
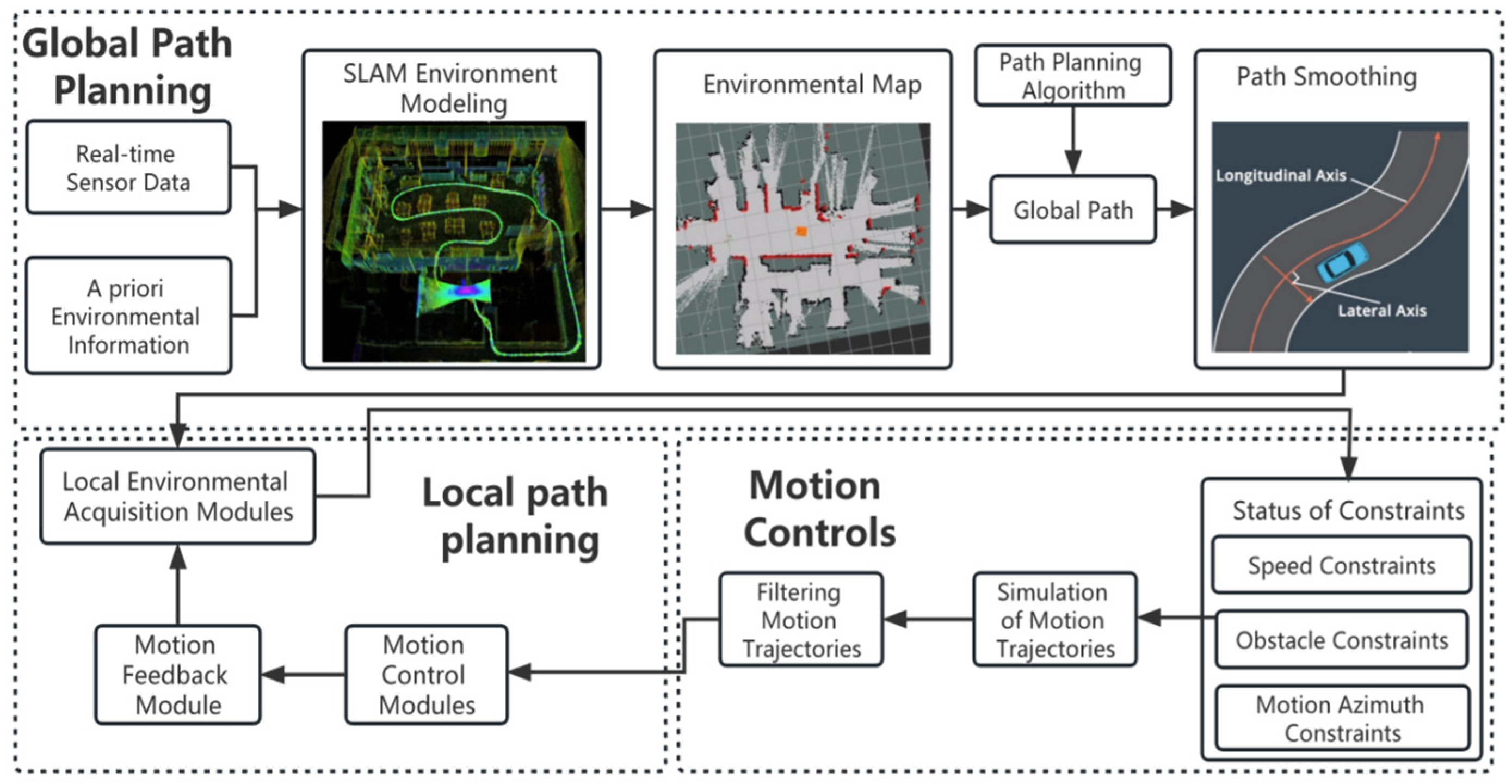
2. Problem Statement
2.1. Working Environment Description of the Robot
2.1.1. SLAM Technology
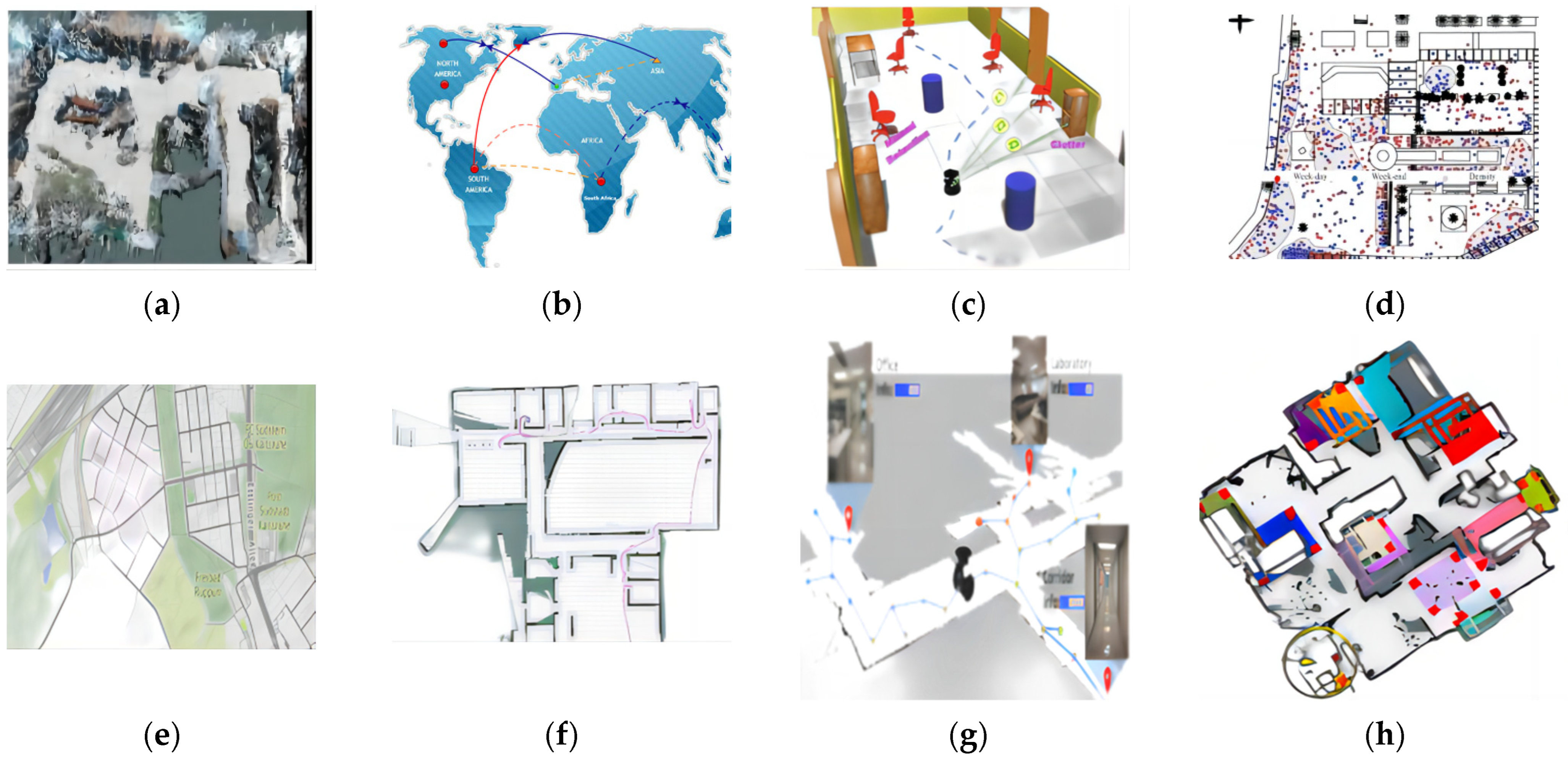
2.1.2. Map Model
- (1)
- Scale Map: Also known as a measurement map, the metric map typically relies on grids or pixels to partition the environment into a series of discrete units. Each unit signifies a state and can represent either free space or obstacles. The metric map can express the physical dimensions of the real world. It encompasses various types such as occupancy grid maps, depth maps, and probabilistic maps.
- (2)
- Topological Map: The description of a robot’s location often does not involve the actual physical dimensions of the world. Instead, it leverages connectivity and distance relationships among different locations to depict the robot’s position. This type of map comprises two main categories: node-based and edge-based topological maps. Topological maps find utility in scenarios where the environment exhibits certain regularities, as seen in city road networks.
- (3)
- Semantic Map: A semantic map is typically feature-based, wherein environmental entities are labeled to enhance the robot’s perception and understanding. This labeling facilitates heightened autonomy and intelligence by imparting a sense of meaning to the robot’s perception of its surroundings.
- (4)
- Behavior Map: Employed to represent a robot’s behavior and task information, the behavior map outlines the actions a robot needs to undertake to accomplish specific tasks. Behavior maps are often generated using robot control systems and planning algorithms, offering utility across decision-making, execution, and autonomous learning applications.
- (1)
- Satellite Map: Leveraging satellite imagery, satellite maps encapsulate ground landscapes to vividly portray actual terrains and natural features such as mountains, forests, lakes, and rivers.
- (2)
- Indoor Map: Specially tailored for navigation within confined environments, indoor maps cater to spaces like shopping complexes, airports, museums, and medical centers. They commonly incorporate intricate floor plans for varying levels, annotated landmarks, directional cues, designated paths, and the precise locations of diverse amenities.
- (3)
- Traffic Map: The domain of traffic maps encompasses roads, traffic signs, signals, and other vehicular infrastructure. Robots adeptly employ these vital data to chart optimal routes, ensuring adherence to traffic regulations and road etiquettes for both safe and efficient navigation.
- (4)
- Hybrid Map: Bridging the attributes of diverse map genres, hybrid maps wield the potential to offer a comprehensive and precise repository of geographic information. These maps are particularly invaluable for navigating complex terrains, facilitating intricate path planning. For instance, integrating a metric map with a topological counterpart can yield precise robot positioning and navigation. Similarly, coupling a semantic map with a behavior map expedites task planning and execution.
2.2. Path Indicators
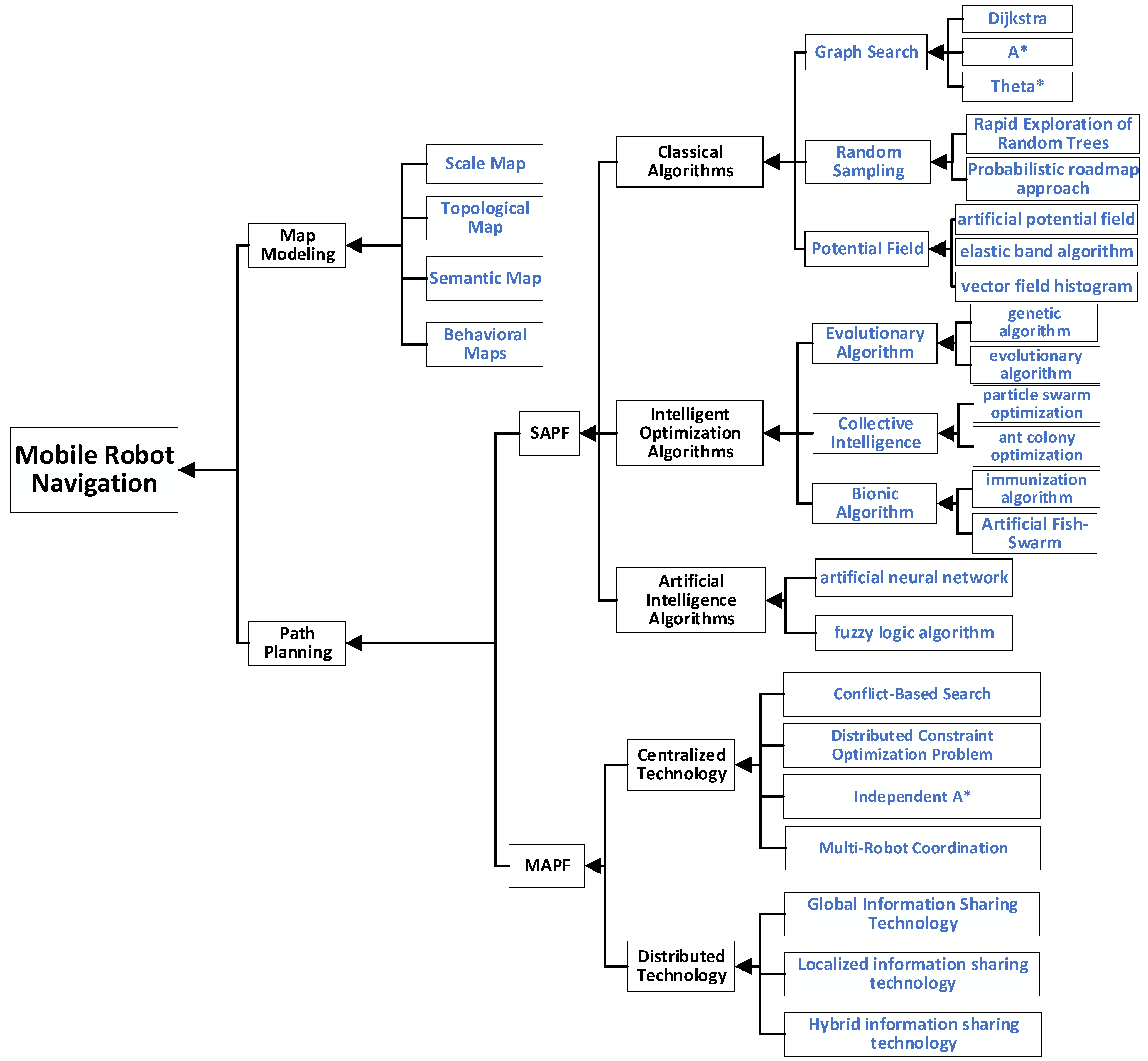
3. Single-Agent Path Planning Algorithm
- (1)
- Classical Algorithms: This category includes graph search algorithms, random sampling algorithms, potential field algorithms, artificial potential field methods, and model predictive control algorithms.
- (2)
- Bio-Inspired Algorithms: The domain of intelligent optimization encompasses this category, incorporating genetic algorithms, ant colony optimization algorithms, particle swarm optimization algorithms, firefly algorithms, bacterial foraging algorithms, cuckoo search algorithms, and artificial bee colony algorithms.
- (3)
- Artificial Intelligence Algorithms: This category primarily comprises algorithms such as fuzzy control algorithms and neural network algorithms.
3.1. Classical Class Algorithms
3.1.1. Graph Search Algorithms
| Algorithm | Time | Characteristics | Research |
|---|---|---|---|
| WA* | - | Fine-tuned heuristic weight factor to adjust the algorithm’s emphasis on heuristic estimates and path costs during exploration. | [53] [58] |
| AA* | - | Updated heuristic function based on the actual exploration path costs to guide the search direction more accurately, thereby enhancing search efficiency. | [54] [58] |
| Theta* | 2010 | Implemented improvements upon the A* algorithm to reduce path deviations and eliminate the need for re-exploring visited nodes. | [55] [59] |
| Lazy-Theta* | 2010 | Computation of path cost is performed only when genuinely required, resulting in an enhancement of search efficiency. | [60] |
| JPS | 2011 | Leveraged map symmetry and accessibility to bypass numerous unnecessary nodes, consequently reducing search overhead. | [56] |
| D* | 1994 | A self-correcting path planning algorithm evolved from the A* algorithm, applicable to dynamic environments. | [61] |
| LPA* | 2001 | Employed two priority queues to manage current path estimates and enhanced path information, adjusting paths incrementally based on cost and heuristic information to achieve optimal routes. | [62] |
| D* Lite | 2002 | Built upon the LPA* approach, incorporated ideas of incremental path updating and repairing to enable efficient path adjustments in dynamic environments. | [63] |
| TLPA* | 2013 | Integrated the concept of suboptimal constraints into the LPA* framework, facilitating a reduction in state expansions. | [64] |
| TD* Lite | 2013 | Introduced a suboptimal re-planning algorithm for navigation, combining TLPA* truncation rules with D* Lite principles. | [64] |
| MOD* Lite | 2016 | A multi-objective incremental search algorithm. | [65] |
| MOPBD* | 2022 | Multi-objective incremental search algorithm with more efficient scaling of nodes | [66] |
3.1.2. Random Sampling Algorithms
| Algorithm | Time | Characteristics | Research |
|---|---|---|---|
| RRT-Connect | 2000 | Finding a feasible path to connect two trees using two RRT trees growing and joining step by step for continuous spaces. | [68,73] |
| RRT* | 2011 | Connect the tree nodes through the minimum spanning tree algorithm and iteratively optimize to find a better path. | [69,74,76] |
| RRT*-Smart | 2012 | Intelligent sampling strategy is introduced to dynamically adjust the distribution of sampling points according to the structure of the tree and the location of the target point to accelerate the path search. | [70,77] |
| RRT*-Connect | 2015 | The iterative process of RRT-Connect algorithm is optimized to improve the path quality. | [71,78] |
| Informed RRT*-connect | 2020 | Heuristic information is introduced to improve the RRT*-Connect algorithm, which makes the path planning more efficient and better quality. | [72] |
3.1.3. Potential Field Algorithms
3.2. Intelligent Optimization Class Algorithms
- (1)
- Evolutionary Algorithms: Evolutionary algorithms simulate the process of biological evolution, incorporating operations such as selection, crossover, and mutation to search for optimal solutions within solution spaces. Prominent algorithms in this category include genetic algorithms and evolution strategies.
- (2)
- Swarm Intelligence Algorithms: Swarm intelligence algorithms emphasize collaboration and communication among individuals in a group. They utilize information sharing and coordination among members to collectively solve problems. Notable algorithms in this category include particle swarm optimization and ant colony optimization.
- (3)
- Bio-inspired Algorithms: Bio-inspired algorithms mimic the behavior, structures, and mechanisms of living organisms to address problems. These algorithms draw inspiration and principles from biology. Representative examples are immune algorithms and artificial fish swarm algorithms.
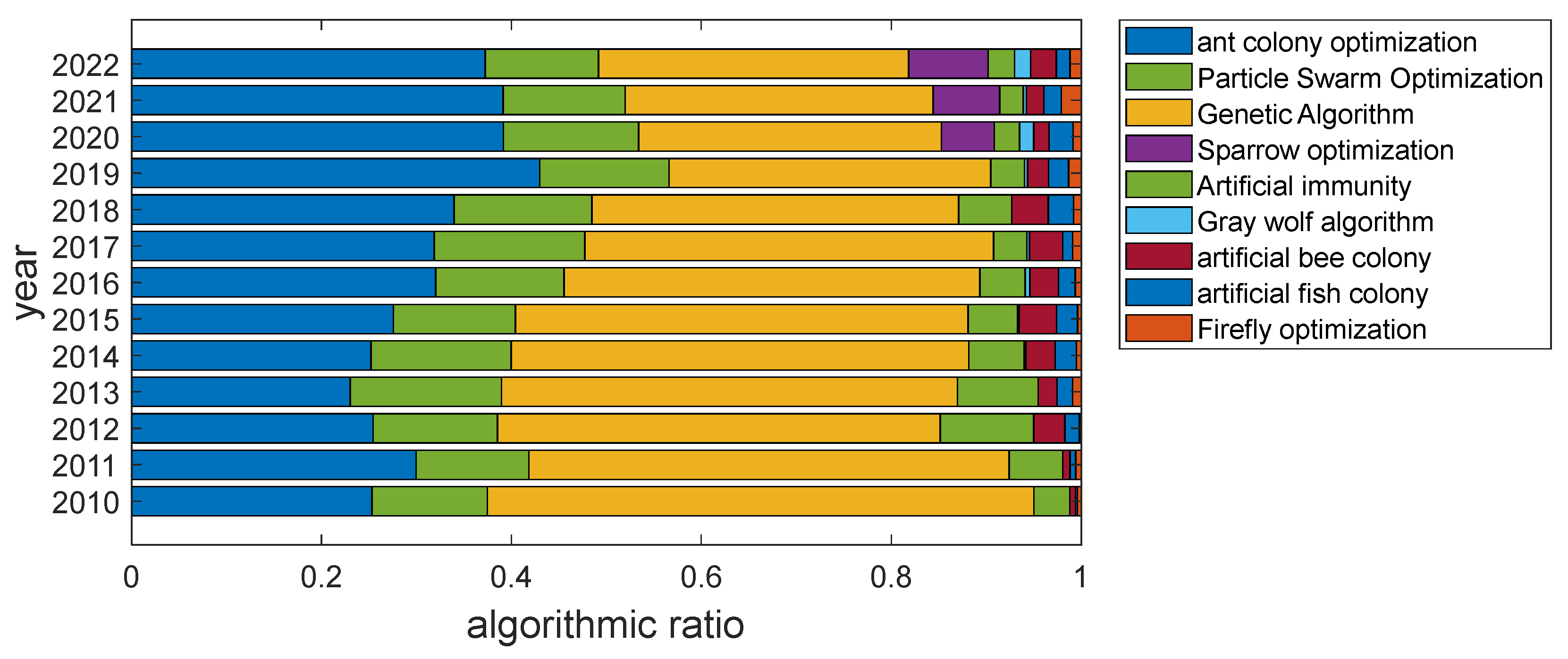
3.2.1. Ant Colony Optimization
- (1)
- In Homogeneous Multi-Population, each population employs similar search strategies to independently explore, while communication of information is facilitated through mechanisms like pheromone updates. For instance, Yang et al. [110] introduced an efficient Leader-Follower Ant Colony Optimization (LF-ACO) to address multi-robot formation path planning. They integrated pheromones from both leader ants and follower ants into the ACO’s pheromone update rules to enhance the quality of the formation path search.
- (2)
- In Heterogeneous Multi-Population, each population maintains the same number of ants with distinct search strategies, focusing on different optimization objectives. Yang et al. [111] presented a parallel ACO approach employing two independent, concurrently operating ACO populations to expand search diversity. This method generates an initial collision-free path in complex environments. To enhance mobile robot path planning, Zhang et al. [112] proposed an improved dual-layer Ant Colony Optimization. They divided the ants into guiding-layer ants emphasizing smoothness and regular-layer ants focusing on the shortest path, effectively exploiting collaborative advantages during the search process.
- (3)
- In Collaborative Populations, distinct populations handle different subproblems while sharing pheromones or experiential knowledge between populations to accelerate convergence and improve solution quality. For instance, Deng et al. [113] introduced an enhanced ACO algorithm based on a multi-population strategy, cooperative evolution mechanism, pheromone update strategy, and pheromone diffusion mechanism, enhancing optimization performance for large-scale problems.
3.2.2. Particle Swarm Optimization
3.2.3. Genetic Algorithm
3.3. Artificial Intelligence Class Algorithms
3.3.1. Neural Network Algorithm
3.3.2. Fuzzy Logic Algorithm
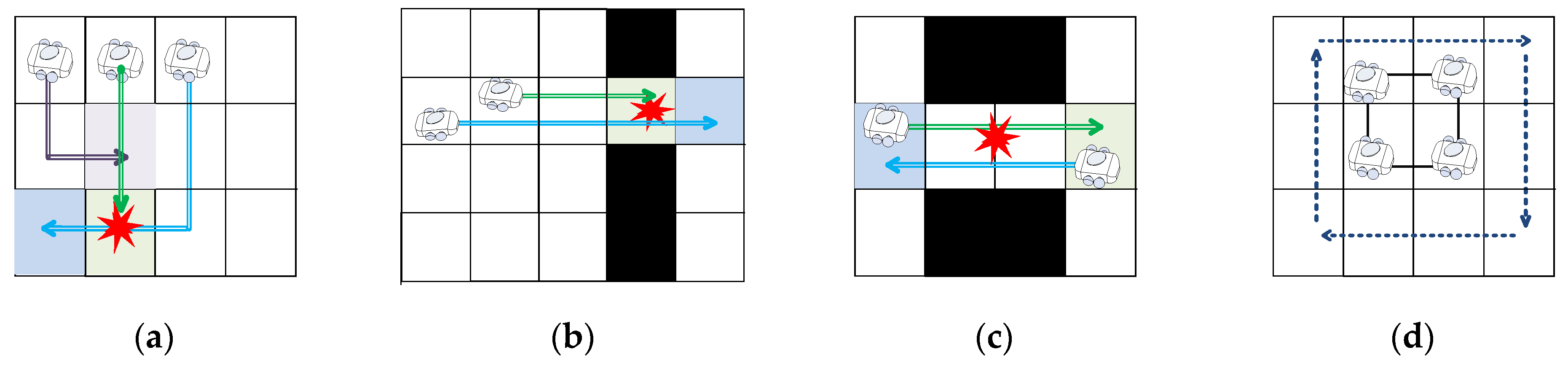
4. Multi-Agent Path Planning Algorithms
4.1. Centralized Planning
4.1.1. Problem Description
4.1.2. Solution
4.2. Distributed Planning
4.2.1. Problem Description
4.2.2. Solution
- (1)
- In the context of localized information sharing, robots interact exclusively with their immediate neighbors. Amoolya et al. [213] and Lijina et al. [214] employed WiFi and Bluetooth technologies, respectively for localized information exchange. Liu et al. [215] proposed a decoupled multi-robot path planning technique, blending an enhanced ant colony algorithm and distributed navigation. Global paths are determined via Ant Colony Optimization (ACO), while local navigation relies on a “first-come, first-served” collision avoidance strategy. Chang et al. [216] addressed the challenge of unknown environments with static and dynamic obstacles, introducing a layered multi-robot navigation and formation approach driven by deep reinforcement learning and distributed optimization. This hierarchical framework empowers each robot to navigate to a global goal based on its local perception within the unfamiliar environment, resulting in optimal formations with minimal communication.
- (2)
- In the context of global information sharing, all robots access global information to attain optimal solutions. Dong et al. [217] proposed a Collaborative Complete Coverage Path Planning (CCPP) algorithm for multiple agents in unknown environments. Causa et al. [218] devised a multi-UAV path planning algorithm catering to scenarios with heterogeneous global navigation satellite system coverage. Addressing the issue of unnecessary detours due to dynamic obstacle avoidance through re-planning, Wang et al. [219] introduced the Globally Guided Reinforcement Learning (G2RL) method, addressing multi-robot path planning in a fully distributed reactive manner.
- (3)
- Hybrid information sharing involves establishing local information sharing regions around each robot, interconnected to form a global information sharing network. Each robot considers neighbor information while also accessing global data to attain an optimal global solution. To address dynamic multi-robot path planning [220,221], an adaptive hybrid algorithm was introduced. This algorithm ensures safety in unknown dynamic environments through dynamic obstacle avoidance rules and enables collaborative obstacle avoidance within the motion conflict range using proposed priority obstacle avoidance rules. Fan et al. [222] introduced a method utilizing Received Signal Strength Indicator (RSSI) to gauge distributed robot motion conflicts. In case of a conflict, one robot proceeds, and upon reaching an RSSI threshold or designated avoidance wait-time, the other robot navigates.
5. Conclusions and Prospects
5.1. Conclusions
5.2. Prospects
- (1)
- Perception and environmental modeling: In light of the ongoing evolution of sensor technology, upcoming developments should optimally harness sophisticated perception tools such as LiDAR, cameras, and depth sensors. Furthermore, the integration of diverse perception techniques, including deep learning and computer vision, should be a focal point, enhancing a robot’s understanding and perception of its surroundings.
- (2)
- Adaptability and learning capabilities: Upcoming advancements should prioritize the adaptability and learning capabilities of SAPF algorithms and MAPF algorithms, empowering them to autonomously adjust strategies in response to changing environments and task requirements. Techniques such as machine learning and deep reinforcement learning can be harnessed to imbue robots with the ability to make independent motion decisions through interactions with their surroundings, such as highly dynamic environments and non-flat terrain. This, in turn, will bolster system robustness and adaptability.
- (3)
- Multi-modal path planning technology: Future path planning technologies should consider the multi-modal behavior of robots and the possibility of multiple path choices, including different motion modes, travel speeds, and planning objectives. By integrating the physical characteristics of robots and task requirements, more flexible and efficient path planning can be achieved. This is especially important for multi-agent systems, where the extension to multi-modal and multi-objective MAPF may be necessary to better meet practical needs.
- (4)
- Multi-robot collaborative path planning technology: In complex scenarios, the cooperative efforts of multiple mobile robots may be required to collectively fulfill tasks. In this regard, future innovations should emphasize collaborative decision-making mechanisms and effective information-sharing paradigms among multiple robots. This will yield heightened efficiency and safety, with applications in fields like factory automation and logistics.
- (5)
- Challenges in large-scale scenarios: As the field of automation continues to expand, including areas such as logistics management and autonomous driving, both SAPF and MAPF are required to address increasingly larger-scale scenarios. Consequently, the future challenges will revolve around finding solutions for these large-scale problems.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path Planning Techniques for Mobile Robots: Review and Prospect. Expert Syst. Appl. 2023, 227, 120254. [Google Scholar] [CrossRef]
- Khan, M.T.R.; Muhammad Saad, M.; Ru, Y.; Seo, J.; Kim, D. Aspects of Unmanned Aerial Vehicles Path Planning: Overview and Applications. Int. J. Commun. Syst. 2021, 34, 14827. [Google Scholar] [CrossRef]
- Tan, C.S.; Mohd-Mokhtar, R.; Arshad, M.R. A Comprehensive Review of Coverage Path Planning in Robotics Using Classical and Heuristic Algorithms. IEEE Access 2021, 9, 119310–119342. [Google Scholar] [CrossRef]
- Chen, S.L.; Wu, J.J. RGB-D SLAM: A Survey. Comput. Eng. Appl. 2019, 55, 30–39+126. (In Chinese) [Google Scholar] [CrossRef]
- Ali, W.; Liu, P.; Ying, R.; Gong, Z. A Feature Based Laser SLAM Using Rasterized Images of 3D Point Cloud. IEEE Sens. J. 2021, 21, 24422–24430. [Google Scholar] [CrossRef]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-Time Single Camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed]
- Kerl, C.; Sturm, J.; Cremers, D. Robust odometry estimation for RGB-D cameras. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3748–3754. [Google Scholar] [CrossRef]
- Endres, F.; Hess, J.; Sturm, J.; Burgard, W. 3-D Mapping With an RGB-D Camera. IEEE Trans. Robot. 2014, 30, 177–187. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Schneider, T.; Dymczyk, M.; Fehr, M.; Egger, K.; Lynen, S.; Gilitschenski, l.; Siegwart, R. Maplab: An Open Framework for Research in Visual-Inertial Mapping and Localization. IEEE Robot. Autom. Lett. 2018, 3, 1418–1425. [Google Scholar] [CrossRef]
- Vineet, V.; Miksik, O.; Lidegaard, M.; Nießner, M.; Golodetzet, S.; Prisacariu, V.A.; Kähler, O.; Murray, D.W.; Izadi, S.; Pérez, P.; et al. Incremental dense semantic stereo fusion for large-scale semantic scene reconstruction. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 75–82. [Google Scholar] [CrossRef]
- Bowman, S.L.; Atanasov, N.; Daniilidis, K.; Pappas, G.J. Probabilistic data association for semantic SLAM. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Marina Bay Sands, Singapore, 29 May–3 June 2017; pp. 1722–1729. [Google Scholar] [CrossRef]
- Schönberger, J.L.; Pollefeys, M.; Geiger, A.; Sattle, T. Semantic visual localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6896–6906. [Google Scholar] [CrossRef]
- Yu, C.; Liu, Z.; Liu, X.J.; Xie, F.; Yang, Y.; Wei, Q.; Fei, Q. DS-SLAM: A Semantic Visual SLAM towards Dynamic Environments. In Proceedings of the 2018 IEEE International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1168–1174. [Google Scholar] [CrossRef]
- Cui, L.; Ma, C. SOF-SLAM: A Semantic Visual SLAM for Dynamic Environments. IEEE Access 2019, 7, 166528–166539. [Google Scholar] [CrossRef]
- Yousif, K.; Bab-Hadiashar, A.; Hoseinnezhad, R. An Overview of Visual Odometry and Visual SLAM: Applications to Mobile Robotics. Intell. Ind. Syst. 2015, 1, 289–311. [Google Scholar] [CrossRef]
- Saeedi, S.; Trentini, M.; Seto, M.; Li, H. Multiple-Robot Simultaneous Localization and Mapping: A Review. J. Field Robot. 2016, 33, 3–46. [Google Scholar] [CrossRef]
- Taketomi, T.; Uchiyama, H.; Ikeda, S. Visual SLAM algorithms: A survey from 2010 to 2016. IEEE Trans. Comput. Vis. Appl. 2017, 9, 16. [Google Scholar] [CrossRef]
- Jamiruddin, R.; Sari, A.O.; Shabbir, J.; Anwer, T. RGB-depth SLAM review. arXiv 2018, arXiv:1805.07696. [Google Scholar] [CrossRef]
- Duan, C.; Junginger, S.; Huang, J.; Jin, K.; Thurow, K. Deep learning for visual SLAM in transportation robotics: A review. Transp. Saf. Environ. 2019, 1, 177–184. [Google Scholar] [CrossRef]
- Xia, L.; Cui, J.; Shen, R.; Xu, X.; Gao, Y.P.; Li, X.Y. A survey of image semantics-based visual simultaneous localization and mapping: Application-oriented solutions to autonomous navigation of mobile robots. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420919185. [Google Scholar] [CrossRef]
- Nam, D.V.; Gon-Woo, K. Solid-State LiDAR based-SLAM: A Concise Review and Application. In Proceedings of the 2021 IEEE International Conference on Big Data and Smart Computing (bigcomp), Jeju Island, Republic of Korea, 17–20 January 2021; pp. 302–305. [Google Scholar] [CrossRef]
- Kazerouni, I.A.; Fitzgerald, L.; Dooly, G.; Toal, D. A survey of state-of-the-art on visual SLAM. Expert Syst. Appl. 2022, 205, 117734. [Google Scholar] [CrossRef]
- Pu, H.Y.; Luo, J.; Wang, G.; Huang, T.; Liu, H.I.; Luo, J. Visual SLAM Integration with Semantic Segmentation and Deep Learning: A Review. IEEE Sens. J. 2023, 23, 22119–22138. [Google Scholar] [CrossRef]
- Li, Y.; Wan, Y.; Zhang, Y.; Kuang, H. Path planning for warehouse robots based on artificial bee colony-adaptive genetic algorithm. J. Instrum. 2022, 43, 282–290. (In Chinese) [Google Scholar] [CrossRef]
- Wen, S.; Jiang, Y.; Cui, B.; Gao, K.; Wang, F. A Hierarchical Path Planning Approach with Multi-SARSA Based on Topological Map. Sensors 2022, 22, 2367. [Google Scholar] [CrossRef]
- Zurbrügg, R.; Blum, H.; Cadena, C.; Siegwart, R.; Schmid, L. Embodied Active Domain Adaptation for Semantic Segmentation via Informative Path Planning. IEEE Robot. Autom. Lett. 2022, 7, 8691–8698. [Google Scholar] [CrossRef]
- Wang, J.; Li, T.; Li, B.; Meng, M.Q. GMR-RRT*: Sampling-Based Path Planning Using Gaussian Mixture Regression. IEEE Trans. Intell. Veh. 2022, 7, 690–700. [Google Scholar] [CrossRef]
- Borges, C.D.B.; Almeida, A.M.A.; Júnior, J.J.D.M. A strategy and evaluation method for ground global path planning based on aerial images. Expert Syst. Appl. 2019, 137, 232–252. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, K.; Song, C.; Zhang, X.; Cheng, J.C.; Li, D. Global path planning based on BIM and physics engine for UGVs in indoor environments. Autom. Constr. 2022, 139, 104263. [Google Scholar] [CrossRef]
- Diaz-diaz, A.; Ocaña, M.; Llamazares, Á.; Gómez-huélamo, C.; Revenga, P.; Bergasa, L.M. HD maps: Exploiting OpenDRIVE potential for Path Planning and Map Monitoring. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 4–9 June 2022; IEEE: New York, NY, USA, 2022; pp. 1211–1217. [Google Scholar] [CrossRef]
- Wang, Z.; Tian, G. Hybrid offline and online task planning for service robot using object-level semantic map and probabilistic inference. Inf. Sci. 2022, 593, 78–98. [Google Scholar] [CrossRef]
- Leung, T.H.Y.; Ignatyev, D.; Zolotas, A. Hybrid Terrain Traversability Analysis in Off-road Environments. In Proceedings of the 2022 8th International Conference on Automation, Robotics and Applications (ICARA), Prague, Czech Republic, 18–20 February 2022; IEEE: New York, NY, USA, 2022; pp. 50–56. [Google Scholar] [CrossRef]
- Sturtevant, N.R. Benchmarks for Grid-Based Pathfinding. IEEE Trans. Comput. Intell. AI Games 2012, 4, 144–148. [Google Scholar] [CrossRef]
- Stern, R.; Sturtevant, N.; Felner, A.; Koenig, S.; Ma, H.; Walker, T.; Li, J.; Atzmon, D.; Cohen, L.; Kumar, T.K.; et al. Multi-agent pathfinding: Definitions, variants, and benchmarks. In Proceedings of the International Symposium on Combinatorial Search, Napa, CA, USA, 16–17 July 2019; pp. 151–158. [Google Scholar] [CrossRef]
- Xiang, D.; Lin, H.; Ouyang, J.; Huang, D. Combined improved A* and greedy algorithm for path planning of multi-objective mobile robot. Sci. Rep. 2022, 12, 13273. [Google Scholar] [CrossRef]
- Li, P.; Yang, L. Conflict-free and energy-efficient path planning for multi-robots based on priority free ant colony optimization. Math. Biosci. Eng. 2023, 20, 3528–3565. [Google Scholar] [CrossRef]
- Yu, Z.; Duan, P.; Meng, L.; Han, Y.; Ye, F. Multi-objective path planning for mobile robot with an improved artificial bee colony algorithm. Math. Biosci. Eng. 2023, 20, 2501–2529. [Google Scholar] [CrossRef]
- Ghambari, S.; Golabi, M.; Lepagnot, J.; Brévilliers, M.; Jourdan, L.; Idoumghar, L. An Enhanced NSGA-II for Multiobjective UAV Path Planning in Urban Environments. In Proceedings of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA, 9–11 November 2020; IEEE: New York, NY, USA, 2020; pp. 106–111. [Google Scholar] [CrossRef]
- Dong, Q.; Cao, M.; Gu, F.; Gong, W.; Cai, Q. Method for puncture trajectory planning in liver tumors thermal ablation based on NSGA-III. Technol. Health Care 2022, 30, 1243–1256. [Google Scholar] [CrossRef]
- Xia, M.; Zhang, C.; Weng, L.; Liu, J.; Wang, Y. Robot path planning based on multi-objective optimization with local search. J. Intell. Fuzzy Syst. 2018, 35, 1755–1764. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, H.; Chen, Y.; Cheng, L.; Zhang, B. Patrol robot path planning in nuclear power plant using an interval multi-objective particle swarm optimization algorithm. Appl. Soft Comput. 2022, 116, 108192. [Google Scholar] [CrossRef]
- Miao, C.; Chen, G.; Yan, C.; Wu, Y. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm. Comput. Ind. Eng. 2021, 156, 107230. [Google Scholar] [CrossRef]
- Yang, L.; Fu, L.; Guo, N.; Yang, Z.; Guo, H.; Xu, X. Multifactor improved ant colony algorithm for path planning. Comput. Integr. Manuf. Syst. 2023, 1–18. (In Chinese) [Google Scholar] [CrossRef]
- Ntakolia, C.; Platanitis, K.S.; Kladis, G.P.; Skliros, C.; Zagorianos, A.D. A Genetic Algorithm enhanced with Fuzzy-Logic for multi-objective Unmanned Aircraft Vehicle path planning missions. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; IEEE: New York, NY, USA, 2022; pp. 114–123. [Google Scholar] [CrossRef]
- Chang, L.; Shan, L.; Jiang, C.; Dai, Y. Reinforcement based mobile robot path planning with improved dynamic window approach in unknown environment. Auton. Robot. 2021, 45, 51–76. [Google Scholar] [CrossRef]
- Fang, T.; Ding, Y. A sampling-based motion planning method for active visual measurement with an industrial robot. Robot. Comput.-Integr. Manuf. 2022, 76, 102322. [Google Scholar] [CrossRef]
- Tsardoulias, E.G.; Iliakopoulou, A.; Kargakos, A.; Petrou, L. A review of global path planning methods for occupancy grid maps regardless of obstacle density. J. Intell. Robot. Syst. 2016, 84, 829–858. [Google Scholar] [CrossRef]
- Yang, X.; Wang, R.; Zhang, T. A review of intelligent optimization algorithms for UAV cluster path planning. Control Theory Appl. 2020, 37, 2291–2302. [Google Scholar] [CrossRef]
- Di Franco, C.; Buttazzo, G. Coverage Path Planning for UAVs Photogrammetry with Energy and Resolution Constraints. J. Intell. Robot. Syst. 2016, 83, 445–462. [Google Scholar] [CrossRef]
- Dijkstra, E.W. Edsger Wybe Dijkstra: His Life, Work, and Legacy; Krzysztof, R., Apt, A., Tony Hoare, B., Eds.; Association for Computing Machinery: New York, NY, USA, 2022; p. 576. [Google Scholar]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Liang, Q.; Zhou, L.; Lu, W.; Zhou, H. An improved algorithm for 3D A* path planning based on adaptive weights. J. Xian Univ. Posts Telecommun. 2022, 27, 84–89. (In Chinese) [Google Scholar] [CrossRef]
- Chi, X.; Li, H.; Fei, J. Research on random obstacle avoidance method for robots based on the fusion of improved A* algorithm and dynamic window method. J. Instrum. 2021, 42, 132–140. (In Chinese) [Google Scholar] [CrossRef]
- Luo, Y.; Lu, J.; Qin, Q.; Liu, Y. Improved JPS Path Optimization for Mobile Robots Based on Angle-Propagation Theta* Algorithm. Algorithms 2022, 15, 198. [Google Scholar] [CrossRef]
- Luo, Y.; Lu, J.; Zhang, Y.; Qin, Q.; Liu, Y. 3D JPS Path Optimization Algorithm and Dynamic-Obstacle Avoidance Design Based on Near-Ground Search Drone. Appl. Sci. 2022, 12, 7333. [Google Scholar] [CrossRef]
- Pu, X.; Zhang, C.; Zhang, J. Multi-target Real-time Path Planning Using Double Adaptive A Algorithm. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4301–4312. [Google Scholar] [CrossRef]
- Lai, X.; Li, J.; Chambers, J. Enhanced Center Constraint Weighted A* Algorithm for Path Planning of Petrochemical Inspection Robot. J. Intell. Robot. Syst. 2021, 102, 78. [Google Scholar] [CrossRef]
- Daniel, K.; Nash, A.; Koenig, S.; Felner, A. Theta*: Any-angle path planning on grids. J. Artif. Intell. Res. 2010, 39, 533–579. [Google Scholar] [CrossRef]
- Nash, A.; Koenig, S.; Tovey, C. Lazy Theta*: Any-angle path planning and path length analysis in 3D. In Proceedings of the AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; pp. 147–154. [Google Scholar] [CrossRef]
- Stentz, A. Optimal and efficient path planning for partially-known environments. In Proceedings of the IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 3310–3317. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M.; Furcy, D. Lifelong planning A∗. Artif. Intell. 2004, 155, 93–146. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M. D* Lite; AAAI/IAAI: Washington, DC, USA, 2002; Volume 15, pp. 476–483. [Google Scholar]
- Aine, S.; Likhachev, M. Truncated incremental search: Faster replanning by exploiting suboptimality. In Proceedings of the AAAI Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013; pp. 16–24. [Google Scholar] [CrossRef]
- Oral, T.; Polat, F. MOD* Lite: An Incremental Path Planning Algorithm Taking Care of Multiple Objectives. IEEE Trans. Cybern. 2016, 46, 245–257. [Google Scholar] [CrossRef]
- Ren, Z.; Rathinam, S.; Likhachev, M.; Choset, H. Multi-Objective Path-Based D* Lite. IEEE Robot. Autom. Lett. 2022, 7, 3318–3325. [Google Scholar] [CrossRef]
- Lavalle, S.M. Rapidly-exploring random trees: A new tool for path planning. In The Annual Research Report; Department of Computer Science, Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Kuffner, J.J.; Lavalle, S.M. RRT-connect: An efficient approach to single-query path planning. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; pp. 995–1001. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Islam, F.; Nasir, J.; Malik, U.; Ayaz, Y.; Hasan, O. RRT*-Smart: Rapid convergence implementation of RRT* towards optimal solution. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Chengdu, China, 5–8 August 2012; pp. 1651–1656. [Google Scholar] [CrossRef]
- Klemm, S.; Oberländer, J.; Hermann, A.; Roennau, A.; Schamm, T.; Zollner, J.M.; Dillmann, R. RRT*-Connect: Faster, asymptotically optimal motion planning. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 1670–1677. [Google Scholar] [CrossRef]
- Mashayekhi, R.; Idris, M.Y.I.; Anisi, M.H.; Ahmedy, I.; Ali, I. Informed RRT*-Connect: An Asymptotically Optimal Single-Query Path Planning Method. IEEE Access 2020, 8, 19842–19852. [Google Scholar] [CrossRef]
- Kang, J.; Lim, D.; Choi, Y.; Jang, W.; Jung, J. Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning. Sensors 2021, 21, 333. [Google Scholar] [CrossRef] [PubMed]
- Jeong, I.; Lee, S.; Kim, J. Quick-RRT*: Triangular inequality-based implementation of RRT* with improved initial solution and convergence rate. Expert Syst. Appl. 2019, 123, 82–90. [Google Scholar] [CrossRef]
- Qian, K.; Liu, Y.; Tian, L.; Bao, J. Robot path planning optimization method based on heuristic multi-directional rapidly-exploring tree. Comput. Electr. Eng. 2020, 85, 106688. [Google Scholar] [CrossRef]
- Qureshi, A.H.; Ayaz, Y. Intelligent bidirectional rapidly-exploring random trees for optimal motion planning in complex cluttered environments. Robot. Auton. Syst. 2015, 68, 1–11. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.J.; Liu, X.Y.; Nan, L.; Yang, K.Q.; Zhu, H. Navigation Method Based on Improved Rapid Exploration Random Tree Star-Smart (RRT*-Smart) and Deep Reinforcement Learning. J. Donghua Univ. 2022, 39, 490–495. [Google Scholar]
- Chen, Y.; Wang, L. Adaptively Dynamic RRT*-Connect: Path Planning for UAVs Against Dynamic Obstacles. In Proceedings of the 2022 7th International Conference on Automation, Control and Robotics Engineering (CACRE), Xi’an, China, 14–16 July 2022; IEEE: New York, NY, USA, 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Kavraki, L.; Svestka, P.; Latombe, J.; Overmars, M. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Incremental sampling-based algorithms for optimal motion planning. Robot. Sci. Syst. VI 2010, arXiv:1005.0416. [Google Scholar] [CrossRef]
- Bohlin, R.; Kavraki, L. Path planning using lazy PRM. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; pp. 521–528. [Google Scholar] [CrossRef]
- Liu, C.; Xie, S.; Sui, X.; Huang, Y.; Ma, X.; Guo, N.; Yang, F. PRM-D* Method for Mobile Robot Path Planning. Sensors 2023, 23, 3512. [Google Scholar] [CrossRef]
- Ravankar, A.A.; Ravankar, A.; Emaru, T.; Kobayashi, Y. HPPRM: Hybrid Potential Based Probabilistic Roadmap Algorithm for Improved Dynamic Path Planning of Mobile Robots. IEEE Access 2020, 8, 221743–221766. [Google Scholar] [CrossRef]
- Mohanta, J.; Keshari, A. A knowledge based fuzzy-probabilistic roadmap method for mobile robot navigation. Appl. Soft Comput. 2019, 79, 391–409. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Fan, X.; Guo, Y.; Liu, H.; Wei, B.; Lyu, W. Improved artificial potential field method applied for AUV path planning. Math. Probl. Eng. 2020, 2020, 6523158. [Google Scholar] [CrossRef]
- Lin, X.; Wang, Z.; Chen, X. Path Planning with Improved Artificial Potential Field Method Based on Decision Tree. In Proceedings of the 2020 27th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), Saint Petersburg, Russia, 25–27 May 2020; IEEE: New York, NY, USA, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Lu, Y.F.; Wu, A.P.; Chen, Q.Y.; Wu, Y.J. An improved UAV path planning method based on RRT-APF hybrid strategy. In Proceedings of the 2020 5th International Conference on Automation, Control and Robotics Engineering (CACRE), Dalian, China, 19–20 September 2020; IEEE: New York, NY, USA, 2020; pp. 81–86. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, J.; Zhu, Z.; Yang, D.; Wu, J. Tangent navigated robot path planning strategy using particle swarm optimized artificial potential field. Optik 2018, 158, 639–651. [Google Scholar] [CrossRef]
- Tong, X.; Yu, S.; Liu, G.; Niu, X.; Xia, C.; Chen, J.; Yang, Z.; Sun, Y. A hybrid formation path planning based on A* and multi-target improved artificial potential field algorithm in the 2D random environments. Adv. Eng. Inform. 2022, 54, 101755. [Google Scholar] [CrossRef]
- Quinlan, S.; Khatib, O. Elastic bands: Connecting path planning and control. In Proceedings of the 1993 Proceedings IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; IEEE: New York, NY, USA, 1993; pp. 802–807. [Google Scholar] [CrossRef]
- Reclik, D.; Kost, G. The comparison of elastic band and B-Spline polynomials methods in smoothing process of collision-free robot trajectory. J. Achiev. Mater. Manuf. Eng. 2008, 29, 187–190. [Google Scholar]
- Wen, Y.; Huang, J.; Jiang, T.; Su, X. An improved time elastic band trajectory planning algorithm with safety and smoothness. Control Decis. 2022, 37, 2008–2016. (In Chinese) [Google Scholar] [CrossRef]
- Rösmann, C.; Feiten, W.; Wösch, T.; Hoffmann, F.; Bertram, T. Trajectory modification considering dynamic constraints of autonomous robots. In Proceedings of the Robotik 2012, 7th German Conference on Robotics, Munich, Germany, 21–22 May 2012; VDE: Frankfurt, Germany, 2012; pp. 1–6. [Google Scholar]
- Nguyen, L.A.; Pham, T.D.; Ngo, T.D.; Truong, X.T. A proactive trajectory planning algorithm for autonomous mobile robots in dynamic social environments. In Proceedings of the 2020 17th International Conference on Ubiquitous Robots (UR), Kyoto, Japan, 22–26 June 2020; IEEE: New York, NY, USA, 2020; pp. 309–314. [Google Scholar] [CrossRef]
- Sun, J.; Sun, Z.; Wei, P.; Liu, B.; Wang, Y.; Zhang, T.; Yan, C. Path Planning Algorithm for a Wheel-Legged Robot Based on the Theta* and Timed Elastic Band Algorithms. Symmetry 2023, 15, 1091. [Google Scholar] [CrossRef]
- Borenstein, J.; Koren, Y. The vector field histogram-fast obstacle avoidance for mobile robots. IEEE Trans. Robot. Autom. 1991, 7, 278–288. [Google Scholar] [CrossRef]
- Ulrich, I.; Borenstein, J. VFH+: Reliable obstacle avoidance for fast mobile robots. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation, Leuven, Belgium, 20 May 1998; IEEE: New York, NY, USA, 1998; pp. 1572–1577. [Google Scholar] [CrossRef]
- Ulrich, I.; Borenstein, J. VFH*: Local obstacle avoidance with look-ahead verification. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings, San Francisco, CA, USA, 24–28 April 2000; IEEE: New York, NY, USA, 2000; pp. 2505–2511. [Google Scholar] [CrossRef]
- Sary, I.P.; Nugraha, Y.P.; Megayanti, M.; Hidayat, E.; Trilaksono, B.R. Design of obstacle avoidance system on hexacopter using vector field histogram-plus. In Proceedings of the 2018 IEEE 8th International Conference on System Engineering and Technology (ICSET), Bandung, Indonesia, 15–16 October 2018; IEEE: New York, NY, USA, 2018; pp. 18–23. [Google Scholar] [CrossRef]
- Díaz, D.; Marín, L. VFH+D: An Improvement on the VFH+ Algorithm for Dynamic Obstacle Avoidance and Local Planning. IFAC-Pap. 2020, 53, 9590–9595. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, S.; Xu, J.; Zhou, S. Kalman prediction based VFH of dynamic obstacle avoidance for intelligent vehicles. In Proceedings of the 2010 International Conference on Computer Application and System Modeling (ICCASM 2010), Taiyuan, China, 22–24 October 2010; IEEE: New York, NY, USA, 2010; p. V3-6. [Google Scholar] [CrossRef]
- Dorigo, M.; Caro, G.D. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; IEEE: New York, NY, USA, 1999; pp. 1470–1477. [Google Scholar] [CrossRef]
- Wang, X.; Yang, L.; Zhang, Y.; Meng, S. Robot path planning based on improved potential field ant colony algorithm. Control Decis. 2018, 33, 1775–1781. (In Chinese) [Google Scholar] [CrossRef]
- Jiao, Z.; Ma, K.; Rong, Y.; Wang, P.; Zhang, H.; Wang, S. A path planning method using adaptive polymorphic ant colony algorithm for smart wheelchairs. J. Comput. Sci. 2018, 25, 50–57. [Google Scholar] [CrossRef]
- Akka, K.; Khaber, F. Mobile robot path planning using an improved ant colony optimization. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418774673. [Google Scholar] [CrossRef]
- Li, L.; Li, H.; Shan, N. Path planning based on ant colony algorithm with multiple heuristic factors. Comput. Eng. Appl. 2019, 55, 219–225. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, S.; Pu, J.; Si, Y.; Sun, L. Review on application of ant colony algorithm in mobile robot path planning. Comput. Eng. Appl. 2020, 56, 10–19. (In Chinese) [Google Scholar] [CrossRef]
- Twomey, C.; Stützle, T.; Dorigo, M.; Manfrin, M.; Birattari, M. An analysis of communication policies for homogeneous multi-colony ACO algorithms. Inf. Sci. 2010, 180, 2390–2404. [Google Scholar] [CrossRef]
- Yang, L.; Fu, L.; Li, P.; Mao, J.; Guo, N.; Du, L. LF-ACO: An effective formation path planning for multi-mobile robot. Math. Biosci. Eng. 2022, 19, 225–252. [Google Scholar] [CrossRef]
- Yang, H.; Qi, J.; Miao, Y.; Sun, H.; Li, J. A new robot navigation algorithm based on a double-layer ant algorithm and trajectory optimization. IEEE Trans. Ind. Electron. 2019, 66, 8557–8566. [Google Scholar] [CrossRef]
- Zhang, H.; He, L.; Yuan, L.; Ran, T. Mobile robot path planning based on improved double-layer ant colony algorithm. Control Decis. 2022, 37, 303–313. (In Chinese) [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.; Zhao, H. An improved ant colony optimization algorithm based on hybrid strategies for scheduling problem. IEEE Access 2019, 7, 20281–20292. [Google Scholar] [CrossRef]
- Liu, J.; Yang, J.; Liu, H.; Tian, X.; Gao, M. An improved ant colony algorithm for robot path planning. Soft Comput. 2017, 21, 5829–5839. [Google Scholar] [CrossRef]
- Dai, X.; Long, S.; Zhang, Z.; Gong, D. Mobile robot path planning based on ant colony algorithm with A* heuristic method. Front. Neurorobotics 2019, 13, 15. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Fu, L.; Li, P.; Mao, J.; Guo, N. An effective dynamic path planning approach for mobile robots based on ant colony fusion dynamic windows. Machines 2022, 10, 50. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Proceedings of ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Aydilek, İ.B.; Nacar, M.A.; Gümüşçü, A.; Salur, M.U. Comparing inertia weights of particle swarm optimization in multimodal functions. In Proceedings of the 2017 International Artificial Intelligence and Data Processing Symposium (IDAP), Malatya, Turkey, 16–17 September 2017; IEEE: New York, NY, USA, 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Nayeem, G.M.; Fan, M.; Akhter, Y. A Time-Varying Adaptive Inertia Weight based Modified PSO Algorithm for UAV Path Planning. In Proceedings of the 2021 2nd International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 5–7 January 2021; IEEE: New York, NY, USA, 2021; pp. 573–576. [Google Scholar] [CrossRef]
- Dai, H.; Chen, D.; Zheng, Z. Effects of Random Values for Particle Swarm Optimization Algorithm. Algorithms 2018, 11, 23. [Google Scholar] [CrossRef]
- Maina, R.M.; Lang’at, P.K.; Kihato, P.K. Collaborative beamforming in wireless sensor networks using a novel particle swarm optimization algorithm variant. Heliyon 2021, 7, e08247. [Google Scholar] [CrossRef] [PubMed]
- Jingjing, H.; Xun, L.; Wenzhe, M.; Xin, Y.; Dong, Y. Path Planning Method for Mobile Robot Based on Multiple Improved PSO. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; IEEE: New York, NY, USA, 2021; pp. 1485–1489. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Yuan, Y.; Zeng, N.; Hone, K.; Liu, X. A novel sigmoid-function-based adaptive weighted particle swarm optimizer. IEEE Trans. Cybern. 2019, 51, 1085–1093. [Google Scholar] [CrossRef] [PubMed]
- Liang, B.; Zhao, Y.; Li, Y. A hybrid particle swarm optimization with crisscross learning strategy. Eng. Appl. Artif. Intell. 2021, 105, 104418. [Google Scholar] [CrossRef]
- Phung, M.D.; Ha, Q.P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization. Appl. Soft Comput. 2021, 107, 107376. [Google Scholar] [CrossRef]
- Guo, X.; Ji, M.; Zhao, Z.; Wen, D.; Zhang, W. Global path planning and multi-objective path control for unmanned surface vehicle based on modified particle swarm optimization (PSO) algorithm. Ocean Eng. 2020, 216, 107693. [Google Scholar] [CrossRef]
- Fu, Y.; Ding, M.; Zhou, C. Phase angle-encoded and quantum-behaved particle swarm optimization applied to three-dimensional route planning for UAV. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2011, 42, 511–526. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, E.Z.; Chen, Q.W. Rotary unmanned aerial vehicles path planning in rough terrain based on multi-objective particle swarm optimization. J. Syst. Eng. Electron. 2020, 31, 130–141. [Google Scholar] [CrossRef]
- Thammachantuek, I.; Ketcham, M. Path planning for autonomous mobile robots using multi-objective evolutionary particle swarm optimization. PLoS ONE 2022, 17, e0271924. [Google Scholar] [CrossRef] [PubMed]
- Sathiya, V.; Chinnadurai, M.; Ramabalan, S. Mobile robot path planning using fuzzy enhanced improved Multi-Objective particle swarm optimization (FIMOPSO). Expert Syst. Appl. 2022, 198, 116875. [Google Scholar] [CrossRef]
- Chen, Q.; Zheng, Y.; Jiang, H. Improved particle swarm optimization algorithm based on neural network for dynamic path planning. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2012, 49, 51–55. [Google Scholar] [CrossRef]
- Wu, J.; Song, C.; Ma, J.; Wu, J.; Han, G. Reinforcement learning and particle swarm optimization supporting real-time rescue assignments for multiple autonomous underwater vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 23, 6807–6820. [Google Scholar] [CrossRef]
- Lin, S.; Liu, A.; Wang, J.; Kong, X. An intelligence-based hybrid PSO-SA for mobile robot path planning in warehouse. J. Comput. Sci. 2022, 67, 101938. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms and the optimal allocation of trials. SIAM J. Comput. 1973, 2, 88–105. [Google Scholar] [CrossRef]
- Forrest, S.; Mitchell, M. Adaptive computation: The multidisciplinary legacy of John H. Holland. Commun. ACM 2016, 59, 58–63. [Google Scholar] [CrossRef]
- Hao, K.; Zhao, J.; Yu, K.; Li, C.; Wang, C. Path Planning of Mobile Robots Based on a Multi-Population Migration Genetic Algorithm. Sensors 2020, 20, 5873. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Y.; Deng, N.; Guo, K. Dynamic Path Planning Algorithm for a Mobile Robot Based on Visible Space and an Improved Genetic Algorithm. Int. J. Adv. Robot. Syst. 2016, 13, 91. [Google Scholar] [CrossRef]
- Lamini, C.; Benhlima, S.; Elbekri, A. Genetic Algorithm Based Approach for Autonomous Mobile Robot Path Planning. Procedia Comput. Sci. 2018, 127, 180–189. [Google Scholar] [CrossRef]
- Guo, H.; Shang, Y.; Qu, W. A Mobile Robot Path Planning Algorithm Based on Multi-objective Optimization. In Proceedings of the 2020 3rd International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE), Shenzhen, China, 24–26 April 2020; pp. 35–40. [Google Scholar] [CrossRef]
- Li, K.; Hu, Q.; Liu, J.; Bazzi, A. Path Planning of Mobile Robot Based on Improved Multiobjective Genetic Algorithm. Wirel. Commun. Mob. Comput. 2021, 2021, 8836615. [Google Scholar] [CrossRef]
- Ramabalan, S.; Sathiya, V.; Chinnadurai, M. Wheeled Mobile Robot Trajectory Planning Using Evolutionary Techniques. In Robotics and Mechatronics; Springer Singapore: Singapore, 2021; pp. 291–301. [Google Scholar] [CrossRef]
- Bhesdadiya, R.H.; Trivedi, I.N.; Jangir, P.; Jangir, N.; Kumar, A. An NSGA-III algorithm for solving multi-objective economic/environmental dispatch problem. Cogent Eng. 2016, 3, 1269383. [Google Scholar] [CrossRef]
- Mahmud, M.S.A.; Abidin, M.S.Z.; Mohamed, Z.; Rahman, M.K.I.A.; Iida, M. Multi-objective path planner for an agricultural mobile robot in a virtual greenhouse environment. Comput. Electron. Agric. 2019, 157, 488–499. [Google Scholar] [CrossRef]
- Orozco-rosas, U.; Picos, K.; Montiel, O. Hybrid Path Planning Algorithm Based on Membrane Pseudo-Bacterial Potential Field for Autonomous Mobile Robots. IEEE Access 2019, 7, 156787–156803. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, G.; Zhan, X.; Han, T. A new hybrid algorithm for path planning of mobile robot. J. Supercomput. 2022, 78, 4158–4181. [Google Scholar] [CrossRef]
- Wang, J.; Shang, X.; Guo, T.; Zhou, J.; Jia, S.; Wang, C. Optimal Path Planning Based on Hybrid Genetic-Cuckoo Search Algorithm. In Proceedings of the 2019 6th International Conference on Systems and Informatics (ICSAI), Shanghai, China, 2–4 November 2019; pp. 165–169. [Google Scholar] [CrossRef]
- Elmousalami, H.H. Artificial intelligence and parametric construction cost estimate modeling: State-of-the-art review. J. Constr. Eng. Manag. 2020, 146, 03119008. [Google Scholar] [CrossRef]
- Huang, H.; Zhu, D.; Ding, F. Dynamic task assignment and path planning for multi-AUV system in variable ocean current environment. J. Intell. Robot. Syst. 2014, 74, 999–1012. [Google Scholar] [CrossRef]
- Arena, P.; Blanco, C.F.; Li Noce, A.; Taffara, S.; Patanè, L. Learning Traversability Map of Different Robotic Platforms for Unstructured Terrains Path Planning. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, P.; Liang, H.; Mei, T. Motion Planning for Autonomous Vehicle Based on Radial Basis Function Neural Network in Unstructured Environment. Sensors 2014, 14, 17548–17566. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Jin, M.; Lu, E.; Yang, S. Path planning of arbitrary shaped mobile robots with safety consideration. IEEE Trans. Intell. Transp. Syst. 2021, 23, 16474–16483. [Google Scholar] [CrossRef]
- Manchella, K.; Umrawal, A.K.; Aggarwal, V. Flexpool: A distributed model-free deep reinforcement learning algorithm for joint passengers and goods transportation. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2035–2047. [Google Scholar] [CrossRef]
- Wu, P.; Cao, Y.; He, Y.; Li, D. VVision-Based Robot Path Planning with Deep Learning; Springer International Publishing: Cham, Switzerland, 2017; pp. 101–111. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.; Li, Y. Path planning for indoor Mobile robot based on deep learning. Optik 2020, 219, 165096. [Google Scholar] [CrossRef]
- Gao, R.; Gao, X.; Liang, P.; Han, F.; Lan, B.; Li, J.; Li, J.; Li, S. Motion Control of Non-Holonomic Constrained Mobile Robot Using Deep Reinforcement Learning. In Proceedings of the 2019 IEEE 4th International Conference on Advanced Robotics and Mechatronics (ICARM), Toyonaka, Japan, 3–5 July 2019; pp. 348–353. [Google Scholar] [CrossRef]
- Yu, J.; Su, Y.; Liao, Y. The path planning of mobile robot by neural networks and hierarchical reinforcement learning. Front. Neurorobotics 2020, 14, 63. [Google Scholar] [CrossRef]
- Semnani, S.H.; Liu, H.; Everett, M.; De ruiter, A.; How, J.P. Multi-Agent Motion Planning for Dense and Dynamic Environments via Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 3221–3226. [Google Scholar] [CrossRef]
- Wen, S.; Zhao, Y.; Yuan, X.; Wang, Z.; Zhang, D.; Manfredi, L. Path planning for active SLAM based on deep reinforcement learning under unknown environments. Intell. Serv. Robot. 2020, 13, 263–272. [Google Scholar] [CrossRef]
- Lei, X.; Zhang, Z.; Dong, P. Dynamic path planning of unknown environment based on deep reinforcement learning. J. Robot. 2018, 2018, 5781591. [Google Scholar] [CrossRef]
- Wang, P.; Li, X.; Song, C.; Zhai, S. Research on dynamic path planning of wheeled robot based on deep reinforcement learning on the slope ground. J. Robot. 2020, 2020, 7167243. [Google Scholar] [CrossRef]
- Taghavifar, H.; Xu, B.; Taghavifar, L.; Qin, Y. Optimal Path-Planning of Nonholonomic Terrain Robots for Dynamic Obstacle Avoidance Using Single-Time Velocity Estimator and Reinforcement Learning Approach. IEEE Access 2019, 7, 159347–159356. [Google Scholar] [CrossRef]
- Ruan, X.; Ren, D.; Zhu, X.; Huang, J. Mobile Robot Navigation based on Deep Reinforcement Learning. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 6174–6178. [Google Scholar] [CrossRef]
- Song, S.; Kidziński, Ł.; Peng, X.B.; Ong, C.; Hicks, J.; Levine, S.; Atkeson, C.G.; Delp, S.L. Deep reinforcement learning for modeling human locomotion control in neuromechanical simulation. J. Neuroeng. Rehabil. 2021, 18, 126. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhang, Y.; Wang, S. A Review of Mobile Robot Path Planning Based on Deep Reinforcement Learning Algorithm. J. Phys. Conf. Ser. 2021, 2138, 012011. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, W.; Yu, R.; Zhang, Y. Motion Planning for Mobile Robots—Focusing on Deep Reinforcement Learning: A Systematic Review. IEEE Access 2021, 9, 69061–69081. [Google Scholar] [CrossRef]
- Hichri, B.; Gallala, A.; Giovannini, F.; Kedziora, S. Mobile robots path planning and mobile multirobots control: A review. Robotica 2022, 40, 4257–4270. [Google Scholar] [CrossRef]
- Bakdi, A.; Hentout, A.; Boutami, H.; Maoudj, A.; Hachour, O.; Bouzouia, B. Optimal path planning and execution for mobile robots using genetic algorithm and adaptive fuzzy-logic control. Robot. Auton. Syst. 2017, 89, 95–109. [Google Scholar] [CrossRef]
- Raguraman, S.; Tamilselvi, D.; Shivakumar, N. Mobile robot navigation using fuzzy logic controller. In Proceedings of the 2009 International Conference on Control, Automation, Communication and Energy Conservation, Perundurai, Erode, India, 4–6 June 2009; IEEE: New York, NY, USA, 2009; pp. 1–5. [Google Scholar]
- Selekwa, M.F.; Dunlap, D.D.; Shi, D.; Collins Jr, E.G. Robot navigation in very cluttered environments by preference-based fuzzy behaviors. Robot. Auton. Syst. 2008, 56, 231–246. [Google Scholar] [CrossRef]
- Pandey, A.; Kumar, S.; Pandey, K.K.; Parhi, D.R. Mobile Robot Navigation in Unknown Static Environments Using ANFIS Controller. Perspect. Sci. 2016, 8, 421–423. [Google Scholar] [CrossRef]
- Al-Dahhan, M.R.H.; Ali, M.M. Path Tracking Control of a Mobile Robot Using Fuzzy Logic. In Proceedings of the 2016 13th International Multi-conference on Systems, Signals & Devices (SSD), Leipzig, Germany, 21–24 March 2016; pp. 82–88. [Google Scholar] [CrossRef]
- Guo, J.; Li, C.; Guo, S. A Novel Step Optimal Path Planning Algorithm for the Spherical Mobile Robot Based on Fuzzy Control. IEEE Access 2020, 8, 1394–1405. [Google Scholar] [CrossRef]
- Kumar, P.B.; Muni, M.K.; Parhi, D.R. Navigational analysis of multiple humanoids using a hybrid regression-fuzzy logic control approach in complex terrains. Appl. Soft Comput. 2020, 89, 106088. [Google Scholar] [CrossRef]
- Rath, A.K.; Parhi, D.R.; Das, H.C.; Muni, M.K.; Kumar, P.B. Analysis and use of fuzzy intelligent technique for navigation of humanoid robot in obstacle-prone zone. Def. Technol. 2018, 14, 677–682. [Google Scholar] [CrossRef]
- Muni, M.K.; Parhi, D.R.; Kumar, P.; Pandey, K.K.; Kumar, S.; Chhotray, A. Sugeno fuzzy logic analysis: Navigation of multiple humanoids in complex environments. In Proceedings of the International Conference on Artificial Intelligence in Manufacturing & Renewable Energy (ICAIMRE), Bhubaneswar, Odisha, India, 25–26 October 2019. [Google Scholar] [CrossRef]
- Pham, D.T.; Awadalla, M. Fuzzy-logic-based behavior coordination in a multi-robot system. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2004, 218, 583–598. [Google Scholar] [CrossRef]
- Zagradjanin, N.; Rodic, A.; Pamucar, D.; Pavkovic, B. Cloud-based multi-robot path planning in complex and crowded environment using fuzzy logic and online learning. Inf. Technol. Control 2021, 50, 357–374. [Google Scholar] [CrossRef]
- Kumar, S.; Parhi, D.R. Trajectory planning and control of multiple mobile robots using hybrid MKH-fuzzy logic controller. Robotica 2022, 40, 3952–3975. [Google Scholar] [CrossRef]
- Song, Q.; Zhao, Q.L.; Wang, S.X.; Liu, Q.; Chen, X.H. Dynamic Path Planning for Unmanned Vehicles Based on Fuzzy Logic and Improved Ant Colony Optimization. IEEE Access 2020, 8, 62107–62115. [Google Scholar] [CrossRef]
- Lyridis, D.V. An improved ant colony optimization algorithm for unmanned surface vehicle local path planning with multi-modality constraints. Ocean Eng. 2021, 241, 109890. [Google Scholar] [CrossRef]
- Azouaoui, O.; Ouadah, N.; Mansour, I.; Semani, A. Neural Networks and Fuzzy Logic navigation approach for a bi-steerable mobile robot. In Proceedings of the 2011 8th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Incheon, Republic of Korea, 23–26 November 2011; pp. 44–49. [Google Scholar] [CrossRef]
- Al Yahmedi, A.S.; Fatmi, M.A. Fuzzy logic-based navigation of mobile robots. In Recent Advances in Mobile Robotics; Intech: London, UK, 2011; pp. 287–310. [Google Scholar]
- Shi, H.; Li, X.; Pan, W.; Hwang, K.; Li, Z. A novel fuzzy three-dimensional grid navigation method for mobile robots. Int. J. Adv. Robot. Syst. 2017, 14, 3. [Google Scholar] [CrossRef]
- Lin, Z.; Yue, M.; Chen, G.; Sun, J. Path planning of mobile robot with PSO-based APF and fuzzy-based DWA subject to moving obstacles. Trans. Inst. Meas. Control 2022, 44, 121–132. [Google Scholar] [CrossRef]
- Sangeetha, V.; Krishankumar, R.; Ravichandran, K.S.; Cavallaro, F.; Kar, S.; Pamucar, D.; Mardani, A. A fuzzy gain-based dynamic ant colony optimization for path planning in dynamic environments. Symmetry 2021, 13, 280. [Google Scholar] [CrossRef]
- Hentout, A.; Maoudj, A.; Aouache, M. A review of the literature on fuzzy-logic approaches for collision-free path planning of manipulator robots. Artif. Intell. Rev. 2023, 56, 3369–3444. [Google Scholar] [CrossRef]
- Yanik, P.; Ford, G.; McDaniel, W. An introduction and literature review of fuzzy logic applications for robot motion planning. In Proceedings of the ASEE Southeast Section Conference, Blacksburg, VA, USA, 18–20 April 2010; pp. 1–10. [Google Scholar]
- Liu, Z.; Cao, L.; Lai, J.; Chen, X.; Chen, Y. A review of multi-intelligent body path planning. Comput. Eng. Appl. 2022, 58, 43–62. (In Chinese) [Google Scholar] [CrossRef]
- Li, J.; Tinka, A.; Kiesel, S.; Durham, J.; Kumar, T.; Koenig, S. Lifelong Multi-Agent Path Finding in Large-Scale Warehouses. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence (AAAI 2019), Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar] [CrossRef]
- Sharan, P. MMAPA: Simulation Study of Multi-Robot for Intelligent Transportation System. In Proceedings of the 2014 Annual IEEE India Conference (INDICON), Pune, India, 11–13 December 2014. [Google Scholar] [CrossRef]
- Zhang, K.; Mao, J.; Xuan, Z.; Xiang, F.; Fu, L. Hierarchical scheduling multi-robot path planning for pass terrain. Comput. Integr. Manuf. Syst. 2022, 1–16. (In Chinese) [Google Scholar]
- Ratner, D.; Warmuth, M. Finding a Shortest Solution for the NxN Extension of the 15-Puzzle is Intractable. In Proceedings of the Fifth AAAI National Conference on Artificial Intelligence, Philadelphia, PA, USA, 11–15 August 1986; AAAI Press: Washington, DC, USA, 1986. [Google Scholar] [CrossRef]
- Banfi, J.; Basilico, N.; Amigoni, F. Intractability of Time-Optimal Multirobot Path Planning on 2D Grid Graphs with Holes. IEEE Robot. Autom. Lett. 2017, 2, 1941–1947. [Google Scholar] [CrossRef]
- Huang, S.; Yang, D.; Zhong, C.; Yan, S.; Zhang, L. An Improved Ant Colony Optimization Algorithm for Multi-Agent Path Planning. In Proceedings of the 2021 International Conference on Networking Systems of AI (INSAI), Shanghai, China, 19–20 November 2021; IEEE: New York, NY, USA, 2021; pp. 95–100. [Google Scholar] [CrossRef]
- Wen, L.; Liu, Y.; Li, H. CL-MAPF: Multi-Agent Path Finding for Car-Like robots with kinematic and spatiotemporal constraints. Robot. Auton. Syst. 2022, 150, 103997. [Google Scholar] [CrossRef]
- Cap, M.; Novak, P.; Kleiner, A.; Selecky, M. Prioritized Planning Algorithms for Trajectory Coordination of Multiple Mobile Robots. IEEE Trans. Autom. Sci. Eng. 2015, 12, 835–849. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Jiang, W.; Wang, P.; Cao, Q. Combined Priority and Path Planning through a Double-layer Structure for Multiple Robots. In Proceedings of the ICARM 2020–2020 5th IEEE International Conference on Advanced Robotics and Mechatronics, Shenzhen, China, 18–21 December 2020; pp. 257–262. [Google Scholar] [CrossRef]
- Li, H.; Zhao, T.; Dian, S. Prioritized planning algorithm for multi-robot collision avoidance based on artificial untraversable vertex. Appl. Intell. 2022, 52, 429–451. [Google Scholar] [CrossRef]
- Wu, W.; Bhattacharya, S.; Prorok, A. Multi-Robot Path Deconfliction through Prioritization by Path Prospects. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Dewangan, R.K.; Shukla, A.; Godfrey, W.W. A solution for priority-based multi-robot path planning problem with obstacles using ant lion optimization. Mod. Phys. Lett. B 2020, 34, 2050137. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Y.; Hu, J.; Zhang, J. A multi-robot path planning algorithm based on improved conflict search. Control Decis. Mak. 2022, 1–7. (In Chinese) [Google Scholar] [CrossRef]
- Gange, G.; Harabor, D.; Stuckey, P.J. Lazy CBS: Implicit conflict-based search using lazy clause generation. In Proceedings of the International Conference on Automated Planning and Scheduling, Berkeley, CA, USA, 11–15 July 2019; pp. 155–162. [Google Scholar] [CrossRef]
- Li, J.; Boyarski, E.; Felner, A.; Ma, H.; Koenig, S. Improved heuristics for multi-agent path finding with conflict-based search: Preliminary results. In Proceedings of the International Symposium on Combinatorial Search, Napa, CA, USA, 16–17 July 2019; pp. 182–183. [Google Scholar] [CrossRef]
- Barer, M.; Sharon, G.; Stern, R.; Felner, A. Suboptimal variants of the conflict-based search algorithm for the multi-agent pathfinding problem. In Proceedings of the International Symposium on Combinatorial Search, Prague, Czech Republic, 15–17 August 2014; pp. 19–27. [Google Scholar] [CrossRef]
- Chan, S.; Li, J.; Gange, G.; Harabor, D.; Stuckey, P.J.; Koenig, S. ECBS with flex distribution for bounded-suboptimal multi-agent path finding. Proc. Int. Symp. Comb. Search 2021, 159–161. [Google Scholar] [CrossRef]
- Rahman, M.; Alam, M.A.; Islam, M.M.; Rahman, I.; Khan, M.M.; Iqbal, T. An Adaptive Agent-Specific Sub-Optimal Bounding Approach for Multi-Agent Path Finding. IEEE Access 2022, 10, 22226–22237. [Google Scholar] [CrossRef]
- Han, S.D.; Yu, J. Optimizing Space Utilization for More Effective Multi-Robot Path Planning. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: New York, NY, USA, 2022; pp. 10709–10715. [Google Scholar] [CrossRef]
- Liu, J.; Anavatti, S.; Garratt, M.; Abbass, H.A. Modified continuous Ant Colony Optimisation for multiple Unmanned Ground Vehicle path planning. Expert Syst. Appl. 2022, 196, 116605. [Google Scholar] [CrossRef]
- Ma, Z.; Luo, Y.; Ma, H. Distributed Heuristic Multi-Agent Path Finding with Communication. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: New York, NY, USA, 2021; pp. 8699–8705. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Mo, Y.; Miao, Z.; Wang, H.; Feng, M.; Wang, S. Multi-Agent Path Finding Using Deep Reinforcement Learning Coupled With Hot Supervision Contrastive Loss. IEEE Trans. Ind. Electron. 2022, 1–9. [Google Scholar] [CrossRef]
- Matoui, F.; Boussaid, B.; Abdelkrim, M.N. Distributed path planning of a multi-robot system based on the neighborhood artificial potential field approach. Simulation 2019, 637–657. [Google Scholar] [CrossRef]
- Contreras-Cruz, M.A.; Lopez-Perez, J.J.; Ayala-Ramirez, V. Distributed path planning for multi-robot teams based on Artificial Bee Colony. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; IEEE: New York, NY, USA, 2017; pp. 541–548. [Google Scholar] [CrossRef]
- Amoolya, G.; Lavanya, K.L.; Sudheer, A. Wi-fi RSSI based optimal path planning and collision avoidance in a multi-robot environment. In Proceedings of the 2019 IEEE International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS), Tamilnadu, India, 11–13 April 2019; IEEE: New York, NY, USA, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Lijina, P.; Nippun, K.A. Bluetooth RSSI based collision avoidance in multirobot environment. In Proceedings of the 2016 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Jaipur, India, 21–24 September 2016; IEEE: New York, NY, USA, 2016; pp. 2168–2174. [Google Scholar] [CrossRef]
- Liu, S.; Mao, L.; Yu, J. Path Planning Based on Ant Colony Algorithm and Distributed Local Navigation for Multi-Robot Systems. In Proceedings of the 2006 International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; IEEE: New York, NY, USA, 2006; pp. 1733–1738. [Google Scholar] [CrossRef]
- Chang, L.; Shan, L.; Zhang, W.; Dai, Y. Hierarchical multi-robot navigation and formation in unknown environments via deep reinforcement learning and distributed optimization. Robot. Comput.-Integr. Manuf. 2023, 83, 102570. [Google Scholar] [CrossRef]
- Dong, Q.; Zhang, J. Distributed Cooperative Complete Coverage Path Planning in an Unknown Environment Based on a Heuristic Method. Unmanned Syst. 2023, 1–12. [Google Scholar] [CrossRef]
- Causa, F.; Fasano, G. Multi-UAV Path Planning for Autonomous Missions in Mixed GNSS Coverage Scenarios. Sensors 2018, 18, 4188. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Li, Q.; Prorok, A. Mobile Robot Path Planning in Dynamic Environments Through Globally Guided Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 6932–6939. [Google Scholar] [CrossRef]
- Yang, Z.; Li, J.; Yang, L.; Wang, Q.; Li, P.; Xia, G. Path planning and collision avoidance methods for distributed multi-robot systems in complex dynamic environments. Math. Biosci. Eng. 2023, 20, 145–178. [Google Scholar] [CrossRef]
- Wang, Q.; Li, J.; Yang, L.; Yang, Z.; Li, P.; Xia, G. Distributed Multi-Mobile Robot Path Planning and Obstacle Avoidance Based on ACO–DWA in Unknown Complex Terrain. Electronics 2022, 11, 2144. [Google Scholar] [CrossRef]
- Fan, N.; Bao, N.; Zuo, J.; Sun, X. Decentralized Multi-robot Collision Avoidance Algorithm Based on RSSI. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Nayak, A.; Rathinam, S. Heuristics and Learning Models for Dubins MinMax Traveling Salesman Problem. Sensors 2023, 23, 6432. [Google Scholar] [CrossRef]
- Patle, B.; Pandey, A.; Parhi, D.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Boscariol, P.; Gasparetto, A.; Scalera, L. Path Planning for Special Robotic Operations. In Robot Design: From Theory to Service Applications; Springer International Publishing: Cham, Switzerland, 2022; pp. 69–95. [Google Scholar] [CrossRef]
- Lin, S.; Liu, A.; Wang, J.; Kong, X. A Review of Path-Planning Approaches for Multiple Mobile Robots. Machines 2022, 10, 0773. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Q.; Xu, X.; Yang, J.; Chen, Y. Research Progress of Nature-Inspired Metaheuristic Algorithms in Mobile Robot Path Planning. Electronics 2023, 12, 3263. [Google Scholar] [CrossRef]
- Wijayathunga, L.; Rassau, A.; Chai, D. Challenges and Solutions for Autonomous Ground Robot Scene Understanding and Navigation in Unstructured Outdoor Environments: A Review. Appl. Sci. 2023, 13, 214. [Google Scholar] [CrossRef]
- Qu, H.; Xing, K.; Alexander, T. An improved genetic algorithm with co-evolutionary strategy for global path planning of multiple mobile robots. Neurocomputing 2013, 120, 509–517. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, H. An improved constrained differential evolution algorithm for unmanned aerial vehicle global route planning. Appl. Soft Comput. 2015, 26, 270–284. [Google Scholar] [CrossRef]
- Chakraborty, J.; Konar, A.; Chakraborty, U.K.; Jain, L.C. Distributed cooperative multi-robot path planning using differential evolution. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 718–725. [Google Scholar] [CrossRef]
- Chai, R.; Savvaris, A.; Tsourdos, A.; Xia, Y.; Chai, S. Solving Multiobjective Constrained Trajectory Optimization Problem by an Extended Evolutionary Algorithm. IEEE Trans. Cybern. 2020, 50, 1630–1643. [Google Scholar] [CrossRef]
- Orozco-Rosas, U.; Montiel, O.; Sepúlveda, R. Mobile robot path planning using membrane evolutionary artificial potential field. Appl. Soft Comput. 2019, 77, 236–251. [Google Scholar] [CrossRef]
- Contreras-Cruz, M.A.; Ayala-Ramirez, V.; Hernandez-Belmonte, U.H. Mobile robot path planning using artificial bee colony and evolutionary programming. Appl. Soft Comput. 2015, 30, 319–328. [Google Scholar] [CrossRef]
- Shrivastava, K.; Jha, S.S.; Nair, S.B. Autonomous mobile robot navigation using artificial immune system. In Proceedings of the Conference on Advances in Robotic, Pune, India, 4–6 July 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Yiping, Z.; Fang, L. Path Planning of Mobile Robot Based on Improved Artificial Immune Algorithm. Open Autom. Control Syst. J. 2015, 7, 1768–1775. [Google Scholar] [CrossRef]
- He, T.; Zhang, Y.; Sun, F.; Shi, X. Immune optimization based multi-objective six-DOF trajectory planning for industrial robot manipulators. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; pp. 2945–2950. [Google Scholar] [CrossRef]
- Chen, D.; Li, S.; Wang, J.; Feng, Y.; Liu, Y. A multi-objective trajectory planning method based on the improved immune clonal selection algorithm. Robot. Comput.-Integr. Manuf. 2019, 59, 431–442. [Google Scholar] [CrossRef]
- Yan, C.; Chen, G.; Li, Y.; Sun, F.; Wu, Y. Immune deep reinforcement learning-based path planning for mobile robot in unknown environment. Appl. Soft Comput. 2023, 145, 110601. [Google Scholar] [CrossRef]
- Feng, K.; He, X.; Wang, M.; Chu, X.; Wang, D.; Yue, D. Path Optimization of Agricultural Robot Based on Immune Ant Colony: B-Spline Interpolation Algorithm. Math. Probl. Eng. 2022, 2022, 2585910. [Google Scholar] [CrossRef]
- Peng, J.; Li, X.; Qin, Z.; Luo, G. Robot global path planning based on improved artificial fish-swarm algorithm. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 2042–2047. [Google Scholar] [CrossRef]
- Li, F.; Du, Y.; Jia, K. Path planning and smoothing of mobile robot based on improved artificial fish swarm algorithm. Sci. Rep. 2022, 12, 659. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Wang, F.; Bai, Y. Route planning for autonomous vessels based on improved artificial fish swarm algorithm. Ships Offshore Struct. 2023, 18, 897–906. [Google Scholar] [CrossRef]
- Zuo, J.; Chen, J.; Tan, Y.; Wang, M.; Wen, L. A Multi-Agent Collaborative Work Planning Strategy Based on AFSA-PSO Algorithm. In Proceedings of the 2019 International Conference on Robots & Intelligent System (ICRIS), Haikou, China, 15–16 June 2019; pp. 254–257. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Z.; Jiang, Y.; Cheng, L. Cooperative Path Planning for Multiple Mobile Robots via HAFSA and an Expansion Logic Strategy. Appl. Sci. 2019, 9, 672. [Google Scholar] [CrossRef]
- Zhang, K.; Mao, J.; Xiang, F.; Xuan, Z. A B-IHCA* multi-robot path planning algorithm based on bargaining game mechanism. J. Autom. 2022, 1–15. (In Chinese) [Google Scholar] [CrossRef]
- Gautier, A.; Stephens, A.; Lacerda, B.; Hawes, N.; Wooldridge, M. Negotiated path planning for non-cooperative multi-robot systems. Assoc. Comput. Mach. 2022, 1, 472–480. [Google Scholar] [CrossRef]
- Zhu, M.; Otte, M.; Chaudhari, P.; Frazzoli, E. Game theoretic controller synthesis for multi-robot motion planning Part I: Trajectory based algorithms. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1646–1651. [Google Scholar] [CrossRef]
- Silver, D. Cooperative pathfinding. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, Salt Lake, UT, USA, 8–12 October 2005; pp. 117–122. [Google Scholar] [CrossRef]
- Fan, N. Design of Conflict Avoidance Path Optimization Algorithm for Multi-Mobile Robots. Master’s Thesis, Nanjing University of Posts and Telecommunications, Nanjing, China, 2022. (In Chinese). [Google Scholar] [CrossRef]
- Mondada, F.; Gambardella, L.; Floreano, D.; Nolfi, S.; Deneuborg, J.; Dorigo, M. The cooperation of swarm-bots: Physical interactions in collective robotics. IEEE Robot. Autom. Mag. 2005, 12, 21–28. [Google Scholar] [CrossRef]
- Wang, Y.; Silva, C.W. A machine-learning approach to multi-robot coordination. Eng. Appl. Artif. Intell. 2008, 21, 470–484. [Google Scholar] [CrossRef]
- Verma, J.K.; Ranga, V. Multi-robot coordination analysis, taxonomy, challenges and future scope. J. Intell. Robot. Syst. 2021, 102, 1–36. [Google Scholar] [CrossRef] [PubMed]




| Type | Principle | Advantages | Disadvantages | Hardware Cost | Research Cost |
|---|---|---|---|---|---|
| LIDAR | Emit lasers to calculate distance and position. | High precision, accuracy, suitable for complexity. | Costly, limited field of view, bulky. | High | High |
| Camera (Visual Sensor) | Capture images, extract features for localization and mapping. | Affordable, lightweight, versatile. | Sensitive to lighting and texture, data-hungry. | Low | High |
| Semantic Sensor (e.g., Camera + Depth Sensor) | Capture images, recognize objects, landmarks, scenes, etc., providing semantics. | Rich semantic data. | High computational complexity, limited view. | Medium | High |
| Inertial Measurement Unit (IMU) | Measure linear acceleration and angular velocity for attitude and velocity estimation. | Lightweight, rapid response, indoor-friendly. | Accumulates errors, not suitable for long-term positioning. | Low | Low |
| Ultrasonic Sensor | Emit ultrasonic pulses for distance measurement. | Ideal for obstacle detection. | Limited range, lower precision. | Low | Low |
| GPS | Receive satellite signals for location determination. | Global coverage, outdoor suitability. | Insufficient precision, susceptible to obstructions. | Low | Low |
| Millimeter-Wave Radar | Use high-frequency radar waves to detect object positions. | Long-range capability, works well in harsh weather. | Expensive, larger size. | High | High |
| Thematic | Year | Results |
|---|---|---|
| Visual odometry and visual SLAM for mobile robots | 2015 | [16] |
| Multi-robot SLAM systems | 2016 | [17] |
| Vision SLAM Algorithms | 2017 | [18] |
| RGB-D SLAM | 2018 | [19] |
| Deep Learning for Visual SLAM in Transportation Robotics | 2019 | [20] |
| Semantic SLAM | 2020 | [21] |
| Solid State LiDAR(SSL) | 2021 | [22] |
| V-SLAM | 2022 | [23] |
| Deep Learning and Semantic Segmentation combined with Visual SLAM | 2023 | [24] |
| Types | Advantages | Disadvantages | Applications | Results |
|---|---|---|---|---|
| Scale Map | Simplifies construction; supports various navigation algorithms. | Mapping precision is hard to measure; struggles with unstructured environments. | Robot path and motion planning in static settings. | [25] |
| Topological Map | Handles complex environments; suitable for large-scale areas. | Difficulty representing detailed information; manual topological definitions needed. | Highways traffic management systems; large-scale robot formations. | [26] |
| Semantic Map | Describes object semantics; aids advanced robot tasks. | Requires advanced sensors and algorithms, struggles with dynamic objects. | Semantic setting modeling and robot speech interaction. | [27] |
| Behavior Map | Provides essential behavioral information; supports autonomous learning. | High construction and maintenance costs, limited accuracy and scope. | Autonomous planning, learning, and multitasking for robots. | [28] |
| Satellite Map | Offers genuine terrain and natural features. | Maps may lack real-time accuracy and updates. | Outdoor navigation and exploration for robots. | [29] |
| Indoor Map | Facilitates indoor navigation and localization. | Costly map creation and maintenance, necessitating real-time updates. | Indoor robot. | [30] |
| Traffic Map | Improves traffic efficiency, safety, and energy conservation. | Challenges in data acquisition and high maintenance costs; complex systems. | Security patrols and logistics robots. | [31] |
| Hybrid Map | Integrates multiple map types for comprehensive environmental data. | Persistent high costs in map creation and maintenance. | Autonomous vehicles and intelligent inspection robots. | [32,33] |
| Maps | Types | Numbers |
|---|---|---|
| Game | Dragon Age: Origins | 156 |
| Dragon Age 2 | 68 | |
| Warcraft III | 36 | |
| Baldurs Gate II (512 × 512) | 36 | |
| Baldurs Gate II | 120 | |
| Starcraft | 75 | |
| Real-World | City/street | 90 |
| Artificial | Mazes | 60 |
| Random | 40 | |
| Room | 40 | |
| Terrain | 20 |
| Maps | Cases | Map Scale |
|---|---|---|
| City | Berlin_1_256 | 256 × 256 |
| Game | den312d | 65 × 81 |
| Empty | empty-16-16 | 16 × 16 |
| Maze | maze-32-32-2 | 32 × 32 |
| Random | random-32-32-10 | 32 × 32 |
| Warehouse | warehouse-10-20-10-2-2 | 161 × 63 |
| Indicators | Definition | Performance Measurement | Evaluation Methodology | Focus Area |
|---|---|---|---|---|
| Path Length | Path length from start to end, possibly with multiple points. | Actual path length, optimal path length. | Compare robot and planned path lengths to assess algorithm effectiveness. | Autonomous navigation, including drones. |
| Safety | Robot’s hazard avoidance capability (e.g., narrow terrains). | Robotic collision detection, path safety assessment. | Evaluate planned path adaptability based on robot motion capabilities. | Autonomous vehicles, industrial and service robots. |
| Energy consumption | Energy needed for path planning. | Consider energy consumption in path metrics and robot energy management strategies. | Evaluate motion costs using energy models in simulations or real-world. | Agricultural and exploration robots. |
| Smoothness | Path curvature assessment. | Number of turns, curvature values. | Calculate path curvature through smoothing algorithms. | Industrial assembly and handling robots. |
| Path Deviation | Actual vs. planned path deviation. | Path offset, maximum path offset, offset distance. | Determine actual path-to-theory distance with offsets. | Medical robotics and precision machining. |
| Coverage Rate | Efficiency and completion ratio in defined areas. | Area coverage, point coverage, time coverage, distance coverage. | Calculate coverage metrics based on planning and area partitioning. | Detection and cleaning robots. |
| Time Efficiency | Path planning time. | Factors include algorithm time and space complexity, along with the robot’s real-world execution efficiency. | Analyze algorithm complexity, real-world performance, and comparisons. | Industrial automation, emergency rescue. |
| Robustness | Algorithm’s interference resistance. | Success rate or stability, tolerance of algorithms to robot hardware errors. | Compare algorithms in simulations and on real robots. | Robot exploration and rescue. |
| Real-time | Path planning response speed. | Response time, path planning algorithms to solve the balance of accuracy and speed. | Evaluate algorithm performance across different environments. | Self-driving cars, military robots. |
| Algorithm | Time | Characteristics | Research |
|---|---|---|---|
| PRM* | 2010 | A roadmap is constructed using an incremental approach that continuously improves the quality of the paths using a shortest path search algorithm as it samples and connects nodes. | [80] |
| Lazy PRM | 2000 | Minimizes the number of collision checks performed during planning, thus minimizing the planner’s runtime. | [81] |
| HPPRM | 2020 | Improved adaptability of the algorithm to multi-class complex environments. | [83] |
| Fuzzy-PRM | 2019 | Achieved dual metric optimization of path length and smoothness. | [84] |
| PRM-D* | 2023 | Dynamically adapts to environmental changes and unknown dynamic obstacles during the planning process. | [82] |
| Algorithms | Time Complexity |
|---|---|
| RRT-Connect | |
| RRT* | |
| RRT*-Smart | |
| RRT*-Connect | |
| PRM* | |
| Lazy PRM | |
| PRM-D* |
| Characteristics | Neural Network Algorithm | Fuzzy Logic Algorithm |
|---|---|---|
| Principle | Simulates biological neural system principles | Based on the theory of fuzzy set for inference |
| Advantages | Adapt to complex nonlinear problems with strong learning and generalization skills. | Manages fuzziness and uncertainty with interpretable rules. |
| Disadvantages | Demands abundant training data and computational resources, yielding less interpretable output. | Relies on manually defined fuzzy rules and membership functions; less adaptable to complex nonlinear problems. |
| MAPF | Advantages | Disadvantages |
|---|---|---|
| Centralized | Centralized planner for all agents in static or small-scale environments, fast and high-quality. | As the number of agents and environmental complexity increase, replanning becomes time-consuming |
| Distributed | Independent actions based on current observations, scalable to large-scale environments, and real-time path replanning. | Slower planning and learning in small, static environments compared to centralized algorithms. |
| Conflict Type | Recognition Methods | Constraints Type | |
|---|---|---|---|
| Basic Conflicts | Node Conflict | Two robots occupy the same grid center at the same time step | Obstacle constraints |
| Alignment Conflict | Two robots exchange positions within a time step | Obstacle constraints | |
| Deep Conflicts | Placeholder conflict | Robot path step is larger than conflict time step and solution space exists | Length Constraints |
| Target Conflict | The robot path step is much larger than the conflict time step. | Length constraints | |
| Blocking conflicts | When two or more robots try to pass through a narrow passage in opposite directions | Range Constraints | |
| Cycle conflict | When each robot moves to a vertex previously occupied by another robot, a “rotating loop” pattern is formed within the same time step. | Range Constraints | |
| Algorithm | Machines | Characteristics | Research |
|---|---|---|---|
| Lazy-CBS | Replaces the high-level solver of CBS with an inertly constructed constraint planning model that explores the conflict space using a core-guided depth-first search too and detects reusable branches along each branch. | Significantly improves the optimal MAPF problem under cost metrics | [202] |
| HCBS | Adds a heuristic function to the high-level search to better prune the constraint tree. | Ability to achieve better results with less computational cost | [203] |
| ECBS | Relaxing the optimal solution condition for the CBS runtime | Significant reduction in runtime | [204] |
| FECBS | Further reduce the number of conflicts that need to be resolved at high levels by using more relaxed suboptimal bounds for low-level search, while still providing bounded suboptimal solutions. | FECBS can solve more MAPF instances than ECBS within 5 min | [205] |
| ASB-ECBS | An adaptive intelligence-specific suboptimal bounds method, which can be executed statically or dynamically, allows suboptimal bounds to be assigned based on the requirements of individual intelligences. | Significantly improves the runtime while reducing the search space | [206] |
| Paper | Year | SAPF | MAPF | Environment Description | Path Metrics Description | Traditional Methods | AI Methods |
|---|---|---|---|---|---|---|---|
| [1] | 2023 | Y | N | Y | Y | Y | Y |
| [3] | 2021 | Y | N | N | Y | Y | Y |
| [35] | 2019 | N | Y | Y | Y | Y | N |
| [48] | 2016 | Y | N | N | Y | Y | N |
| [49] | 2020 | Y | N | Y | Y | Y | N |
| [108] | 2020 | Y | N | N | N | Y | N |
| [147] | 2020 | - | N | Y | |||
| [164] | 2021 | Y | N | N | N | N | Y |
| [165] | 2021 | N | Y | N | N | N | Y |
| [166] | 2022 | Y | Y | N | N | Y | N |
| [186] | 2023 | Y | N | N | N | N | Y |
| [187] | 2010 | Y | N | N | N | N | Y |
| [188] | 2022 | N | Y | N | N | Y | N |
| [224] | 2019 | Y | Y | N | N | Y | Y |
| [225] | 2013 | Y | Y | N | N | Y | N |
| [226] | 2023 | Y | N | N | N | Y | N |
| [227] | 2022 | N | Y | N | N | Y | Y |
| [228] | 2023 | Y | N | N | N | Y | N |
| [229] | 2023 | Y | N | Y | N | Y | Y |
| Ours | 2023 | Y | Y | Y | Y | Y | Y |
| SAPF | Category | Typical | Mechanisms | Advantages | Disadvantages | Improvements | ||
|---|---|---|---|---|---|---|---|---|
| Methods | Results | |||||||
| Classical Class Algorithms | Graph Search Algorithms | A* | Heuristic Search Based on Improved Dijkstra | Completeness and rapidity | May be limited by state space expansion in complex environments | Weights A* | [53,58] | |
| Adaptive A* | [54,58] | |||||||
| Theta* | [55,59] | |||||||
| Lazy-Theta* | [60] | |||||||
| JPS | [56] | |||||||
| LPA* | Incremental Heuristic Search Based on Improved A* | Dynamically updated path planning for dynamic environments | Requires local updates and global fixes, with some delay in response to environmental changes | TLPA* | [64] | |||
| TD* Lite | [64] | |||||||
| D* | Real-time update path planning for unknown and dynamic environments | Path oscillations and frequent replanning may exist | D* Lite | [63] | ||||
| MOD* Lite | [65] | |||||||
| MOPBD* | [66] | |||||||
| Randomized Sampling Algorithm | RRT | Randomized Sampling Search | Applicable to high-dimensional spaces and discontinuous problems | Limitations in solving globally optimal paths. | RRT-Connect | [68,73] | ||
| RRT* | [69,74,76] | |||||||
| RRT*-Smart | [70,77] | |||||||
| RRT*-Connect | [71,78] | |||||||
| Informed RRT*-connect | [72] | |||||||
| PRM | Sampling and connecting paths | Applicable to high-dimensional spaces and discontinuous problems | The distribution of sampling points and connection strategies may affect the quality of path planning. | PRM* | [80] | |||
| Lazy PRM | [81] | |||||||
| HPPRM | [83] | |||||||
| Fuzzy-PRM | [84] | |||||||
| PRM-D* | [82] | |||||||
| potential field algorithm | APF | Modeling of interaction forces between objects | Fast calculations and real-time updates | May fall into local minima, unable to pass through narrow passages, more sensitive to parameter selection and adjustment | Optimization of gravitational and repulsive structures | [86] [87] | ||
| Integrated algorithms | [88] [89] [90] | |||||||
| EBA | Path planning based on elastic band modeling | Adaptable to dynamic environments and obstacle avoidance | Parameter selection and tuning is more sensitive and may be less responsive to environmental changes | Considers time and dynamic constraints | [94,95] | |||
| Integrated algorithms | [96] | |||||||
| VFH | Construct vector fields and histograms of the environment | Suitable for complex environments and dynamic changes | May have computational complexity issues in high dimensional spaces and large-scale environments | VFH+ | [98] | |||
| VFH* | [99] | |||||||
| Integrated algorithms | [100,101] [102] | |||||||
| Intelligent Optimization Class Algorithms | Evolutionary Algorithms | GA | Modeling the Process of Biological Heredity | Global search capability and maintenance of diversity | Poor localized search capability; genetic factors are difficult to determine; chromosome coding method affects the solution | Improving individual quality, avoiding local optimal solutions, and improving poor population diversity | [136,137,138] | |
| Multi-objective GA | MOGA | [139,140,141] | ||||||
| NSGA-II | [39,141] | |||||||
| NSGA-III | [40,143] | |||||||
| Integrated algorithms | [144,145,146] | |||||||
| EA | Simulating the process of biological evolution | Suitable for global optimization and multi-objective optimization problems. | Search efficiency may be limited in complex environments and high-dimensional spaces | Evolutionary Strategies | [230] | |||
| Differential Evolutionary Algorithms | [231,232] | |||||||
| Multi-objective evolutionary algorithms | [233] | |||||||
| Heuristic Evolutionary Algorithms | [234] | |||||||
| Integrated algorithms | [234,235] | |||||||
| Group Intelligence Algorithms | ACO | Simulating the foraging behavior of ants | Fast convergence at the backend, memorable | Longer search time in the early stage; many parameters and difficult to set up | Structure, parameter selection and pheromones of optimization algorithms | [104,105,106] | ||
| Multi-objective ACO | [43,107] | |||||||
| Multi-cluster ACO | [109,110,111,112,113] | |||||||
| Integrated algorithms | [114,115,116] | |||||||
| PSO | Simulating the movement of particles in search space and sharing information | Few parameters; fast convergence in the early stage; memorability | Need to choose appropriate parameters and neighborhood search strategy | Parameter optimization | [118,119,120,121,122,123] | |||
| Increasing population diversity and avoiding local optimization | [124,125,126,127] | |||||||
| Multi-objective PSO | [42,128,129,130] | |||||||
| Integrated algorithms | [131,132,133] | |||||||
| Bionic Algorithms | Artificial Immune Algorithm (AIA) | Simulated antibody and immune memory mechanisms of the immune system | Global search and diversity maintenance | The choice of parameters and the design of immunization mechanism may affect the performance of the algorithm | Optimization algorithms for operations such as selection, mutation and cloning | [236,237] | ||
| Multi-objective AIA | [238,239] | |||||||
| Integrated algorithms | [240,241] | |||||||
| Artificial Fish Swarming Algorithm (AFSA) | Simulated the process of fish feeding and migration | Global search and group collaboration | Sensitive to parameter selection and tuning, the effectiveness of the algorithm is affected by the problem characteristics and environment | Adjustment of the behavioral capacity of the fish | [242,243] | |||
| Improve convergence and optimization | [244] | |||||||
| Integrated algorithms | [245,246] | |||||||
| Artificial Intelligence-like Algorithms | Neural Networks | Simulation of connections between neurons and activation functions for information processing | Strong learning ability to adapt to complex non-linear relationships | Requires a large amount of data for training, long training time, poor model interpretation | Self-organizing mapping NN | [148,149,150,151] | ||
| Deep Learning | Multi-layer neural networks for feature extraction and learning | Strong characterization ability, can automatically learn features and apply to large-scale data | Complex training process, requires large number of computational resources and data, may have overfitting problems | Deep Convolutional Neural Networks | [153,155,158] | |||
| Integrated algorithms | [154,156] | |||||||
| Reinforcement Learning | Learning behavioral strategies through trial and error and reward mechanisms | Can learn and make decisions autonomously in unsupervised environments with high adaptability | Requires a large amount of training time and number of interactions, low exploration efficiency, high requirements for environment modeling and reward design | Q-learning | [159,163] | |||
| DQN | [160,163] | |||||||
| DRL | [155,157,163] | |||||||
| Other | [161,164,165] | |||||||
| Fuzzy Logic | Fuzzy sets and fuzzy rule inference | Capable of handling uncertainty and ambiguity information, applicable to complex fuzzy environments | The design of knowledge representation and inference rules is complex and requires a lot of domain expert knowledge. | Solving Robot Uncertainty Navigation Problems | [167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] | |||
| MAPF | Characteristics | Advantages | Disadvantages | Results | |
|---|---|---|---|---|---|
| CMAPF | PP | The Prioritized Planning (PP) algorithm adopts a priority-based method to harmonize the actions of multiple robots, effectively addressing the challenge of waiting indefinitely for other robots to conclude tasks. |
|
| [196,197,198,199,200,201] |
| CBS | The Conflict-Based Search (CBS) algorithm stands as a conflict-detection-centered path planning strategy, tackling the intricacies of multi-robot path planning by identifying conflicts among the trajectories of robots. |
|
| [201,202,203,204,205,206] | |
| M* | The Market-Based Multi-Robot Path Planning (M*) algorithm introduces a market-driven mechanism to multi-robot path planning. It employs a trading framework to orchestrate both task allocation and path planning among a cohort of robots. |
|
| [247,248,249] | |
| IA* | The Improved A* (IA*) algorithm treats the path planning for individual robots as distinct endeavors. Each robot autonomously employs the A* algorithm for charting its path. |
|
| [250,251] | |
| MRC | The Multi-Robot Coordination (MRC) algorithm functions on the premise of cooperative coordination, forming the basis for multi-robot path planning. It segments robots into discrete teams, with each team collectively devising paths for its members. |
|
| [252,253,254] | |
| DMAPF | Local Informing Sharing | Robots share path planning-relevant information that they observe only with other robots within a specific range while executing tasks. | Low computational complexity; high system robustness. | Global optimal solution is difficult to guarantee; high probability of robot conflict. | [208,213,214,215,216] |
| Global Informing Sharing | All robots in the robot team share information they observe, including maps, sensor data, target locations, etc., in a global scope through communication and coordination. | Global optimal solution can be obtained; robot motion conflicts can be avoided as much as possible. | High computational complexity; poor robustness. | [210,211,212,217,219] | |
| Hybrid Informing Sharing | The approach involves integrating both localized and global information for collaborative path planning and decision-making. | Local and global information are utilized at the same time, and a better path planning scheme can be obtained. | Difficult to realize; requires more communication and computational resources. | [209,220,221,222] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Li, P.; Qian, S.; Quan, H.; Miao, J.; Liu, M.; Hu, Y.; Memetimin, E. Path Planning Technique for Mobile Robots: A Review. Machines 2023, 11, 980. https://doi.org/10.3390/machines11100980
Yang L, Li P, Qian S, Quan H, Miao J, Liu M, Hu Y, Memetimin E. Path Planning Technique for Mobile Robots: A Review. Machines. 2023; 11(10):980. https://doi.org/10.3390/machines11100980
Chicago/Turabian StyleYang, Liwei, Ping Li, Song Qian, He Quan, Jinchao Miao, Mengqi Liu, Yanpei Hu, and Erexidin Memetimin. 2023. "Path Planning Technique for Mobile Robots: A Review" Machines 11, no. 10: 980. https://doi.org/10.3390/machines11100980
APA StyleYang, L., Li, P., Qian, S., Quan, H., Miao, J., Liu, M., Hu, Y., & Memetimin, E. (2023). Path Planning Technique for Mobile Robots: A Review. Machines, 11(10), 980. https://doi.org/10.3390/machines11100980






