Tachometer-Less Synchronous Sampling for Large Speed Fluctuations and Its Application in the Monitoring of Wind Turbine Drive Train Condition

Abstract

Accurate shaft speed extraction is crucial for synchronous sampling in the fault diagnosis of wind turbines. However, traditional narrow-bandpass filtering techniques face limitations when dealing with large fluctuations in rotational speed, hindering the accurate construction of an instantaneous phase for synchronous resampling of a shaft. To overcome this, we propose a tachometer-less synchronous sampling based on Scaling-Basis Chirplet Transform, tailored to a wind turbine’s structure and operating conditions. The algorithm generates a time–frequency representation of the vibration response, revealing time-varying characteristics even under large speed fluctuations. Using maximum tracking on the time–frequency spectrum, we extract instantaneous speed and compare its accuracy with tachometer-acquired results. The instantaneous phase is obtained through numerical integration, and vibration data are resampled synchronously using inverse function interpolation in the digital domain. Numerical simulations and practical cases of wind turbines demonstrate the effectiveness and the engineering applicability of our methodology.

1. Introduction

The escalating global demand for clean energy, coupled with remarkable advancements in wind turbine manufacturing technology, has resulted in a consistent upward trajectory in installed wind turbine capacity. Notably, maintenance costs associated with onshore and offshore wind turbines constitute a substantial proportion of wind farm revenues, estimated to range from 10 to 15% for onshore turbines and 20–35% for offshore turbines [1]. Among the various types of faults encountered in wind turbines, the mechanical components within the drive chain pose the most significant financial burden in terms of removal and repair [2]. Consequently, the implementation of condition monitoring systems specifically designed to diagnose and address drive-chain-related issues has become standard practice. Recent overviews on wind turbine condition monitoring systems can be found in the open literature, such as in references [3,4,5]. Within the industry, vibration-sensor-based condition monitoring has gained prominence due to its well-established maturity and cost-effectiveness [6].

Wind turbines operate under time-varying speed conditions, leading to frequency modulation and spectrum dispersion. This poses challenges for fault diagnosis based solely on spectrum analysis. To address these issues, the synchronous technique has emerged as an effective approach. Unlike traditional equal-time sampling methods, synchronous sampling involves resampling the vibration response at constant angular intervals. This approach mitigates the impact of speed fluctuations on the order spectrum, enabling more accurate fault diagnosis. Furthermore, the synchronous technique can be combined with synchronous averaging to eliminate asynchronous periodic components as well as the noise. As a result, the synchronous technique has gained wide recognition for its utility in early fault diagnosis of wind turbines.

Traditionally, synchronous techniques for fault diagnosis in wind turbines relied on auxiliary equipment like tachometers or encoders to provide shaft speed references for signal resampling. However, this approach is limited by constraints in shaft mounting space, sensor technology, and operational conditions. These limitations result in increased costs. Consequently, engineers have been actively exploring methods to extract rotational speed directly from vibration. Bonnardot et al. [7] proposed a band-pass-filter-based synchronous sampling method that isolates the gear mesh response or its harmonics, enabling resampling of the vibration response based on the phase of the isolated signal. Building upon this approach, Combet et al. [8] improved the scheme by automating the selection of mesh harmonics. However, the conventional method of extracting a single component using a traditional band-pass filter is suitable only for cases with small speed variations where adjacent harmonic frequency bands can be separated in the frequency domain. In situations with significant speed fluctuations, the overlapping of harmonic bands makes it challenging to extract individual harmonics from the signal using the band-pass filtering method. This limitation restricts the application of synchronous techniques in fault diagnosis.

Time–frequency analysis (TFA) offers a promising approach to address the challenges posed by large speed fluctuations. By mapping the one-dimensional time series onto a two-dimensional time–frequency plane, it visually represents the time-varying characteristics of the frequency. Urbanek et al. [9] proposed a shaft speed extraction scheme based on TFA. Short-Time Fourier Transform (STFT) was applied to obtain the time–frequency representation (TFR) of the vibration response. The estimated speed derived from the spectrogram was utilized for angular resampling. Subsequently, the desired components were extracted in the angular domain using a band-pass filter and resampled back to the time domain. Wang et al. [10] employed a fast spectral kurtosis algorithm to obtain the bearing envelope signal adaptively. Subsequently, the instantaneous fault characteristic frequency was extracted for signal resampling based on the TFR of STFT. Zhu et al. [11] estimated the instantaneous speed using STFT and resampled the vibration in the angular domain. The Teager–Kaiser energy operator was then applied to enhance the fault components in the signal, followed by processing the enhanced signal using fast spectral correlation. Envelope analysis was performed to extract the fault characteristics of rolling bearings. Nonetheless, because of inherent limitations in time–frequency resolution, this conventional TFA method results in a substantial error in identifying the shaft speed.

In order to achieve high-resolution representations, numerous advanced TFA methods have been developed in the past decade. Among these methods, the basis transform approach has garnered significant interest from researchers. Linear chirp basis is a prominent example, and it is commonly used in Chirplet Transform (CT) [12] for analyzing chirp-like signals with linear frequency conversions. Zhao et al. [13] employed the CT to obtain the TFR and extract a specific harmonic of the rotational frequency. The identification results were then utilized in Vold–Kalman filters to extract the harmonics for synchronous resampling of the original signal based on its instantaneous phase. Polynomial Chirplet Transform (PCT) [14] replaces the linear basis with a polynomial basis to analyze single-component signals with nonlinear frequency trajectories. Wang et al. [15] utilized the PCT to estimate the instantaneous rotational frequency of rolling bearings. On this basis, a maximum correlated kurtosis deconvolution-based envelope order spectrum was employed to detect the bearing fault characteristic order. While the abovementioned algorithms provide good TFR for single-component signals, they do not yield satisfactory results for multi-component signals since the chirp basis cannot simultaneously match the instantaneous frequency (IF) trajectories of multiple components. To tackle the analysis of practical multicomponent signals, which are commonly encountered, General Linear Chirplet Transform (GLCT) [16] was developed. This method obtains a set of TFRs using various chirp parameters and selects the TFR with the highest amplitude at each point to form the final TFR. GLCT has demonstrated favorable results for both single-component and multicomponent signals. Liu et al. [17] applied GLCT to estimate the instantaneous rotation frequency. The angular domain signal was then purified using an adaptive cross-validation threshold denoising algorithm, aiming to enhance the fault feature extraction performance of the envelope order spectrum method. However, these TFA methods are less effective in dealing with multicomponent signals with small intervals between adjacent frequency components.

During wind turbine operation, the complex structure of the gearbox introduces intricate amplitude and frequency modulation, especially when gear damage occurs. These modulation components manifest as time–frequency ridges close to the meshing frequency and its harmonics in TFR [18]. However, identifying the meshing frequencies that are associated with shaft speeds using TFA faces significant challenges. At low wind speeds, neighboring frequency ridges are closely spaced, while variable speed conditions lead to the blurring of time–frequency ridges. These factors pose difficulties for conventional TFA methods.

Li et al. introduced the Scaling-Basis Chirplet Transform (SBCT) [19], which employs a second-order polynomial to construct the chirplet basis function. This time–frequency basis can adaptively scale within a specified window and utilizes the kurtosis criterion to determine optimal parameters for matching the desired frequency trajectory. Consequently, it generates a time and frequency varying linear chirp basis. Compared to other TFA methods, SBCT exhibits notable advantages in effectively handling synchronous signals characterized by dense frequency content and nonlinear variations, including harmonic components of vibration signals, modulated signals with complex sidebands, and signals with strong noise backgrounds.

Therefore, a simple and yet effective approach is proposed in this paper. The SBCT is employed to perform time–frequency transformation of wind turbine vibration data first. The instantaneous shaft speed is identified from the time–frequency spectrogram by the maxima tracking. The phase information of the target shaft speed is derived by numerical integration. The original signal is then resampled synchronously using an inverse function interpolation method. Order analysis without tachometer assistance is finally achieved and the damage feature is extracted from the order spectrum.

The rest of this paper is structured as follows: Section 2 illustrates the principle of SBCT algorithm. Section 3 describes the process of the SBCT-based instantaneous shaft speed identification method. Section 4 details the process of this methodology through numerical simulation signals. Section 5 verifies the proposed methodology with two practical cases of wind turbines. Finally, Section 6 provides the conclusion.

2. SBCT Algorithm

Time–frequency analysis expands the signal from a one-dimensional time series to a two-dimensional time–frequency plane in order to observe the IF of the signal. CT is the inner product between the signal and the chirp basis, and the CT of the signal $x\left(t\right)$ can be expressed as follows:

$$\begin{array}{c}CT(\tau ,f,c)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}s\left(t\right)w(t-\tau )\exp (-j2\pi \frac{c}{2}(t-\tau {)}^2)\exp (-j2\pi ft)dt\\ ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}s\left(t\right)w\left(t-\tau \right)\exp (-j2\pi \phi \left(\tau ,f,t\right))dt\end{array}$$

(1)

$$s(t)=x(t)+j\frac{1}{\pi }{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{x\left(\tau \right)}{t-\tau }d\tau$$

(2)

$$w\left(t\right)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{1}{2}{\left(\frac{t}{\sigma }\right)}^2\right)$$

(3)

$$\phi (\tau ,f,t)=ft+\frac{c}{2}(t-\tau {)}^2$$

(4)

where $s\left(t\right)$ is the analytic signal of $x\left(t\right)$ generated by the Hilbert transform; $w\left(t\right)$ denotes a real, nonnegative, symmetric and normalized window function, usually denoted as a Gaussian function; $\mathsf{\sigma }$ denotes the standard deviation; $\phi (\tau ,f,t)$ is the phase function; $f\in \mathbb{R}$ and $t\in \mathbb{R}$ represent the frequency center and time center, respectively; and $c\in \mathbb{R}$ represents the chirp rate, which is a constant.

The first- and second-order derivatives of $\phi (\tau ,f,t)$ are expressed as:

$$\phi \prime \left(\tau ,f,t\right)=\frac{\partial \phi }{\partial t}=f+c(t-\tau )$$

(5)

$$\frac{\partial \phi \prime }{\partial t}=c=-\tan \theta$$

(6)

where $\phi \prime \left(\tau ,f,t\right)$ denotes the IF and $\theta$ is the rotation angle of the IF trajectory, which varies from $-\pi /2$ to $\pi /2$.

The CT is essentially a windowed transformation. The ultimate TFR is constructed by processing each segment of the windowed signal. The degree of energy concentration in the TFR increases with improved alignment between the TF bases and the IF trajectory. The TFR demonstrates maximum energy concentration when the TF bases entirely coincide with the IF trajectories [20]. This happens when the tangent value of the rotation angle matches the slope of the target IF trajectory.

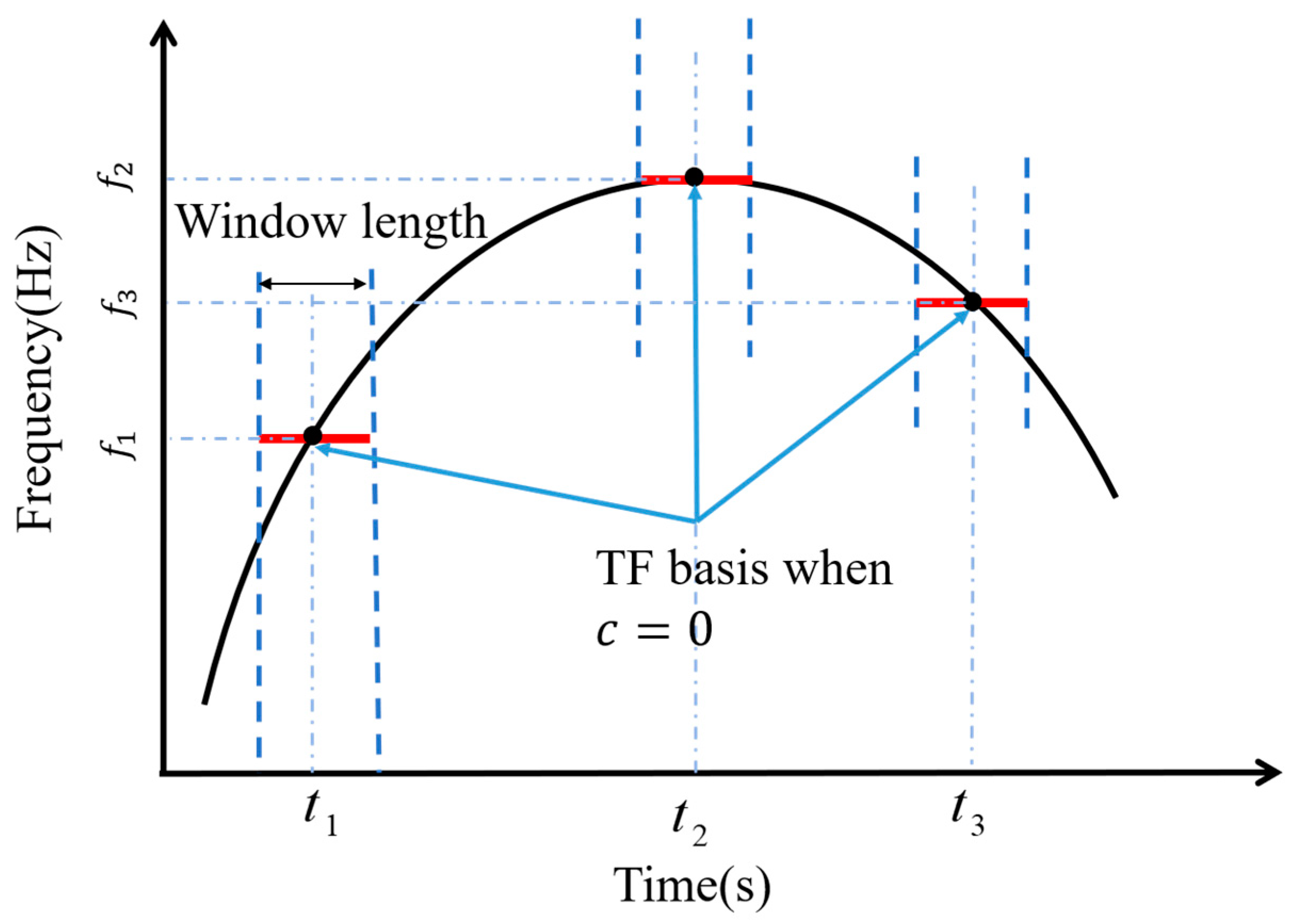
The matching principle between the TF bases and target IF trajectories within a specific window length is elucidated in the following three figures. The black line is the true IF, the red line denotes the TF base, and the blue dashed line denotes the analysis window.

A point on the IF is represented by a black dot, and its time and frequency values are marked with a light blue dashed line.

As per Equation (6), when $c$ is set to zero, the CT becomes equivalent to the STFT, as illustrated in Figure 1. In essence, the STFT can be seen as a simplified variant of the CT when $c$ equals zero. In such instances, the TF bases run parallel to the time axis, aligning exclusively at the time center $t_2$. Mismatches occurring elsewhere lead to notably diminished energy concentration.

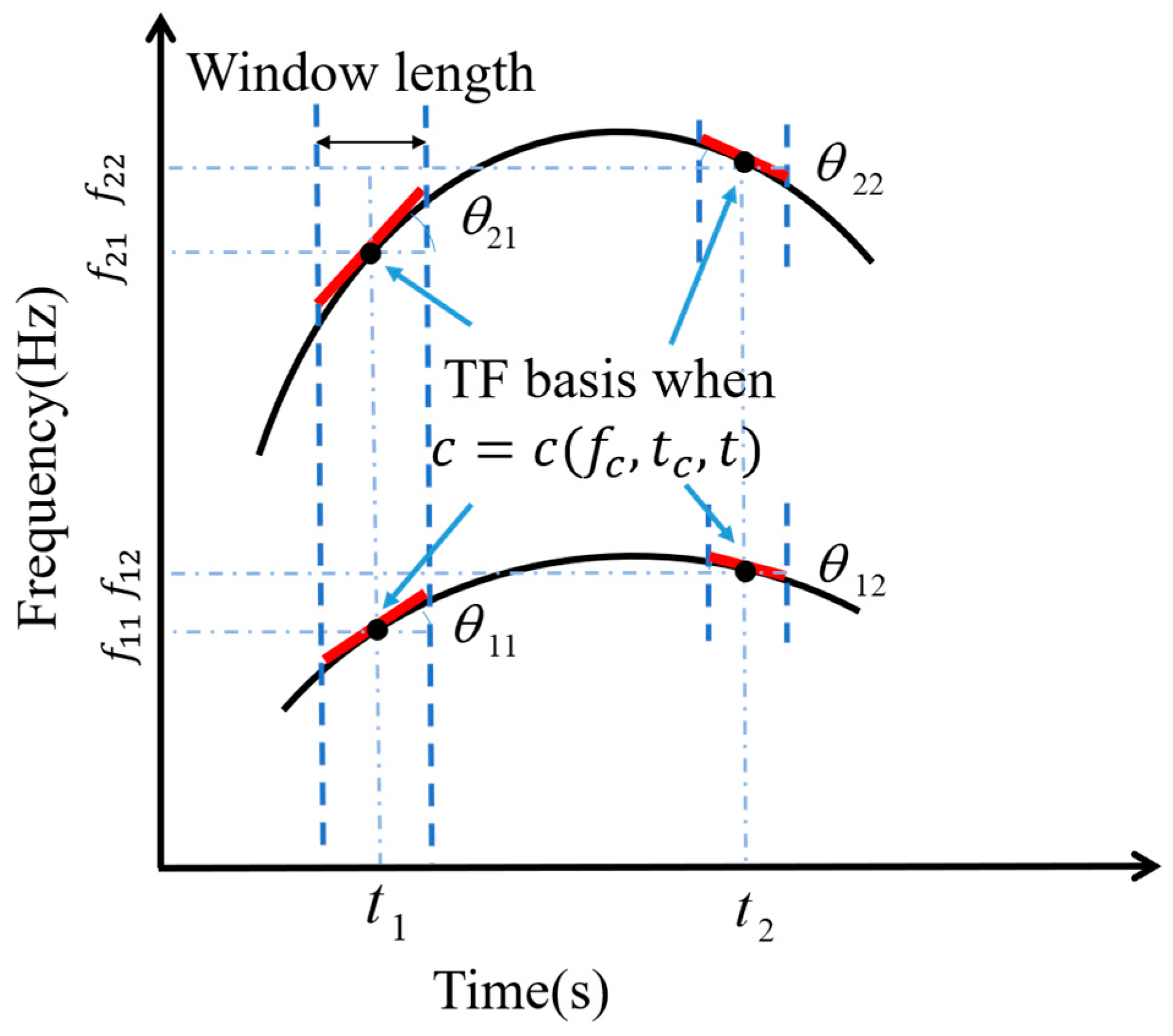
If C represents a nonzero constant, the TF bases undergo rotation by an angle $\theta =-\arctan \left(c\right)$ around the points ($t_i$, $f_i$) ($i=\mathrm{1,2},3)$, as depicted in Figure 2. When the chirp rate closely matches the slope of the time–frequency ridge or, in simpler terms, the rotation angle of the bases closely matches the inclination angle of the IF trajectory, this results in higher energy concentration within the TFR. Consequently, CT exhibits superior performance in processing linear frequency modulation (FM) signals when compared to STFT.

However, the CT’s constant chirp parameters impose limitations when analyzing highly nonlinear FM signals. When handling nonlinear FM signals, both STFT and CT struggle to achieve significant energy concentration at specific time points. For instance, the STFT results at $t_1$ and the CT results at $t_3$.

SBCT constructs the chirp basis by means of a second-order polynomial. Its second-order derivative, i.e., the chirp parameter, varies adaptively with frequency and time, and matches the time–frequency trajectories of different frequency components and time centers. The new phase function is constructed in the following form:

$${\phi }_s\left(f,t,\tau ,a_1,a_2,\cdots ,a_n\right)=f\times \left[t+\sum _{k=1}^n{a}_k{\left(t-\tau \right)}^{1+k}\right]$$

(7)

The corresponding first-order and second-order derivatives are expressed as follows:

$${\phi }_s^{\prime }=\frac{\partial {\phi }_s}{\partial t}=f\times \left[1+\sum _{k=1}^n\left(1+k\right)a_k{\left(t-\tau \right)}^k\right]$$

(8)

$$-\tan \theta =\frac{\partial {\phi }_s^{\prime }}{\partial t}=f\times \left[\sum _{k=1}^n\left(1+k\right)k{a}_k{\left(t-\tau \right)}^{k-1}\right]$$

(9)

Equation (9) can be rewritten when $t$ is equal to the time center $\tau$ as follows:

$$-\tan \theta =2f{a}_1+\sum _{k=2}^{K}f(k+1)k(t-\tau {)}^{k-1}=2f{a}_1$$

(10)

where $\theta$ is the rotation angle of the time–frequency basis at the time center $\tau$. From Equation (10), it can be seen that the value of $\theta$ varies with the frequency center, that is, the chirp rate varies with the range of the frequency trajectory. For a multicomponent signal with $N$ frequency components at the time center $\tau$, the chirp rate can be calculated as follows:

$$-\tan \left({\theta }_n\right)=2f_n{a}_1, n=\mathrm{1,2},\cdots N$$

(11)

Considering $t=\tau +\mathsf{\Delta }t$, Equation (11) can be rewritten as follows:

$$-\tan ({\theta }_n)=\sum _{k=1}^K{f}_n(k+1)k{a}_k(\mathsf{\Delta }t{)}^{k-1},n=\mathrm{1,2},\cdots ,N$$

(12)

In summary, the SBCT of the signal $x\left(t\right)$ is expressed as follows:

$$SBCT\left(f,\tau ,a_1,a_2\cdots ,a_n\right)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}s\left(t\right)w\left(t-\tau \right)\exp \left(-j2\pi f\times \left(t+\sum _{k=1}^n{a}_k{\left(t-\tau \right)}^{1+k}\right)\right)dt$$

(13)

where $a_1,a_2,\cdots ,a_n$ are parameters that need to be determined before performing SBCT. Considering the balance between accuracy and cost of the calculation, the value $n$ is usually taken as 2.

According to the theory proposed by Ville, the analytic signal can be written as follows:

$$s(t)=A(t)\exp (j2\pi \int f\left(t\right)dt)$$

(14)

where $A\left(t\right)$ denotes the instantaneous amplitude and $f\left(t\right)$ denotes the IF.

Based on the Taylor expansion, the IF within the window length can be written as follows:

$$f\left(t\right)\approx f\left(\tau \right)+f\prime (\tau )(t-\tau )+\frac{f^{″}(\tau )}{2}(t-\tau {)}^2$$

(15)

where $f\left(\tau \right)$ is the value of the IF at the moment $\tau$; $f\prime \left(\tau \right)$ and $f^{″}\left(\tau \right)$ are the first and second order derivatives of the IF. Higher-order terms are neglected in Equation (15).

Substituting Equations (14) and (15) into Equation (13), the following expressions are obtained:

$$\begin{array}{l}\left|SBCT\left(f,\tau ,a_1,a_2\right)\right|\\ =\left|{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}A\left(t\right)\exp \left(j2\pi \int f\left(t\right)\mathit{dt}\right) w\left(t-\tau \right)\exp \left(\left.-j2\pi {\phi }_s(f,\tau ,t,a_1,a_2\right)\right)dt\right|\\ =\left|{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}A\left(t\right)w\left(t-\tau \right)exp\left(j2\pi {\left(t-\tau \right)}^2\left(\frac{f^{\prime }\left(\tau \right)}{2}-a_{1}f\left(\tau \right)\right)\right)exp\left(j2\pi {\left(t-\tau \right)}^3\left(\frac{f^{″}\left(\tau \right)}{6}-a_{2}f\left(\tau \right)\right)\right)dt\right|\\ \le \left|{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}A\left(t\right)w(t-\tau )dt\right|\end{array}$$

(16)

When the two following equations are satisfied, the equation in Equation (16) holds and $\left|SBCT\left(f,\tau ,a_1,a_2\right)\right|$ takes the maximum value, i.e., the highest energy concentration level.

$$\frac{f\prime \left(\tau \right)}{2}-a_{1}f(\tau )=0$$

(17)

$$\frac{f^{″}\left(\tau \right)}{6}-a_{2}f(\tau )=0$$

(18)

Equations (17) and (18) can be rewritten as follows:

$$a_1=\frac{f\prime \left(\tau \right)}{2f\left(\tau \right)}$$

(19)

$$a_2=\frac{f^{″}\left(\tau \right)}{6f\left(\tau \right)}=\frac{f^{″}\left(\tau \right)}{3f\prime \left(\tau \right)}{a}_1$$

(20)

Usually, the IF of an arbitrary signal is not known a priori, but the trajectory inclination $\gamma$ of the IF must vary from $-\pi /2$ to $\pi /2$. Therefore, $\gamma$ can be discretized in the following form:

$${\gamma }_1(i)=-\frac{\pi }{2}+\frac{\pi }{M+1}i i=\mathrm{1,2},3,\cdots M$$

(21)

$${\gamma }_2(i)=-\frac{\pi }{2}+\frac{\pi }{N+1}i i=\mathrm{1,2},3,\cdots N$$

(22)

where $M$ and $N$ denote the number of discretization points in the angle range from $-\pi /2$ to $\pi /2$.

Therefore, there exist ${\gamma }_{1i}$ and ${\gamma }_{2i}$ approximating the following equation:

$$a_1\approx \mathrm{t}\mathrm{a}\mathrm{n} \left({\gamma }_{1i}\right)$$

(23)

$$a_2\approx \mathrm{t}\mathrm{a}\mathrm{n} \left({\gamma }_{1i}\right)\mathrm{t}\mathrm{a}\mathrm{n} \left({\gamma }_{2i}\right)$$

(24)

The finer the discretization of $\gamma$, the more accurate the values of $a_1$ and $a_2$. This facilitates the coincidence of the basis with the IF trajectory. Hence, $M$ and $N$ are usually taken as large values to satisfy $a_1$ and $a_2$ in Equations (23) and (24).

In order to further reduce the computational burden, a common practice is to introduce factors $m_0$ and $n_0$ and redefine as follows:

$$a_1\approx \frac{\mathrm{t}\mathrm{a}\mathrm{n} \left({\gamma }_1\right)}{m_0}$$

(25)

$$a_2\approx \frac{\mathrm{t}\mathrm{a}\mathrm{n} \left({\gamma }_1\right)\mathrm{t}\mathrm{a}\mathrm{n} \left({\gamma }_2\right)}{n_0}$$

(26)

where $m_0$ and $n_0$ are parameters generally larger than 1 that produce moderate variations in $\mathrm{t}\mathrm{a}\mathrm{n} \left(\gamma \right)$ when $M$ and $N$ are set to low values. If the target IF trajectory changes drastically, the values of $m_0$ and $n_0$ will be set to lower values, e.g., 1.

When the rotation angle of the basis is approximately equivalent to the inclination angle of the IF trajectory, the amplitude of the frequency component reaches the maximum. The kurtosis reaches the maximum as well under this condition. Therefore, ${\gamma }_1\left(\tau \right)$ and ${\gamma }_2\left(\tau \right)$ can be determined in accordance with the following kurtosis theory:

$$\left({\mathsf{\gamma }}_1\left(\tau \right),{\mathsf{\gamma }}_2\left(\tau \right)\right)=\underset{({\mathsf{\gamma }}_1,{\mathsf{\gamma }}_2)}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}\left(\frac{\left({\int }_0^{V}SBC{T}^4(f,\tau ,{\gamma }_1,{\gamma }_2)dv\right)/V}{{\left(\left({\int }_0^{V}SBC{T}^2(f,\tau ,{\gamma }_1,{\gamma }_2)dv\right)/V\right)}^2}\right)$$

(27)

where the frequency range in TFR is $\left[0,V\right]$.

Hence, SBCT can be expressed as:

$$SBCT\left(\tau ,f,a_1,a_2\right)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}x\left(t\right)w\left(t-\tau \right)\exp (-j2\pi f\times (t+a_1{\left(t-\tau \right)}^2+a_2{\left(t-\tau \right)}^3))dt$$

(28)

The schematic diagram of SBCT is shown in Figure 3. The chirp rate varies with both frequency and time, achieved by searching for the best parameters around the respective time centers $t_c$ by kurtosis theory. By assigning reasonable values to $a_{1 }\mathrm{a}\mathrm{n}\mathrm{d} a_{2 }$, the TF base is “scaled” within a certain window length. This scaling enables the bases to effectively match the nonlinear IF trajectory of a multicomponent signal and thus improves the TFR energy concentration.

3. Synchronous Sampling with SBCT

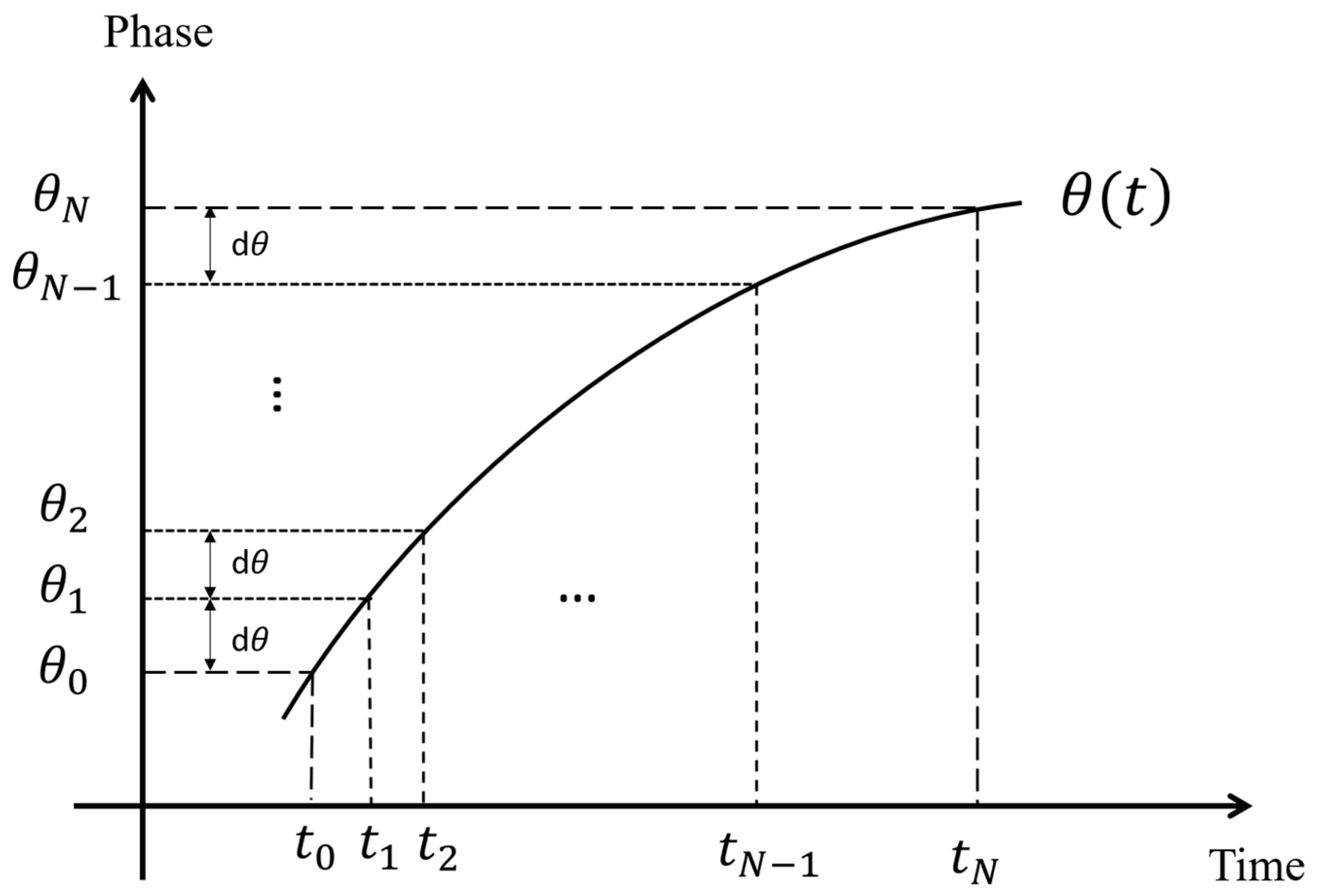
During the operation of rotating machinery, the failure characteristic frequency of a mechanical component, such as shaft unbalance response or damage characteristics of bearings and gears, are directly related to the speed of the shaft to which the component is connected. When the shaft speed changes, discretizing the vibration response signal in an equal-delta-time manner can lead to the dispersion of frequency components in the spectrum, making it difficult to identify fault features (as shown in Figure 4A). By resampling the vibration data with equal shaft circumferential angles, the response signal is converted into a cyclostationary waveform over the shaft period, which makes it achieve minimal or no energy leakage on the order spectrum, and therefore, a higher-precision fault feature can be extracted (as shown in Figure 4B).

The key to performing synchronous sampling is to acquire an accurate shaft rotational speed. There are many ways to extract the instantaneous speed from the vibration response. Time–frequency spectrogram-based maximum tracking is a technique that is easy to understand and implement. Figure 5 shows the flow chart of this methodology, where the SBCT is employed in TFA due to its IF energy concentration and closely spaced frequency component separation capabilities.

The main steps of the procedure are as follows:

• Convert vibration response into TFR by SBCT.

For a discrete vibration time series, perform SBCT to form a TFR:

$$\begin{gathered} SBCT(a,b)=\sum _{t=0}^{T-1}s\left(t\right)w\left(t-b\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-j2\pi \frac{a}{T}(t+a_1(t-b{)}^2+a_2\left(t-b{)}^3\right)\right) \\ a=\mathrm{0,1},\cdots ,T-1 \end{gathered}$$

(29)

where $T$ is the window size.

2.

Track the maxima value to extract the instantaneous speed. The maximal tracking algorithm tracks the maximum magnitude point in the frequency direction at each time point. Assume that in the acceleration-based time–frequency spectrogram the rotational frequency is $f\left(t\right)$. The most significant component of the vibration response is not necessarily the shaft response itself, but some other frequency response, such as the gear mesh response or its harmonics, that may have a better overall signal-to-noise ratio (SNR). To improve the detection accuracy, the maximum value can be tracked at the frequency component of $cf\left(t\right)$, where $c$ is a constant determined by the kinematics of the mechanical system. From the identified frequency, the shaft speed can be established.

3.

Identify the instantaneous phase $\theta \left(t\right)$. From the identified IF $f\left(t\right)$, assuming $\theta \left(0\right)=0$, the instantaneous phase is obtained by integration of $f\left(t\right)$:

$$\theta (t)={\int }_{t_0}^{t}f\left(\tau \right)d\tau$$

(30)

4.

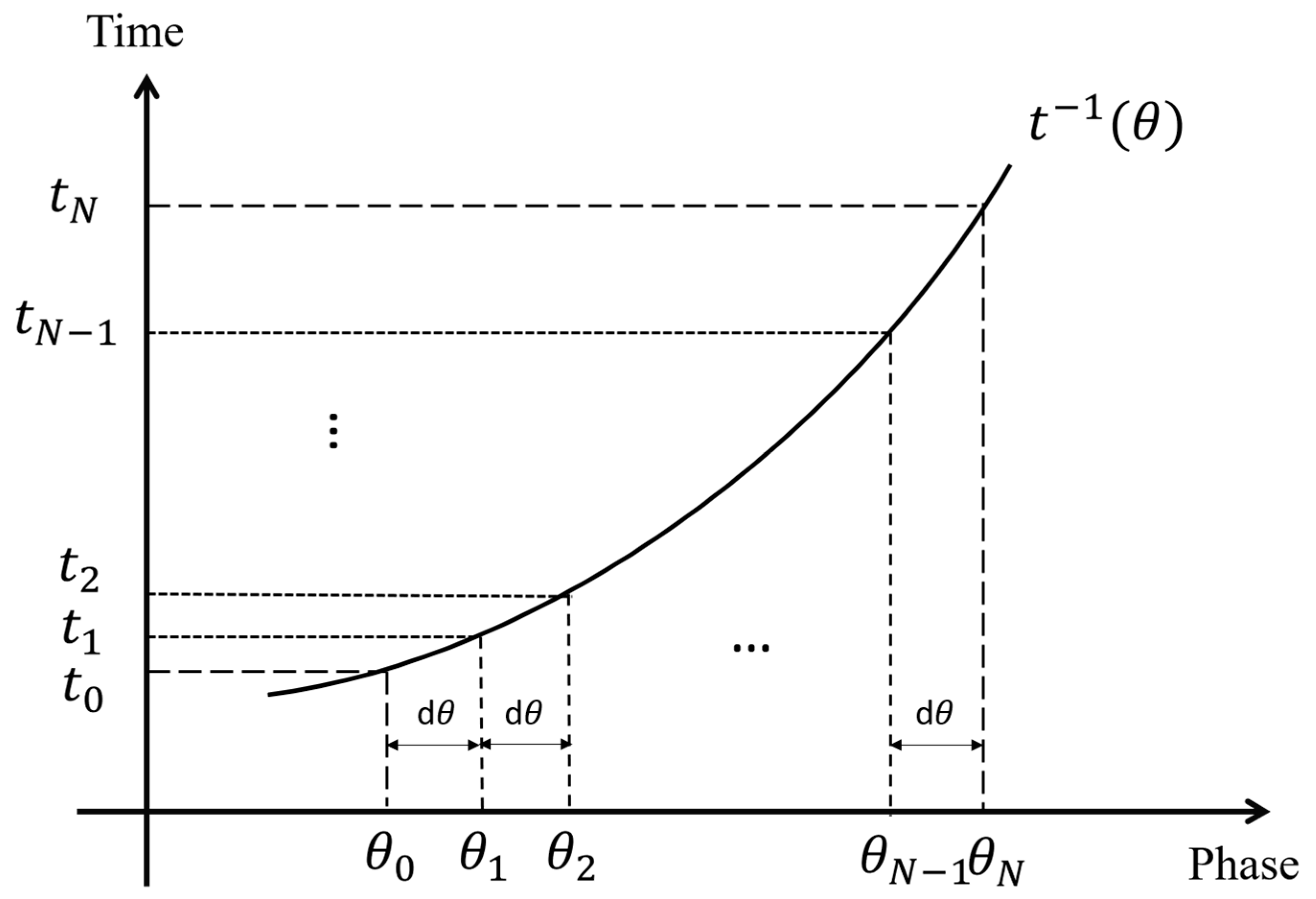
Determine the synchronous sampling time locations based on inverse function interpolation. As shown in Figure 6, suppose the shaft rotates one circle from $t_0$ to $t_N$, and the number of points sampled synchronously is $N$. Then, the time point of each equal rotation angle, $t_i(i=\mathrm{1,2},\cdots N)$, can be resolved by the following equation in turn:

$$\theta \left(t_i\right)-\theta \left(t_{i-1}\right)=\frac{1}{N},i=\mathrm{1,2},\cdots N$$

(31)

where $\mathrm{d}\theta$ (y-axis direction) stays equalized. However, solving Equation (31) by conventional methods requires numerical iterations, and is thus time consuming. If only the unidirectional shaft rotation is considered, the instantaneous phase function $phase=\theta \left(t\right)$ is a time-monotonic function. Its inverse function $t={\theta }^{-1}\left(phase\right)$ exists and is an equally monotonic property. As shown in Figure 7, assuming that the discrete points ${phase}_i\left(i=\mathrm{0,1},\cdots ,N\right)$, it follows that

$$phas{e}_N-phas{e}_0=1$$

(32)

$$phas{e}_i-phas{e}_{i-1}=\frac{1}{N},i=\mathrm{1,2}\cdots N$$

(33)

where $\mathrm{d}\theta$ (x-axis direction) stays equalized. The discrete sampling time points, $t_i(i=\mathrm{1,2},\cdots N)$, can be obtained by interpolating (evaluating) the inverse function $t={\theta }^{-1}\left(phase\right)$, i.e.,

$$t_i={\theta }^{-1}\left(phas{e}_i\right),i=\mathrm{1,2}\cdots ,N$$

(34)

By employing this approach, the computation of time stamps corresponding to shaft equal rotation angles is accomplished through a dependent variable evaluation process, rather than an iterative process. As a result, the computational time cost is significantly reduced. Furthermore, since there is no approximation involved in the evaluation of the inverse function, the synchronous resampling based on the inverse function of the instantaneous phase is expected to yield higher accuracy.

4. Numerical Simulation

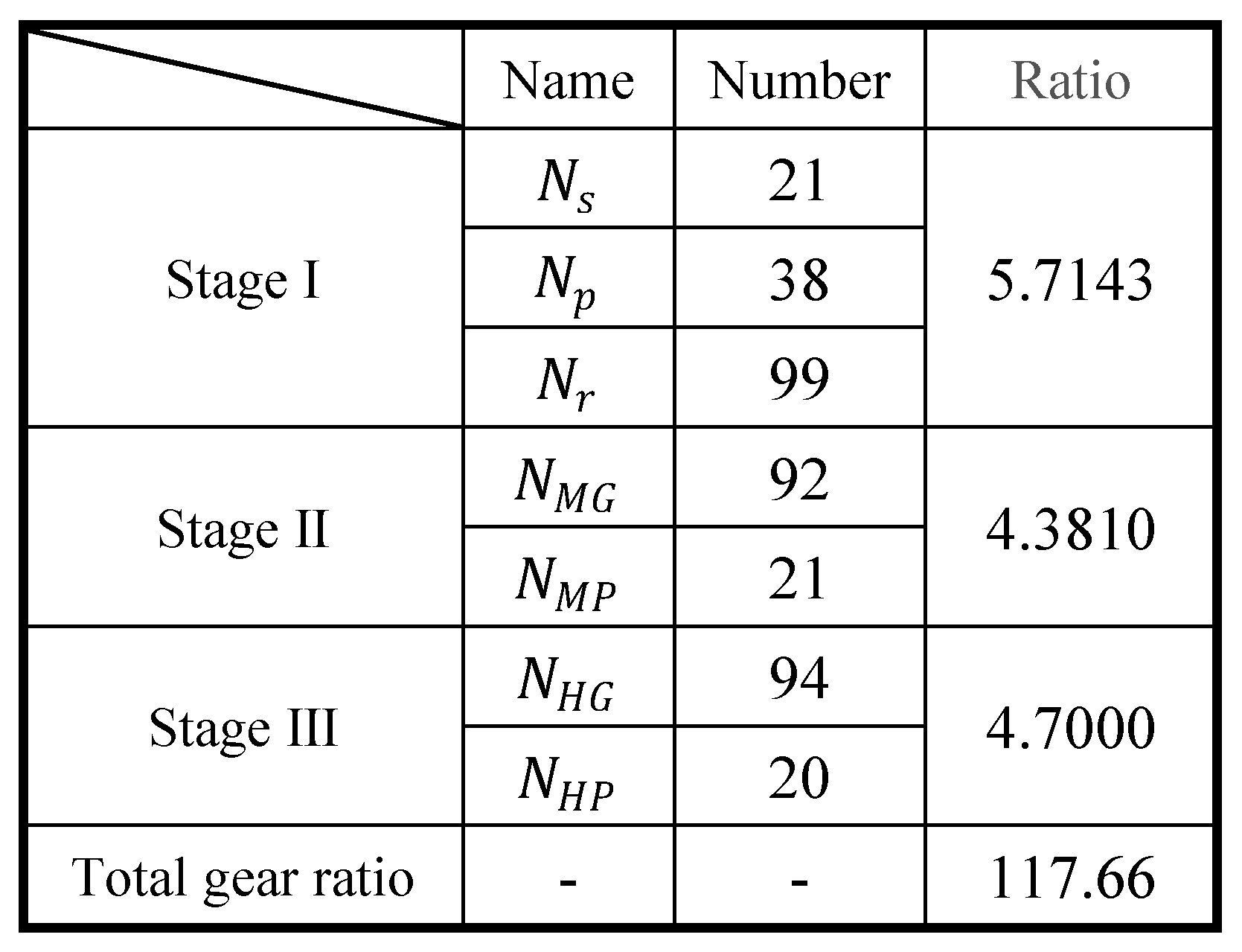
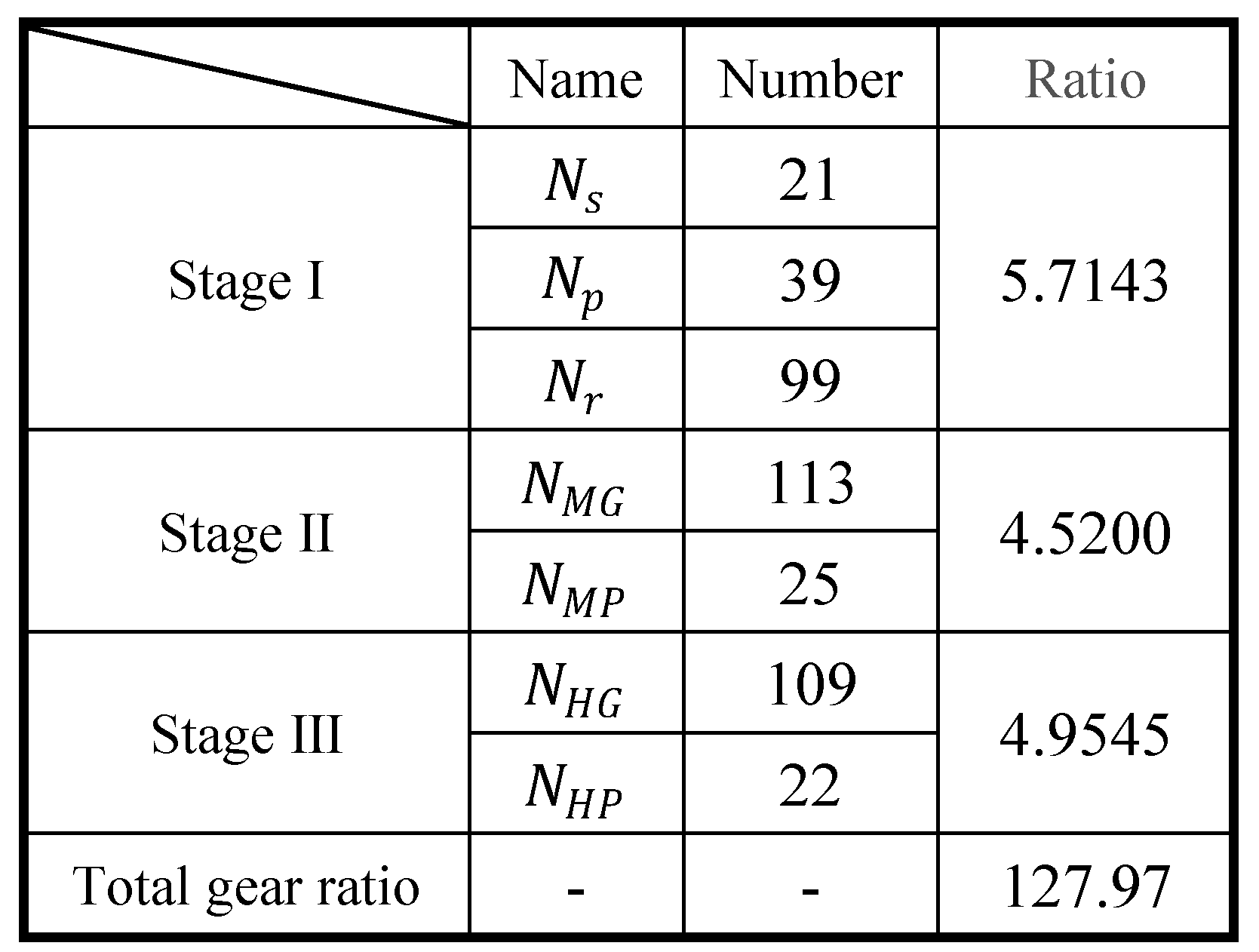
To demonstrate the advantages of the proposed methodology, a faulty parallel gear meshing signal $s\left(t\right)$ is simulated with speed fluctuation. Without loss of generality, the gear mesh signal is assumed to be sinusoidal with three higher-order harmonics as described in Equations (35) and (36). The amplitude rises with increasing order.

$$s(t)=\sin \left(2\pi \int f_{rs}dt\right)+\sum _{i=1}^{3}3i[1+\beta \cos (2\pi \int 3f_{\mathit{rs}}\mathit{dt}\left)\right]\cos \left(2\pi \int i{N}_p{f}_{rs}dt\right)$$

(35)

$$f_{rs}=2+\cos (\frac{\pi }{2}t)$$

(36)

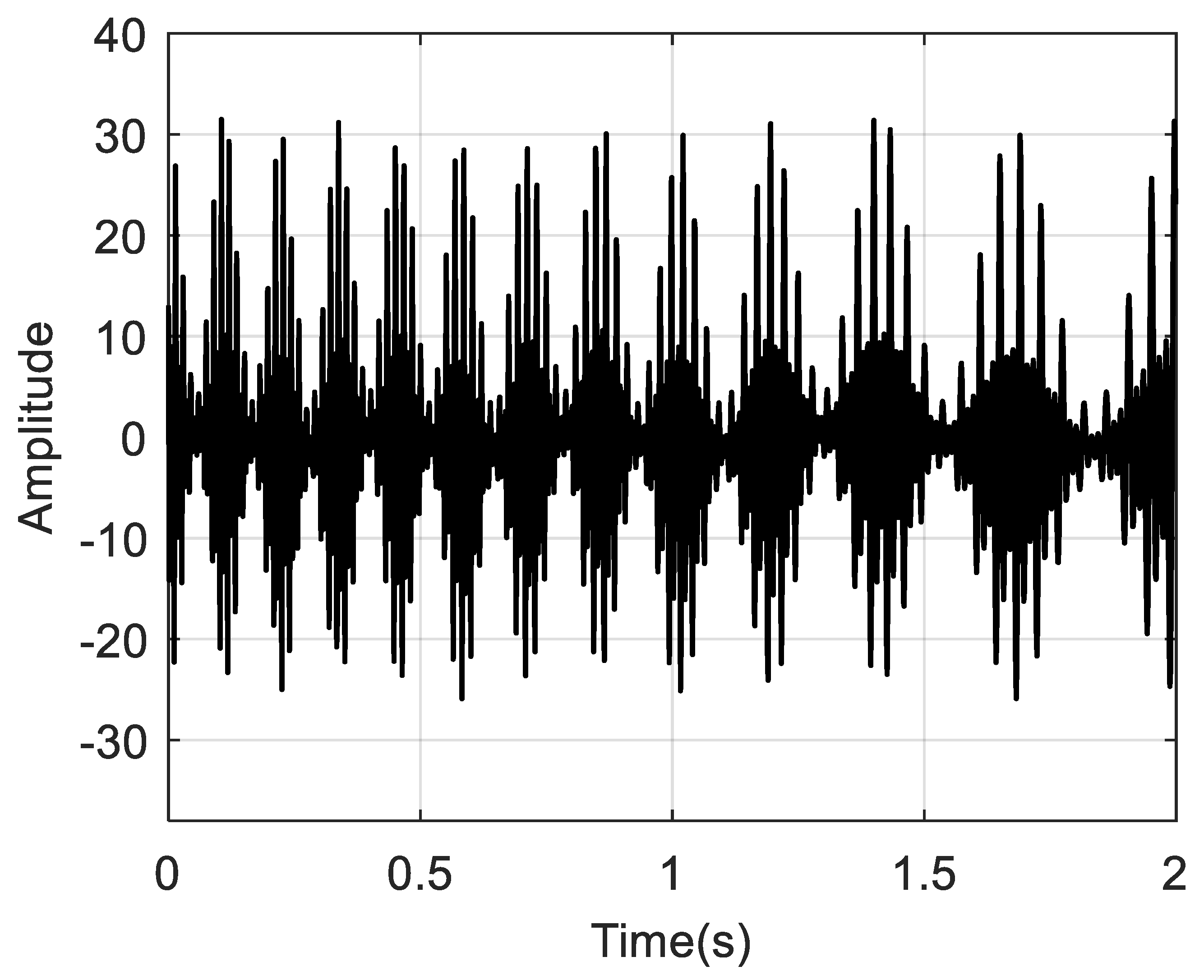
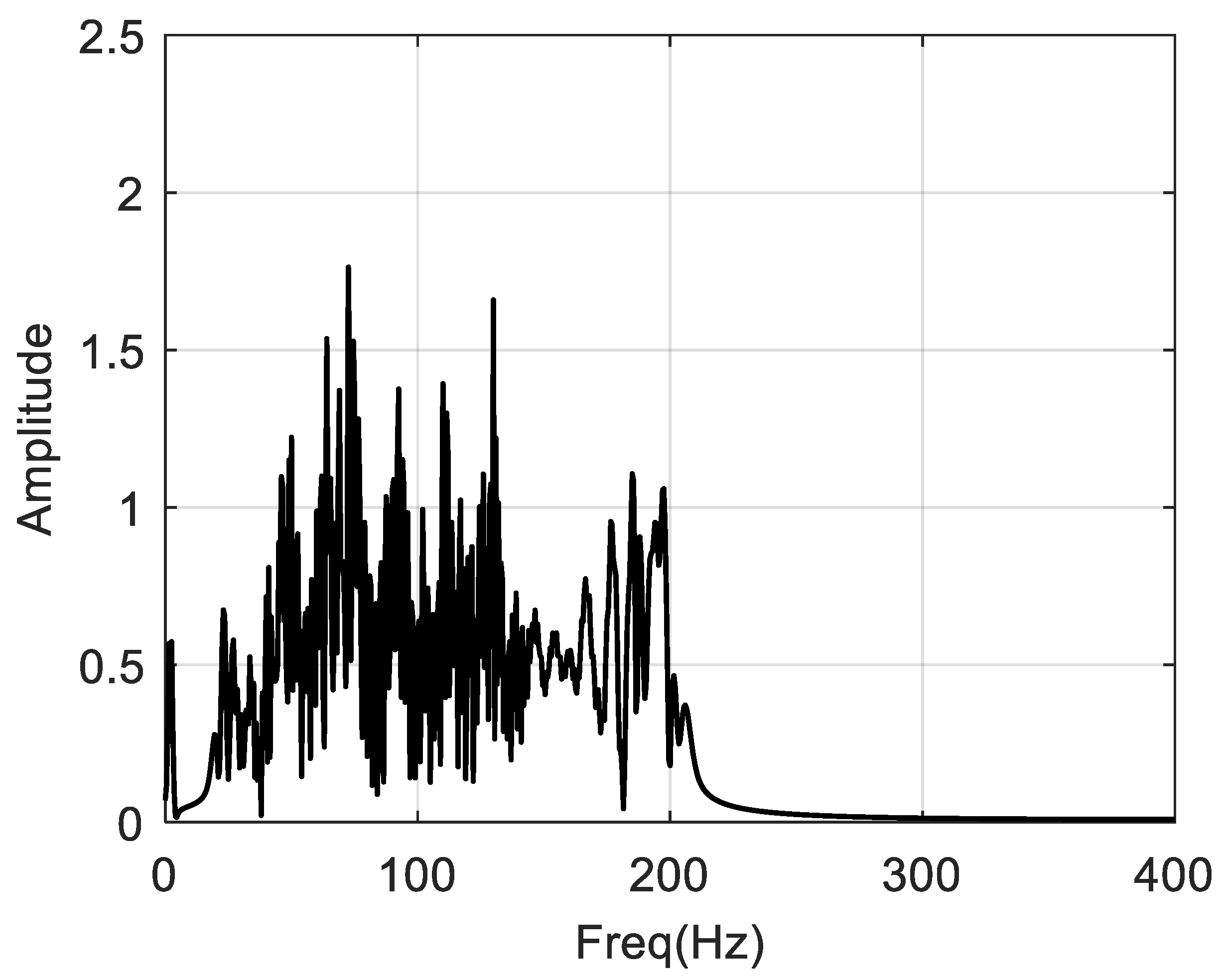
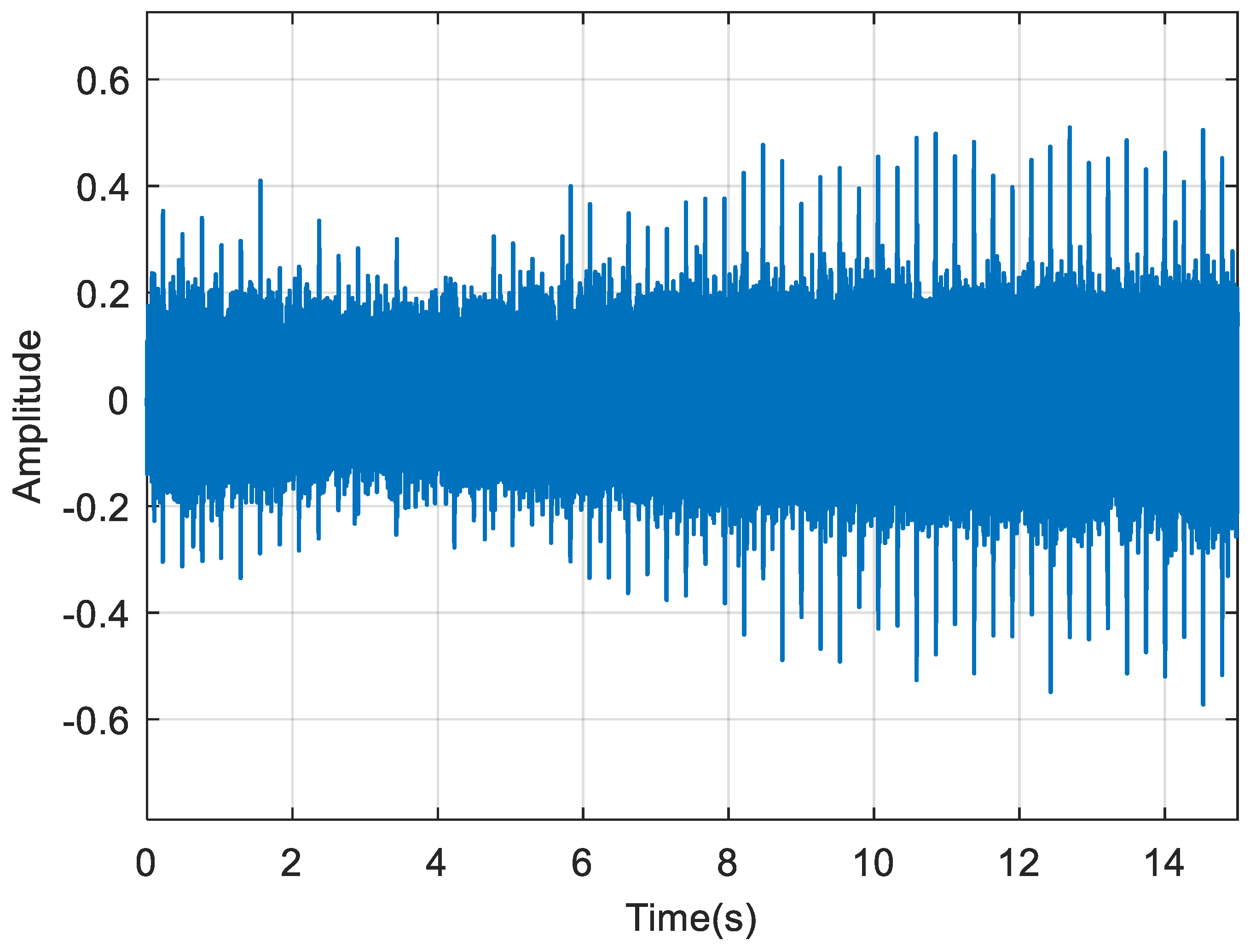
where $f_{rs}$ is the shaft speed frequency; $\beta$ is the modulation coefficient. The gear tooth number $N_p$ is 22. The sampling frequency is 800 Hz, and the sampling duration is 2 s. The simulated time history, the reference speed, and the corresponding spectrum are shown in Figure 8, Figure 9 and Figure 10, respectively. Under such speed fluctuations, a significant energy dispersion in the spectrum is observed.

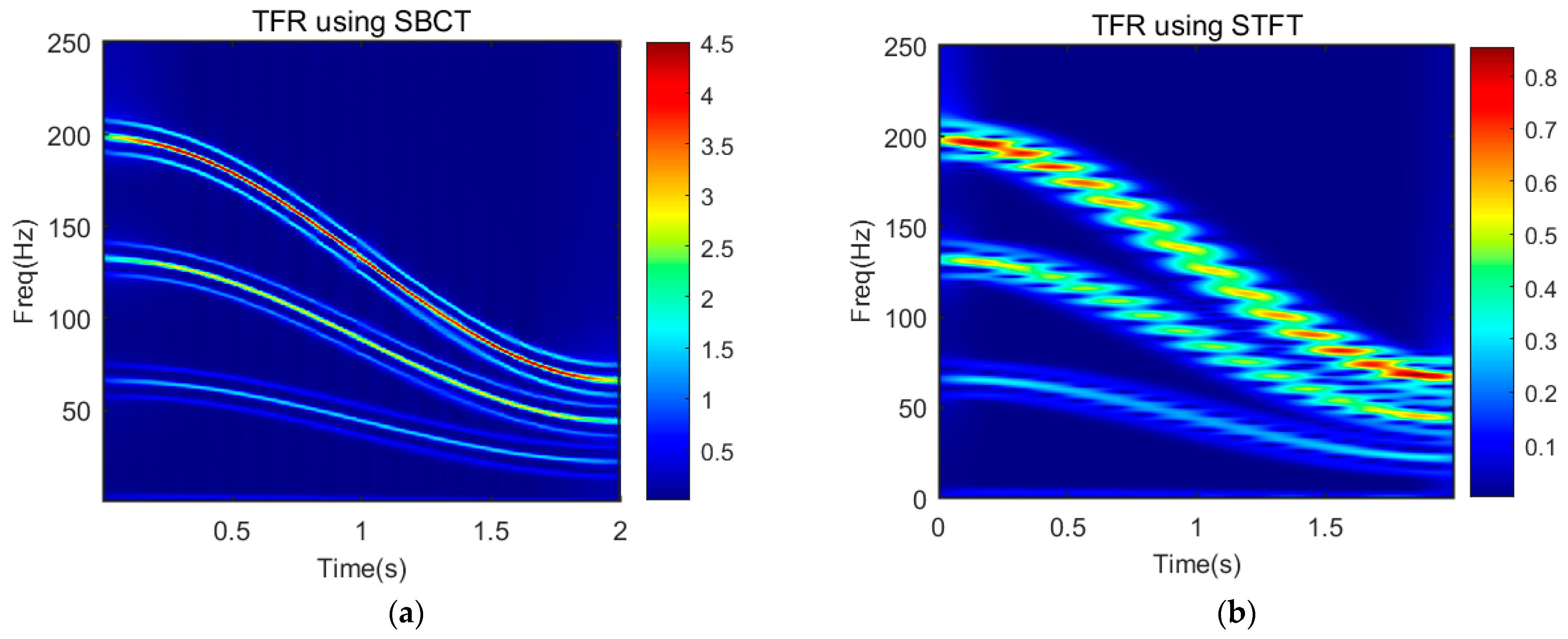
Figure 11 illustrates the TFR obtained using SBCT and STFT. The SBCT analysis yields a continuous and clear time–frequency representation, allowing for precise differentiation between gear meshing frequencies and closely-spaced modulation components. Conversely, the STFT analysis results in energy dispersion due to the speed variation, leading to overlapping among the meshing frequencies and modulation components.

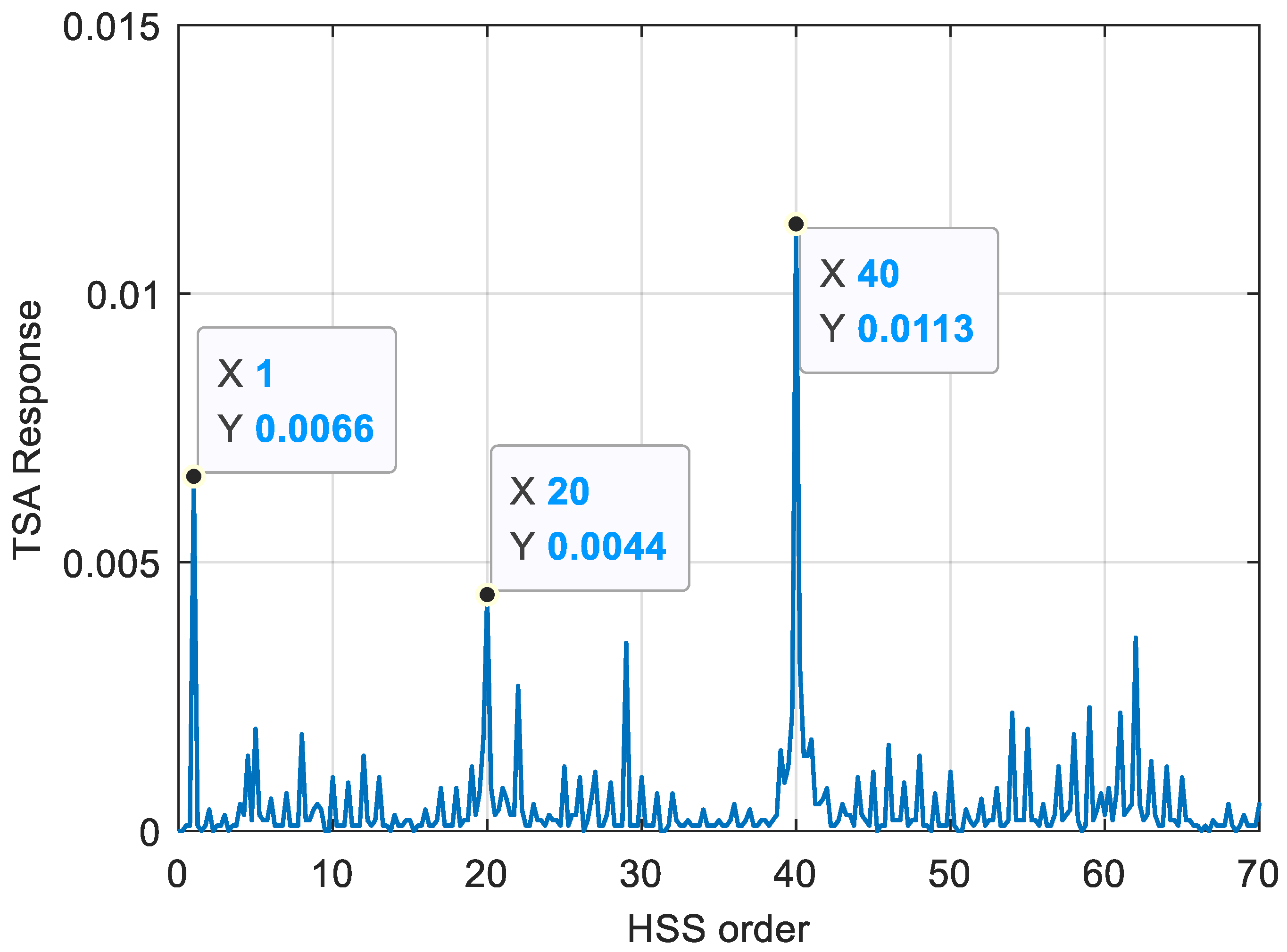
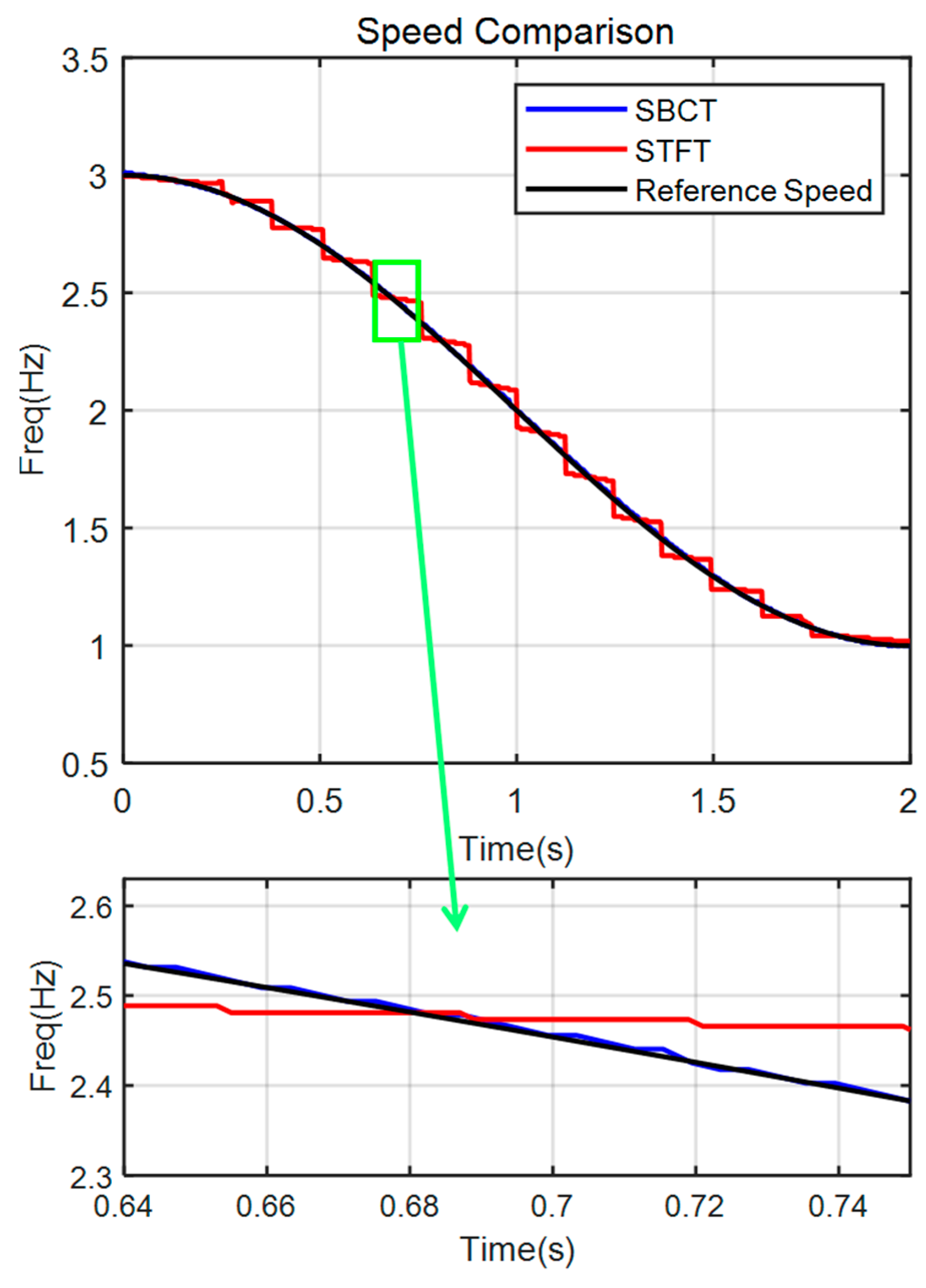
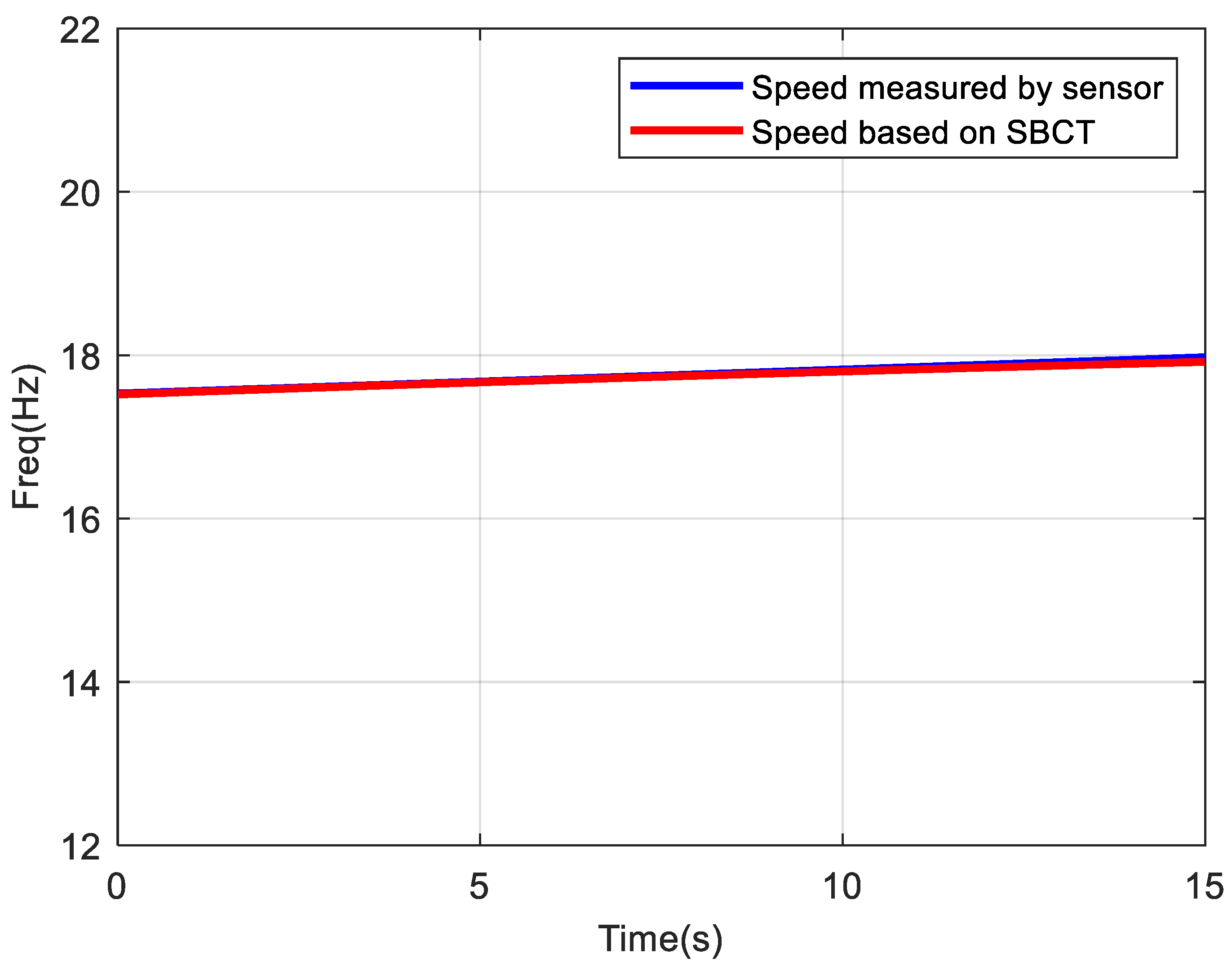
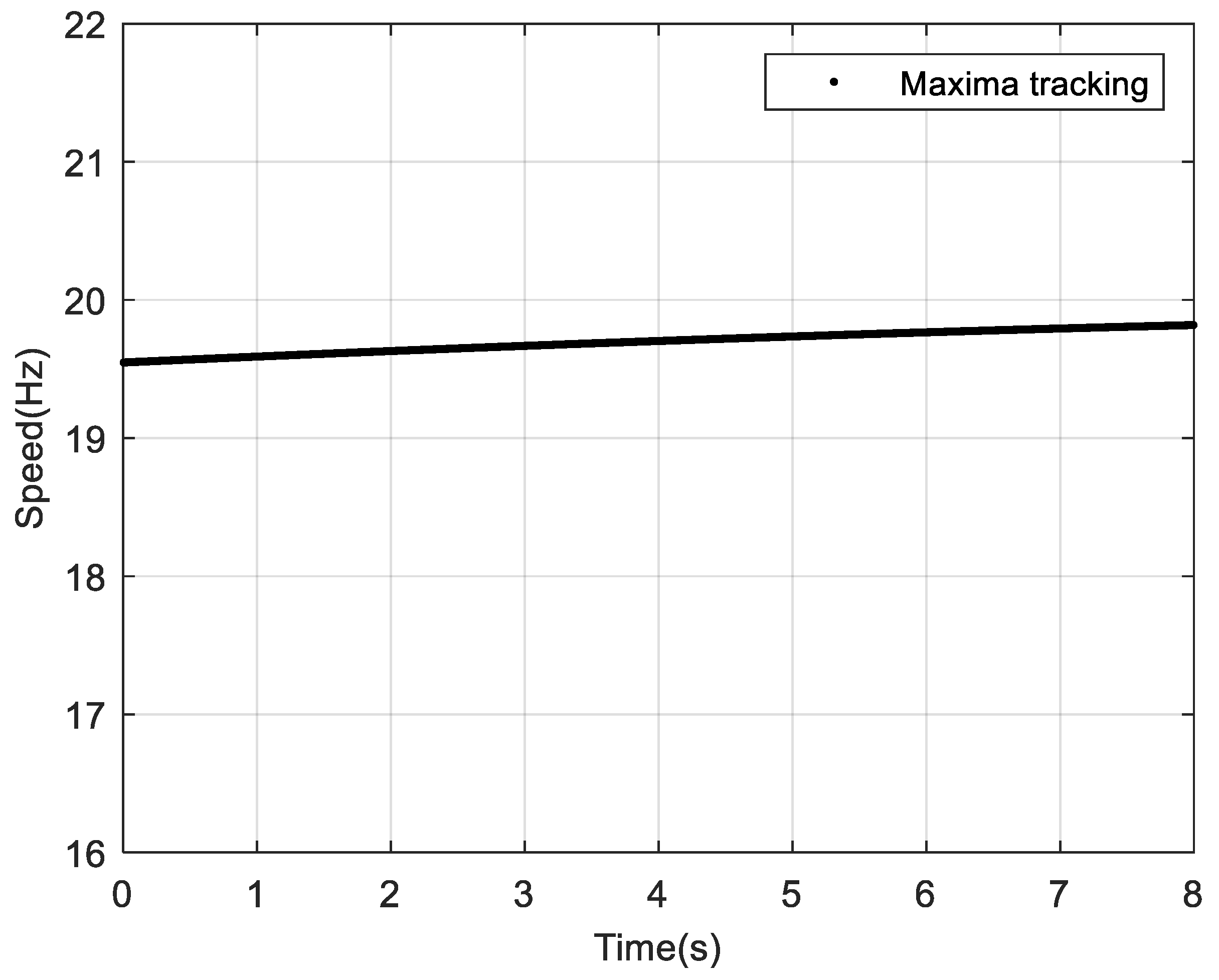
The maximum tracking technique is employed to extract the 3rd harmonic of the meshing frequency, which exhibits the highest energy concentration, and consequently, a better SNR. The shaft speed is determined by dividing three times the tooth count (${3N}_p$). Figure 12 compares the speed extracted from the SBCT’s TFR with that obtained from STFT and zoomed 0.64 s to 0.75 s in detail. The results clearly demonstrate that the SBCT-based speed estimation closely aligns with the simulated speed.

To quantify the accuracy, an error measure is defined as follows:

$$Error=\sqrt{\frac{{\left(Speed-Spee{d}_{real}\right)}^2}{Spee{d}_{real}^2}}\times 100\%$$

(37)

where $Speed$ is the detected result and $Spee{d}_{real}$ is the simulated speed.

According to the Equation (37), the two errors are as follows:

$$Error\left(SBCT\right)=0.08\mathrm{\%}$$

$$Error\left(STFT\right)=2.87\mathrm{\%}$$

Evidently, the speed extracted using SBCT exhibits better accuracy compared to that obtained through the conventional STFT method.

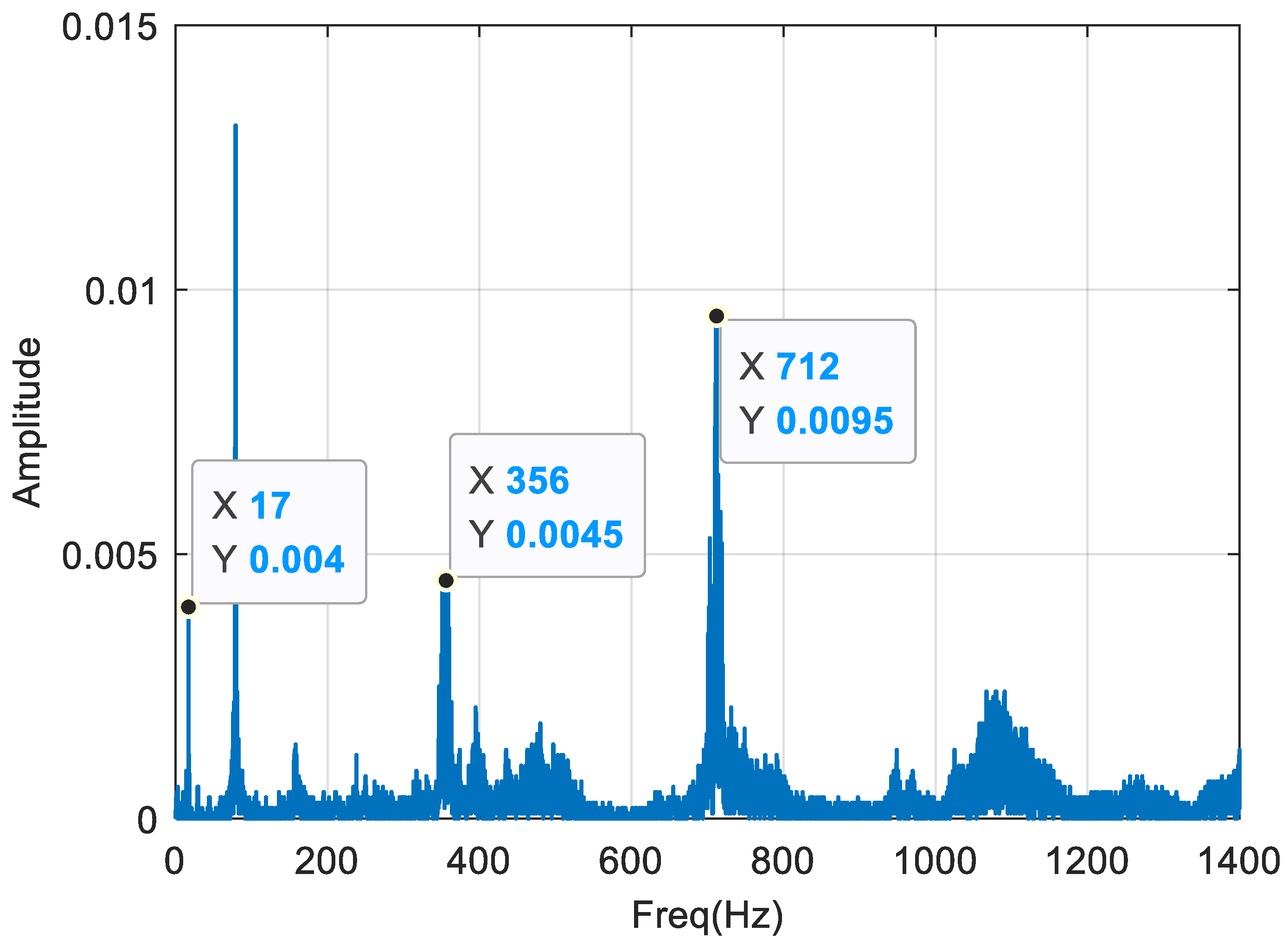
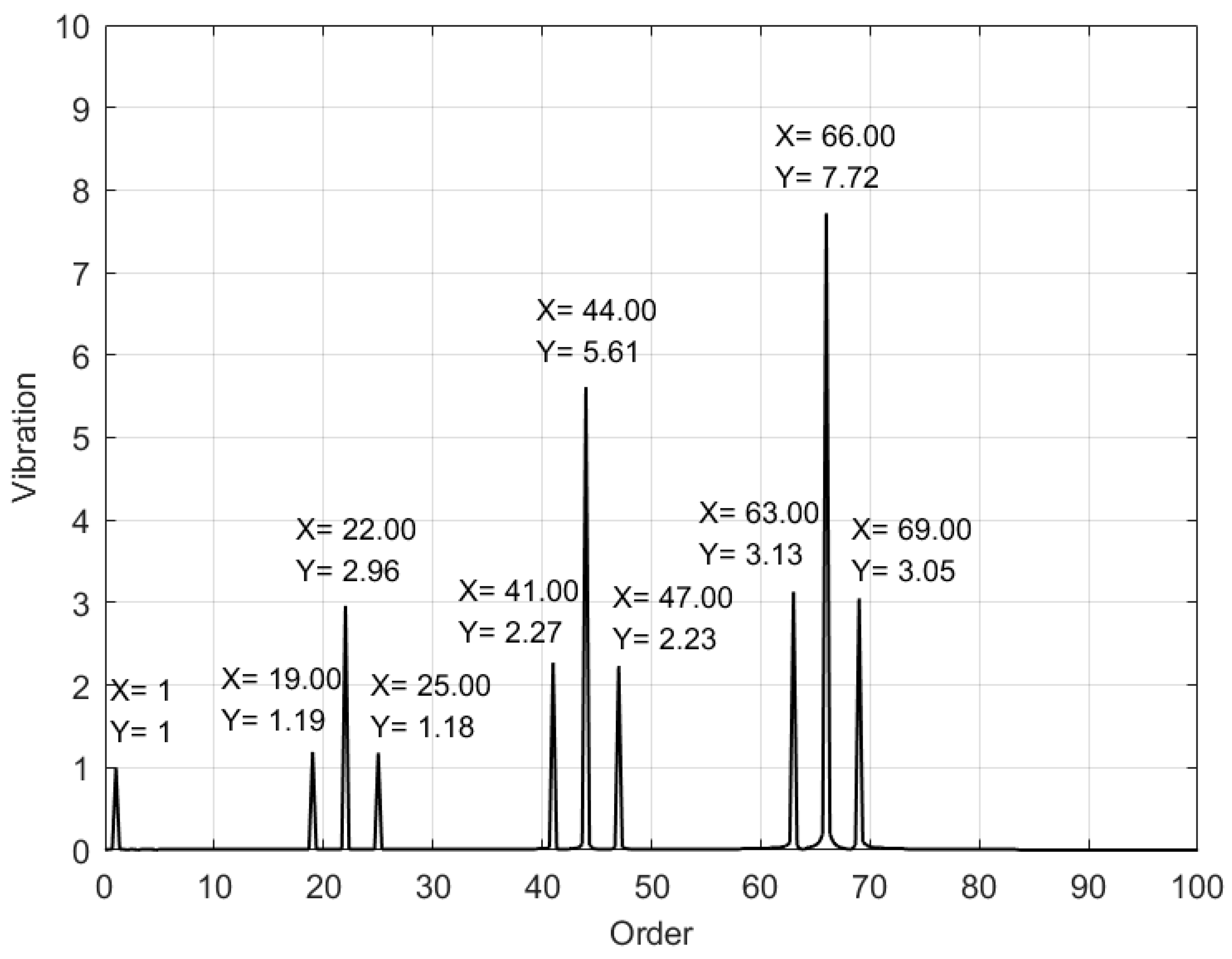
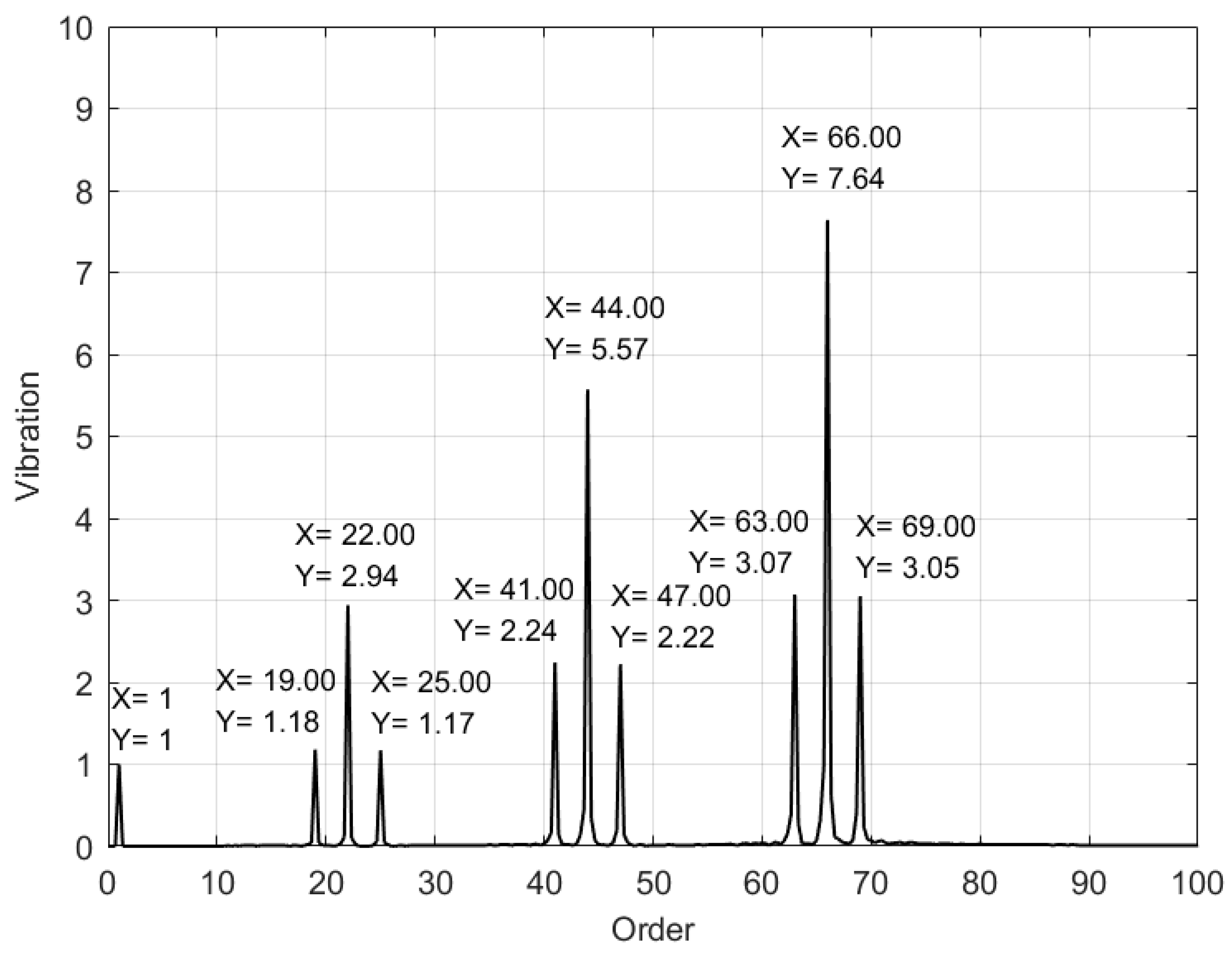
Synchronous resampling to the vibration data is conducted based on the detected speeds and order analysis is carried out accordingly. Figure 13 displays the order spectrum based on the simulated reference speed. In Figure 14 and Figure 15, the order spectra using the identified speeds with the SBCT and the STFT are shown, respectively.

By comparing the waveform in Figure 14 and Figure 15 to that in the Figure 13, it is evident that the order spectrum obtained from synchronous sampling using the speed identified by SBCT better aligns with the theoretical values.

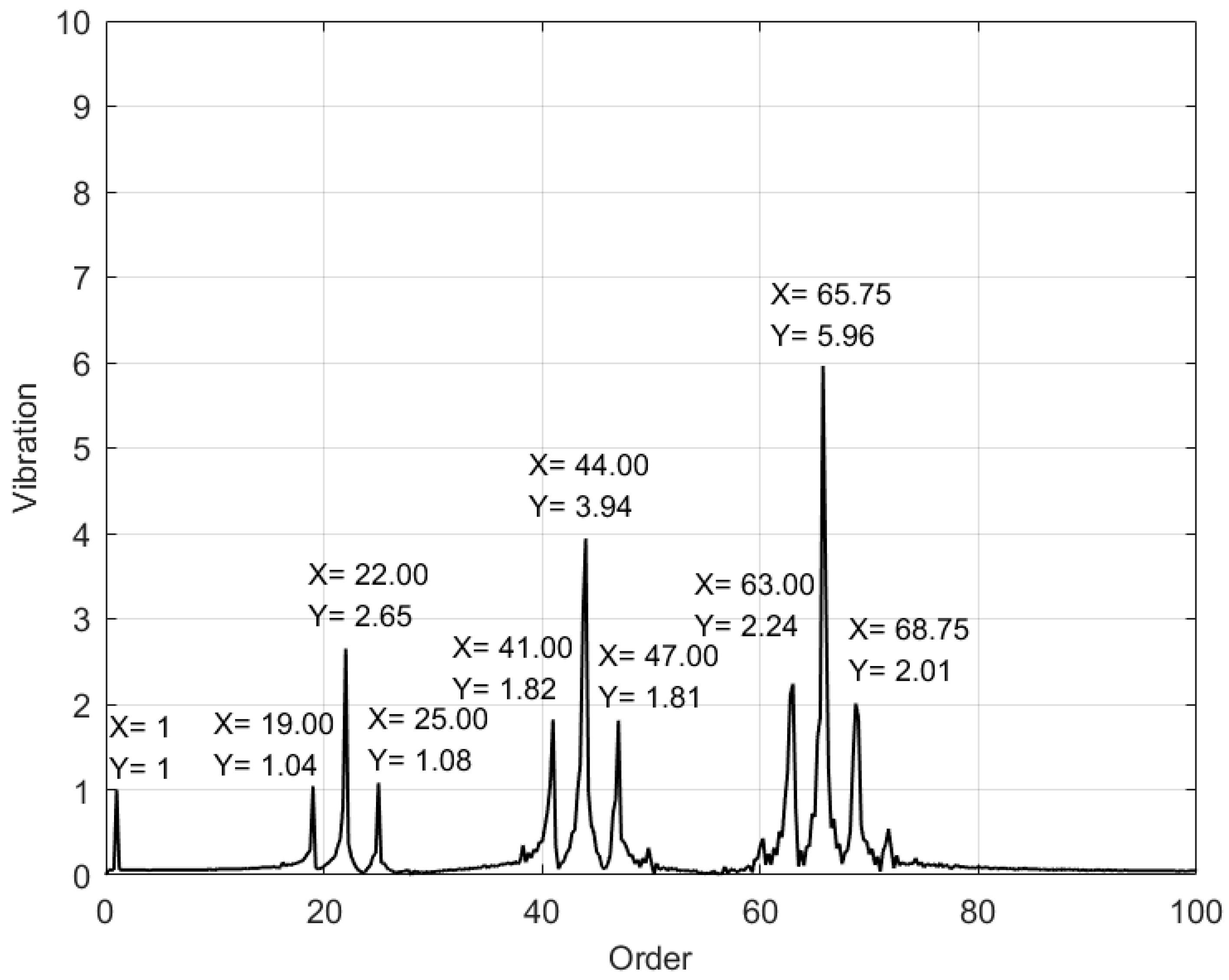
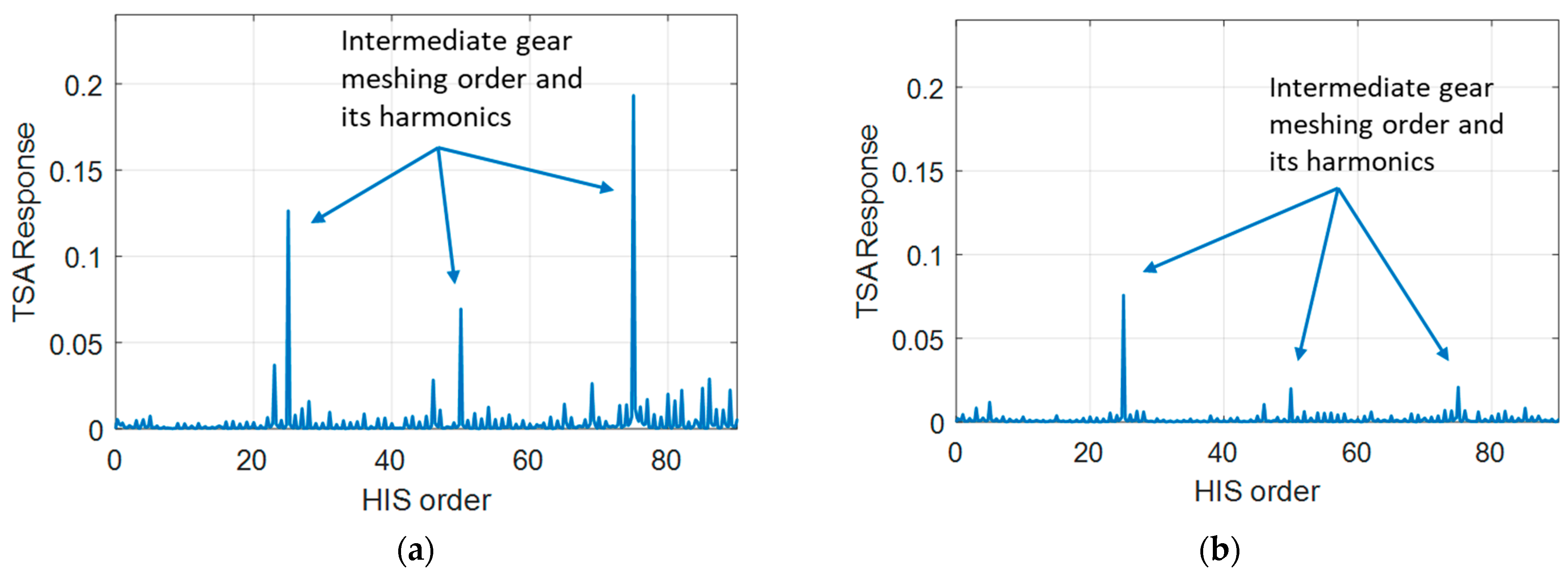
In addition, the speed identification error may also cause the deviation of the characteristic orders. For example, as shown in Figure 15, the error in the STFT speed identification caused 0.25 order deviation in the 3rd harmonics of the gear meshing characteristic order (65.75 and 68.75).

To quantitatively evaluate the difference in amplitudes, the error measure similar to the one described in the Equation (37) was employed as an indicator.

Table 1. The error of each order amplitude.

	SBCT	STFT
1st order and its sideband	0.84%	12.61%
	0.68%	10.47%
	0.85%	8.47%
2nd order and its sideband	1.32%	19.82%
	0.71%	29.77%
	0.45%	18.83%
3rd order and its sideband	1.92%	28.43%
	1.04%	22.80%
	0.00%	34.10%

displays the errors in the amplitudes of the gear meshing order and its sidebands with respect to the theoretical values. The maximum error in the SBCT speed identification is 1.92%. By contrast, the maximum error from STFT speed identification reaches up to 34.1%. This indicates that the SBCT-based speed has a higher level of energy concentration than that obtained by the STFT-based speed.

5. Engineering Applications

To demonstrate the practicality of the proposed methodology, two real wind farm cases are used as examples. The software used is MATLAB R2021b. The configuration of the computer used is as follows: Intel i7-11700 QM 3.6 GHz CPU, 32 GB DDR3 RAM.

5.1. Field Case I: Vibration Data with Shaft Speed Reference

In this case, real wind turbine data measured from a wind farm is utilized to demonstrate the reliability of the proposed methodology in extracting shaft speed. As shown in Figure 16, the wind turbine features a three-stage gearbox structure, which includes a planetary gear and two parallel gears. The number of planets is 3. The parallel stage consists of two pairs of fixed-shaft cylindrical gears. Gearbox parameters are given in the Appendix A Figure A1. One speed sensor, specifically positioned to measure the speed of the high-speed shaft (HSS), and six accelerometers were installed along the drive train. All channels were digitized simultaneously at a sampling rate of 25.6 kHz. The length of the data-acquisition time was 15 s.

For this analysis, the vibration signals obtained from the #4 accelerometer serve as an example. Figure 17 displays the time history of the accelerometer’s response, while Figure 18 displays the speed variation of the HSS measured by the speed sensor, ranging from 17.5 Hz to 18 Hz.

To identify the instantaneous shaft speed from the response only, the vibration signal passes through the signal processing procedure as shown in Figure 5. The TFR based on SBCT is shown in Figure 19, offering a clear visualization of the signal characteristics. Then, the HSS speed $\left(f_{HSS}\right)$ is identified based on the maxima tracking technique. The identified HSS speed is overlaid on the time–frequency spectrum in Figure 20, demonstrating a strong alignment between the two.

The reference speed of the HSS was also measured during data acquisition once per revolution and then identified through a pulse-counting algorithm. As depicted in Figure 21, the speed estimated using SBCT closely aligns with the measured speed. Based on the error measure provided in Equation (37), the deviation between the measured speed and the identified speed from the vibration signal is 0.14%, demonstrating the accuracy of IF identification based on SBCT analysis.

Finally, the HSS synchronous signal and corresponding order spectrum are obtained by resampling with the SBCT-based speed. The synchronous signal is shown in Figure 22. By comparing the order spectrum (Figure 23) with the spectrum of the raw data (Figure 24), it is clearly seen that the proposed synchronous method is able to clean up the signal from two aspects: 1. cleaning up the frequency smearing caused by the speed variation; 2. alleviating or eliminating the non-synchronous component, such as the response component associated with other shafts. In addition, the deciphering of the order spectrum becomes much easier because, in the TSA response spectrum, major response components are all associated with the shaft. For example, the $f_{HSS}$ appears at the 1st order, and the fundamental order and the second harmonic of the gear meshing are located in the 20th and 40th orders.

5.2. Field Case II: Vibration Data without Shaft Speed Measurement

In this case, the proposed methodology is applied to diagnose faults on a wind turbine operating in a wind farm. The available data for analysis comprises vibration data collected from a faulty wind turbine. The shaft speed was not provided.

Figure 25 shows the sketch of the wind turbine drive chain structure. It features a gearbox with a planetary stage and two parallel gear stages. Gearbox parameters are provided in the Appendix A Figure A2. Seven accelerometers were installed along the drive train.

Borescope examination of the gearbox shows that there was tooth flaking on the intermediate-stage gear. As can be seen in Figure 26, the damage was evaluated as at an initial damage stage.

The vibration response time history is shown in Figure 27, which was measured by the #5 acceleration sensor on the high-speed-stage bearing house. The digitization was performed at a sampling rate of 25.6 kHz. The duration of the data acquisition period was 8 s. The smearing in the frequency domain caused by the variable speed operation of the wind turbine is visible in the Figure 28. Owing to this smearing effect, the gear meshing sidebands are not obvious in the frequency spectrum.

The SBCT-based time–frequency spectrum is shown in Figure 29. The proposed algorithm is applied to identify the instantaneous speed of the high-speed shaft and the speed variation curve as shown in Figure 30.

Based on the identified speed and gearbox kinematic relationships, the vibration signal is resampled synchronously in a digital domain with respect to the high-intermediate shaft (HIS) adopting an arbitrary shaft-synchronous sampling technique proposed in the open literature [21]. The results of the time-synchronous averaging (TSA) analysis are shown in Figure 31a, and the order spectrum corresponding to the HIS is shown in Figure 32a.

The TSA results illustrates the occurrence of impulsive events during the rotation of the HIS. Additionally, the order spectrum demonstrates the modulation of the HIS pinion meshing order by the HIS shaft speed, indicating damage to the pinion during the intermediate-stage gear meshing. It validates the results reported in the borescope inspection report.

For comparison, a set of vibration data was selected, which is 2 weeks prior to the time when the damage was not detectable by the borescope inspection. It is reasonable to assume that the pinion gear flaking was not initiated at that moment. With the similar processing procedure, the TSA results of the HIS is shown in Figure 31b, and the corresponding HIS order spectrum is shown in Figure 32b. By comparing Figure 31a,b, the gear tooth spalling increased the impulsive vibration contents in the TSA signal. This is also validated by the corresponding order spectrum as seen in Figure 32a,b, where the gear tooth spalling has shown more gear meshing sideband energy contents.

6. Conclusions

The proposed method in this paper introduces a time–frequency analysis approach for the detection of wind turbine drive train component faults, aiming to overcome the limitations of traditional tachometer-less synchronous sampling in the presence of significant speed fluctuations. By applying the algorithm to numerical simulations, the TFR from SBCT achieves a higher concentration of energy in the gear-meshing vibration signals for large speed fluctuations. Consequently, the shaft speed identified through maximum tracking based on the TFR of SBCT exhibits better accuracy compared to that from TFR of the STFT. The instantaneous phase is obtained through numerical integration. The vibration signals are then synchronously resampled in the digital domain using inverse function interpolation. The subsequent synchronous analysis demonstrates that the order spectrum obtained with the speed identified by the SBCT has a higher level of energy concentration than that obtained by the conventional STFT method.

The methodology is validated using real wind turbine failure data, effectively detecting early gear faults and demonstrating the practical applicability of the proposed approach. Furthermore, the comparison underscores the methodology’s ability to achieve high-precision shaft speed estimation, even in the presence of significant speed fluctuations. The implementation of this methodology may provide a better tool for rotating machinery condition monitoring, especially for situations with variable speed operations without the measurement of the shaft speed.