Muscle Fatigue Regulation through Muscle Activation Control in a Knee Hybrid Exoskeleton: Simulation Study
Abstract
:1. Introduction
2. Methods and Materials
2.1. Joint Dynamic Equation
2.2. Muscle Dynamic Equations
2.3. State Space Equations
3. Proposed Control Method
3.1. Motor Control Signal
3.2. Muscle Controller
3.2.1. Muscle Fatigue Regulation
3.2.2. Estimation of Muscle Activation Time Parameter
3.2.3. FES Control Signal
3.2.4. Stability Analysis
4. Simulation Results
4.1. Assessment of Controllers Performance
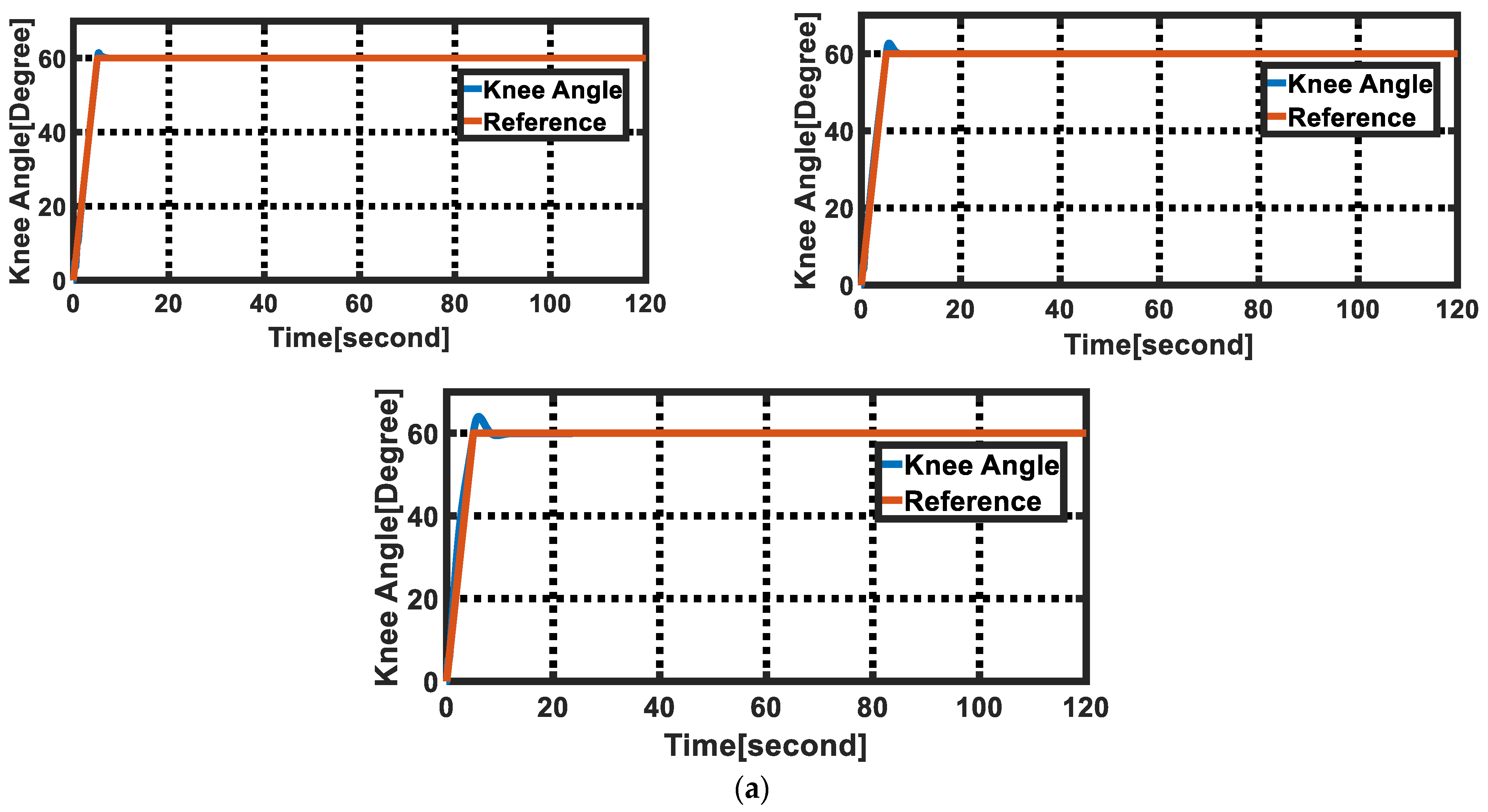
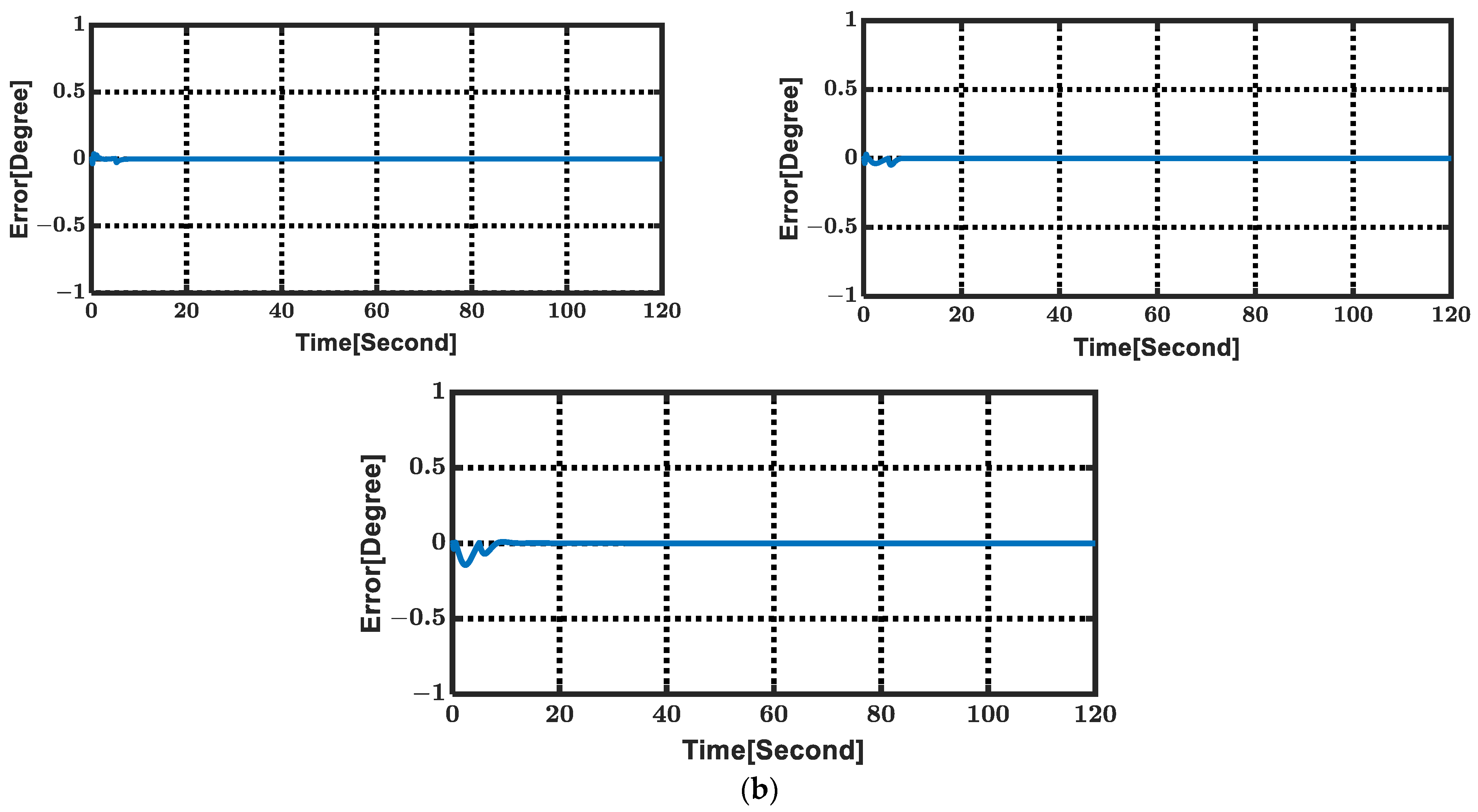
4.1.1. Regulation Results
4.1.2. Control Signals and Torques
4.1.3. Assessment of Muscle Fatigue Regulation
4.1.4. Assessment of Control Structure Performance
4.2. Comparison with Other Methods
4.2.1. Comparison with MPC Methods
4.2.2. Comparison with Switching Methods
5. Discussion
5.1. Proposed Method Assessment
5.2. Proposed Method Advantages in Comparison with Other Methods
5.3. Proposed Method Advantages in Clinical Implementation
5.4. Limitations
6. Conclusions
Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anaya, F.; Thangavel, P.; Yu, H. Hybrid FES–robotic gait rehabilitation technologies: A review on mechanical design, actuation, and control strategies. Int. J. Intell. Robot. Appl. 2018, 2, 1–28. [Google Scholar] [CrossRef]
- Cimolato, A.; Driessen, J.J.; Mattos, L.S.; De Momi, E.; Laffranchi, M.; De Michieli, L. EMG-driven control in lower limb prostheses: A topic-based systematic review. J. NeuroEngineering Rehabil. 2022, 19, 43. [Google Scholar] [CrossRef] [PubMed]
- Voloshina, A.S.; Collins, S.H. Lower limb active prosthetic systems—Overview. Wearable Robot. 2020, 469–486. [Google Scholar] [CrossRef]
- Dunkelberger, N.; Schearer, E.M.; O’Malley, M.K. A review of methods for achieving upper limb movement following spinal cord injury through hybrid muscle stimulation and robotic assistance. J. Exp. Neurol. 2020, 328, 113274. [Google Scholar] [CrossRef] [PubMed]
- Gil-Castillo, J.; Alnajjar, F.; Koutsou, A.; Torricelli, D.; Moreno, J.C. Advances in neuroprosthetic management of foot drop: A review. J. Neuroeng. Rehabil. 2020, 17, 46. [Google Scholar] [CrossRef]
- Masengo, G.; Zhang, X.; Dong, R.; Alhassan, A.B.; Hamza, K.; Mudaheranwa, E. Lower limb exoskeleton robot and its cooperative control: A review, trends, and challenges for future research. Front. Neurorobot. 2023, 16, 913748. [Google Scholar] [CrossRef]
- Sheng, Z.; Iyer, A.; Sun, Z.; Kim, K.; Sharma, N. A hybrid knee exoskeleton using real-time ultrasound-based muscle fatigue assessment. IEEE/ASME Trans. Mechatron. 2022, 27, 1854–1862. [Google Scholar] [CrossRef]
- Kirsch, N.; Alibeji, N.; Dicianno, B.E.; Sharma, N. Switching control of FES and motor assist for muscle fatigue compensation. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; IEEE: Washington, DC, USA, 2016; Volume 16193830. [Google Scholar] [CrossRef]
- Molazadeh, V.; Sheng, Z.; Sharma, N. A Within-Stride Switching Controller for Walking with Virtual Constraints: Application to a Hybrid Neuroprosthesis. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; IEEE: Washington, DC, USA, 2018; Volume 18008171, pp. 5286–5291. [Google Scholar]
- Sheng, Z.; Molazadeh, V.; Sharma, N. Hybrid dynamical system model and robust control of a hybrid neuroprosthesis under fatigue based switching. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; IEEE: Washington, DC, USA, 2018; Volume 18008786, pp. 1446–1451. [Google Scholar] [CrossRef]
- Molazadeh, V.; Sheng, Z.; Bao, X.; Sharma, N. A robust iterative learning switching controller for following virtual constraints: Application to a hybrid neuroprosthesis. IFAC-PapersOnLine 2019, 51, 28–33. [Google Scholar] [CrossRef]
- Sheng, Z.; Sun, Z.; Molazadeh, V.; Sharma, N. Switched control of an N-degree-of-freedom input delayed wearable robotic system. Automatica 2021, 125, 109455. [Google Scholar] [CrossRef]
- Molazadeh, V.; Zhang, Q.; Bao, X.; Sharma, N. An iterative learning controller for a switched cooperative allocation strategy during sit-to-stand tasks with a hybrid exoskeleton. IEEE Trans. Control Syst. Technol. 2021, 30, 1021–1036. [Google Scholar] [CrossRef]
- Ghajari, S.; Moghaddam, R.K.; Kobravi, H.R.; Pariz, N. Knee Joint Movement Control Using Hybrid Neuro-prosthesis Based on Persistent D-well Time Allocation Strategy with Muscle Fatigue Overcoming: Simulation Approach. JRRS 2022, 18, 12–23. [Google Scholar]
- Zhang, D.; Yong, R.; Gui, K.; Jia, J.; Wendong, X. Cooperative Control for A Hybrid Rehabilitation System Combining FES and Robotic Exoskeleton. Front. Neurosci. 2017, 11, 725. [Google Scholar] [CrossRef]
- Bao, X.; Molazadeh, V.; Dodson, A.; Dicianno, B.E.; Sharma, N. Using person-specific muscle fatigue characteristics to optimally allocate control in a hybrid exoskeleton—Preliminary results. IEEE Trans. Med. Robot. Bionics 2020, 2, 226–235. [Google Scholar] [CrossRef] [PubMed]
- Molazadeh, V.; Zhang, Q.; Bao, X.; Dicianno, B.E.; Sharma, N. Shared control of a powered exoskeleton and functional electrical stimulation using iterative learning. Front. Robot. AI 2021, 8, 711388. [Google Scholar] [CrossRef]
- Kirsch, N.; Alibeji, N.; Sharma, N. Model predictive control-based dynamic control allocation in a hybrid neuroprosthesis. In Proceedings of the ASME 2014 Dynamic Systems and Control Conference, San Antonio, TX, USA, 22–24 October 2014; American Society of Mechanical Engineers: Washington, DC, USA, 2014; Volume 46209, p. V003T43A003. [Google Scholar] [CrossRef]
- Kirsch, N.; Bao, X.; Alibeji, N.; Dicianno, B.; Sharma, N. Model-based dynamic control allocation in a hybrid neuroprosthesis. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 26, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Bao, X.; Kirsch, N.; Dodson, A.; Sharma, N. Model Predictive Control of a Feedback Linearized Hybrid Neuroprosthetic System with a Barrier Penalty. ASME. J. 2019, 14, 101009. [Google Scholar] [CrossRef]
- Bao, X.; Sheng, Z.; Dicianno, B.E.; Sharma, N. A Tube-Based Model Predictive Control Method to Regulate a Knee Joint with FES and Electric Motor Assist. IEEE Trans. Control Syst. Technol. 2020, 9, 2180–2191. [Google Scholar] [CrossRef]
- Bao, X.; Mao, Z.H.; Munro, P.; Sun, Z.; Sharma, N. Sub-optimally solving actuator redundancy in a hybrid neuroprosthetic system with a multi-layer neural network structure. Int. J. Intell. Robot. Appl. 2019, 3, 298–313. [Google Scholar] [CrossRef] [PubMed]
- Tu, X.; Li, J.; Li, J.; Su, C.; Zhang, S.; Li, H.; Cao, J.; He, J. Model-based hybrid cooperative control of hip-knee exoskeleton and FES induced ankle muscles for gait rehabilitation. Intern. J. Pattern Recognit. Artif. Intell. 2017, 31, 1759019. [Google Scholar] [CrossRef]
- Alibeji, N.; Molazadeh, V.; Dicianno, B.E.; Sharma, N. A, control scheme that uses dynamic postural synergies to coordinate a hybrid walking neuroprosthesis: Theory and experiments. Front. Neurosci. 2018, 12, 159. [Google Scholar] [CrossRef]
- Del-Ama, A.J.; Gil-Agudo, Á.; Pons, J.L.; Moreno, J.C. Hybrid FES-robot cooperative control of ambulatory gait rehabilitation exoskeleton. J. Neuroeng. Rehabil. 2014, 11, 27. [Google Scholar] [CrossRef] [PubMed]
- Del-Ama, A.J.; Gil-Agudo, Á.; Pons, J.L.; Moreno, J.C. Characterization of a Dual PID-ILC FES Controller for FES-Robot Control of Swing Phase of Walking. In Replace, Repair, Restore, Relieve–Bridging Clinical and Engineering Solutions in Neurorehabilitation, 1st ed.; Jensen, W., Andersen, O., Pons, J., Moreno, J.C., Eds.; Springer: Cham, Switzerland, 2014; Volume 7, pp. 341–349. [Google Scholar] [CrossRef]
- De Sousa, A.C.; Freire, J.P.; Bo, A.P. Integrating hip exosuit and FES for lower limb rehabilitation in a simulation environment. IFAC-PapersOnLine 2019, 51, 302–307. [Google Scholar] [CrossRef]
- Wan, J.J.; Qin, Z.; Wang, P.Y.; Sun, Y.; Liu, X. Muscle fatigue: General understanding and treatment. Exp. Mol. Med. 2017, 49, e384. [Google Scholar] [CrossRef] [PubMed]
- Bulea, T.C.; Sharma, N.; Sikdar, S.; Su, H. Next generation user-adaptive wearable robots. Front. Robot. AI 2022, 9, 920655. [Google Scholar] [CrossRef] [PubMed]
- Müller, P.; Del Ama, A.J.; Moreno, J.C.; Schauer, T. Adaptive multichannel FES neuroprosthesis with learning control and automatic gait assessment. J. Neuroeng. Rehabil. 2020, 17, 36. [Google Scholar] [CrossRef]
- Popovic, D.; Stein, R.B.; Oguztoreli, M.N.; Lebiedowska, M.; Jonic, S. Optimal control of walking with functional electrical stimulation: A computer simulation study. IEEE Trans. Neural Syst. Rehabil. Eng. 1999, 7, 69–79. [Google Scholar] [CrossRef]
- Kirsch, N.; Alibeji, N.; Sharma, N. Nonlinear model predictive control of FES. Control Eng. Pract. 2017, 58, 319–331. [Google Scholar] [CrossRef]
- Ober-Blöbaum, S.; Offen, C. Variational learning of Euler–Lagrange dynamics from data. J. Comput. Appl. Math. 2023, 421, 114780. [Google Scholar] [CrossRef]
- Riener, R.; Quintern, J.; Schmidt, G. Biomechanical model of the human knee evaluated by neuromuscular stimulation. J. Biomech. 1996, 29, 1157–1167. [Google Scholar] [CrossRef]
- Veltink, P.H.; Chizeck, H.J.; Crago, P.E.; El-Bialy, A. Nonlinear joint angle control for artificially stimulated muscle. IEEE Trans. Biomed. Eng. 1992, 39, 368–380. [Google Scholar] [CrossRef]
- Carsten, B.; Siedler, K. Adaptive PID-tracking Control of Muscle-like Actuated Compliant Robotic Systems with Input Constraints. Appl. Math. Mode 2019, 67, 9–21. [Google Scholar] [CrossRef]
- Alif, T.; Bhasin, S.; Garg, K.; Joshi, D. An Enhanced Model Free Adaptive Control Approach for Functional Electrical Stimulation Assisted Knee Joint Regulation and Control. IEEE Trans. Neural Syst. Rehabilitation Eng. 2023, 31, 1584–1593. [Google Scholar] [CrossRef] [PubMed]
- Khalil, H. Nonlinear Systems; Pearson: London, UK, 2003; pp. 400–401. [Google Scholar]
- Astrom, K.J.; Wittenmark, B. Adaptive Control; Dover Publications Inc.: Boston, MA, USA, 2008; pp. 100–105. [Google Scholar]
- Xu, J.X. A survey on iterative learning control for nonlinear systems. Int. J. Control 2011, 84, 1275–1294. [Google Scholar] [CrossRef]
- Ding, Z. Nonlinear and Adaptive Control Systems; The Institution of Engineering and Technology: London, UK, 2013; pp. 150–152. [Google Scholar]
- Baek, J.; Jin, M.; Han, S. A new adaptive sliding-mode control scheme for application to robot manipulators. IEEE Trans. Ind. Electron. 2016, 63, 3628–3637. [Google Scholar] [CrossRef]
- Nunes, W.R.; Alves, U.N.; Sanches, M.A.; Teixeira, M.C.; De Carvalho, A.A. Electrically Stimulated Lower Limb using a Takagi-Sugeno Fuzzy Model and Robust Switched Controller Subject to Actuator Saturation and Fault under Nonideal Conditions. Int. J. Fuzzy Syst. 2022, 24, 57–72. [Google Scholar] [CrossRef]
- Sa-e, S.; Freeman, C.T.; Yang, K. Iterative learning control of FES in the presence of voluntary user effort. Control Eng. Pract. 2020, 96, 104303. [Google Scholar] [CrossRef]
- Alibeji, N.; Kirsch, N.; Sharma, N. An adaptive low-dimensional control to compensate for actuator redundancy and FES-induced muscle fatigue in a hybrid neuroprosthesis. Control Eng. Pract. 2017, 59, 204–219. [Google Scholar] [CrossRef]
- Michelle, H.; Cameron, M. Physical Agents in Rehabilitation: An Evidence-Based Approach to Practice; Elsevier: Berkeley, CA, USA; Saunders: Philadelphia, PA, USA, 2017; pp. 77–84. [Google Scholar]
- Rakhtala, S.M. Adaptive gain super twisting algorithm to control a knee exoskeleton disturbed by unknown bounds. Int. J. Dyn. Control 2021, 9, 711–726. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, C.; Zhang, M.; Wu, J.; Tang, Z. Research on the Recognition of Various Muscle Fatigue States in Resistance Strength Training. Healthcare 2022, 10, 2292. [Google Scholar] [CrossRef]
- Frey-Law, L.A.; Schaffer, M.; Urban, F.K. Muscle fatigue modelling: Solving for fatigue and recovery parameter values using fewer maximum effort assessments. Int. J. Ind. Ergon. 2021, 82, 103104. [Google Scholar] [CrossRef]
- Zhang, Q.; Iyer, A.; Lambeth, K.; Kim, K.; Sharma, N. Ultrasound echogenicity as an indicator of muscle fatigue during functional electrical stimulation. Sensors 2022, 22, 335. [Google Scholar] [CrossRef] [PubMed]
- Tran, H.T.; Tan, L.N.; Han, S.H. Model-Learning-Based Partitioned Control of a Human-Powered Augmentation Lower Exoskeleton. J. Electr. Eng. Technol. 2022, 17, 533–550. [Google Scholar] [CrossRef]
- Luo, S.; Androwis, G.; Adamovich, S.; Su, H.; Nunez, E.; Zhou, X. Reinforcement learning and control of a lower extremity exoskeleton for squat assistance. Front. Robot. AI 2021, 8, 702845. [Google Scholar] [CrossRef] [PubMed]
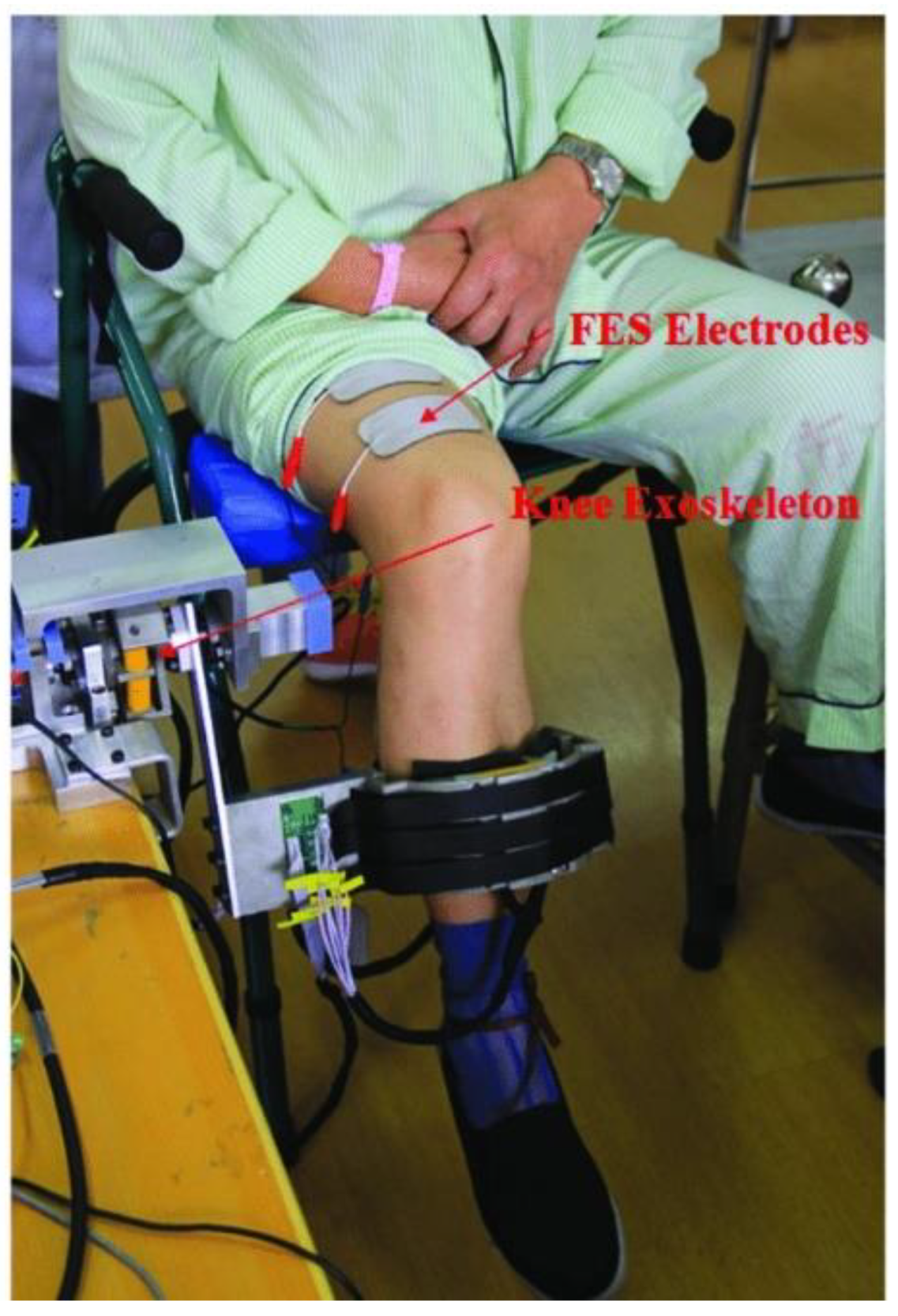
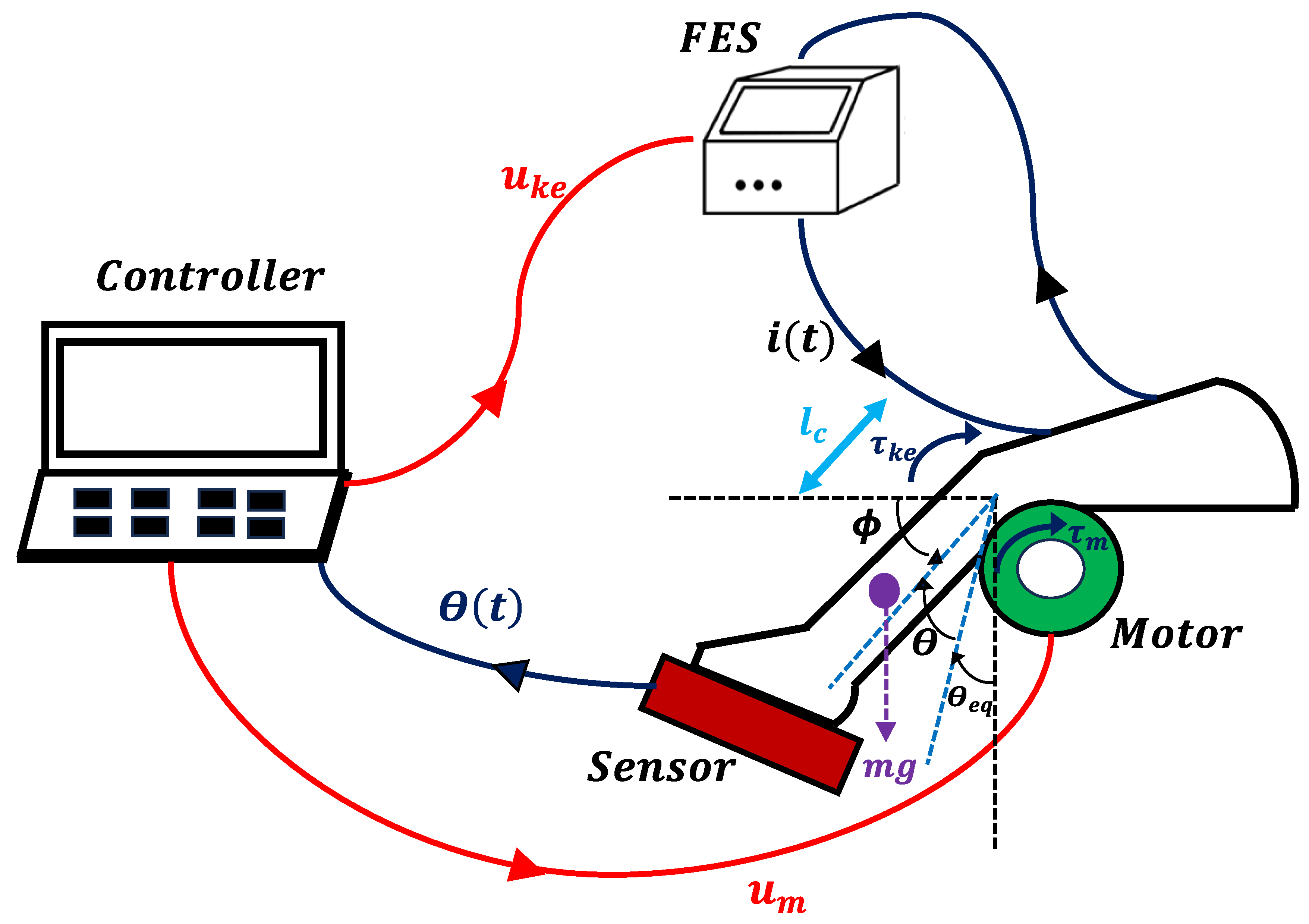



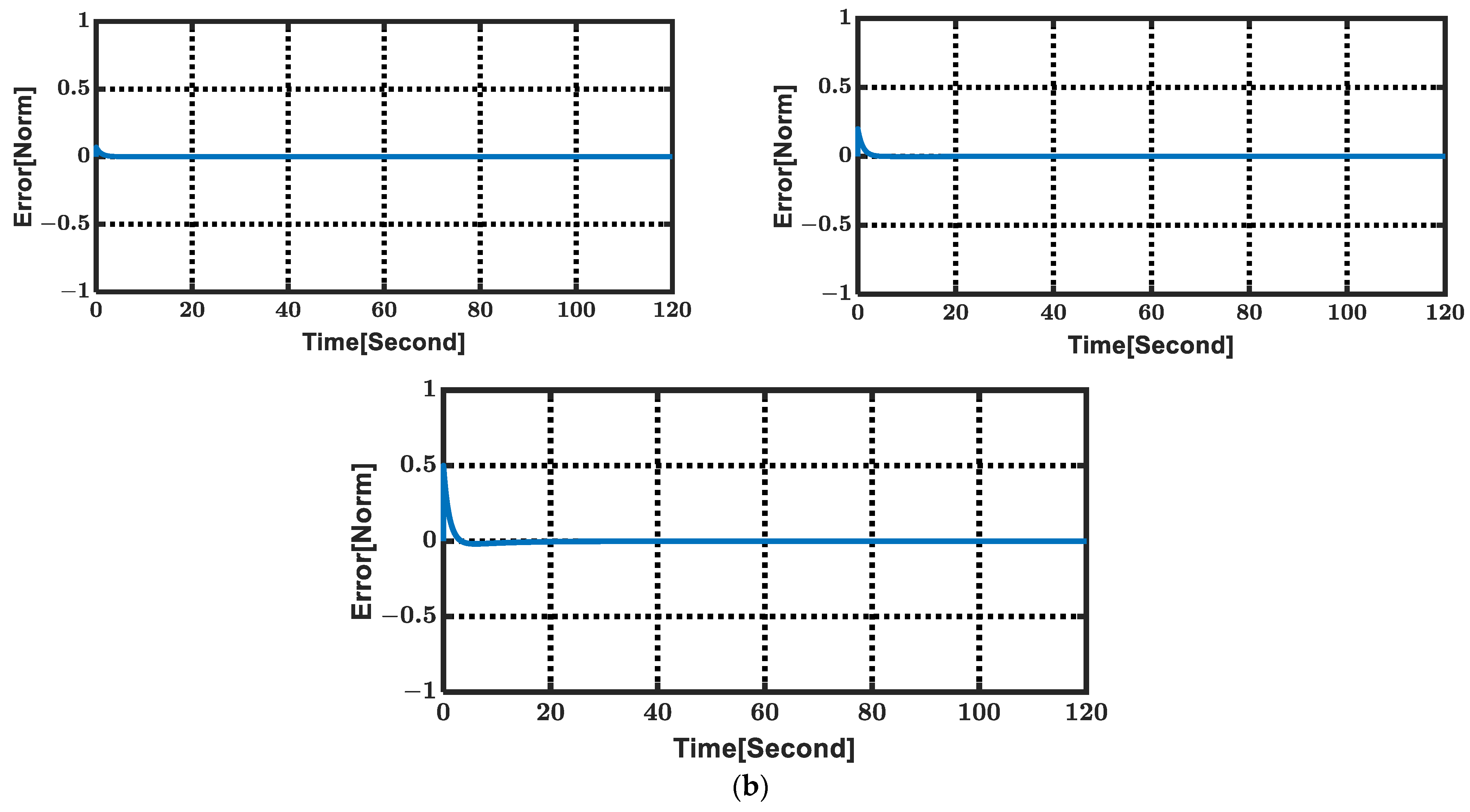

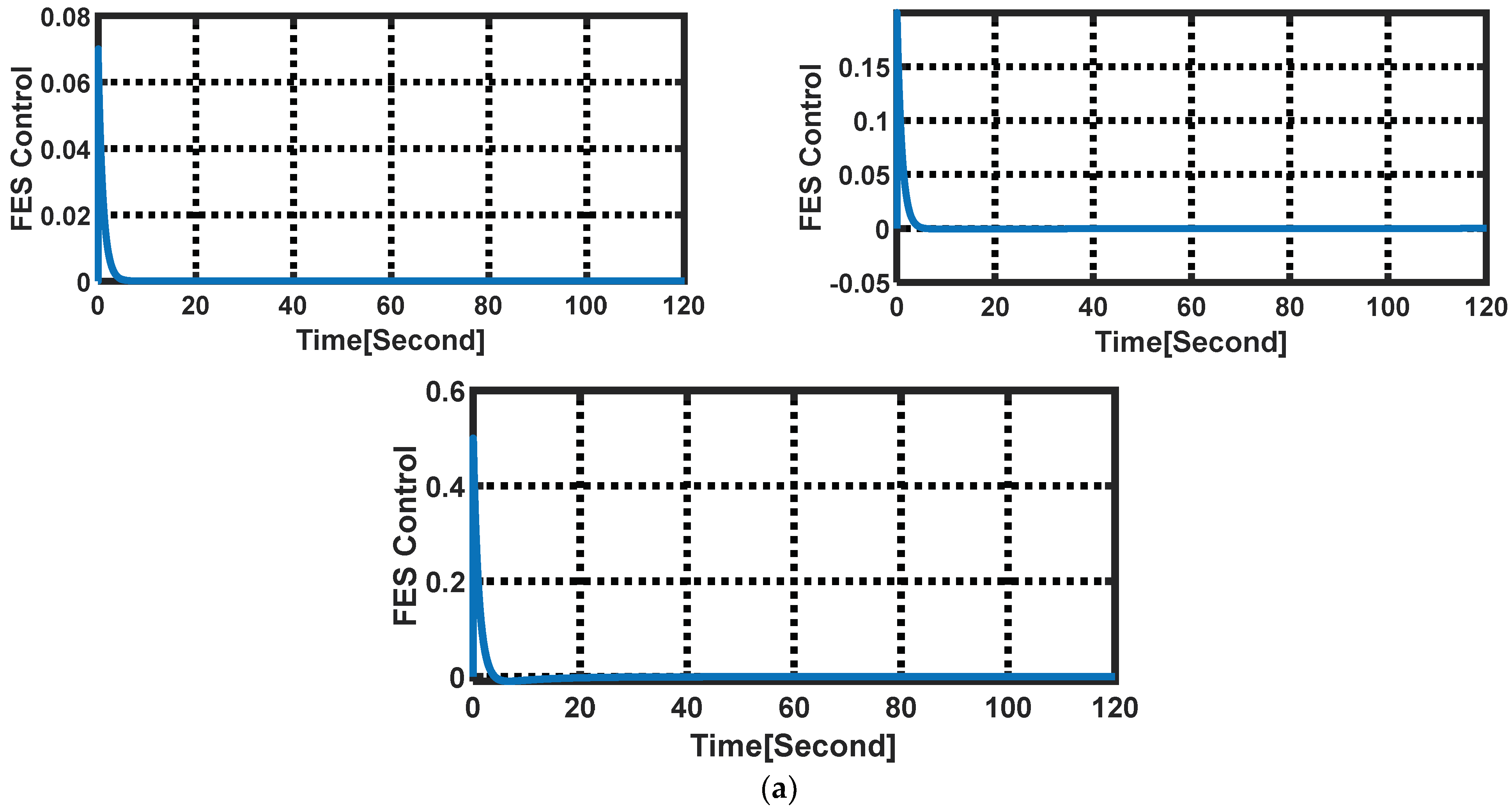
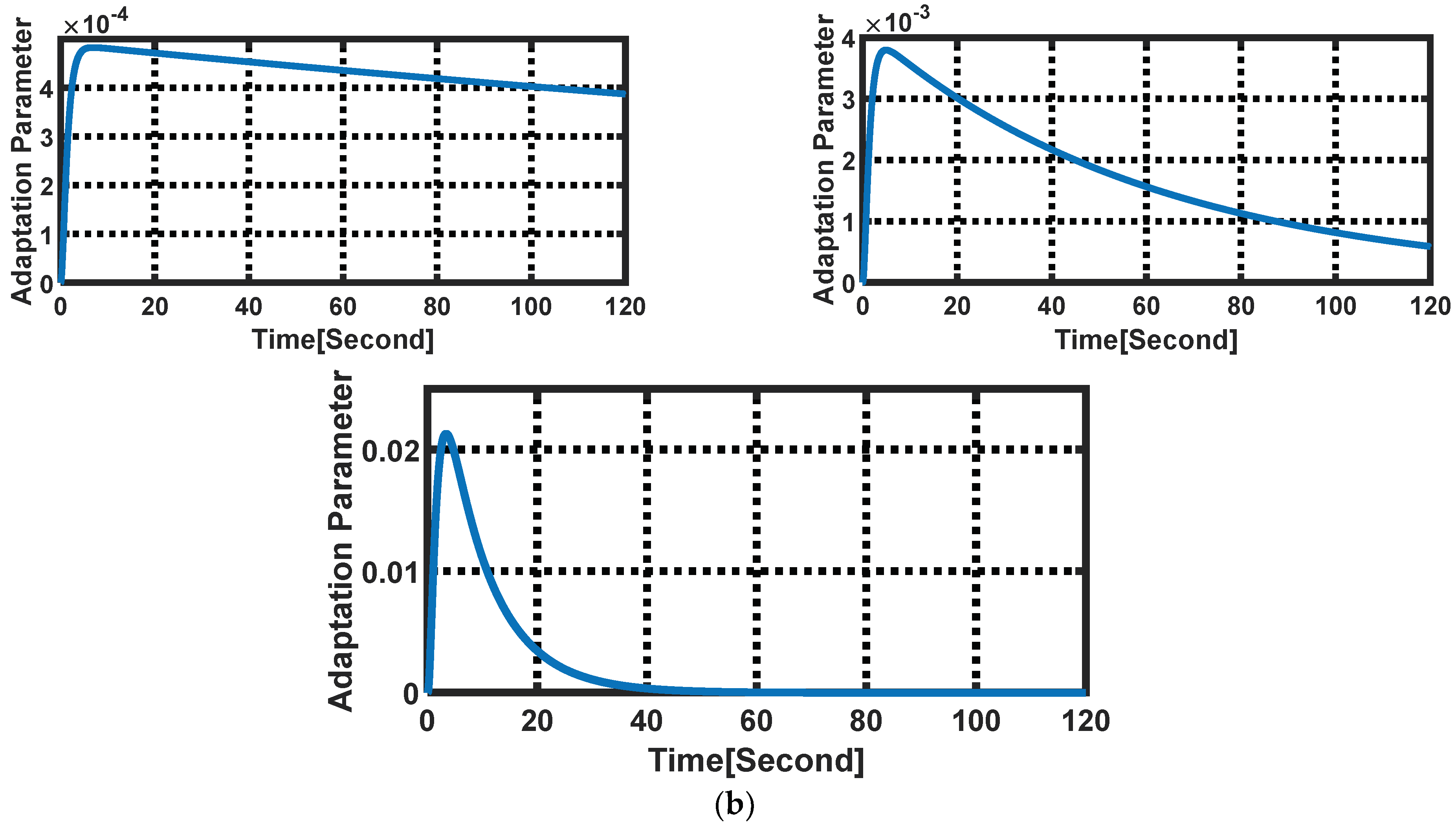

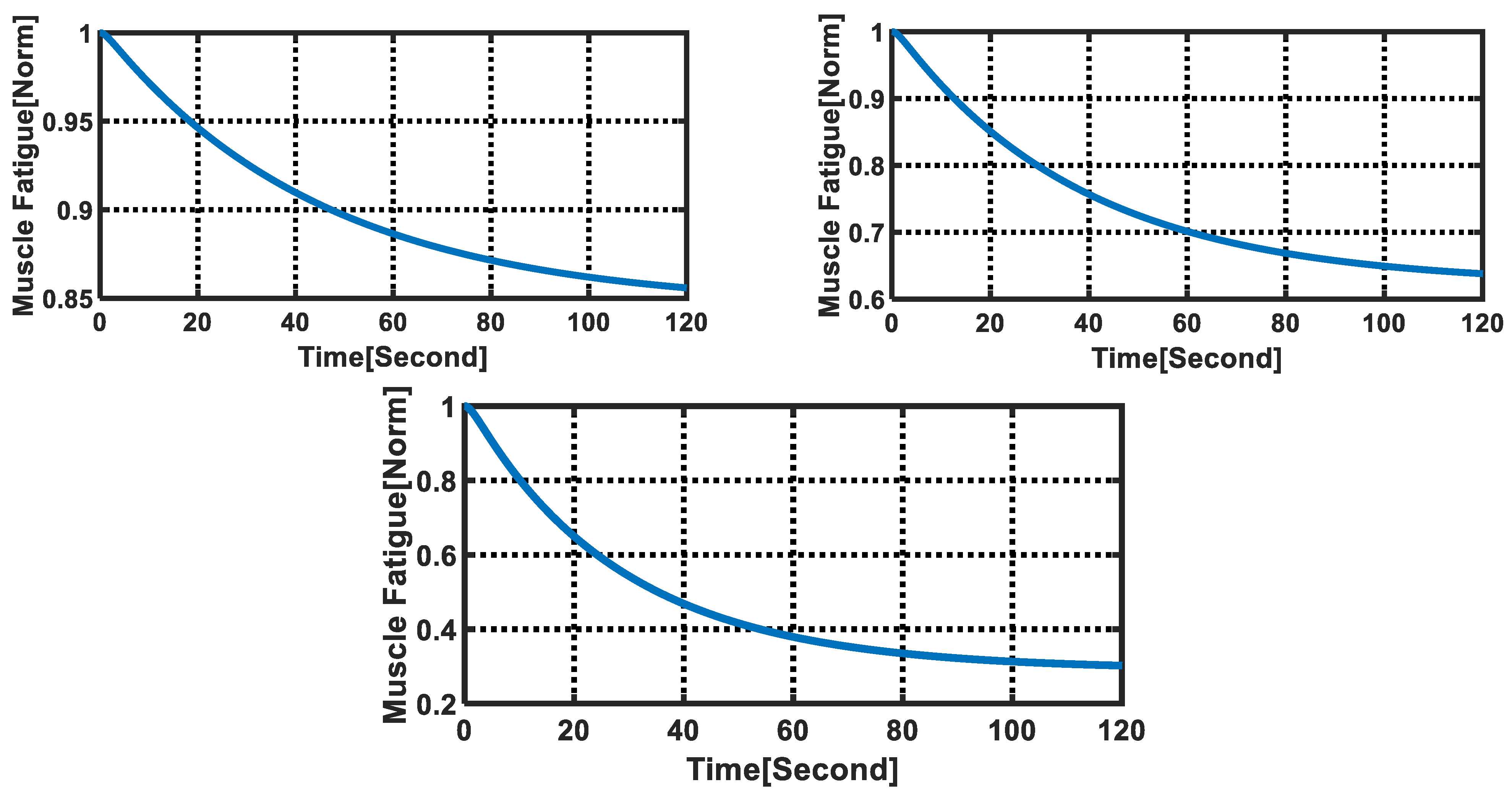
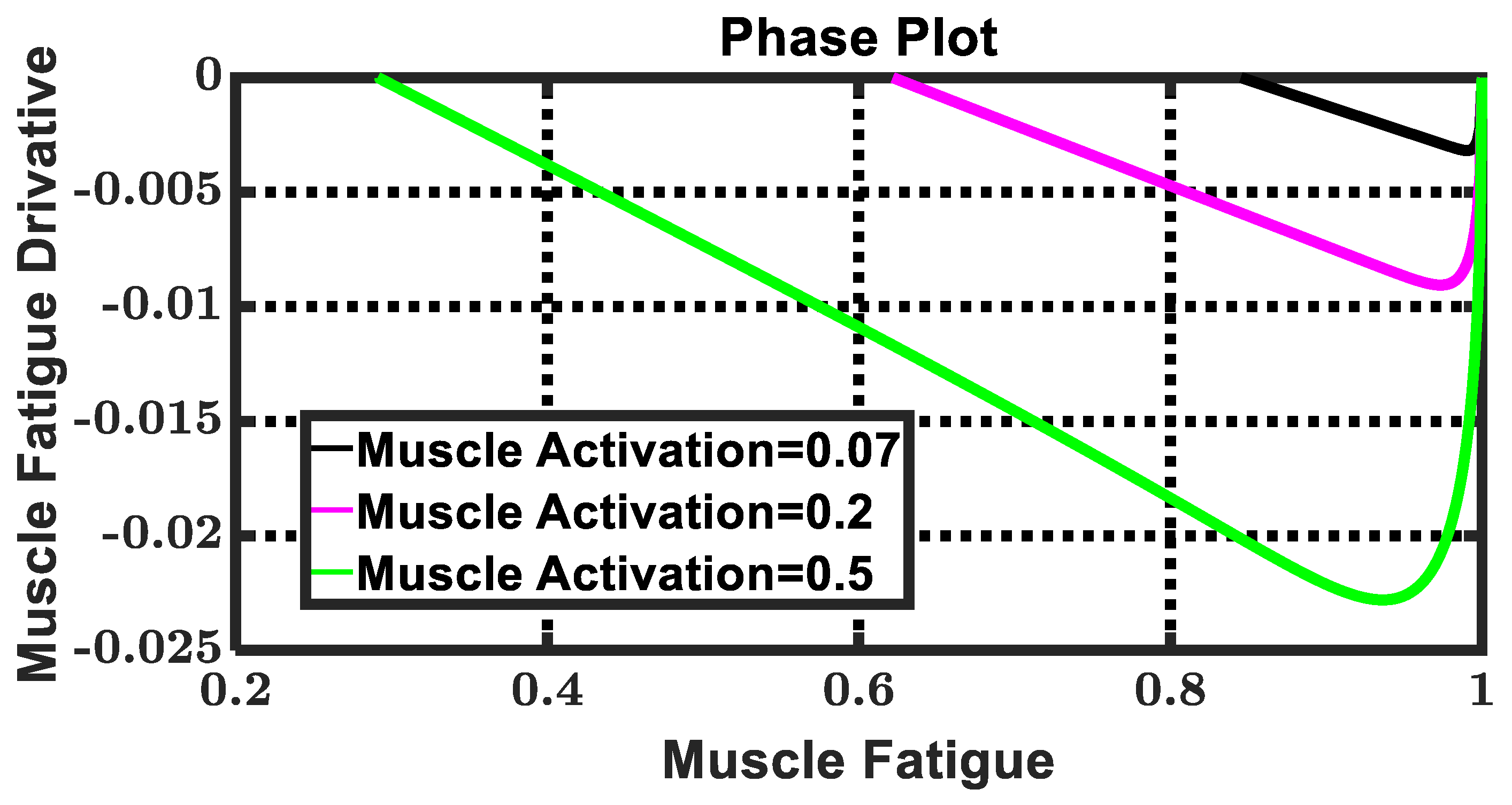
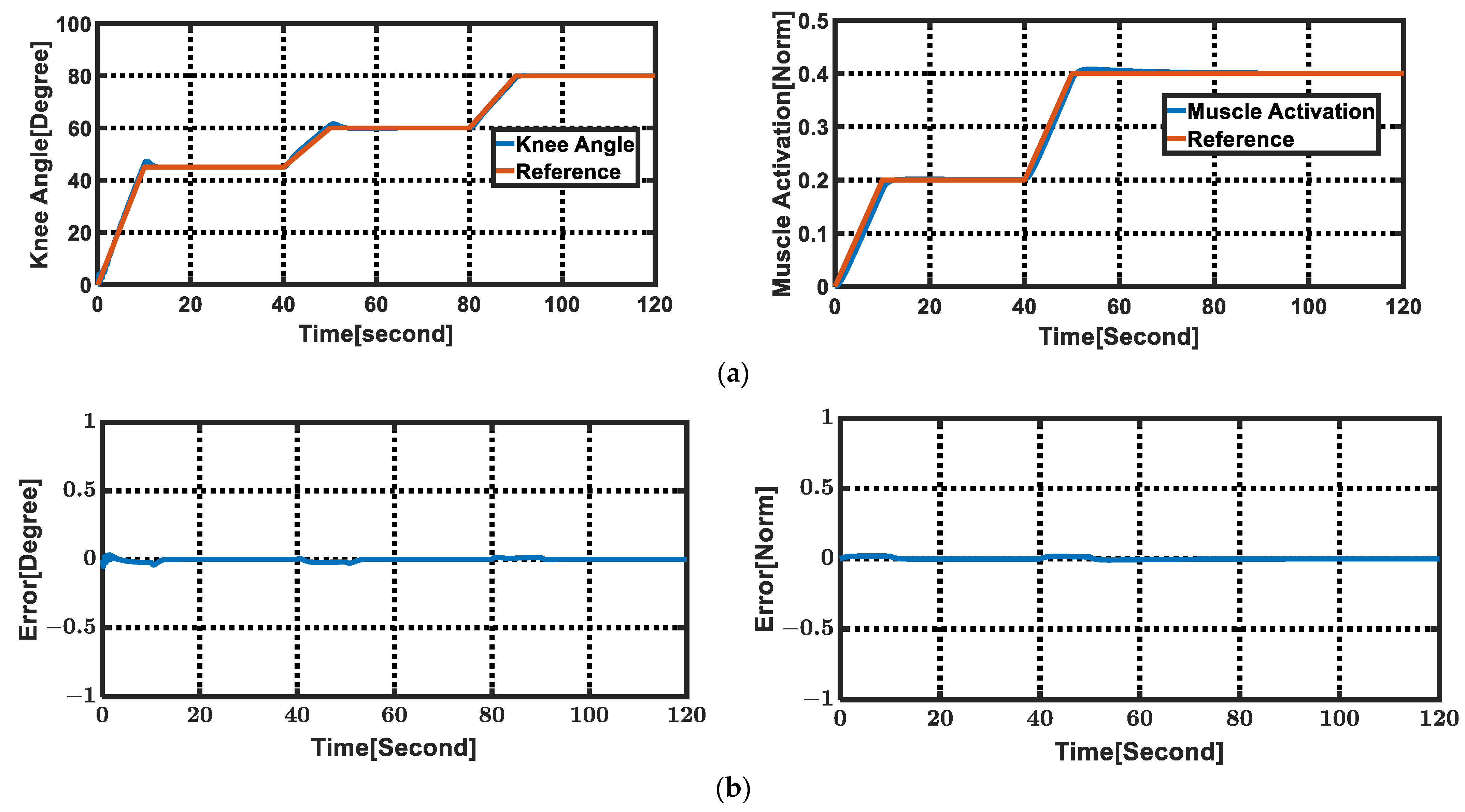
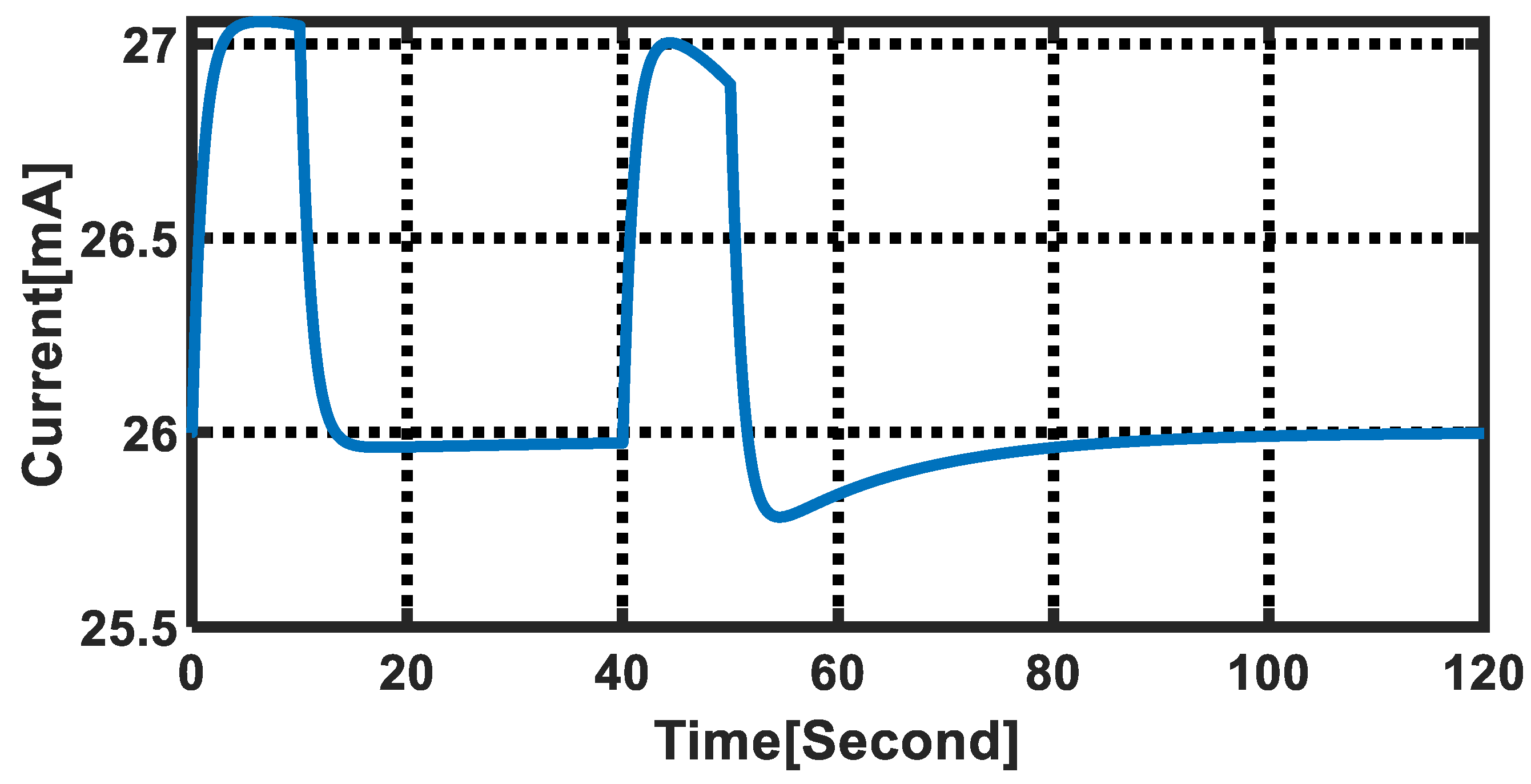

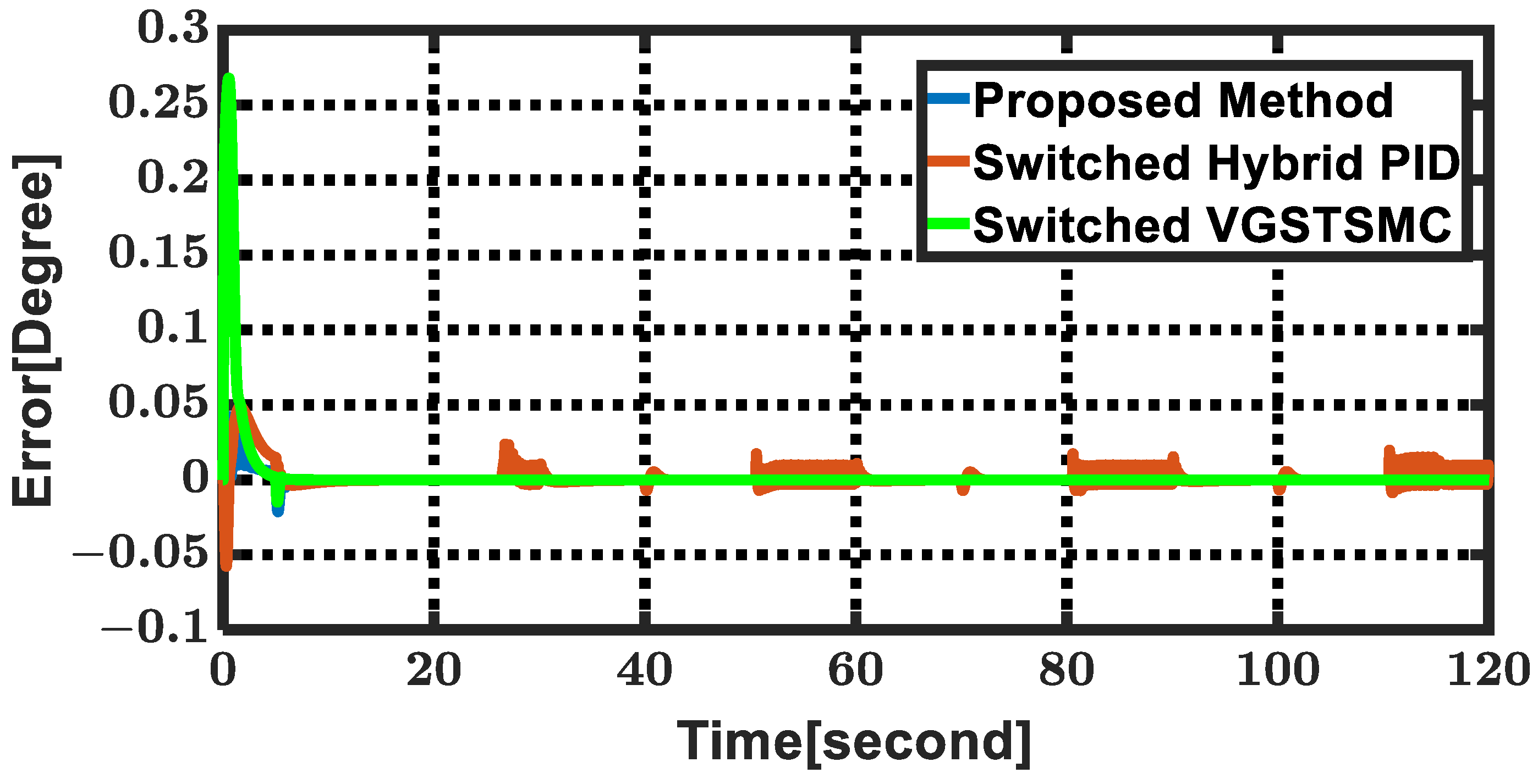
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|---|---|
| It [mA] | 18.1 | 2.66 | [rad] | 5.29 | 48.09 | ||
| Is [mA] | 60 | 1.68 | 78.78 | 0.26 | |||
| M [kg] | 4.69 | 1.64 | 55.76 | 29.17 | |||
| lc [m] | 37 | 1.59 | −49.02 | ||||
| J [kg/m] | 0.19 | 0.76 | 1.44 | ||||
| 1.2 | −39.09 | 2.61 |
| Maximum Current [mA] | Current Steady Value [mA] | RMS Error [Degree] | Overshoot [Degree] | |
|---|---|---|---|---|
| 0.07 | 29.67 | 25.99 | 0.17 | 1.51 |
| 0.2 | 36.49 | 25.99 | 0.36 | 2.73 |
| 0.5 | 52.50 | 26 | 1.14 | 3.99 |
| Converged Value | Muscle Fatigue Converged Value |
|---|---|
| 0.07 | 0.84 |
| 0.2 | 0.62 |
| 0.5 | 0.29 |
| Controller | Average Current [mA] | Maximum Current [mA] |
|---|---|---|
| Proposed Method | 20 | 26 |
| NMPC | 38 | 55 |
| Controller | Minimum Muscle Fatigue |
|---|---|
| Proposed Method | 0.8 |
| Tube based NMPC | 0.4 |
| Feedback linearized NMPC | 0.7 |
| Controller | |||
|---|---|---|---|
| Motor | 0.65 | 0.92 | 1.87 |
| FES | 454.32 | 45.39 | 431.17 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 248.7 | 1 | ||
| 1.38 | 30 | ||
| 0.82 | 5 | ||
| 0.587 | 1 | ||
| 1.38 |
| Control Methods | RMS Error [Degree] | Transient RMS Error [Degree] | Steady RMS Error [Degree] |
|---|---|---|---|
| Proposed Method | 0.19 | 0.68 | 6.27 |
| Switched Hybrid PID | 0.16 | 1.33 | 0.16 |
| Switched VGSTSMC | 1.26 | 4.38 | 2.25 |
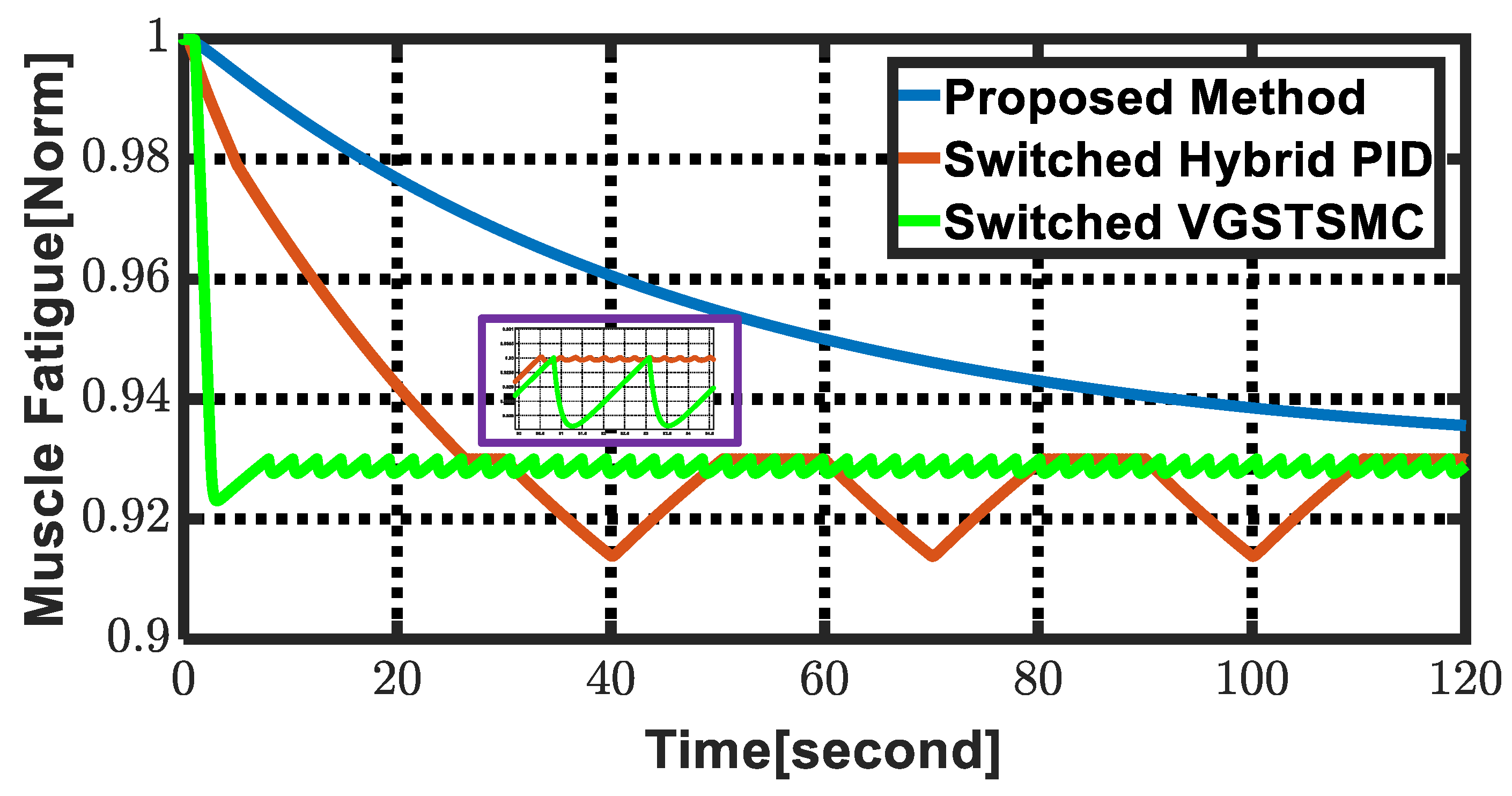
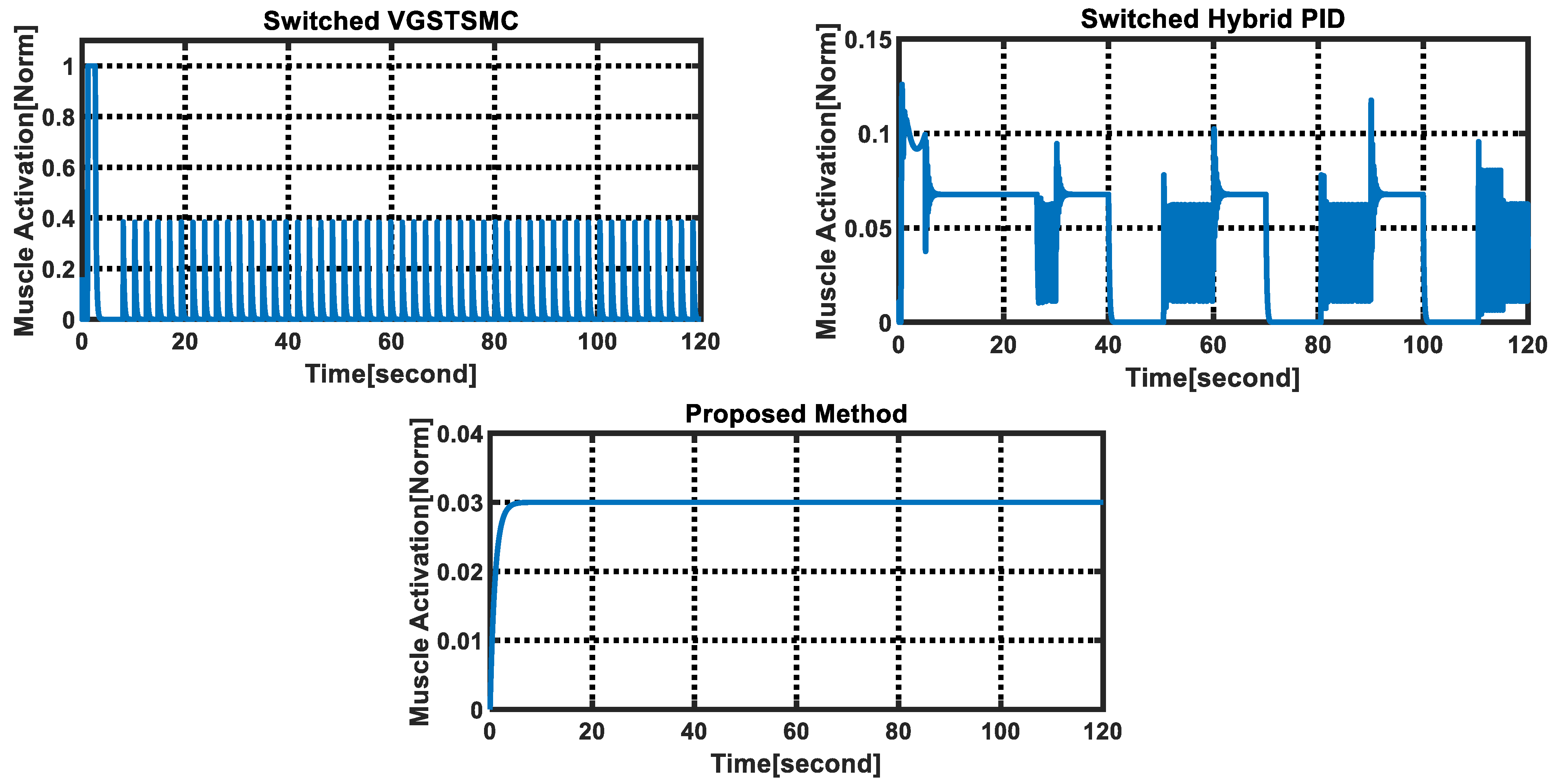
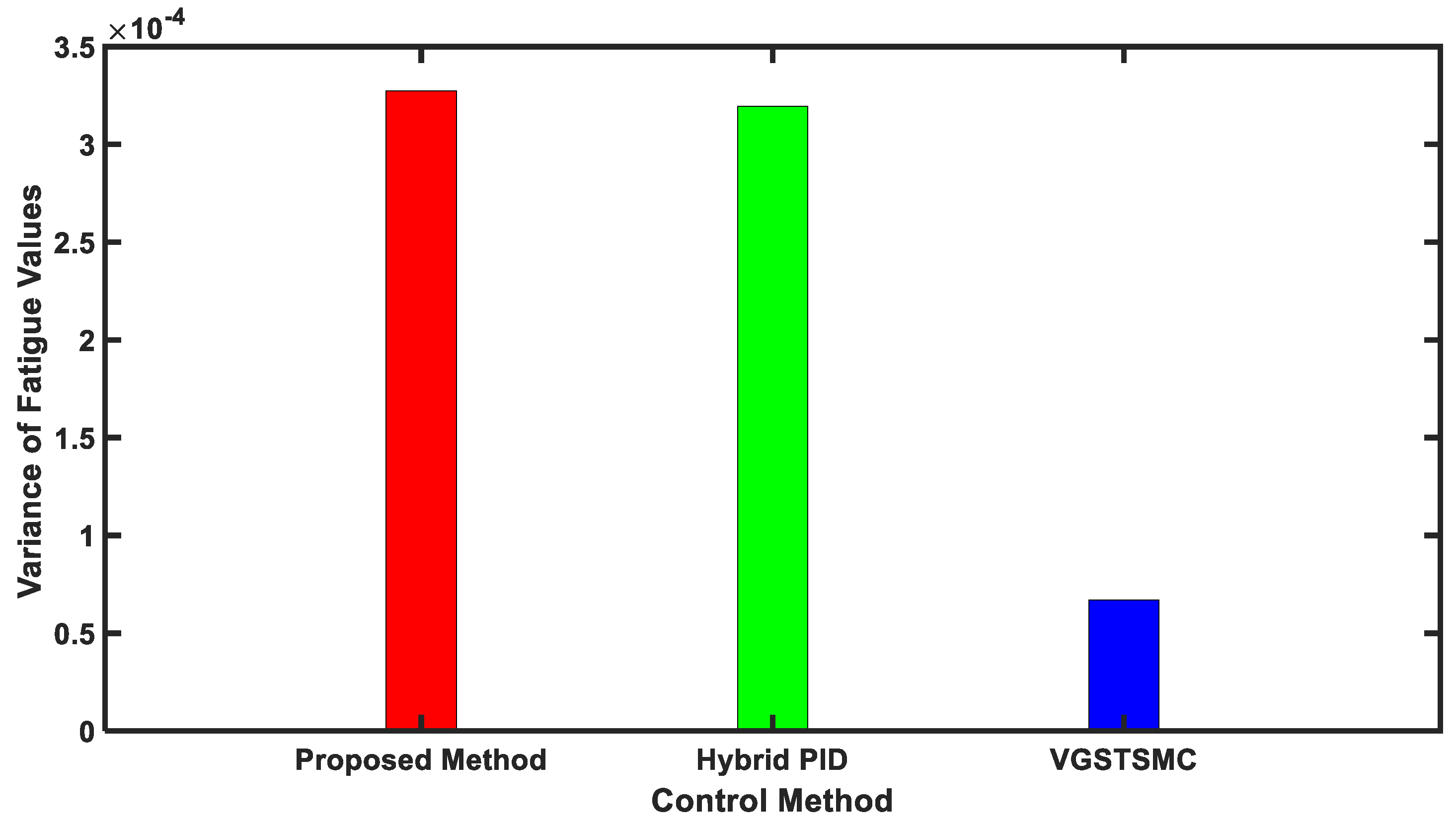
| Control Methods | Muscle Fatigue Values Mean | Muscle Fatigue Values Variance | Fatigue Instant [Second] | ||
|---|---|---|---|---|---|
| Proposed Method | 0.95 | 0.93 | 0.03 | t > 120 | |
| Switched Hybrid PID | 0.93 | 0.91 | 0.12 | 26.35 | |
| Switched VGSTSMC | 0.92 | 0.92 | 1 | 2.55 |
| Control Method | RMS Error of Angle [Degree] | Converged Fatigue Value [Norm] | RMS Error Improvement | Muscle Fatigue Improvement |
|---|---|---|---|---|
| Proposed Method | 0.19 | 0.95 | - | - |
| NMPC | 0.52 | 0.8 | 63% | 18.75% |
| Linearized MPC | 2.23 | 0.7 | 91.47% | 35.71% |
| Shared ILC | 1.91 | Not reported | 90.05% | - |
| ALDC | 2.82 | 0.75 | 93.26% | 26.66% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghajari, S.; Moghaddam, R.K.; Kobravi, H.; Pariz, N. Muscle Fatigue Regulation through Muscle Activation Control in a Knee Hybrid Exoskeleton: Simulation Study. Machines 2023, 11, 937. https://doi.org/10.3390/machines11100937
Ghajari S, Moghaddam RK, Kobravi H, Pariz N. Muscle Fatigue Regulation through Muscle Activation Control in a Knee Hybrid Exoskeleton: Simulation Study. Machines. 2023; 11(10):937. https://doi.org/10.3390/machines11100937
Chicago/Turabian StyleGhajari, Shazan, Reihaneh Kardehi Moghaddam, Hamidreza Kobravi, and Naser Pariz. 2023. "Muscle Fatigue Regulation through Muscle Activation Control in a Knee Hybrid Exoskeleton: Simulation Study" Machines 11, no. 10: 937. https://doi.org/10.3390/machines11100937
APA StyleGhajari, S., Moghaddam, R. K., Kobravi, H., & Pariz, N. (2023). Muscle Fatigue Regulation through Muscle Activation Control in a Knee Hybrid Exoskeleton: Simulation Study. Machines, 11(10), 937. https://doi.org/10.3390/machines11100937







