Abstract
High-speed permanent magnet synchronous motors (PMSMs) are usually started with the hybrid low-speed open-loop and high-speed closed-loop control mode. However, low-speed open-loop control produces large starting current, or even current overload, resulting in demagnetization and motor damage. Therefore, there is an urgent need to develop a high-speed permanent magnet synchronous motor with self-starting ability at low speed, that is, a permanent magnet hysteresis motor (PMHM). This paper takes the permanent magnet ring hysteresis column rotor structure as the research object. Firstly, the performance of this type of rotor is improved using the micro level of effective layer material AlNiCo, and the mechanical properties of AlNiCo are calculated. Secondly, based on the thick-walled cylinder theory, the analytical model for calculating the strength of the composite rotor considering the temperature effect is deduced, and the tangential and radial stress distribution for each part of the rotor under no-load and load conditions are obtained. Then, the electromagnetic losses and temperature field distribution of the rotor are obtained using the magneto-thermal bidirectional coupling finite element method. Finally, strength of the thermal rotor is analyzed by substituting the temperature rise curve function and AlNiCo parameters at the operating temperature. The comparison of the stress calculation results of the semi-analytical solution and the finite element method showed that the error between both of them is less than 5%, which verified that the semi-analytical solution can accurately analyze the thermal stress distribution of the rotor during high-speed rotation.
1. Introduction
High-speed permanent magnet synchronous motor (PMSM) is one of the most important energy recovery or drive unit, which has attracted much attention because of its simple structure, high power density, no excitation loss and high efficiency [1,2,3,4]. PMSM is the key to develop high-end energy power equipment such as hydrogen fuel cell air compressor, flywheel energy storage and micro gas turbine. However, factors such as the rotor with no starting winding, the existence of permanent magnet braking torque, and foil-bearing preload cause starting difficulties for the motor [5,6]. In reference [7], a sensorless control strategy was used to control the drive of a permanent magnet synchronous motor (PMSM). A sensorless stator resistance tracking strategy based on switching PI control based on MRAS observer was proposed. Meanwhile, a double closed-loop FLC was designed to control speed and current to improve the response performance of speed regulation and the accuracy of command voltage. As the high-speed permanent magnet rotor has no salient pole structure, low-speed open-loop and high-speed closed-loop hybrid control methods are commonly used for motor starting [8]. However, low-speed open-loop control will produce large starting current and even current overload, causing permanent magnet demagnetization and motor damage. The existing methods of asynchronous starting [9,10] and closed-loop control starting [11] can only solve the starting problem for medium and low-speed motors due to the limitation of rotor structure. Due to the problem of starting current overload of high-speed rotors, the open-loop control mode of constant voltage frequency ratio (V/F) or constant current frequency ratio (I/F) is not adopted in the low-speed section [8]. Hysteresis ring can be added to the rotor to induce self-starting ability in low speed [12,13]. This kind of permanent magnet synchronous motor with hysteresis structures, that is, permanent magnet hysteresis motor (PMHM), has the advantages of both the high starting torque of the hysteresis motor and the high power factor of the permanent magnet synchronous motor. This structure avoids the complex rotor position detection and control technology in the low-speed section, enhances the reliability of the system, and reduces the cost and pulsating torque of the whole machine [14]. However, due to factors such as very low-force density and insufficient starting torque, the radial rotor structure is prone to slip. And the strength of the hysteresis ring is not high enough to limit the high-speed applications. Therefore, to ensure rotor strength, there is an urgent need to solve the problems associated with the rotors of high-speed PMHM slip due to insufficient starting torque.
Scholars have proposed three rotor structures: block permanent magnet hysteresis ring rotor I [15,16], spherical permanent magnet hysteresis ring rotor II [17], and block permanent magnet hysteresis disk rotor III [13]. For rotor I, under the speed of 3000 rpm, hysteresis loop can avoid complex control and enable the rotor to start itself. During steady-state operation, there is less heat dissipation and low power loss because of no-slip power loss. For rotor II, the shape and position of permanent magnet are different from those of rotor I. Under a rated speed of 50,000 rpm and a rated torque of 0.09 Nm, the starting torque for rotor II can reach 0.3 Nm, and the starting multiple is as high as 3.3, in which the experimental results prove that the permanent magnet hysteresis hybrid rotor structure is feasible for the starting of high-speed PMSM. However, it is easy for the rotor to slip during self-starting, and the ratio of permanent magnet to hysteresis ring is not clarified when the motor performance is optimal. In rotor III, that is, hysteresis disk rotor structure, the starting characteristics and synchronization capabilities are good; it has already been mentioned that the development of semi-hard magnetic materials can improve the power range of the motor. Due to the small moment of inertia, the high peak torque and locked torque, and the low strength of the hysteresis ring material for the motor rotor, it is only suitable for low speed operation. The volume of permanent magnet and hysteresis disk in the disc rotor structure is large. Thus, this disc structure is not the best choice for high-speed motors considering the economy of permanent magnet or the lack of rare earth elements. Based on the above analysis, it is found that the rotor structure of PMHM is very important for the starting characteristics of the motor. Therefore, in this paper, the hysteresis column made of semi-hard magnetic material is used to replace the rotor shaft, that is, the permanent magnet ring and the hysteresis column structure.
It is universally acknowledged that eddy current and hysteresis loss of the rotor are determined by the conductivity and hysteresis characteristics of the material itself, which are closely related to the morphology and structure of the material. At present, the Al-Ni-Co material is commonly used in the rotor effective layer, but its eddy current loss is large, and there are holes and cracks at the phase interface [18,19], so its strength and hysteresis characteristics cannot be directly applied to the high-speed motor rotor. However, the development of high-speed PMHM has higher requirements for hysteresis materials including high hysteresis characteristics, higher strength, and lower eddy current, which are difficult to meet using the existing magnetic materials. The existing magnetic material, Al-Ni-Co permanent magnet alloy [20], which is commonly used in hysteresis ring, has a very good temperature stability () and a high operating temperature of 500 °C. Although its magnetic property is lower than those of rare earth permanent magnet materials, its outstanding magnetic stability makes it irreplaceable in the application of aerospace and other fields, especially for high-precision and high-stability equipment and instrument.
At present, in the rotor structure of permanent magnet motor, the permanent magnet mostly uses sintered NdFeB or sintered samarium cobalt material, which has high compressive strength, but the tensile strength is too low to withstand the demands of high-speed motors. Several research has been conducted on the theoretical analysis of rotor strength, mainly on the establishment of stress analytical models to optimize rotor structure. Ref. [21] investigated the effects of fit tolerance on the strength of permanent magnet and protection sleeve, but the stress distribution of the whole rotor was not considered in the analysis. Zhang [22] studied the influence of different protective sleeves on stress distribution using an analytical method. Chen [23,24] established a rotor stress analytical model based on the plane stress problem for a high-speed surface-mounted permanent magnet synchronous motor rotor, and then analyzed the relationship between speed, protective sleeve thickness, fit amount and rotor strength.
However, the above studies did not take into account the influence of rotor temperature rise on stress. Aiming for the development of a three-layer rotor structure, an analytical model of rotor strength considering both temperature field and rotor loss was established [25,26,27], but it did not consider the influence of coupling field. N. Hanappier [28] calculated the solid-thermal coupling field of the motor rotor using the basic principles of continuum mechanics and thermodynamics. Then, the electromagnetic field and the temperature field distribution of a permanent magnet motor based on the magnetic-thermal coupling analysis method was calculated. Reference [29] calculated the electromagnetic field, temperature field and stress field of the motor via unidirectional coupling. Although the coupling analysis of the electromagnetic field, temperature field and stress field have been carried out in the above studies, they are all two-field coupling or three-field unidirectional coupling calculation. Under high temperature conditions, the error of calculation results of electromagnetic field and temperature field is large. This is very harmful to the structure design of the motor. The research object of this paper is the four-layer rotor structure, as shown in Figure 1. Firstly, the composition design and temperature stability should be analyzed from the requirement of the rotor effective layer material AlNiCo at a micro level. Secondly, the magnetic-thermal bidirectional coupling strength of the rotor should be calculated considering dynamic elasticity modulus and Poisson’s for the AlNiCo material under the actual operating conditions.
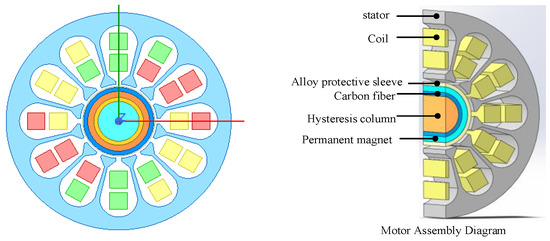
Figure 1.
Rotor structure of PMHM.
2. Temperature Stability Calculation of AlNiCo
AlNiCo, which is used in a hysteresis motor, has very good temperature stability and high operating temperature [30], and this outstanding magnetic stability is especially suitable for high-precision high-stability equipment and instruments. In order to meet the requirements of high-speed PMHM with self-starting ability at low speed and with low eddy current at high speed, we need to improve the properties of the material itself. When the motor runs stably, the rotor temperature is within 300 °C; hence, the thermal properties of the improved AlNiCo material will be calculated as the physical parameters of the hysteresis material for rotor strength analysis. The first 300 °C physical parameter values such as density, Poisson’s ratio and elastic modulus are selected, and then the middle values are subjected to approximate processing, which provides reliable data for motor strength calculation.
An appropriate amount of Ti and Nb elements is added to AlNiCo to improve the coercivity of the material [31], and a small amount of Si and Zr is added to reduce the critical cooling rate of the material [32]. The AlNiCo ratio adopted in this paper is based on AlNiCo8 which has high coercivity; its composition is shown in Table 1. It can be seen that the Fe content of the improved AlNiCo composition is higher than that of the traditional AlNiCo. It is because the improved material also contains an insulating Fe-coated element. At the same time, in order to reduce the content of FeCo phase generated by the reaction of Fe and Co elements, it is necessary to reduce the content of Co in the component.

Table 1.
Improved AlNiCo permanent magnet alloy composition.
After phase calculation, the relationship between phase transformation and heat treatment temperature of the improved AlNiCo alloy is obtained, as shown in Figure 2. In this figure, the combination of and is the BCC phase, in which mainly contains Fe and Co elements, while contains a small amount of Cu, Al, Ti and other elements. and are mainly composed of Ni, Al, and Ti elements. The and phases are face-centered cubic structure, in which the content of Fe element can be as high as 55~60%, and it also contains a small amount of Ti, Ni, Co and other elements. The G phase mainly contains Ni, Nb, and Si elements, and a small amount of Fe and Ti, and tiny amounts of Co. The phase mainly contains 80% Ni and 22% Ti, and tiny amounts of Co, Cu, Fe and other elements. According to Figure 2, phase is precipitated between 750 °C and 1200 °C. To avoid the formation of this phase, 730 °C was selected as the heat treatment temperature. The relationship between phase transformation and temperature after heat treatment is shown in Figure 2b. It can be seen that the improved AlNiCo material contains 50% BCC phase, 38% NiAl phase, 9% phase, 3% phase and a small amount of G phase under 730 °C.
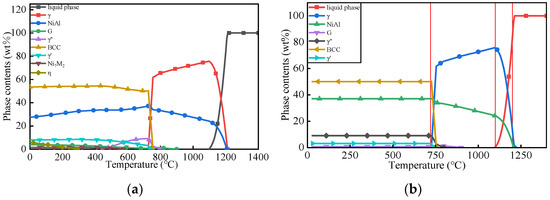
Figure 2.
The relationship between alloy phase content and temperature: (a) before heat treatment; (b) after heat treatment.
Figure 3 shows the relationship between the mechanical properties and the operating temperature of the improved AlNiCo material. It can be seen that its density is 7.15 g/cm3 at room temperature, and it linearly decreases with the increase in temperature before the liquefaction begins at 1100 °C. For the permanent magnet hysteresis column rotor, the actual operating temperature is less than 300 °C, as shown in the dotted box, and the corresponding density is about 7.08 g/cm3. The variation trends of the elastic modulus and the shear modulus are consistent with density; at 300 °C, the values are 170 GPa and 65 GPa, respectively. However, the change trend in Poisson’s ratio is the opposite. Before the liquid phase appears, Poisson’s ratio linearly increases from 0.32 at room temperature to 0.37 with the increase in temperature. During the production of the liquid phase, it rapidly increases to 0.49, and remains at 0.49 after complete liquefaction.
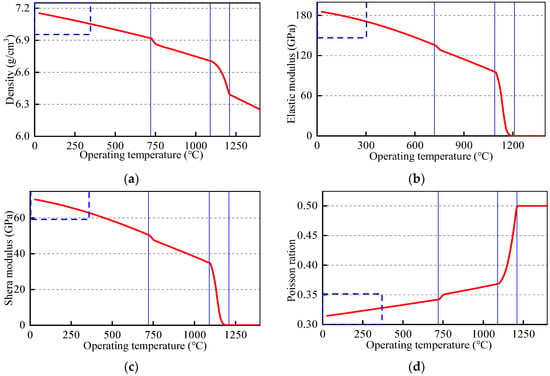
Figure 3.
Relationship between mechanical properties and operating temperature for the improved AlNiCo material: (a) density; (b) elastic modulus; (c) shear modulus; (d) Poisson’s ratio.
Thermal and electrical conductivities are two key parameters that have a direct impact on the temperature distribution for each part of the permanent magnet hysteresis column rotor. As shown in Figure 4a, the thermal conductivity of the material linearly increases before 730 °C, reaching 35 W/m·K at 300 °C, which is 3.4% higher than that at room temperature. The conductivity parabolically decreased before the formation of the liquid phase. The conductivity is 3.3 × 106 1/Ω·m at room temperature, and it decreases to 1.3 × 106 1/Ω·m with the increase in temperature. At 300 °C, the conductivity is 2.25 × 106 1/Ω·m, which is slightly smaller than the pre-designed value because the insulation coating on the surface of pure iron is not taken into account in the calculation of material properties.
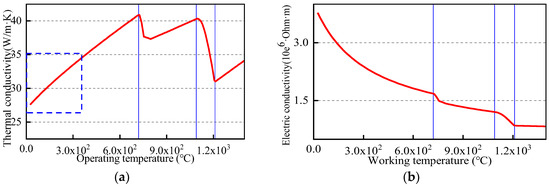
Figure 4.
The variation in thermal conductivity and electrical conductivity with operating temperature for the improved AlNiCo material: (a) thermal conductivity; (b) conductivity.
3. Structure and Strength Analysis of Permanent Magnet Hysteresis Column Rotor
The composite rotor structure, as shown in Figure 1, can be divided into thick-walled cylinders and disks. Figure 5 shows the force model of the rotor plane. The outer surface of the hysteresis column is subjected to a uniform distribution of contact pressure . Carbon fiber, permanent magnet, and alloy sleeve are the thick-walled cylinder structures. The outer surface is subjected to a uniform distribution of contact pressure , and the inner surface is subjected to a uniform distribution of contact pressure , where n is 1–3 or I–IV. Under the influence of interference fit, the rotor has strain in all directions, which further generates tangential and axial stress, and the axial stress has an effect on the radial strain and tangential strain of the rotor.
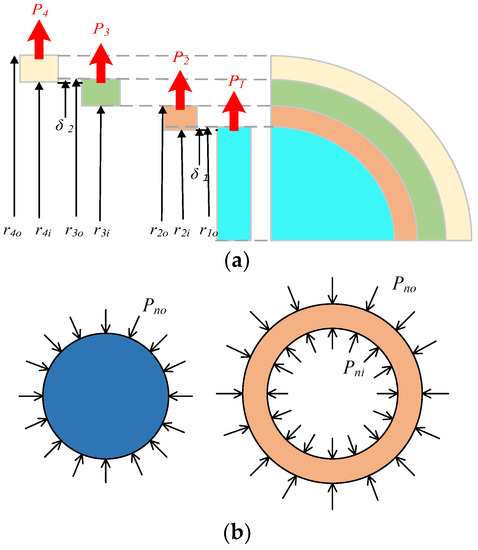
Figure 5.
Mechanical model for the rotor: (a) disk; (b) thick-walled cylinders.
In order to describe the rotor strength more accurately, the temperature effect should be considered in strength calculation. Hysteresis column, permanent magnet, and alloy sleeve are regarded as isotropic materials, but carbon fiber is anisotropic. Different kinds of material property parameters in the paper are defined, as shown in Table 2 and Table 3.

Table 2.
Nomenclature.

Table 3.
Greek letters.
According to the generalized Hooke’s law and thermodynamics, the physical equation of rotor structure in Figure 5 can be expressed as
After ignoring the axial strain of the rotor while considering the centrifugal force of the rotor speed, the equilibrium differential equation of each part in the polar coordinate system is
The corresponding geometric equation is
By combining Equations (1)–(3), the displacement field of the rotor can be obtained.
Isotropic material:
Anisotropic material:
where , and are undetermined coefficients, and each part corresponds to different expressions, which can be obtained according to the boundary conditions.
Substituting Equation (2) into Equation (1), the stress field of the rotor can be obtained.
The analytic expression of stress can be obtained by substituting the displacement Equations (4) and (5) into the stress Equation (6).
Isotropic material:
Anisotropic material:
To obtain the static pre-stress for each part of the rotor, the stress needs to be solved using the following stress boundary conditions. The stress in the rotor structure is continuous, so it can be assumed that the contact stresses from inside to outside, as shown in Figure 5, are , , and , respectively. The relation formulas are , , and , respectively. Because the outer diameter of the rotor is not restricted, it meets the condition of , . The stress boundary conditions of the rotor structure can be written as follows.
The above boundary conditions are substituted into the stress and displacement equations of each part, and then the undetermined coefficients , and contact stress of each part are obtained. The obtained contact stress is substituted into the stress equation of each part to further obtain the analytical solution of the stress.
4. Magneto-Thermal Bidirectional Coupling Strength of Rotor
The overall model and assembly diagram of the motor used in the calculation are shown in Figure 1. The parameters are as follows: the inner diameter of the stator is 18.5 mm, the outer diameter of the stator is 55 mm, the number of slots is 12, the number of slot conductors is 20, and the polar logarithm is 1. In this structure, the permanent magnet adopts a parallel magnetization mode. Firstly, the current load is inputted into the PMHM, and then the rotor loss under load (50 A) and no-load (0 A) conditions are calculated; the total loss distribution of the rotor after the smooth operation of the motor is then obtained. Then, the loss is applied to the temperature field as a heat source, and the temperature field results are iterated to the electromagnetic field through workbench for the bidirectional coupling solution. By reducing the iteration error, the temperature rise trend of the rotor can be calculated more accurately. Since the rotor temperature during the stable operation of the motor is within 300 °C, only the performance parameters of the AlNiCo material before 300 °C are selected, and the intermediate value is considered in the strength calculation. The specific parameters are shown in Table 4.

Table 4.
Material parameters.
4.1. Loss Analysis of Magneto-Thermal Bidirectional Coupling
Taking the speed of 120,000 rad/min as an example, the interference fit for the composite rotor with = 0.01 mm and = 0.06 mm was selected, as shown in Figure 5. When it runs at 1.38 ms, the motor enters a stable operation state at the allowable temperature; the magnetic density distribution under no-load and load conditions are shown in Figure 6. Among them, the maximum magnetic density of 1.54 T occurs in the stator part at no-load; in the rotor part, the maximum magnetic density of 0.99 T occurs on the permanent magnet. The maximum magnetic density of 1.13 T in the rotor part also occurs on the permanent magnet under load. For a pair of pole motors, the magnetic density is symmetrically distributed. According to the B–H curve of the motor materials, the magnetic density of each part does not reach magnetic saturation when the motor is running, which meets the design requirements of the motor. The losses under the two conditions are shown in Figure 7a,b, respectively. The rotor losses are concentrated in the outer metal sleeve due to the skin effect.
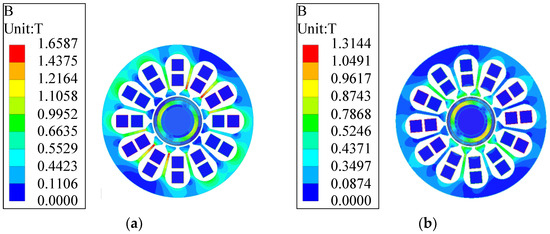
Figure 6.
Magnetic density distribution of the PMHM: (a) no-load; (b) under load.
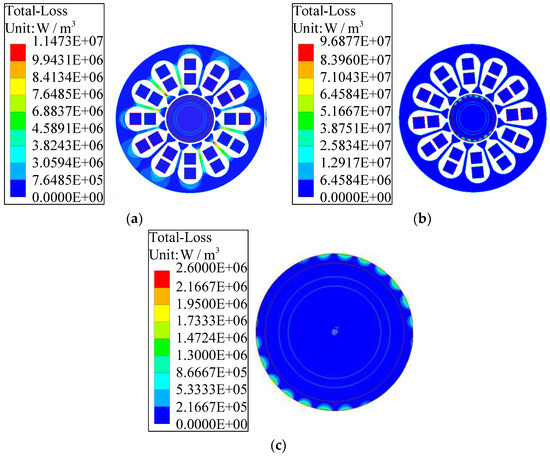
Figure 7.
Loss distribution of the PMHM: (a) no-load; (b) under load. (c) topography of (a).
The bidirectional coupling of the electromagnetic field and the temperature field is solved, and their distribution under two working conditions is obtained, as shown in Figure 8. Due to the cooling of the outer surface of the rotor after being in contact with the air, change in the temperature gradient mainly occurs in the metal protective sleeve of the rotor, while the temperatures of the hysteresis column, carbon fiber, and permanent magnet are almost the same. The average temperature of the rotor under no-load is about 26 °C, while it reaches about 160 °C under load. Under the same working condition, the temperature gradient error, calculated using the electromagnetic field and the temperature field, is about 0.7%.
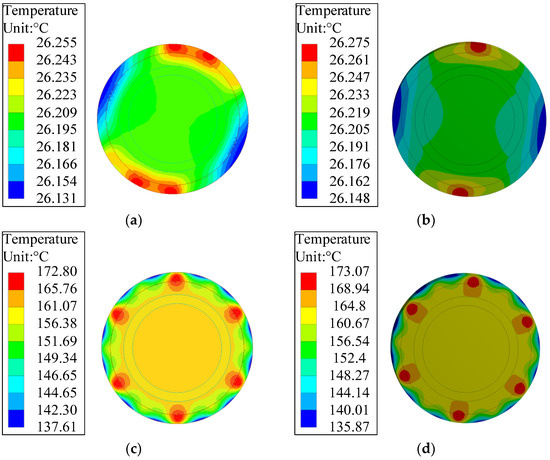
Figure 8.
Temperature distribution of the rotor under different conditions: (a) no-load for electromagnetic field; (b) no-load for temperature field; (c) under load for electromagnetic field; (d) under load for temperature field.
In order to obtain the analytical solution of the strength under the magnetic-thermal bidirectional coupling field, the unit loss density converted by the rotor loss, varying with the current magnetic field position, is uniformly applied to the rotor. The heat transfer coefficient of 100 is selected, and the room temperature is set to 22 °C for the coupling field solution. The calculation results are shown in Figure 9. Compared with the temperature field distribution changing with the magnetic field position, the homogenization loss method reduced the overall temperature by 4.3%, which proves that this method is feasible. In Figure 9, the fit of the curve of the rotor temperature field is shown. To obtain the corresponding temperature rise curve function, under no-load and load is calculated, as shown in Equations (11) and (12), respectively. The stress can be obtained by substituting the temperature rise function into the stress analytic formula. Similarly, in the finite element method, the simulation value of rotor stress distribution is obtained by adding the rotor temperature distribution into the strength analysis module as a load for thermal-structural coupling analysis.
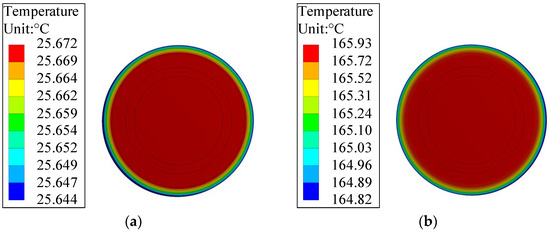
Figure 9.
Temperature distribution of the rotor: (a) no-load; (b) under load.
4.2. Rotor Strength under No-Load and Load
Taking the rotor with the same interference fit for = 0.01 mm and = 0.06 mm and speed of 120,000 rad/min as the analysis object, the thermal stress of the motor rotor under electromagnetic action is analyzed. Figure 10 shows the radial and tangential stress distribution of the rotor under no-load and load conditions. The comparison of the thermal stress of the rotor obtained with the analytical method and the finite element method is shown in Figure 11. Due to the influence of the two-layer interference fits, the whole rotor is under radial compression stress, which is more conducive to protect the hysteresis material from damage. At the same time, under the action of pre-stress and centrifugal force, the rotor has a peak at the interference fit.
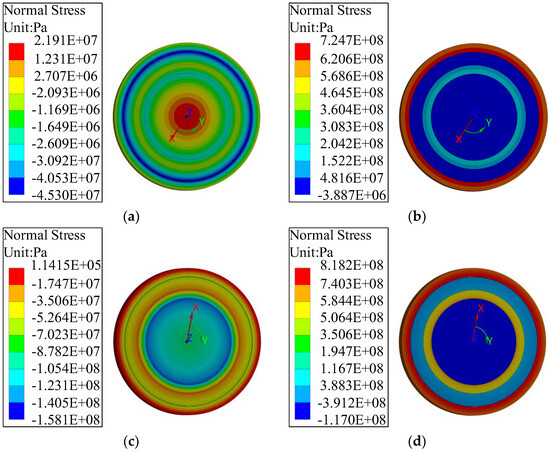
Figure 10.
Stress distribution of the rotor under different working conditions: (a) no-load radial force; (b) no-load tangential force; (c) load radial force; (d) load tangential force.
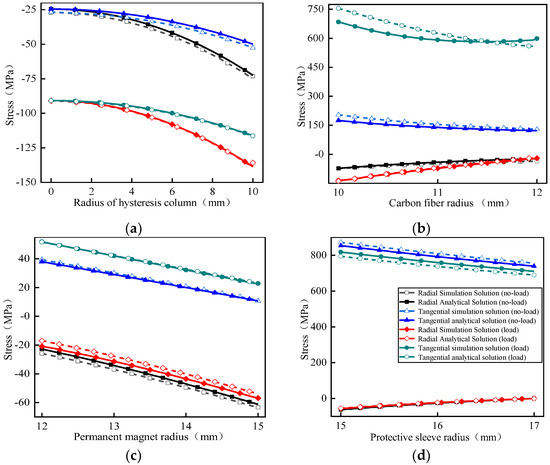
Figure 11.
The stress values for each part of the rotor under two working conditions: (a) hysteresis column; (b) carbon fiber; (c) permanent magnet; (d) protective sheath. Symbol descriptions in (a–c) is the same to that in (d).
As shown in Figure 11a, with the increase in the radius of the hysteresis column, the stress difference between the conditions under no-load and load increases continually; the maximum difference is 70 Mpa, which is caused by the temperature difference of 140 °C between the two conditions. The two kinds of stresses increase with the increase in the radius of the hysteresis column due to the influence of pre-stress and thermal expansion of the material. In addition, the radial and tangential stresses at the rotor center are −25 MPa and −90 MPa, respectively, which is due to the fact that tangential driving force is greater than centrifugal force. As shown in Figure 11b, since carbon fiber is an anisotropic material, its tangential and radial stresses g vary greatly at the inner diameter, whether it is loaded or unloaded. Taking the analytical solution of load as an example, the amplitude change of radial stress is about 70 MPa, and the amplitude change of tangential stress is nearly twice that of radial stress, which is because of the fact that the tangential elastic modulus is much larger than the radial elastic modulus. Under the high speed 120 kr/min condition, the interference fit between the carbon fiber and the hysteresis column is 0.01 mm, which increases the pre-stress of the hysteresis column. Therefore, the whole hysteresis column presents a compression state, and its stress direction is opposite to that of the carbon fiber. The carbon fiber sleeve presents a state of radial compression and tangential tension as a whole, and the stresses in two directions decrease with the increase in radius which yields the minimum value at the outer diameter. Under the two working conditions, the error of the semi-analytical solution and simulation results of the tangential stress for the carbon fiber is less than 6%, among which the error is the largest under load. On one hand, the carbon fiber is regarded as a whole in modeling, which is different from the actual laminated winding. On the other hand, due to the influence of thermal expansion coefficient and elastic modulus at high speed and high temperature, the tangential stress error becomes larger. According to the above analysis, both material strength and the temperature gradient errors meet the engineering design requirements.
As shown in Figure 11c, the radial compressive stress of the permanent magnet increases with the increase in the radius in the range of −20 MPa~−60 MPa, and reaches the maximum value at the outer diameter. The inner diameter of the permanent magnet needs to bear the stress caused by the deformation of the carbon fiber. At the same time, the outer diameter is constrained by the sleeve, resulting in the decrease in tangential stress, with the radius under no-load and load conditions in the range of 40 MPa~10 MPa and 52 MPa~23 MPa, respectively.
As shown in Figure 11d, the maximum tensile stress of the rotor appears in the protective sleeve, and the tangential stress decreases with the increase in radius. The ranges of change are 850~800 MPa and 800~750 MPa under no-load and load conditions, respectively. This is mainly because the protective sleeve as the outermost structure of the rotor needs to bear large centrifugal force inside, resulting in huge tangential tensile stress. In addition, the different ranges of stress variation under the two conditions indicates that the influence of temperature rise on the tangential force of the protective sleeve cannot be ignored. The difference of the radial stress between the two conditions is about 20 MPa, and it gradually decreases with the radius until 0. This is because the outer diameter is not subjected to any constraints, and there is interference fit at the inner diameter. According to the tensile strength (1390 MPa) of the selected material Inconel718 and the first strength theory, the tensile stress of the protective sleeve can meet the requirement of the strength of the material.
In summary, the error between the semi-analytical solution and the finite element result is very small, which verifies the correctness of the proposed analytical method of magneto-thermal bidirectional coupling strength. The two-layer interference fit design introduced in this paper has played a certain role in protecting the hysteresis material while ensuring the continuity of stress. Under both conditions, each material used in the rotor meets the allowable strength criterion, and ensures that the motor can operate safely.
5. Discussion and Conclusions
To solve the problem associated with the lack of starting winding in the rotor of high-speed PMSM, a rotor structure with a permanent magnet hysteresis column is proposed in this paper. Considering the low tensile strength for both the hysteresis and permanent magnet materials, the strength of the hysteresis material and the composite rotor are respectively studied to analyze if the motor rotor can ensure the operation strength at the rated speed of 120,000 rad/min. The main conclusions are as follows:
(1) The composition of the existing AlNiCo is improved, and the soft magnetic phase is pretreated with insulation coating technology to reduce the high-frequency eddy current loss. After obtaining the thermodynamic calculation results, the heat treatment temperature is determined to be 730 °C, in order to avoid the precipitation of harmful components. The relationship between the properties (mechanical properties, thermal conductivity and conductivity) and the working temperature of AlNiCo is analyzed. The physical parameters of the motor at the highest possible operating temperature of 300 °C are obtained, which provide a basis for the strength analysis of the hot rotor.
(2) Based on the thick-walled cylinder theory, the analytical model of composite rotor strength considering temperature rise and high-speed centrifugal force is derived. The magnetic-thermal coupled finite element method is used to study the rotor loss distribution and the temperature field distribution under no-load (0 A) and load (50 A) conditions, respectively. The obtained temperature function is put into the rotor stress field for calculation, and the stress values of the semi-analytical method and the finite element method are compared and analyzed. The error is within 6%, which verifies the correctness of the semi-analytical method. According to the first strength theory, the materials used in the rotor can meet the strength requirements, confirming the feasibility of the permanent magnet hysteresis column rotor structure.
Author Contributions
L.X.: Conceptualization, methodology, funding access, resources, supervision, writing—review, and editing. S.Z.: Concept, method, software, investigation, formal analysis, writing. J.D.: Data management, writing visualization, investigation. W.C.: Software, literature search. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by National Natural Science Foundation of China (Grant No. 52275271), Shaanxi Natural Science Foundation (2020JM-531, 2022JM-194).
Data Availability Statement
Due to privacy issues, we do not disclose the data from the study. If you have questions, please contact the corresponding author to discuss them with us.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhao, W.; Yang, Z.; Liu, Y.; Wang, X. Analysis of a Novel Surface-Mounted Permanent Magnet Motor with Hybrid Magnets for Low Cost and Low Torque Pulsation. IEEE Trans. Magn. 2021, 57, 1–4. [Google Scholar] [CrossRef]
- Gerada, D.; Mebarki, A.; Brown, N.L.; Gerada, C.; Cavagnino, A.; Boglietti, A. High-Speed Electrical Machines: Technologies, Trends, and Developments. IEEE Trans. Ind. Electron. 2013, 61, 2946–2959. [Google Scholar] [CrossRef]
- Cheng, W.; Li, W.; Xiao, L.; Li, M.; Tian, Y.; Sun, Y.; Yu, L. Transient line starting analysis of the ultra-high speed PMSM. AIP Adv. 2017, 7, 903–910. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Du, G.; Wang, T.; Liu, G.; Cao, W. Rotor Retaining Sleeve Design for a 1.12-MW High-Speed PM Machine. IEEE Trans. Ind. Appl. 2015, 51, 3675–3685. [Google Scholar] [CrossRef]
- Zhao, L.; Ham, C.; Zheng, L.; Wu, T.; Sundaram, K.; Kapat, J.; Chow, L. A highly efficient 200000 RPM permanent magnet motor system. IEEE Trans. Magn. 2007, 43, 2528–2530. [Google Scholar] [CrossRef]
- Rahman, M.A.; Chiba, A.; Fukao, T. Super high speed electrical machines-Summary. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; pp. 1272–1275. [Google Scholar]
- Liu, Z.H.; Nie, J.; Wei, H.L.; Chen, L.; Li, X.H.; Lv, M.Y. Switched PI Control Based MRAS for Sensorless Control of PMSM Drives UsingFuzzy-Logic-Controller. IEEE Open J. Power Electron. 2022, 3, 368–381. [Google Scholar] [CrossRef]
- Nair, S.V.; Hatua, K.; Prasad, N.D.; Reddy, D.K. A Quick I-f Starting of PMSM Drive with Pole Slipping Prevention and ReducedSpeed Oscillations. IEEE Trans. Ind. Electron. 2021, 68, 6650–6660. [Google Scholar] [CrossRef]
- Rabbi, S.F.; Rahman, M.A. Analysis of Starting and Synchronization Process for Line Start IPM Motors. In Proceedings of the 2012 7th International Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, 20–22 December 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 311–314. [Google Scholar]
- Xu, F.; Chen, A.; Yang, S.; Cao, J.; Liu, X.; Li, L. AC Loss Prediction in BSCCO-Tape Armature Winding Design of a Synchronous Motor. IEEE Trans. Appl. Supercond. 2010, 20, 1005–1008. [Google Scholar]
- Yamazaki, K.; Kokubu, S. Induction Motor Analysis by Considering Hysteresis Loops in Stator and Rotor. IEEE Trans. Magn. 2021, 57, 1–4. [Google Scholar] [CrossRef]
- Behniafar, A.; Darabi, A. Analytical modeling of disc-type permanent magnet hysteresis motor in steady-state operational conditions. Int. J. Comput. Math. Electr. Electron. Eng. 2017, 36, 991–1007. [Google Scholar] [CrossRef]
- Qian, J.H.; Rahman, M.A. Analysis of field oriented control for permanent magnet hysteresis synchronous motors. IEEE Trans. Ind. Appl. 2002, 29, 1156–1163. [Google Scholar] [CrossRef]
- Rehman, S.U.; Huang, Q.; Sagar, R.U.R.; Jiang, Q.; Yang, M.; Zhong, Z. Interaction mechanism, magnetic properties and microstructure of Ce-Fe-B/Alnico spark plasma sintered magnets. J. Magn. Magn. Mater. 2021, 537, 168237. [Google Scholar] [CrossRef]
- Gallicchio, G.; Palmieri, M.; Di Nardo, M.; Cupertino, F. Fast Torque Computation of Hysteresis Motors and Clutches Using Magneto-static Finite Element Simulation. Energies 2019, 12, 3311–3327. [Google Scholar] [CrossRef]
- Jagiela, M.; Garbiec, T.; Kowol, M. Design of High-Speed Hybrid Hysteresis Motor Rotor Using Finite Element Model and Decision Process. IEEE Trans. Magn. 2014, 50, 861–864. [Google Scholar] [CrossRef]
- Pyrhonen, J.; Ruoho, S.; Nerg, J. Hysteresis losses in Sintered NdFeB permanent magnets in rotating electrical machines. IEEE Trans. Ind. Electron. 2015, 62, 857–865. [Google Scholar] [CrossRef]
- Mohapatra, J.; Xing, M.; Elkins, J.; Liu, J.P. Hard and semi-hard magnetic materials based on cobalt and cobalt alloys. J. Alloys Compd. 2020, 824, 153874. [Google Scholar] [CrossRef]
- Duan, N.; Xu, W.; Feng, H.; Wang, S.; Guo, Z.; Li, Y.; Wang, S.; Zhu, J. A Scalar Hysteresis Model of Ferromagnetic Materials Based on the Elemental Operators. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Ma, H.J.; Zhang, J.T.; Li, G.H.; Zhang, W.X.; Wang, W.M. Effect of Zr on the thermal stability and magnetic properties of Fe78Si9B13, glassyalloy. J. Alloys Compd. 2010, 501, 227–232. [Google Scholar] [CrossRef]
- Wang, J.; Wang, F.; Bao, W.; Guan, E. Rotor Design and Strength Analysis of High Speed Permanent magnet Motor. Proc. CSEE 2005, 25, 140–145. (In Chinese) [Google Scholar]
- Zhang, F.; Du, G.; Wang, T.; Huang, N. Strength Analysis of Rotor Protection Measures for High Speed Permanent magnet Motor. Proc. CSEE 2013, 33, 195–202. (In Chinese) [Google Scholar]
- Cheng, W.; Deng, Z.; Xiao, L.; Zhong, B.; Zhang, B. Strength analytical solution to ultra-high-speed permanent magnet rotor considering temperature gradient and segmental permanent magnet effect. Adv. Mech. Eng. 2019, 11, 1–4. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, C.; Qiao, X. Strength Analysis of High Speed Split SPMSM Rotor fixed with Carbon Fiber. Electr. Mach. Control 2019, 23, 93–103. (In Chinese) [Google Scholar]
- Chen, L.; Zhu, C.; Jiang, K. Rotor Strength Analysis of High Speed Surface Mount Permanent Magnet Synchronous Motor with interelectrode Filling Block. J. Zhejiang Univ. Eng. Ed. 2015, 9, 1738–1748. (In Chinese) [Google Scholar]
- Mo, L.; Zhu, X.; Zhang, T.; Quan, L.; Wang, Y.; Huang, J. Temperature Rise Calculation of a Flux-Switching Permanent-Magnet Double-Rotor Machine Using Electromagnetic-Thermal Coupling Analysis. IEEE Trans. Magn. 2017, 54, 1–4. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, J.; Liu, X.; Han, B. Loss Calculation and Thermal Analysis of Rotors Supported by Active Magnetic Bearings for High-Speed Permanent-Magnet Electrical Machines. IEEE Trans. Ind. Electron. 2015, 63, 1. [Google Scholar] [CrossRef]
- Hanappier, N.; Charkaluk, E.; Triantafyllidis, N. A coupled electromagnetic–thermomechanical approach for the modeling of a electric motors. J. Mech. Phys. Solids 2021, 149, 2567–2569. [Google Scholar] [CrossRef]
- Preis, K.; Biro, O.; Dyczijedlinger, R. Application of FEM to coupled electric, thermal and mechanical problems. IEEE Trans. Magn. 1994, 30, 3316–3319. [Google Scholar] [CrossRef]
- Maroufian, S.S.; Pillay, P. Design and Analysis of a Novel PM-Assisted Synchronous Reluctance Machine Topology with AlNiCo Magnets. IEEE Trans. Ind. Appl. 2019, 55, 4733–4742. [Google Scholar] [CrossRef]
- Rehman, S.U.; Wei, C.; Huang, Q.; Jiang, Q.; Haq, A.U.; Wang, J.; Zhong, Z. Tailoring the microstructure, magnetic properties and interaction mechanisms of Alnico-Ta alloys by magnetic field treatment. J. Alloys Compd. 2021, 857, 157586. [Google Scholar] [CrossRef]
- Zhang, S.-D.; Wang, S.; Chen, S.-Y.; Yu, X.; Sun, J.-B. Structure and magnetic properties of alnico 8 ribbons. Phys. B Condens. Matter 2020, 597, 412423. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).