Analysis of Synchronous Generator Self-Excitation under Capacitive Load Condition in Variable-Frequency Aviation Power System

Featured Application

This research will be useful for load configuration design in the case of variable-frequency aviation power systems with a reduced risk of synchronous generator self-excitation under capacitive load conditions.

Abstract

As power electronic converters become more widely used in aviation power systems, the associated capacitive loads in the harmonic filter circuits increase accordingly. The risk of self-excitation of aeronautical synchronous generators due to capacitive loads is thus increased. Compared with the self-excitation of a generator in a conventional fixed-frequency power system, this process is more complicated in a variable-frequency aviation power supply (360–800 Hz), as both the varied frequency and the loading conditions contribute to the self-excitation. To quantify this effect, in our study, a series-parallel model of simplified RLC loads under a variable-frequency power supply was built. The criterion of generator self-excitation, given in terms of the generator impedance and the load impedance, was then derived. To facilitate the load configuration design in the case of an aviation power system, a comprehensive analysis of the influences of the varied load power and system frequency on the load impedance was conducted. A graphical approach was proposed to determine self-excitation by comparing the series load reactance and resistor with three critical impedances corresponding to three self-excitation criteria, which is more intuitive and enables one to visualize the tendency of self-excitation with varied frequencies and loading conditions more effectively. Finally, the influence of variable frequency on the self-excitation of the aeronautical synchronous generator was verified by the simulation results.

1. Introduction

Recent decades have witnessed the trend of aviation electrification, led by the concept of more electric aircraft (MEA) and all electric aircraft, with traditional hydraulic and pneumatic energy replaced by more electrical energy in airplanes [1]. This has resulted in significant growth in the number of motor and power electronic devices in aircraft power systems, which exhibit nonlinear load characteristics and adversely affect power quality [2]. To address this issue, filters with capacitors are commonly used, leading to an increase in the capacitive loads. Nonetheless, capacitive loads also lead to certain stability issues, such as resonance with other inductive devices [3]. According to the principle of synchronous generators, capacitive loads may result in the hazardous self-excitation phenomenon, malfunction of the voltage regulators, and even the collapse of the entire system.

The self-excitation of synchronous generators has been extensively studied in the context of utility AC power systems with a nominal frequency of 50 or 60 Hz [4,5,6,7,8]. The main research methods include the state variable approach and phasor analysis approach. As previously reported, the major culprits in causing the self-excitation of synchronous generators include the saliency of the generator rotor, long transmission line, capacitive loads, and filters. However, as the frequency of the utility grid is fixed at around 50 or 60 Hz, the relevant conclusions cannot be directly applied to aircraft AC power systems, partly due to the difference in the grid frequency. Generally, higher frequencies are adopted to reduce the volume and weight of the transformers and inductors in aircraft. Two schemes of grid frequencies exist in AC aviation power systems, of which one is constant frequency (or “CF”, in brief) at 400 Hz, such as that used in the Boeing 767 and Boeing 777 [9,10], and the other is variable frequency (or “VF”), ranging from 360 to 800 Hz, such as that used in the Boeing 787 and Airbus A380 [11,12]. Currently, the VF scheme is gaining dominance due to its advantages of a reduced weight, higher reliability, and adaptability to variable-speed motors.

Until now, the self-excitation of synchronous generators under a VF power supply has not been fully investigated. As an isolated power system, the traditional loads in aircraft are mainly inductive and exhibit a lagging power factor. With the greater uptake of capacitive loads in aircraft power systems, the grid characteristics will undergo essential changes. Among these, the induced self-excitation of synchronous generators is one of the difficult issues, causing voltage instability and reduced safety and reliability. As is well-known, self-excitation may result in abrupt over-voltage and over-current in the generator stator and power system network, drive the field-winding current to become negative, whereupon the excitation system will normally cease to function, and even cause overall system failure and the reduced reliability performance of the aviation power supply [13].

Given the significance of functional reliability in complex systems such as aircrafts, it is worth conducting a thorough analysis to assess the self-excitation process of synchronous generators under VF power supply and capacitive load conditions [14]. In [15], the power factor of VF power systems was analyzed by deriving the impedance characteristics of the inductive filter and capacitive loads with varying grid frequencies. The same authors studied the load characteristics of an asynchronous motor with a terminal capacitor [16]. The self-excitation criterion of a synchronous generator feeding capacitive loads under 115 V/400 Hz grid conditions was studied in [17]. A simplified generator–load model was developed, while the stability criterion was provided from the perspective of the load impedance, load capacity, and power factor. However, the influence of variable frequency was not considered [18].

With the nonlinear characteristics of load impedance under a varied frequency of 360–800 Hz, the self-excitation of a synchronous generator will be more complex than that of its fixed-frequency counterpart. To address this issue, here, the impacts of frequency and load variation on the load impedance are studied. A graphical tool applied to the frequency domain, similar to the bode plots used in stability analysis, is proposed, whereby the criterion of self-excitation is reformulated as the equivalent series load impedance, compared with three critical impedances that are determined by the generator parameters. The mechanism through which a reduced active power load or increased capacitive load leads to self-excitation is revealed by observing the intersection of the relevant impedance curves as the power and frequency change. This research will provide a reference for power supply compliance in variable-frequency aviation power systems.

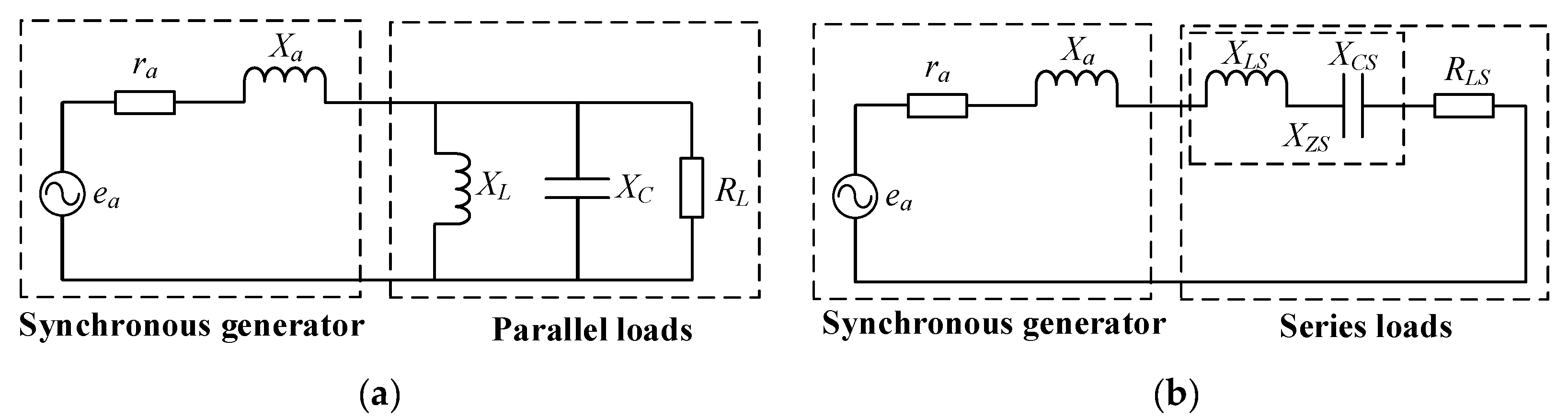
2. Capacitive Loads and Self-Excitation of Aviation Synchronous Generators

The traditional three-stage aero-synchronous generator in a three-phase, four-wire system is considered, with the main generator being electrically excited and possessing a salient rotor.

2.1. Simplified Model of Generator–Load System

For simplicity, the per-phase model of an aero-generator serving parallel RLC loads was developed, as shown in Figure 1a, where R_L, X_L, and X_C denote the resistive load, inductive load, and capacitive load, respectively. The synchronous generator is characterized by a steady-state phase voltage e_a, inner resistance r_a, and inductance X_a. The parallel load is transformed to the equivalent series load, as shown in Figure 1b. The relationship between R_L, X_L, X_C, and the series resistance R_LS, inductance X_LS, and capacitance X_CS are given by (1), where |Z_L| is the magnitude of the load impedance:

$$\{\begin{array}{c}{R}_{LS}={\left|Z_L\right|}^2/R_L\\ X_{LS}={\left|Z_L\right|}^2/X_L\\ X_{CS}={\left|Z_L\right|}^2/X_C\end{array},{\left|Z_L\right|}^2=\frac{{(R_L{X}_L{X}_C)}^2}{{(X_L{X}_C)}^2+R_L{}^2{(X_L-X_C)}^2}$$

(1)

In Figure 1b, the sum of the inductance and capacitance on the load side is given by (2), corresponding to the net reactive power:

$$X_{ZS}=X_{CS}-X_{LS}={\left|Z_L\right|}^2\frac{X_L-X_C}{X_C{X}_L}$$

(2)

Based on the two-reaction theory, the voltage equation of the generator–load system in the dq reference frame is given by (3), where v_d, v_q, and v_F denote the voltage in the d-axis, q-axis, and field winding; i_d, i_q, and i_F denote the current in the d-axis, q-axis, and field winding; and X_md is the mutual inductance between the field winding and the virtual d-axis winding [19,20].

$$\left[\begin{array}{c}{v}_d\\ v_q\\ v_F\end{array}\right]=\left[\begin{array}{ccc}{r}_a+R_{LS}& X_q-X_{ZS}& -X_{md}\\ -X_d+X_{ZS}& r_a+R_{LS}& 0\\ X_{md}& 0& R_F\end{array}\right]\left[\begin{array}{c}{i}_d\\ i_q\\ i_F\end{array}\right]$$

(3)

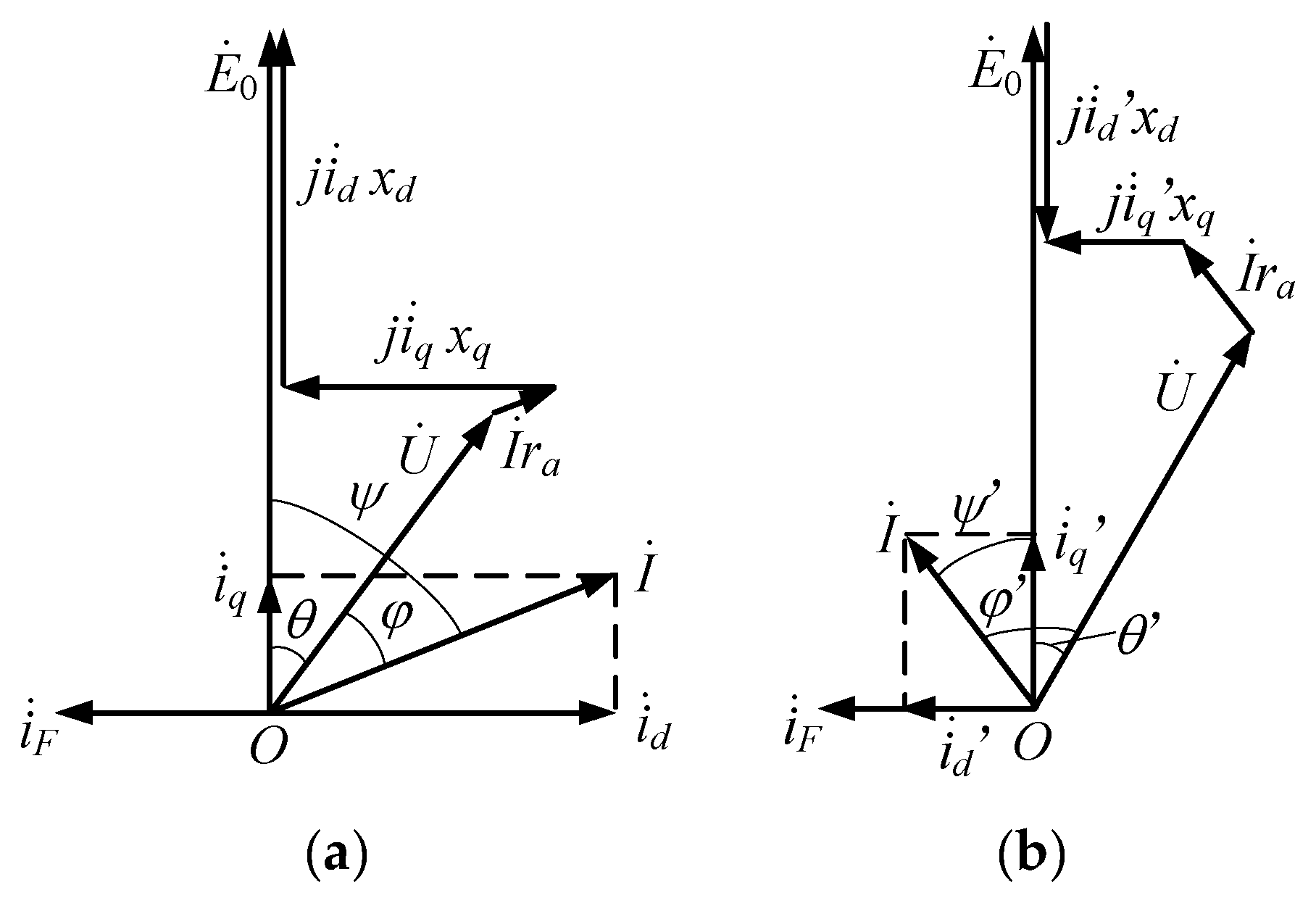
2.2. Criterion of Synchronous Generator Self-Excitation

The voltage–current relationship (3) can be represented by the phasor diagram in Figure 2. When the load is inductive, the current phasor will lag behind the voltage phasor. In this case, i_d is oppositive to i_F; thus, the armature reaction will have a demagnetizing effect. When the load is capacitive, the current phasor will lead ahead of the voltage phasor. i_d aligns with i_F, indicating a magnetizing effect of the armature reaction.

As observed, if i_d is too large in the capacitive load condition, it will establish the main magnetic flux instead of i_F. The synchronous generator will then enter the self-excitation state, which indicates that self-excitation will occur when the excitation current is negative. Based on [21], if the salient-pole synchronous generator is not self-excited, its reactance X_ZS and resistance R_ZS should meet condition (4), whose solution is given by (5):

$${\left(X_{ZS}-\frac{X_d+X_q}{2}\right)}^2+{\left(r_a+R_{LS}\right)}^2>{\left(\frac{X_d-X_q}{2}\right)}^2$$

(4)

$$\{\begin{array}{c}{X}_{ZS}>\frac{X_d+X_q-\sqrt{{\left(X_d-X_q\right)}^2-4{\left(r_a+R_{LS}\right)}^2}}{2}\\ X_{ZS}<\frac{X_d+X_q+\sqrt{{\left(X_d-X_q\right)}^2-4{\left(r_a+R_{LS}\right)}^2}}{2}\end{array}$$

(5)

2.3. The Loading Condition of Self-Excitation

Clearly, the self-excitation condition of a synchronous generator, based on (5), is not so comprehensible, partly due to its square root formulation. The region of the series load impedance R_LS and X_ZS for self-excitation is depicted in Figure 3, beyond which the synchronous generator will be self-excited.

In the boundary of the half circle, three critical points, Z₁, Z₂, and Z₃, are found, which constitute the sufficient but not necessary conditions for self-excitation, as shown in (6), among which if one is satisfied, then it will be safe.

$$\begin{array}{ll}{Z}_1:\hfill & X_{ZS}>X_d\hfill \\ Z_2:\hfill & X_{ZS}<X_q\hfill \\ Z_3:\hfill & R_{LS}>\frac{1}{2}\left(X_d-X_q\right)-r_a\hfill \end{array}\begin{array}{c}\\ \\ \end{array}\}$$

(6)

3. The Variable Frequency Characteristics of the Load Impedance

When the grid frequency is variable, the impedance of a synchronous generator and the load as well as the region of the synchronous generator self-excitation will be affected.

3.1. Impact of Variable Frequency on the Load Impedance

The inductive or capacitive loads change as the power supply frequency varies. The normal voltage of the power supply is 115 V, and the frequency ranges from f_min = 360 Hz to f_max = 800 Hz, with ω = 2πf. For convenience, here, a frequency of 400 Hz is selected as the base value.

The value of the paralleled impedance for a random frequency ω is quantified by (7):

$$\{\begin{array}{c}{X}_C\left(\omega \right)=1/(\omega C_P)\\ X_L\left(\omega \right)=\omega L_P\end{array}$$

(7)

As seen above, both X_ZS and R_LS exhibit nonlinear characteristics with a varied frequency. Assuming resistive, inductive, and capacitive loads of 4 kW, 3 kVA (400 Hz), and 5 kVA (400 Hz), the impedance characteristics under a variable frequency are shown in Figure 4.

The load impedance has two obvious features: (1) For f < 400 Hz and X_ZS < 0, the load is inductive. Specifically, for f = 360 Hz, the power factor is 0.97 lagging. (2) For f > 400 Hz and X_ZS > 0, the load is capacitive. Specifically, for f = 800 Hz, the power factor is 0.56 leading.

3.2. Admittance Model of the Series Load

In the load configuration design of an aviation power system, such as that shown in Figure 1a, it is necessary to analyze the influences of the resistive, inductive, and capacitive load capacities on the generator’s self-excitation characteristics. In (6), the impedances X_ZS and R_LS are used to determine whether the load is within the self-excitation range of the generator.

Firstly, the formulation of X_ZS and R_LS are derived in terms of the original parallel impedances, R_L, X_L, and X_C. Equation (1), in this case, is simplified as (8), where X_Z is the impedance of the total reactive power load in parallel:

$$\{\begin{array}{c}{R}_{LS}=\frac{R_L{X}_Z{}^2}{R_L{}^2+X_Z{}^2}\\ X_{ZS}=\frac{R_L{}^2{X}_Z}{R_L{}^2+X_Z{}^2}\end{array}, X_Z=\frac{X_L{X}_C}{X_L-X_C}$$

(8)

By rewriting the load impedance as the admittance in (9), the relationship between the load capacity and the self-excitation of the generator can be more effectively analyzed. The admittance of the reactive power load in parallel is then obtained as shown in (10):

$$\begin{array}{ll}{Y}_R=1/R_L\hfill & \hfill \\ Y_L=1/X_L=1/(\omega L_P)\hfill & \hfill \\ Y_C=1/X_C=\omega C_P\hfill & \hfill \end{array}\}$$

(9)

$$Y_Z=\frac{1}{X_z}=Y_C-Y_L=\omega C_P-\frac{1}{\omega L_P}=\frac{{\omega }^2{L}_P{C}_P-1}{\omega L_P}$$

(10)

Clearly, the load appears to be capacitive if Y_Z > 0 and inductive if Y_Z < 0. The impedance of the equivalent series load system, represented by the admittance, is:

$$X_{ZS}=\frac{Y_Z}{Y_Z{}^2+Y_R{}^2},R_{LS}=\frac{Y_R}{Y_Z{}^2+Y_R{}^2}$$

(11)

Since Y_Z has better linear frequency characteristics than X_Z, it is more suitable for the analysis of the frequency characteristics of X_ZS and R_LS.

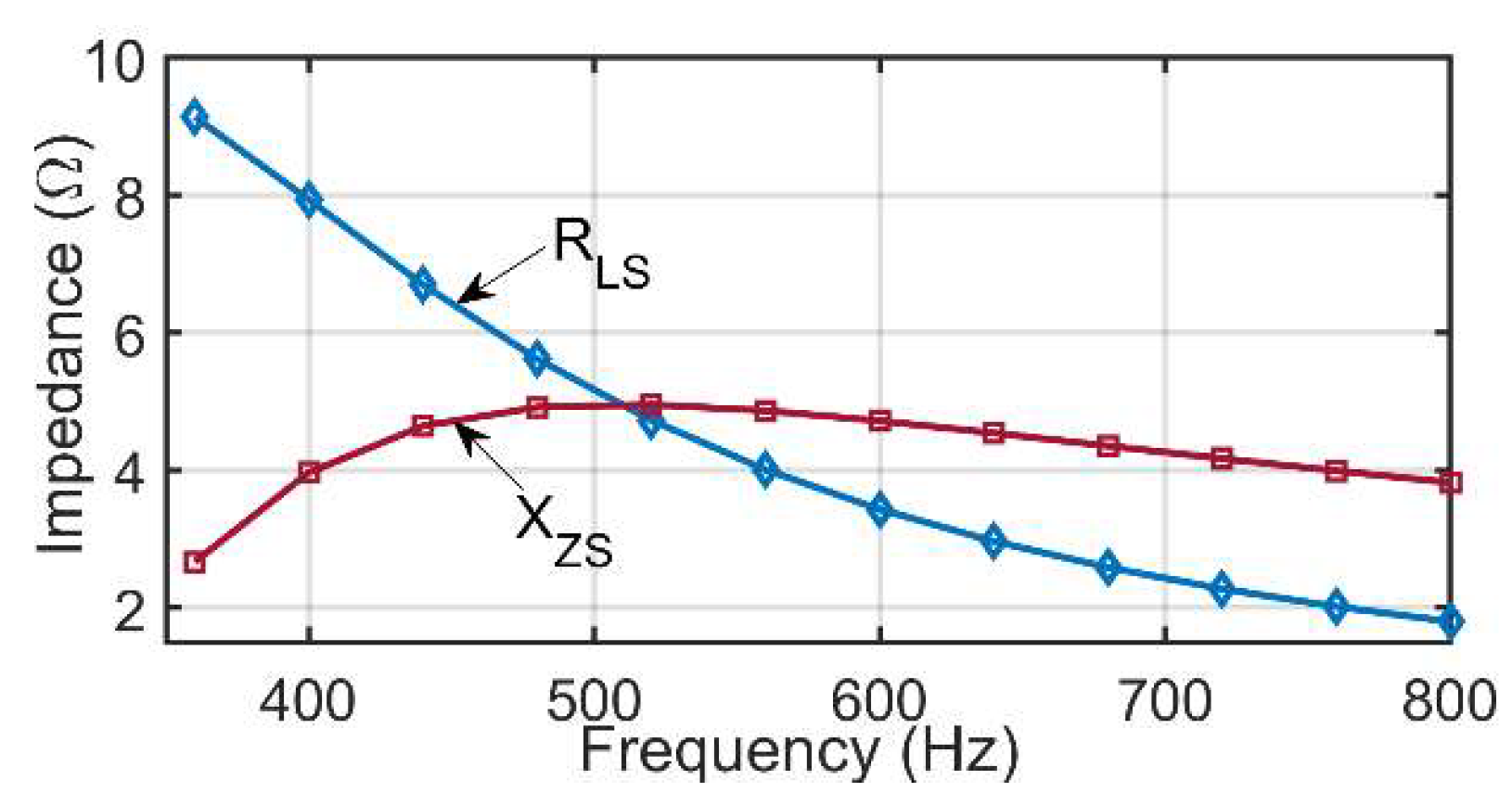
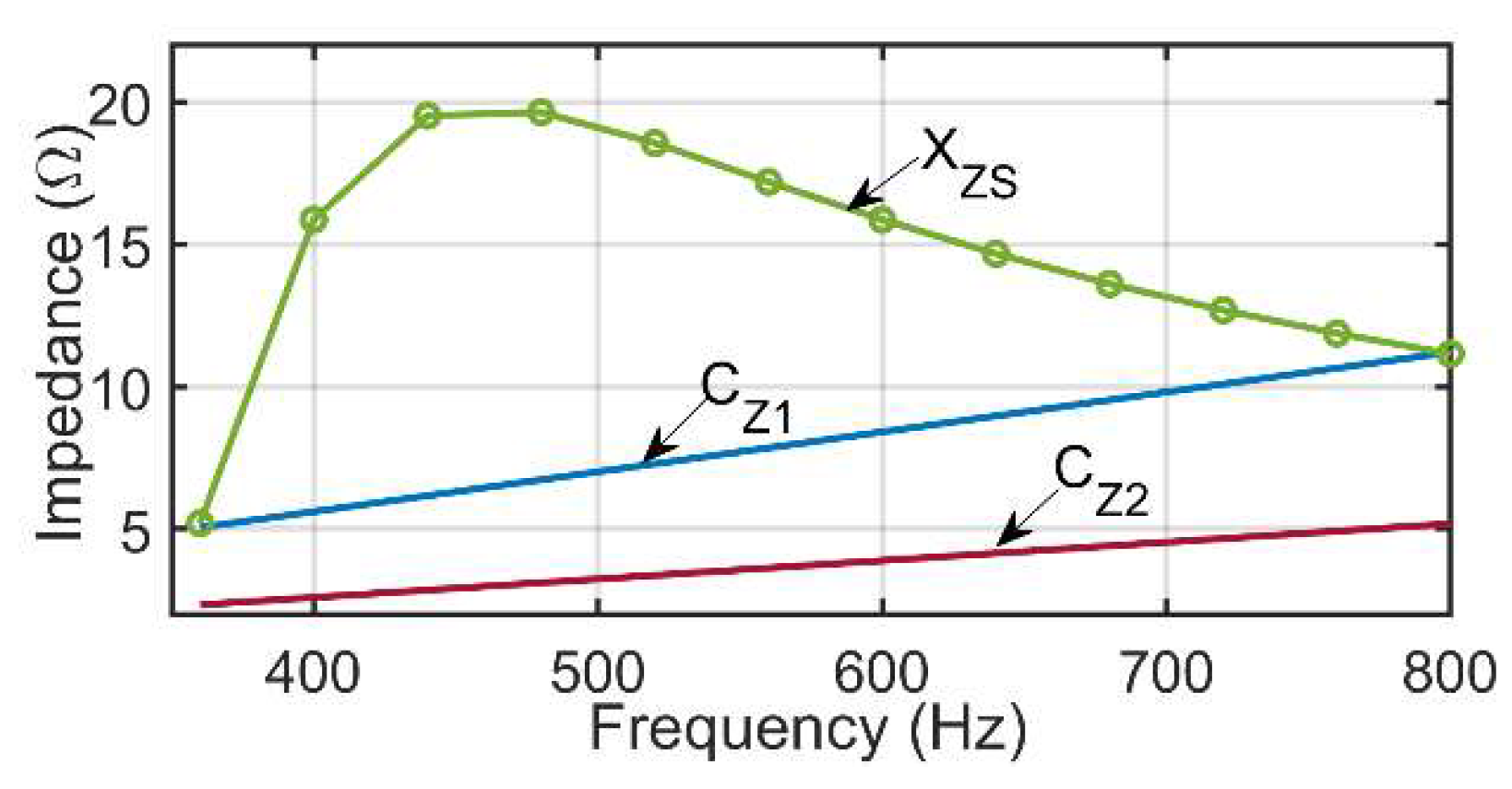
3.3. Frequency Characteristics of the Series Load Impedance

3.3.1. Frequency characteristics of reactance X_ZS

As seen from Figure 4, there is an extreme point A in the curve of reactance X_ZS, which satisfies Y_Z = Y_R by setting the derivative of X_ZS as 0 with respect to Y_Z:

$$\frac{d{X}_{ZS}}{d{Y}_Z}=\frac{Y_R{}^2-Y_Z{}^2}{{\left(Y_Z{}^2+Y_R{}^2\right)}^2}=0$$

Furthermore, the values of X_ZS and R_LS on point A can be obtained as:

$$\begin{array}{ll}{X}_{ZSA}=\frac{Y_Z}{Y_Z{}^2+Y_R{}^2}=\frac{1}{2}{R}_L\hfill & \hfill \\ R_{LSA}=\frac{Y_R}{Y_Z{}^2+Y_R{}^2}=\frac{1}{2}{R}_L\hfill & \hfill \end{array}\}$$

(12)

According to (10), we have (13), indicating the admittance Y_Z and frequency ω_A at point A:

$$Y_Z\left({\omega }_A\right)=\frac{{\omega }_A{}^2{L}_P{C}_P-1}{{\omega }_A{L}_P}=Y_R=\frac{1}{R_L}$$

(13)

$${\omega }_A=\frac{1}{2R_L{C}_P}\left(1+\sqrt{1+\frac{4R_L^2{C}_P}{L_P}}\right)$$

Note that there may be cases of f_A < 360 Hz or f_A > 800 Hz when X_ZS becomes monotonically decreasing or increasing in the full frequency range.

3.3.2. Frequency Characteristics of Resistance R_LS

The derivative of R_LS with respect to Y_Z is given by (14), indicating that R_LS will increase as the frequency increases for the capacitive load (Y_Z > 0) and decrease for the inductive load (Y_Z < 0). When studying the synchronous generator self-excitation characteristics, the capacitive load (Y_Z > 0) is considered.

$$\frac{d{R}_{LS}}{d{Y}_Z}=\frac{-2Y_R{Y}_Z}{{\left(Y_Z{}^2+Y_R{}^2\right)}^2}$$

(14)

3.4. The Series Impedance Expressed by the Load Capacity

Assuming a constant voltage magnitude U_s, the power capacity is proportional to the load admittance. The active power P_Z and reactive power Q_Z of the load are:

$$\begin{array}{ll}{P}_Z=U_s^2{Y}_R=\frac{U_s^2}{R_L}\hfill & \hfill \\ Q_Z=Q_C-Q_L=U_s^2\left(Y_C-Y_L\right)=U_s^2{Y}_Z=U_s^2\left(\omega C_p-\frac{1}{\omega L_p}\right)\hfill & \hfill \end{array}\}$$

(15)

The series load impedance in terms of the power capacity is given by (16). The variation in Q_Z may result from the change in Q_C or Q_L, but their effects on R_LS and X_ZS are the same.

$$\begin{array}{ll}{X}_{ZS}=\frac{Q_Z{U}_s}{Q_Z{}^2+P_Z{}^2}\hfill & \hfill \\ R_{LS}=\frac{P_Z{U}_s}{Q_Z{}^2+P_Z{}^2}\hfill & \hfill \end{array}\}$$

(16)

4. Application of the Self-Excitation Criterion to a VF Generator

When applying criterion (6) to a VF aviation power system, the frequency characteristics of the load impedance and synchronous generator impedance, as analyzed in Section 3, are considered, and detailed below.

4.1. The Threshold of Synchronous Generator Self-Excitation

In the sufficient condition (6) of self-excitation, there are three thresholds determined by the generator parameters, defined in (17):

$$\begin{array}{ll}{C}_{Z1}\left(\omega \right)=X_d\left(\omega \right)=L_d\omega \hfill & \\ C_{Z2}\left(\omega \right)=X_q\left(\omega \right)=L_d\omega \hfill & \\ C_{Z3}\left(\omega \right)=\frac{1}{2}\left[X_d\left(\omega \right)-X_q\left(\omega \right)\right]-r_a\hfill & \end{array}\}$$

(17)

As we can see, all the three threshold values increase linearly with the frequency. Among them, C_Z1 and C_Z2 are related to the reactance X_ZS, and C_Z3 is related to R_LS. Without a loss of generality, the data on the synchronous generator in

Table 1. Parameters of the studied aircraft synchronous generator.

Nominal Voltage (V)	Nominal Power (kVA)	Ld (mH)	Lq (mH)	ra (Ω)
115	20	2.23	1.03	0.05

were used in our analysis of the self-excitation characteristics.

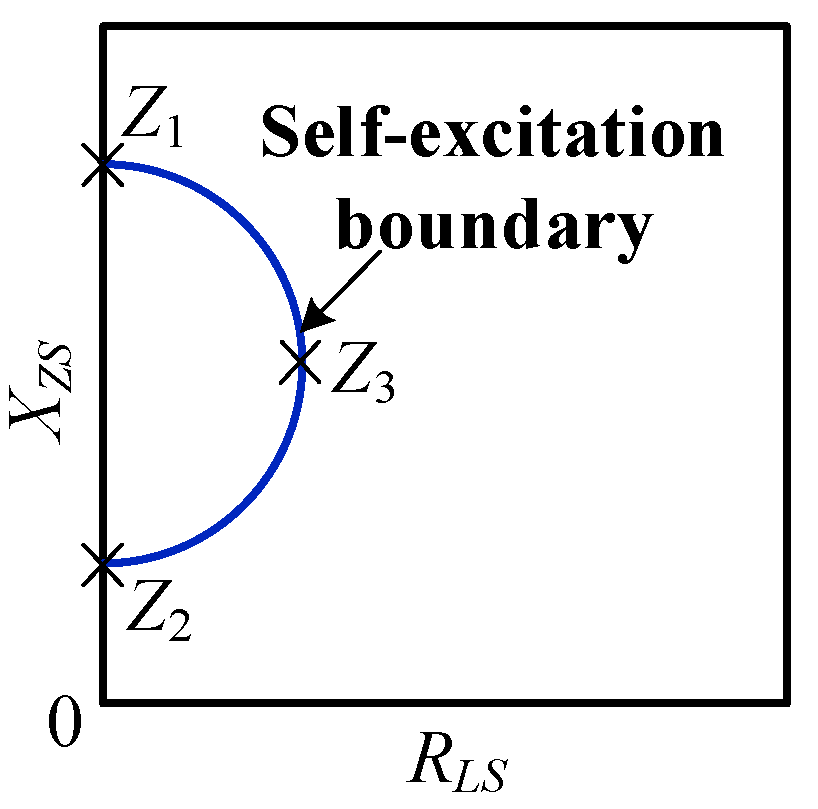
4.2. Individual Criterion for the Self-Excitation of the Synchronous Generator

Any of the sufficient conditions in Equation (6) can be used as an independent criterion. The three load systems in

Table 2. Three cases of the load system.

Cases	Resistive Load Power PZ	Inductive Load Power QL	Capacitive Load Power QC	Total Reactive Power QZ
#1	1 kW	1.5 kVA	2 kVA	0.5 kVA
#2	5 kW	5 kVA	4.5 kVA	−0.5 kVA
#3	3 kW	5 kVA	4 kVA	−1 kVA

were selected for the case studies in our research. The capacities of Q_L, Q_C, and Q_Z are all given at the nominal frequency of 400 Hz.

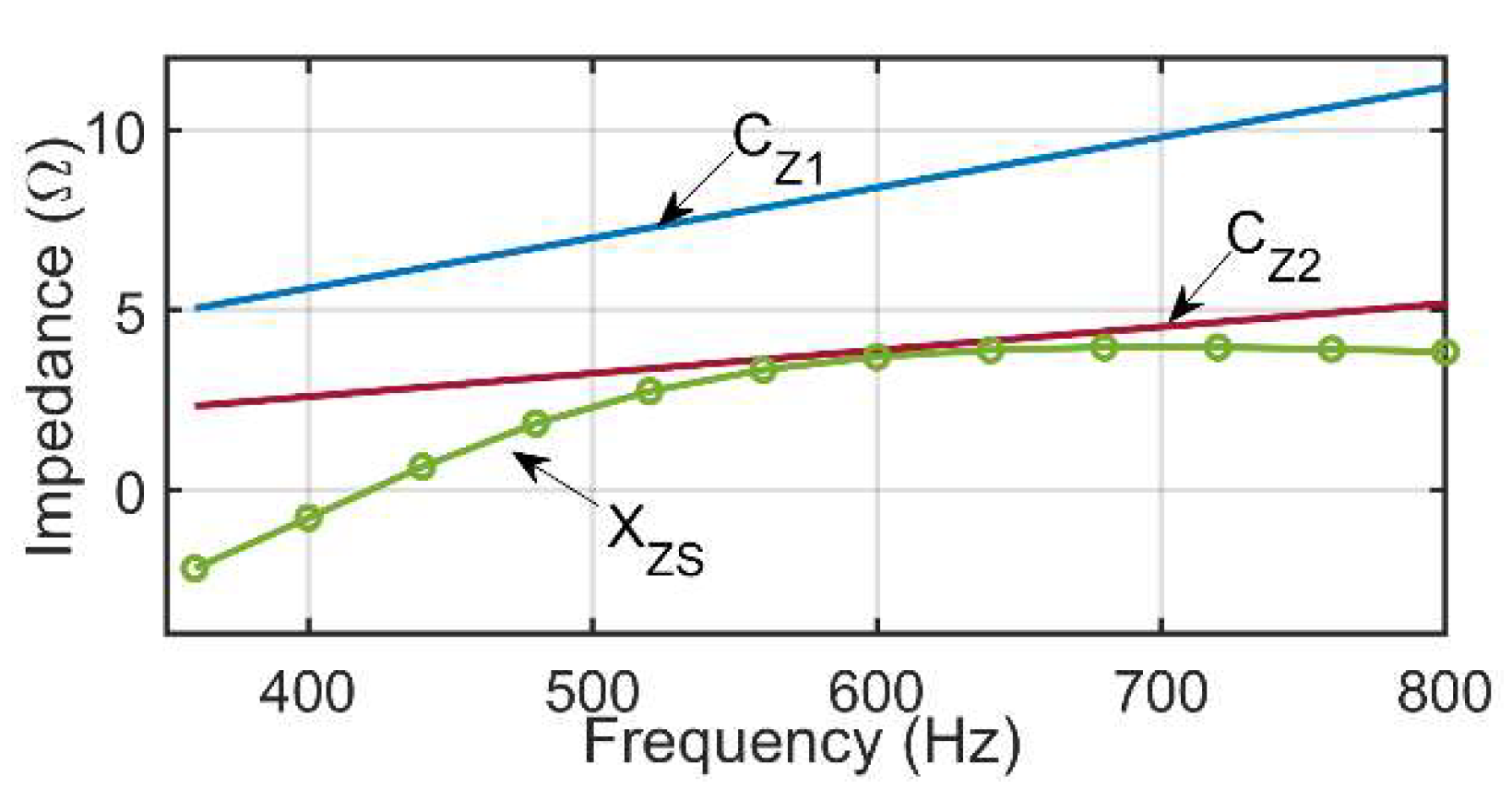
4.2.1. Application of Criterion Z₁

The Z₁ criterion requires that X_ZS satisfy (18) in the considered frequency range of f_min–f_max:

$$X_{ZS}\left(f\right)>C_{Z1}(f)=2\pi f{L}_d$$

(18)

According to the frequency characteristics of X_ZS analyzed earlier, the minimum value will appear at the lowest frequency f_min or the highest frequency f_max. Based on the property of the convex function, if the following condition (19) holds, then X_ZS > C_Z1 in the full range from f_min to f_max:

$$\begin{array}{ll}{X}_{ZS}\left(f_{\max }\right)>C_{Z1}\left(f_{\max }\right)\hfill & \hfill \\ X_{ZS}\left(f_{\min }\right)>C_{Z1}\left(f_{\min }\right)\hfill & \hfill \end{array}\}$$

(19)

For the generator in Table 1 and the load in Case 1 in Table 2, the frequency characteristics of X_ZS and threshold values C_Z1 and C_Z2 are as shown in Figure 5. As we can see, X_ZS is larger than C_Z1 in the full frequency range; thus, the generator will not be self-excited.

4.2.2. Application of Criterion Z₂

If the Z₂ criterion is used, X_ZS should meet the requirement of (20) in the full frequency range:

$$X_{ZS}\left(f\right)<C_{Z2}(f)=2\pi L_{q}f$$

(20)

According to the frequency characteristics of X_ZS analyzed earlier, there are two situations that arise in the application of the Z₂ criterion:

(a) If f_A < f_min or f_A > f_max, X_ZS monotonically decreases or increases over the whole frequency range, which requires:

$$\begin{gathered} X_{ZS}\left(f_{\min }\right)<C_{Z2}\left(f_{\min }\right)=2\pi L_q{f}_{\min } \mathrm{or} \\ {X}_{ZS}\left(f_{\max }\right)<C_{Z2}\left(f_{\max }\right)=2\pi L_q{f}_{\max }; \end{gathered}$$

and (b) If f_min < f_A < f_max, X_ZS is a convex curve with a maximum value. If the following condition holds, then it can be concluded X_ZS satisfies the Z₂ criterion in the full range:

$$X_{ZS}\left(f_A\right)<C_{Z2}\left(f_A\right)$$

Additionally, using the generator data in Table 1 and the load in Case 2 in Table 2, the frequency characteristics of X_ZS and the thresholds C_Z1 and C_Z2 are as shown in Figure 6. As we can see, the maximum point is reached at f_A = 640 Hz, where X_ZS < C_Z2. However, at f = 600 Hz, where X_ZS is closest to C_Z2, we must verify whether X_ZS is in the self-excited safe zone.

4.2.3. Application of Criterion Z₃

C_Z3 (the threshold of the Z₃ criterion) increases with the increase in the power supply frequency. Therefore, if the relation in (21) holds, then the Z₃ criterion is satisfied from f_min to f_max, and the generator is in the self-excitation safe zone. For the generator data in Table 1 and the load in Case 3 in Table 2, the frequency characteristics R_LS, shown in Equation (13), decrease as the frequency increases. The frequency characteristics of R_LS and C_Z3 are shown in Figure 7. As we can see, because R_LS is greater than C_Z3 in the full frequency range, the generator will not be self-excited.

$$R_{LS}\left(f_{\max }\right)>C_{Z3}\left(f_{\max }\right)$$

(21)

4.3. “Complementary” Property of the Self-Excitation Criteria

The independent application of the Z₁, Z₂, or Z₃ criterion to determine whether the generator will be self-excited is a “harsh” sufficient condition. According to (13), R_LS decreases with the increased grid frequency; thus, the Z₃ criterion can be met more easily in low-frequency ranges. If X_ZS satisfies the Z₁ or Z₂ criterion in the high-frequency range, then the combination of the Z₃ criterion with the Z₁ or Z₂ criterion will constitute a “complementary” sufficient condition.

For example, if the Q_C of the capacitive load in Case 2 in Table 2 is increased to 7.5 kVA, i.e., Q_Z = 2.5 kVA, the series impedance characteristics will be as shown in Figure 8. As we can see, X_ZS violates the Z₂ and Z₃ criteria at f < 570 Hz, and R_LS violates the Z₃ criterion at f > 600 Hz. However, since the two frequency ranges are staggered, there are no intervals that violate all three criteria. Therefore, the generator will not be self-excited over the full frequency range.

5. Impact of the Load Capacity on Generator Self-Excitation

In aviation power systems, countermeasures should be taken to avoid the self-excitation of the generator by adjusting the load capacity. Here, the influence of the load capacity on the self-excitation characteristics is studied by analyzing the relationship between the load capacity and its impedance.

5.1. Impact of Active Power Variation on the Series Load Impedance

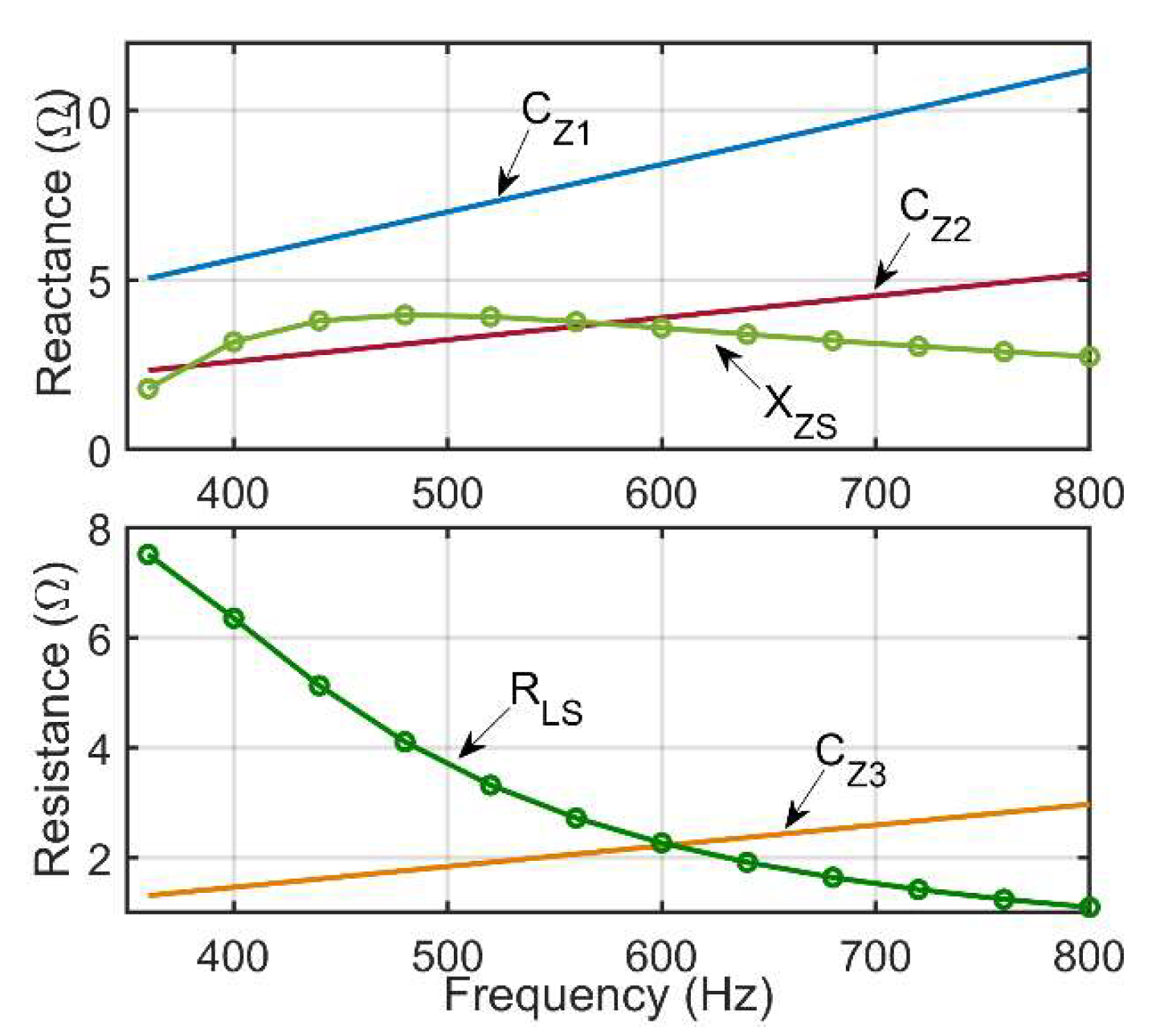
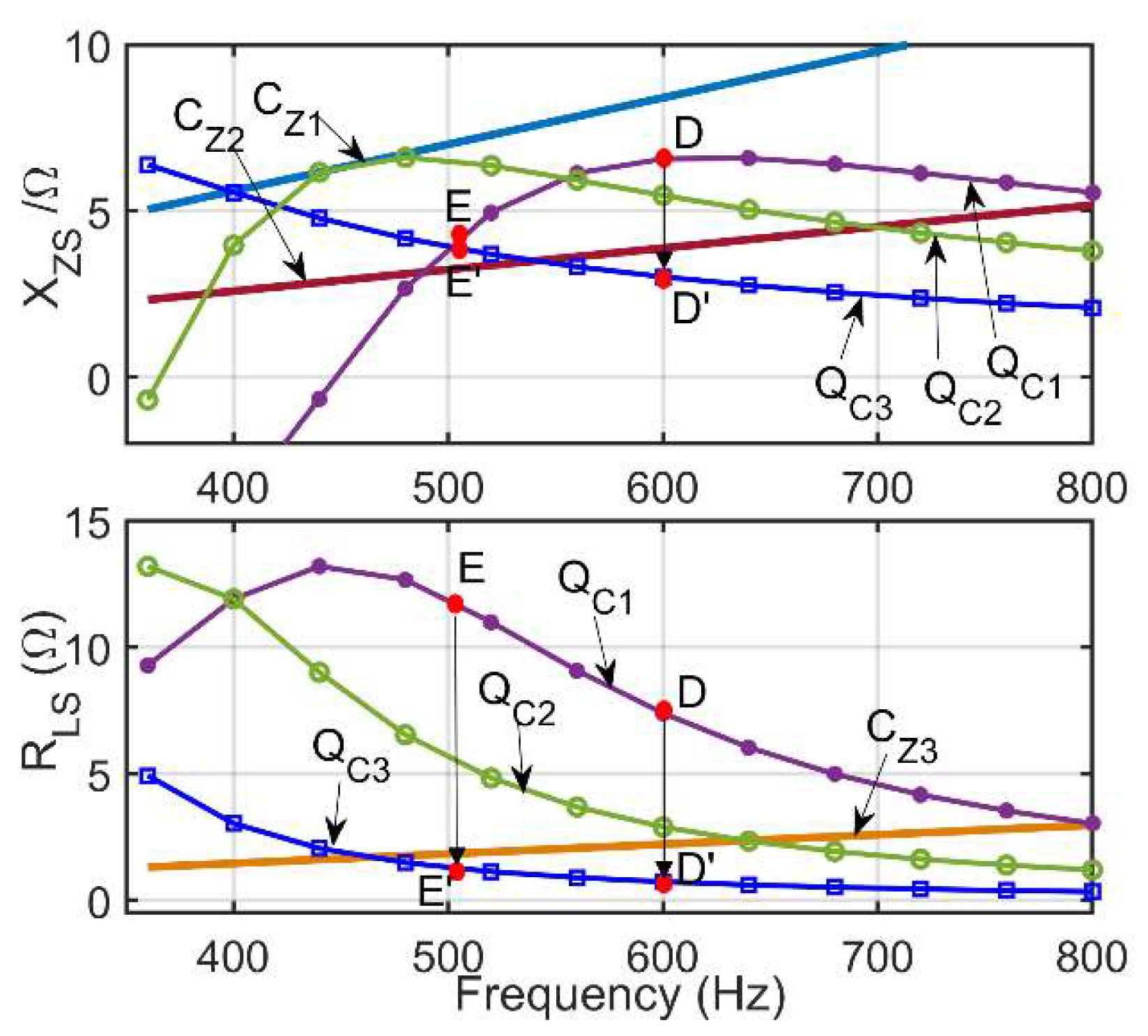
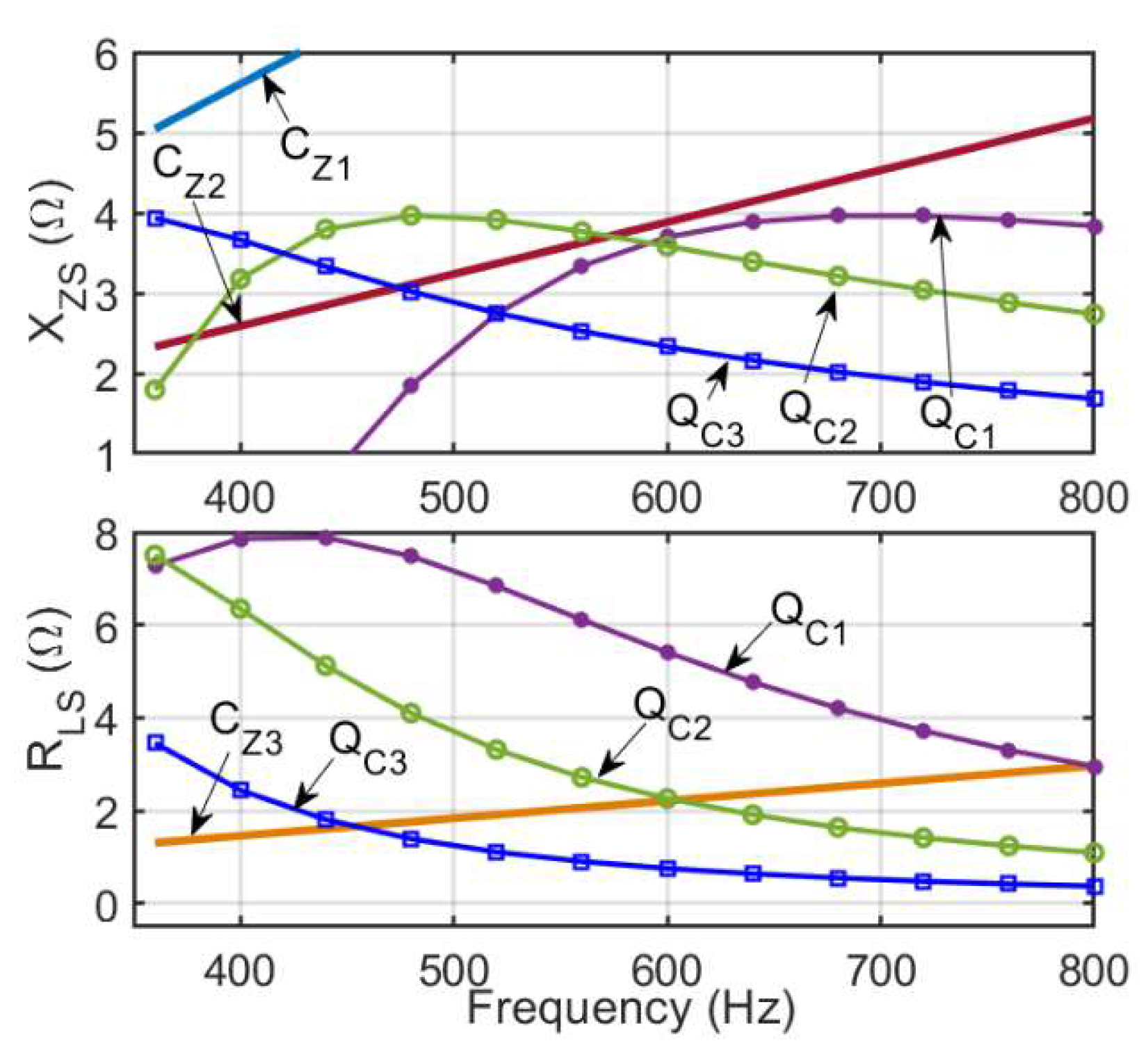
5.1.1. Impact of P_Z variation on X_ZS

According to equation (16), when Q_Z > 0, the increase in P_Z will lead to a decrease in X_ZS, and conversely, the decrease in P_Z will lead to an increase in X_ZS. According to (12), the maximum X_ZSA is determined by the resistance R_L. That is, X_ZSA is inversely proportional to P_Z:

$$X_{ZSA}=\frac{R_L}{2}=\frac{U_s^2}{2P_Z}$$

(22)

For the Case 3 load system shown in Table 2, setting P_Z to P_Z1 = 1.5 kW, P_Z2 = 3 kW, and P_Z3 = 5 kW, respectively, the frequency characteristics of X_ZS and R_LS are as shown in Figure 9.

For load P_Z1, the X_ZS curve has a large “peak” at X_ZSA, and part of the curve is above the threshold C_Z1. For load P_Z2, the decrease in X_ZSA causes the X_ZS curve to become “flatter”, and most of the curve lies between C_Z1 and C_Z2. For load P_Z3, the X_ZSA is further reduced, so that the X_ZS curve becomes even “flatter”, and all the curves are below C_Z2. The generator is completely within the self-excitation safe zone.

5.1.2. Impact of P_Z variation on R_LS

Firstly, the derivative of R_LS with respect to P_Z is obtained as shown in (23). As we can see, R_LS will increase as P_Z increases for Q_Z > P_Z, and the opposite occurs for Q_Z < P_Z. Since the frequency characteristics of Q_Z increases under capacitive loading, Q_Z >P_Z is often satisfied in the high-frequency range, and R_LS will thus increase as P_Z increases. In the low-frequency range, R_LS will decrease as P_Z increases for Q_Z < P_Z.

$$\frac{\partial R_{LS}}{\partial P_Z}=\frac{U_s\left(Q_Z{}^2-P_Z{}^2\right)}{{\left(Q_Z{}^2+P_Z{}^2\right)}^2}$$

(23)

According to (14), the frequency characteristics of R_LS are decreasing. The increase in P_Z will reduce the decreasing speed of R_LS based on (23) and, thus, increase the value of R_LS in the high-frequency range, rendering it easier to meet the Z₃ criterion. Conversely, as P_Z decreases, the R_LS decreasing speed increases, which is not conducive to meeting the Z₃ criterion in the high-frequency range.

As shown in the R_LS part of Figure 9, for a large P_Z, such as P_Z2 or P_Z3, the decrement rate of R_LS in the high-frequency range decreases. Therefore, the value of R_LS increases, which satisfies the Z₃ criterion. At P_Z1, the R_LS curve falls too quickly, which violates the Z₃ criterion in the high-frequency range. The above analysis shows that P_Z affects the “slope” of R_LS. As P_Z increases, the high-frequency characteristics of R_LS are improved, rendering it easier to meet the Z₃ criterion.

Combining the observations in Section 5.1.1 and Section 5.1.2, it is found that the active power variation mainly affects the “vertical” characteristics of the impedance curves, similar to the way in which the quality factor defined in the RLC circuit affects the sharpness of the impedance curves. Namely, decreased P_Z will result in sharper curves with higher peaks, steeper slopes, and narrower “bandwidths”. Consequently, there is an increased likelihood that X_ZS and R_LS will cross the critical impedances Z₁, Z₂, and Z₃, resulting in a higher probability of generator self-excitation.

5.2. Impact of Reactive Power Variation on the Series Load Impedance

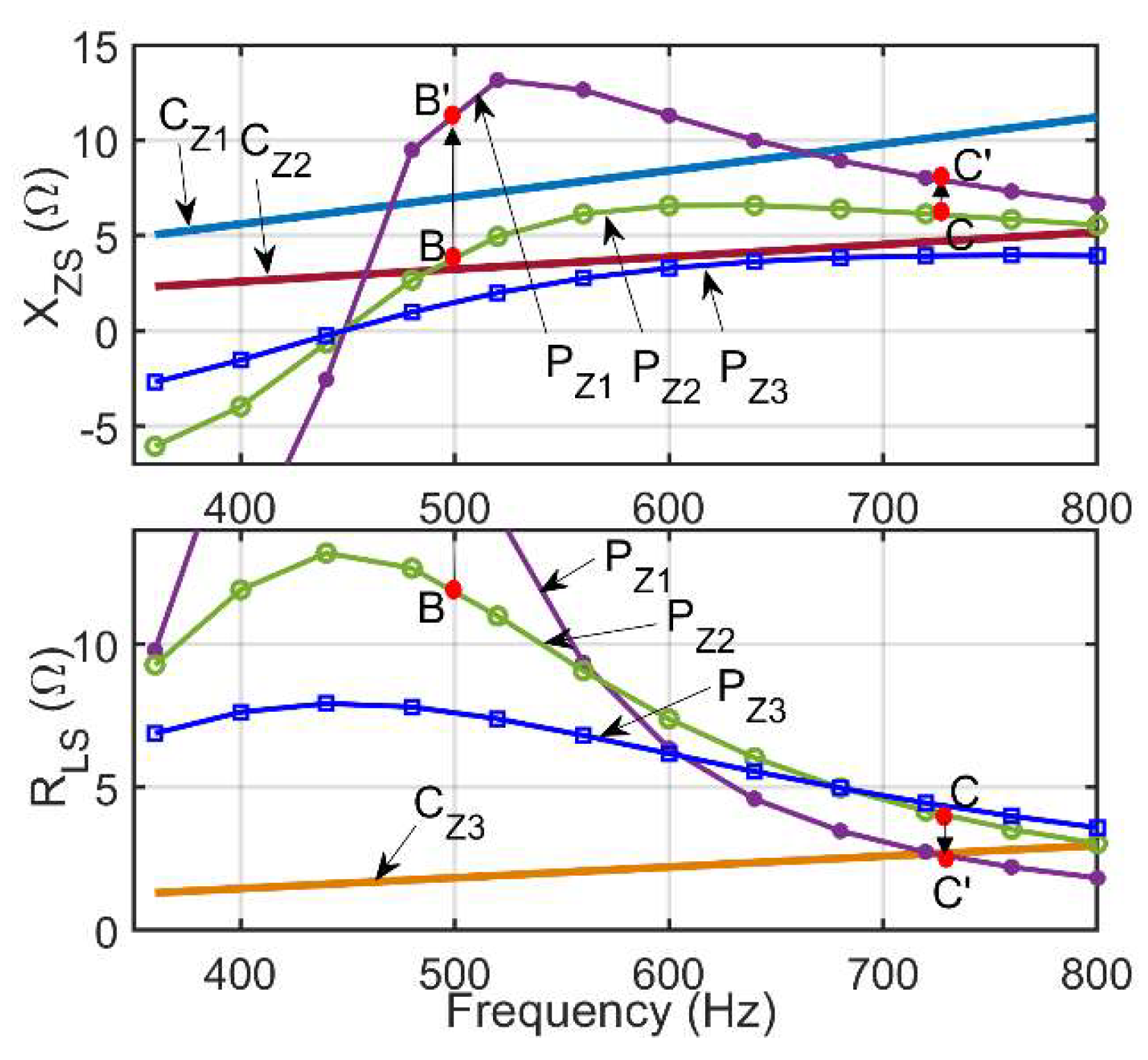
5.2.1. Impact of Q_Z variation on X_ZS

According to (12) and (13), the change in the capacitive load C_P will affect the extreme point frequency f_A on the curve of X_ZS but will not affect the value of X_ZSA. As we can see, the increase in Q_Z (or Q_C) will shift f_A to a lower frequency, and the decrease in Q_Z will shift f_A to a higher frequency. If the Q_C in Case 3 in Table 2 is changed from Q_C1 = 4 kVA to Q_C2 = 6 kVA and Q_C3 = 10.5 kVA, the frequency characteristics of X_ZS and R_LS will be as shown in Figure 10.

As we can see, part of the X_ZS curve lies between C_Z1 and C_Z2. As Q_C increases, X_ZS moves to the lower range, rendering X_ZS smaller than C_Z2 in the high range. The interval in which X_ZS lies lower than C_Z2 in the high-frequency range, i.e., the frequency range meeting the Z₂ criterion, expands.

5.2.2. Impact of Q_Z Variation on R_LS

According to (16), the reactive power Q_Z is in the denominator of R_LS formulation. Therefore, the increase in Q_Z will cause R_LS to decrease, and vice versa.

As we can see from the R_LS part of Figure 10, if Q_C increases, the intersection of R_LS and C_Z3 shifts to the lower range, and R_LS, in the high-frequency range, no longer satisfies the Z₃ criterion due to the decrease in R_LS. That is, the frequency range that satisfies the Z₃ criterion shrinks.

Based on the observations in Section 5.2.1 and Section 5.2.2, it is found that the reactive power variation mainly affects the “horizontal” characteristics of the impedance curves. Increasing the capacitive load will cause both the reactance and resistance curves to move leftward. The frequency range in which X_ZS and R_LS cross the critical impedances Z₁, Z₂, and Z₃ will expand, resulting in a higher probability of generator self-excitation.

5.3. Impact of Q_Z Variation on the Complementary Property of the Z₂ and Z₃ Criteria

For the load system in Case 2 in Table 2, it can be seen in Figure 11 that X_ZS lies between C_Z1 and C_Z2. Here, the self-excitation characteristics are analyzed when the X_ZS curves move horizontally as Q_C varies (Q_C1 = 4.5 kVA, Q_C2 = 7.5 kVA, Q_C3 = 12.5 kVA).

Compared with Figure 8, it can be seen that as Q_C increases, the high-frequency range in which X_ZS satisfies the Z₂ criterion expands, while the low-frequency range in which R_LS satisfies the Z₃ criterion shrinks. The two ranges complement each other to a certain extent.

However, with the capacitive load Q_C3, X_ZS satisfies the Z₂ criterion in the frequency range of f > 475 Hz, while R_LS satisfies the Z₃ criterion in the frequency range of f < 450 Hz. In this case, the complementary property of the Z₂ and Z₃ criteria is lost, and self-excitation may occur in the frequency range of 450 < f < 475 Hz. More generally, when the X_ZS curve crosses C_Z2, the complementary property of the Z₂ and Z₃ criteria will deteriorate or even disappear with the increase in Q_C.

6. Simulation Verification

To verify the relationship of the self-excitation with the loading composition analyzed above, a simulation was conducted based on the aviation generator modeled, as depicted in Table 1. The three-phase synchronous generator provides a 115 V/360–800 Hz power supply, and the load is a variable RLC parallel branch.

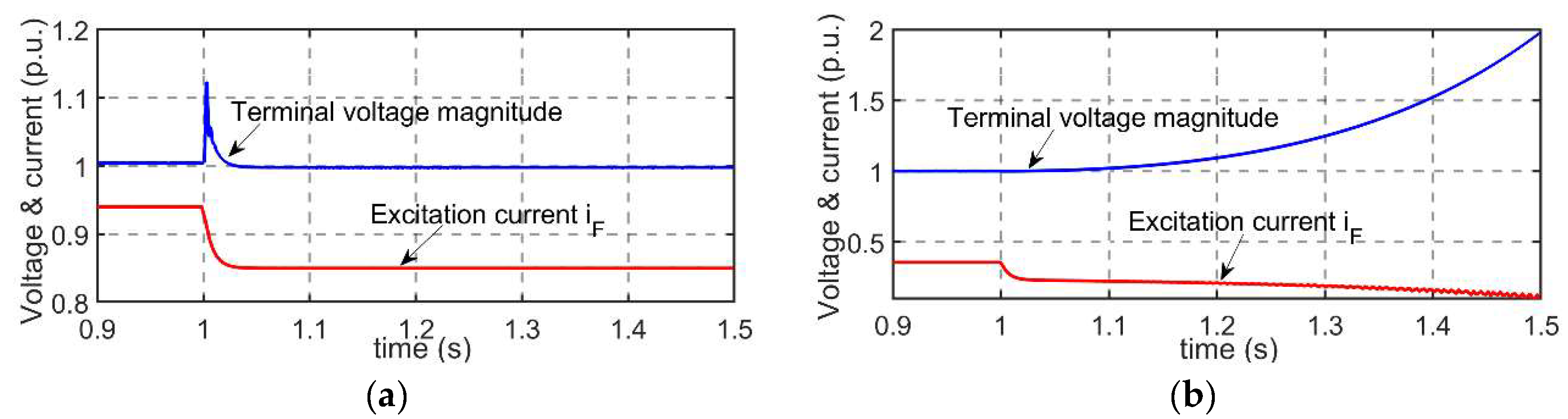
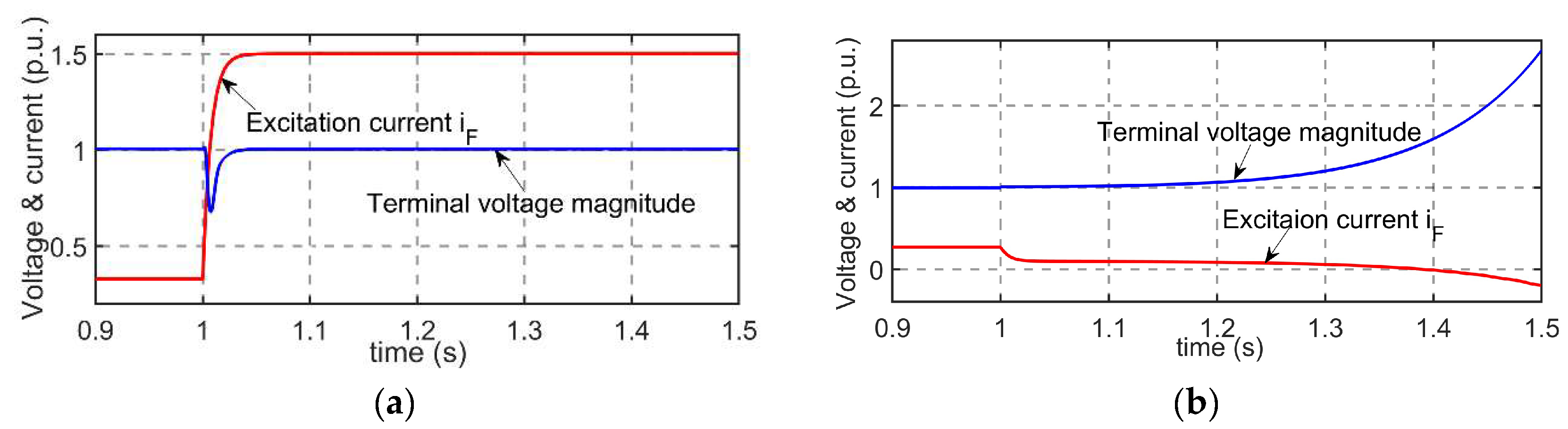
6.1. Self-Excitation Characteristics as the Active Power Changes

Here, Case 3 in Table 2 is used as the base loading case. According to the series load characteristics shown in Figure 10, the operation under frequencies of 500 Hz (points B and B′ in Figure 9) and 726 Hz (points C and C′ in Figure 9) is simulated. The resistive load P_Z varies from 3 kW to 1.5 kW at 1 s.

The simulation results are shown in Figure 12. At the frequency of 500 Hz, the generator can regulate the voltage normally. However, at the frequency of 726 Hz, the generator is self-excited. The excitation current decreases, and the voltage becomes unstable. This is consistent with the analysis shown in Figure 9.

6.2. Self-Excitation Characteristics as the Reactive Power Changes

Again, using the data for Case 3 in Table 2, the generator’s operation at frequencies of 600 Hz (points D and D′ in Figure 10) and 505 Hz (points E and E′ in Figure 10) is simulated according to the series load characteristics in Figure 10. In the simulation, the capacitive load Q_C varies to 10.5 kVA at 1 s.

The simulation results are shown in Figure 13. At the frequency of 600 Hz, the generator works normally. However, at the frequency of 505 Hz, the generator is self-excited, the excitation current drops, and the voltage becomes unstable. This result is consistent with the conclusions shown in Figure 10.

7. Conclusions

In this paper, the range of capacitive loads invoking the self-excitation of a synchronous generator was obtained by analyzing the frequency characteristics of the load impedance under variable aviation frequencies (360–800 Hz). The relationship between the power supply frequency, load capacity, and synchronous generator self-excitation was revealed. The key conclusions are summarized below:

(1) The criterion of synchronous generator self-excitation is changed from its original form of square root inequality without explicitly showing frequency into the problem of two parabola curves intersecting with three linear curves corresponding to the three sufficient conditions identified herein. With the frequency as the abscissa and the impedance of the machine side and the load side as the ordinate, the method is intuitive, enabling us to directly observe the trend of the system impedance and generator self-excitation as the supply frequency and load power change.

(2) The change in the active power load mainly affects the peak and slope of the resistance and the reactance curve under a variable-frequency power supply. Increasing the active power load will alleviate the risk of self-excitation of the synchronous generator.

(3) The change in the reactive power load mainly affects the horizontal characteristics of the resistance and reactance curves. Increasing the capacitive load will enlarge the frequency range, violating the self-excitation criterion.

The analysis approach and the findings of this research will be useful for the design of variable-frequency power system in more electric aircraft, especially the configuration of capacitive loads.