Anti-Rollover Control and HIL Verification for an Independently Driven Heavy Vehicle Based on Improved LTR
Abstract
1. Introduction
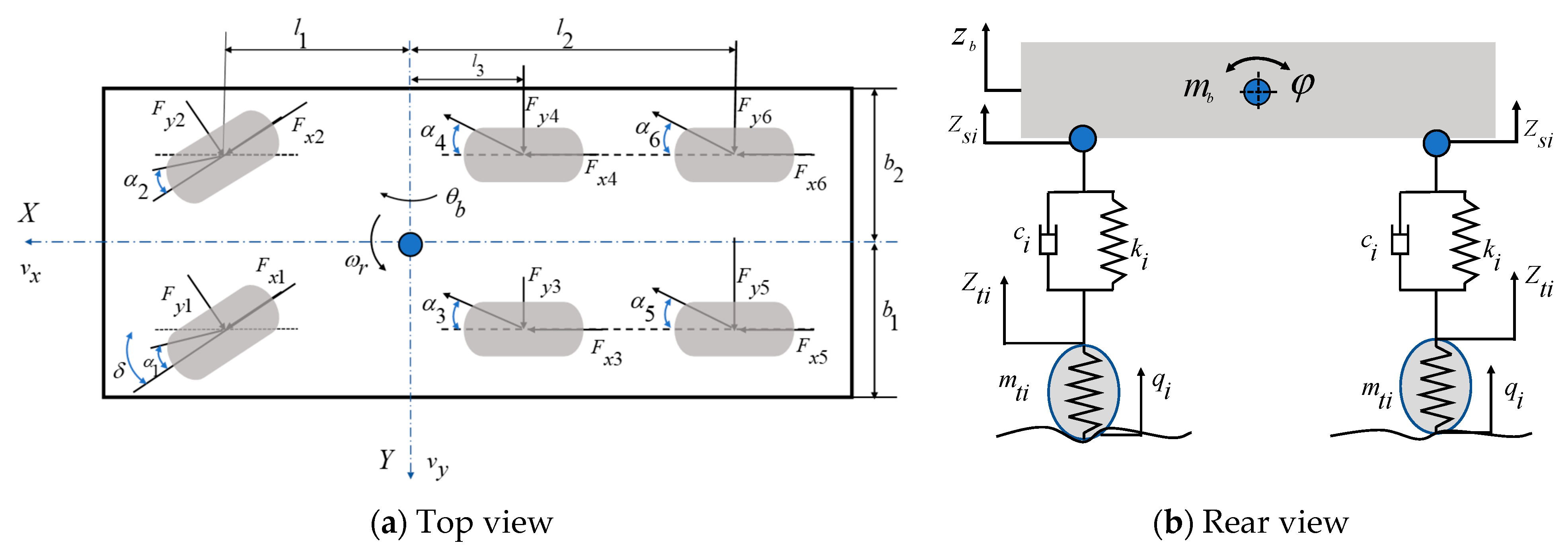
2. Heavy-Vehicle-Dynamics Model
2.1. Vehicle Model
2.2. Tire Model
2.3. Improving LTR Rollover Indicators
2.4. NLTR Index Validation
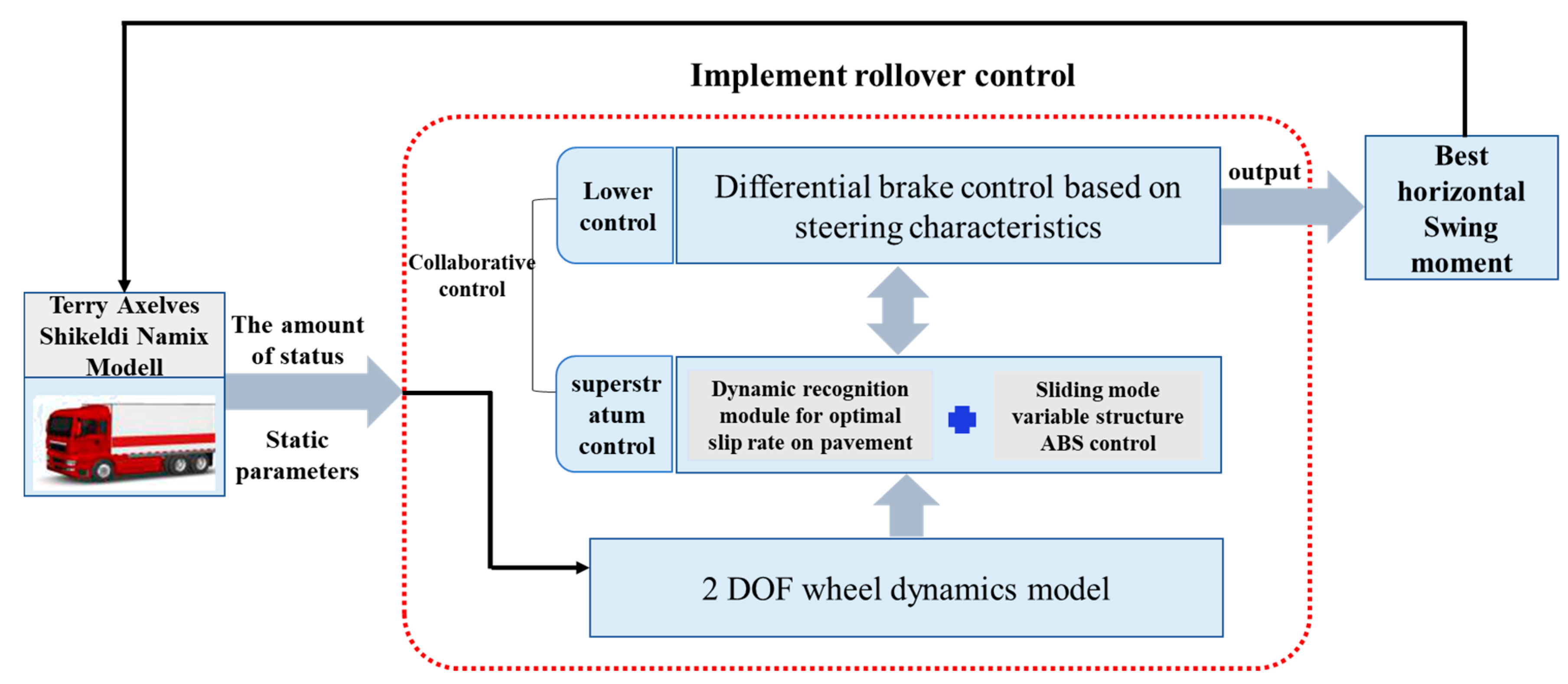
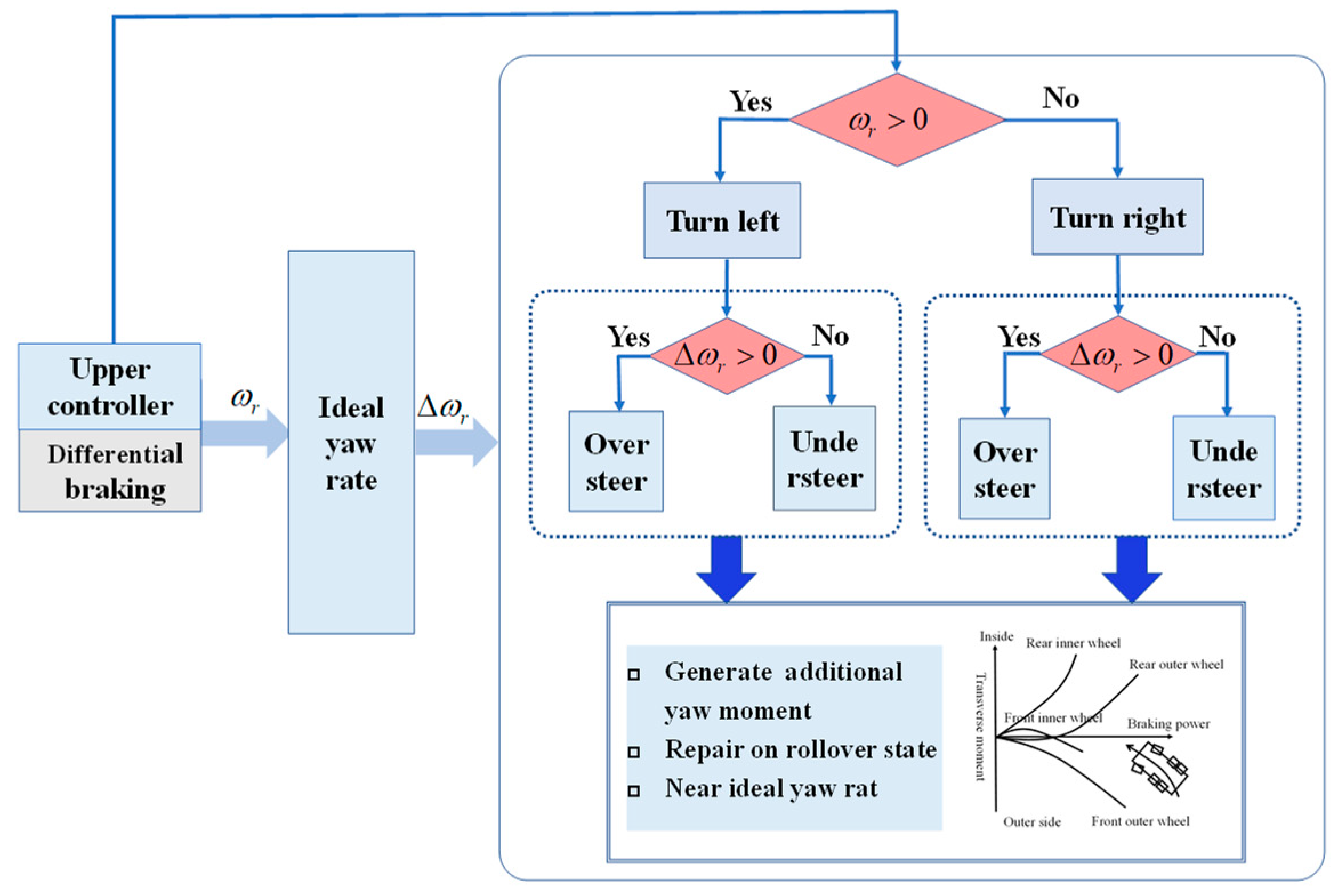
3. NLTR-Based Hierarchy Control Strategy for Anti-Rollover
3.1. Anti-Rollover Upper-Level Controller
3.1.1. Optimal Slip Rate Identification
3.1.2. Sliding-Mode Variable-Structure Controller
3.2. Anti-Rollover Lower-Level Controller
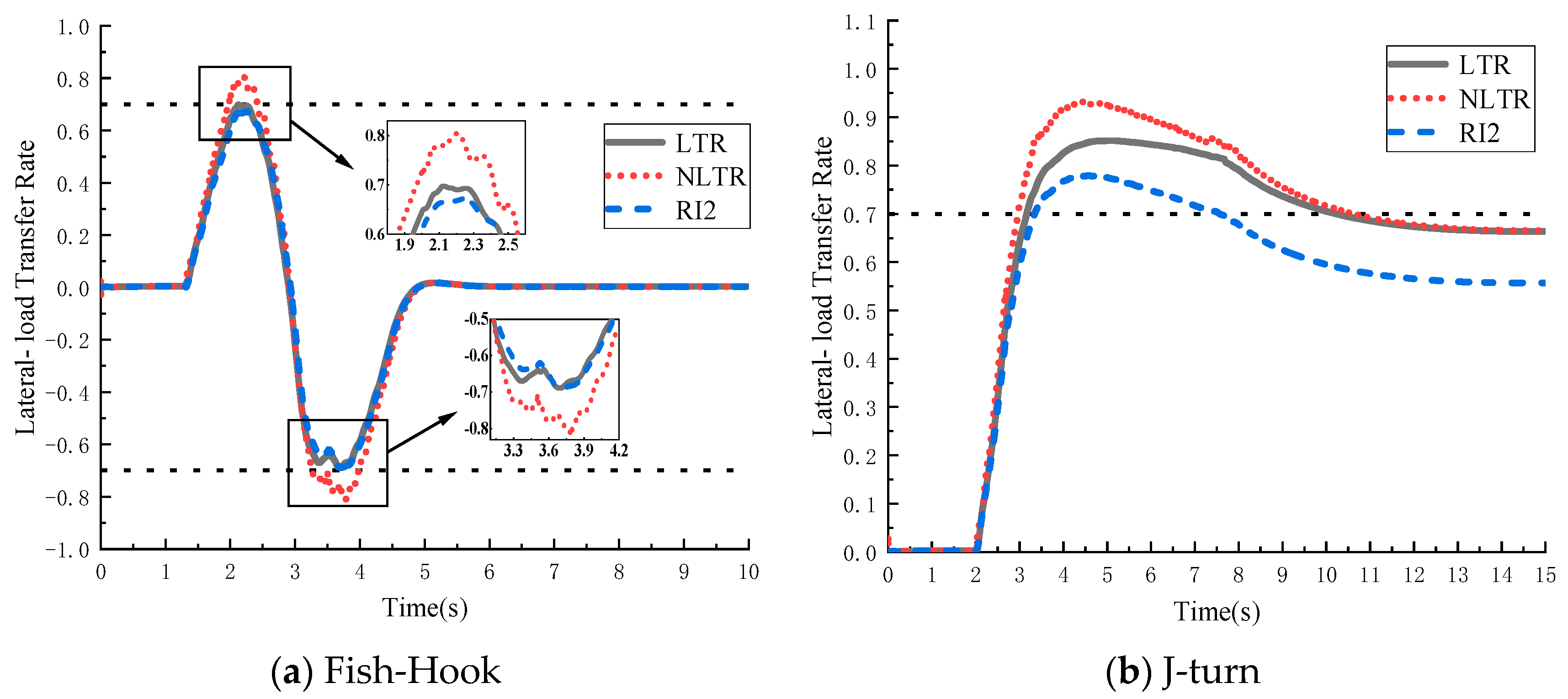
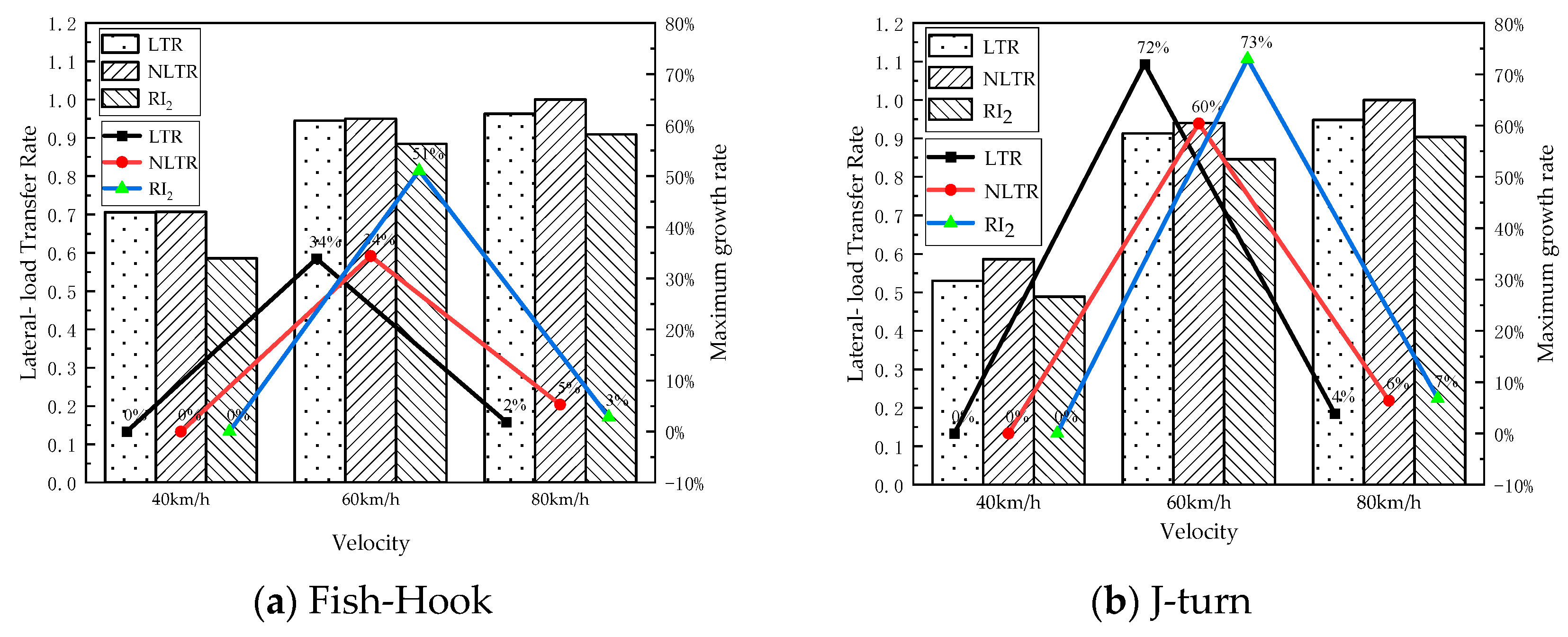
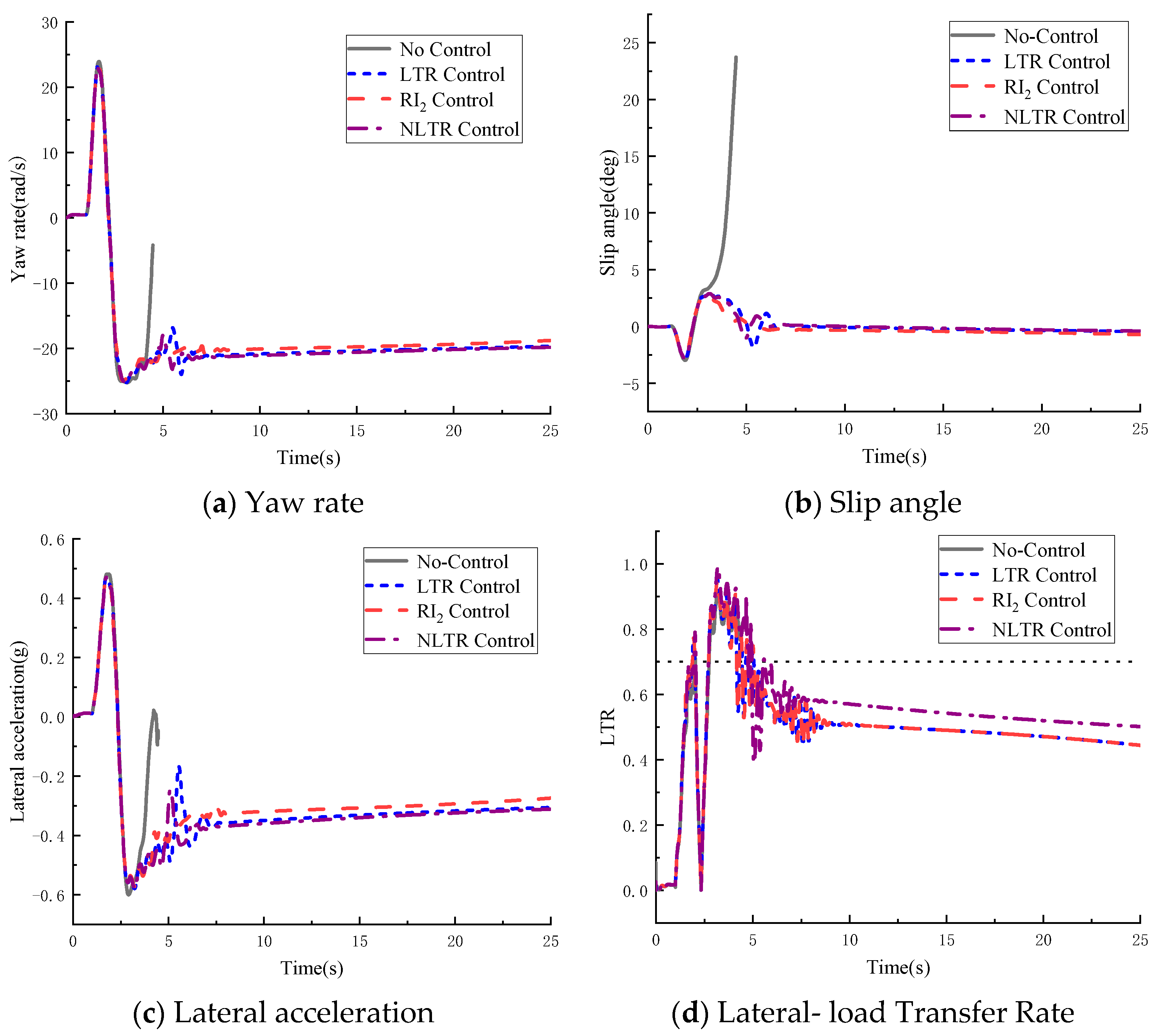
4. Heavy-Vehicle-Rollover Prevention Simulation Analysis
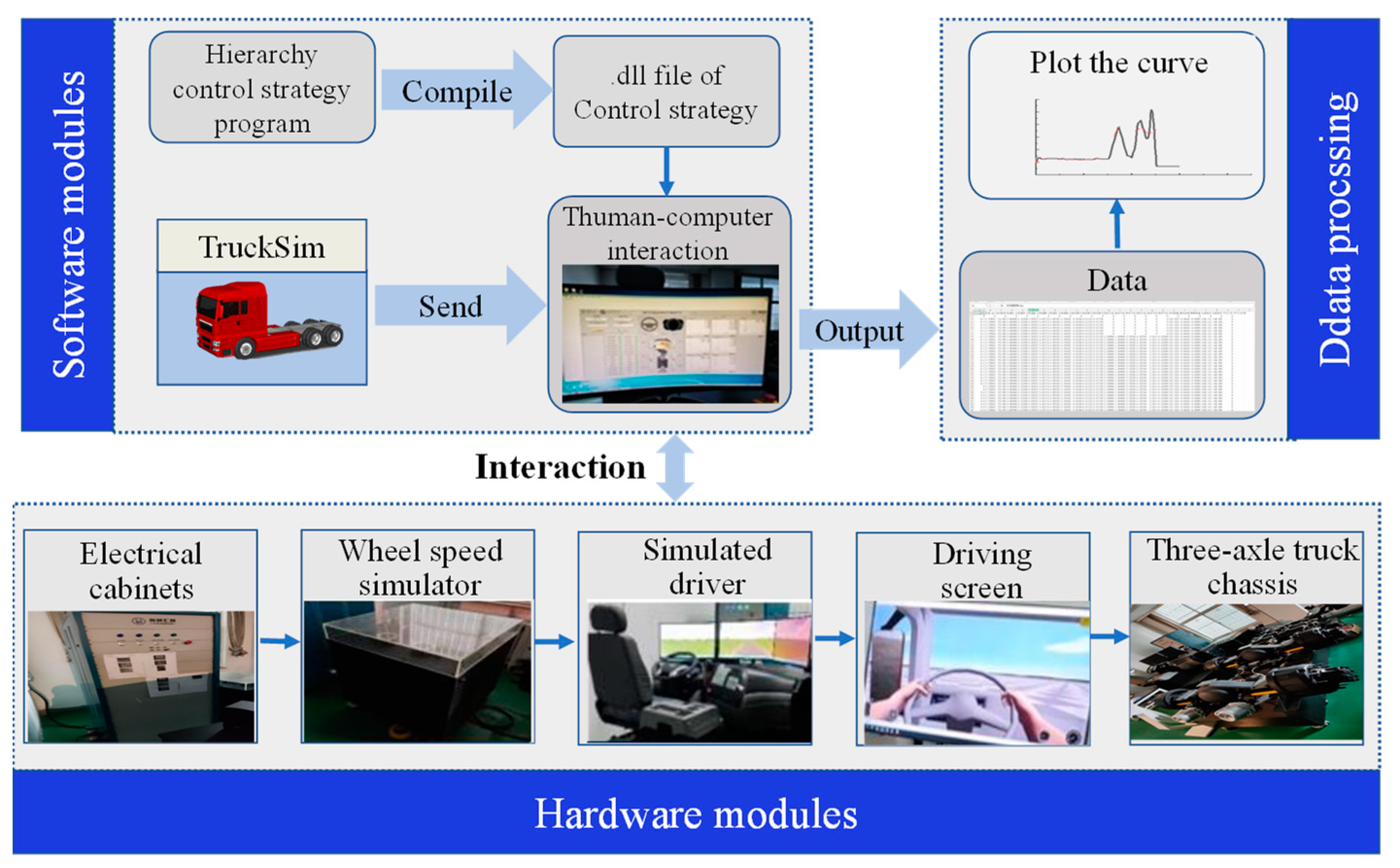
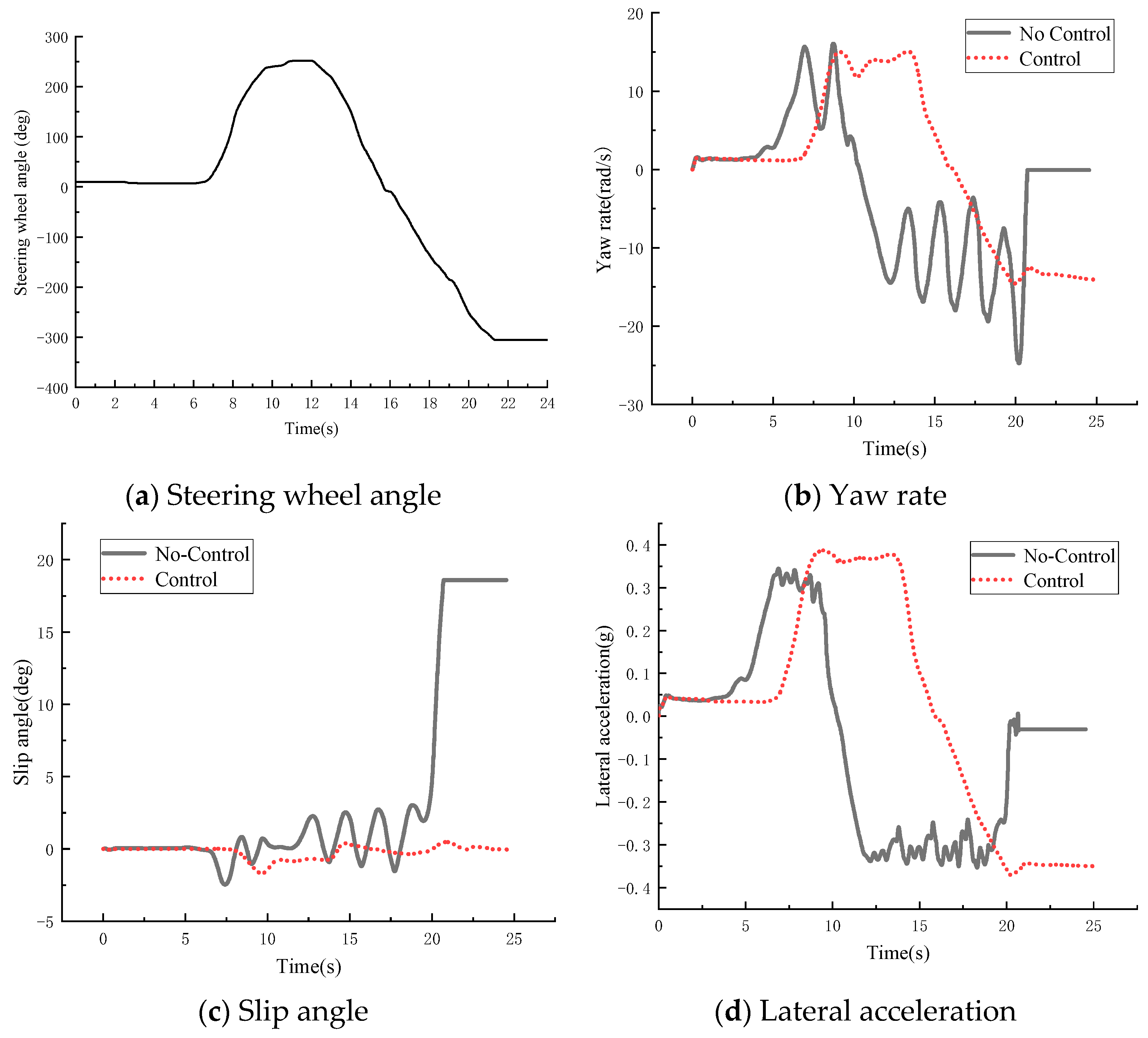
5. HIL Test Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- National Highway Traffic Safety Administration. Traffic Safety Facts 2016: A Compilation of Motor Vehicle Crash Date from the Fatality Analysis Reporting System and the General Estimates System; US Department of Transportation: Washington, DC, USA, 2018; pp. 70–77.
- Abu-Zidan, F.M.; Eid, H.O. Factors affecting injury severity of vehicle occupants following road traffic collisions. Injury 2015, 46, 136–141. [Google Scholar] [CrossRef] [PubMed]
- Kordani, A.A.; Molan, A.M. The effect of combined horizontal curve and longitudinal grade on side friction factors. KSCE J. Civ. Eng. 2015, 19, 303–310. [Google Scholar] [CrossRef]
- Doumiati, M.; Sename, O.; Dugard, L.; Martinez-Molina, J.-J.; Gaspar, P.; Szabo, Z. Integrated vehicle dynamics control via coordination of active front steering and rear braking. Eur. J. Control. 2013, 19, 121–143. [Google Scholar] [CrossRef]
- Ye, Z.; Xie, W.; Yin, Y.; Fu, Z. Dynamic Rollover Prediction of Heavy Vehicles Considering Critical Frequency. Automot. Innov. 2020, 3, 158–168. [Google Scholar] [CrossRef]
- Huang, G.; Yuan, X.; Shi, K.; Wu, X. A BP-PID controller-based multi-model control system for lateral stability of distributed drive electric vehicle. J. Frankl. Inst. 2019, 356, 7290–7311. [Google Scholar] [CrossRef]
- Jin, Z.L.; Chen, G.Y.; Zhao, W.Z. Rollover stability analysis and control of in-wheel motor drive electric vehicles. China Mech. Eng. 2018, 29, 1772–1779. [Google Scholar]
- Shi, K.; Yuan, X.; Liu, L. Model predictive controller-based multi-model control system for longitudinal stability of distributed drive electric vehicle. ISA Trans. 2018, 72, 44–55. [Google Scholar] [CrossRef]
- Zhang, L.P.; Duan, J.Y.; Su, T.; Ren, C.H. Cooperative control of spatial stability chassis for electric wheel drive vehicles. J. Mech. Eng. 2022, 58, 209–221. [Google Scholar]
- Saglam, F.; Unlusoy, Y.S. Adaptive ride comfort and attitude control of vehicles equipped with active hydro-pneumatic suspension. Int. J. Veh. Des. 2016, 71, 31. [Google Scholar] [CrossRef]
- Jin, Z.; Li, J.; Huang, Y.; Khajepour, A. Study on Rollover Index and Stability for a Triaxle Bus. Chin. J. Mech. Eng. 2019, 32, 64. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, H.D.; Wu, H.D.; Zhang, F.J.; Jiang, X.Y. Research on vehicle anti-rollover based on combined control of active lateral stabilizer bar and differential braking. Automot. Eng. 2019, 41, 1043–1049. [Google Scholar]
- Pourasad, Y.; Mahmoodi-k, M.; Oveisi, M. Design of an optimal active stabilizer mechanism for enhancing vehicle rolling resistance. J. Central South Univ. 2016, 23, 1142–1151. [Google Scholar] [CrossRef]
- Yakub, F.; Lee, S.; Mori, Y. Comparative study of MPC and LQC with disturbance rejection control for heavy vehicle rollover prevention in an inclement environment. Mech. Sci. Technol. 2016, 30, 3835–3845. [Google Scholar] [CrossRef]
- Liu, C.W.; Xu, T.S.; Li, T.; Zhang, J.H.; Lin, J.W.; Jia, H.J.; Li, Y.H.; Wang, J.C. Ride comfort simulation and optimization of heavy-duty trucks based on human-vehicle coupling dynamics model. J. Tianjin Univ. (Nat. Sci. Eng. Technol. Ed.) 2020, 53, 736–744. [Google Scholar]
- Wang, Y.; Yuan, L.; Chen, H.; Du, P.; Lian, X. An anti-slip control strategy with modifying target and torque reallocation for heavy in-wheel motor vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 2625–2644. [Google Scholar] [CrossRef]
- Tota, A.; Dimauro, L.; Velardocchia, F.; Paciullo, G.; Velardocchia, M. An Intelligent Predictive Algorithm for the Anti-Rollover Prevention of Heavy Vehicles for Off-Road Applications. Machines 2022, 10, 835. [Google Scholar] [CrossRef]
- Liu, J. Optimal Design and Analysis of Intelligent Vehicle Suspension System Based on ADAMS and Artificial Intelligence Algorithms. J. Physics: Conf. Ser. 2021, 2074, 012023. [Google Scholar] [CrossRef]
- Sivaramakrishnan, P.; Prakash, A.K.M.; Sekulic, D.; Jacobson, B.; Selvi, C.; Johannesen, S.M. Methods to introduce floating bridge motion and wind excitation on a model for the investigation of heavy vehicle dynamics. Appl. Math. Model. 2023, 117, 118–141. [Google Scholar] [CrossRef]
- Deng, Z.W.; Zhao, Y.Q.; Wang, B.H.; Gao, W.; Kong, X. A preview driver model based on sliding-mode and fuzzy control for articulated heavy vehicle. Meccanica 2022, 57, 1853–1878. [Google Scholar] [CrossRef]
- Arslan, M.S.; Sever, M. Vehicle stability enhancement and rollover prevention by a nonlinear predictive control method. Trans. Inst. Meas. Control. 2019, 41, 2135–2149. [Google Scholar] [CrossRef]
- Saeedi, M.A.; Kazemi, R.; Azadi, S. Improvement in the rollover stability of a liquid-carrying articulated vehicle via a new robust controller. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 322–346. [Google Scholar] [CrossRef]
- Jin, X.; Wang, J.; He, H.; Yan, Z.; Xu, L.; Wei, C.; Yin, G. Improving Vibration Performance of Electric Vehicles Based on In-Wheel Motor-Active Suspension System via Robust Finite Frequency Control. IEEE Trans. Intell. Transp. Syst. 2022. [Google Scholar] [CrossRef]
- Odenthal, D.; Bünte, T.; Ackermann, J. Nonlinear steering and braking control for vehicle rollover avoidance. In Proceedings of the 1999 European Control Conference (ECC), Karlsruhe, Germany, 31 August–3 September 1999; pp. 598–603. [Google Scholar]
- Phanomchoeng, G.; Rajamani, R. New rollover index for the detection of tripped and untripped rollovers. IEEE Trans. Ind. Electron. 2012, 60, 4726–4736. [Google Scholar] [CrossRef]
- Dahmani, H.; Chadli, M.; Rabhi, A.; El Hajjaji, A. Detection of impending vehicle rollover with road bank angle consideration using a robust fuzzy observer. Int. J. Autom. Comput. 2015, 12, 93–101. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, L.; Zhang, J.; Khajepour, A. Stability and optimised H∞ control of tripped and untripped vehicle rollover. Veh. Syst. Dyn. 2016, 54, 1405–1427. [Google Scholar] [CrossRef]
- Jin, Z.; Li, J.; Huang, S. Rollover detection and prevention of a heavy-duty vehicle on banked and graded uneven road. Int. J. Veh. Des. 2021, 87, 218–248. [Google Scholar] [CrossRef]
- Ataei, M.; Khajepour, A.; Jeon, S. Model predictive rollover prevention for steer-by-wire vehicles with a new rollover index. Int. J. Control. 2020, 93, 140–155. [Google Scholar] [CrossRef]
- Zhao, W.; Ji, L.; Wang, C. H∞ control of integrated rollover prevention system based on improved lateral load transfer rate. Trans. Inst. Meas. Control. 2019, 41, 859–874. [Google Scholar] [CrossRef]
- Shin, D.; Woo, S.; Park, M. Rollover Index for Rollover Mitigation Function of Intelligent Commercial Vehicle’s Electronic Stability Control. Electronics 2021, 10, 2605. [Google Scholar] [CrossRef]
- Vempaty, S.; He, Y.; Zhao, L. An overview of control schemes for improving the lateral stability of car-trailer combinations. Int. J. Veh. Perform. 2020, 6, 151–199. [Google Scholar] [CrossRef]
- Liu, W.; He, H.; Sun, F.; Lv, J. Integrated chassis control for a three-axle electric bus with distributed driving motors and active rear steering system. Veh. Syst. Dyn. 2017, 55, 601–625. [Google Scholar] [CrossRef]
- Soltani, A.; Bagheri, A.; Azadi, S. Integrated vehicle dynamics control using semi-active suspension and active braking systems. Proc. Inst. Mech. Eng. Part K J. Multi Body Dyn. 2018, 232, 314–329. [Google Scholar] [CrossRef]
- Dong, E.; Zhang, L.; Zhang, K.; Qin, C. Research for vehicle anti-rollover control based on differential braking. In Proceedings of the 2019 International Conference on Computer Network, Electronic and Automation (ICCNEA), Xi’an, China, 27–29 September 2019; pp. 486–490. [Google Scholar]
- Termous, H.; Shraïm, H.; Talj, R.; Francis, C.; Charara, A. Coordinated control strategies for active steering, differential braking and active suspension for vehicle stability, handling and safety improvement. Veh. Syst. Dyn. 2019, 57, 1494–1529. [Google Scholar] [CrossRef]
- Chang, X.; Zhang, H.; Yan, S.; Hu, S.; Meng, Y. Analysis and roll prevention control for distributed drive electric vehicles. World Electr. Veh. J. 2022, 13, 210. [Google Scholar] [CrossRef]
- Zang, L.; Wu, Y.; Wang, X.; Wang, Z.; Li, Y. Stability control of a vehicle with tire blowout based on active steering and differential braking. Int. J. Model. Simul. Sci. Comput. 2022, 13, 2250032. [Google Scholar] [CrossRef]
- Wang, G.; Liu, L.; Meng, Y.; Gu, Q.; Bai, G. Integrated Path Tracking Control of Steering and Differential Braking Based on Tire Force Distribution. Int. J. Control. Autom. Syst. 2022, 20, 536–550. [Google Scholar] [CrossRef]
- Lu, Y.; Han, Y.; Huang, W.; Wang, Y. Sliding mode control for overturning prevention and hardware-in-loop experiment of heavy-duty vehicles based on dynamical load transfer ratio prediction. Proc. Inst. Mech. Eng. Part K J. Multi Body Dyn. 2022, 236, 68–83. [Google Scholar] [CrossRef]
- Jin, X.; Wang, J.; Yan, Z.; Xu, L.; Yin, G.; Chen, N. Robust Vibration Control for Active Suspension System of In-Wheel-Motor-Driven Electric Vehicle Via μ-Synthesis Methodology. ASME Trans. J. Dyn. Syst. Meas. 2022, 144, 051007. [Google Scholar] [CrossRef]
- He, L.; Pan, Y.; He, Y.; Li, Z.; Królczyk, G.; Du, H. Control strategy for vibration suppression of a vehicle multibody system on a bumpy road. Mech. Mach. Theory 2022, 174, 104891. [Google Scholar] [CrossRef]
- Silva, F.L.; Silva, L.C.; Eckert, J.J.; Lourenço, M.A. Robust fuzzy stability control optimization by multi-objective for modular vehicle. Mech. Mach. Theory 2022, 167, 104554. [Google Scholar] [CrossRef]
- Chu, D.; Li, H.; Zhao, C.; Zhou, T. Trajectory Tracking of Autonomous Vehicle Based on Model Predictive Control With PID Feedback. IEEE Trans. Intell. Transp. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Li, D.F.; Qin, F.; Wang, W.W.; Xu, H.; Liu, J.Q. Design and verification of hardware-in-the-loop virtual test system for unmanned vehicle. J. Chang‘an Univ. (Nat. Sci. Ed.) 2021, 41, 116–126. [Google Scholar]
- Guo, Y.S.; Zhang, H.J.; Fu, R.; Wang, C. Research on lateral control model of intelligent vehicle based on neuro-ergonomics. Automot. Eng. 2021, 43, 1057–1065. [Google Scholar]
- Ma, Y.Z.; Yan, T.Y.; Zhao, Y.L. Research on integrated control strategy of new electronically controlled air suspension system. Automot. Eng. 2021, 43, 1394–1401. [Google Scholar]
- Xu, N.; Li, X.Y. Handling stability control of four-wheel drive electric vehicle under combined conditions. J. Mech. Eng. 2021, 57, 205–220. [Google Scholar]
- Pacejka, H.B. Tyre and Vehicle Dynamics; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Zhang, H.X. Study on Vertical-Lateral Coupling Dynamic Model and Control of Heavy-Duty Vehicles; Shijiazhuang University of Railways: Shijiazhuang, China, 2019. [Google Scholar]
- Mehrtash, M.; Yuen, T.; Balan, L. Implementation of experiential learning for vehicle dynamic in automotive engineering: Roll-over and fishhook test. Procedia Manuf. 2019, 32, 768–774. [Google Scholar] [CrossRef]
- Huang, W.H. Research on Anti-Rollover Sliding Mode Control of Heavy Vehicles Based on Kalman Filter Warning; Shijiazhuang Railway University: Shijiazhuang, China, 2020. [Google Scholar] [CrossRef]
- Gu, B.; Cong, J.; Zhao, J.; Chen, H.; Fatemi Golshan, M. A novel robust finite time control approach for a nonlinear disturbed quarter-vehicle suspension system with time delay actuation. Automatika 2022, 63, 627–639. [Google Scholar] [CrossRef]
- Sun, X.-Q.; Cai, Y.-F.; Yuan, C.-C.; Wang, S.-H.; Chen, L. Fuzzy Sliding Mode Control for the Vehicle Height and Leveling Adjustment System of an Electronic Air Suspension. Chin. J. Mech. Eng. 2018, 31, 25. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, H.; Wei, Y.; Iu, H.H.-C.; Fernando, T. Robust adaptive finite-time tracking control for Intervention-AUV with input saturation and output constraints using high-order control barrier function. Ocean. Eng. 2023, 268, 113219. [Google Scholar] [CrossRef]
- Li, L.; Guo, T.; Xu, S. Simulation Analysis of Vehicle Handling Stability Based on Trucksim. J. Phys. Conf. Ser. IOP Publ. 2021, 1885, 032043. [Google Scholar] [CrossRef]




| Pavement Type | |||
|---|---|---|---|
| Dry Asphalt | 1.28 | 23.99 | 0.52 |
| Wet asphalt | 0.875 | 33.822 | 0.374 |
| Cement | 1.197 | 25.17 | 0.54 |
| Dry cobblestone | 1.37 | 6.46 | 0.669 |
| Wet pebbles | 0.41 | 33.71 | 0.12 |
| Ice | 0.05 | 306.39 | 0.001 |
| Snow | 0.195 | 94.13 | 0.065 |
| Symbol | Value | Unit |
|---|---|---|
| 20,000 | kg | |
| 17,860 | kg | |
| 2 | m | |
| 1.5 | m | |
| 2.7 | m | |
| 1.173 | m | |
| 2284.9 | Kg·m2 | |
| 35,408 | Kg·m2 | |
| 34,823 | Kg·m2 | |
| 1626 | Kg·m2 | |
| 1.863 | m | |
| , | 0.9315 | m |
| 250,000 | N/m | |
| 700,000 | N/m | |
| 15,000 | N/m/s | |
| 30,000 | N/m/s | |
| , | 285 | kg |
| , , , | 392.5 | kg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Lu, Y.; Li, H.; Zhang, J. Anti-Rollover Control and HIL Verification for an Independently Driven Heavy Vehicle Based on Improved LTR. Machines 2023, 11, 117. https://doi.org/10.3390/machines11010117
Zheng L, Lu Y, Li H, Zhang J. Anti-Rollover Control and HIL Verification for an Independently Driven Heavy Vehicle Based on Improved LTR. Machines. 2023; 11(1):117. https://doi.org/10.3390/machines11010117
Chicago/Turabian StyleZheng, Lufeng, Yongjie Lu, Haoyu Li, and Junning Zhang. 2023. "Anti-Rollover Control and HIL Verification for an Independently Driven Heavy Vehicle Based on Improved LTR" Machines 11, no. 1: 117. https://doi.org/10.3390/machines11010117
APA StyleZheng, L., Lu, Y., Li, H., & Zhang, J. (2023). Anti-Rollover Control and HIL Verification for an Independently Driven Heavy Vehicle Based on Improved LTR. Machines, 11(1), 117. https://doi.org/10.3390/machines11010117










