High-Performance Control Strategy for Low-Speed Torque of IPMSM in Electric Construction Machinery
Abstract
:1. Introduction
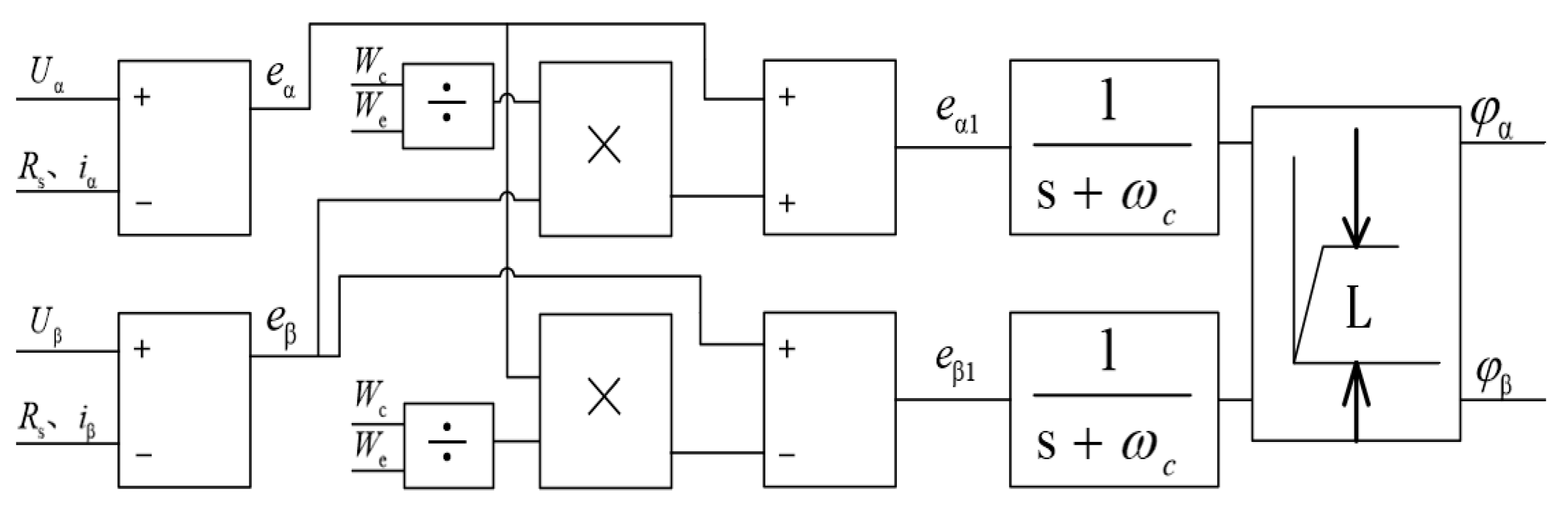
2. Voltage and Current Composite Observation Algorithm Framework
3. Torque Improvement Model Design of IPMSM
3.1. MTPA Control
3.2. EM Temperature Prediction Model
3.3. Voltage Observation Model
3.4. Current Observation Model
4. Experimental Research
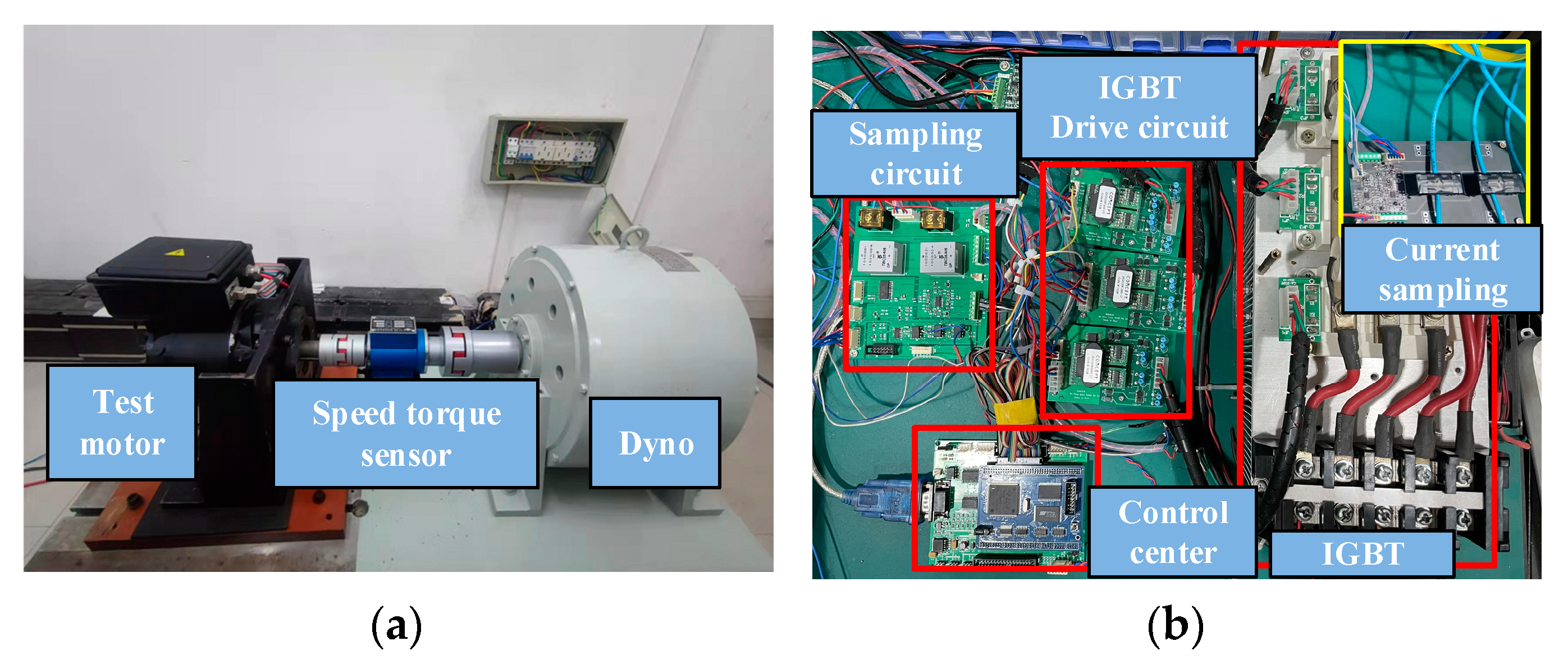
4.1. Experimental Platform
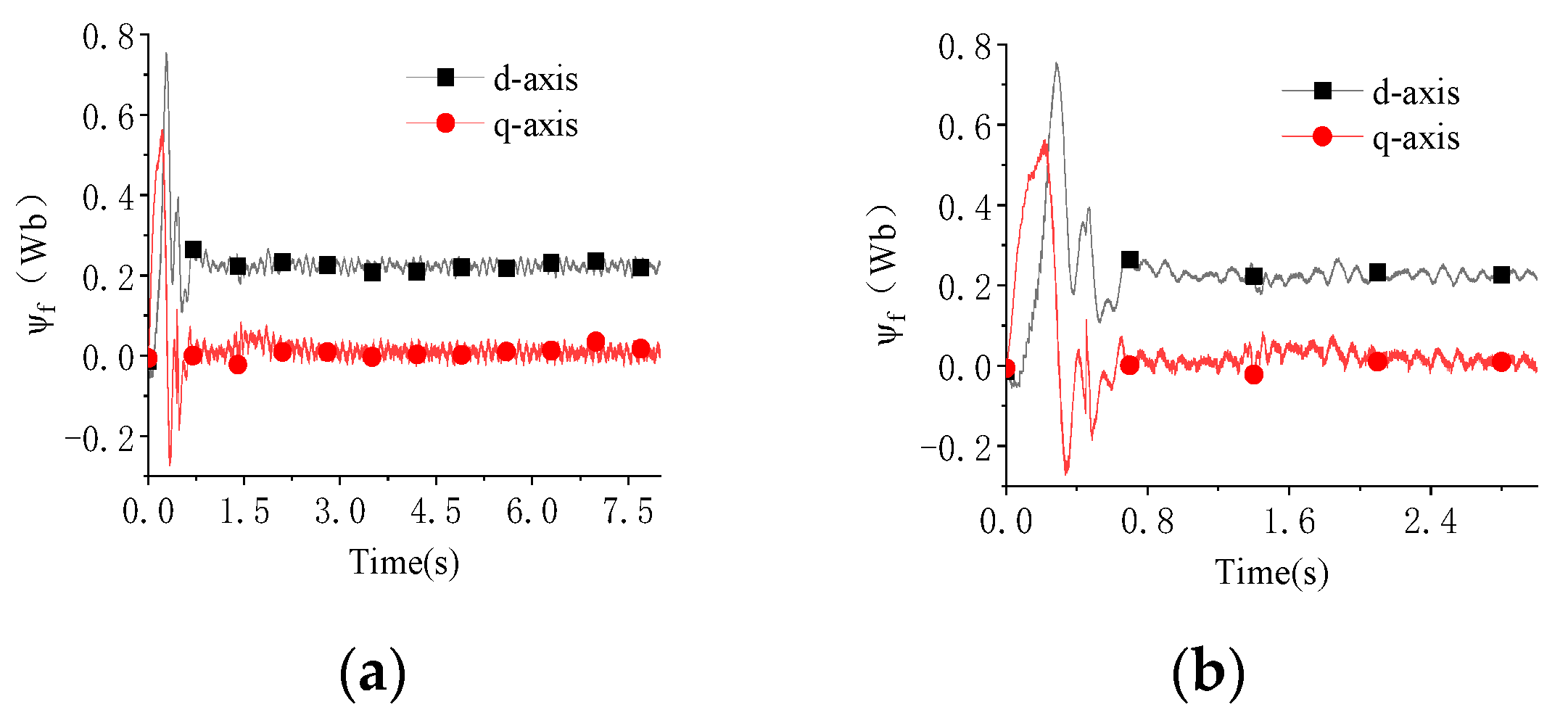
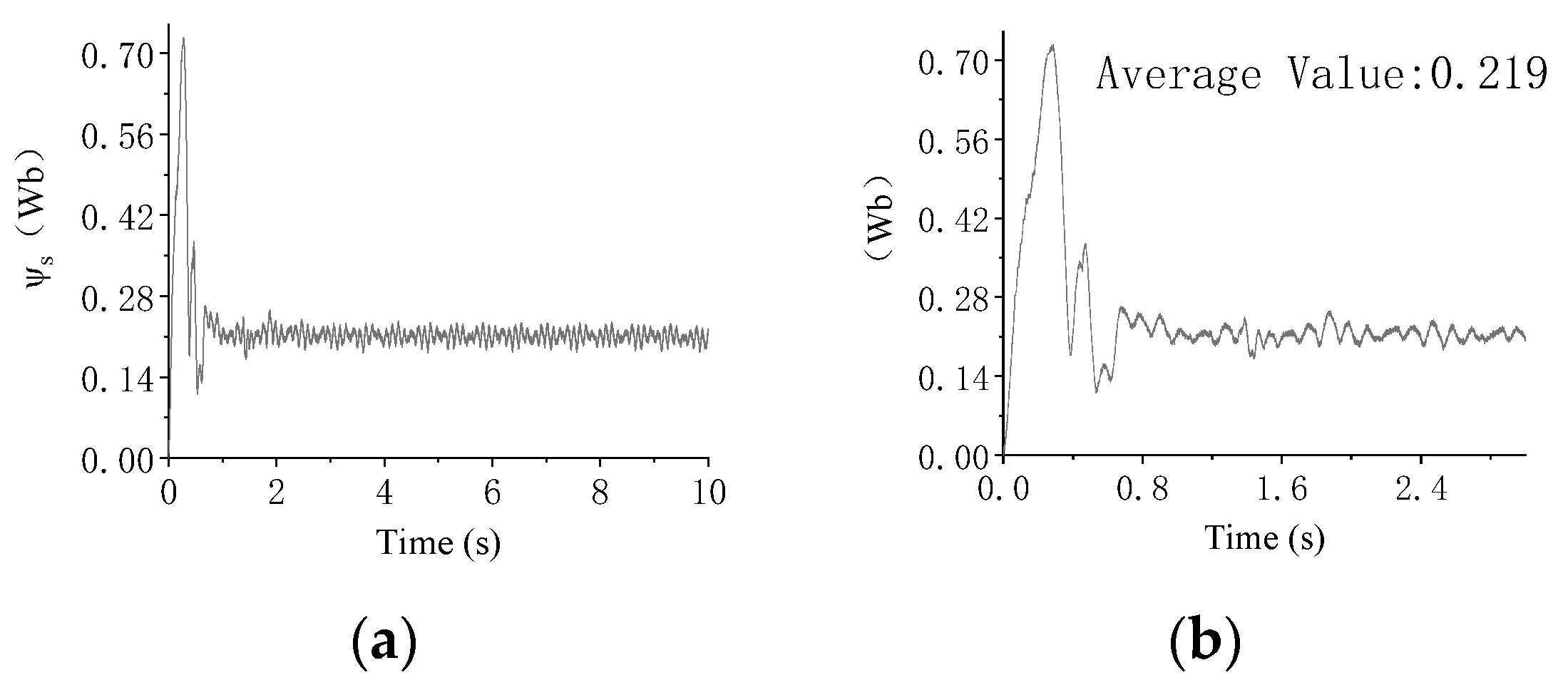
4.2. Test and Analysis of No-Load On-Line Parameter Identification
4.3. Test and Analysis of On-Line Parameter Identification in Loaded Condition
4.4. Comparative Test Analysis of Parameter Identification MTPA Control and Fixed Parameter MTPA Control
5. Conclusions
- (1)
- Electric construction machinery is considered to be an important trend in the future. However, electric construction machinery has more stringent requirements for EM control. It is often necessary for the EM to work under the condition of low speed, large torque, and high efficiency.
- (2)
- Based on the vector control of the MTPA for an IPMSM, we studied a voltage and current composite observation algorithm. By establishing the EM temperature model and observing the temperature change during the low-speed condition of the EM, the real-time stator resistance value and the PM flux linkage of the EM were observed, and then sent into the voltage observation model. During the operation of the EM, the amplitude limited compensation voltage flux linkage observation method was used to observe the stator flux, and then combined with the current observation model. The parameters in the real-time operation of the EM were identified.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, T.; Lin, Y.; Ren, H.; Chen, H.; Chen, Q.; Li, Z. Development and key technologies of pure electric construction machinery. Renew. Sustain. Energy Rev. 2020, 132, 110090. [Google Scholar] [CrossRef]
- Lin, T.; Lin, Y.; Ren, H.; Chen, H.; Li, Z.; Chen, Q. A Double Variable Control Load Sensing System for Electric Hydraulic Excavator. Energy 2021, 223, 119999. [Google Scholar] [CrossRef]
- Ge, L.; Quan, L.; Zhang, X.; Dong, Z.; Yang, J. Power Matching and Energy Efficiency Improvement of Hydraulic Excavator Driven with Speed and Displacement Variable Power Source. Chin. J. Mech. Eng. 2019, 32, 100. [Google Scholar] [CrossRef]
- Qiu, Z.; Chen, Y.; Liu, X.; Zhang, L.; Cheng, H. Evaluation and comparison of sideband harmonics and acoustic responses with continuous and discontinuous PWM strategies in permanent magnet synchronous motor for electric vehicles. Int. J. Hydromechatron. 2022, 5, 109–123. [Google Scholar] [CrossRef]
- Guo, T.; Cai, S.L.; Chen, Q.-H.; Lin, T.-L.; Chen, H.-B.; Fu, S.-J.; Guo, H.-B. Electro-hydraulic shift system and control strategy for pure electric loader based pressure feedback. Chin. Hydraul. Pneum. 2020, 12, 22–29. [Google Scholar]
- Chen, T.; Chen, P.; Liang, J.; Li, S.; Fahimi, B. Maximum torque per ampere control of interior permanent magnet synchronous motor via optimal current excitation. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 28 September–2 October 2019. [Google Scholar]
- Han, Z.; Liu, J.; Yang, W.; Pinhal, D.B.; Reiland, N.; Gerling, D. Improved online maximum-torque-per-ampere algorithm for speed controlled interior permanent magnet synchronous machine. IEEE Trans. Ind. Electron. 2019, 67, 3398–3408. [Google Scholar] [CrossRef]
- Sun, T.; Wang, J.; Chen, X. Maximum torque per ampere (MTPA) control for interior permanent magnet synchronous machine drives based on virtual signal injection. IEEE Trans. Power Electron. 2014, 30, 5036–5045. [Google Scholar] [CrossRef]
- Djeriou, A.; Houari, A.; Machmoum, M.; Mesbahi, T.; Ghanes, M. Cascade GW Controllers for Speed Ripple Minimization at Low-Speed Operation of PMSM Drives for EV. In Proceedings of the 46th Annual Conference of the IEEE Industrial Electronics Society, Electr Network, Singapore, 19–21 October 2020. [Google Scholar]
- Elsonbaty, N.A.; Enany, M.A.; Hassanin, M.I. An Efficient Vector Control Policy for EV-Hybrid Excited Permanent-Magnet Synchronous Motor. World Electr. Veh. J. 2020, 11, 42. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, X.; Zhu, Y. IPMSM Dead Time Compensation Method Based on NNBPF-EKF. Proc. CSEE 2020, 40, 5011–5019. [Google Scholar]
- Fu, S.; Ren, H.; Lin, T. SM-PI Control Strategy of Electric Motor-pump for Pure Electric Construction Machinery. IEEE Access 2020, 8, 100241–100250. [Google Scholar] [CrossRef]
- Chen, Q.; Lin, T.; Ren, H. A novel direct torque control of a permanent magnet synchronous machine for hybrid hydraulic excavator. IET Electr. Power Appl. 2019, 13, 222–228. [Google Scholar] [CrossRef]
- Bobtsov, A.; Pyrkin, A.; Aranovskiy, S.; Nikolaev, N.; Slita, O.; Kozachek, O.; Quoc, D.V. Stator flux and load torque observers for PMSM. IFAC-PapersOnLine 2020, 53, 5051–5056. [Google Scholar] [CrossRef]
- Pulvirenti, M.; Scarcella, G.; Scelba, G.; Testa, A.; Harbaugh, M.M. On-Line Stator Resistance and Permanent Magnet Flux Linkage Identification on Open-End Winding PMSM Drives. IEEE Trans. Ind. Appl. 2019, 55, 504–515. [Google Scholar] [CrossRef]
- Shi, Y. Online Identification of Permanent Magnet Flux Based on Extended Kalman Filter for IPMSM Drive with Position Sensorless Control. IEEE Trans. Ind. Electron. 2012, 59, 4169–4178. [Google Scholar] [CrossRef]
- Ding, X.; Wang, S.; Zou, M.; Liu, M. Predictive Current Control for Permanent Magnet Synchronous Motor Based on MRAS Parameter Identification. In Proceedings of the IEEE International Power Electronics and Application Conference and Exposition, Shenzhen, China, 4–7 November 2018. [Google Scholar]





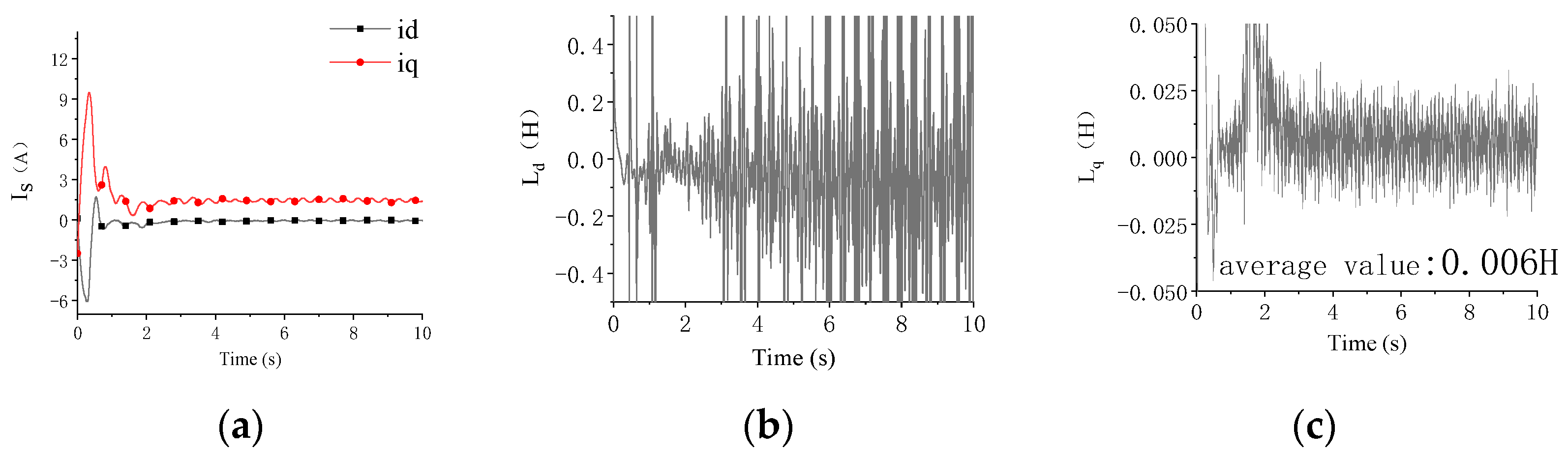


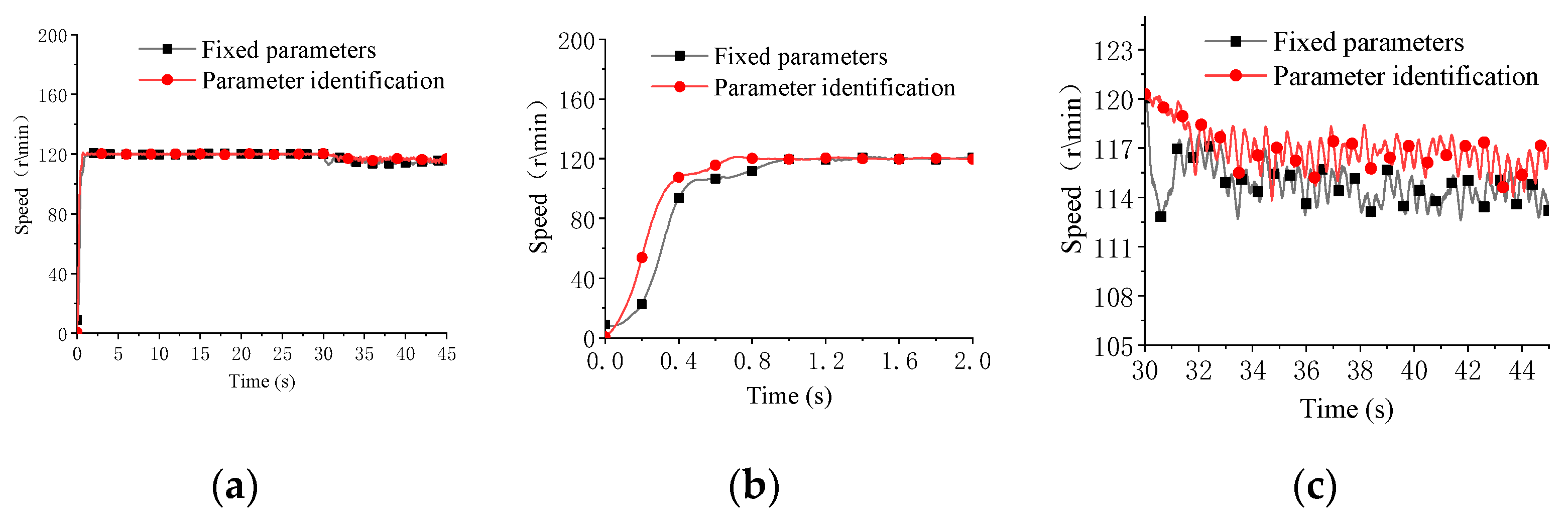
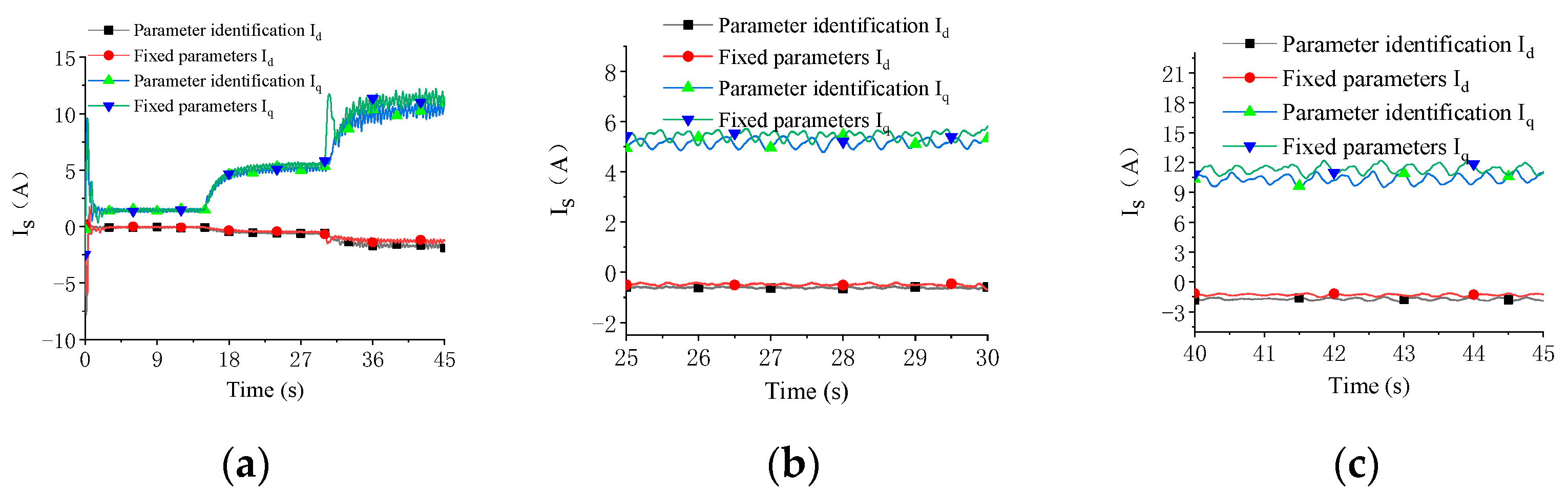
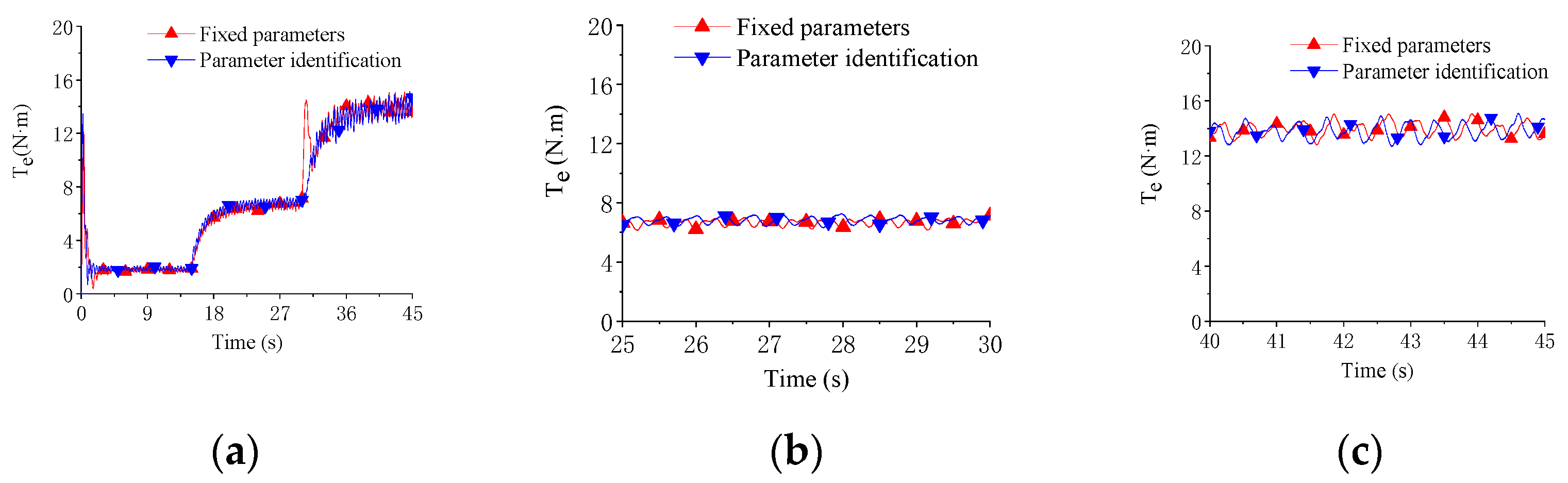

| Rated Power (kW) | Rated Speed (rpm) | Rated Torque (N·m) | Rated Current (A) | Ld (mH) | Lq (mH) | Pole Pair |
|---|---|---|---|---|---|---|
| 9 | 1800 | 44 | 35 | 2.5 | 5.5 | 4 |
| Target Torque (N·m) | Target Speed (r/min) | Time (s) |
|---|---|---|
| 7 | 120 | 15~30 |
| 14 | 120 | 30~50 |
| Manufacturer Parameters | Identification Value | |
|---|---|---|
| Flux linkage (Wb) | 0.203 | 0.219 |
| Ld (mH) | 2.5 | 2.5 |
| Lq (mH) | 5.5 | 6 |
| Fixed Parameter | Novel Control | |
|---|---|---|
| Target speed (r/min) | 120 | 120 |
| Dynamometer given torque (N·m) | 0~7~14 | 0~7~14 |
| Time (s) | 0~15~30~45 | 0~15~30~45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chen, Q.; Chen, Y.; Lin, T.; Ren, H.; Gong, W. High-Performance Control Strategy for Low-Speed Torque of IPMSM in Electric Construction Machinery. Machines 2022, 10, 810. https://doi.org/10.3390/machines10090810
Li Z, Chen Q, Chen Y, Lin T, Ren H, Gong W. High-Performance Control Strategy for Low-Speed Torque of IPMSM in Electric Construction Machinery. Machines. 2022; 10(9):810. https://doi.org/10.3390/machines10090810
Chicago/Turabian StyleLi, Zhongshen, Qihuai Chen, Yongjie Chen, Tianliang Lin, Haoling Ren, and Wen Gong. 2022. "High-Performance Control Strategy for Low-Speed Torque of IPMSM in Electric Construction Machinery" Machines 10, no. 9: 810. https://doi.org/10.3390/machines10090810
APA StyleLi, Z., Chen, Q., Chen, Y., Lin, T., Ren, H., & Gong, W. (2022). High-Performance Control Strategy for Low-Speed Torque of IPMSM in Electric Construction Machinery. Machines, 10(9), 810. https://doi.org/10.3390/machines10090810







