Multiobjective Design Optimization of Lightweight Gears
Abstract
:1. Introduction
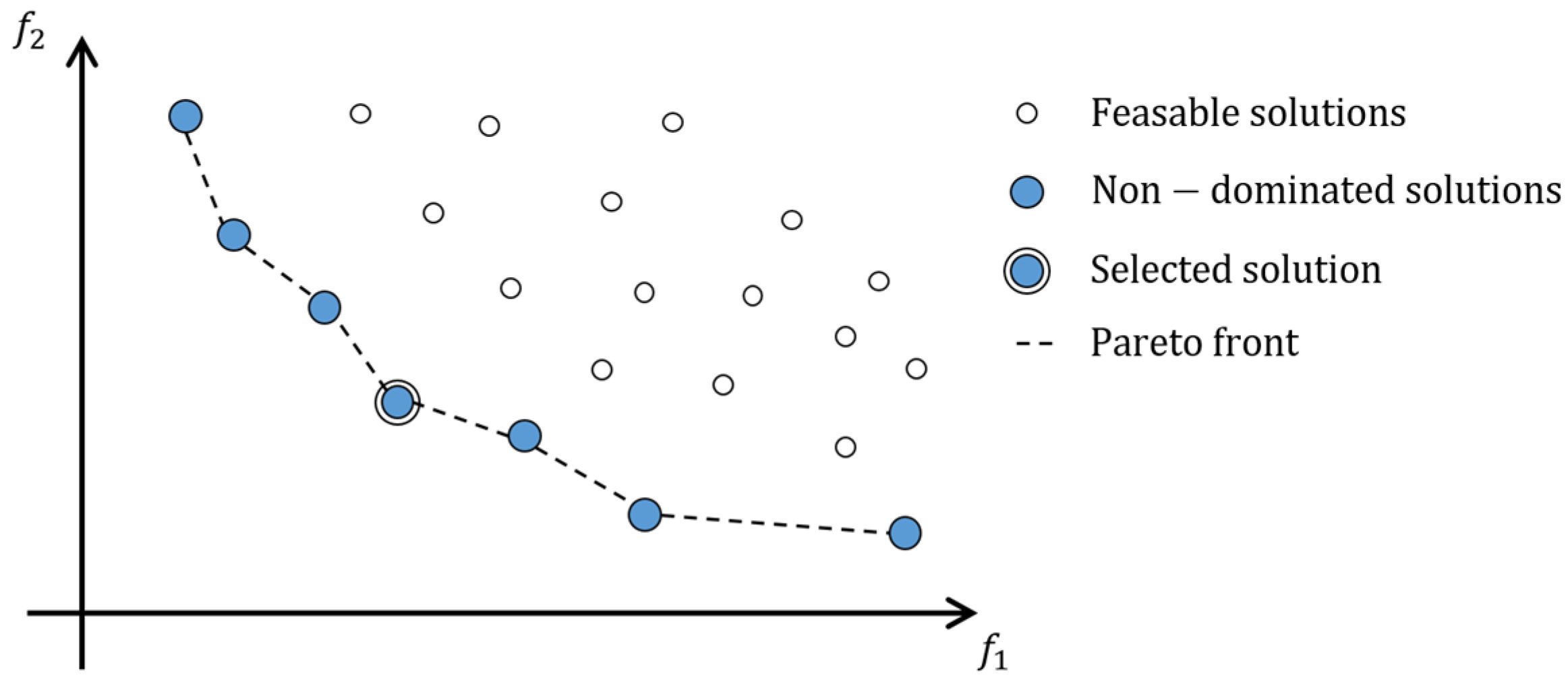
2. Multiobjective Optimization Strategy
HEEDS|MDO Optimization Software
3. Modeling Strategy for Gear Meshing Analysis
- Lumped-parameter (LP) modeling [16,17,18,19,20] aims to (semi)analytically lump mechanical and contact properties of a system through the most relevant, yet few, parameters (e.g., meshing stiffness, damping, and inertias) and states (e.g., angular positions and velocities). It allows for efficiently representing the overall load distribution and approximating the system-level statics/dynamics with simple and quick-to-solve equations. However, it is limited to simple gear topologies and geometry-dependent parameter sets that are often difficult to obtain [21,22]. Therefore, although they are very computationally efficient, LP models require the careful parameterization of the design space (not always possible) to be used in optimization problems.
- Finite-element (FE) modeling a gear train [12,23,24] relies on using finite elements to achieve a geometrical domain discretization and approximate the behavior of the continuous bodies through numerical integrations. It is a general modeling approach since it does not rely on any gear topologies assumption and is a first-principle-based strategy. It can account for micro- and macrogeometry deviations from the nominal operating conditions, teeth coupling, and the contacting bodies’ dynamic behavior. Nevertheless, it usually requires the fine discretization of the contacting bodies in the contact zones due to the high-stress gradients involved, and computationally expensive contact detection, which renders the FE method computationally prohibitive to use in design optimization problems.
- Multibody (MB) modeling [25,26,27,28] is used to analyze the dynamics of systems composed of several components interconnected in space with different specifications. It enables the representation of the different bodies as rigid or deformable (flexible) components linked together through permanent (e.g., bushings) or variable (e.g., meshing gears) connection elements. It is modular, efficient (depending on the formulation and system topology), and allows for including other modeling strategies, i.e., LP and FE. Moreover, it accounts for large and complex body motions in space, macro misalignments, and microgeometry modifications [29] with respect to nominal operating and geometrical specifications. Nevertheless, it is challenging to accurately and efficiently formulate the body flexibility effects in a MB environment jointly with contact phenomena. In particular, most MB formulations are based on small (body) deformations that represent a limitation under high loading conditions.
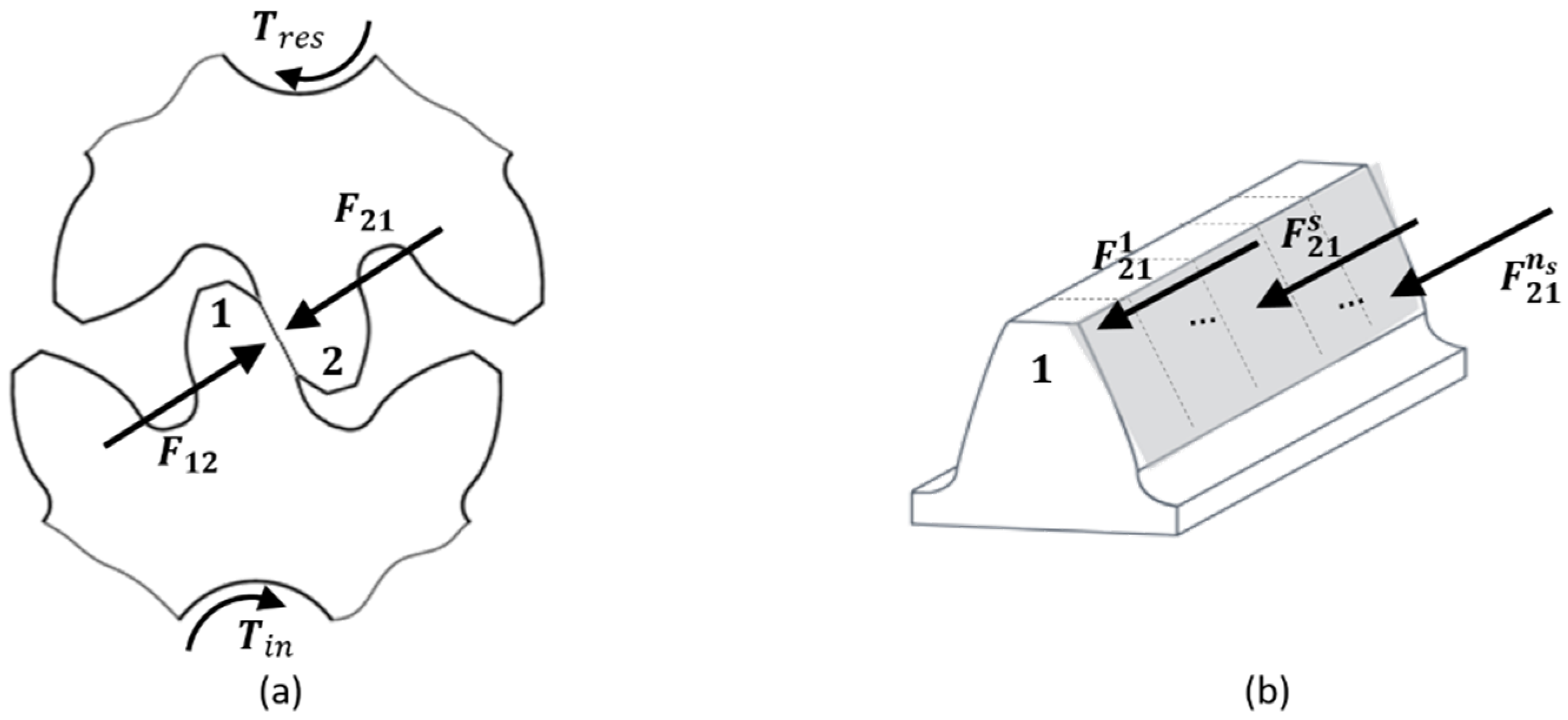
3.1. Advanced Contact Strategy in Multibody Simulations
- Detecting the contact locations of the meshing bodies.
- Formulating the amount of contact deformation (compliance) or inversely the contact stiffness.
- Formulating the contact problem to be solved.
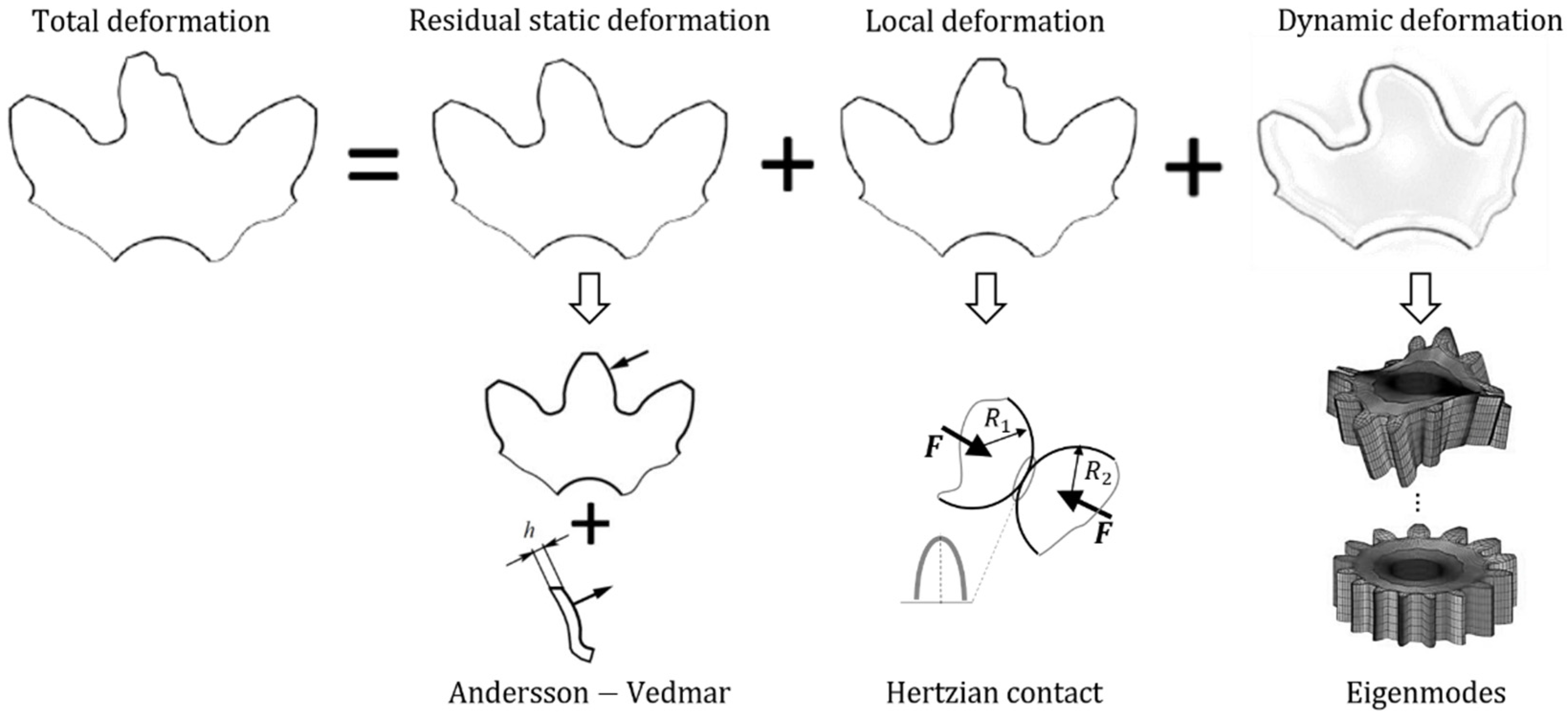
- The residual static deformation based on the Andersson and Vedmar idea is described in [32]. It is computed through an FE-based approach [21,33] where a static unit nodal load, normal to the tooth surface, is applied in a preprocessing step; subsequently, the deformation pattern is subtracted from the previous one considering the same loading condition while clamping the tooth in its middle plane. In this way, a locally incorrect solution is overcome [12].
- The nonlinear local contact deformation is approximated as two contacting cylinders in line contact according to Hertz theory, and theWeber and Banaschek formula [34].
3.2. Performance Metric: Transmission Error
4. Adopted Optimization Strategy
4.1. Optimization Workflow
4.2. Alterer
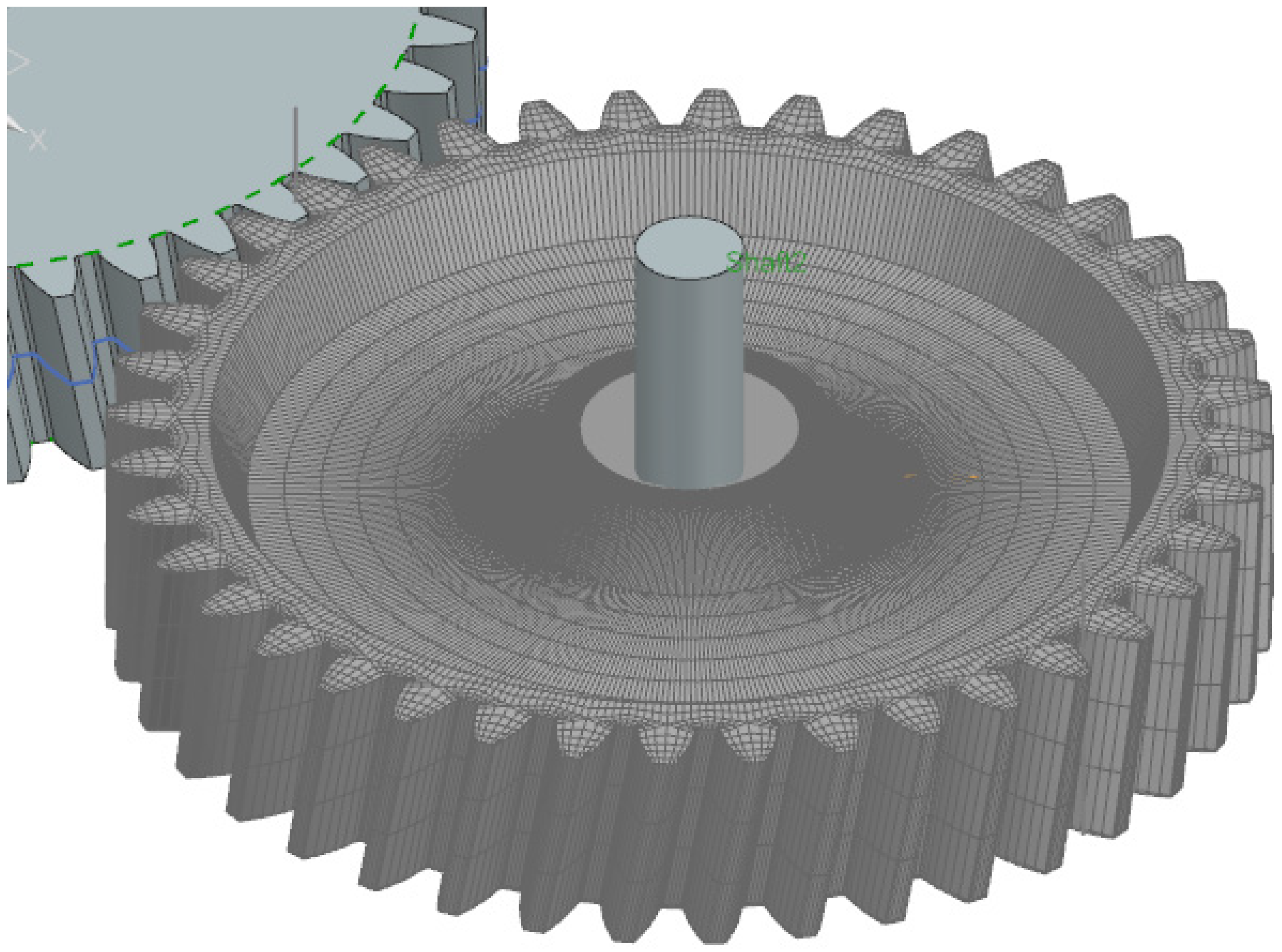
5. Application Case
5.1. Use-Case Description
5.2. Optimization Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dobrzański, L.; Tański, T.; Čížek, L.; Brytan, Z. Structure and properties of magnesium cast alloys. J. Mater. Process. Technol. 2007, 192–193, 567–574. [Google Scholar] [CrossRef]
- New Equipment Digest. NASA’s Revolutionary Hybrid Gear Lightens Your Load. Available online: https://www.newequipment.com/research-and-development/article/22058083/nasas-revolutionary-hybrid-gear-lightens-your-load (accessed on 10 June 2022).
- Ohrn, K.E. Aircraft Energy Use. In Encyclopedia of Energy Engineering and Technology, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 32–38. [Google Scholar] [CrossRef]
- Shweiki, S.; Palermo, A.; Mundo, D. A Study on the Dynamic Behaviour of Lightweight Gears. Shock Vib. 2017, 2017, 7982170. [Google Scholar] [CrossRef]
- Benaïcha, Y.; Mélot, A.; Rigaud, E.; Beley, J.-D.; Thouverez, F.; Perret-Liaudet, J. A decomposition method for the fast computation of the transmission error of gears with holes. J. Sound Vib. 2022, 532, 116927. [Google Scholar] [CrossRef]
- Catera, P.G.; Mundo, D.; Gagliardi, F.; Treviso, A. A comparative analysis of adhesive bonding and interference fitting as joining technologies for hybrid metal-composite gear manufacturing. Int. J. Interact. Des. Manuf. 2020, 14, 535–550. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y.; Lee, C.-H. Multi-parameter optimization-based design of lightweight vibration-reduction gear bodies. J. Mech. Sci. Technol. 2022, 36, 1879–1887. [Google Scholar] [CrossRef]
- Ramadani, R.; Belsak, A.; Kegl, M.; Predan, J.; Pehan, S. Topology Optimization Based Design of Lightweight and Low Vibration Gear Bodies. Int. J. Simul. Model. 2018, 17, 92–104. [Google Scholar] [CrossRef]
- Hou, L.; Lei, Y.; Fu, Y.; Hu, J. Effects of Lightweight Gear Blank on Noise, Vibration and Harshness for Electric Drive System in Electric Vehicles. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2020, 234, 447–464. [Google Scholar] [CrossRef]
- Shweiki, S.; Rezayat, A.; Tamarozzi, T.; Mundo, D. Transmission Error and strain analysis of lightweight gears by using a hybrid FE-analytical gear contact model. Mech. Syst. Signal Process. 2019, 123, 573–590. [Google Scholar] [CrossRef]
- Vivet, M.; Tamarozzi, T.; Desmet, W.; Mundo, D. On the modelling of gear alignment errors in the tooth contact analysis of spiral bevel gears. Mech. Mach. Theory 2021, 155, 104065. [Google Scholar] [CrossRef]
- Cappellini, N.; Tamarozzi, T.; Blockmans, B.; Fiszer, J.; Cosco, F.; Desmet, W. Semi-analytic contact technique in a non-linear parametric model order reduction method for gear simulations. Meccanica 2017, 53, 49–75. [Google Scholar] [CrossRef]
- Simcenter. HEEDS. Available online: https://www.plm.automation.siemens.com/global/en/products/simcenter/simcenter-heeds.html (accessed on 22 June 2022).
- Siemens PLM Software. Boosting Productivity in Gearbox Engineering Using a Revolutionary Approach to Multibody Simulation. Available online: https://resources.sw.siemens.com/en-US/white-paper-gearbox-multibody-simulation (accessed on 22 June 2022).
- Simcenter 3D Motion: Siemens PLM Software. Advanced FE-Preprocessor. Available online: https://www.plm.automation.siemens.com/global/en/products/simcenter/simcenter-3d.html (accessed on 22 June 2022).
- Cai, Y.; Hayashi, T. The Linear Approximated Equation of Vibration of a Pair of Spur Gears (Theory and Experiment). J. Mech. Des. 1994, 116, 558–564. [Google Scholar] [CrossRef]
- Cai, Y. Simulation on the Rotational Vibration of Helical Gears in Consideration of the Tooth Separation Phenomenon (A New Stiffness Function of Helical Involute Tooth Pair). J. Mech. Des. 1995, 117, 460–469. [Google Scholar] [CrossRef]
- Parker, R.G.; Vijayakar, S.M.; Imajo, T. Non-linear dynamic response of a spur gear pair: Modelling and experimental comparisons. J. Sound Vib. 2000, 237, 435–455. [Google Scholar] [CrossRef]
- Shweiki, S.; Korta, J.; Palermo, A.; Adduci, R.; Mundo, D. Combining Finite Element Analysis and Analytical Modelling for Efficient Simulations of Non-Linear Gear Dynamics. In Proceedings of the 7th European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece, 5–10 June 2016. [Google Scholar]
- ISO. ISO 6336-1:1996—Calculation of Load Capacity of Spur and Helical Gears—Part 1: Basic Principles, Introduction and General Influence Factors. Available online: https://www.iso.org/standard/12632.html (accessed on 20 June 2022).
- Shen, Y.; Yang, S.; Liu, X. Nonlinear dynamics of a spur gear pair with time-varying stiffness and backlash based on incremental harmonic balance method. Int. J. Mech. Sci. 2006, 48, 1256–1263. [Google Scholar] [CrossRef]
- Vivet, M.; Mundo, D.; Tamarozzi, T.; Desmet, W. An analytical model for accurate and numerically efficient tooth contact analysis under load, applied to face-milled spiral bevel gears. Mech. Mach. Theory 2018, 130, 137–156. [Google Scholar] [CrossRef]
- Blockmans, B.; Adduci, R.; Fiszer, J.; Cappellini, N.; Desmet, W. Finite Element Based Simulation of Planetary Gearboxes Using Model-Order Reduction. In Proceedings of the International Gear Conference, Lyon, France, 29 August 2018; Chartridge Books: Oxford, UK, 2018; pp. 1024–1033. [Google Scholar]
- Korta, J.A.; Mundo, D. Multi-objective micro-geometry optimization of gear tooth supported by response surface methodology. Mech. Mach. Theory 2017, 109, 278–295. [Google Scholar] [CrossRef]
- Blockmans, B. Model Reduction of Contact Problems in Flexible Multibody Dynamics with Emphasis on Dynamic Gear Contact Problems; KU Leuven: Leuven, Belgium, 2018. [Google Scholar]
- Vivet, M.; Verhoogen, J.; Jiránek, P.; Tamarozzi, T. A New Gear Contact Method for the Tooth Contact Analysis of Spiral Bevel Gear Drives in Multibody Simulations. In Proceedings of the NAFEMS International Seminar Advances in Structural Dynamic Simulation, Online, 29–30 March 2022. [Google Scholar]
- Tamarozzi, T.; Blockmans, B.; Desmet, W. Dynamic Stress Analysis of the High-Speed Stage of a Wind Turbine Gearbox Using a Coupled Flexible Multibody Approach. In Proceedings of the Conference for Wind Power Drives 2015, Aachen, Germany, 10–12 March 2015; Books on Demand: Canfield, OH, USA, 2018; p. 87. [Google Scholar]
- Palermo, A.; Mundo, D.; Hadjit, R.; Desmet, W. Multibody element for spur and helical gear meshing based on detailed three-dimensional contact calculations. Mech. Mach. Theory 2013, 62, 13–30. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; ISBN 9780521815178. [Google Scholar]
- Siemens. White Paper: Boosting Productivity in Gearbox Engineering; 2019; Available online: http://www.fp7demetra.eu/images/files/Siemens-PLM-Boosting-Productivity-in-Gearbox-Engineering-wp-65217-A20.pdf (accessed on 30 July 2022).
- Shabana, A.A. Dynamics of Multibody Systems, 5th ed.; Cambridge University Press: Cambridge, UK, 2020; ISBN 1108485642. [Google Scholar]
- Andersson, A.; Vedmar, L. A dynamic model to determine vibrations in involute helical gears. J. Sound Vib. 2003, 260, 195–212. [Google Scholar] [CrossRef]
- Heirman, G.; Cappellini, N.; Tamarozzi, T.; Toso, A. Contact Modeling between Objects. US Patent 10,423,730, 24 September 2019. [Google Scholar]
- Weber, C.; Banaschek, K.; Niemann, G. Formänderung und Profilrücknahme Bei Gerad-und Schrägverzahnten Rädern; F. Vieweg: Brunswick, Germany, 1955. [Google Scholar]
- Craig, R.R.; Bampton, M.C.C. Coupling of substructures for dynamic analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, O.P.; Shabana, A.A. Dynamic analysis of multibody systems using component modes. Comput. Struct. 1985, 21, 1303–1312. [Google Scholar] [CrossRef]
- Blockmans, B.; Tamarozzi, T.; Naets, F.; Desmet, W. A nonlinear parametric model reduction method for efficient gear contact simulations. Int. J. Numer. Methods Eng. 2015, 102, 1162–1191. [Google Scholar] [CrossRef]
- Ascher, U.M.; Petzold, L.R. Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations; Siam: Philadelphia, PA, USA, 1998; Volume 61. [Google Scholar]
- Palermo, A.; Britte, L.; Janssens, K.; Mundo, D.; Desmet, W. The measurement of Gear Transmission Error as an NVH indicator: Theoretical discussion and industrial application via low-cost digital encoders to an all-electric vehicle gearbox. Mech. Syst. Signal Process. 2018, 110, 368–389. [Google Scholar] [CrossRef]
- Choi, C.; Ahn, H.; Park, Y.J.; Lee, G.H.; Kim, S.C. Influence of gear tooth addendum and dedendum on the helical gear optimization considering mass, efficiency, and transmission error. Mech. Mach. Theory 2021, 166, 104476. [Google Scholar] [CrossRef]
- Kim, S.-C.; Moon, S.-G.; Sohn, J.-H.; Park, Y.-J.; Choi, C.-H.; Lee, G.-H. Macro geometry optimization of a helical gear pair for mass, efficiency, and transmission error. Mech. Mach. Theory 2020, 144, 103634. [Google Scholar] [CrossRef]
- Garambois, P.; Perret-Liaudet, J.; Rigaud, E. NVH robust optimization of gear macro and microgeometries using an efficient tooth contact model. Mech. Mach. Theory 2017, 117, 78–95. [Google Scholar] [CrossRef] [Green Version]
- Chase, N.; Rademacher, M.; Goodman, E.; Averill, R.; Sidhu, R. A Benchmark Study of Multi-Objective Optimization Methods. BMK-3021 Rev. 2009, 6, 1–24. [Google Scholar]




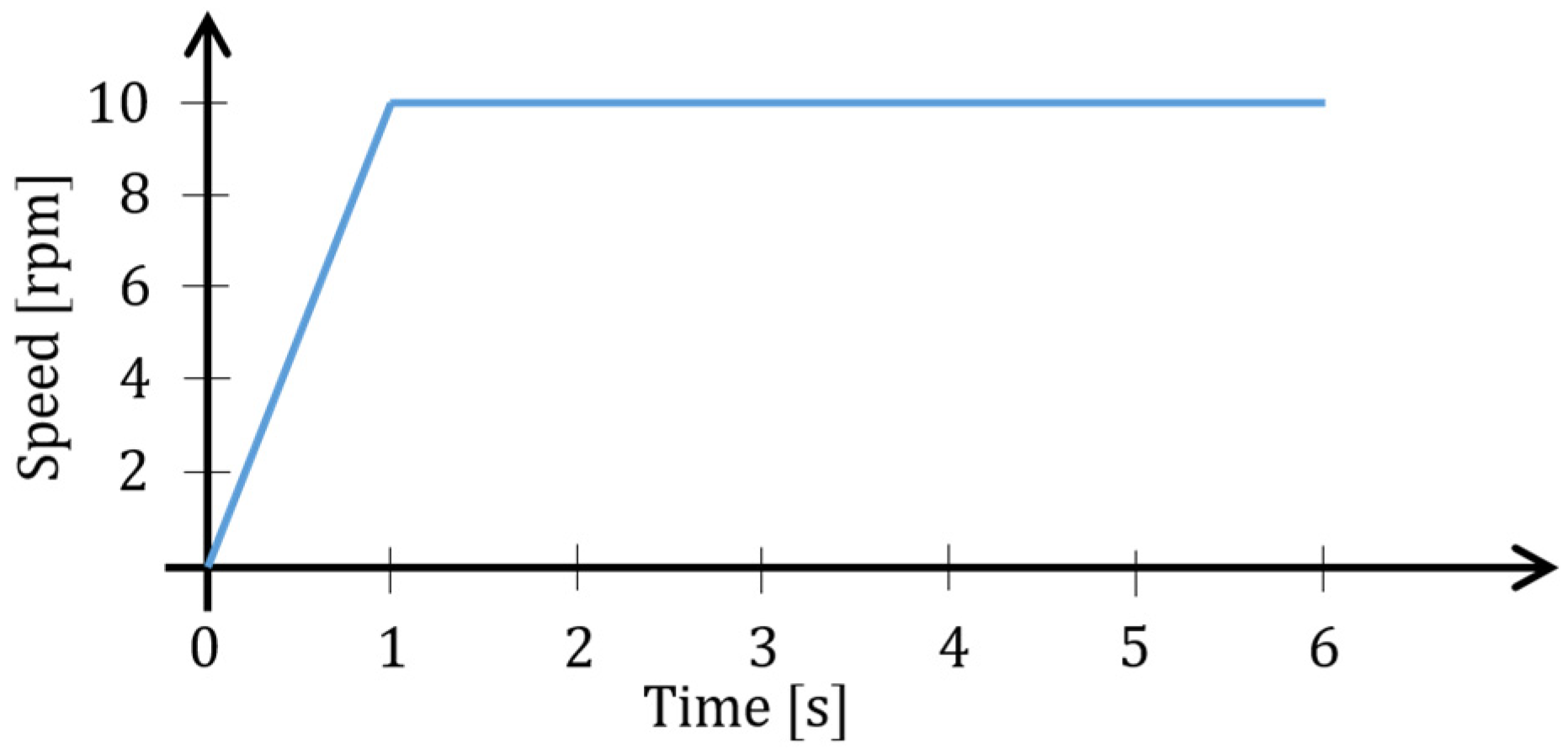
| Parameter Name | Baseline Gears |
|---|---|
| Teeth number | 40 |
| Normal module (m) | 2.5 mm |
| Normal pressure angle | 20 deg |
| Helical angle | 10 deg |
| Tooth width | 20 mm |
| Addendum | 1 |
| Dedendum | 1.25 |
| Working center distance | 101.6 mm |
| Rim width | - |
| Web thickness | 20 mm |
| Decision Variable | Min | Max | Baseline |
|---|---|---|---|
| Web thickness (mm) | 5 | 20 | 20 |
| Rim length (mm) | 36.25 | 43.75 | 43.75 |
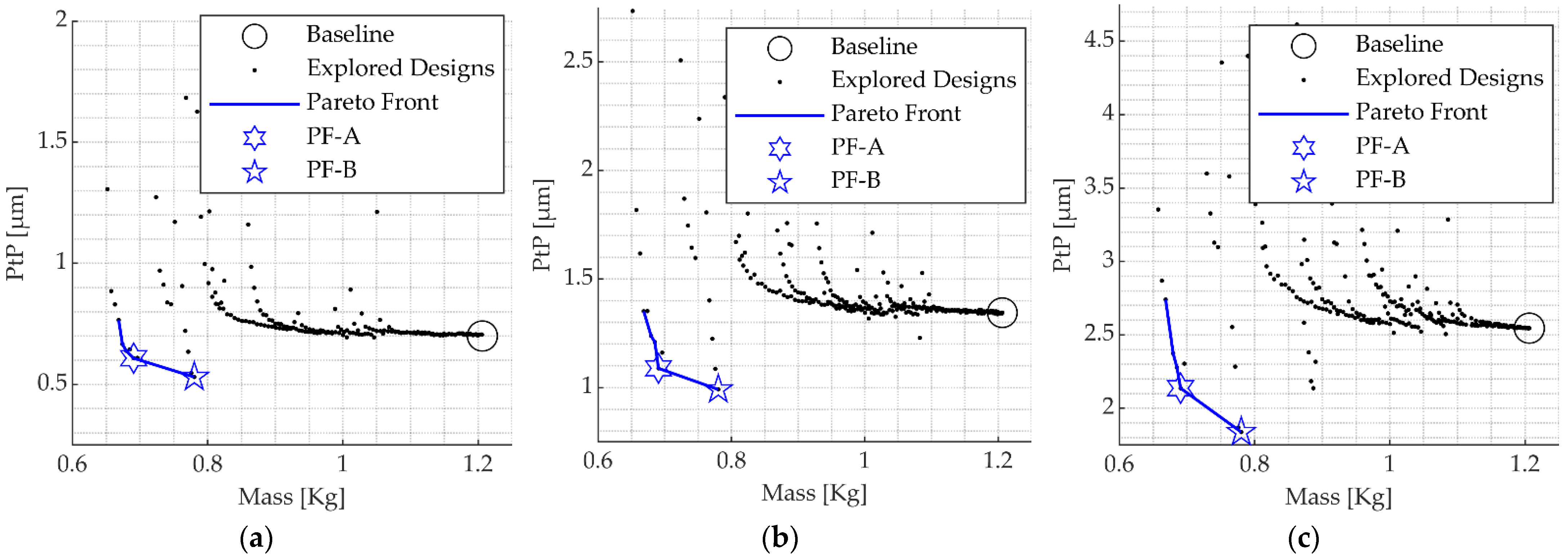
| Design Parameters | Design Goals | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Web Thickness | Rim Length | Mass | PtP | |||||||
| (kg) | (%) | 50 nm | 100 nm | 200 nm | ||||||
| (mm) | (mm) | (μm) | (%) | (μm) | (%) | (μm) | (%) | |||
| Baseline | 20 | 43.75 | 1.205 | 0.75 | 1.35 | 2.54 | ||||
| PF-A | 6.04 | 43.75 | 0.691 | −42.7% | 0.61. | −19.0% | 1.09 | −19.1% | 2.14 | −15.7% |
| PF-B | 5.60 | 40 | 0.780 | −35.3% | 0.53 | −29.3% | 0.99 | −26.3% | 1.84 | −27.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cosco, F.; Adduci, R.; Muzzi, L.; Rezayat, A.; Mundo, D. Multiobjective Design Optimization of Lightweight Gears. Machines 2022, 10, 779. https://doi.org/10.3390/machines10090779
Cosco F, Adduci R, Muzzi L, Rezayat A, Mundo D. Multiobjective Design Optimization of Lightweight Gears. Machines. 2022; 10(9):779. https://doi.org/10.3390/machines10090779
Chicago/Turabian StyleCosco, Francesco, Rocco Adduci, Leonardo Muzzi, Ali Rezayat, and Domenico Mundo. 2022. "Multiobjective Design Optimization of Lightweight Gears" Machines 10, no. 9: 779. https://doi.org/10.3390/machines10090779
APA StyleCosco, F., Adduci, R., Muzzi, L., Rezayat, A., & Mundo, D. (2022). Multiobjective Design Optimization of Lightweight Gears. Machines, 10(9), 779. https://doi.org/10.3390/machines10090779








