Optimal Design for Vibration Mitigation of a Planar Parallel Mechanism for a Fast Automatic Machine

Abstract

This work studies a planar parallel mechanism installed on a fast-operating automatic machine. In particular, the mechanism design is optimized to mitigate experimentally-observed vibrations. The latter are a frequent issue in mechanisms operating at high speeds, since they may lead to low-quality products and, ultimately, to permanent damage to the goods that are processed. In order to identify the vibration cause, several possible factors are explored, such as resonance phenomena, elastic deformations of the components, and joint deformations under operation loads. Then, two design optimization are performed, which result in a significant improvement in the vibrational behaviour, with oscillations being strongly reduced in comparison to the initial design.

1. Introduction

Parallel mechanisms were proposed in the literature for the most disparate tasks [1], since they present significant performances in terms of accuracy and rigidity, as well as the ability to operate at high speed. For fast pick-and-place operations, the problem of vibration mitigation is of paramount importance.

In this work, we analyze and optimize a planar parallel mechanism employed in a fast automatic machine. Our study is driven by the fact that the mechanism experiences vibrations of unacceptable magnitude, and we seek to mitigate this phenomenon by optimizing its design. First, we investigate the possible sources of vibrations. By using a multibody simulation software, we develop FEM-based modal and elastodynamic analyses to investigate the possible occurrence of resonance phenomena and elastic deformation of the mechanism components. We also investigate possible vibrations generated by the joint compliance. On the basis of these analyses, we mitigate vibrations by optimizing the mechanism design based on (i) reduction of the moving masses, and (ii) change of the link geometry.

The paper is structured as follows. Section 2 describes the main components of the studied mechanism and its working principle. Section 3 investigates the possible sources of vibrations through the dynamic simulation of the mechanism: in particular, modal, elastodynamic, and joint-compliance analyses are conducted. Then, Section 4 proposes two design optimizations aiming at reducing the mechanism vibrations. Finally, conclusions are drawn in Section 5.

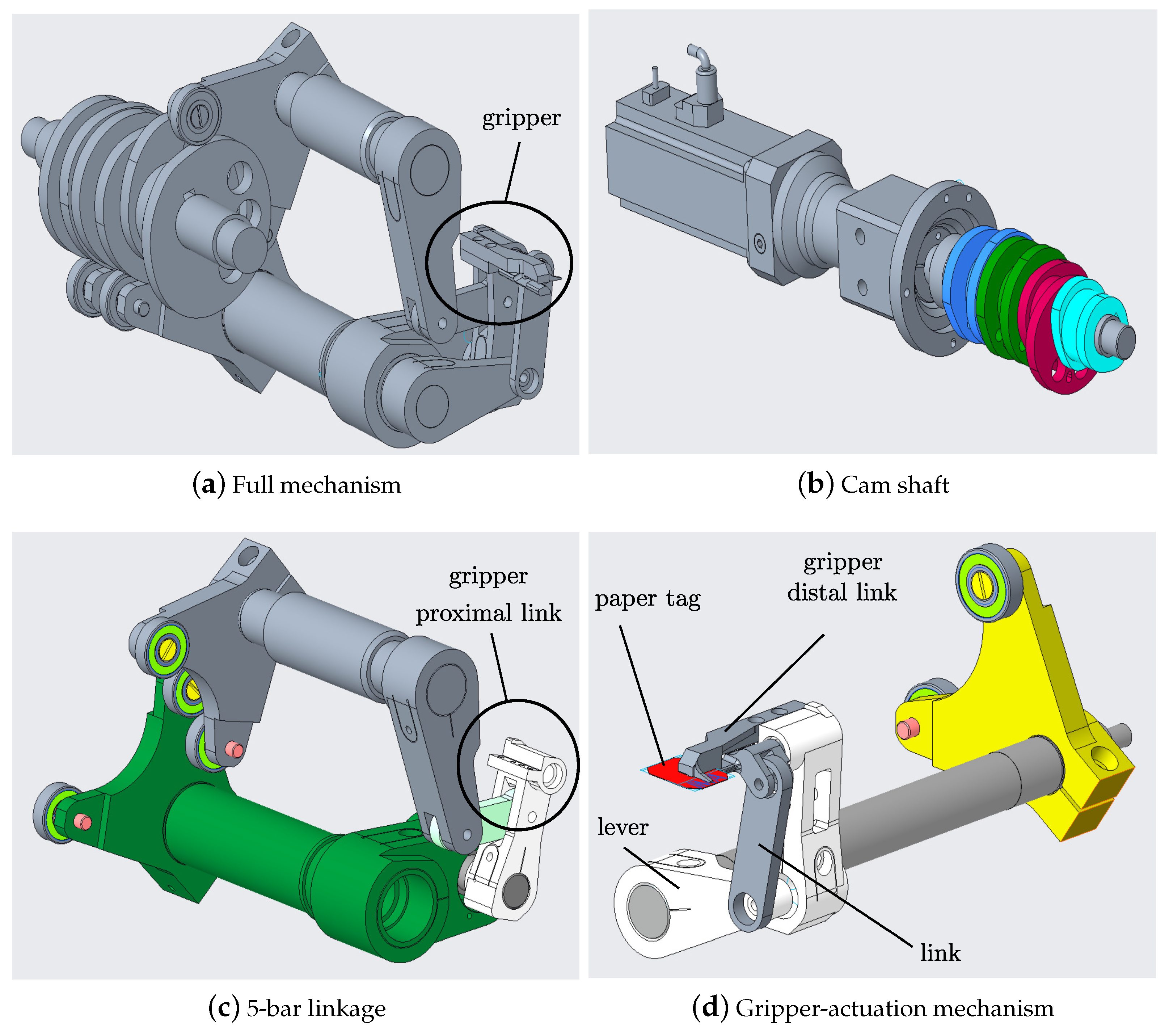
2. Mechanism Description

In this paper, we focus on the mechanism illustrated in Figure 1a, which serves as a connection between two stages of a more complex automatic machine. Paper tags are taken from the exit location of the previous machine stage by a custom gripper, and then delivered to the entry station of the next stage. Thus, the aim of the mechanism is to execute a pick-and-place task at high rate (specifically, 1000 cycles/min). In particular, since the components to be delivered are light and thin (i.e., paper tags), high accuracy is required to safely perform the pick-and-place task.

The device in Figure 1a comprises two submechanisms: one, with two degree of freedom (DoF), displaces the gripper over a plane, whereas the other actuates the gripper opening/closing motion. Despite the possibility of employing three different motors to position and actuate the gripper, a single motor rotating at constant speed is preferred coupled to a set of cams. This is mainly done because the two extreme poses of the gripper are assigned, and also to avoid motor-synchronization problems at high speed.

In order to give a detailed description of the mechanism operation, we can consider three main subgroups: a motorized shaft equipped with cams, a five-bar 2-DoF linkage, and a gripper-actuation mechanism. The aim of the cam-shaft group (Figure 1b) is to convert the continuous rotation of the electric drive to the prescribed alternate motions of a set of rocking levers. While the first set of cams is devoted to actuate the five-bar linkage, a second cam set is employed for the gripper actuation. Each cam group is made by a principal and a conjugate profile, in order to avoid the use of call-back springs. The five-bar mechanism is used to displace the gripper between two assigned locations (Figure 1c). Two levers receive the alternate motion from the first cam group and, by means of two shafts, actuate the five-bar input links. The five-bar is composed of four mobile aluminum members connected by revolute joints, and the distal end of a member serves as a proximal link of the gripper (see Figure 1c) Finally, the gripper-actuation subgroup (Figure 1d) receives actuation by a cam through another lever and a shaft. The latter rotation actuates a leverage that displaces the distal link of the gripper; the movement of the lever combined with that of the proximal link enables the closing/opening motion that allows paper tags to be grasped.

Given the required high production rate, and the light weight of the products to be handled (a few grams), the accuracy of the pick-and-place task must be relevant. The mechanism is supposed to operate among the two poses depicted in Figure 2. For each rotation of the main motor shaft, the working cycle of the mechanism can be summarized as follows:

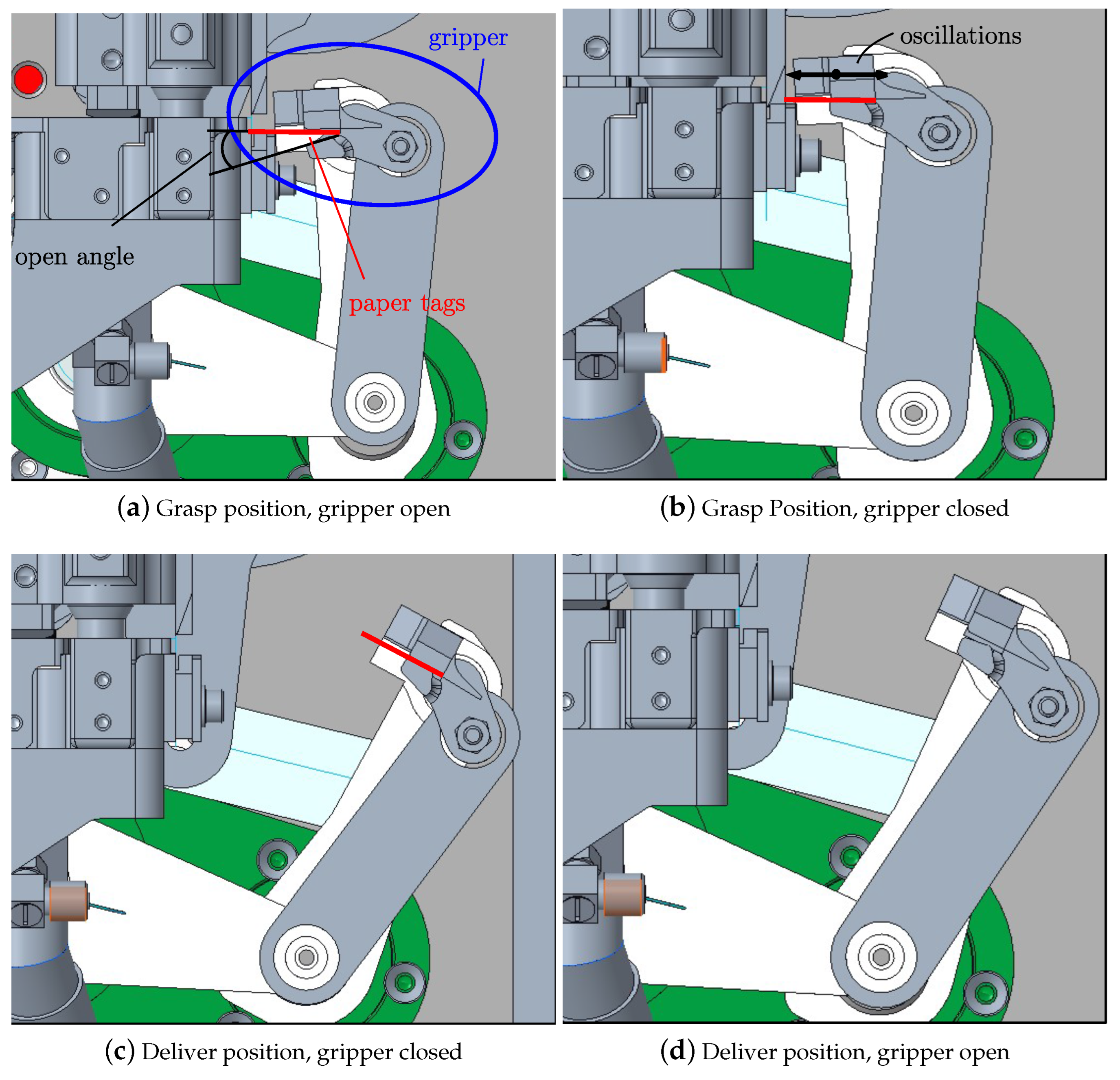
• The gripper is positioned at the grasp position (Figure 2a) and it is open, waiting for paper tags to be received;
• Once a paper tag is available, the gripper closes and the product is grasped thanks to the movement of the gripper-actuation mechanism (Figure 2b);
• The gripper moves to the deliver position (Figure 2c) thanks to the movement of the five-bar linkage;
• At the deliver position, the gripper opens and the product is released (Figure 2d);
• The gripper moves back to the grasp position and the cycle restarts.

The mechanism operation was monitored at its nominal production rate of 1000 cycles/min, and oscillations were experimentally observed when the gripper was at the grasp position (Figure 2a), where on the contrary it was supposed to remain still. Oscillations were measured to reach an amplitude of 1 mm, which is unacceptable for the quality standards of the products that are to be delivered. In the next section, we investigate the possible causes of such vibrations.

3. Dynamic Analysis

The main aim of this section is to identify the possible causes of the vibratory phenomena observed in the real mechanism. We start from a rigid-body dynamic simulation of the five-bar mechanism, and then we carry out a modal analysis to explore possible resonance phenomena. Then, the flexibility of the system is taken into account by performing an elastodynamic simulation of the parallel linkage. Finally, we investigate the compliance of the base joints and possible solutions.

3.1. Rigid-Body Dynamic Analysis

The first step toward the identification of the vibration cause is the computation of the ideal behavior of the system. This is performed by developing a rigid-body dynamic analysis where, for a given input of the motor, we identify the position, velocity, and accelerations of each component of the system.

At this stage, we focus on the five-bar mechanism illustrated in Figure 3, and we consider the angles ${\theta }_1,{\theta }_4$ provided by the cams as assigned inputs. By assuming all components as rigid, the closure-loop equations of the five-bar linkage can be solved to obtain the theoretical location $x,y$ of the gripper reference point E, and the intermediate angles ${\theta }_2,{\theta }_3$. Then, the velocities and acceleration of each component of the five-bar may be determined by the solution of the velocity/acceleration linear systems obtained by successive derivation of the closure-loop equations for given velocities ${\dot{\theta }}_1,{\dot{\theta }}_4$ and accelerations ${\ddot{\theta }}_1,{\ddot{\theta }}_4$. By knowing the mass distribution of each component, the inverse dynamic problem can then be solved to obtain the joint reactions that stress the system, as well as the actuation actions. By employing the Newton–Euler approach [2], unknown reaction forces are introduced at each joint of the mechanism. Then, the dynamic equilibrium of the forces and couples is established for each mechanism member. The corresponding equations can be written as a linear system of the form:

$$\mathbf{A}\mathbf{F}=\mathbf{B}$$

(1)

with $\mathbf{F}$ being the vector of unknown joint reaction forces and actuation actions, $\mathbf{B}$ a known term including inertial and Coriolis effects, and $\mathbf{A}$ a matrix that collects the coefficients that multiply the unknown force array $\mathbf{F}$. These coefficients, which depend on the mechanism configurations, can be obtained by the solution of the kinematic problem.

The inverse dynamic problem is solved by a multibody simulation software (ANSYS), where all the components are modeled as rigid, and friction is disregarded. Revolute joints model the bearings that support the rotating shafts and the hinges between components, whereas ideal contact constraints are used to simulate the cam-lever motion transmission. As a result of the simulation, we obtain the position, velocity, and acceleration of each body, as well as joint reactions. As an example, the magnitude of the base reaction ${\mathbf{F}}_0$ for a single cycle, which will play a crucial role in the mechanism optimization, is depicted in Figure 4.

3.2. Modal Analysis

Modal analysis is the process of determining the dynamic properties of mechanical systems in the form of natural frequencies and/or mode shapes [3]. When a system is excited or it is working close to one of its natural frequencies, resonance occurs and the system may display large vibrations.

In general, two different approaches are employed for modal analysis: numerical simulations and experimental analysis [3]. When a mechanism is subjected to a known external excitation, frequency response functions can be experimentally measured to obtain the natural frequencies and mode shape characteristics of the system. However, this approach generally requires complex measurements that may not be easily carried out in a complex machine. On the opposite, numerical simulations aim at predicting the dynamic behavior of the system by the use of a mathematical model [4]. In this context, the finite-element method is commonly used to derive the model of complex systems such as parallel mechanisms, leading to an eigenproblem in the form:

$$\left(\mathbf{M}-{\omega }_j^2\mathbf{K}\right){\varphi }_j=\mathbf{0}$$

(2)

where $\mathbf{M}$ is the mass matrix, $\mathbf{K}$ is the stiffness matrix, ${\omega }_j$, and ${\varphi }_j$ are the natural frequency and the vibration mode associated to the j-th resonance, respectively.

In order to investigate the possible occurrence of resonance, we considered the mechanism at the grasp configuration (Figure 2a), where oscillations were measured. The full mechanism is discretized according to the finite-element approach. The coupling between the mechanical components is modeled in the same fashion as in rigid-body simulation: revolute joints represent bearings and rotative connections between links, and contact joints represent the motion transmission by cams. Damping is assumed to be negligible. The material properties are those of aluminum components, and solid elements are used to discretize the geometry. The number of elements is gradually increased until convergence is achieved, and the final discretization is represented in Figure 5. The finite-element discretization and the modal analysis are performed in a multibody simulation software (ANSYS), and the first six natural frequencies associated with vibration modes are reported in

Table 1. Natural frequencies associated with the first six resonance modes.

Mode Number	Frequency [Hz]
1	463.52
2	596.44
3	695.68
4	866.64
5	1182.60
6	1269.10

. By inspection of mode shapes, only the first two correspond with the vibratory phenomena that were experimentally observed, and these two modes have frequencies considerably distant from the frequencies that excite the system. Therefore, we can assume that the oscillations of the gripper are not caused by resonance phenomena.

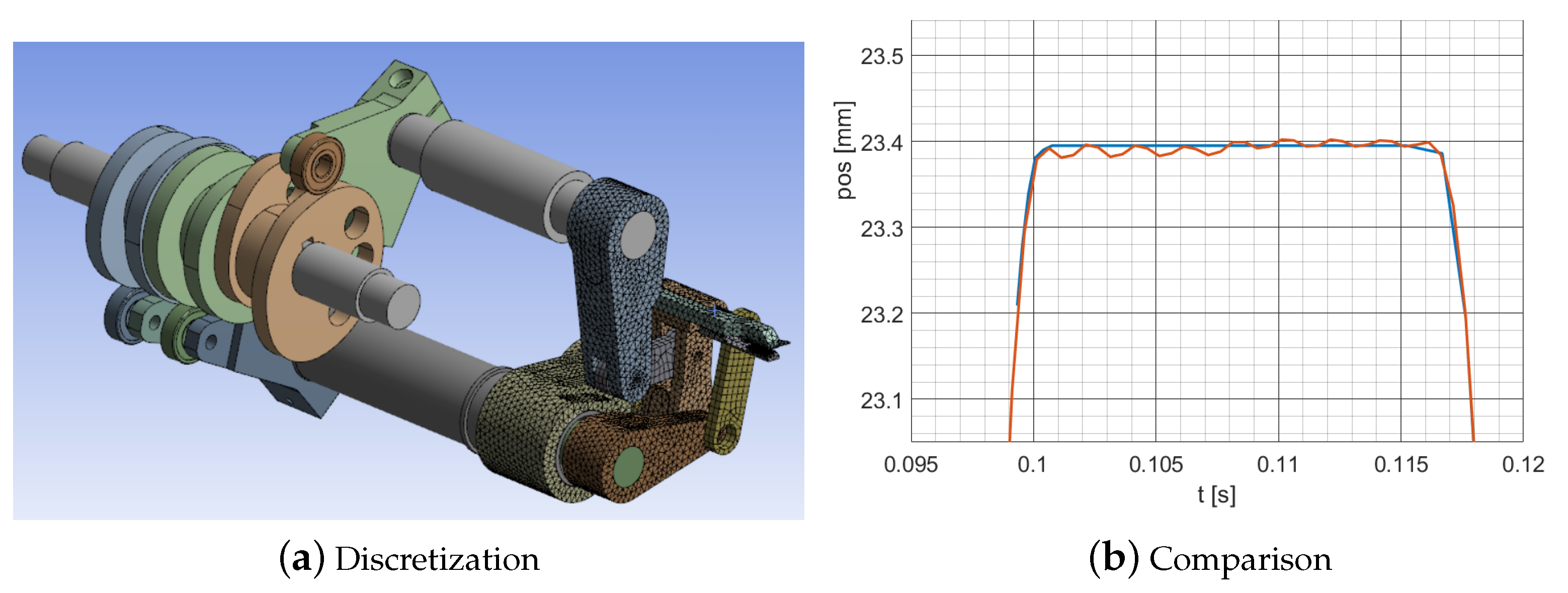
3.3. Elastodynamic Simulation

A typical cause of oscillations in mechanisms working at high frequency is the intrinsic elasticity of their components. In order to reduce the high inertial forces and actuation torques required to operate at high speed, mechanisms for fast-operating machines are usually made as lightweight as possible. However, light members generally bring reduced stiffness and elastic deformations may occur. The performance of the mechanism, in terms of position accuracy, may consequently be reduced by elastic oscillations.

While rigid simulations play a dominant role in the design and synthesis of standard mechanisms, elastodynamic simulations are usually performed when the operating speed is relevant, and the influence of the component elasticity is not negligible [5]. Continuous elastic systems and lumped parameter models aim at finding approximate solutions in reduced computational time [6]. On the other hand, the finite-element method [7,8] provides a more general and accurate modeling technique for complex mechanisms, and the resulting dynamic model is a set of differential equations that can be formulated as:

$$\mathbf{M}\ddot{\mathbf{q}}+\mathbf{C}\dot{\mathbf{q}}+\mathbf{K}\mathbf{q}=\mathbf{f}$$

(3)

where $\mathbf{q}$ is the vector of the nodal coordinate of the discretized system, $\mathbf{C}$ is the compliance matrix, and $\mathbf{f}$ is the vector of external forces. Thus, by the numerical integration of Equation (3) over a defined temporal interval, the position, velocity, and acceleration of each member of the mechanism can be evaluated with the inclusion of elastic effects.

In this work, we used the finite-element approach to investigate the effect of elasticity on the vibrations of the mechanism. Despite the possibility of considering the elasticity of all members of the mechanism, in order to reduce the computational cost, we decided to evaluate the influence of the five-bar linkage deformations only, and to assume the other components as rigid. This decision is mainly driven by the considerable computational time needed to achieve accurate solutions if the full mechanism is discretized. Solid elements are employed to discretize the five-bar mechanism, and the resulting discretization is displayed in Figure 6a. As for the modal analysis, the number of elements is gradually increased to achieve convergence of the numerical results. Because of the high speed of the mechanism, the material damping is assumed to be negligible. The mechanism is simulated for a single cycle at the operating speed of 1000 cycles/min. At the end of the simulation, we compare the displacement of the gripper between the theoretical position given by a rigid simulation, and the prediction of the elastic model. As shown in Figure 6b, slight oscillations are predicted by the flexible model, with an amplitude on the order of 0.02 mm. We can consequently assume that the cause of the vibrations is not the elasticity of the system, since the predicted amplitude is significantly different from the measured displacement of 1 mm.

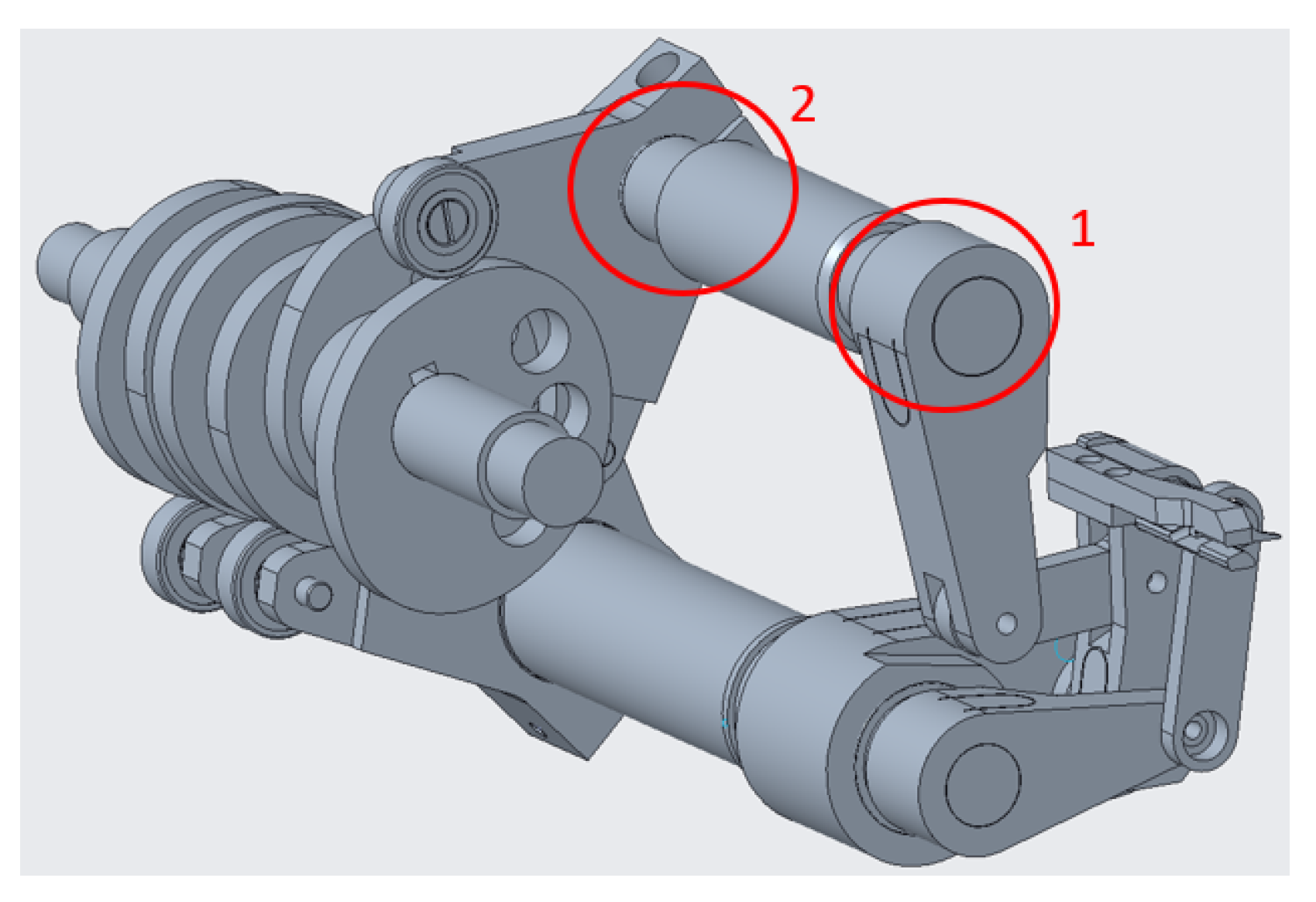
3.4. Joint Stiffness and Possible Solutions

Joint clearance and deformation under external load is a known cause of oscillations, especially for high-speed mechanisms [9].

The influence of joint clearance and deformation under external loads can be numerically evaluated by establishing the kinetostatic model of each joint affected by clearance/deformation, and then evaluating the corresponding effect on the mechanism end-effector [10]. However, in this work, we are interested in understanding if joint compliance is the source of the experimentally-measured vibrations, and then mitigating such oscillations. As shown in Ref. [11], vibrations induced by such phenomena are mainly governed by the entity of the joint clearance, the magnitude of forces that act on the joint, and the joint stiffness.

In comparison to complex mathematical models, a more practical way to evaluate if joint deformation may influence the mechanical behavior is to stress the mechanism in static configuration with loads corresponding to the operating efforts, and experimentally measure if joint displacements are relevant.

To this purpose, the five-bar linkage was statically positioned in the grasp configuration, and by means of a dynamometer we applied to joint A (see Figure 3b) an external load that corresponds to the peak load simulated during the rigid-body analysis described in Section 3.1. When this load was statically applied, we measured joint displacements of 0.020 mm and 0.050 mm at points 1 and 2 of Figure 7, respectively. These deformations may significantly influence the behavior of the system at the nominal speed of 1000 cycles/min. A possible solution aims at increasing the joint stiffness, which requires the re-design of the base joints. However, due to the high complexity and interconnection of the whole machine, we preferred to aim at a force magnitude reduction by introducing modifications to the five-bar mechanism only.

4. Optimization

In this Section, we discuss two possible strategies that aim at reducing the gripper oscillations. Since we consider the base joint deformation under operative loads as the cause of vibrations, we seek at reducing the base reaction force ${\mathbf{F}}_0$. Additional changes in the overall mechanism may be considered, but we limit ourselves to modifications of the five-bar only, to reduce the cost of the intervention. First, we discuss an iterative optimization process that reduces the base reaction magnitude by reducing the overall moving mass of the parallel linkage. Then, a second optimization is proposed where the lengths of the five-bar links are varied to reduce the base joint efforts.

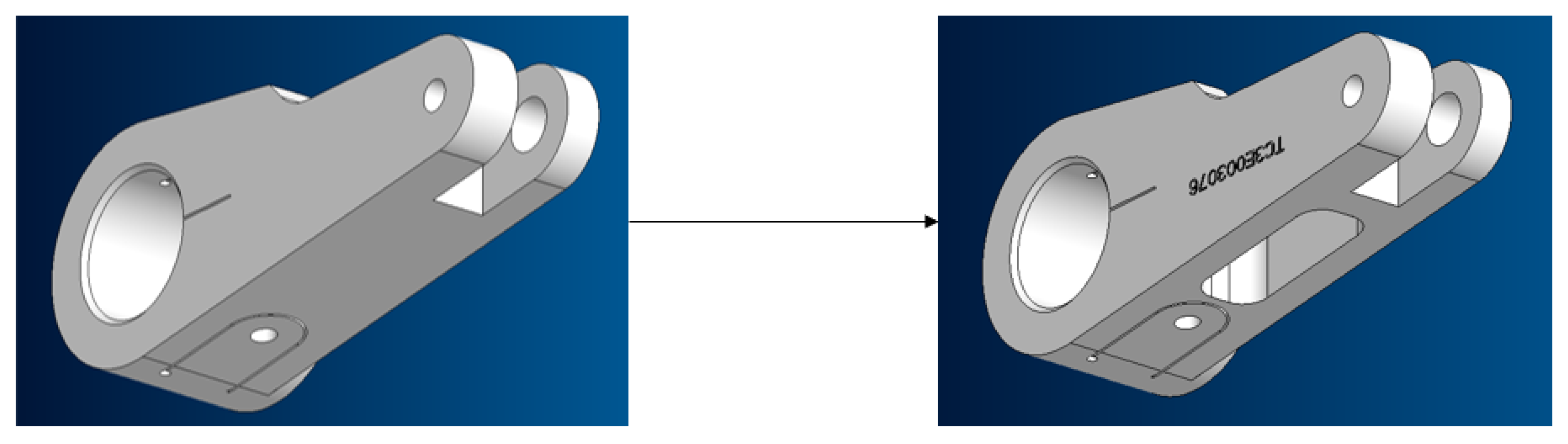
4.1. Mass Reduction

In parallel mechanisms working at high speed, the main source of stress on components is given by their own inertial effects. Thus, it is legitimate to assume that a reduction of the overall moving masses may reduce the base joints reaction and, consequently, reduce the gripper vibrations.

Topology optimization can be a solution to reduce the mass of each component by reallocating the material only where needed [12]. In topology optimization, a mathematical method is employed to optimize the distribution of the material in a finite domain, while satisfying the given constraints. Usually, based on the constrained minimization of a cost function, the main steps of topology optimization requires the identification of design variables, the cost function, and the constraints to be satisfied. However, the result of topology optimization frequently conducts to components with highly complex geometries, which can be difficult to realize with traditional tools or which requires long production times.

A more practical solution is to directly modify the existing components, in order to save production time and to keep modifications to a minimum. In this way, simple mechanical modifications can be carried out to remove material on the components (e.g., drilling, holes, chambers, as shown in Figure 8). However, these modifications influence the dynamic properties of the system, and verifications are required to check if the mechanism performance is not deteriorated. To do that, an iterative process can be set up, as follows:

• Each five-bar linkage component is manually modified with simple geometry modifications;
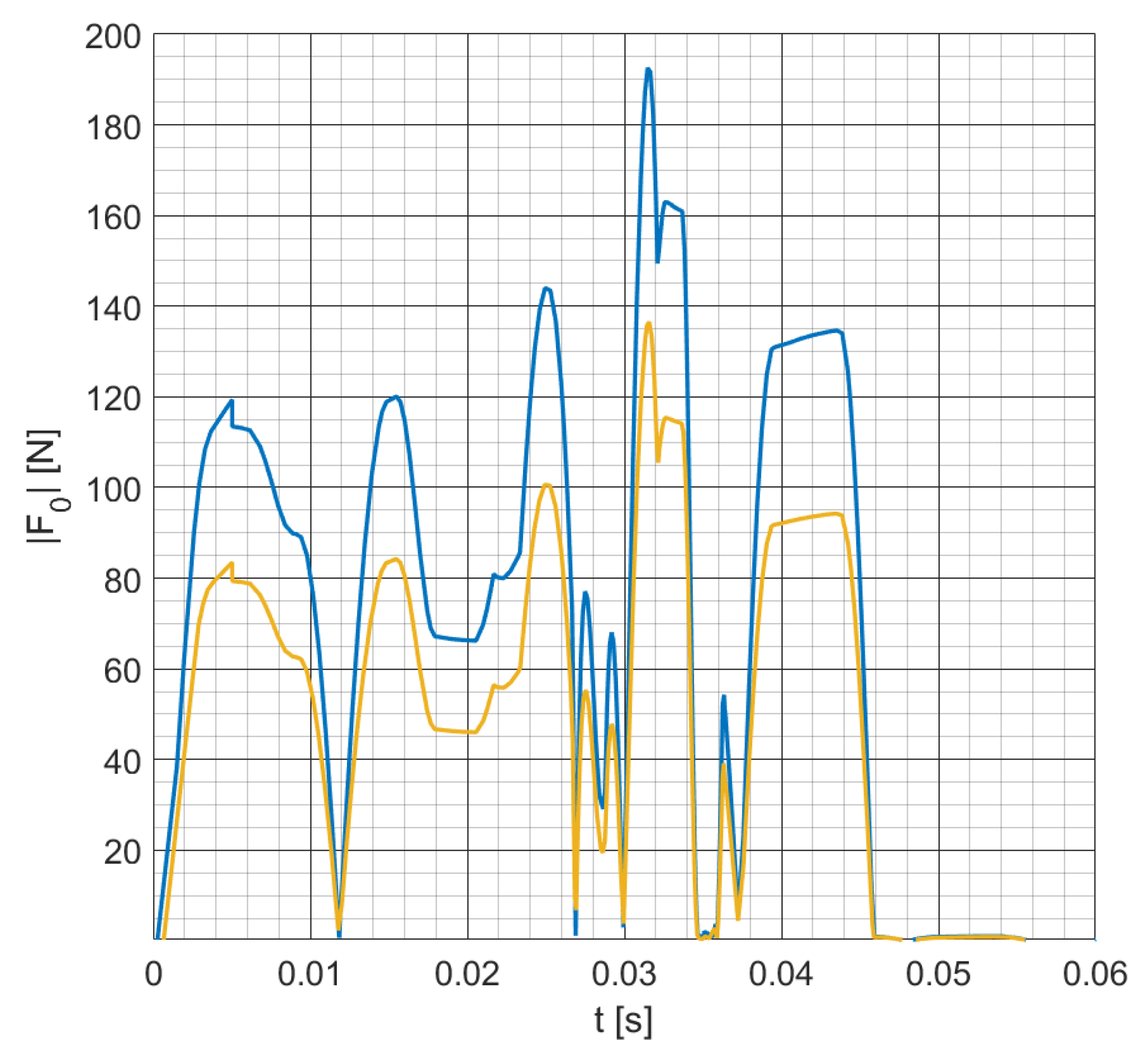
• The modified mechanism is rigidly simulated by means of a multibody simulation software (ANSYS) in order to calculate the reaction force that acts on each joint;
• Then, each link is independently simulated by taking into account its elasticity to estimate the corresponding deformations. Despite the possibility of simulating the overall system in a single time, we preferred to independently verify each component to reduce the simulation time;
• If deformations are negligible, the process continues;
• Modifications are repeated until the base force reaches a sufficiently low value.

We performed the previously described iterative process on the five-bar linkage. Starting from an initial mass of the mechanism of 0.460 kg, a 19% reduction is obtained with a corresponding final mass of 0.373 kg. Then, a rigid dynamic simulation is performed to quantify the joint load reduction, whose magnitude is displayed in Figure 9 and compared with the original values. The peak magnitude of ${\mathbf{F}}_0$ is reduced by roughly 30%, passing from 230 N to 160 N.

Before manufacturing the mechanism, several tests were conducted to verify that other issues were not introduced. Firstly, a modal analysis was conducted and we verified that no resonance was excited. Then, a flexible dynamic simulation was performed, and oscillations were predicted with a magnitude of 0.02 mm, as in Section 3.3. Finally, the real mechanism was manufactured and tested at nominal working conditions of 1000 cycle/min. Oscillations were observed with a magnitude of 0.3 mm, thus significantly smaller that the original ones.

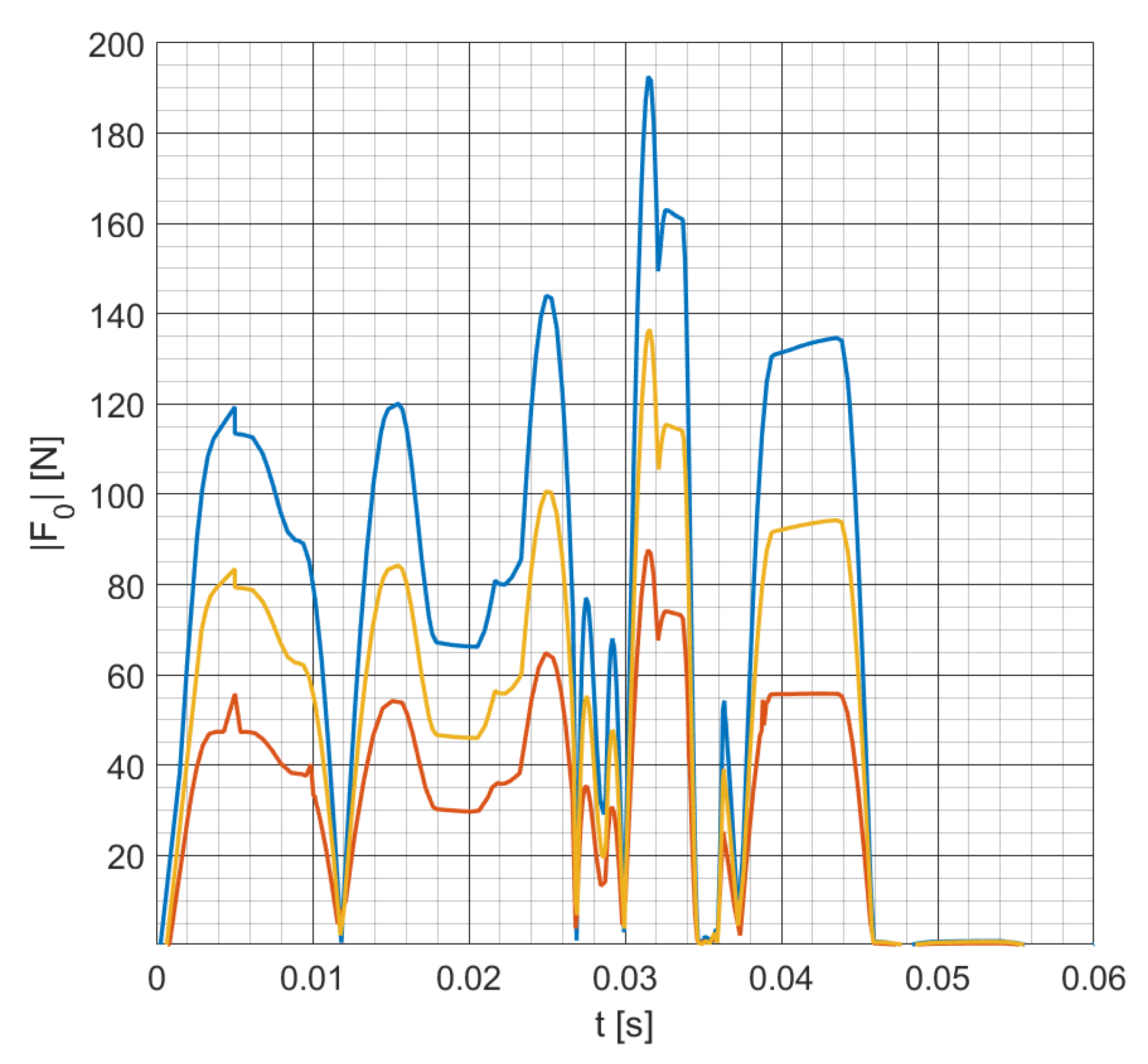
4.2. Dimension Optimization

Oscillations were drastically reduced by designing a lighter mechanism. However, the presence of residual vibrations can still be an issue, which may cause early wear. Therefore, we tried to further reduce the vibrations of the gripper at its grasp configuration.

In general, all lengths of the five-bar components can be varied to minimize the base reaction forces. This may lead to a constrained optimization problem where we seek to minimize the base force reactions while preserving the original trajectory of the gripper. Optimality conditions may be formally derived, and the optimization problem may be solved by numerical schemes. However, the modification of links 3 and 4 would also require the re-design of the gripper actuation mechanism, with further cost and production time.

Therefore, we proceeded in a different direction, by considering links 3 and 4 as assigned, and consider as design variables the lengths $l_1,l_2$, and the placement of the joint B over link 3 defined by the distance $l_B$ (see Figure 3b). Due to mechanical limitations of the available space, $l_1,l_2,l_B$ can be chosen with predefined boundaries. Since the number of design variables is limited to 3, we decided to simply sample the design space at uniform steps and to select the triplet $l_1,l_2,l_B$ that ensures the minimum magnitude of the base joint reaction ${\mathbf{F}}_0$, among the design set. In particular, the optimization process is carried out as follows.

• Considering the initial design, we extracted the joint values ${\theta }_3,{\theta }_4,{\dot{\theta }}_3,{\dot{\theta }}_4,{\ddot{\theta }}_3,{\ddot{\theta }}_4$ for a single cycle;
• Then, we studied the five-bar mechanism by considering joints Q and C in Figure 3b as motorized. Since the motion of the kinematic chain $QCE$ is not varied in comparison to the original design, the $x,y$ trajectory of the gripper is preserved;
• By the solution of the inverse dynamic problem with new inputs, we can recover the new joint values, and the joint reactions.

The aforementioned design optimization is performed by means of a custom Matlab code, where the inverse dynamic problem is solved for each sample of the design variables. The design space is defined as $l_1\in [61,85]$ mm, $l_2\in [48,60]$ mm, $l_B\in [41,65]$ mm, and the lengths are explored with a 1 mm sampling. At the end of the design optimization, the optimal triplet is identified as $l_1=71$ mm, $l_2=48$ mm, $l_B=65$ mm. In particular, the peak value of the ${\mathbf{F}}_0$ magnitude is reduced to 118 N (Figure 10), which corresponds to a reduction of 49% with respect to the 230 N of the initial mechanism.

Before prototyping the mechanism, several tests were conducted to exclude the presence of other issues. Modal analysis resulted in no natural frequencies excited, and a flexible dynamic simulation predicted negligible vibrations due to the elasticity of the components. Finally, the mechanism was manufactured and monitored at its nominal speed of 1000 cycle/min: no vibration was observed at all.

5. Conclusions

In this work, we investigated the vibration phenomena of a planar parallel mechanism for application in a fast-operating industrial automatic machine. We firstly investigated the possible sources of vibrations, by excluding the presence of resonance phenomena, and oscillations inducted by the intrinsic elasticity of components. We identified as the cause of vibrations the deformation that occurs at the base joints during the operation at the nominal speed. Then, in order to reduce vibrations, two optimization approaches were conducted to reduce the loads that act on the base joints. By reducing the overall mass of the mechanism, the vibrations were strongly reduced. Then, a second optimization was carried out by modifying links lengths, achieving a further reduction of vibrations up to negligible values.