Investigation on the Cage Whirl State of Cylindrical Roller Bearings under High Speed and Light Load

Abstract

This paper explores the cage whirl state under different operating conditions based on the cylindrical roller bearing dynamics model. The stability and whirl characteristics of the cage whirl are evaluated by considering the rotation and force of the cage and roller. The results demonstrate that the cage whirl state is divided into three types according to the cage whirl orbit: disordered whirl, local periodic whirl and regular circular whirl. With disordered whirl, the whirl speed and whirl radius of the cage are unpredictable, and the force of the cage changes frequently. With local periodic whirl, the rotation speed, whirl speed and the force on the cage change periodically or stay constant. In the case of a regular circular whirl, the force on the cage should be considered to evaluate the stability of the cage whirl. In addition, the collision force between the roller and cage determines whether the cage whirl speed is stable or not, and the bearing slipping has no obvious effect on cage whirl stability.

1. Introduction

A cage is a component of a rolling bearing, which is the most complicated component subjected to force. It not only distributes the roller evenly but also guides the roller movement in the unloaded area. Since the cage is subject to frequent collisions in operation, the cage mass center will be offset relative to the bearing center. This motion is called the cage whirl. The cage mass center eddy state can evaluate the running stability of the cage, which helps to reduce the risk of cage failure.

The cage whirl state is a comprehensive representation of the force and motion of the cage; Figure 1 shows the cage whirl diagram. Here, $\left\{O;X,Y,Z\right\}$ represents the bearing’s global coordinate system, $\left\{O_c;X_c,Y_c,Z_c\right\}$ represents the cage coordinate system, $O$ and $O_c$ are the mass center mass of the bearing and cage, respectively, $P$ is the point on the cage, and $S$ is the mass center of the rolling element. $\alpha$ is the deflection angle of the cage mass center, $\beta$ is the position angle of the cage, and $\gamma$ is the position angle of the rolling element.

Kingsbury [1] first discovered that cage whirl affects the torque of angular contact ball bearings and proposed the cage whirl model (squeal model). The author characterized three cage whirl states, which are:

• Synchronous whirl. If the cage whirl speed is equal to the outer ring speed, then the position of the cage mass center and the outer ring center mass center are the same. If the outer ring is stationary, the cage center position is fixed at one point; if the outer ring is rotating, the cage mass center does a circular whirl. This situation is caused by the unbalance of the outer ring and only occurs under light load conditions;
• Stable whirl. If the cage whirl speed is equal to the cage rotation speed (rolling elements rotational speed), then the cage mass center around the bearing mass center does a circular whirl;

Figure 1. Schematic diagram of cage whirl.

Figure 1. Schematic diagram of cage whirl.

Ball-jump whirl. There is a deviation between the cage whirl speed and the cage rotation speed, which is much smaller than the cage rotation speed. The deviation is related to the collision frequency between the cage and the guide ring. Since then, more scholars have paid attention to cage stability and conducted related research. Gupta [2,3,4,5,6] established a six degrees of freedom dynamics model for rolling bearings to study the effects of factors on the dynamic characteristics of the cage under high speed and light loads, such as cage clearance ratio, cage guidance method and load type. In addition, he evaluated the operational stability of the cage according to whether the cage wear amount reached a stable value. Kingsbury et al. [7] regarded the cage as a rigid body and considered the geometric and frictional coupling between the pocket hole and the rolling body to reveal the mechanism of angular contact ball-bearing cage whirl generation. Niranjan et al. [8] found that when the cage clearance ratio is less than 1 and the radial clearance is small for the cylindrical roller bearings, the cage whirl orbit is regularly circular. Increasing or decreasing the diameter of one rolling element can destabilize the cage and lead to intermittent and substantial collision forces between the cage and guide ring. SolJi Ryu et al. [9] monitored the acoustic vibration of deep groove ball-bearing cage operation under rich/spent oil and used it to evaluate the cage stability. They discovered that the cage operation was more stable under oil-rich conditions. Zhang et al. [10] analyzed the cage whirl orbit of cylindrical roller bearings under four types of lubricants. They applied the cage mass center nonlinear whirl cycle to evaluate the cage operational stability and finally recommended the type of lubricant to be used at different speed loads. Niu et al. [11] compared the forces on the cage during steady and unsteady operation, including the cage centrifugal force, the contact force and friction between the rolling elements and pockets, and the contact force and friction between the cage and guide ring. The authors explored the forces affecting and maintaining the whirl radius and whirl speed of the cage mass center and found that the uneven distribution of rolling elements characterized the stable cage whirl. Takashi et al. [12] classified the stable cage operation into two categories. One is where the cage whirl speed is the same as the rotation speed, and the other is where the amplitude of cage deflection is less than the cage guide clearance. The authors analyzed the influence of the friction coefficient on the cage whirl stability and proposed a formula for calculating the critical friction coefficient of the cage whirl. Niu et al. [13,14] found that the corrugation of the raceway and the unbalanced quality of the cage will increase the collision force between the rolling elements and pockets, which will intensify the cage wear and decrease the stability of the cage whirl. Arya et al. [15] compared the whirl stability of brass, plastic, and steel cages. The results indicated that brass cages had the most stable whirl, plastic cages had the most circular whirl orbit, and steel cages had the largest collision force between rolling elements and pockets. Liu et al. [16,17,18] found that high-speed cylindrical roller bearings with spherical pockets and V-shaped pockets can not only decrease the cage slip rate but also improve the stability of the cage whirl. Gao et al. [19,20] investigated the effect of pocket shapes and different combinations of pocket shapes on the cage whirl stability of angular contact ball bearing. The results showed that the cage whirl radius with a spherical pocket was equal to half of the pocket clearance, and those with a combined pocket shape had a smaller whirl radius than those with a single pocket shape.

In summary, many scholars have studied the mechanism and influencing factors of rolling bearing cage whirl, particularly for angular contact ball bearings. For cylindrical roller bearings, the existing research on cage whirl stability is generally based on the Kingsbury angular contact ball bearing cage vortex model, but the whirl model of cylindrical roller bearing cage has not been explored in detail. This paper investigates the cage whirl stability of cylindrical roller bearings under high speed and light load based on Gupta’s dynamics model. Four different cage mass center whirl orbits are obtained by changing the operating parameters of the bearing, and the whirl radius and whirl speed corresponding to each whirl orbit are compared. Further, the cage whirl stability is evaluated by combining the cage force characteristics, such as the contact force between the cage and rolling elements or guide ring.

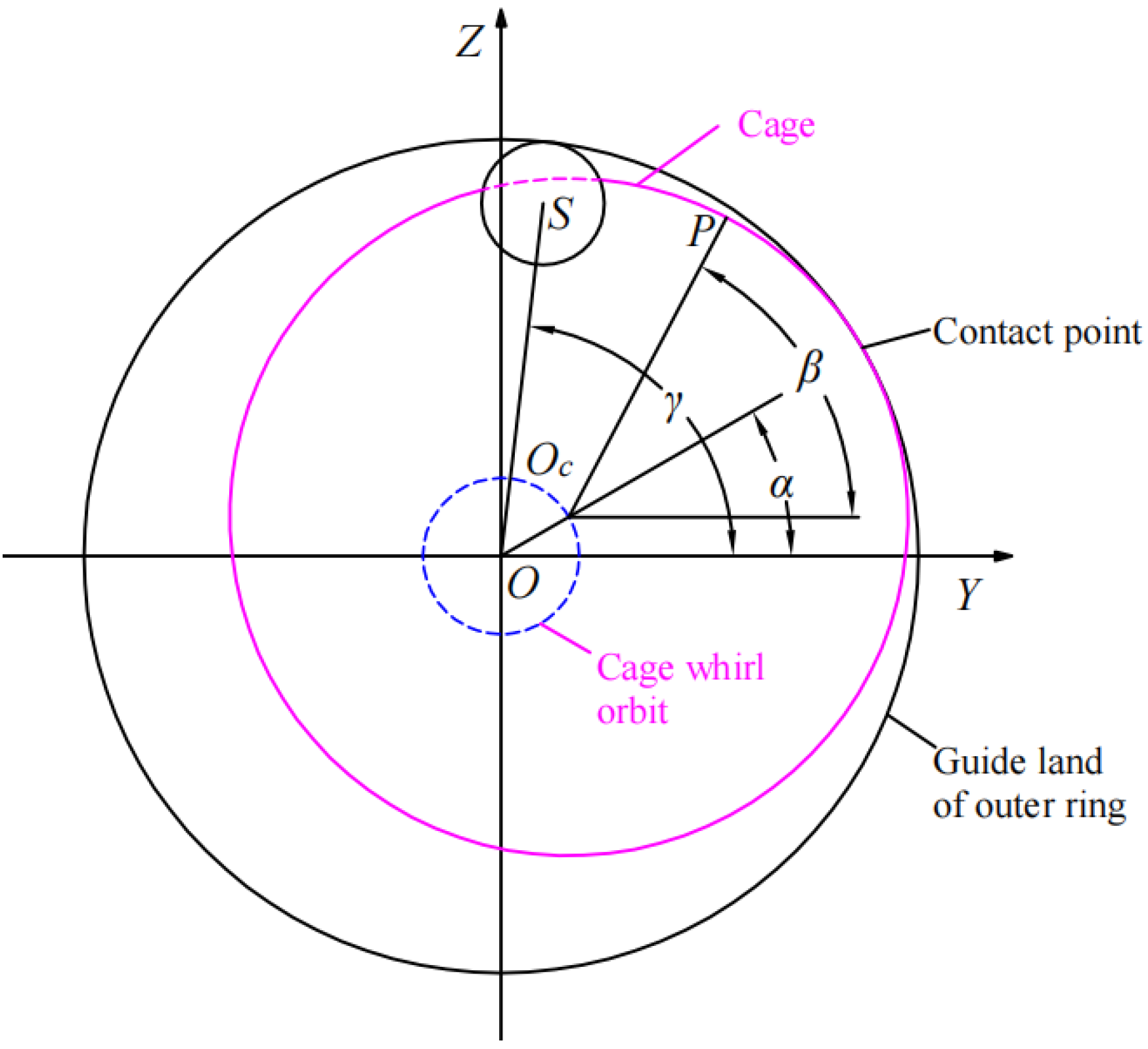
2. Model Description and Verification

2.1. Bearing Structure Parameters

The object of investigation is an NU1007 cylindrical roller bearing, which has a fixed outer ring and a rotating inner ring. Some structural parameters are shown in

Table 1. Some structural parameters of the bearing.

Structural Parameter	Value	Structural Parameter	Value
Inner diameter	35 mm	Roller number	16
Outer diameter	62 mm	Roller diameter	6.5 mm
Bearing width	14 mm	Roller length	6.5 mm
Guide method	Outer ring	Guide clearance	0.2 mm

.

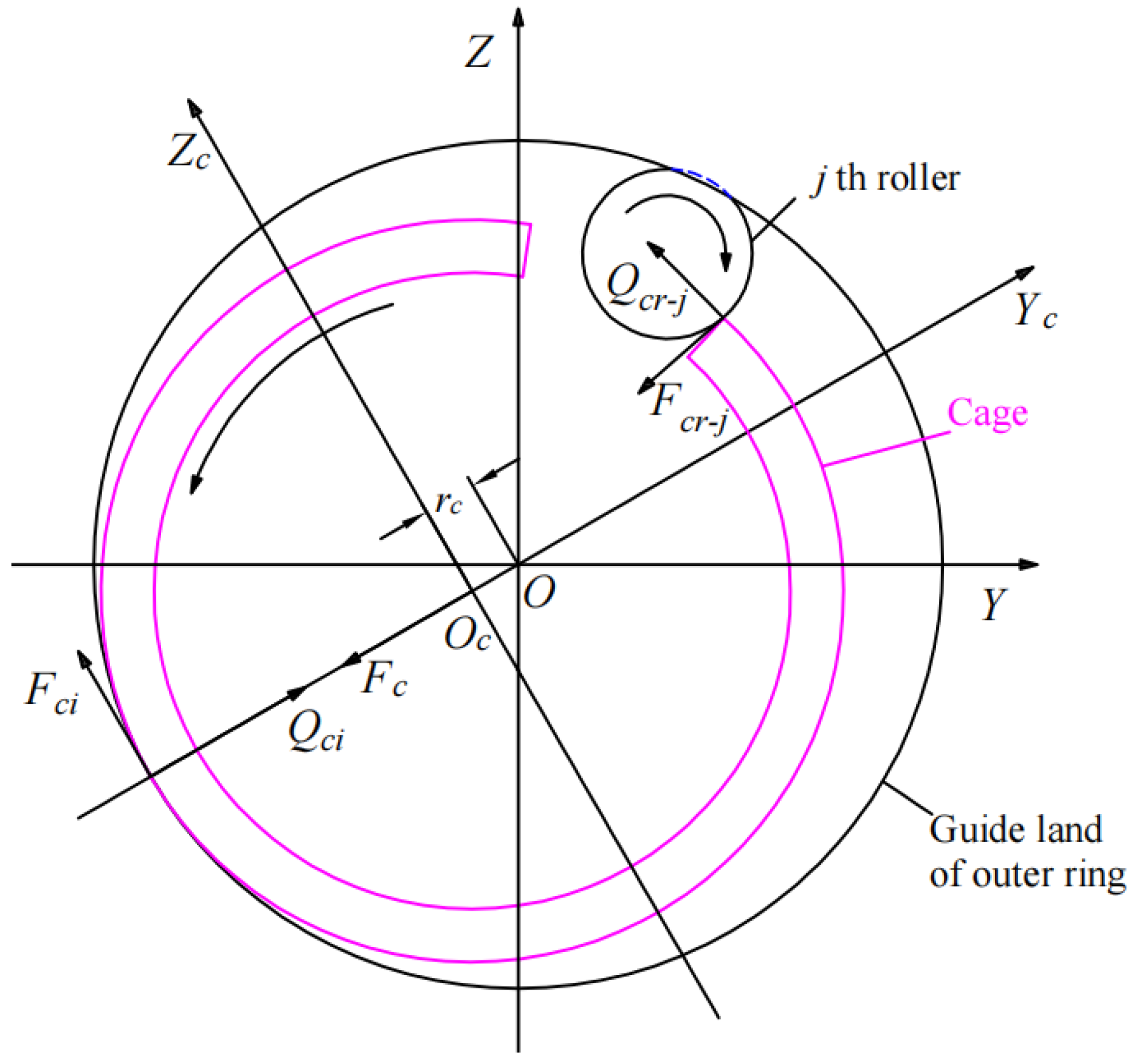
2.2. Cage Contact Model

The contact model between the cage and the guide collar or rolling elements is established [21], and the following hypothesis is made:

• We assume that the cage is a rigid object and ignore its flexible deformation;
• When the cage is not in contact with the guide ring and rolling body, we assume that there is hydrodynamic action between them, and the elastic deformation caused by hydrodynamic action is not considered;
• We assume that the local contact deformation between the cage, guide ring and rolling elements is elastic deformation.

Based on the above assumptions, the geometric relationship between the cage and rolling elements and guide ring is firstly determined, such as the mass whirl speed, contact clearance, etc. Secondly, according to the given cage pocket clearance and guide clearance, the contact model of the cage with rolling elements and guide ring is established. In turn, the normal load and friction force at the contact position are obtained. Figure 2 shows the force on the cage; the cage is mainly subjected to the contact force and friction force from the roller and the guide ring. $Q_{cr-j}$ and $F_{cr-j}$ are the contact force and friction force between the jth roller and cage, $Q_{ci}$ and $F_{ci}$ are the contact force and friction force between the cage and guide ring,$r_c$ is the relative offset of cage mass center, and $F_c$ is the centrifugal force of cage.

2.3. Experimental Verification

A high-speed bearing cage motion state testing machine and a high-speed camera were used to measure the whirl orbit of the cage mass center. This was compared with the model calculation results to verify the accuracy of the model.

2.3.1. Testing Equipment

The high-speed bearing cage motion state testing machine consisted of a main structure, drive system, hydraulic loading system, high-temperature lubrication system, electric control and computer software system. The main structure is shown in Figure 3. The test bearing is located at the leftmost end of the spindle, and its motion can be observed through the observation window. The temperature sensor is used to monitor the temperature of the outer ring of the test bearing, accompanying test bearing and support bearing. The vibration sensor is used to monitor the vibration acceleration of the main structure. The bearings are lubricated and cooled by spraying oil with 4050 aviation lubricant.

The process of cage motion is captured by a high-speed camera, and the coordinates of markers are obtained by capturing the marker points on the cage with image post-processing software. The center coordinates of the circle at each marker are calculated as the position of the cage mass center in the $YOZ$ plane. The cage mass center whirl orbit in the $YOZ$ plane is derived, as shown in Figure 4.

2.3.2. Experimental and Simulation Results

The inner ring rotated at 10,000 r/min and 30,000 r/min, respectively, and the radial load was 200 N (about 0.95% of the rated dynamic load of this bearing). The measured cage mass center whirl orbit is shown in Figure 5, and the simulation model calculated the cage mass center whirl orbit as shown in Figure 6. The red dashed line in the figure is the circle ⊙_center with the radius of the guide clearance, and the cage mass center is the whirl in ⊙_center. The results show that the cage mass center obtained from the experiment and simulation at the inner ring speed of 10,000 r/min has a disordered whirl in the local area. The cage mass center whirl orbit obtained from the experiment and simulation at the inner ring speed of 30,000 r/min is comparatively regular circular, and the whirl radius is approximately equal to the guide clearance. It can be seen that the shape and range of cage mass center whirl obtained from the simulation are close to the experimental results. Consequently, the simulation model can be used to simulate the cage whirl characteristics of cylindrical roller bearings under high speed and light load.

3. Cage Whirl State

The whirl orbit, whirl speed $\dot{\alpha }$ and whirl radius $r_c$ are important parameters of the cage whirl. The cage mass center whirl orbit reflects the stability of the cage operation and wear [3,20]. The constant whirl speed $\dot{\alpha }$ and whirl radius $r_c$ indicate that the cage is in a stable whirl state [1]. In order to obtain different cage whirl states, the operating parameters of the bearing are changed, as shown in

Table 2. Bearing operating parameters.

No.	Inner Ring Speed ${\mathit{n}}_{\mathit{i}}/\mathbf{r}/\mathbf{min}$	Radial Loads ${\mathit{F}}_{\mathit{r}}/\mathbf{N}$	Cage Theoretical Speed ${\mathit{n}}_{\mathit{c}\mathit{a}\mathit{g}\mathit{e}}/\mathbf{r}/\mathbf{min}$
1	10,000	200	4329.90
2	15,000	200	6494.85
3	20,000	200	8659.79
4	30,000	200	12,989.70

.

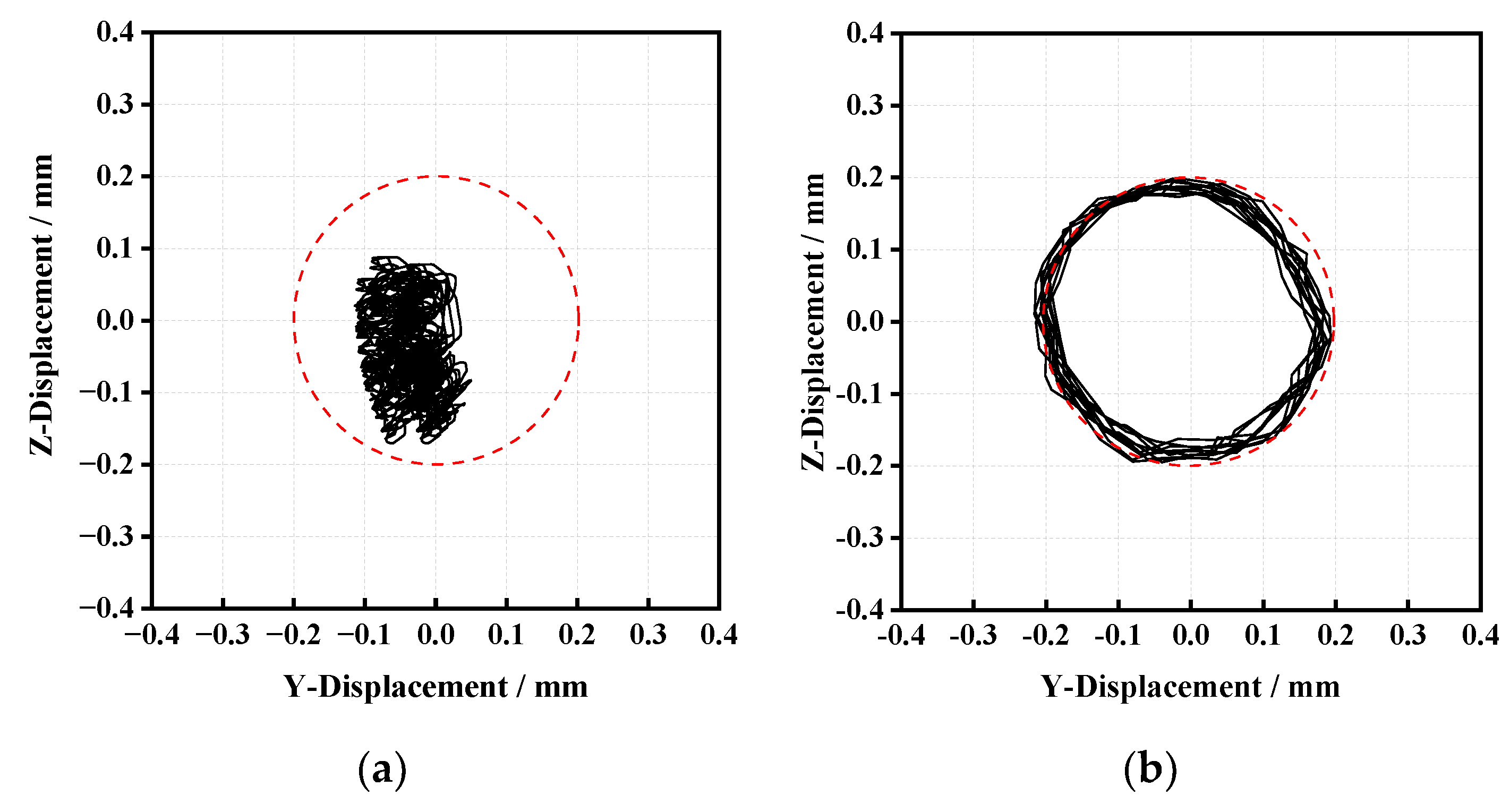
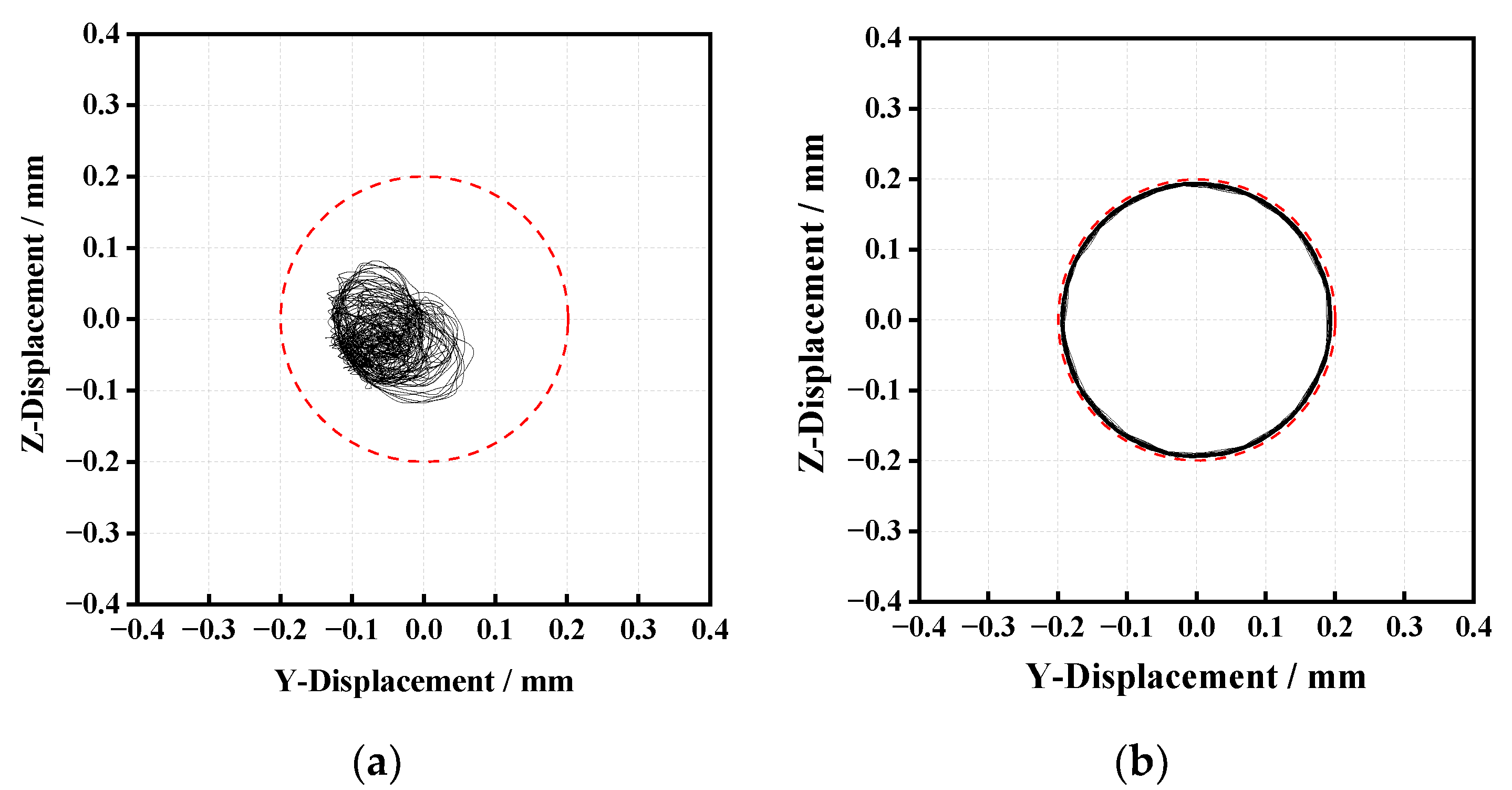
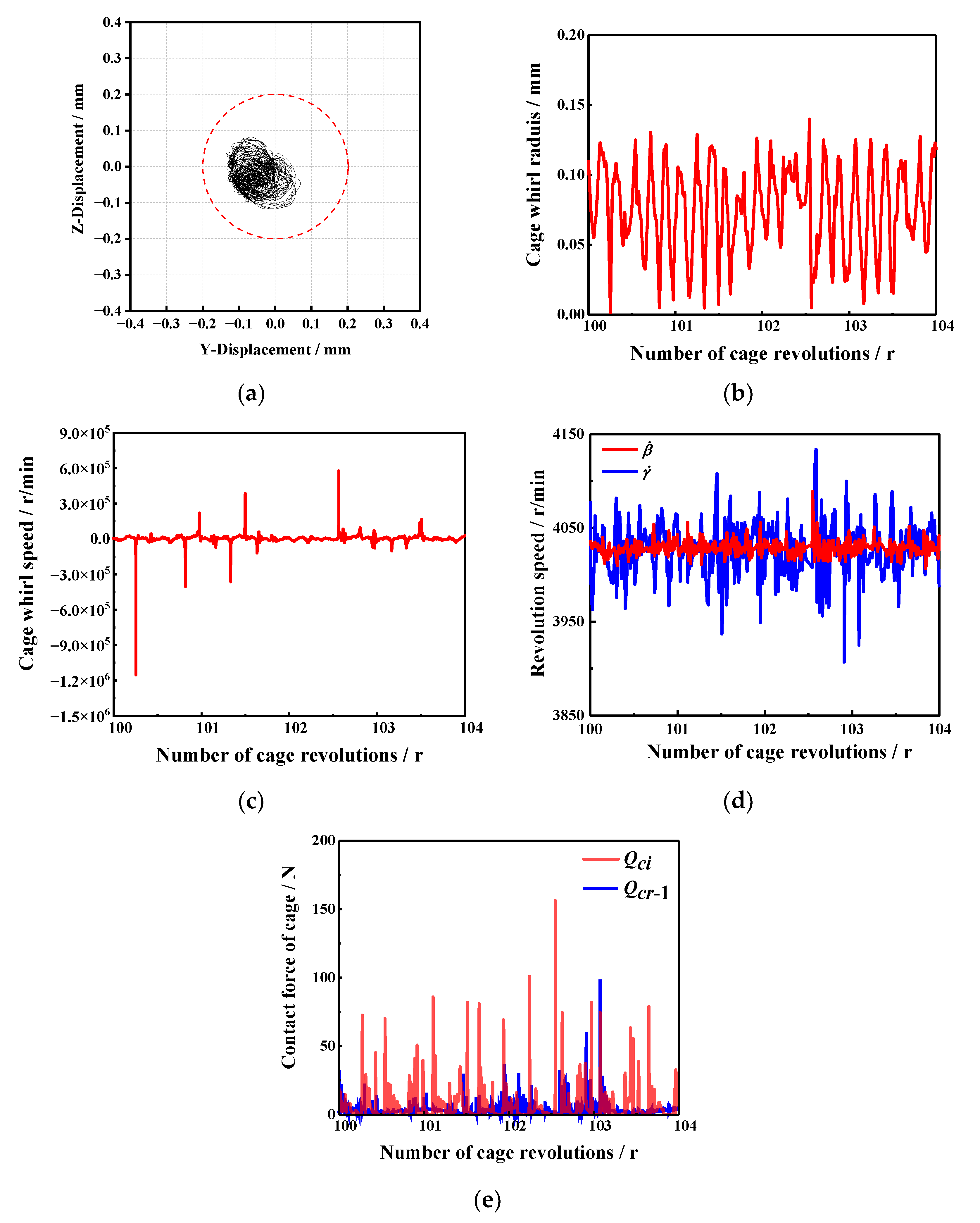
3.1. Disordered Whirl

Under operation condition 1, shown in Figure 7, the cage mass center whirls irregularly in circle ⊙_center. The whirl radius $r_c$ varies disorderly, and the cage whirl speed $\dot{\alpha }$ varies dramatically. Figure 7d shows the variation in cage speed $\dot{\beta }$ and roller speed $\dot{\gamma }$. There is a significant difference in the values, and both are lower than the theoretical cage speed. The continuous variation of $\dot{\gamma }$ will cause shock to the cage and affect the force $Q_{cr-1}$ and motion $\dot{\beta }$ of the cage. In the term of the face of the cage, $Q_{cr-1}$ and $Q_{ci}$ vary continuously, and their RMS is 4.58 N and 12.54 N, respectively. The level of force on the cage is low. However, influenced by the unstable impact of the roller, the fluctuation of $Q_{cr-1}$ and $Q_{ci}$ is large, and there is no obvious regularity, which will cause the whirl radius and whirl speed to fluctuate, making the cage mass center create a disordered whirl.

3.2. Local Periodic Whirl

The cage mass center is gradually stabilized at one point under operating condition 2, shown in Figure 8, i.e., the position of the mass center does not change. Accordingly, the cage whirl radius $r_c$ is always equal to 0.153 mm, and the cage whirl speed $\dot{\alpha }$ is stabilized at 0 r/min with a little variation. Figure 8d shows that the bearing is slipping, but the cage rotation speed $\dot{\beta }$ is constant and the roller speed $\dot{\gamma }$ varies approximately sinusoidally with $\dot{\beta }$ as the axis. The regular variation of $\dot{\gamma }$ avoids the violent collision between the roller and cage, which enables $Q_{cr-1}$ to vary periodically. Meanwhile, a constant and extremely weak force (hydrodynamic force) exists between the cage and guide ring. According to the definition of the cage whirl state by Kingsbury [7], the cage can be considered to be in a “synchronous whirl state” at this time. Therefore, in terms of motion and force, the stability cage whirl is higher in case 2.

The cage mass center under operating condition 3, shown in Figure 9, has a fixed and periodic whirl orbit in a local area within circle ⊙_center. The cage whirl radius $r_c$ and whirl speed $\dot{\alpha }$ both vary periodically. At this time, the bearing center O is outside the whirl range of the cage mass center, so the whirl speed $\dot{\alpha }$ has some negative values. It can be regarded as the cage mass center around the point (–0.015, –0.115) to carry out periodic motion, the motion radius and the motion speed, as shown in Figure 9d,e. It can be seen that the motion radius and motion speed of the cage mass center also vary periodically. From the motion speed of the cage and roller, $\dot{\beta }$ varies in a small amplitude period, and $\dot{\gamma }$ varies similarly to operating condition 2 but is not completely sinusoidal, corresponding to $Q_{cr-1}$ and $Q_{ci}$, which show a periodic variation, but the amplitude of each period of $Q_{cr-1}$ is different.

Compared with operating condition 2, the stability of the force on the cage in operating condition 3 decreases, but there is periodicity, and it is maintained at a low level. Simultaneously, the whirl radius and whirl speed of the cage vary periodically with time. Thus, the cage whirl under operating condition 3 has a certain degree of stability.

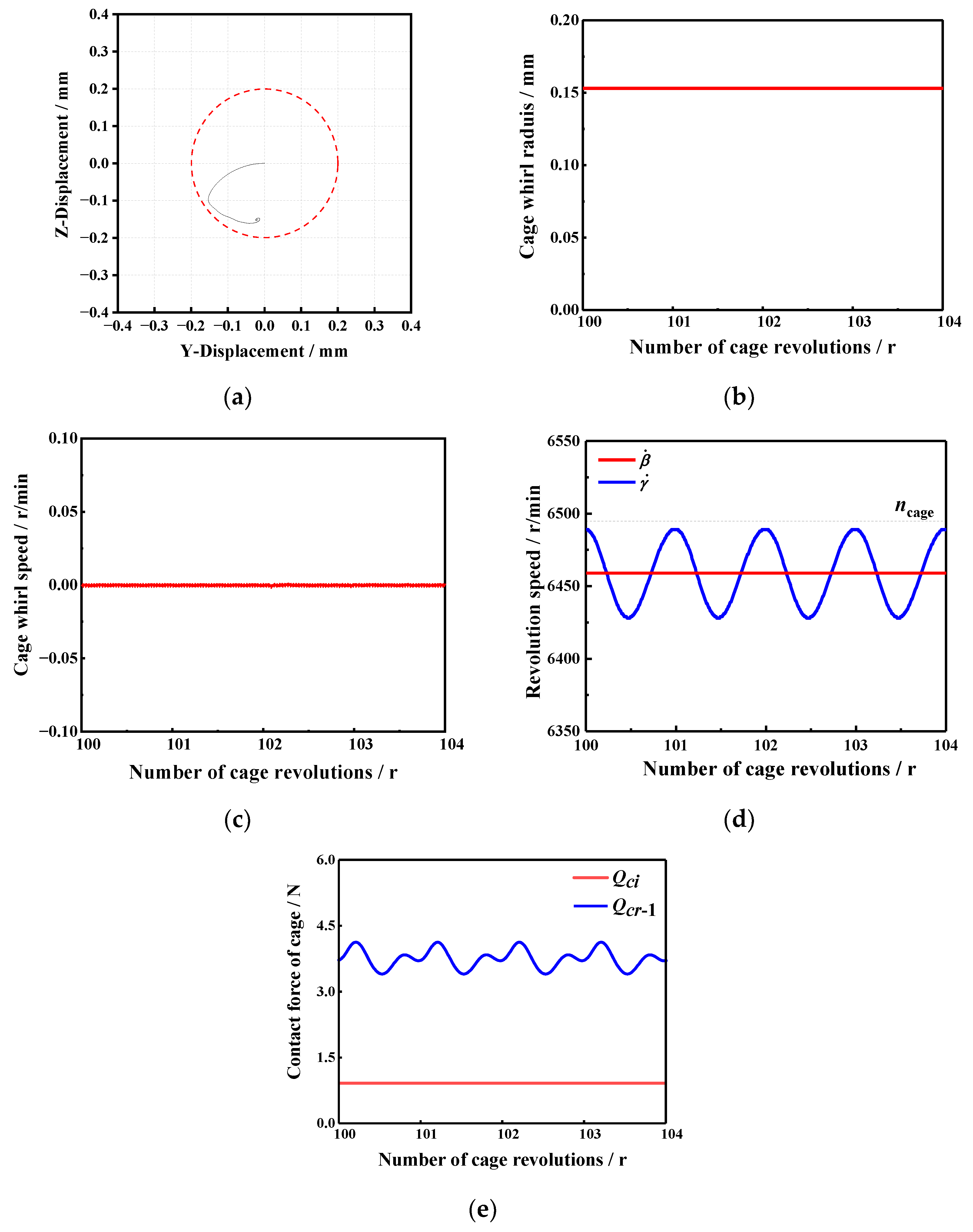
3.3. Regular Circular Whirl

The whirl orbit of the cage mass center under operating condition 4, shown in Figure 10, is close to circle ⊙_center and is regularly circular. The cage whirl radius $r_c$ varies between 0.187 and 0.197 mm in a small range but does not display periodicity. The cage whirl speed $\dot{\alpha }$ varies frequently and is much higher than the cage rotational speed. Figure 10d shows that the rotational speed of the cage and roller gradually decreases, implying that the degree of bearing slipping increases. Relative to $\dot{\beta }$, $\dot{\gamma }$ fluctuates violently, which in turn causes violent collisions between the roller and the cage. In addition, the extremely high whirl speed results in a considerable centrifugal force on the cage, which greatly increases the collision force between the cage and the guide ring.

If the stability of the cage whirl is judged only by the cage mass center whirl orbit, there is no doubt that the cage whirl is stable under operating condition 4. However, if considering the whirl speed and force on the cage, the stability of the cage whirl is relatively worse. Therefore, the evaluation of the stability of the cage whirl is not only according to the cage whirl orbit [10,22] but also needs to combine the cage whirl state and the force on the cage.

In summary, compared with operating conditions 2 and 3, the stability of the cage whirl under operating conditions 1 and 4 is worse, especially under operating condition 4, when there is a violent collision between the cage and roller or guide ring, which will increase the risk of cage breakage. Under operating conditions 2 and 3, the cage whirl is more stable, and the force on the cage is smaller and relatively steady. Among them, the cage whirl radius and whirl speed are constant under operating condition 2, and the cage whirl stability is the highest at this time. It is worth noting that the existing studies on the cage whirl characteristics of cylindrical roller bearings have not been reported to be similar to the cage whirl state of “cage whirl at one point” under operating condition 2.

4. Conclusions

In this paper, a rolling bearing dynamics model is established, and the accuracy of the model is verified through experiments. Based on the model, the cage whirl state and the force on the cage are investigated under different operating conditions, and the stability of the cage whirl is evaluated. The main conclusions are as follows:

• The irregular variation of the rotational speed of the roller will produce a frequent impact on the cage, which will cause the cage to suffer violent collision force and lead to the unstable whirl of the cage, which is expressed as the irregular variation of the cage whirl speed.
• When the cage mass center is a disordered whirl, the whirl speed and rotational speed of the cage are unstable, and the force between the cage and roller or guide ring fluctuates greatly. The cage mass center whirl orbit is regular circular (whirl radius is about equal to the guide clearance), which does not mean that the cage whirl state and the force on the cage are stable.
• The cage mass center in a local area for a cycle whirl, rotational speed, whirl speed and the force of the cage is a periodic variation or remains constant. At this time, the force between the cage and the roller or guide ring is minor.
• The stability of the cage mass center whirl is not affected by the degree of bearing slipping.