An Experimental and Numerical Study of Damage Due to Particle Impact on Sapphire Orifices Used in High-Pressure Water Jet Cutting

Abstract

In the present study, the damage mechanisms that cause premature failure of sapphire water jet orifices were analyzed using a combined experimental and finite element modeling (FEM) approach. Depending on the operating behavior and local conditions, the service life of orifices for high-pressure water jet cutting often deviates considerably from the manufacturer’s specifications. Literature states a typical service life of 50 to 100 h, while in some cases, premature failure after a few hours or even minutes of operation can be observed. The focus of this paper is on the interaction of particles that impact the orifice surface but also the effect of faulty orifice assembly is taken into account. To estimate the risk of failure, the stress distribution in critical parts of the orifice were calculated via FEM, which is fed with experimental data. The modified Mohr failure criterion was then used to evaluate the stress distributions with respect to the possible failure of the orifice jewel. The results revealed that the risk of damage caused by excessive assembly preload forces is marginal. The stress caused by the impact of particles of different sizes is up to four orders of magnitude higher than the stress caused by assembly forces and is therefore identified as the main risk for orifices to fail prematurely. Experimental data shows mainly particles of calcium carbonate and iron–aluminum silicates, which are compounds that originate from the process water itself. It is demonstrated that particles are more critical than formerly assumed in the literature. This paper identifies particles with a diameter of more than 10 µm as critical when there are no other loads present. In operation, even particles as small as 2 µm in diameter can cause damage to the orifice jewel. To prevent premature orifice failure due to foreign particles, water filtration with a 2 µm mesh is recommended, while future research needs to focus on the interior cutting head design to prevent precipitation from the process water.

1. Introduction

High-pressure water jet cutting is an efficient machining process that allows the cutting of almost any material without heat input into the cutting surface [1]. Because of this particular advantage, waterjet cutting is, e.g., used in research for the preparation of welding specimens, as described by Kumar, Chattopadhyaya et al. [2]. Furthermore, cutting forces are low and cutting quality and accuracy are relatively high [3]. This makes water jet cutting attractive, particularly for the machining of modern complex high-performance materials [4,5,6]. Currently, various factors limit a broader use in the industry. In addition to the general challenge of ensuring the geometry of the workpiece being cut, Natajaran et al., in particular, cite a low penetration depth of the waterjet resulting from a lack of energy transfer between the nozzle and the workpiece [7]. The cutting geometry determines the achievable manufacturing accuracy. This is particularly important when machining modern composite materials and is limited by the water jet’s geometry. Kumar, Kumar et al. demonstrated the importance of the kerf geometry when machining Inconel 718 [8], while other work by Sutowska et al. evaluated the geometrical deviations of the workpiece when cutting soda lime glass [9]. Banon et al. described that the waterjet consists of different zones and how their characteristics affect the kerf [10]. Above a certain standoff distance, the water jet breaks down into drops. A droplet jet is used for material removal processes [11] but is not useful for cutting applications. Therefore, it is necessary to create a water jet with high coherence. The decisive factors here are the cutting head design and the condition of the orifice.

There are two main process variants—pure water jet cutting and abrasive water jet cutting. Both processes require a high-pressure pump for compressing the process medium, which is usually compressed up to a pressure of 400 MPa [12]. A piping system feeds the compressed water to a cutting head mounted on a guide system. The cutting head contains the orifice and other components. Pure and abrasive water jet cutting have in common that they rely on a fine and coherent water jet to cut the different materials and to achieve high productivity and accuracy. Both process variants use the same type of orifice to convert the potential energy of the compressed water into kinetic energy of the fast-flowing water jet. Thus, in a high-pressure water jet cutting system, the orifice represents a component of central importance. It determines the achievable manufacturing accuracy, performance, and efficiency of the process. The dependencies of the overall process on the cutting head and the contained orifice are already known [13]. In addition, some damaging potentials and their respective effect on the cutting system are briefly investigated. Hashish mentioned foreign particles that move upstream at switching operations [14], Jegaraj et al. connected orifice damage with salt particles on the orifice surface [15], and Urazmetov et al. emphasized the importance of the orifice’s geometric integrity for the jet quality [16].

To illustrate the dependence on the orifice that is shared by pure and abrasive water jet cutting, a comparison of both process variants is shown in Figure 1. It shows that the same type of orifice is used for the generation of the actual water jet. The orifice has contact with pure water only. In the case of injector jet cutting, an abrasive is added after the water jet has been generated; the water jet then accelerates the abrasive particles. For this purpose, a so-called nozzle limits the expansion of the resulting abrasive water jet resulting from air friction over a defined length [17]. In pure water jet cutting, the orifice is the only functional component of the cutting head, whereas injector jet cutting features additional downstream components.

Since the orifice is the only functional component in the cutting head for pure water, its condition and alignment exclusively determine the quality of the water jet [14]. In the case of the abrasive water jet, it is often mistakenly assumed that the nozzle is of paramount importance for the jet quality, as it represents the last part of the cutting head before the water jet exits into the atmosphere. The wear mechanisms affecting the nozzle are relatively easy to investigate as they are similar to those of conventional cutting tools [18]. The inner diameter of the nozzle increases almost linearly with operating time, which results in a larger abrasive water jet diameter [19]. Most research regarding wear in water jet systems deals with nozzle wear, as Hashish stated in his study of the wear of nozzle materials [20]. Pi and Tuan also modeled the wear of carbide nozzles [21]. Even though research by Kumar, Gupta et al. clearly proves that the wear of the nozzle causes a decreasing jet quality and leads to a low process performance [22], the orifice condition must be considered as well.

The nozzle and orifice must be matched to each other in such a way that the orifice provides a water jet that is suitable to enter the nozzle in the designed way. Due to air friction, the water jet expands with increasing orifice distance. The inner nozzle diameter is, therefore, larger compared to the orifice bore diameter. Typical values are an orifice diameter of d_o = 300 µm with a nozzle diameter of d_n = 800 µm. The diameters and the distance between the orifice and nozzle have to be matched so that the water jet is able to enter the nozzle approximately tangentially. If this is not the case, the nozzle walls deflect the water, and it subsequently exits the nozzle with low coherence [18], even if the nozzle is still in perfect condition. Thus, as the orifice is damaged during operation, the water jet no longer matches its design geometry, and the emitted jet’s coherence decreases, resulting in a decline in production quality and process productivity [23].

To ensure jet coherence and a small jet diameter, the orifice bore needs sharp edges [24]. Due to the action of high loads, orifices usually contain a sapphire or ruby jewel. The jewel is the central component of the orifice and contains the actual orifice bore. Typically, it is set into a stainless steel orifice mount with an aluminum bronze frame [14]. Literature data suggest a nominal life of sapphire orifices between 50 [12] and 100 [15] operating hours. In practice, the achievable service life often differs significantly. The mechanisms that lead to orifice damage and result in failure are not fully understood. The literature gives some hints to the prevailing damaging mechanisms but lacks studies that focus especially on the interactions between the orifice and its surroundings. Particles flowing in the water might impact the orifice surface, and this impact is often assumed as the reason for orifice damage [25]. Investigations in this field are rare and rely on few empirical data, mainly due to the poor accessibility of the orifice during operation. The present study was designed to shed light on the effect of particles impacting on the orifice and to test the main hypothesis:

H1: 

Particles within the fluid flow can lead to orifice damage and premature failure. Their appearance is critical when their diameter exceeds a specific value.

To investigate the interaction between particles and the orifice jewel and to overcome the restricted accessibility, numerical methods were used to supplement the experiments. The widely established Modified Mohr failure criterion [26] was employed to interpret the numerical results regarding the particle’s damaging potential on the orifice jewel. The insight obtained can be exploited to derive measures to extend orifice service lives.

2. Materials and Methods

This chapter describes the orifice type investigated, including the basic properties of the orifice jewel material, as well as the equipment and analysis technology used. In addition, the numerical approach used to gain insight into the interaction between particles and the orifice jewel inside the cutting head is described.

2.1. Experimental

2.1.1. Sapphire Orifice Jewels—Material Properties

Given their excellent wear resistance, sapphire (single-crystalline aluminum oxide) or ruby are the materials of choice for orifices. These materials have good wear resistance and high hardness (1900–2100 HK orthogonal to c-axis [27]). Both materials have trigonal elementary cells and thus have anisotropic material properties. Ruby differs from sapphire in the additional doping with chromium oxides [28], but material properties relevant in the current context do not differ [27]. A decisive disadvantage of these ceramic materials lies in their brittleness, which makes service life predictions difficult. Starting with material defects or external damage to the material surface, microscopic cracks can grow rapidly once the stress intensity factor K_I exceeds a certain threshold. The stress intensity factor is given by the external load, σ, the geometry factor of the crack, Y, and its length a as [29]:

$$K_{\mathrm{I}}=\sigma ·\sqrt{a} ·Y.$$

(1)

For sapphire, the threshold value is around 1 MNm^−3/2 and the critical value intensity factor, where the crack becomes unstable is also low, i.e., K_IC,sapphire = 1.6 MNm^−3/2 [28]. By assuming a typical operating pressure of a commercially used water jet cutting system of σ = 300 MPa and a geometry factor of Y = 1.7725 [28], the critical crack length calculated from Equation (1) becomes a₃₀₀ ≈ 3.5 µm. Such small defects may rapidly form upon the impact of foreign particles and lead to rapid edge chipping [15].

2.1.2. Water Quality

To assess and classify the wear progress and damage patterns of orifices, the operation of commercial orifices on a 3-axis water jet cutting machine were monitored. The resulting data set represents a sample of damage patterns occurring during the operation of orifices, which was then used as a basis for further investigations. In all experiments, the water jet system was fed with tap water provided by the local water supplier.

Table 1. Extract from the official water analysis, provided by the local water supplier [30].

	Amount	Unit
copper	<0.02	mg/L
nickel	<0.006	mg/L
aluminum	<0.02	mg/L
iron	<0.02	mg/L
manganese	<0.01	mg/L
sodium	34	mg/L
potassium	3.4	mg/L
calcium	86	mg/L
sulfate	170	mg/L
total hardness	2.9	mmol/L
pH value	8.3	-

shows an extract from the official water analysis.

2.1.3. Experimental Setup

The tap water was fed into a hydraulic pressure intensifier of type BFT Servotron 40.37. This system can compress water to up to 400 MPa and deliver a fluid flow of 3.8 L/min. After compression, the pressure intensifier fed the water into a high-pressure piping system. It had an overall length of 20 m, after which the water was fed through a switching valve and to the cutting head. The cutting head was mounted to a 3-axis guiding system and contained the sapphire orifice.

Figure 2 gives a schematic overview of the water jet cutting system. The pressure intensifier (b) compresses the tap water to the required operating pressure of up to 400 MPa. The pump used was equipped with several pre-filters with a mesh size of 10 or 5 µm (a). The compressed water is then fed via a piping system (c) through the cutting head (d), which consists of a switching valve (e) the orifice (f), and the nozzle (g). The cutting head from BFT GmbH corresponds to the design shown in Figure 1b). The orifices used were sapphire orifices of type 91 manufactured by Allfi AG with a bore diameter of 300 µm.

Depending on the conditions, the lifetime of an orifice in real operation typically is about 10 to 50 operating hours. End of life is reached as soon as the jet quality decreases in such a way that satisfactory cutting quality can no longer be guaranteed. In industrial applications, the decrease in cutting quality is usually determined by measuring the workpiece and not meeting the required manufacturing tolerances. To determine the jet quality in this study, a jet-focused approach was chosen by defining a dimensionless quality index Q_Jet as follows:

$$Q_{\mathrm{Jet}}=\frac{d_{\mathrm{nominal}}}{d}.$$

(2)

The index of a new orifice starts at Q_Jet = 1, as the actual jet diameter d matches the nominal jet diameter d_nominal. During operation, the index decreases due to the fact that the actual diameter of the water jet d increases. The end of orifice life was defined as Q_Jet ≤ 0.7. The orifice was then replaced and analyzed using imaging techniques. In the present study, a total of nine orifices were analyzed. Orifices with characteristic damage patterns were selected from the samples and are discussed in the following chapter.

2.2. Numerical Simulation

To further investigate the potential contributions to the observed scatter in orifice lifetimes and the different damage phenomena, a backward numerical approach was adopted. For the numerical investigations, the software ANSYS Workbench was used, which includes both a mechanical and a fluent module. This allowed modeling of the flow field through the orifice and addressed the suspected two main causes of premature orifice failure, i.e., the effect of excessive loading upon assembly of the orifice in the cutting head and the presence of solid particles in the process water.

The greatest computational effort was expected in the study of particle impact. Due to the high dynamics of the event of impact and the small dimensions of the particle, explicit algorithms were used to quantify the tensile and compressive stresses. With this approach, good simulation performance was achieved when using the commercial FEM software package 2022 R1. It was made possible to perform the calculations with the following specifications: i5-10505 CPU (3.2 GHz), 8 GB RAM, 1 TB storage space with a typical calculation time between 20 and 40 min for each case addressed with this study.

2.2.1. Material Definition

Due to its trigonal lattice, sapphire does not have isotropic material properties, i.e., it exhibits higher mechanical strength along its c-axis than normal to it. For modeling, it was assumed that all orifice jewels are oriented such that their c-axis coincides with the orifice bore and an orthotropic material model was used for the calculations. Furthermore, the material behavior was assumed as linear elastic, and thus the stress-strain relationship was obtained as

$$\left(\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{33}\\ {\sigma }_{12}\\ {\sigma }_{13}\\ {\sigma }_{23}\end{array}\right)=\frac{1}{E} \left(\begin{array}{cccccc}{D}_{1111}& D_{1122}& D_{1133}& 0& 0& 0\\ D_{1122}& D_{2222}& D_{2233}& 0& 0& 0\\ D_{1133}& D_{2233}& D_{3333}& 0& 0& 0\\ 0& 0& 0& D_{1212}& 0& 0\\ 0& 0& 0& 0& D_{1313}& 0\\ 0& 0& 0& 0& 0& D_{2323}\end{array}\right)\left(\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ {\epsilon }_{33}\\ {\epsilon }_{12}\\ {\epsilon }_{13}\\ {\epsilon }_{23}\end{array}\right),$$

(3)

with σ_ij and ε_ij being the stresses and strains, respectively. E is Young’s modulus and the entries D are

$$D_{1111}=E_1\left(1-{\nu }_{23}{\nu }_{32}\right){\rm Y},$$

(4)

$$D_{2222}=E_2\left(1-{\nu }_{13}{\nu }_{31}\right){\rm Y},$$

(5)

$$D_{3333}=E_1\left(1-{\nu }_{12}{\nu }_{21}\right){\rm Y},$$

(6)

$$D_{1122}=E_1\left({\nu }_{21}-{\nu }_{31}{\nu }_{23}\right){\rm Y},$$

(7)

$$D_{1133}=E_1\left({\nu }_{31}-{\nu }_{21}{\nu }_{32}\right){\rm Y},$$

(8)

$$D_{2233}=E_2\left({\nu }_{32}-{\nu }_{12}{\nu }_{31}\right){\rm Y},$$

(9)

$$D_{1212}=G_{12},$$

(10)

$$D_{1313}=G_{13},$$

(11)

$$D_{2323}=G_{23},$$

(12)

where ν_ij are Poisson’s ratios, Y as follows:

$${\rm Y}=\frac{1}{1-{\nu }_{12}{\nu }_{21}-{\nu }_{23}{\nu }_{32}-{\nu }_{31}{\nu }_{13}-2{\nu }_{21}{\nu }_{32}{\nu }_{13}},$$

(13)

and G_ij are the shear moduli

$$G_{\mathrm{ij}}=\frac{E_{\mathrm{i}}}{2\left(1+{\nu }_{\mathrm{ij}}\right)},$$

(14)

as shown by LeVeque [31]. The material behavior of the particles, carbonate, and silica, was assumed to be isotropic. For isotropic material properties, Equations (3)–(14) can be simplified by considering symmetry constraints. In addition, isotropic material properties were used for the aluminum bronze (orifice mount) and the stainless steel (orifice body), as shown in

Table 2. Mechanical properties of sapphire (Al₂O₃), calcium carbonate (CaCO₃), iron–aluminum silicate (Fe₃Al₂[SiO₄]₃), stainless steel, and aluminum bronze used for modeling.

	Orthotropic Material Properties
	ρ, kg/mm³	EX, GPa	EY, GPa	EZ, GPa	νXY	νYZ	νXZ	GXY, GPa	GYZ, GPa	GXZ, GPa
sapphire	3.96 × 10−6	386	435	386	0.3	0.3	0.3	156	156	156
	Isotropic Material Properties
	ρ, kg/mm³		E, GPa		ν		G, GPa		K, GPa
calcium carbonate	2.71 × 10−6		97		0.38		35.00		139.57
iron–aluminum silicate	2.27 × 10−6		66		0.17		28.21		33.33
stainless steel 1.4571	8.00 × 10−6		200		0.31		76.34		175.44
aluminum bronze	2.77 × 10−6		71		0.33		26.69		69.61

. In addition to the previously mentioned properties, it contains the bulk modulus K for the isotropic materials.

2.2.2. Orifice Assembly

To prevent that damage due to the orifice mounting is mistakenly assumed as damage caused by particles, the stress field after orifice mounting was investigated. The mounting situation of the orifice was modeled, taking into account the rotational and axial symmetry of the component. The model encompassed the entire orifice assembly, i.e., the orifice body, the orifice mount, and the orifice jewel. Frictional contacts were applied between the individual parts so that the contact could transmit pressure and shear forces. The following boundary conditions were used: (i) a fixed bearing located at the bottom of the orifice body (A in Figure 3); and (ii) a support was applied to surface B, which ensures a displacement restraint in the y-direction but allows displacement in the x-direction. This corresponds to the real installation situation, where there is a clearance fit between the shell surface (C) of the orifice assembly and the cutting head.

Depending on the torque applied when the cutting head is mounted, a corresponding preload force is set, which acts parallel to the jet axis on the conical sealing and centering chamfer of the orifice assembly. Figure 3 shows the applied force vector F_a. The chamfer on the orifice body, which is required for sealing and centering the orifice in the collimation tube, causes the axial assembly preload force to be converted into additional radial components. The assembly is typically performed by tightening an M14 × 1.5 thread with a torque of 70 Nm. The resulting force is then obtained as [32]

$$F_{\mathrm{a}}=\frac{M_{\mathrm{a}}}{\frac{d_{\mathrm{p}}}{2}\left(\frac{{\mu }_{\mathrm{t}}}{\cos \left(\beta /2\right)}+\tan \phi +{\mu }_{\mathrm{k}} \frac{d_{\mathrm{w}}+d_{\mathrm{h}}}{2d_{\mathrm{p}}}\right)},$$

(15)

with

Ma	tightening torque
dp	pitch diameter
µt	total coefficient of friction
β	thread angle
φ	pitch angle
dw	outer support diameter of the screw head
dh	through hole diameter

and was used as a boundary condition in the model.

The model was then used to test whether excessively high tightening torques of up to 100 Nm would contribute significantly to the damaging of the orifice jewel and whether very low tightening torques of only 20 Nm would lead to a significant reduction of the stress field. In the case that low tightening torques would lead to a substantially lower damage potential, additional measures would of course be necessary to seal the connection, as the metallic surface pressure ensures the high-pressure sealing.

After calculating the stress states induced by orifice mounting, different operating pressures were added to the orifice jewel. Thus, the stress state after orifice mounting could be compared with the operational loads on the orifice. The operating pressure p_in was applied on the orifice jewel surface as shown in Figure 3 and was varied between 200 and 400 MPa in 50 MPa steps. Quadrilateral elements with a size of 0.12 mm were used for the mesh, and a refined mesh (factor of 5) was employed at the critical locations. The orifice jewel itself was meshed with a smaller element size of 0.01 mm due to its geometric dimensions. The model was meshed with a total of 20,597 cells and 60,260 nodes. A convergence test showed that finer meshing of the assembly did not lead to further changes in the stress distribution.

The contacts between the three bodies were assumed to be frictional.

Table 3. Friction coefficients used in the numeric simulation.

Body	Friction Coefficient
orifice body/frame	μ = 0.45
orifice body/orifice jewel	μ = 0.15
frame/orifice jewel	μ = 0.20

shows the friction coefficients for the different material pairings.

In the simulation, the loads were applied in two time-steps. In the first step, only the tightening torque and the resulting preload force were considered. In the second step, the operating pressure was then superimposed. The calculations were made in the static structural regime. Fluctuations of the operating conditions were not considered.

2.2.3. Flow Simulation

The aim of the flow simulation was to calculate the velocity distribution around the orifice body. Then, the fluid’s velocity distribution was used to define boundary conditions for particle movement, which allowed investigating the influence that particles can have on the orifice jewel surface. The mesh consisted of two-dimensional rectangular cells with the smallest elements having a size of 4.5 µm and the largest ones of 40 µm. The fluid volume was meshed with 40,650 quadrilateral elements. All the elements near the wall were refined in order to achieve convergence. The water inlet pressure p_in was varied from 200 MPa to 400 MPa with steps of 50 MPa. The outlet pressure p_out was always set to 0.1 MPa, which equals the atmospheric pressure. Water with a temperature of 295.15 K was used as the flow medium. According to Figure 4, its flow direction is from top to bottom, as p_in >> p_out.

To obtain the steady-state regime of the orifice flow field, the k-ω model (SST) of ANSYS Fluent was employed. The model calculates the transport effects of the principal turbulent shear stress with a modified turbulent viscosity. The coupled algorithm ensures an efficient single-phase solution for steady-state flow [33]. As convergence criteria, the residuals of continuity, x-velocity, y-velocity, energy, k, and ω were set to 10⁻³. Figure 4 shows the mesh and the boundary conditions used.

2.2.4. Particle Impact

In the following, it is assumed that there are particles within the flow field, which can strike the orifice jewel’s surface. In order to investigate the effect that these particles have on the surface, their motion and contact with the orifice jewel were modeled in an explicit dynamic regime. The velocity vector c of the particle was calculated from the flow field simulation. The mesh used involved rectangular and trapezoidal elements. The mesh was refined at the contact zone to ensure convergence. With increasing distance from the surface, the mesh was continuously coarsened. The smallest element size was 12 nm and the largest was 35 µm. The geometry was meshed with a total of 70,726 cells and 71,453 nodes as shown in Figure 5.

The following boundary conditions defined the model: Fixed support was applied on the down surface of the orifice and a velocity was applied to all elements of the particle. The ambient temperature for all simulations in this study was T = 295.15 K. Explicit integration is usually employed for simulating particles or parts with high velocity, where non-linearities may occur, which coincides with the present case. The contact between the two components was defined as frictional, with a friction coefficient of µ = 0.3.

3. Results and Discussion

This chapter presents experimental data of damaged orifices after short-time operation and the results of the numerical calculations. Images of the damaged orifices during the short-time operation were obtained by scanning electron microscopy (SEM). The damage patterns and possible causes, like remaining particles, their number and size then served as boundary conditions for the numerical calculations. Calculating the interaction between those observed particles and the orifice jewel then allowed to estimate their individual damaging potential for given operating conditions.

The challenge in investigating processes in the high-pressure part of the waterjet system is that this area is very difficult or not accessible for measuring devices due to the required pressure resistance. Accordingly, in-situ observation is not possible. In addition, the particles and areas to be observed are extremely small. The advantage of combining experimental and numerical approaches is that measured data can be used to model processes that cannot be measured. Because of the experimental data, the boundary conditions always correlate with real measured values and can also be easily modified and thus the model can be adapted in case of changing operating conditions. The disadvantage of modeling and discussing processes that cannot be measured is the difficult or sometimes impossible validation of the numerically calculated data. In reality, other factors that are not represented in the model can also contribute to the damage of the orifices. The importance of the modeled factors can be exaggerated in the interpretation.

3.1. Damaged Orifices

The following orifices were subjected to regular operation at an operating pressure of 300 MPa and failure of these orifices occurred after short-time operation already. The operating time was between 35 min and 7:12 h. Because the orifices have such a short service life, cavitation was excluded as the major damage mechanism. Cavitation occurs in the orifice channel due to the high flow velocities. It is known that this constantly contributes to wear and damage of the orifices during their service life due to discontinuous impact loads on the material. However, as there are many cavitation-induced events in a very short time [34], the intensity of this load can be assumed to be quasi-stationary when investigated in the context of orifice service life [35]. Thus, cavitation as the main reason for early orifice failure was ruled out and the focus was on faulty assembly or particles hitting the orifice jewel. Hashish [14], Wright [25], and Powell [13] have published empirical observations about the damage that particles can cause at orifice jewels or metallic orifices. They emphasize the general need for filtration of the process water and state that solid matter hitting the orifice might lead to premature failure.

The presence of particles in filtered water is a statistical phenomenon that occurs only sporadically. Thus, particle impact can contribute to orifice damage after many hours as well as directly at the beginning of the operation. Figure 6 shows images of a virgin and a damaged orifice. After production, the orifices have a very low roundness tolerance (Figure 6a). The round bore, in conjunction with the sharp edge on the top of the orifice jewel [23], provides high jet coherence as well as constriction of the jet to a diameter that is below the bore diameter [36]. On the damaged orifice (Figure 6b), there are various areas of edge chipping. These occur statistically distributed over the bore circumference with increasing operating time due to material defects, external load, cavitation, or particle impact. The observed damage patterns correlate with data published by other authors, like Hashish [14], Powell [13], and Li [37]. The research by Li proved the general problem of edge chipping at sharp-edged holes in ceramic materials, while Hashish and Powell connect this type of failure to the coherence of the water jet. However, they do not provide evidence for the mechanisms, leading to these material breakouts. For early premature failure, it is very likely that particle impact caused these damages. If the density of chipped areas in a region is high, it finally results in large material breakouts.

It can be assumed that the edge chipping is the result of cracks propagating in the area near the bore edge. Material defects in the sapphire can serve as the starting point for these cracks, as known from conventional fracture mechanics [28,29]. Manufacturing processes cause material defects and they are always present in real materials. However, these material defects are statistically distributed inside the material and between different orifices. Clearly, this does not explain the preferred localized damage nor high variations in service life for apparently similar loading conditions.

A possible cause for variations in service lives is additional crack initiation caused by externally-induced damage. As published by Powell, faulty assembly, particle impact, or cavitation can cause these damages [13]. Figure 7 shows particles on the surface of the orifice jewel and at the orifice bore. This observation does clearly support the theory of particles potentially damaging the orifice. Such particles may have their origin in the tap water supplied by the local supplier. In addition, the process water can transport abrasions from other components of the cutting system to the orifice. Another possible source of particles can be traced back to the chemical composition of the process water itself. The process water is not a pure substance but rather serves as a universal solvent for a wide variety of material compounds. These dissolved components may precipitate out of the solution during operation and subsequently have a tribological effect as particles.

Figure 7b demonstrates the influence that particles can have on the orifice jewel, where a larger crack is present on the surface, and a small crack around the orifice bore can be noted. Both cracks have already exceeded the estimated critical crack length of a ≈ 3.5 µm. However, one must note that this estimate assumes a tensile load, whereas the stress state at a bore is more complex, and a crack can be stopped when compressive stresses prevail.

It was assumed that particles from the process water are the main reason for initiating the cracks in the orifice jewel, as this explains the large variation in service life seen between different operating sites. The fact that precipitates from the water can form on the orifice surface have already been described by Jegaraj et al. [15]. The authors also suspect a relation between different salt particles and the chipping of the orifice bore’s edge. However, the authors can examine the orifices only after operation. Therefore, only the assumption of the connection of precipitates and orifice damage remains.

Figure 8 shows that, in this study, substantial amounts of particles can also be detected on the jewel for low operation time with more switching operations. As can be seen in Figure 8a, the particles occur more frequently in the orifice bore area where high fluid velocities are present and less frequently at the outer rim. Thus, it was concluded that particles tend to precipitate out of the solution due to fluid dynamic effects, which can occur due to local cavitation-induced evaporation. In areas such as biotechnology [38] or the production of nanoparticles [39], this effect is deliberately utilized. To further investigate the effect of particles on the orifice jewel, their size and their chemical composition was measured, as detailed in the next chapter.

3.2. Particle Analysis

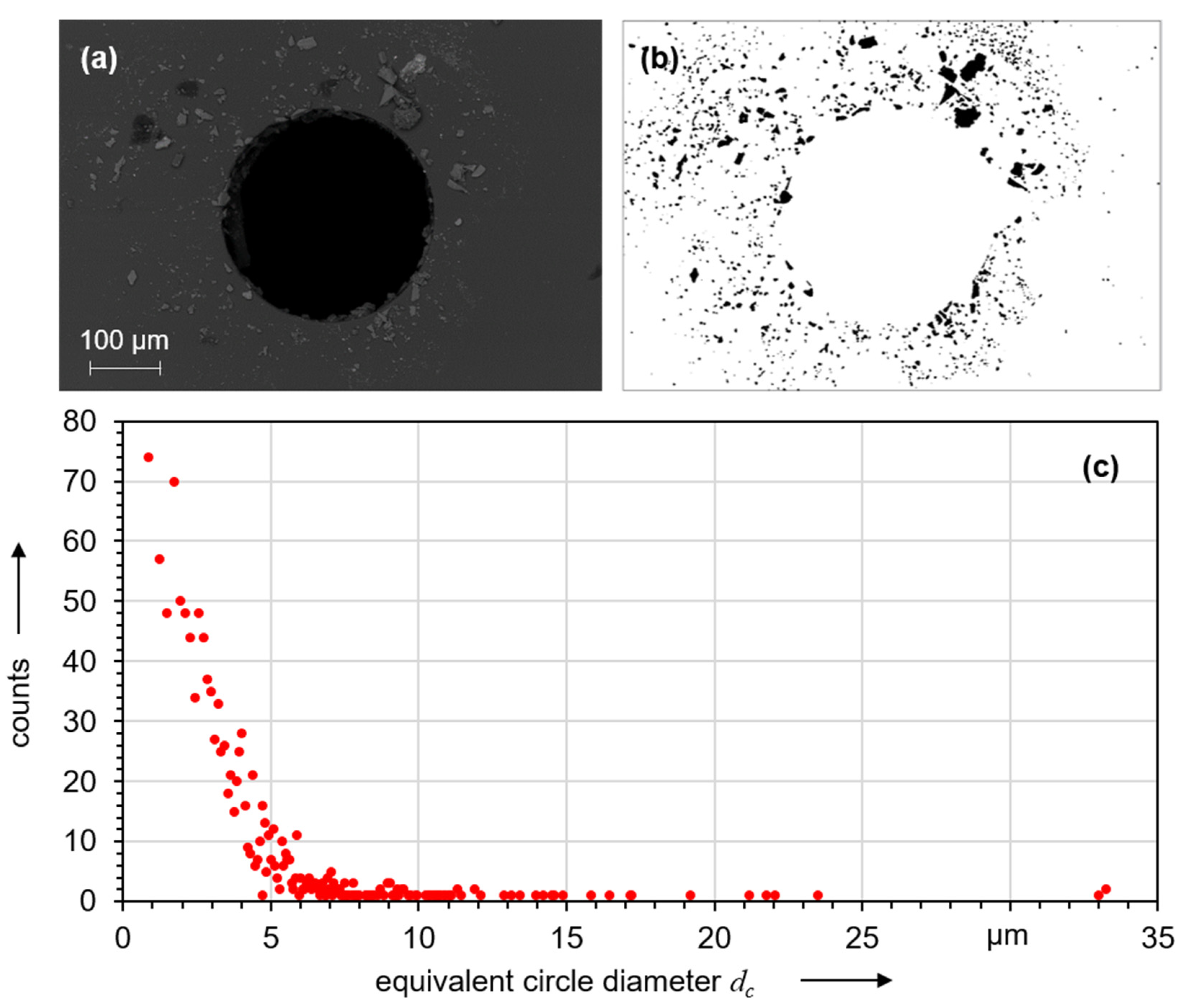
The particle size distribution was determined using digital image processing. The images were processed to obtain binary images (Figure 9b) using threshold values. Based on the different shapes of the individual particles, the diameter of a circle with the same area was then calculated. Figure 9c shows the distribution of the diameters of these equivalent circles. For an equivalent diameter below 5 µm, the number of particles increases exponentially. The largest particles observed had an equivalent diameter of 33 µm. Large particles generally have a higher damaging potential, which is why they are also more strongly represented in the remainder of this study. The investigated orifices all originated from a system that had a 5 µm pre-filtration on the pump side. This filtration exceeds the recommendations given in the literature. For example, Wright recommends filtration with a filter mesh size of 10 µm [25]. Despite the higher quality filtration of the process water, particles can still be found on the orifice jewel. The high number of particles below this filter mesh size can, therefore, be explained as foreign particles. Yet, the particles with equivalent diameters of more than 5 µm have a different origin.

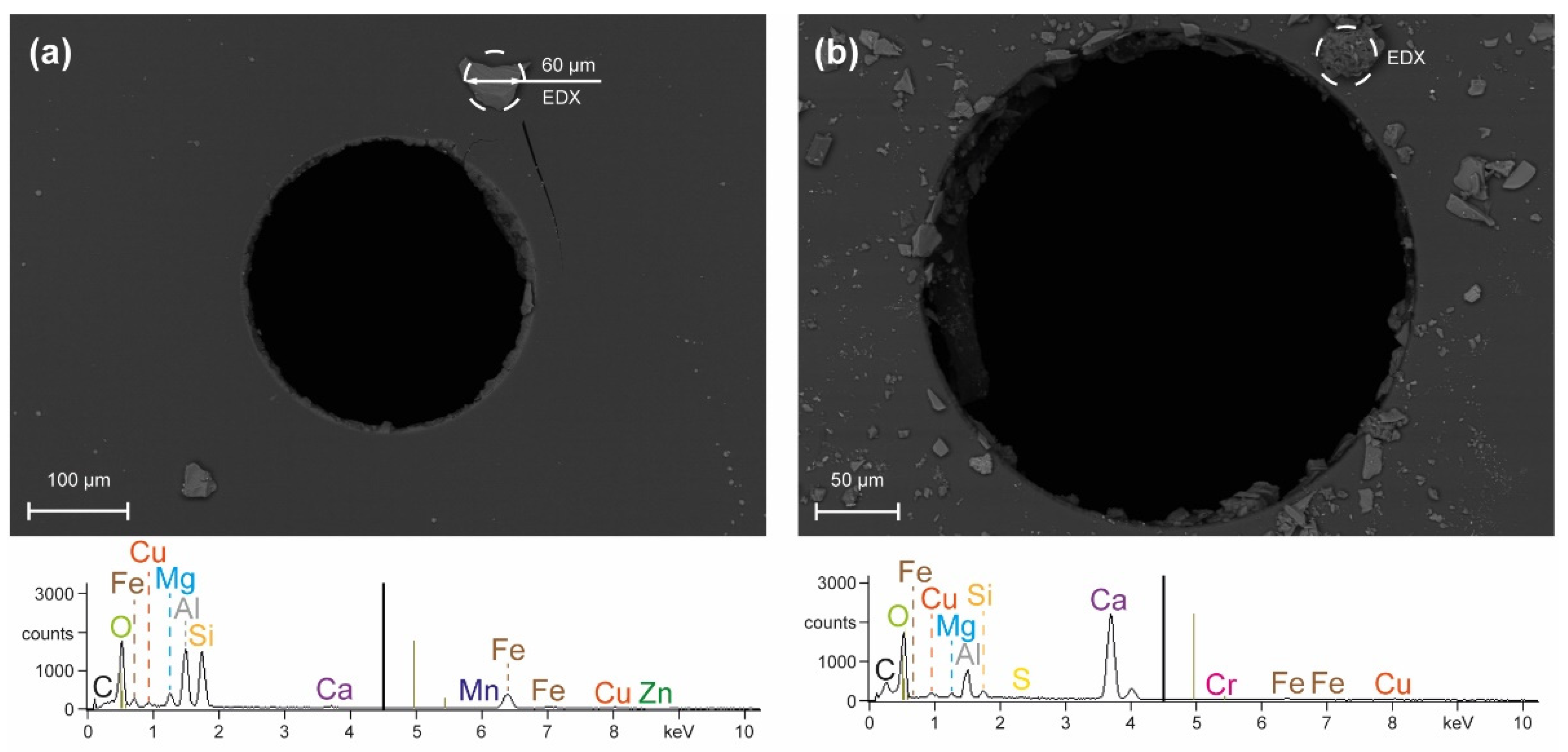
Energy-dispersive analysis of X-rays (EDX) of selected particles was performed to more comprehensively determine the origin and nature of these particles. The analysis in Figure 10a shows the elements oxygen, aluminum, silicon, and iron and traces of the elements copper, calcium, magnesium, and zinc. It should be noted that light elements are difficult to quantify with EDX. Still, the element composition demonstrates that the investigated particles had their origin in the tap water itself, i.e., all elements detected occur dissolved in the tap water. Specifically, the major element silicon should not originate from the pump, piping system, or other plant components. The element aluminum is the main component of the orifice sapphire itself and is thus present upon analysis of thin particles. The element iron is contained in almost all components of the water jet cutting system and can pass into the tap water dissolved or as abrasion.

Although EDX can only be used to determine elemental compositions and not molecular structures or chemical compounds, further conclusions can still be drawn based on known chemical–physical relationships. For example, the presence of silicon indicates the formation of a silicate particle. It is known that silicates can exist dissolved in water and that their solubility is pressure-dependent [40]. In conjunction with the other elements detected, it is concluded that the present particle consists of an iron–aluminum silicate (Fe₃Al₂[SiO₄]₃).

Analysis of other particles showed similar chemical composition. However, the proportion of trace elements that can no longer be clearly identified increased in the case shown in Figure 10b. In this case, the strongest EDX signal was obtained for the element calcium, and the particle is assumed to be of calcium carbonate (CaCO₃) type. This assumption appears valid as calcium carbonate occurs as a solid that is present in almost all water-bearing systems.

Based on the EDX analysis, all particles were assumed to be calcium carbonate or iron–aluminum silicates in the numerical analysis. These two particles have different chemical–physical properties. Specifically, the mechanical properties of the iron–aluminum silicate almandine and the calcium carbonate calcite were used for further numerical investigations.

3.3. Numerical Calculations

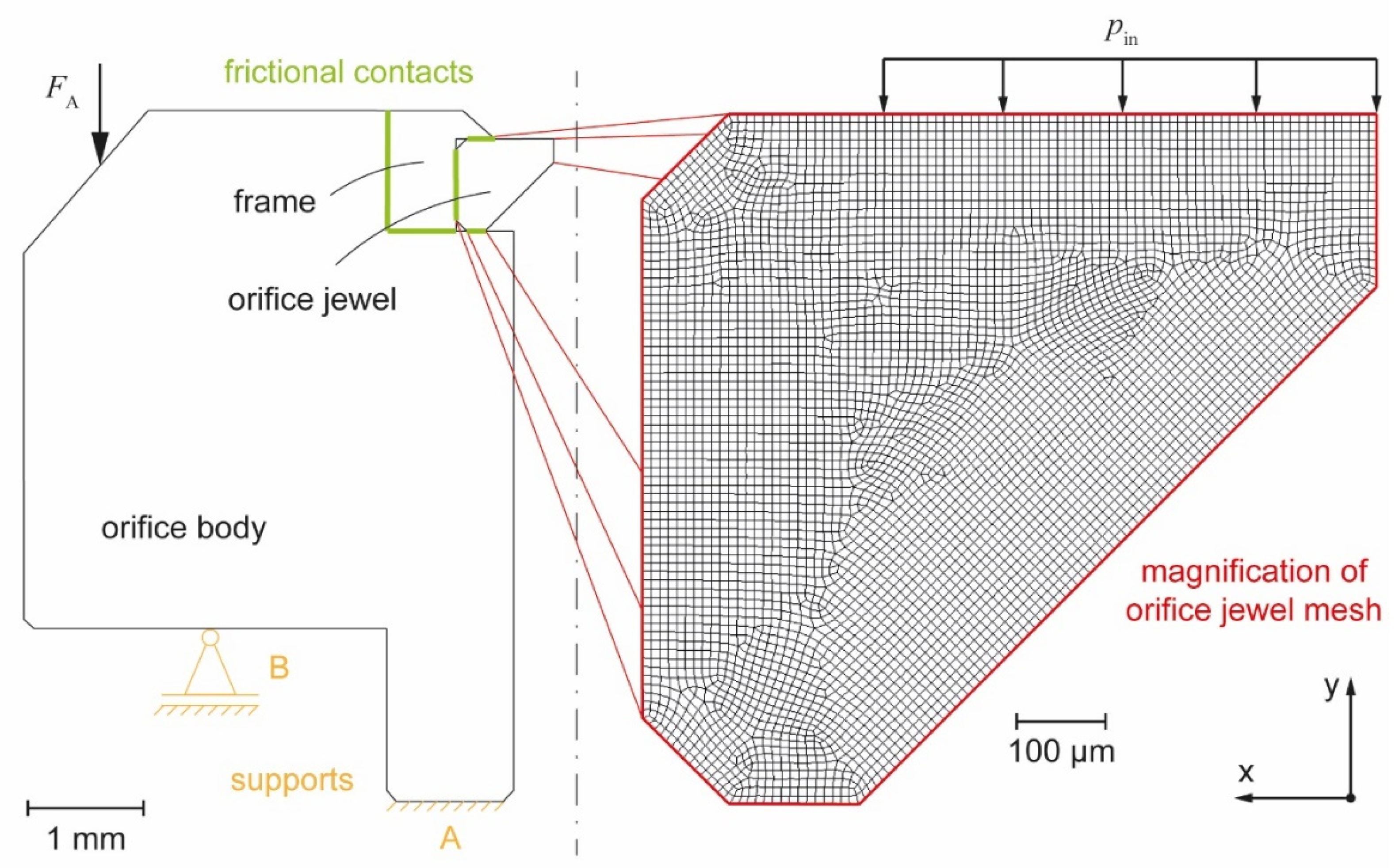
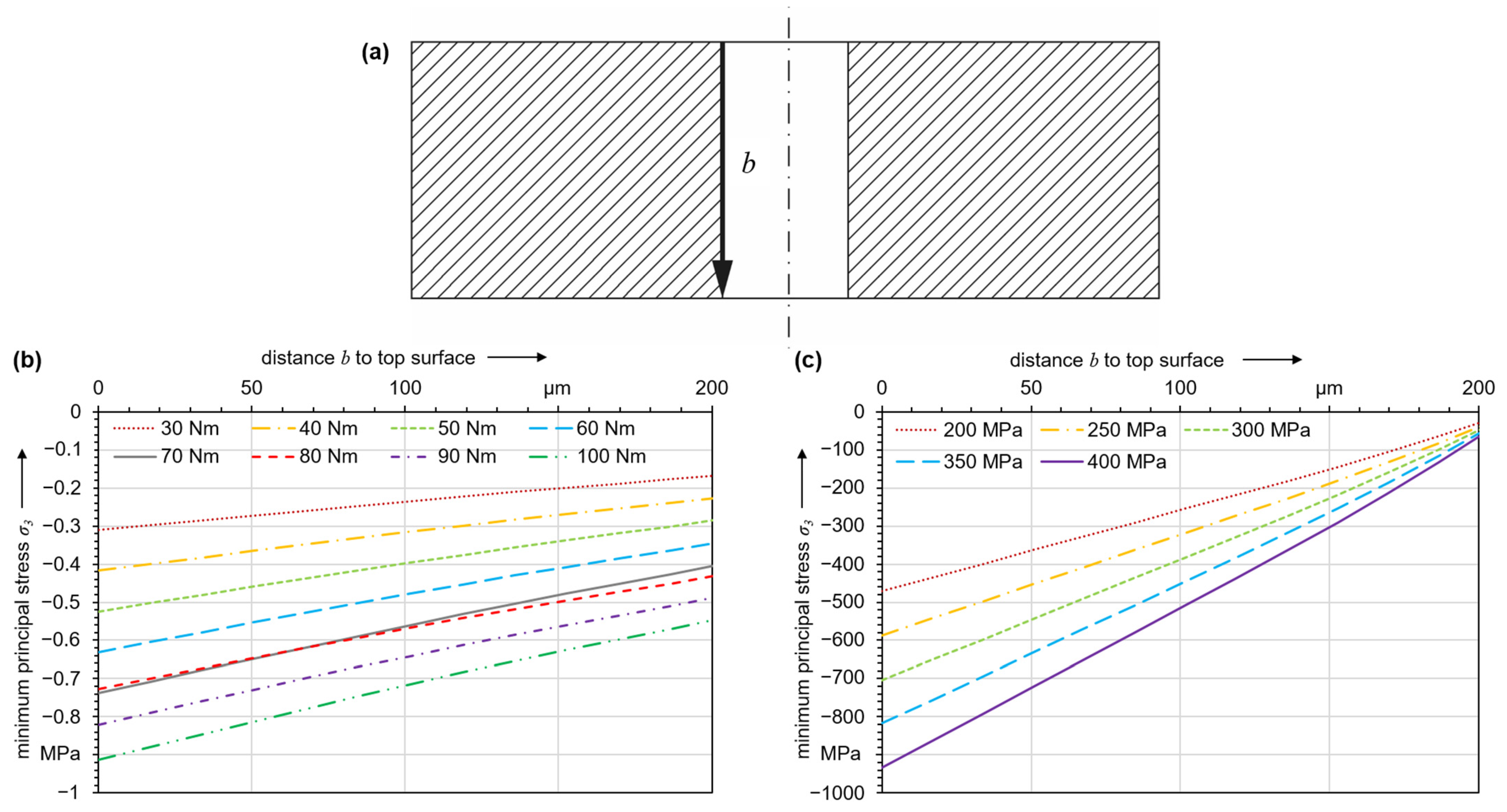
For brittle materials like sapphire, fracture occurs due to a separation normal to the maximum principal stress for a given multiaxial stress state. Already the assembly of an orifice in the water jet cutting system establishes a stress state, and Figure 11a shows the effect that different tightening torques have on the main stress in the orifice jewel. The curves shown in Figure 11a are for tightening torques of 30 to 100 Nm. The compressive strength of sapphire is σ_c = 2 GPa, whereas the tensile strength, σ_t, is only about 200 MPa [27]. Along the orifice bore, only compressive stresses are present. They exhibit a local maximum directly at the edge of the orifice bore and decrease with increasing distance from the top surface. By convention, compressive stresses are plotted negatively, so the compressive stress with the highest magnitude is equal to the minimum principal stress. Higher tightening torques lead to higher compressive stress, but they are about three orders of magnitude lower than the material strength. The calculated stresses due to assembly are negligible, and thus it is extremely unlikely that a tightening torque exceeding the specification by a reasonable amount will lead to damage to the orifice jewel.

Figure 11b shows the stresses after assembly with a tightening torque of 70 Nm under operating pressures between 200 and 400 MPa. Still, the local maximum is present at the upper edge of the orifice bore, but the magnitudes of the induced stresses are higher by factors between 5 ∙ 10² and 10³ compared with the unpressurized state. Clearly, the stress state is by far dominated by the operating conditions, whereas initial tightening has only a minor effect.

The stress field caused by the operating pressure will slightly oscillate due to fluctuations occurring from the operation of the pump. When using a hydraulic pressure intensifier, these fluctuations are approximately in the range of ±1% of the nominal pressure [41]. Therefore, these fluctuations are neglected in the following, as fatigue limits in ceramics tend to be close to monotonic strength values.

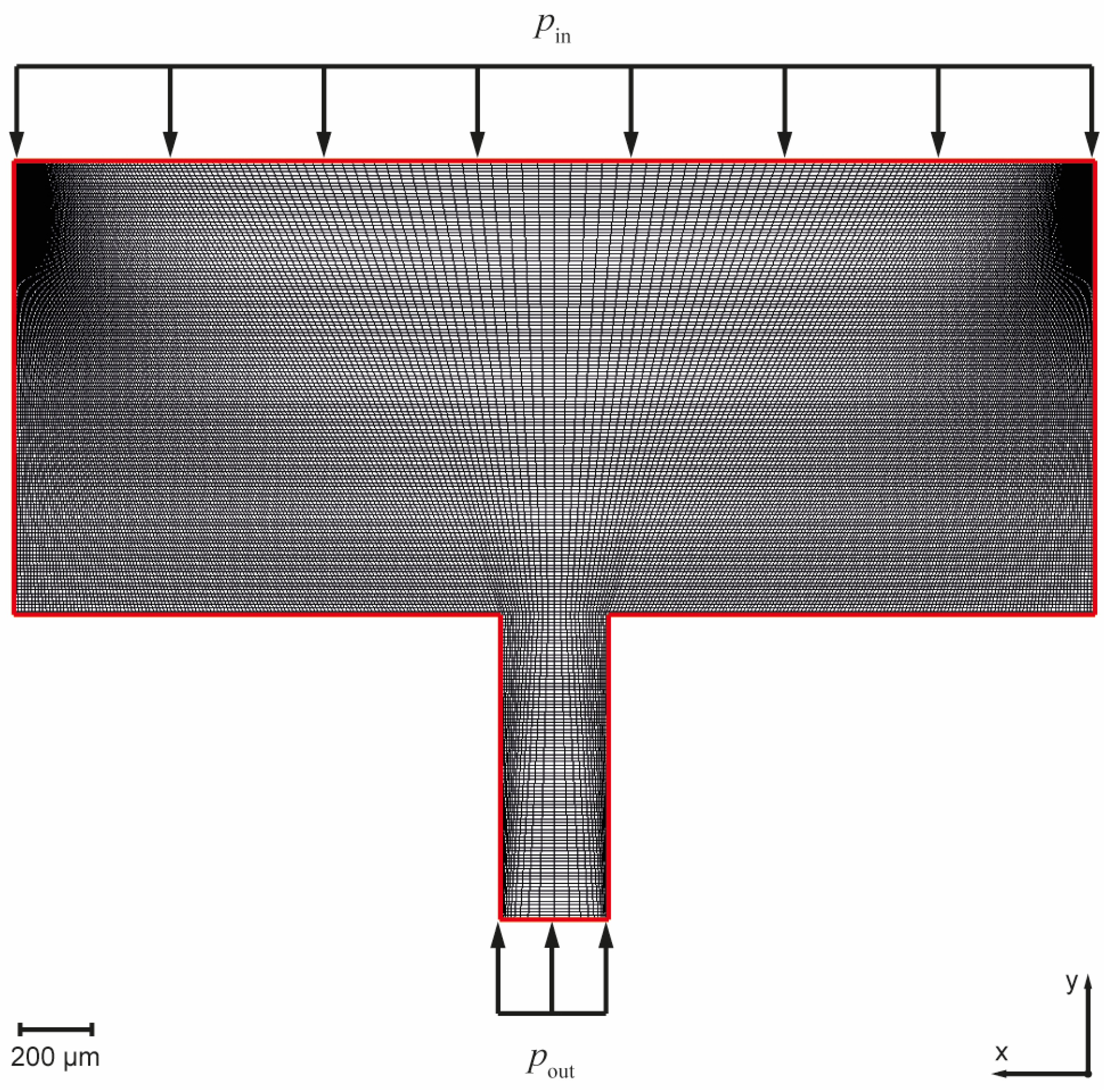
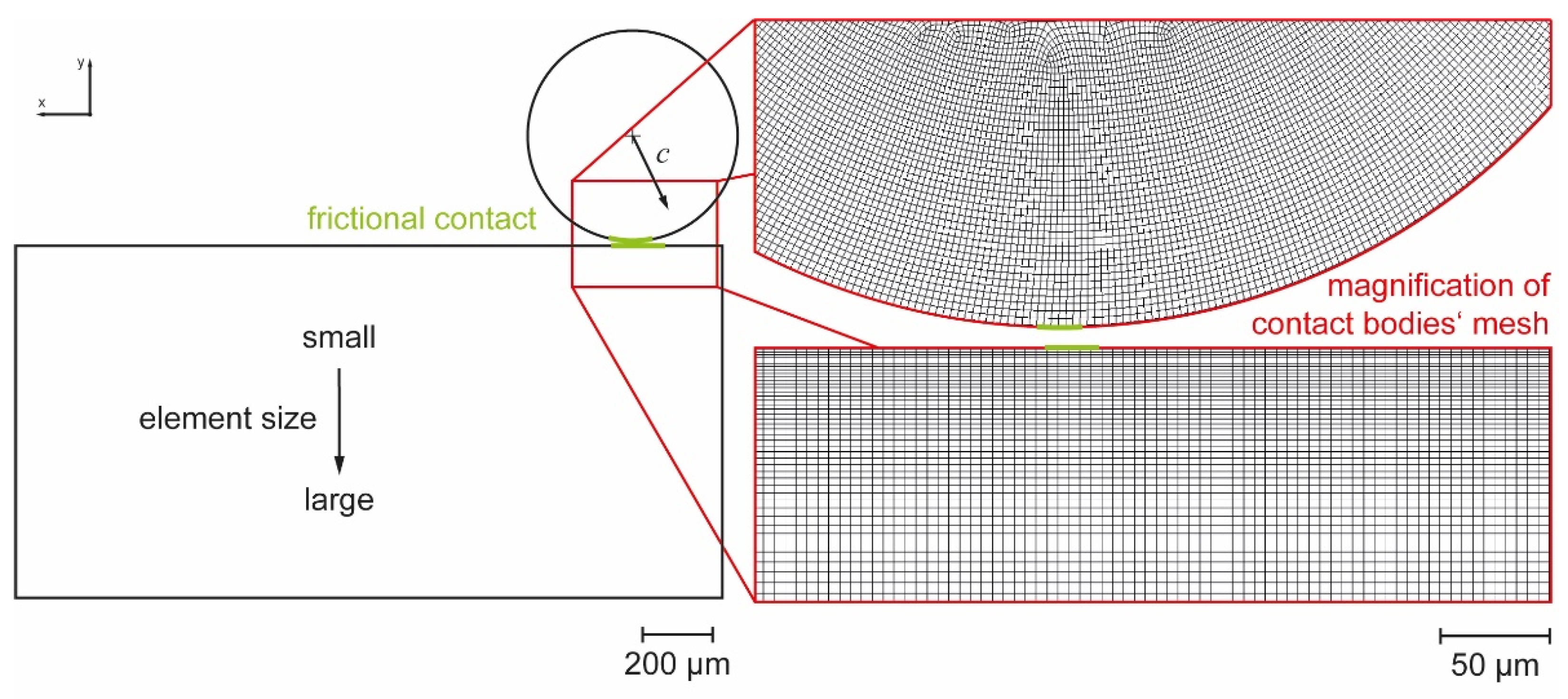
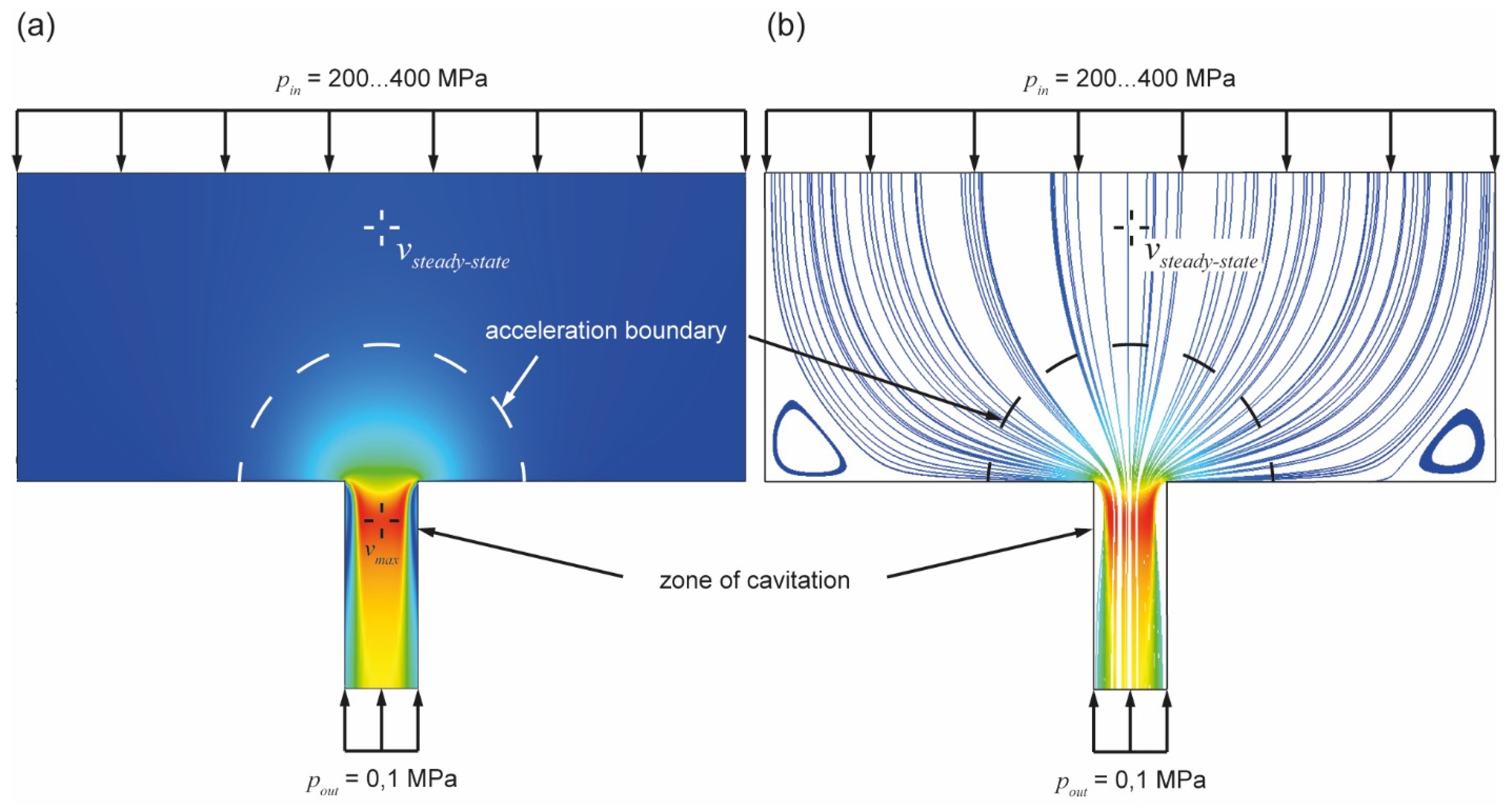
Upon impact, particles transported in the water can locally change the state of stress resulting from the operating pressure. Particles cause short-time discontinuous effects during operation. Particles follow the direction of the water flow through the orifice. For the modeling of the interactions of particles and the orifice jewel, the characteristics of the flow field around the orifice bore were obtained from numerical simulation. The flow field for operating pressures between 200 and 400 MPa was modeled as a steady-state one, i.e., it represents the condition in operation of a water jet cutting system after a sufficiently long time after actuating the pump and cutting valve. Figure 12a shows a representation of the flow field, where the velocity data are normalized with respect to the maximum value. The direction of the flow field vectors is shown by the representation of the streamlines in Figure 12b. At a larger distance from the orifice bore, the flow velocity in the collimation tube changes only slightly over the cross-section, and this value is referred to as the steady-state velocity. In the area around the edge of the orifice bore, a strong acceleration of the flow occurs due to the cross-sectional constriction. In addition to the magnitude, the direction of the velocity vectors of the flow field also changes drastically near the orifice bore. These results are in accord with the studies of Annoni [42], Basha et al. [24], and Urazmetov [16]. Basha et al. also observed the constriction of the water jet inside the orifice bore because of zones of cavitation. Additionally, the calculated flow velocities correlate with the author’s results [24]. The calculated velocity profile of Annoni et al. also matched the results presented in this paper [42]. Differences occur because of their slightly different orifice geometry, but they can be neglected as they are present at the orifice bore exit, which is not taken into account within the context of this study. The results of Urazmetov et al. [16] match the results of Annoni et al. [42] very well and correlate with this study as well. The flow field calculations can therefore be considered as valid.

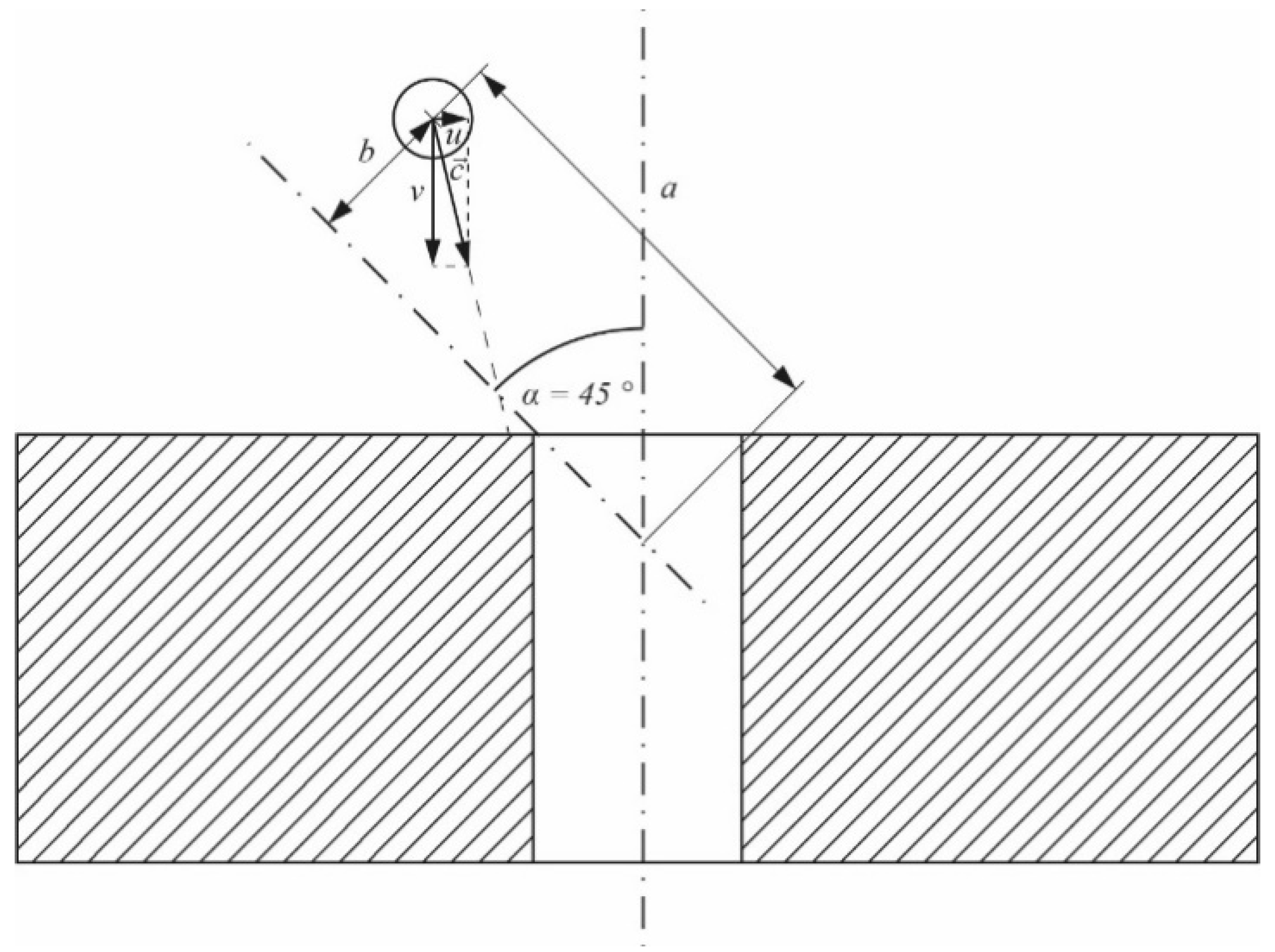
Given the velocity gradient and the deflection of the flow in the acceleration zone, individual particles can continue their trajectory and impact the orifice jewel. In Figure 13, a point of the flow field is shown where it can be assumed that the impact of the particle on the orifice jewel occurs with a high normal component, and thus, a high damage potential.

The magnitude and direction of the velocity vectors for the critical particle position differ depending on the pressurization of the system. The components of the vectors at different operating pressures are shown in

Table 4. Components of velocity vectors at different operating pressures p for the critical particle trajectories; the velocity vector c consists of two components, i.e., in the x-direction (u) and y-direction (v).

p, MPa	u, m/s	v, m/s	|c|, m/s
200	−33.5	−65.4	73.5
250	−36.9	−72.1	81.0
300	−39.9	−77.9	87.5
350	−42.6	−83.1	93.4
400	−45.0	−87.8	98.7

.

For each operating pressure, particles with diameters between 5 and 60 µm consisting of the two observed materials, calcium carbonate and iron–aluminum silicate, were modeled. The parameter selection covers a wide range of experimentally observed particles without excessively increasing the computational effort. The computational effort was further reduced by utilizing axis symmetry and setting up the simulation in a 2-dimensional space. Additionally, the movement of the individual particles was kept to a minimum before contact. With this approach, a runtime of 36 min was realized on average for each case.

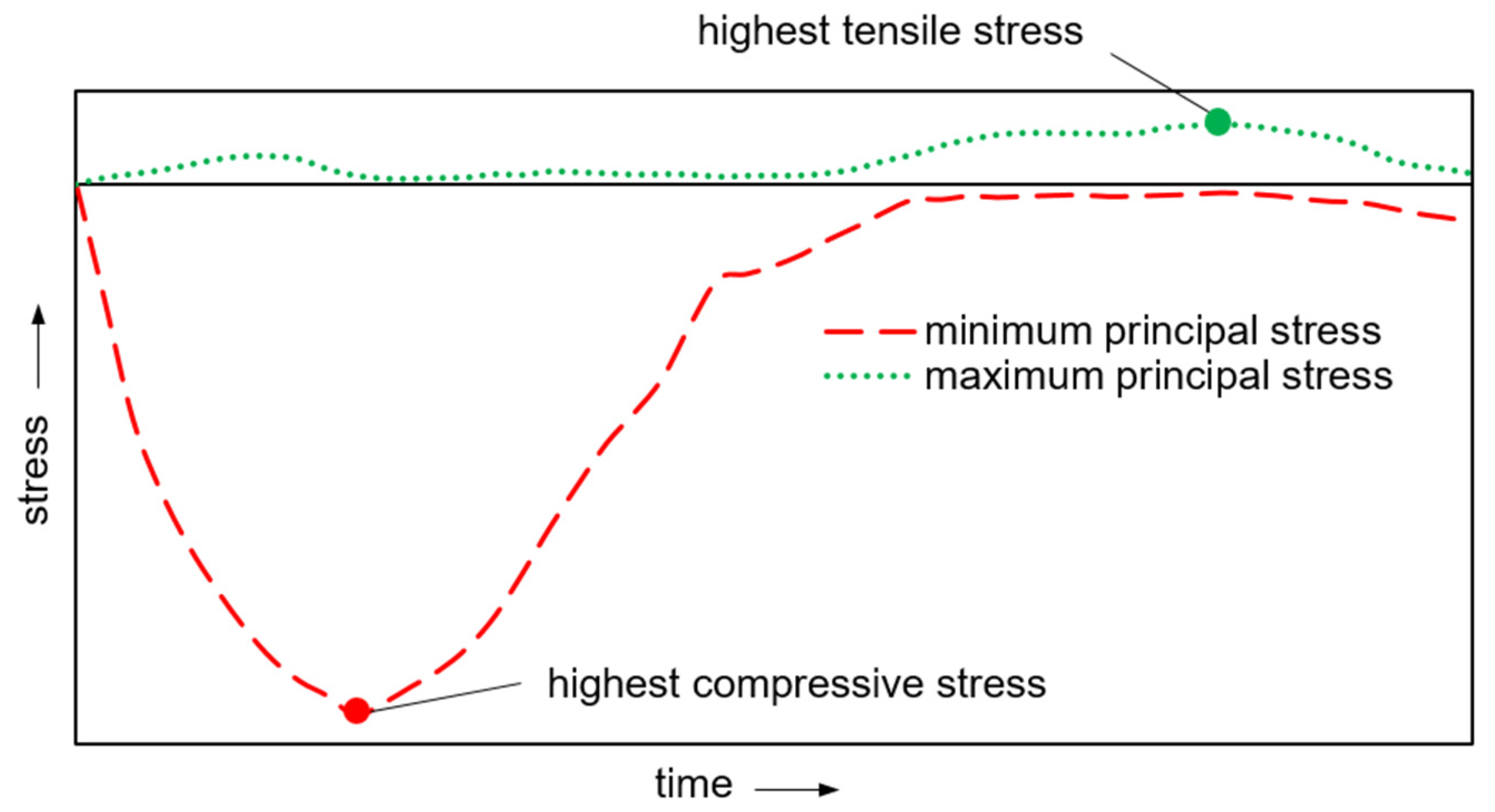
Because of the dynamics of particle impact, the stress state is time-dependent. Principal stresses with high magnitudes can arise when the particle contacts the orifice jewel’s surface. In the following, the maximum and the minimum principal stresses are considered. In the described case of particle impact on an orifice jewel’s surface, these represent the maximum tensile and the maximum compressive stresses, respectively, in the principal coordinate system. Taking the time dependence of the load during particle impact into account, a shift between the maximum tensile stress (temporal maximum of maximum principal stress) and the maximum compressive stress (temporal minimum of minimum principal stress) occurs. Figure 14 qualitatively shows the induced stress at particle impact over time. For further investigation, the time points with the respective highest magnitude of tensile and compressive stresses were determined, as it was not known a priori which stress state is critical for failure. The two maxima occur at different times so that both principal stresses never have their maximum value at the same time.

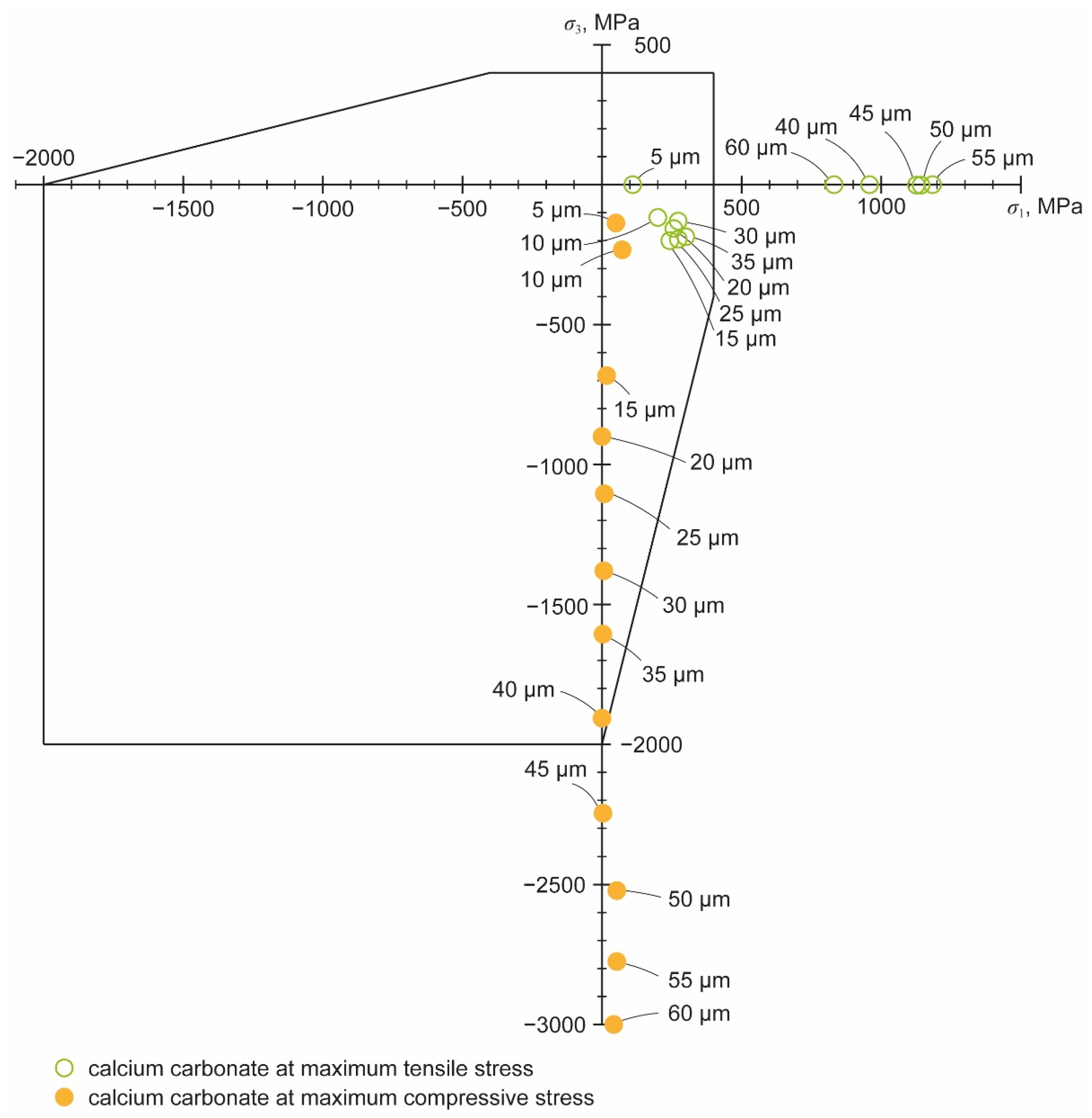
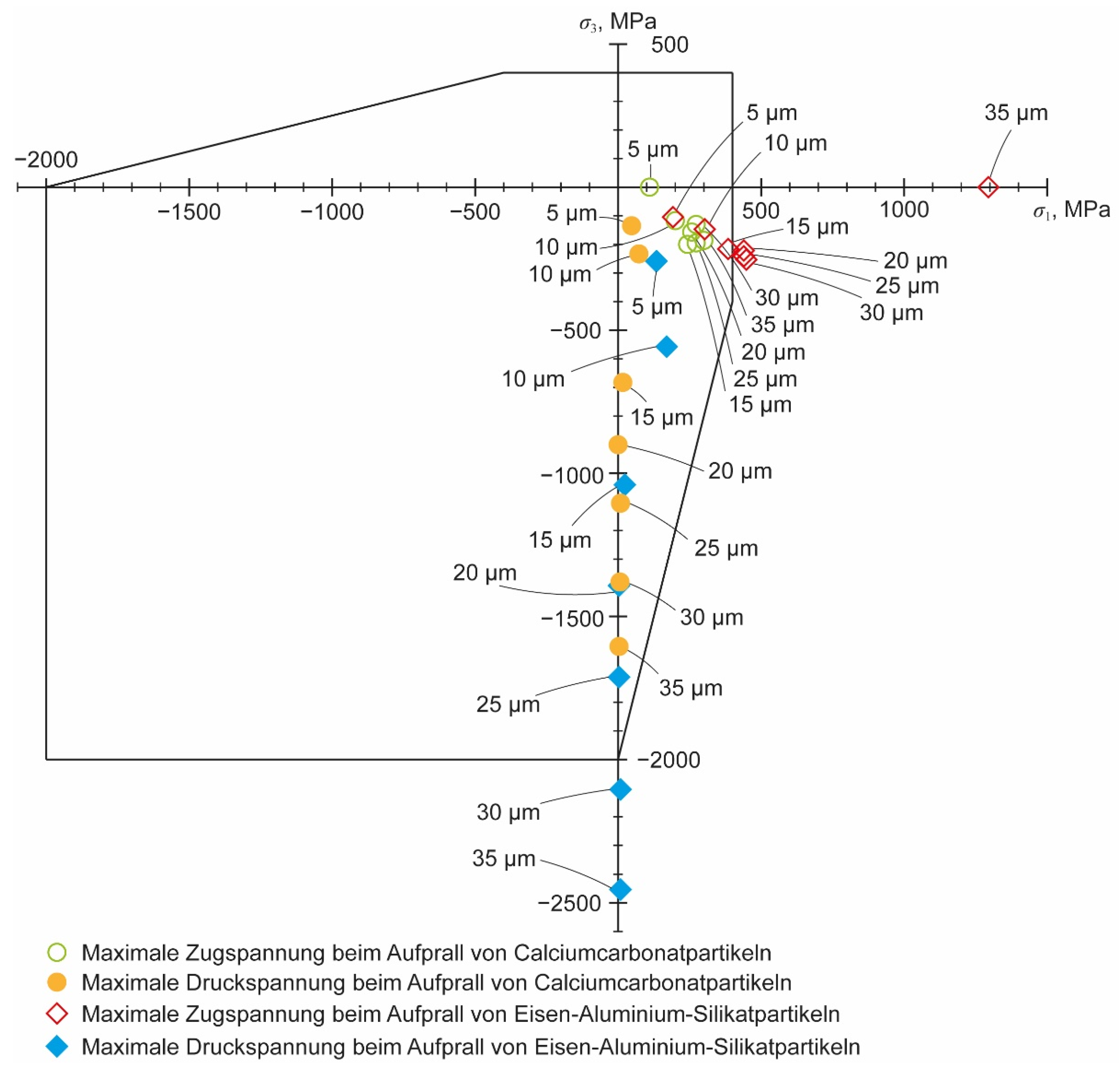
The stresses caused by a particle impact depend on particle diameter, operating pressure, and particle material. For evaluating a particle’s damage potential, the modified-Mohr failure criterion was employed. The criterion is widely used to predict the failure of brittle materials and fits experimental data better than the Coulomb–Mohr criterion, even though it is less conservative [43]. Figure 15 shows the failure envelope obtained for the stresses caused by the impact of calcium carbonate particles of different diameters at 300 MPa operating pressure. The diagram illustrates the position of the principal stresses in relation to the mechanical strength of the material. Damage to the orifice jewel occurs as soon as a point lies outside the failure envelope. These loads, which exceed the material strength, then result in initial damage to the surface during operation, which in turn is the starting point for further crack growth and can lead to the final failure of the orifice.

For the carbonate particles at an operating pressure of 300 MPa, the limit of acceptable particle size appears to be around 30 µm. At this diameter, the principal stress is not yet outside the envelope at the moment of either the greatest tensile or the greatest compressive stress. With a particle diameter of 40 µm, the third principal stress at the moment of the highest compressive stress is still inside, but the first principal stress at the moment of the highest tensile stress is outside the envelope. Next, for particle diameters of 30 µm and below and an operating pressure of 300 MPa, silicate particles of the same diameters were added. Figure 16 shows the increased damaging potential of the particle assembly. The silicate particles have a higher damaging potential, so the critical particle diameter has now dropped to 15 µm. As with the impact of the carbonate particle, failure also occurs in the bore due to tensile stresses when a silicate particle impacts. The diagram clearly shows that for the same particle diameter, there is a much larger safety factor in the region of compressive stresses. Considering only the moment of greatest compressive stress, the critical particle diameter would not be 15 µm but 25 µm. In essence, crack initiation due to particle impact can occur because of the high induced tensile stresses with silicate particles having the higher damage potential. Therefore, when considering the pressure dependence, only these stresses resulting from the impact of silicate particles are plotted in the remainder of this paper.

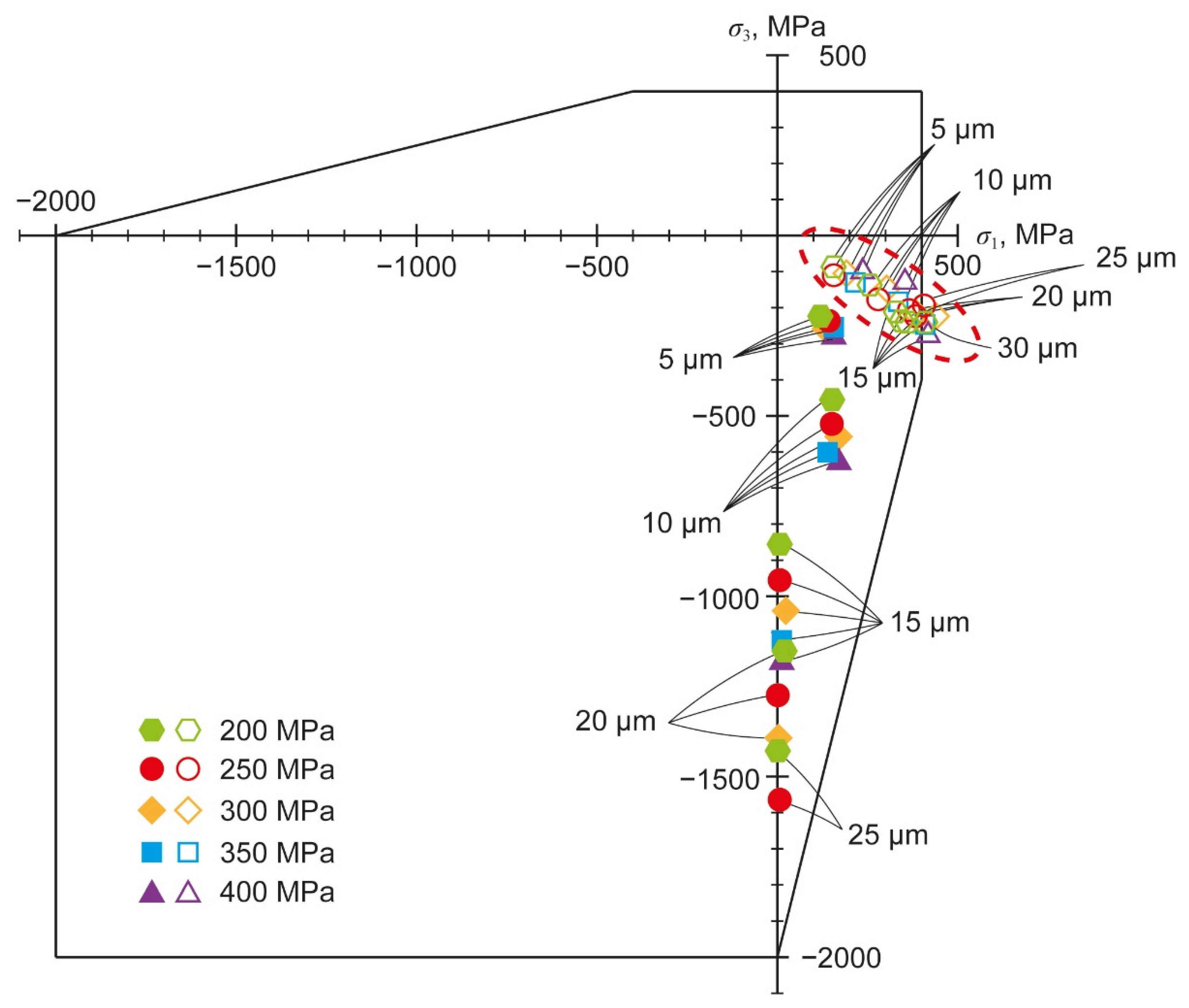
Figure 17 shows the dependence of principal stresses on the operating pressure, and only the stresses caused by the more damaging silicate particles are plotted.

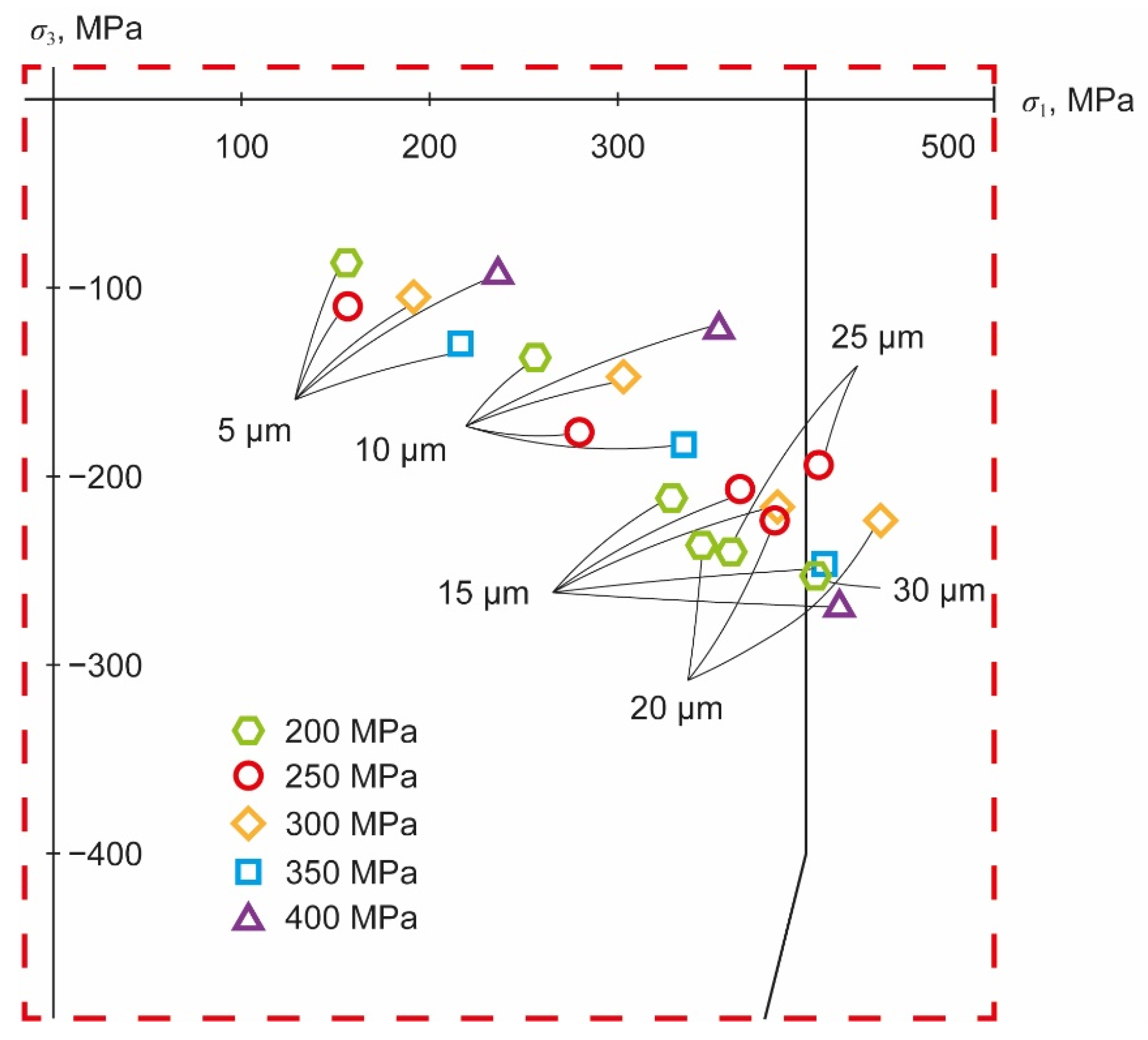
To determine the critical particle diameters, Figure 18 shows a magnification of the dashed area outlined in Figure 17. In Figure 18, only the principal stresses at the moment of the largest tensile stress are given. Considering the different operating pressures investigated, the critical particle diameter varies from 25 µm at 200 MPa to 10 µm at 400 MPa. Silicate particles with diameters as small as 10 µm can therefore contribute to the initiation of cracks in the orifice jewel. This accords with the empiric observations and the recommendations for filtration that are given in the literature. Orifice testing leads to the recommendation of a 10 µm filtration, as stated by Wright [25]. Taking the results shown in Figure 18 into account, the assumption seems to be valid. Even if earlier studies did not differentiate between different types of particles and did not look into their origin, it is plausible that their experiment contained silicate particles that did have the same damaging potential as the particles in this study.

Clearly, the effect of an impacting particle on service life of an orifice depends on the operating pressure as well. A reduction in the operating pressure leads to an increase in the critical diameter. An increase of operating pressure, on the other hand, would place increased demands on the particle-free nature of the water. Momber published that a filter mesh size of 10 µm is already mandatory for operating pressures above 100 MPa and that the manufacturer’s recommendations should be applied to further increase operating pressure [44].

Even if the details of the interaction of individual particles with the orifice jewel surface were not modeled, the damaging effect of particles on orifices is clear. The impact of particles induces stress in the region of the orifice bore, which locally leads to material failure, i.e., initiation of cracks in the sapphire. High loads are particularly critical in the orifice bore since, in additional to the operating pressure, loads are expected there due to the flowing fluid because of the quasi-stationary state of cavitation. The presence of cavitation load is proven by many authors, such as Hashish [14], Annoni et al. [42], Basha et al. [24], and Urazmetov et al. [16]. Additional stresses due to mounting and alignment, mentioned by Powell [13], can not be confirmed within this study.

Stresses due to particle impact and cavitation may coincide with damage sites seen in worn orifices obtained in this study. The damage sites also correlate with the damage sites observed by other authors, like Jegaraj et al. [15] and Li et al. [37]. It is possible that crack growth starts from the orifice bore and progresses to the orifice jewel surface. Even without cavitation, the present results already demonstrate the presence of critical stress for the usual operating pressure of 300 MPa with common carbonate particles with a diameter of 40 µm. Other substances, such as silicates, which are present in almost all process waters, can cause damage even at smaller particle diameters of 15 µm under these conditions. Increasing the operating pressure further decreases the critical particle size. This result has led to the recommendation of a 10 µm filtration in the past [25].

Adding the factor of additional loads and assuming that the discontinuous loads from particle impacts and cavitation are equal, a safety factor of S ≥ 2 would be required considering the particle diameter. According to the modified-Mohr failure envelope, this leads to a maximum tolerable particle size of about 5 µm at the maximum operating pressure of 400 MPa.

With regard to foreign particles, this boundary condition is satisfied today in most modern water jet cutting systems by sufficiently fine pre-filtering. Taking the load resulting from the pressurization of the orifice due to the operating pressure into account, an additional stress of more than 900 MPa affects the bore edge at an operating pressure of 400 MPa. Since this additional compressive stress results in a shift in the modified-Mohr diagram in the negative y direction, the stresses are then outside the failure envelope for a particle diameter of more than 5 µm. By adding the assumed cavitation safety factor, this leads to a need for a pre-filtering with a mesh of 2 µm or less.

Other studies give different recommendations for filtering high-pressure water. Wright [25] recommends a filter mesh size of 10 µm for waterjet cutting, whereas Momber [44] suggests 25 µm. Even if the given recommendations seemed to be valid without taking additional loads into account, it can be shown that the safety margin was very low. As these studies were made almost two decades ago and there have been no other recommendations so far, these large values may explain the fluctuations in orifice service life observed in practice. Thus, this study provides new data for a better understanding of the water treatment required in waterjet cutting to reduce premature orifice failure.

The present study also showed the range of particles precipitating from the water during operation, which filtering of the tap water cannot prevent. Commercially available filters allow filter mesh sizes around 1 µm. However, high-pressure filters can only be installed at some distance in front of the switching valve and the actual cutting head. Thus, there is still a risk of precipitation, especially in the cutting head. The avoidance of these precipitates by physical-chemical or design measures will be of central importance for future high-pressure water cutting systems to increase the service life of the orifices.

4. Conclusions

The premature failure of high-pressure water jet orifices was studied using a combined numerical and experimental approach. The main results can be summarized as follows:

• High local stresses resulting from particle impact on the brittle orifice jewel were identified as a major cause for premature crack initiation and formation of edge chipping at the orifice bore.
• Depending on the chemical composition of the particles, a critical particle size of around 10 µm was calculated for typical operating conditions of a high-pressure water cutting system.
• In the presence of further loads, such as cavitation, particles with a diameter of 2 µm can already damage the orifice jewel.
• Pre-filtering of water is not sufficient to avoid the presence of particles of a critical size, as particles can precipitate from the water within the cutting head.
• Chemical analysis showed that the particles present on the orifice were of the iron–aluminum silicate (Fe₃Al₂[SiO₄]₃) and calcium carbonate (CaCO₃) type. Their different damage potential can be accounted for using the modified-Mohr failure criterion.
• Stresses induced by applying excessive torque upon assembly were found to have only a minor effect.

This study provides key data on the damage potential of particles, although it was limited to sapphire orifices of type 91 that are frequently used for pure and abrasive water jet cutting. The implementation of the interaction between particles and the orifice jewel in a numerical model allows estimation of the damage potential of particles impacting on the orifice jewel, and also enables the prediction of the stresses in the orifice jewel with high lateral resolution. In the future, this database can be exploited for targeted design and tailored material modifications at potentially vulnerable areas of the orifice to minimize the risk of premature failure, extend the overall service life and increase process reliability and manufacturing accuracy in waterjet cutting.