Experimental Research of the Hydrodynamic Processes of an Axial Piston Water Hydraulic Pump

Abstract

Water hydraulic components and systems play pivotal roles in the development of modern hydraulics. Sustainable development and environmental protection cannot be imagined without the use of water as a working medium in modern hydraulic systems. An axial piston pump is the main component of these systems. This paper presents analytical and experimental methods for the development of an axial piston pump. The presented mathematical model is rooted in numerous research results in the literature and in our own experience. It is based on mathematical modelling of hydrodynamic processes of a water hydraulic axial piston pump which, combined with experimental research, provides a great tool to analyse the influence of different factors on the operating process and to optimise the pump parameters. The experimental equipment used in our tests simulates a real hydraulic installation, and the obtained results are very close to the actual operating parameters. This research included a modification of the swash plate in order to achieve ideal operating parameters and, thus, extend the service life of the pump. Water has a number of advantages over conventional hydraulic oils. It is a sustainable, environmentally friendly resource, more readily available than oil (lower transportation costs), cheaper to dispose of, non-flammable and non-toxic, and its high thermal conductivity aids in cooling.

1. Introduction

Modern water hydraulics should enable the use of water as a working fluid and, thus, provide an environmentally friendly alternative to the widespread oil hydraulics. Water hydraulics is particularly suitable for industrial activities such as food processing, seawater desalination, steel production, mining, packaging industry, pulp and paper industry, nuclear power production, and the production of mobile machinery for environmentally sensitive areas. Researchers face great challenges in the search for innovative solutions in order to make water hydraulics more competitive and reliable than hydraulic and pneumatic systems. Due to technical imperatives and application requirements, there is a need for continuous research. Sustainable development and environmental protection are strong global trends that ensure the important role of water hydraulics in the future. The modern development of pumps sets the standards in these systems, both in terms of increasingly strict operating modes and their quality and reliability.

Water has low viscosity, so the use of water as a lubricant can cause solid friction and wear in water hydraulic axial piston pumps under challenging operating conditions [1]. The testing of a physical prototype over a range of different operating conditions showed significant wear on the bores, indicating that the grooves in the pistons of this unit, which are likely to be responsible for much of this wear, should be removed.

The modern methods of development and design of hydraulic components and systems are inconceivable without the use of appropriate mathematical models of phenomena and processes [2,3,4]. A mathematical model of a process represents an analytical interpretation of the process with certain assumptions [5,6,7]. The formulation of a mathematical model requires detailed theoretical research based on the laws of fundamental sciences and scientific disciplines in order to fully understand and interpret the process in question, adopt certain assumptions, and define the equations of the model [8,9,10].

Water is used as a hydraulic transmission medium instead of mineral oil in order to transfer energy, power, and resources in a sustainable way and to the extent that it does not endanger the environment [10]. Due to the increasing demands of society for environmental protection [11], sustainable development, and production safety [12], hydraulic power transmission has drawn attention as a technology that needs to be renewed and modernised [13,14]. Water hydraulics is becoming one of the most important areas of research in the field of power and energy transmission by fluids due to its exceptional performance characteristics, cleanliness, and energy savings [15]. Due to their significant advantages, water hydraulic systems are increasingly replacing oil, pneumatic, and electrical systems in many areas. New construction solutions and constant development have contributed to the fact that water hydraulic systems have a wide range of applications in various industrial areas [16].

Since the axial piston pump is one of the crucial elements of hydraulic systems for the transfer of mechanical into hydraulic energy, it has a wide application in various industries [17]. The hydraulic axial piston pump is essential in the application of water hydraulics [18,19,20]. Compared with mineral oil, water has lower viscosity which makes it difficult to achieve good lubrication [21,22]. The kinematic viscosity of oil is approximately 30 times higher than water viscosity at representative operating temperatures [23].

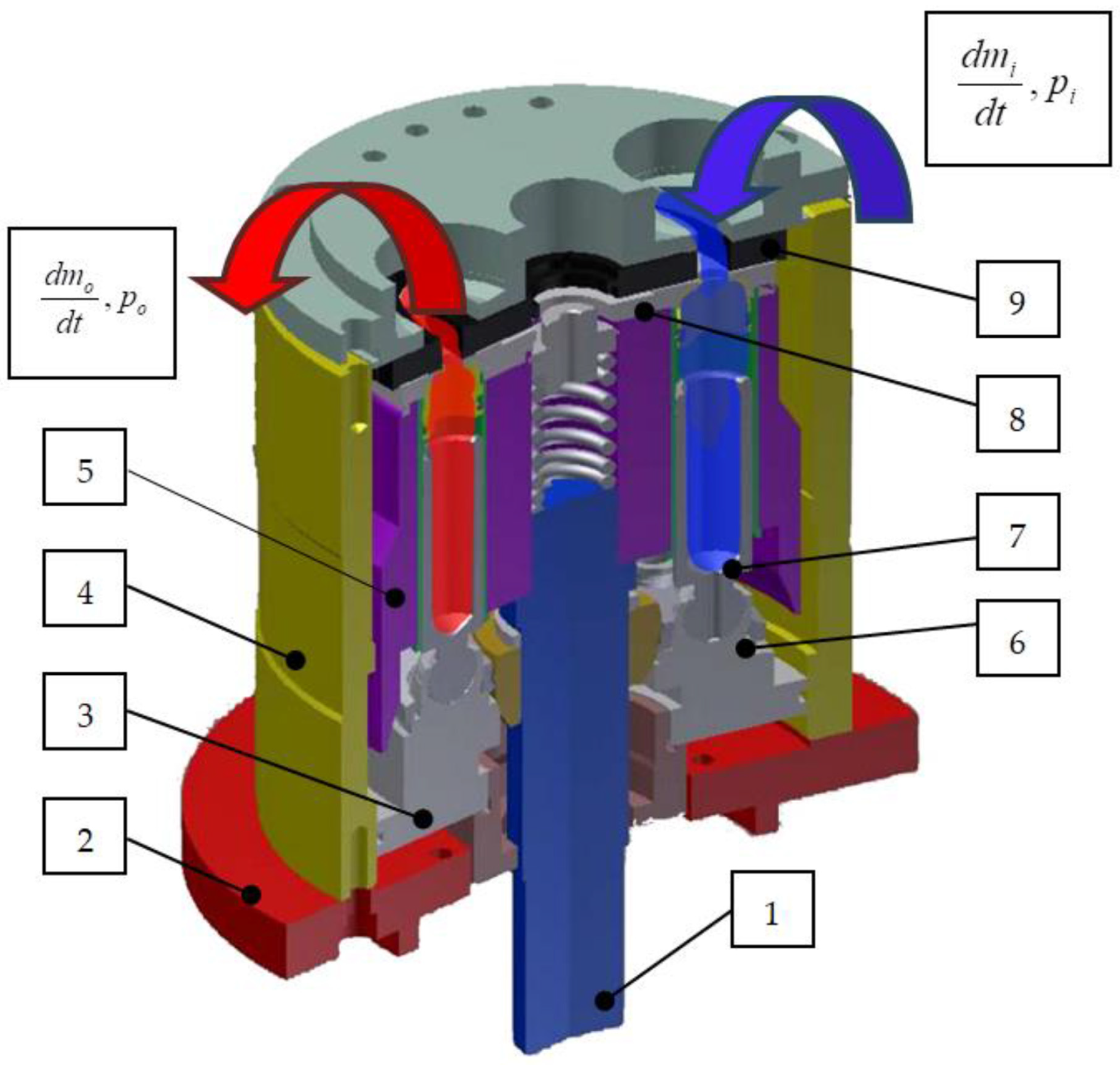
An axial piston pump (Figure 1) was tested using an installation specially designed for this experiment and mounted on an existing test bench at the Development and Research Laboratory “PPT—Namenska”. Due to the complex hydrodynamic processes of the pump, a large number of the experimental studies conducted in laboratories around the world cover only a limited number of the processes that occur inside the pump. The tests presented in [24,25] include various parameters of pump operation processes.

The interface between the piston slipper and the swash plate is one of the most important friction pairs in piston axial pumps. Zhou et al. [21] presented a new prototype pump and test equipment for studying the dynamic lubricating performance of the slipper/swash plate interface in axial piston pumps. In order to confirm the results of the numerical simulation, Yin et al. [26] performed an experimental study of a prototype pump under different inlet pressures and drive shaft speeds. They measured the outlet flow pressure under various conditions of insufficient suction flow rates due to cavitation. In addition, they performed experimental measurements of pump vibrations in order to examine the pump’s performance under the influence of cavitation. The wear between the piston and the cylinder bore is considered the primary cause of fault in axial piston pumps. Thus, the deviation of flow characteristics from a normal flow rate due to an increased leakage gap is considered one of the parameters for pump health monitoring [27].

2. Mathematical Model of Hydrodynamic Processes in the Pump Cylinders

Water hydraulic axial piston pumps are characterised by extremely complex dynamic and hydrodynamic processes that occur in the pump’s operating area. These processes are non-stationary, but they periodically repeat with each subsequent cycle in the stationary mode. The analysis of these processes requires knowledge and use of laws of mechanics, fluid mechanics, and mathematics [27,28]. Thus far, fundamental research has not explained the mechanisms associated with these processes, particularly under non-stationary conditions. For these reasons, mathematical models are not purely analytical but to a certain extent rely on empirical correlations and approximations. The suction, compression, and displacement of the working fluid in the cylinder and in the suction and discharge areas of the pump are modelled by applying the law of conservation of mass and the equation of state of the fluid.

Having formulated the mathematical model, it is necessary to make a mathematical interpretation of everything occurring in the entire physical system, i.e., it is necessary to simulate the physical system. When analysing a physical system, it is also necessary to precisely define system boundaries, the subsystems that constitute it, and their mutual relations, as well as the processes that occur in it. Then, the assumptions and mathematical models of all the previously defined processes have to be defined. The obtained system of equations and their mutual relations is a simulation of that physical model.

Applying the law of conservation of mass to the pump cylinder [29], it follows that a change in the mass of the fluid in the pump cylinder is caused by its flow into the cylinder during the suction phase and its flow out of the cylinder in the displacement phase which will be:

$$\frac{d{m}_c}{dt}=\frac{d{m}_i}{dt}-\frac{d{m}_o}{dt}$$

(1)

where the mass flow rate of the working fluid which fills the cylinders in the suction phase is defined by the Bernoulli equation:

$$\frac{d{m}_i}{dt}=k_1{\mu }_1{A}_1\sqrt{2{\rho }_p\left|p_i-p_p\right|}$$

(2)

The values of the constants are:

k₁= 1 for p_i ≥ p_p;

k₁ = −1 for p_i < p_p

The mass flow rate of the fluid in the displacement phase is defined by the following equation:

$$\frac{d{m}_o}{dt}=k_o{\mu }_o{A}_o\sqrt{2{\rho }_o\left|p_c-p_o\right|}$$

(3)

The values of the constants are:

k_o = 1 for p_c ≥ p_o;

k_o = −1 for p_c < p_o.

The following differential equation of the pressure in the cylinder is obtained:

$$\frac{d{p}_c}{dt}=\frac{1}{\epsilon V_c}\left[\frac{1}{{\rho }_c}\left(\frac{d{m}_i}{dt}-\frac{d{m}_o}{dt}\right)-\frac{d{V}_c}{dt}\right]$$

(4)

The current volume of the cylinder is:

$$V_c=V_{c\min }+V_{cx};\hspace{0.17em}{V}_{cx}\hspace{0.17em}=A_c\cdot x_k$$

(5)

The change in the cylinder volume caused by the piston movement and calculated as

$$\frac{d{V}_c}{dt}=-A_c{v}_k$$

(6)

If we introduce the change determined by Equation (6) into Equation (4), as well as the relation dϕ = ω·dt and the modulus of elasticity E, we obtain the following equation:

$$\frac{d{p}_c}{d\varphi }=\frac{E}{V_c}\left[\frac{A_c{v}_k}{\omega }+\frac{1}{{\rho }_c}\left(\frac{d{m}_u}{d\varphi }-\frac{d{m}_i}{d\varphi }\right)\right]$$

(7)

The cylinder block, together with the shaft, performs a rotational movement, while the piston moves in a straight line inside the cylinder block. The swash plate is fixed to the pump housing, while the piston slipper slides on it during pump operation.

The piston stroke is defined by the following expression:

$$x_k=Rtg\beta \left(1-\cos \varphi \right)$$

(8)

where the symbols stand for

p_i—inlet pressure;

p_p—pressure of the suction chamber;

ρ_p—fluid density in the suction chamber;

Α₁—geometric flow intersection of the inlet opening;

μ₁—constant of the flow coefficient of the inlet opening;

p_c—pressure in the cylinder;

p_o—pressure in the displacement chamber;

ρ_o—fluid density in the displacement chamber;

Α_o—geometric flow intersection of the displacement chamber;

μ_o—constant of the flow coefficient of the displacement chamber;

V_c—volume of the cylinder;

ρ_c—fluid density in the cylinder;

ε—compressibility coefficient;

x_k—current piston stroke;

Ac—geometric flow intersection of the cylinder;

E—modulus of elasticity;

$v_k$—speed of the piston;

$\omega$—current angular velocity of the pump’s drive shaft;

$\beta$—plate inclination angle;

$\varphi$—rotation angle of the drive shaft;

R—radius of the cylinder’s axis.

Solution of the Mathematical Model

The pump’s operating processes defined by this mathematical model are represented using the following differential equation:

$$\frac{d{y}_n}{d\varphi }=f_n(\varphi ,y_1,....y_{\mathrm{K}})$$

(9)

where n is in the range of 1 to K differential parameters. The variable $\varphi$ represents the value of the rotation angle of the axis of the pump’s drive shaft. The equations in which the quantities are defined as functions of time are reduced to the angle $\varphi$, using the expression $\varphi =\omega \cdot t$. Here, $\omega$ is the angular velocity of the pump shaft.

For the simultaneous integration of non-linear differential equations of the boundary conditions and partial differential flow equations, it is necessary to use computers and develop appropriate computer programs. A program that connects and simultaneously solves all the above differential equations, equations of characteristic cross-sectional changes, and changes in the fluid’s physical characteristics requires an appropriate structure and organisation. Thus, in this study, the program was written in the programming language Digital Visual Fortan 5.0. and was realised in a Quantum X measurement and control system. Structural and modular programming principles were used. The program consists of the main program and a module. Important programs are written as rounded modules connected to each other or the main program, but they can also be used independently. The WHAKSIP software system has been specifically developed for the mathematical modelling of current and hydrodynamic processes during the entire operating cycle of axial piston water hydraulic pumps.

3. Experimental Testing with Results

In order to verify the theoretical analysis and the mathematical model of the hydrodynamic processes of the axial piston water hydraulic pump, experimental tests were performed at the Development and Research Laboratory “PPT—Namenska”. As part of this experiment, a test installation was specially designed.

The basic component of the installation was a 37 kW electric motor with regulated speed and torque. Figure 2 shows the experimental hydraulic installation used to test the characteristic parameters of the axial piston pump consisting of a drive motor, an axial piston pump (test object), a speed and torque sensor, a module for data acquisition and processing, temperature and pressure sensors, an auxiliary feed pump, and secondary hydraulic installation components. The auxiliary feed pump was installed at the inlet port of the test pump in order to ensure a safe and predetermined supply of the working fluid to the test pump. The test stand was equipped with a water tank with a capacity of 1000 litres and a temperature control system, which would ensure stable conditions during the test. The temperature of the working fluid during the test was maintained in the range from 2 to 50 °C. Figure 3 shows the test pump installed on the test stand. In

Table 1. Sensors and equipment used in the experimental test installation.

Symbol	Name	Characteristics
P1, P2, P3	Gauge pressure	P3MA Hottinger Measuring range from 1 to 50 MPa Accuracy class 0.1
Q1	Flow meter	RE3-300 Hydrotechnik Measuring range from 15 to 300 L/min Accuracy class 0.2
T	Speed and torque meter	T30FN, HBM, Measuring range up to 3000 rpm and 500 Nm Accuracy class 0.2
T1, T2, T3	Thermometer	Omega K-type thermocouple Range: 0–120 °C 1% accuracy
M	Electro motor	37 kW

, more detailed information about the sensors and equipment used on the test stand is provided.

For data acquisition and processing, a QuantumX MX840B universal acquisition system produced by HBM (Figure 3), with an accuracy class of up to 0.01, was used. This system uses the MX Assistant software and enables the continuous measurement and calculation of the characteristic parameters of the pump’s operating cycle in real time. The QuantumX system has 8 channels with 24-bit A/D converters per channel and simultaneous measurement on 8 channels. For the purposes of this experiment, simultaneous measurements were performed on 5 channels. The sampling rate was 192 kHz per channel. The software allows the measurement of cyclic and non-cyclic rapidly changing processes with graphical visualisation. The acquired data were stored in different file types for further analysis and calculation.

In the experiment, special attention was paid to the change in the pump’s effective flow rate measured for different speeds of the pump’s drive shaft. For each rotation speed, a pump load was applied through the valve at the pump’s outlet, so that the outlet pressure was in the range of 1–8 MPa, in accordance with the test plan shown in

Table 2. Operating modes used during the experimental testing process.

Ordinal Number	Symbol	Speed (rpm)	Pressure at the Test Pump Inlet (MPa)	Pressure at the Test Pump Outlet (MPa)
1	IR1	1000	0.3	from 1 to 8
2	IR2	900	0.3	from 1 to 8
3	IR3	800	0.3	from 1 to 8
4	IR4	700	0.3	from 1 to 8
5	IR5	600	0.3	from 1 to 8
6	IR6	500	0.3	from 1 to 8

. The test interval during which the pump parameters were measured was 50 ms.

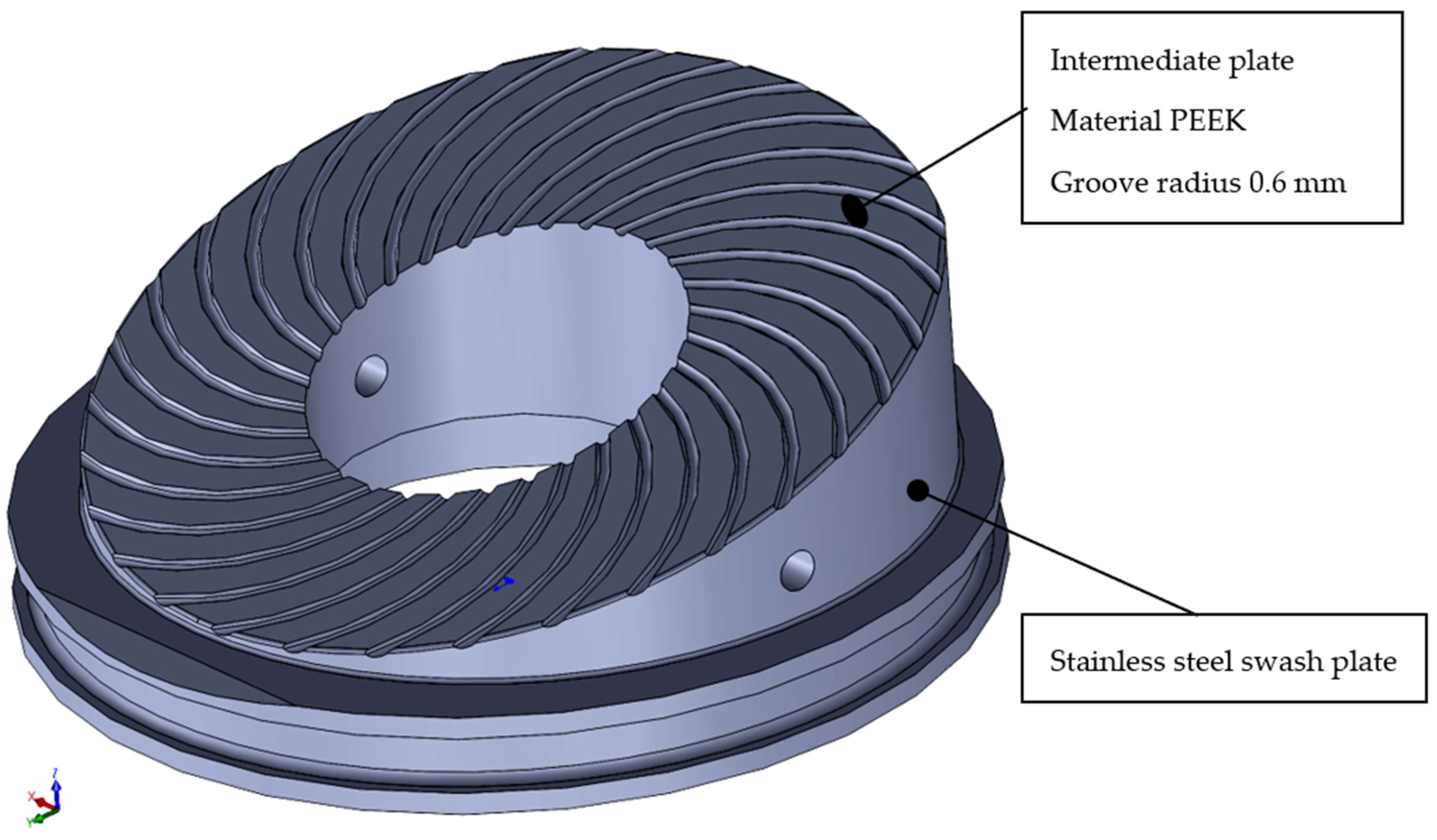
The tests presented in this paper were performed using modified swash plates in order to extend the service life of the pump. The modification involved the installation of intermediate plates (Figure 4) on the contact surface of the piston slipper and the swash plate. The intermediate plates were made of polyetheretherketone (PEEK) [30], and they had some grooves, as shown in Figure 4. The geometry of the plate was optimised for the output operating parameters and working life of the pump.

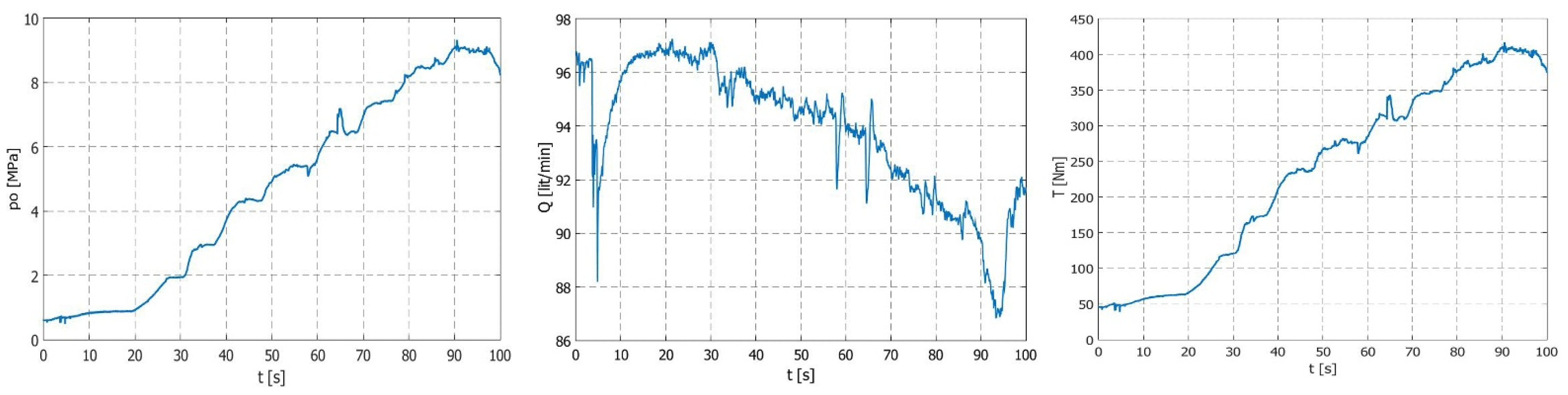
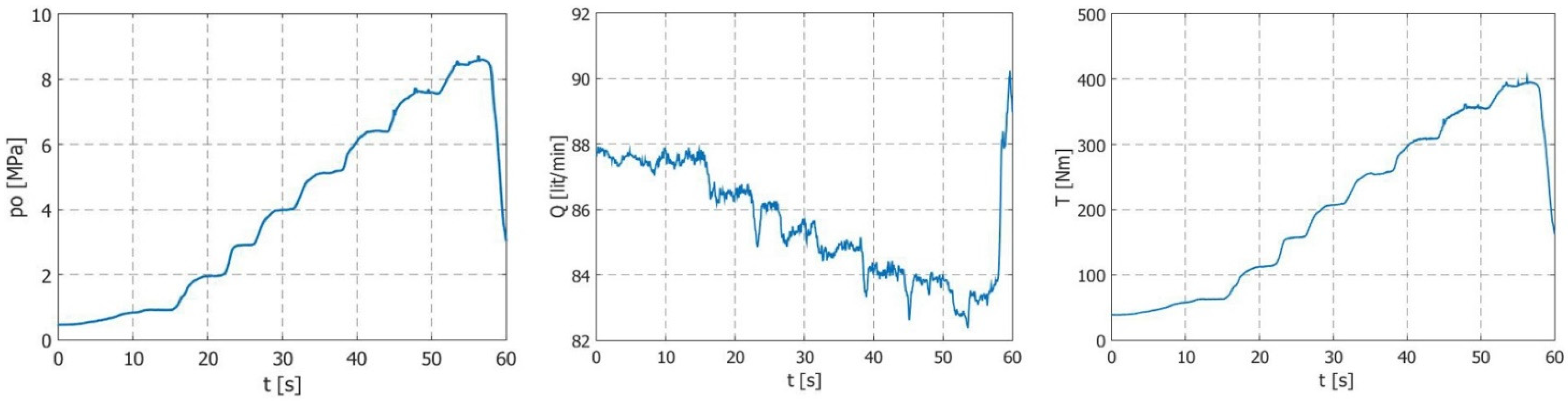
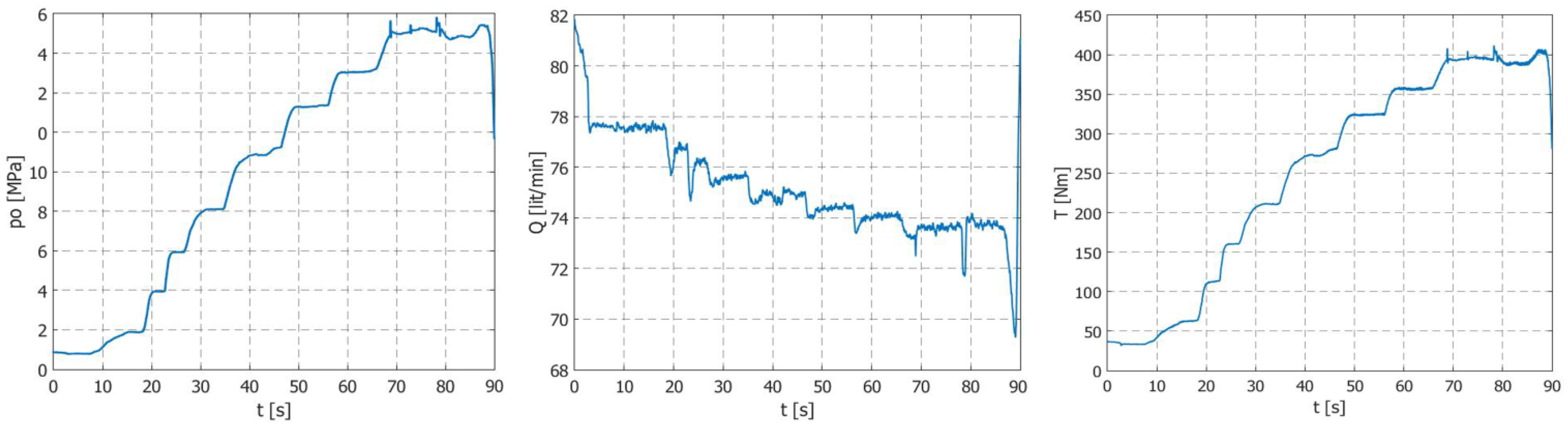
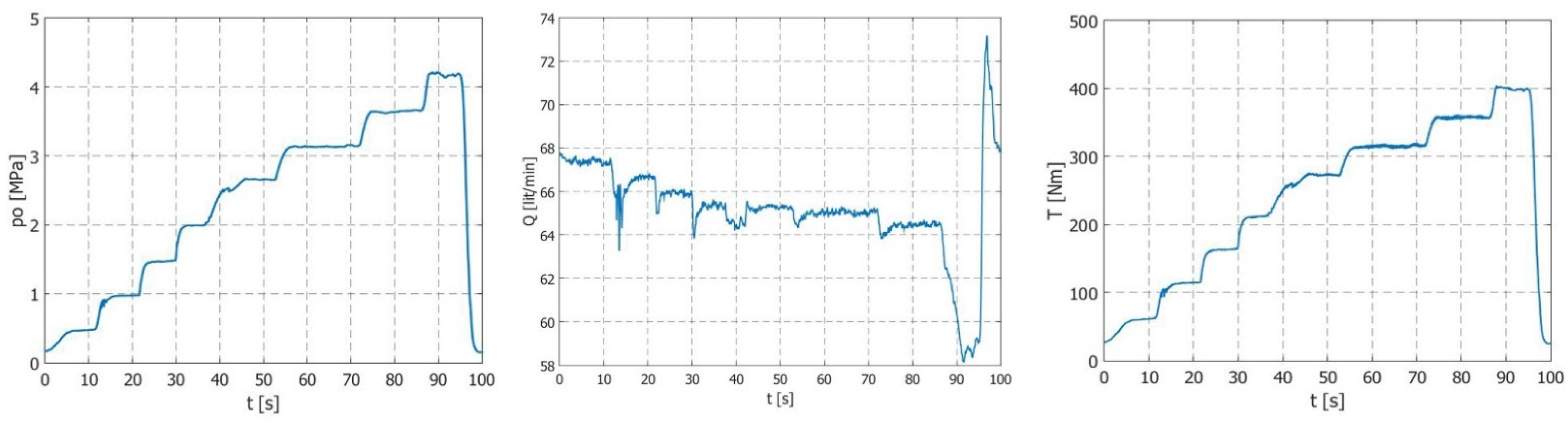
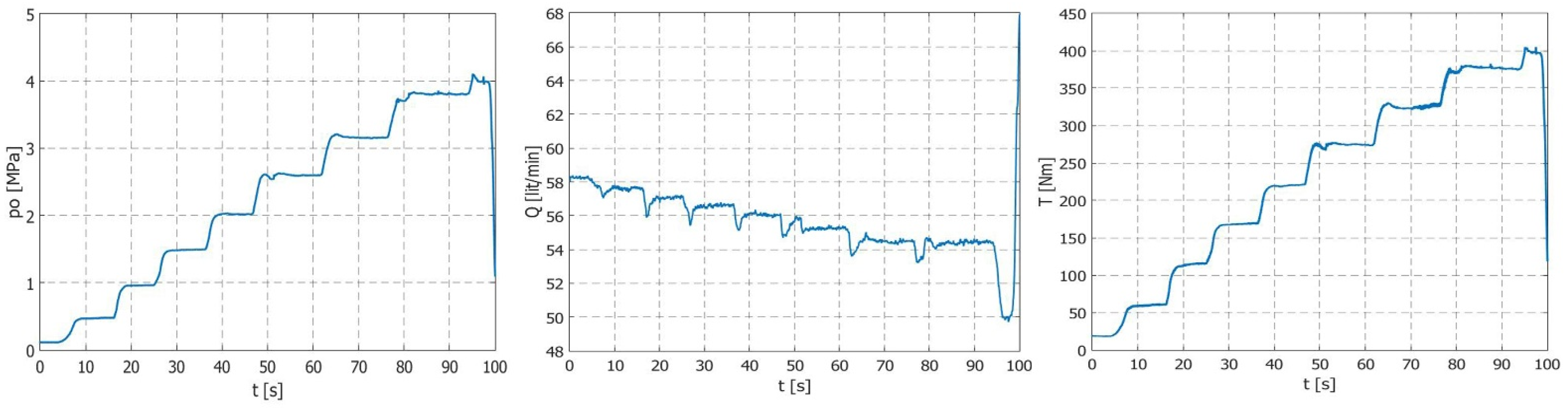
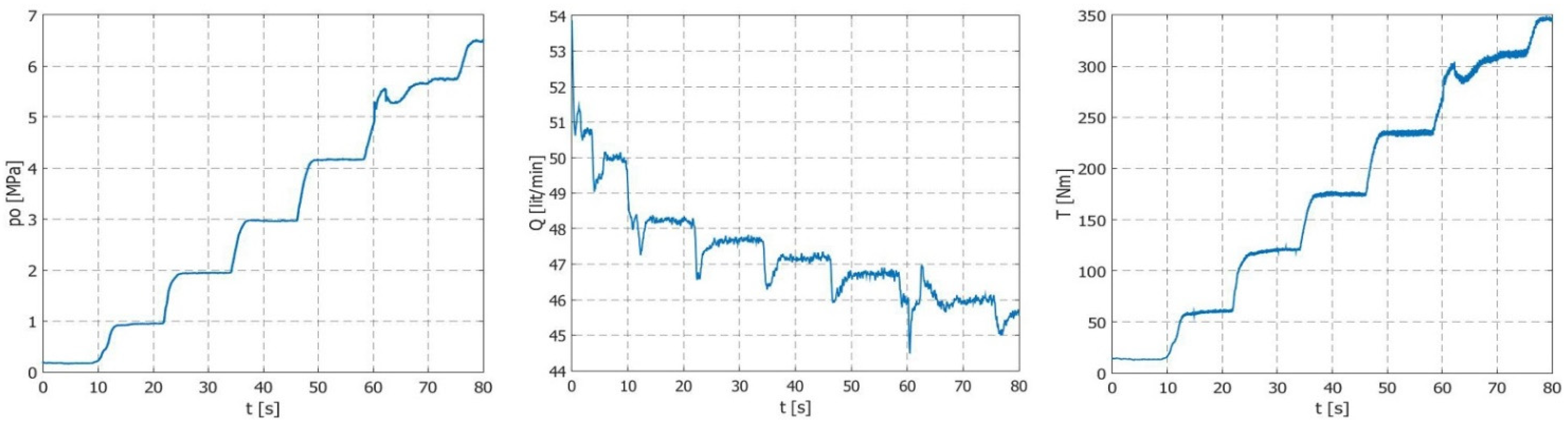
Test results are given in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. Diagrams of changes in the output pressure, as well as the flow and torque values of the drive shaft, are shown. It can be noticed that the pump’s flow rate decreased with an increase in the pump’s outlet pressure, whereas the torque increased with an increase in the output pressure.

Figure 11 shows a summary diagram of the measured values of the pump’s operating parameters depending on the testing time.

Small vibrations seen in the diagram of the rotation speed of the pump shaft were the result of errors in the measuring equipment. The peaks that can be noticed in the diagram of the pump’s flow rates are due to an uneven pump inlet pressure. Moreover, the pump’s flow rate decreased with a smaller number of revolutions in the pump’s drive shaft.

4. Discussion

This experimental research highlighted the behaviour of the sliding surface between slippers and swash plates when the pressure level increases. It is possible to use slippers at higher pressure levels. The slipper is designed to be safe, and the hydrostatic balance is quite low, which also means that its PV rate values are higher. The behaviour of the slipper significantly changes at high-pressure levels, and the hydrostatic equilibrium increases beyond the limit [30].

It is possible to realise the rotation of the swash plate because the influence on the behaviour of the slipper can be controlled. However, the area of rotation and changes in behaviour should be considered in the design process of slippers.

To reduce leakage, the ratio between the inner and outer radii of the slipper should be as small as possible. In practice, it is obvious that the outer radius cannot be increased indefinitely. However, it is possible to increase the outer radius. In this way, many benefits are achieved: The leakage flow and the PV rates are reduced, while the hydrostatic balance and the load capacity are increased. The disadvantage is that the frictional force accumulates, but this should be accepted because otherwise, the leakage will be too high.

5. Conclusions

The parameters of hydrodynamic processes of an axial piston water hydraulic pump cannot be accurately determined using only an experimental or a mathematical model. More accurate parameters can only be obtained by a combination of experimental methods measuring pump operating parameters and the mathematical modelling of the actual hydrodynamic process.

The testing of the axial piston water hydraulic pump presented in this paper was carried out on an installation specially made for this experiment at the Development and Research Laboratory “PPT—Namenska”. The tested PPT NW10 pump had a constant flow rate, a working volume of 101 cm³, a maximum output pressure of 8 MPa, and its operating speed ranged from 500 to 1000 rpm.

During the experimental testing, six operating modes were applied. For each of these operating modes, the diagrams of changes in the output pressure, the working fluid’s flow rate, and the torque values of the drive shaft were presented. Pulsations were observed in the pump’s pressure, flow rate, and torque, and they significantly affected the capacity and efficiency of the pump. These pulsations are related to the working fluid and the friction of the working fluid, which is considered to have low viscosity. In that sense, the issue of the materials used in the pump components exposed to wear and tear has to also be addressed, as well as the tribological demands they have to meet.

The suggestions found in the literature concerning the materials of the parts exposed to wear were taken into account by choosing the PEEK material.

Water as a working fluid is a challenging medium in hydraulic components because a water-based film is thin, and water has a low viscosity coefficient. Water as a medium under pressure imposes a number of limitations on the material, and industrial plastics are widely used in water hydraulic components. Therefore, deformations play major roles in the behaviour of the components. The deformations of the components in the sliding joint between the piston slipper and the intermediate plate affect the pressure field under the sliding surface and this, in turn, changes the hydrostatic balance of the slipper and the leakage flow rate.

Using basic equations, it is possible to determine the size of the contact between the slipper and the swash plate near the boundary. All different requirements can be met, and high pressure or an adjustable swash plate angle will not be a problem. However, the greatest challenge is that the basic equations are only applicable in ideal situations. In real situations, many interferences make the basic equations incorrect. The deformation of the sliding surfaces causes the largest error.

The most important dimensions of the contact slipper/swash plate are the inner and the outer radii of the sliding surface because the behaviour of the slipper mainly depends on them. Although there are many different forces acting on the slipper, pressure-dependent forces are dominant, and the desired properties cannot be properly achieved if the hydrostatic balance of the slipper and the intermediate plate is not in the right range.

Some of the challenges in future research include finding the optimised structure of the components of the axial piston water hydraulic pump. This means that the combination of stainless steel and industrial plastic should be optimised in order to avoid deformation. The result would be a more stable structure of the pump components in a wider operating range. The use of ceramics instead of industrial plastics would solve many problems, though it is entangled with many challenges. Ceramics should be taken into consideration when seeking solutions for higher pressure.

The mathematical model used in this paper takes into account the characteristics of other materials used in the construction of the pump; hence, our further research will involve testing the model using an appropriate software program and a comparison of the obtained results with experimental tests.