A Study on Gear Defect Detection via Frequency Analysis Based on DNN
Abstract
:1. Introduction
2. Materials and Methods
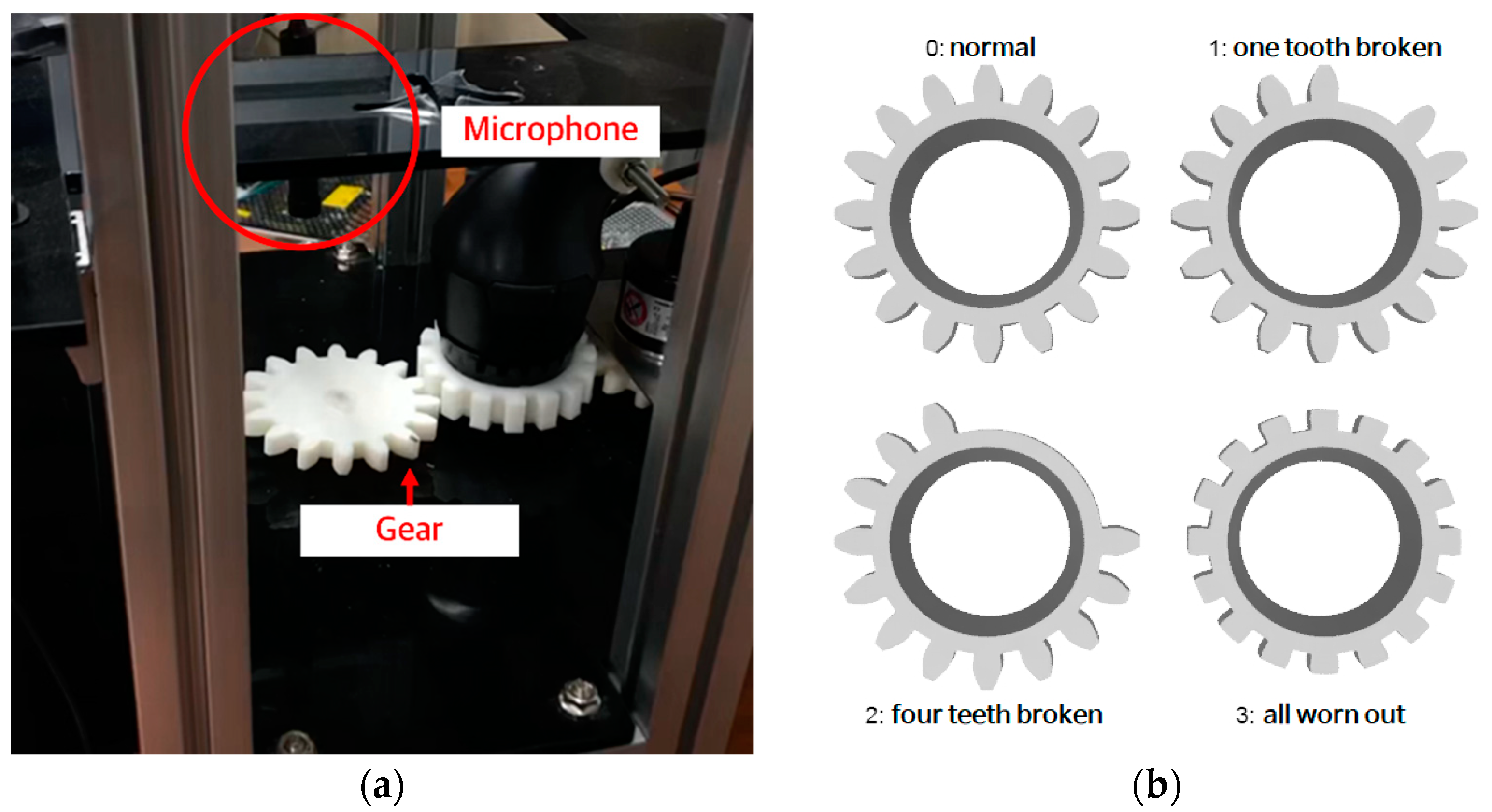
2.1. Sound Data Collection for Acoustic Analysis
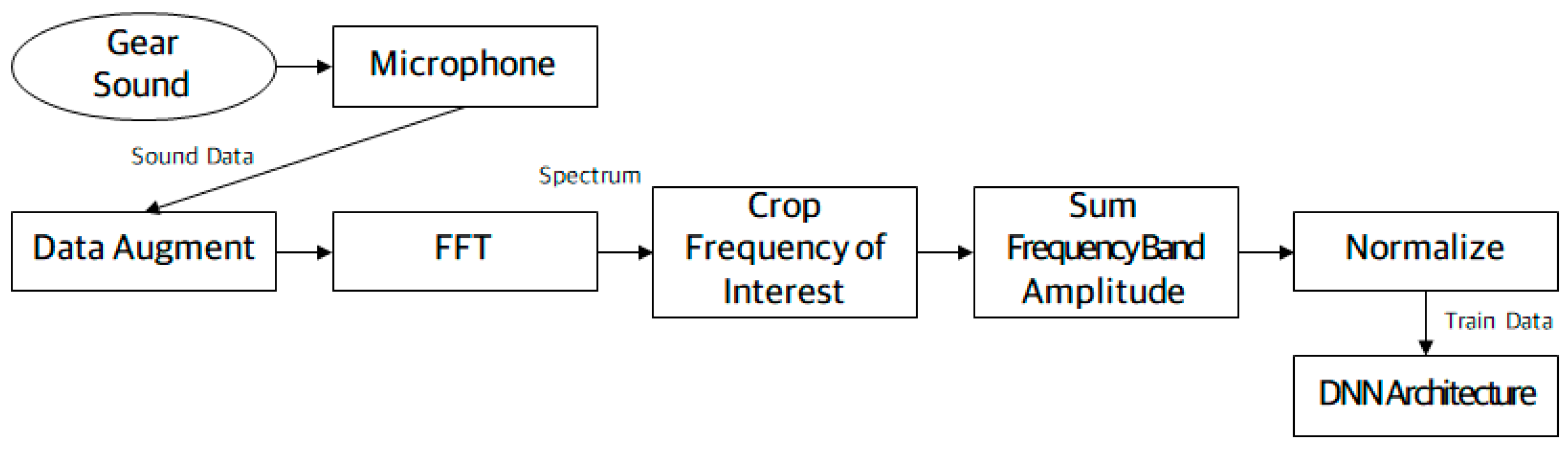
2.2. Sound Data Pre-Processing
2.2.1. Data Augmentation
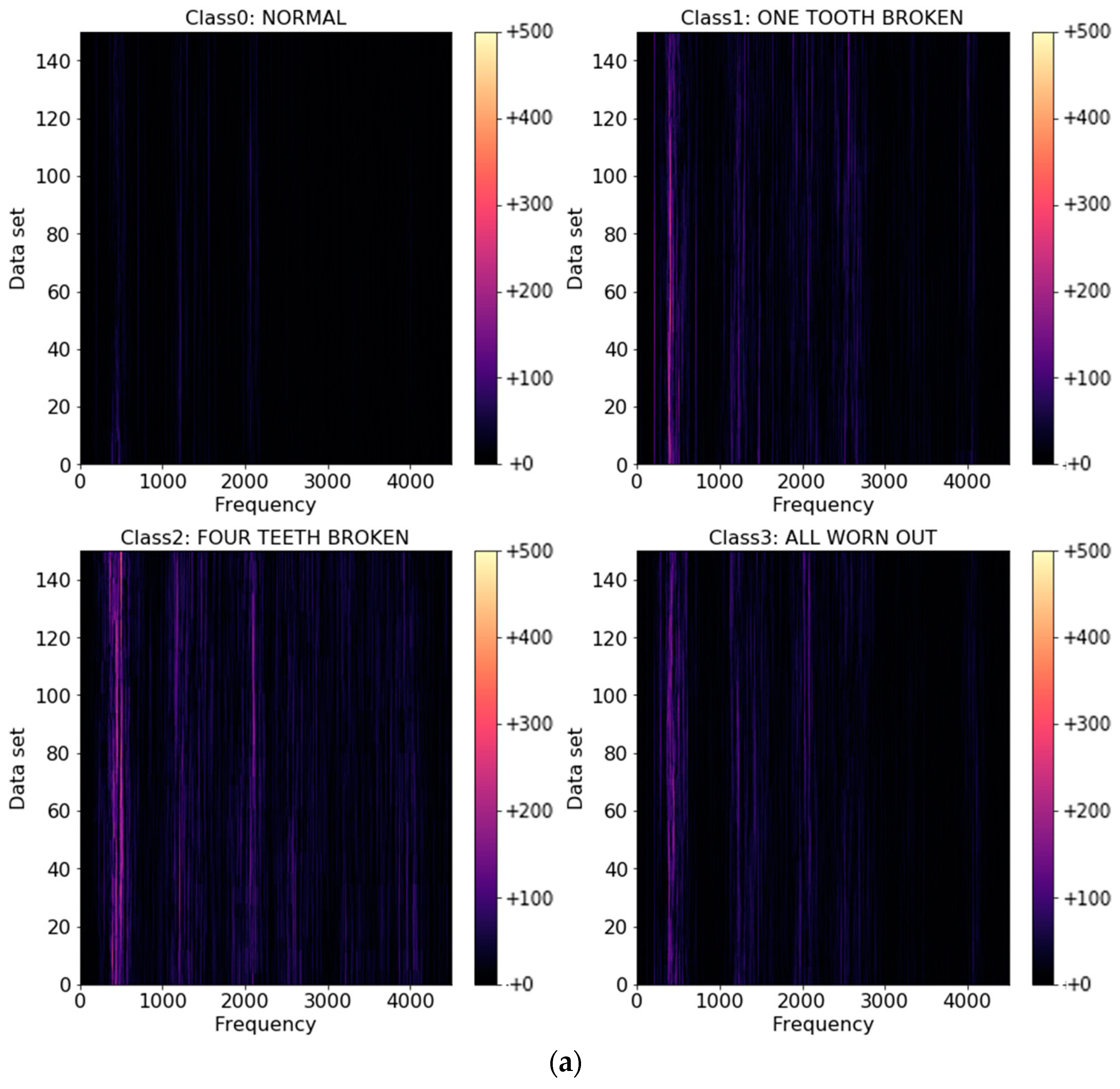
2.2.2. Acoustic Spectral Analysis
2.3. Train Dataset
2.4. Training
3. Experiment and Results
3.1. Experiment Environment
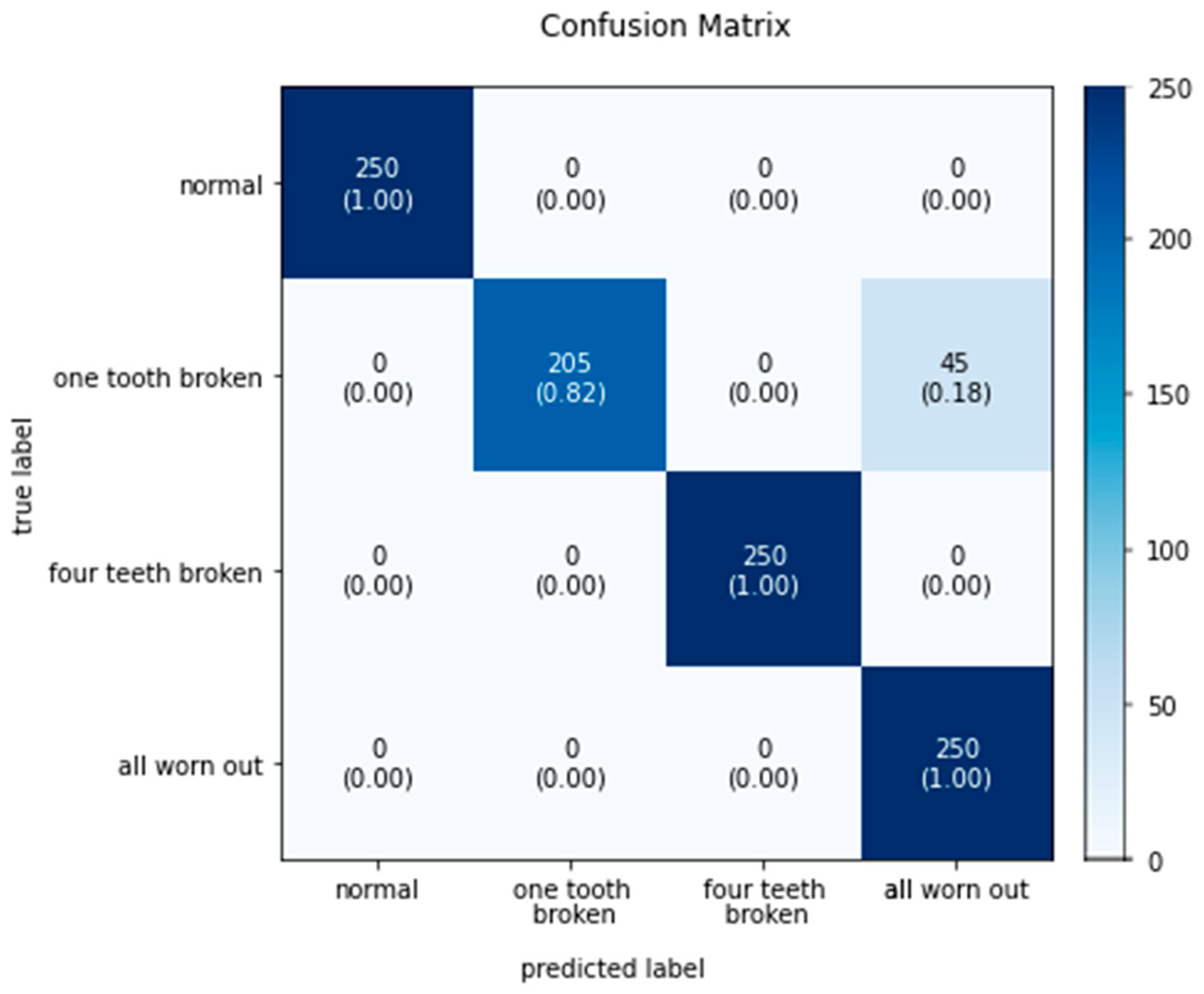
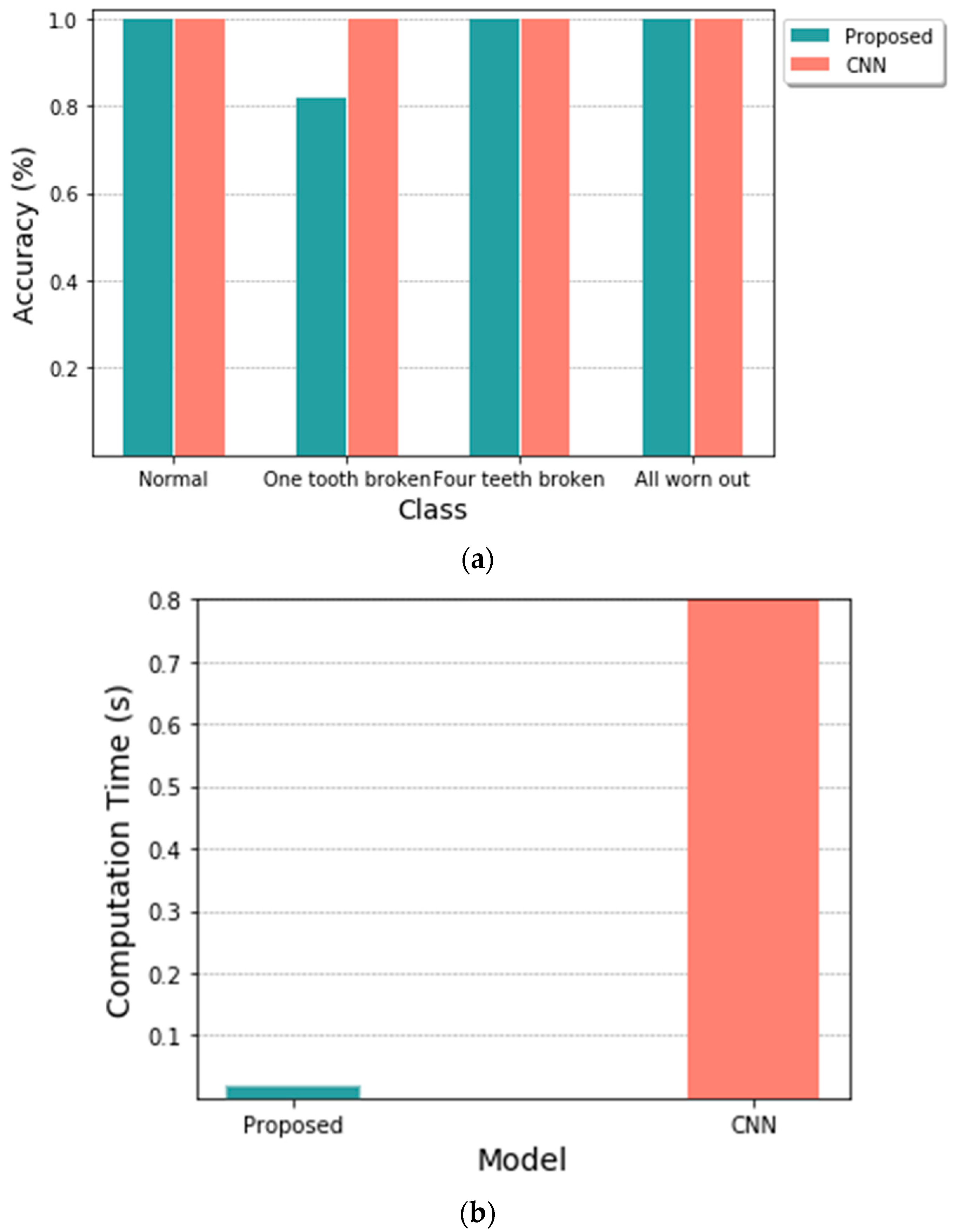
3.2. Result of Experiment with Test Dataset
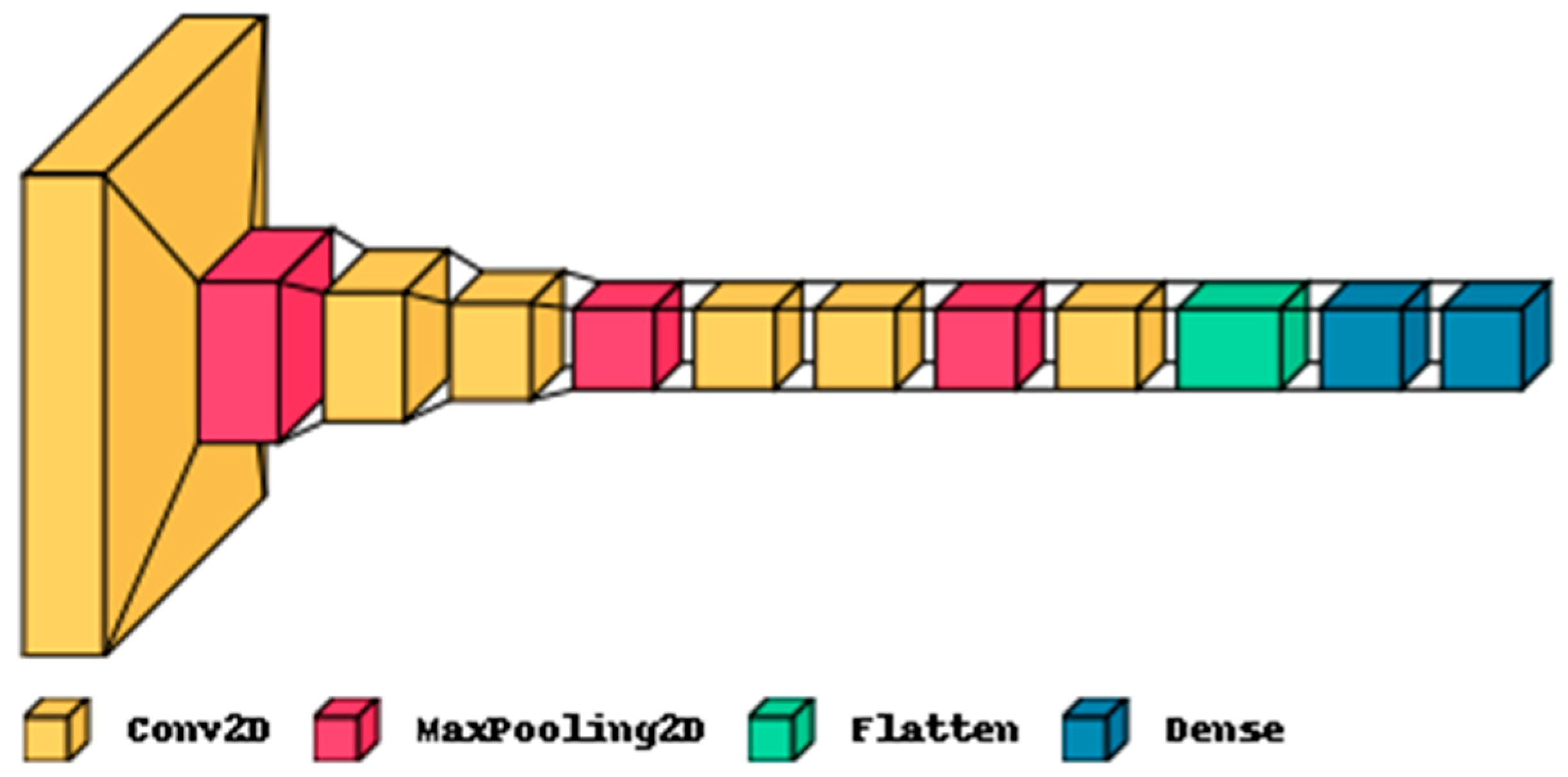
3.3. Comparison between CNN Classifiers
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cooper, C.; Kaplinsky, R. Technology and Development in the Third Industrial Revolution; Routledge: London, UK, 2005. [Google Scholar]
- Mowery, D.C. Plus ca change: Industrial R&D in the “third industrial revolution”. Ind. Corp. Change 2009, 18, 1–50. [Google Scholar]
- Greenwood, J. The Third Industrial Revolution: Technology, Productivity, and Income Inequality; Number 435; American Enterprise Institute: Washington, DC, USA, 1997. [Google Scholar]
- Carlsson, B. Technological Systems and Economic Performance: The Case of Factory Automation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 5. [Google Scholar]
- Wang, B.; Tao, F.; Fang, X.; Liu, C.; Liu, Y.; Freiheit, T. Smart manufacturing and intelligent manufacturing: A comparative review. Engineering 2021, 7, 738–757. [Google Scholar] [CrossRef]
- Dotoli, M.; Fay, A.; Mi’skowicz, M.; Seatzu, C. An overview of current technologies and emerging trends in factory automation. Int. J. Prod. Res. 2019, 57, 5047–5067. [Google Scholar] [CrossRef]
- Majchrzak, A. The Human Side of Factory Automation: Managerial and Human Resource Strategies for Making Automation Succeed; Jossey-Bass: Hoboken, NJ, USA, 1988. [Google Scholar]
- Jäntti, M.; Toroi, T.; Eerola, A. Difficulties in establishing a defect management process: A case study. In Proceedings of the International Conference on Product Focused Software Process Improvement, Amsterdam, The Netherlands, 12–14 June 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 142–150. [Google Scholar]
- Adams, R.; Cawley, P.; Pye, C.; Stone, B. A vibration technique for non-destructively assessing the integrity of structures. J. Mech. Eng. Sci. 1978, 20, 93–100. [Google Scholar] [CrossRef]
- Maraaba, L.S.; Twaha, S.; Memon, A.; Al-Hamouz, Z. Recognition of stator winding inter-turn fault in interior-mount LSPMSM using acoustic signals. Symmetry 2020, 12, 1370. [Google Scholar] [CrossRef]
- Zaki, A.; Chai, H.K.; Aggelis, D.G.; Alver, N. Non-destructive evaluation for corrosion monitoring in concrete: A review and capability of acoustic emission technique. Sensors 2015, 15, 19069–19101. [Google Scholar] [CrossRef]
- Qian, S.; Chen, D. Joint time-frequency analysis. IEEE Signal Process. Mag. 1999, 16, 52–67. [Google Scholar] [CrossRef]
- Wyse, L. Audio spectrogram representations for processing with convolutional neural networks. arXiv 2017, arXiv:1706.09559. [Google Scholar]
- Hess-Nielsen, N.; Wickerhauser, M.V. Wavelets and time-frequency analysis. Proc. IEEE 1996, 84, 523–540. [Google Scholar] [CrossRef] [Green Version]
- Muda, L.; Begam, M.; Elamvazuthi, I. Voice recognition algorithms using mel frequency cepstral coefficient (MFCC) and dynamic time warping (DTW) techniques. arXiv 2010, arXiv:1003.4083. [Google Scholar]
- Kang, M.; Kim, J.; Wills, L.M.; Kim, J.M. Time-Varying and Multiresolution Envelope Analysis and Discriminative Feature Analysis for Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2015, 62, 7749–7761. [Google Scholar] [CrossRef]
- Feng, Z.; Chen, X.; Wang, T. Time-varying demodulation analysis for rolling bearing fault diagnosis under variable speed conditions. J. Sound Vib. 2017, 400, 71–85. [Google Scholar] [CrossRef]
- Stefani, A.; Bellini, A.; Filippetti, F. Diagnosis of Induction Machines’ Rotor Faults in Time-Varying Conditions. IEEE Trans. Ind. Electron. 2009, 56, 4548–4556. [Google Scholar] [CrossRef]
- Zhou, K.; Tang, J. Harnessing fuzzy neural network for gear fault diagnosis with limited data labels. Int. J. Adv. Manuf. Technol. 2021, 115, 1005–1019. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Allam, A.; Moussa, M.; Tarry, C.; Veres, M. Detecting Teeth Defects on Automotive Gears Using Deep Learning. Sensors 2021, 21, 8480. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Qu, Y.; He, D. Gear Pitting Fault Diagnosis Using Integrated CNN and GRU Network with Both Vibration and Acoustic Emission Signals. Appl. Sci. 2019, 9, 768. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Li, L.; Ma, J. Rolling bearing fault diagnosis based on STFT-deep learning and sound signals. Shock. Vib. 2016, 2016, 6127479. [Google Scholar] [CrossRef] [Green Version]
- Verstraete, D.; Ferrada, A.; Droguett, E.L.; Meruane, V.; Modarres, M. Deep learning enabled fault diagnosis using time-frequency image analysis of rolling element bearings. Shock. Vib. 2017, 2017, 5067651. [Google Scholar] [CrossRef]
- Kang, K.W.; Lee, K.M. CNN-based Automatic Machine Fault Diagnosis Method Using Spectrogram Images. J. Inst. Converg. Signal Process. 2020, 21, 121–126. [Google Scholar]
- Kim, M.S.; Yun, J.P.; Park, P.G. Supervised and Unsupervised Learning Based Fault Detection Using Spectrogram. 2019. Available online: https://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE09306024 (accessed on 2 August 2022).
- Nam, J.; Park, H.J. A Neural Network based Fault Detection and Classification System Using Acoustic Measurement. J. Korean Soc. Manuf. Technol. Eng. 2020, 29, 210–215. [Google Scholar]
- Yun, J.P.; Kim, M.S.; Koo, G.; Shin, W. Fault Diagnosis and Analysis Based on Transfer Learning and Vibration Signals. IEMEK J. Embed. Syst. Appl. 2019, 14, 287–294. [Google Scholar]
- Shen, S.; Lu, H.; Sadoughi, M.; Hu, C.; Nemani, V.; Thelen, A.; Webster, K.; Darr, M.; Sidon, J.; Kenny, S. A physics-informed deep learning approach for bearing fault detection. Eng. Appl. Artif. Intell. 2021, 103, 104295. [Google Scholar] [CrossRef]
- Shrestha, A.; Mahmood, A. Review of deep learning algorithms and architectures. IEEE Access 2019, 7, 53040–53065. [Google Scholar] [CrossRef]
- Titze, I.R.; Winholtz, W.S. Effect of microphone type and placement on voice perturbation measurements. J. Speech Lang. Hear Res. 1993, 36, 1177–1190. [Google Scholar] [CrossRef]
- Pham, H. Pyaudio: Portaudio v19 Python Bindings. 2006. Available online: https://people.csail.mit.edu/hubert/pyaudio (accessed on 2 August 2022).
- Landau, H. Sampling, data transmission, and the Nyquist rate. Proc. IEEE 1967, 55, 1701–1706. [Google Scholar] [CrossRef]
- Rebuffi, S.A.; Gowal, S.; Calian, D.A.; Stimberg, F.; Wiles, O.; Mann, T.A. Data augmentation can improve robustness. Adv. Neural Inf. Process. Syst. 2021, 34, 29935–29948. [Google Scholar]
- Psobot, Pedalboard, GitHub Repository. 2021. Available online: https://github.com/spotify/pedalboard (accessed on 27 July 2022).
- Eklund, V.V. Data Augmentation Techniques for Robust Audio Analysis. Master’s Thesis, Tampere University, Tampere, Finland, 2019. [Google Scholar]
- István, L.; Vér, L.L.B. Noise and Vibration Control Engineering: Principles and Applications; John Wiley Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Van Der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy array: A structure for efficient numerical computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Khor, J.Z.S.; Gopalai, A.A.; Lan, B.L.; Gouwanda, D.; Ahmad, S.A. The effects of mechanical noise bandwidth on balance across flat and compliant surfaces. Sci. Rep. 2021, 11, 12276. [Google Scholar] [CrossRef]
- Sola, J.; Sevilla, J. Importance of input data normalization for the application of neural networks to complex industrial problems. IEEE Trans. Nucl. Sci. 1997, 44, 1464–1468. [Google Scholar] [CrossRef]
- Komer, B.; Bergstra, J.; Eliasmith, C. Hyperopt-sklearn: Automatic hyperparameter configuration for scikit-learn. In Proceedings of the ICML Workshop on AutoML, Austin, TX, USA, 6–13 July 2006; Citeseer: Austin, TX, USA, 2014; Volume 9, p. 50. [Google Scholar]
- Solanki, A.; Pandey, S. Music instrument recognition using deep convolutional neural networks. Int. J. Inf. Technol. 2019, 14, 1659–1668. [Google Scholar] [CrossRef]

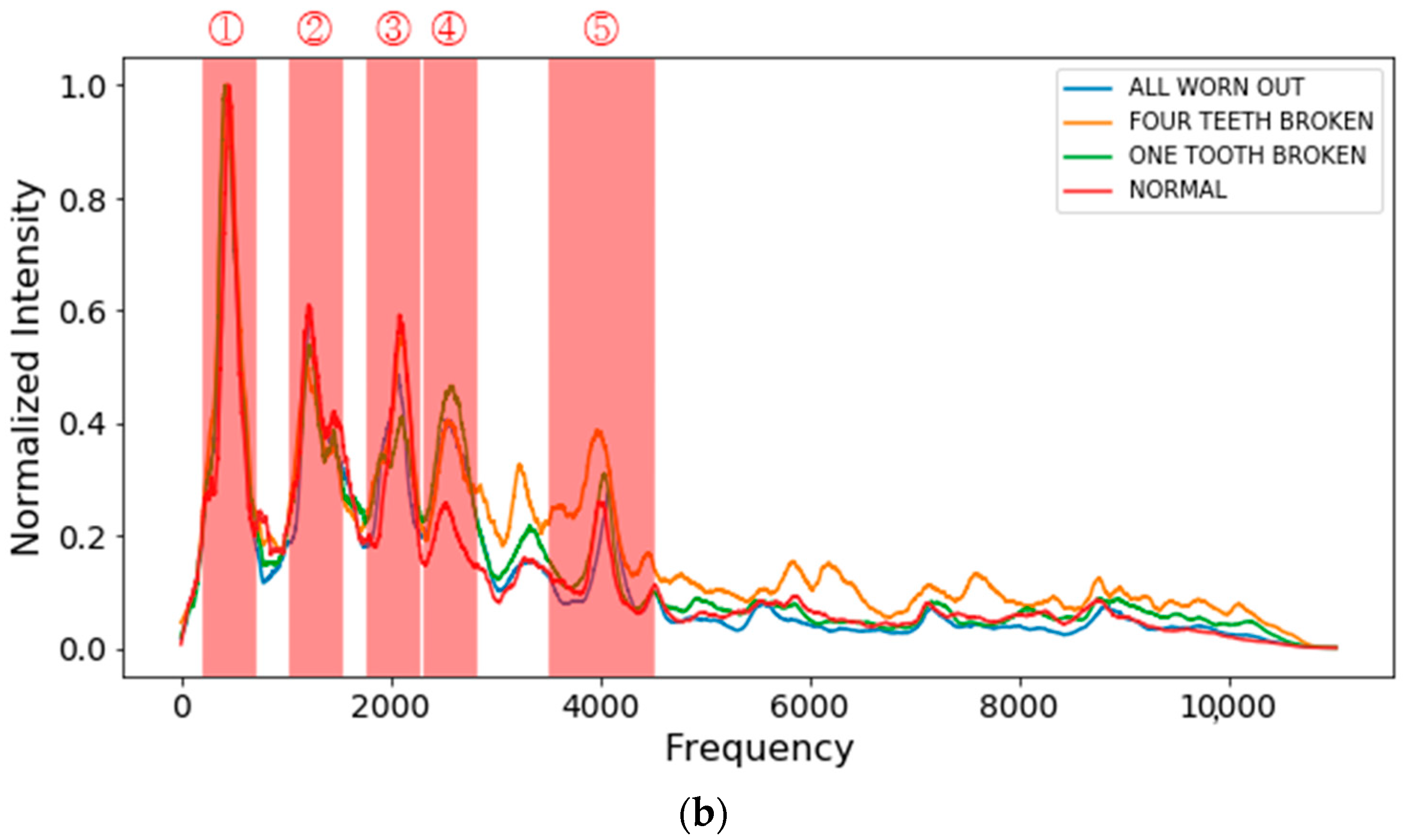
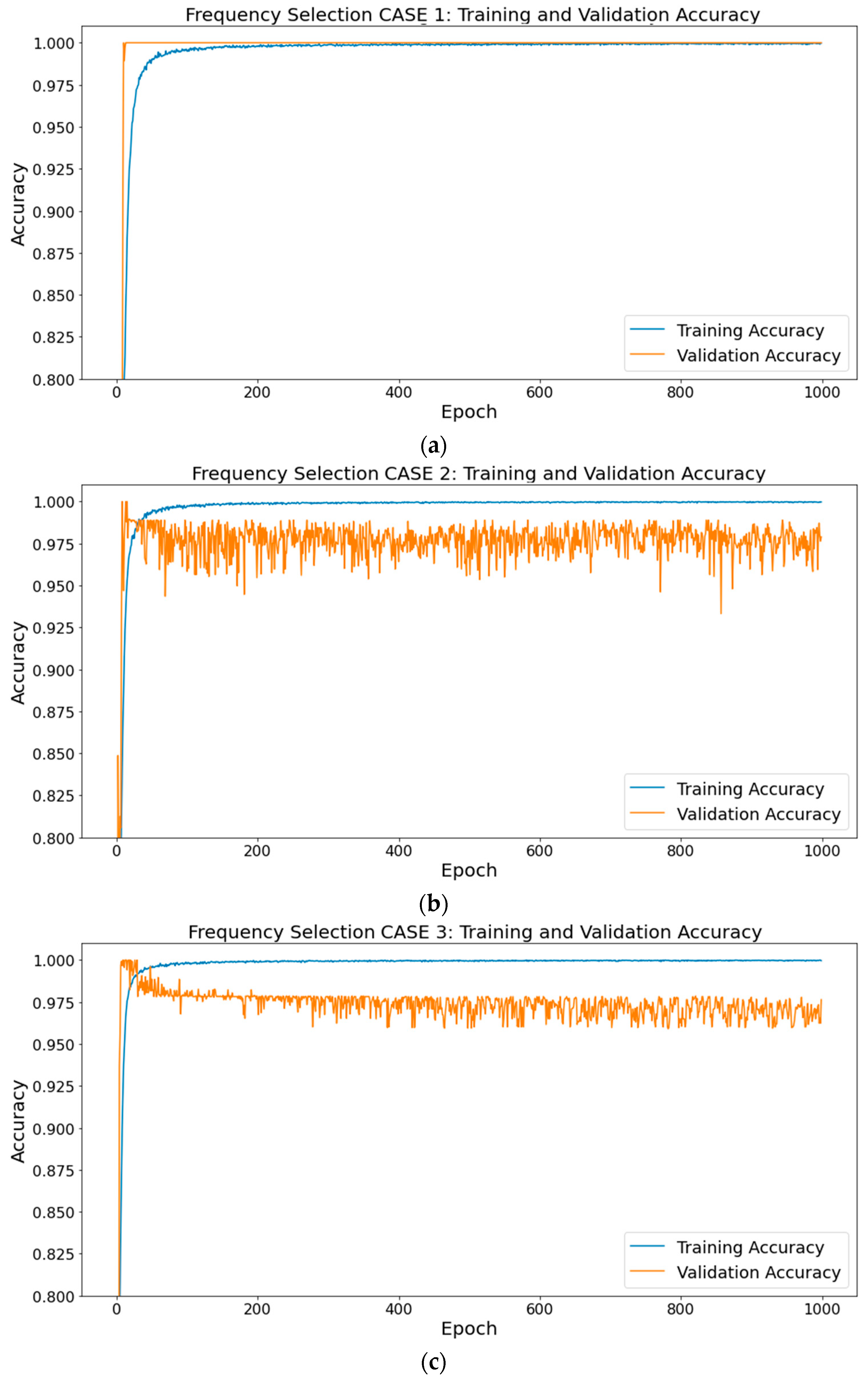
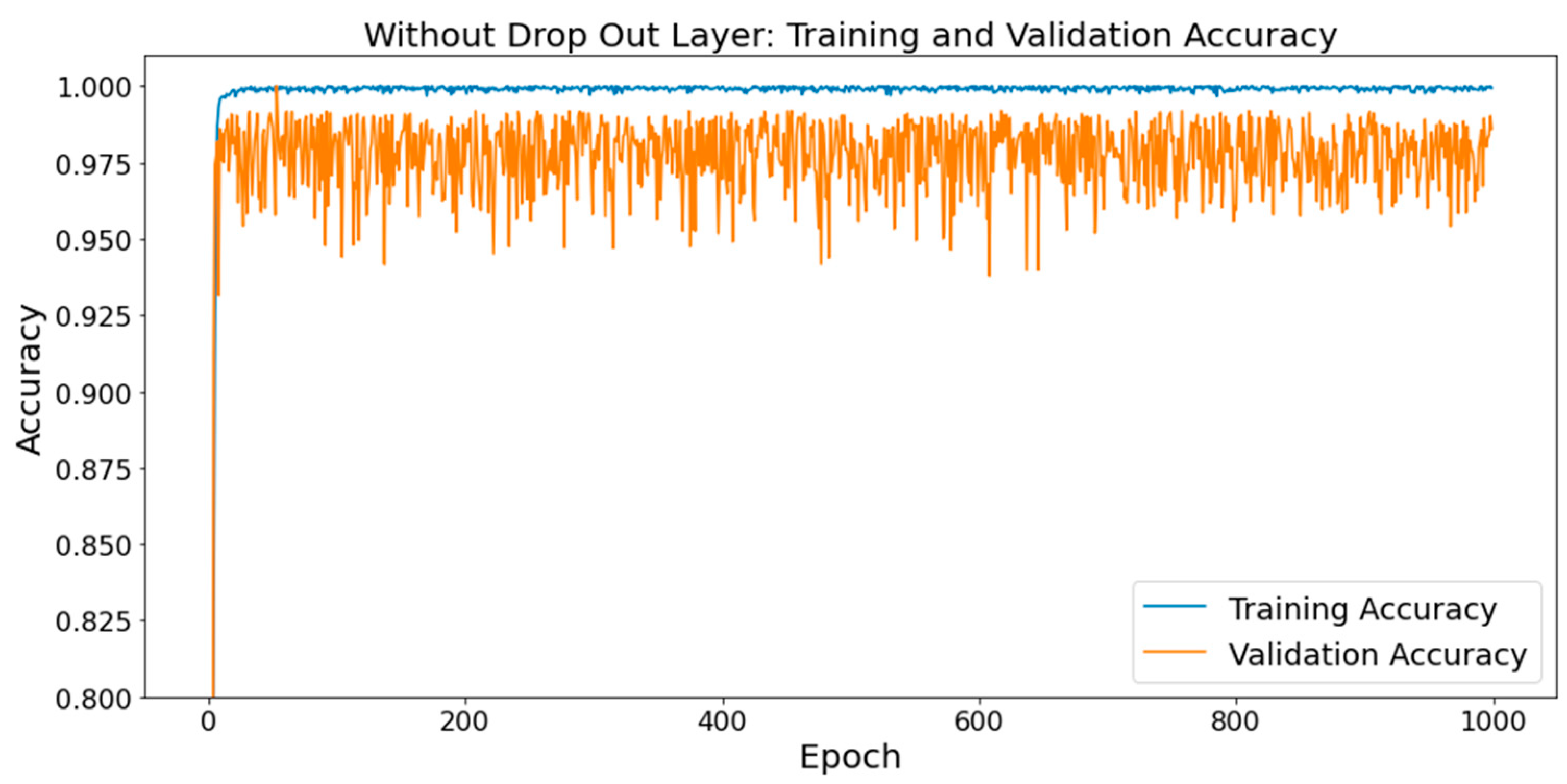

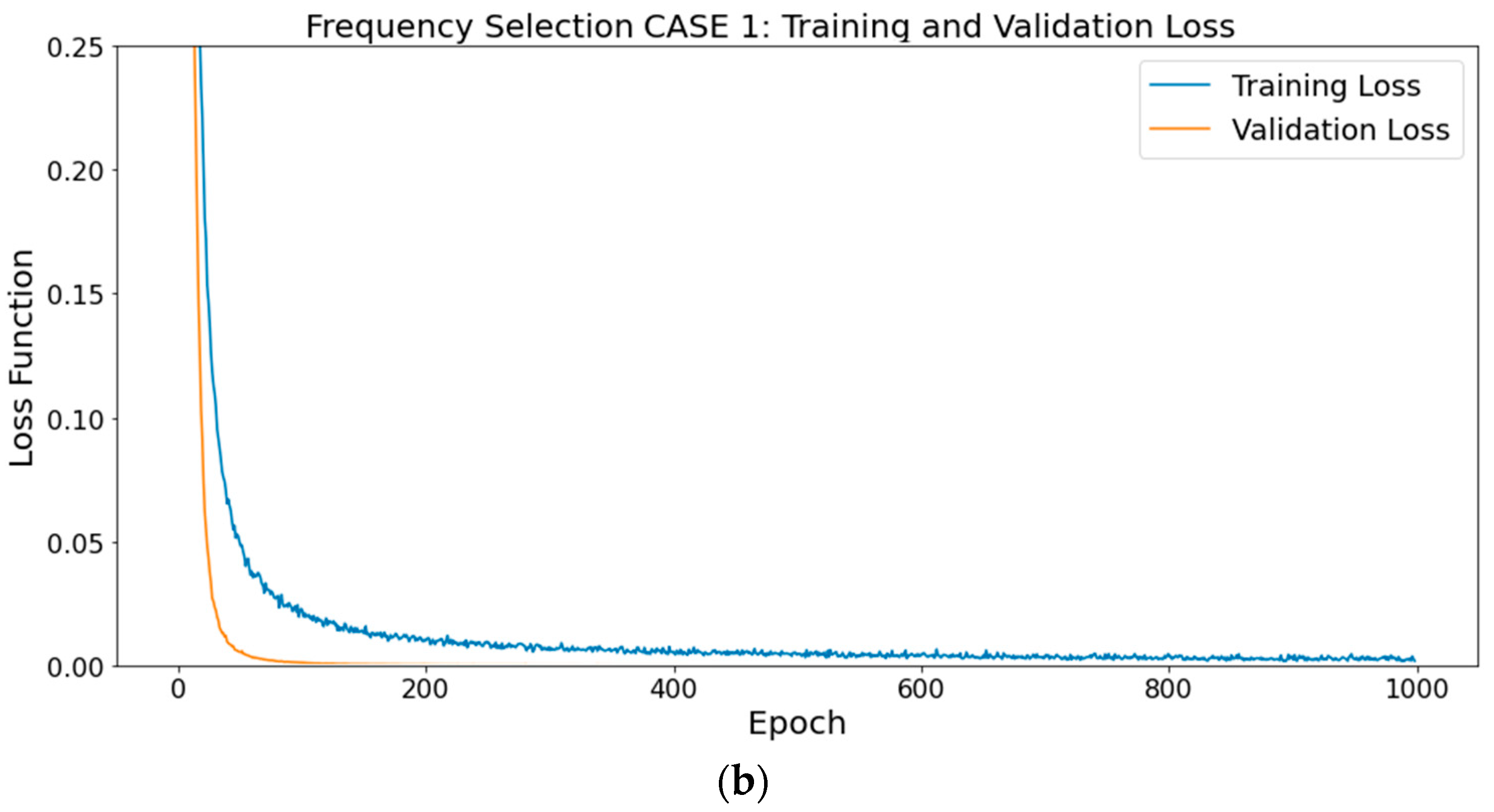

| Frequency Selection Case 1 | Frequency Selection Case 2 | Frequency Selection Case 3 | |
|---|---|---|---|
| ① | 200~700 | 200~700 | 1900~2400 |
| ② | 1000~1500 | 1000~1500 | 2400~2900 |
| ③ | 1700~2200 | 1700~2200 | 3000~3500 |
| ④ | 2200~2700 | 2200~2700 | 3800~4300 |
| ⑤ | 3500~4500 | 3000~3500 | 5500~6500 |
| ⑥ | N/A | 3500~4500 | 7000~8000 |
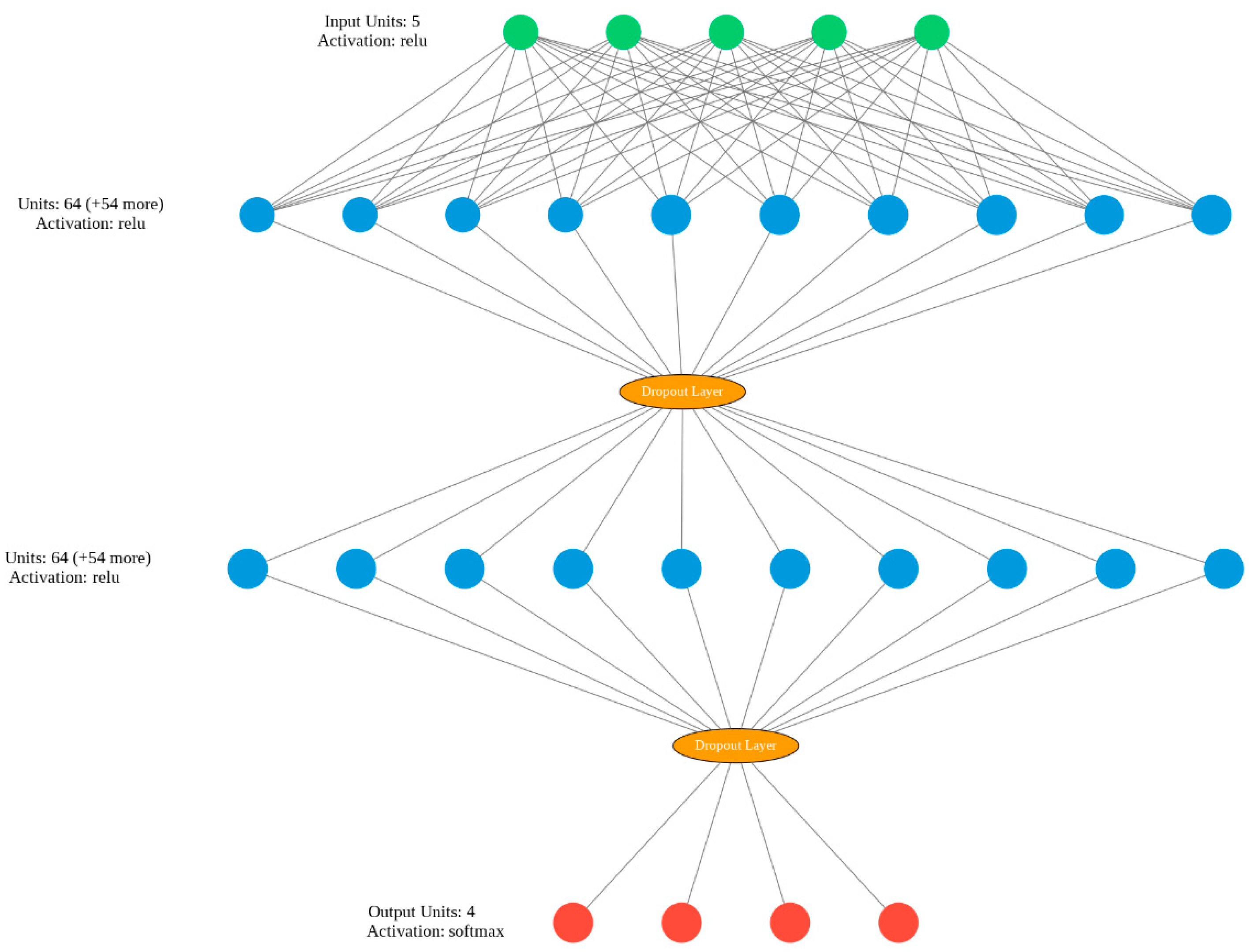
| Layer | Output Shape | Parameter |
|---|---|---|
| Dense | (None, 64) | 384 |
| Dropout | (None, 64) | 0 |
| Dense | (None, 64) | 4160 |
| Dropout | (None, 64) | 0 |
| Dense | (None, 4) | 260 |
| OS | CPU | RAM |
|---|---|---|
| Windows 10 Edu 64 bit | Intel i3-7100U 2.4 GHz | 8 GB |
| Layer (Type) | Output Shape | Parameter |
|---|---|---|
| conv2d (Conv2D) | (None, 150, 150, 32) | 896 |
| max_pooling2d | (None, 50, 50, 32) | 0 |
| conv2d (Conv2D) | (None, 48, 48, 32) | 9248 |
| conv2d (Conv2D) | (None, 48, 48, 32) | 9248 |
| max_pooling2d | (None, 15, 15, 32) | 0 |
| conv2d (Conv2D) | (None, 13, 13, 32) | 9248 |
| conv2d (Conv2D) | (None, 11, 11, 64) | 18,496 |
| max_pooling2d | (None, 3, 3, 64) | 0 |
| conv2d (Conv2D) | (None, 1, 1, 64) | 36,928 |
| flatten (Flatten) | (None, 64) | 0 |
| dense (Dense) | (None, 64) | 4160 |
| dense (Dense) | (None, 4) | 260 |
| Proposed (DNN) | CNN |
|---|---|
| 18.48 ms | 0.80 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Kim, J.; Kim, H. A Study on Gear Defect Detection via Frequency Analysis Based on DNN. Machines 2022, 10, 659. https://doi.org/10.3390/machines10080659
Kim J, Kim J, Kim H. A Study on Gear Defect Detection via Frequency Analysis Based on DNN. Machines. 2022; 10(8):659. https://doi.org/10.3390/machines10080659
Chicago/Turabian StyleKim, Jeonghyeon, Jonghoek Kim, and Hyuntai Kim. 2022. "A Study on Gear Defect Detection via Frequency Analysis Based on DNN" Machines 10, no. 8: 659. https://doi.org/10.3390/machines10080659
APA StyleKim, J., Kim, J., & Kim, H. (2022). A Study on Gear Defect Detection via Frequency Analysis Based on DNN. Machines, 10(8), 659. https://doi.org/10.3390/machines10080659







