Dynamic Simulation and Experimental Study of Electric Vehicle Motor-Gear System Based on State Space Method
Abstract
:1. Introduction
2. Modeling Process
2.1. Improved Dynamic Model of Motor-Gear System
2.2. Model Parameters
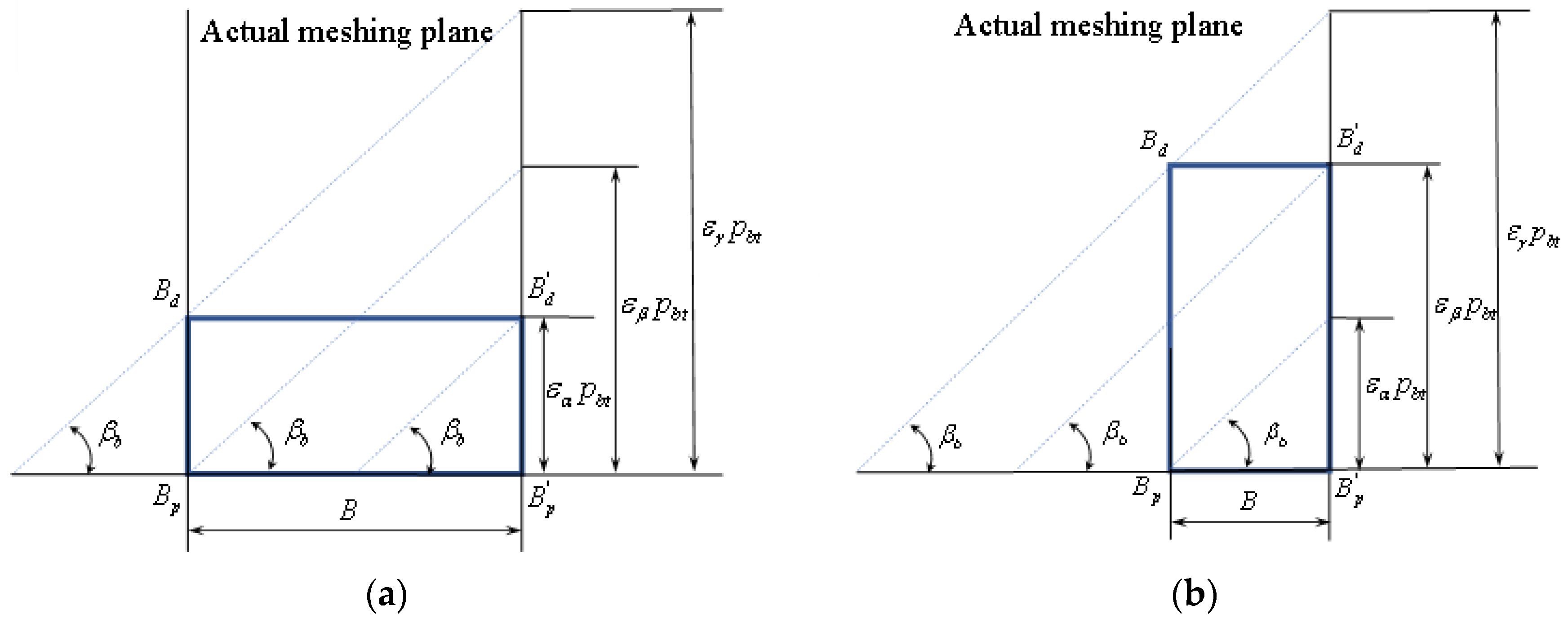
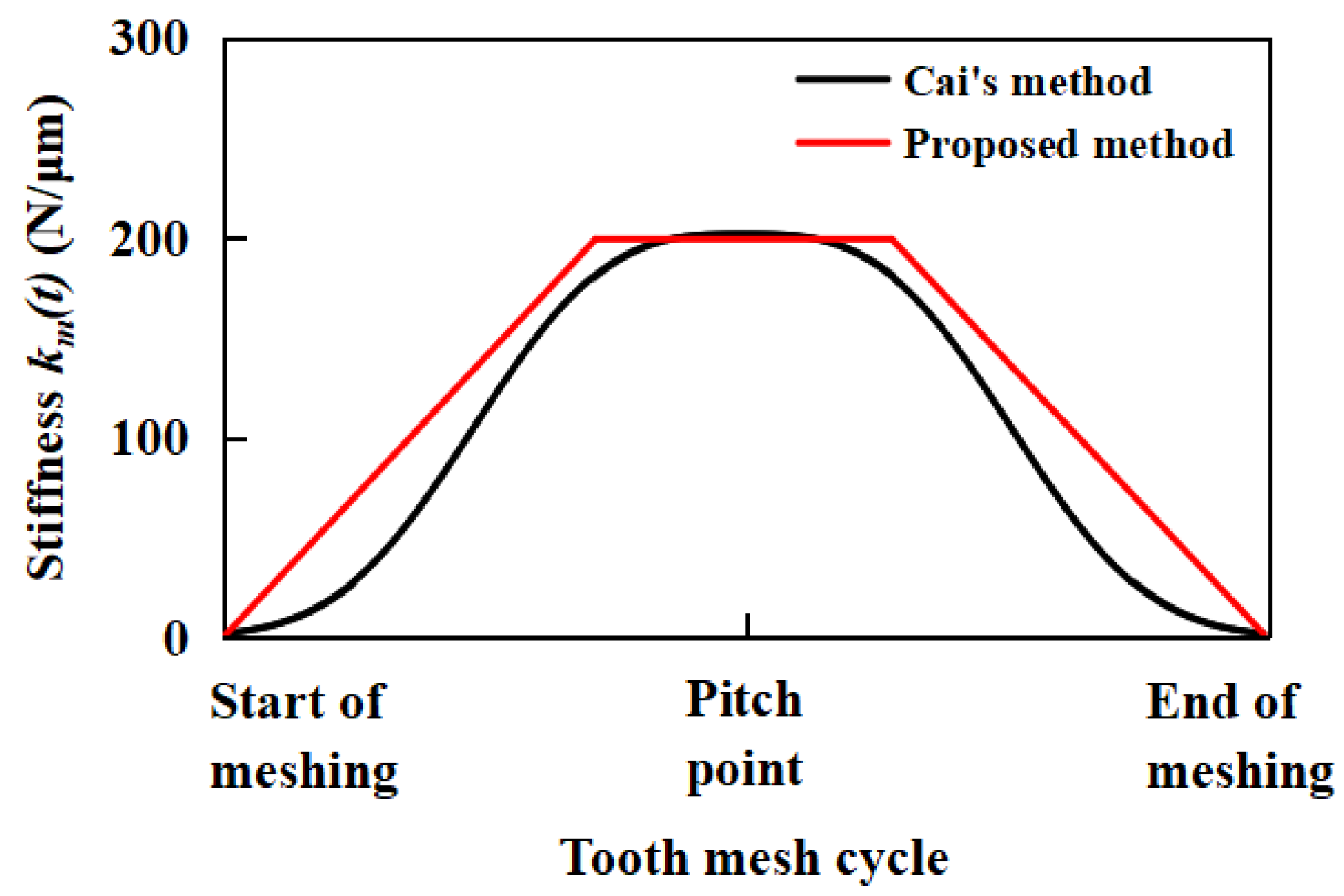
2.2.1. Stiffness
2.2.2. Damping
2.2.3. Errors
2.2.4. Elements
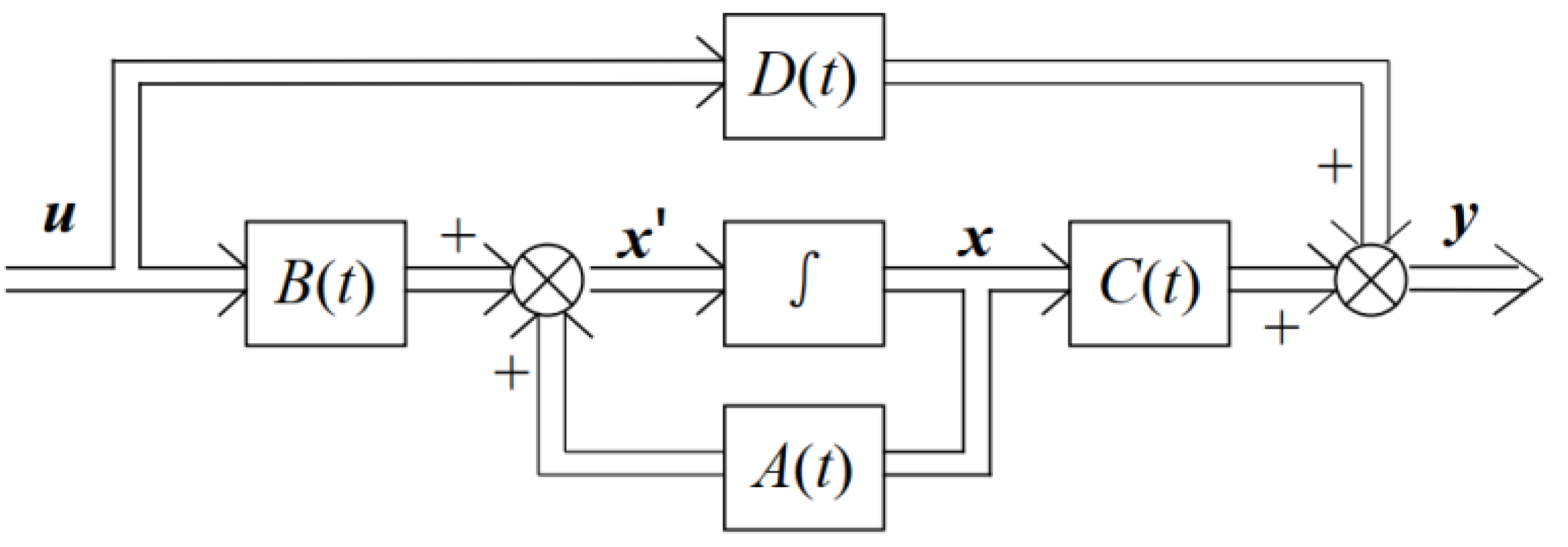
2.3. State Space Method
3. Experimental Test and Measurement
3.1. Test Equipment
3.2. Test Method
4. Results and Discussion
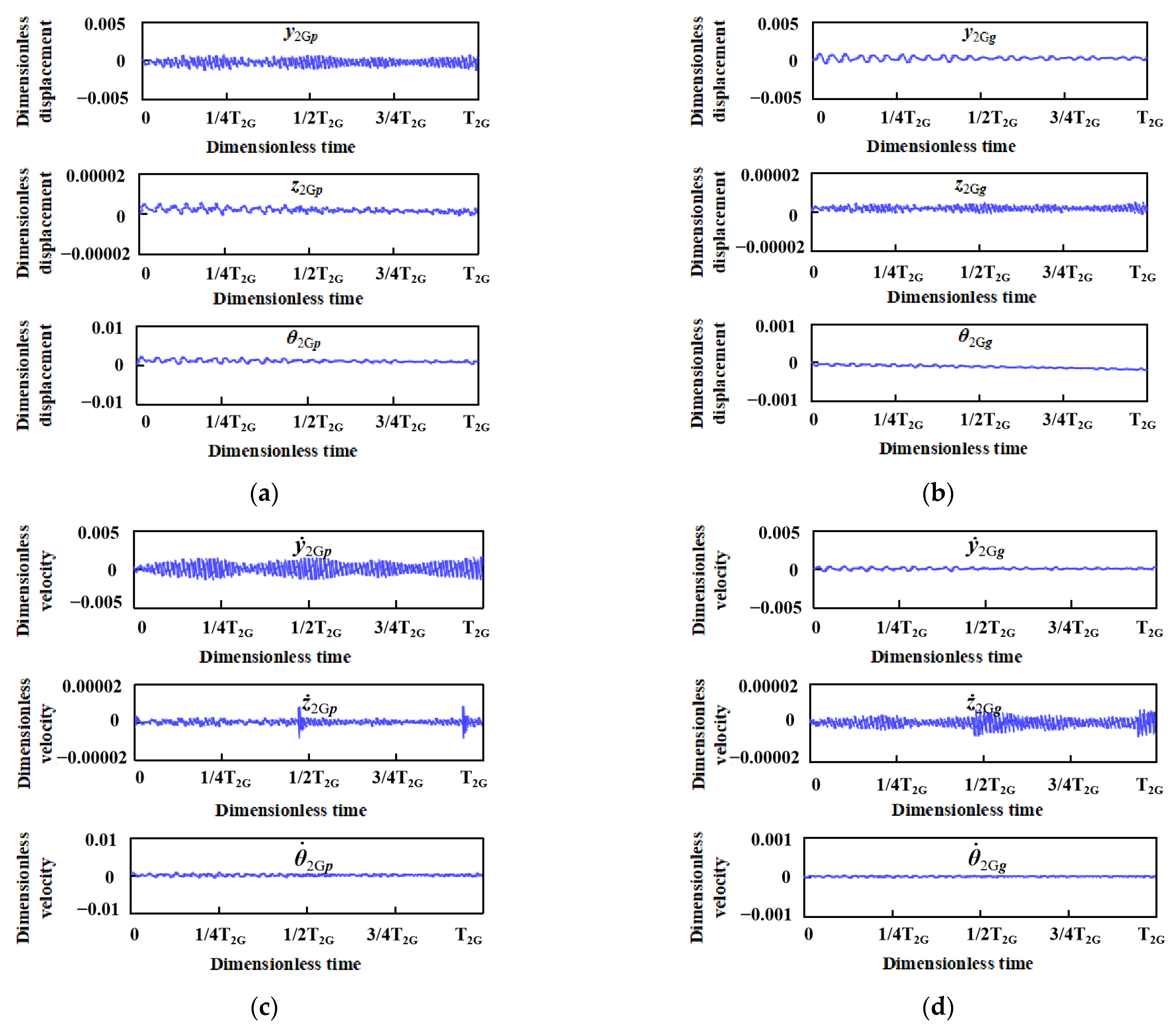
4.1. State Space Calculation
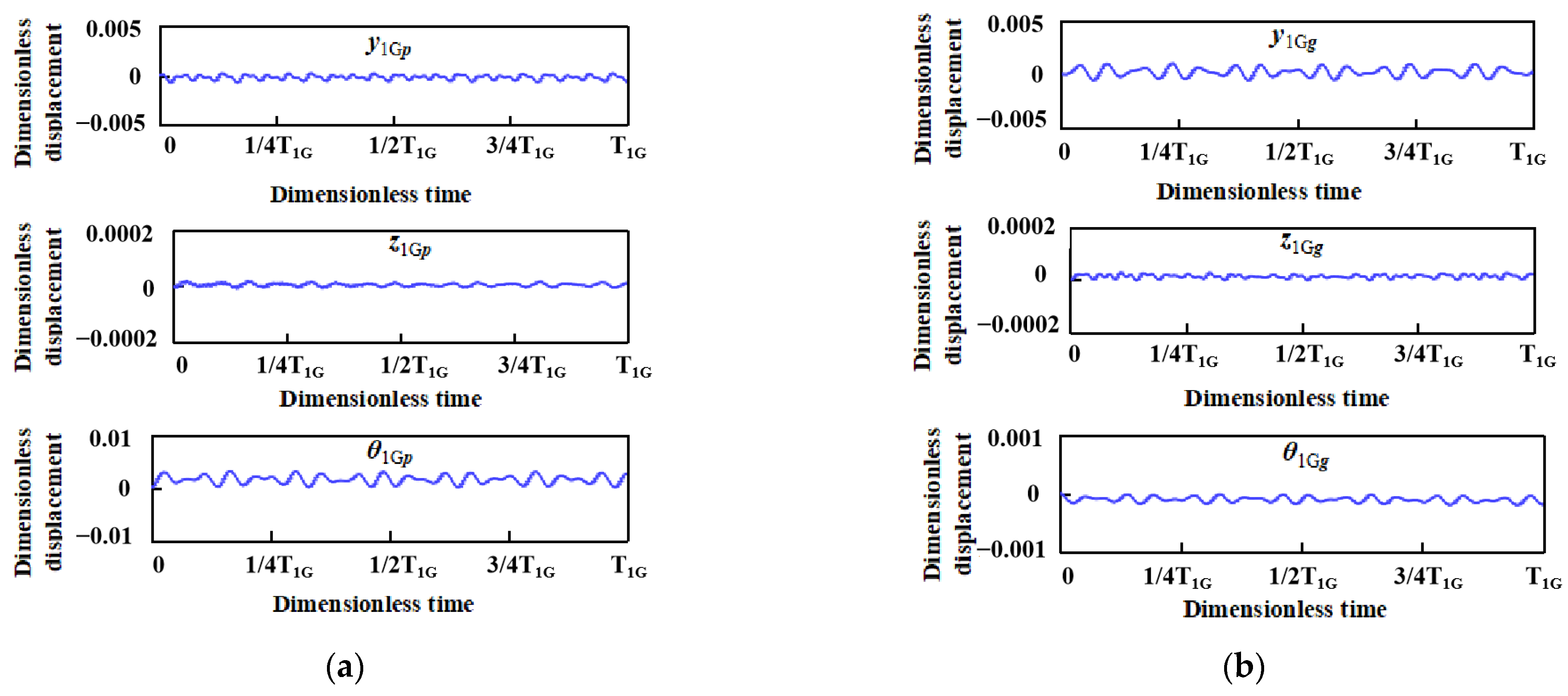
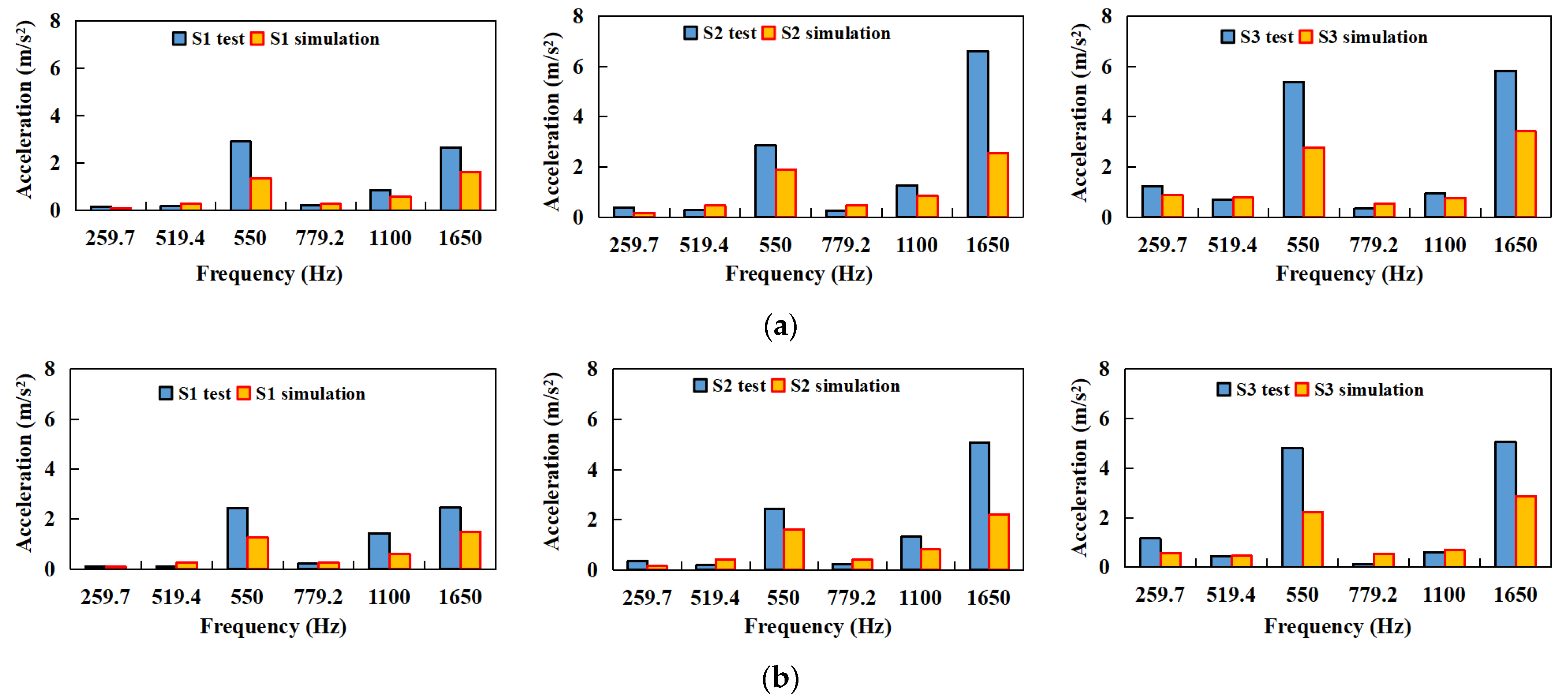
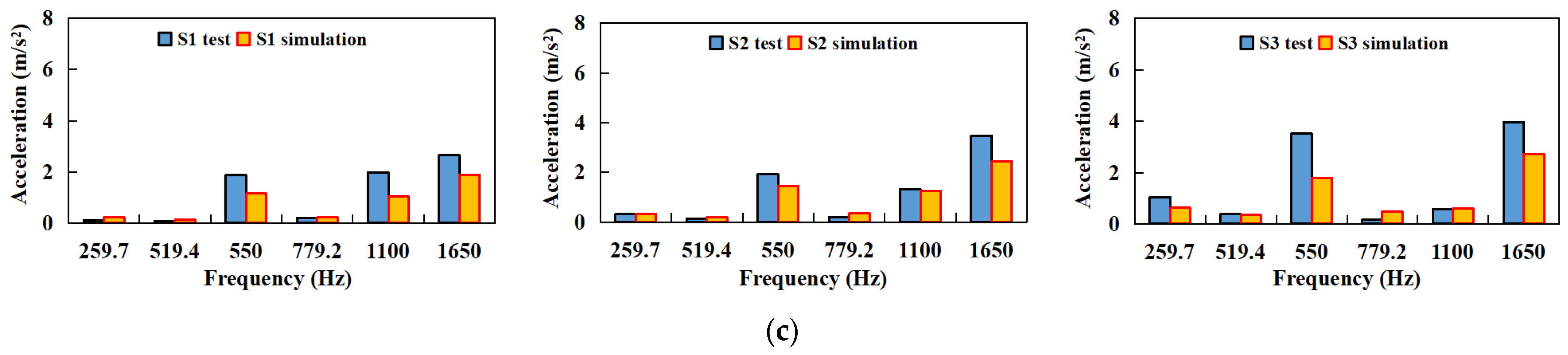
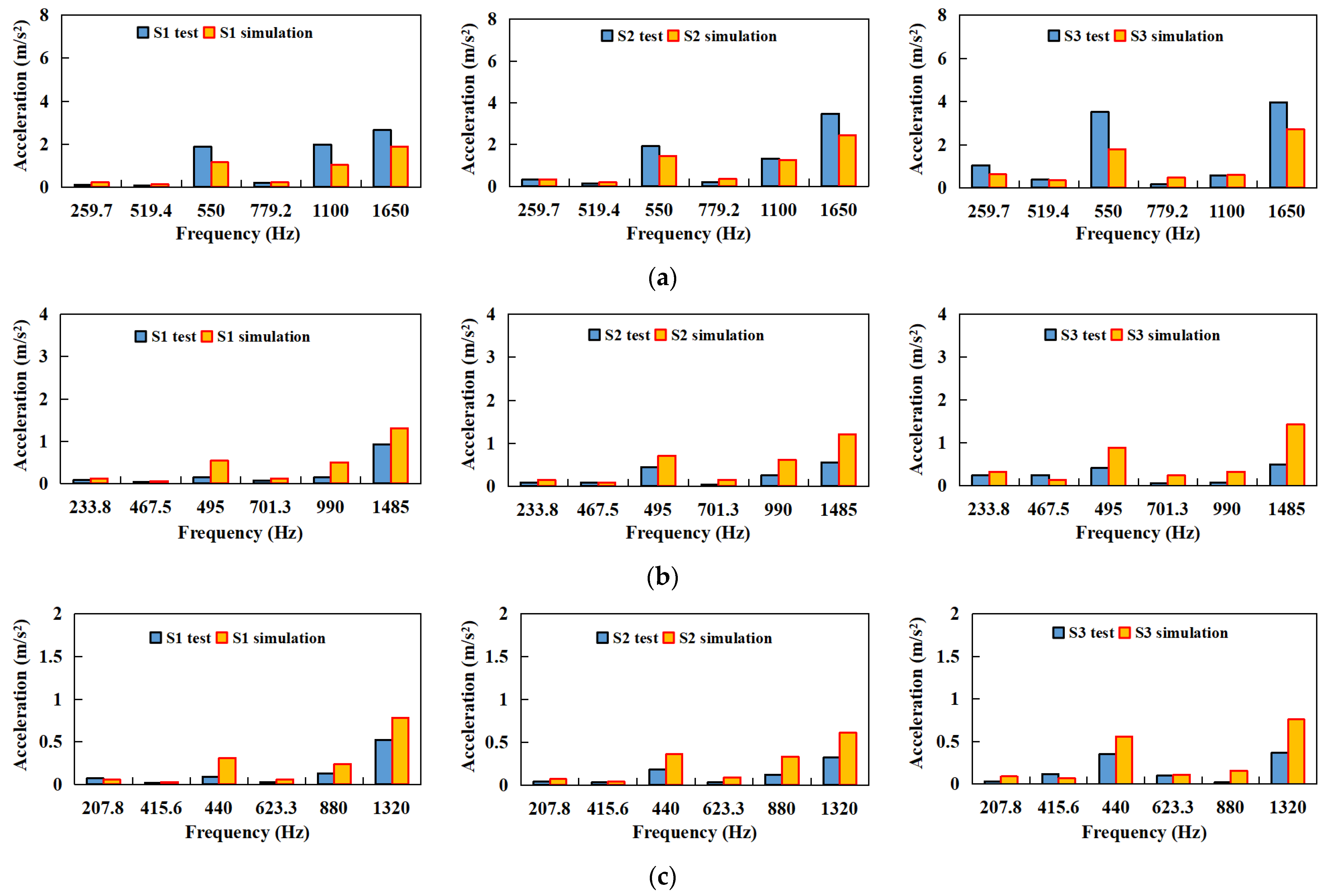
4.2. Transmission Housing Vibration Response
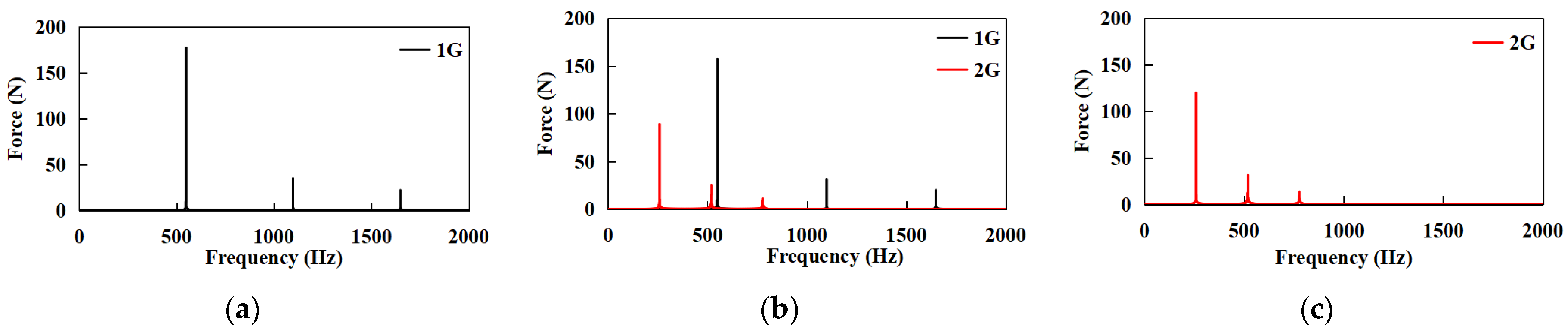
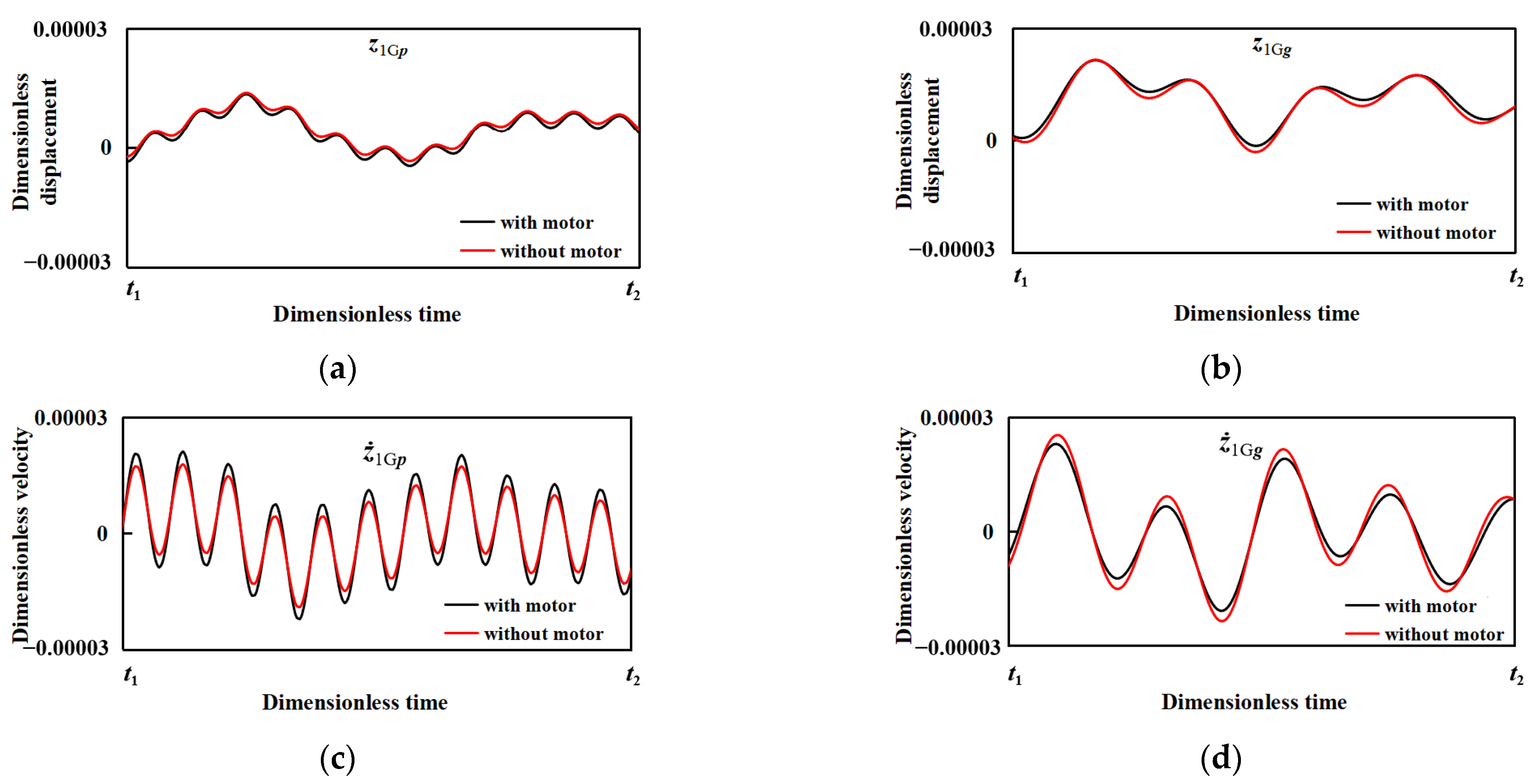
4.3. Influence of Motor Excitation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Chen, R.; Zhou, J.; Sun, W. Dynamic characteristics of a planetary gear system based on contact status of the tooth surface. J. Mech. Sci. Technol. 2018, 32, 69–80. [Google Scholar] [CrossRef]
- Luo, B.; Li, W. Experimental study on thermal dynamic characteristics of gear transmission system. Measurement 2019, 136, 154–162. [Google Scholar] [CrossRef]
- Zhu, C.; Xu, X.; Liu, H.; Luo, T.; Zhai, H. Research on dynamical characteristics of wind turbine gearboxes with flexible pins. Renew. Energy 2014, 68, 724–732. [Google Scholar] [CrossRef]
- Guo, D.; Zhou, Y.; Wang, Y.; Chen, F.; Shi, X. Numerical and experimental study of gear rattle based on a refined dynamic model. Appl. Acoust. 2022, 185, 108407. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, Y.; Zang, L. Model-based transmission acoustic analysis and improvement. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 1572–1584. [Google Scholar] [CrossRef]
- Wei, S.; Zhao, J.; Han, Q.; Chu, F. Dynamic response analysis on torsional vibrations of wind turbine geared transmission system with uncertainty. Renew. Energy 2015, 78, 60–67. [Google Scholar] [CrossRef]
- Inalpolat, M.; Handschuh, M.; Kahraman, A. Influence of indexing errors on dynamic response of spur gear pairs. Mech. Syst. Signal Process. 2015, 60–61, 391–405. [Google Scholar] [CrossRef]
- Duan, T.; Wei, J.; Zhang, A.; Xu, Z.; Lim, T.C. Transmission error investigation of gearbox using rigid-flexible coupling dynamic model: Theoretical analysis and experiments. Mech. Mach. Theory 2021, 157, 104213. [Google Scholar] [CrossRef]
- Garambois, P.; Perret-Liaudet, J.; Rigaud, E. NVH robust optimization of gear macro and microgeometries using an efficient tooth contact model. Mech. Mach. Theory 2017, 117, 78–95. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; He, G.; Zhang, J.; Zhao, Y.; Yao, Y. Nonlinear dynamics analysis of the spur gear system for railway locomotive. Mech. Syst. Signal Process. 2017, 85, 41–55. [Google Scholar] [CrossRef]
- Wang, X. Stability research of multistage gear transmission system with crack fault. J. Sound Vib. 2018, 434, 63–77. [Google Scholar] [CrossRef]
- Abboudi, K.; Walha, L.; Driss, Y.; Maatar, M.; Fakhfakh, T.; Haddar, M. Dynamic behavior of a two-stage gear train used in a fixed-speed wind turbine. Mech. Mach. Theory 2011, 12, 1888–1900. [Google Scholar] [CrossRef]
- Walha, L.; Driss, Y.; Khabou, M.T.; Fakhfakh, T.; Haddar, M. Effects of eccentricity defect on the nonlinear dynamic behavior of the mechanism clutch-helical two stage gear. Mech. Mach. Theory 2011, 7, 986–997. [Google Scholar] [CrossRef]
- Cai, Y.; Hayashi, T. The Linear Approximated Equation of Vibration of a Pair of Spur Gears (Theory and Experiment). J. Mech. Des. 1994, 116, 558–564. [Google Scholar] [CrossRef]
- Cai, Y. Simulation on the Rotational Vibration of Helical Gears in Consideration of the Tooth Separation Phenomenon (A New Stiffness Function of Helical Involute Tooth Pair). J. Mech. Des. 1995, 117, 460–469. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, A.; Wang, G.; Qin, D.; Lim, T.C.; Wang, Y.; Lin, T. A study of nonlinear excitation modeling of helical gears with Modification: Theoretical analysis and experiments. Mech. Mach. Theory 2018, 128, 314–335. [Google Scholar] [CrossRef]
- Wu, X.; He, H.; Chen, G. A new state-space method for exponentially damped linear systems. Comput. Struct. 2019, 212, 137–144. [Google Scholar] [CrossRef]
- Lu, K.; Zhou, W.; Zeng, G.; Du, W. Design of PID controller based on a self-adaptive state-space predictive functional control using extremal optimization method. J. Frankl. Inst. 2018, 355, 2197–2220. [Google Scholar] [CrossRef]
- Demirhan, P.A.; Taskin, V. Bending and free vibration analysis of Levy-type porous functionally graded plate using state space approach. Compos. Part B Eng. 2019, 160, 661–676. [Google Scholar] [CrossRef]
- Vaseghi, N.; Abrishamian, M.S. Analysis of electromagnetic scattering from anisotropic cylindrical structures using state space method. AEU-Int. J. Electron. Commun. 2018, 89, 24–33. [Google Scholar] [CrossRef]
- Scheel, M.; Kleyman, G.; Tatar, A.; Brake, M.R.W.; Peter, S.; Noël, J.-P.; Allen, M.S.; Krack, M. Experimental assessment of polynomial nonlinear state-space and nonlinear-mode models for near-resonant vibrations. Mech. Syst. Signal Process. 2020, 143, 106796. [Google Scholar] [CrossRef]
- Fang, Y.; Zhang, T.; Yu, P.; Guo, R. Effect of tangential electromagnetic force on vibration and noise of electric powertrain. Electric Mach. Control 2016, 20, 90–95. [Google Scholar]
- Li, B. Calculation Method for Axial Force of Motor Based on Two-dimensional Electromagnetic Field Simulation. Micromotors 2019, 52, 28–33. [Google Scholar]
- Chen, S.; Tang, J.; Wu, L. Dynamics analysis of a crowned gear transmission system with impact damping: Based on experimental transmission error. Mech. Mach. Theory 2014, 74, 354–369. [Google Scholar] [CrossRef]
- Amabili, M.; Fregolent, A. A method to identify modal parameters and gear errors by vibrations of a spur gear pair. J. Sound Vib. 1998, 214, 339–357. [Google Scholar] [CrossRef]
- Chang, L.; He, Z.; Liu, G. A generalized dynamic model for parallel shaft gear transmissions and the influences of dynamic excitations. J. Vib. Shock 2016, 35, 7–14. [Google Scholar] [CrossRef]
- Alptekin, A.; Broadstock, D.C.; Chen, X.; Wang, D. Time-varying parameter energy demand functions: Benchmarking state-space methods against rolling-regressions. Energy Econ. 2019, 82, 26–41. [Google Scholar] [CrossRef]
- Ding, Z.; Li, L.; Hu, Y.; Li, X.; Deng, W. State-space based time integration method for structural systems involving multiple nonviscous damping models. Comput. Struct. 2016, 171, 31–45. [Google Scholar] [CrossRef]
- Zandi-Mehran, N.; Nazarimehr, F.; Rajagopal, K.; Ghosh, D.; Jafari, S.; Chen, G. FFT bifurcation: A tool for spectrum analyzing of dynamical systems. Appl. Math. Comput. 2022, 422, 126986. [Google Scholar] [CrossRef]
- Han, J.; Liu, Y.; Yu, S.; Zhao, S.; Ma, H. Acoustic-vibration analysis of the gear-bearing-housing coupled system. Appl. Acoust. 2021, 178, 108024. [Google Scholar] [CrossRef]
- Xu, B.; Ye, S.; Zhang, J. Numerical and experimental studies on housing optimization for noise reduction of an axial piston pump. Appl. Acoust. 2016, 110, 43–52. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, Y.; Xu, H. Effects of multi-excitation on vibration characteristics of planetary gear system. Alex. Eng. J. 2022, 61, 10593–10602. [Google Scholar] [CrossRef]






| Elements | Parameters | Values | |||
|---|---|---|---|---|---|
| Gears | Gear No. | First-stage gear pair | Second-stage gear pair | ||
| Gear Z1 | Gear Z2 | Gear Z3 | Gear Z4 | ||
| Number of teeth | 11 | 36 | 17 | 62 | |
| Normal module (mm) | 2.5 | 2.25 | |||
| Pressure angle (deg) | 20 | 20 | |||
| Helix angle (deg) | 25.5 | 30 | |||
| Face width (mm) | 14.00 | 12.50 | 28.10 | 25.00 | |
| Profile shift coefficient (mm) | 0.35 | −0.43 | 0.32 | 0.32 | |
| Base diameter (mm) | 28.26 | 92.48 | 40.72 | 148.50 | |
| Reference diameter (mm) | 30.47 | 99.71 | 44.17 | 161.08 | |
| Tip diameter (mm) | 38.25 | 102.00 | 51.30 | 167.41 | |
| Root diameter (mm) | 27.85 | 90.54 | 38.96 | 155.57 | |
| Center distance (mm) | 65 | 104 | |||
| Gear ratio | 3.27 | 3.65 | |||
| Moment of inertia (kg·mm2) | 13 | 865 | 89 | 6355 | |
| Shafts | Shaft No. | Shaft S1 | Shaft S2 | Shaft S3 | |
| Diameter (mm) | 23 | 30 | 40 | ||
| Length (mm) | 82.5 | 61.1 | 82.9 | ||
| Motor | Number of poles | 10 | |||
| Number of slots | 72 | ||||
| Length of effective stator (mm) | 240 | ||||
| Armature radius (mm) | 360 | ||||
| Axial air gap flux (T) | 0.84 | ||||
| Air permeability (H/m) | 4 × 10−7 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Chen, Y.; Li, G.; Zang, L.; Wang, D.; Qiu, Z.; Wei, G. Dynamic Simulation and Experimental Study of Electric Vehicle Motor-Gear System Based on State Space Method. Machines 2022, 10, 589. https://doi.org/10.3390/machines10070589
Cao Z, Chen Y, Li G, Zang L, Wang D, Qiu Z, Wei G. Dynamic Simulation and Experimental Study of Electric Vehicle Motor-Gear System Based on State Space Method. Machines. 2022; 10(7):589. https://doi.org/10.3390/machines10070589
Chicago/Turabian StyleCao, Zhan, Yong Chen, Guangxin Li, Libin Zang, Dong Wang, Zizhen Qiu, and Guangyan Wei. 2022. "Dynamic Simulation and Experimental Study of Electric Vehicle Motor-Gear System Based on State Space Method" Machines 10, no. 7: 589. https://doi.org/10.3390/machines10070589
APA StyleCao, Z., Chen, Y., Li, G., Zang, L., Wang, D., Qiu, Z., & Wei, G. (2022). Dynamic Simulation and Experimental Study of Electric Vehicle Motor-Gear System Based on State Space Method. Machines, 10(7), 589. https://doi.org/10.3390/machines10070589







