Abstract
Heavy fuel combustion problems with startup and operation may significantly reduce the microturbine efficiency in small APUs (Auxiliary Power Units). The use of commercial automotive-derived turbochargers solves the design problems of compressors and turbines but introduces large issues with combustors. The radial combustor proved to be the best design. Unfortunately, high-pressure injection is not practical for small units. For this reason, primary air and low-pressure fuel spray are heated and mixed. In any case, a high air swirl must achieve a satisfactory combustion efficiency. This swirl should be almost eliminated at the turbine intake. CFD analysis of the combustor design was, therefore, performed with several different geometries and design solutions. In the end, a large offset of the fresh pipe from the compressor proved to be the best solution for a high swirl in the combustion region. The combustion tends to eliminate the swirl, but an undesired tumble motion at the turbine intake takes place. To eliminate the tumble, two small fins were added to straighten the flow to the turbine.
1. Introduction
Small turbogas generators are even more critical than standard turbogas generators due to problems with miniaturization, low Re (Reynold number) and tip play. Efficiency and reliability are achieved only if the development problems are correctly addressed. Debugging a faulty design may easily result in disasters. Therefore, the combustor has several tasks to accomplish. First, it should be easy to start. Then, it should produce a stable and resonance-free combustion of the fuel in most, theoretically any, working conditions of the turbogas. The combustor should also be efficient and should keep the temperature in a proper range to avoid excess NOx. Finally, the combustor should deliver a homogeneous and vortex-free gas flow to the turbine. The velocity vectors at the turbine intake must have the proper direction and the right intensity pattern.
In the first part of this paper [1], it was shown that the design of a turbogas generator with a centrifugal compressor and radial turbine is not easy. The compressor introduces a swirl motion that is difficult to correct in an axial flow combustor. The difficulty is because the swirl energy content and the velocity vectors depend on the shaft speed and the load on the turbogas generator. Therefore, a compromise should be met between the necessity to have an easy start and a reasonable efficiency, at least in nominal conditions. In our case, as described in the first part of this paper [1], a variable geometry compressor was used to obtain reasonable performance. In the end, a radial combustor with a fixed geometry compressor and turbine proved to be the optimal solution. Even with a radial compressor and turbine, which are more flexible than the axial ones, the off-design efficiency is not the best quality of the turbogas generator when compared with piston engines. The necessity of an easy coupling of the turbogas generator with a brushless generator is the origin of the second part of this paper [2]. This second part demonstrates that, in most cases, for loads over 50% of the maximum, the turbogas generator can be easily matched to a brushless generator. This third part is focused on the improvement of combustor design. The combustion of heavy fuel requires turbulence in the combustion airflow. A stable swirl motion is required for optimal combustion. However, this swirl motion should be eliminated at the turbine intake. Luckily, the combustion process with the gas expansion helps to fulfill this requirement. CFD (Computational Flow Dynamic) analysis was used to find out more efficient geometry.
This study is focused on the improvement of the combustion chamber design. The combustion chamber has been the most problematic part of the design. The initial axial solution proved to be prohibitive due to difficulties in off-design performance to the point that starting the machine proved to be problematic or impossible. The radial configuration and the design of Don Giandomenico are effective. As briefly introduced in this paper, microturbines are not very efficient even at the design point. The introduction of a heat-recovery system eliminates the only true advantage of turbine-APUs: the exceedingly small size. For this reason, design choices are extremely limited. Micro axial compressors are inherently inefficient, difficult to design, unreliable due to boundary layer problems and due to a large amount of very tiny parts, which adversely impact manufacturing tolerances and maintainability [3]. Radial turbines and compressors are easier to manufacture but face a significant efficiency reduction below 200,000 Re [4,5,6]. The efficiency problem becomes important below 100,000. Exceptionally large automotive turbochargers used in trucks usually work below 150,000 Re. For this reason, they are an exceptionally good starting point for microturbines. Automotive turbochargers are designed for optimum off-design performance and minimum inertia. For this reason, the impeller wheel is usually as small as possible, and the diffuser is also slightly sub-sized. However, especially for large turbochargers, several diffusers are available for the compressor. The largest one is close to the design of maximum efficiency. For this reason, it is very convenient to use a commercial turbocharger. The turbine wheel can be replaced with the best commercial elevated temperature one that can withstand 1050 DEG C continuously. A good honing of the parts, improved balance, and the addition of a polymeric liner to the compressor case completes the preparation. The radial combustor uses an insulated pipe with the largest bend possible to bring the “fresh” air of the compressor to the combustor. The combustor is cylindrical and contains a holed pipe for primary and secondary air separation. A very short duct is interfaced with the radial turbine intake. A high-pressure fuel injection system is not convenient due to weight and size. A low fuel pressure injection system would not satisfy the atomization requirement for heavy fuel. The third part of the study aims to improve the combustor efficiency by changing the design of the combustion chamber to obtain homogeneous and parallel air at the turbine intake while increasing the vortex inside the chamber.
Summary of Previous Papers
The first two papers of this study aimed to develop a highly cost-effective turbogenerator derived from an up-to-date and commercial turbocharger. In the first paper, design development is introduced. The design starts from a modern, simple, reliable, cost-effective automotive turbo generator with its inherent advantages and limits. For this purpose, the exceptionally large Garrett GTX5533-98 turbocharger is used due to its modern and optimized design. Large units have the advantage of high Re that are closer to the most efficient ones. A few cost-effective modifications are introduced to the off-the-shelf turbocharger. First, to increase the efficiency and power, a higher temperature turbine wheel was installed. This new turbine has the best material commercially available that can withstand a constant temperature of 1050 DEG C. Then, a polymeric liner was painted on the inner part of the compressor casing to decrease the gap at the impeller-blade-tip. In this way, the impeller can carve the gap in operation without damage. As a further step, the impeller and the diffuser of the compressor were polished to the best quality available. In this way, the compressor map narrows, but the maximum pressure and the efficiency of the compressor are improved. Finally, the combustion chamber design reached an acceptable design. In the initial configuration, the purely axial design of the heavy fuel combustion chamber proved to be poor to the point that it prevented the turbogas generator from starting. A variable geometry vaned diffuser was added to the initial geometry to improve the performance of the design both at starting and in nominal conditions. Unfortunately, it increased costs enormously with concerns about the reliability of so many tiny parts. The best solution is the one used by Mr Don Giandomenico. Giandomenico designed a radial combustor, which solves many flow problems inside the turbogas generator. In addition, according to that system, the combustor has a heating system inside to improve fuel vaporization, which increases the combustion efficiency up to 95% with automotive diesel fuel [1,2]. In the second part of this paper, the off-design performance of a turbocharger-derived APU (Auxiliary Power Unit) has been studied. This study was performed by using the Mach number similitude, which is perfect to evaluate the turboshaft power output at different intake temperatures, altitudes, and humidity values. The Mach number varies with temperature and humidity. The original compressor map was measured by the manufacturer with the volumetric flow on the x-axis about OA (Outside Air) conditions. In our case, it is the Garrett reference OA. For a given turbocharger, volumetric flow is equivalent to velocity. If you express this nominal velocity in terms of Mach, it is possible to calculate in reverse the velocity for different OA conditions. This evaluation is extremely accurate due to the huge amount of work in the calculation of the sonic speed for acoustics. In this method, the turbocharger rpm is also substituted with the ratio of the peripheral impeller velocity and the sound speed. Turbine power output is then calculated from equations corrected by very few experimental coefficients, and these calculations are shown with different OA conditions. OA temperature affects the max power output as well as density. With altitude, the power loss is linear due to the reduction in temperature that partially compensates for the decline in pressure. In most cases, for power output exceeding 50% of the maximum available, the coupling with a brushless generator proved to be easy [1,2].
Experimental tests on several prototypes demonstrated that the development of turbogas from a turbocharger is not easy. Centrifugal compressors are not an easy match to axial combustors. If you want to use the wide map of the centrifugal compressor in every working condition from startup to partial load and for most environmental conditions, it is better to use a tangential combustor that will match the intake of the centripetal turbine. This is because the speed at the turbine intake is very high, even if the Mach number is well below unitary. Turbine intake temperatures reach 1023.15 K for commercial grade turbochargers and up to 1323.15 K for premium commercial ones. Therefore, the absolute speed that should stay subsonic (below~0.9 Mach) can be quite high in absolute terms. The equation of perfect gas in which the Mach speed is proportional to the square of gas temperature (K) holds with good approximation. For this reason, the pipes to the turbine should be as straight as possible to reduce pressure drop. On the other hand, the tangential combustor makes it possible to optimize combustor geometry for primary, secondary and tertiary air. A small duct of primary air in the combustor is necessary to reduce the size of the heating device for cold starting. The secondary air duct is necessary to achieve the necessary condition of efficient combustion with heavy fuel with the necessary swirl even when a low-pressure injection is adopted. In fact, high-pressure injection is too expensive both in terms of the sheer cost and power requirement. The tertiary air is necessary to cool down and control the secondary air exit temperature, which can easily be over 2000 K. For acceptable turbine efficiency and turbine power output, the exit flow from the combustor is uniform and coaxial to the turbine intake as possible. This paper offers a design of a combustor that has good efficiency and straight output flow. The combustion efficiency depends essentially on the swirl rate: a higher swirl allows higher combustion efficiency. However, the swirl motion is extremely stable and survives the combustion down to the combustor exit/turbine intake. It is, therefore, important to design a combustor with low-pressure drop and well-aligned, uniform velocity vectors at the exit. The uniformity of the intake flow to the small turbine is critical for turbine efficiency (75% max), which is already not high when compared with large axial turbines (97% max). This low efficiency is compensated, for axial turbines and compressors, by a wider range of acceptable efficiency in terms of volumetric and mass flow. Furthermore, small centrifugal compressors suffer from the same problem with a maximum efficiency of 76% compared with large axial compressors (88% max).
2. Materials and Methods
2.1. Small Turbogas Issues
Small turbogas generators have always been problematic for efficiency and reliability. The reason lies in small Re and miniaturization. For example, an LM2500 marine turbogas requires only 8.23 × 2.74 × 3.05 m (68.77 m3) of ship space to deliver 40,200 HP (30 MW). A 100 kW turbogas generator with equivalent volumetric power density would theoretically need only 27 × 9 × 10 mm (2.57 10−6 m3). Even if the Reynolds numbers (Re) (boundary layer) and blade gaps required a larger volume, the size of a turbogas unit when compared with a piston engine is appeasing. Centrifugal compressors are the premium choice for microgas turbines (100−1000 kW), being simpler than the axial counterparts and theoretically much smaller than piston engines. In addition, the small-scale centrifugal compressors of turbochargers have theoretically immense potential improvement due to their low efficiency. In fact, the small size of many centrifugal compressors with an impeller outlet diameter of less than 30 mm gives a low Reynolds number (Re), leading to a much lower efficiency than that of larger units. A reduction of 96% in the Reynolds number (Re) may result in 15 percentage points lower efficiency in a centrifugal compressor [3]. Unfortunately, modern piston engines are incredibly good competitors, with an efficiency that can exceed 50% and multifuel capability (hydrogen, natural gas, ammonia, diesel, gasoline, etc.). The possibility of embedding the generator in the flywheel and the electronic control of most automotive-derived engines make the conversion to APU easy. Commercially, microturbine APUs are available, but the necessity to adopt at least a 30% recuperator makes the microturbine uncompetitive with the equivalent piston-powered APUs in terms of volume [7]. Another large limitation is that the cooling of the turbogas is provided by intake air. In ground applications, the intake air should be filtered, resulting in large filters that require frequent maintenance. Finally, the extremely poor off-design performance of a turbogas generator makes it very inefficient to work at partial power output. Most of the problems of miniaturization come from the compressor, which has been and still is the most critical part of a turbogas generator.
2.1.1. Small Axial Compressors Losses
In axial compressors, the pressure rise depends on aerodynamic diffusion efficiency performance that is strongly influenced by the boundary layer (BL) over the blade surfaces. In fact, the diffusion-induced adverse pressure gradients tend to separate the boundary layers with negative effects on pressure rise capability. The large volume/area occupied by BL makes the situation more critical. Therefore, the boundary layer influences efficiency and loss in small compressors more than in larger ones. Furthermore, laminar-to-turbulent transition influences the development of unsteady boundary layers on blades significantly, and in multistage compressors, this transition process depends on the unsteadiness of the flow. As in many other applications, unsteady natural disturbances in the background are gradually amplified, generating three-dimensional secondary instabilities with local flow breakdown with turbulent spots that rapidly result in a fully turbulent BL. This phenomenon is added to the classical bypass transition. The high freestream turbulence and upstream wakes affect the laminar to turbulence transition of the BL as they spread downstream. Finally, in decelerating flow, the laminar boundary layer tends to separate from the surface and tends to roll up the separated shear layer into coherent turbulent vortices. Therefore, it is not possible to scale down existing compressors, but an innovative design is needed. In addition, the large clearances needed in small machines make the aerodynamics of the system even more complicated. The miniaturization of parts and the necessity for smooth surfaces makes axial compressors in microturbines prohibitively expensive.
2.1.2. Small Centrifugal Compressors Losses
In centrifugal compressors, a low Reynolds number (Re) increases the BL thickness and the friction losses leading to deteriorated performance for both efficiency and pressure ratio. For turbogas, the decrease in the Reynolds number (Re) depends on a change in the compressor size and the environmental conditions. In centrifugal compressors, the reference length of the Reynolds number (Re) is based on distance c between the mid-spans of the blade leading edge and blade trailing edge. The velocity w1 is the inlet one (3). The deterioration process begins at Re lower than 200,000 and becomes important below 100,000. Re also affects the compressor map, moving the surge line on the right.
The adiabatic compression process is assumed as a maximum reference to the compressor performance, and Equation (4) holds for total-to-total isentropic efficiency η. The t stands for total pressure and temperature. Cp is the heat capacity at constant pressure. R is the universal gas constant. Section 1 refers to the inlet, while 2 is the compressor output. For the units, it is necessary to use the SI.
Earliest Re correction equations were published by Moody (1925) and Ackeret (1930) [1]. The most common correction equation is (5).
Unfortunately, the exponent n ranges from 0.1 to 0.5 depending on the compressor type, and the Re independent losses a range from 0 to 0.5. The authors of [8] stated that the strong deterioration of the compressor performance depends on Reynolds number (Re) and the laminar behavior of the BL under 200,000. Figure 1 shows the different correction curves depending on coefficient values of a and n. Substantially, Equation (5) does not hold, and the real efficiency should at least be evaluated with the CFD (Computational Flow Dynamic) simulation. In any case, the loss can be huge under 200,000. Re of 140,000 or less is common even in large automotive turbochargers.
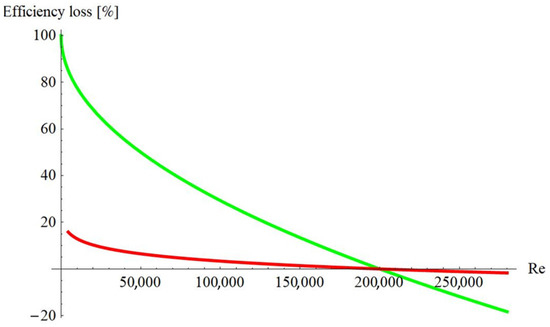
Figure 1.
Efficiency loss according to Equation (3). The red line is for a = 0.5 and n = 0.1, while the green line is for a = 0 and n = 0.5. In this case, Reref is 200,000.
Due to the small efficiency, it would be necessary to add a heat exchanger to recycle power from the exhaust to the intake. A 30% heat recovery is common [9,10]. However, this approach increases the overall volume of the turbogas generator with a size that is similar to the one of piston engines. This makes turbine-based APU noncompetitive. In fact, diesel APUs reach and pass 50% efficiency with the additional advantage of having a flat efficiency value for most loads and off-design conditions. Therefore, in this paper, the turbine-APU is without heat recovery with the advantage of an exceedingly small overall size, which is the real advantage of these units.
2.2. CFD Implementation
In this paper, Flow Simulation, the CFD software and automatic mesh generator of SolidWorks was used. Complete and accurate CAD 3D models are the beginning stage for all virtual prototyping and actual reproductions. The integration of CAD 3D models with Computational Fluid Dynamics, (CFD) and FE (Finite Element) in CAE (Computer Aided Engineering) software can altogether speed up the development phase. In any case, this approach has the disadvantage of expanding development time. This reality unavoidably builds the resistance to outer “specific” software and enhancements such as FE and CFD. Previous findings suggested that FE-related simulations are able to portray feasible results for material and mechanical design analysis [11], even for composite structures [12]. However, the consistent improvement of CAD-implanted interfaces consistently reduced this additional time. In addition, the new CFD software has reduced the computational time by two orders of magnitude in the last 10 years. To make CFD usable for most mechanical and aerospace engineers, CFD programming bundles have been robotized to limit the expert mastery expected to work with conventional CFD programming. The abilities of CAD-installed CFD to deal with genuinely complex calculations and, furthermore, to adapt to different boundary conditions and geometries with heat and mass exchange is then critical, along with the automatic boundary layer generation. Today, the SolidWorks-inserted Flow Simulation software is a ten-year-old mature code with thousands of simulations successfully conducted. It uses a modified k-ϵ 2-condition model that fits a wide range of flow conditions [13]. It utilizes a modified k-ϵ two-equation turbulence model optimized for a wide range of turbulence scenarios. An immersed boundary Cartesian meshing technique gives a sufficiently accurate flow field estimation with low cell mesh densities [14] (Figure 2).
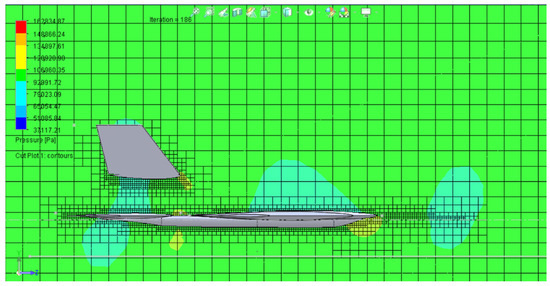
Figure 2.
Cartesian mesh with impingement of the model. Impingement means that elements are adapted to the model boundary layer.
The submerged limit techniques are genuinely basic. From the model and the initial mesh, the pre-processor recognizes the computational cells that are cut by the body with the boundary layer. The cells are then separated into those that are inside and outside of the body and the boundary layer. The cut cells are isolated in two sorts of cells relating to the area of their cell place. The first type of cell that has its mathematical focus outside or on the outer layer of the body is marked as a point of interaction cells. The second type of cell is dealt with similarly to inside cells. The flow variable φ, which addresses a disturbance variable, is set to focus within cells. At the connection point cells, the closing of the divider is demonstrated with an off-divider limit condition, which, overall, comprises a straight introduction design amended with a (non-direct) rectification. The scalar variable φ in the point of the interaction cell (i, j) is inserted in two stages, utilizing just the adjoining cells that are further away from the body. At first, a straight interjection is completed along with the ordinary to the divider up to a transitional area that has a similar distance to the divider as the point of interaction cell focus (i, j) for each adjoining cell. The subsequent addition takes on a surface that corresponds to the divider. Here, the converse distance weighted strategy proposed by [15] saves nearby maxima and produces smooth reproductions. The introduction of φ (i, j) in the connection point cell is:
with
and
where φm are the recently added values, hm is the distance between the place of φ (i, j) and the place of φm and H is the limit of the upsides of hm. The aggregate is over the adjoining cells, where m recognizes the cell over (N-Nord), under (S-South) on the left (E-East) and the right (W-West) of the present cell. The loads wm = 0 for all non-qualifying neighbors. For every connection point cell, the portrayed direct insertion brings about a bunch of loads βn, which sum up the effect of each neighbor cell on the point of interaction cell:
By considering only the adjoining cells (W, E, S, N) that have a typical face with the connection point cell (i, j), the straight insertion (4) can, without much of a stretch, be treated in a verifiable manner. Truth be told, in the computational CFD RANS (Reynolds Averaged Navier–Stokes) code, a second request of an understood, cell-focused Cartesian lattice is utilized inside a strain speed coupling calculation with an isolated arrangement of the field conditions [16]. These conditions are discretized in three aspects with a 7-point design. In any case, in this short presentation, we will allude to the straightforwardness of the relating two-layered conditions. In this manner, for every cell (i, j), the discretized field condition for force, scalar and tension adjustment can be written as:
The certain lattice of the situation (5) can be modified with the loads βm without presenting new diagonals with non-zero components. Notwithstanding the incorporation of mathematical individual focuses, for example, corners ought to be constructed unequivocally. For a non-direct conduct of φ close to the divider, an unequivocal stabilator ∆φcorr is added to the right-hand side of condition (4). This network generator can be applied to develop all-inclusive profiles related to Van Driest [17]. These profiles can be utilized to portray two classes of violent limit layers. The thick limit layer model is utilized when the liquid mass habitats of the close divider network cells are situated inside the limit layer. The meager limit layer model substitutes the first when the liquid mass places of the close divider network cells are situated external to the limit layer. These limit layer models overcome the issue of an extremely fine lattice thickness close to the dividers in the estimation. The Launder Spalding capacities determine the divider limit conditions for the RANS in an improved disturbance k-ϵ model. In different districts of the computational area, the k-ϵ with the damping model of Lamand Bremhorst [18] portrays laminar, tempestuous, and temporary progressions of homogeneous liquids comprising disturbance energy preservation conditions [18,19].
with
where Cij = 0.09, Ct1 = 1.44, Ct2 = 1.92, σk = 1, σε = 1.3, σB = 0.9 and CB = 1 or CB = 0 for PB > 0 and PB < 0.
Lam and Brembhorst’s damping function is used in the turbulent viscosity term (8) (9).
y is the distance of the point from the wall, and
Lam and Bremhorst’s damping functions fµ, f1, f2 decrease turbulent viscosity and turbulence energy and increase the turbulence dissipation rate. These boundaries are constrained by the Reynolds number Ry. Ry is determined by the normal speed of variances and distance from the divider. When fµ = 1, f1 = 1, f2 = 1, the methodology obtains the first k-ε model. A liquid’s limit layer requires an extremely high thickness lattice to give precise outcomes. This approach debilitates the computational proficiency of the reproduction and typically requires significant PC (Personal Computer) time on high-performing computers. Thus, the computational cross section utilized in our CFD code is a vivid limit non-body-fitted Cartesian lattice. For this reason, the dimensionless distance boundary from the divider boundary y+ is utilized (10). Accordingly, the dimensionless separation from the tempestuous harmony area’s external limit up to y+ = 300 follows the exploratory information introduced by [19]. With this approach, the CFD explicitly obtains the energy, heat transition, and limit conditions for the RANS. This approach improves the meshing and decreases the computational time even in huge areas. Acquiring genuinely exact outcomes with standard PCs is then feasible.
2.3. Reference Cycle of the Turbogas
In this paper, the reference cycle of our turbogas generator is at “Garrett standard conditions” (T0 = 302.6 K, p0 = 0.962 bar, humidity = 0%). A pressure drop of 0.0135 bar on the intake and an overpressure on the exhaust are included in the calculations. The data shown in Table 1 are extrapolated from tests on the real APU [1].

Table 1.
Reference cycle data.
It is possible to run the turbogas generator efficiently from 62,000 up to 84,000 rpm with variable power output. Maximum efficiency is always met with maximum allowable temperature T3 = 1050 DEG C. In this condition, the torque to rpm curve is compatible with a brushless generator being linear for a power output of 50–100%.
Figure 3 shows the general arrangement layout of the turbine. The OA aspires through the filter (6) to the airbox (5) that contains the generator. The air is then compressed by the centrifugal compressor (4) that is connected to the combustor (1) through an insulated pipe (2). The hot and pressurized air from the combustor (1) moves the radial turbine (3). A truly short diffuser (8) slows down the exhaust velocity.
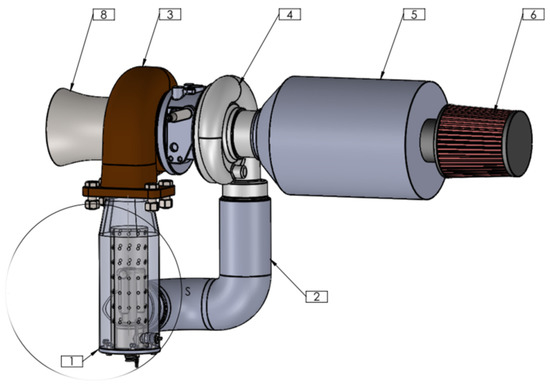
Figure 3.
Layout of microgas turbine. 1. Combustor. 2. Fresh air pipe to combustor. 3. Radial turbine. 4. Centrifugal Compressor. 5. Airbox (that contains the generator). 6. Air filter. 8. Diffuser.
2.4. Improvement of Combustion Chamber Design
The combustion chamber is composed of a vaporizing pipe (1.2), which has a slot in the bottom part (Figure 4). The fuel is sprayed through a low-pressure nozzle (1.5). The air coming from the compressor hits the perforated pipe (1.4). Part of this air passes through the holes (secondary air) and reaches the slot (primary air) at the bottom of the vaporization pipe (1.2). This pipe is extremely hot and helps to vaporize the fuel spray and to heat this primary air. The primary air meets the secondary air at the end of the “horns” of the vaporization pipe. In this area, the main combustion takes place. Then the primary and secondary air exits the combustor and is conveyed to the turbine intake. The glow plug (1.1) is used for starting the combustion process. A heated injector with a small blower (1.3) is used to start the turbine by heating the vaporization pipe (1.2). This paper is aimed at optimizing the combustor to increase the vortex and the combustion efficiency according to the highest EGT (Exhaust Gas Temperature) T3 and reference pressure p3. For optimum combustion, a high swirl is needed in the combustion area inside the holed pipe. On the contrary, at the turbine intake, it is necessary to have a homogeneous velocity pattern, with velocity vectors parallel to the turbine intake axis. Geometrical parameters such as diameter, radius and length were changed. In addition, the position of the intake pipe in the combustion chamber was varied. A combustion simulation is beyond our computational capability. Therefore, the airflow simulation at the combustion conditions was implemented.
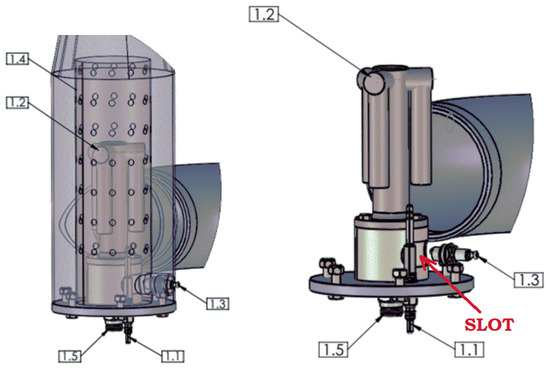
Figure 4.
Layout of the combustor. Transparent view on the right and inner view on the left. 1.1. Restart glow plug. 1.2. Vaporization piping system. 1.3. Heated injector for starting. 1.4. Mixing holed pipe. 1.5. Fuel spray nozzle.
CFD Analysis with Distinctive Design Solutions
In this scenario, the general settings for atmospheric conditions were used. However, the input and the output parameters of the combustion were given to reach the required value at the intake of the turbine. The output parameters should be 310,000 Pa [19] and 1323 K. To obtain these results, the temperature of the holed pipe is increased up to 3000 K. In this way, the temperature at the intake of the turbine reaches the required value of 1323 K. The CFD analysis of these design solutions is implemented with SolidWorks. These identified values are applied to our design as boundary conditions. Figure 5a shows the pressure (350,000 Pa) and temperature value (436 K) at the combustion intake, whilst Figure 5b shows the output values of the combustion, which are 310,000 Pa and 1323 K, and Figure 5c shows the temperature of the holed pipe (perforated sheet) inside the combustion chamber.
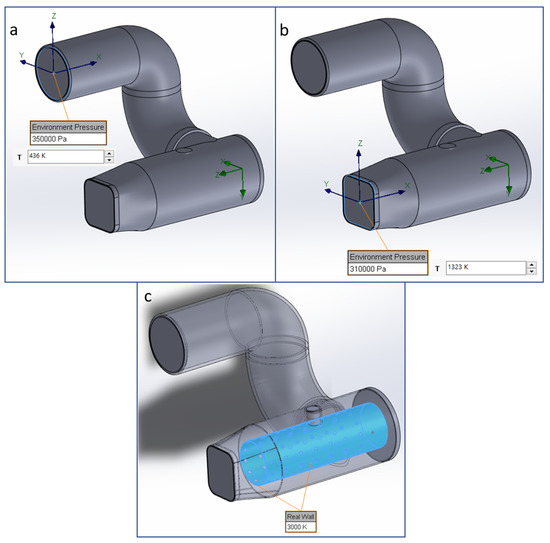
Figure 5.
(a) Input parameters of the combustor. (b) Output parameters of the combustor (turbine intake). (c) Perforated sheet temperature.
For the general settings of this simulation, “air” was chosen as a fluid. According to these values and settings, the simulation was implemented, and the flow trajectory results were analyzed for each design solution. This initial simulation is shown in Figure 6.
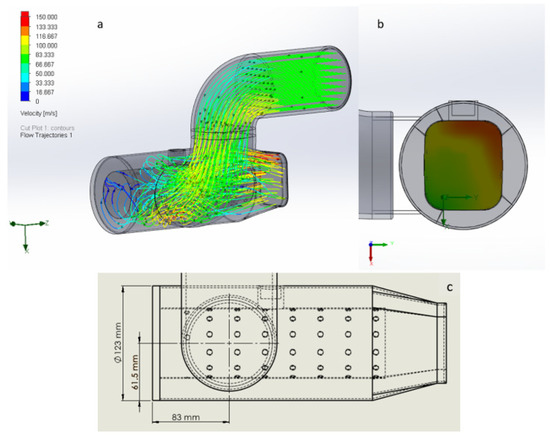
Figure 6.
(a) CFD simulation of the original Giandomenico design. (b) Velocity distribution of the outflow. (c) Technical detail of the middle-middle position for air pipe.
The original approved design shows an improvement in the CFD simulation. Inside the holed pipe, the flow has a robust swirl. At the turbine inlet, the velocity pattern is quite regular even if the upper red vectors indicate that the velocity is not perfectly uniform (Figure 6b), and an undesired moderate tumble is present at the turbine intake. It is probable that this velocity pattern is acceptable for the turbine. A high swirl inside the holed pipe has a direct influence on the combustion efficiency. Therefore, the geometry is modified to improve the swirl inside the holed pipe. In the first design solution of Figure 7, the offset from the duct of the compressor is displaced by increasing the offset from the holed pipe axis. The technical details of this position for the air pipe are given in Figure 7c. In this way, the swirl is increased for better combustion efficiency. As a result, our innovative design showed an unacceptable increase in the swirl at the turbine intake, and the distribution of the airflow was less homogeneous (Figure 7b) than the results of the previous design. This simulation was not satisfactory, with a significant deterioration of the velocity pattern at the output of the combustor.
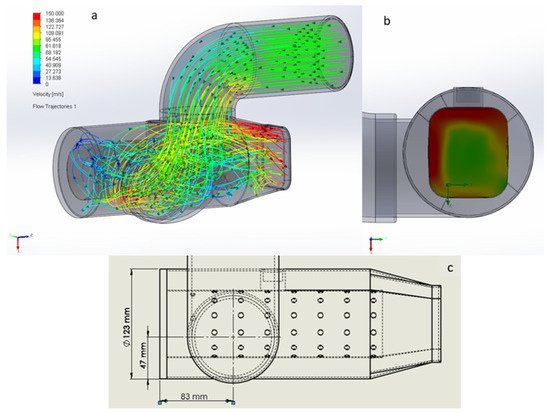
Figure 7.
(a) The duct from the compressor is displaced at the bottom of the combustor, increasing the offset. (b) Velocity distribution of outflow. (c) Technical detail of bottom-middle position for air pipe.
To increase the straightness of the outflow, the intake hole of the combustion chamber is displaced at the bottom of the combustor, keeping the offset that proved to be beneficial for the swirl (Figure 8). The details of the repositioning of the air pipe are given in Figure 8c.
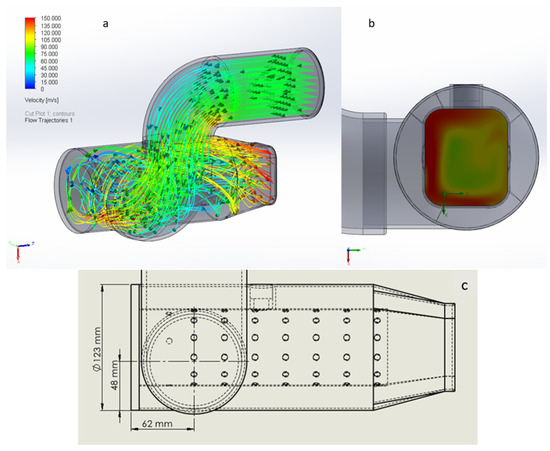
Figure 8.
(a) The duct from the compressor is displaced at the bottom of the combustor, increasing the offset. In addition, the duct was displaced at the end of the combustor on the side of the fuel nozzle. (b) Velocity distribution of outflow. (c) Technical detail of bottom-end position for air pipe.
The swirl is still improved as in the previous solution (Figure 7). In addition, the outflow motion at the turbine intake is slightly more evenly distributed than in the previous analysis, especially in the outer area (Figure 8b). Therefore, the solution in Figure 8 shows a considerable improvement. The next design solution (Figure 9) aims to have a straighter outflow at the turbine intake without losing the swirl motion inside the chamber. Thus, a fin is added at the turbine intake. The dimension details of the fin are given in Figure 10.
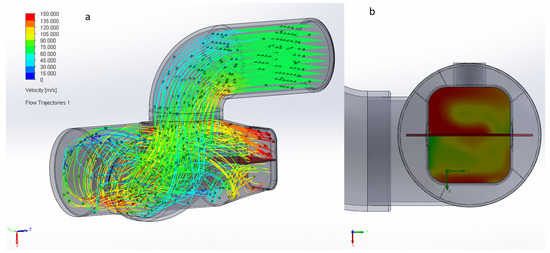
Figure 9.
(a) The fin added design. (b) Velocity distribution of outflow.
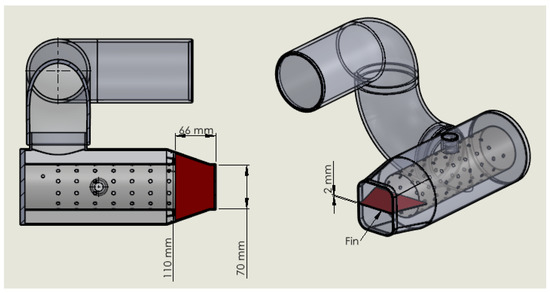
Figure 10.
Dimensions of the fin added to the turbine intake.
Results showed that the fin can assist in obtaining a more regular airflow distribution at the turbine intake. In particular, the fin divided the area not only for the XY plane but also for the XZ plane. Thus, a second fin was used to achieve a better result (Figure 11). Details of the double fin design can be seen in Figure 12.
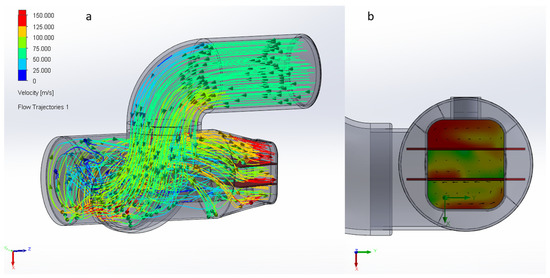
Figure 11.
(a) The double fin added design. (b) Velocity distribution of outflow for double fin design.
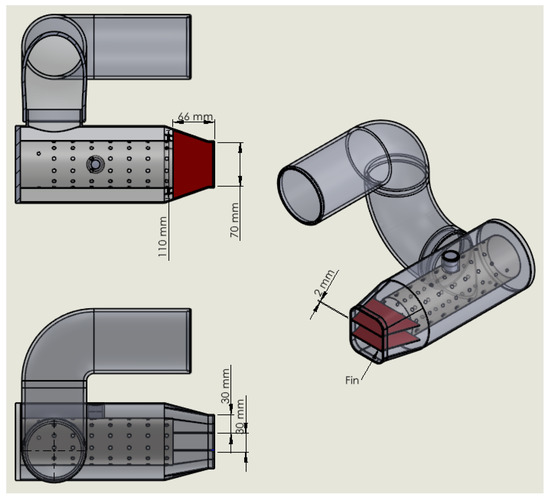
Figure 12.
Details of the second fin added to the design.
3. Results
The main purpose of this study of increasing the swirl motion inside the combustion chamber is achieved by changing the position of the intake hole on the design. The highest vortex was achieved with the design in Figure 8. In addition, although we made a positive contribution to the efficiency by increasing the vortex in the combustion chamber, the increase in the vortex at the combustion chamber outlet required a reduction.
In Figure 13, the difference of the swirl of the air in the case of a (fin) plate being added is shown. As seen from the flow trajectory vectors of the air, the fin had a beneficial effect on the fluid to decrease the swirl motion at the turbine intake. Figure 13a shows the optimum design solution before using any plate (fin) at the end of the combustion chamber; in this case, the swirl motion of the air seems quite irregular, but 13b clearly shows how the vortex is reduced in the airflow due to the use of the (fin) plate, and 13c shows the better solution for the whole design, which provided a straighter flow than the other solutions. Furthermore, Figure 13d–f shows the turbulent viscosity of the airflow during the simulations. These two types of flow results show that the fin addition at the turbine intake has the benefit of making the outflow straighter.
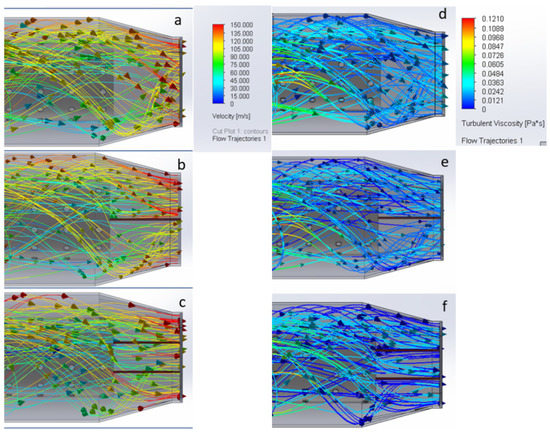
Figure 13.
(a) The velocity flow trajectory results of the air for the no-fin design at the exit of the combustion chamber, (b) the velocity flow trajectory of the air for the one-fin design, (c) the velocity flow trajectory for the two-fin design, (d) the turbulent viscosity flow trajectory results for the no-fin design, (e) the turbulent viscosity flow trajectory of the air for the one-fin design, (f) the turbulent viscosity flow trajectory results for the two-fin design.
In addition to the flow trajectory results, the numerical results are added in Table 2, Table 3 and Table 4. Additionally, in Figure 14, Figure 15 and Figure 16, graphs show the mass and volume flow rate of each design.

Table 2.
Numerical results of mass and volume flow rate for the compressor outflow (Figure 8).

Table 3.
Numerical results of mass and volume flow rate for the compressor outflow (Figure 9).

Table 4.
Numerical results of mass and volume flow rate for the compressor outflow (Figure 11).
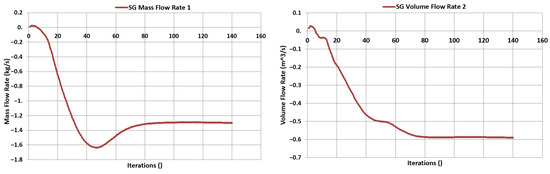
Figure 14.
Mass and Volume Flow Rate of turbine intake for Figure 8.
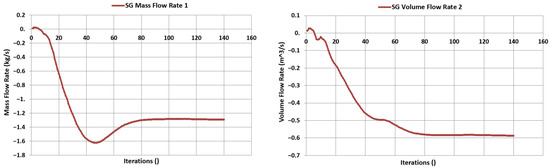
Figure 15.
Mass and volume flow rate of turbine intake for Figure 9.
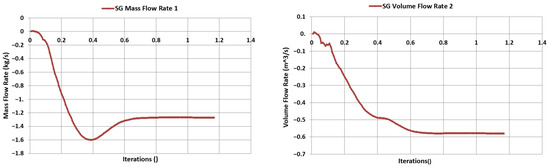
Figure 16.
Mass and volume flow rate of turbine intake for Figure 11.
According to these results, mass and volume flow rates are slightly decreased after the addition of a fin to the design. Negative flow rate values indicate that air is leaving the system. This might be the consequence of the area of the fin at the XY plane because these results are for the same simulation scenario. Furthermore, there is a minor decrement in overall velocity, while the velocity in the Z direction hardly increased. This vectorial velocity increment might be the consequence of the outflow area reduction. Still, it can be seen from comparing the tables that there is no important difference between the total pressure for Figure 8, Figure 9 and Figure 11. These results essentially proved that this small fin addition does not have a big impact on pressure, velocity, and the flow rate of the airflow while helping to get straight flow.
4. Discussion
Even if the overall velocity of this design hardly decreased, as seen comparatively in Table 2, Table 3 and Table 4, the velocity in the Z direction slightly increased. This slight change might be due to the inverse relation between volume flow rate and flow velocity because adding some fin parts decreased the total area for the airflow.
is volumetric flow rate, v is flow velocity and A is cross-sectional vector area for the flow. Results show that surface velocity at the turbine intake was reduced, which means the mass and volume flow rate must reduce proportionally. However, these three designs do not have the same outflow area. Thus, again, the relationship between flow velocity and flow area must be taken into consideration. In addition, the straightness of airflow has to be the main target in these kinds of systems to keep the efficiency high while changing the geometry.
5. Conclusions
In this paper, an improvement of the combustion system design was achieved in the initial design. The presence of a high swirl in the combustion area is especially important to obtain a high combustion efficiency. For this reason, several positions of the combustor intake duct were assessed with CFD simulation. The improved design solution is a compromise because the turbine needs very stable air with a homogeneous air velocity parallel to the intake axis. Since software for combustion simulation was not available, the combustor was simplified by eliminating the heating pipe and by assigning an extremely high temperature to the holed tube. In this way, the required nominal temperature of 1050 °C at the turbine intake was obtained.
- The best configuration proved to be positioning the combustor intake at the bottom of the combustor to the most offset position from the combustor axis. A variation of the length of the combustor or the diameter has an extremely limited effect on the swirl motion and the turbine intake velocity pattern.
- Putting the combustion intake pipe at the bottom and the rearmost position helped increase the swirl motion of air inside the combustion chamber. However, additional solutions are required to reduce the outflow vortex.
- The insertion of fins at the turbine intake is proved to be beneficial in the case of making the airflow more stable and straighter. Additionally, due to the double fin solution, the design has straighter airflow.
- Overall values prove that there is not much pressure difference at turbine intake between the designs even if the outflow area slightly decreased because of fin parts.
- Further design solutions for this concept can be developed with the addition of enthalpy values of the combustion chamber by using equations and some additional boundary conditions in the simulation to analyze the thermal effects in this design.
Author Contributions
Conceptualization, L.P.; methodology, M.S.; software, M.S.; validation, L.P., M.S.; formal analysis, L.P.; investigation, M.S.; resources, L.P.; data curation, M.S.; writing—original draft preparation, L.P.; writing—review and editing, L.P. and C.L.-C.; visualization, M.S.; supervision, L.P.; project administration, L.P.; funding acquisition, L.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Piancastelli, L.; Ferretti, P.; Santi, G.M.; Scaltrini, A.; Cassani, S.; Calzini, F. Critical Design Issues of Heavy Fuel APUs Derived from Automotive Turbochargers. Part 1: Nominal Ambient Conditions. Technol. Ital. J. Eng. Sci. 2021, 65, 53–57. [Google Scholar] [CrossRef]
- Piancastelli, L.; Scaltrini, A.; Santi, G.M.; Risorgimento, V. Critical Design Issues of Heavy Fuel Turbogas Generators Derived from Automotive Turbochargers. Part II: The Improved Mach Method for off Design Performance Tuning. Technol. Ital. J. Eng. Sci. 2020, 64, 325–330. [Google Scholar] [CrossRef]
- Tiainen, J. Losses in Low-Reynolds-Number Centrifugal Compressors; LUT Yliopistopaino: Lappeenranta, Finland, 2018; ISBN 9789523352490. [Google Scholar]
- Piancastelli, L.; Gatti, A.; Frizziero, L.; Ragazzi, L.; Cremonini, M. CFD Analysis of the Zimmerman’s V173 Stol Aircraft. ARPN J. Eng. Appl. Sci. 2015, 10, 8063–8070. [Google Scholar]
- Frizziero, L.; Rocchi, I.; Donnici, G.; Pezzuti, E. Aircraft diesel engine turbocompound optimized. JP J. Heat Mass Transf. 2015, 11, 133–150. [Google Scholar] [CrossRef]
- Piancastelli, L.; Frizziero, L.; Bombardi, T. Bézier Based Shape Parameterization in High Speed Mandrel Design. Int. J. Heat Technol. 2014, 32, 57–63. [Google Scholar]
- Casey, M.; Robinson, C. A method to estimate the performance map of a centrifugal compressor stage. In Turbo Expo: Power for Land, Sea, and Air; ASME: New York, NY, USA, 2011; Volume 54679, pp. 1981–1993. [Google Scholar] [CrossRef]
- Xiao, G.; Yang, T.; Liu, H.; Ni, D.; Ferrari, M.L.; Li, M.; Luo, Z.; Cen, K.; Ni, M. Recuperators for Micro Gas Turbines: A Review. Appl. Energy 2017, 197, 83–99. [Google Scholar] [CrossRef]
- Ansaldo Energia AE-T100E Datasheet. 2017. Available online: https://www.ansaldoenergia.com/microturbines/Pages/Products.aspx (accessed on 4 July 2022).
- Ferretti, P.; Santi, G.M.; Leon-Cardenas, C.; Fusari, E.; Donnici, G.; Frizziero, L. Representative Volume Element (RVE) Analysis for Mechanical Characterization of Fused Deposition Modeled Components. Polymers 2021, 13, 3555. [Google Scholar] [CrossRef] [PubMed]
- Ferretti, P.; Santi, G.M.; Leon-Cardenas, C.; Freddi, M.; Donnici, G.; Frizziero, L.; Liverani, A. Molds with Advanced Materials for Carbon Fiber Manufacturing with 3D Printing Technology. Polymers 2021, 13, 3700. [Google Scholar] [CrossRef] [PubMed]
- Gavrilyuk, V.N.; Denisov, O.P.; Nakonechnyj, V.P.; Odintsov, E.V.; Sergienko, A.A.; Sobach, R. Numerical Simulation of Working Processes in Rocket Engine Combustion Chamber. In Proceedings of the Graz International Astronautical Federation Congress, Graz, Austria, 16–22 October 1993. [Google Scholar]
- Kalitzin, G.; Iaccarino, G. Turbulence Modeling in an Immersed-Boundary RANS Method. Cent. Turbul. Res. Annu. Res. Briefs 2002, 29, 415–426. [Google Scholar]
- Franke, R. Scattered Data Interpolation: Tests of Some Method. Math. Comput. 1982, 38, 181–200. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2002; ISBN 3540420746. [Google Scholar]
- Van Driest, E.R. On Turbulent Flow near a Wall. J. Aeronaut. Sci. 1956, 23, 1007–1011. [Google Scholar] [CrossRef]
- Lam, C.K.G.; Bremhorst, K. A Modified Form of the K-ε Model for Predicting Wall Turbulence. J. Fluids Eng. 1981, 103, 456–460. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries: Mumbai, India, 2006; Volume 2006. [Google Scholar]
- Silva, R.; Lacava, P. Preliminary Design of a Combustion Chamber for Microturbine Based in an Automotive Turbocharger. In Proceedings of the 22nd International Congress of Mechanical Engineering (COBEM 2013), Ribeirão Preto, Brazil, 3–7 November 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).