Gravity-Compensation Design Approaches for Flexure-Pivot Time Bases
Abstract
:1. Introduction
- Minimizing the difference in pivot stiffness for gravity orientations lying within the rotation plane (i.e., oscillator in vertical position with respect to gravity). Design approaches to mitigate these in-plane effects are described in Section 2.1.
- Minimizing the difference between the mean pivot stiffness for gravity orientations within the rotation plane (step 1) and the stiffness when gravity acts along the rotation axis (i.e., oscillator in horizontal position with respect to gravity). Design approaches to mitigate these out-of-plane effects are described in Section 2.2.
- The novelty of the out-of-plane effects mitigation technique;
- The combination of both aforementioned steps to reach new levels of frequency stability;
- The evaluation of these approaches in terms of chronometric accuracy on designs and prototypes satisfying realistic mechanical watch specifications.
2. Gravity-Compensation Design Approaches
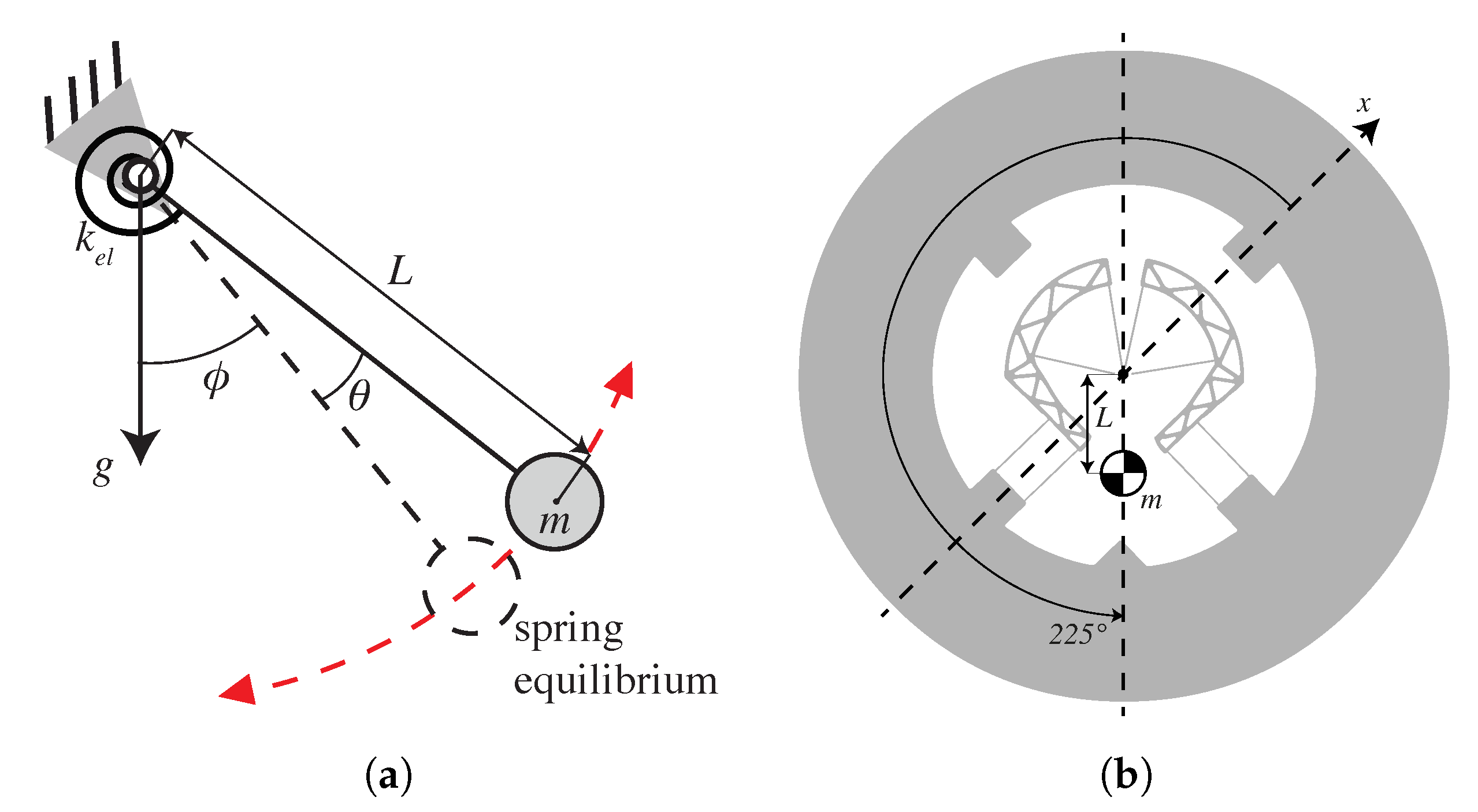
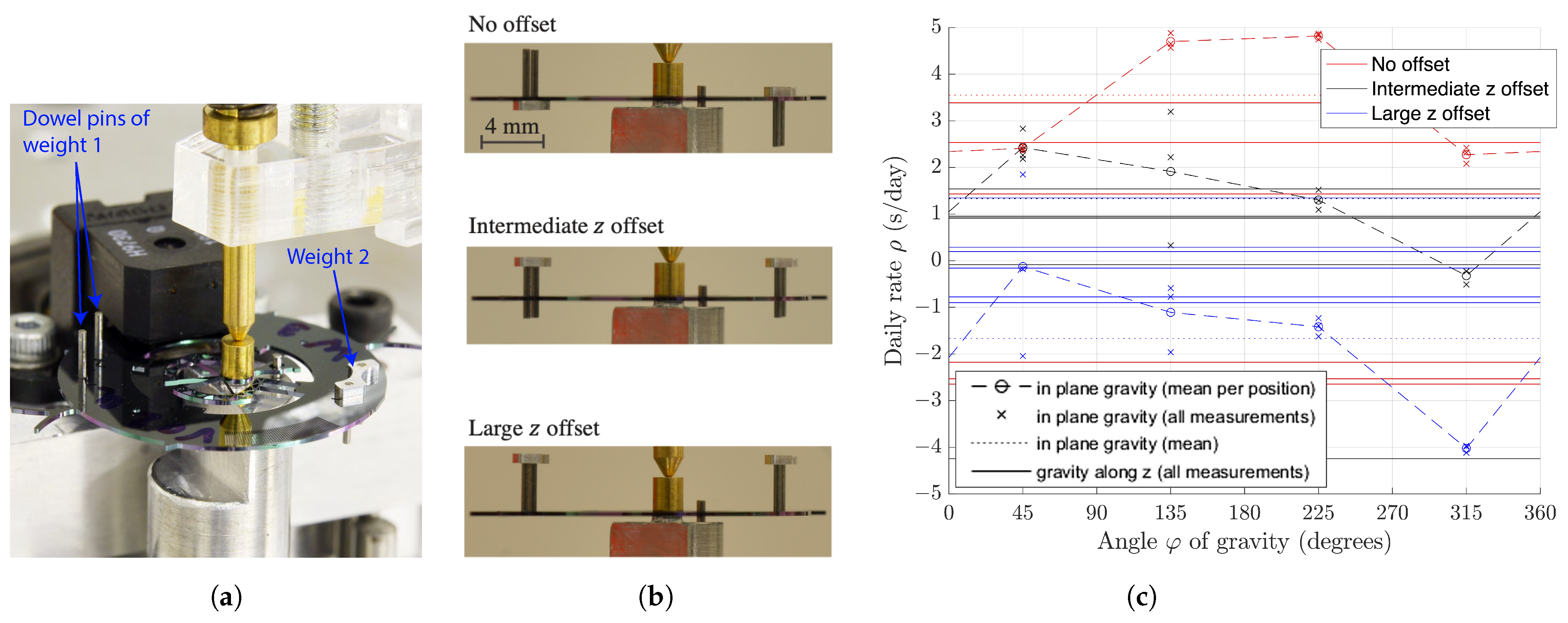
2.1. In-Plane Gravity Effects Mitigation
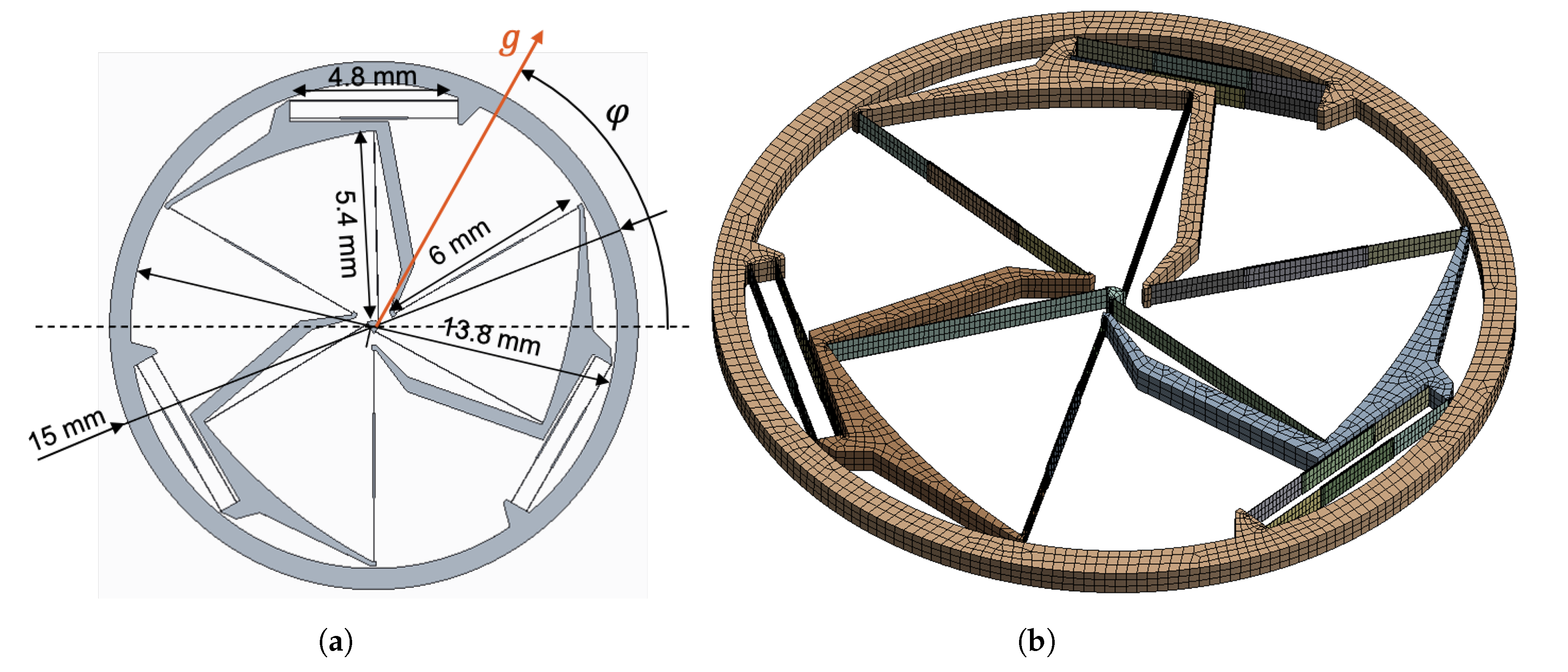
2.1.1. Reducing the Parasitic Center Shift
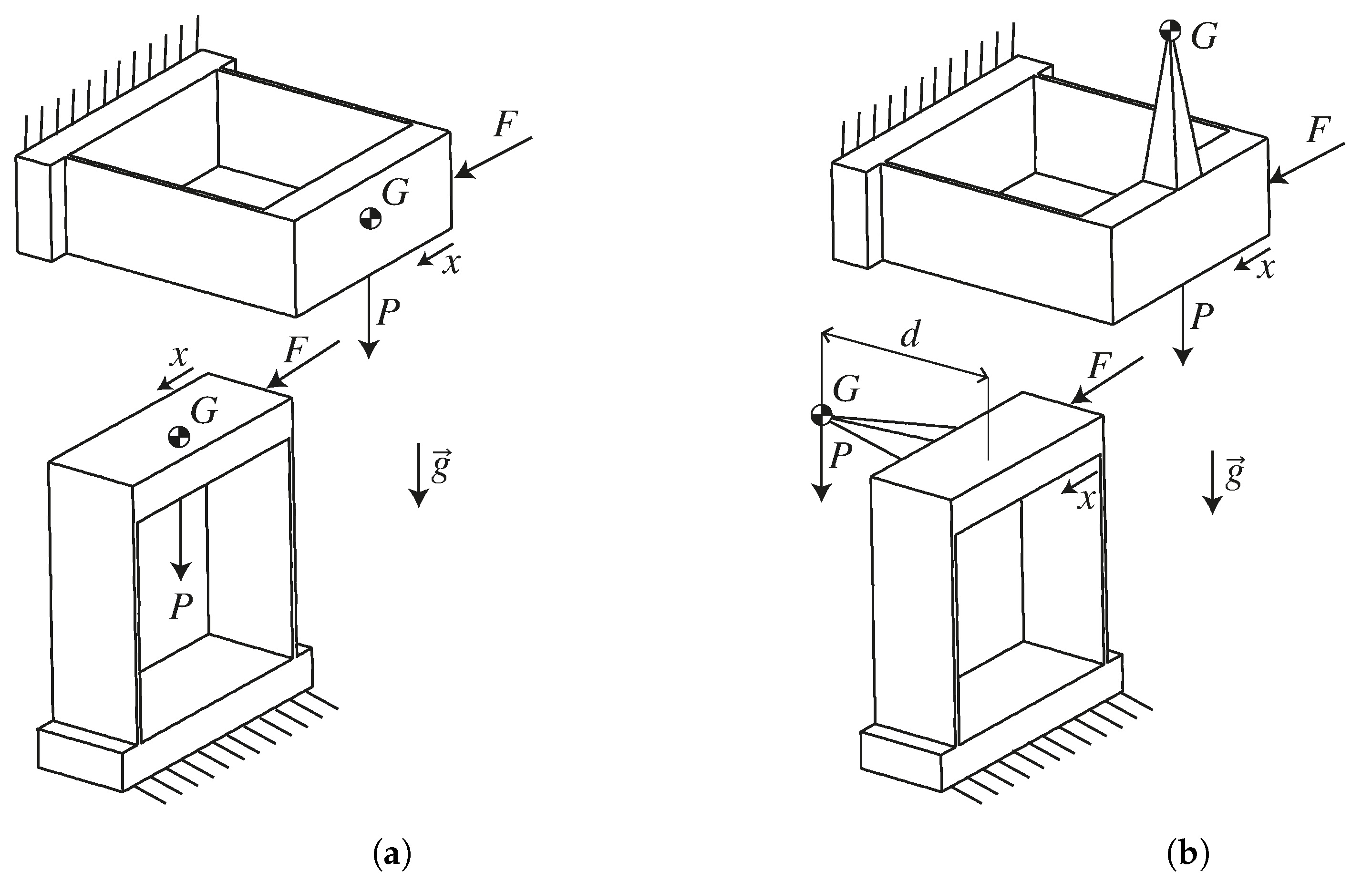
2.1.2. Offsetting the COM along the In-Plane Axis of Symmetry
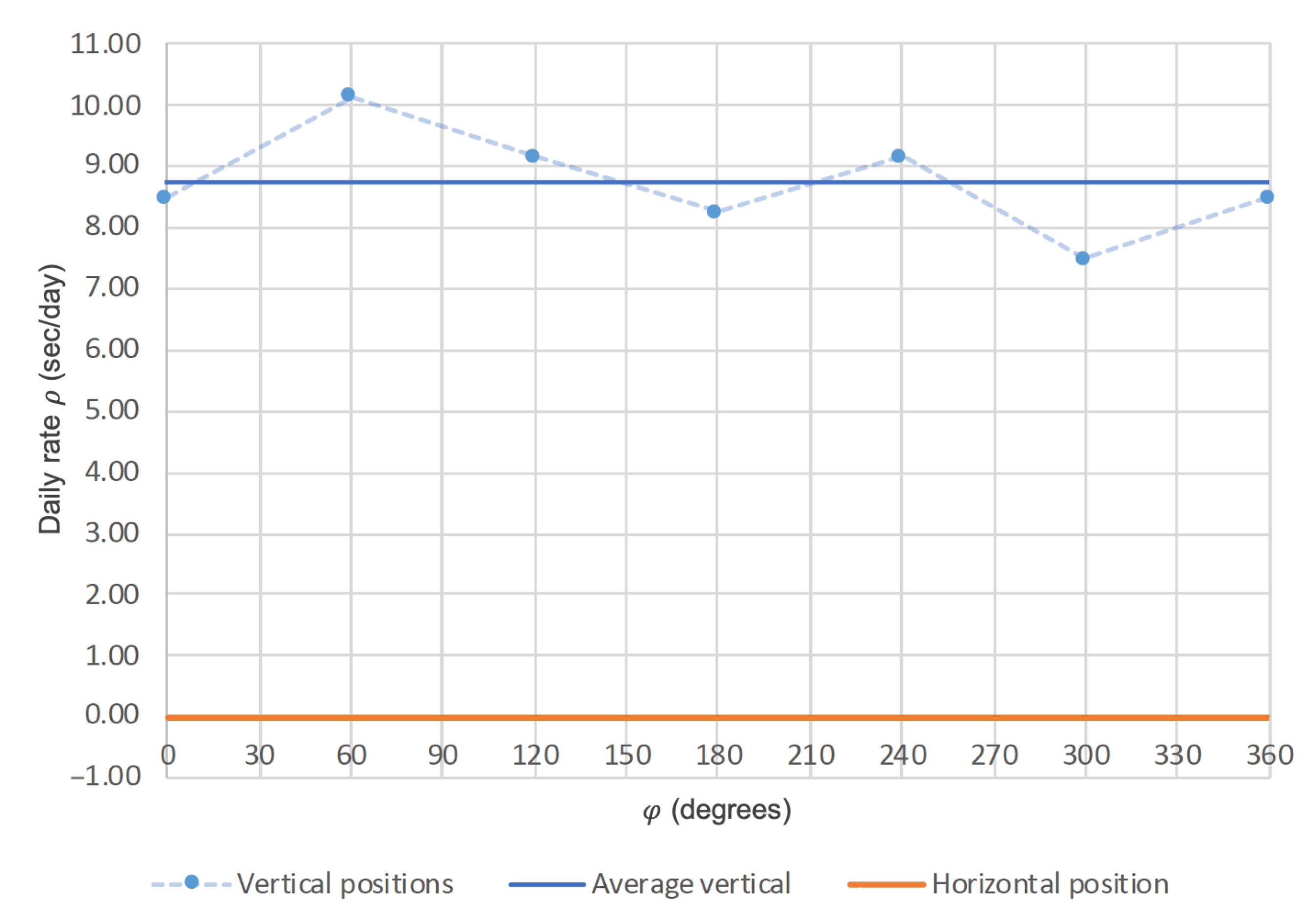
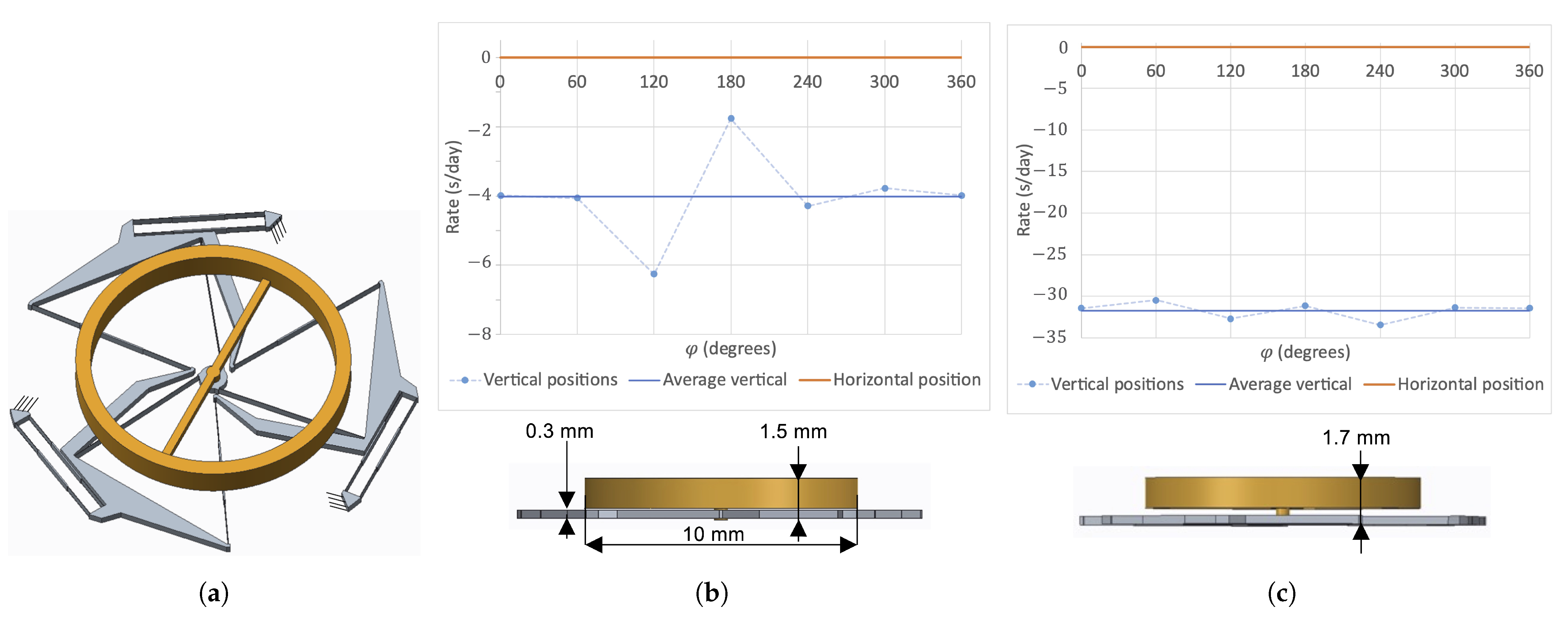
2.2. Out-of-Plane Gravity Effects Mitigation
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barrot, F.; Dubochet, O.; Henein, S.; Genequand, P.; Giriens, L.; Kjelberg, I.; Renevey, P.; Schwab, P.; Ganny, F. Un Nouveau Régulateur Mécanique pour une Réserve de Marche Exceptionnelle. In Proceedings of the Journée d’Etude de la Société Suisse de Chronométrie 2014, Lausanne, Switzerland, 17 September 2014; pp. 43–48. [Google Scholar]
- Barrot, F.; Musy, G.; Cosandier, F.; Kjelberg, I.; Renevey, P.; Giriens, L.; Schwab, P.; Genequand, P.; Petremand, Y.; Dubochet, O.; et al. GENEQUAND, A Novel Watch Regulator Based on Compliant Mechanisms; CSEM Scientific and Technical Report 2015; CSEM: Neuchâtel, Switzerland, 2015. [Google Scholar]
- Henein, S.; Vardi, I.; Rubbert, L.; Bitterli, R.; Ferrier, N.; Fifanski, S.; Lengacher, D. IsoSpring: Vers la Montre sans échappement. In Proceedings of the Journée d’Etude de la Société Suisse de Chronométrie 2014, Lausanne, Switzerland, 17 September 2014; pp. 49–58. [Google Scholar] [CrossRef]
- Thalmann, E. Flexure Pivot Oscillators for Mechanical Watches. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 2020. [Google Scholar] [CrossRef]
- Kahrobaiyan, M.H.; Thalmann, E.; Rubbert, L.; Vardi, I.; Henein, S. Gravity-Insensitive Flexure Pivot Oscillators. J. Mech. Des. 2018, 140, 075002-9. [Google Scholar] [CrossRef] [Green Version]
- Thalmann, E.; Kahrobaiyan, M.H.; Vardi, I.; Henein, S. Flexure Pivot Oscillator with Intrinsically Tuned Isochronism. J. Mech. Des. 2020, 142, 075001. [Google Scholar] [CrossRef]
- Thalmann, E.; Henein, S. Design of a Flexure Rotational Time Base with Varying Inertia. J. Mech. Des. 2021, 143, 115001. [Google Scholar] [CrossRef]
- Thalmann, E.; Henein, S. Optical measurement method for mechanical time base characterization. In Proceedings of the 21st International Conference of the European Society for Precision Engineering and Nanotechnology, EUSPEN 2021, Virtual, 7–10 June 2021; pp. 469–472. [Google Scholar]
- Schneegans, H.; Thalmann, E.; Henein, S. Shaking force balancing of a 2-DOF isotropic horological oscillator. Precis. Eng. 2021, 72, 502–520. [Google Scholar] [CrossRef]
- Thalmann, E.; Henein, S. Triple Crossed Flexure Pivot Based on a Zero Parasitic Center Shift Kinematic Design. J. Mech. Robot. 2022, 14, 045001. [Google Scholar] [CrossRef]
- Roulet, C. Zenith’s Quantum Leap. Available online: http://journal.hautehorlogerie.org/en/zeniths-quantum-leap/ (accessed on 19 February 2019).
- Markl, X. Introducing Ulysse Nardin Freak NeXt. Available online: http://monochrome-watches.com/ulysse-nardin-freak-next-a-new-concept-with-revolutionary-3d-flying-oscillator-live-pics/ (accessed on 30 October 2019).
- Forster, J. In-Depth: The Silicon-Powered Speed of the Frederique Constant Slimline Monolithic Manufacture-40 Hz. Available online: www.hodinkee.com/articles/the-silicon-powered-speed-of-the-frederique-constant-slimline-monolithic-manufacture-40hz (accessed on 15 May 2022).
- Eastman, F.S. Flexure Pivots to Replace Knife Edges and Ball Bearings, an Adaptation of Beam-Column Analysis; Engineering Experiment Station Series; University of Washington: Seattle, WA, USA, 1935. [Google Scholar]
- Howell, L.L. Compliant Mechanisms; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Cosandier, F.; Henein, S.; Richard, M.; Rubbert, L. The Art of Flexure Mechanism Design; EPFL Press: Lausanne, Switzerland, 2017. [Google Scholar]
- Scheibner, D.; Wibbeler, J.; Mehner, J. Frequency selective sensor arrays for vibration measurement. In Proceedings of the 2002 IEEE SENSORS, Orlando, FL, USA, 12–14 June 2002; Volume 1, pp. 675–679. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q. Design and Optimization of an XYZ Parallel Micromanipulator with Flexure Hinges. J. Intell. Robot. Syst. 2008, 55, 377. [Google Scholar] [CrossRef]
- Lu, S.; Tian, C.; Yan, P. Adaptive Extended State Observer-Based Synergetic Control for a Long-Stroke Compliant Microstage With Stress Stiffening. IEEE/ASME Trans. Mechatron. 2020, 25, 259–270. [Google Scholar] [CrossRef]
- Hetzel, M. Le diapason et son influence sur l’horlogerie. Bull. Annu. Soc. Suisse Chronométrie 1962, IV-1962, 666–679. [Google Scholar]
- Thalmann, E.; Henein, S. Design of a Triple Crossed Flexure Pivot with Minimized Parasitic Shift. In Proceedings of the ASME 2021 IDETC-CIE Conference, Virtual, 17–19 August 2021; p. V08AT08A003. [Google Scholar] [CrossRef]
- Wittrick, W. The properties of crossed flexure pivots, and the influence of the point at which the strips cross. Aeronaut. Q. 1951, 2, 272–292. [Google Scholar] [CrossRef]
- Zhao, H.; Bi, S. Accuracy characteristics of the generalized cross-spring pivot. Mech. Mach. Theory 2010, 45, 1434–1448. [Google Scholar] [CrossRef]
- Marković, K.; Zelenika, S. Characterization of cross-spring pivots for micropositioning applications. In Proceedings of the SPIE 9517, Smart Sensors, Actuators, and MEMS VII; and Cyber Physical Systems, Barcelona, Spain, 4–6 May 2015; p. 951727. [Google Scholar] [CrossRef]
- Marković, K.; Zelenika, S. Optimized cross-spring pivot configurations with minimized parasitic shifts and stiffness variations investigated via nonlinear FEA. Mech. Based Des. Struct. Mach. 2017, 45, 380–394. [Google Scholar] [CrossRef]
- Wittrick, W. The Theory of Symmetrical Crossed Flexure Pivots. Aust. J. Sci. Res. Phys. Sci. 1948, 1, 121. [Google Scholar] [CrossRef]
- Haringx, J.A. The cross-spring pivot as a constructional element. Flow Turbul. Combust. 1949, 1, 313. [Google Scholar] [CrossRef]
- Van Eijk, J. On the Design of Plate-Spring Mechanisms. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 1985. [Google Scholar]
- von Gunten, S.; Gygax, P.; Humair, L. Oscillateur Mécanique. EP2273323B1, 16 December 2015. [Google Scholar]
- Weeke, S.L.; Tolou, N.; Semon, G.; Herder, J.L. A Fully Compliant Force Balanced Oscillator. In Proceedings of the ASME 2016 IDETC-CIE Conference, Charlotte, NC, USA, 21–24 August 2016; p. V05AT07A008. [Google Scholar] [CrossRef]
- Robuschi, N.; Braghin, F.; Corigliano, A.; Ghisi, A.; Tasora, A. On the dynamics of a high frequency oscillator for mechanical watches. Mech. Mach. Theory 2017, 117, 276–293. [Google Scholar] [CrossRef]
- Di Domenico, G.; Léchot, D.; Helfer, J.L.; Winkler, P. Timepiece Resonator Mechanism. EP3206089A1, 10 August 2017. [Google Scholar]
- Semon, G.; Van Zoest, W.P.; Tolou, N. Monolithic Timepiece Regulator, Timepiece Movement and Timepiece Having Such a Timepiece Regulator. WO2016079068A1, 26 May 2016. [Google Scholar]
- Ypma, W.J.B.; Weeke, S.L. Mechanical Watch Oscillator. WO2019156552A1, 15 August 2019. [Google Scholar]
- Chabloz, D. Timepiece Component with a Flexible Pivot. EP3410229A1, 5 December 2018. [Google Scholar]




| Prototype | Imbalance B | Analytical Daily Rate Compensation 1 | FEM Daily Rate | FEM Daily Rate Compensation 1 | Experimental Daily Rate | Experimental Daily Rate Compensation 1 |
|---|---|---|---|---|---|---|
| B2a | 1.83 nNm | - | s/day | - | s/day | - |
| B2b | 1.83 nNm | - | s/day | - | s/day | - |
| B13a | 12.6 nNm | s/day | s/day | s/day | s/day | s/day |
| B13b | 12.6 nNm | s/day | s/day | s/day | s/day | s/day |
| B25a | 24.7 nNm | s/day | s/day | s/day | s/day | s/day |
| B25b | 24.7 nNm | s/day | s/day | s/day | s/day | s/day |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thalmann, E.; Gubler, Q.; Henein, S. Gravity-Compensation Design Approaches for Flexure-Pivot Time Bases. Machines 2022, 10, 580. https://doi.org/10.3390/machines10070580
Thalmann E, Gubler Q, Henein S. Gravity-Compensation Design Approaches for Flexure-Pivot Time Bases. Machines. 2022; 10(7):580. https://doi.org/10.3390/machines10070580
Chicago/Turabian StyleThalmann, Etienne, Quentin Gubler, and Simon Henein. 2022. "Gravity-Compensation Design Approaches for Flexure-Pivot Time Bases" Machines 10, no. 7: 580. https://doi.org/10.3390/machines10070580
APA StyleThalmann, E., Gubler, Q., & Henein, S. (2022). Gravity-Compensation Design Approaches for Flexure-Pivot Time Bases. Machines, 10(7), 580. https://doi.org/10.3390/machines10070580






