1. Introduction
Grinding is a widely used abrasive process for the finishing of various types of mechanical parts with high accuracy and surface quality. Currently, the increased use of hard-to-cut materials, such as superalloys or ceramic materials, in various high-end applications requires that the processing of these materials should meet various necessary requirements, avoiding damage and other adverse effects on workpiece integrity. In particular, the high brittleness of ceramic materials renders them susceptible to fracture. When their processing is conducted under unfavorable conditions, reduced part integrity and life is expected, as well as rapid wear on cutting tools, which is undesirable from a financial point of view.
Superhard materials pose a difficult task for manufacturers due to their superior properties, compared to more easily processed materials such as aluminum, copper alloys, and steel. Common superhard materials are diamond and diamond-related mono and polycrystalline materials, cubic boron nitride, and composite materials, such as (TiN/SiN)
x nanocomposites [
1,
2]. More specifically, the main characteristics of superhard materials include high hardness, often exceeding 40 or even 80 GPa [
1,
3], high bulk modulus, high melting point, wear resistance, and chemical inertness. These are the reasons why they are often selected as preferable materials for heavy duty applications, such as cutting and abrasive tools, drilling bits in petrochemical industry, etc. [
1,
4]. On the other hand, they may also exhibit some undesirable properties, such as inferior thermal stability or impact toughness, which limit their possible range of applications, which can be modified by appropriate synthesis procedure, e.g., sintering [
1,
4].
Synthetic diamonds (SD) belong to the category of superhard materials and are unique in their physical and mechanical properties, which are widely used in the creation of cutting tools for various industries. However, since diamond is the hardest material in nature, it becomes difficult to sharpen and finish such a tool, since the classical requirement of the cutting theory that the hardness of the tool material exceeds the machined material is not met. Cutting edge processing performance is largely determined by the quality of tool sharpening. Therefore, for example, with the appropriate quality of sharpening and finishing of tools made of SD, they can successfully replace natural diamond.
Various authors have conducted experimental research on the grinding of hard and superhard materials. In order to increase the efficiency of grinding these materials, some researchers have proposed the use of assistive technologies, such as ultrasonic vibrations or laser beams. Regarding laser-assisted grinding (LAG), Li et al. [
5] noted that, during LAG of RB-SiC ceramics, plastic removal becomes easier due to the reduction of hardness and mechanical strength of workpiece material, and also surface quality and subsurface damage can be reduced by effectively regulating process parameters, especially feed rate and laser power. Kumar et al. [
6] conducted LAG of silicon nitride workpieces and found that grinding forces and tool wear can be effectively decreased in comparison to traditional grinding, enabling larger material removal rates. Ma et al. [
7] conducted LAG on zirconia ceramic workpieces, revealing that ductile regime machining can be achieved by LAG. Regarding ultrasonic grinding, Wang et al. [
8] studied the surface generation during rotary ultrasonic grinding of Si
3N
4 ceramic material, and established the correlation between surface topography, ultrasonic energy, and grinding parameters. Baraheni and Amini [
9] showed that rotary ultrasonic-assisted face grinding can improve machined part quality by considerably reducing subsurface damage, especially at higher values of vibration amplitude and frequency. Chen et al. [
10] investigated the suitable parameter values during elliptical ultrasonic-assisted grinding of brittle materials and suggested that, apart from high grinding speed, the magnitude of axial and vertical vibration affect significantly the brittle–ductile mode transition. Guo and Zao [
11] performed grinding on micro-structures and observed that, apart from the vibration amplitude and frequency, which lead to lower surface roughness and sharper edges of the structures, the use of a high tilt angle leads to further reduction of surface roughness.
Apart from applying non-conventional techniques for improving the conditions of hard and superhard material grinding, the choice of the appropriate grinding wheel that possesses favorable characteristics is essential. Moreover, it is important to take into consideration the special conditions that occur during the grinding of superhard materials such as SD, in which the requirements of the cutting theory about the cutting tool hardness exceeding that of the processed material are not met. Thus, in this process, the hardness of the tool material and the processed material is almost equal and, in this case, the grinding process is not a cutting process in its classical sense, but is transformed into a process of a mutual micro-fracture of two equally hard materials, since the processed superhard material has the same hardness as the abrasive grains.
Various studies have been conducted regarding the characteristics of diamond grinding wheels. In order to achieve low wear rates of the grinding wheel, research should be conducted in order to understand the tribological phenomena during the grinding of superhard materials [
12,
13], the role of fabrication method of the wheel [
14], and its properties. The most important grinding wheel characteristics are the abrasive material and grain size, the bonding material, as well as the wheel grade and structure [
15]. Ding et al. [
16] created a brazed diamond wheel with defined grain distribution, and observed that this wheel had grains with greater protrusion heights and more uniform height distribution than electroplated wheels and that it could lead to lower grinding forces and force ratio. Moreover, it was noted that microstructured diamond wheels can produce surfaces with high precision and reduced cracks under certain conditions. Wu et al. [
17] fabricated microstructured wheels with the use of laser beams, and observed ductile regime cutting and minimization of dimensional errors on hard ceramic workpieces. In other studies [
18,
19], different types of patterns or produced features such as microgrooves and holes were created on the wheel surface using laser technology, leading to the reduction of grinding forces, surface roughness, better self-sharpening ability, and the promotion of shearing instead of an ironing action of the wheel.
The diamond grinding wheel bond is another element whose physical and mechanical properties can be varied in a fairly wide range, and can play a decisive role in the efficiency of the grinding process, as it determines the fixing strength of the grains and their service life [
20,
21]. The efficiency of the grinding process with SD and cubic boron nitride wheels using porous metal bonds was investigated in various works in the relevant literature [
22,
23]. In these studies, the authors studied the design and characteristics of metal-bonded diamond grinding wheels made by selective laser melting, observing the grinding temperature and wear of superabrasive boron wheels for highly efficient deep grinding. Moreover, it was found [
24] that the ultimate load causing the fracture of diamond grains depends not only on the compressive strength of the diamond grains, but also on the compressive strength of the bond, as well as on the coefficient of the embedding of diamond grains within it. The classification of the types of wear of diamond wheels using various bonds and possible models of the fracture of diamond grinding wheels is given in [
25,
26]. The use of additions on bonding material can assist to obtain favorable mechanical, thermal, or chemical properties, such as microhardness, bending strength, and chemical durability, for both CBN and diamond grinding wheels [
27,
28].
In order to design the appropriate grinding wheel for processing superhard materials, it is necessary to develop computational models for the grinding process, apart from experimental work. Usually the grinding process can be modeled using FEM models [
29], but models based on soft computing methods exist as well [
30]. M. Mahdi and L. Zhang [
31] used the finite element method (FEM) to simulate stresses caused by mechanical loading, thermal cycling, and phase transitions. H. Sakamoto [
32] applied FEM to study the wear and deformation of diamond cutting wheels with different structures by determining the conditions that ensure the minimum temperature during grinding and its uniform distribution. In the works of V. Yadava [
33,
34] using the FEM, the residual stresses arising during high-speed grinding are determined. Wan et al. [
35] developed a thermo-mechanical model using multiple abrasive grains for grinding or zirconia ceramic workpieces in order to determine subsurface damage. Wang et al. [
36] developed a model for the simulation of surface topography during grinding with diamond wheels, taking into account the kinematics of grinding and various geometrical characteristics of the grain geometry in order to optimize the grain arrangement. Denkena et al. [
37] simulated the sintering process of metal-bonded grinding wheels by means of FEM and DEM models. Li et al. [
38] studied the formation of surface topography produced by an electroplated diamond wheel for both fresh and worn wheels.
From a review of the literature, it can be concluded that although several authors have studied different aspects of diamond grinding wheel characteristics, there is still limited research on the effect of bond material mechanical properties during the grinding of superhard materials in order to determine the most suitable grinding wheel bond type for processing these materials even at higher speeds. Thus, in the present work, the effect of the bond’s elastic modulus on the stress state of the workpiece, critical embedding of grain into the bond, micro-fracture possibility, process efficiency, and specific consumption is investigated by means of theoretical models and FE simulation. The results show that the elastic modulus of the bond plays a considerable role in the efficiency of the grinding process of superhard materials, as higher values of bond elastic modulus can improve diamond grain retention, facilitate material removal through mutual micro-fracture of grain and workpiece material, reduce specific consumption, and allow the use of higher speeds.
2. Materials and Methods
The aim of the current work initially is to investigate the effect of the mechanical properties of the bond material of the diamond abrasive wheel on the stress distribution of the workpiece material during the contact with the diamond abrasive grain. The investigation is carried out by using both FE simulation and theoretical models. The FE models use six different types of metal bonds, all based on Enterprise Standard (ES), the exact material composition of which is shown in
Table 1.
As can be seen in
Table 1, where the physical and mechanical properties of bond materials are presented, different types of bonds exhibit different elasticity parameters and yield stress, which can affect grinding process considerably.
For the determination of stress distribution during the grinding of superhard materials using diamond grinding wheels, an FE model is employed, presented in
Figure 1.
In this figure, the system of the abrasive wheel and workpiece is depicted. The abrasive wheel model includes bond material and single diamond abrasive grains with metal inclusion acting on the workpiece surface. The grain is modeled in the form of an octahedron with rounded tips, and, since the grains in fact are randomly located in the wheel, three options for the contact of the grain with the material being processed and with the bond are considered—the top of the grain, the edge, and the face. The grade and graininess of the grinding wheel is AC6 250/200, which means that the average grain size is 225 μm, equal to the dimension of the grain in the model. The size of the workpiece is 630 × 300 × 150 μm, whereas the size of the part representing the bond in which the abrasive grains are embedded has the dimensions of 630 × 220 × 150 μm.
Finite element analysis was performed using 8-node SOLID elements. In the finite element software, the type of finite elements from the package library for each component of the system was selected, and a grid of finite elements was built and selectively refined. HexDominant and Tetrahedron elements were used to create the grid for the metal phases. Refinement of the mesh was performed in the areas of abrasive grains in the connection, in the places of contact of grains with the workpiece and the inclusion of the metal phase, as well as on the contact surfaces of the system elements. This approach allowed for a more accurate simulation of the deformation of model fragments, taking into account the remoteness of the zones of boundary effects. The elements on the workpiece have an average edge size of 80 μm, which is gradually reduced to almost 60 μm close to the upper surface that contacts the abrasive grains, whereas close to the surface the average edge size is reduced to almost 20 μm. In the part representing the bonding material, the edge size varies between 40–80 μm except for the regions near the grains, where it is reduced to 20 μm. The edge size of the elements in the grains is 50 μm. The contact type between the grains and bonding material is bonded, whereas the contact type between the metallic phase and grain, as well as the grain and workpiece, is “no penetration,” which allows deformation of materials due to their interactions with contacting bodies, but does not allow the penetration of one material into the other.
In the example of model calculations (
Figure 1), the physical and mechanical properties of the elements of the “grain-metal phase-bond-processed SHM” system were used, and are shown in
Table 2.
The study is static structural, thus thermal effects are not taken into account. As can be seen in
Figure 1c, a static, uniformly distributed load of 2N is exerted on the outer surfaces of the bond, in the form of a hold-down pressure. On the bottom face of the workpiece, displacements are restricted in order to avoid rigid body motion.
Afterwards, the value of critical embedding of diamond grain on the bond material (
hcr) is determined from the appropriate FE model, presented in
Figure 2, for three different percentages of grain embedment (
hemb), namely 20, 50, and 65%, as well as from empirical models, for which the coefficients values were calculated using the FE model. Finally, the developed FE model is also used in order to calculate the penetration depth of abrasive grain into the bond material at various positions of the grain–bond contact, which is related to the grain retention strength of the wheel.
3. Results and Discussion
3.1. Effect of Bond Properties on Critical Embedding Depth of Grains
After the simulations of the 3D stress–strain state of the “SHM–grain–bond” system were carried out, the essential role of the elastic modulus of the bond in the mutual destruction of the system elements and the grain retention strength was able to be revealed. It is worth mentioning that the mechanical properties of the grain have a considerable effect on the magnitude of the stresses in the contact area between the grain and the SHM workpiece. Subsequently, the properties of the bond affect the fracture process of both grains and the workpiece material, which is related to the grinding performance and wear of the grinding wheel. Moreover, the bond properties have a direct effect on the embedding depth of grains into the bond and the number of working grains, which affect the size of the contact area between SHM and WWS and loads exerted on each grain. Bond stiffness directly affects the vibration of grains and surface quality of the workpiece [
39]. Usually, during grinding of superhard materials such as diamond, the bond is considered to be the weakest part of the system, as its elastic modulus is at least 10 times less than that of the workpiece and grains’ material, as can be seen from the properties depicted in
Table 2.
At the first stage of the investigations, the influence of the physical and mechanical properties of the bond and the conditions of interaction of the system elements on the value of the critical embedding of grains in the bond are evaluated. This parameter is necessary to determine the number of actually working grains and the actual contact area in the “SHM–grain–bond” system. As a fracture criterion, the excess of the reduced stress of the yield point of the bond material or the impact toughness value, which for the strongest bonds M6-16 and M6-14, is 66 and 61.4 kJ/m
2, respectively, is used [
40]. The yield points of bonds based on aluminum, bronze, and iron are 200, 270, and 470 MPa, respectively [
41]. As can be observed, the iron-based bond has the greatest elasticity. Of the commercially available metal bonds, the M6-16 bond has the highest modulus of elasticity (
E = 193.7 GPa). Some indicative results regarding the influence of bond properties of the stress state of the workpiece during grinding of superhard materials are depicted in
Figure 3a.
The value of the critical embedding of diamond grains in the bond
hcr is determined based on the results of the 3D model of the stress-strain state of the “SHM–grain–bond” system. Visualization of stress fields in the “SHM–grain–bond” system, depending on the amount of grain embedment in the bond (
hemb) at the top contact, is shown in
Figure 4.
Based on the processing of the simulations’ results in the MathCAD environment, we obtain analytical dependences of the effect of the elastic modulus of the bond
Eb, the working grain height
hw, normal pressure
Pn, grinding speed
Vwh, and cross feed on the critical value of the embedding of grains into the binder
hcr:
where
K1,2,3–coefficients are obtained by calculating 3D SSS of the “SHM-grain-bond” system with the FEM method [
21];
Eb–elastic modulus of the bond, [GPa];
hw–working grain height, [µm];
Pn–normal pressure at the “WWS-SHM” contact, [MPa];
Scrf–cross feed, [µm]/double run;
Vwh–wheel speed, [m/s].
The results of calculating the critical value of the embedment from Equations (1)–(3) and the results of 3D modeling of the stress-strain state of the system are presented in
Table 3. It can be seen that the elastic modulus has a negative correlation with the critical embedding value, indicating that the higher the elastic modulus of the bond is, the lowest the critical embedding value of the grains in the bond becomes. Thus, when grinding wheels with bond types such as M2-01 or M3-16 are used, based on the properties depicted in
Table 1, the grains can be more easily embedded in the bond than in the case of M1-01 or M1-05 type bonding material. Moreover, the critical embedding value varies in respect to different regions of contact between grain and bonding material.
Regarding the effect of loading conditions on the critical embedding value of grains, it was determined that an increase of cross feed value leads to an increase of the critical embedding value of the grains, thus decreasing the possibility of grain retention. Furthermore, the increase of wheel speed also increases the critical embedding value of the grains; thus, in order to be able to use higher cross feed values or wheel speed values, a grinding wheel with higher elastic modulus of the bond is required.
The results of calculations on these dependencies are used to determine the efficiency of manipulating the properties of diamond grains. Since the elastic modulus of diamond grains and the processed material are practically the same (without taking into account the anisotropy of properties) and have natural limiting values inherent in diamond structures, and the process of stock removal is carried out mainly due to extremely high contact pressures, for a productive process, it is necessary to create contact pressures similar to real grinding conditions.
As a result, it was found that the bond has a dominant effect on the parameters of the SSS system and on the value of contact pressures in the “grain–SHM” system and, therefore, largely determines the intensity of mutual fracture of the SHM and grains.
Calculations show that the degree of influence of the elastic modulus of grain, SHM, and bond on the value of reduced stresses (or deformation energy density) in SHM is estimated at 0.02–0.036–0.164, respectively, and it turns out that the elastic modulus of the bond affects the magnitude of stresses in the “grain–SHM” eight times more than the elastic modulus of the grain and five times more than the elastic modulus of SHM. For example, with diamond grinding of SHM with the wheel on the M1-01 bond (E = 72 GPa), the volume of the fractured SHM in a one-step interaction with a diamond grain is 4 × 10–10 mm3, and, when grinding with the wheel on the M6-14 bond (E = 196 GPa), under the same conditions, this volume is already 34 × 10–10 mm3.
3.2. Effect of Bond Elastic Modulus on Grain Penetration Depth into Bonding Material and Process Efficiency
Apart from the effect of the mechanical properties of the bond on the critical embedding of the grain into the bond, the effect of the elastic modulus of the bond on the penetration of grains into bonding material and process efficiency has also been investigated. In the conditions of 3D modeling of the stress-strain state of the “SHM–grain–bond” system, the possible value of grain embedding into the bond was also analyzed. Under conditions of rigid grinding, when extremely rigid materials “grain–SHM” come into contact on one side in the “WWS–SHM” contact, it is obvious that the main value of the cross feed (
Scrf) should be compensated by the elasticity of the bond and the amount of embedding of diamond grains into it. With certain assumptions, the process of diamond grinding is similar to the impregnation [
26] or the process of profiling diamond wheels by the method of plastic deformation [
23,
31], where an extremely rigid SHM acts as a lap, and the material to be impregnated is a metal bond based on aluminum, bronze, iron, or cobalt. In this case, as shown in [
31], even diamond grains of the AC6 grade with a grain size of 63/40 can be completely embedded (pressed) into the bond without fracture.
Our studies, carried out with the finite element method, have shown that the smaller the working height of the grains, the lower the probability of fracture of diamond grains. This fully confirms our position that the process of diamond grinding of SHM should be carried out not with the maximum (as stated earlier in [
39]), but with the minimum possible, excluding the contact of the bond with SHM and the height of the protrusion of grains from the bond
hw.
Since during diamond grinding of SHM there is practically no intrusion of grains into the PM, the load from the cross feed (
Scrf) turns into elastic deformation (indentation) of diamond grains into the bond, while new tops of grains that are in the layer come into contact with the PM, with a thickness equal to that of the grains embedded into the bond (
a). Thus, when calculating the number of working (contacting) grains in the process of grinding SHM, it is necessary to take into account the elastic deformation (indentation) of the most protruding grains in the bond and, due to this, the coming into contact of new grain tops located in the layer with the depth of the grains embedded into the bond (
a) from lines of protrusions. The calculated values of elastic deformation (indentation) of the grains into the bond (
a), the values of which were obtained in 3D modeling of the stress-strain state of the system, are given in
Table 4.
From the results presented in
Table 4, it can be seen that the penetration depth of the grains into the bond varies considerably depending on the contact region with the bond, more than one order of magnitude in some cases. Moreover, in each case, the penetration depth of the grains is also increasing significantly with an increase in the cross feed value, exceeding an order of magnitude in most cases.
The authors of [
26] obtained the optimal values of the bond hardness for various grades of diamond grains and the dependence of the relative grain penetration into the bond on the pressing force
P [kgf]:
where
HVb is the micro-hardness of the bond;
dg is the grain size in µm;
ξ =
a/
Rg,
a is thegrain embedment into the bond in µm, and
Rg it the radius at the top of the grain in µm.
It has been found that the stronger the diamond grain, the harder the bond that should be used. In our case, when the introduction of diamond grains into the material being processed is negligible and can be neglected, the elastic modulus of the bond will be determined from the condition of the dynamic indentation of the grain into the bond without fracturing it; that is, in fact, by the dynamic strength of the grains, determined by our proposed method [
39].
Thus, the modulus of elasticity of the bond should ensure the strength of retention of grains in the bond and the sufficient load on the grain for one-step micro-fracture of the grain at the top with its gradual deepening into the bond. The introduction of the energy of ultrasonic vibrations into the grinding area and/or into the control area [
39] significantly increases the likelihood of diamond grains embedment into the bond, which naturally prolongs their active life. This effect was used by the authors in the method of impregnation of the surface with abrasive grains [
26].
The value of the elastic modulus of the bond also affects the frequency of natural vibrations of diamond grains in the bond, which was determined by using the finite element method [
21]. The stiffness of the bond is also important when tracing the anisotropy of the properties of SHM crystallites—the more rigid the bond, the greater the probability of fixing the anisotropy and more efficient the process. [
21]. Since during diamond grinding of SHM the main obstacle for stock removal is the formation of wear areas on the cutting grains and the transformation of the machining process into a wear-resistant friction pair of “SHM-diamond grains,” we proposed a method of forced micro-fracture of wear areas [
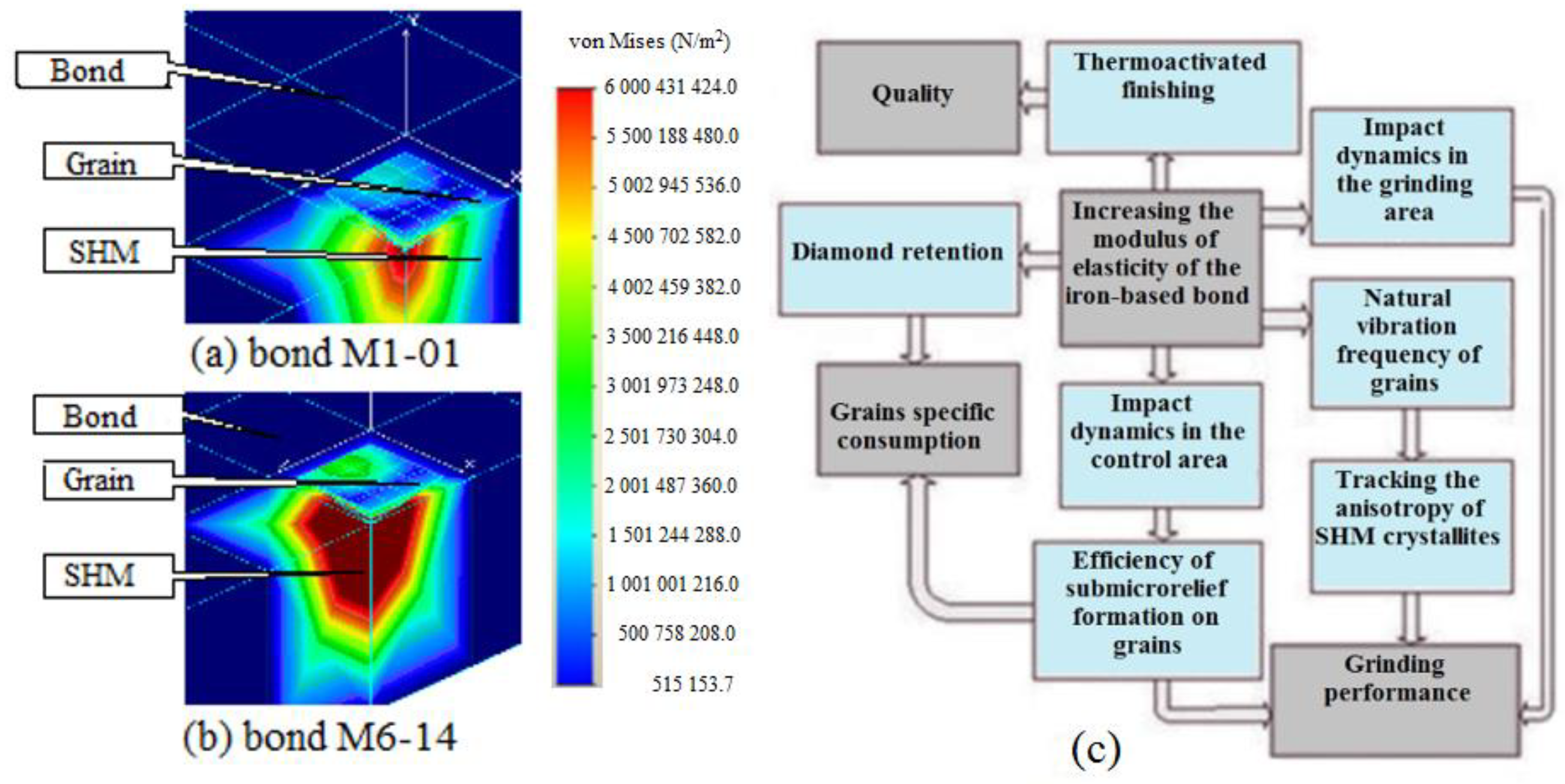
39]. Outside the grinding area, an ultrasonic effect is carried out on the working surface of the wheel with a special prismatic impact tool with a size of 10 × 20 × 30 mm, consisting of a composite of strong diamond grains (AC 160T) and a hard-alloy bond. The effect of the modulus of elasticity of the bond between the wheel and the impact tool, which forms the submicrorelief on the wear areas of the grains, on the output parameters of the SHM grinding process is shown in
Figure 5.
Thus, the calculations of the 3D stress–strain state of the “SHM–grain–bond” system showed that the elastic modulus of the metal bond is the most significant parameter determining the efficiency of mutual fracture of the elements of the “SHM–grain–bond” system during diamond grinding. A two-fold increase in the stiffness of the metal bond can increase the stress in the “grain–SHM” contact by a factor of seven and, therefore, significantly increase the grinding performance.
An increase in the elastic modulus (stiffness) of the bond can provide various positive effects during grinding. At first, it can increase the strength of diamond retention, as, in wheels with bonding material with higher elastic modulus, the grains can be more easily embedded in the bond, as can be seen from
Figure 5b. Moreover, it can increase the efficiency of the mutual micro-fracture in the “grain–SHM” contact by increasing the force of impact during grinding of superhard materials. Finally, as can be seen in
Figure 5b, the specific consumption during grinding of superhard materials with higher elastic modulus is reduced.
Thus, it is possible that by optimal selection of the ratio of stiffnesses (elastic modulus) of the metal bond of the wheel and the bond of the impact tool, conditions under which the diamond grains of the wheel will be maximally micro-fractured upon impact, can be determined. As we have formulated and proved the position on the important role of the stiffness of the metal bond in the efficiency of mutual micro-fracture of the elements of the “SHM–grain–bond” system due to an increase in the impact force in the “grain–SHM” contact (an increase in the grinding performance and reduction of specific consumption of diamonds in the wheel), it becomes obvious that the selection of a grinding wheel with the appropriate bonding material in each case is crucial in order to increase the efficiency during grinding of superhard materials with diamond grinding wheels without deteriorating surface quality and the wear of the grinding wheel.
4. Conclusions
Under conditions when uniformly hard materials (ground SHM and diamond grains) are in contact and the value of elastic penetration of grains into SHM is by one order of magnitude less than their elastic penetration into the bond, even a slight increase in the elastic modulus of the bond provides a significant increase in the level of stresses in the “grain–SHM” contact and, as a consequence, an increase in the intensity of their micro-fracture. Thus, in the current work, the essential role of the elastic modulus of the metal bond in increasing the efficiency during grinding of superhard materials is investigated for various types of bonding materials using an appropriate FE model.
At first, based on the simulation results and an analytical model, the critical embedding value of grains in the bonding material was determined for various values of elastic modulus, corresponding to different bonding material types, at different contact regions of grain and bond as well as different values of cross feed and wheel speed. The results indicate that a higher elastic modulus of the bond decreases the critical embedding value of grains, whereas grinding at higher cross feed or wheel speed values increases the critical embedding value of grains. Thus, in order to maintain sufficient grain retention when grinding is conducted at higher cross feeds or wheel speeds, grinding wheels with stiffer bond materials are required.
Afterwards, the penetration depth of grains into the bond at various regions of grain-bond contact was determined, and the effect of bond properties on workpiece stress condition, grinding performance, and specific consumption during grinding was determined. It was found that a higher elastic modulus of the bond can increase the strength of diamond retention, which provides an increase in grinding performance and a reduction in the specific consumption of diamonds. Hence, it is concluded that it is necessary to select the optimal combination of elements of the system “SHM grade–grain grade–bond grade” to intensify the process of removing PM, as the bond with the optimum elastic modulus can increase the likelihood of grain–workpiece fracture, the processing efficiency, and the possibility of self-sharpening of diamond grains.