Abstract
Resource-constrained product general assembly lines with complex processes face significant challenges in delivering orders on time. Accurate and efficient resources allocation of assembly lines remain a critical factor for punctual order delivery, full use of resources and associated customer satisfaction in complex production systems. In order to quickly solve the order-based dynamic resource allocation problem, in this paper a metamodel-based, multi-response optimization method is proposed for a complex product assembly line, which has the characteristics of order-based production, long working time of processes, multiple work area re-entry and restricted operator quantity. Considering the complexity of the assembly line and the uncertainty of orders, the correlation between system performance indicators and resource parameters is investigated. Multiple metamodels are constructed by the Response Surface Methodology to predict and optimize the system performance. The adequacy of the constructed metamodels is verified and validated based on the bootstrap resampling method. Under the condition of ensuring the throughput demand of the assembly line, the desirability function is applied to simultaneously optimize the multi-response, and the resource allocation solution is generated. The method in this paper can be used to rapidly adjust the resource configuration of the assembly line when considering the order changes.
1. Introduction
Aerospace products are typically complex products based on a discrete manufacturing system. Considering the specificity of the product’s use, small batches are made according to customer orders [1]. Aerospace products are generally high-value products that are not suitable for long-term storage, such as rockets and satellites. The demand for aerospace products is unstable due to their special purpose. Because product performance can be directly affected by long-term storage, manufacturers are required to deliver products strictly according to customer order requirements. It indicates that the manufacturer needs to strictly control the throughput of the product assembly line without either advanced or delayed deliveries.
The general assembly process of a kind of aerospace product consists of many parallel assembly workstations with a re-entry process and resource constraints. There are many resource constraints, such as operators, workstations and transportation. Especially regarding operators and workstations, there are only more than a dozen operators in the assembly line, but there are nearly 100 workstations overall. Its production mode is neither a traditional assembly flow line [2] nor a pulsating line [3], where the products flow through the fixed stations with regular operators at each station. The operator resource of the assembly line is made up of a certain number of master and auxiliary operators, who work together to complete the assembly tasks of a workstation. The station number is far greater than the number of operators. The operators should change their station after completing the jobs on the current station. Because of large volume and weight with extensive parts, aerospace products always have a longer manufacturing cycle and a complex assembly process. The duration of the processes at a workstation may be minutes, hours or days. Due to the long process time of some works, there are several large areas with multiple parallel workstations. Re-entry during the assembly process is more common due to process requirements and long working-time processes. The above-mentioned resources of product assembly line should be changed in time to ensure that production capacity meet the customer’s requirements.
For such an aerospace products assembly line, fast and reasonable adjustment of production resource configuration is indispensable to ensure the order delivery time and decrease the waste of resources. Traditionally, simulation methods are often used to solve such problems. But the time spent on iterative simulation becomes longer and longer as the complexity of the model increases [4]. Metamodel methods are favorited by scholars and practitioners for their rapidity and accuracy in solving resource allocation problems [5]. Digital Twin is also a popular method to solve production resource allocation problems [6]. Its core is models and algorithms for optimization and prediction. Compared to traditional simulation and metamodel approaches, Digital Twin pays more attention to real-time performance. In this paper, considering the assembly resources adjusted by month for the aerospace product, we use the second-order response surface metamodel method to predict the complex system performance under different resources configurations in an aerospace product line. The stability of the metamodel output is verified by the bootstrap resampling method. The resource allocation scheme satisfying the throughput target of orders is quickly obtained based on the desirability function.
The remainder of the paper is organized as follows. Section 2 reviews the methods in solving resource configuration problems. Section 3 explains the basic scenario of the problem and proposes solution ideas. Section 4 constructs a second-order response surface metamodel for the case assembly line and applies the desirability function for resource allocation. Section 5 concludes and gives an outlook on future works.
2. Literature Review
2.1. Simulation-Based Method for Resource Configuration of Manufacturing Systems
Simulation is the process of building visible models of real systems for experimental study of real systems [7]. Especially when different system configurations or processes need to be validated [8], simulation is a significant tool for modelling and analyzing the true performance of manufacturing systems. It has functions such as identifying and dealing with bottlenecks in manufacturing plants, predicting plant capacity, observing machine operating efficiency and so on [9,10,11,12].
A simulation-based method can find the resource configuration that gives the ideal performance by changing the resource parameters in the model [13,14,15]. Imseitif et al. [16] established a serial manufacturing line model in Simul8 software. They studied the impact of multiple resource factors on throughput, such as the cycle time of workstations, the length of a manufacturing line and the capacity of internal buffers through simulation. A simulation-based method for port capacity assessment and expansion planning was proposed in [17], which can associate a capacity value to a given resource configuration. The method pointed out the optimal resource configuration for a given expected throughput. For an electric device re-manufacturing system, Calvi et al. [18] presented a simulation model in Simio software with an activity-based costing method to evaluate different system configurations. The model analyzed the impact of configurations (e.g., resources and workstations) on system throughput, resource utilization and equipment costs.
Recently, more and more scholars have integrated metaheuristic algorithms into simulation to analyze the resource allocation problem of the production line, so as to predict and optimize system performance [19,20]. For the resource configuration of the reconfigurable manufacturing systems, Diaz et al. [21] proposed a simulation method based on the Non-dominated Sequential Genetic Algorithm (NSGA-Il) to get the optimal allocation of work tasks and workstations. Yegul et al. [22] studied the resource allocation problem of electric vehicle component production lines. A simulation optimization method based on a Simulated Annealing algorithm was used to solve configuration problems of nine resources, such as the number of machines and workers at workstations that maximize annual profit. For a water heater production line [23], an integrated simulation and metaheuristic algorithm (Genetic Algorithm and Particle Swarm Optimization) method was proposed to obtain the optimal buffer allocation.
However, the simulation model must be verified after establishment [6]. It may take several iterations to obtain the optimal resource allocation solution when the optimization algorithm is integrated into the simulation model. Because the simulation itself may take a long time to run, iterative simulation will consume a lot of time.
2.2. Metamodel-Based Method for Performance Prediction and Resource Configuration
Metamodels are mathematical approaches used to approximate simulation models. Especially when the simulation cost is expensive due to the complexity of the model, it is helpful to use the metamodel [24]. The metamodel can capture the input/output relationship of simulation models and generate predictive value faster than simulation models [25,26,27]. When the number of possible solutions is too large, it is impractical to evaluate all possible solutions, making it necessary to use a metamodel-based method [28,29].
The most popular metamodel-based method is the Response Surface Methodology (RSM) [4,30,31,32]. Azadeh et al. [33] optimized the performance of a steelmaking plant based on a second-order RSM metamodel, where the effect of four factors (e.g., the number of converters and mixing machines) on plant capacity was studied. For the problem of assigning buffers in a production line, Nuñez-Piña et al. [34] found the optimal output values through the construction of a predictive four-order RSM metamodel. In their work, the relationship among the number of buffer slots, the number of workstations and the production rate is studied. In order to solve the buffer allocation problem for unreliable and unbalanced production lines, Motlagh et al. [35] developed a second-order RSM metamodel of throughput. The parameters are workstation operating time and buffer capacity. The NSGA-Il and the Non-dominated Sequential Genetic Algorithm (NRGA) were applied to maximize the capacity and minimize the cost of an automotive body rear-floor production line.
The other metamodel methods are also used for production resource allocation [36,37,38,39]. In order to predict the production throughput of surface mount technology production lines, Li et al. [40] presented a Symbiotic Organism Search Algorithm-based Support Vector Regression metamodel considering the production line configurations, which include the printed circuit broad board type, machine configurations and so on. Facing the buffer allocation problem, an Artificial Neural Network (ANN) metamodel was applied to establish the decision support system for searching the optimal buffer allocation solution [41]. A Kriging metamodel was established with three input variables (e.g., solid mass fraction in the reactor, enzymatic load and hydrolysis reaction time) to analyze the production of bioethanol in [42].
The most important advantage of a metamodel-based method is to approximate and replace expensive simulation models, making optimization faster [43]. However, when training metamodels, a certain number of observations (training set) are obtained through simulation model experiments, which is time consuming because of the larger size of the training set [44].
Considering the complexity of order-based complex production systems, this paper is committed to solving the resource allocation problem of such systems using the metamodel-based method. There are two contributions of this paper: (1) It provides decision support for such assembly lines with re-entry, long processes, personnel constraints, etc. A metamodel-based, multi-responses optimization method is used to optimize resource configuration considering the delivery time of an order, which can also analyze and predict the system’s performance. (2) A complex aerospace product general assembly line in real life with extremely unbalanced working time of processes is used to verify the approach for dynamic resource allocation based on the order requirement.
3. Problem Statement and Method Description
3.1. Assembly Process of Aerospace Products
In the face of unstable orders and strict delivery requirements, the resource-constrained aerospace product assembly system requires rapid adjustment of resource allocation. Our goal is to find a reasonable resource allocation solution while ensuring on-time delivery of orders.
In the aerospace product assembly line, workers are usually classified into two types based on skill level: master operator (MO) and auxiliary operator (AO). The MO can complete the work of the AO, but the AO cannot complete the work of the MO. Because of the special requirements of the assembly line, there is an upper limit for the number of master and auxiliary operators in the general assembly workshop, which are workers in total.
The basic assembly process of the aerospace product studied in this paper is shown in Figure 1, including assembly, testing, repair, painting, and measurement, etc. In the figure, () indicates the number of workers required to complete the process, () is the minimum number of master operators required, and is much smaller than the sum of . Processes in a dashed box are completed at the same station in the same area. The working time required by the process has been written in the process flow. From the process flow, we can see that the working time of the dry process can be up to several days. For example, the working time of process 10 is seven days and that of process 25 is four days. The rest of the process operating time is basically measured in minutes. In addition, the sum of long processes working-hours accounts for 97.2% of the total assembly working hours. There are multiple tests, measurements and repairs in the whole assembly process.
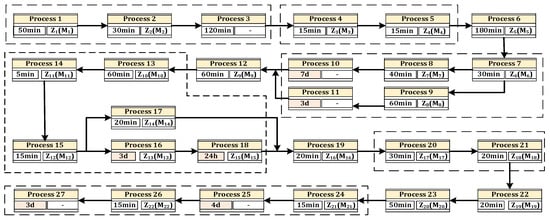
Figure 1.
The assembly process of case product.
A typical assembly line layout for the aerospace product studied is shown in Figure 2. There are a number of areas, such as the manual assembly area, automatic assembly area, quality control area, special process area, measurement area, packing area, finishing area and parts warehouse. In the figure, the arrow is the logistics route of the assembly process according to the process flow. ) indicates the number of stations in each area. In order to reduce the impact of long working hours on production efficiency, some parallel workstations () have been configured in areas where working hours are too long according to process requirements. The logistics road map shows that there are re-entries in the quality control area, special process area and measurement area. There are three types of transfer tools in the general assembly line, which are AGV-1, AGV-2 and trolley.
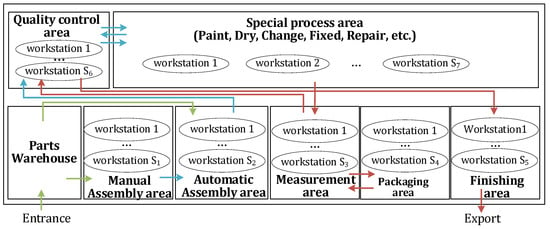
Figure 2.
The layout of general assembly workshop.
3.2. Metamodel-Based, Multi-Response Optimization Method
The metamodel represented by the RSM method has the function expression, which can directly optimize under feasible constraints. The ANN metamodel can only predict the output based on the input, which requires the addition of other optimization algorithms to find the optimal solution. Moreover, the RSM has many important advantages for solving resource configuration problems. It allows the use of statistical tools to evaluate the fitness of the approximated RSM metamodel. A small number of experiments can reveal the influence of factors (input variables) and their interactions on system performance. The RSM is quite effective with a limited number of design variables [38]. In this paper, considering the prediction and optimization achieved simultaneously, the second-order RSM metamodel that takes into account interactions between resources is chosen. Multiple response metamodels are used to analyze, predict and optimize system performance indicators.
A simulation optimization method based on multiple RSM metamodels is proposed to solve the problem of order-oriented rapid resource allocation. In order to obtain the resource allocation solution that meets the demand of the order, we should optimize multiple responses simultaneously. The response surface metamodel of the performance indicator m is built as shown in Equation (1).
where denotes the resource factor. There are resource factors and performance indicators selected. For the response , is the random error with zero mean and variance. , are the coefficients of and , respectively.
The individual desirability of the response is calculated as shown in Equation (2).
where is the predicted value of response, , is the lowest value for response, , is the target value of response and . is the weight corresponding to the response.
Therefore, the objective is to maximize the composite desirability value (), as shown in Equation (3), where the throughput response meets the target demand and the remaining response values are maximized. The ranges from 0 to 1, and the closer to 1, the better the resource allocation solution is.
The constraints are as follows:
where is the number of MO and is the number of AO, is the maximum number of workstations in the corresponding area and is the response of throughput. Equation (4) demonstrates that the sum of the number of MO and AO cannot exceed the upper limit number of workers in the workshop. Equation (5) shows that the number of workstations in area is less than or equal to the maximum number of workstations limited in that area. Equation (6) means that the number of AO is non-negative. Equation (7) denotes that the number of MO is not less than the maximum number of workers to complete the entire assembly process. The minimum number of workers to complete the entire assembly process is the maximum value of the number of workers required to complete each process. Equation (8) represents that the response–throughput needs to meet the order demand .
The metamodel-based, multi-response optimization method is shown in Figure 3. There are two main processes, i.e., multiple-response surface metamodels’ construction and multi-responses optimization. For an order-driven complex product assembly system, a simulation model is built to reflect the real system. It is known that not all changes of system performance caused by changes in resources are directly perceived. Because resource factors with insignificant effects can be ignored in production control, the variables that have a major impact on system performance must be identified by sensitivity analysis. Based on the resource constraints of the assembly system, the correlation between multiple resource factors and system performance responses is investigated through the simulation data obtained by DOE. Then, the metamodels are constructed and validated. The multi-responses optimization is shown on the left side. After receiving an order with product quantity and the delivery time in months, we need to split the order on the basis of each month and get the target value of the throughput response. To obtain the value of and the optimal resource allocation scheme, we apply the desirability function to optimize multiple responses. Finally, the optimal resource configuration is sent to the assembly line.
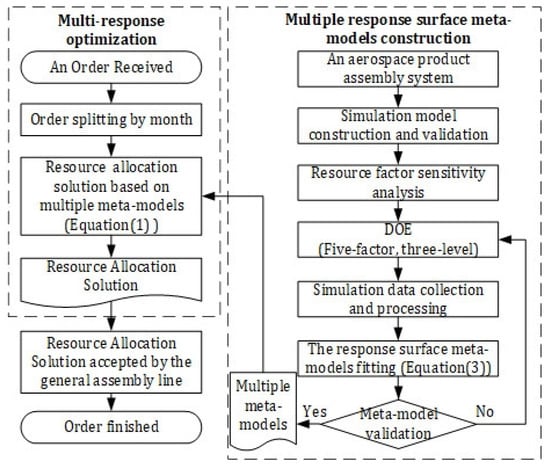
Figure 3.
Metamodel-based, multi-response optimization method.
4. Case Study
4.1. Simulation Model of the Assembly Line
As shown in Figure 4, through process modelling, data collection and stochastic distribution fitting of process time, a discrete event simulation model of the aerospace product general assembly line is built in Anylogic software (8.7.6, the Anylogic Company, Chicago, IL, USA).
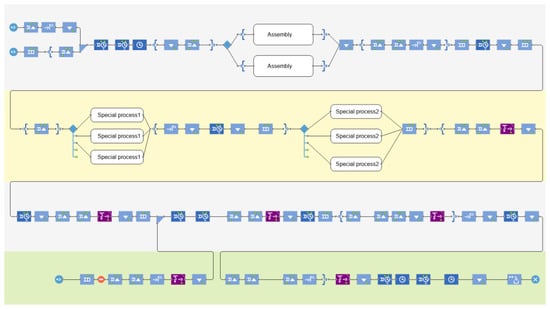
Figure 4.
The simulation model of the general assembly line.
The established simulation model is verified by the following work. (1) The model check function provided by Anylogic is performed to ensure the logic and structural correctness of model. (2) The manual check of generated simulation model in Anylogic is also carried out one by one to affirm that the simulation model is consistent with the exact one constructed through a traditional method by a simulation expert. (3) After the debugger completes the logic correction, the Anylogic animation is used to check the material flow and operational rules of the system, particularly for reasonableness under the various settings of input parameters. (4) The visual tool of Anylogic is applied to show real-time data of several key indicators and to ensure that the variations of the indicators are reasonable.
The system performance data is collected from the simulation model during the steady-state operation period after warm-up. To ensure the accuracy of the simulation data, the simulation is repeated 10 times for each experiment. The average value of the 10-times results is taken as the final data of this experiment. Each simulation is run for a year with 8 working hours per day and 5 days per week.
4.2. Sensitivity Analysis and DOE of Resource Factors
In this paper, the influence of various resource factors on system performance indicators is investigated through sensitivity analysis. Sensitivity analysis is an uncertainty analysis technique that studies the influence of a certain change of relevant factors on a key indicator or a group of key indicators from the perspective of quantitative analysis [45]. Using the control variable method, the resource parameters are changed one by one in the simulation model, whereas other factors are kept in their initial state. The system performance data is collected to analyze the positive or negative impact of each factor. Since the purpose of this paper is to meet the order demand while maximizing resources utilization, the impact of resources on system throughput should be analyzed. After the sensitivity analysis, the factors that have main effects on the general assembly line performance are determined as follows:
- the number of master operators ;
- the number of total operators ;
- the number of quality-control workstations ;
- the number of packaging workstations ;
- the number of finishing workstations .
In order to better capture representative groups among all resource combinations and to appropriately reduce the number of experiments, the level ranges of the studied resource factors are shown in Table 1, where −1 refers to the lowest level, +1 refers to the highest level and 0 refers to the middle level.

Table 1.
Factor Level of Assembly Resources.
A DOE method is used to address the selection of independent factors and investigate how to choose the level combination of independent factors suitable for the target. The commonly used DOE methods are usually factorial design, Central Composite Design and Box-Behnken Design [40,46]. The choice of the appropriate DOE method depends on the function under study, the metamodel used, and the limitations of the problem [37]. Considering the resource factor level and the sample size comprehensively, a complete 35 factorial design with two centers is chosen to study the overall factor influence of the general assembly line. This would require a simulation running for a total of 243 different design points.
4.3. Metamodel Construction Based on Second-Order RSM
A fully quadratic regression analysis is chosen to establish the second-order RSM metamodels, as shown in Equation (1). There are seven second-order RSM metamodels representing the system performance indicators studied, as listed in Table 2. Before its application, the metamodel is tested for fitting to determine if it properly represents the data of the simulation model. A key indicator of fitting is the value, which evaluates the internal data performance of the model [30]. The value ranges from 0 to 1. The higher the is, the better the model is. And its value is calculated from the same data used to construct the RSM metamodel. Because this paper studies the influence of multiple factors on performance, it is a multivariate statistic. Thus, the adjusted value is used to measure the fitness from analysis of variance (ANOVA), excluding the influence caused by the number of factors on the value.

Table 2.
Responses of System Performance Indicators.
The ANOVA results of the response throughput are listed in Table 3. The F-value is 379.33 and the p-value is 0.000. The p-value is less than 0.05, indicating that the meta-model is statistically significant at the 95% confidence level. The F-value is above the critical value 2.253. The larger the F-value, the higher the significance level of the model. In addition, the adjusted value is 96.90%, indicating that the data fit well with the regression line. Therefore, the fitness of the metamodel is supported by sufficient evidence. Thus, the metamodel is accepted to determine the predicted optimal value for the throughput. The metamodel of throughput response is shown in Equation (9).

Table 3.
ANOVA for Response Throughput.
The main ANOVA results of the seven responses ( to ) are shown in Table 4, including the F-value, the p-value and the adjusted value. It can be found that all p-values are less than 0.05, all F-values are more than 2.253 and all the adjusted values are greater than 70%. Therefore, the metamodels of the responses to all satisfy the acceptance conditions and can be used directly for subsequent optimization.

Table 4.
The main ANOVA results of the responses –.
4.4. Validation of Throughput Response Meta-Model
The fitness of the metamodel for the non-training data in the solution space should be validated. This is because the indicates how well the model fits the existing data (training data set), but it does not measure how well the model fits the new data set. The main methods to validate the metamodel’s fitness are the cross-validation method and the bootstrap resampling validation method [25,40]. The cross-validation method is commonly used when the data set is large. The bootstrap resampling validation method can be used to measure the accuracy of the prediction model and also to evaluate the uncertainty of the model, which is slightly more complex but more robust than cross-validation. The factors in this study have a wide range of values and a huge solution space. The experimental design only takes a small part of the solution space with a small data set. To better validate the fitness of the metamodel, the fitted throughput RSM metamodel is validated using the bootstrap resampling method.
The Root Mean Squared Error () and the Correlation Coefficient () are two popular indicators to measure the performance of the metamodel [34].
- (a)
- The Root Mean Square Error ().
- (b)
- Correlation Coefficient ().
Bootstrap resampling requires a suitable number of repetitions to test the fitness of the metamodel. Too few repetitions are insufficient to account for fitness, and too many repetitions are time consuming. In this paper, the normal distribution is randomly sampled from the solution space five times repeatedly, and twenty-seven sets of observations are taken each time as the validation set for verification. The validation results of throughput are shown in Table 5. The minimum and maximum values of five validations are 34.3170 and 42.9624, respectively. The mean value of is 37.3359. In addition, all five values fluctuate slightly around the mean value. All the values of five validations are above 0.98, which is very close to 1. The above results show that the throughput RSM metamodel has good and stable prediction performance for out-of-fit data.

Table 5.
Results of Five Validations for the Throughput RSM Meta-Model.
4.5. Order Driven Dynamic Resource Configuration
Assume there is an order A, which has a total of 345 products delivered in 8 months with four times. The first delivery is at the end of the third month with 180 products. A total of 70 products are needed to be delivered in the fifth month. The third delivery is at the end of the sixth month with 45 products. Moreover, 50 products need to be delivered in the last month. The product quantity of order A is divided into monthly throughput as shown in Table 6.

Table 6.
Information of Order A.
As seen in Table 6, four different throughputs, i.e., 60, 35, 40 and 25, are required over an eight-month period. Thus, a total of four resource allocations are required in order to complete the production task. The optimal resource allocation scheme should ensure the system throughput and the utilization rate of resources should be maximized. The weight of the response throughput is 8. The weight is 0.5 for the response of personnel utilization. The utilization of workstations with a weight of 0.2 except for the testing workstation, whose weight is 0.4. And the optimal resource configuration result is generated using Minitab. The four resource configuration solutions and the maximum of the composite desirability of the assembly line are shown in Table 7.

Table 7.
Resource Allocation Solution Validation.
For instance, Figure 5 shows the results of the second resource allocation based on multi-responses optimization. It can be seen that the optimal factor levels for factors (= 1, 2,⋯, 5) are 6, 14, 2, 2, and 8, respectively. The desirability of the resource allocation is 0.9108. Accordingly, there should be 14 operators including 6 master operators, 2 testing workstations, 2 packaging workstations and 8 finishing workstations. Given these optimal resource factor combinations, the predicted values of the special process workstations utilization (85.24%) and throughput (424) are obtained. The curves reflect the trend that each resource factor influences the individual desirability of each response of the meta-model. For example, the impact of resource factors and on the composite desirability has the extreme value point. The resource factor has a positive effect on the throughput .
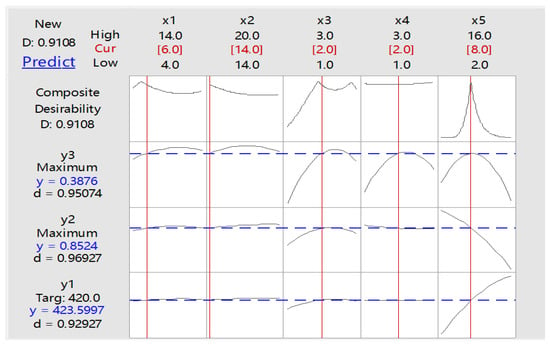
Figure 5.
Multi-response optimization results of the second delivery period.
In order to confirm the results of the four resource allocation solutions, the simulation model is used to validate the solution for each resource allocation. The simulation data is shown in Table 7. In production planning, when inventory is available, the current production produced can be less than the order demand, as long as the total production is satisfied at the time of delivery [47]. The sum of the first delivery throughput is 198, which can meet the demand of a first-delivery order (A) of 180 and generates inventory. The inventory can make up for the lack of second and fourth throughput. The sum of all eight-month throughput is 358, meeting the demand of order A. The simulation data show that the solution is feasible. Therefore, the reliability of the metamodel and the optimization method is verified.
5. Conclusions
For system performance prediction and the resource allocation problem of a general assembly line with workforce constraints, long working-hour process, multiple work area re-entry phenomena and order-based production, a simulation optimization method based on an RSM metamodel is proposed. The sensitivity analysis was conducted to determine the impact of multiple resource factors on system performance. A factorial design of experiments was carried out to collect data through the simulation model. Multiple RSM metamodels were developed for the number of master operators, the total number of shop workers, as well as the number of workstations in the quality control area, the packaging area and the finishing area on several system performance indicators (throughput, workforce utilization, work area utilization, etc.). The stability of the most important throughput RSM metamodel over the entire solution space was verified using the bootstrap resampling validation method. The seven performance indicators are optimized by the desirability function together, where the throughput indicator is ensured to satisfy the target demand and the utilization indicators are maximized. The effective resource configuration solutions under the satisfied throughput target are obtained for timely delivery in multiple stages.
Compared to traditional simulation modeling methods, the RSM metamodel allows for a faster initial prediction and determination of the overall performance of the assembly line based on resource allocation solutions. It can assist workshop managers in making quick and correct decisions in the face of order changes. The method also provides a management reference for complex assembly lines. In the future work, a Digital Twin model can be constructed to realize real-time data collection and performance analysis. Meanwhile, other multi-objective decision-making methods will be tried to determine resource allocation.
Author Contributions
Conceptualization, D.T. and J.W.; methodology, D.T. and J.W.; software, D.T. and X.D.; validation, D.T. and X.D.; formal analysis, X.D.; investigation, D.T.; resources, D.T. and X.D.; writing—original draft preparation, D.T.; writing—review and editing, J.W.; project administration, J.W.; funding acquisition, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Defense Industrial Technology Development Program of China, grant number JCKY2016204A502.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, W.; Li, S.; Huang, Y.; Wang, J. Simulation-based Planning of a Kind of Complex Product General Assembly Line. Procedia CIRP 2018, 76, 25–30. [Google Scholar] [CrossRef]
- Li, M.; Huang, G.Q. Production-intralogistics synchronization of industry 4.0 flexible assembly lines under graduation intelli-gent manufacturing system. Int. J. Prod. Econ. 2021, 241, 108272. [Google Scholar] [CrossRef]
- Wang, X.; Lu, J.; Chen, R.; Xu, M.; Xia, L. Research on design and planning of pulsating aero-engine assembly line based on plant simulation. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference ITNEC 2020, Chongqing, China, 12–14 June 2020. [Google Scholar] [CrossRef]
- Chen, J.C.; Chen, T.-L.; Teng, Y.-C. Meta-model based simulation optimization for automated guided vehicle system under different charging mechanisms. Simul. Model. Pr. Theory 2020, 106, 102208. [Google Scholar] [CrossRef]
- Long, T.; Li, Y.; Chen, J. Productivity prediction in aircraft final assembly lines: Comparisons and insights in different productivity ranges. J. Manuf. Syst. 2021, 62, 377–389. [Google Scholar] [CrossRef]
- Bécue, A.; Maia, E.; Feeken, L.; Borchers, P.; Praça, I. A New Concept of Digital Twin Supporting Optimization and Resilience of Factories of the Future. Appl. Sci. 2020, 10, 4482. [Google Scholar] [CrossRef]
- Junior, W.T.S.; Montevechi, J.A.B.; Miranda, R.C.; Campos, A.T. Discrete simulation-based optimization methods for industrial engineering problems: A systematic literature review. Comput. Ind. Eng. 2019, 128, 526–540. [Google Scholar] [CrossRef]
- Mourtzis, D. Simulation in the design and operation of manufacturing systems: State of the art and new trends. Int. J. Prod. Res. 2019, 58, 1927–1949. [Google Scholar] [CrossRef]
- Greinacher, S.; Overbeck, L.; Kuhnle, A.; Krahe, C.; Lanza, G. Multi-objective optimization of lean and resource efficient manufacturing systems. Prod. Eng. 2020, 14, 165–176. [Google Scholar] [CrossRef]
- Zhao, R.; Zou, G.; Su, Q.; Zou, S.; Deng, W.; Yu, A.; Zhang, H. Digital Twins-Based Production Line Design and Simulation Optimization of Large-Scale Mobile Phone Assembly Workshop. Machines 2022, 10, 367. [Google Scholar] [CrossRef]
- Zhang, M.; Matta, A.; Pedrielli, G. Discrete event optimization: Workstation and buffer allocation problem in manufacturing flow lines. In Proceedings of the Winter Simul Conference, 2016, Washington, DC, USA, 11–14 December 2016. [Google Scholar] [CrossRef]
- Daniyan, I.; Mpofu, K.; Ramatsetse, B.; Zeferino, E.; Monzambe, G.; Sekano, E. Design and simulation of a flexible manufacturing system for manufacturing operations of railcar subassemblies. Procedia Manuf. 2021, 54, 112–117. [Google Scholar] [CrossRef]
- Andrade, P.F.; Pereira, V.G.; Del Conte, E.G. Value stream mapping and lean simulation: A case study in automotive company. Int. J. Adv. Manuf. Technol. 2015, 85, 547–555. [Google Scholar] [CrossRef]
- Schönemann, M.; Bockholt, H.; Thiede, S.; Kwade, A.; Herrmann, C. Multiscale simulation approach for production systems. Int. J. Adv. Manuf. Technol. 2019, 102, 1373–1390. [Google Scholar] [CrossRef]
- Grabowik, C.; Kalinowski, K.; Cwikla, G.; Niemiec, K.; Paprocka, I. A computer simulation as a tool for a production system analysis and optimization. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Constanta, Romania, 13–16 June 2018. [Google Scholar] [CrossRef] [Green Version]
- Imseitif, J.; Tang, H.; Smith, M. Throughput Analysis of Manufacturing Systems with Buffers Considering Reliability and Cycle Time Using DES and DOE. Procedia Manuf. 2019, 39, 814–823. [Google Scholar] [CrossRef]
- Triska, Y.; Frazzon, E.M.; Silva, V.M.D. Proposition of a simulation-based method for port capacity assessment and expansion planning. Simul. Model. Pr. Theory 2020, 103, 102098. [Google Scholar] [CrossRef]
- Calvi, K.; Halawa, F.; Economou, M.; Kulkarni, R.; Chung, S.H. Simulation study integrated with activity-based costing for an electronic device re-manufacturing system. Int. J. Adv. Manuf. Technol. 2019, 103, 127–140. [Google Scholar] [CrossRef]
- Zaplana, I.; Cepolina, E.; Gagliardi, R.; Faieta, F.; D’Imperio, M.; Cannella, F. A novel strategy for workload balance of industrial processes based on a genetic algorithm. In Proceeding of the 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vienna, Austria, 8–11 June 2020; pp. 785–792. [Google Scholar] [CrossRef]
- Yang, S.L.; Xu, Z.G.; Wang, J.Y. Modelling and Production Configuration Optimization for an Assembly Shop. Int. J. Simul. Model. 2019, 18, 366–377. [Google Scholar] [CrossRef]
- Diaz, C.A.B.; Aslam, T.; Ng, A.H.C. Optimizing Reconfigurable Manufacturing Systems for Fluctuating Production Volumes: A Simulation-Based Multi-Objective Approach. IEEE Access 2021, 9, 144195–144210. [Google Scholar] [CrossRef]
- Yegul, M.F.; Erenay, F.S.; Striepe, S.; Yavuz, M. Improving configuration of complex production lines via simulation-based optimization. Comput. Ind. Eng. 2017, 109, 295–312. [Google Scholar] [CrossRef]
- Zandieh, M.; Joreir-Ahmadi, M.N.; Fadaei-Rafsanjani, A. Buffer allocation problem and preventive maintenance planning in non-homogenous unreliable production lines. Int. J. Adv. Manuf. Technol. 2017, 91, 2581–2593. [Google Scholar] [CrossRef]
- Can, B.; Heavey, C. Comparison of experimental designs for simulation-based symbolic regression of manufacturing systems. Comput. Ind. Eng. 2011, 61, 447–462. [Google Scholar] [CrossRef]
- Kleijnen, J. Simulation-optimization via Kriging and bootstrapping: A survey. J. Simul. 2014, 8, 241–250. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, J.; Ng, S.H. Gaussian process based optimization algorithms with input uncertainty. IISE Trans. 2019, 52, 377–393. [Google Scholar] [CrossRef]
- Li, B.; Tian, X.; Zhang, M. Modeling and multi-objective optimization of cutting parameters in the high-speed milling using RSM and improved TLBO algorithm. Int. J. Adv. Manuf. Technol. 2020, 111, 2323–2335. [Google Scholar] [CrossRef]
- Storti, B.A.; Dorella, J.J.; Roman, N.D.; Peralta, I.; Albanesi, A.E. Improving the efficiency of a Savonius wind turbine by designing a set of deflector plates with a metamodel-based optimization approach. Energy 2019, 186, 115814. [Google Scholar] [CrossRef]
- Amaral, J.V.S.D.; Montevechi, J.A.B.; Miranda, R.D.C.; Junior, W.T.D.S. Metamodel-based simulation optimization: A systematic literature review. Simul. Model. Pr. Theory 2021, 114, 102403. [Google Scholar] [CrossRef]
- Amiri, M.; Mohtashami, A. Buffer allocation in unreliable production lines based on design of experiments, simulation, and genetic algorithm. Int. J. Adv. Manuf. Technol. 2011, 62, 371–383. [Google Scholar] [CrossRef]
- de Oliveira, L.G.; de Paiva, A.P.; Balestrassi, P.P.; Ferreira, J.R.; da Costa, S.C.; Campos, P.H.D.S. Response surface methodology for advanced manufacturing technology optimization: Theoretical fundamentals, practical guidelines, and survey literature review. Int. J. Adv. Manuf. Technol. 2019, 104, 1785–1837. [Google Scholar] [CrossRef]
- Dengiz, B.; Belgin, O. Simulation optimization of a multi-stage multi-product paint shop line with Response Surface Methodology. Simulation 2014, 90, 265–274. [Google Scholar] [CrossRef]
- Azadeh, A.; Maghsoudi, A. Optimization of production systems through integration of computer simulation, design of experiment, and Tabu search: The case of a large steelmaking workshop. Int. J. Adv. Manuf. Technol. 2009, 48, 785–800. [Google Scholar] [CrossRef]
- Nuñez-Piña, F.; Medina-Marin, J.; Seck-Tuoh-Mora, J.C.; Hernandez-Romero, N.; Hernandez-Gress, E.S. Modeling of Throughput in Production Lines Using Response Surface Methodology and Artificial Neural Networks. Complexity 2018, 2018, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Motlagh, M.M.; Azimi, P.; Amiri, M.; Madraki, G. An efficient simulation optimization methodology to solve a multi-objective problem in unreliable unbalanced production lines. Expert Syst. Appl. 2019, 138, 112836. [Google Scholar] [CrossRef]
- Batur, D.; Bekki, J.M.; Chen, X. Quantile regression metamodeling: Toward improved responsiveness in the high-tech electronics manufacturing industry. Eur. J. Oper. Res. 2018, 264, 212–224. [Google Scholar] [CrossRef]
- Zeinali, F.; Mahootchi, M.; Sepehri, M.M. Resource planning in the emergency departments: A simulation-based metamodeling approach. Simul. Model. Pr. Theory 2015, 53, 123–138. [Google Scholar] [CrossRef]
- Bandaru, S.; Ng, A.H.C. On the Scalability of Meta-Models in Simulation-Based Optimization of Production Systems. In Proceedings of the Winter Simulation Conference, Huntington Beach, CA, USA, 6–9 December 2015. [Google Scholar] [CrossRef]
- Dengiz, B.; Iç, Y.T.; Belgin, O. A meta-model based simulation optimization using hybrid simulation-analytical modeling to increase the productivity in automotive industry. Math. Comput. Simul. 2016, 120, 120–128. [Google Scholar] [CrossRef]
- Li, D.; Wang, L.; Huang, Q. A case study of SOS-SVR model for PCB throughput estimation in SMT production lines. In Proceedings of the 2019 International Conference on Industrial Engineering and Systems Management (IESM), Shanghai, China, 25–27 September 2019. [Google Scholar] [CrossRef]
- Tsadiras, A.; Papadopoulos, C.; O’Kelly, M. An artificial neural network based decision support system for solving the buffer allocation problem in reliable production lines. Comput. Ind. Eng. 2013, 66, 1150–1162. [Google Scholar] [CrossRef]
- Carpio, R.R.; Furlan, F.F.; Giordano, R.C.; Secchi, A.R. A Kriging-based approach for conjugating specific dynamic models into whole plant stationary simulations. Comput. Chem. Eng. 2018, 119, 190–194. [Google Scholar] [CrossRef]
- Junior, W.T.D.S.; Montevechi, J.A.B.; Miranda, R.; Rocha, F.; Vilela, F. Economic Lot-Size Using Machine Learning, Parallelism, Metaheuristic and Simulation. Int. J. Simul. Model. 2019, 18, 205–216. [Google Scholar] [CrossRef]
- Barton, R.R. Simulation optimization using metamodels. In Proceedings of the 2009 Winter Simulation Conference, Austin, TX, USA, 13–16 December 2009. [Google Scholar] [CrossRef] [Green Version]
- Durieux, S.; Pierreval, H. Regression metamodeling for the design of automated manufacturing system composed of parallel machines sharing a material handling resource. Int. J. Prod. Econ. 2004, 89, 21–30. [Google Scholar] [CrossRef]
- Hassannayebi, E.; Boroun, M.; Jordehi, S.A.; Kor, H. Train schedule optimization in a high-speed railway system using a hybrid simulation and meta-model approach. Comput. Ind. Eng. 2019, 138, 106110. [Google Scholar] [CrossRef]
- Rossi, T.; Pozzi, R.; Pero, M.; Cigolini, R. Improving production planning through finite-capacity MRP. Int. J. Prod. Res. 2016, 55, 377–391. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).