An Improved Residual-Based Detection Method for Stealthy Anomalies on Mobile Robots
Abstract
:1. Introduction
- To address the problem that normal residual detection methods cannot detect the existence of stealthy anomalies purposefully imposed on mobile robots, this paper proposes to apply an improved residual-based detection method to the anomaly detection of mobile robots.
- Three ways to achieve stealthy anomalies purposefully imposed on the OMR, zero-dynamic attacks, covert attacks and replay attacks are implemented on the OMR, and their implementation results are analyzed and summarized, then some new conclusions are obtained.
- The application of the improved residual-based method is implemented on the OMR, and the detection performance of this method can meet the requirements for general anomaly detection.
2. Materials and Methods
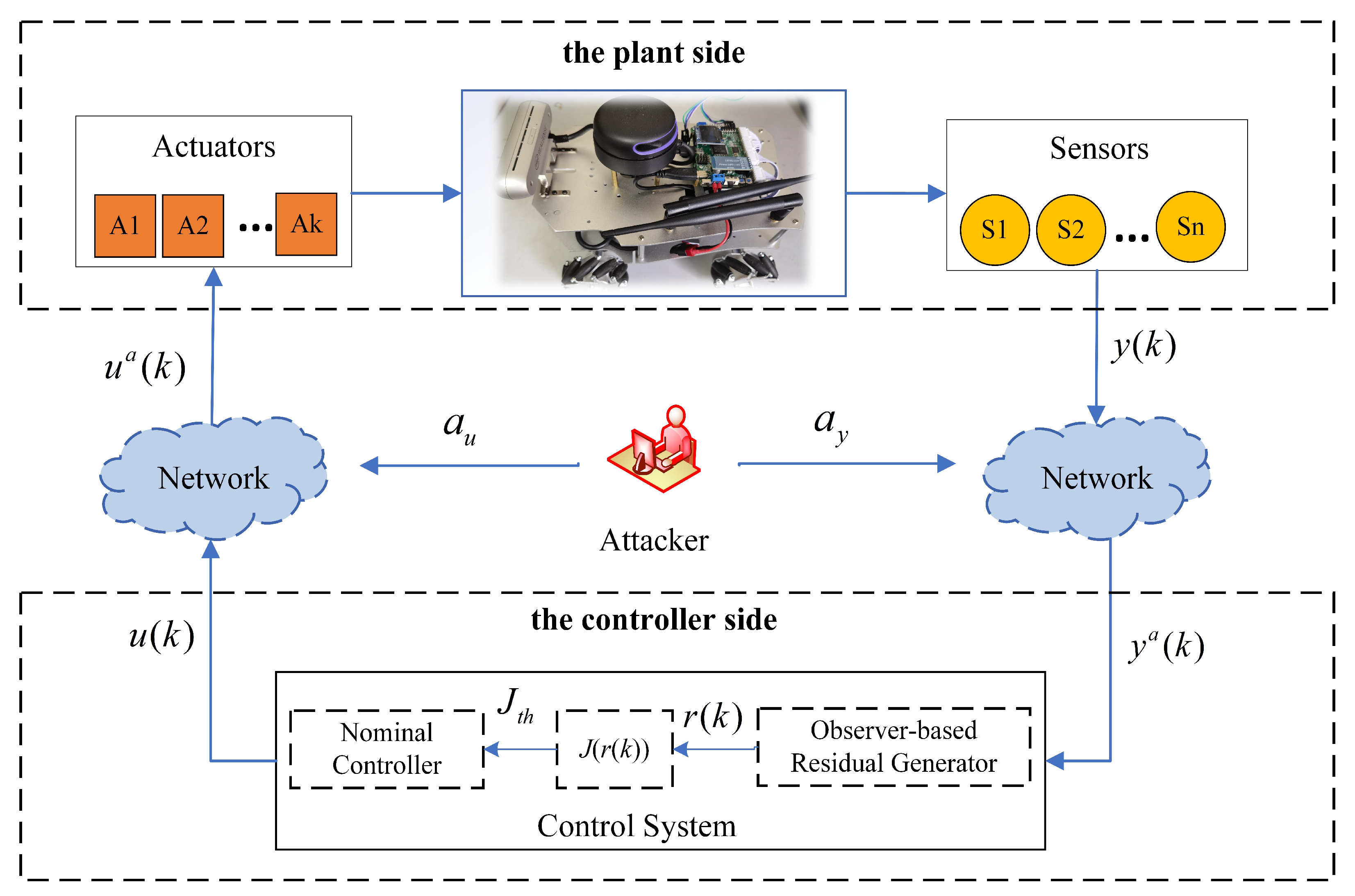
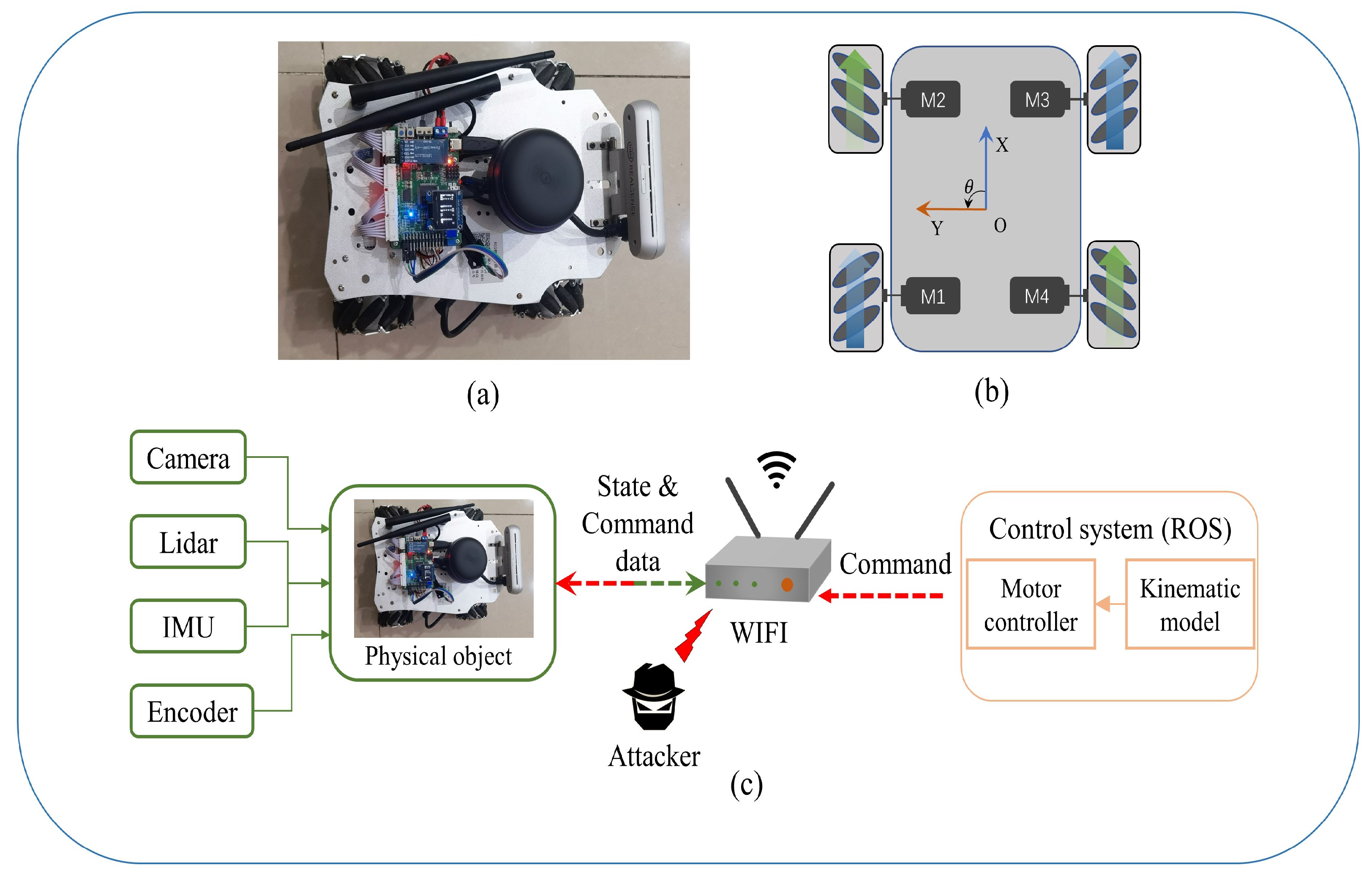
2.1. System Description
2.2. Stealthy Attacks
2.2.1. Zero-Dynamic Attacks
2.2.2. Covert Attacks
2.2.3. Replay Attacks
3. Theory and Calculation
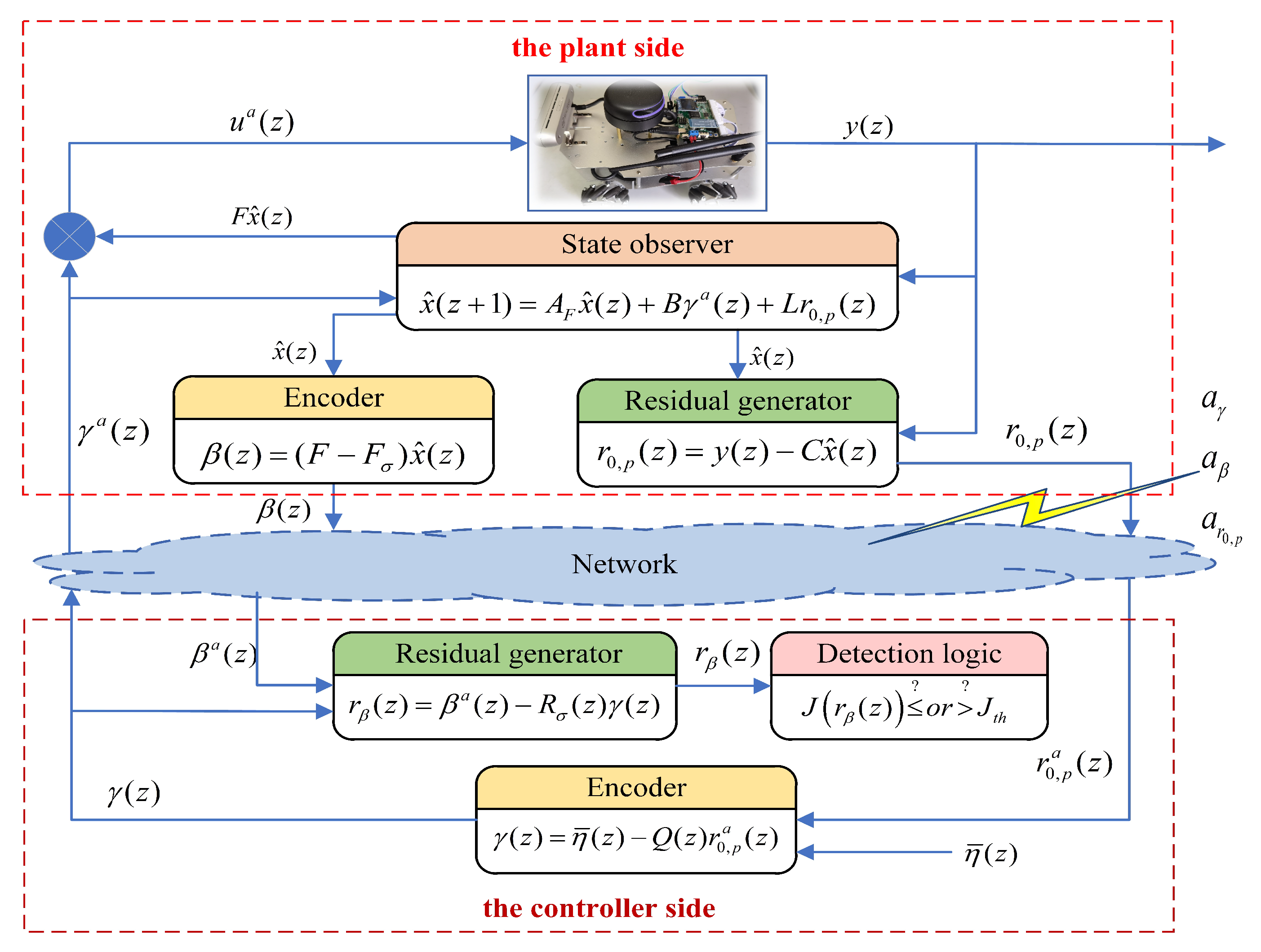
3.1. The Construction of Improved Residual Method
| Algorithm 1: Detection Process Based on |
|
3.2. Detection Logic and Scheme Realization
4. Results and Discussions
4.1. Realization of the Stealthy Attacks
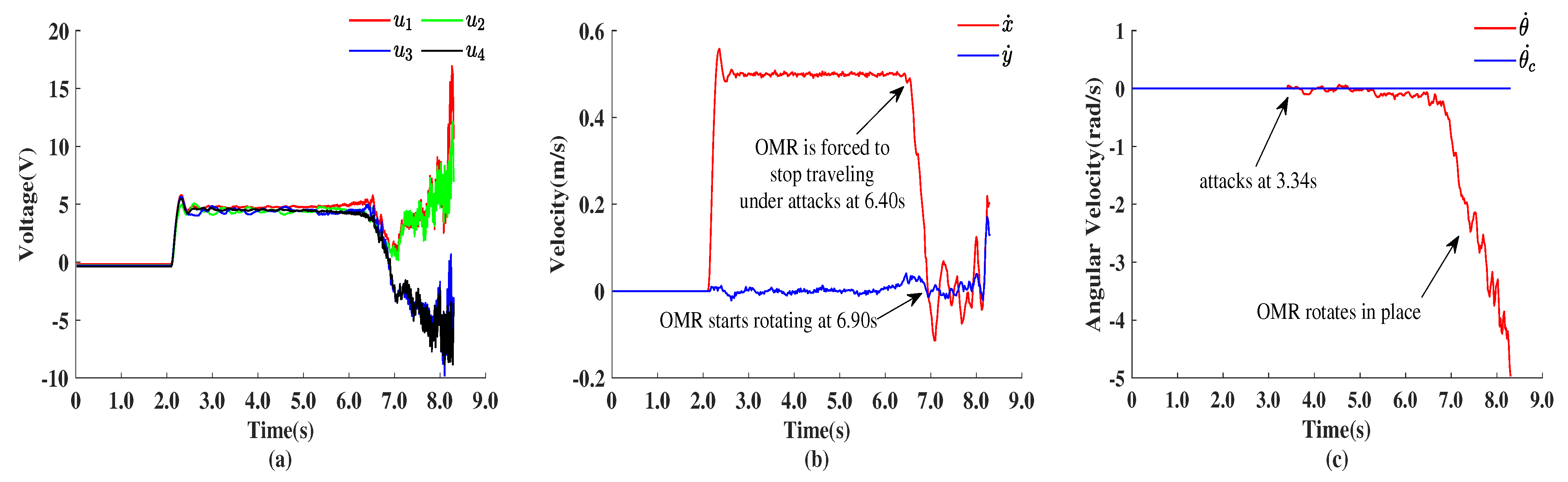
4.1.1. Realization of Zero-Dynamic Attacks
4.1.2. Realization of Covert Attacks
4.1.3. Realization of Replay Attacks
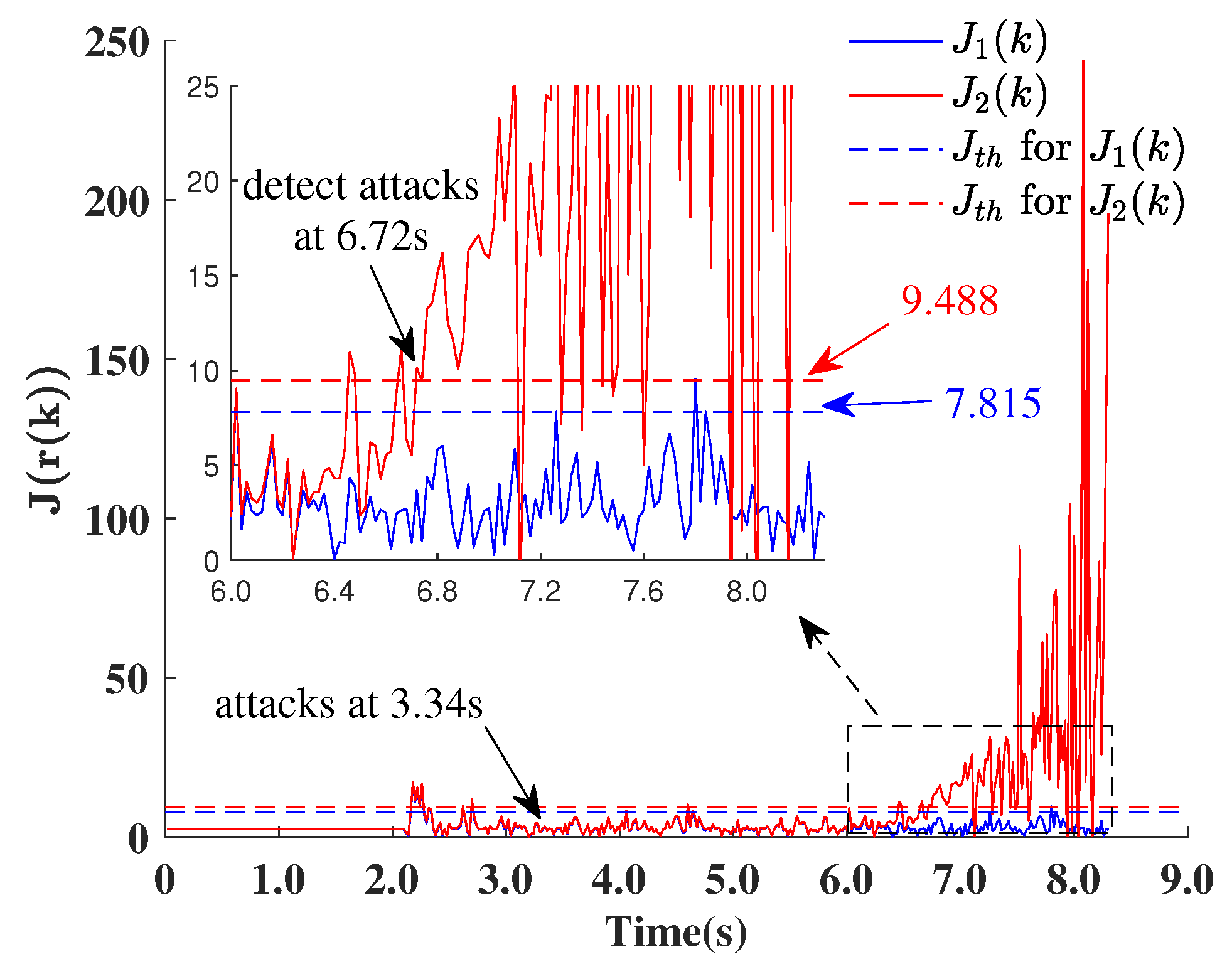
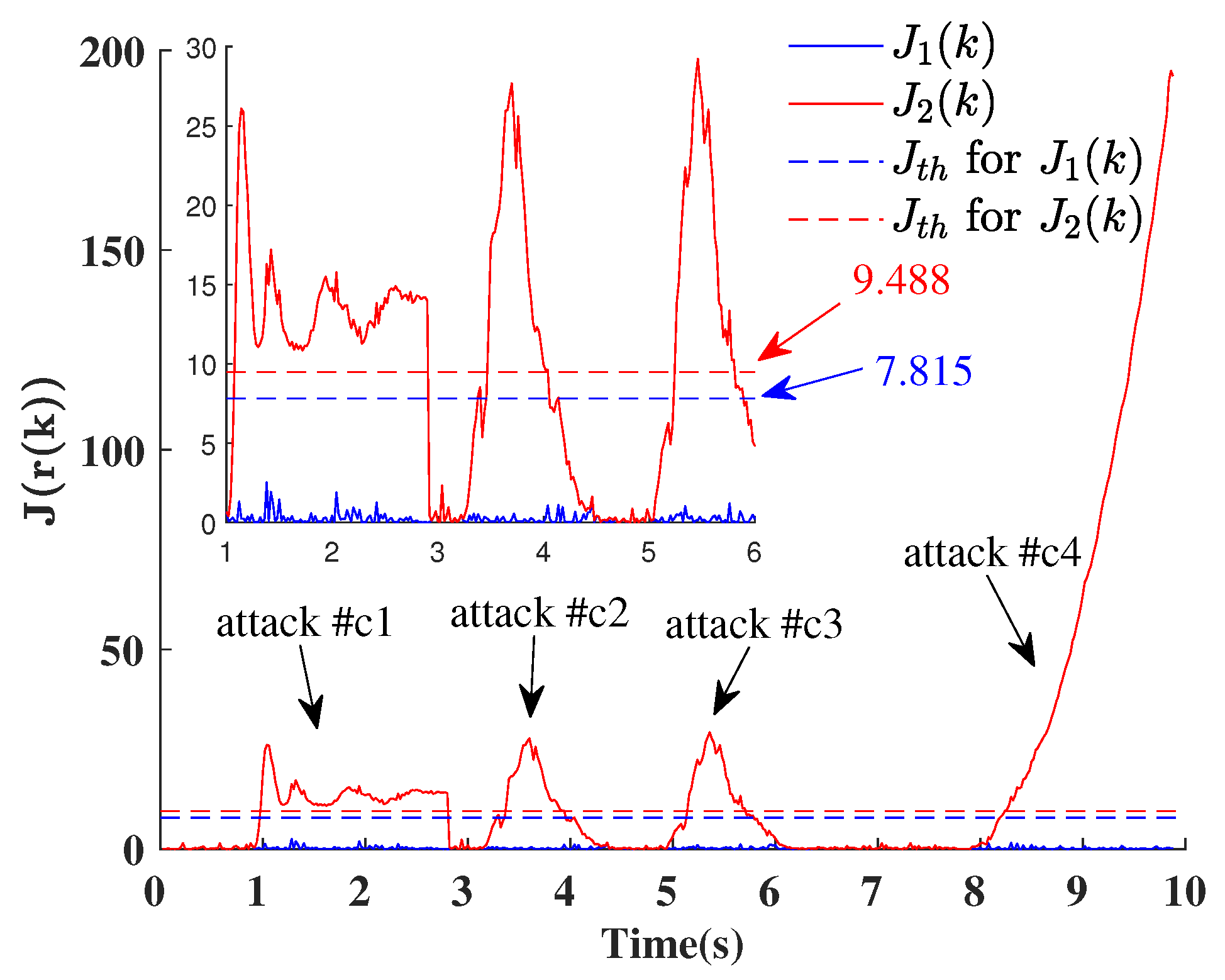
4.2. Analysis of the Detection Results
4.2.1. Detection Mechanism
4.2.2. Detection Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sztipanovits, J.; Koutsoukos, X.; Karsai, G.; Sastry, S.; Tomlin, C.; Damm, W.; Fränzle, M.; Rieger, J.; Pretschner, A.; Köster, F. Science of design for societal-scale cyber-physical systems: Challenges and opportunities. Cyber-Phys. Syst. 2019, 5, 145–172. [Google Scholar] [CrossRef]
- Biró, M.; Mashkoor, A.; Sametinger, J. Safe and Secure Cyber-Physical Systems. J. Softw. Evol. Process 2021, 33, e2340. [Google Scholar] [CrossRef]
- Wright, A. On Sapphire and Type-Safe Languages. Commun. ACM 2003, 46, 120. [Google Scholar] [CrossRef]
- Farwell, J.; Rohozinski, R. Stuxnet and the Future of Cyber War. Survival 2011, 53, 23–40. [Google Scholar] [CrossRef]
- Herrington, L.; Aldrich, R. The Future of Cyber-Resilience in an Age of Global Complexity. Politics 2013, 33, 299–310. [Google Scholar] [CrossRef]
- Adams, C. Learning the lessons of WannaCry. Comput. Fraud. Secur. 2018, 2018, 6–9. [Google Scholar] [CrossRef]
- Dibaji, S.M.; Pirani, M.; Flamholz, D.B.; Annaswamy, A.M.; Johansson, K.H.; Chakrabortty, A. A systems and control perspective of CPS security. Annu. Rev. Control 2019, 47, 394–411. [Google Scholar] [CrossRef] [Green Version]
- Giraldo, J.; Urbina, D.; Cardenas, A.; Valente, J.; Faisal, M.; Ruths, J.; Tippenhauer, N.O.; Sandberg, H.; Candell, R. A Survey of Physics-Based Attack Detection in Cyber-Physical Systems. ACM Comput. Surv. 2018, 51, 1–36. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Luo, X.; Zhang, M.; Guan, X. Distributed detection and isolation of false data injection attacks in smart grids via nonlinear unknown input observers. Int. J. Electr. Power Energy Syst. 2019, 110, 208–222. [Google Scholar] [CrossRef]
- Al-Dabbagh, A.W.; Li, Y.; Chen, T. An Intrusion Detection System for Cyber Attacks in Wireless Networked Control Systems. IEEE Trans. Circuits Syst. Part II Express Briefs 2018, 65, 1049–1053. [Google Scholar] [CrossRef]
- Alcaraz, C.; Bernieri, G.; Pascucci, F.; Lopez, J.; Setola, R. Covert Channels-Based Stealth Attacks in Industry 4.0. IEEE Syst. J. 2019, 13, 3980–3988. [Google Scholar] [CrossRef] [Green Version]
- Ding, S.X.; Yang, G.; Zhang, P.; Ding, E.L.; Jeinsch, T.; Weinhold, N.; Schultalbers, M. Feedback Control Structures, Embedded Residual Signals, and Feedback Control Schemes With an Integrated Residual Access. IEEE Trans. Control. Syst. Technol. 2010, 18, 352–367. [Google Scholar] [CrossRef]
- Mo, Y.; Weerakkody, S.; Sinopoli, B. Physical Authentication of Control Systems: Designing Watermarked Control Inputs to Detect Counterfeit Sensor Outputs. IEEE Control Syst. 2015, 35, 93–109. [Google Scholar]
- Yang, W.; Zheng, Z.; Chen, G.; Tang, Y.; Wang, X. Security Analysis of a Distributed Networked System Under Eavesdropping Attacks. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1254–1258. [Google Scholar] [CrossRef]
- Ding, S.X.; Li, L.; Zhao, D.; Louen, C.; Liu, T. Application of the unified control and detection framework to detecting stealthy integrity cyber-attacks on feedback control systems. Automatica 2022, 142, 110352. [Google Scholar] [CrossRef]
- Scherer, C.W. An efficient solution to multi-objective control problems with LMI objectives. Syst. Control Lett. 2000, 40, 43–57. [Google Scholar] [CrossRef]
- Teixeira, A.; Shames, I.; Sandberg, H.; Johansson, K.H. A secure control framework for resource-limited adversaries. Automatica 2015, 51, 135–148. [Google Scholar] [CrossRef] [Green Version]
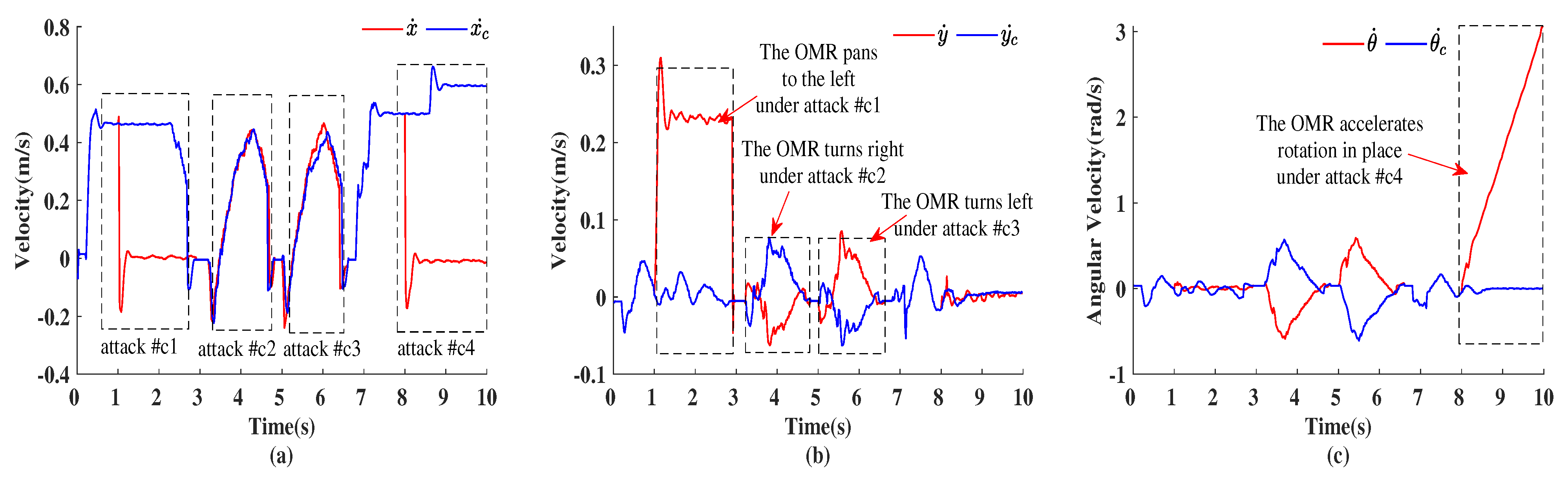
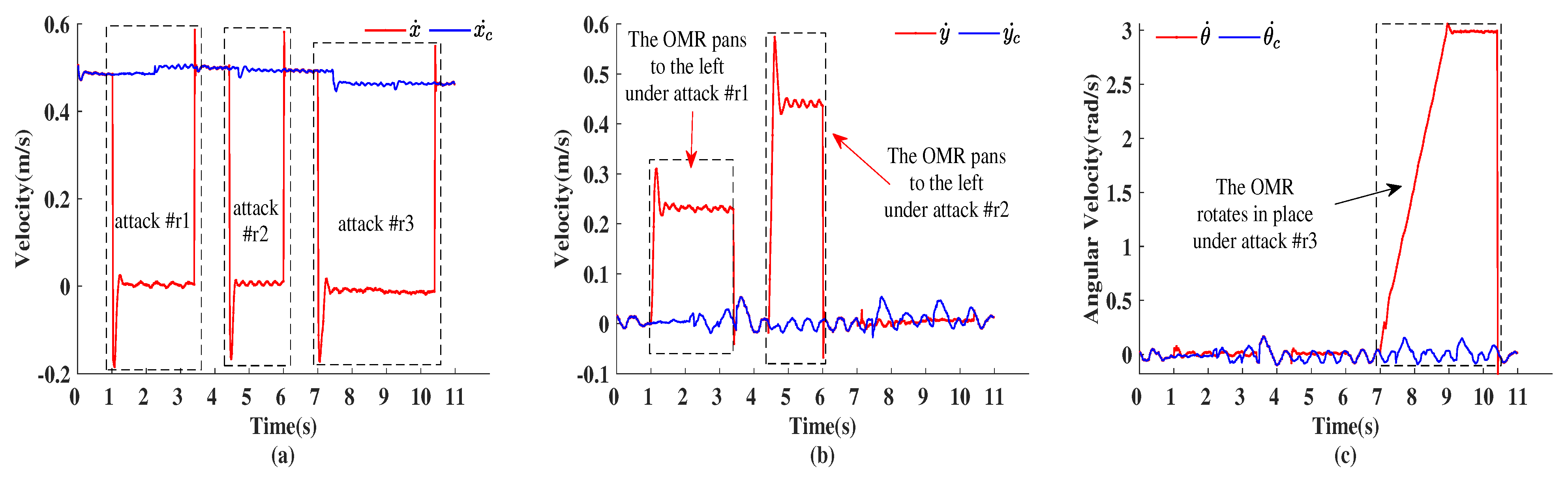
| The Expected Movements of the OMR | Descriptions of Movements | Time of Movement | Time of Attacks | Types of Attacks | Attack Effects |
|---|---|---|---|---|---|
| the first stage | straight ahead at 0.5 m/s | 0 s~2.9 s | 1.0 s~2.9 s | attack #c1 | pan to the left at 0.23 m/s |
| the second stage | turn left | 3.2 s~4.8 s | 3.2 s~4.8 s | attack #c2 | turn right under attacks |
| the third stage | turn right | 5.0 s~6.6 s | 5.0 s~6.6 s | attack #c3 | turn left under attacks |
| the fourth stage | straight ahead at different speeds | 6.8 s~10.0 s | 8.0 s~10.0 s | attack #c4 | accelerate rotation in place |
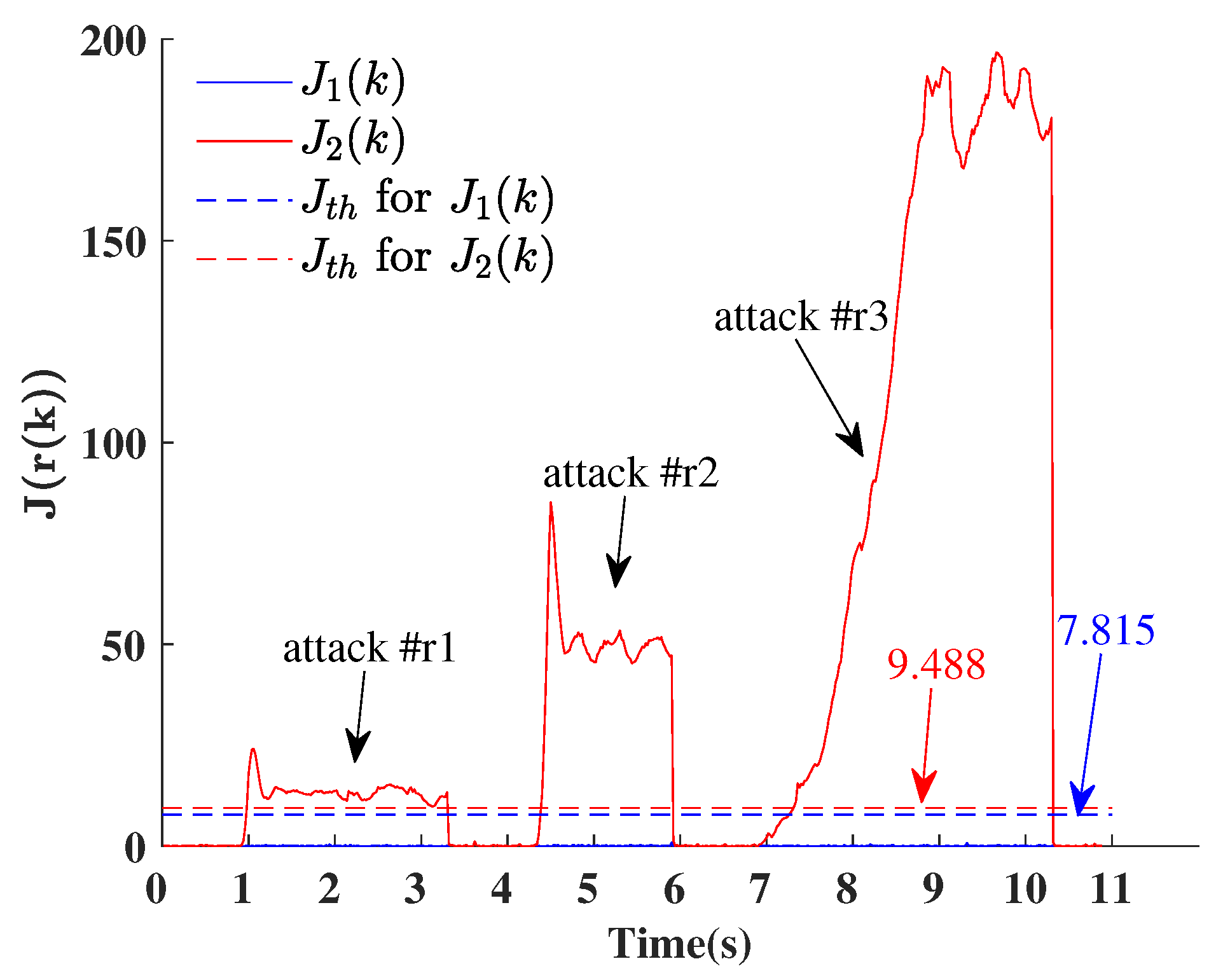
| The Expected Movement | Time of Attacks | Types of Attacks | Attack Effects |
|---|---|---|---|
| the OMR travels in a straight line at 0.5 m/s | 1.0 s~3.4 s | attack #r1 | pan to the left at 0.23 m/s |
| 4.4 s~6.0 s | attack #r2 | pan to the left at 0.44 m/s | |
| 7.0 s~10.4 s | attack #r3 | accelerate rotation in place |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Xin, L.; Long, Z. An Improved Residual-Based Detection Method for Stealthy Anomalies on Mobile Robots. Machines 2022, 10, 446. https://doi.org/10.3390/machines10060446
Yang B, Xin L, Long Z. An Improved Residual-Based Detection Method for Stealthy Anomalies on Mobile Robots. Machines. 2022; 10(6):446. https://doi.org/10.3390/machines10060446
Chicago/Turabian StyleYang, Biao, Liang Xin, and Zhiqiang Long. 2022. "An Improved Residual-Based Detection Method for Stealthy Anomalies on Mobile Robots" Machines 10, no. 6: 446. https://doi.org/10.3390/machines10060446
APA StyleYang, B., Xin, L., & Long, Z. (2022). An Improved Residual-Based Detection Method for Stealthy Anomalies on Mobile Robots. Machines, 10(6), 446. https://doi.org/10.3390/machines10060446







