X-Shaped Structure-Based Modeling and Control for a Stable Platform with a Series Elastic Actuator
Abstract
:1. Introduction
- 1
- The X-shaped structure is introduced to generate the dynamic reference trajectory;
- 2
- A backstepping controller is proposed for the stable platform;
- 3
- Comparative simulations are carried out to verify the effectiveness of the proposed method.
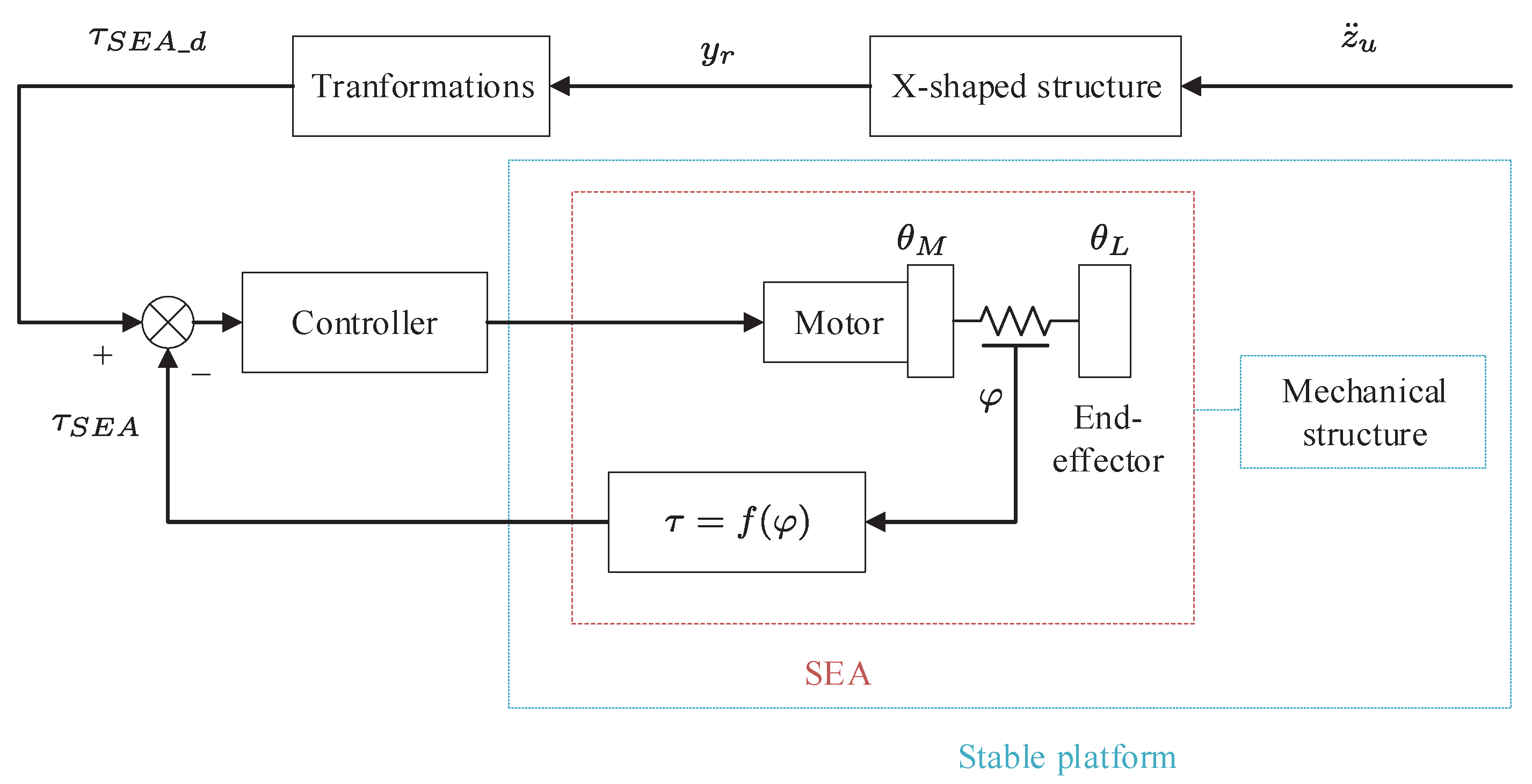
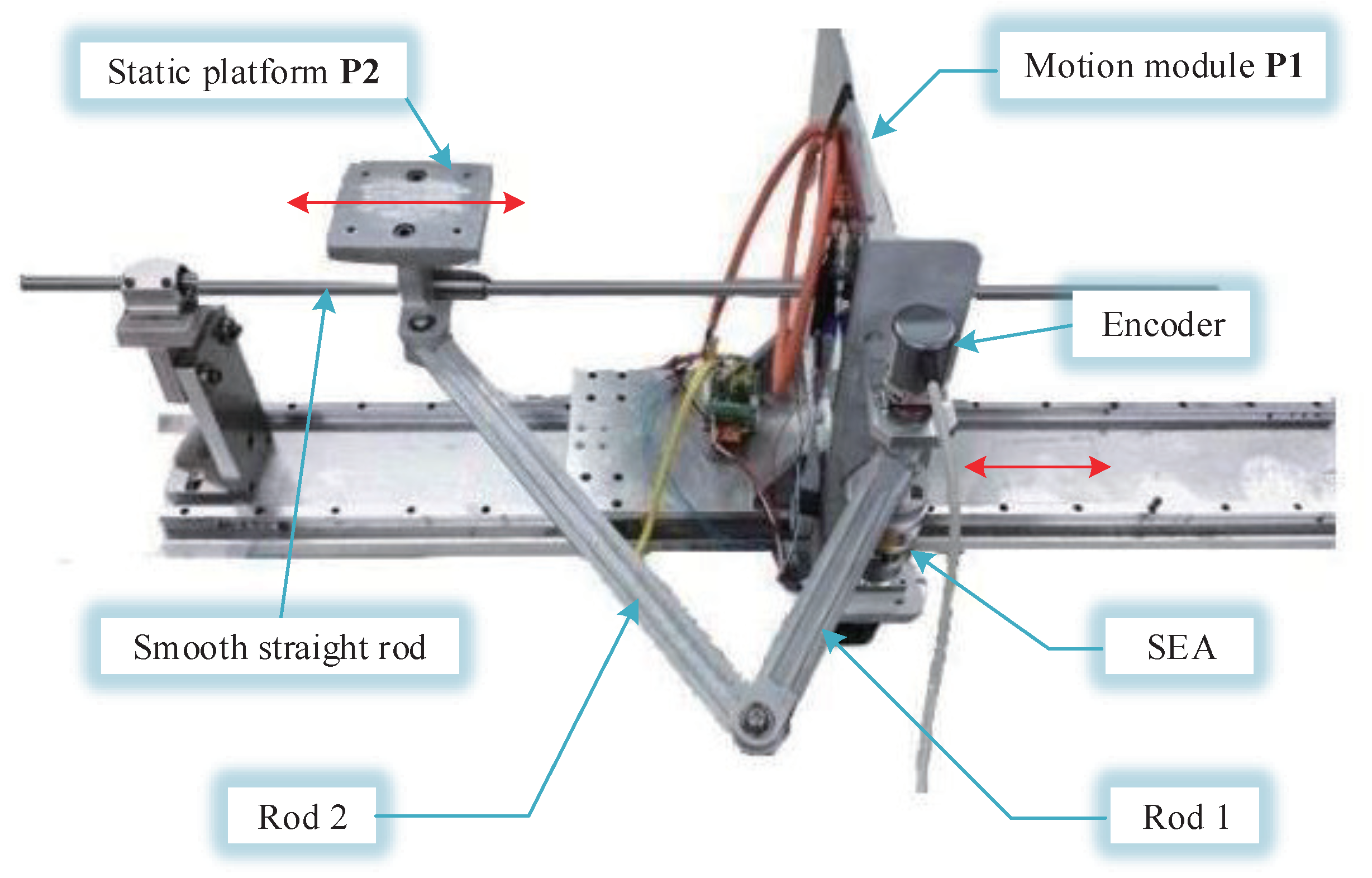
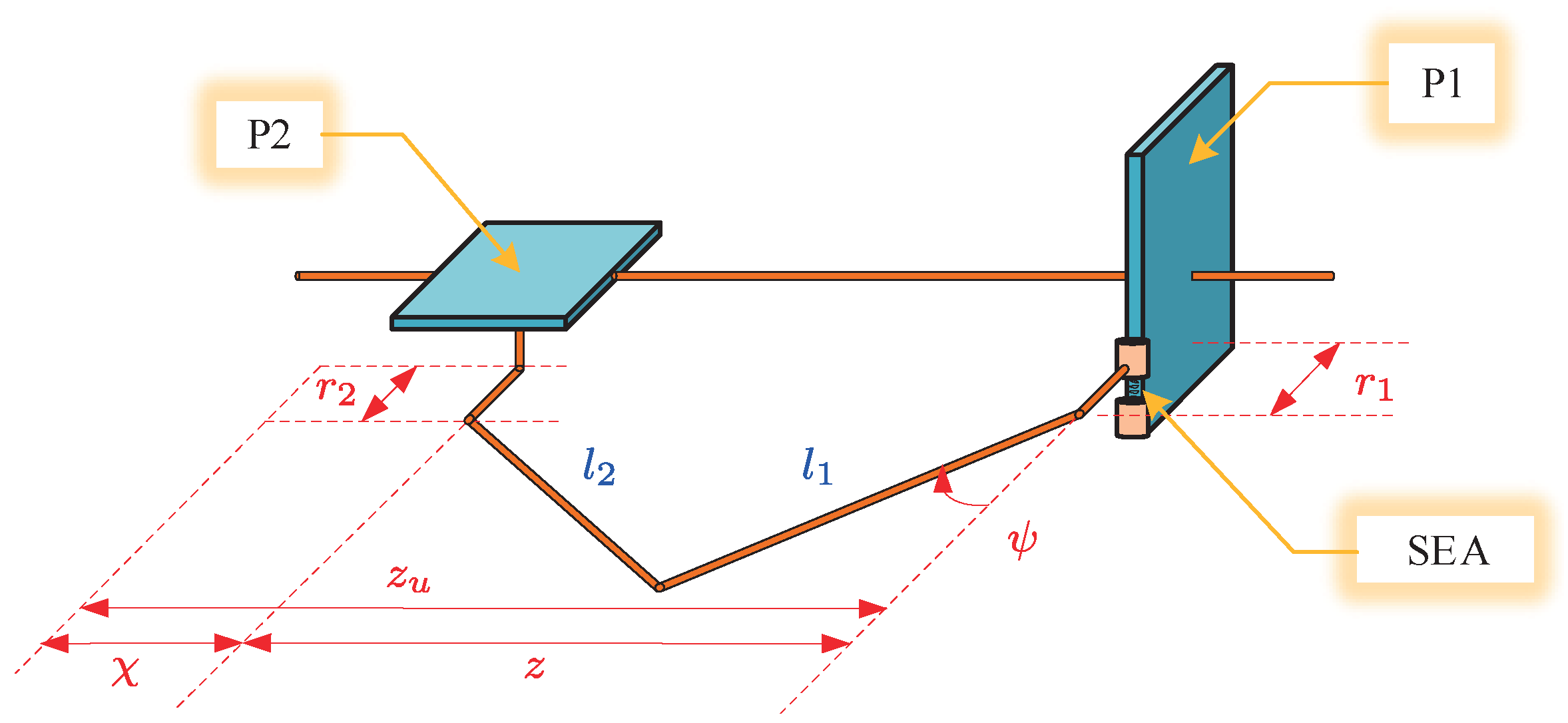
2. X-Shaped Structure-Based Modeling for the Stable Platform with the SEA
2.1. Modeling of the Stable Platform
2.2. Modeling of the SEA
2.3. Dynamic Trajectory Based on the X-Shaped Structure
3. Controller Design
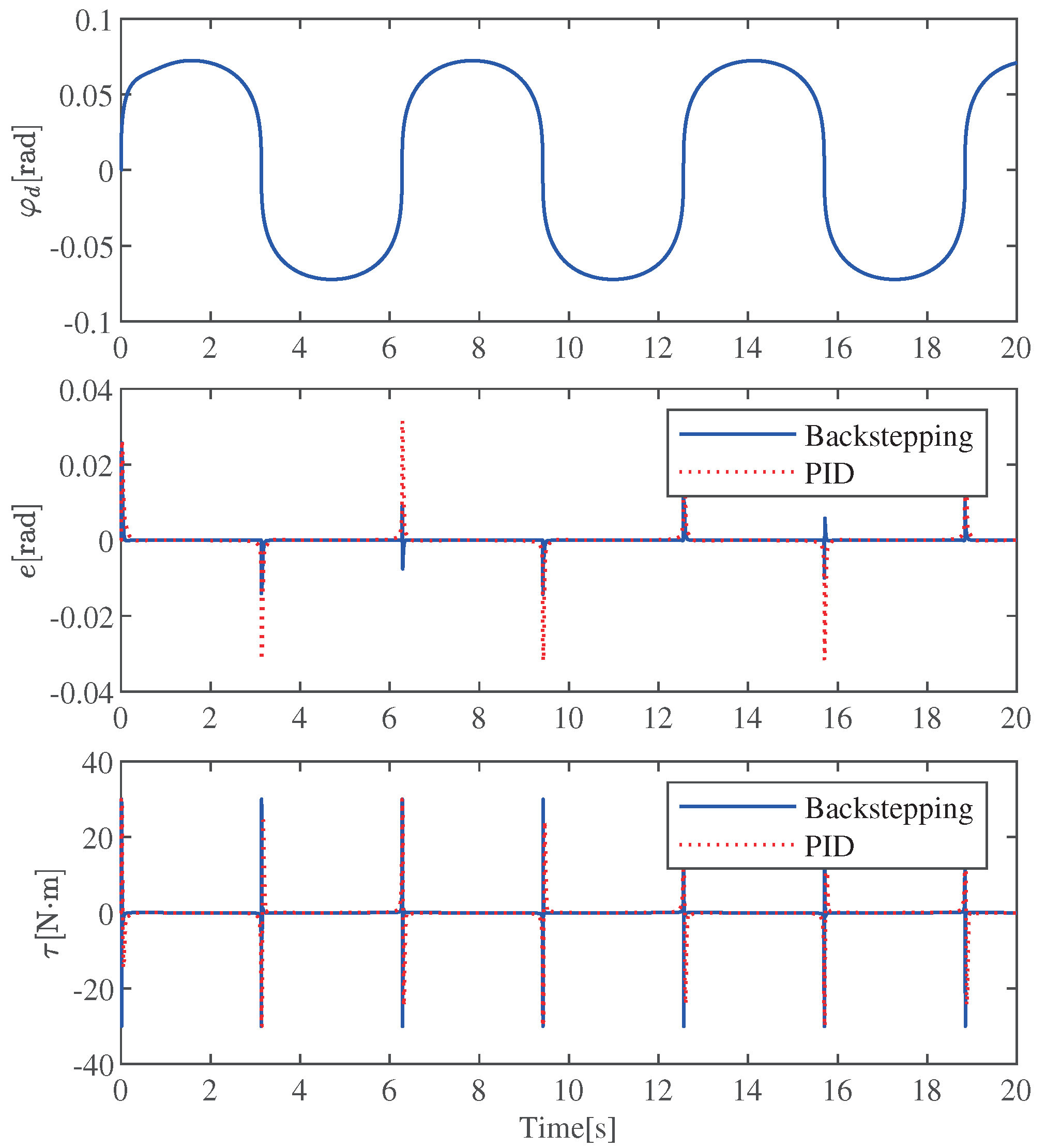
4. Simulation Results
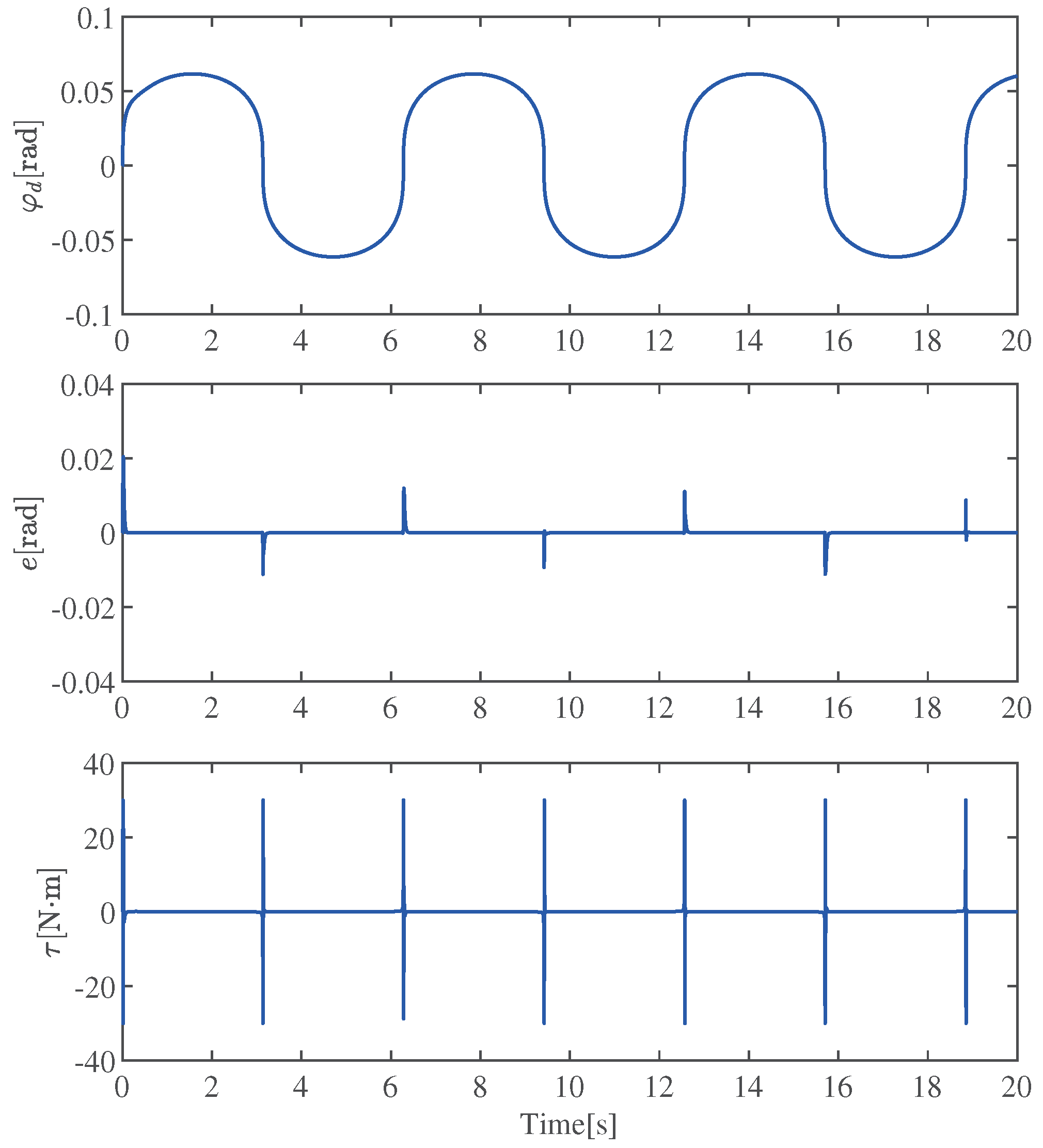
4.1. Simulation 1: Effectiveness Verification
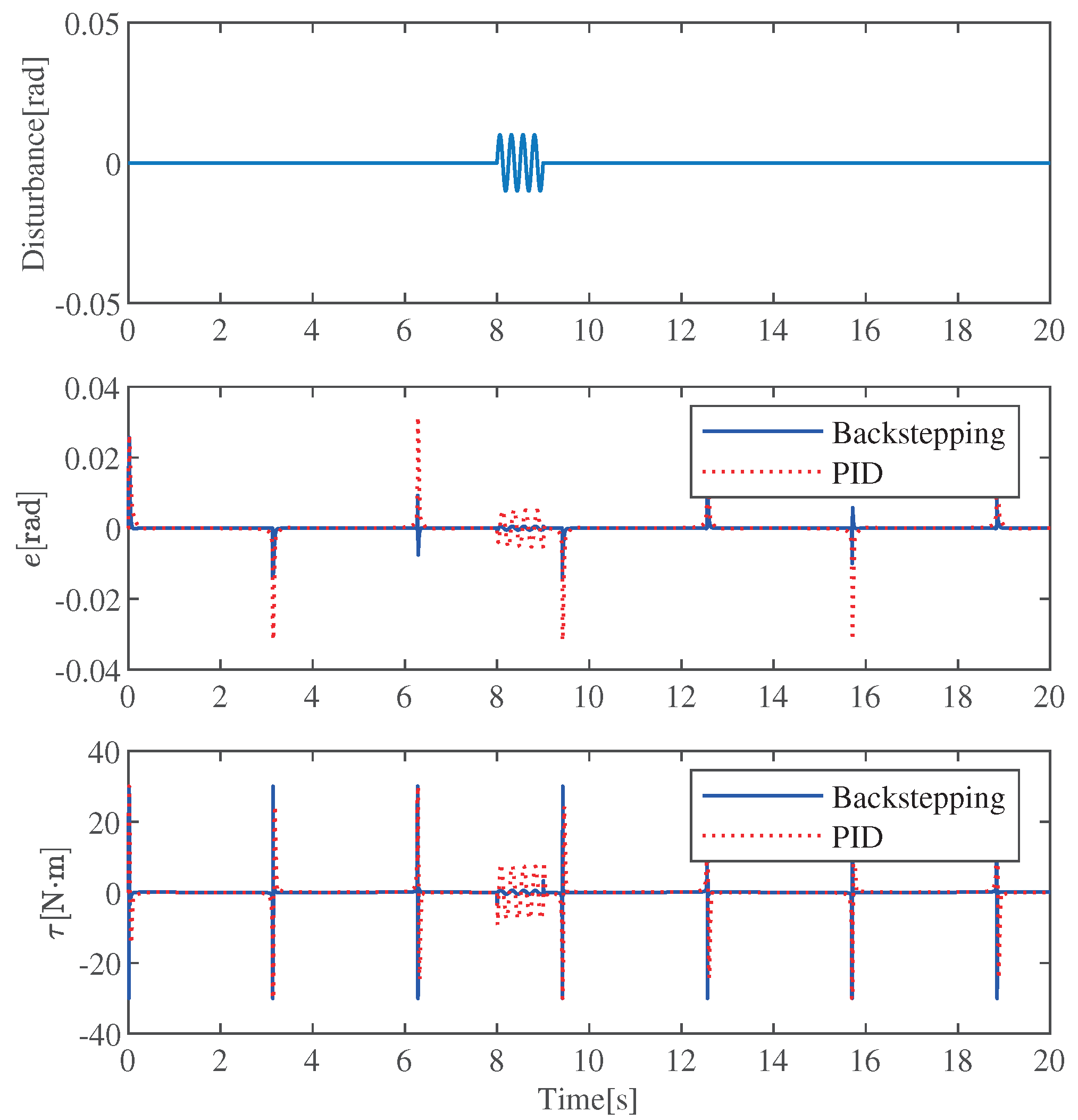
4.2. Simulation 2: With Disturbances
4.3. Simulation 3: With Parameter Uncertainty
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SEA | Series elastic actuator |
| PID | Proportional integral derivative |
References
- Ouyang, H.; Xu, X.; Zhang, G. Energy-shaping-based nonlinear controller design for rotary cranes with double-pendulum effect considering actuator saturation. Autom. Constr. 2020, 111, 103054. [Google Scholar] [CrossRef]
- Sun, W.; Su, S.F.; Xia, J.; Nguyen, V.T. Adaptive fuzzy tracking control of flexible-joint robots with full-state constraints. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 2201–2209. [Google Scholar] [CrossRef]
- Yang, T.; Sun, N.; Fang, Y. Neuroadaptive control for complicated underactuated systems with simultaneous output and velocity constraints exerted on both actuated and unactuated states. IEEE Trans. Neural Netw. Learn. Syst. 2021; to be published. [Google Scholar] [CrossRef]
- Liang, D.; Sun, N.; Wu, Y.; Chen, Y.; Fang, Y.; Liu, L. Energy-based motion control for pneumatic artificial muscle actuated robots with experiments. IEEE Trans. Ind. Electron. 2022, 69, 7295–7306. [Google Scholar] [CrossRef]
- Hilkert, J. Inertially stabilized platform technology concepts and principles. IEEE Control Syst. Mag. 2008, 28, 26–46. [Google Scholar]
- Pan, H.; Jing, X.; Sun, W.; Gao, H. A bioinspired dynamics-based adaptive tracking control for nonlinear suspension systems. IEEE Trans. Control Syst. Technol. 2017, 26, 903–914. [Google Scholar] [CrossRef]
- Iqbal, S.; Bhatti, A.I.; Akhtar, M.; Ullah, S. Design and robustness evaluation of an H∞ loop shaping controller for a 2DOF stabilized platform. In Proceedings of the 2007 European Control Conference (ECC), Kos, Greece, 2–5 July 2007; pp. 2098–2104. [Google Scholar]
- Patel, B.; Warren, M.; Schoellig, A. Point me in the right direction: Improving visual localization on UAVs with active gimballed camera pointing. In Proceedings of the 2019 16th Conference on Computer and Robot Vision (CRV), Kingston, QC, Canada, 29–31 May 2019; pp. 105–112. [Google Scholar]
- Bolívar Nieto, E.A.; Rezazadeh, S.; Gregg, R.D. Minimizing energy consumption and peak power of series elastic actuators: A convex optimization framework for elastic element design. IEEE/ASME Trans. Mechatron. 2019, 24, 1334–1345. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oh, S.; Kong, K. High-precision robust force control of a series elastic actuator. IEEE/ASME Trans. Mechatron. 2017, 22, 71–80. [Google Scholar] [CrossRef]
- Sun, Y.; Tang, P.; Zheng, J.; Dong, D.; Chen, X.; Bai, L.; Ge, W. Optimal design of a nonlinear series elastic actuator for the prosthetic knee joint based on the conjugate cylindrical cam. IEEE Access 2019, 7, 140846–140859. [Google Scholar] [CrossRef]
- Bolivar, E.; Allen, D.; Ellson, G.; Cossio, J.; Voit, W.; Gregg, R. Towards a series elastic actuator with electrically modulated stiffness for powered ankle-foot orthoses. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–25 August 2016; pp. 1086–1093. [Google Scholar]
- Hurst, J.W.; Rizzi, A.A. Series compliance for an efficient running gait. IEEE Robot. Autom. Mag. 2008, 15, 42–51. [Google Scholar] [CrossRef]
- Jafari, A.; Tsagarakis, N.G.; Caldwell, D.G. Exploiting natural dynamics for energy minimization using an Actuator with Adjustable Stiffness (AwAS). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4632–4637. [Google Scholar]
- Jarrett, C.; McDaid, A. A model inversion procedure for control of nonlinear series elastic actuators. In Proceedings of the 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), Toronto, ON, Canada, 24–28 June 2019; pp. 453–458. [Google Scholar]
- Junior, A.G.L.; de Andrade, R.M.; Filho, A.B. Series elastic actuator: Design, analysis and comparison. In Recent Advances in Robotic Systems; IntechOpen: London, UK, 2016. [Google Scholar]
- Li, J.; Jing, X.; Li, Z.; Huang, X. Fuzzy adaptive control for nonlinear suspension systems based on a bioinspired reference model with deliberately designed nonlinear damping. IEEE Trans. Ind. Electron. 2018, 66, 8713–8723. [Google Scholar] [CrossRef]
- Zhang, M.; Jing, X.; Wang, G. Bioinspired nonlinear dynamics-based adaptive neural network control for vehicle suspension systems with uncertain/unknown dynamics and input delay. IEEE Trans. Ind. Electron. 2020, 68, 12646–12656. [Google Scholar] [CrossRef]
- Zhang, M.; Jing, X. A bioinspired dynamics-based adaptive fuzzy SMC method for half-car active suspension systems with input dead zones and saturations. IEEE Trans. Cybern. 2020, 51, 1743–1755. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Jing, X. Energy-saving robust saturated control for active suspension systems via employing beneficial nonlinearity and disturbance. IEEE Trans. Cybern. 2021; to be published. [Google Scholar] [CrossRef]
- Li, M.; Sun, L.; Zhao, W.; Liu, J. Robust control approach for novel stabilized platform with series elastic actuator. In Proceedings of the 2019 IEEE International Conference on Advanced Robotics and its Social Impacts (ARSO), Beijing, China, 31 October–2 November 2019; pp. 141–146. [Google Scholar]
- Wang, M.; Sun, L.; Yin, W.; Dong, S.; Liu, J. A novel sliding mode control for series elastic actuator torque tracking with an extended disturbance observer. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 2407–2412. [Google Scholar]
- Gong, X.R.; Chen, X.W.; Yin, W.; Sun, W.C.; Sun, L. Accurate estimation of the spring stiffness in series elastic actuators. In Proceedings of the 2017 IEEE International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Honolulu, HI, USA, 31 July–4 August 2017; pp. 382–387. [Google Scholar]
- Wang, M.; Sun, L.; Yin, W.; Dong, S.; Liu, J. Continuous robust control for series elastic actuator with unknown payload parameters and external disturbances. IEEE/CAA J. Autom. Sin. 2017, 4, 620–627. [Google Scholar] [CrossRef]
- Wang, M.; Sun, L.; Yin, W.; Dong, S.; Liu, J. Continuous finite-time control approach for series elastic actuator. In Proceedings of the 2016 IEEE Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 843–848. [Google Scholar]



| Parameters | Pysical Meanings | Values |
|---|---|---|
| length of Rod 1 | 0.2 m | |
| length of Rod 2 | 0.3 m | |
| distance from P1 to the SEA | 0.15 m | |
| distance from P2 to Rod 2 | 0.05 m | |
| mass of Rod 1 | 0.15 kg | |
| mass of Rod 2 | 0.14 kg | |
| mass of the load | 10 kg |
| Parameters | Values |
|---|---|
| 13,600 N/m | |
| c | 0.018 m |
| R | 0.020 m |
| r | 0.005 m |
| 0.082 | |
| 0.75 |
| Parameters | Values |
|---|---|
| 500 N/m | |
| 250 N/m | |
| 0.1 m | |
| 0.2 m | |
| 0.167 rad | |
| 1 Ns/m | |
| 0.155 Ns/m |
| Controllers | (s) | (rad) | (rad) |
|---|---|---|---|
| Backstepping | 0.020 | 0.026 | 0.014 |
| PID | 0.135 | 0.032 | 0.032 |
| Improvement | 85.19% | 37.50% | 56.25% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, A.; Wu, Q.; Yang, T.; Sun, L.; Sun, N. X-Shaped Structure-Based Modeling and Control for a Stable Platform with a Series Elastic Actuator. Machines 2022, 10, 430. https://doi.org/10.3390/machines10060430
Teng A, Wu Q, Yang T, Sun L, Sun N. X-Shaped Structure-Based Modeling and Control for a Stable Platform with a Series Elastic Actuator. Machines. 2022; 10(6):430. https://doi.org/10.3390/machines10060430
Chicago/Turabian StyleTeng, Ai, Qingxiang Wu, Tong Yang, Lei Sun, and Ning Sun. 2022. "X-Shaped Structure-Based Modeling and Control for a Stable Platform with a Series Elastic Actuator" Machines 10, no. 6: 430. https://doi.org/10.3390/machines10060430
APA StyleTeng, A., Wu, Q., Yang, T., Sun, L., & Sun, N. (2022). X-Shaped Structure-Based Modeling and Control for a Stable Platform with a Series Elastic Actuator. Machines, 10(6), 430. https://doi.org/10.3390/machines10060430








