Temperature-Sensitive Point Selection and Thermal Error Model Adaptive Update Method of CNC Machine Tools
Abstract
:1. Introduction
2. Typical Thermal Error Modeling Methods
2.1. TSP Selection Method
- (1)
- Build a fuzzy similarity matrix , where is the correlation coefficient of and .
- (2)
- Convert similarity matrix to equivalent matrix. Perform multiple square fuzzy operations on fuzzy similarity matrices as follows:
- (3)
- Set as the threshold. If and are in the same group, then (,) > . The number of groups and the number of TSPs are determined .
2.2. Thermal Error Modeling Algorithms
3. TSP Selection and Thermal Error Model Update Method
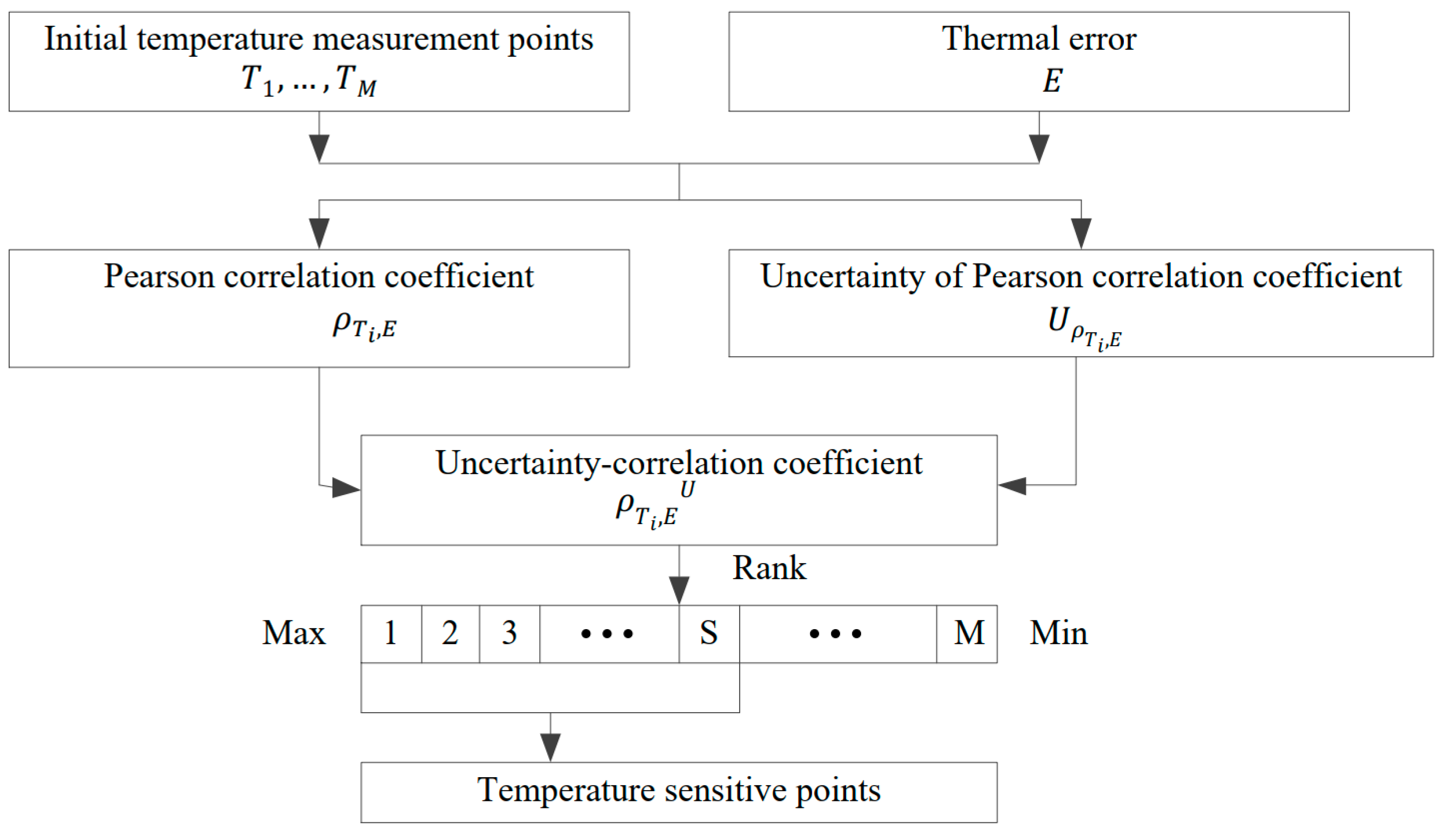
3.1. Stability TSP Selection Method
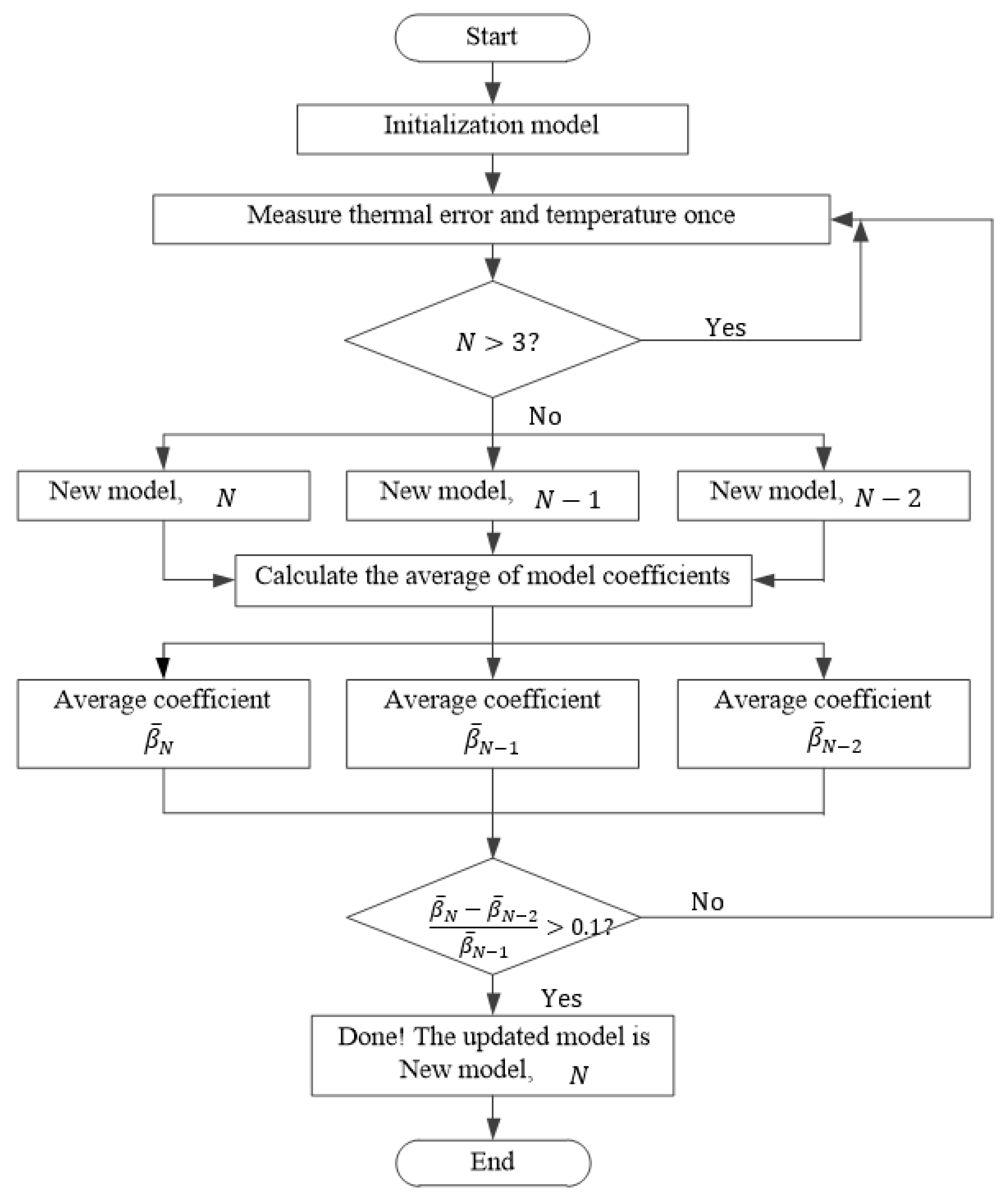
3.2. Update Method of Thermal Error Model Based on Update Regression
4. Experimental Verification
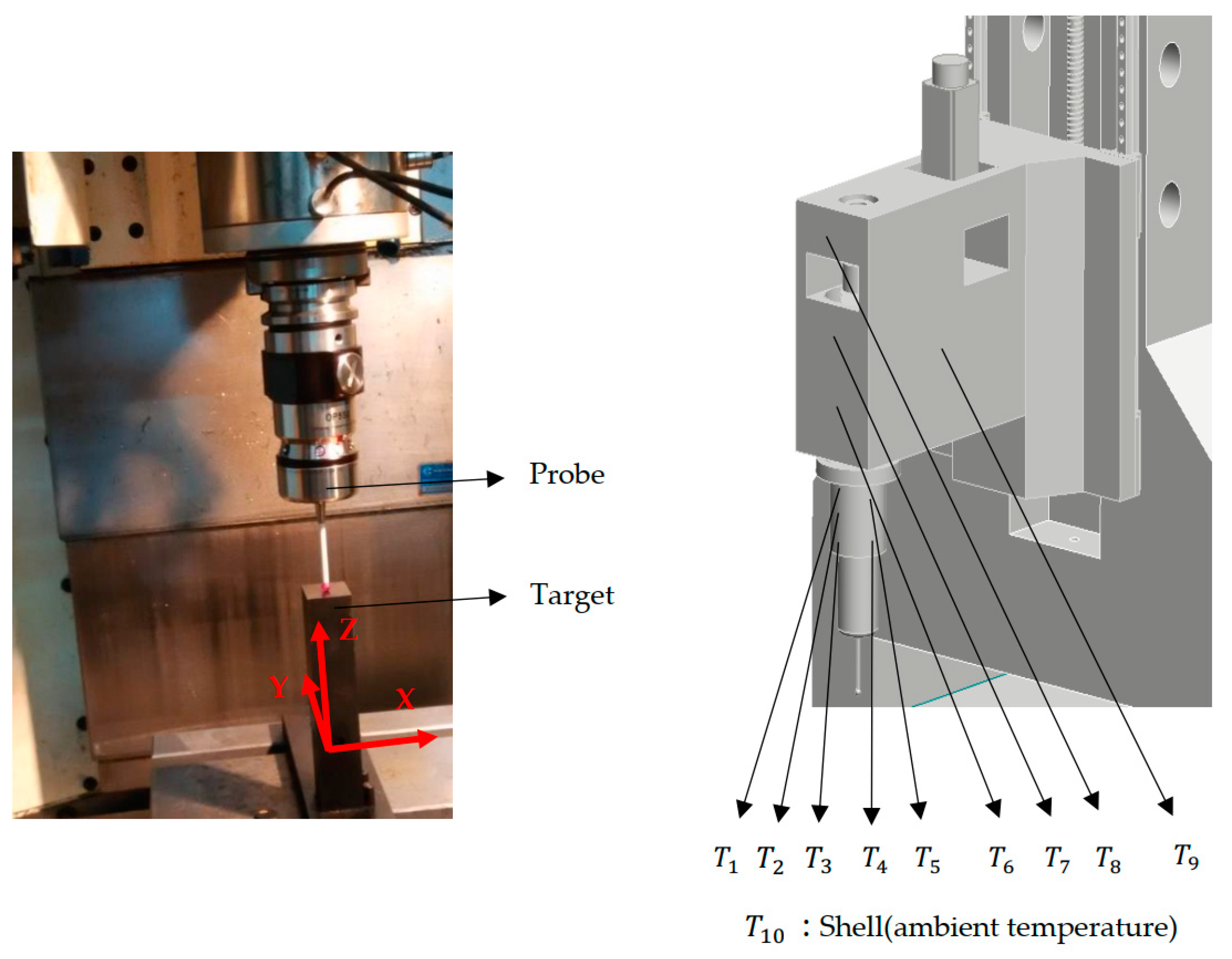
4.1. Experimental Plan

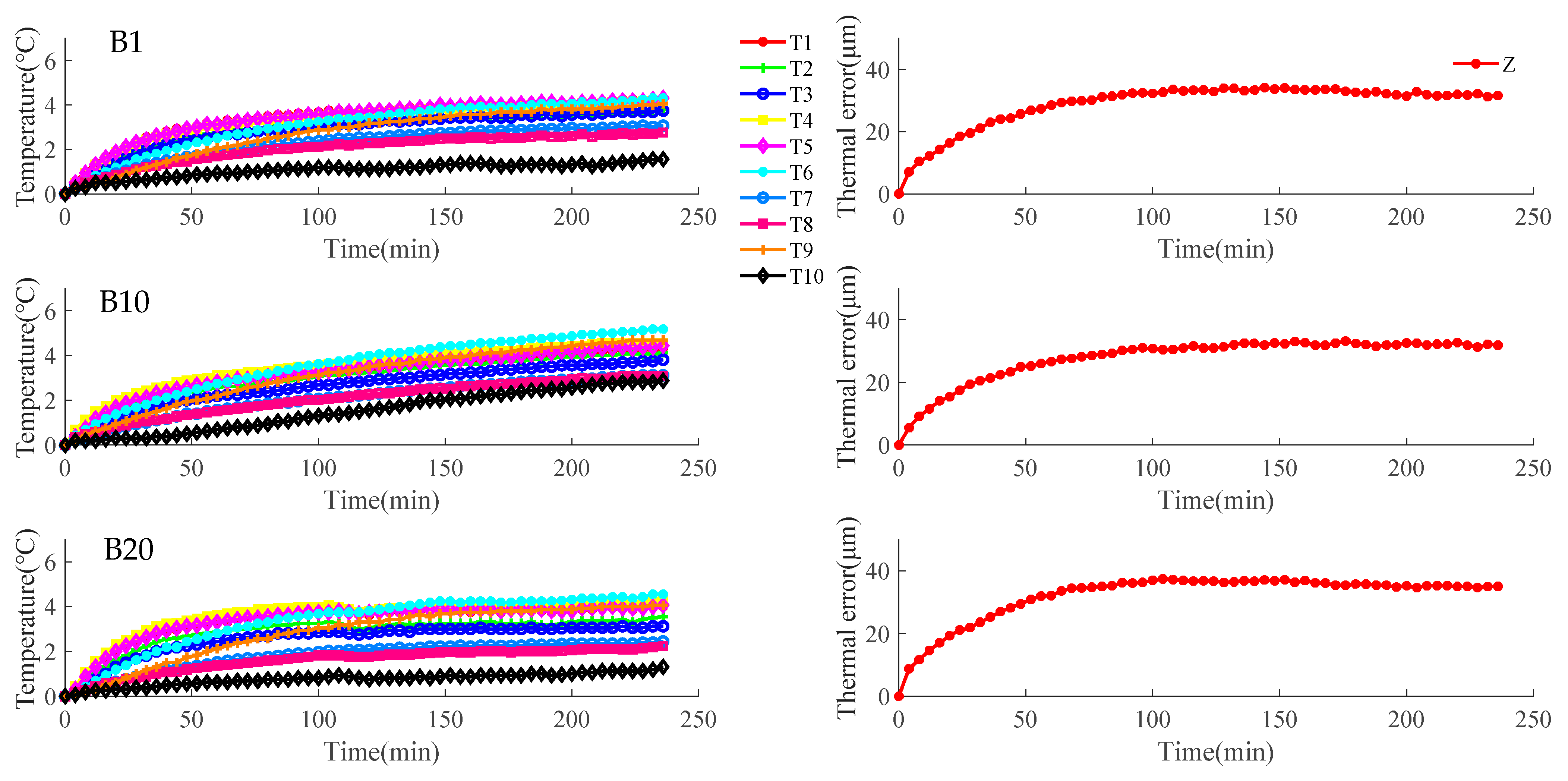
4.2. Experimental Result
4.2.1. Comparison Results of TSP Selection Methods
- (1)
- Fuzzy clustering and correlation coefficient. First, the initial temperature measurement points are divided into two groups. Then, for each group, the point with the highest correlation is selected as a TSP.
- (2)
- Stability TSP selection method. The two points with the highest uncertainty-correlation coefficients are selected as TSPs.
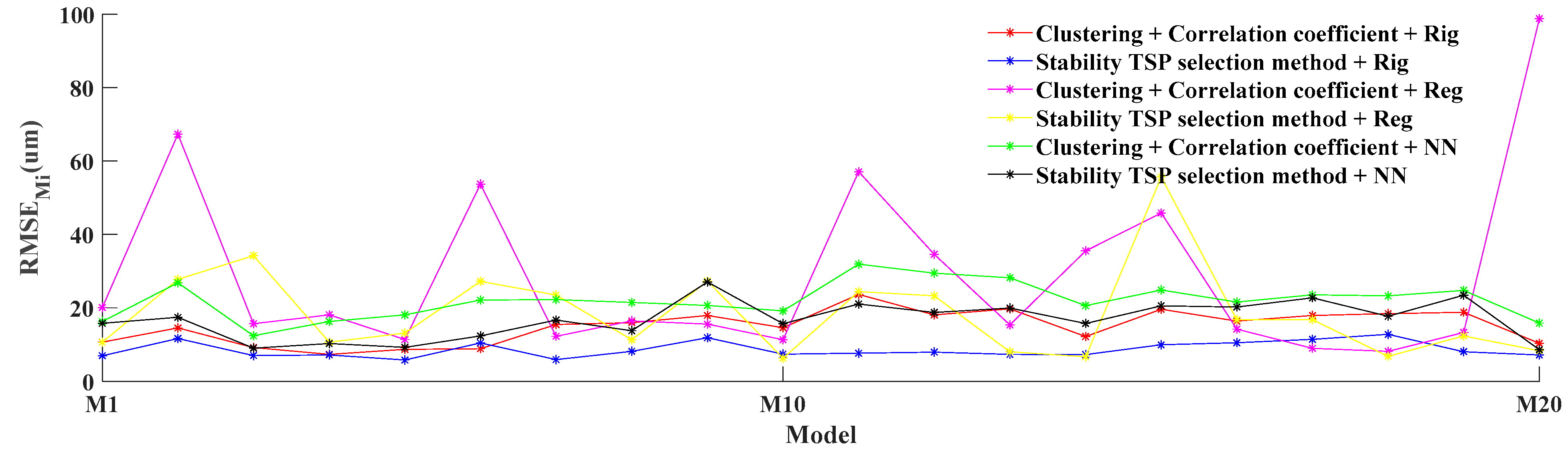
4.2.2. Comparison Results of Modeling Accuracy of TSP Selection Methods
- (1)
- Clustering + Correlation coefficient + Rig: Fuzzy clustering and correlation coefficient for TSP selection, and ridge regression for modeling.
- (2)
- Stability TSP selection method + Rig: Stability TSP selection method for TSP selection, and ridge regression for modeling.
- (3)
- Clustering + Correlation coefficient + Reg: Fuzzy clustering and correlation coefficient for TSP selection, and ordinary multiple regression for modeling.
- (4)
- Stability TSP selection method + Reg: Stability TSP selection method for TSP selection, and the ordinary multiple regression for modeling.
- (5)
- Clustering + Correlation coefficient + NN: Fuzzy clustering and correlation coefficient for TSP selection, and neural network for modeling.
- (6)
- Stability TSP selection method + NN: Stability TSP selection method for TSP selection, and neural network for modeling.
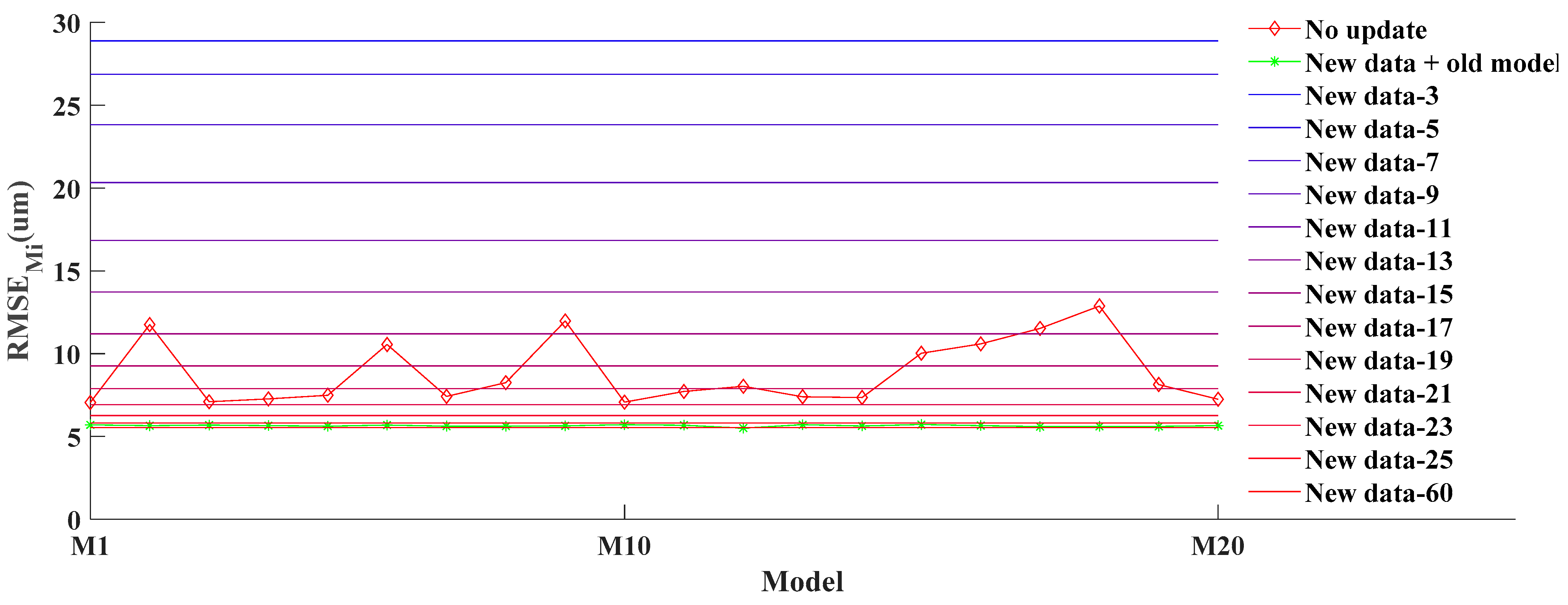
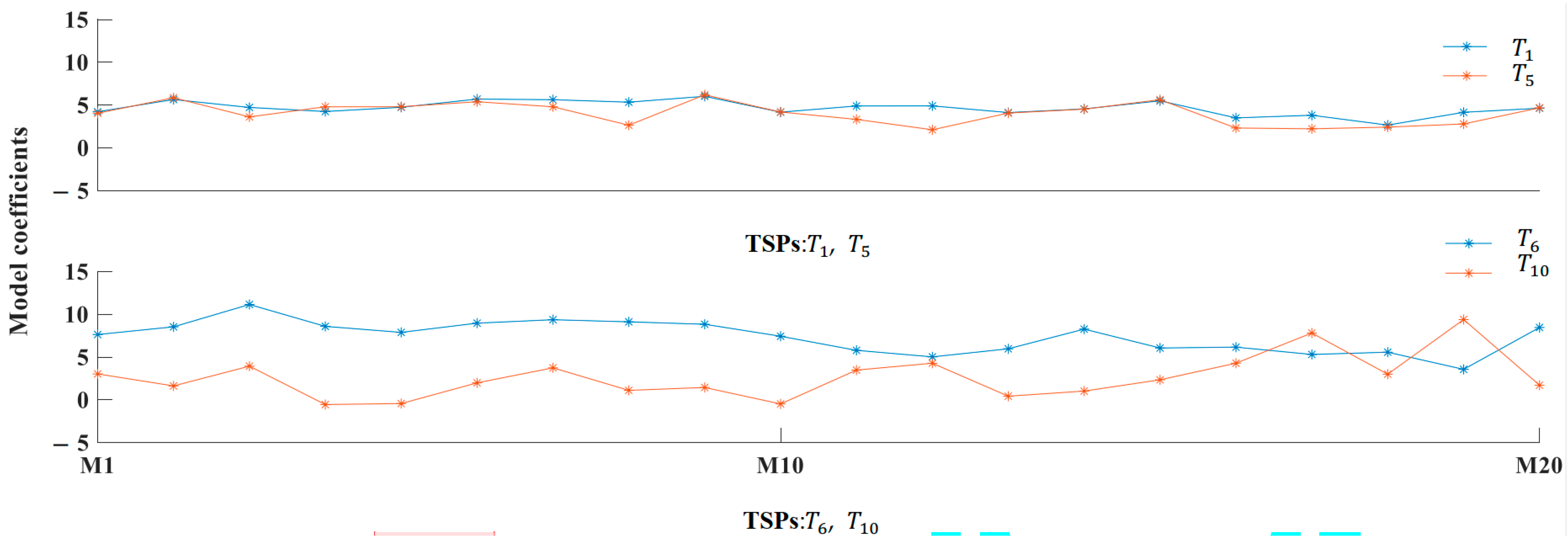
4.2.3. Comparison Results of the Adaptive Model Update Algorithm
- (1)
- No update model (“No update” in Figure 8): Models M1–M20 are established by B1–B20, respectively. The modeling method is “Stability TSP selection method + Rig”. No updates are made when predicting the new data.
- (2)
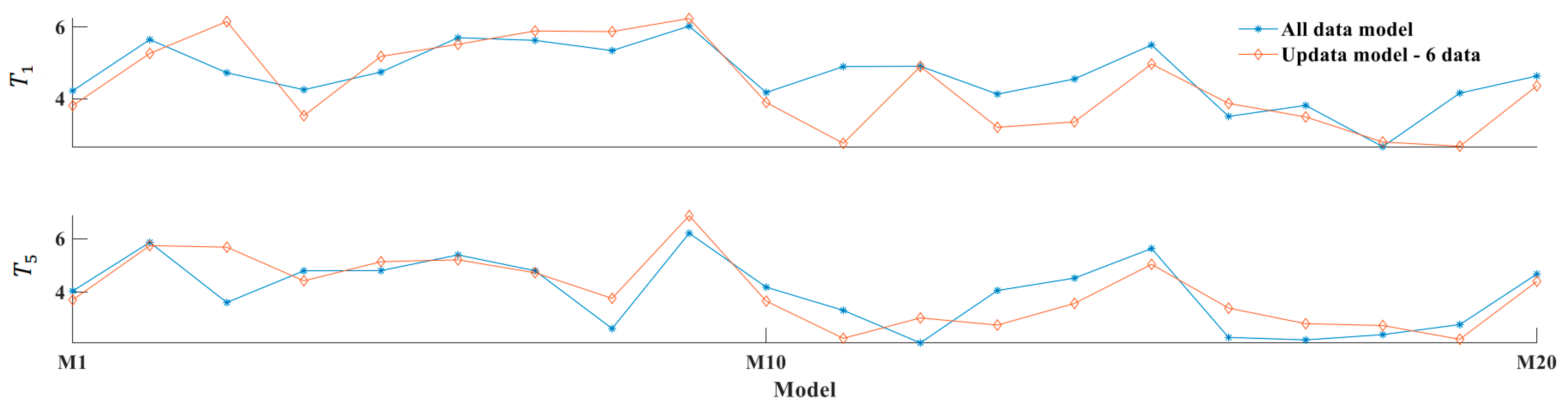
- Update model by new data + old model (“New data + old model” in Figure 8): When predicting the data Bj, the old model and new data are both used to build the model. The old model refers to M1–M20 of the “No update” model. A segment of data Bj from beginning is used for the updating model as new data. The model updating algorithm is update regression. The Mi of means old model.
- (3)
- Update model only by new data (“New data-” in Figure 8, where is the length of the new data): When predicting the data Bj, a segment of data Bj from the beginning is used to build the model as new data. The lengths of the new data are 3, 5, 7, 9, 11, ..., 25, 60, respectively. The modeling method is “Stability TSP selection method + Rig”. Since no old model is involved in prediction, .
4.3. Validation of the Proposed Model
4.3.1. Model Precision
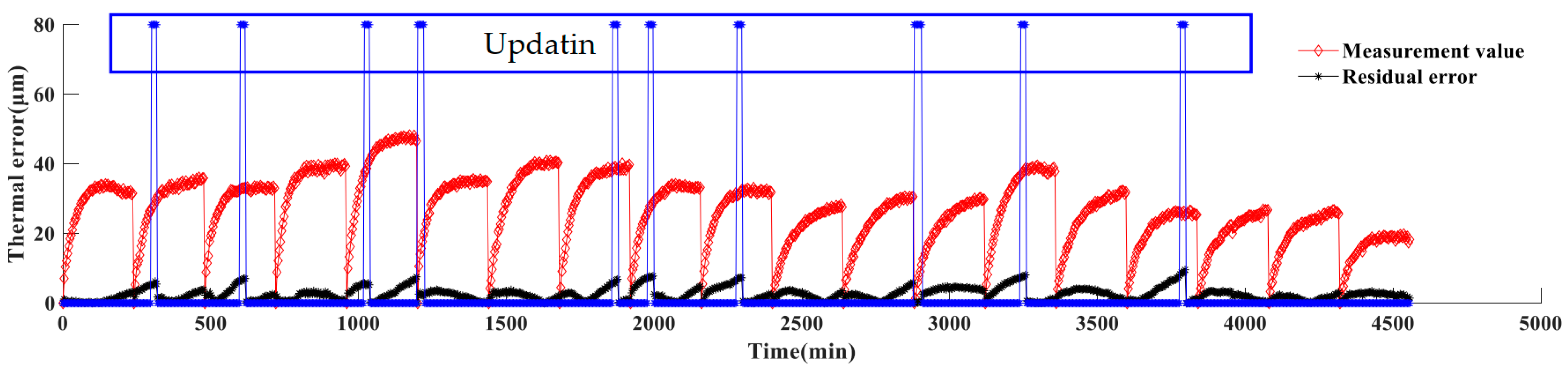
4.3.2. Computation Time of Model Update
5. Discussion
5.1. Discussion of Comparison Results of TSP Selection Methods
- (1)
- For each temperature measurement point, the mean correlation of all batch data was calculated by two correlation calculation methods shown in the following equation. This process indicates the long-term correlation. The results are shown in Figure 11.
- (2)
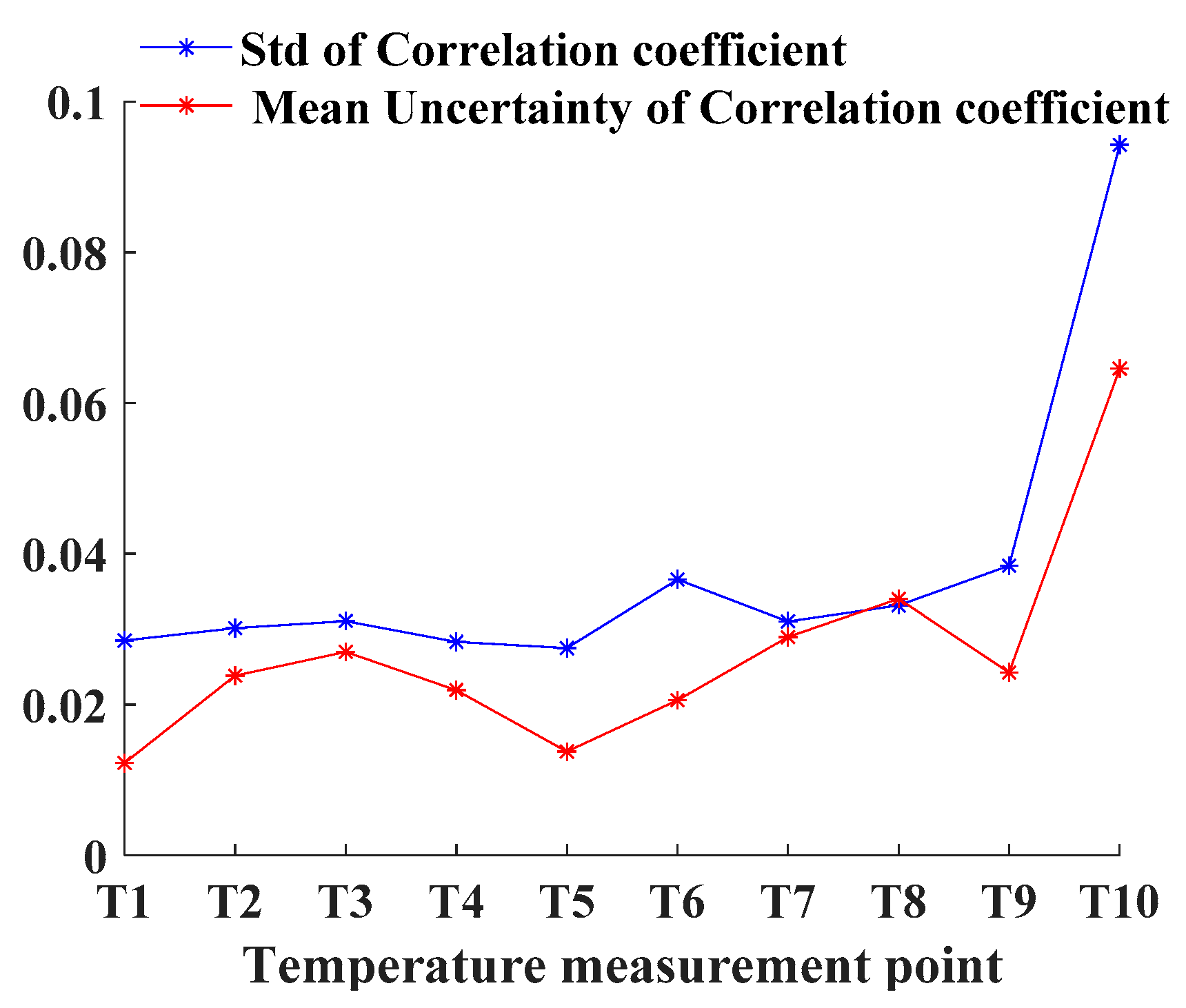
- For each temperature measurement point, the standard deviation () and mean uncertainty of the correlation coefficient of all batch data were calculated. The specific calculation methods are expressed by the following equation. The results are depicted in Figure 12. This process indicates the stability of the correlation.
- (3)
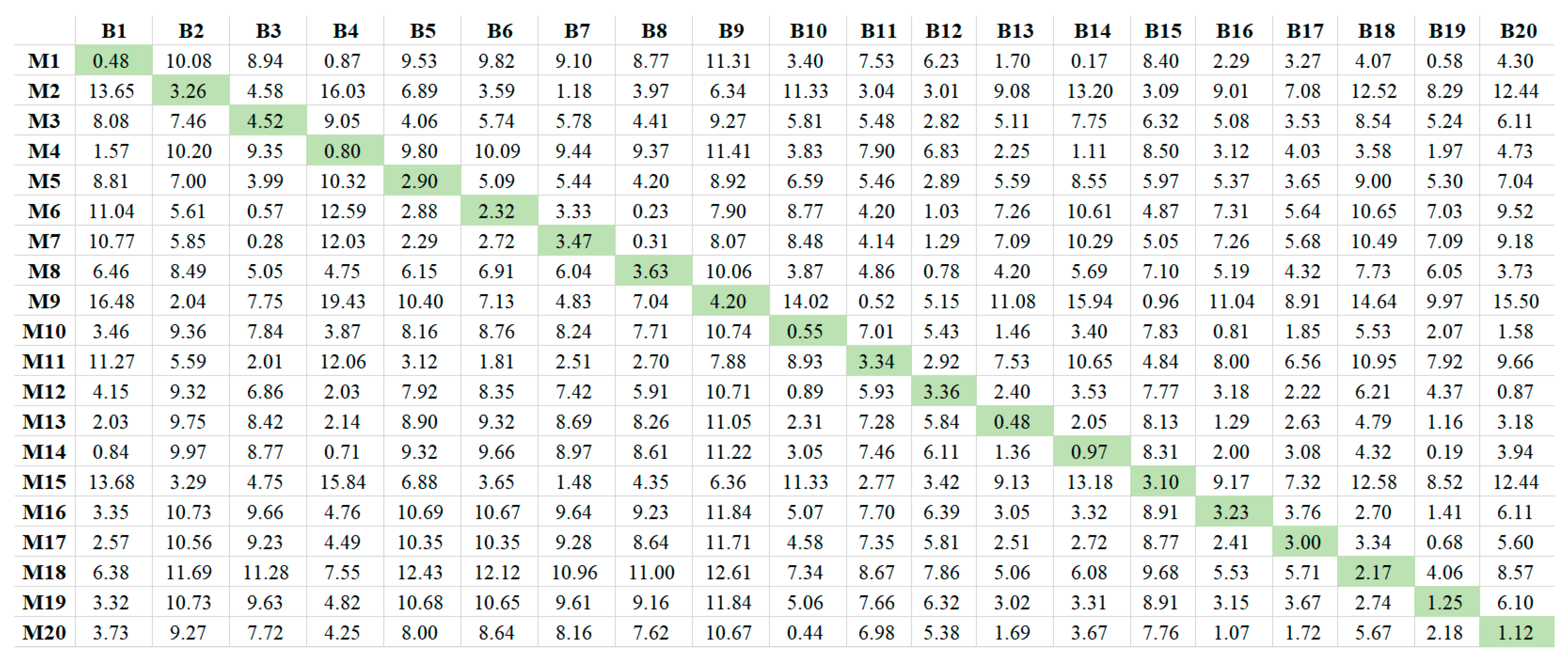
- The fuzzy clustering results of T1–T10 in B1–B20, are listed in Table 4.
- (1)
- The low collinearity and high correlation of TSPs are conflicting, resulting in a low correlation for one of the TSPs selected by the “Fuzzy clustering and correlation coefficient”. There is no grouping process in the “Stability TSP selection method”, so high correlation TSPs can be selected. According to Figure 11, it can be seen that the correlation of – is significantly higher, and the correlation of is lower. According to Table 4, in most cases, the “Fuzzy clustering and correlation coefficient” method will group – into the same group, indicating that the collinearity between and is also high. This confirms the theoretical analysis in the introduction that the correlation of temperature measurement points is transitive. Therefore, reducing the collinearity of TSPs and improving the correlation at the same time are in conflict. This results in the “Fuzzy clustering and correlation coefficient” method always grouping alone, eventually causing one of the TSPs to have a low correlation. According to Figure 12, the correlation of temperature measurement points with low correlation is also more unstable. Since correlation is the basis for the selection of TSPs, low correlation is one of the reasons for the variability of TSPs. The “Stability TSP selection method” directly selects TSPs with a strong correlation, so this problem does not exist.
- (2)
- The uncertainty of the correlation coefficient is an effective indicator to evaluate the stability of the correlation of the temperature measuring points, and it can be used to select TSPs with more stable correlation. According to Figure 12, the Std and uncertainty of the correlation coefficient have the same effect on measuring stability. However, there is an important difference between them. In particular, the Std calculation of the correlation coefficient needs all batches of data, which means multiple long-term experiments with the machine. The uncertainty of the correlation coefficient can be calculated only by one batch of data. This means that the uncertainty of the correlation coefficient can calculate the stability of the correlation in a short time. Furthermore, according to Figure 11, when the correlation of temperature measurement points is similar, the uncertainty-correlation coefficient promotes the selection of TSPs with a stable correlation, thereby significantly reducing the variability of TSPs.
5.2. Discussion of Comparison Results of Modeling Accuracy of TSP Selection Methods
5.3. Discussion of Comparison Results of the Adaptive Model Update Algorithm
6. Conclusions
- (1)
- When selecting the TSPs, the grouping method could cause the conflict of the collinearity and correlation of the TSPs and result in the low correlation of the selected TSPs. The stability of the correlation should also be considered when performing the correlation calculation in TSP selection. These two problems lead to the variability of TSPs, which reduces the prediction accuracy of thermal error models. This means that the TSPs selection method is unstable and may lead to inappropriate TSPs. In this regard, a stability TSP selection method was proposed in this study. In the proposed method, the correlation is the primary basis for the selection of TSPs. Furthermore, when calculating the correlation, the stability of correlation is calculated simultaneously so that the TSPs with high and stable correlations can be selected. After experimental verification, the variability of TSPs selected by the proposed method almost disappeared. In addition, for a variety of thermal error modeling algorithms, higher thermal error prediction accuracy could be obtained.
- (2)
- This study proposed a new thermal error model adaptive update method. This approach adds a regularization term that tends to the old model coefficients in the loss function of the regression algorithm. Based on the new loss function, the new data can be fused with the old model. Many experiments verified by that the proposed method could complete the update of the thermal error model with an average of six new data. Moreover, the prediction accuracy was close to the highest accuracy (fitting accuracy) of the linear regression algorithm, which greatly reduced the model update time and improved the accuracy of the updated model.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Bryan, J.B. International Status of Thermal Error Research. CIRP Ann. 1990, 39, 645–656. [Google Scholar] [CrossRef]
- Aronson, R.B. War against thermal expansion. Manuf. Eng. 1996, 116, 45–50. [Google Scholar]
- Yang, J.G. Error Synthetic Compensation Technique and Application for NCMachine Tools. Ph.D. Thesis, Shanghai Jiao Tong University, Shangha, China, 1998. [Google Scholar]
- Yang, L.; Zhao, W.; Lan, J.S.; Ni, J.; Wu, W.; Lu, B. A review on spindle thermal error compensation in machine tools. Int. J. Mach. Tools Manuf. 2015, 95, 20–38. [Google Scholar]
- Lo, C.H.; Yuan, J.; Ni, J. Optimal temperature variable selection by grouping approach for thermal error modeling and compensation. Int. J. Mach. Tools Manuf. 1999, 39, 1383–1396. [Google Scholar] [CrossRef]
- Yang, A.S.; Yu, X.H.; Zhuang, J.R.; Lee, C.Y.; Hsieh, W.H. DOE-FEM based design improvement to minimize thermal errors of a high speed spindle system. Therm. Sci. Eng. Prog. 2018, 8, 525–536. [Google Scholar] [CrossRef]
- Wei, X.; Gao, F.; Li, Y.; Zhang, D.Y. Study on optimal independent variables for the thermal error model of CNC machine tools. Int. J. Adv. Manuf. Technol. 2018, 98, 657–669. [Google Scholar] [CrossRef]
- Zhang, L.L.; Xuan, J.P.; Shi, T.L.; Li, R.; He, S.; Tang, L. Robust, fractal theory, and FEM-based temperature field analysis for machine tool spindle. Int. J. Adv. Manuf. Technol. 2020, 111, 1571–1586. [Google Scholar] [CrossRef]
- Naumann, A.; Ruprecht, D.; Wunsch, J. Toward transient finite element simulation of thermal deformation of machine tools in real-time. Comput. Mech. 2018, 62, 929–942. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.F.; Zhang, Y.J.; Zhao, Y.Q.; Shi, X.J. Thermal-mechanical coupling calculation method for deformation error of motorized spindle of machine tool. Eng. Fail. Anal. 2021, 128, 105597. [Google Scholar] [CrossRef]
- Liu, P.L.; Yao, X.D.; Ge, G.Y.; Du, Z.C.; Feng, X.B.; Yang, J.G. A Dynamic Linearization Modeling of Thermally Induced Error Based on Data-Driven Control for CNC Machine Tools. Int. J. Precis. Eng. Manuf. 2021, 22, 241–258. [Google Scholar] [CrossRef]
- Li, Y.; Yu, M.L.; Bai, Y.M.; Hou, Z.Y.; Wu, W.W. A Review of Thermal Error Modeling Methods for Machine Tools. Appl. Sci. 2021, 11, 5216. [Google Scholar] [CrossRef]
- Liu, Y.S.; Miao, E.M.; Liu, H.; Chen, Y.Y. Robust machine tool thermal error compensation modelling based on temperature-sensitive interval segmentation modelling technology. Int. J. Adv. Manuf. Technol. 2020, 160, 655–669. [Google Scholar] [CrossRef]
- Blaser, P.; Pavliček, F.; Mori, K.; Mayr, J.; Weikert, S.; Wegener, K. Adaptive learning control for thermal error compensation of 5-axis machine tools. J. Manuf. Syst. 2017, 44, 302–309. [Google Scholar] [CrossRef]
- Mayr, J.; Blasér, P.; Ryser, A.; Hernandez-Becerroa, P. An adaptive self-learning compensation approach for thermal errors on 5-axis machine tools handling an arbitrary set of sample rates. CIRP Ann. 2018, 67, 551–554. [Google Scholar] [CrossRef]
- Zimmermann, N.; Lang, S.; Blaser, P.; Mayr, J. Adaptive input selection for thermal error compensation models. CIRP Ann. 2020, 69, 485–488. [Google Scholar] [CrossRef]
- Zimmermann, N.; Breu, M.; Mayr, J.; Wegener, K. Autonomously triggered model updates for self-learning thermal error compensation. CIRP Ann. 2021, 70, 431–434. [Google Scholar] [CrossRef]
- Miao, E.M.; Liu, Y.; Liu, H.; Gao, Z.H.; Li, W. Study on the effects of changes in temperature-sensitive points on thermal error compensation model for CNC machine tool. Int. J. Mach. Tools Manuf. 2015, 97, 50–59. [Google Scholar] [CrossRef]
- Yang, J.G.; Deng, W.G.; Ren, Y.Q.; Li, Y.S.; Dou, X.L. Grouping optimization modeling by selection of temperature variables for the thermal error compensation on machine tools. China Mech. Eng. 2004, 15, 478–481. [Google Scholar]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J. The collinearity problem in linear Regression. The partial least squares (PLS) approach to generalized inverses. Siam J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef] [Green Version]
- Miao, E.M.; Gong, Y.Y.; Dang, L.C.; Miao, J.C. Temperature-sensitive point selection of thermal error model of CNC machining center. Int. J. Adv. Manuf. Technol. 2014, 74, 681–691. [Google Scholar]
- Abdulshahed, A.M.; Longstaff, A.P.; Fletcher, S.; Myers, A. Thermal error modelling of machine tools based on ANFIS with fuzzy c-means clustering using a thermal imaging camera. Appl. Math. Model. 2015, 39, 1837–1852. [Google Scholar] [CrossRef]
- Zhang, T.; Ye, W.H.; Shan, Y.C. Application of sliced inverse regression with fuzzy clustering for thermal error modeling of CNC machine tool. Int. J. Adv. Manuf. Technol. 2016, 85, 2761–2771. [Google Scholar] [CrossRef]
- Yin, Q.; Feng, H.X.; Yin, G.F. Spindle thermal error modeling based on selective ensemble BP neural networks. Int. J. Adv. Manuf. Technol. 2019, 101, 1699–1713. [Google Scholar] [CrossRef]
- Li, Z.Y.; Li, G.L.; Xu, K.; Tang, X.D.; Dong, X. Temperature-sensitive point selection and thermal error modeling of spindle based on synthetical temperature information. Int. J. Adv. Manuf. Technol. 2021, 113, 1029–1043. [Google Scholar] [CrossRef]
- Tsai, P.C.; Cheng, C.C.; Chen, W.J.; Su, S.J. Sensor placement methodology for spindle thermal compensation of machine tools. Int. J. Adv. Manuf. Technol. 2020, 106, 5429–5440. [Google Scholar] [CrossRef]
- Fu, G.Q.; Tao, C.; Xie, Y.P.; Lu, C.J.; Gao, H.L. Temperature-sensitive point selection for thermal error modeling of machine tool spindle by considering heat source regions. Int. J. Adv. Manuf. Technol. 2021, 112, 2447–2460. [Google Scholar] [CrossRef]
- Li, G.L.; Tang, X.D.; Li, Z.Y.; Xu, K.; Li, C.Z. The temperature-sensitive point screening for spindle thermal error modeling based on IBGOA-feature selection. Precis. Eng. 2021, 73, 140–152. [Google Scholar] [CrossRef]
- Zhan, W.R.; Yu, H. The Transitivity of Correlation Coefficient. Coll. Math. 2013, 29, 91–94. [Google Scholar]
- Liu, H.; Miao, E.M.; Zhang, L.Y.; Tang, D.F.; Hou, Y.L. Correlation Stability Problem in Selecting Temperature-Sensitive Points of CNC Machine Tools. Machines 2022, 10, 132. [Google Scholar] [CrossRef]
- Socha, K.; Blum, C. An ant colony optimization algorithm for continuous optimization: Application to feed-forward neural network training. Neural Comput. Appl. 2007, 16, 235–247. [Google Scholar] [CrossRef]
- Whitley, D.; Starkweather, T.; Bogart, C. Genetic algorithms and neural networks: Optimizing connections and connectivity. Parallel Comput. 1990, 14, 347–361. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, J.; Ji, S.J. Thermal positioning error modeling of machine tools using a bat algorithm-based back propagation neural network. Int. J. Adv. Manuf. Technol. 2018, 97, 2575–2586. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, Y.C.; Du, L.; Yang, H. Thermal error analysis, modeling and compensation of five-axis machine tools. J. Mech. Sci. Technol. 2020, 34, 4295–4305. [Google Scholar] [CrossRef]
- Liu, H.; Miao, E.; Wei, X.Y.; Zhuang, X.D. Robustness Modeling Method for Thermal Error of CNC Machine Tools Based on Ridge Regression Algorithm. Int. J. Mach. Tools Manuf. 2017, 113, 35–48. [Google Scholar] [CrossRef]
- Fu, C.B.; Tian, A.H.; Yau, H.T.; Hoang, M.C. Thermal monitoring and thermal deformation prediction for spherical machine tool spindles. Therm. Sci. 2019, 23, 2271–2279. [Google Scholar] [CrossRef]
- Chen, C.C.; Hung, W.C. Thermal Error Modeling of CNC Machine Tool Spindle Based on Multiple Regression and Features Selection. In Proceedings of the 2021 IEEE 3rd Eurasia Conference on IOT, Communication and Engineering (ECICE), Yunlin, Taiwan, China, 29–31 October 2021. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 42, 80–86. [Google Scholar] [CrossRef]

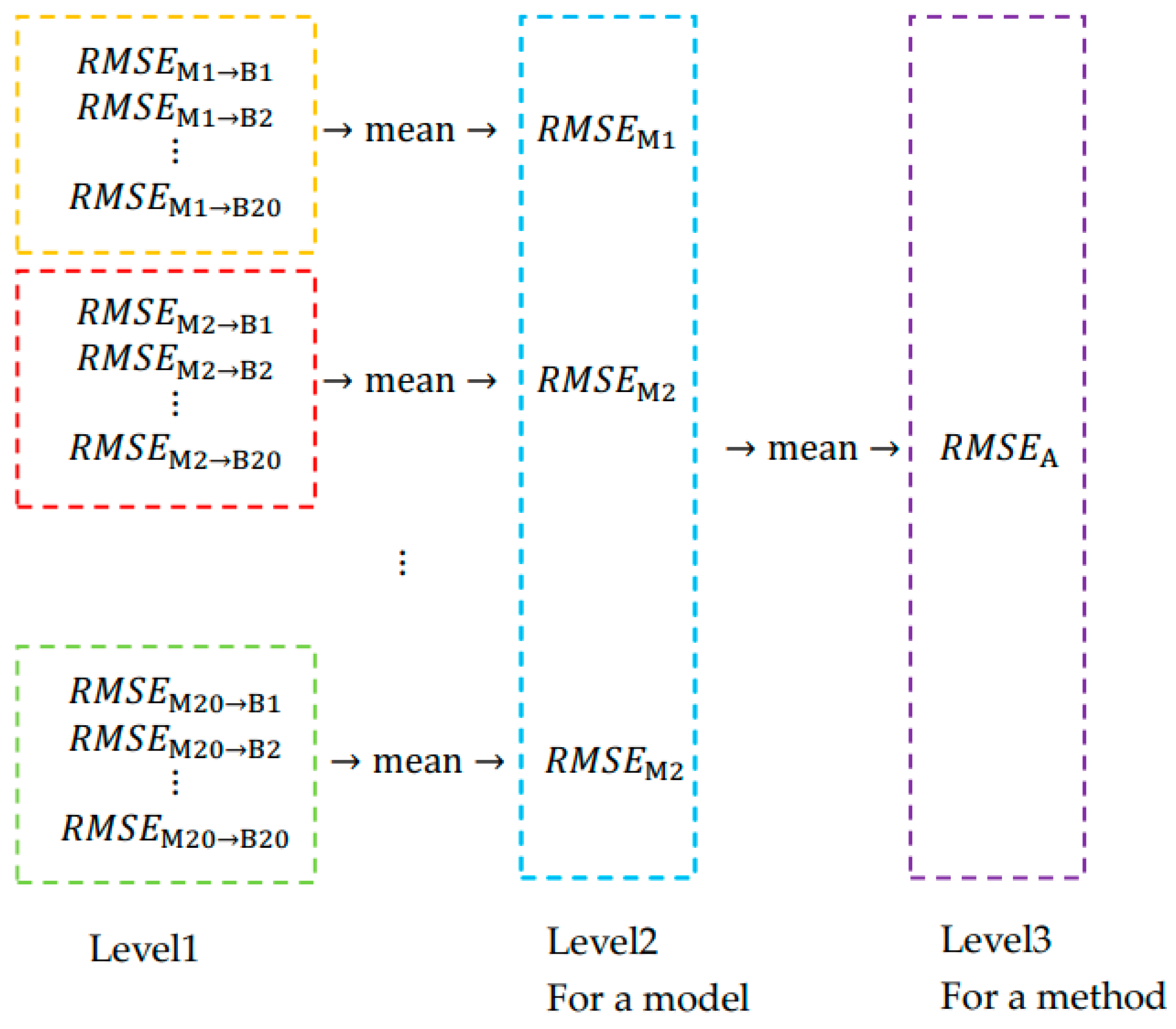

| Batch | Rotating Speed (rpm) | Feed (mm/min) | Cutting Depth (μm) |
|---|---|---|---|
| B1 | 1000 | 400 | 100 |
| B2 | 500 | 600 | 100 |
| B3 | 1500 | 600 | 50 |
| B4 | 1500 | 600 | 100 |
| B5 | 1500 | 600 | 100 |
| B6 | 1000 | 600 | 50 |
| B7 | 1000 | 600 | 150 |
| B8 | 1500 | 400 | 150 |
| B9 | 500 | 400 | 50 |
| B10 | 1000 | 600 | 100 |
| B11 | 500 | 400 | 50 |
| B12 | 1000 | 600 | 150 |
| B13 | 1500 | 800 | 100 |
| B14 | 1000 | 600 | 150 |
| B15 | 1500 | 800 | 100 |
| B16 | 1000 | 400 | 100 |
| B17 | 800 | 500 | 150 |
| B18 | 1500 | 600 | 50 |
| B19 | 1000 | 400 | 100 |
| B20 | 1500 | 800 | 100 |
| Batch | TSPs Selected by Fuzzy Clustering and Correlation Coefficient | TSPs Selected by Stability TSP Selection Method |
|---|---|---|
| B1 | ||
| B2 | ||
| B3 | ||
| B4 | ||
| B5 | ||
| B6 | ||
| B7 | ||
| B8 | ||
| B9 | ||
| B10 | ||
| B11 | ||
| B12 | ||
| B13 | ||
| B14 | ||
| B15 | ||
| B16 | ||
| B17 | ||
| B18 | ||
| B19 | ||
| B20 |
| Modeling Methods | |
|---|---|
| Clustering + Correlation coefficient + Rig | 14.95 |
| Stability TSP selection method + Rig | 8.65 |
| Clustering + Correlation coefficient + Reg | 28.7 |
| Stability TSP selection method + Reg | 18.6 |
| Clustering + Correlation coefficient + NN | 21.9 |
| Stability TSP selection method + NN | 16.4 |
| Batch | Group1 | Group2 | Batch | Group1 | Group2 |
|---|---|---|---|---|---|
| B1 | B2 | ||||
| B3 | B4 | ||||
| B5 | B6 | ||||
| B7 | B8 | ||||
| B9 | B10 | ||||
| B11 | B12 | ||||
| B13 | B14 | ||||
| B15 | B16 | ||||
| B17 | B18 | ||||
| B19 | B20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Miao, E.; Wang, J.; Zhang, L.; Zhao, S. Temperature-Sensitive Point Selection and Thermal Error Model Adaptive Update Method of CNC Machine Tools. Machines 2022, 10, 427. https://doi.org/10.3390/machines10060427
Liu H, Miao E, Wang J, Zhang L, Zhao S. Temperature-Sensitive Point Selection and Thermal Error Model Adaptive Update Method of CNC Machine Tools. Machines. 2022; 10(6):427. https://doi.org/10.3390/machines10060427
Chicago/Turabian StyleLiu, Hui, Enming Miao, Jingfan Wang, Liyin Zhang, and Siyu Zhao. 2022. "Temperature-Sensitive Point Selection and Thermal Error Model Adaptive Update Method of CNC Machine Tools" Machines 10, no. 6: 427. https://doi.org/10.3390/machines10060427
APA StyleLiu, H., Miao, E., Wang, J., Zhang, L., & Zhao, S. (2022). Temperature-Sensitive Point Selection and Thermal Error Model Adaptive Update Method of CNC Machine Tools. Machines, 10(6), 427. https://doi.org/10.3390/machines10060427





