Design and Characterization of a Rolling-Contact Involute Joint and Its Applications in Finger Exoskeletons
Abstract
:1. Introduction
- (1)
- A rolling contact involute joint model was proposed, and we applied the joint as a motion-fitting solution for finger exoskeletons. When designing the involute finger exoskeleton, an optimization algorithm was introduced, and the driving position and spring mechanism were analyzed.
- (2)
- A series of experiments was performed to measure the kinematic and dynamic properties of the finger exoskeleton. The results show that the proposed finger exoskeleton provides fingertip force with a maximum of 10 N, which is enough to support people in grasping daily heavy objects, such as a water bottle.
- (3)
- We developed an EMG-controlled exoskeleton glove and conducted experimental verification of the exoskeleton. The wearability and functionality performance of the exoskeleton were verified.
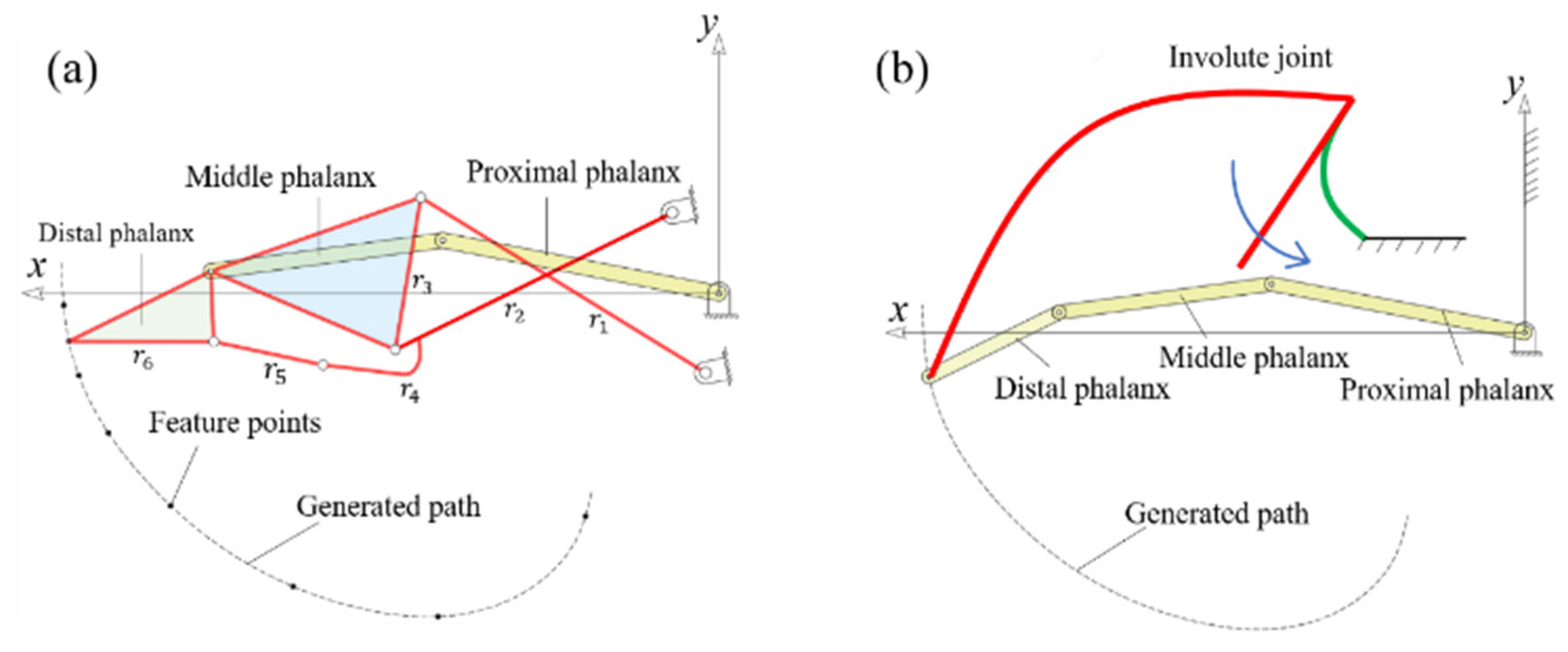
2. Design of an Involute Rolling-Contact Finger Exoskeleton
2.1. Optimization of an Involute Joint for Path Generation
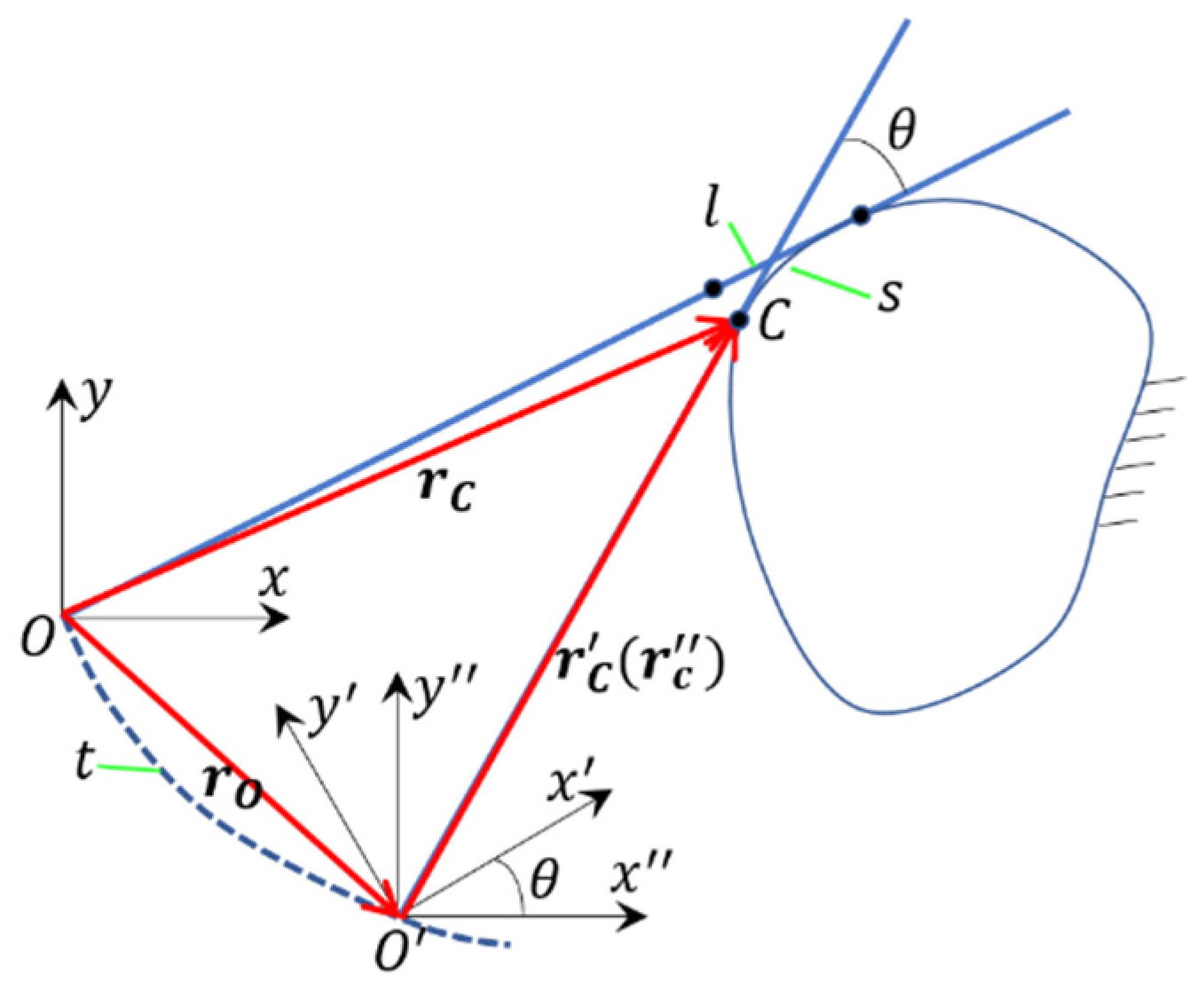
2.1.1. Kinematic Model of an Involute Joint
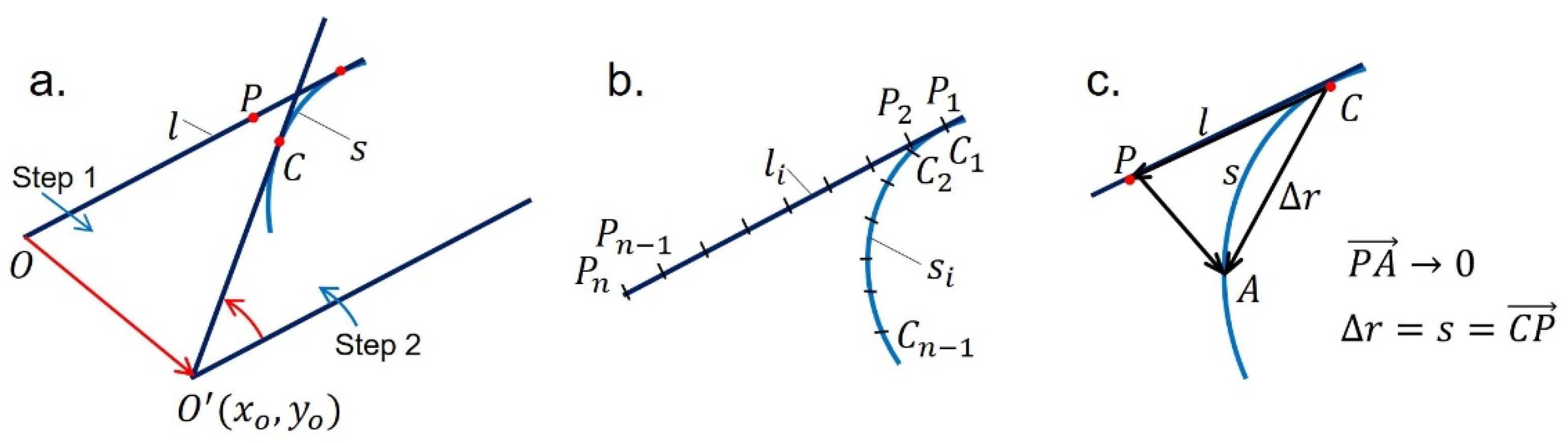
2.1.2. Optimization of the Meshing Curve
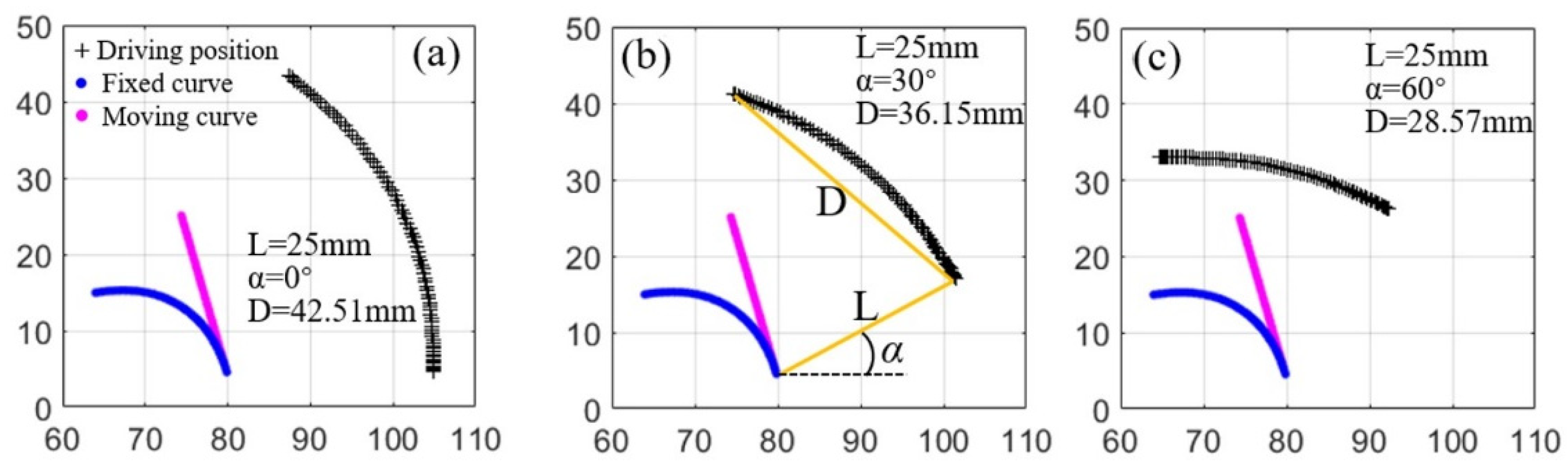
2.1.3. Design of an Involute Joint for an End-Effect Finger Device
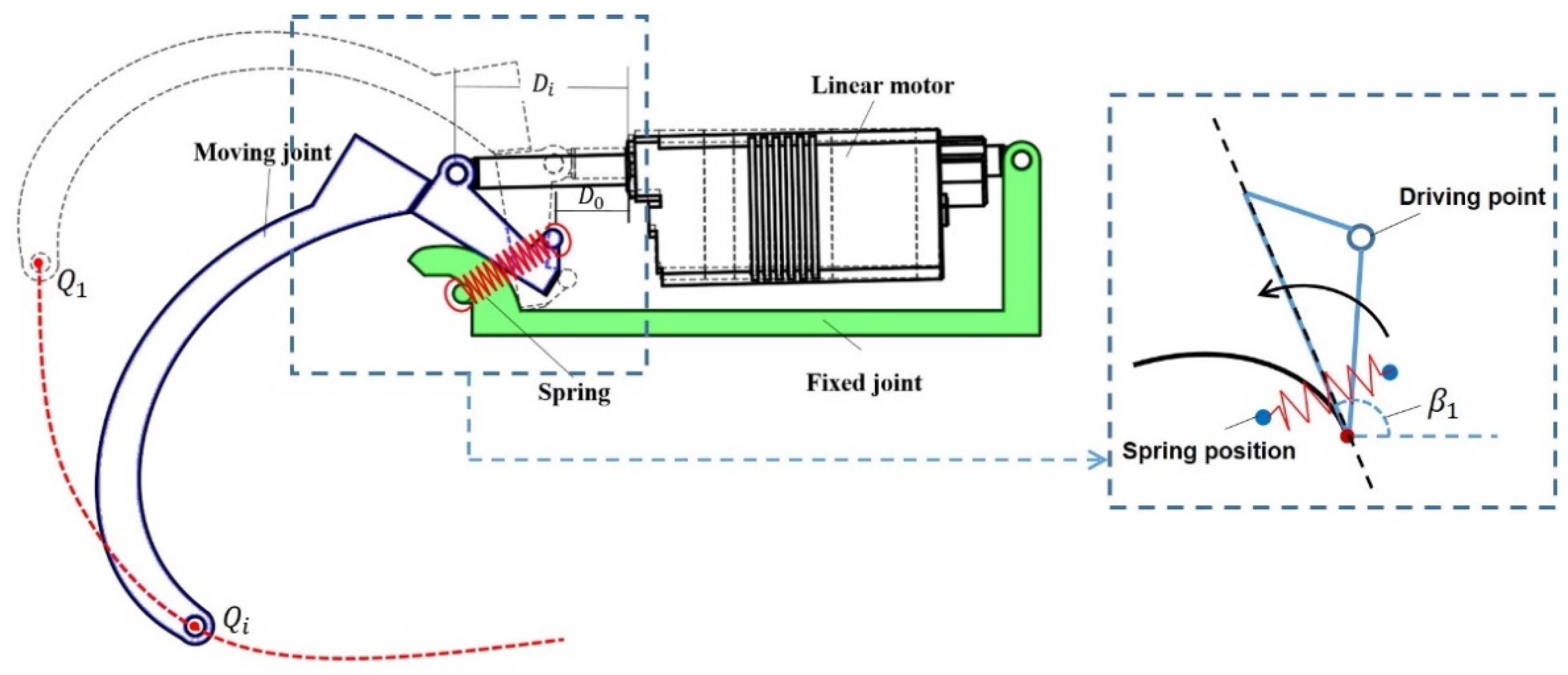
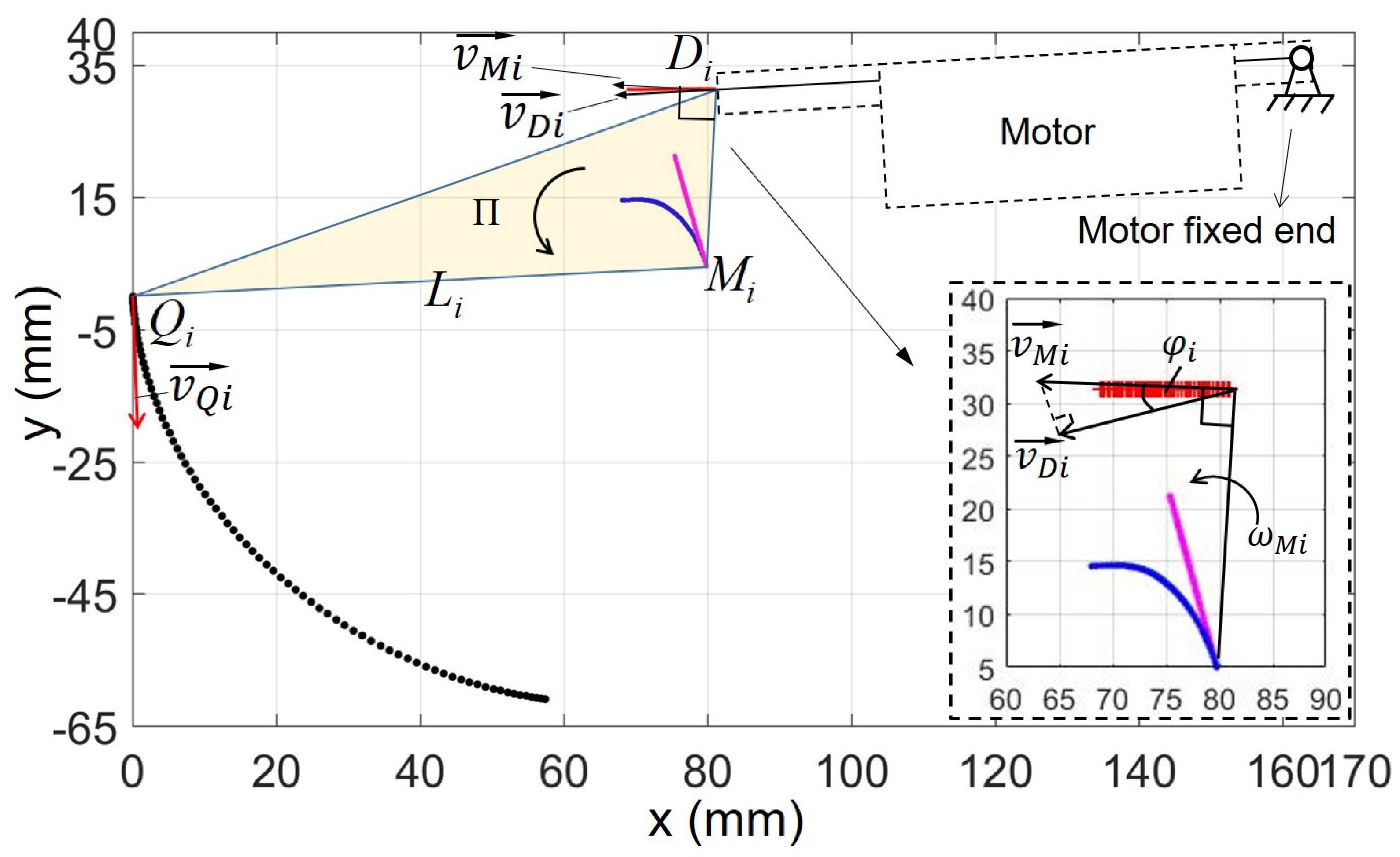
2.2. Optimization of the Driving Position and Spring Mechanism
2.2.1. Optimization of the Driving Position
2.2.2. Spring Mechanism
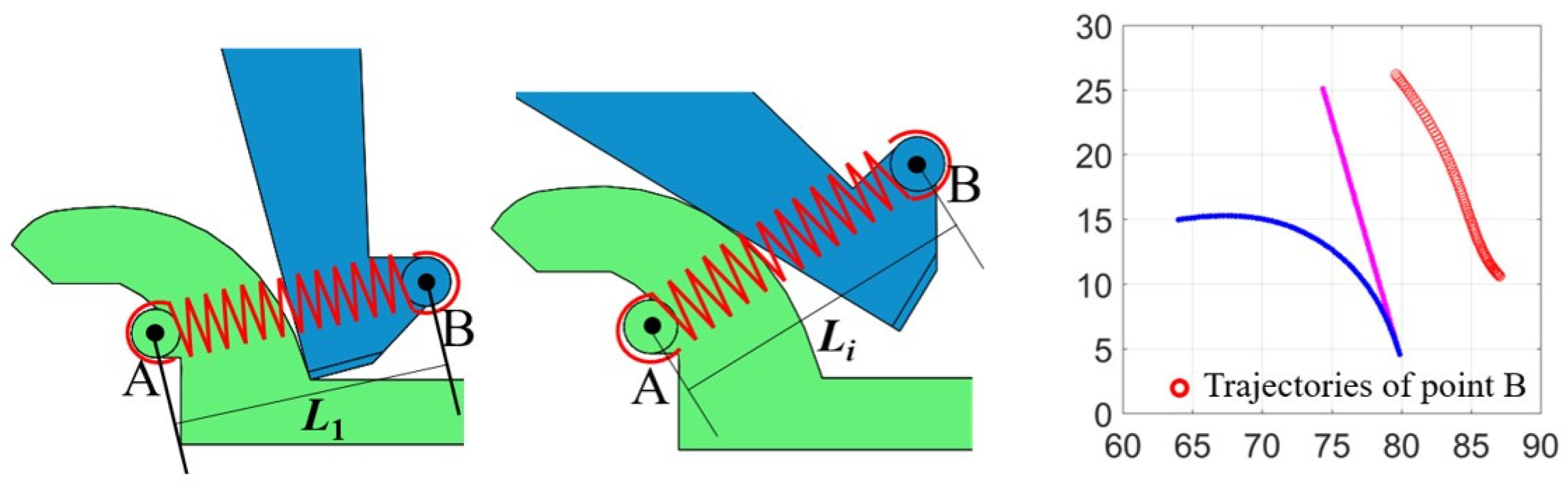
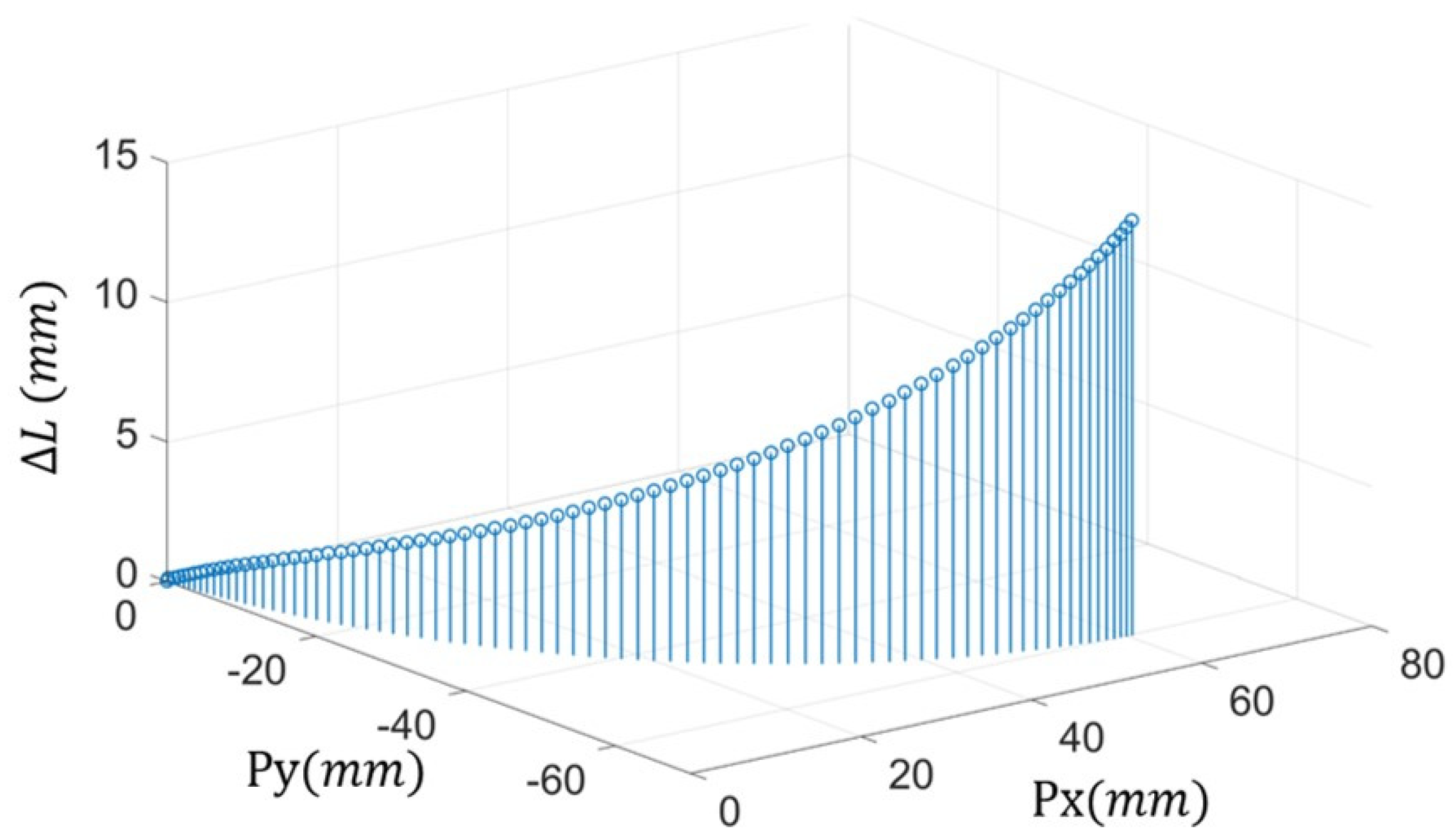
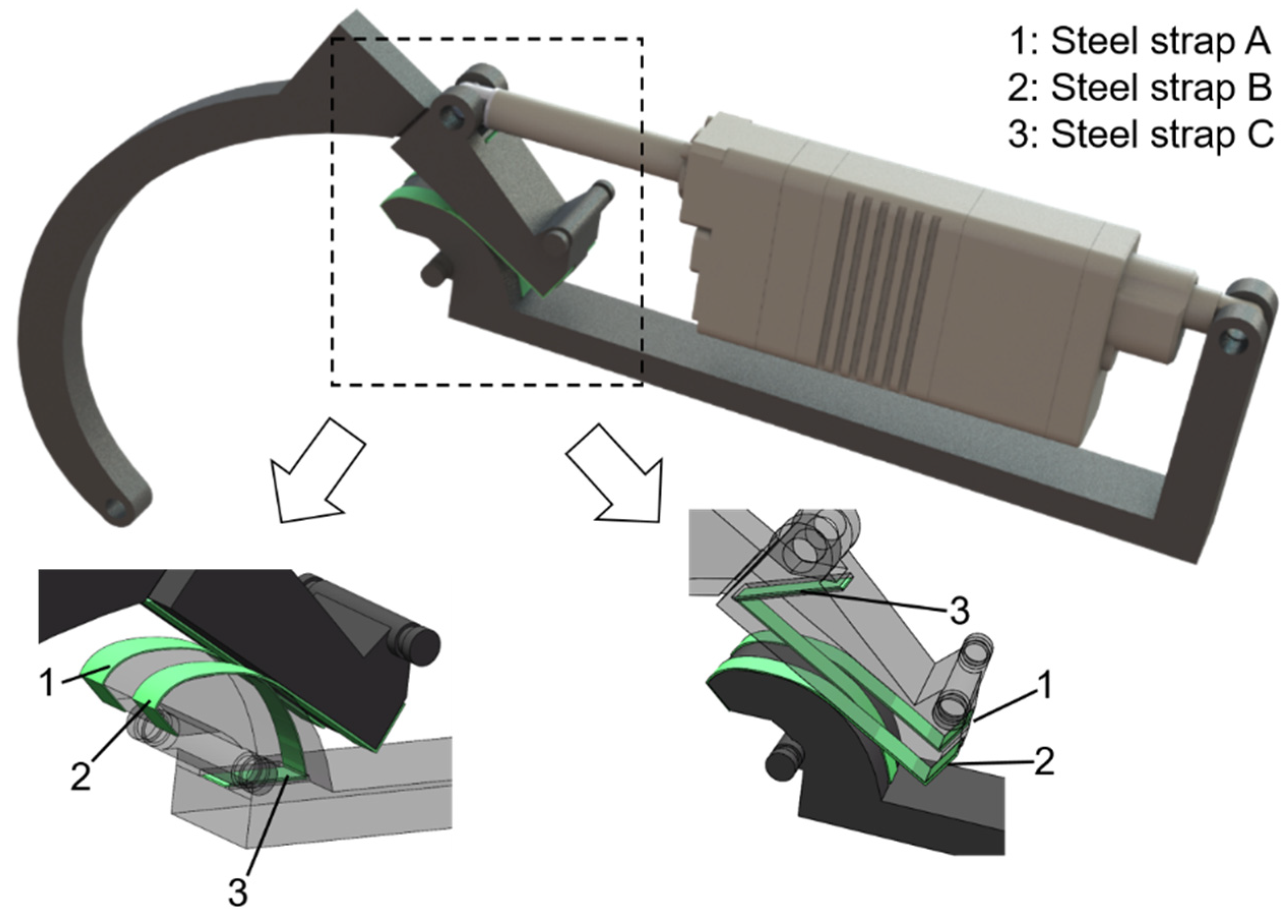
2.2.3. Rolling Contact Design of Involute Surfaces
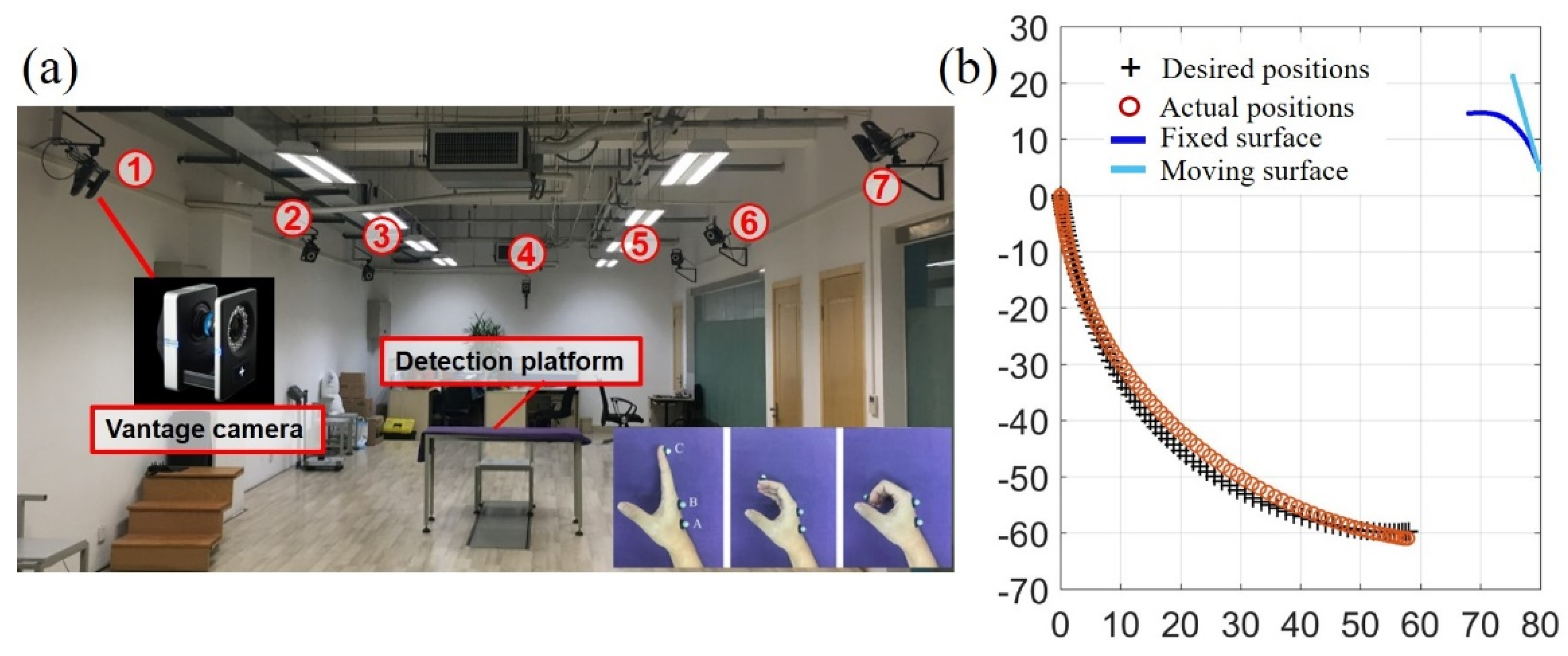
3. Performance Verification
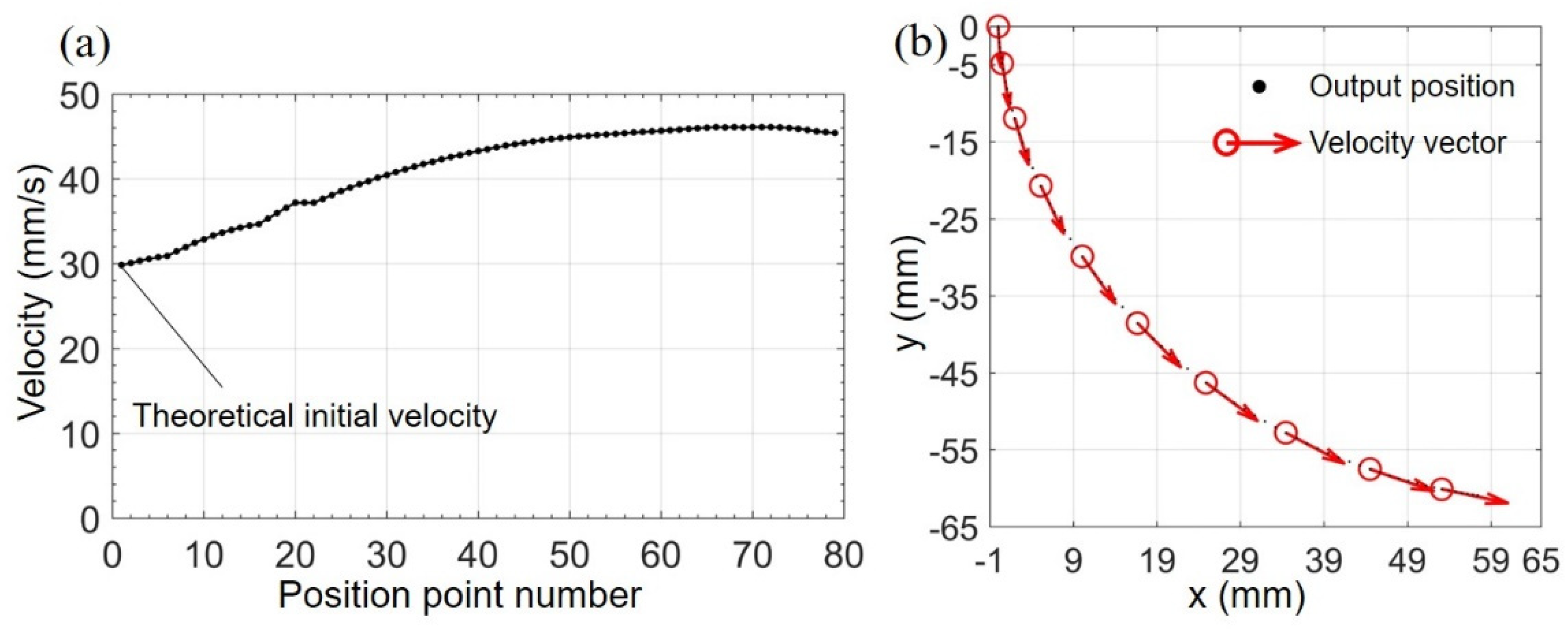
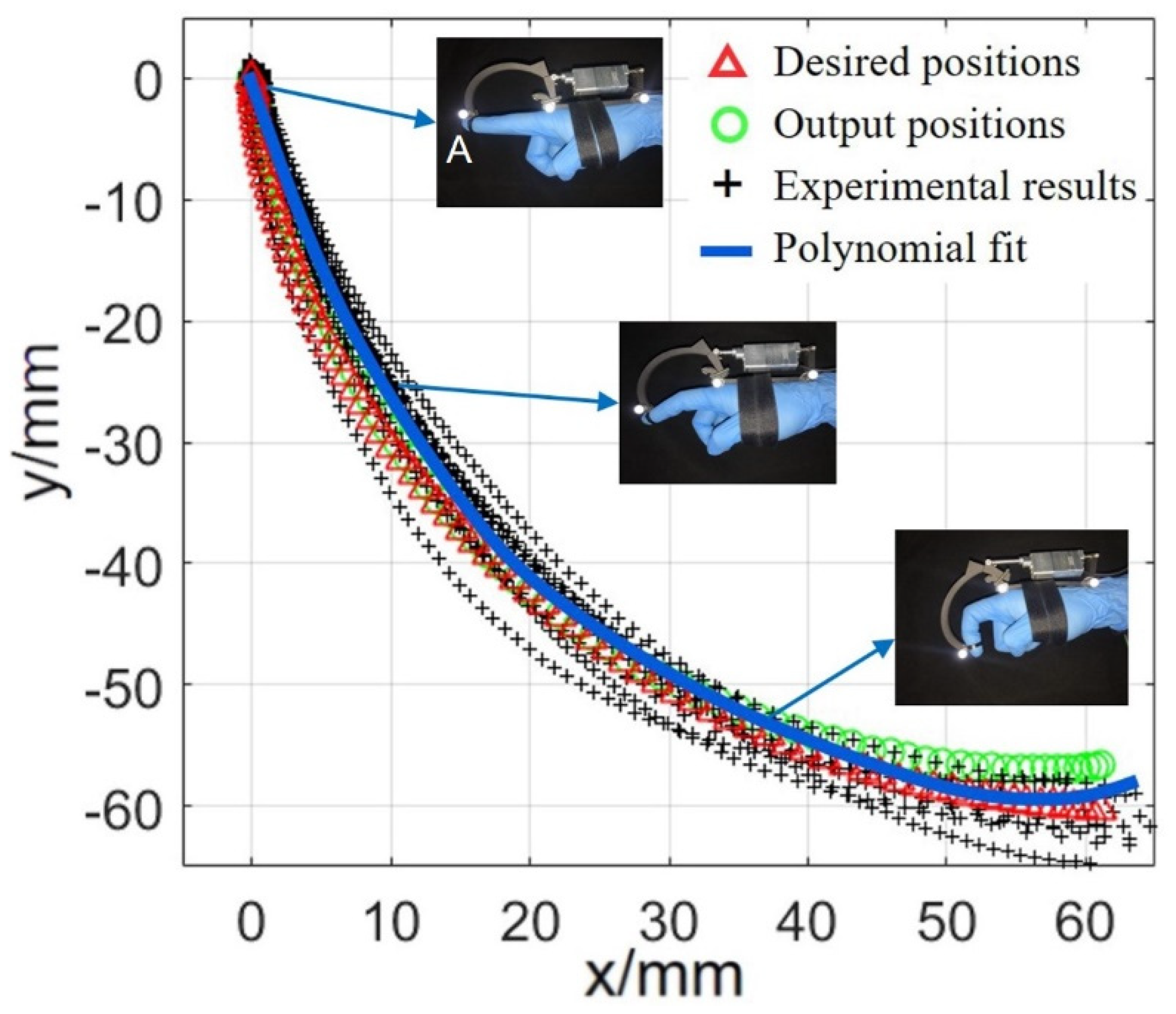
3.1. Output Trajectory of the Exoskeleton
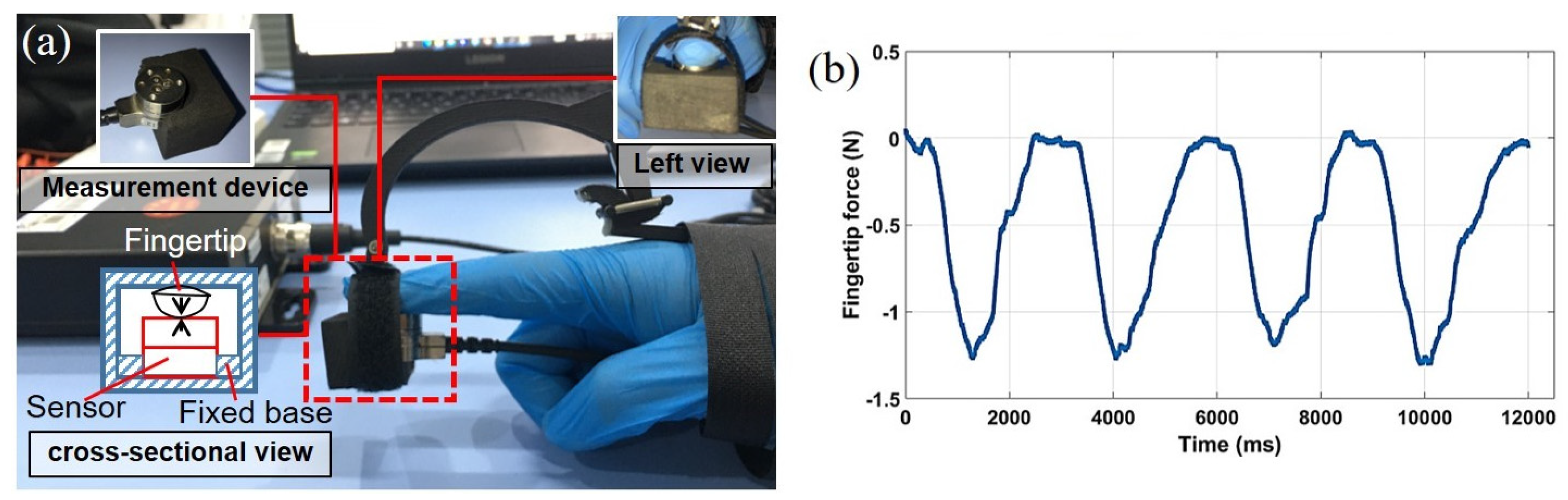
3.2. Performance of the Free-Space Simulation
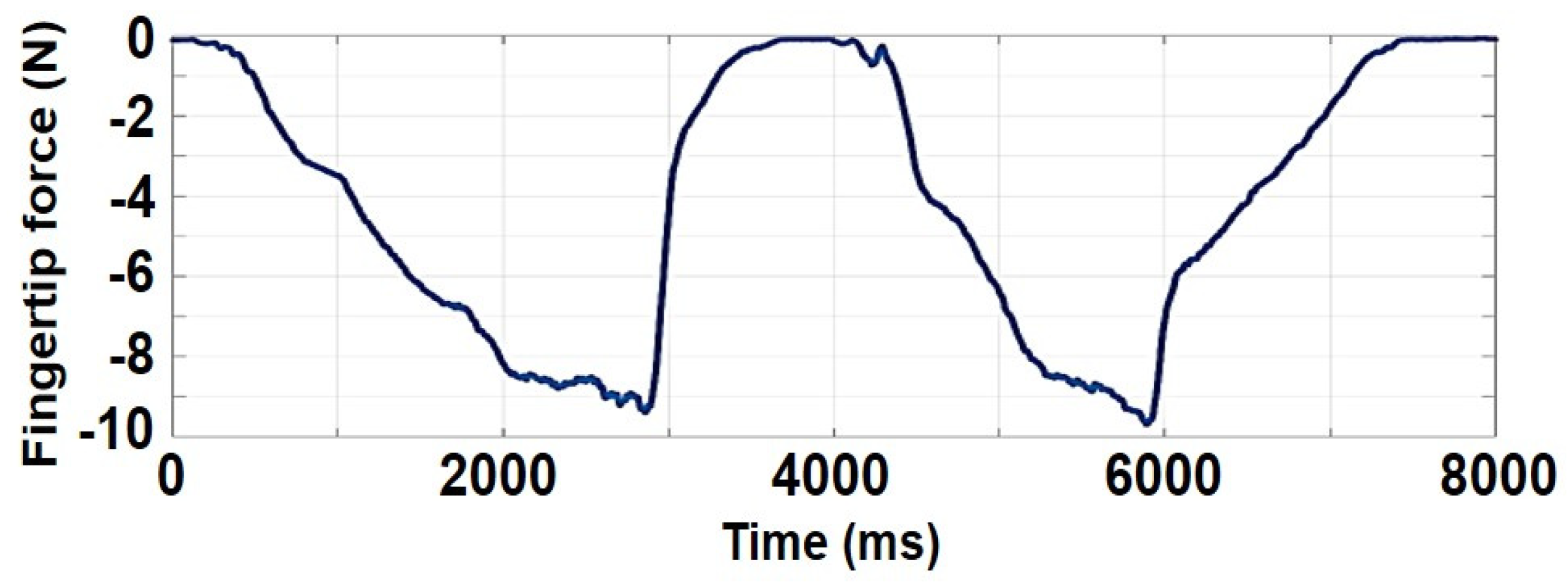
3.3. Performance of the Grasping Simulation
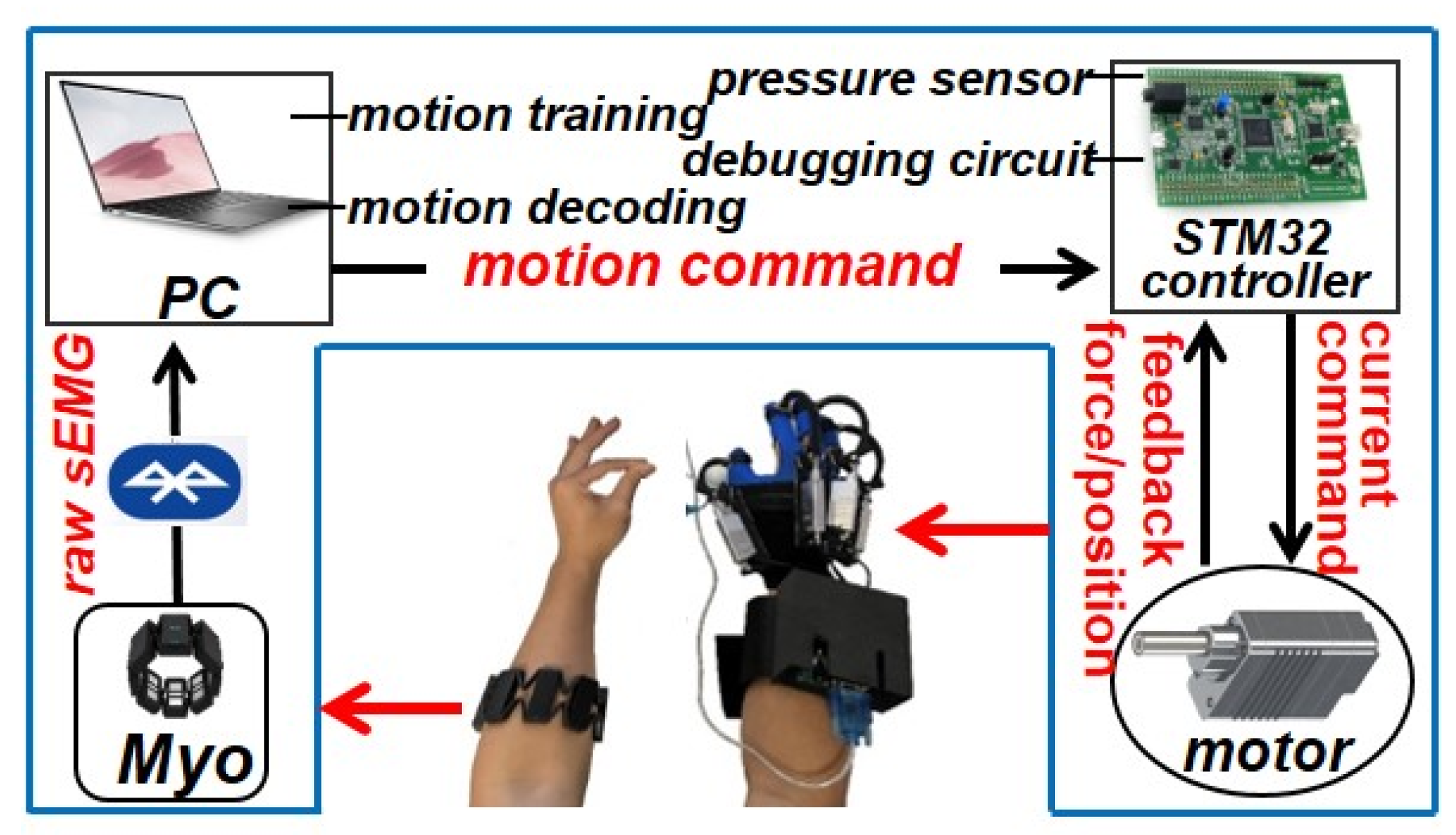
4. An EMG-Controlled Robotic Hand Rehabilitation System
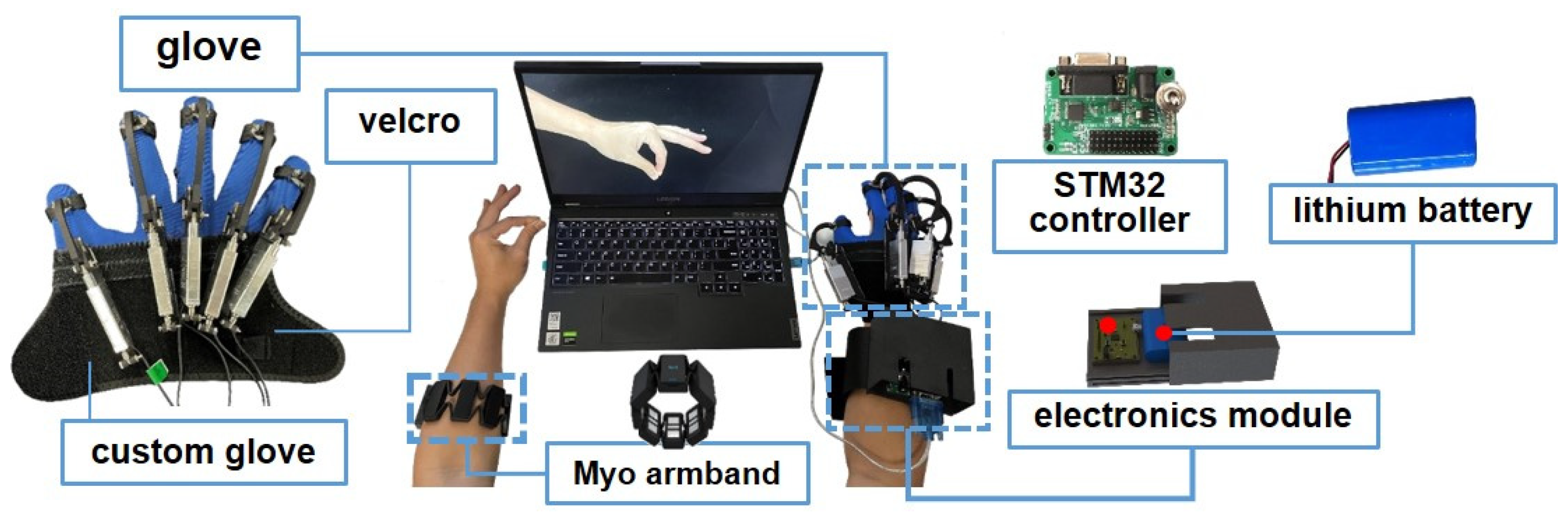
4.1. Design Implementation
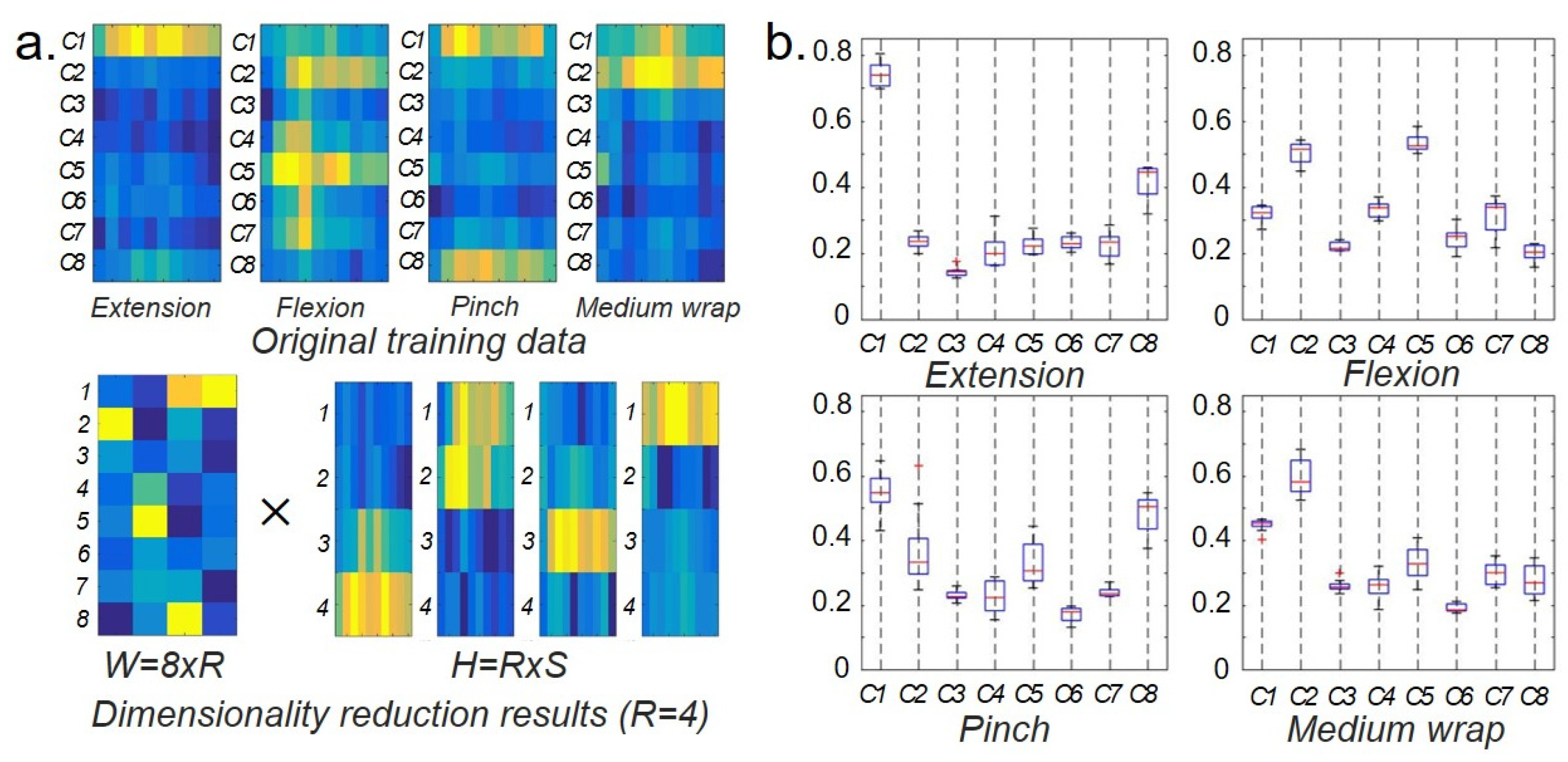
4.2. Motion Intention Detection
4.3. Wearability and Functionality Testing
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jones, C.L.; Wang, F.; Morrison, R.; Sarkar, N.; Kamper, D.G. Design and Development of the Cable Actuated Finger Exoskeleton for Hand Rehabilitation Following Stroke. IEEE/ASME Trans. Mechatron. 2014, 19, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Ferris, D.P. The exoskeletons are here. J. Neuroeng. Rehabil. 2009, 6, 17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, A.; Yin, R.; Cao, L.; Yuan, C.; Ding, H.; Zhang, W. Soft robotics: Definition and research issues. In Proceedings of the 2017 24th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Auckland, New Zealand, 21–23 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 366–370. [Google Scholar]
- Li, H.; Cheng, L.; Li, Z.; Xue, W. Active Disturbance Rejection Control for a Fluid-Driven Hand Rehabilitation Device. IEEE/ASME Trans. Mechatron. 2020, 26, 841–853. [Google Scholar] [CrossRef]
- Zhang, H.; Kumar, A.S.; Chen, F.; Fuh, J.Y.H.; Wang, M.Y. Topology Optimized Multimaterial Soft Fingers for Applications on Grippers, Rehabilitation, and Artificial Hands. IEEE/ASME Trans. Mechatronics 2019, 24, 120–131. [Google Scholar] [CrossRef]
- Yap, H.K.; Khin, P.M.; Koh, T.H.; Sun, Y.; Liang, X.; Lim, J.H.; Yeow, C.H. A fully fabric-based bidirectional soft robotic glove for assistance and rehabilitation of hand impaired patients. IEEE Robot. Autom. Lett. 2017, 2, 1383–1390. [Google Scholar] [CrossRef]
- Li, C.; Gu, X.; Ren, H. A Cable-Driven Flexible Robotic Grasper With Lego-Like Modular and Reconfigurable Joints. IEEE/ASME Trans. Mechatron. 2017, 22, 2757–2767. [Google Scholar] [CrossRef]
- Sun, N.; Li, G.; Cheng, L. Design and Validation of a Self-Aligning Index Finger Exoskeleton for Post-Stroke Rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 1513–1523. [Google Scholar] [CrossRef]
- Bützer, T.; Lambercy, O.; Arata, J.; Gassert, R. Fully Wearable Actuated Soft Exoskeleton for Grasping Assistance in Everyday Activities. Soft Robot. 2021, 8, 128–143. [Google Scholar] [CrossRef]
- Zheng, Y.; Cao, L.; Qian, Z.; Chen, A.; Zhang, W. Topology optimization of a fully compliant prosthetic finger: Design and testing. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics, Singapore, 26–29 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1029–1034. [Google Scholar]
- Bos, R.A.; Haarman, C.J.; Stortelder, T.; Nizamis, K.; Herder, J.L.; Stienen, A.H.; Plettenburg, D.H. A structured overview of trends and technologies used in dynamic hand orthoses. J. Neuroeng. Rehabil. 2016, 13, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Tong, R.K.-Y.; Zhang, X.; Li, S.; Zhou, P. Myoelectric Pattern Recognition for Controlling a Robotic Hand: A Feasibility Study in Stroke. IEEE Trans. Biomed. Eng. 2018, 66, 365–372. [Google Scholar] [CrossRef]
- Esposito, D.; Centracchio, J.; Andreozzi, E.; Savino, S.; Gargiulo, G.D.; Naik, G.R.; Bifulco, P. Design of a 3D-Printed Hand Exoskeleton Based on Force-Myography Control for Assistance and Rehabilitation. Machines 2022, 10, 57. [Google Scholar] [CrossRef]
- Orlando, M.F.; Behera, L.; Dutta, A.; Saxena, A. Optimal Design and Redundancy Resolution of a Novel Robotic Two-Fingered Exoskeleton. IEEE Trans. Med. Robot. Bionics 2020, 2, 59–75. [Google Scholar] [CrossRef]
- Secciani, N.; Bianchi, M.; Ridolfi, A.; Volpe, F.V.Y.; Governi, L.; Bianchini, M.; Allotta, B. Tailor-Made Hand Exoskeletons at the University of Florence: From Kinematics to Mechatronic Design. Machines 2019, 7, 22. [Google Scholar] [CrossRef] [Green Version]
- Fontana, M.; Dettori, A.; Salsedo, F.; Bergamasco, M. Mechanical design of a novel Hand Exoskeleton for accurate force displaying. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009. [Google Scholar] [CrossRef]
- Gabardi, M.; Solazzi, M.; Leonardis, D.; Frisoli, A. Design and Evaluation of a Novel 5 DoF Underactuated Thumb-Exoskeleton. IEEE Robot. Autom. Lett. 2018, 3, 2322–2329. [Google Scholar] [CrossRef]
- Leonardis, D.; Barsotti, M.; Loconsole, C.; Solazzi, M.; Troncossi, M.; Mazzotti, C.; Castelli, V.P.; Procopio, C.; Lamola, G.; Chisari, C.; et al. An EMG-Controlled Robotic Hand Exoskeleton for Bilateral Rehabilitation. IEEE Trans. Haptics 2015, 8, 140–151. [Google Scholar] [CrossRef] [PubMed]
- Linde-Medina, M. Adaptation or exaptation? The case of the human hand. J. Biosci. 2011, 36, 575–585. [Google Scholar] [CrossRef]
- Kamper, D.G.; Cruz, E.G.; Siegel, M.P. Stereotypical fingertip trajectories during grasp. J. Neurophysiol. 2003, 90, 3702–3710. [Google Scholar] [CrossRef]
- Borghesan, G.; Palli, G.; Melchiorri, C. Design of tendon-driven robotic fingers: Modeling and control issues. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 793–798. [Google Scholar]
- Omarkulov, N.; Telegenov, K.; Zeinullin, M.; Begalinova, A.; Shintemirov, A. Design and analysis of an underactuated anthropomorphic finger for upper limb prosthetics. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; IEEE: Piscataway, NJ, USA, 2015; Volume 2015, pp. 2474–2477. [Google Scholar]
- Kang, L.; Seo, J.T.; Kim, S.H.; Kim, W.J.; Yi, B.J. Design and implementation of a multi-function gripper for grasping general objects. Appl. Sci. 2019, 9, 5266. [Google Scholar] [CrossRef] [Green Version]
- Liang, R.; Xu, G.; Teng, Z.; Li, M.; Zhang, S.; Zheng, X.; Zhang, K.; He, B. A General Arthropod Joint Model and its Applications in Modeling Human Robotic Joints. IEEE Access 2021, 9, 7814–7822. [Google Scholar] [CrossRef]
- Neumann, D.A. Kinesiology of the Musculoskeletal System-e-Book: Foundations for Rehabilitation; Elsevier Health Sciences: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Zheng, Y.; Wang, D.; Wang, Z.; Zhang, Y.; Zhang, Y.; Xu, W. Design of a Lightweight Force-Feedback Glove with a Large Workspace. Engineering 2018, 4, 869–880. [Google Scholar] [CrossRef]
- Tran, P.; Jeong, S.; Wolf, S.L.; Desai, J.P. Patient-Specific, Voice-Controlled, Robotic FLEXotendon Glove-II System for Spinal Cord Injury. IEEE Robot. Autom. Lett. 2020, 5, 898–905. [Google Scholar] [CrossRef]
- Chang, P.H.; Lee, S.H.; Koo, K.M.; Lee, S.H.; Jin, S.H.; Yeo, S.S.; Seo, J.P.; Jang, S.H. The cortical activation pattern by a rehabilitation robotic hand: A functional NIRS study. Front. Hum. Neurosci. 2014, 8, 49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Susanto, E.A.; Tong, R.K.; Ockenfeld, C.; Ho, N.S. Efficacy of robot-assisted fingers training in chronic stroke survivors: A pilot randomized-controlled trial. J. Neuroeng. Rehabil. 2015, 12, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, R.; Xu, G.; Li, M.; He, B.; Khalique, U. Fusing Topology Optimization and Pseudo-Rigid-Body Method For the Development of a Finger Exoskeleton. IEEE Robot. Autom. Lett. 2021, 7, 1721–1728. [Google Scholar] [CrossRef]
- Randazzo, L.; Iturrate, I.; Perdikis, S.; Millan, J.D.R. mano: A Wearable Hand Exoskeleton for Activities of Daily Living and Neurorehabilitation. IEEE Robot. Autom. Lett. 2018, 3, 500–507. [Google Scholar] [CrossRef] [Green Version]
- Yap, H.K.; Lim, J.H.; Nasrallah, F.; Goh, J.C.; Yeow, R.C. A soft exoskeleton for hand assistive and rehabilitation application using pneumatic actuators with variable stiffness. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4967–4972. [Google Scholar]
- Cappello, L.; Galloway, K.C.; Sanan, S.; Wagner, D.A.; Granberry, R.; Engelhardt, S.; Haufe, F.L.; Peisner, J.D.; Walsh, C.J. Exploiting Textile Mechanical Anisotropy for Fabric-Based Pneumatic Actuators. Soft Robot. 2018, 5, 662–674. [Google Scholar] [CrossRef]
- Nassour, J.; Hamker, F.H.; Cheng, G. High-Performance Perpendicularly-Enfolded-Textile Actuators for Soft Wearable Robots: Design and Realization. IEEE Trans. Med Robot. Bionics 2020, 2, 309–319. [Google Scholar] [CrossRef]
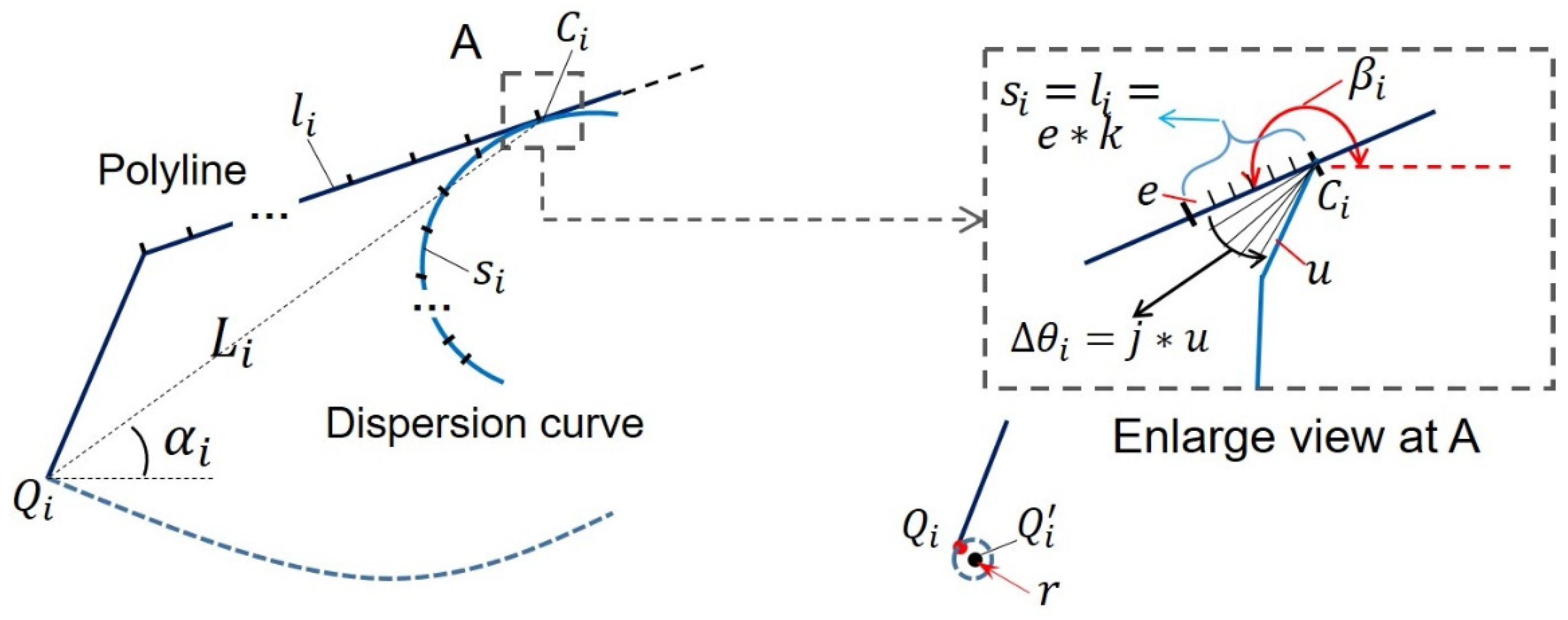




| Initial Values | Threshold Radius (mm) | Rotation Radius (mm) | Step Size of Δθi (mm) | Step Size of si (rad) | Initial Position (rad) | Initial Angle (rad) |
|---|---|---|---|---|---|---|
| Symbol | r | L(1) | U | e | α1 | β1 |
| Value | 2 | 80 | 0.001 | 0.005 | 56π/55 | 7π/12 |
| Wearing Step | Donning(s) | Doffing(s) | ||
|---|---|---|---|---|
| 1st Trial | 2nd Trial | 1st Trial | 2nd Trial | |
| 1 | 7.74 | 5.96 | 4.89 | 5.35 |
| 2 | 30.06 | 31.35 | 9.47 | 8.57 |
| Hand Exoskeleton | Weight (g) | Finger Number | Fingertip Force (N) | Actuation Method |
|---|---|---|---|---|
| Involute joint exoskeleton | 175 (without actuator) 376.5 (with actuator) | 5 | 10 | Linear motor |
| FLEXotendon Glove-II [27] | n/a | 3 | 5.03 | DC motor (cable driven) |
| RELab tenoexo [9] | 148 (without actuator) 788 (with actuator) | 5 | 6.4 | DC motor (cable driven + spring blade) |
| Exo-Glove [28] | 194 (without actuator) | 3 | 12 | DC motor (cable driven) |
| Force-feedback glove [26] | 245 (without actuator) | 5 | 4 | Pneumatic pump |
| Evan et al. [29] | 700 (without actuator) | 5 | n/a | Linear motor |
| Thumb-Exoskeleton [17] | n/a | 5 | 3.11 | DC motor |
| Rigid-soft exoskeleton [30] | 95 (without actuator) 324 (with actuator) | 5 | 6 | Linear motor |
| Mano [31] | 50 (without actuator) 930 (with actuator) | 5 | 5 | cable driven |
| ExoGlove [32] | 200 (without actuator) | 5 | 3.59 | Pneumatic pump |
| Fabric-Based Actuators [33] | 78.6 (without actuator) | 5 | n/a | Pneumatic pump |
| Enfolded-Textile Actuator [34] | 160 (without actuator) | 5 | n/a | Pneumatic pump |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, R.; Xu, G.; Zhang, Q.; Jiang, K.; Li, M.; He, B. Design and Characterization of a Rolling-Contact Involute Joint and Its Applications in Finger Exoskeletons. Machines 2022, 10, 301. https://doi.org/10.3390/machines10050301
Liang R, Xu G, Zhang Q, Jiang K, Li M, He B. Design and Characterization of a Rolling-Contact Involute Joint and Its Applications in Finger Exoskeletons. Machines. 2022; 10(5):301. https://doi.org/10.3390/machines10050301
Chicago/Turabian StyleLiang, Renghao, Guanghua Xu, Qiuxiang Zhang, Kaiyuan Jiang, Min Li, and Bo He. 2022. "Design and Characterization of a Rolling-Contact Involute Joint and Its Applications in Finger Exoskeletons" Machines 10, no. 5: 301. https://doi.org/10.3390/machines10050301
APA StyleLiang, R., Xu, G., Zhang, Q., Jiang, K., Li, M., & He, B. (2022). Design and Characterization of a Rolling-Contact Involute Joint and Its Applications in Finger Exoskeletons. Machines, 10(5), 301. https://doi.org/10.3390/machines10050301






