Development of an Anthropomorphic and Dexterous Dual-Arm System for Aerial Cooperative Bimanual Manipulation
Abstract
:1. Introduction
2. System Description
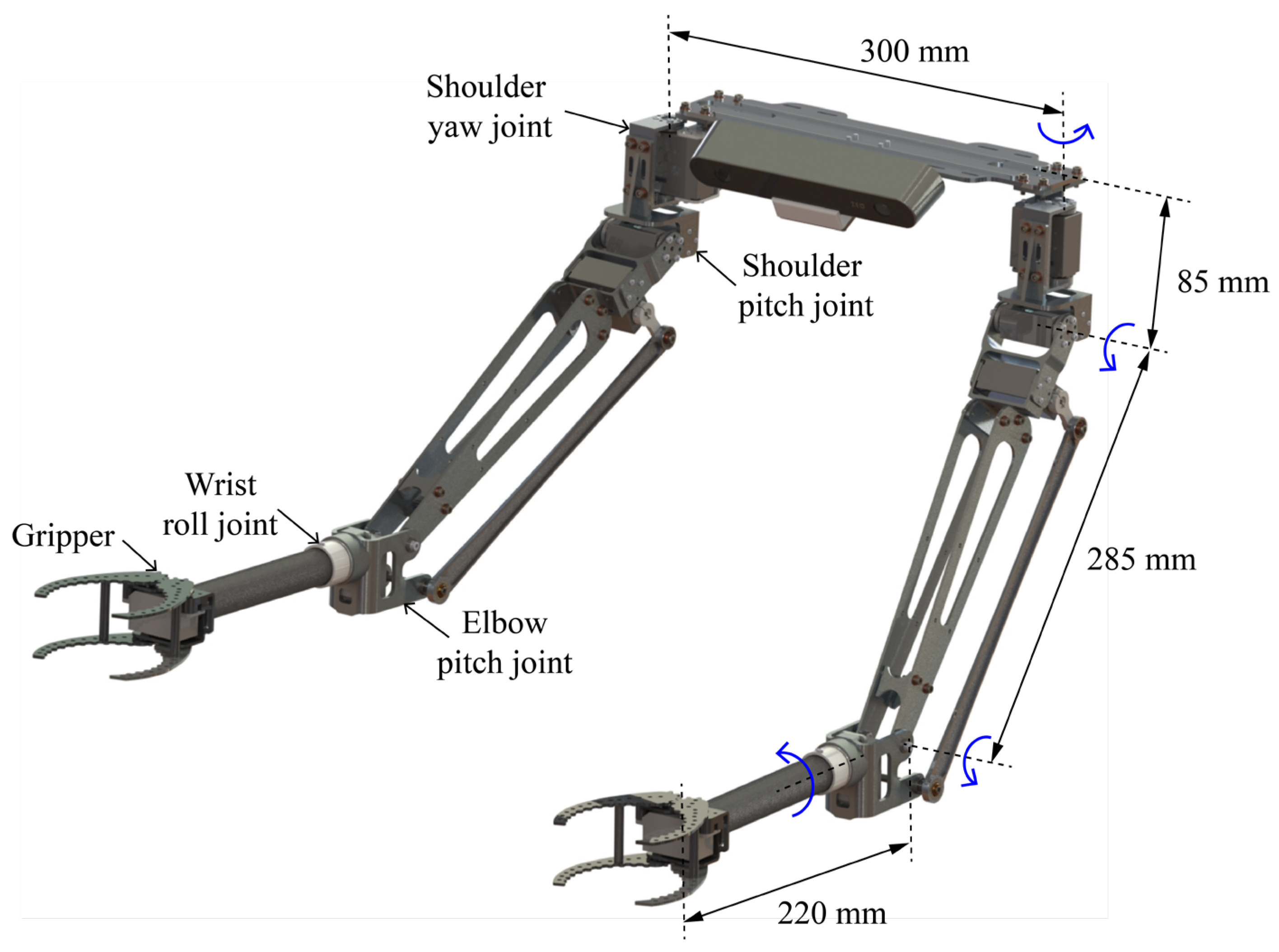
2.1. Dual-Arm Manipulator
2.1.1. General Overview
2.1.2. Materials for the Frame Structure
2.1.3. Workspace
2.2. Aerial Manipulation System
2.2.1. Aerial Platform
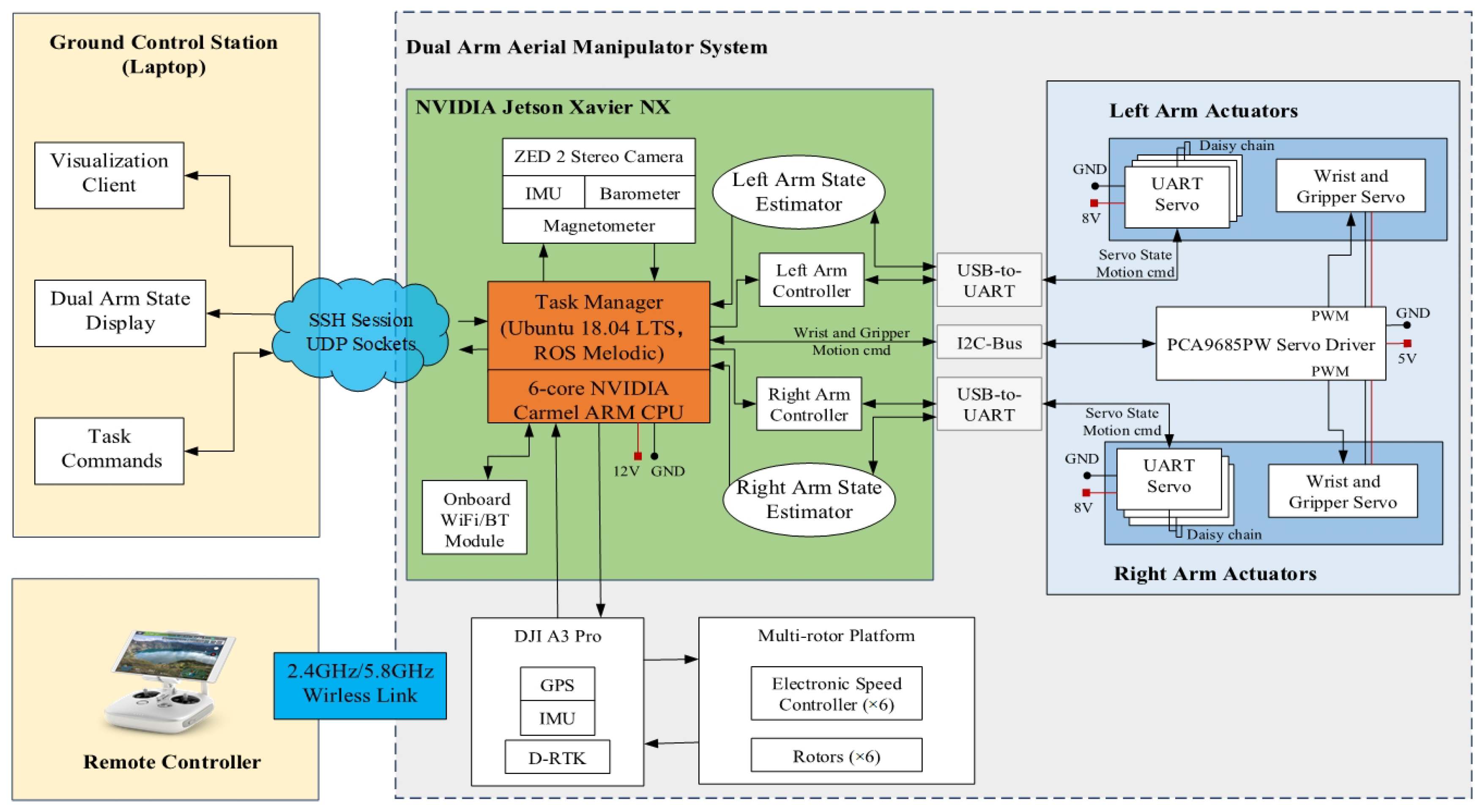
2.2.2. Hardware/Software Architecture
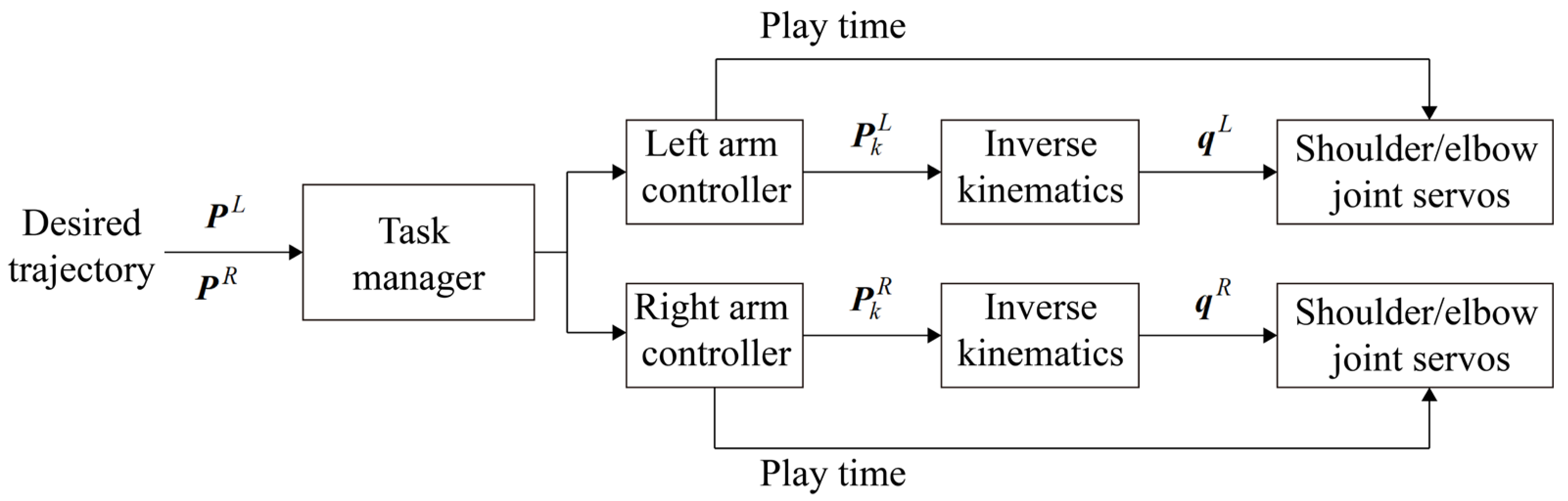
2.2.3. Control
3. Modeling
3.1. Kinematic Model
3.2. Dynamic Model
4. Experimental Results
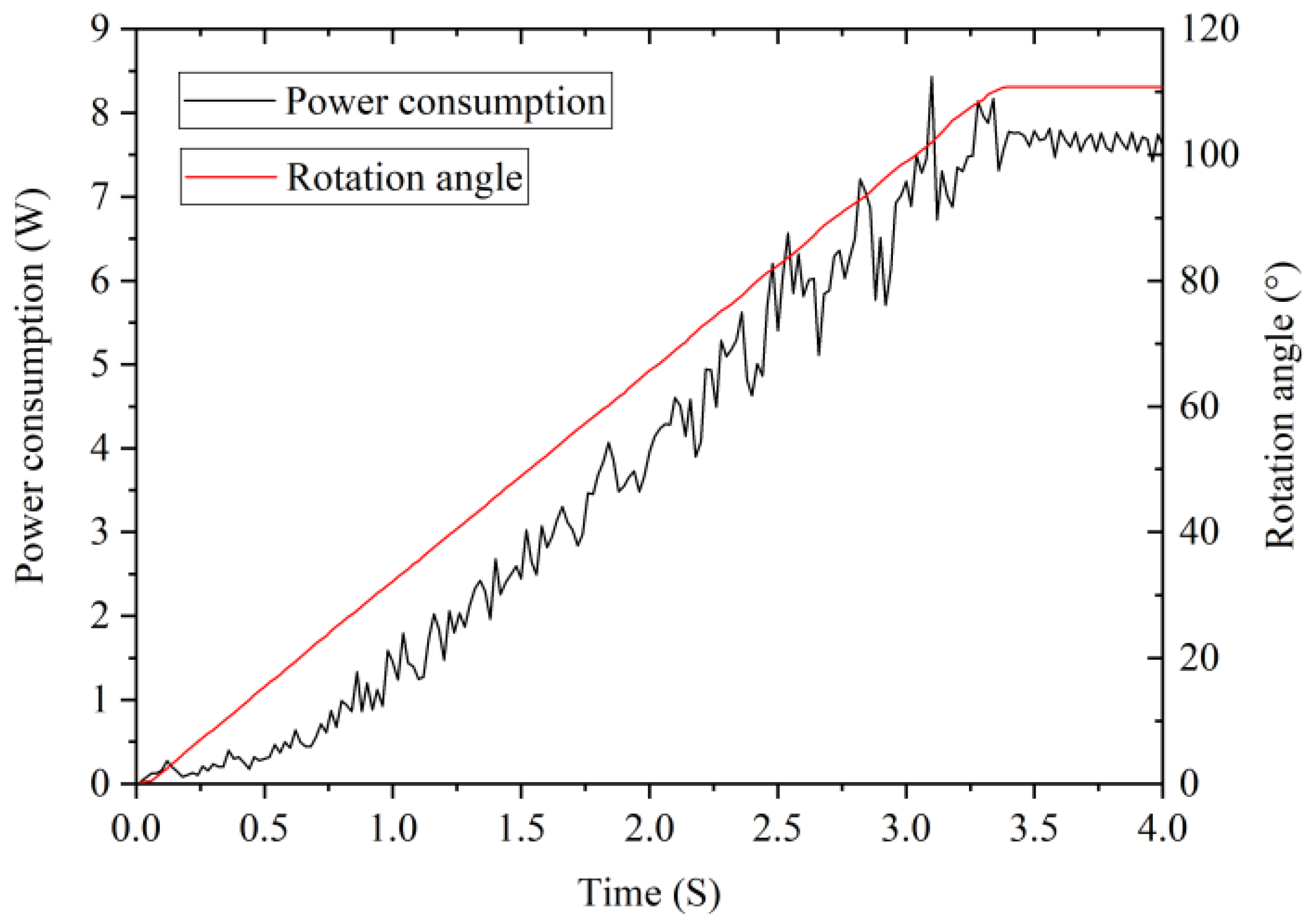
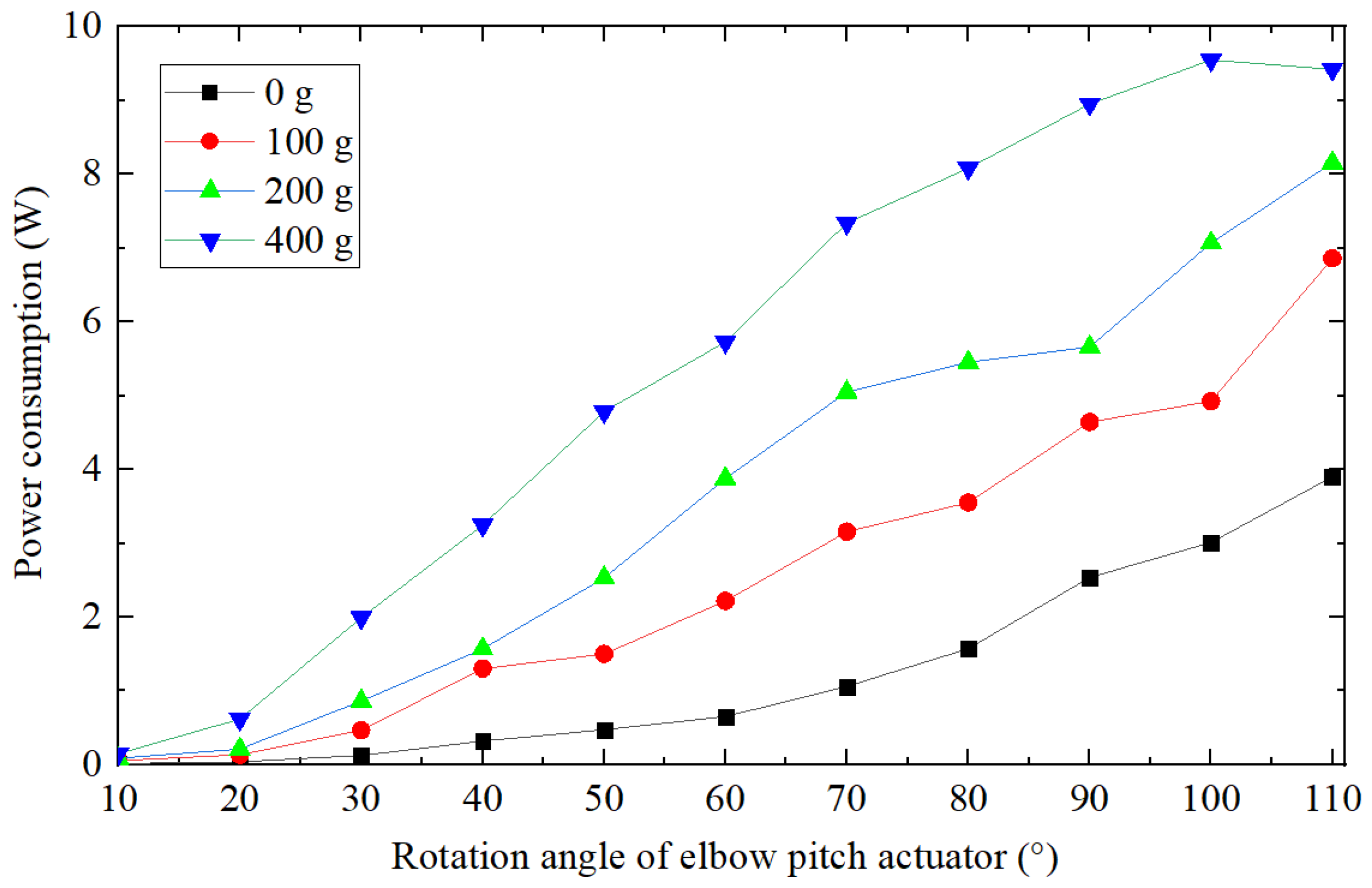
4.1. Lift Load
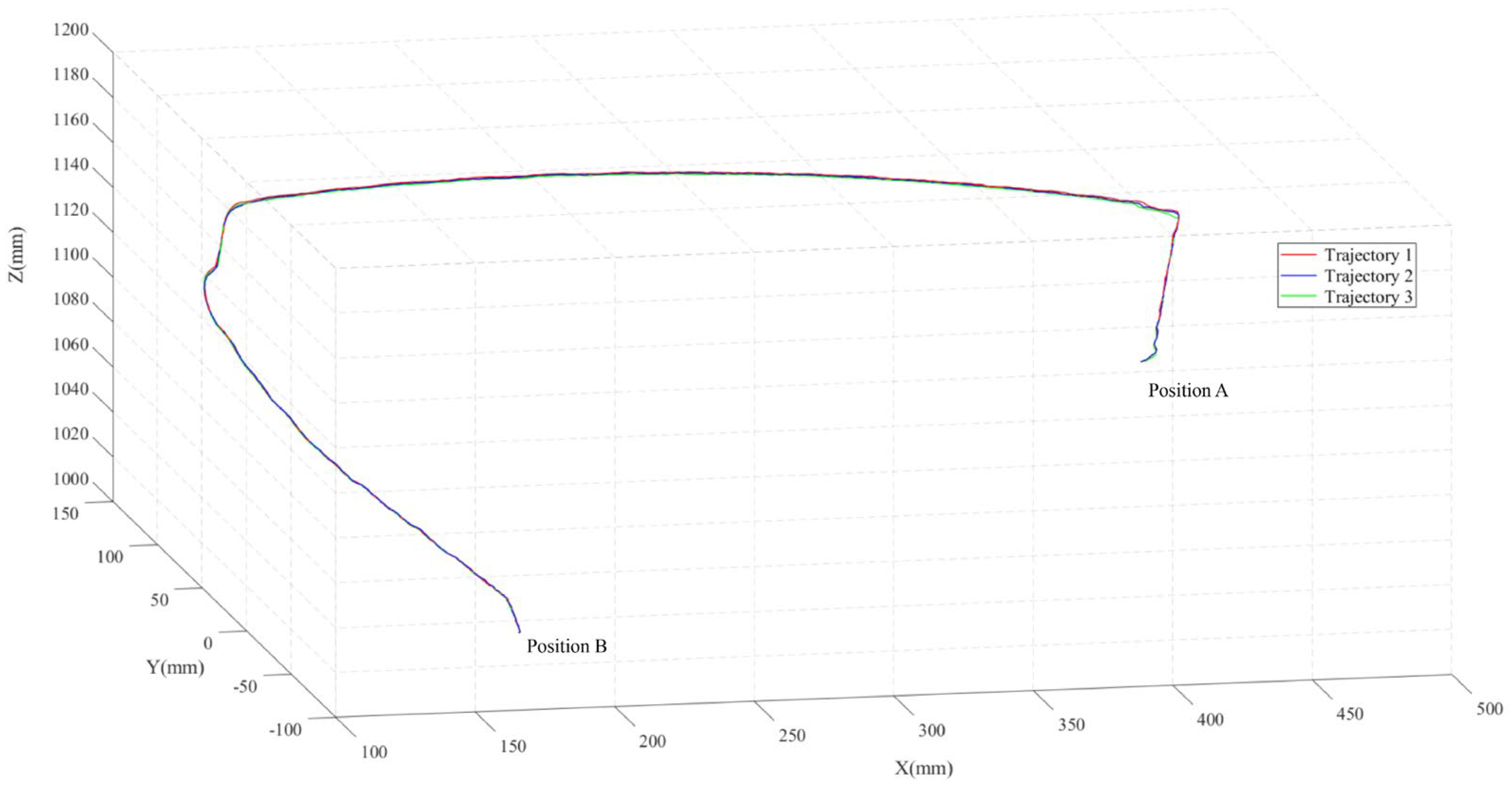
4.2. Accuracy and Repeatability
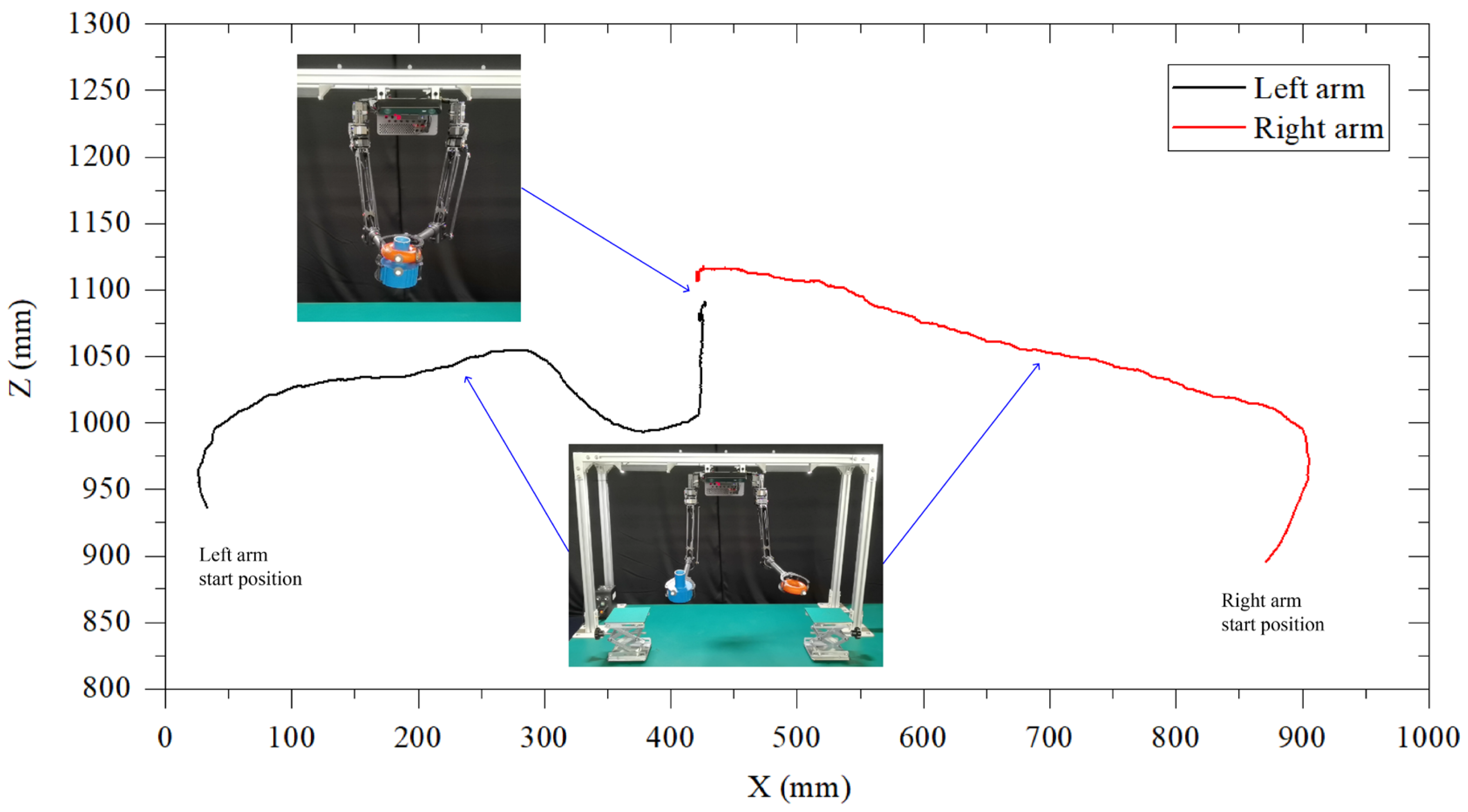
4.3. Cooperative Bimanual Manipulation
4.4. Outdoor Flight Tests
- (1)
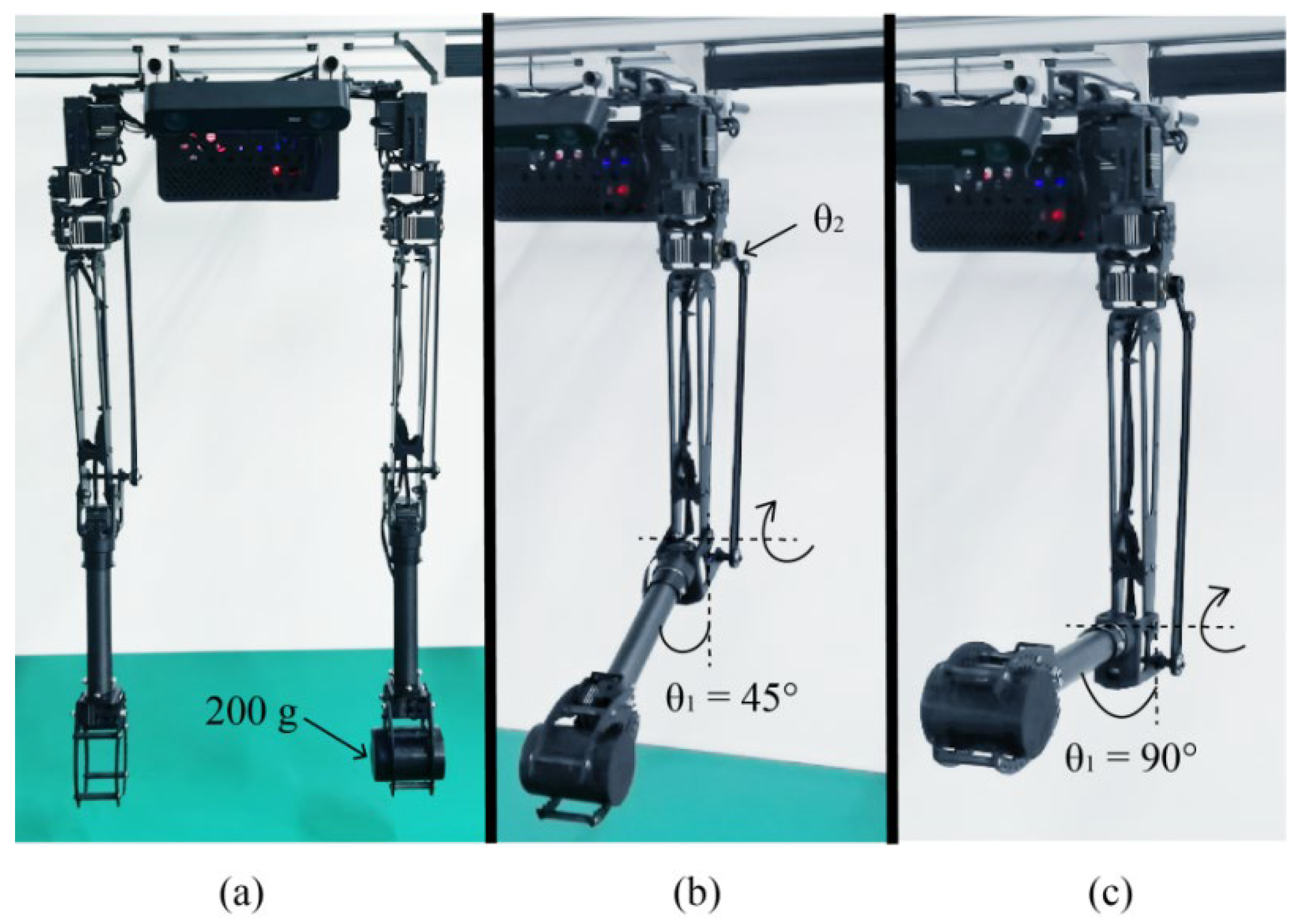
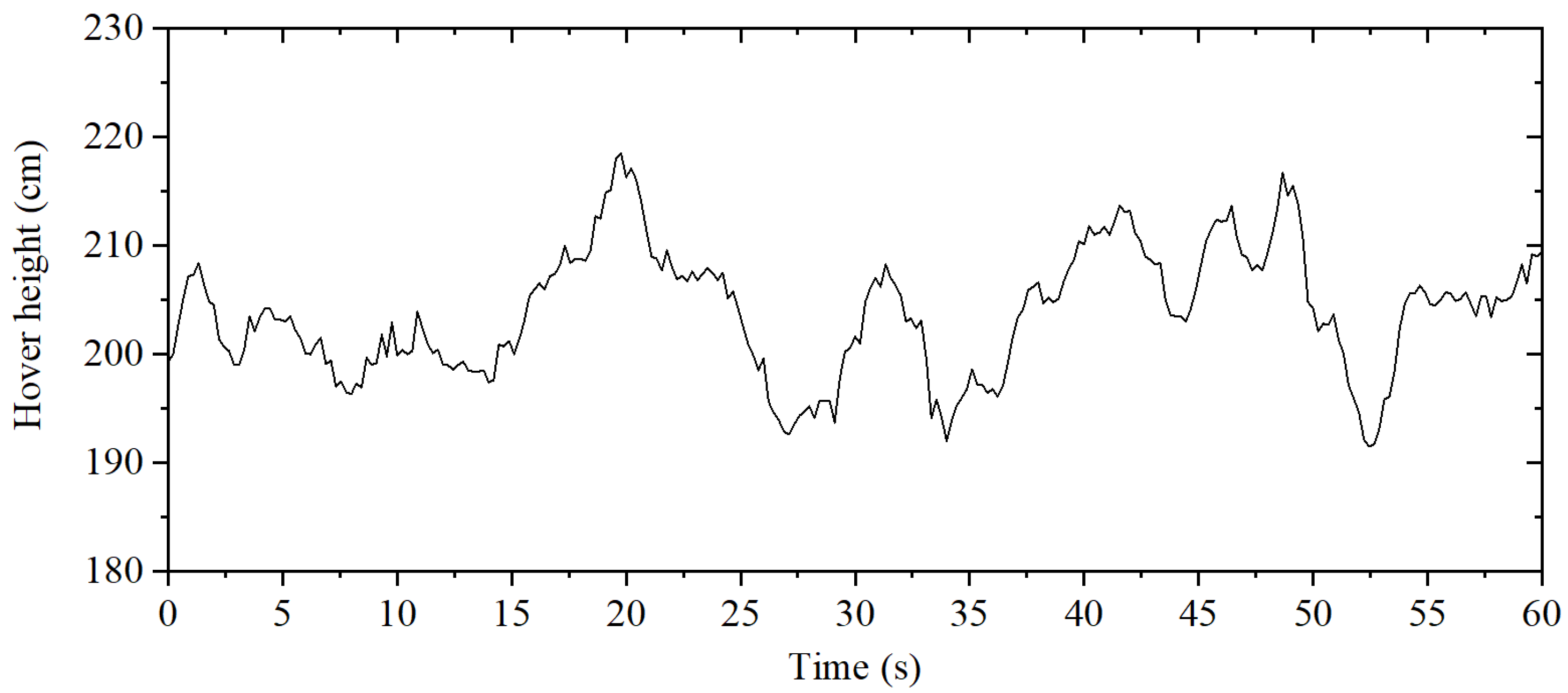
- Test 1: The mechanical arm is vertically stationary, and each joint actuator does not move. Testing the height position change of the whole system when hovering at 2 m.
- (2)
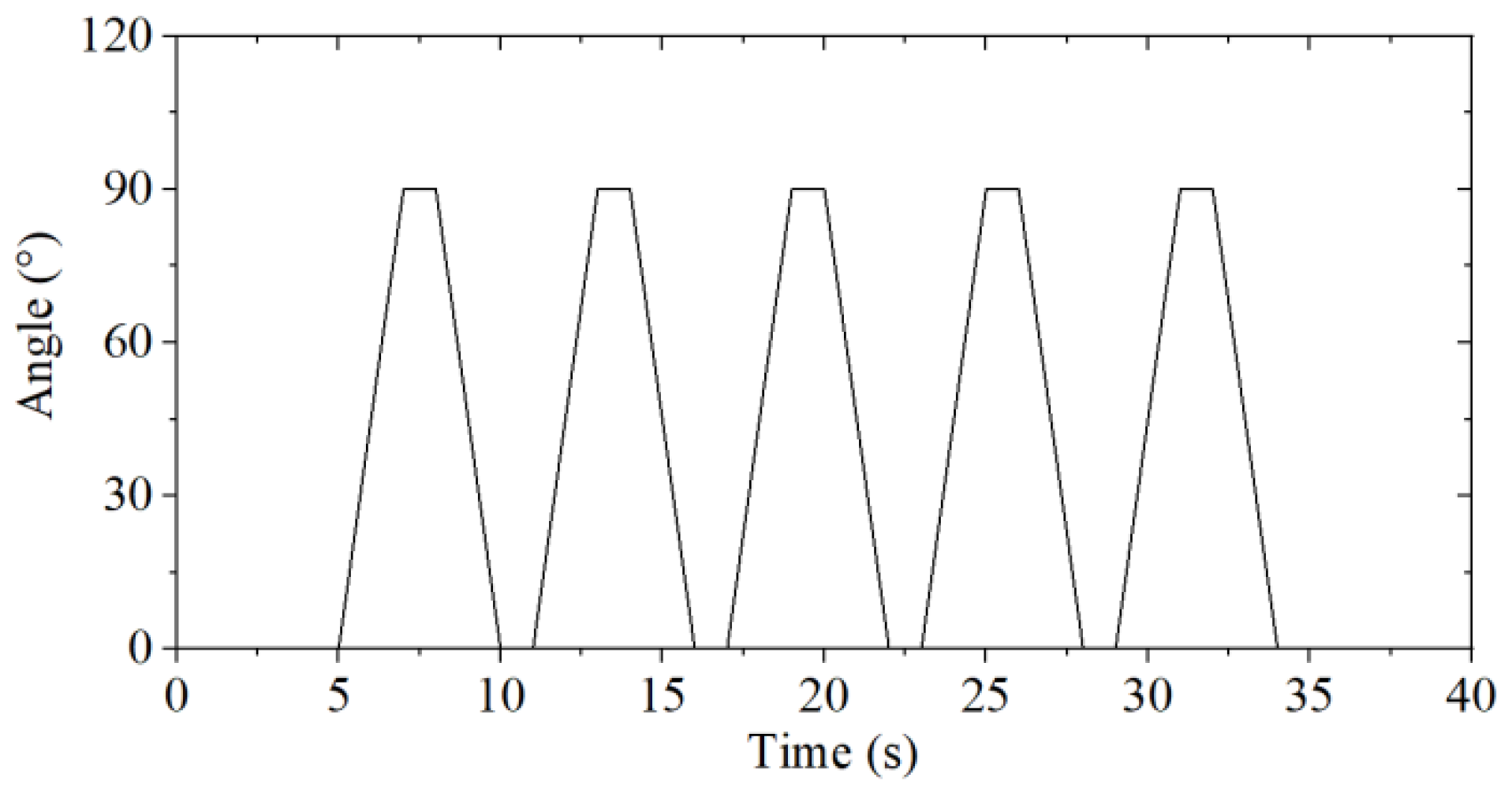
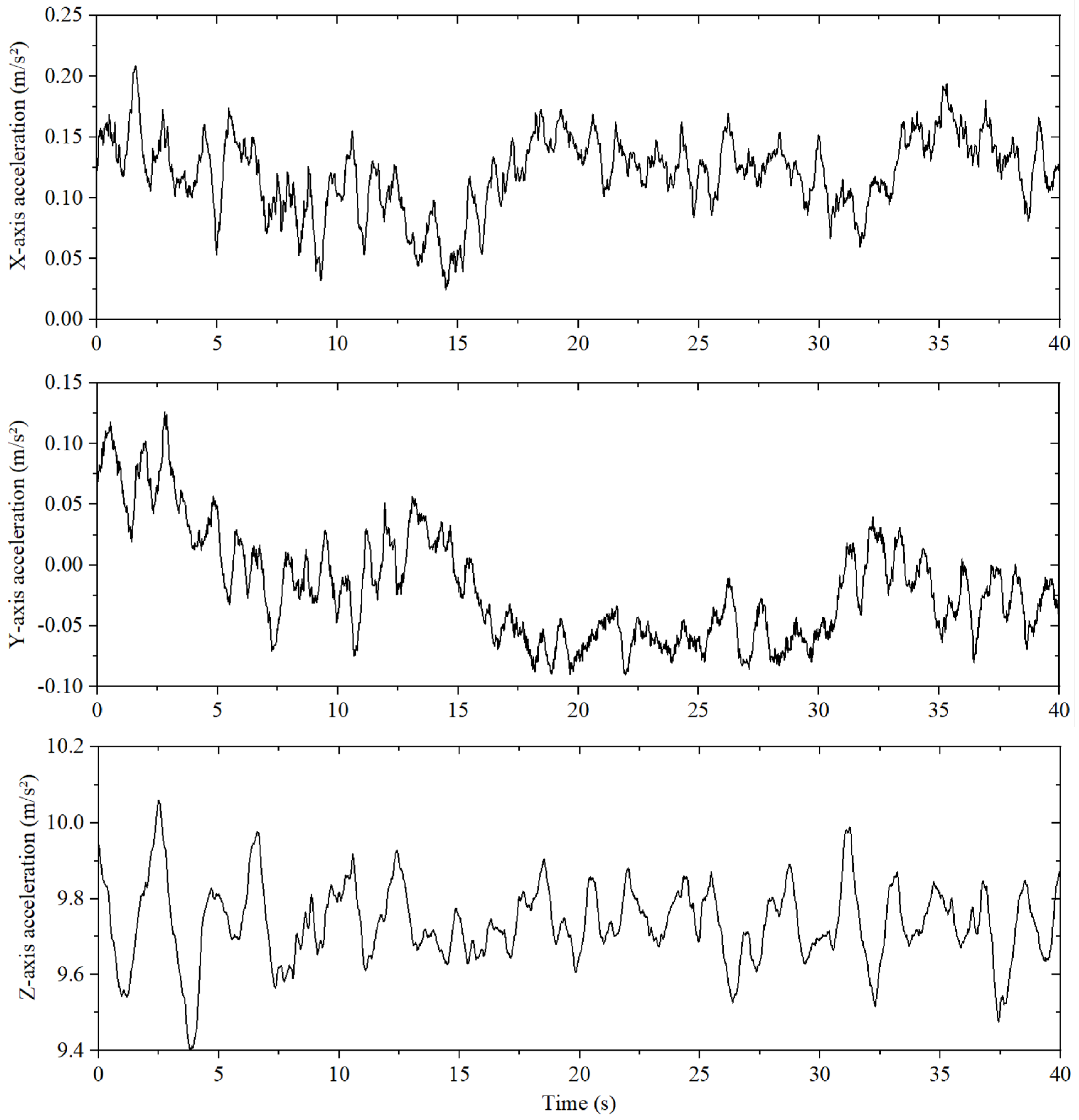
- Test 2: The left mechanical arm does not move vertically, the shoulder yaw actuator angle of the right mechanical arm rotates, as shown in Figure 15, and other joint actuators do not move. Testing the influence of single-arm wide range motion on the stability of the system. The image sequence of the test process is shown in Figure 16a.
- (3)
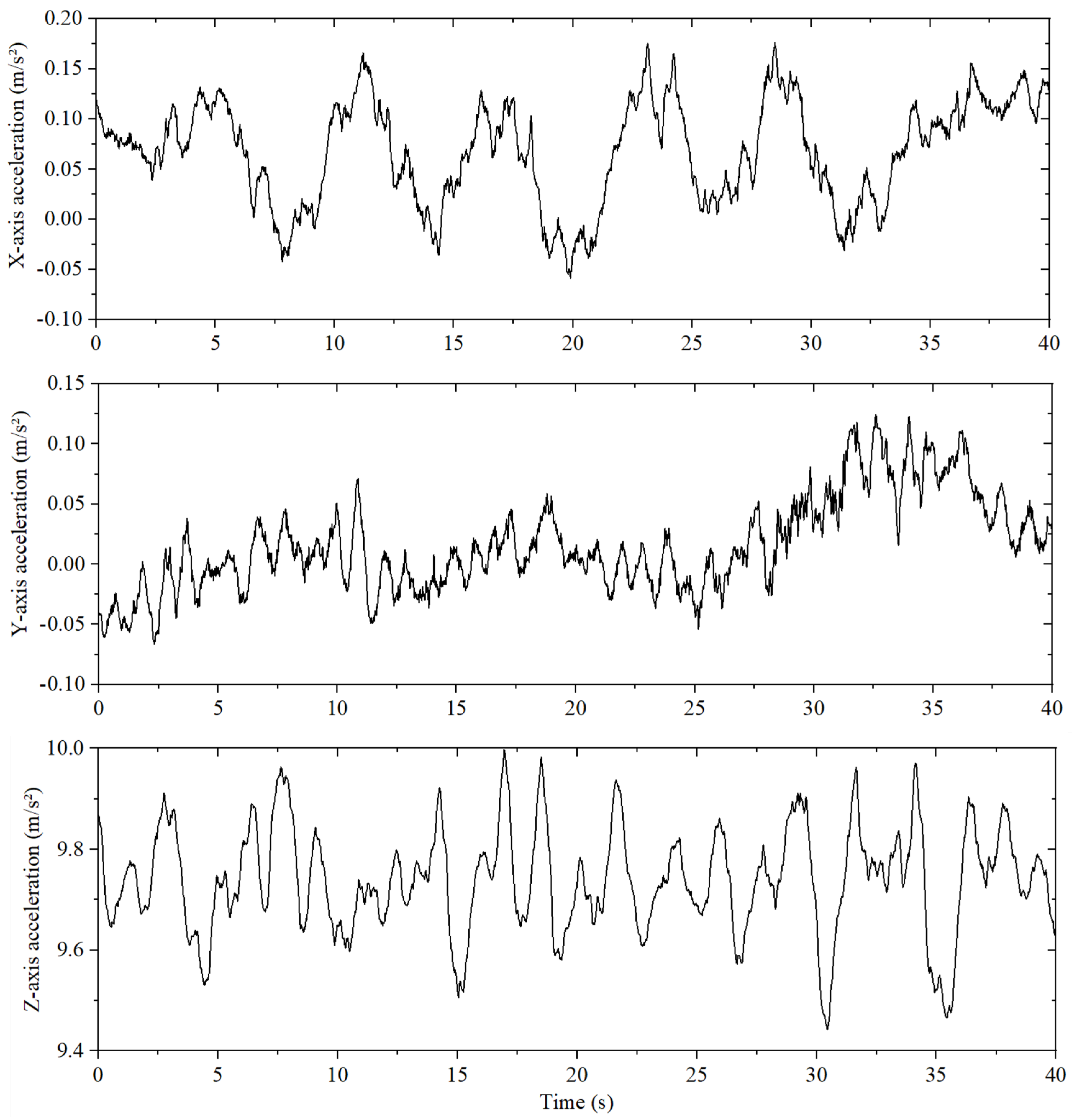
- Test 3: The angles of the shoulder yaw actuators of the left and right manipulator arms rotate, as shown in Figure 15, at the same time, and the other joint actuators do not move. Testing the influence of two arms' motion on the stability of the system. The image sequence of the test process is shown in Figure 16b.
5. Conclusions
- (1)
- A dual-arm manipulator system with low weight, low inertia, and a humanoid arm structure for aerial manipulation was developed. The weight of the dual-arm manipulator is 1.9 kg, and the arm frame structure supporting the servo actuator is composed of 41 customized aluminum parts. Each manipulator contains four degrees of freedom, similar to the arrangement of human joints, including shoulder yaw, shoulder pitch, elbow pitch, and wrist roll. The workspace of the dual-arm manipulator was simulated and analyzed, and the relevant kinematic and dynamic models were deduced.
- (2)
- Through various types of tests, the related performance of the dual-arm aerial manipulator system was analyzed and verified. Through the lift load, accuracy and repeatability, and cooperative bimanual manipulation tests on the test bench, the relevant operating performance of the designed dual-arm manipulator system was quantitatively evaluated. In the outdoor test, the manipulator was integrated on the commercial six-rotor platform, and the characteristics of low weight and low inertia of the designed dual-arm manipulator were verified through several groups of tests. At the same time, the test results showed the feasibility of the designed dual-arm aerial manipulator system for outdoor operation.
Author Contributions
Funding
Conflicts of Interest
References
- Reinoso, J.F.; Gonçalves, J.E.; Pereira, C.; Bleninger, T. Cartography for civil engineering projects: Photogrammetry supported by unmanned aerial vehicles. Iran. J. Sci. Technol. Trans. Civ. Eng. 2018, 42, 91–96. [Google Scholar] [CrossRef]
- Yang, L.; Fan, J.; Liu, Y.; Li, E.; Peng, J.; Liang, Z. A review on state-of-the-art power line inspection techniques. IEEE Trans. Instrum. Meas. 2020, 69, 9350–9365. [Google Scholar] [CrossRef]
- Annis, A.; Nardi, F.; Petroselli, A.; Apollonio, C.; Arcangeletti, E.; Tauro, F.; Belli, C.; Bianconi, R.; Grimaldi, S. UAV-DEMs for small-scale flood hazard mapping. Water 2020, 12, 1717. [Google Scholar] [CrossRef]
- Yu, Y.; Ding, X.; Zhu, J.J. Dynamic modeling and control for aerial arm-operating of a multi-propeller multifunction aerial robot. Adv. Robot. 2017, 31, 665–679. [Google Scholar] [CrossRef]
- Sun, Y.; Jing, Z.; Dong, P.; Huang, J.; Chen, W.; Leung, H. A Switchable Unmanned Aerial Manipulator System for Window-Cleaning Robot Installation. IEEE Robot. Autom. Lett. 2021, 6, 3483–3490. [Google Scholar] [CrossRef]
- Meng, X.; He, Y.; Han, J. Survey on aerial manipulator: System, modeling, and control. Robotica 2020, 38, 1288–1317. [Google Scholar] [CrossRef]
- Mimmo, N.; Macchelli, A.; Naldi, R.; Marconi, L. Robust motion control of aerial manipulators. Annu. Rev. Control 2020, 49, 230–238. [Google Scholar] [CrossRef]
- Hamaza, S.; Georgilas, I.; Fernandez, M.; Sanchez, P.; Richardson, T.; Heredia, G.; Ollero, A. Sensor installation and retrieval operations using an unmanned aerial manipulator. IEEE Robot. Autom. Lett. 2019, 4, 2793–2800. [Google Scholar] [CrossRef] [Green Version]
- Ollero, A.; Heredia, G.; Franchi, A.; Antonelli, A.; Kondak, K.; Sanfeliu, A.; Viguria, A.; Dios, J.R.M.; Pierri, F.; Cortes, J.; et al. The aeroarms project: Aerial robots with advanced manipulation capabilities for inspection and maintenance. IEEE Robot. Autom. Mag. 2018, 25, 12–23. [Google Scholar] [CrossRef] [Green Version]
- Chermprayong, P.; Zhang, K.; Xiao, F.; Kovac, M. An integrated delta manipulator for aerial repair: A new aerial robotic system. IEEE Robot. Autom. Mag. 2019, 26, 54–66. [Google Scholar] [CrossRef]
- Kutia, J.R.; Stol, K.A.; Xu, W. Aerial manipulator interactions with trees for canopy sampling. IEEE/ASME Trans. Mechatron. 2018, 23, 1740–1749. [Google Scholar] [CrossRef]
- Khamseh, H.B.; Janabi-Sharifi, F.; Abdessameud, A. Aerial manipulation—A literature survey. Robot. Auton. Syst. 2018, 107, 221–235. [Google Scholar] [CrossRef]
- Trujillo, M.Á.; Martínez-de Dios, J.R.; Martín, C.; Viguria, A.; Ollero, A. Novel aerial manipulator for accurate and robust industrial NDT contact inspection: A new tool for the oil and gas inspection industry. Sensors 2019, 19, 1305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hamaza, S.; Georgilas, I.; Heredia, G.; Ollero, A.; Richardson, T. Design, modeling, and control of an aerial manipulator for placement and retrieval of sensors in the environment. J. Field Robot. 2020, 37, 1224–1245. [Google Scholar] [CrossRef]
- Bartelds, T.; Capra, A.; Hamaza, S.; Fumagalli, M. Compliant aerial manipulators: Toward a new generation of aerial robotic workers. IEEE Robot. Autom. Lett. 2016, 1, 477–483. [Google Scholar] [CrossRef] [Green Version]
- Ruggiero, F.; Lippiello, V.; Ollero, A. Aerial manipulation: A literature review. IEEE Robot. Autom. Lett. 2018, 3, 1957–1964. [Google Scholar] [CrossRef] [Green Version]
- Mohiuddin, A.; Tarek, T.; Zweiri, Y.; Gan, D. A survey of single and multi-UAV aerial manipulation. Unmanned Syst. 2020, 8, 119–147. [Google Scholar] [CrossRef]
- Tognon, M.; Chávez, H.A.T.; Gasparin, E.; Sable, Q.; Bicego, D.; Mallet, A.; Lany, M.; Santi, G.; Revaz, B.; Cortes, J.; et al. A truly-redundant aerial manipulator system with application to push-and-slide inspection in industrial plants. IEEE Robot. Autom. Lett. 2019, 4, 1846–1851. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; He, Y.; Dai, B.; Gu, F.; Yang, L.; Han, J.; Liu, G. Aerial grasping of an object in the strong wind: Robust control of an aerial manipulator. Appl. Sci. 2019, 9, 2230. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Seo, H.; Shin, J.; Kim, H.J. Cooperative aerial manipulation using multirotors with multi-dof robotic arms. IEEE/ASME Trans. Mechatron. 2018, 23, 702–713. [Google Scholar] [CrossRef]
- Korpela, C.; Orsag, M.; Pekala, M.; Oh, P. Dynamic stability of a mobile manipulating unmanned aerial vehicle. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4922–4927. [Google Scholar]
- Caccavale, F.; Giglio, G.; Muscio, G.; Pierri, F. Adaptive control for UAVs equipped with a robotic arm. IFAC Proc. Vol. 2014, 47, 11049–11054. [Google Scholar] [CrossRef] [Green Version]
- Ruggiero, F.; Trujillo, M.A.; Cano, R.; Ascorbe, H.; Viguria, A.; Peréz, C.; Lippiello, V.; Ollero, A.; Siciliano, B. A multilayer control for multirotor UAVs equipped with a servo robot arm. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4014–4020. [Google Scholar]
- Jimenez-Cano, A.E.; Martin, J.; Heredia, G.; Ollero, A.; Cano, R. Control of an aerial robot with multi-link arm for assembly tasks. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4916–4921. [Google Scholar]
- Suarez, A.; Jimenez-Cano, A.E.; Vega, V.M.; Heredia, G.; Rodriguez-Castaño, A.; Ollero, A. Design of a lightweight dual arm system for aerial manipulation. Mechatronics 2018, 50, 30–44. [Google Scholar] [CrossRef] [Green Version]
- Suarez, A.; Heredia, G.; Ollero, A. Physical-virtual impedance control in ultralightweight and compliant dual-arm aerial manipulators. IEEE Robot. Autom. Lett. 2018, 3, 2553–2560. [Google Scholar] [CrossRef] [Green Version]
- Suarez, A.; Grau, P.; Heredia, G.; Ollero, A. Winged aerial manipulation robot with dual arm and tail. Appl. Sci. 2020, 10, 4783. [Google Scholar] [CrossRef]
- Suarez, A.; Real, F.; Vega, V.M.; Heredia, G.; Rodriguez-Castano, A.; Ollero, A. Compliant bimanual aerial manipulation: Standard and long reach configurations. IEEE Access 2020, 8, 88844–88865. [Google Scholar] [CrossRef]
- Suarez, A.; Heredia, G.; Ollero, A. Design of an anthropomorphic, compliant, and lightweight dual arm for aerial manipulation. IEEE Access 2018, 6, 29173–29189. [Google Scholar] [CrossRef]
- Cacace, J.; Orozco-Soto, S.M.; Suarez, A.; Caballero, A.; Orsag, M.; Bogdan, S.; Vasiljevic, G.; Ebeid, E.; Rodriguez, J.; Ollero, A. Safe Local Aerial Manipulation for the Installation of Devices on Power Lines: AERIAL-CORE First Year Results and Designs. Appl. Sci. 2021, 11, 6220. [Google Scholar] [CrossRef]
- Korpela, C.; Orsag, M.; Oh, P. Towards valve turning using a dual-arm aerial manipulator. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 3411–3416. [Google Scholar]
- Orsag, M.; Korpela, C.; Bogdan, S.; Oh, P. Dexterous aerial robots—Mobile manipulation using unmanned aerial systems. IEEE Trans. Robot. 2017, 33, 1453–1466. [Google Scholar] [CrossRef]
- Ramon-Soria, P.; Arrue, B.C.; Ollero, A. Grasp planning and visual servoing for an outdoors aerial dual manipulator. Engineering 2020, 6, 77–88. [Google Scholar] [CrossRef]
- Perez-Jimenez, M.; Ramon-Soria, P.; Arrue, B.C.; Ollero, A. Hecatonquiros: Open-source hardware for aerial manipulation applications. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420921622. [Google Scholar] [CrossRef]
- Yu, Y.; Ding, X. Safe landing analysis of a quadrotor aircraft with two legs. J. Intell. Robot. Syst. 2014, 76, 527–537. [Google Scholar] [CrossRef]
- Aguirre, O.A.; Nacato, J.C.; Andaluz, V.H. Virtual simulator for collaborative tasks of aerial manipulator robots. In Proceedings of the 2020 15th Iberian Conference on Information Systems and Technologies (CISTI), Seville, Spain, 15 July 2020; pp. 1–6. [Google Scholar]
- Caballero, A.; Béjar, M.; Rodriguez-Castaño, A.; Ollero, A. Motion planning for long reach manipulation in aerial robotic systems with two arms. In Proceedings of the 2017 European Conference on Mobile Robots (ECMR), Paris, France, 6–8 September 2017; pp. 1–7. [Google Scholar]
- Yu, P.; Wang, Z.; Wong, K.C. Exploring aerial perching and grasping with dual symmetric manipulators and compliant end-effectors. Int. J. Micro Air Veh. 2019, 11, 1756829319877416. [Google Scholar] [CrossRef] [Green Version]
- Lippiello, V.; Fontanelli, G.A.; Ruggiero, F. Image-based visual-impedance control of a dual-arm aerial manipulator. IEEE Robot. Autom. Lett. 2018, 3, 1856–1863. [Google Scholar] [CrossRef]
- Paul, H.; Miyazaki, R.; Ladig, R.; Shimonomura, K. TAMS: Development of a multipurpose three-arm aerial manipulator system. Adv. Robot. 2021, 35, 31–47. [Google Scholar] [CrossRef]
- Peidró, A.; Reinoso, Ó.; Gil, A.; Marín, J.M.; Payá, L. An improved Monte Carlo method based on Gaussian growth to calculate the workspace of robots. Eng. Appl. Artif. Intell. 2017, 64, 197–207. [Google Scholar] [CrossRef]
- Suarez, A.; Sanchez-Cuevas, P.J.; Heredia, G.; Ollero, A. Aerial Physical Interaction in Grabbing Conditions with Lightweight and Compliant Dual Arms. Appl. Sci. 2020, 10, 8927. [Google Scholar] [CrossRef]
- Suarez, A.; Vega, V.M.; Fernandez, M.; Heredia, G.; Ollero, A. Benchmarks for aerial manipulation. IEEE Robot. Autom. Lett. 2020, 5, 2650–2657. [Google Scholar] [CrossRef]








| Joint | Servo Model | Stall Torque (N·m) | No-Load Speed (rad/s) | Rotation Range (°) | Actuator Weight (g) |
|---|---|---|---|---|---|
| Shoulder yaw | RX8-U45H-M | 4.5 | 9.52 | [0,120] | 82 |
| Shoulder pitch | RX8-U45H-M | 4.5 | 9.52 | [0,100] | 82 |
| Elbow pitch | RX8-U45H-M | 4.5 | 9.52 | [0,110] | 82 |
| Wrist roll | Power HD-S15 | 1.5 | 14.5 | ±90 | 52 |
| Gripper | Power HD-S15 | 1.5 | 14.5 | [0,90] | 52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Wang, H.; Liu, Z.; Dong, Z.; Zhang, L. Development of an Anthropomorphic and Dexterous Dual-Arm System for Aerial Cooperative Bimanual Manipulation. Machines 2022, 10, 273. https://doi.org/10.3390/machines10040273
Yang P, Wang H, Liu Z, Dong Z, Zhang L. Development of an Anthropomorphic and Dexterous Dual-Arm System for Aerial Cooperative Bimanual Manipulation. Machines. 2022; 10(4):273. https://doi.org/10.3390/machines10040273
Chicago/Turabian StyleYang, Peng, Hao Wang, Zhen Liu, Zhiyan Dong, and Lihua Zhang. 2022. "Development of an Anthropomorphic and Dexterous Dual-Arm System for Aerial Cooperative Bimanual Manipulation" Machines 10, no. 4: 273. https://doi.org/10.3390/machines10040273
APA StyleYang, P., Wang, H., Liu, Z., Dong, Z., & Zhang, L. (2022). Development of an Anthropomorphic and Dexterous Dual-Arm System for Aerial Cooperative Bimanual Manipulation. Machines, 10(4), 273. https://doi.org/10.3390/machines10040273






