RPEOD: A Real-Time Pose Estimation and Object Detection System for Aerial Robot Target Tracking

Abstract

Pose estimation and environmental perception are the fundamental capabilities of autonomous robots. In this paper, a novel real-time pose estimation and object detection (RPEOD) strategy for aerial robot target tracking is presented. The aerial robot is equipped with a binocular fisheye camera for pose estimation and a depth camera to capture the spatial position of the tracked target. The RPEOD system uses a sparse optical flow algorithm to track image corner features, and the local bundle adjustment is restricted in a sliding window. Ulteriorly, we proposed YZNet, a lightweight neural inference structure, and took it as the backbone in YOLOV5 (the state-of-the-art real-time object detector). The RPEOD system can dramatically reduce the computational complexity in reprojection error minimization and the neural network inference process; Thus, it can calculate real-time on the onboard computer carried by the aerial robot. The RPEOD system is evaluated using both simulated and real-world experiments, demonstrating clear advantages over state-of-the-art approaches, and is significantly more fast.

1. Introduction

Micro aerial vehicles (MAVs) will soon play a significant role in industrial inspection, accident warning, and national defense [1,2,3]. For such operations, flight mode dependent on the human remote control can no longer meet the mission requirements under complex conditions. Ulteriorly, MAVs navigation based on GNSS information only is not sufficient. Precise fully autonomous operation requires the aerial robot to rely on accurate environmental perception and a robust state estimation system [4]. Once an embedded computer is implemented on an ordinary MAV and sends flight commands directly without human manipulation, this intelligent MAV will become an aerial robot. Due to the quadrotor MAVs’ swing during moving, the robot navigation system requires that the pose estimator have extraordinary robustness. This leads to the existing state estimation methods being usually unsatisfactory. Furthermore, it is urgent to implement a pattern recognition system for the aerial robot in order to obtain the environmental semantic information around the aerial robot.

Unfortunately, there are still some difficulties for implementing state estimation and target tracking system directly on the aerial robot computer. In recent years, in the field of pattern recognition, researchers tend to build deeper and more complex object detection architecture in order to pursue higher detection accuracy [5,6,7]. However, these innovative architectures to improve the mean average precision (mAP) of the target detection system do not necessarily make the detection system more effective in inferring speed and memory occupation. In the aerial robot target-tracking task, the aerial robot state estimator and object detector need to run in real time on airborne hardware equipment with limited computing and storage. Nevertheless, the deep neural model has the characteristics of computing intensive structure, which makes it difficult for the high-performance convolution model to be implemented on the airborne computer with limited computing power [8].

In this paper, we demonstrate RPEOD, a simultaneous real-time pose estimation and object detection system for aerial robot target tracking, which combines inertial measurement and sparse optical flow tracking algorithms [9] to estimate the MAV motion between consecutive video frames. Meanwhile, the object detection module will lock the target in the environment and locate the spatial position of the tracked target, as shown in Figure 1. The RPEOD system can achieve real-time performance with CUDA acceleration on an airborne platform (the input video resolution is: 640 × 480). The main novelties of RPEOD are as follows:

Figure 1. The aerial robot equipped with the RPEOD system.

• The RPEOD system uses a sparse optical flow algorithm to track the Shi-Tomasi [10] corner, and the feature describing and matching are not required in this process. After CUDA acceleration, the whole state estimator can calculate in real time on the onboard computer carried by the MAV.
• The local bundle adjustment is restricted in a narrow sliding window, which dramatically reduces the number of variables in the back-end optimization process. Meanwhile, the computation complexity of the RPEOD system is bound by the additional marginalization scheme.
• We proposed YZNet, an extremely lightweight neural inference structure, and took it as the backbone in YOLOV5, which can prominently reduce the number of neural network weights and inference delay on the premise of maintaining object detection accuracy so that the deep neural network can run in real time on the low-power onboard computer.

2. Related Work

2.1. Robot Pose Estimation

Robot pose estimator can immediately provide the current position and orientation with high frequency. It is an essential part of the intelligent robot. In the process of aerial robot target tracking, the performance of the pose estimator will directly affect the success of the tracking task. Due to the limitations of the congeneric sensor, researchers usually prefer to use the method of multi-sensor fusion in recent years [11,12,13,14,15]. Compared with Lidar, stereo cameras have the characteristics of portability, which is inexpensive and has low power consumption. It is more suitable as the positioning source of micro robots.

At present, vision-based state estimation methods are mainly divided into direct methods [16,17] and feature methods [18,19,20]. Direct methods estimate camera motion directly from pixel gray levels in the consecutive video frames. The local intensity gradient magnitude and direction are used in the robot pose solving process compared to feature-based methods [17]. The feature-based methods are mainly completed by the following steps: firstly, extracting a sparse set of image corner points (e.g., SIFT, ORB, Shi-Tomasi) in consecutive video frames; secondly, matching these corner points separately in each image using invariant feature descriptors; thirdly, recovering robot pose by spatial epipolar geometry constraint; finally, optimizing the position and orientation through reprojection error minimization. The computation of the direct methods with photometric error minimization is more intensive than the feature-based methods with reprojection error minimization, and the direct methods have unstable robustness to illumination variations. Therefore, researchers began to use feature-based methods to incrementally estimate robot pose.

2.2. Neural Inference Acceleration Technology

The lightweight technologies for deep neural networks are mainly divided into pruning the trained model and redesigning the compact neural architecture. Neural network pruning refers to directly discarding the parameters that have little impact on the model performance according to the importance of the weights in the trained model [8]. Network pruning and quantization are the most direct and effective means to compress convolutional neural networks (CNNs). In practical engineering applications, the absolute values of these weights are often close to zero. The weights approximately equal to zero in the deep model can be deleted directly, which has little impact on the performance of the whole neural network. The detection mean average precision before pruning can be quickly restored through finetuning. In numerical operation, the digit capacity determines the calculation accuracy. In the field of deep learning, model quantization further compresses the pruned deep model by reducing the digit capacity required to represent each parameter in the onboard computer. Making multiple connections share the same weight to limit the number of effective weights to be stored, and then finetuning these shared weights to achieves the purpose of compressing the depth neural network [8].

Designing the new convolution structure to realize the optimal trade-off between accuracy and efficiency is an important research direction in recent years. In SqueezeNet [21], 1 × 1 convolution is widely used to reduce the number of model parameters. In recent years, the neural network lightweight research focus has transformed from reducing the number of model parameters to reducing the actual amount of calculation and hardware delay. For example, the deep separable convolution structure [22] has attracted more and more attention, as shown in Figure 2. The convolution structure decomposes the traditional three-dimensional convolution into a combination of two-dimensional surface convolution and 1 × 1 convolution, which can reduce the amount of calculation by more than eight times. Deep separable convolution is widely used in MobileNet series networks [23,24] to construct an efficient convolution calculation module with linear bottleneck structure, and then build a high-efficiency and low-power deep convolutional network, which is suitable for operation on airborne hardware devices equipped with tensor processors. ShuffleNet series networks [25,26] further reduce the floating-point computation by using grouped convolution structure and channeling random crisscrossing operation. CondenseNet [27] proposes a fusion convolution structure to maintain the dense connection between layers useful for prominent features, which can facilitate feature reuse and greatly improve computational efficiency.

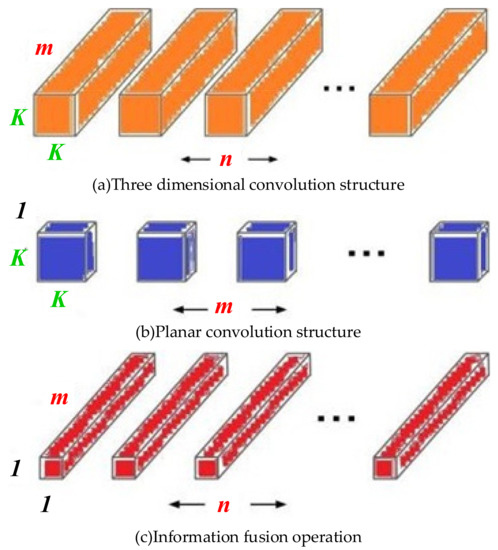
Figure 2. The depthwise separable convolutional structure.

3. Aerial Robot Pose Estimator

3.1. Feature Extracting and Tracking

The feature tracking process is mainly responsible for corner feature extraction and sparse optical flow tracking, and sends the tracking results to the MAV pose estimator. For each input video frame, when the number of feature points is less than the preseted threshold (120), new corner features are extracted to maintain a sufficient number of corner features. Meanwhile, a uniform corner distribution is implemented by setting a minimum pixel interval between adjacent features. Considering the motion instability of the quadrotor aerial robot, we extract the Shi-Tomasi [10] corners for sparse optical flow tracking [9]. It is worth noting that the feature extraction and sparse optical flow tracking algorithms can run in real time on the airborne-embedded platform carried by the quadrotor aerial robot after being accelerated by CUDA.

Another primary function of the feature tracking process is the video keyframe deciding. If the pixel parallax of video frames exceeds the threshold between the current frame and contiguous keyframe, the current frame will be treated as a new keyframe. Not only the image translation, but also image rotation is regarded as a pixel parallax. Meanwhile, to avoid tracking disconnection caused by too few corners in the surrounding environment, another keyframe selection strategy [28] is enabled when the number of tracked Shi-Tomasi [10] corners goes below a preset threshold.

3.2. Inertial Measurements Preintegration

In the world coordinate system (w), the quadrotor MAV orientation, position, and speed can be obtained by the inertial measurement unit (IMU) measurements that are measured in the quadrotor robot body frame and are disturbed by stochastic noise n, acceleration bias b_a, and gyroscope bias b_ω, which are approximated to a Brownian motion. The moments of two video frames (r_k and r_k+1) are approximated to be t_k and t_k+1; the quadrotor MAV orientation, velocity, and position are derived as the following:

$$\left\{\begin{array}{c}{o}_{rk+1}^w=o_{rk}^w\otimes {\displaystyle {\int }_{t\in [tk,tk+1]}\frac{1}{2}}\mathsf{\Phi }({\widehat{\omega }}_t-b_{\omega t}-n_{\omega })o_t^{rk}dt\hfill \\ v_{rk+1}^w=v_{rk}^w+{\displaystyle {\int }_{t\in [tk,tk+1]}(R_t^w}({\widehat{a}}_t-b_{at}-n_a)-g^w)dt\hfill \\ p_{rk+1}^w=p_{rk}^w+\Delta t_k{v}_{rk}^w+{\displaystyle {\iint }_{t\in [tk,tk+1]}(R_t^w}({\widehat{a}}_t-b_{at}-n_a)-g^w)d{t}^2,\end{array}\right.$$

(1)

where $\widehat{\omega }$ and $\widehat{a}$ are the gyroscope and accelerometer measurements, symbol $\otimes$ defined quaternion multiplication, n_ω and n_a are Gaussian white noise, and Δt_k is the duration between the neighbouring frames.

$$\mathsf{\Phi }(\omega )=\left[\begin{array}{cc}-{⌊\omega ⌋}_{\times }& \omega \\ -{\omega }^T& 0\end{array}\right],{⌊\omega ⌋}_{\times }=\left[\begin{array}{ccc}0& -{\omega }_z& {\omega }_y\\ {\omega }_z& 0& -{\omega }_x\\ -{\omega }_y& {\omega }_x& 0\end{array}\right],$$

(2)

The accelerometer integral term contains the gravitational acceleration in the world coordinate system. Because the gravity vector does not change over time, it does not need to propagate with the accelerometer measurements [29,30]. In the process of the aerial robot tracking target, the state of quadrotor MAV is changing all the time, and we have to reintegrate IMU measurements between them. To alleviate the computational load of the robot pose estimator, we can adopt the inertial measurement preintegration scheme.

The influence of gravitational acceleration can be eliminated by changing the reference coordinate from the world coordinate to the quadrotor body coordinate. We can only preintegrate the portions that are related to gyroscope measurements $\widehat{\omega }$ and accelerometer measurements $\widehat{a}$, as follows:

$$\left\{\begin{array}{c}{o}_w^{rk}\otimes o_{rk+1}^w={\alpha }_{rk+1}^{rk}\hfill \\ R_w^{rk}{v}_{rk+1}^w=R_w^{rk}(v_{rk}^w-\Delta t_k{g}^w)+{\beta }_{rk+1}^{rk}\hfill \\ R_w^{rk}{p}_{rk+1}^w=R_w^{rk}(p_{rk}^w+\Delta t_k{v}_{rk}^w-\frac{1}{2}\Delta t_k^2{g}^w)+{\gamma }_{rk+1}^{rk},\end{array}\right.$$

(3)

where

$$\left\{\begin{array}{c}{\alpha }_{rk+1}^{rk}={\displaystyle {\int }_{t\in [tk,tk+1]}\frac{1}{2}}\mathsf{\Phi }({\widehat{\omega }}_t-b_{\omega t}-n_{\omega }){\alpha }_t^{rk}dt\hfill \\ {\beta }_{rk+1}^{rk}={\displaystyle {\int }_{t\in [tk,tk+1]}{R}_t^{rk}}({\widehat{a}}_t-b_{at}-n_a)dt\hfill \\ {\gamma }_{rk+1}^{rk}={\displaystyle {\iint }_{t\in [tk,tk+1]}{R}_t^{rk}}({\widehat{a}}_t-b_{at}-n_a)d{t}^2,\hfill \end{array}\right.$$

(4)

Preintegrate terms α, β, and γ are only effected by IMU biases instead of other quadrotor MAV motion from video frame k to k + 1. When the bias changes slightly, we can only adjust α, β, and γ by their first-order Jacobian approximations. In the graph optimization-based state estimation system, the quadrotor MAV states are changed every time. Therefore, this inertial measurement preintegrate trick saves a large number of computational resources, because the IMU measurements do not need to be integrated repeatedly. The first-order approximation of preintegrate terms, α, β, and γ, can be formulated as follows:

$$\left\{\begin{array}{c}{\alpha }_{rk+1}^{rk}\approx {\widehat{\alpha }}_{rk+1}^{rk}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{J}_{b\omega }^{\alpha }\Delta b_{\omega k}\end{array}\right]\hfill \\ {\beta }_{rk+1}^{rk}\approx {\widehat{\beta }}_{rk+1}^{rk}+J_{ba}^{\beta }\Delta b_{ak}+J_{b\omega }^{\beta }\Delta b_{\omega k}\\ {\gamma }_{rk+1}^{rk}\approx {\widehat{\gamma }}_{rk+1}^{rk}+J_{ba}^{\gamma }\Delta b_{ak}+J_{b\omega }^{\gamma }\Delta b_{\omega k},\end{array}\right.$$

(5)

where J^α indicates the subblock Jacobian matrix J_ck+1, and the same meaning is also used for the others. When the inertial measurement bias changes, we can utilize Equation (5) to adjust inertial measurement preintegration results approximately, instead of integrating them repeatedly.

3.3. Tightly Coupled Aerial Robot Pose Estimation

One of the advantages of the binocular camera is that we do not need a specific structure from motion (SFM) initialization as in the monocular case, as the depth information of two-dimensional pixels has been obtained by visual geometry constraint. First, a keyframe with the initial video frame is created, then its pose is set, as the world coordinates the origin. Meanwhile, e an initial local map from all stereo points is created. To obtain a quadrotor MAV state more immediately, we proceed with a tightly-coupled pose estimation with a narrow sliding window-based strategy that delimits computational complexity in a tolerable boundary. The state vector in a sliding window can be written as:

$$\left\{\begin{array}{c}\chi ={\left[x_0,x_1,\dots x_n,{\lambda }_1,{\lambda }_2,\dots {\lambda }_m\right]}^T\\ xk={\left[o_{rk}^w,v_{rk}^w,p_{rk}^w,b_a,b_g\right]}^T,k\in \left[0,n\right],\end{array}\right.$$

(6)

where n and m are the numbers of keyframes and Shi-Tomasi corners, respectively, in the sliding window. λ is the pixel corners depth from Intel Realsense T265 binocular camera observation. x_k is the aerial robot odometry vector at the time that the kth frame is captured. It contains the robot pose and velocity in the world coordinate frame.

The maximum posteriori estimation can be formulated by minimizing the summation of prior and all sensor measurement errors.

$$\widehat{\chi }=\underset{\chi }{argmin}\left({‖P‖}^2+{\displaystyle \sum _{k\in I}{‖E_I‖}^2+{\displaystyle \sum _{(l,j)\in C}\rho {‖E_c‖}^2}}\right),$$

(7)

where the P, E_I, E_c and p are defined as:

$$\left\{\begin{array}{c}P=ep-H_p\chi \\ E_I=e_I({\widehat{m}}_{rk+1}^{rk},\chi )\\ E_c=e_c({\widehat{m}}_l^{Cj},\chi )\end{array}\right.,$$

(8)

$$\rho (x)=\left\{\begin{array}{cc}x& x<1\\ 2\sqrt{x}-1& x\ge 1\end{array}\right.,$$

(9)

where e_p and H_p are the prior information from marginalization. E_I and E_c are error function from IMU and Intel Realsense T265 camera, respectively. This maximum posteriori estimation is solved by Ceres solver.

4. Designing Efficient CNNs for Real-Time Object Detection

Object detection aims at searching for all interested objects in a video frame and predicting their bounding boxes and categories. Many excellent target detectors have been implemented in engineering applications, achieving inspiring results, such as: the YOLO series [31,32,33], Sparse-RCNN [5], and TSP-FCOS [6], etc. Unfortunately, these detectors have some limitations without strong GPU support. In this section, to improve the inference speed of the real-time object detector, we will try to redesign a lightweight CNNs as the backbone of YOLOV5.

4.1. Channel Attention Module

Differently from the traditional visual saliency mechanism, the channel attention mechanism can be considered as a general network optimization method, which can directs the limited system computing resources to deal with the most sensitive part of the input signal [34]. From the recognizing and understanding of specific targets to the construction of sequence-based deep models, the advantages of the channel attention mechanism have been reflected in a series of pattern recognition tasks. The channel attention mechanism module in a deep neural network is usually realized by gating functions (such as swish or sigmoid) and information-sorting technology.

A channel attention module [35] called squeeze and excitation (SE) is introduced in this paper to explore another crucial potential factor for improving the performance of convolutional neural networks. The purpose of embedding channel attention module in a deep neural network is to explicitly construct the relationship between each channel in convolutional layers, and selectively enhance or suppress the overall weights of some channels, so as to improve the feature extraction ability of the convolutional neural network. To achieve this goal, a channel adaptive selection mechanism is fused to allow recalibrating the image features. Through this mechanism, the convolutional neural network can learn the global information, then selectively enhance the image features that are useful for correct recognition results, but also suppress the irrelevant ones.

The channel attention module is shown in Figure 3. For any given function mapping F: X → Y, the feature channels in a certain convolutional layer are reordered by constructing a corresponding SE attention module. The feature map X is transformed into the feature map Y through three-dimensional convolution, then the dimension of feature map is pooled from H to 1 through the “squeeze” operation, which generates a channel descriptor corresponding to each feature map one by one. The global distribution of the channel-wise feature response is embedded into those one-dimensional channel descriptors, so that the underlying receptive field information, which is more important to the detection results, can be used by the deeper convolutional layer. The neural network learns the importance of each channel to the final detection result by a gating function that can describe the channel dependence. Then, each feature map is reordered on the basis of its importance to generate the output from the attention module. Finally, the recalibrated feature map is directly input into the subsequent convolutional layers.

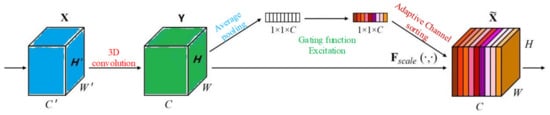
Figure 3. The squeeze-and-excitation block schematic diagram.

4.2. Nonlinear Activation Function

Researchers usually employ S-type activation functions, such as sigmoid or softmax, in the early stage of convolutional neural network research. Unfortunately, S-type activation functions often make the neural network difficult to converge. Due to the local linear properties of the ReLU [36] nonlinear activation function, it can complete nonlinear activation at a low computational cost, which enables researchers to build a deeper neural network. Elfwing et al. [37] proposed a nonlinear activation function called swish, as shown in Formula 10. Compared with the ReLU [36] activation function, swish activation can improve the accuracy of a neural network to a certain extent. However, because the cost of solving sigmoid nonlinear function on an embedded computing platform is much higher, swish activation function is unsuitable for lightweight convolutional neural networks.

$$swish(x)=x\times sigmoid(x).$$

(10)

Engineering practice demonstrates that most of the weights in convolutional neural networks are distributed between [−10, 10]. Therefore, only the nonlinearity of the activation function near 0 can be retained, and other intervals can be adjusted as linear operations to reduce the complexity of the activation function and the amount of system calculation. According to this conception, we change the sigmoid nonlinear part of the swish function to the ReLU linear operation, as shown in Formula (11). Then, the smooth part of the swish curve will become sharper, which is conducive to the rapid calculation of the embedded hardware platform. Figure 4 shows the difference between the swish and hardswish function.

$$hardswish(x)=x\times \frac{ReLU6(x+3)}{6}.$$

(11)

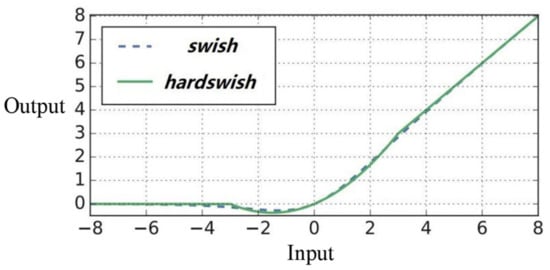
Figure 4. The swish and hardswish nonlinearity counterparts.

As shown in Figure 4, the relatively sharper hardwise function and smoother swish function can match well, and there is no obvious difference in the accuracy of object detection between the two nonlinear functions. However, the hardswish activation function with a sharp curve has more advantages for the task requirements of aerial robot target tracking. Firstly, almost all current deep learning frameworks contain ReLU6-based nonlinear activation. Secondly, under the condition of numerical quantization, the hardswish function resolves the potential calculation error caused by sigmoid singularity. The hardswish nonlinear activation can be solved as a piecewise function in an airborne-embedded computer to further reduce the access times of running memory. Therefore, the response speed of the neural network inference is dramatically improved.

4.3. Normalization of the Network Activation

There is a fundamental premise in deep learning: the training set and test set containing the same category should have the same probability distribution [38]. This assumption is a prerequisite for the trained deep neural network to perform well on the test set. As the input of each convolution layer will be affected by all previous nonlinear layers, the small disturbance of network parameters will be amplified with the deepening of the network [39], which results in the difficulty of depth model training. The change of input probability distribution from each nonlinear layer in the neural network training process is called the hierarchical covariate shift [24]. Eliminating the covariate shift in each convolutional layer can accelerate the convergence of the model. In this section, a processing mechanism called hierarchical batch normalization is embedded into the object detection system, then the input of each nonlinear layer is transformed into the standard probability distribution with zero mean and unit variance. Thus, the covariate shift in the nonlinear layers is effectively reduced and the convergence speed of the deep neural network is simultaneously accelerated. Hierarchical batch normalization reduces the dependence of back propagation on parameter initialization and gradient disturbance, so that the neural network can be trained with higher learning rate without divergence. The detailed operations are as follows:

Firstly, the input distribution of each nonlinear layer in the neural network is transformed into zero mean and unit variance, and the input characteristics of each layer are independently standardized. For the n-dimensional input data of each layer, x = {x₁, x₂,…, x_n} are normalized, respectively:

$${\widehat{x}}_n=\frac{x_n-E(x_n)}{\sqrt{Var(x_n)}}.$$

(12)

The mean and variance are obtained by calculating the training data. However, directly normalizing the input of each convolutional layer may weaken the characterization ability. To eliminate this effect, it is necessary to ensure that the hierarchical normalization embedded in the neural network can be restored to the original irregular distribution state for the input data. Corresponding to the activation x_n of each layer, a set of proportion and weighting parameters can be interposed as α_k, β_k to solve this problem:

$$y_k={\alpha }_k\times {\widehat{x}}_n+{\beta }_k,$$

(13)

These scale parameters, α_k and weighted parameters β_k, participate in the training together with the original model parameters, and restore the expression ability of convolutional neural networks as much as possible. In the process of hierarchical normalization, the hierarchical input is normalized by calculating the mathematical expectation and variance of all training images. However, this processing method is not compatible with the mainstream random gradient descent algorithm. Each batch of input images can produce their corresponding estimates of mathematical expectation and variance by using a small batch of image input in the training process of the convolutional neural network. In the case of data association, the regularization process needs to be performed, because the size of the input batch may be less than the number of normalized activations, resulting in the singularity of the covariance matrix. Hierarchical batch normalization for neural network input can limit the distribution of the input tensor to a specific range, which greatly shortens the training time of the target recognition system.

4.4. Efficient Blocks for Inference

In the field of sparse representation and low-rank decomposition, the concept of residual mapping has been proposed as early as 2007. For example, VLAD vector [40] and Fisher vector [41] are familiar residual descriptors. The degradation problem in deep convolution neural networks demonstrates that it is difficult for airborne-embedded equipment to use nonlinear convolution operation to fit linear identity mapping. In the actual numerical quantization process, however, the airborne computer coding residual vector is more efficient than directly calculating the original vector, which makes the model convergence speed faster. In a typical convolutional neural network it is difficult to directly use the nonlinear function to match the linear identity map; thus, the model degradation problem will become more and more serious with the increase of network depth. In the residual representation structure, when the linear identity mapping is optimal, the airborne embedded system can set the weights of several continuous nonlinear convolutional layers to zero, which can directly construct the linear mapping inside the neural network. Therefore, residual neural networks usually have a more substantial probability distribution fitting ability than the typical convolutional neural networks.

Sandler et al. [23] found that if the input feature map can be inserted into a subspace with lower input dimension in the deep neural network, the convolution operation will not destroy the original information contained in the input tensor. It is also pointed out that to ensure the high-dimensional fitting ability of the depth model, the use of linear mapping in some narrow nonlinear layers can improve the overall performance to a certain extent. If we deconvolute a feature map in the convolution network, the visualization contained in the feature map actually exists in the low-dimensional subspace of the high-dimensional space of the deep neural network. Assuming that the interest tensor in the aerial robot object detection system is low dimensional, the low-dimensional features that play a role in the final detection results can be captured by constructing a linear bottleneck structure in the deep neural network.

According to the above principles, based on the linear bottleneck convolution structure, we integrated the attention mechanism model with feature channel to construct a reverse residual representation structure that can retain the primary feature information to the greatest extent, as shown in Figure 5. The reverse residual convolutional block can selectively utilize different types of nonlinear activation according to the dimensional change of input tensor. Linear transformation is used to reduce the dimension of the feature map, which prominently retains the integrity of the initial input information.

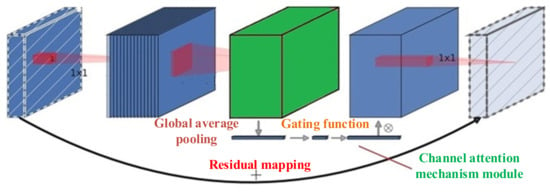
Figure 5. Inverted residual convolutional block.

4.5. Building Efficient CNNs

Inspired by the reverse residual mapping structure proposed in the previous section, we embed hierarchical batch normalization modules in each nonlinear layer, and build a lightweight convolutional neural network architecture YZNet for the micro aerial robot object detection task, as shown in Table 1. The model inserts a hyper-parameter called the “expansion factor” into the 2D planar convolution operation in the reverse residual module, which can expand the feature map before the 2D planar convolution, and greatly improve the feature extraction ability of the reverse residual block. YZNet contains about 1.74 × 10⁶ network parameters. When the input is a 224 × 224 dimensional three channel color image, about 5.9 × 10⁷ times of multiplication is required in the process of model inference.

Table 1. The structure configuration of YZNet.

Input	Function Block	Kernel Size	Expansion	Output Channels
224 × 224 × 3	3 × 3 convolution	3 × 3	-	16
112 × 112 × 16	Reflection residual module	3 × 3	1	16
56 × 56 × 16	Reflection residual module	3 × 3	4.5	24
28 × 28 × 24	Reflection residual module	3 × 3	3.7	24
28 × 28 × 24	Reflection residual module	3 × 3	4	40
14 × 14 × 40	Reflection residual module	5 × 5	5	40
14 × 14 × 40	Reflection residual module	3 × 3	6	60
14 × 14 × 60	Reflection residual module	5 × 5	4	60
14 × 14 × 60	Reflection residual module	3 × 3	4	80
14 × 14 × 80	Reflection residual module	5 × 5	6	80
7 × 7 × 80	Reflection residual module	5 × 5	6	100
7 × 7 × 100	Reflection residual module	5 × 5	6	120
7 × 7 × 120	1 × 1 convolution	1 × 1	-	600
7 × 7 × 600	Average pooling	7 × 7	-	600
1 × 1 × 600	Full connection layer	-	-	1200
1 × 1 × 1200	Classifier	-	-	20

5. Implementation for Target-Tracking System

We chose the NVIDIA jetson NX-embedded platform as the onboard computer for the micro aerial robot, utilized Intel Realsense T265 binocular camera to provide pose estimation for the aerial robot, and used Intel Realsense D435i stereo camera as the input of the depth neural network. The 410 mm wheelbase quadrotor MAV serves as the carrier of onboard computer and cameras. Pixhawk4 is used as the flight control hardware platform, and the PX4 is chosen as the flight control firmware. The ground station is connected with the Pixhawk4 and airborne computer through WiFi and Ethernet, respectively. Before the aerial robot can fly, it is necessary to implement the offline pre-trained object detection system to the airborne computer in advance. The detailed description is shown in Figure 6.

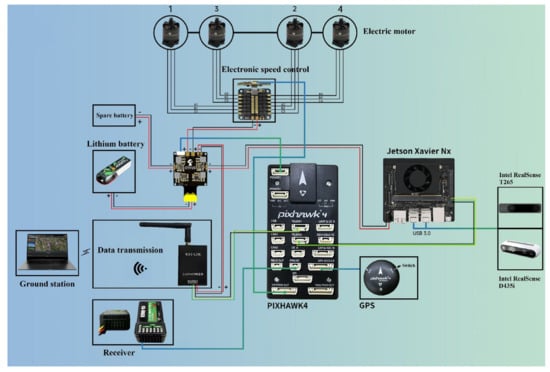
Figure 6. The connecting scheme of aerial robot.

6. Experiments

6.1. Pose Estimator

The EuRoC datasets [42] are collected from a binocular fisheye camera (global shutter, 20 frames per second) and synchronized IMU (maximum 200 Hz) carried by a micro aerial robot. The EuRoC datasets [42] contain 11 sequences, which include different objects, different lighting conditions, and different environments. We compare the proposed RPEOD with OKVIS [11], Kimera-VIO [14] and ORB-SLAM3 [15] in EuRoC datasets. Kimera-VIO is the state-of-the-art optical flow-based SLAM system, and ORB-SLAM3 is the state-of-the-art feature matching-based SLAM system supporting various camera models. All comparative experiments were run in NVIDIA Jetson Xavier NX, as shown in Figure 7. This embedded onboard computer is different from other similar products in that it has a GPU with 384 cores (the maximum frequency per core is 1.1 GHZ), which allows the RPEOD system to perform parallel acceleration with CUDA. The root-mean-square error (RMSE) and average time consumed per frame are shown in Table 2, which is evaluated by an absolute pose error (APE). The default configuration file is used for ORB-SLAM3 [15]. Figure 8 shows the change of absolute pose error (APE) as time goes on in first sequence. The experimental results show that, on the NVIDIA Jetson Xavier NX hardware equipment, RPEOD can achieve real-time performance but other algorithms cannot (input videos are 20 frames per second).

Figure 7. NVIDIA Jetson Xavier NX.

Table 2. Performance comparison in the EUROC dataset (Time in ms, RMSE in m.).

Sequence	OKVIS		Kimera-VIO		ORB-SLAM3		RPEOD
	RMSE	Time	RMSE	Time	RMSE	Time	RMSE	Time
MH01	0.16	113.8	0.15	75.6	0.07	126.4	0.16	48.6
MH02	0.22	107.4	0.13	73.2	0.05	124.3	0.14	48.2
MH03	0.24	105.6	0.18	73.4	0.15	121.7	0.13	46.8
MH04	0.34	104.8	0.27	72.6	0.12	118.5	0.23	45.2
MH05	0.47	105.2	0.41	72.8	0.21	119.7	0.38	45.2
V101	0.09	110.6	0.12	75.2	0.07	120.6	0.14	48.4
V102	0.20	107.2	0.13	74.4	0.03	113.4	0.05	43.6
V103	0.24	106.4	0.07	74.6	0.05	116.5	0.13	44.8
V201	0.13	108.4	0.09	75.2	0.09	122.7	0.07	47.2
V202	0.16	105.2	0.14	73.8	0.03	119.5	0.09	46.8
V203	0.29	105.6	0.23	74.6	0.06	122.3	0.20	47.2
Average	0.23	107.2	0.17	74.1	0.09	120.5	0.15	46.5

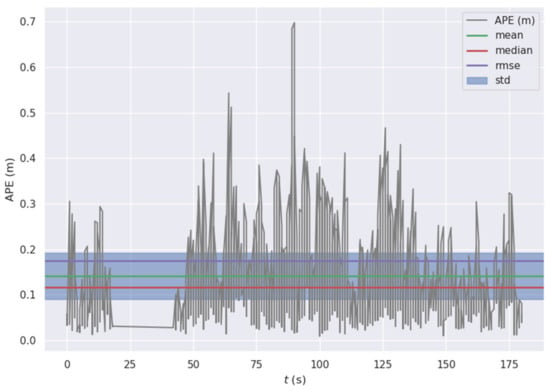
Figure 8. The change of absolute pose error (APE) as time goes on in sequence MH01. RPEOD will inevitably drift over time, which is an inherent characteristic of all visual odometers. Fortunately, thanks to the local bundle adjustment, the APE of the RPEOD system is always within a reasonable range.

6.2. Object Detector

Considering the limited onboard computing resources, we use YOLOV5, the state-of-the-art object detection architecture, as the predominant framework for target tracking. In order to further improve the real-time performance of the detection module, we replace the backbone in YOLOV5 with YZNet, as proposed in Section 4, which requires fewer parameters and computation. We randomly selected 2500 images from the VOC2007 dataset as the training set, then, we selected about 2500 images from the remaining images as the test set without repetition.

The GPU employed in the neural network training process is NVIDIA GTX1660. The development environment is pytorch1.8, the initial learning rate during YZNet training is 0.01, the weight attenuation rate is 1 × 10⁻⁵, the momentum is set to 0.9, and the batchsize is set to 8. Rmsprop is selected as the neural network training optimizer. The resolution of the three channel color image is 640 × 480. After 60 epochs, the network converges completely, and the whole training process takes about 9 h. Because the network structure of YZNet has been reasonably optimized, and each convolution module is embedded with a hierarchical batch normalization module, even if the pretrained parameters are not imported for initialization, the model training process can fully converge in a short time. We recorded the PR curve generated by each category during the neural network training, as shown in the Figure 9.

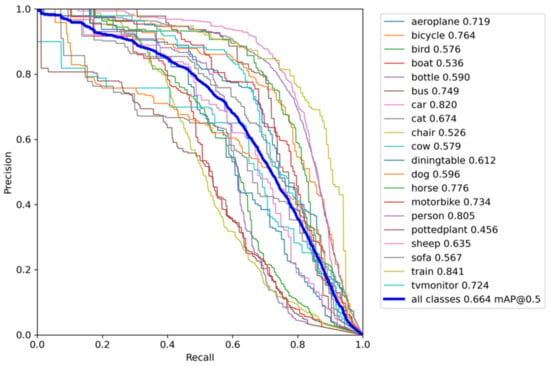
Figure 9. The precision and recall of the YZNet-YOLOV5-tiny (IOU = 0.5).

To verify the practical application performance and low power consumption characteristics, desktop computer-based X86 architecture should not be used. We selected the Xavier Jetson NX-embedded development board with only 15W power consumption as a test platform for aerial robot object detection, as shown in Figure 7. As no test images have been used in the process of model training, the test results can reflect the generalization ability of YZNet to a certain extent. In order to more clearly demonstrate the comprehensive performance advantages of YZNet, we carried out comparative experiments with the original YOLOV5. The training set and test set are exactly the same from the VOC2007 dataset. Each convolutional neural network is optimized by the same training method. The experimental results are shown in Table 3. The acronym “mAP” means mean average precision, and the acronym ”IoU” means intersection over union, where the numerator is the bounding boxes predicted by the detector, and the denominator is the real bounding boxes. Specifically we use 10 IoU thresholds of IoU = 05:0.95, which can average over IoU rewards detectors with better localization. The acronym “FPS” means frames per second. The real-time performance test for YZNet-YOLOV5-tiny detector is shown in Figure 10.

Table 3. The performance indexes for YZNet against YOLOV5.

Detectors	mAP (IoU = 0.5)	mAP (IoU = 0.5:0.95)	Backbone Parameters	Mean FPS (Jetson NX)
YOLOV5	76.1%	52.8%	20.8M	8.1
YOLOV5-tiny	72.1%	45.9%	6.9M	15.2
YZNet-YOLOV5	76.9%	55.6%	28.5M	7.3
YZNet-YOLOV5-tiny	66.4%	38.6%	1.7M	23.8

Figure 10. The real-time performance test for object detection on the NVIDIA Jetson NX embedded platform. The YZNet-YOLOV5-tiny system can simultaneously capture the target category with the distance provided by the depth image from the D435i camera. The complete video is available at: https://www.bilibili.com/video/BV1G44y1J76B?share_source=copy_web (19 December 2021).

6.3. Real-World Target Tracking

Due to the instability of the aerial robot control system, a simulation test is usually needed before real-world flight, which can effectively avoid the aerial robot crash caused by a program error, as shown in Figure 11. After taking off, the aerial robot uses a T265 binocular camera to obtain the relative relationship between the body coordinate system and the world coordinate system. Secondly, YZNet-YOLOV5 is used to find the preseted target (which can be modified manually), and the depth information captured by the D435i stereo camera is fused to obtain the transformation matrix between the tracked target and the D435i camera, so as to further calculate the position of the tracked target in the world coordinate system. When the positions of MAV and target are determined, the aerial robot will automatically generate a desired position in the world coordinate system, then, fly to the desired destination and keep a fixed distance from the tracked target. If the target moves, the aerial robot will automatically follow the target.

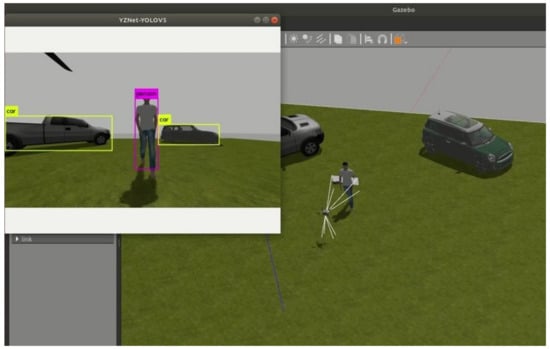
Figure 11. The target-tracking test is carried out in the Gazebo simulator.

In order to verify the robustness and feasibility of the RPEOD system, we also built a real-world test similar to the Gazebo experiment. The real-world experiment was conducted on a university playground, and the target tracked by the aerial robot is an ordinary pedestrian, as shown in Figure 12. The aerial robot will change its position with the person’s movement and always maintain a relatively fixed spatial position relationship with the person. In the process of aerial robot tracking, all flight commands are issued by the airborne computer without any external manual control commands.

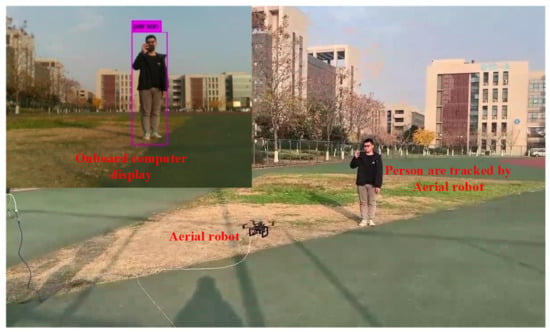
Figure 12. The real-world tracking test was conducted on a university playground. The complete video is available at: https://www.bilibili.com/video/BV1cb4y1v7cX?share_source=copy_web (19 December 2021).

7. Conclusions and Future Work

In this paper, we proposed RPEOD: a real-time simultaneous pose estimation and object detection system for aerial robot target tracking, which combines inertial measurement and sparse optical flow tracking algorithms to estimate aerial robot motion between consecutive video frames. Meanwhile, the object detection module will find the target in the environment and locate the spatial position of the tracked target. The RPEOD system is evaluated using both simulated and real-world experiments, demonstrating clear advantages over state-of-the-art approaches.

Although the RPEOD system has already reached the maturity of real-world deployment, we still see many directions for future work. The assumption of scene rigidity is typical in robot state estimation algorithms. Therefore, the robot state estimator can only handle small parts of the dynamic environment by classifying them as outliers to such a static model, which limits the use of the RPEOD system in cluttered environments. We are interested in multi-view geometry, deep learning or both methods to detect moving objects in dynamic scenarios, and generating a static map of the scene to replenish the frame background, so as to achieve the effect of eliminating dynamic targets in the environment.