Optimization Design of Y-Shaped Settling Diversion Wall Based on Orthogonal Test
Abstract
:1. Introduction
2. Study Area and Method
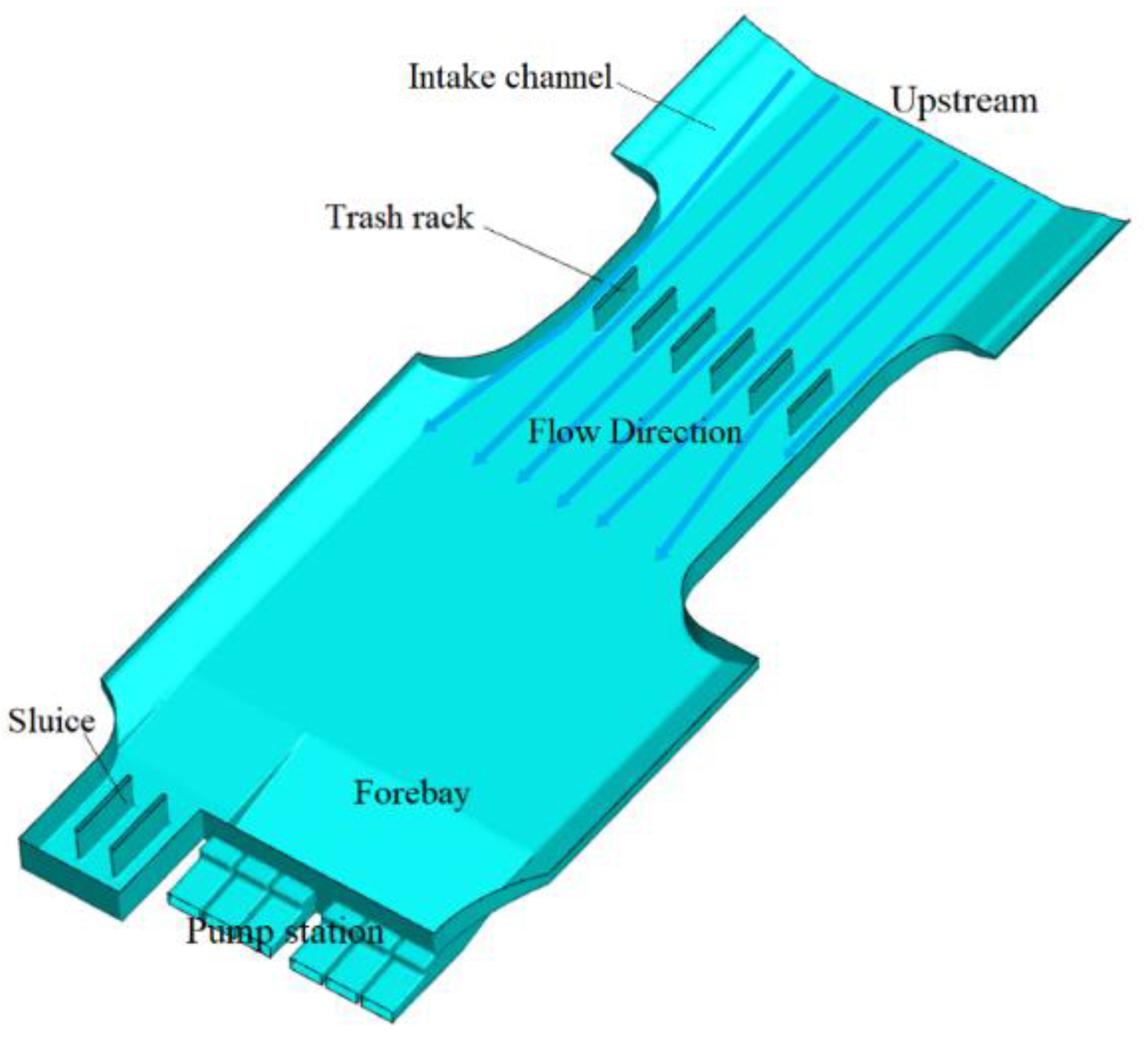
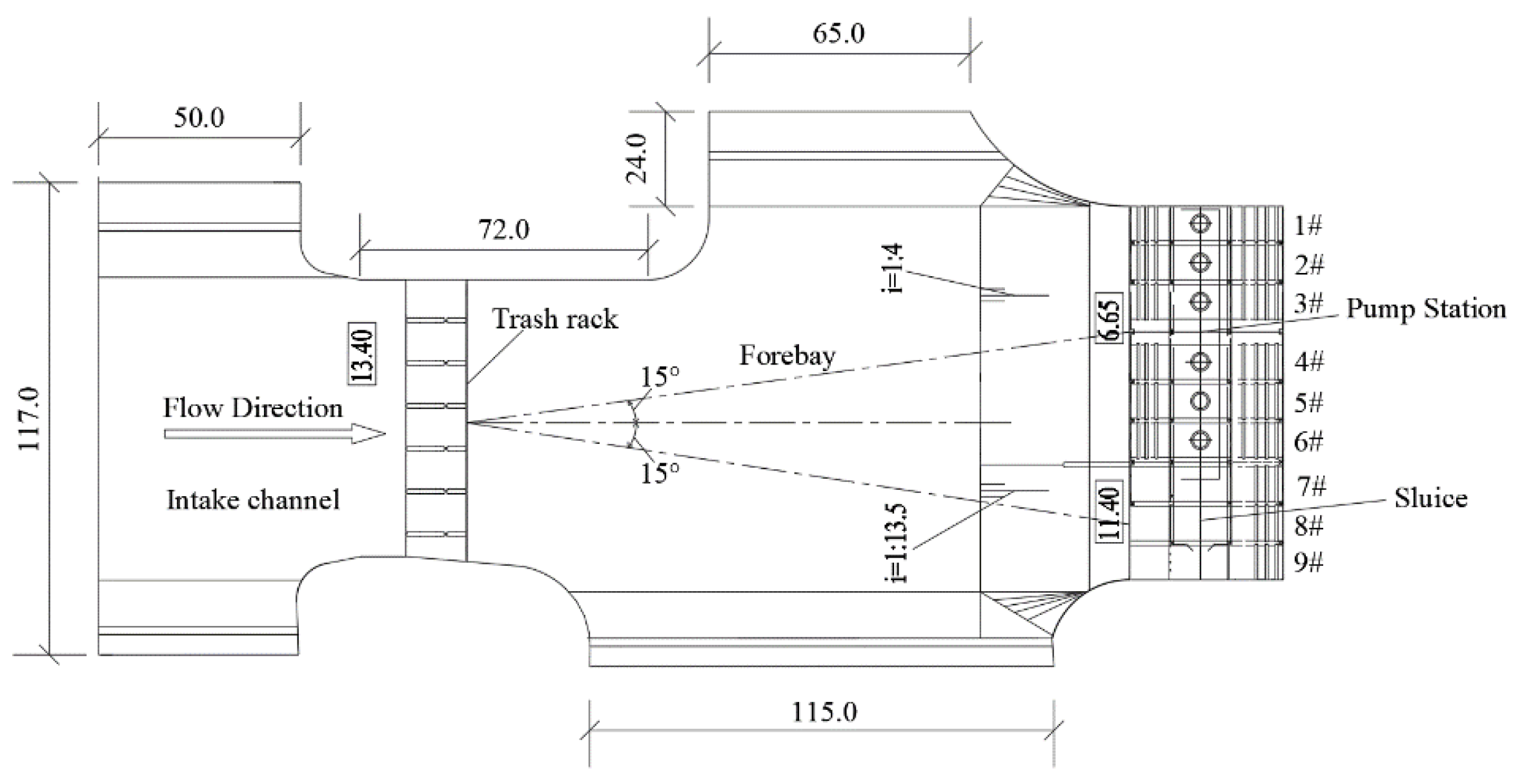
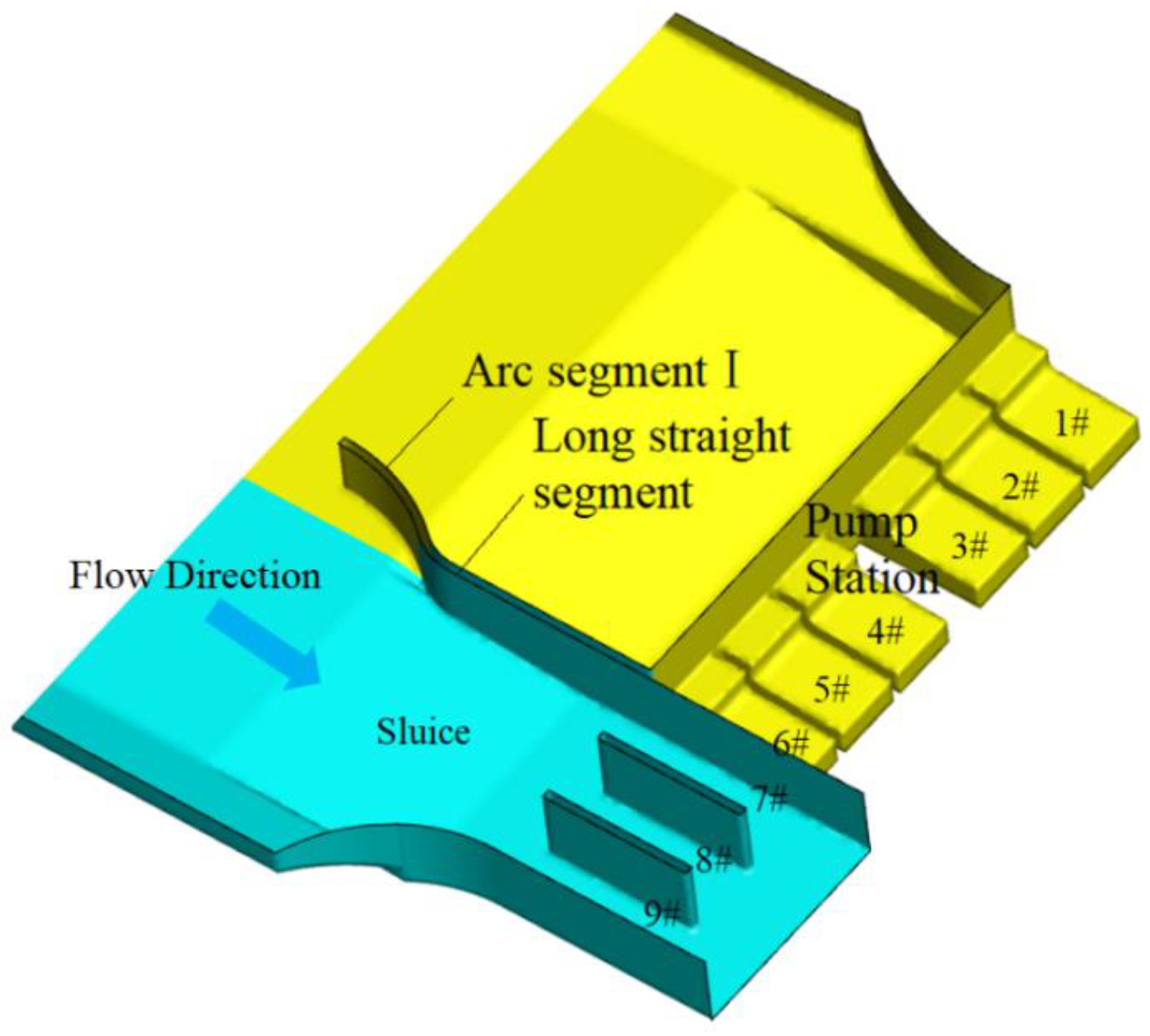
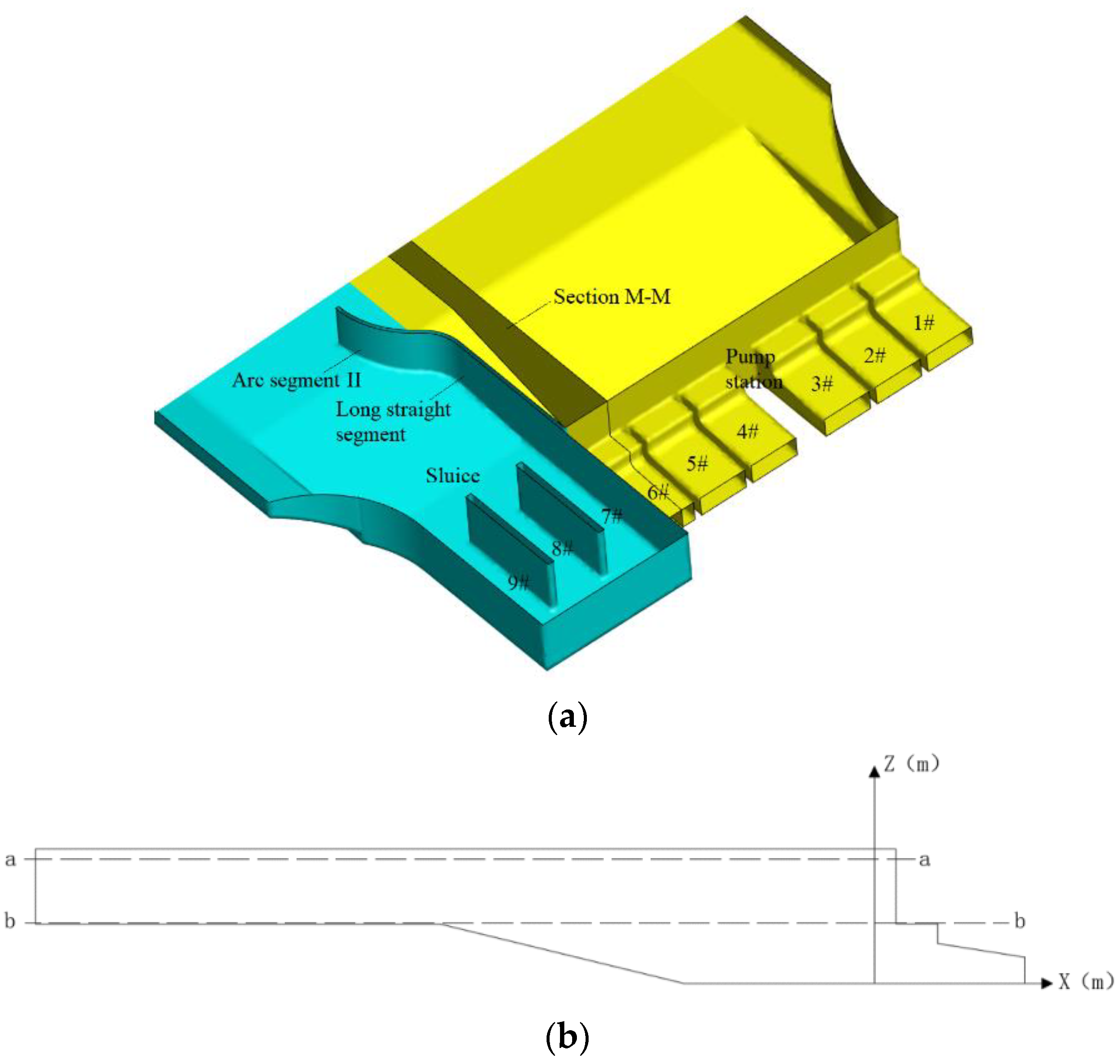
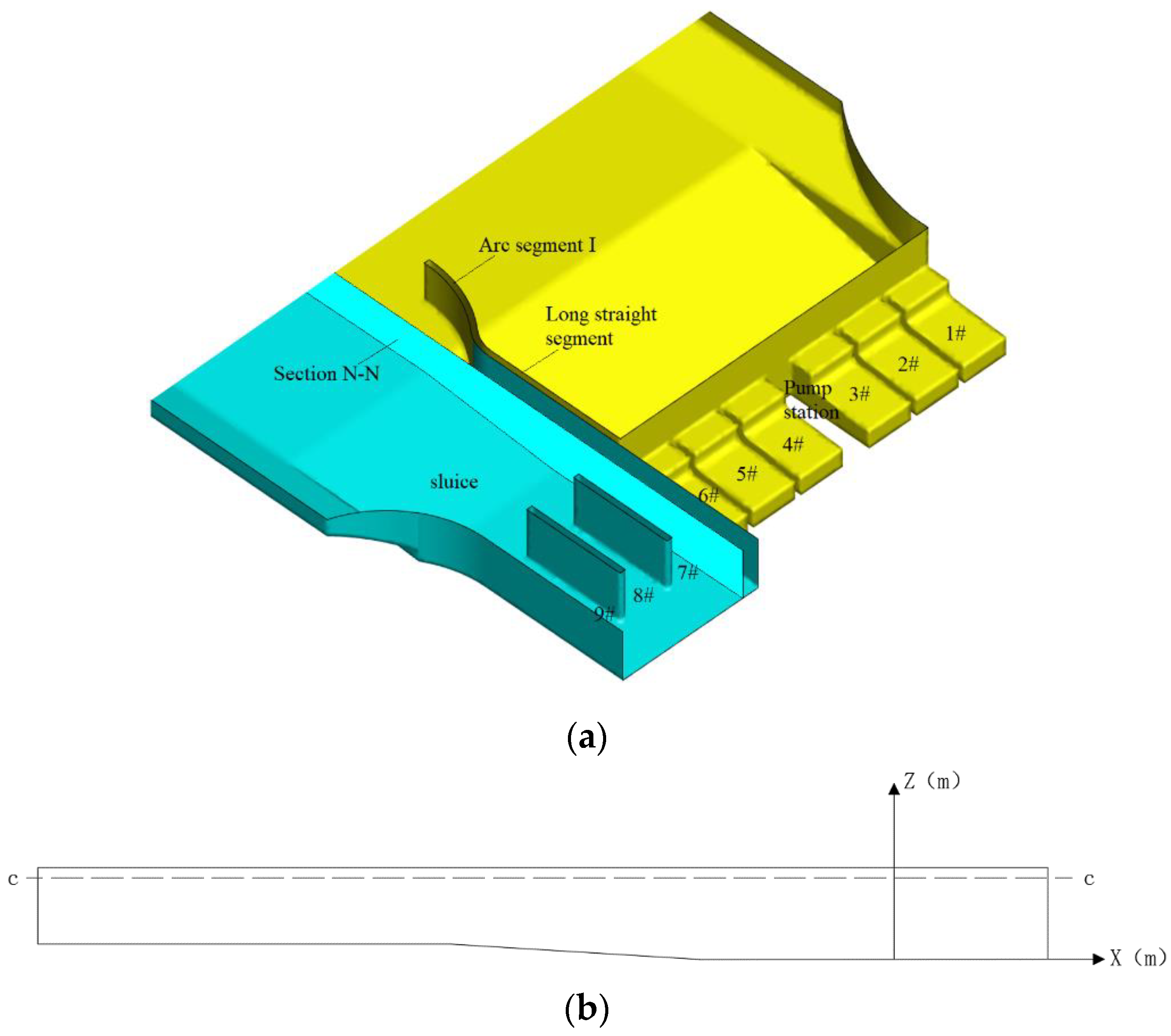
2.1. Study Area
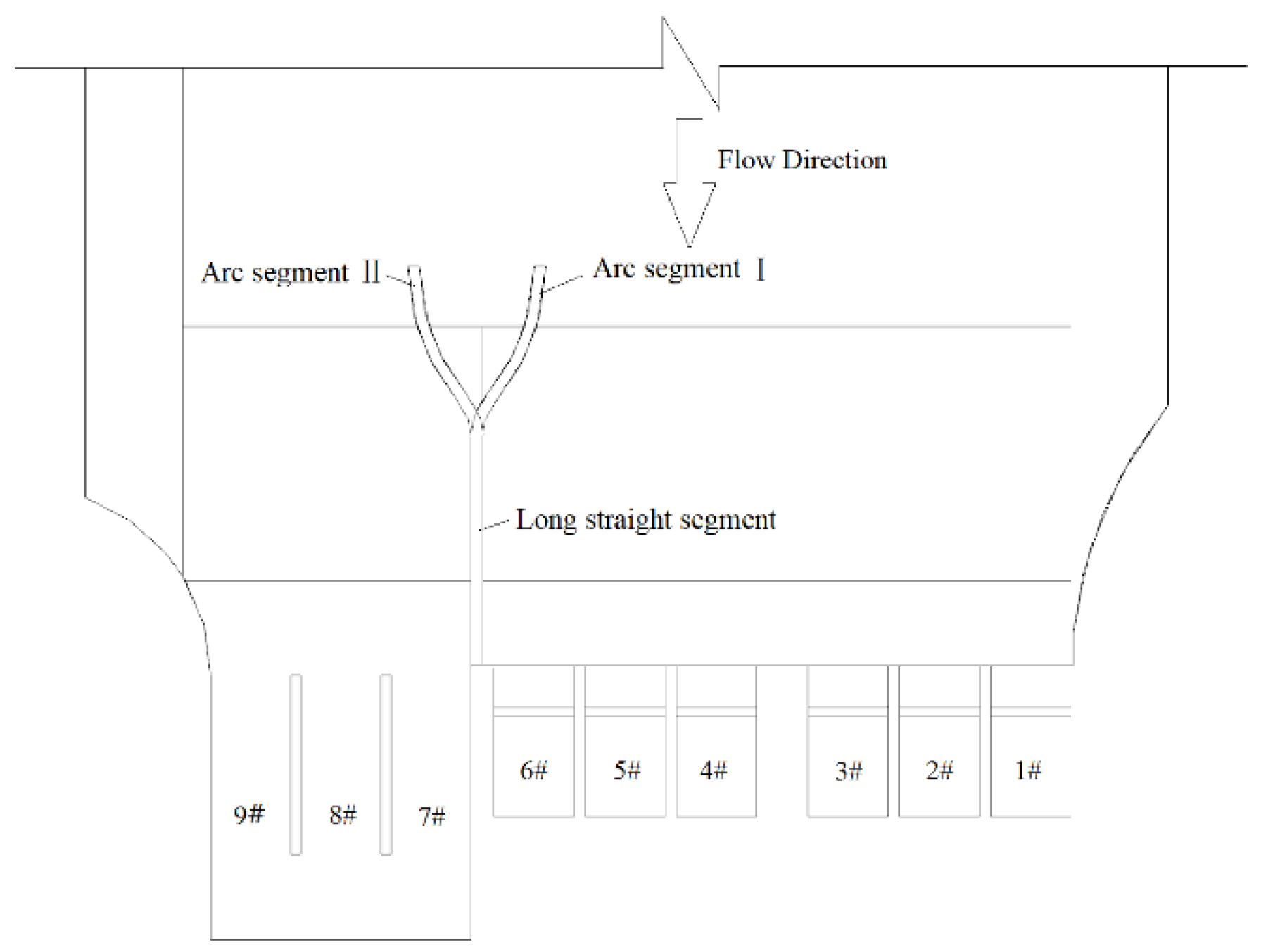
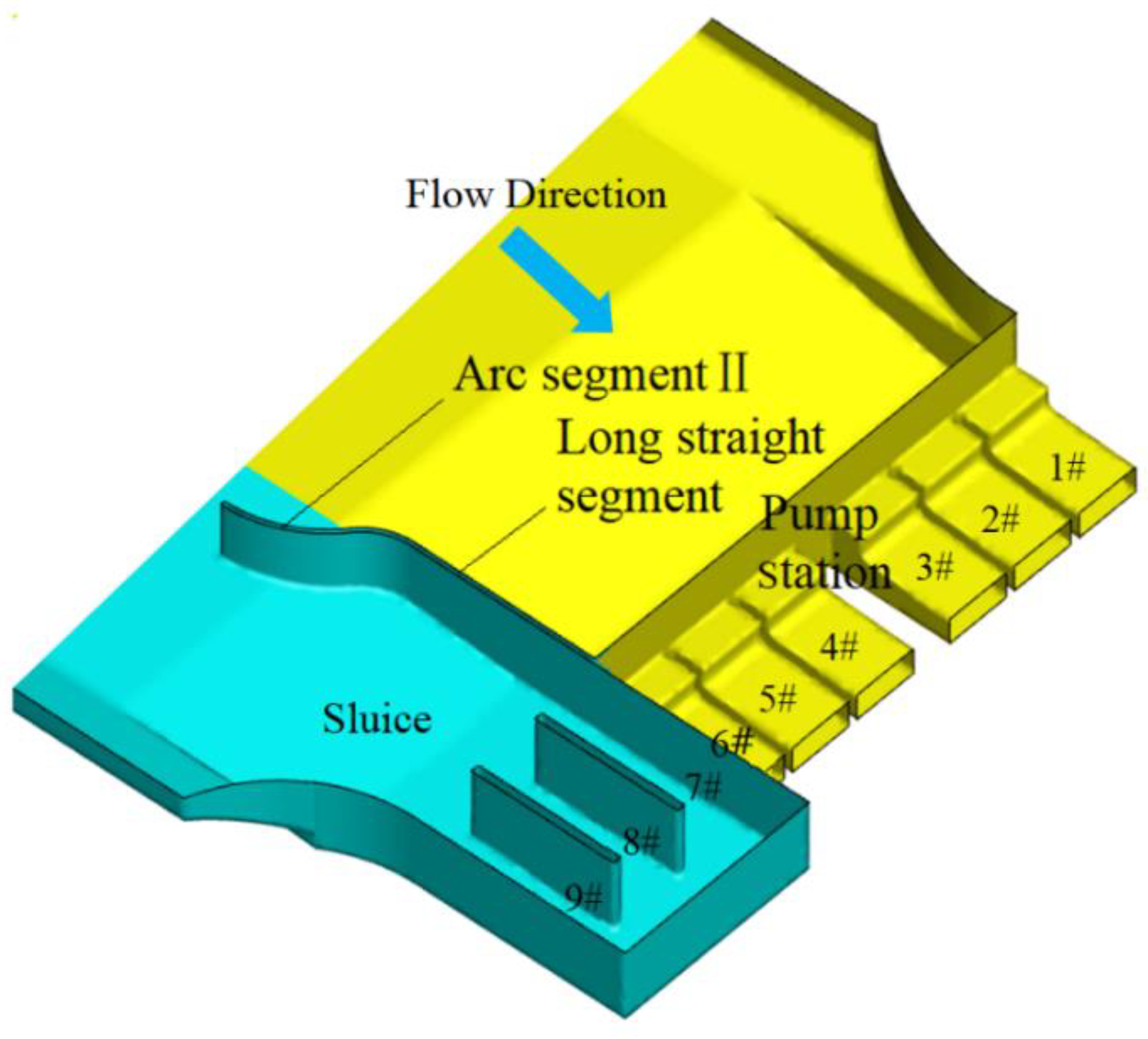
2.2. Study Method
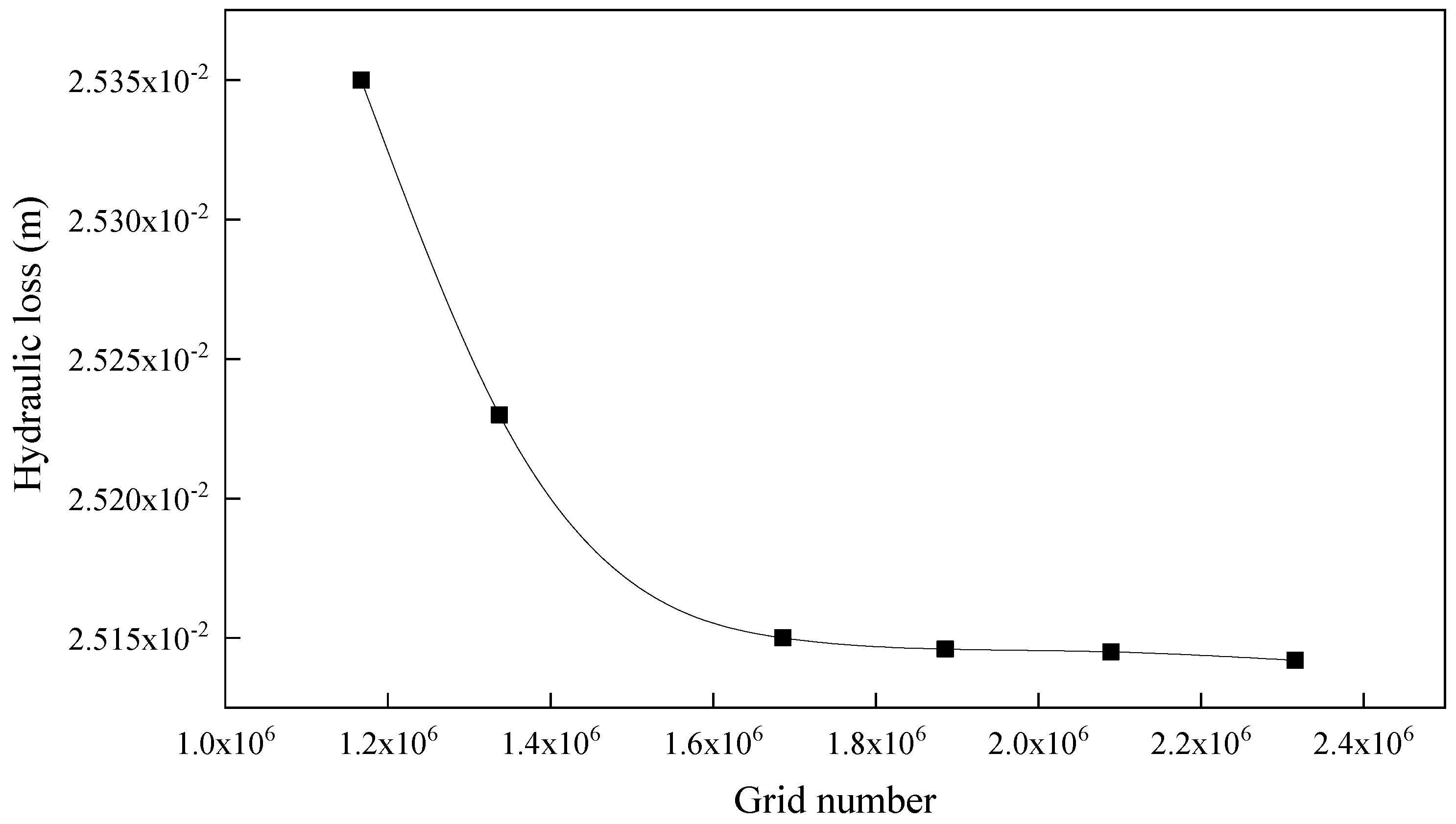
2.2.1. Grid Division
2.2.2. Boundary Condition
2.2.3. Turbulence Model
3. Orthogonal Experimental Design
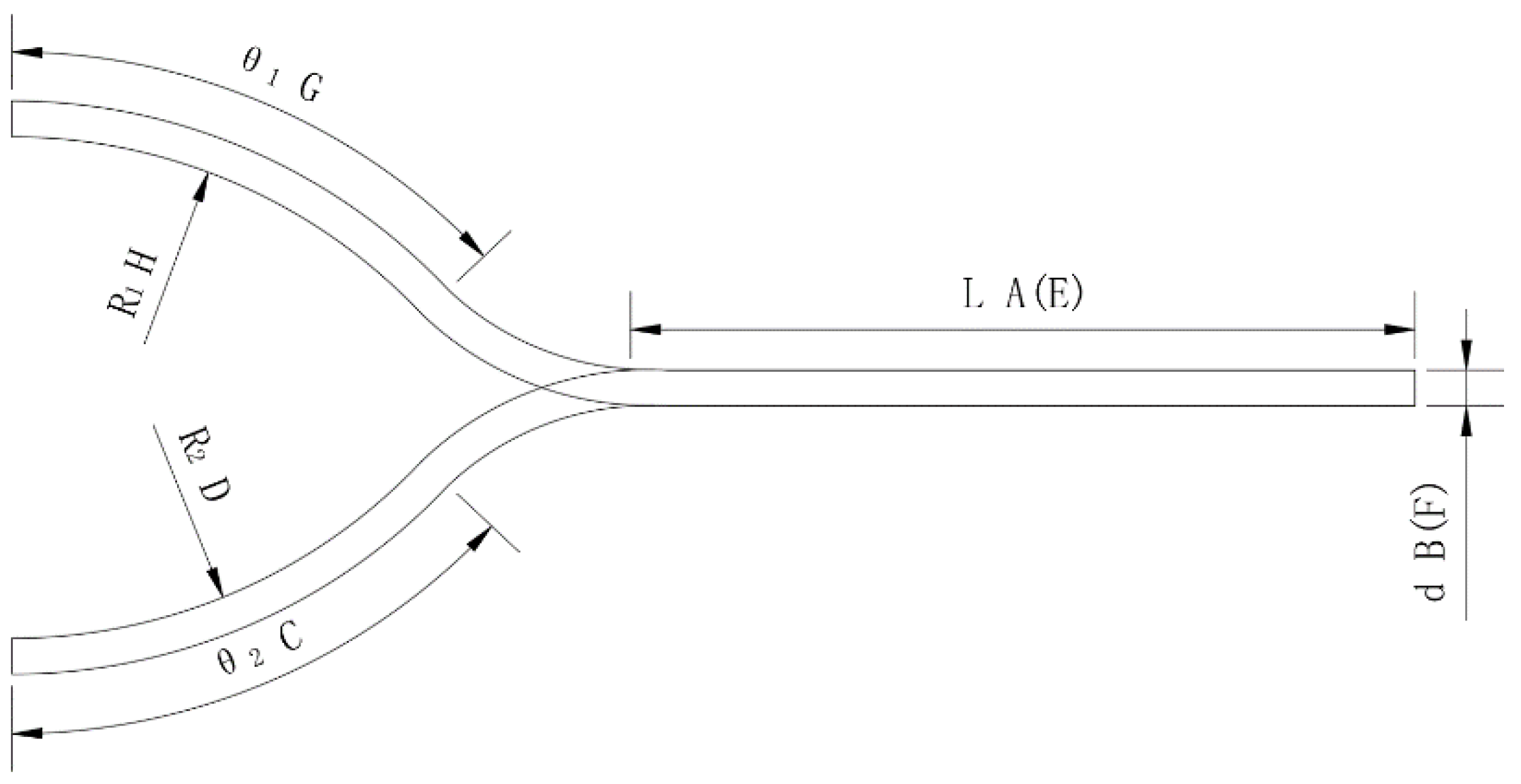
3.1. Selection of Factors and Levels Tested
3.2. Orthogonal Table
3.3. Orthogonal Test Results of the Geometric Parameters of the Diversion Wall
3.4. Variance Analysis
3.5. Determination of Optimal Solution
4. Analysis of Numerical Simulation Results Based on Orthogonal Experimental Design
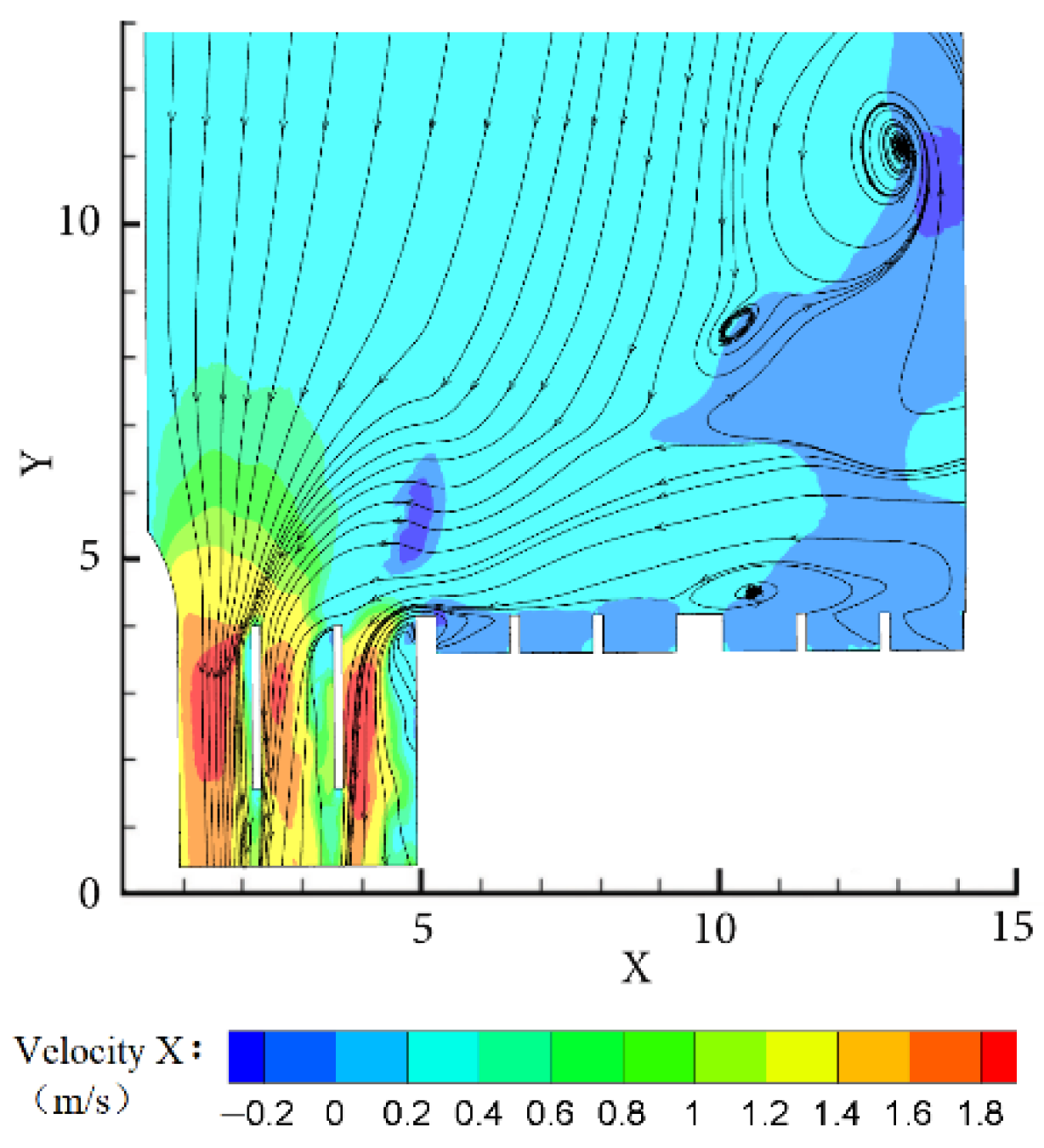
4.1. Feature Section Selection
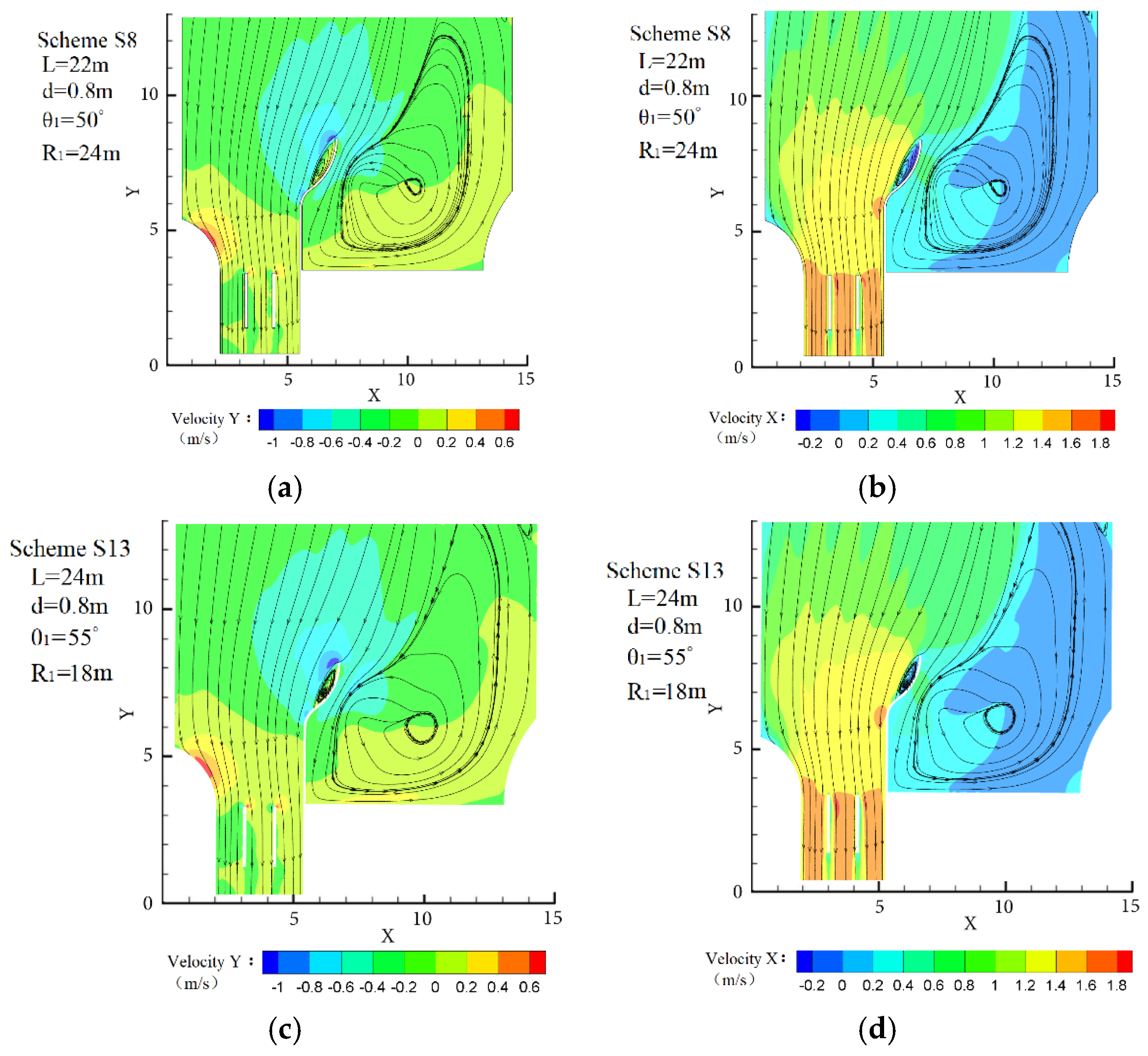
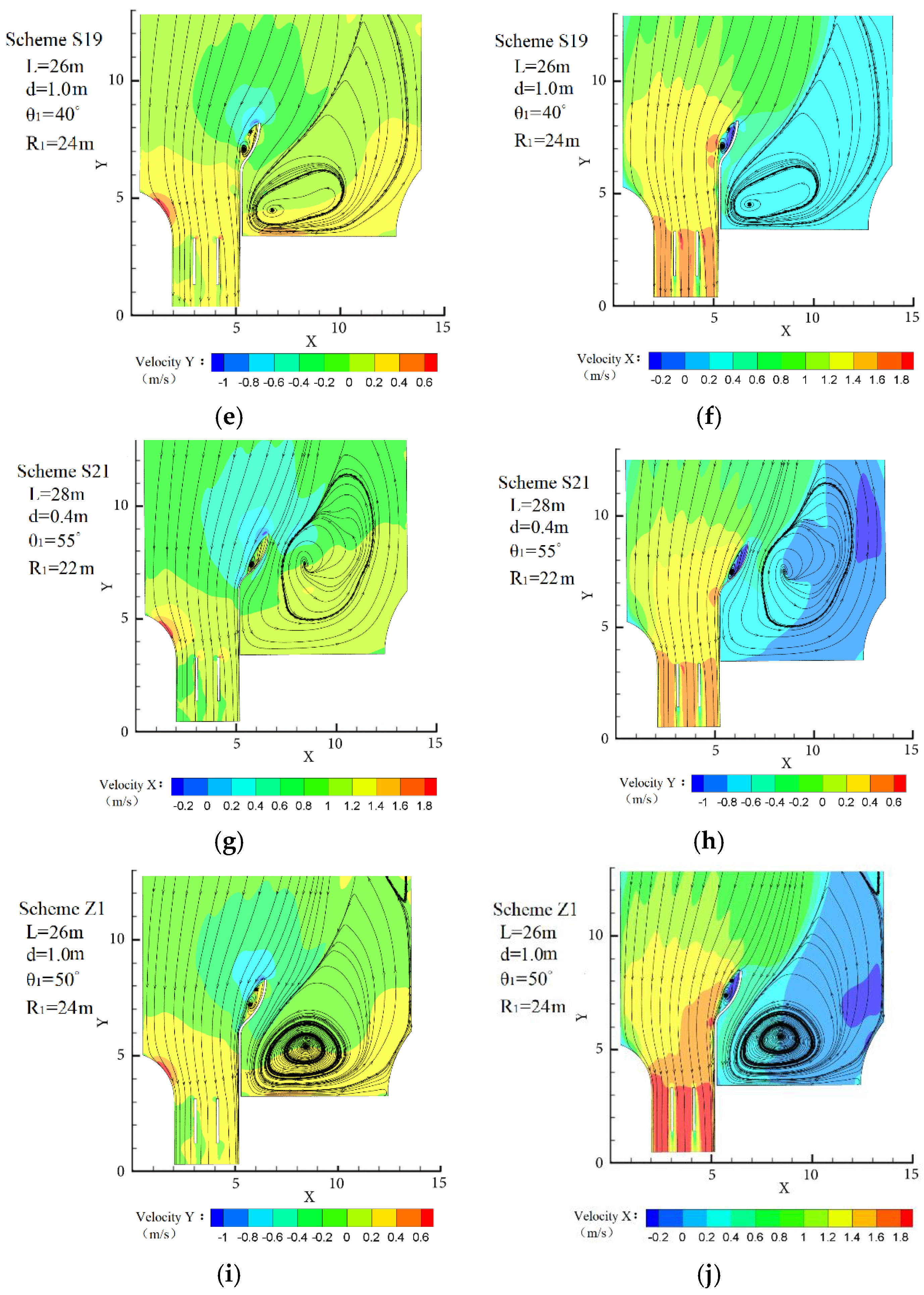
4.2. Selection of the Typical Schemes
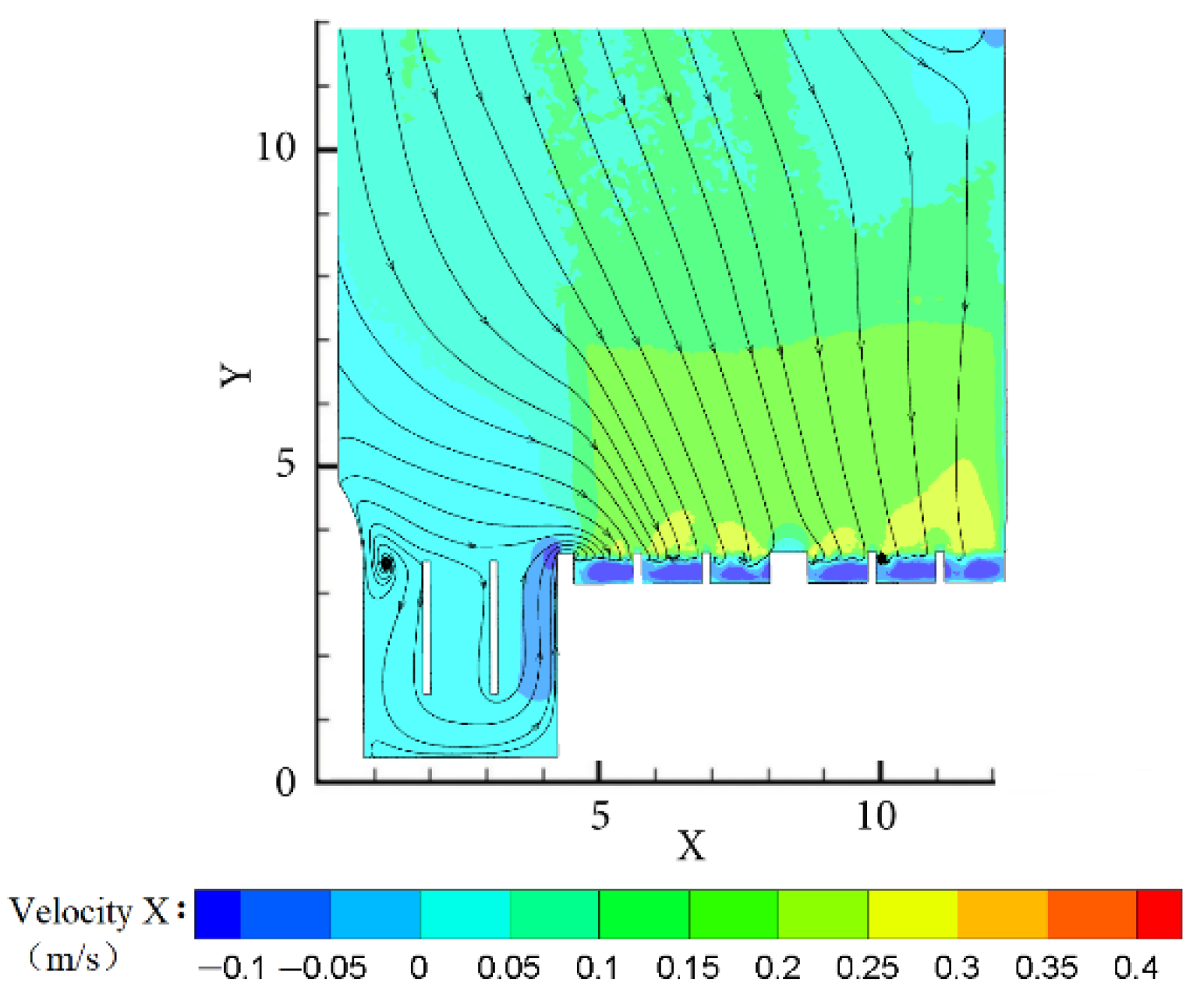
4.3. Analysis of the Numerical Simulation Results
4.3.1. Condition of Pumping
4.3.2. Condition of Self-Draining
5. Discussion
6. Conclusions
- Adding a Y-shaped settling diversion wall between the sluice and the pump station can effectively improve the inlet flow pattern of the combined sluice-pumping station, and the orthogonal test is of great scientific value to analyze such a fluid mechanical engineering issue to obtain the influence degree of various factors on the index.
- The geometric parameters of different diversion walls have different effects on the uniformity of axial velocity in front of the sluice and in the inlet section of the inlet channel. Under the condition of pumping, among the four factors affecting the rectification effect of the diversion wall, the radian of arc segment II of the diversion wall is the key factor, and the arc radius of arc segment II, the width of the diversion wall and the length of the long straight section are all general factors. Under the condition of self-draining, the most influential factor on the index change is still the radian of arc segment I of the diversion wall, followed by the width of the diversion wall and the arc radius of arc segment I, and the length of the long straight segment is the secondary factor with the least influence on the index change.
- For the combined sluice-pumping station with a 15° lateral angle, the parameter combination A4B4C3D4G4H4 of the Y-shaped settling diversion wall is adopted as the optimal experimental scheme, that is, under the condition of pumping, when the length of the long straight segment is 26 m, the width of the diversion wall is 1.0 m, the radian of arc segment II is 45° and the arc radius of arc section II is 24 m, the two test index values are the maximum. Under the condition of self-draining, when the length of the long straight segment is 26 m, the width of the diversion wall is 1.0 m, the radian of the arc section II is 50°, and the arc radius of the arc section I is 24 m, the test index value is the maximum.
- The Y-shaped settling diversion wall studied in this paper optimizes the inlet conditions of the side wall by isolating the backflow, which can achieve the optimal inlet flow pattern under the conditions of pumping and self-drainage. So, it can be well applied in the combined sluice-pumping station with a 15° transverse lateral angle. The results of this research provide a scientific basis and technical reference for the design of the combined sluice-pumping station with a diversion pier under other lateral corners or other operating conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Yang, J.; Yu, J.; Fu, Z.; Chen, Q. Flow Expansion and Deflection Downstream of a Symmetric Multi-gate Sluice Structure. KSCE J. Civ. Eng. 2020, 24, 471–482. [Google Scholar] [CrossRef]
- Mohamed, I.M.; Abdelhaleem, F.S. Flow Downstream Sluice Gate with Orifice. KSCE J. Civ. Eng. 2020, 24, 3692–3702. [Google Scholar] [CrossRef]
- Song, W.; Pang, Y.; Shi, X.; Xu, Q. Study on the rectification of forebay in pumping station. Math. Probl. Eng. 2018, 1, 1–16. [Google Scholar] [CrossRef]
- Xi, W.; Lu, W.; Wang, C.; Xu, B. Optimization of the Hollow Rectification Sill in the Forebay of the Pump Station Based on the PSO-GP Collaborative Algorithm. Shock. Vib. 2021, 1, 1–11. [Google Scholar] [CrossRef]
- Fan, J.; Lu, D.; Shi, Z.; Hou, H. Lateral Water Pumping Station Forebay of Jingtai Electric Power Irrigation District Flow State Numerical Simulation and Preventing Silt Research. Int. J. Comput. Eng. 2016, 1, 30–32. [Google Scholar]
- Teaima, I.R.; El-Gamal, T. Improving flow performance of irrigation pump station intake. J. Appl. Water Eng. Res. 2017, 5, 9–21. [Google Scholar] [CrossRef]
- Zhao, Z.; Qian, Z.; Guo, Z.; Wu, P. Experimental study of subsurface vortices in pump intake with an improved diversion-cone. In Proceedings of the IOP International Conference Series of Earth and Environmental Science, Shanghai, China, 25–26 March 2019; p. 32. [Google Scholar]
- Zhang, L.; Wang, C.; Zhang, Y.; Xiang, W.; He, Z.; Shi, W. Numerical study of coupled flow in blocking pulsed jet impinging on a rotating wall. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 508. [Google Scholar] [CrossRef]
- Tang, S.; Yuan, S.; Zhu, Y. Deep learning-based intelligent fault diagnosis methods toward rotating machinery. IEEE Access 2019, 8, 9335–9346. [Google Scholar] [CrossRef]
- Tang, S.; Yuan, S.; Zhu, Y. Data preprocessing techniques in convolutional neural network based on fault diagnosis towards rotating machinery. IEEE Access 2020, 8, 149487–149496. [Google Scholar] [CrossRef]
- Wang, H.; Qian, Z.; Zhang, D.; Wang, T.; Wang, C. Numerical study of the normal impinging water jet at different impinging height, based on Wray–Agarwal turbulence model. Energies 2020, 13, 1744. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Zhang, C.; Li, Z.; Gao, C.; Bi, C. Study on the influence of geometric parameters of diversion pier on navigable flow conditions of gate station joint hub based on CFD. J. Irrig. Drain. 2019, 38, 115–122. (In Chinese) [Google Scholar]
- Zhao, M.; Jia, J.; Qin, J.; Liang, J.; Yang, F. Simulation of diversion pier rectification of gate station combined with pump station forebay. China Rural. Water Resour. Hydropower 2018, 4, 125–130. (In Chinese) [Google Scholar]
- Zhang, C.; Zhou, C.; Zhou, Y.; Xu, L. Influence of geometric parameters of ‘Y’ diversion pier on flow pattern in forebay of lateral intake pump station. S. N. Water Transf. Water Conserv. Sci. Technol. 2020, 18, 192–200. (In Chinese) [Google Scholar]
- Cheng, L.; Qi, W.; Luo, C.; Shang, Y.; Yuan, H. Effect of geometric parameters of Y-shaped diversion piers on flow pattern in forebay of pumping station. Adv. Sci. Technol. Water Resour. 2014, 34, 68–72. [Google Scholar]
- Xi, B.; Zhen, Y.; Duan, Y.; Yang, X.; Lu, R. Optimization of flow pattern in forebay of gate station combined pump station. J. Chang. Acad. Sci. 2021, 1, 9–28. (In Chinese) [Google Scholar]
- Zhou, J.; Zhao, M.; Wang, C.; Gao, Z. Optimal design of diversion piers of lateral intake pumping station based on orthogonal test. Shock. Vib. 2021, 5, 1–9. [Google Scholar] [CrossRef]
- Zhou, L.; Shi, W.; Lu, W.; Xu, R.; Wang, C. Orthogonal test and optimization design of submersible pump guide vanes. J. Drain. Irrig. Mach. Eng. 2011, 29, 312–315. [Google Scholar]
- Shi, G.; Li, H.; Liu, X.; Liu, Z.; Wang, B. Transport Performance Improvement of a Multiphase Pump for Gas–Liquid Mixture Based on the Orthogonal Test Method. Processes 2021, 9, 1402. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, L.; Zhou, H.; Lv, W.; Wang, J.; Shi, W.; He, Z. Optimal Design of Slit Impeller for Low Specific Speed Centrifugal Pump Based on Orthogonal Test. J. Mar. Sci. Eng. 2021, 9, 121. [Google Scholar] [CrossRef]
- Bouhmala, N.; Cai, X. Partition of unstructured finite element meshes by a multilevel approach. In Proceedings of the International Workshop on Applied Parallel Computing in Springer, Heidelberg/Berlin, Germany, 20–23 June 2000; pp. 187–195. [Google Scholar]
- Lee, M.H.; Kim, C.M.; Park, G.Y.; Choi, C.H.; Park, C.Y. Grid Independence Test of Computational Fluid Dynamics Model for Indoor Airflow Analysis. J. Korean Inst. Archit. Sustain. Environ. Build. Syst. 2020, 10, 183–194. [Google Scholar]
- Xu, L.; Lu, W.; Lu, L.; Dong, L.; Wang, Z. Flow patterns and boundary conditions for inlet and outlet conduits of large pump system with low head. Appl. Math. Mech. 2014, 35, 675–688. [Google Scholar] [CrossRef]
- Ismail, M.; Fartaj, A.; Karimi, M. Numerical investigation on heat transfer and fluid flow behaviors of viscous fluids in a minichannel heat exchanger. Numer. Heat Transf. Part A Appl. 2013, 64, 1–29. [Google Scholar] [CrossRef]
- Axell, L.B.; Liungman, O. A one-equation turbulence model for geophysical applications: Comparison with data and the k—ε model. Environ. Fluid Mech. 2001, 1, 71–106. [Google Scholar] [CrossRef]
- Mousavi, S.F.; Hosseini, K.; Fouladfar, H.; Mohammadian, M. Comparison of different turbulence models in predicting cohesive fluid mud gravity current propagation. Int. J. Sediment Res. 2020, 35, 504–515. [Google Scholar]
- Ying, Z.; Seberry, J.; Xia, T.; Wysocki, B.J.; Wysocki, T.A. Construction of amicable orthogonal designs of quaternions. Australas. J. Comb. 2009, 44, 19–35. [Google Scholar]
- Xu, B.; Gao, C.; Xia, H.; Lu, W. Influence of geometric parameters of perforated diversion pier on rectification effect of forebay of gate station project. J. Chang. Acad. Sci. 2019, 36, 58–62. (In Chinese) [Google Scholar]
- China Communications Planning and Design Institute for Water Transportation. Code for Master Design of Shiplocks, 1st ed.; Nanhai Press: Haikou, China, 2002; pp. 305–2001. [Google Scholar]



| Level | Factor | |||
|---|---|---|---|---|
| A [m] | B [m] | C [°] | D [m] | |
| 1 | 20 | 0.4 | 35 | 18 |
| 2 | 22 | 0.6 | 40 | 20 |
| 3 | 24 | 0.8 | 45 | 22 |
| 4 | 26 | 1.0 | 50 | 24 |
| 5 | 28 | 1.2 | 55 | 26 |
| Level | Factor | |||
|---|---|---|---|---|
| E [m] | F [m] | G [°] | H [m] | |
| 1 | 20 | 0.4 | 35 | 18 |
| 2 | 22 | 0.6 | 40 | 20 |
| 3 | 24 | 0.8 | 45 | 22 |
| 4 | 26 | 1.0 | 50 | 24 |
| 5 | 28 | 1.2 | 55 | 26 |
| Schemes | Length A [m] | Width B [m] | Radian C [°] | Arc Radius D [m] | Error | Flow Rate Uniformity (5# Channel) [%] | Flow Rate Uniformity (6# Channel) [%] | |
|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | 1 | 62.84 | 62.44 | |
| P2 | 1 | 2 | 2 | 2 | 2 | 63.23 | 65.55 | |
| P3 | 1 | 3 | 3 | 3 | 3 | 77.56 | 78.22 | |
| P4 | 1 | 4 | 4 | 4 | 4 | 76.49 | 76.22 | |
| P5 | 1 | 5 | 5 | 5 | 5 | 74.22 | 73.14 | |
| P6 | 2 | 1 | 2 | 3 | 4 | 64.96 | 63.95 | |
| P7 | 2 | 2 | 3 | 4 | 5 | 77.32 | 78.89 | |
| P8 | 2 | 3 | 4 | 5 | 1 | 75.32 | 76.23 | |
| P9 | 2 | 4 | 5 | 1 | 2 | 77.28 | 77.74 | |
| P10 | 2 | 5 | 1 | 2 | 3 | 63.26 | 61.31 | |
| P11 | 3 | 1 | 3 | 5 | 2 | 75.86 | 75.56 | |
| P12 | 3 | 2 | 4 | 1 | 3 | 80.22 | 79.95 | |
| P13 | 3 | 3 | 5 | 2 | 4 | 77.28 | 78.20 | |
| P14 | 3 | 4 | 1 | 3 | 5 | 67.64 | 67.74 | |
| P15 | 3 | 5 | 2 | 4 | 1 | 70.24 | 69.09 | |
| P16 | 4 | 1 | 4 | 2 | 5 | 74.91 | 71.37 | |
| P17 | 4 | 2 | 5 | 3 | 1 | 75.66 | 76.48 | |
| P18 | 4 | 3 | 1 | 4 | 2 | 72.50 | 71.67 | |
| P19 | 4 | 4 | 2 | 5 | 3 | 73.08 | 75.09 | |
| P20 | 4 | 5 | 3 | 1 | 4 | 78.61 | 77.91 | |
| P21 | 5 | 1 | 5 | 4 | 3 | 77.27 | 76.73 | |
| P22 | 5 | 2 | 1 | 5 | 4 | 73.52 | 68.72 | |
| P23 | 5 | 3 | 2 | 1 | 5 | 63.51 | 64.55 | |
| P24 | 5 | 4 | 3 | 2 | 1 | 78.92 | 78.54 | |
| P25 | 5 | 5 | 4 | 3 | 2 | 77.01 | 79.01 | |
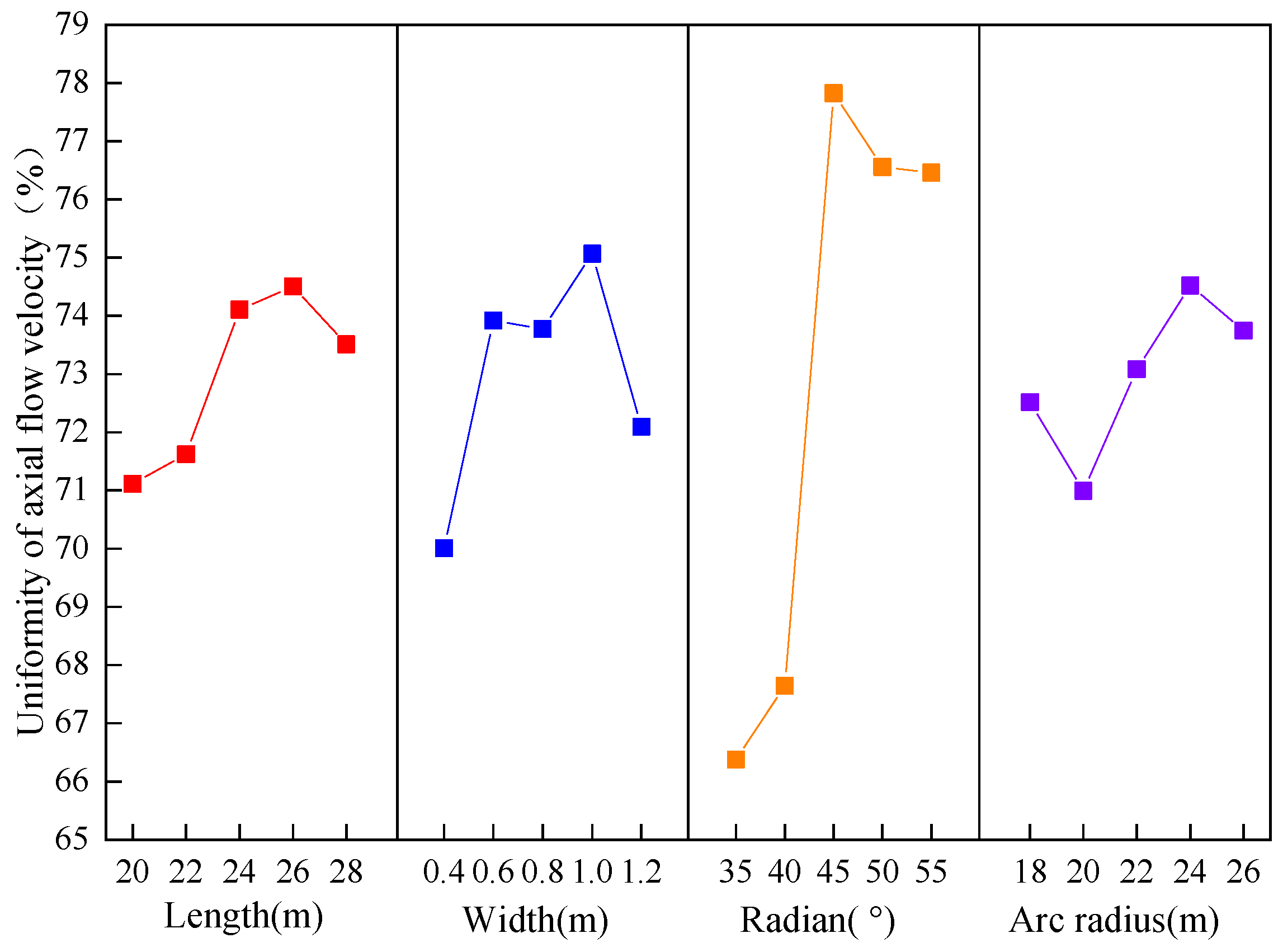
| Flow rate uniformity (5#) | k1 | 70.87 | 71.17 | 67.95 | 72.49 | 72.60 | ||
| k2 | 71.63 | 73.99 | 67.00 | 71.52 | 73.18 | |||
| k3 | 74.25 | 73.23 | 77.65 | 72.57 | 74.28 | |||
| k4 | 74.95 | 74.68 | 76.79 | 74.76 | 74.17 | |||
| k5 | 74.05 | 72.67 | 76.34 | 74.40 | 71.52 | |||
| r | 4.08 | 3.51 | 10.65 | 3.24 | 2.76 | |||
| Flow rate uniformity (6#) | k1 | 71.11 | 70.01 | 66.38 | 72.52 | 72.56 | ||
| k2 | 71.62 | 73.92 | 67.65 | 70.99 | 73.91 | |||
| k3 | 74.11 | 73.77 | 77.82 | 73.08 | 74.26 | |||
| k4 | 74.50 | 75.07 | 76.56 | 74.52 | 73.00 | |||
| k5 | 73.51 | 72.09 | 76.46 | 73.75 | 71.14 | |||
| r | 3.39 | 5.06 | 11.45 | 3.53 | 3.12 | |||
| Schemes | Length E [m] | Width F [m] | Radian G [°] | Arc Radius H [m] | Error | Flow Rate Uniformity (7# Sluice) [%] | |
|---|---|---|---|---|---|---|---|
| S1 | 1 | 1 | 1 | 1 | 1 | 72.41 | |
| S2 | 1 | 2 | 2 | 2 | 2 | 84.81 | |
| S3 | 1 | 3 | 3 | 3 | 3 | 84.15 | |
| S4 | 1 | 4 | 4 | 4 | 4 | 86.49 | |
| S5 | 1 | 5 | 5 | 5 | 5 | 81.26 | |
| S6 | 2 | 1 | 2 | 3 | 4 | 77.72 | |
| S7 | 2 | 2 | 3 | 4 | 5 | 85.16 | |
| S8 | 2 | 3 | 4 | 5 | 1 | 85.96 | |
| S9 | 2 | 4 | 5 | 1 | 2 | 85.73 | |
| S10 | 2 | 5 | 1 | 2 | 3 | 73.78 | |
| S11 | 3 | 1 | 3 | 5 | 2 | 84.61 | |
| S12 | 3 | 2 | 4 | 1 | 3 | 84.10 | |
| S13 | 3 | 3 | 5 | 2 | 4 | 86.24 | |
| S14 | 3 | 4 | 1 | 3 | 5 | 78.33 | |
| S15 | 3 | 5 | 2 | 4 | 1 | 81.55 | |
| S16 | 4 | 1 | 4 | 2 | 5 | 84.94 | |
| S17 | 4 | 2 | 5 | 3 | 1 | 82.74 | |
| S18 | 4 | 3 | 1 | 4 | 2 | 80.43 | |
| S19 | 4 | 4 | 2 | 5 | 3 | 85.73 | |
| S20 | 4 | 5 | 3 | 1 | 4 | 85.28 | |
| S21 | 5 | 1 | 5 | 4 | 3 | 84.65 | |
| S22 | 5 | 2 | 1 | 5 | 4 | 78.23 | |
| S23 | 5 | 3 | 2 | 1 | 5 | 77.91 | |
| S24 | 5 | 4 | 3 | 2 | 1 | 84.52 | |
| S25 | 5 | 5 | 4 | 3 | 2 | 85.00 | |
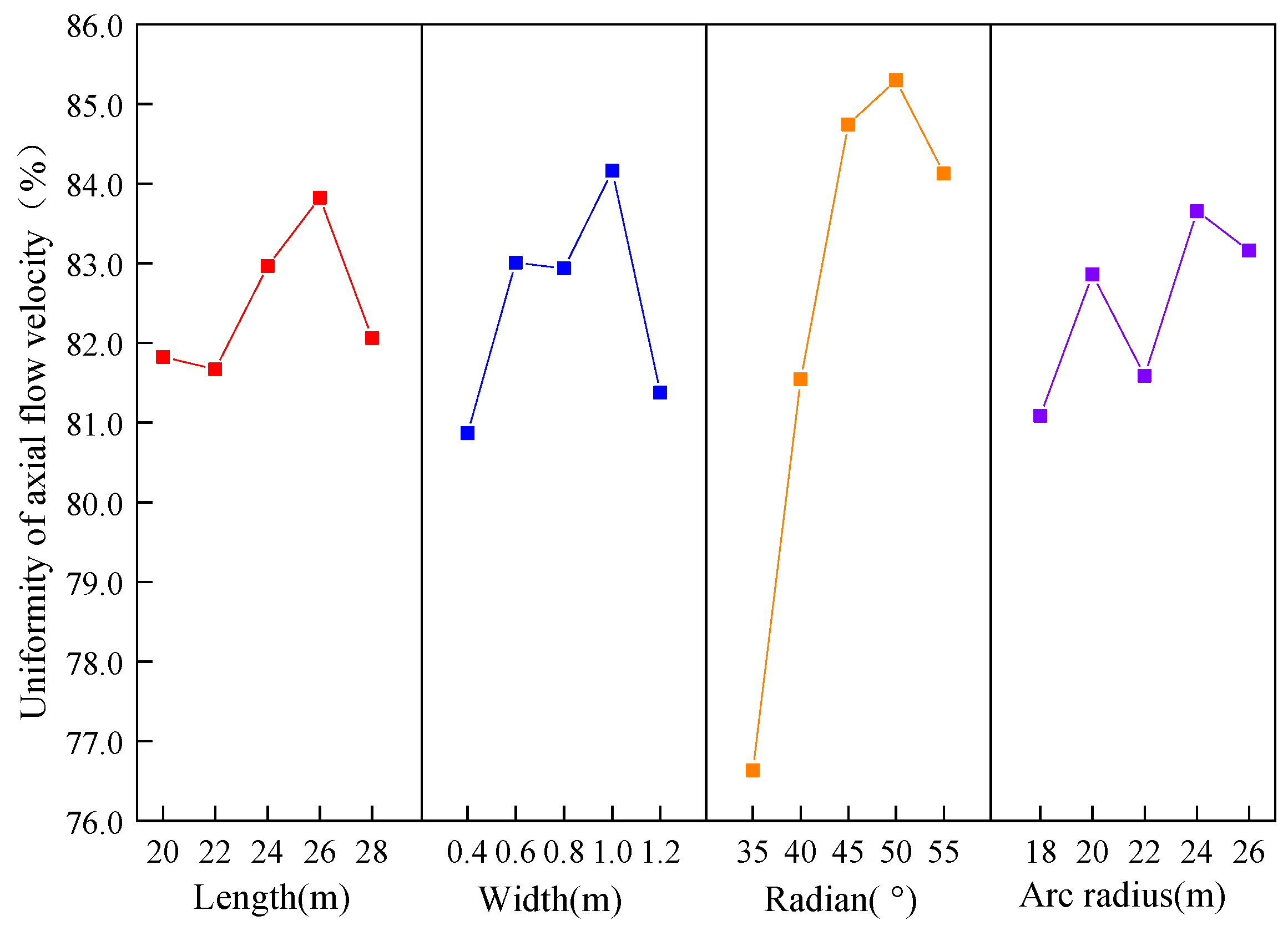
| Flow rate uniformity (7#) | t1 | 82.82 | 80.87 | 76.64 | 81.09 | 81.44 | |
| t2 | 81.67 | 83.01 | 81.54 | 82.86 | 84.12 | ||
| t3 | 82.97 | 82.94 | 84.74 | 81.59 | 82.48 | ||
| t4 | 83.82 | 84.16 | 85.30 | 83.66 | 82.79 | ||
| t5 | 82.06 | 82.37 | 85.12 | 84.16 | 81.52 | ||
| r | 2.15 | 3.29 | 8.66 | 3.07 | 2.68 | ||
| Source of variance | Deviation Sum of Squares | Degree of Freedom | Variance | Variable Values | p |
|---|---|---|---|---|---|
| Length of long straight segment | 63.90 | 4 | 15.98 | 1.80 | 0.222 |
| Width | 36.10 | 4 | 9.03 | 1.02 | 0.454 |
| Radian of arc segment II | 542.58 | 4 | 135.65 | 15.28 | 0.001 |
| Radius of arc segment II | 37.99 | 4 | 9.50 | 1.07 | 0.431 |
| Error | 71.00 | 8 | 8.88 |
| Source of Variance | Deviation Sum of Squares | Degree of Freedom | Variance | Variable Values | p |
|---|---|---|---|---|---|
| Length of long straight segment | 45.98 | 4 | 11.50 | 1.31 | 0.343 |
| Width | 77.35 | 4 | 19.34 | 2.21 | 0.158 |
| Radian of arc segment II | 602.06 | 4 | 150.52 | 17.19 | 0.001 |
| Radius of arc segment II | 35.64 | 4 | 8.91 | 1.02 | 0.453 |
| Error | 70.05 | 8 | 8.76 |
| Source of Variance | Deviation Sum of Squares | Degree of Freedom | Variance | Variable Values | p |
|---|---|---|---|---|---|
| Length of long straight segment | 16.52 | 4 | 4.13 | 0.69 | 0.619 |
| Width | 35.69 | 4 | 8.92 | 1.49 | 0.292 |
| Radian of arc segment I | 253.99 | 4 | 63.50 | 10.61 | 0.003 |
| Radius of arc segment I | 23.62 | 4 | 5.91 | 0.99 | 0.467 |
| Error | 47.86 | 8 | 5.98 |
| Scheme | Diversion Wall Dimension Parameters | |||
|---|---|---|---|---|
| Length [m] | Width[m] | Radian [°] | Arc Radius [m] | |
| P5 | 20 | 1.2 | 55 | 24 |
| P9 | 22 | 1.0 | 55 | 16 |
| P12 | 24 | 1.2 | 50 | 16 |
| P21 | 28 | 1.0 | 55 | 22 |
| C1 | 26 | 1.0 | 45 | 24 |
| Scheme | Diversion Wall Dimension Parameters | |||
|---|---|---|---|---|
| Length [m] | Width[m] | Radian [°] | Arc Radius [m] | |
| S8 | 22 | 0.8 | 50 | 24 |
| S13 | 24 | 0.8 | 55 | 18 |
| S19 | 26 | 1.0 | 40 | 24 |
| S21 | 28 | 0.4 | 55 | 22 |
| Z1 | 26 | 1.0 | 50 | 24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Liu, J.; Lu, W. Optimization Design of Y-Shaped Settling Diversion Wall Based on Orthogonal Test. Machines 2022, 10, 91. https://doi.org/10.3390/machines10020091
Xu B, Liu J, Lu W. Optimization Design of Y-Shaped Settling Diversion Wall Based on Orthogonal Test. Machines. 2022; 10(2):91. https://doi.org/10.3390/machines10020091
Chicago/Turabian StyleXu, Bo, Jianfeng Liu, and Weigang Lu. 2022. "Optimization Design of Y-Shaped Settling Diversion Wall Based on Orthogonal Test" Machines 10, no. 2: 91. https://doi.org/10.3390/machines10020091
APA StyleXu, B., Liu, J., & Lu, W. (2022). Optimization Design of Y-Shaped Settling Diversion Wall Based on Orthogonal Test. Machines, 10(2), 91. https://doi.org/10.3390/machines10020091






