3D-FEM Approach of AISI-52100 Hard Turning: Modelling of Cutting Forces and Cutting Condition Optimization
Abstract
1. Introduction
2. Materials and Methods
2.1. CAD-Based Setup of the Machining Process
2.2. Pre-Processing of the Numerical Model
2.2.1. Analysis Interface Specifications
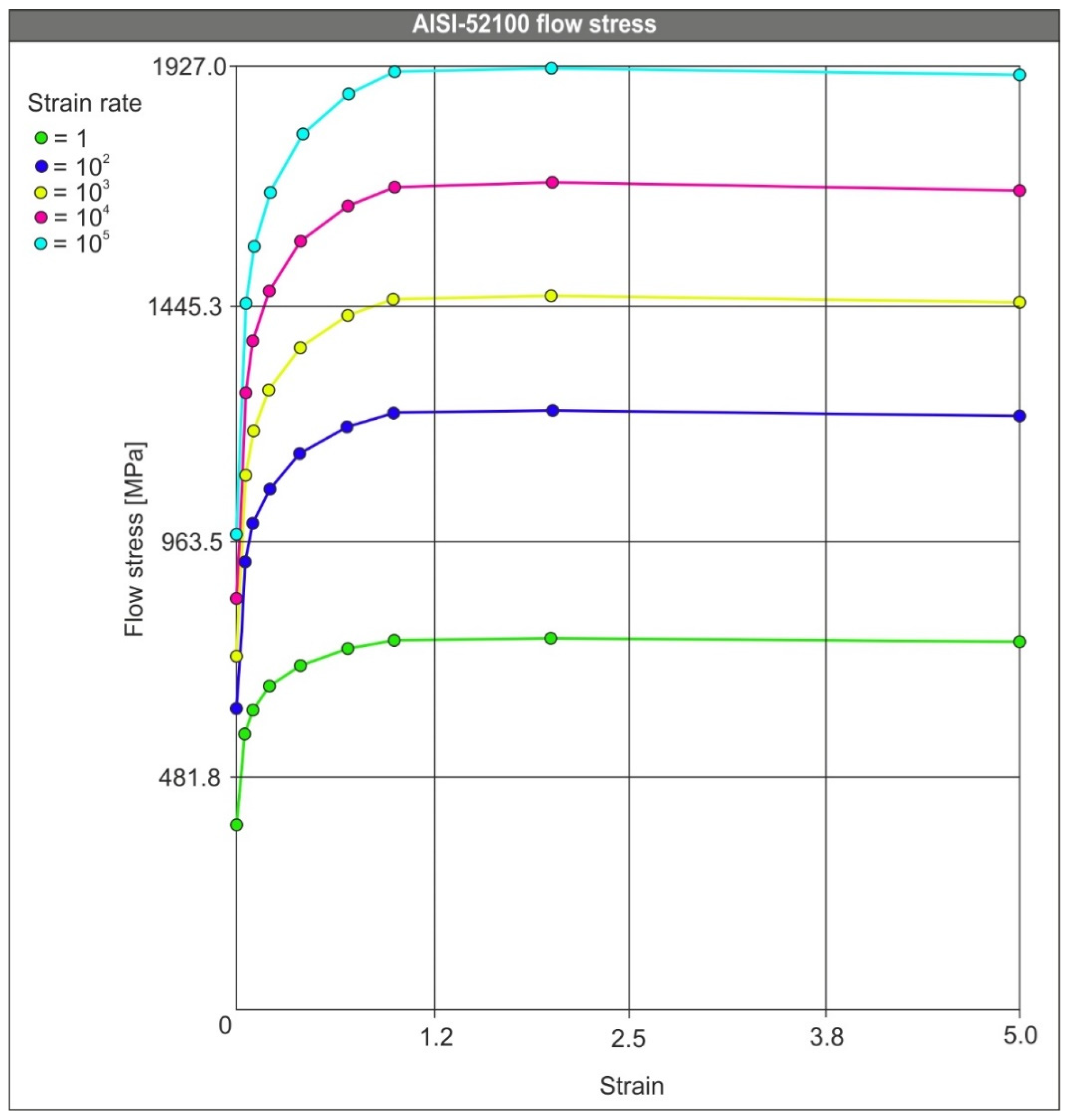
2.2.2. Material Modelling
3. Results and Discussion
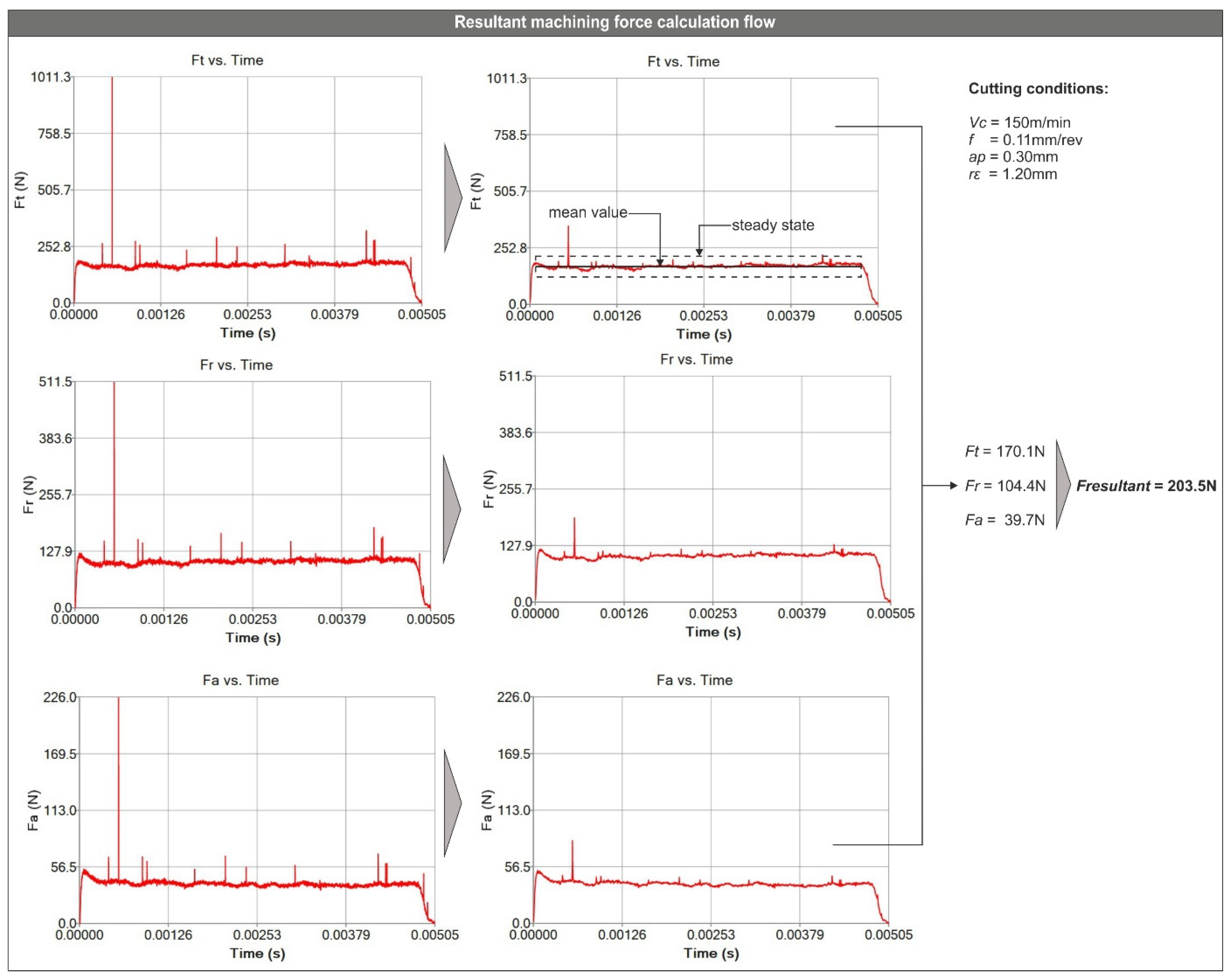
3.1. FEM-Based Evaluation of the Resultant Cutting Force
3.2. Mathematical Modelling of the Resultant Cutting Force
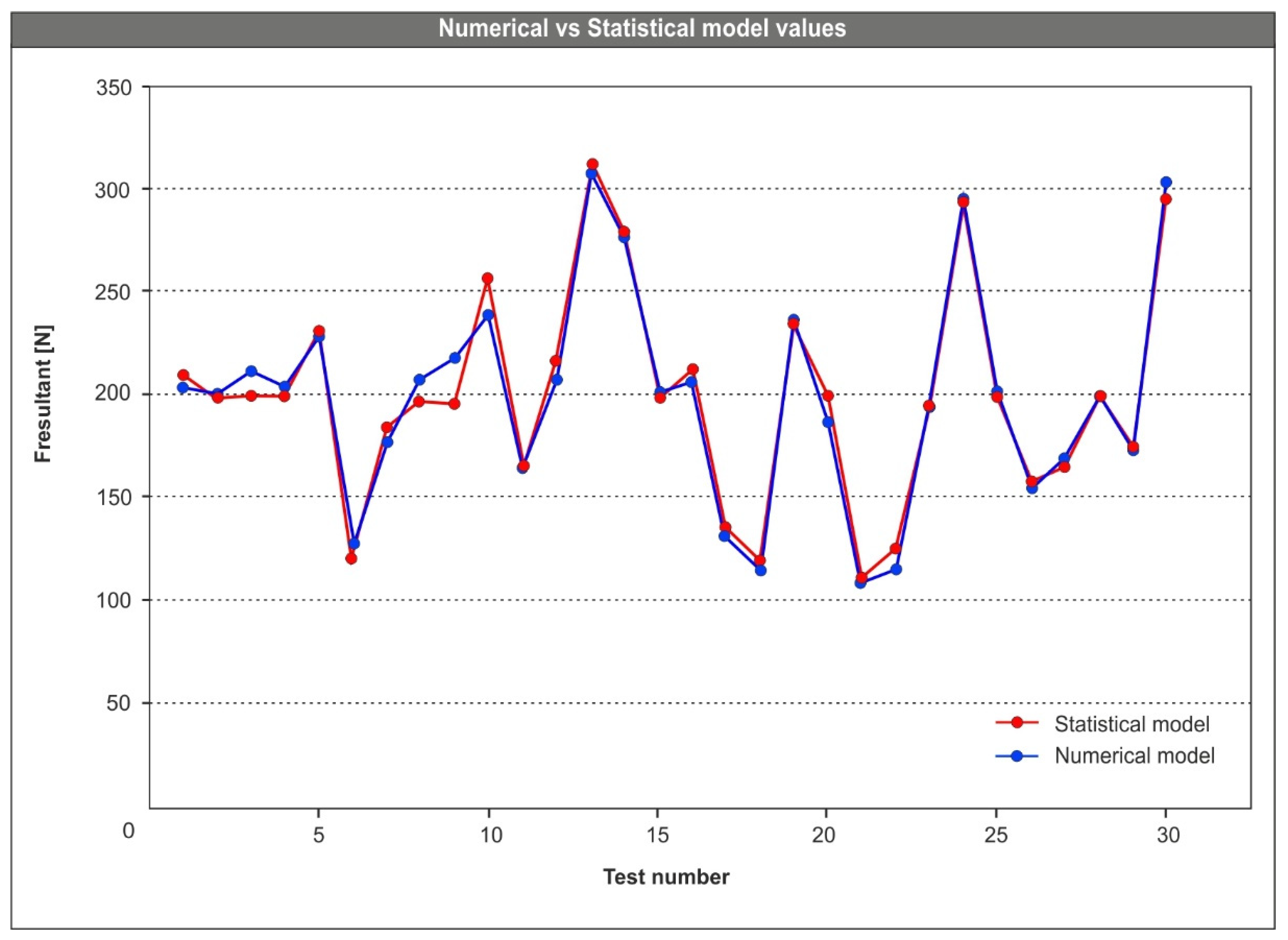
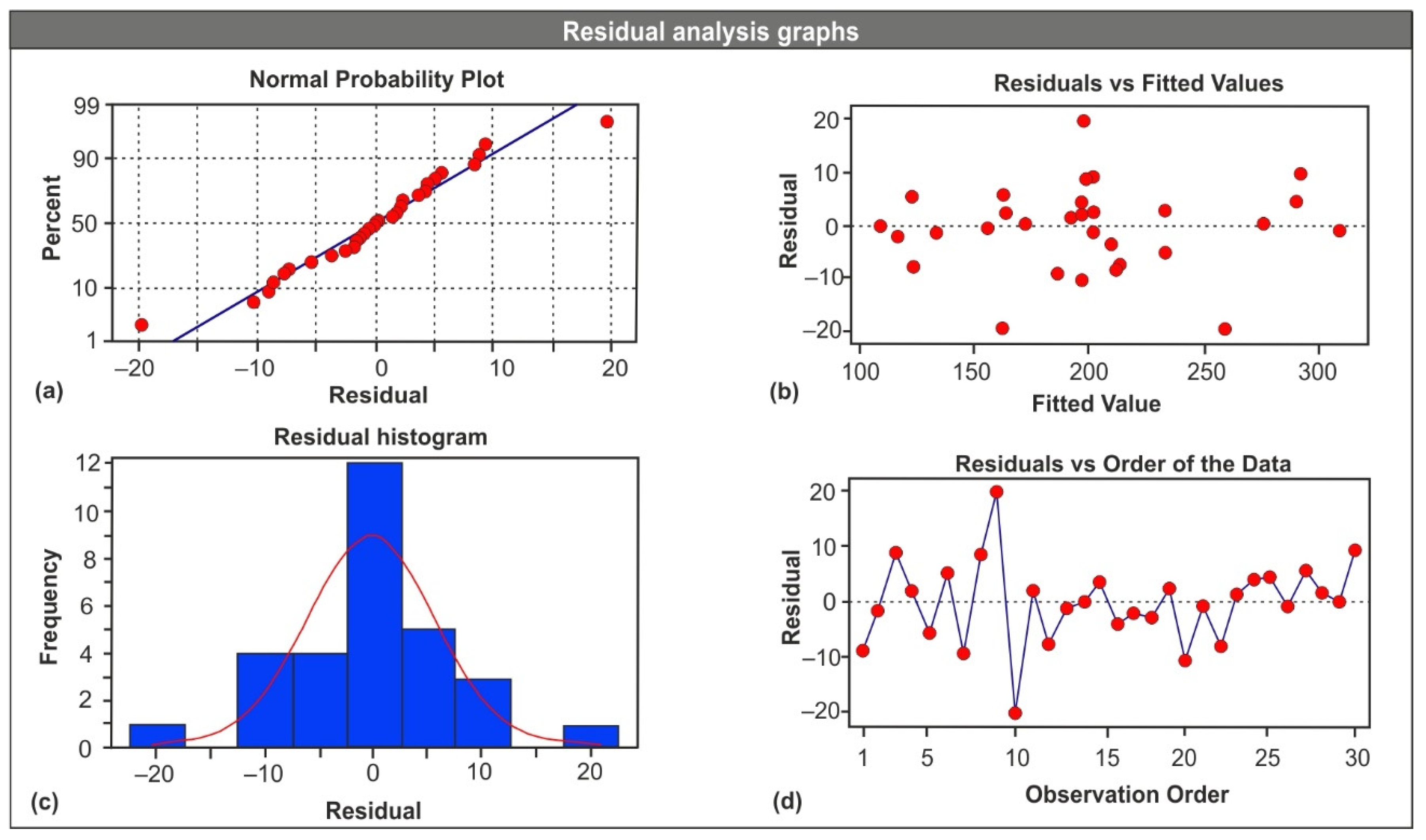
3.3. Analysis and Validation of Mathematical Model
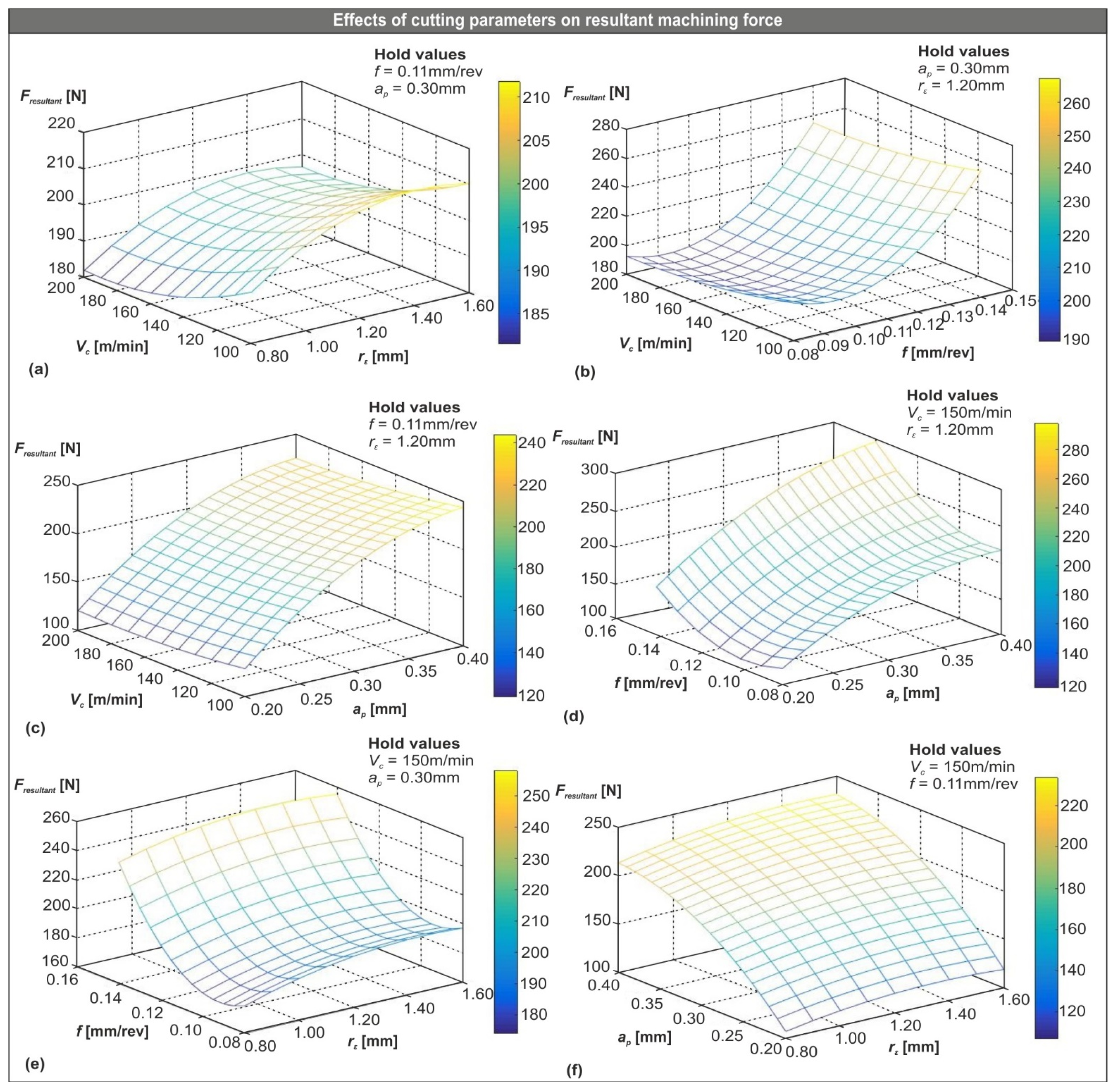
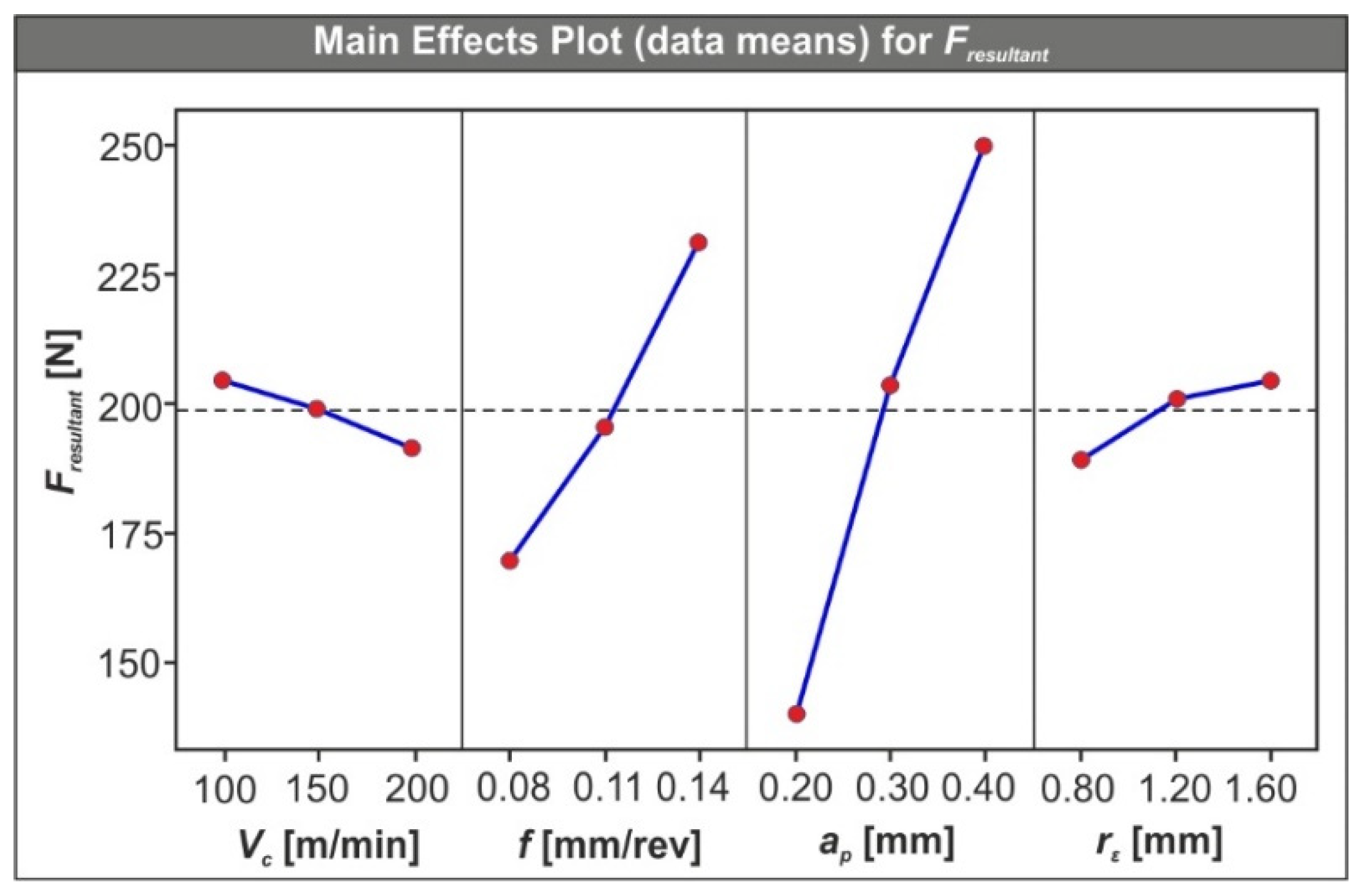
3.4. Investigation of the Cutting Parameters’ Influence
3.5. Optimization Process
3.6. Confirmation of Mathematical Model
4. Conclusions
- Both the established FE model and the mathematical one can predict the generated cutting forces with acceptable errors. The relative error found for the comparison between the numerical and the experimental results ranged between −1.7% and 16.7%, whereas the numerical and the statistical results ranged between −7.9% and 11.3%.
- Especially with the use of the mathematical model, future experimental testing can be skipped and instant results can be delivered for Fresultant within the range of the investigated parameters.
- It was revealed that both depth of cut and feed increasingly act on the generated force, especially depth of cut. The increase percentage when shifting from level one value to level three for feed and depth of cut, is close to 35% and 78%, respectively. Tool nose radius also seems to have an increasing effect, but of no significance, at least compared to the other two parameters. On the other hand, cutting speed seems to lower the produced forces by a small, but not negligible, amount.
- Finally, the optimal cutting conditions were found for three different cutting inserts. Namely, 175.76 m/min cutting speed, 0.097 mm/rev feed and 0.20 mm depth of cut for the 0.80 mm tool, 177.78 m/min cutting speed, 0.098 mm/rev feed and 0.20 mm depth of cut for the 1.20 mm tool and, lastly, 199.73 m/min cutting speed, 0.082 mm/rev feed and 0.20 mm depth of cut for the 1.60 mm tool.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kyratsis, P.; Kakoulis, K.; Markopoulos, A.P. Advances in CAD/CAM/CAE Technologies. Machines 2020, 8, 13. [Google Scholar] [CrossRef]
- Klocke, F.; Raedt, H.-W.; Hoppe, S. 2D-FEM simulation of the orthogonal high speed cutting process. Mach. Sci. Technol. 2001, 5, 323–340. [Google Scholar] [CrossRef]
- Huang, Y.; Liang, S.Y. Modeling of cutting forces under hard turning conditions considering tool wear effect. J. Manuf. Sci. Eng. Trans. ASME 2005, 127, 262–270. [Google Scholar] [CrossRef]
- Yaich, M.; Ayed, Y.; Bouaziz, Z.; Germain, G. Numerical analysis of constitutive coefficients effects on FE simulation of the 2D orthogonal cutting process: Application to the Ti6Al4V. Int. J. Adv. Manuf. Technol. 2017, 93, 283–303. [Google Scholar] [CrossRef]
- Yameogo, D.; Haddag, B.; Makich, H.; Nouari, M. Prediction of the Cutting Forces and Chip Morphology When Machining the Ti6Al4V Alloy Using a Microstructural Coupled Model. Procedia CIRP 2017, 58, 335–340. [Google Scholar] [CrossRef]
- Seshadri, R.; Naveen, I.; Srinivasan, S.; Viswasubrahmanyam, M.; VijaySekar, K.S.; Pradeep Kumar, M. Finite element simulation of the orthogonal machining process with Al 2024 T351 aerospace alloy. Procedia Eng. 2013, 64, 1454–1463. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, H.; Li, A.; Lv, M.; Xue, C.; Zhao, J. FEM simulation-based cutting parameters optimization in machining aluminum-silicon piston alloy ZL109 with PCD tool. J. Mech. Sci. Technol. 2019, 33, 3457–3465. [Google Scholar] [CrossRef]
- Chiappini, E.; Tirelli, S.; Albertelli, P.; Strano, M.; Monno, M. On the mechanics of chip formation in Ti-6Al-4V turning with spindle speed variation. Int. J. Mach. Tools Manuf. 2014, 77, 16–26. [Google Scholar] [CrossRef][Green Version]
- Miller, S.F.; Shih, A.J. Thermo-mechanical finite element modeling of the friction drilling process. J. Manuf. Sci. Eng. Trans. ASME 2007, 129, 531–538. [Google Scholar] [CrossRef]
- Nan, X.; Xie, L.; Zhao, W. On the application of 3D finite element modeling for small-diameter hole drilling of AISI 1045 steel. Int. J. Adv. Manuf. Technol. 2016, 84, 1927–1939. [Google Scholar] [CrossRef]
- Pawar, P.; Ballav, R.; Kumar, A. Modeling and Simulation of Drilling Process in Ti-6Al-4V, Al6061 Using Deform-3D Software. Int. J. ChemTech Res. 2017, 10, 137–142. [Google Scholar]
- Tzotzis, A.; García-Hernández, C.; Huertas-Talón, J.-L.; Kyratsis, P. FEM based mathematical modelling of thrust force during drilling of Al7075-T6. Mech. Ind. 2020, 21, 415. [Google Scholar] [CrossRef]
- Majeed, A.; Iqbal, A.; Lv, J. Enhancement of tool life in drilling of hardened AISI 4340 steel using 3D FEM modeling. Int. J. Adv. Manuf. Technol. 2018, 95, 1875–1889. [Google Scholar] [CrossRef]
- Tzotzis, A.; Markopoulos, A.P.; Karkalos, N.E.; Tzetzis, D.; Kyratsis, P. FEM based investigation on thrust force and torque during Al7075-T6 drilling. In IOP Conference Series: Materials Science and Engineering, Proceedings of the 24th Innovative Manufacturing Engineering and Energy International Conference (IManEE 2020), Athens, Greece,14–15 December 2020; IOP Publishing: Bristol, UK, 2021; Volume 1037, p. 012009. [Google Scholar] [CrossRef]
- Thepsonthi, T.; Özel, T. 3-D finite element process simulation of micro-end milling Ti-6Al-4V titanium alloy: Experimental validations on chip flow and tool wear. J. Mater. Process. Technol. 2015, 221, 128–145. [Google Scholar] [CrossRef]
- Gao, Y.; Ko, J.H.; Lee, H.P. 3D coupled Eulerian-Lagrangian finite element analysis of end milling. Int. J. Adv. Manuf. Technol. 2018, 98, 849–857. [Google Scholar] [CrossRef]
- Pittalà, G.M.; Monno, M. 3D finite element modeling of face milling of continuous chip material. Int. J. Adv. Manuf. Technol. 2010, 47, 543–555. [Google Scholar] [CrossRef]
- Maurel-Pantel, A.; Fontaine, M.; Thibaud, S.; Gelin, J.C. 3D FEM simulations of shoulder milling operations on a 304L stainless steel. Simul. Model. Pract. Theory 2012, 22, 13–27. [Google Scholar] [CrossRef]
- Valiorgue, F.; Rech, J.; Hamdi, H.; Gilles, P.; Bergheau, J.M. 3D modeling of residual stresses induced in finish turning of an AISI304L stainless steel. Int. J. Mach. Tools Manuf. 2012, 53, 77–90. [Google Scholar] [CrossRef]
- Liu, G.; Huang, C.; Su, R.; Özel, T.; Liu, Y.; Xu, L. 3D FEM simulation of the turning process of stainless steel 17-4PH with differently texturized cutting tools. Int. J. Mech. Sci. 2019, 155, 417–429. [Google Scholar] [CrossRef]
- Lotfi, M.; Amini, S.; Aghaei, M. 3D FEM simulation of tool wear in ultrasonic assisted rotary turning. Ultrasonics 2018, 88, 106–114. [Google Scholar] [CrossRef] [PubMed]
- Tzotzis, A.; García-Hernández, C.; Huertas-Talón, J.-L.; Kyratsis, P. 3D FE Modelling of Machining Forces during AISI 4140 Hard Turning. Strojniški Vestn. J. Mech. Eng. 2020, 66, 467–478. [Google Scholar] [CrossRef]
- Mathieu, G.; Frédéric, V.; Vincent, R.; Eric, F. 3D stationary simulation of a turning operation with an Eulerian approach. Appl. Therm. Eng. 2015, 76, 134–146. [Google Scholar] [CrossRef]
- Attanasio, A.; Ceretti, E.; Giardini, C. 3D Fe Modelling Of Superficial Residual Stresses in Turning Operations. Mach. Sci. Technol. 2009, 13, 317–337. [Google Scholar] [CrossRef]
- Kyratsis, P.; Tzotzis, A.; Markopoulos, A.; Tapoglou, N. CAD-Based 3D-FE Modelling of AISI-D3 Turning with Ceramic Tooling. Machines 2021, 9, 4. [Google Scholar] [CrossRef]
- Meddour, I.; Yallese, M.A.; Khattabi, R.; Elbah, M.; Boulanouar, L. Investigation and modeling of cutting forces and surface roughness when hard turning of AISI 52100 steel with mixed ceramic tool: Cutting conditions optimization. Int. J. Adv. Manuf. Technol. 2015, 77, 1387–1399. [Google Scholar] [CrossRef]
- Tzotzis, A.; García-Hernández, C.; Huertas-Talón, J.-L.; Kyratsis, P. Influence of the Nose Radius on the Machining Forces Induced during AISI-4140 Hard Turning: A CAD-Based and 3D FEM Approach. Micromachines 2020, 11, 798. [Google Scholar] [CrossRef] [PubMed]
- DEFORM, Version 11.3 (PC); Documentation; Scientific Forming Technologies Corporation: Columbus, OH, USA, 2016.
- Hu, H.J.; Huang, W.J. Effects of turning speed on high-speed turning by ultrafine-grained ceramic tool based on 3D finite element method and experiments. Int. J. Adv. Manuf. Technol. 2013, 67, 907–915. [Google Scholar] [CrossRef]
- Kobayashi, S.; Lee, C.H. Deformation mechanics and workability in upsetting solid circular cylinders. In Proceedings of the North American Metalworking Research Conference, Hamilton, ON, Canada, 14–15 May 1973; Volume 1. [Google Scholar]
- Oh, S.I.; Chen, C.C.; Kobayashi, S. Ductile Fracture in Axisymmetric Extrusion and Drawing—Part 2: Workability in Extrusion and Drawing. J. Eng. Ind. 1979, 101, 36–44. [Google Scholar] [CrossRef]
- Oyane, M.; Sato, T.; Okimoto, K.; Shima, S. Criteria for ductile fracture and their applications. J. Mech. Work. Technol. 1980, 4, 65–81. [Google Scholar] [CrossRef]
- Cockcroft, M.G.; Latham, D.J. Ductility and the Workability of Metals. J. Institue Met. 1968, 96, 33–39. [Google Scholar]
- Agmell, M. Applied FEM of Metal Removal and Forming, 1st ed.; Studentlitteratur: Lund, Sweden, 2018; ISBN 978-91-44-12507-7. [Google Scholar]
- Arrazola, P.J.; Matsumura, T.; Kortabarria, A.; Garay, A.; Soler, D. Finite Element Modelling of Chip Formation Process Applied to Drilling of Ti64 Alloy. In Proceedings of the International Conference on Leading Edge Manufacturing in 21st Century: LEM21, Omiya Sonic City, Japan, 8–10 November 2011; Volume 6, pp. 1–6. [Google Scholar]
- Haglund, A.J.; Kishawy, H.A.; Rogers, R.J. An exploration of friction models for the chip–tool interface using an Arbitrary Lagrangian–Eulerian finite element model. Wear 2008, 265, 452–460. [Google Scholar] [CrossRef]
- Sateesh, K.; Majumder, H.; Khan, A.; Patel, S.K. Applicability of DLC and WC/C low friction coatings on Al2O3/TiCN mixed ceramic cutting tools for dry machining of hardened 52100 steel. Ceram. Int. 2020, 46, 11889–11897. [Google Scholar] [CrossRef]
- Quiza, R.; Figueira, L.; Paulo Davim, J. Comparing statistical models and artificial neural networks on predicting the tool wear in hard machining D2 AISI steel. Int. J. Adv. Manuf. Technol. 2008, 37, 641–648. [Google Scholar] [CrossRef]
- Horng, J.; Liu, N.; Chiang, K. Investigating the machinability evaluation of Hadfield steel in the hard turning with Al2O3/TiC mixed ceramic tool based on the response surface methodology. J. Mater. Process. Technol. 2008, 208, 532–541. [Google Scholar] [CrossRef]
- Lalwani, D.I.; Mehta, N.K.; Jain, P.K. Experimental investigations of cutting parameters influence on cutting forces and surface roughness in finish hard turning of MDN250 steel. J. Mater. Process. Technol. 2008, 206, 167–179. [Google Scholar] [CrossRef]


| Level | Vc [m/min] | f [mm/rev] | ap [mm] | rε [mm] |
|---|---|---|---|---|
| −1 | 100 | 0.08 | 0.20 | 0.80 |
| 0 | 150 | 0.11 | 0.30 | 1.20 |
| +1 | 200 | 0.14 | 0.40 | 1.60 |
| Mechanical Properties | AISI-52100 | Ceramic |
|---|---|---|
| Young’s Modulus [GPa] | 210 | 415 |
| Density [kg/m3] | 7850 | 3500 |
| Poisson’s ratio | 0.30 | 0.22 |
| Thermal properties | AISI-52100 | Ceramic |
| Heat capacity [J/kgK] | 278 at 93 °C | 334 |
| 324 at 316 °C | ||
| 579 at 649 °C | ||
| 718 at 871 °C | ||
| Thermal expansion [μm/mK] | 11.9 | 8.4 |
| Thermal conductivity [W/mK] | 24.57 at 149 °C | 7.5 |
| 24.4 at 349 °C | ||
| 24.23 at 477 °C | ||
| 24.75 at 604 °C |
| Input | Output | ||||||
|---|---|---|---|---|---|---|---|
| Standard Order | Vc (m/min) | f (mm/rev) | rε (mm) | ap (mm) | Experimental Fresultant (N) | Numerical Fresultant (N) | Relative Error (%) |
| 1 | 100 | 0.08 | 0.80 | 0.25 | 127.1 | 132.8 | 4.5 |
| 2 | 100 | 0.14 | 0.80 | 0.25 | 187.2 | 203.1 | 8.5 |
| 3 | 200 | 0.08 | 0.80 | 0.25 | 119.9 | 126.6 | 5.6 |
| 4 | 200 | 0.14 | 0.80 | 0.25 | 171.7 | 183.3 | 6.8 |
| 5 | 150 | 0.11 | 1.20 | 0.25 | 141.4 | 139.0 | −1.7 |
| 6 | 100 | 0.08 | 1.60 | 0.25 | 146.0 | 161.0 | 10.3 |
| 7 | 100 | 0.14 | 1.60 | 0.25 | 191.6 | 212.4 | 10.8 |
| 8 | 200 | 0.08 | 1.60 | 0.25 | 128.3 | 126.9 | −1.1 |
| 9 | 200 | 0.14 | 1.60 | 0.25 | 183.7 | 214.4 | 16.7 |
| Input | Output | ||||||
|---|---|---|---|---|---|---|---|
| Run | Vc (m/min) | f (mm/rev) | ap (mm) | rε (mm) | Numerical Fresultant (N) | Statistical Fresultant (N) | Relative Error (%) |
| 1 | 100 | 0.11 | 0.3 | 1.2 | 203.2 | 209.6 | −3.0 |
| 2 | 150 | 0.11 | 0.3 | 1.2 | 199.8 | 199.1 | 0.4 |
| 3 | 150 | 0.11 | 0.3 | 1.6 | 210.6 | 199.3 | 5.6 |
| 4 | 150 | 0.11 | 0.3 | 1.2 | 203.5 | 199.1 | 2.2 |
| 5 | 150 | 0.11 | 0.4 | 1.2 | 227.7 | 230.8 | −1.3 |
| 6 | 150 | 0.11 | 0.2 | 1.2 | 127.9 | 120.5 | 6.2 |
| 7 | 150 | 0.11 | 0.3 | 0.8 | 177.1 | 184.0 | −3.7 |
| 8 | 200 | 0.11 | 0.3 | 1.2 | 207.3 | 196.5 | 5.5 |
| 9 | 150 | 0.08 | 0.3 | 1.2 | 217.4 | 195.3 | 11.3 |
| 10 | 150 | 0.14 | 0.3 | 1.2 | 239.2 | 256.9 | −6.9 |
| 11 | 200 | 0.14 | 0.2 | 1.6 | 165.4 | 165.5 | 0.1 |
| 12 | 200 | 0.08 | 0.4 | 1.6 | 206.5 | 216.1 | −4.4 |
| 13 | 100 | 0.14 | 0.4 | 1.6 | 307.8 | 311.1 | −1.0 |
| 14 | 200 | 0.14 | 0.4 | 0.8 | 276.6 | 278.8 | −0.8 |
| 15 | 150 | 0.11 | 0.3 | 1.2 | 200.6 | 199.1 | 0.8 |
| 16 | 100 | 0.08 | 0.4 | 0.8 | 206.0 | 212.0 | −2.8 |
| 17 | 100 | 0.08 | 0.2 | 1.6 | 131.4 | 135.3 | −2.9 |
| 18 | 100 | 0.08 | 0.2 | 0.8 | 114.4 | 119.1 | −3.9 |
| 19 | 100 | 0.08 | 0.4 | 1.6 | 235.2 | 234.8 | 0.2 |
| 20 | 150 | 0.11 | 0.3 | 1.2 | 186.6 | 199.1 | −6.3 |
| 21 | 200 | 0.08 | 0.2 | 0.8 | 108.0 | 110.8 | −2.5 |
| 22 | 200 | 0.08 | 0.2 | 1.6 | 115.5 | 125.4 | −7.9 |
| 23 | 200 | 0.08 | 0.4 | 0.8 | 193.8 | 194.7 | −0.5 |
| 24 | 200 | 0.14 | 0.4 | 1.6 | 295.4 | 293.4 | 0.7 |
| 25 | 150 | 0.11 | 0.3 | 1.2 | 201.4 | 199.1 | 1.2 |
| 26 | 200 | 0.14 | 0.2 | 0.8 | 154.5 | 157.6 | −2.0 |
| 27 | 100 | 0.14 | 0.2 | 0.8 | 168.5 | 165.0 | 2.1 |
| 28 | 150 | 0.11 | 0.3 | 1.2 | 198.7 | 199.1 | −0.2 |
| 29 | 100 | 0.14 | 0.2 | 1.6 | 172.5 | 174.3 | −1.0 |
| 30 | 100 | 0.14 | 0.4 | 0.8 | 302.3 | 295.0 | 2.5 |
| Source | Degree of Freedom | Sum of Squares | Mean Square | f-Value | p-Value |
|---|---|---|---|---|---|
| Model | 15 | 78,097.5 | 5206.5 | 45.63 | 0.000 |
| Error | 14 | 1597.4 | 114.1 | ||
| Total | 29 | 79,694.9 | |||
| R-sq (adj) = 95.85% | |||||
| Term | |||||
| Blocks | 1 | 76.4 | 76.4 | 0.67 | 0.427 |
| Vc | 1 | 779.3 | 779.3 | 6.83 | 0.020 |
| f | 1 | 17,054.7 | 17,054.7 | 149.47 | 0.000 |
| ap | 1 | 54,800.3 | 54,800.3 | 480.28 | 0.000 |
| rε | 1 | 1074.1 | 1074.1 | 9.41 | 0.008 |
| Vc2 | 1 | 40.4 | 40.4 | 0.35 | 0.561 |
| f2 | 1 | 1857.9 | 1875.9 | 16.28 | 0.001 |
| ap2 | 1 | 1391.0 | 1391.0 | 12.19 | 0.004 |
| rε2 | 1 | 139.5 | 139.5 | 1.22 | 0.287 |
| Vc × f | 1 | 1.0 | 1.0 | 0.01 | 0.926 |
| Vc × ap | 1 | 79.2 | 79.2 | 0.69 | 0.419 |
| Vc × rε | 1 | 2.0 | 2.0 | 0.02 | 0.896 |
| f × ap | 1 | 1389.4 | 1389.4 | 12.18 | 0.004 |
| f × rε | 1 | 46.2 | 46.2 | 0.40 | 0.535 |
| ap × rε | 1 | 45.4 | 45.4 | 0.40 | 0.538 |
| Lack of fit | 10 | 1597.4 | 144.7 | 3.86 | 0.102 |
| Pure error | 4 | 1447.4 | 37.5 | ||
| Factor | Goal | Lower Limt | Upper Limit |
|---|---|---|---|
| Vc (m/min) | In range | 100 | 200 |
| f (mm/rev) | In range | 0.08 | 0.14 |
| ap (mm) | In range | 0.20 | 0.40 |
| rε (mm) | In range | 0.80 | 1.60 |
| Fresultant (N) | Minimize | 108.0 | 307.8 |
| Solution | Vc (m/min) | f (mm/rev) | ap (mm) | rε (mm) | Fresultant (N) | Desirability |
|---|---|---|---|---|---|---|
| 1 | 175.76 | 0.097 | 0.20 | 0.80 | 101.0 | 1.000 |
| 2 | 177.78 | 0.098 | 0.20 | 1.20 | 115.0 | 0.965 |
| 3 | 199.73 | 0.082 | 0.20 | 1.60 | 123.4 | 0.923 |
| Test | Vc (m/min) | f (mm/rev) | ap (mm) | rε (mm) | Simulated Fresultant (N) | Predicted Fresultant (N) | Relative Error (%) |
|---|---|---|---|---|---|---|---|
| 1 | 175.75 | 0.097 | 0.20 | 0.80 | 113.7 | 101.0 | 12.5 |
| 2 | 120 | 0.10 | 0.25 | 0.80 | 139.5 | 149.6 | −6.8 |
| 3 | 160 | 0.10 | 0.25 | 1.20 | 141.6 | 159.0 | −10.9 |
| 4 | 160 | 0.12 | 0.25 | 1.60 | 183.1 | 175.2 | 4.5 |
| 5 | 120 | 0.10 | 0.35 | 0.80 | 190.5 | 201.4 | −5.4 |
| 6 | 160 | 0.10 | 0.35 | 1.20 | 229.4 | 210.6 | 8.9 |
| 7 | 160 | 0.12 | 0.35 | 1.60 | 261.7 | 234.7 | 11.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzotzis, A.; Tapoglou, N.; Verma, R.K.; Kyratsis, P. 3D-FEM Approach of AISI-52100 Hard Turning: Modelling of Cutting Forces and Cutting Condition Optimization. Machines 2022, 10, 74. https://doi.org/10.3390/machines10020074
Tzotzis A, Tapoglou N, Verma RK, Kyratsis P. 3D-FEM Approach of AISI-52100 Hard Turning: Modelling of Cutting Forces and Cutting Condition Optimization. Machines. 2022; 10(2):74. https://doi.org/10.3390/machines10020074
Chicago/Turabian StyleTzotzis, Anastasios, Nikolaos Tapoglou, Rajesh Kumar Verma, and Panagiotis Kyratsis. 2022. "3D-FEM Approach of AISI-52100 Hard Turning: Modelling of Cutting Forces and Cutting Condition Optimization" Machines 10, no. 2: 74. https://doi.org/10.3390/machines10020074
APA StyleTzotzis, A., Tapoglou, N., Verma, R. K., & Kyratsis, P. (2022). 3D-FEM Approach of AISI-52100 Hard Turning: Modelling of Cutting Forces and Cutting Condition Optimization. Machines, 10(2), 74. https://doi.org/10.3390/machines10020074








