Design and Analysis of Mechanical Characteristics of EAP Flexible Drivers
Abstract
1. Introduction
2. Materials and Methods
2.1. Analysis of Drive Unit Model
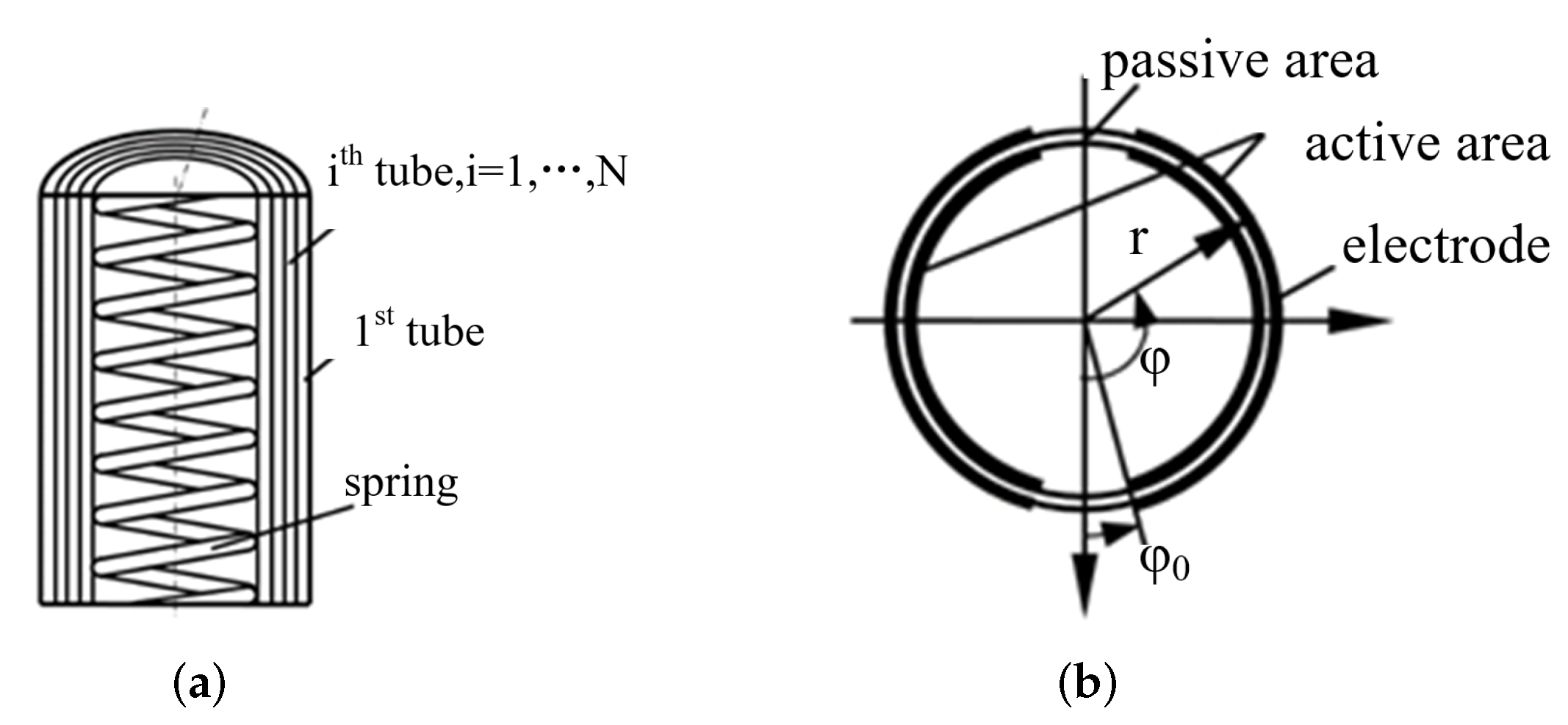
- The unit contains N concentric circular tubes; each tube consists of a circular membrane (Figure 1), and angle is constant and longitudinally symmetric, assuming that the addition of electric drive does not cause a change in the angular position of the active and passive regions.
- In the bending state, the axis of each tube is a circular arc and coincides with the axes of the other tubes, i.e., the curvature of the axes is fixed along the axis direction. In the elongated state, the axes are straight and coincide.
- The spring is a flexible rod with a circular cross-section that supports the EAP membrane from the inside and whose diameter does not vary with the elongation of the spring.
- The EAP membrane is incompressible, superelastic, and time-independent, and the electrodes are soft enough not to prevent the EAP from deforming.
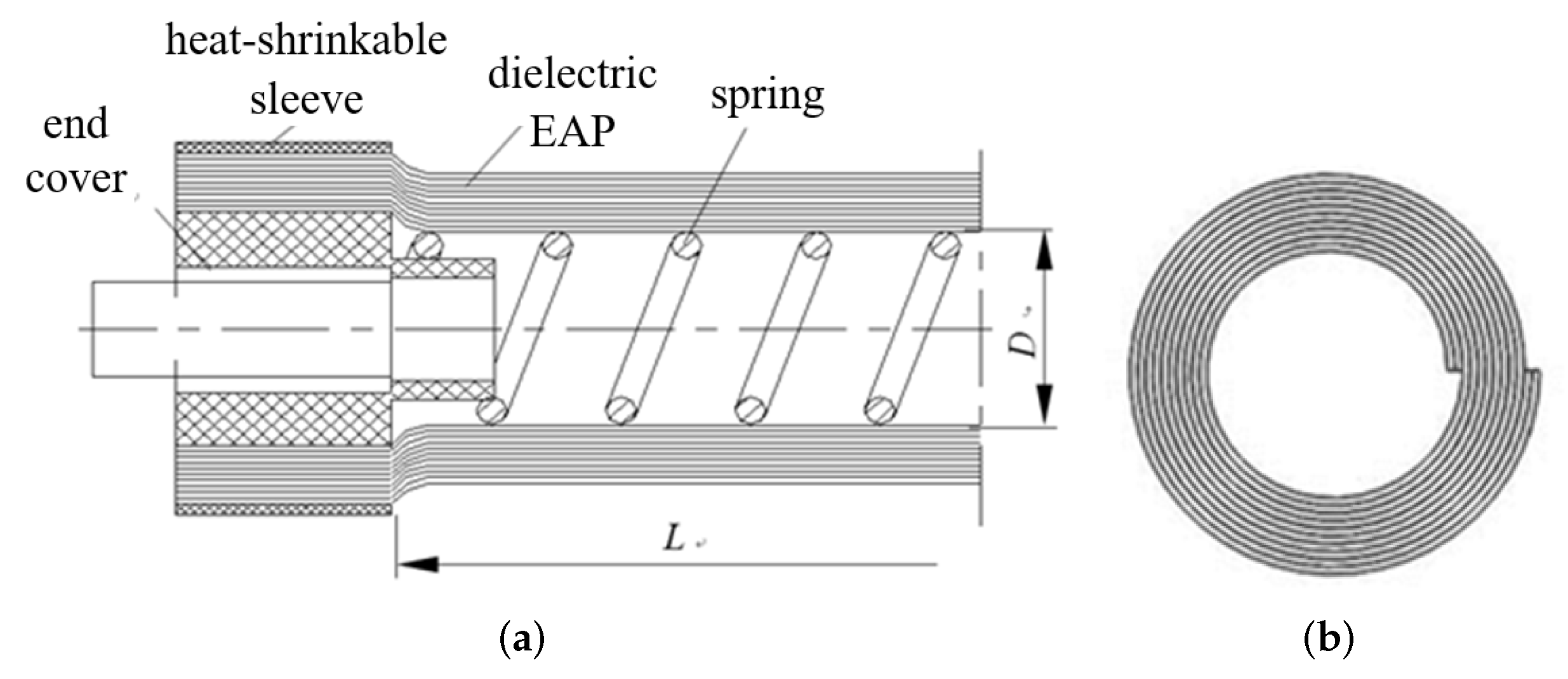
2.2. The Design and Manufacture of Drive Units
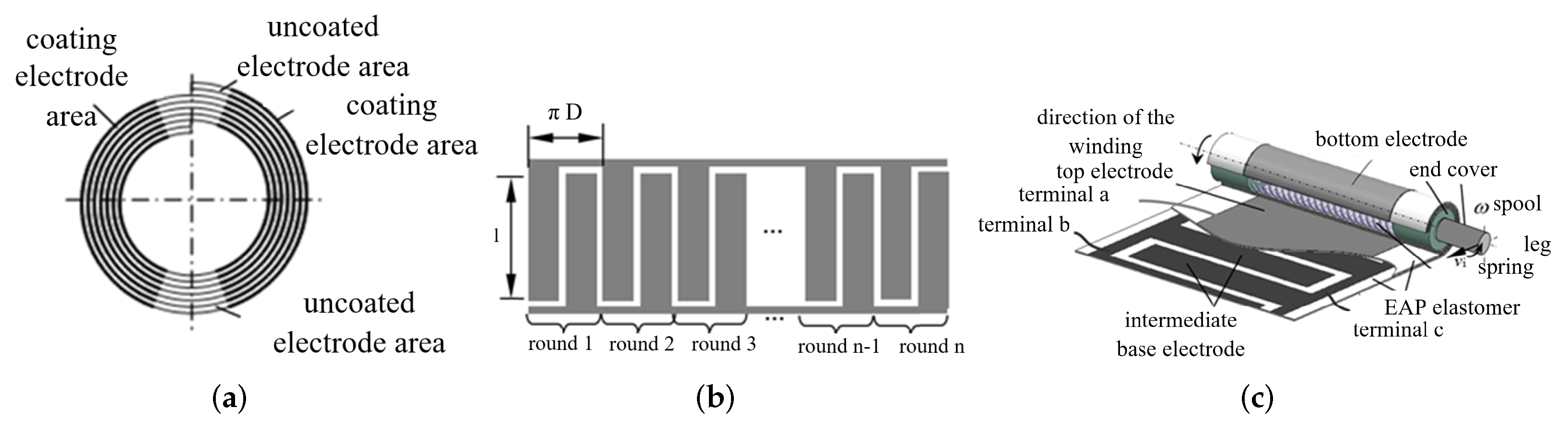
2.2.1. Single-Degree-of-Freedom Actuator
2.2.2. Two-Degree-of-Freedom Actuator
2.3. Manufacture of Drive Units
2.4. The Experiment of Actuating Unit
2.4.1. Uniaxial Tensile Experiment
2.4.2. Experiments of Single-Degree-of-Freedom Actuating Unit
2.4.3. Experiments of Two-Degree-of-Freedom Actuating Unit
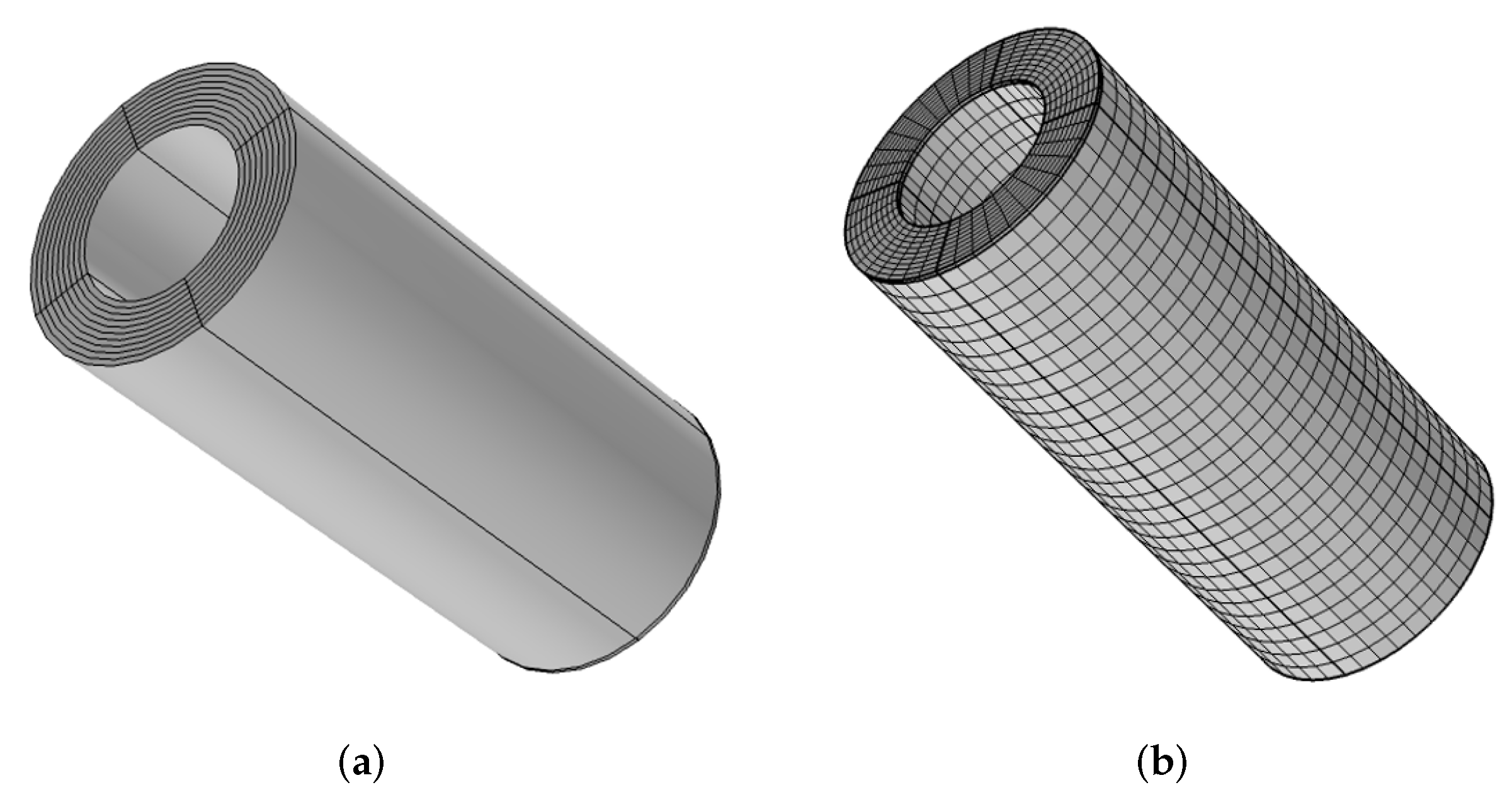
2.5. Simulation of Actuating Unit
2.5.1. Electromechanical Coupling Model
2.5.2. Simulation Content
3. Results and Discussion
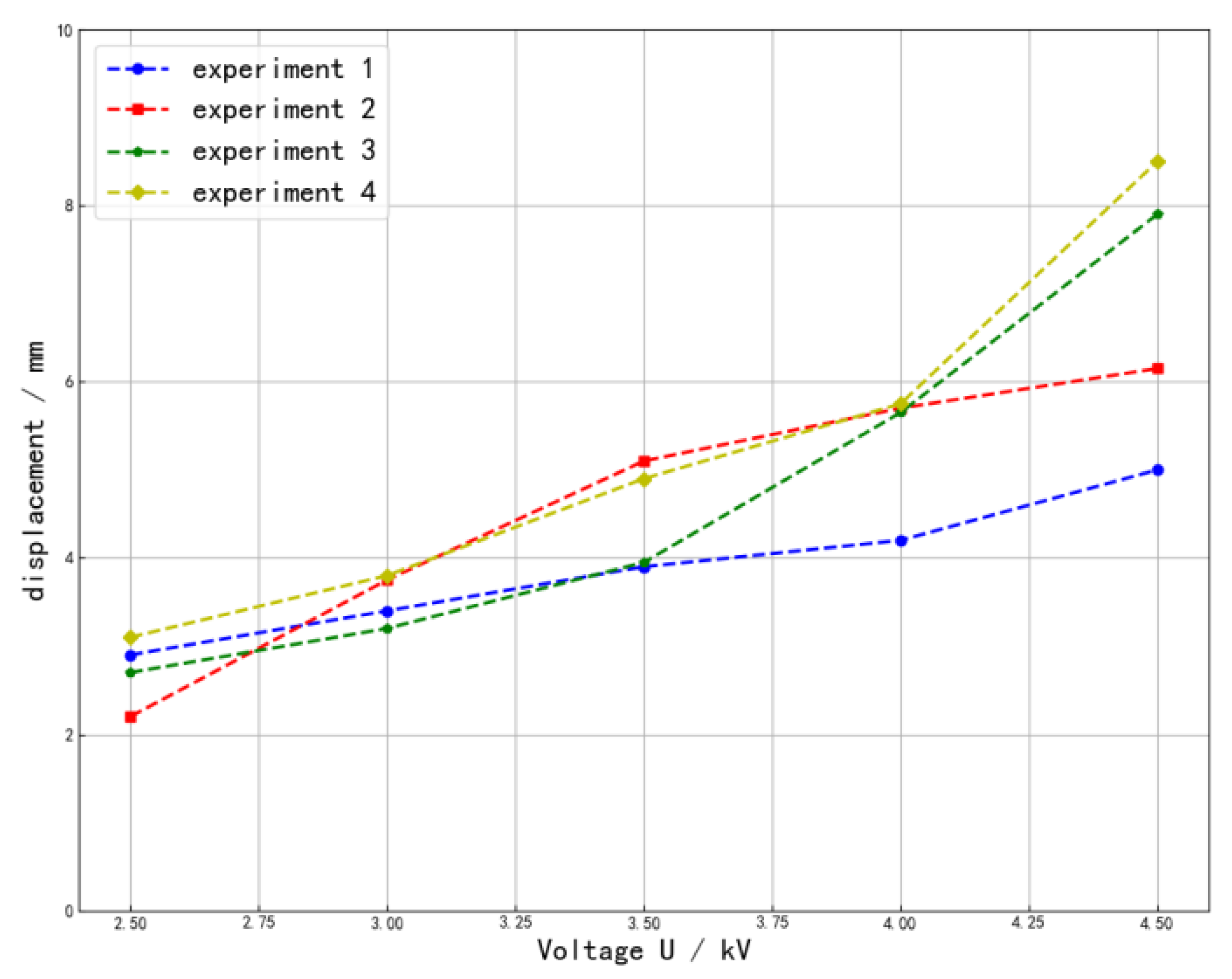
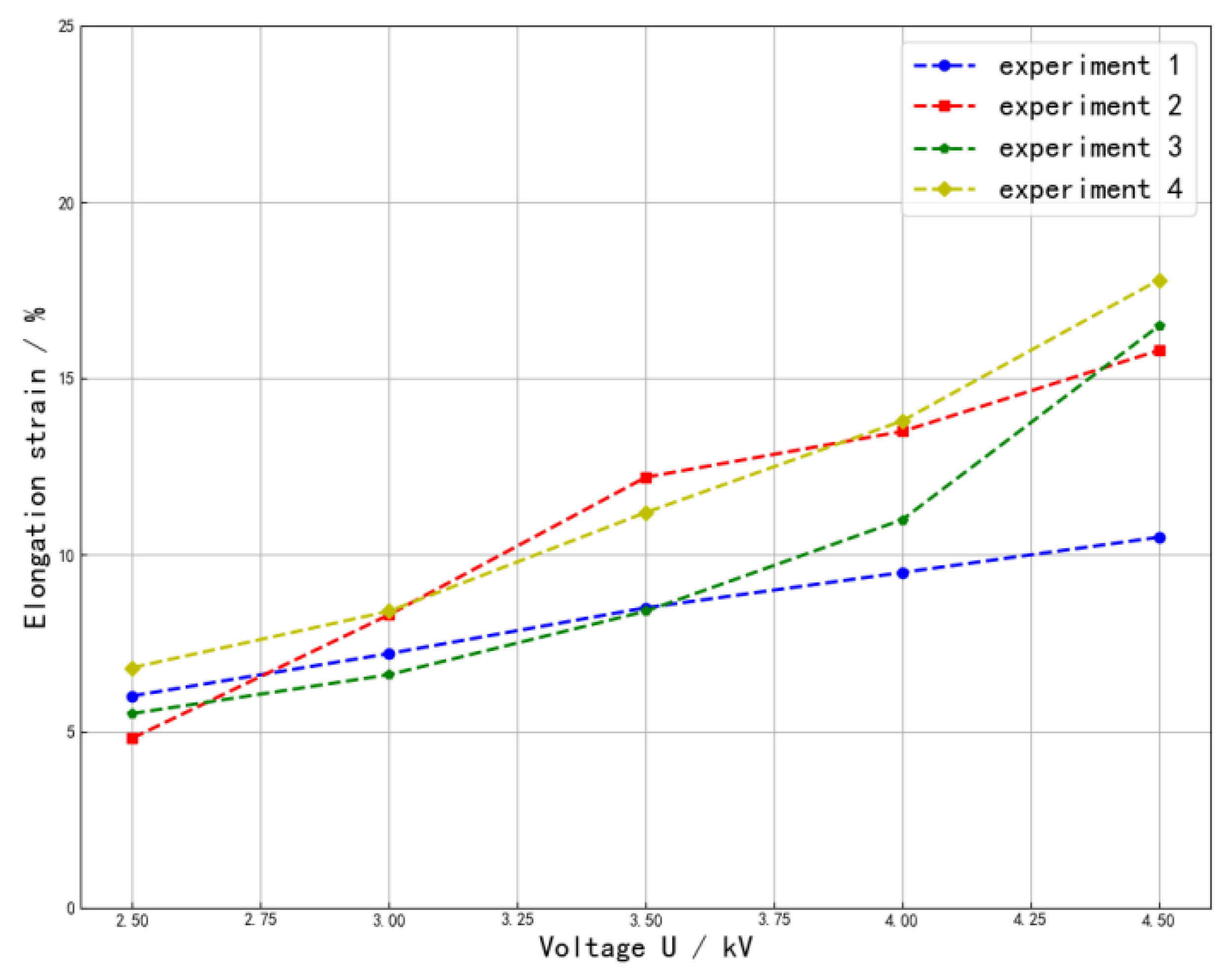
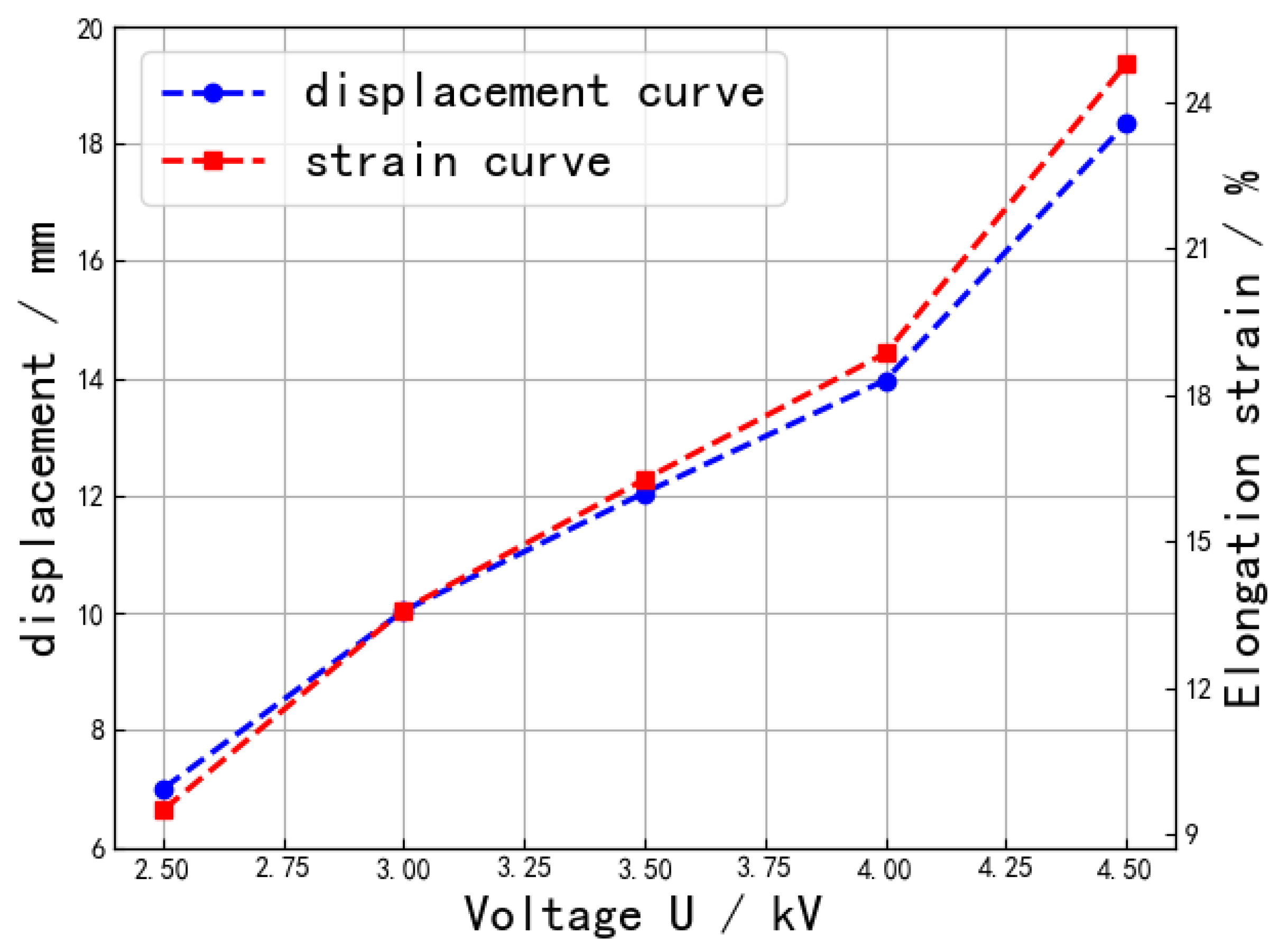
3.1. Single Degree of Freedom
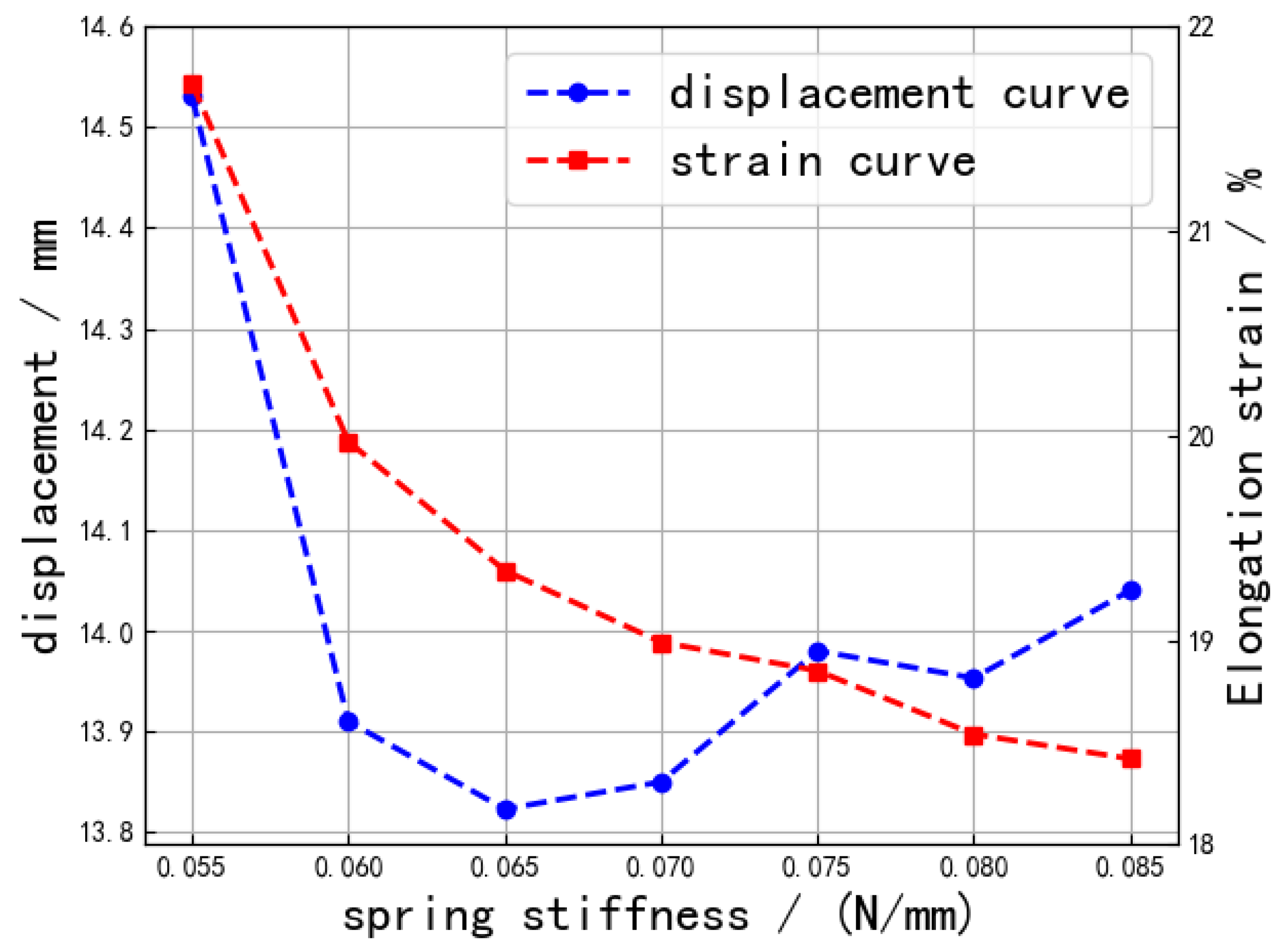
3.2. Two Degree of Freedom
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hollerbach, J.; Hunter, I.; Ballantyne, J. The Robotics Review 2, Chapter A Comparative Analysis of Actuator Technologies for Robotics; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Park, S.; Shrout, T. Ultrahigh strain and piezoelectric behavior in relaxor based ferroelectric single crystals. J. Appl. Phys. 1997, 82, 1804–1811. [Google Scholar] [CrossRef]
- Mirfakhrai, T.; Madden, J.D.; Baughman, R.H. Polymer artificial muscles. Mater. Today 2007, 10, 30–38. [Google Scholar] [CrossRef]
- Bolzmacher, C.; Biggs, J.; Srinivasan, M. Flexible dielectric elastomer actuators for wearable human-machine interfaces. In Proceedings of the Smart Structures and Materials 2006: Electroactive Polymer Actuators and Devices (EAPAD), San Diego, CA, USA, 27 February–2 March 2006; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006; Volume 6168, pp. 27–38. [Google Scholar]
- Bar-Cohen, Y.; Zhang, Q. Electroactive Polymer Actuators and Sensors. MRS Bull. 2008, 33, 173–177. [Google Scholar] [CrossRef]
- Dang, Z.; Wang, L.; Wang, H. Novel smart materials: Progress in electroactive polymers. J. Funct. Mater. 2005, 36, 981–987. [Google Scholar]
- Araromi, O.A.; Gavrilovich, I.; Shintake, J.; Rosset, S.; Richard, M.; Gass, V.; Shea, H.R. Rollable multisegment dielectric elastomer minimum energy structures for a deployable microsatellite gripper. IEEE/ASME Trans. Mechatron. 2014, 20, 438–446. [Google Scholar] [CrossRef]
- Vogan, J.D. Development of Dielectric Elastomer Actuators for MRI Devices. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2004. [Google Scholar]
- Pelrine, R.; Kornbluh, R.; Joseph, J. Electrostriction of polymer dielectrics with compliant electrodes as a means of actuation. Sens. Actuators A Phys. 1998, 64, 77–85. [Google Scholar] [CrossRef]
- Kofod, G.; Sommer-Larsen, P. Silicone dielectric elastomer actuators: Finite-elasticity model of actuation. Sens. Actuators A Phys. 2005, 122, 273–283. [Google Scholar] [CrossRef]
- Suo, Z.; Zhao, X.; Greene, W.H. A nonlinear field theory of deformable dielectrics. J. Mech. Phys. Solids 2008, 56, 467–486. [Google Scholar] [CrossRef]
- Wissler, M.; Mazza, E. Electromechanical coupling in dielectric elastomer actuators. Sens. Actuators A Phys. 2007, 138, 384–393. [Google Scholar] [CrossRef]
- Hossain, M. Modelling the curing process in particle-filled electro-active polymers with a dispersion anisotropy. Contin. Mech. Thermodyn. 2020, 32, 351–367. [Google Scholar] [CrossRef]
- Sharma, R.; Singh, R.; Batish, A. On mechanical and surface properties of electro-active polymer matrix-based 3D printed functionally graded prototypes. J. Thermoplast. Compos. Mater. 2022, 35, 615–630. [Google Scholar] [CrossRef]
- Kanan, A.; Kaliske, M. Finite element modeling of electro-viscoelasticity in fiber reinforced electro-active polymers. Int. J. Numer. Methods Eng. 2021, 122, 2005–2037. [Google Scholar] [CrossRef]
- Mehnert, M.; Steinmann, P. On the influence of the compliant electrodes on the mechanical behavior of VHB 4905. Comput. Mater. Sci. 2019, 160, 287–294. [Google Scholar] [CrossRef]
- Munteanu, L.; Munteanu, A.; Sedlacik, M.; Kutalkova, E.; Kohl, M.; Kalendova, A. Zinc ferrite/polyaniline composite particles: Pigment applicable as electro-active paint. J. Ind. Eng. Chem. 2022, 115, 440–448. [Google Scholar] [CrossRef]
- Du, H.; Cao, J. Electroactive Polymer and Amplification Architectures for Actuators. Aerosp. Control 2005, 23, 92–96. [Google Scholar]
- Zhang, J.; Wang, H.; Li, X. Research on Flexible Dielectric EAP Swinging Actuator. Mach. Des. Manuf. 2012, 41, 75–77+80. [Google Scholar]
- Zhou, L.; Wang, H.; Wei, L.; Yang, W. Research on Linear and Bending Roll Dielectric Electroactive Polymer. In Machinery Design & Manufacture; China Aviation Industry Aviation Power Machinery Research Institute: Zhuzhou, China, 2014; pp. 115–118. [Google Scholar]
- Kornbluh, R.D.; Pelrine, R.; Pei, Q.; Oh, S.; Joseph, J. Ultrahigh strain response of field-actuated elastomeric polymers. In Proceedings of the Smart Structures and Materials 2000: Electroactive Polymer Actuators and Devices (Eapad), Newport Beach, CA, USA, 6–8 March 2000; SRI Int.: Menlo Park, CA, USA, 2000; Volume 3987, pp. 51–64. [Google Scholar]
- Zhang, R.; Kunz, A.; Lochmatter, P.; Kovacs, G. Dielectric elastomer spring roll actuators for a portable force feedback device. In Proceedings of the 2006 14th IEEE Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, Alexandria, VA, USA, 25–26 March 2006; pp. 347–353. [Google Scholar]
- Lochmatter, P.; Kovacs, G. Design and characterization of an actively deformable shell structure composed of interlinked active hinge segments driven by soft dielectric EAPs. Sens. Actuators A Phys. 2008, 141, 588–597. [Google Scholar] [CrossRef]
- Wang, Y. Design of Bionic Robot Fish with Dielectric Elastomer. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Jiang, Z.; Li, Y.; Wang, Q. Dynamic Compensation of Load-Dependent Creep in Dielectric Electro-Active Polymer Actuators. IEEE Sens. J. 2022, 22, 1948–1955. [Google Scholar] [CrossRef]
- Bishara, D.; Jabareen, M. A reduced mixed finite-element formulation for modeling the viscoelastic response of electro-active polymers at finite deformation. Math. Mech. Solids 2019, 24, 1578–1610. [Google Scholar] [CrossRef]
- Bishara, D.; Jabareen, M. A solid-shell formulation based on the assumed natural inhomogeneous strains for modeling the viscoelastic response of electro-active polymers. Comput. Mech. 2020, 66, 1–25. [Google Scholar] [CrossRef]
- Zhu, Y. Research on the Electromechanical Coupling Characteristics of Dielectric Electoactive Polymer (EAP) Transducer. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2012. [Google Scholar]
- Wang, Y.; Guo, J. Study on lateral characteristics of dielectric electroactive polymer cylindrical actuators. Metrol. Meas. Technol. 2022, 42, 43–49. [Google Scholar]
- Bar-Cohen, Y.; Anderson, A.I. Electroactive polymer (EAP) actuators—Background review. Mech. Soft Mater. 2019, 1, 5. [Google Scholar] [CrossRef]





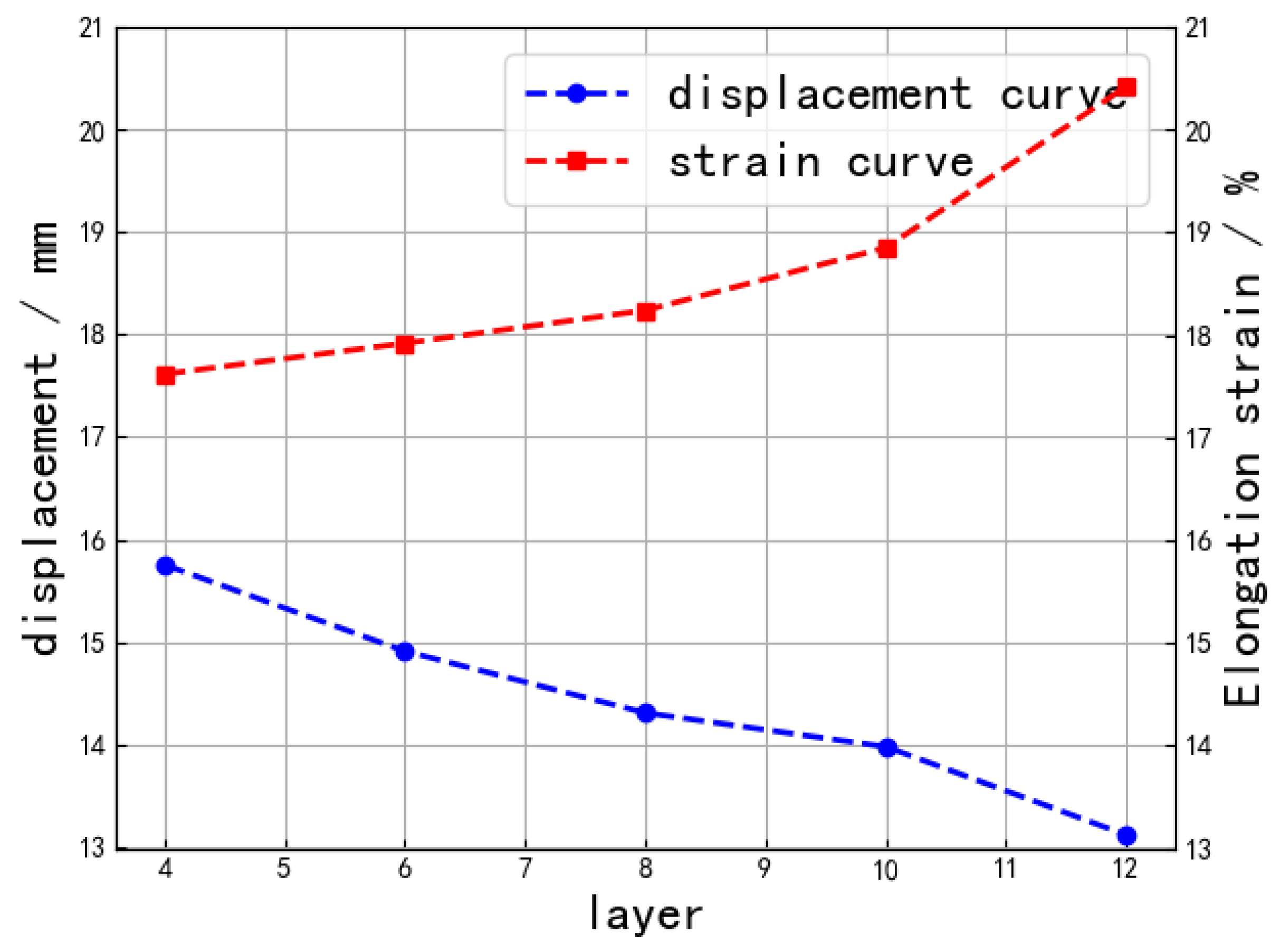
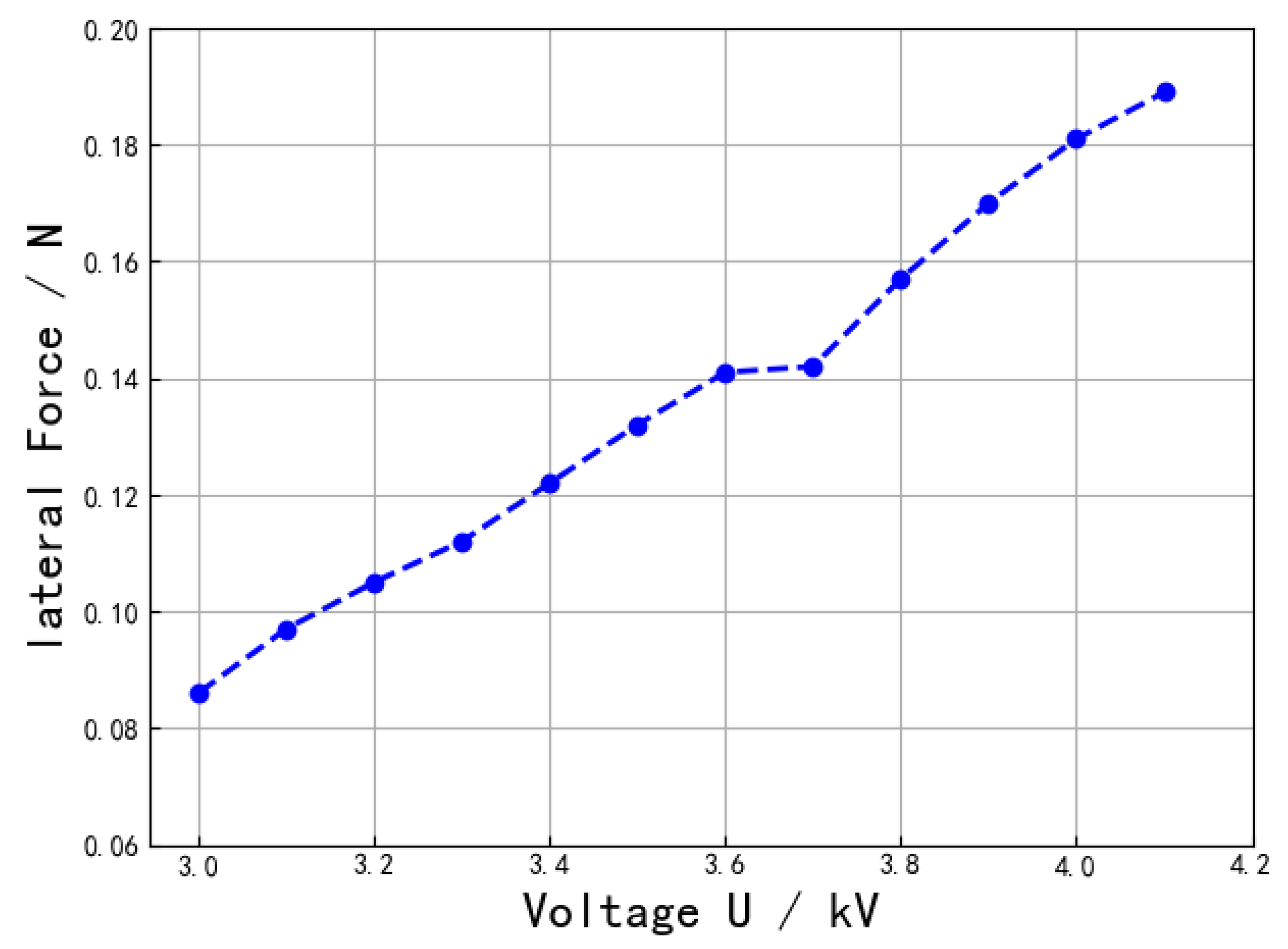
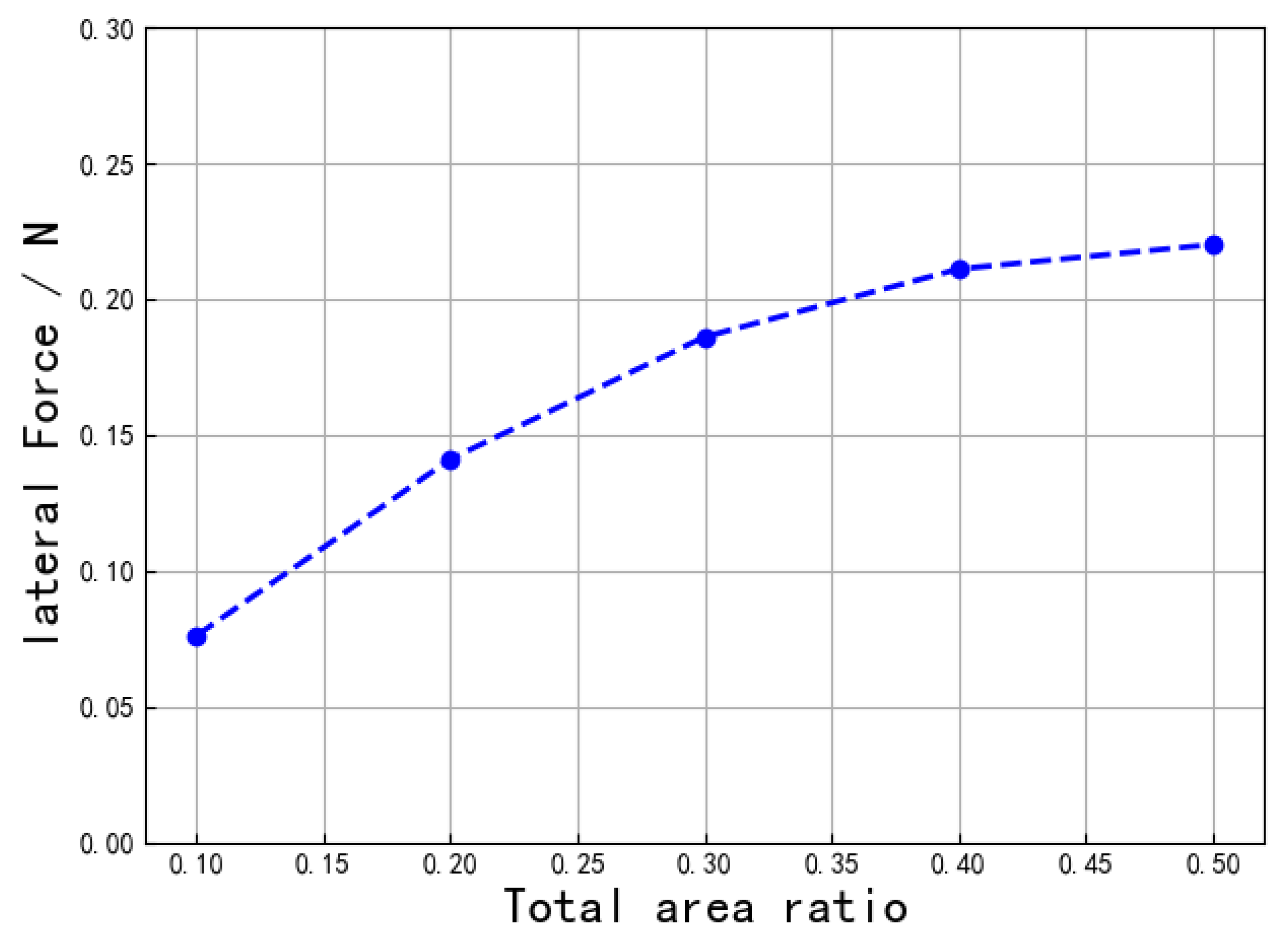
| Factors | Strain/% | Stress/MPa | Drive Voltage/kV | Density/(g/mL) | Fracture Toughness |
|---|---|---|---|---|---|
| EAP | >10 | 0.1~3 | 1~10 | 1~2.5 | Super elastic |
| Piezoelectric ceramics | 0.1~0.3 | 30~40 | 0.001~0.2 | 6~8 | Brittleness |
| Shape memory alloys | <8 | 700 | - | 5~6 | Flexibility |
| Drive Material | Typical Materials | Advantages | Disadvantages |
|---|---|---|---|
| Dielectric EPA materials (DE, etc.) | Silicone Rubber Acrylic | Medium stress (100 KPa–5 MPa), large strain (120–380%), high elastic energy density (10 kJ/m3–3.4 MJ/kg), high electromechanical coupling efficiency (max. 90%), medium-frequency bandwidth (10 Hz–1 kHz), low energy consumption, low current. | High electric field (150 MV/m), low modulus of elasticity (1 MPa). |
| Ionic EAP materials (IPMC, etc.) | Nzfion Flemion | Low voltage (<10 V), large displacement. | Low electromechanical coupling efficiency, requires encapsulation. |
| Parameters | Date | Unit |
|---|---|---|
| 0.026125 | MPa | |
| −0.001623 | MPa | |
| 0.000055 | MPa |
| Test Number | Voltage/kV | Elongation/mm |
|---|---|---|
| Test 1 | 2.5 | 6.8 |
| Test 2 | 3.0 | 9.9 |
| Test 3 | 3.5 | 12.2 |
| Test 4 | 4.0 | 14.0 |
| Test 5 | 4.5 | 18.8 |
| Test Number | Spring Parameters | Prestretch Rate | Number of Winding Turns N | Number of EAP Film Layers |
|---|---|---|---|---|
| Test 1 | mm; mm; mm; ; K = 0.0912 N/mm; material spring. | 325% × 325% | 3 | 6 |
| Test 2 | mm; mm; mm; ; K = 0.0912 N/mm; material spring. | 325% × 325% | 4 | 8 |
| Test 3 | mm; mm; mm; ; K = 0.1543 N/mm; material spring. | 375% × 375% | 3 | 6 |
| Test 4 | mm; mm; mm; ; K = 0.1543 N/mm; material spring. | 375% × 375% | 4 | 8 |
| Test Number | Voltage/kV | Release Stretch Rate |
|---|---|---|
| Test 1 | 2.5 | 0.081 |
| Test 2 | 3.0 | 0.115 |
| Test 3 | 3.5 | 0.141 |
| Test 4 | 4.0 | 0.160 |
| Test 5 | 4.5 | 0.209 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Niu, S.; Li, B.; Wang, P.; Qiao, Y. Design and Analysis of Mechanical Characteristics of EAP Flexible Drivers. Machines 2022, 10, 1241. https://doi.org/10.3390/machines10121241
Li B, Niu S, Li B, Wang P, Qiao Y. Design and Analysis of Mechanical Characteristics of EAP Flexible Drivers. Machines. 2022; 10(12):1241. https://doi.org/10.3390/machines10121241
Chicago/Turabian StyleLi, Bing, Shaohua Niu, Bingyang Li, Pengfei Wang, and Yuli Qiao. 2022. "Design and Analysis of Mechanical Characteristics of EAP Flexible Drivers" Machines 10, no. 12: 1241. https://doi.org/10.3390/machines10121241
APA StyleLi, B., Niu, S., Li, B., Wang, P., & Qiao, Y. (2022). Design and Analysis of Mechanical Characteristics of EAP Flexible Drivers. Machines, 10(12), 1241. https://doi.org/10.3390/machines10121241






