Combination of Thermal and Mechanical Strategies to Compensate for Distortion Effects during Profile Grinding
Abstract
1. Introduction
2. Theoretical Approach
2.1. Thermally Caused Distortions
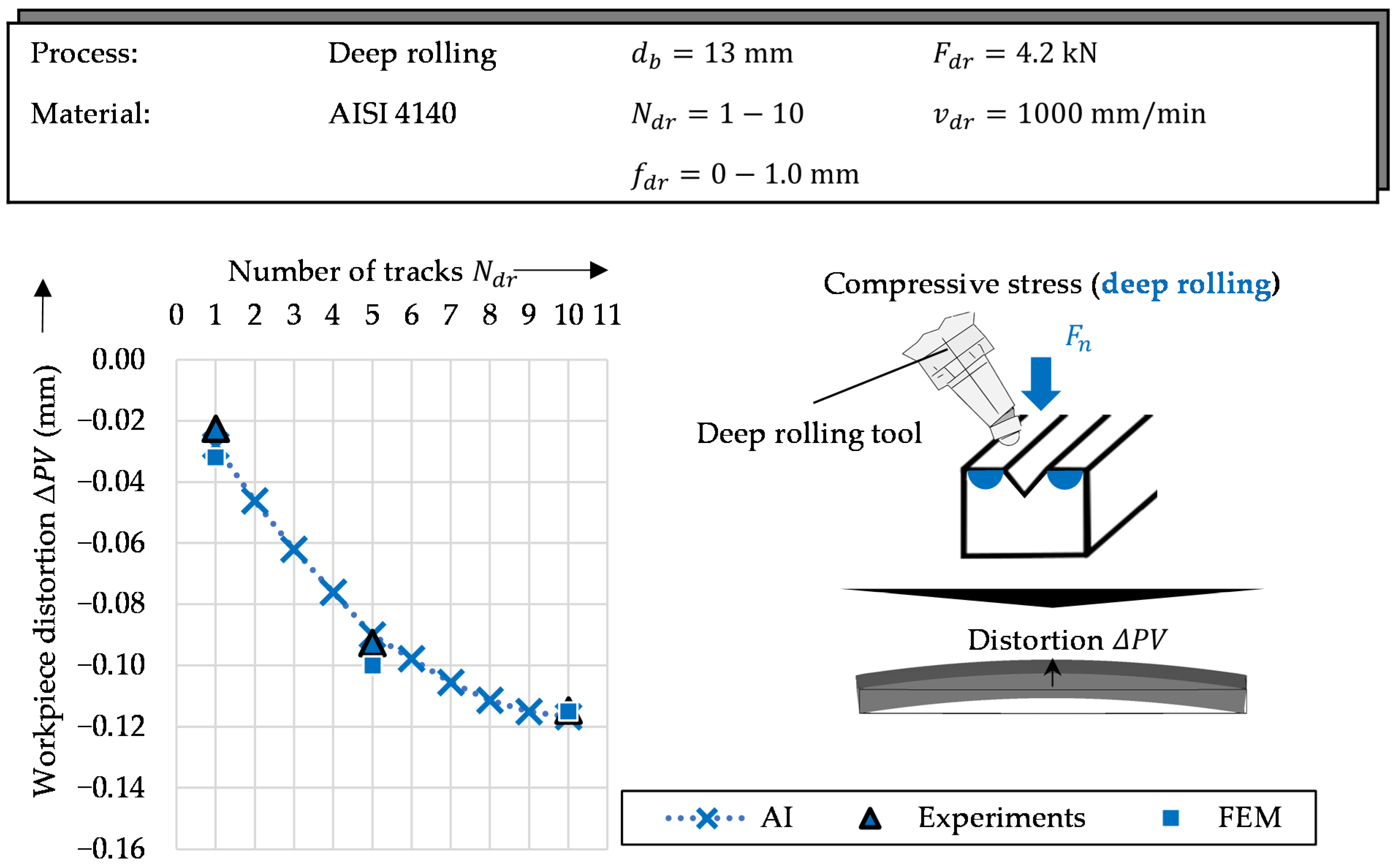
2.2. Deep Rolling
3. Materials and Methods
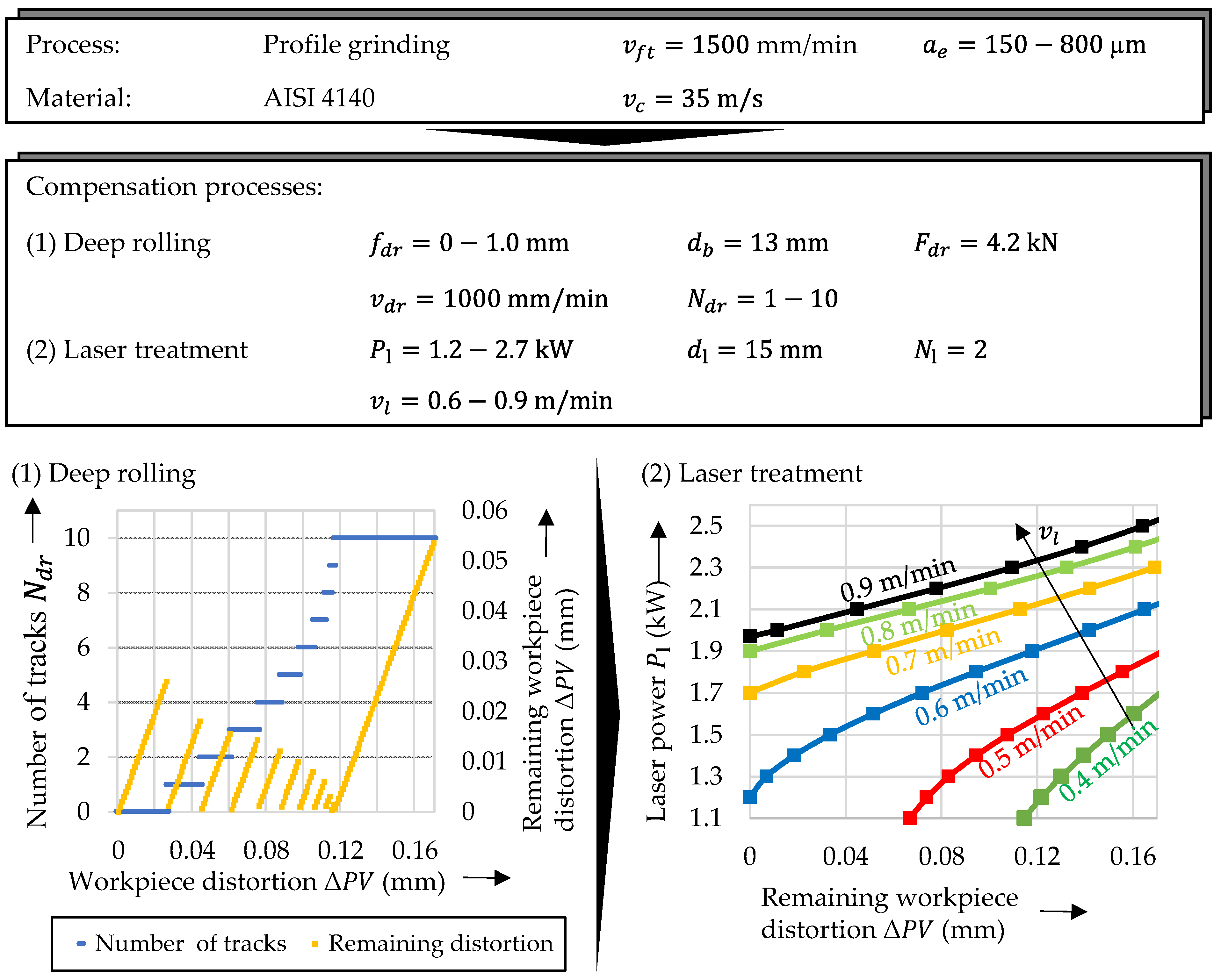
3.1. Workpiece
3.2. Experiments
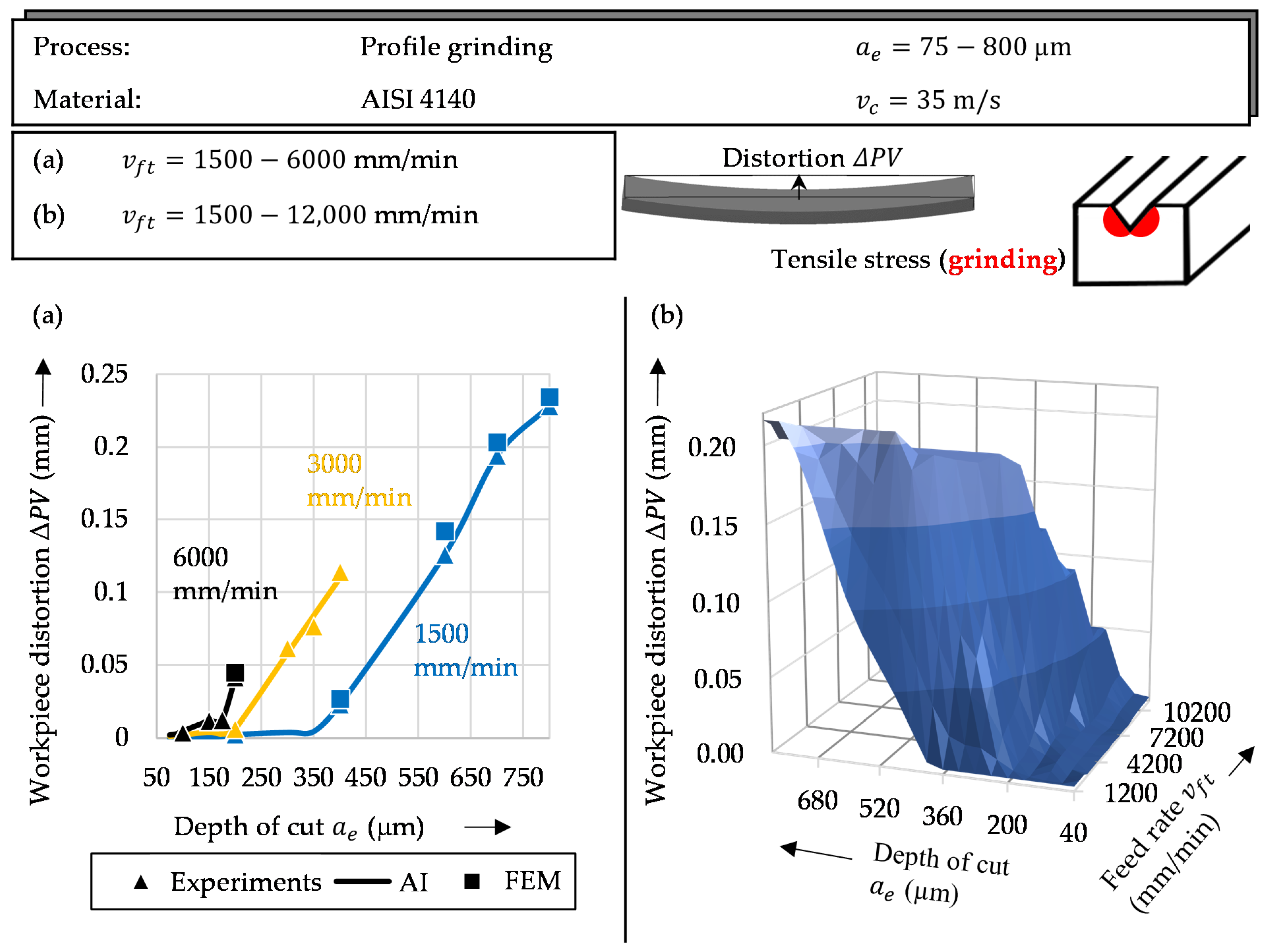
3.2.1. Grinding
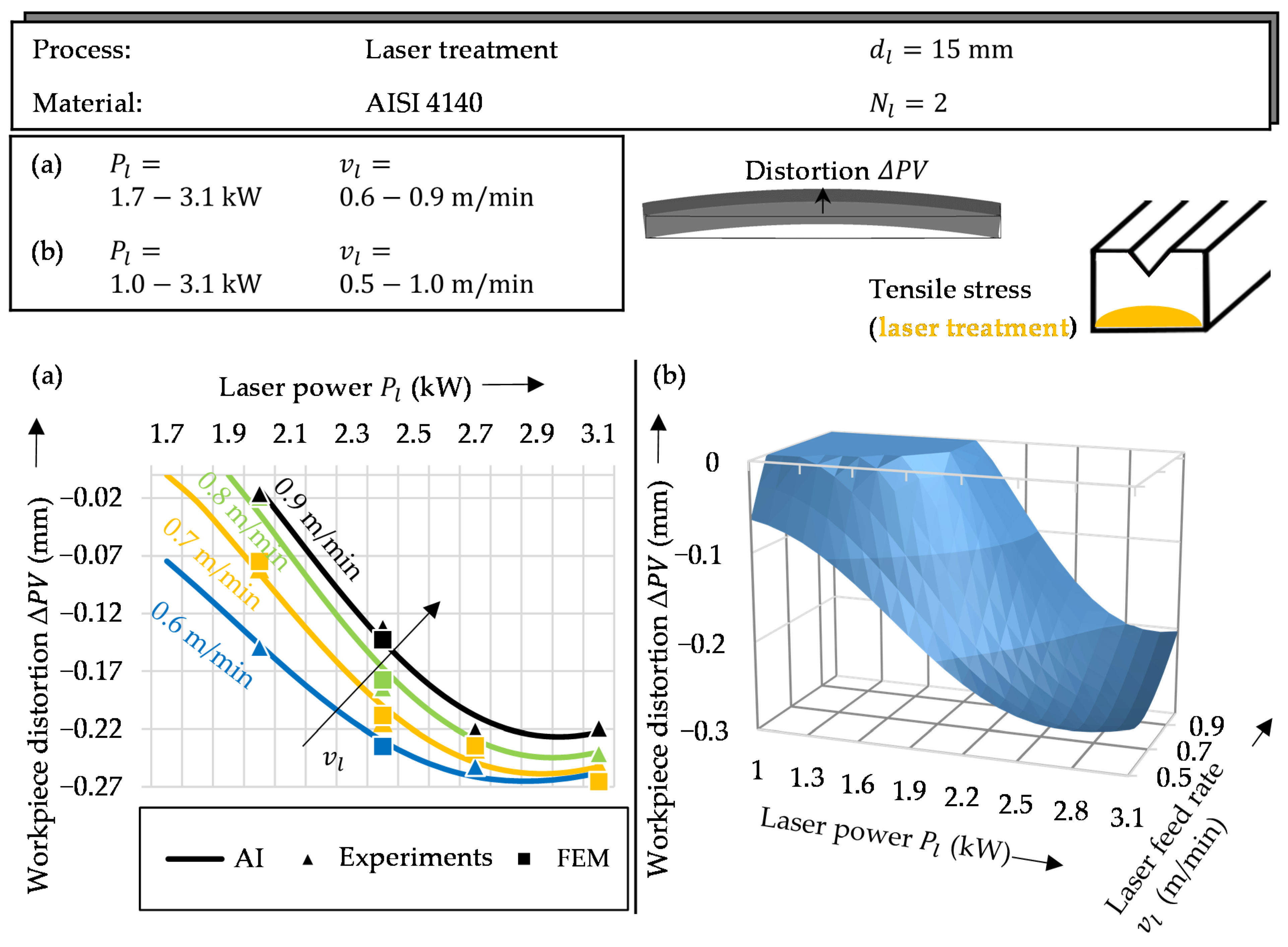
3.2.2. Laser Treatment
3.2.3. Deep Rolling
3.3. Methods
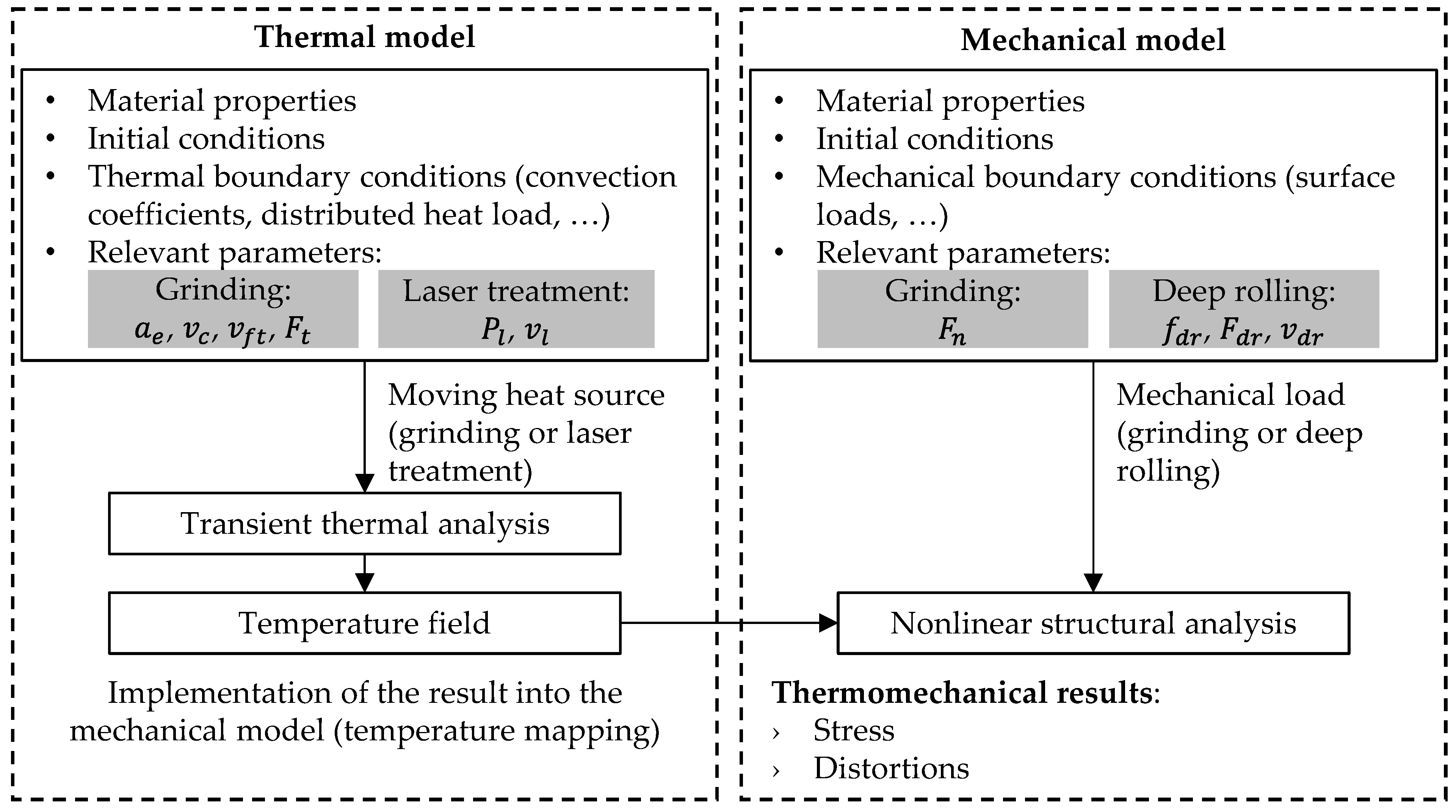
4. Model Development
4.1. Modelling Strategy
4.2. Material Properties
4.3. Thermal Model
4.3.1. Heat Generation
4.3.2. Thermal Diffusion
4.4. Mechanical Model
4.5. Mesh
5. Results and Discussion
5.1. Model Validation and Distortion Prediction
5.2. Prediction of Grinding and Compensation Distortion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Föckerer, T.; Zäh, M.F.; Huntemann, J.-W.; Heinzel, C.; Brinksmeier, E. Simulation of part distortions resulting from heat input during grind-hardening. In Proceedings of the NAFEMS World Congress 2009, Crete, Greece, 16–19 June 2009. [Google Scholar]
- Heinzel, C.; Bleil, N. The use of the size effect in grinding for work-hardening. CIRP Ann. 2007, 56, 327–330. [Google Scholar] [CrossRef]
- Schieber, C.; Hettig, M.; Müller, V.; Zaeh, M.F.; Heinzel, C. Modeling of laser processing as a distortion compensation strategy for profile grinding. Prod. Eng. 2022, 56, 327–330. [Google Scholar] [CrossRef]
- Perenda, J.; Trajkovski, J.; Žerovnik, A.; Prebil, I. Residual stresses after deep rolling of a torsion bar made from high strength steel. J. Mater. Process. Technol. 2015, 218, 89–98. [Google Scholar] [CrossRef]
- Schieber, C.; Hettig, M.; Zaeh, M.F.; Heinzel, C. 3D modeling and simulation of thermal effects during profile grinding. Prod. Eng. 2020, 14, 655–665. [Google Scholar] [CrossRef]
- Jermolajev, S.; Epp, J.; Heinzel, C.; Brinksmeier, E. Material modifications caused by thermal and mechanical load during grinding. Procedia CIRP 2016, 45, 43–46. [Google Scholar] [CrossRef]
- Schieber, C.; Hettig, M.; Zaeh, M.F.; Heinzel, C. Evaluation of approaches to compensate the thermo-mechanical distortion effects during profile grinding. Procedia CIRP 2021, 102, 331–336. [Google Scholar] [CrossRef]
- Guan, Q.; Brown, K.W.; Guo, D.; Cao, J.; Li, C.; Shao, Y.; Liu, J. Method and Apparatus for Low Stress No-Distortion welding of thin-walled structural elements. CN Patent 1987100959, 28 February 1987. [Google Scholar]
- Pilipenko, A. Computer Simulation of Residual Stress and Distortion of thick Plates in Multi-Electrode Submerged Arc Welding. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2001. [Google Scholar]
- Schenk, T. Modelling of Welding Distortion: The Influence of Clamping and Sequencing: Dissertation; Technische Universiteit Delft: Delft, The Netherlands, 2011. [Google Scholar]
- Michaleris, P.; Dantzig, J.; Tortelli, D. Minimization of Welding Residual Stress and Distortion in Large Structures. Weld. J. 1999, 78, 361–366. [Google Scholar]
- Colegrove, P.A.; Coules, H.E.; Fairman, J.; Martina, F.; Kashoob, T.; Mamash, H.; Cozzolino, L.D. Microstructure and residual stress improvement in wire and arc additively manufactured parts through high-pressure rolling. J. Mater. Process. Technol. 2013, 213, 1782–1791. [Google Scholar] [CrossRef]
- Martina, F.; Roy, M.J.; Szost, B.A.; Terzi, S.; Colegrove, P.A.; Williams, S.W.; Withers, P.J.; Meyer, J.; Hofmann, M. Residual stress of as-deposited and rolled wire+arc additive manufacturing Ti–6Al–4V components. Mater. Sci. Technol. 2016, 32, 1439–1448. [Google Scholar] [CrossRef]
- Cordiano, H.V. Effect of Residual Stresses on the Low Cycle Fatigue Life of Large Scale Weldments in High Strength Steel. J. Eng. Ind. 1970, 92, 86–92. [Google Scholar] [CrossRef]
- Webster, G.A.; Ezeilo, A.N. Residual stress distributions and their influence on fatigue lifetimes. Int. J. Fatigue 2001, 23, 375–383. [Google Scholar] [CrossRef]
- Dong, P.; Brust, F.W. Welding Residual Stresses and Effects on Fracture in Pressure Vessel and Piping Components: A Millennium Review and Beyond. J. Press. Vessel. Technol. 2000, 122, 329–338. [Google Scholar] [CrossRef]
- Dong, P. Residual stresses and distortions in welded structures: A perspective for engineering applications. Sci. Technol. Weld. Join. 2005, 10, 389–398. [Google Scholar] [CrossRef]
- Xiong, J.; Lei, Y.; Li, R. Finite element analysis and experimental validation of thermal behavior for thin-walled parts in GMAW-based additive manufacturing with various substrate preheating temperatures. Appl. Therm. Eng. 2017, 126, 43–52. [Google Scholar] [CrossRef]
- Graf, M.; Hälsig, A.; Höfer, K.; Awiszus, B.; Mayr, P. Thermo-Mechanical Modelling of Wire-Arc Additive Manufacturing (WAAM) of Semi-Finished Products. Metals 2018, 8, 1009. [Google Scholar] [CrossRef]
- Montevecchi, F.; Venturini, G.; Grossi, N.; Scippa, A.; Campatelli, G. Finite Element mesh coarsening for effective distortion prediction in Wire Arc Additive Manufacturing. Addit. Manuf. 2017, 18, 145–155. [Google Scholar] [CrossRef]
- Ding, J.; Colegrove, P.; Mehnen, J.; Ganguly, S.; Sequeira Almeida, P.M.; Wang, F.; Williams, S. Thermo-mechanical analysis of Wire and Arc Additive Layer Manufacturing process on large multi-layer parts. Comput. Mater. Sci. 2011, 50, 3315–3322. [Google Scholar] [CrossRef]
- Camilleri, D.; Comlekci, T.; Gray, T.G.F. Computational prediction of out-of-plane welding distortion and experimental investigation. J. Strain Anal. Eng. Des. 2005, 40, 161–176. [Google Scholar] [CrossRef]
- Zhang, L.; Michaleris, P. Investigation of Lagrangian and Eulerian finite element methods for modeling the laser forming process. Finite Elem. Anal. Des. 2004, 40, 383–405. [Google Scholar] [CrossRef]
- Michaleris, P.; Zhang, L.; Bhide, S.R.; Marugabandhu, P. Evaluation of 2D, 3D and applied plastic strain methods for predicting buckling welding distortion and residual stress. Sci. Technol. Weld. Join. 2006, 11, 707–716. [Google Scholar] [CrossRef]
- Liu, W.; Tian, X.; Zhang, X. Preventing Hot Cracking by Synchronous Rolling during Welding. Weld. Res. Suppl. 1996, 75, 297–304. [Google Scholar]
- Yang, Y.P.; Dong, P.; Tian, X.; Zhang, Z. Prevention of Hot Cracking of High Strength Aluminum Alloy by Mechanical Rolling. In Proceedings of the 5th International Conference on Trends in Welding Research, Pine Mountain, Georgia, 1–5 June 1998. [Google Scholar]
- Wen, S.W.; Williams, S.W.; Morgan, S.A.; Wescott, A.; Poad, M. Rolling of Friction Stir Welds for Residual Stress and Distortion Control. Sci. Technol. Weld. Join. 2010, 15, 440–447. [Google Scholar] [CrossRef]
- Klocke, F.; Bäcker, V.; Wegner, H.; Zimmermann, M. Finite Element Analysis of the Roller Burnishing Process for Fatigue Resistance Increase of Engine Components. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 2–11. [Google Scholar] [CrossRef]
- Hettig, M.A.; Meyer, D. Sequential multistage deep rolling under varied contact conditions. Procedia CIRP 2020, 87, 291–296. [Google Scholar] [CrossRef]
- Gornyakov, V.; Sun, Y.; Ding, J.; Williams, S. Computationally Efficient Models of High Pressure Rolling for Wire Arc Additively Manufactured Components. Appl. Sci. 2021, 11, 402. [Google Scholar] [CrossRef]
- Gornyakov, V.; Sun, Y.; Ding, J.; Williams, S. Efficient determination and evaluation of steady-state thermal–mechanical variables generated by wire arc additive manufacturing and high pressure rolling. Model. Simul. Mater. Sci. Eng. 2022, 30, 14001. [Google Scholar] [CrossRef]
- Schieber, C.; Hettig, M.; Zaeh, M.F.; Heinzel, C. Modeling of Deep Rolling as a Distortion Compensation Strategy during Profile Grinding. KEM 2022, 926, 897–905. [Google Scholar] [CrossRef]
- Jiang, F.; Wang, H.; Wang, Y.; Xiang, J. Simulation of Flow and Heat Transfer of Mist/Air Impinging Jet on Grinding Work-Piece. JAFM 2016, 9, 1339–1348. [Google Scholar] [CrossRef]
- Hadad, M.; Sadeghi, B. Thermal analysis of minimum quantity lubrication-MQL grinding process. Int. J. Mach. Tools Manuf. 2012, 63, 1–15. [Google Scholar] [CrossRef]
- Spinu, S.; Frunza, G.; Diaconescu, E. Numerical Simulation of Elastic-Plastic Non-Conforming Contact. In Numerical Simulations-Applications, Examples and Theory; Angermann, L., Ed.; InTech: London, UK, 2011; ISBN 978-953-307-440-5. [Google Scholar]



| C | Cr | Mn | P | S | Si | Mo | Ni | Al | Cu | Sn | Ti | V | Nb | Fe | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AISI 4140 | 0.40 | 1.03 | 0.82 | 0.01 | 0.02 | 0.24 | 0.18 | 0.13 | 0.01 | 0.18 | 0.01 | 0.01 | <0.01 | <0.01 | balanced |
| Parameters | Symbols | Values |
|---|---|---|
| Cutting speed | 35 m/s | |
| Feed rate | 1500–12,000 mm/min | |
| Depth of cut | 75–800 μm | |
| Lubricant flow rate | 50 L/min |
| Parameters | Symbols | Values |
|---|---|---|
| Laser source diameter | dl | 15 mm |
| Laser powers | Pl | 1.7–3.1 kW |
| Number of total passes | Nl | 2 |
| Laser feed rates | vl | 0.5–1.0 m/min |
| Parameters | Symbols | Values |
|---|---|---|
| Tool diameter | db | 13 mm |
| Deep rolling force | Fdr | 4.2 kN |
| Number of total tracks | Ndr | 1–50 |
| Deep rolling velocity | vdr | 1 m/min |
| Lateral feed | fdr | 0–1 mm |
| Lubricant | – | 5% emulsion |
| Properties | Symbols | Values |
|---|---|---|
| Elastic modulus | 210 GPa | |
| Poisson’s ratio | 0.3 | |
| Density | 7830 kg/m³ | |
| Expansion coefficient | ||
| Specific heat capacity | 450 W/(kgK) | |
| Thermal conductivity | 43 W/(mK) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schieber, C.; Hettig, M.; Zaeh, M.F.; Heinzel, C. Combination of Thermal and Mechanical Strategies to Compensate for Distortion Effects during Profile Grinding. Machines 2022, 10, 1240. https://doi.org/10.3390/machines10121240
Schieber C, Hettig M, Zaeh MF, Heinzel C. Combination of Thermal and Mechanical Strategies to Compensate for Distortion Effects during Profile Grinding. Machines. 2022; 10(12):1240. https://doi.org/10.3390/machines10121240
Chicago/Turabian StyleSchieber, Christian, Matthias Hettig, Michael Friedrich Zaeh, and Carsten Heinzel. 2022. "Combination of Thermal and Mechanical Strategies to Compensate for Distortion Effects during Profile Grinding" Machines 10, no. 12: 1240. https://doi.org/10.3390/machines10121240
APA StyleSchieber, C., Hettig, M., Zaeh, M. F., & Heinzel, C. (2022). Combination of Thermal and Mechanical Strategies to Compensate for Distortion Effects during Profile Grinding. Machines, 10(12), 1240. https://doi.org/10.3390/machines10121240







