Experimental and Numerical Study of Collision Attitude Auxiliary Protection Strategy for Subway Vehicles
Abstract
1. Introduction
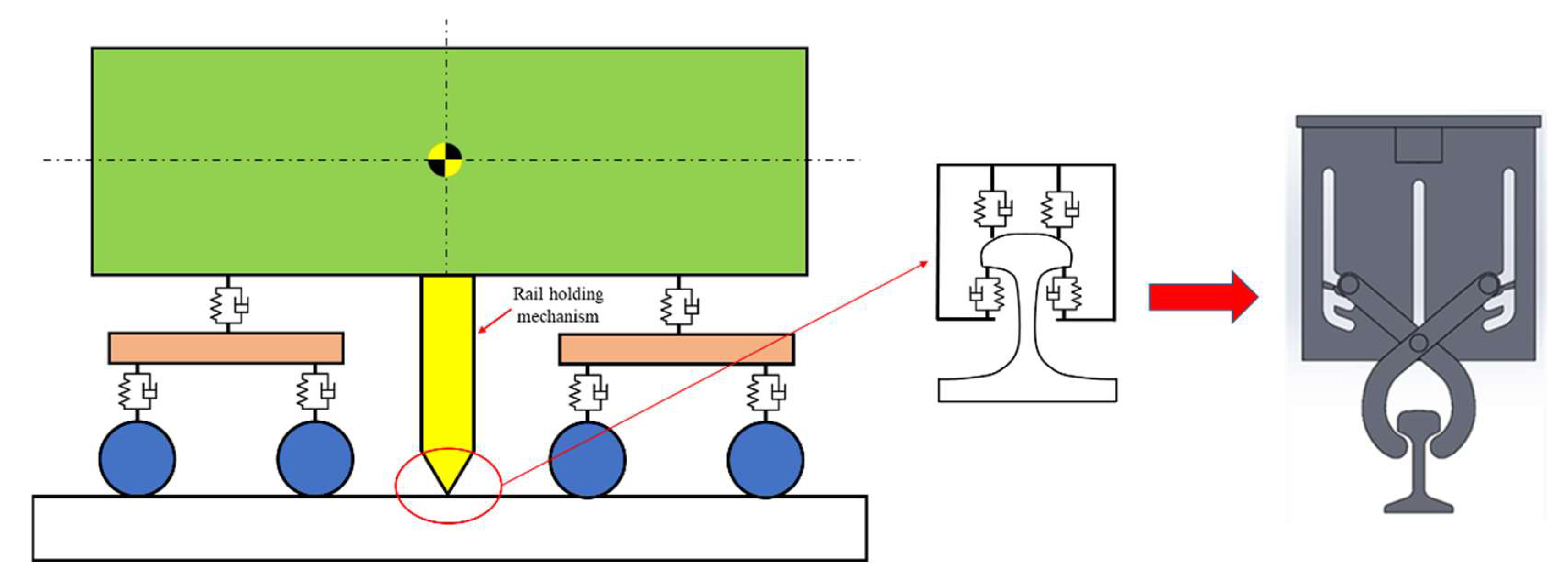
2. Rail Holding Mechanism
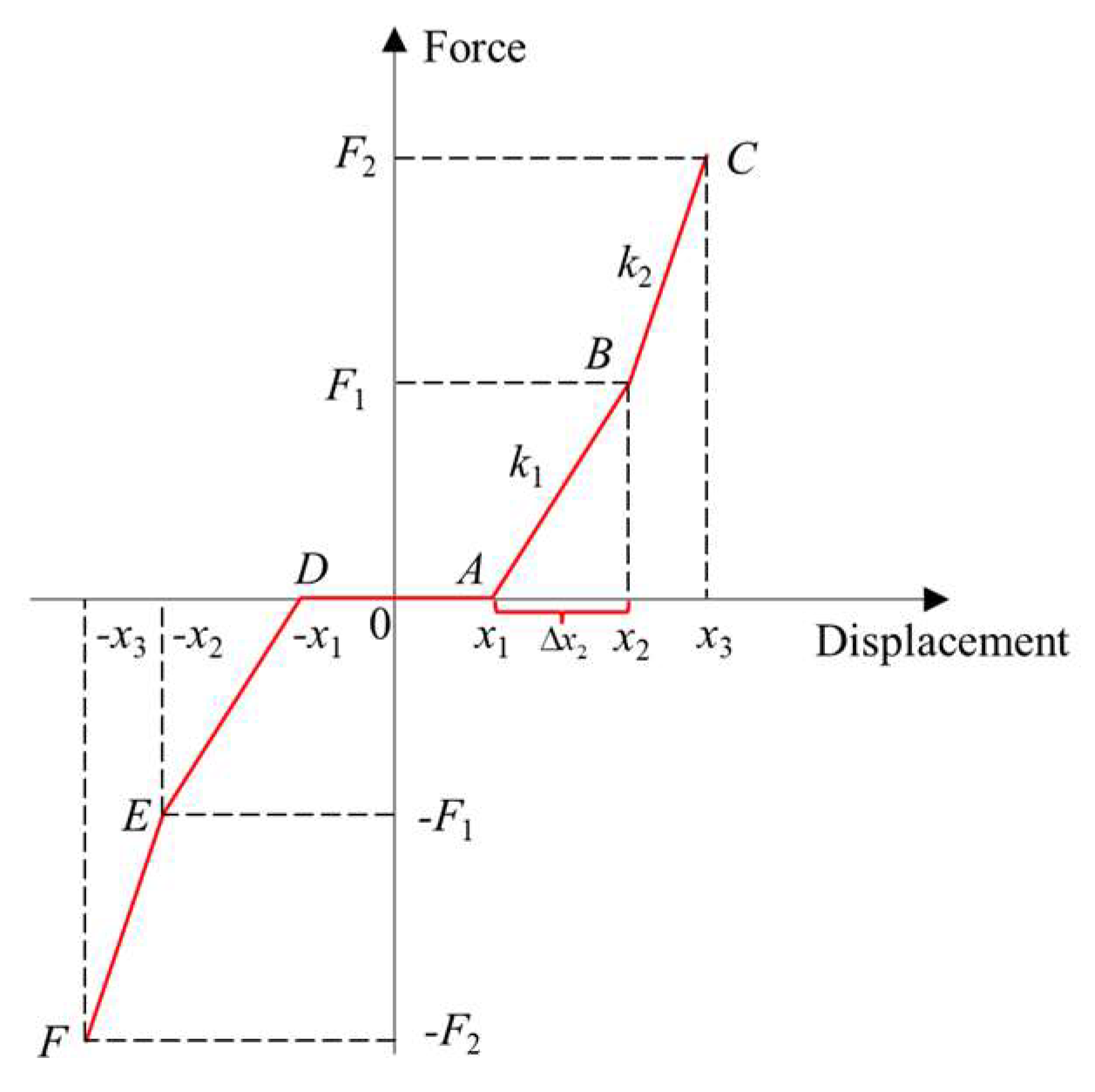
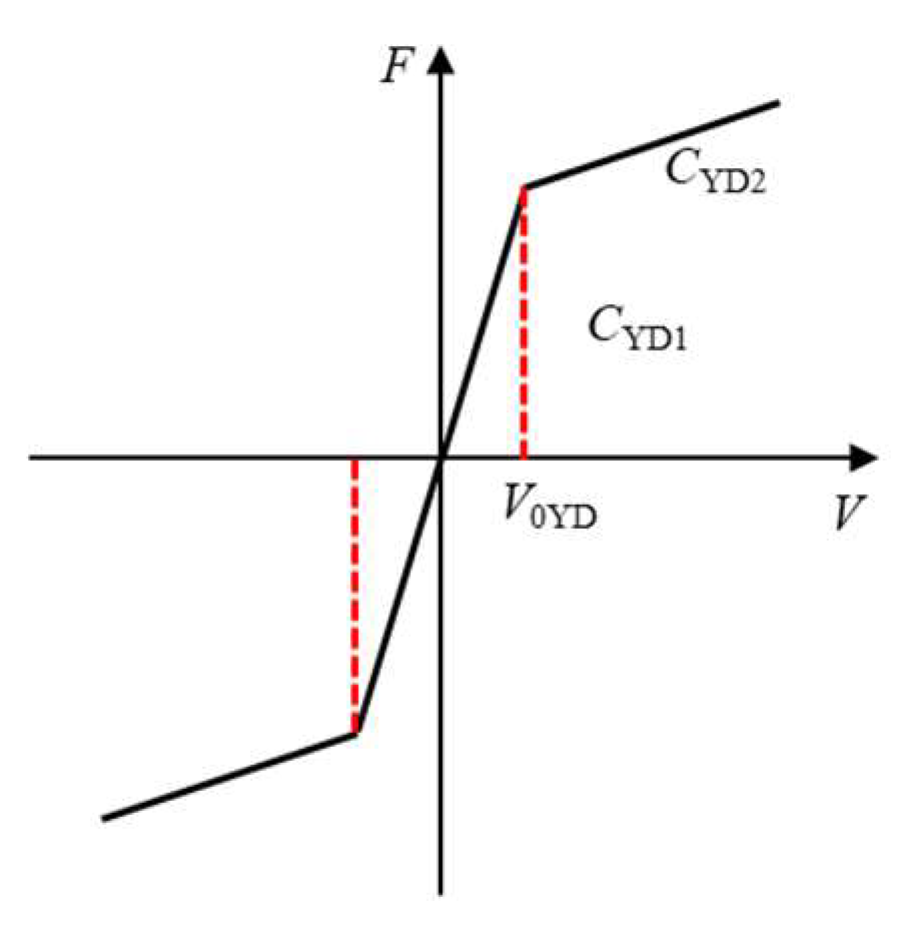
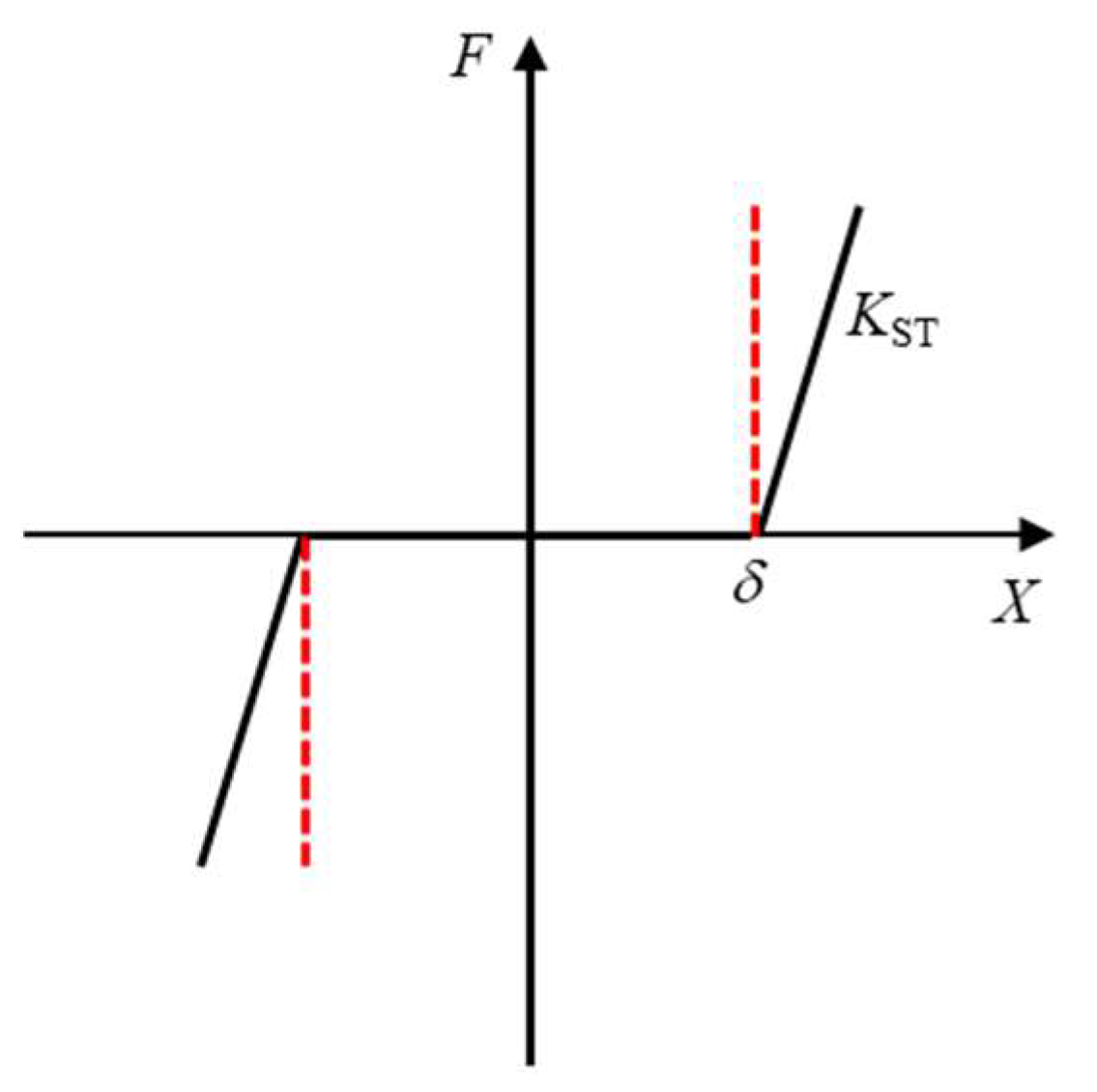
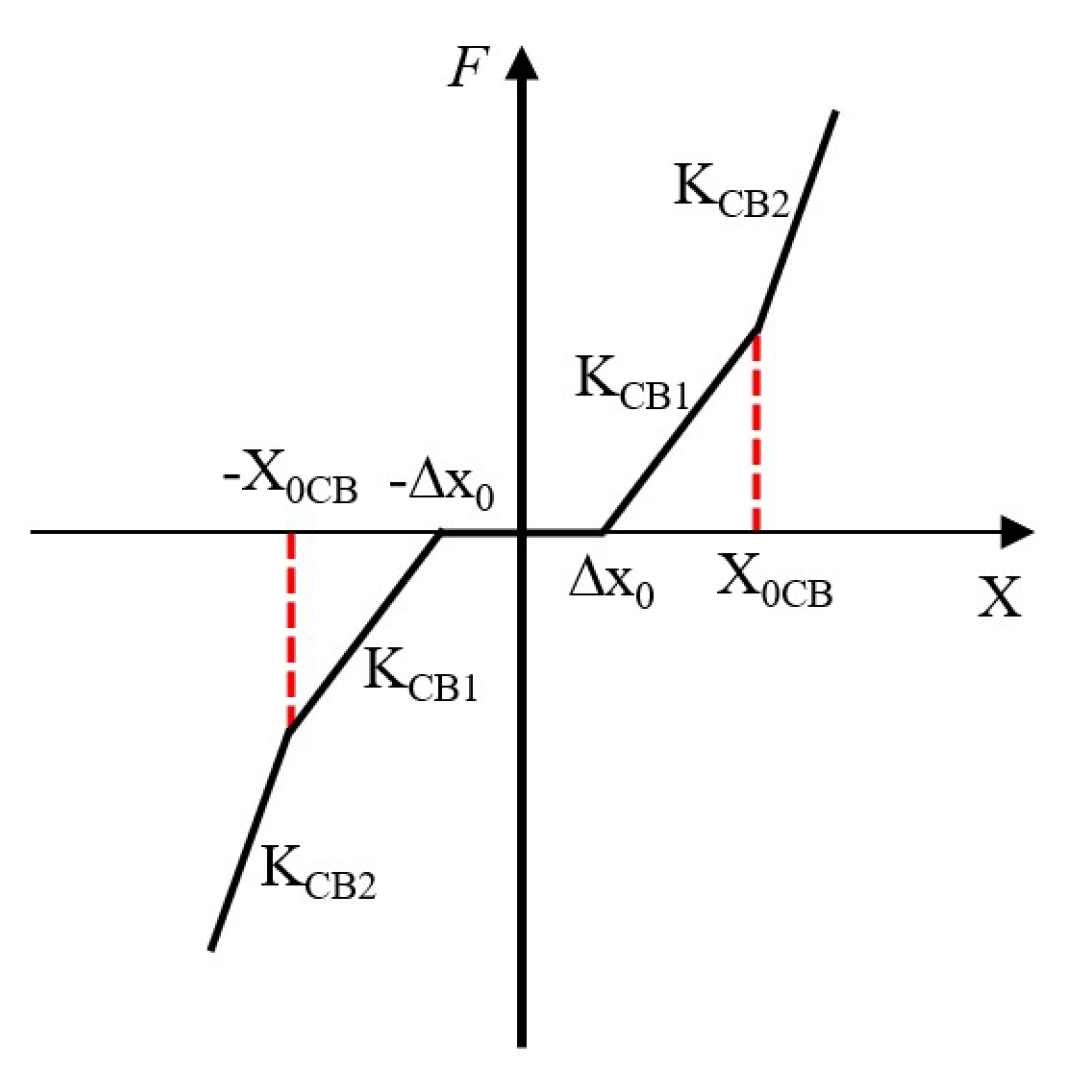
2.1. Equivalent Mechanical Characteristic Curve of a Rail Holding Mechanism
2.2. Vertical Evaluation Index
3. Dynamic Simulation and Experiment Result
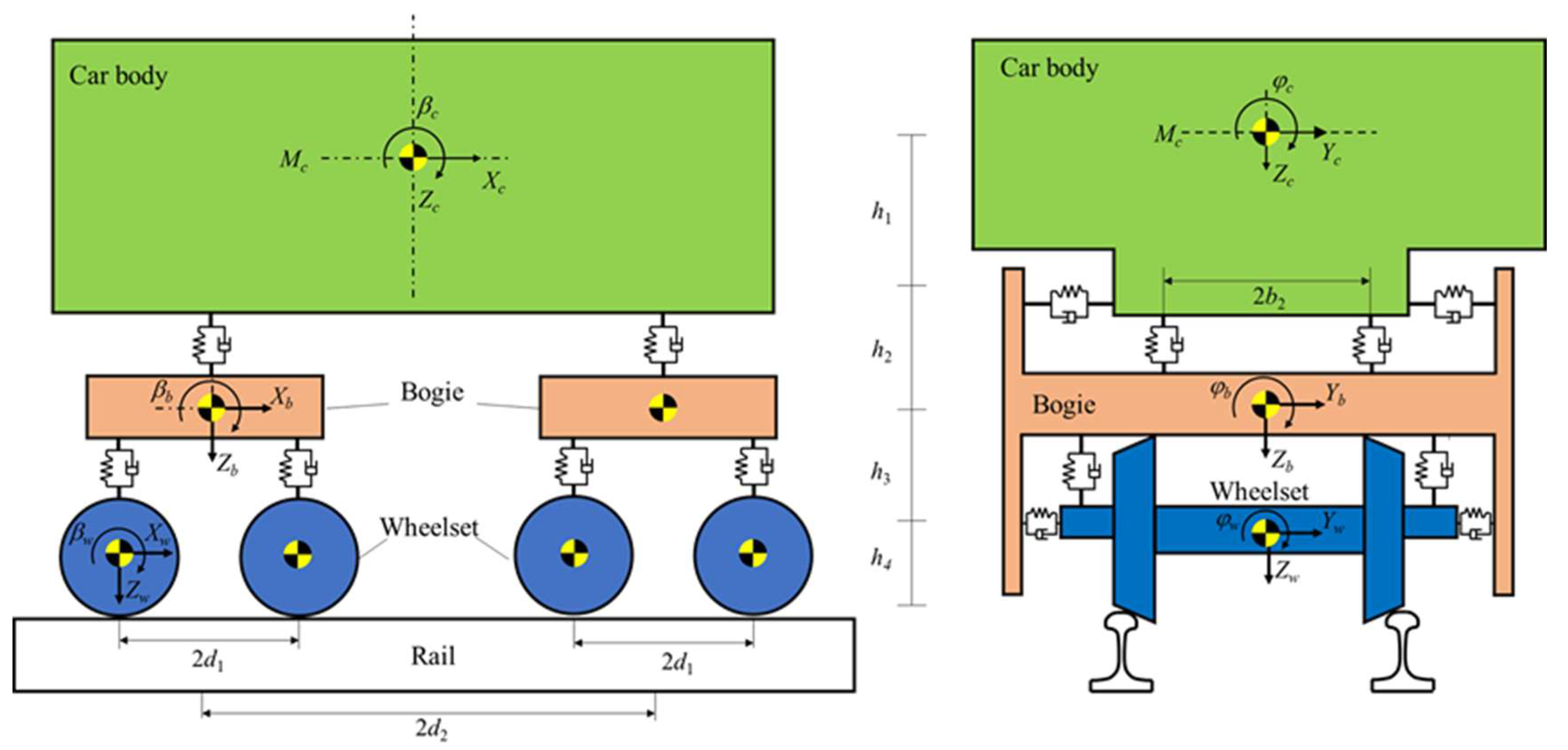
3.1. Equations of Motion of Subway Vehicles
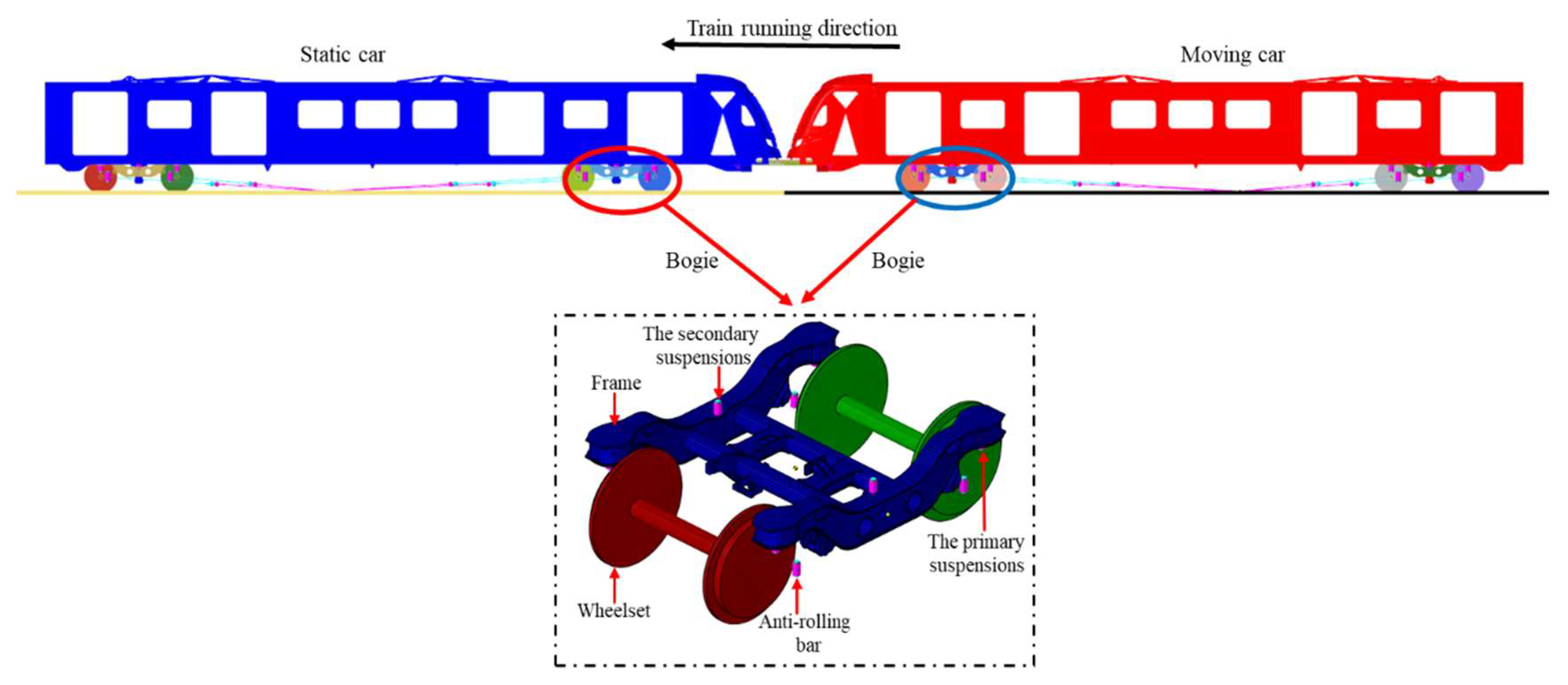
3.2. Dynamic Model of Subway Vehicles
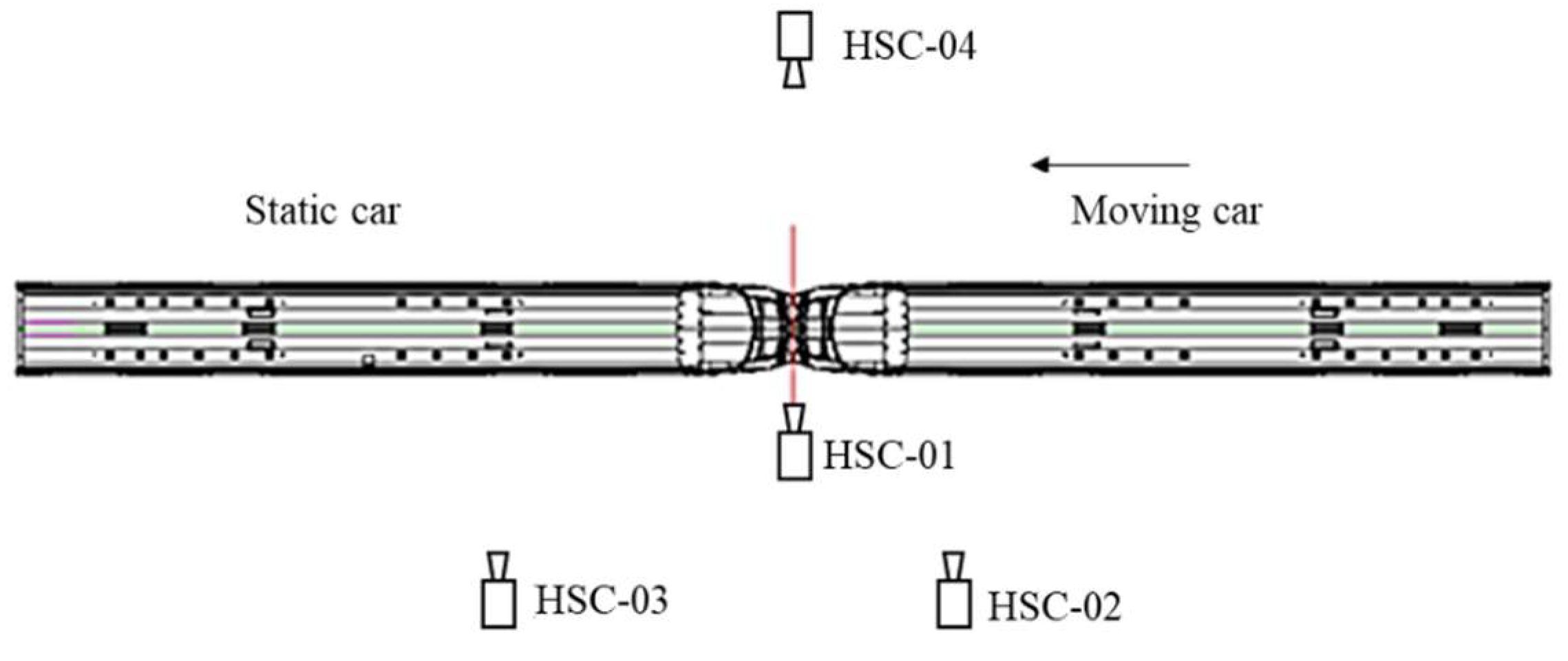
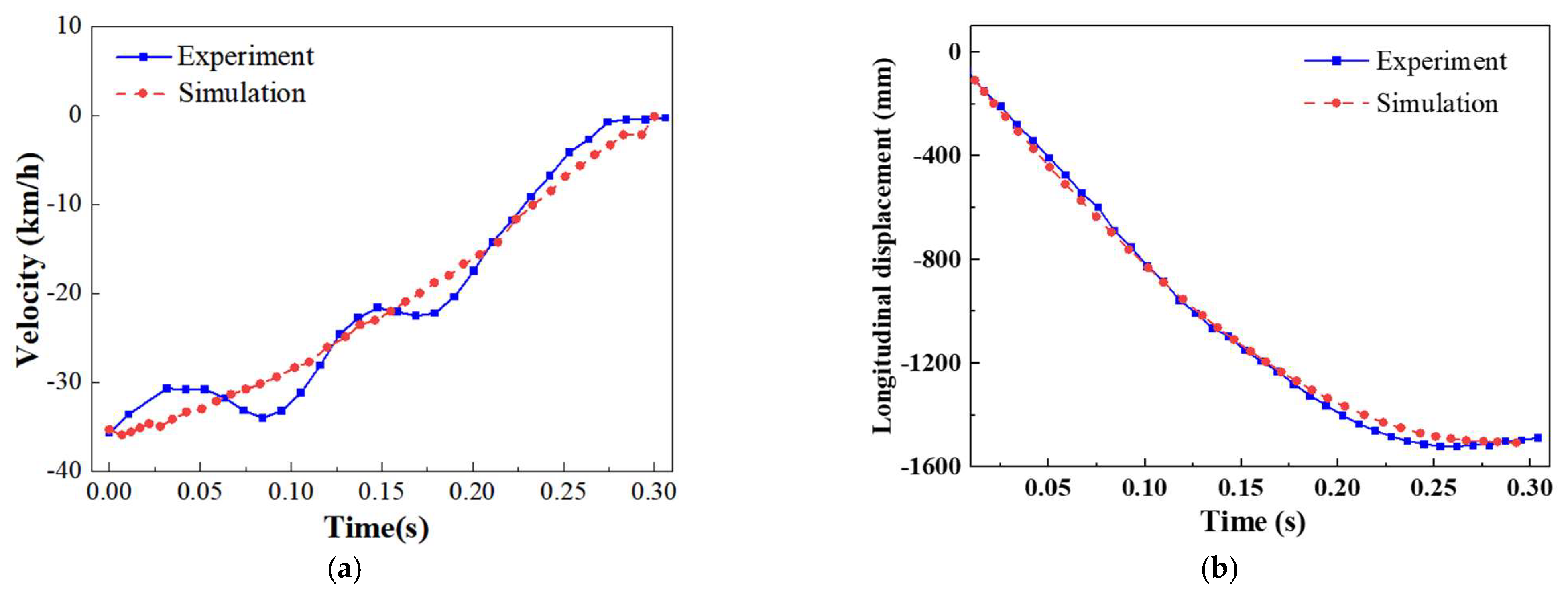
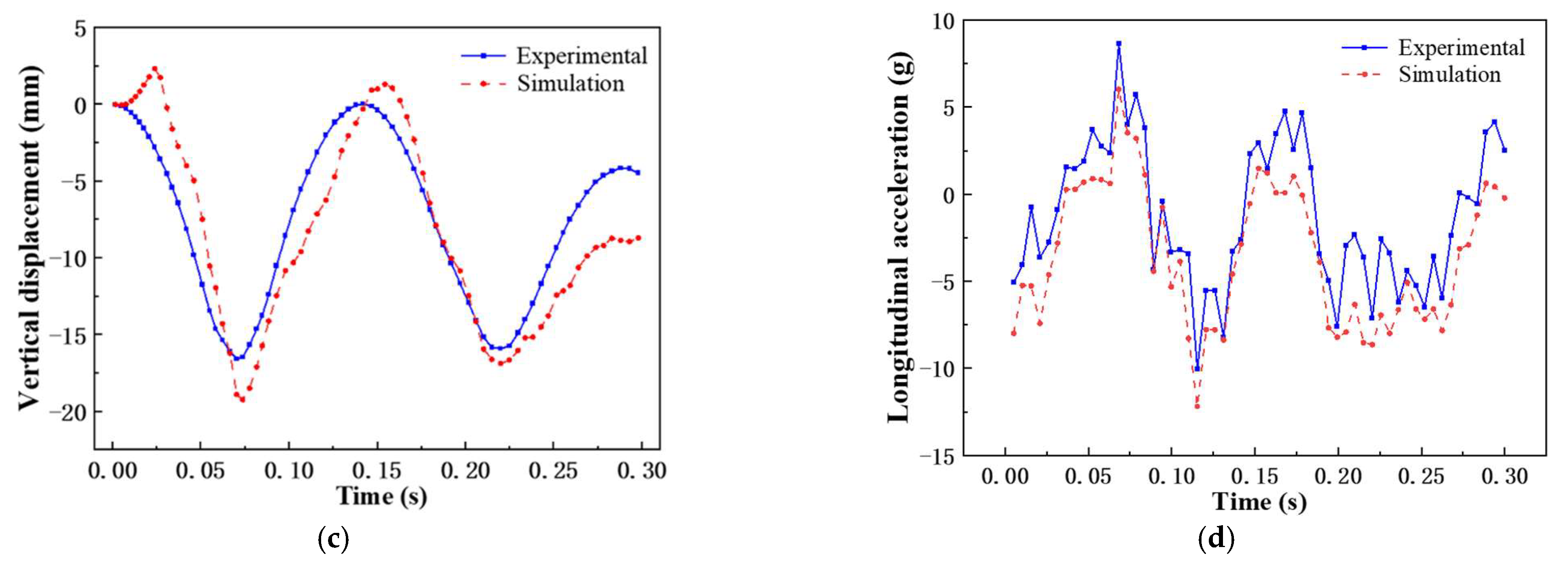
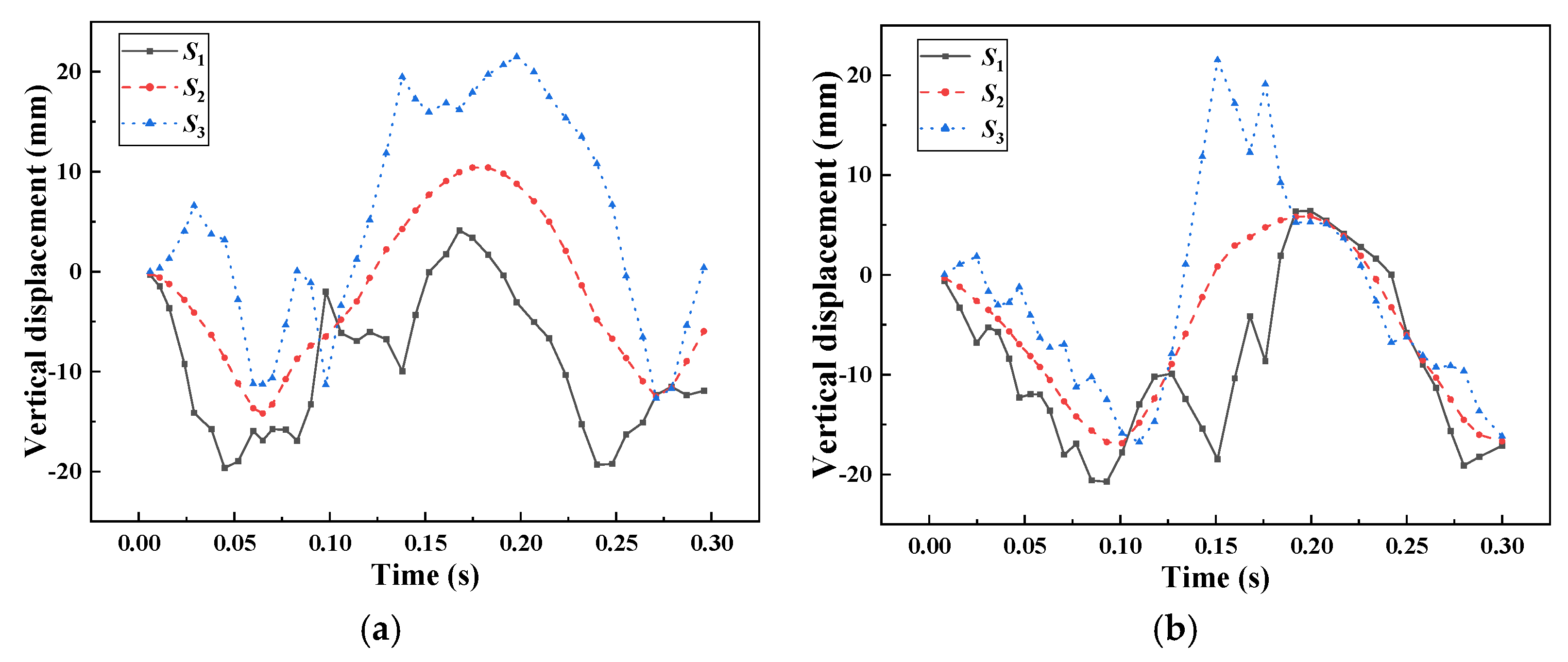
3.3. Crashing Test and Validation
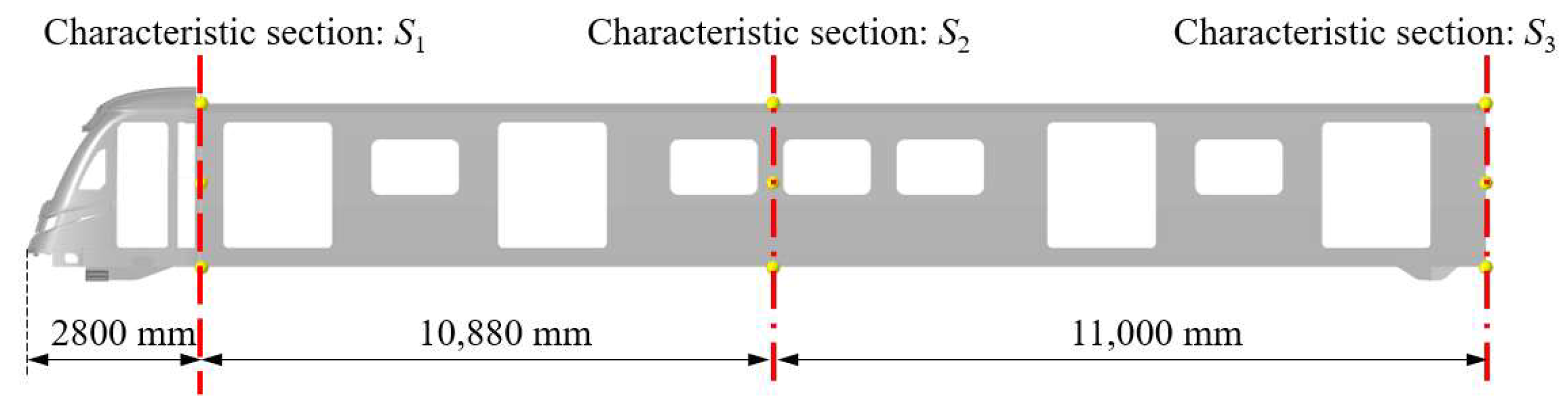
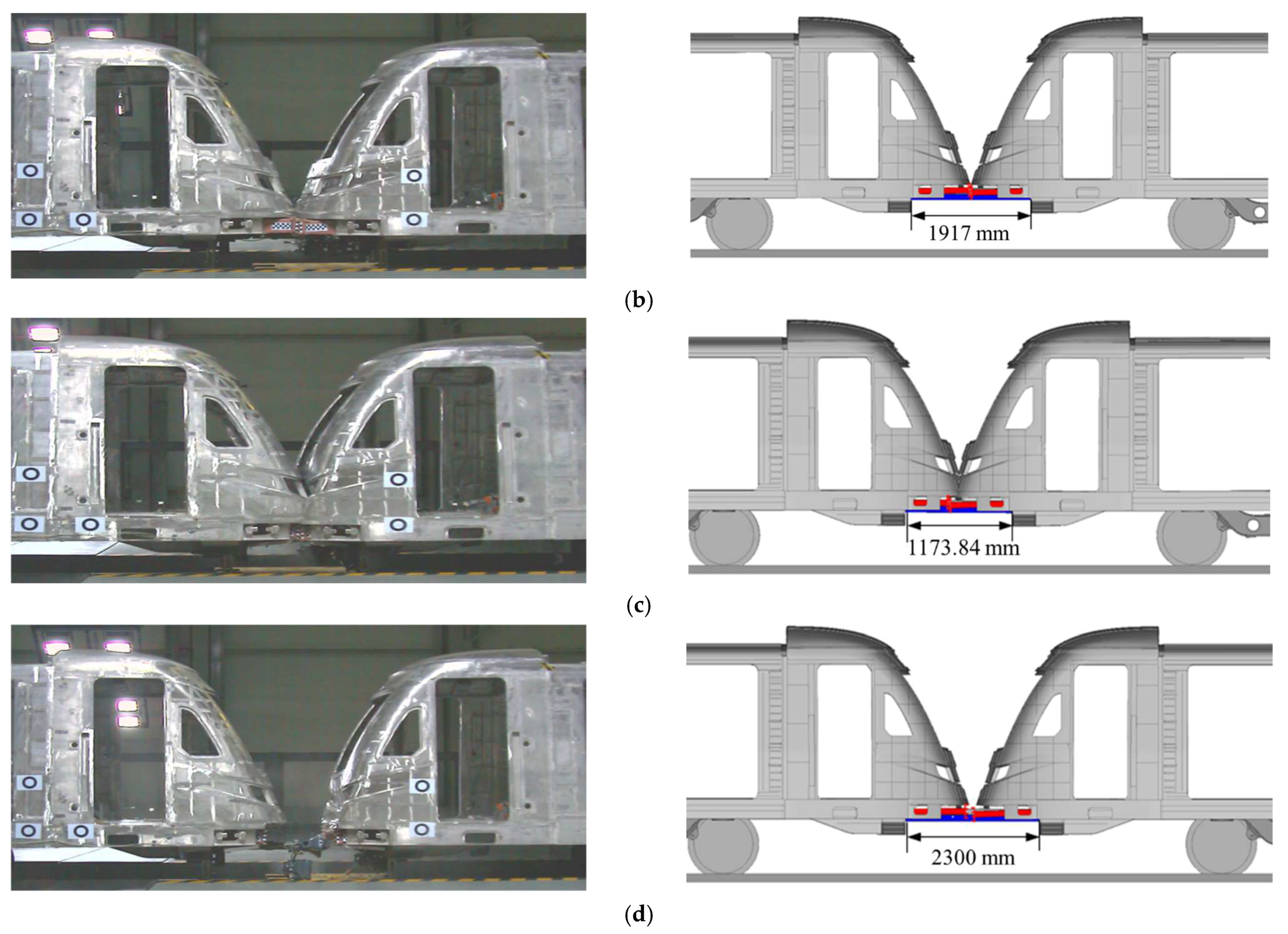
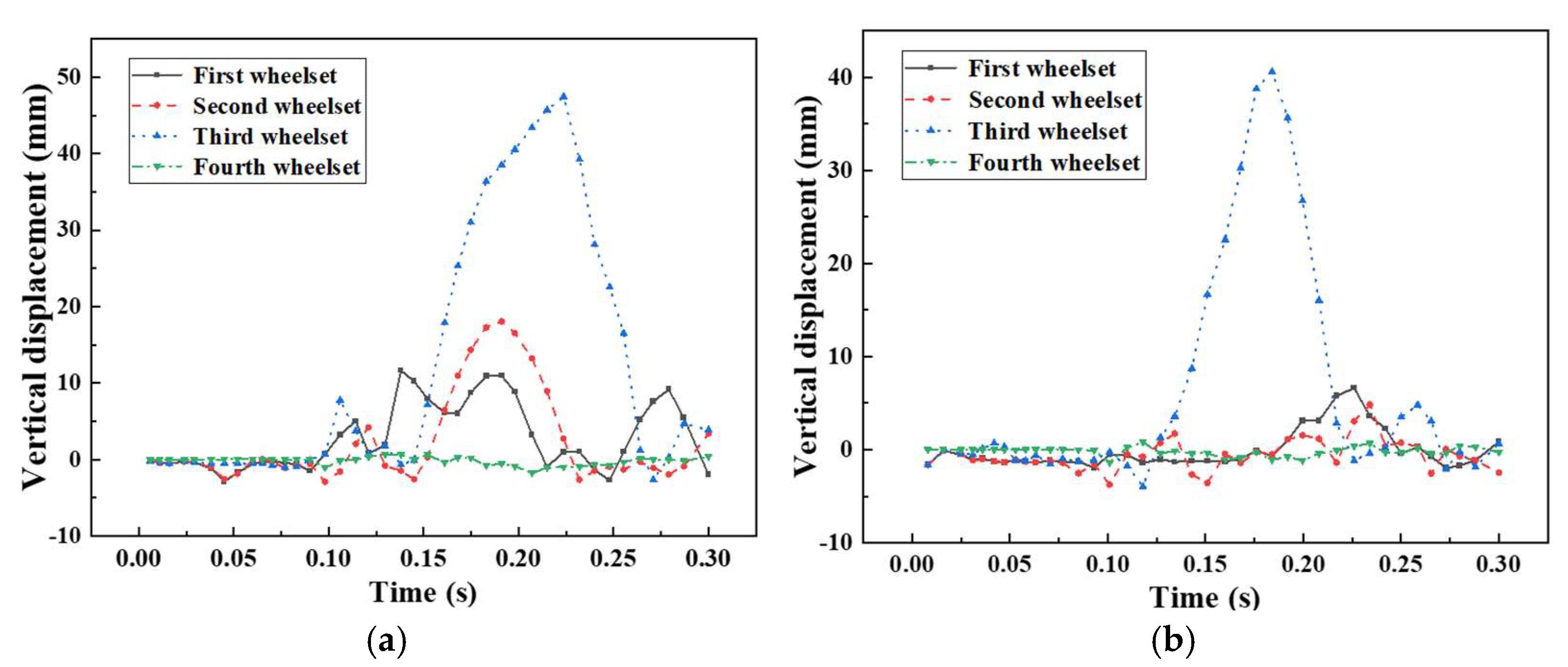
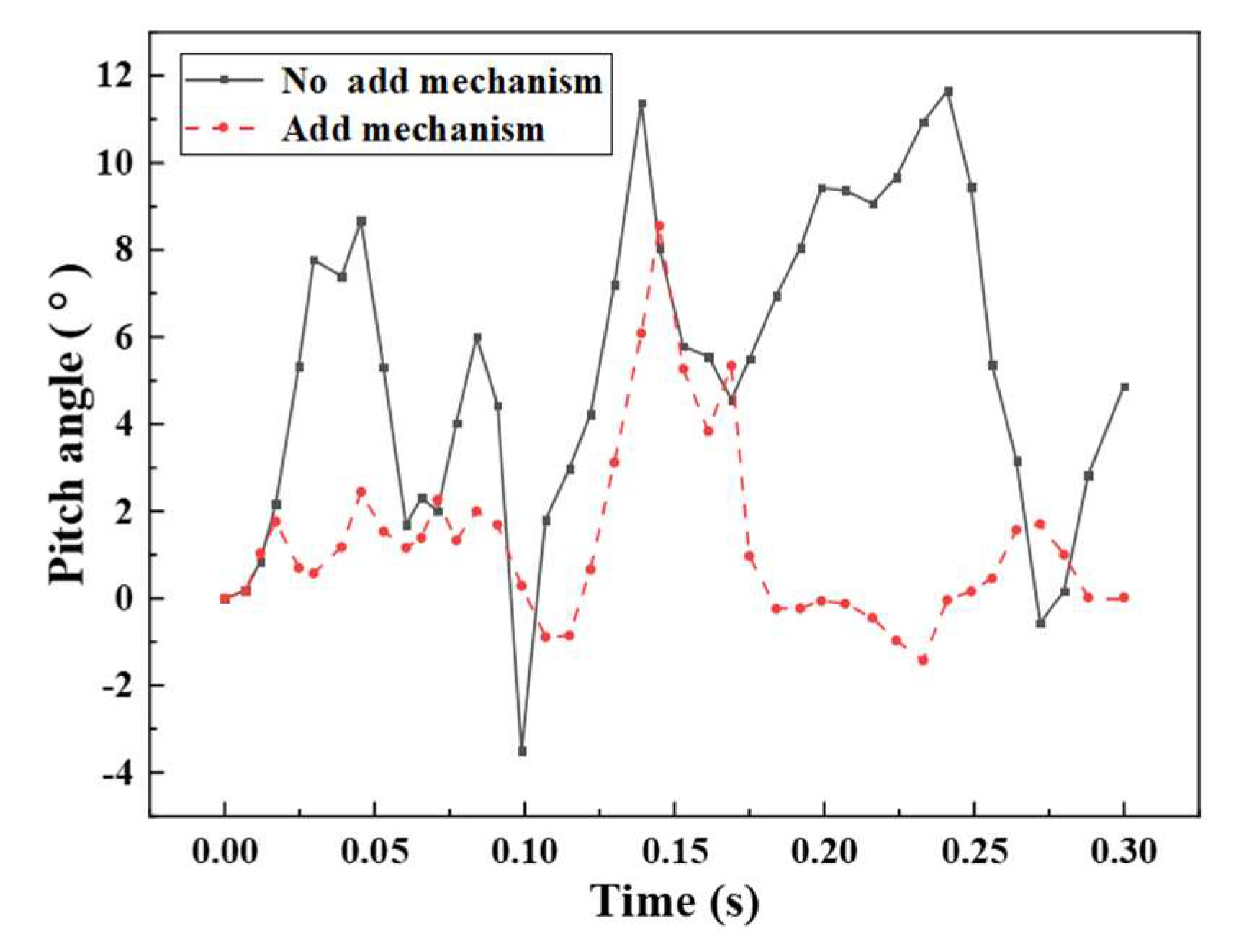
3.4. Comparison of Train Collision Posture
4. Sensitivity Analysis of the Metro Rail Holding Mechanism
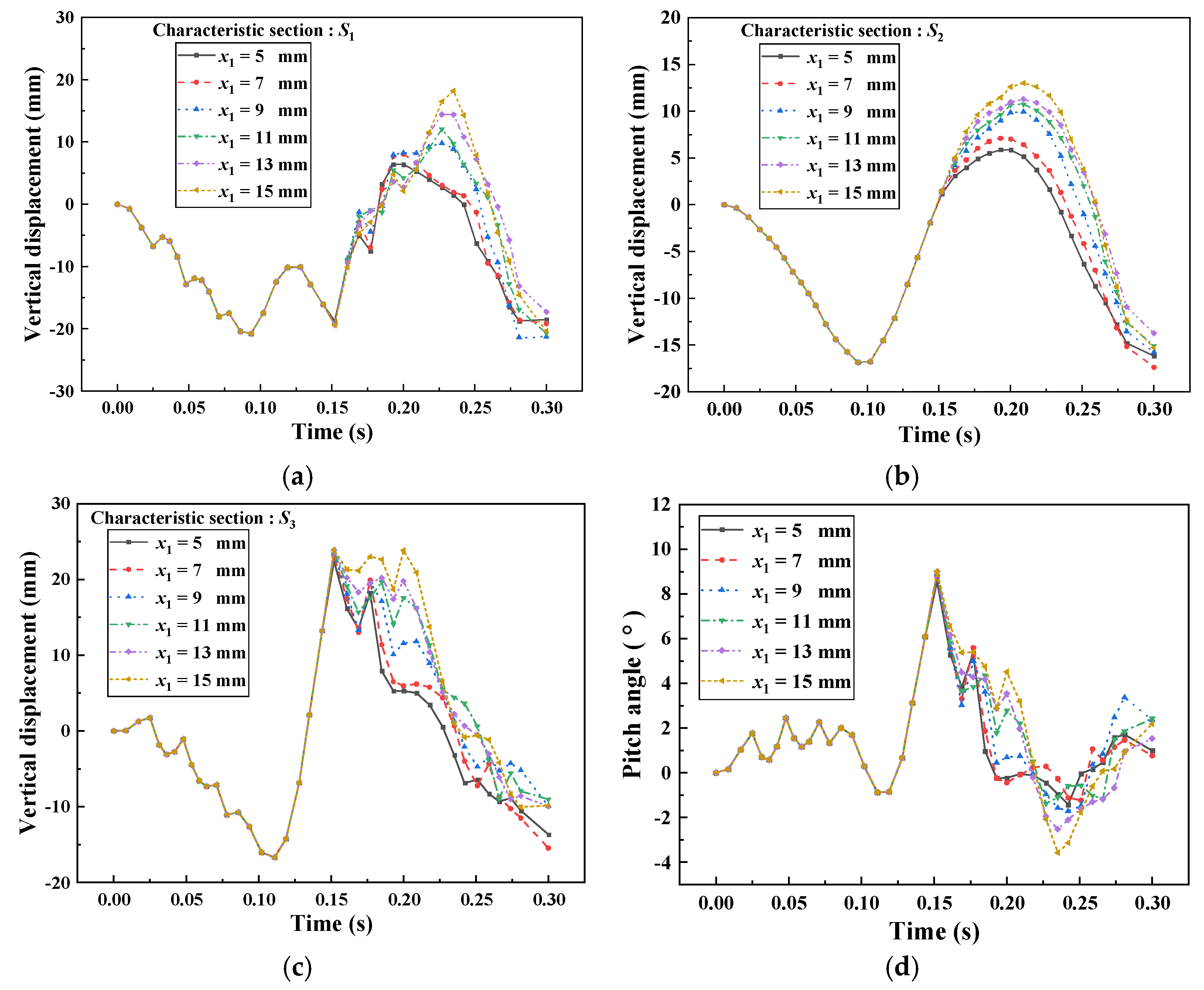
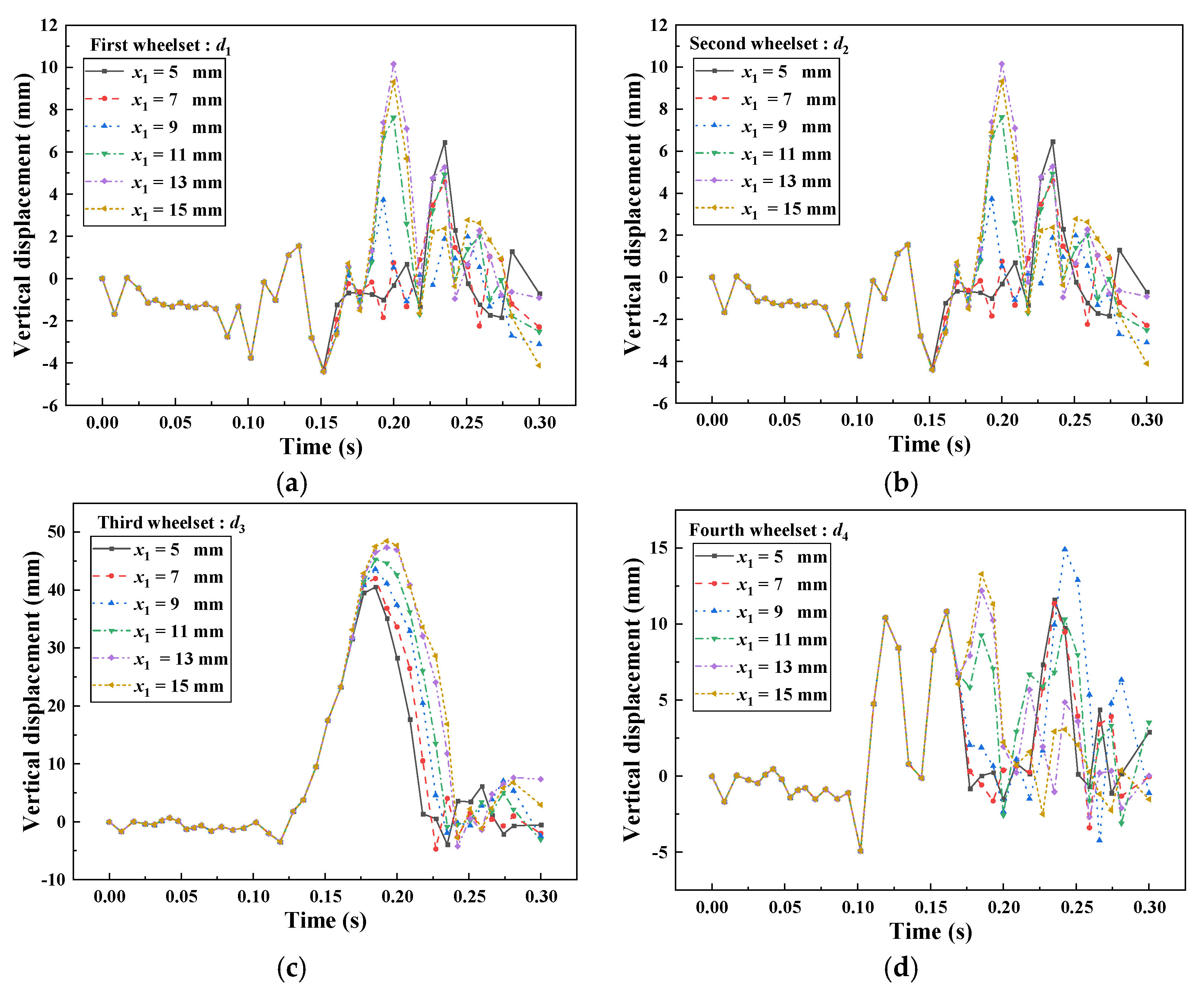
4.1. Effect of Rail Holding Mechanism Distance
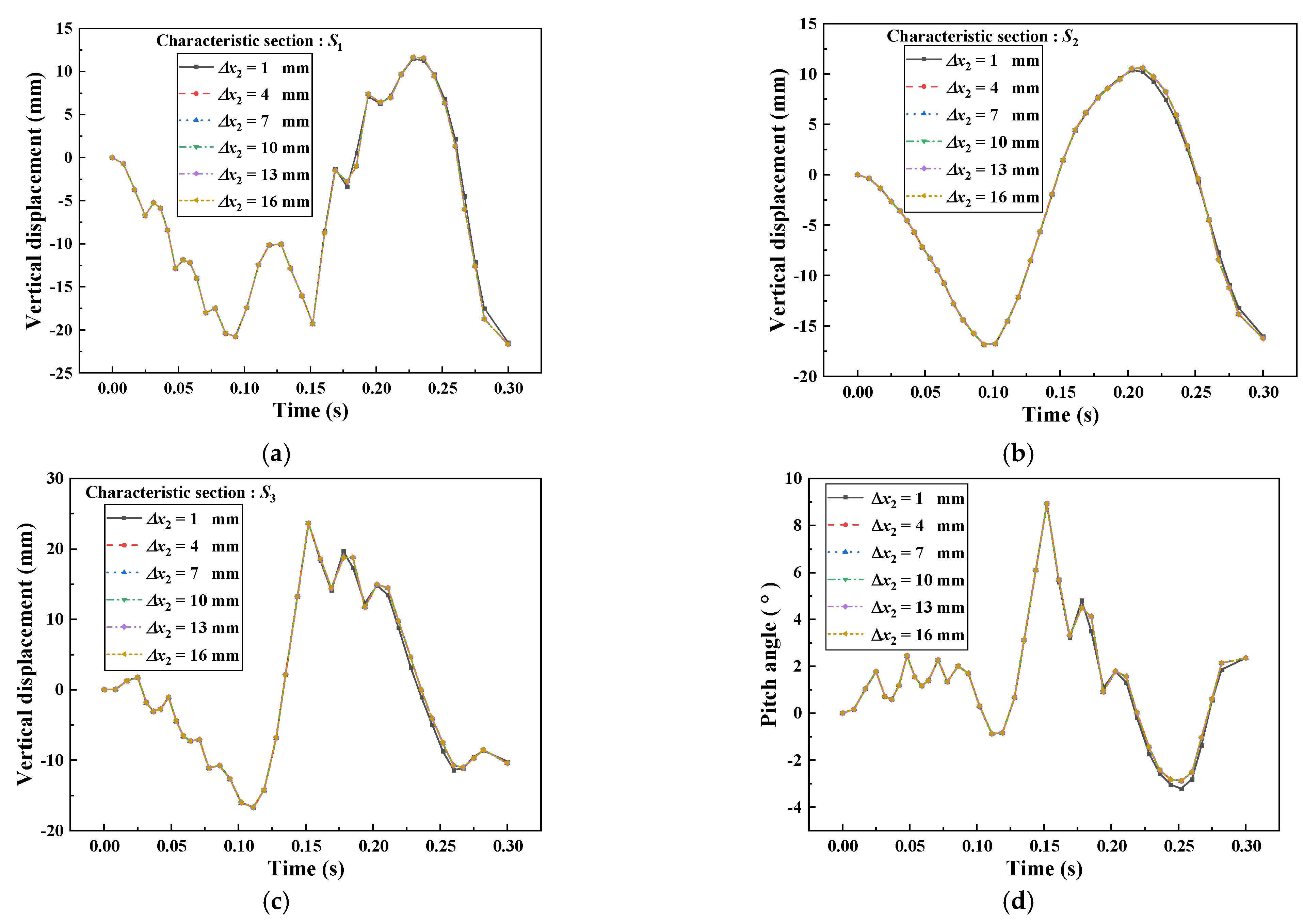
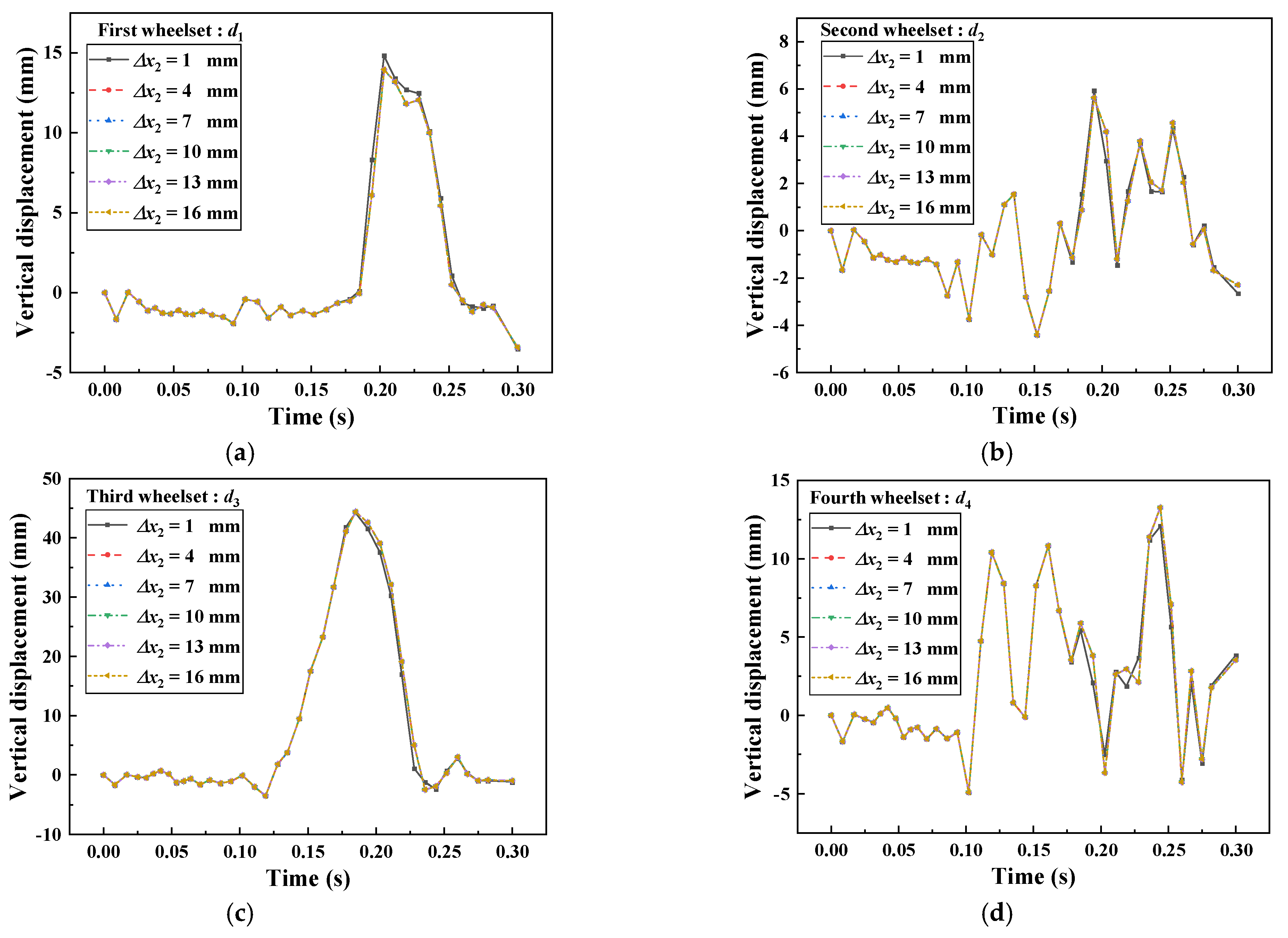
4.2. Effect of Linear Stage Distance of Rail Holding Device
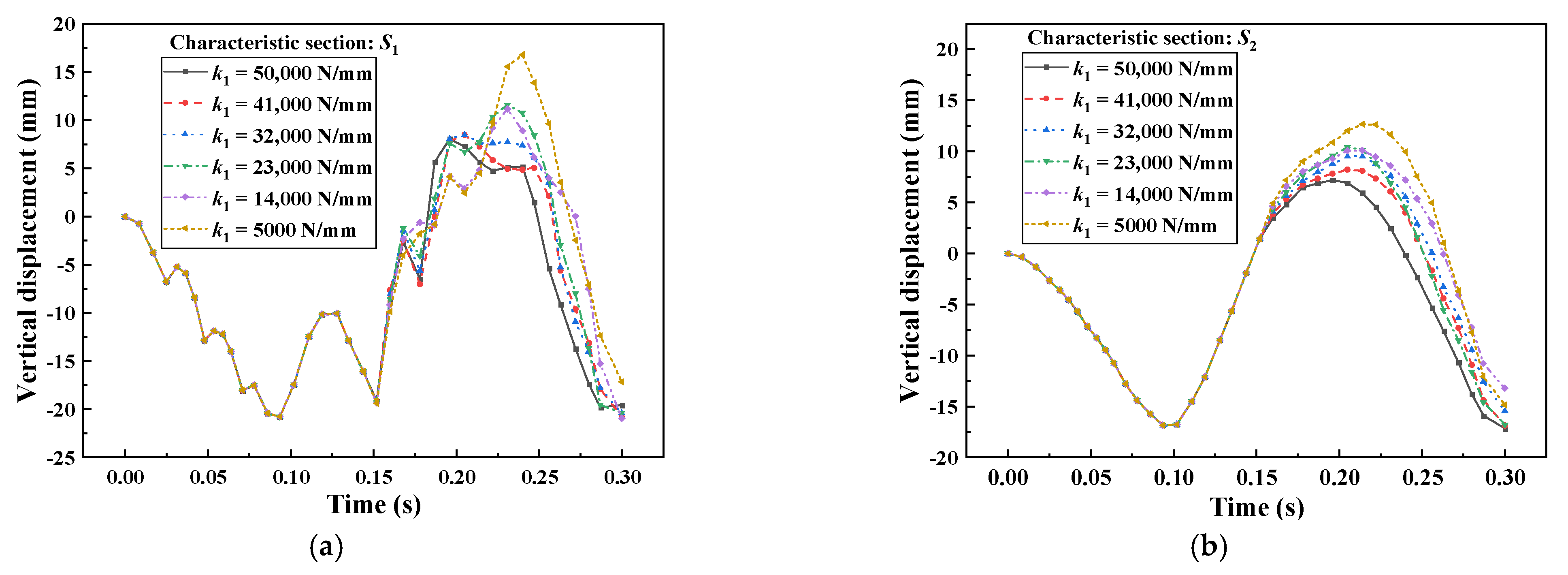
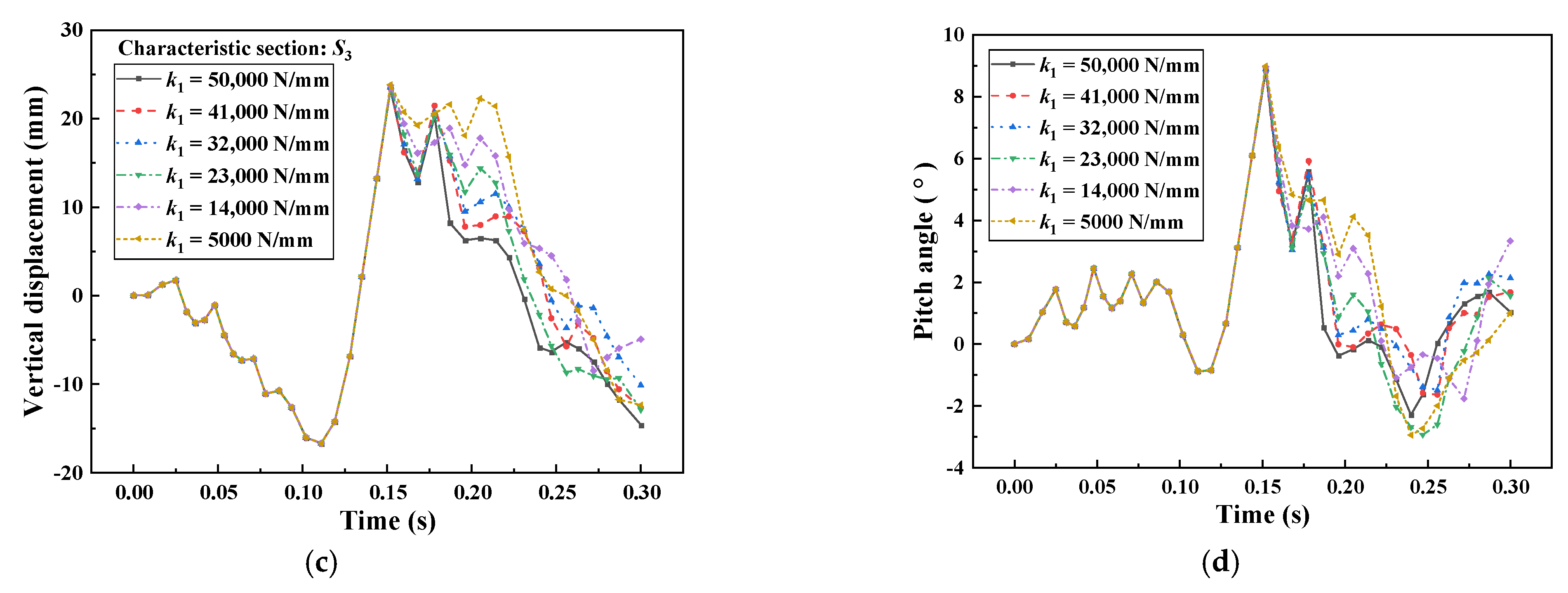
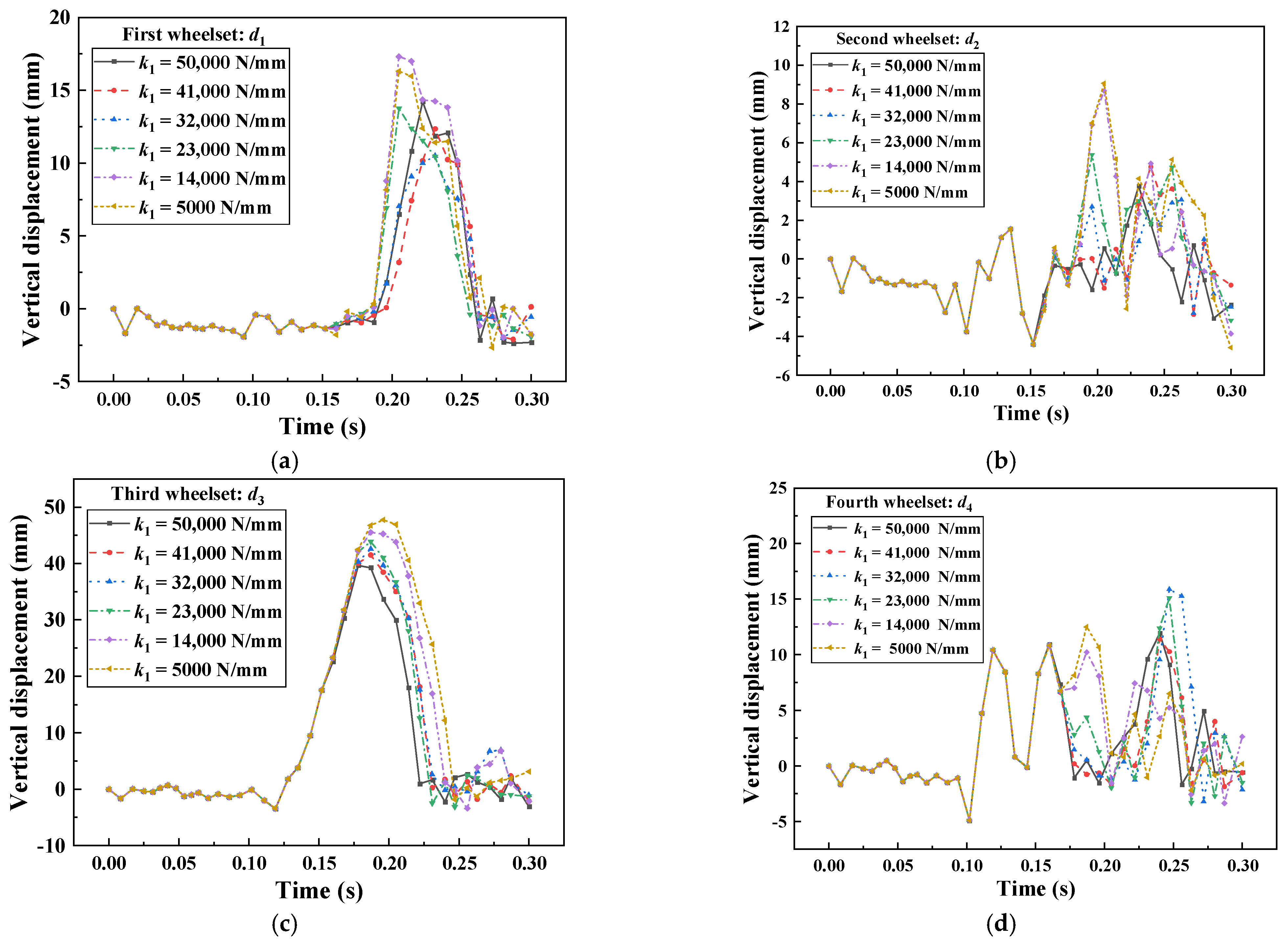
4.3. Effect of the Stiffness of Linear Stage of k1
5. Conclusions
- The maximum vertical lift of the first three wheelsets of the train will increase with the increase in , and the maximum vertical lift of the fourth wheelsets will first decrease and then increase.
- The vertical lift of the three characteristic sections of the car body, the pitch angle of the car body and the vertical lift of the wheelset do not change too much with the change of the linear phase distance , and the linear phase distance of the rail holding device has little effect on the train crash attitude and wheelset lift.
- With the increasing of , the vertical lift of the three characteristic sections of the train and the pitch angle of the car body are decreased, and the maximum vertical lift of the first three wheelsets of the train will keep decreasing with the increasing of , and the maximum vertical lift of the fourth wheelset will appear to increase first and then decrease.
- With the reasonable reduction of the clearance distance and increase in can effectively reduce the vertical lift of the wheelsets and alleviate the nodding phenomenon of the train, and reduce the derailment and jumping phenomenon during the train collision.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baykasoğlu, C.; Sünbüloğlu, E.; Bozdağ, S.E.; Aruk, F.; Toprak, T.; Mugan, A. Railroad passenger car collision analysis and modifications for improved crashworthiness. Int. J. Crashworthiness 2011, 16, 319–329. [Google Scholar] [CrossRef]
- Sutton, A. The development of rail vehicle crashworthiness. Proc. Inst. Mech. Eng. F-J. Rail Rapid Transit 2002, 216, 97–108. [Google Scholar] [CrossRef]
- ASME RT-2–2014. Safety Standard for Structural Requirements for Heavy Rail Transit Vehicles. The American Society of Mechanical Engineers: New York, NY, USA, 2014.
- EN 15227: 2020; Railway Applications Crashworthiness Requirements for Railway Vehicle Bodies. British Standard Published; European Committee for Standardization: London, UK, 2020.
- Li, Y. China Youth Daily. 2022. Available online: http://news.cyol.com/gb/articles/2022-06/04/content_zXzgwCYZo.html (accessed on 4 June 2022).
- Lu, S.; Wang, P.; Ni, W.; Yan, K.; Zhao, S.; Yang, C.; Xu, P. Energy absorption design for crash energy management passenger trains based on scaled model. Struct. Multidiscipl. Optim. 2021, 65, 1–17. [Google Scholar] [CrossRef]
- Zhang, H.; Peng, Y.; Hou, L.; Wang, D.; Tian, G.; Li, Z. Multistage Impact Energy Distribution for Whole Vehicles in High-Speed Train Collisions: Modeling and Solution Methodology. IEEE Trans. Ind. Inform. 2020, 16, 2486–2499. [Google Scholar] [CrossRef]
- Gao, G.; Dong, H.; Tian, H. Collision performance of square tubes with diaphragms. Thin-Walled Struct. 2014, 80, 167–177. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, S.; Yao, S.; Xu, P. Crashworthiness analysis and optimization of a cutting-style energy absorbing structure for subway vehicles. Thin-Walled Struct. 2017, 120, 225–235. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, X.; Xiong, X.; Xu, P. Crashing analysis and multi-objective optimisation of duplex energy-absorbing structure for subway vehicle. Int. J. Crashworthiness 2016, 21, 338–352. [Google Scholar] [CrossRef]
- Xie, S.; Liang, X.; Zhou, H. Design and analysis of a composite energy-absorbing structure for use on railway vehicles. Proc. Inst. Mech. Eng. F-J. Rail Rapid Transit 2015, 230, 825–839. [Google Scholar] [CrossRef]
- Xu, P.; Xing, J.; Yao, S.; Yang, C.; Chen, K.; Li, B. Energy distribution analysis and multi-objective optimization of a gradual energy-absorbing structure for subway vehicles. Thin-Walled Struct. 2017, 115, 255–263. [Google Scholar] [CrossRef]
- Deng, G.; Wang, F.; Yu, C.; Peng, Y.; Xu, H.; Li, Z.; Wang, Z. Assessment of standing passenger traumatic brain injury caused by ground impact in subway collisions. Accid. Anal. Prev. 2022, 166, 106547. [Google Scholar] [CrossRef]
- Hou, L.; Peng, Y.; Sun, D. Neck injury mechanisms in train collisions: Dynamic analysis and data mining of the driver impact injury. Accid. Anal. Prev. 2020, 146, 105725. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Zhang, L. Evaluation and improvement of crashworthiness for high-speed train seats. Int. J. Crashworthiness 2017, 23, 561–568. [Google Scholar] [CrossRef]
- Yang, W.; Xie, S.; Li, H.; Chen, Z. Design and injury analysis of the seated occupant protection posture in train collision. Saf. Sci. 2019, 117, 263–275. [Google Scholar] [CrossRef]
- Yao, S.; Li, X.; Xiao, X.; Xu, P.; Che, Q. Injuries to standing passengers using different handrails in subway train collision accidents. Int. J. Crashworthiness 2019, 26, 53–64. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, T.; Yang, B.; Wang, X.; Xiao, S.; Yang, G.; Li, Y.; Li, B. Influence of wheelset rotational motion on train collision response and wheelset lift mechanism. Int. J. Rail Transp. 2022, 1–25. [Google Scholar] [CrossRef]
- Zhang, T.; Guo, X.; Jin, T.; Yang, Y.; Ling, L.; Wang, K.; Zhai, W. Dynamic derailment behavior of urban tram subjected to lateral collison. Int. J. Rail Transp. 2022, 10, 581–605. [Google Scholar] [CrossRef]
- Xu, P.; Yang, C.; Peng, Y.; Yao, S.; Zhang, D.; Li, B. Crash performance and multi-objective optimization of a gradual energy-absorbing structure for subway vehicles. Int. J. Mech. Sci. 2016, 107, 1–12. [Google Scholar] [CrossRef]
- Guan, W.; Gao, G.; Li, J.; Yu, Y. Crushing analysis and multi-objective optimization of a cutting aluminium tube absorber for railway vehicles under quasi-static loading. Thin-Walled Struct. 2018, 123, 395–408. [Google Scholar] [CrossRef]
- Peng, Y.; Deng, W.; Xu, P.; Yao, S. Study on the collision performance of a composite energy-absorbing structure for subway vehicles. Thin-Walled Struct. 2015, 94, 663–672. [Google Scholar] [CrossRef]
- Kirkpatrick, S.W.; MacNeill, R.A. Development of a computer model for prediction of collision response of a railroad passenger car. In Proceedings of the ASME/IEEE Joint Rail Conference, Washington, DC, USA, 23–25 April 2002. [Google Scholar]
- Tyrell, D.; Jacobsen, K.; Martinez, E.; Perlman, A.B. Train-to-Train Impact Test of Crash Energy Management Passenger Rail Equipment: Structural Results. In Proceedings of the ASME 2006 International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006; The American Society of Mechanical Engineers: New York, NY, USA, 2006. [Google Scholar]
- Liu, Y.; Yang, B.; Li, B.; Xiao, S.; Zhu, T.; Yang, G.; Xiu, R. Experimental and numerical investigation of the design strategy of new anticollision posts for a typical railway vehicle. Int. J. Rail Transp. 2021, 10, 772–799. [Google Scholar] [CrossRef]
- Li, B.; Lu, Z.; Yan, K.; Lu, S.; Kong, L.; Xu, P. Experimental study of a honeycomb energy-absorbing device for high-speed trains. Proc. Inst. Mech. Eng. F-J. Rail Rapid Transit 2019, 234, 1170–1183. [Google Scholar] [CrossRef]
- Li, S.; Zheng, Z. Energy-absorbing structure design and crashworthiness analysis of high-speed trains. Explos. Shock Waves 2015, 35, 164–170. [Google Scholar]
- Yang, C.; Xu, P.; Yao, S.; Xie, S.; Li, Q.; Peng, Y. Optimization of honeycomb strength assignment for a composite energy-absorbing structure. Thin-Walled Struct. 2018, 127, 741–755. [Google Scholar] [CrossRef]
- Zhang, Z.; Yao, S.; Xu, P.; Peng, Y.; Zhang, Y. High-speed train car body front-end energy-absorbing structure of crash simulation and experiment. Locomot. Roll. Stock Technol. 2015, 3, 33–34, 43. [Google Scholar]
- Zhang, Y.; Xu, P.; Peng, Y.; Deng, L.; Che, Q. Crashworthiness optimization of high-speed train front multi-cell energy-absorbing structure. J. Vib. Shock 2017, 36, 31–36. [Google Scholar]
- Baharudin, M.E.; Rouvinen, A.; Korkealaakso, P.; Mikkola, A. Real-time multibody application for tree harvester truck simulator. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2014, 228, 182–198. [Google Scholar] [CrossRef]
- Wu, X.; Chi, M.; Gao, H. The study of post-derailment dynamic behavior of railway vehicle based on running tests. Eng. Fail. Anal. 2014, 44, 382–399. [Google Scholar] [CrossRef]
- Ling, L.; Xiao, X.; Jin, X.-S. Development of a simulation model for dynamic derailment analysis of high-speed trains. Acta Mech. Sin. 2015, 30, 860–875. [Google Scholar] [CrossRef]
- Ling, L.; Dhanasekar, M.; Wang, K.; Zhai, W.; Weston, B. Collision derailments on bridges containing ballastless slab tracks. Eng. Fail. Anal. 2019, 105, 869–882. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, B.; Xiao, S.; Zhu, T.; Yang, G.; Xiu, R. Parameter study and multi-objective optimization for crashworthiness of a B-type metro train. Proc. Inst. Mech. Eng. F-J. Rail Rapid Transit 2021, 236, 91–108. [Google Scholar] [CrossRef]
- Li, R.; Xu, P.; Peng, Y.; Xie, Y. Scaled tests and numerical simulations of rail vehicle collisions for various train sets. Proc. Inst. Mech. Eng. F-J. Rail Rapid Transit 2015, 230, 1590–1600. [Google Scholar] [CrossRef]
- Lu, S.; Xu, P.; Yan, K.; Yao, S.; Li, B. A force/stiffness equivalence method for the scaled modelling of a high-speed train head car. Thin-Walled Struct. 2019, 137, 129–142. [Google Scholar] [CrossRef]
- Yao, S.; Yan, K.; Lu, S.; Xu, P. Energy-absorption optimisation of locomotives and scaled equivalent model validation. Int. J. Crashworthiness 2017, 22, 441–452. [Google Scholar] [CrossRef]
- Wu, X.; Chi, M.; Gao, H.; Zhang, D.; Zeng, J.; Wu, P.; Zhu, M. The study of post-derailment measures to limit the extent of a derailment. Proc. Inst. Mech. Eng. F-J. Rail Rapid Transit 2014, 230, 64–76. [Google Scholar] [CrossRef]
- Yang, C.; Li, D.; Zhu, T.; Xiao, S. Special dynamic behavior of an aluminum alloy and effects on energy absorption in train collisions. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Lai, J.; Xu, J.; Liao, T.; Zheng, Z.; Chen, R.; Wang, P. Investigation on train dynamic derailment in railway turnouts caused by track failure. Eng. Fail. Anal. 2022, 134, 106050. [Google Scholar] [CrossRef]
- Xu, J.; Wang, J.; Wang, P.; Chen, J.; Gao, Y.; Chen, R.; Xie, K. Study on the derailment behaviour of a railway wheelset with solid axles in a railway turnout. Veh. Syst. Dyn. 2019, 58, 123–143. [Google Scholar] [CrossRef]
- Ren, Y. The Influence of the Initial States of the Train on the Collision Responses. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2019. [Google Scholar] [CrossRef]
- Yang, C.; Li, Q.; Wang, X.; Wang, M. Overriding Behavior in Train Collisions Based on Moving Vehicle-Track Coupled Model. J. Southwest Jiaotong Univ. 2019, 54, 1298–1304. [Google Scholar]
- Lv, R. Impact Characteristics of Metro Trains Coupler and Draft Gears and Its Effect on Derailment Behavior. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2021. [Google Scholar] [CrossRef]
- Zhai, W.; Wang, K.; Cai, C. Fundamentals of vehicle–track coupled dynamics. Veh. Syst. Dyn. 2009, 47, 1349–1376. [Google Scholar] [CrossRef]
- Ling, L.; Xiao, X.; Xiong, J.; Zhou, L.; Wen, Z.; Jin, X. A 3D model for coupling dynamics analysis of high-speed train/track system. J. Zhejiang Univ.-Sci. A 2015, 16, 170. [Google Scholar] [CrossRef]
- Marquis, B.; Pascal, J.P. Report on a railway Benchmark simulating a single wheelset without friction impacting a rigid track. Veh. Syst. Dyn. 2008, 46, 93–116. [Google Scholar] [CrossRef]





| Type | Parameters | Unit | Value |
|---|---|---|---|
| Position parameters | Vehicle distance | mm | 13,368 |
| Bogie axis distance | mm | 5032 | |
| Rail distance | mm | 1435 | |
| Wheel rolling circle diameter | mm | 860 | |
| Wheelset distance | mm | 2516 | |
| vehicle parameter | Carbody mass | t | 34 |
| Carbody moment of inertia-X | kg·m2 | 6.67 × 107 | |
| Carbody moment of inertia-Y | kg·m2 | 1.06 × 109 | |
| Carbody moment of inertia-Z | kg·m2 | 1,349,239 | |
| Bogie mass | t | 2.66 | |
| Bogie moment of inertia-X | kg·m2 | 1.29 × 106 | |
| Bogie moment of inertia-Y | kg·m2 | 1.038 × 106 | |
| Bogie moment of inertia-Z | kg·m2 | 2.18 × 106 | |
| Wheelset mass | t | 1.2 | |
| Wheelset moment of inertia-X | kg·m2 | 8.59 × 105 | |
| Wheelset moment of inertia-Y | kg·m2 | 1.57 × 105 | |
| Carbody moment of inertia-Z | kg·m2 | 8.72 × 106 | |
| Suspension parameters | Axlebox spring longitudinal stiffness | N/mm | 13,150 |
| Axlebox spring lateral stiffness | N/mm | 13,150 | |
| Axlebox spring vertical stiffness | N/mm | 3800 | |
| Primary suspension vertical damper | N·s/mm | 20 | |
| Airspring longitudinal stiffness | N/mm | 2500 | |
| Airspring lateral stiffness | N/mm | 2500 | |
| Airspring vertical stiffness | N/mm | 3800 | |
| Secondary suspension longitudinal damper | N·s/mm | 810 | |
| Secondary suspension lateral damper | N·s/mm | 15 | |
| Secondary suspension vertical damper | N·s/mm | 10 |
| Number | Instrument | Model | Brand |
|---|---|---|---|
| 1 | Dynamic data collector | Ki-DAU | Kistler (Winterthur, Switzerland) |
| 2 | Motion sensor | MT2A | Celesco (Chatsworth, CA, USA) |
| 3 | Acceleration sensor | 7264H-360 | ENDEVCO (San Juan Capistrano, CA, USA) |
| 4 | Tape measure | A0481 | TaJima (Tokyo, Japan) |
| 5 | Photograph | HX-6E | NAC (Salem, MA, USA) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Yang, L.; Guo, W.; Yang, C.; Che, Q.; Xu, T. Experimental and Numerical Study of Collision Attitude Auxiliary Protection Strategy for Subway Vehicles. Machines 2022, 10, 1231. https://doi.org/10.3390/machines10121231
Xu P, Yang L, Guo W, Yang C, Che Q, Xu T. Experimental and Numerical Study of Collision Attitude Auxiliary Protection Strategy for Subway Vehicles. Machines. 2022; 10(12):1231. https://doi.org/10.3390/machines10121231
Chicago/Turabian StyleXu, Ping, Liting Yang, Weinian Guo, Chengxing Yang, Quanwei Che, and Tuo Xu. 2022. "Experimental and Numerical Study of Collision Attitude Auxiliary Protection Strategy for Subway Vehicles" Machines 10, no. 12: 1231. https://doi.org/10.3390/machines10121231
APA StyleXu, P., Yang, L., Guo, W., Yang, C., Che, Q., & Xu, T. (2022). Experimental and Numerical Study of Collision Attitude Auxiliary Protection Strategy for Subway Vehicles. Machines, 10(12), 1231. https://doi.org/10.3390/machines10121231







