Research on the Gearbox Fault Diagnosis Method Based on Multi-Model Feature Fusion
Abstract
1. Introduction
- (1)
- Eight time–frequency sensitive features are extracted and selected. The 1DCNN was used to extract the original vibration signal features.
- (2)
- The parallel fusion method was used to fuse the two domain features as the input of the support vector machine (SVM) model.
- (3)
- The improved particle swarm optimization (IPSO) algorithm is used to optimize the SVM classifier to achieve gearbox fault diagnosis and obtain more accurate and effective results.
2. Background
2.1. 1DCNN
2.2. IPSO
2.3. SVM
2.4. Feature Fusion
3. Experimental Platform Construction and Data Collection
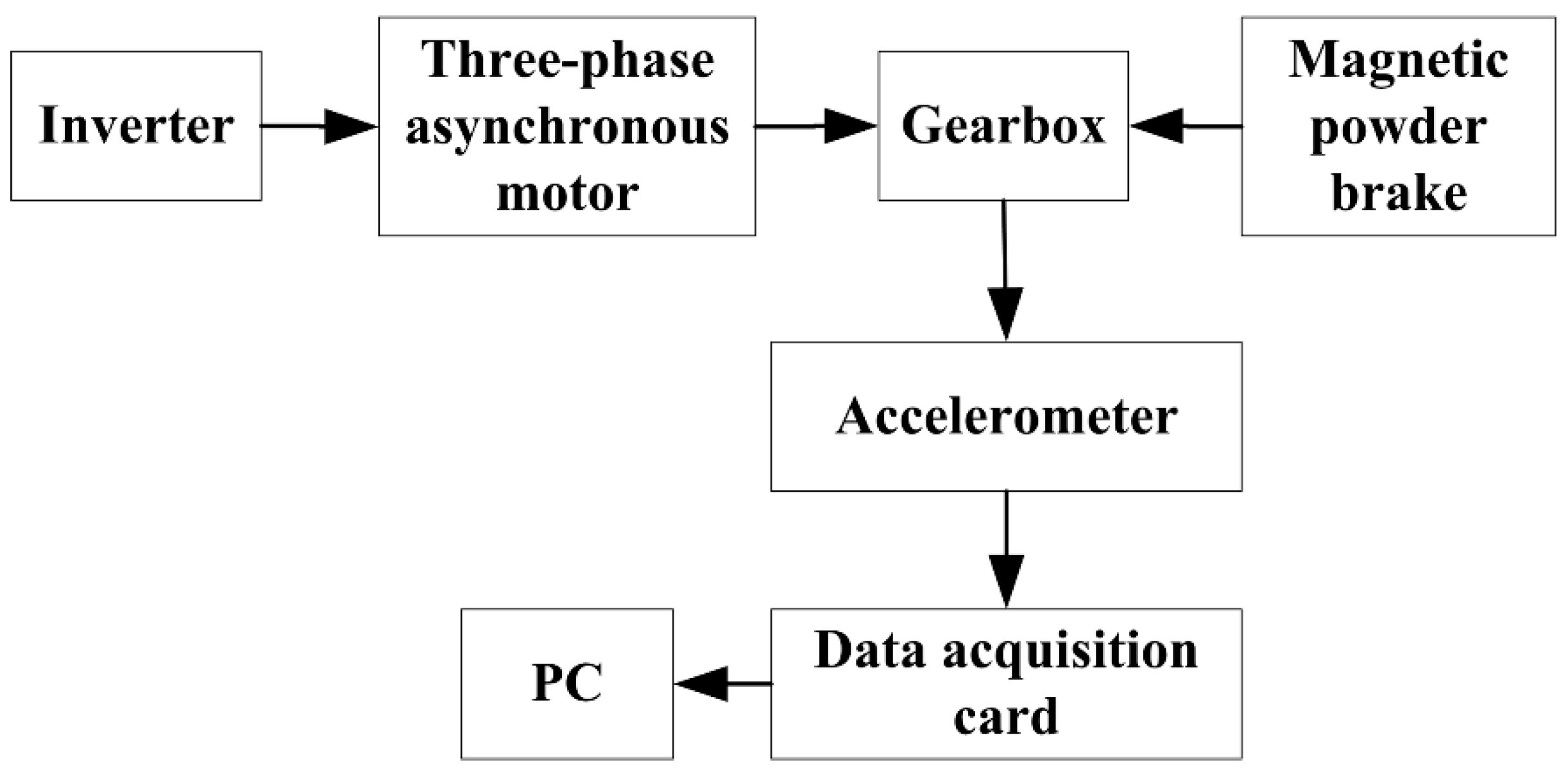
- (1)
- To ensure safety during the experiment, an air switch was installed between the power plug and inverter.
- (2)
- The inverter was connected to the motor, and the motor and gearbox were connected through the belt. The gearbox and the magnetic powder brake were connected through the coupling, and the motor, gearbox, and magnetic powder brake were fixed in the base plate.
- (3)
- A piezoelectric accelerometer was installed at the axial position of the bearing cover of the high-speed shaft of the gearbox, and the sensor, acquisition card, and PC were connected through the signal output line.
- (4)
- Four types of vibration data were obtained from the experiment: normal, wear, pitting, and broken gears. The motor speed was set at 900 rpm, and the sampling frequency was set at 6 kHz. A total of 1.8 million data points were collected for each state. The data groups, data length, sampling frequency, and motor speed of the vibration data obtained from the experiments are listed in Table 1.
4. Fault Diagnosis Model Construction
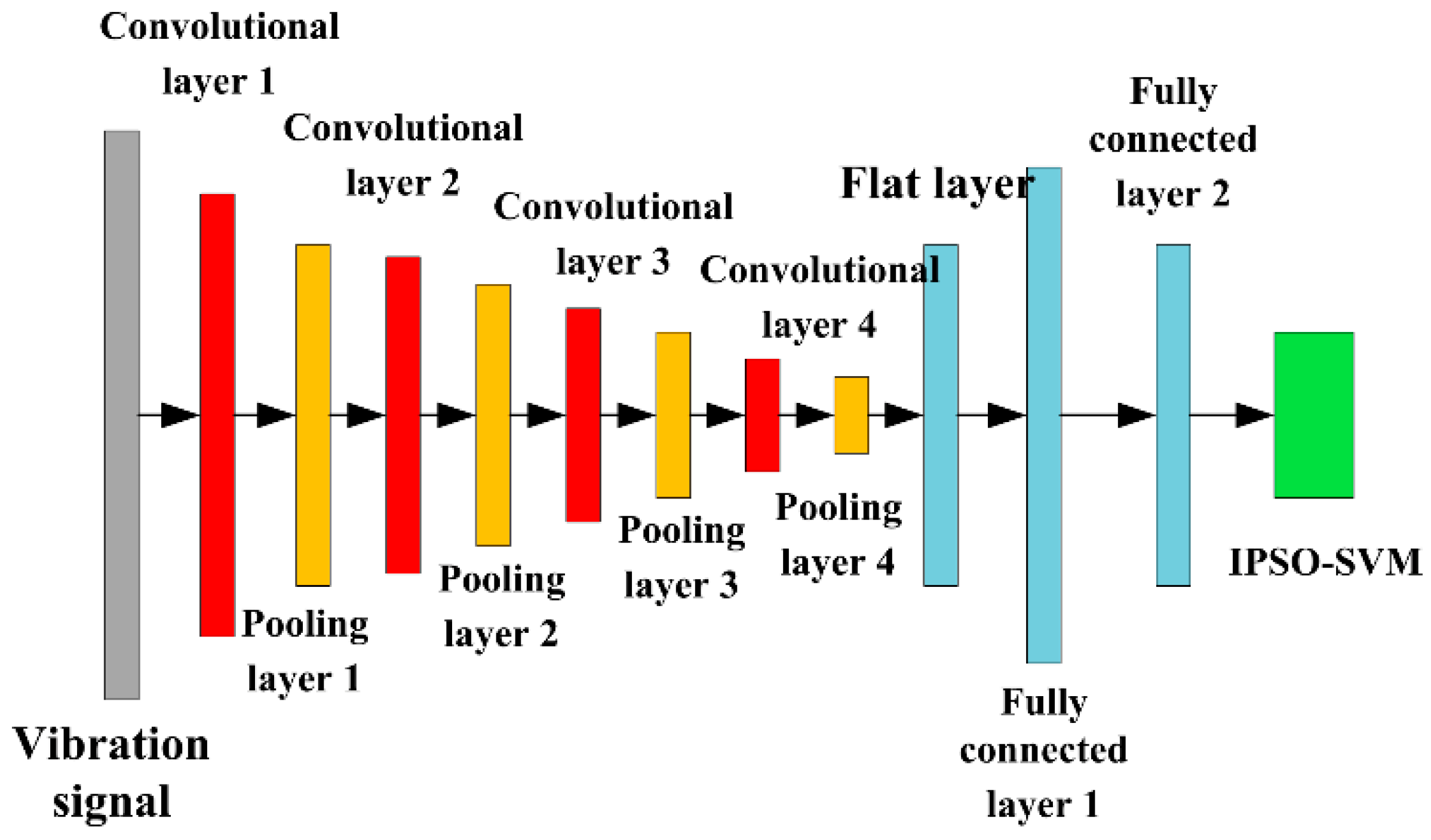
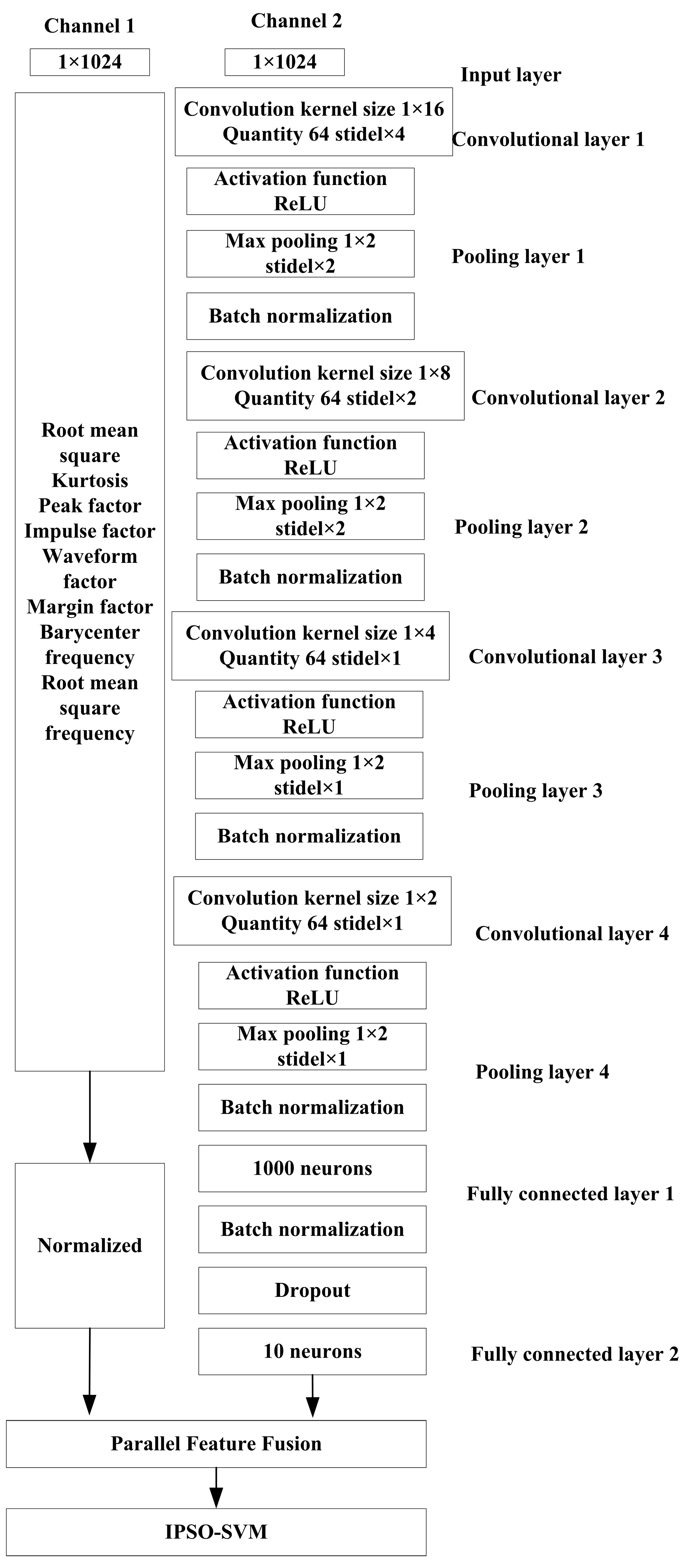
4.1. 1DCNN-IPSO-SVM Model
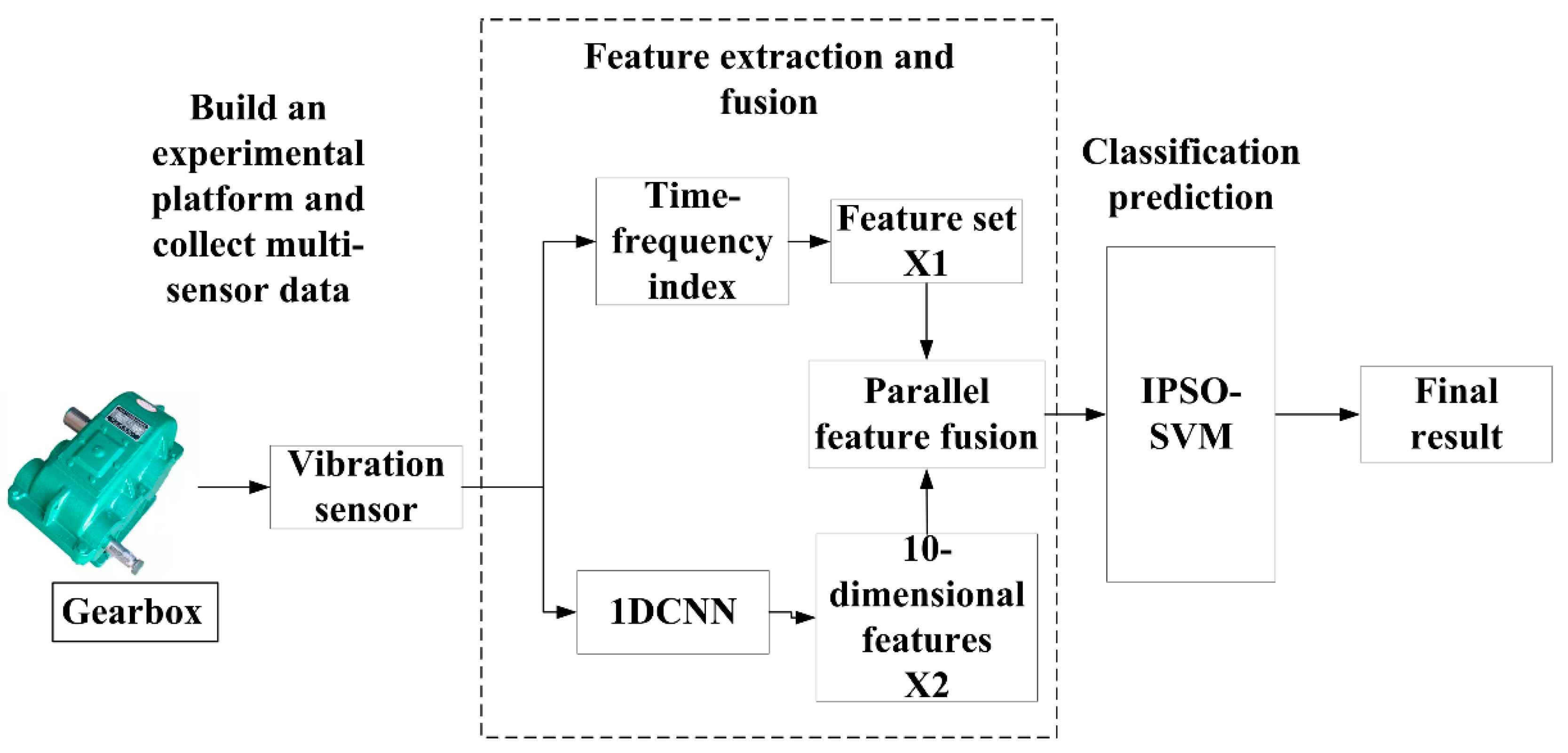
4.2. Multi-Model Feature Fusion Fault Diagnosis Model Framework
5. Experimental Analysis and Verification
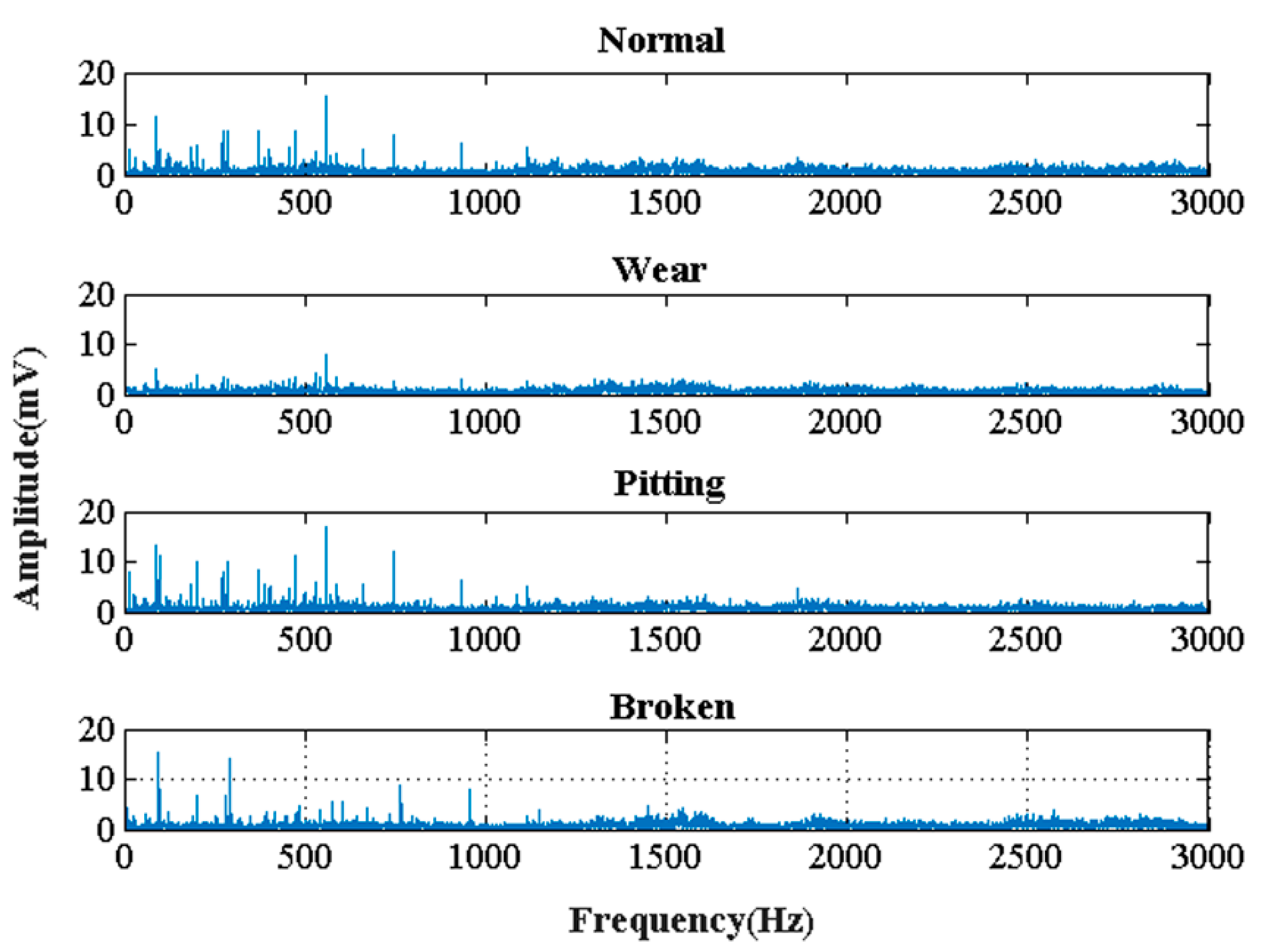
5.1. Time–Frequency Domain Feature Extraction
5.2. Feature Extraction Analysis
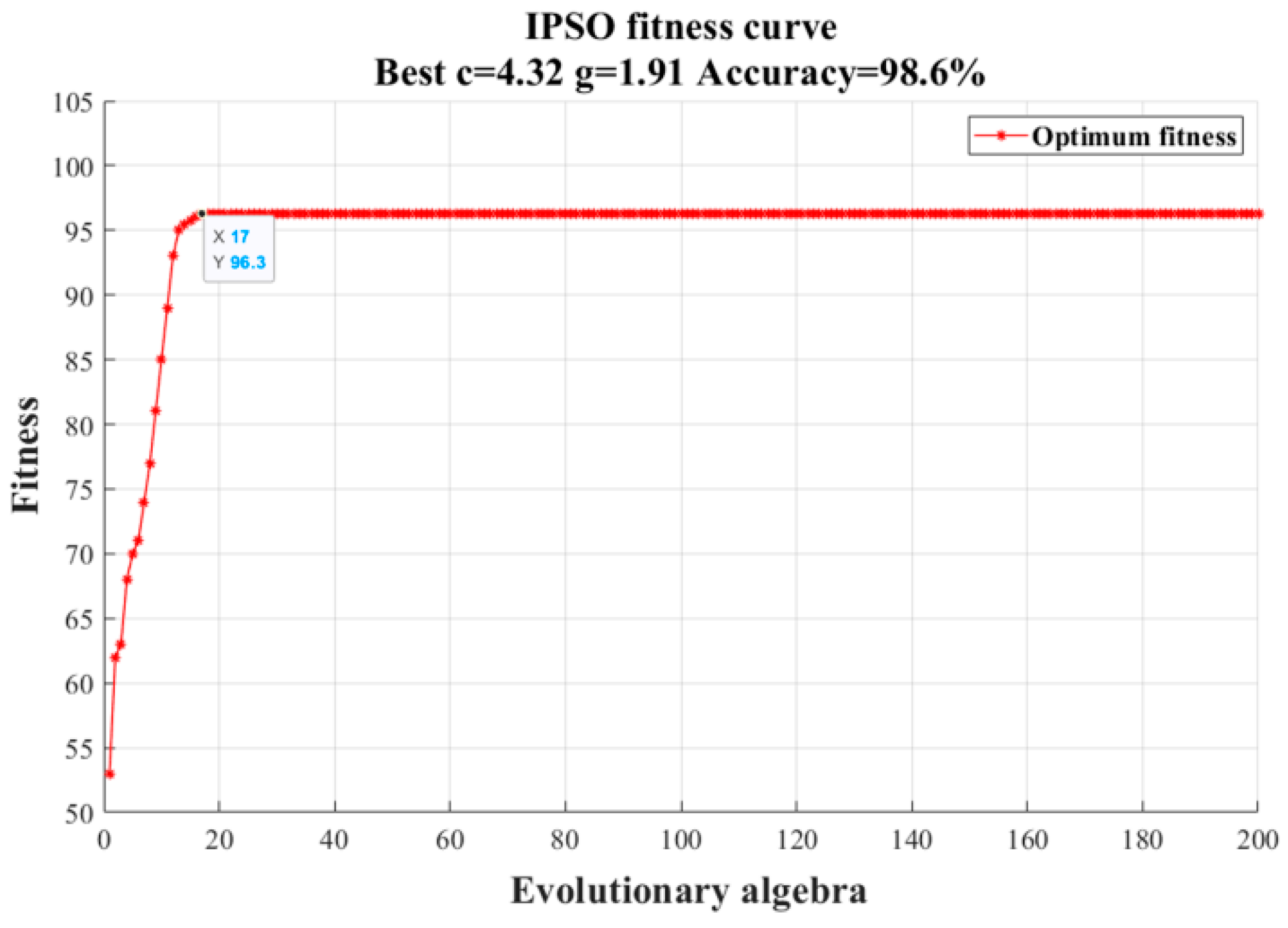
5.3. IPSO-SVM Parameter Analysis
5.4. Model Comparison and Verification
- (1)
- The traditional time–frequency feature extraction has human interference, which easily leads to the loss of valuable information and the reduction of recognition rate.
- (2)
- Using 1DCNN to extract features from original data reduces human interference, improves the reliability of extracted features, and is conducive to improving the recognition rate.
- (3)
- The 1DCNN model takes a long time to operate, the pooling layer will lose valuable information, and it is easy for the commonly used softmax classifier to fall into local optimization.
- (4)
- The proposed multi-model feature fusion model fused traditional time–frequency sensitive features and CNN extracted features through the parallel fusion method to overcome the single feature and effectively improve the recognition rate.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, J.; Lin, C.; Peng, D.; Ge, H. Fault diagnosis of rotating machinery: A review and bibliometric analysis. IEEE Access 2020, 8, 224985–225003. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, X.; Zou, J. The optimized deep belief networks with improved logistic sigmoid units and their application in fault diagnosis for planetary gearboxes of wind turbines. IEEE Trans. Ind. Electron. 2018, 66, 3814–3824. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Miao, Q. Fault diagnosis techniques for planetary gearboxes under variable conditions: A review. In Proceedings of the 2016 Prognostics and System Health Management Conference (PHM-Chengdu), Chengdu, China, 19–21 October 2016; pp. 1–11. [Google Scholar]
- Yu, J.; Zhou, X.; Lu, L.; Zhao, Z. Multiscale dynamic fusion global sparse network for gearbox fault diagnosis. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Tang, S.; Yuan, S.; Zhu, Y. Deep learning-based intelligent fault diagnosis methods toward rotating machinery. IEEE Access 2020, 8, 9335–9346. [Google Scholar] [CrossRef]
- Cerrada, M.; Zurita, G.; Cabrera, D.; Sánchez, R.V.; Artés, M.; Li, C. Gearbox fault diagnosis based on deep random forest fusion of acoustic and vibratory signals. Mech. Syst. Signal Process. 2016, 76, 283–293. [Google Scholar]
- Bao, M.; Zhao, C.S. Researches on gear fault diagnosis techniques. Nanjing Univ. Aeronaut. Astronaut. 1992, 24, 566–573. [Google Scholar]
- Wang, W.; Wong, A.K. Some new signal processing approaches for gear fault diagnosis. In Proceedings of the Fifth International Symposium on Signal Processing and its Applications (IEEE Cat. No.99EX359), Brisbane, QLD, Australia, 22–25 August 1999; Volume 2, pp. 587–590. [Google Scholar]
- Wu, B.; Luo, Y. Research on gear fault diagnosis and feature extraction method. In Proceedings of the 2020 International Conference on Artificial Intelligence and Electromechanical Automation (AIEA), Tianjin, China, 26–28 June 2020; pp. 512–515. [Google Scholar]
- Cao, X.C.; Chen, B.Q.; Yao, B. Combining translation-invariant wavelet frames and convolutional neural network for intelligent tool wear state identification. Comput. Ind. 2019, 106, 71–84. [Google Scholar] [CrossRef]
- Nd, A.; Sm, B.; Rj, C. Multipoint milling tool supervision using artificial neural network approach. Mater. Today Proc. 2020, 45, 1898–1903. [Google Scholar]
- Zhong, J.H.; Zhang, J.; Liang, J.; Wang, H. Multi-fault rapid diagnosis for wind turbine gearbox using sparse bayesian extreme learning machine. IEEE Access 2019, 7, 773–781. [Google Scholar] [CrossRef]
- Kiran, V.; Hemantha, K.; Gangadharan, K.V.; Salih, D.; Bendaya, M. Engine gearbox fault diagnosis using machine learning approach. J. Qual. Maint. Eng. 2018, 24, 345–357. [Google Scholar]
- Wang, H.W.; Sun, W.L.; Zhang, X.D.; He, L. Fault diagnosis method of wind turbine’s gearbox based on composite multiscale dispersion entropy of optimised VMD and LSTM. Acta Energ. Sol. Sin. 2022, 43, 288–295. [Google Scholar]
- Kamat, P.; Sugandhi, R.; Kumar, S. Data-driven bearing fault detection using hybrid autoencoder-LSTM deep learning approach. Int. J. Model. Identif. Control. 2021, 1, 38. [Google Scholar] [CrossRef]
- Khalil, K.; Eldash, O.; Kumar, A.; Bayoumi, M. Machine learning-based approach for hardware faults prediction. IEEE Trans. Circuits Syst. I Reg. Papers. 2020, 67, 3880–3892. [Google Scholar] [CrossRef]
- Khalil, K.; Eldash, O.; Kumar, A.; Bayoumi, M. Intelligent fault-prediction assisted self-healing for embryonic hardware. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 852–866. [Google Scholar] [CrossRef] [PubMed]
- Tian, H.; Chen, S.C. MCA-NN: Multiple correspondence analysis based neural network for disaster information detection. In Proceedings of the 2017 IEEE Third International Conference on Multimedia Big Data (BigMM), Laguna Hills, CA, USA, 19–21 April 2017; pp. 268–275. [Google Scholar]
- Gong, W.F.; Chen, H.; Zhang, Z.H.; Zhang, M.L.; Wang, R.H.; Guan, C.; Wang, Q. A novel deep learning method for intelligent fault diagnosis of rotating machinery based on improved CNN-SVM and multichannel data fusion. Sensors 2019, 19, 1693. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Sun, C.; Yan, R.; Chen, X. Intelligent fault diagnosis for planetary gearbox using time-frequency representation and deep reinforcement learning. IEEE/ASME Trans. Mechatron. 2021, 27, 985–998. [Google Scholar] [CrossRef]
- Zhao, X.L.; Yao, J.Y.; Deng, W.X.; Ding, P.; Ding, Y.F.; Jia, M.P.; Liu, Z. Intelligent fault diagnosis of gearbox under variable working conditions with adaptive intraclass and interclass convolutional neural network. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–15. [Google Scholar] [CrossRef]
- Li, P.; Chen, Z.; Yang, L.T.; Gao, J.; Zhang, Q.; Deen, M.J. An incremental deep convolutional computation model for feature learning on industrial big data. IEEE trans. Ind. Informat. 2019, 15, 1341–1349. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Chen, Y.S.; Zhao, X.; Jia, X.P. Spectral–spatial classification of hyperspectral data based on deep belief network. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Hu, X.; Li, G.; Niu, P.; Wang, J.; Zha, L. A generative adversarial neural network model for industrial boiler data repair. Appl. Soft Comput. 2021, 104, 107214. [Google Scholar] [CrossRef]
- Wu, C.Z.; Jiang, P.F.; Feng, T.; Chen, T.; Chen, X. Faults diagnosis method for gearboxes based on a 1-D convolutional neural network. J. Vib. Shock 2018, 37, 51–56. [Google Scholar]
- Zhang, X.; Han, P.; Xu, L.; Zhang, F.; Wang, Y.; Gao, L. Research on bearing fault diagnosis of wind turbine gearbox based on 1DCNN-PSO-SVM. IEEE Access 2020, 8, 192248–192258. [Google Scholar] [CrossRef]
- Li, Y.; Jia, H.; Qi, J.; Sun, H.; Fan, X. An Acquisition method of agricultural equipment roll angle based on multi-source information fusion. Sensors 2020, 20, 2082. [Google Scholar] [CrossRef]
- Xuan, Y.; Si, W.; Zhu, J.; Sun, Z.; Zhao, J.; Xu, M.; Xu, S. Multi-model fusion short-term load forecasting based on random forest feature selection and hybrid neural network. IEEE Access 2021, 9, 69002–69009. [Google Scholar] [CrossRef]
- Tian, Z.; Chen, H. Multi-step short-term wind speed prediction based on integrated multi-model fusion. Appl. Energy 2021, 298, 117248. [Google Scholar] [CrossRef]
- Sercu, T.; Puhrsch, C.; Kingsbury, B.; Lecun, Y. Very deep multilingual convolutional neural networks for LVCSR. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 4955–4959. [Google Scholar]
- Gao, X.; Wang, Y.W. Recognition of similar handwritten Chinese characters based on CNN and random elastic deformation. J. South China Univ. Technol. 2014, 42, 72–76+83. [Google Scholar]
- Zhang, M.; Zhang, X.; Mo, J.; Xiang, Z.; Zheng, P. Brake uneven wear of high-speed train intelligent monitoring using an ensemble model based on multi-sensor feature fusion and deep learning. Eng. Fai. Anal. 2022, 137, 106219. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.S.; Gu, D.S.; Choi, B.K. Intelligent fault diagnosis system of induction motor based on transient current signal. Mechatronics 2009, 19, 680–689. [Google Scholar] [CrossRef]
- Lin, F.J.; Chen, S.Y.; Teng, L.T.; Chu, H. Recurrent functional-link-based fuzzy neural network controller with improved particle swarm optimization for a linear synchronous motor drive. IEEE Trans. Magnet. 2009, 45, 3151–3165. [Google Scholar]
- Song, X.; Zhao, J.; Song, J.; Dong, F.; Xu, L.; Zhao, J. Local demagnetization fault recognition of permanent magnet synchronous linear motor based on S-transform and PSO–LSSVM. IEEE Trans. Power Electron. 2020, 35, 7816–7825. [Google Scholar] [CrossRef]
- Zaharis, Z.D.; Gravas, I.P.; Yioultsis, T.V.; Lazaridid, P.I.; Xenors, T.D. Exponential log-periodic antenna design using improved particle swarm optimization with velocity mutation. In 2016 IEEE Conference on Electromagnetic Fied Computation (CEFC); IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm: Explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Ding, S.F.; Qi, B.J.; Tan, H.Y. An overview on theory and algorithm of support vector machines. J. Univ. Electron. Sci. Technol. China 2011, 40, 2–10. [Google Scholar]
- Zhu, X.; Xiong, J.; Liang, Q. Fault diagnosis of rotation machinery based on support vector machine optimized by quantum genetic algorithm. IEEE Access 2018, 6, 33583–33588. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q.; Wang, K.; Wang, J.; Zhou, T.; Zhang, Y. Optimal dissolved gas ratios selected by genetic algorithm for power transformer fault diagnosis based on support vector machine. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1198–1206. [Google Scholar] [CrossRef]
- Qi, W. Fuzzy fault diagnosis based on fuzzy robust v-support vector classifier and modified genetic algorithm. Expert Syst. Appl. 2011, 38, 4882–4888. [Google Scholar]
- Song, G.M.; Wang, H.J.; Liu, H.; Jiang, S.Y. Analog Circuit Fault Diagnosis Using Lifting Wavelet Transform and SVM. J. Electron. Meas. Instrum. 2010, 24, 17–22. [Google Scholar] [CrossRef]
- Cheng, Y.; Yuan, H.; Liu, H.; Lu, C. Fault diagnosis for rolling bearing based on SIFT-KPCA and SVM. Eng. Computation 2017, 34, 53–65. [Google Scholar] [CrossRef]
- Ge, J.; Niu, T.; Xu, D.; Yin, G.; Wang, Y. A rolling bearing fault diagnosis method based on EEMD-WSST signal reconstruction and multi-scale entropy. Entropy 2020, 22, 290. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Two-stream convolutional network for action recognition in videos. Adv. Neural Inf. Proc. Syst. 2014, 27, 568–576. [Google Scholar]
- Bagheri, M.A.; Hu, G.; Gao, Q.; Escalera, S. A framework of multi-classifier fusion for human action recognition. In Proceedings of the 2014 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; pp. 1260–1265. [Google Scholar]
- Chen, Z.; Jin, T.; Zheng, X. An innovative method-based CEEMDAN–IGWO–GRU hybrid algorithm for short-term load forecasting. Electr. Eng. 2022, 5, 3137–3156. [Google Scholar] [CrossRef]

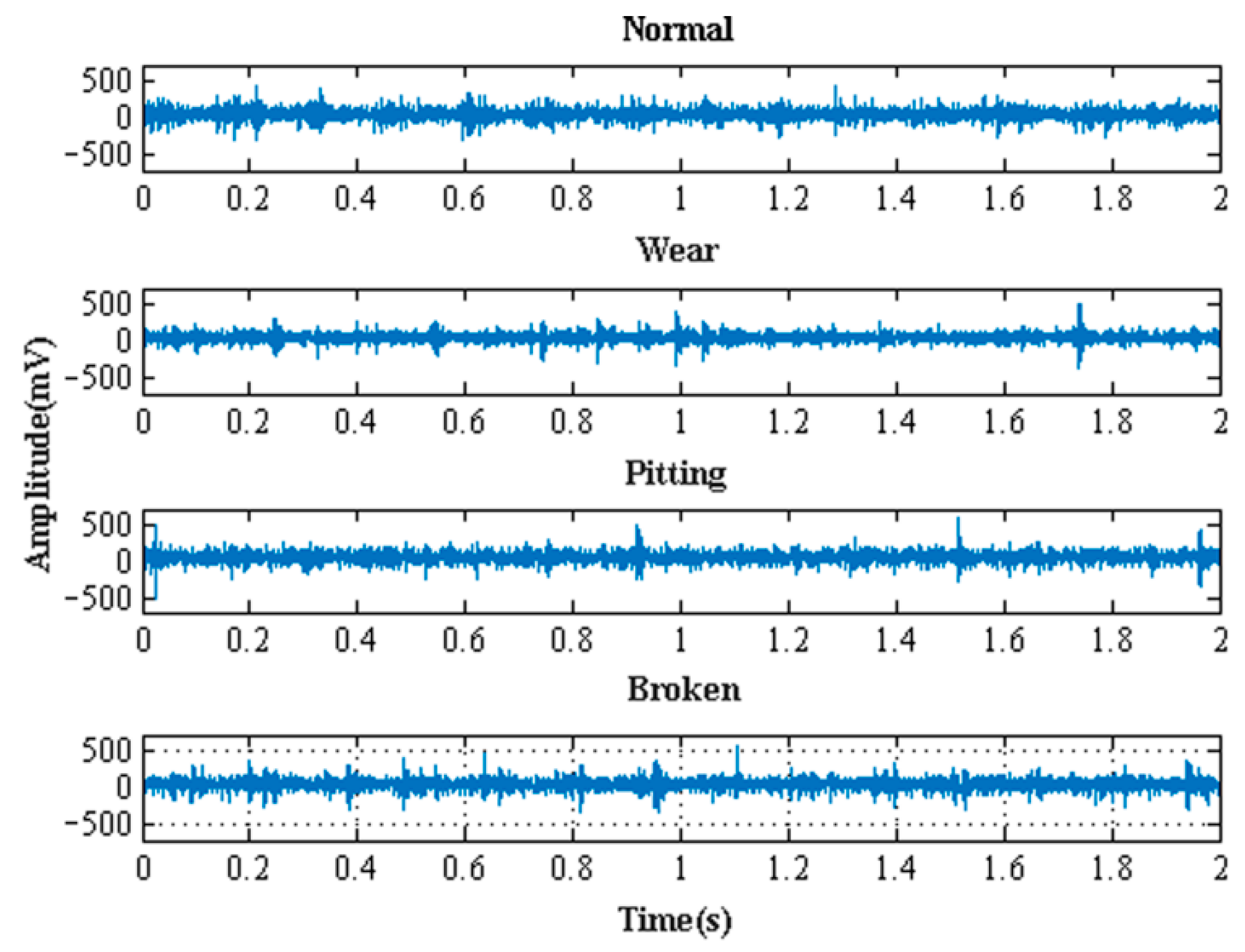
| Type | Gearbox Status | Data Length | Motor Speed (rpm) | Sampling Frequency (kHz) | Number of Data Groups | Expected Output |
|---|---|---|---|---|---|---|
| 1 | Normal | 1024 | 900 | 6 | 1500 | 0 |
| 2 | Wear | 1024 | 900 | 6 | 1500 | 1 |
| 3 | pitting | 1024 | 900 | 6 | 1500 | 2 |
| 4 | Broken | 1024 | 900 | 6 | 1500 | 3 |
| Layer | Kernel Size | Step | Output Size |
|---|---|---|---|
| Conv1 | 1 × 16 | 1 × 4 | 64 × 256 |
| Max Pooling1 | 1 × 2 | 1 × 2 | 64 × 128 |
| Conv2 | 1 × 8 | 1 × 2 | 64 × 64 |
| Max Pooling2 | 1 × 2 | 1 × 2 | 64 × 32 |
| Conv3 | 1 × 4 | 1 × 2 | 32 × 16 |
| Max Pooling3 | 1 × 2 | 1 × 1 | 32 × 16 |
| Conv4 | 1 × 2 | 1 × 1 | 16 × 16 |
| Max Pooling4 | 1 × 2 | 1 × 1 | 16 × 16 |
| FC1 | 1000 | 1000 | |
| FC2 | 10 | 10 |
| Number | Indicator Name | Equation | Annotation |
|---|---|---|---|
| 1 | Root mean square | xi is the ith value of the signal x; N is the total number of data | |
| 2 | Kurtosis | is the signal mean; is the standard deviation | |
| 3 | Peak factor | is the peak | |
| 4 | Impulse factor | is the average of the absolute values | |
| 5 | Waveform factor | is the root mean square value | |
| 6 | Margin factor | is the square root amplitude | |
| 7 | Barycenter frequency | is the power spectrum of the signal | |
| 8 | Root mean square frequency | is the power spectrum of the signal |
| State | Normal | Wear | Pitting | Broken | |
|---|---|---|---|---|---|
| Feature | |||||
| Root mean square | 0.3679 | 0.2077 | 0.2196 | 0.4183 | |
| Kurtosis | 0.0657 | 0.3004 | 0.0905 | 0.3676 | |
| Peak factor | 0.1702 | 0.3968 | 0.2359 | 0.5132 | |
| Impulse factor | 0.1772 | 0.3688 | 0.2176 | 0.4937 | |
| Waveform factor | 0.3089 | 0.2458 | 0.1861 | 0.3442 | |
| Margin factor | 0.1861 | 0.3595 | 0.2138 | 0.4862 | |
| Barycenter frequency | 0.5261 | 0.5451 | 0.4054 | 0.5020 | |
| Root mean square frequency | 0.5750 | 0.5749 | 0.4188 | 0.5235 | |
| Complemented feature 1 and 2 | 0 | 0 | 0 | 0 | |
| State | Normal | Wear | Pitting | Broken | |
|---|---|---|---|---|---|
| Feature | |||||
| f1 | 0.99997 | 0.00010 | 0.99999 | 0.99636 | |
| f2 | 0.00038 | 0.99992 | 0.98999 | 0.00005 | |
| f3 | 0.99998 | 0.99956 | 0.99997 | 0.00012 | |
| f4 | 0.00009 | 0.00044 | 0.00003 | 0.99981 | |
| f5 | 0.00039 | 0.99992 | 0.99341 | 0.00002 | |
| f6 | 0.99996 | 0.00022 | 0.99999 | 0.99947 | |
| f7 | 0.99940 | 0.00014 | 0.99999 | 0.00006 | |
| f8 | 0.00283 | 0.00040 | 0.98495 | 0.99878 | |
| f9 | 0.99987 | 0.99994 | 0.00795 | 0.99799 | |
| f10 | 0.00170 | 0.99996 | 0.00002 | 0.99997 | |
| State | Normal | Wear | Pitting | Broken | |
|---|---|---|---|---|---|
| Feature | |||||
| d1 | 1.00213 | 0.30040 | 1.06542 | 1.00046 | |
| d2 | 0.36790 | 1.02126 | 1.07473 | 0.21960 | |
| d3 | 1.01436 | 1.07544 | 1.12397 | 0.23590 | |
| d4 | 0.17720 | 0.36880 | 0.49370 | 1.02322 | |
| d5 | 0.30890 | 1.02969 | 1.05135 | 0.18610 | |
| d6 | 1.01713 | 0.35950 | 1.11192 | 1.02208 | |
| d7 | 1.12942 | 0.54510 | 1.11892 | 0.40540 | |
| d8 | 0.57501 | 0.57490 | 1.11543 | 1.08303 | |
| d9 | 0.99987 | 0.99994 | 0.00795 | 0.99799 | |
| d10 | 0.00170 | 0.99996 | 0.00002 | 0.99997 | |
| Diagnosis Method | Time–Frequency Features + IPSO-SVM | 1DCNN-Softmax | 1DCNN-IPSO-SVM | Multi-Feature Fusion Model |
|---|---|---|---|---|
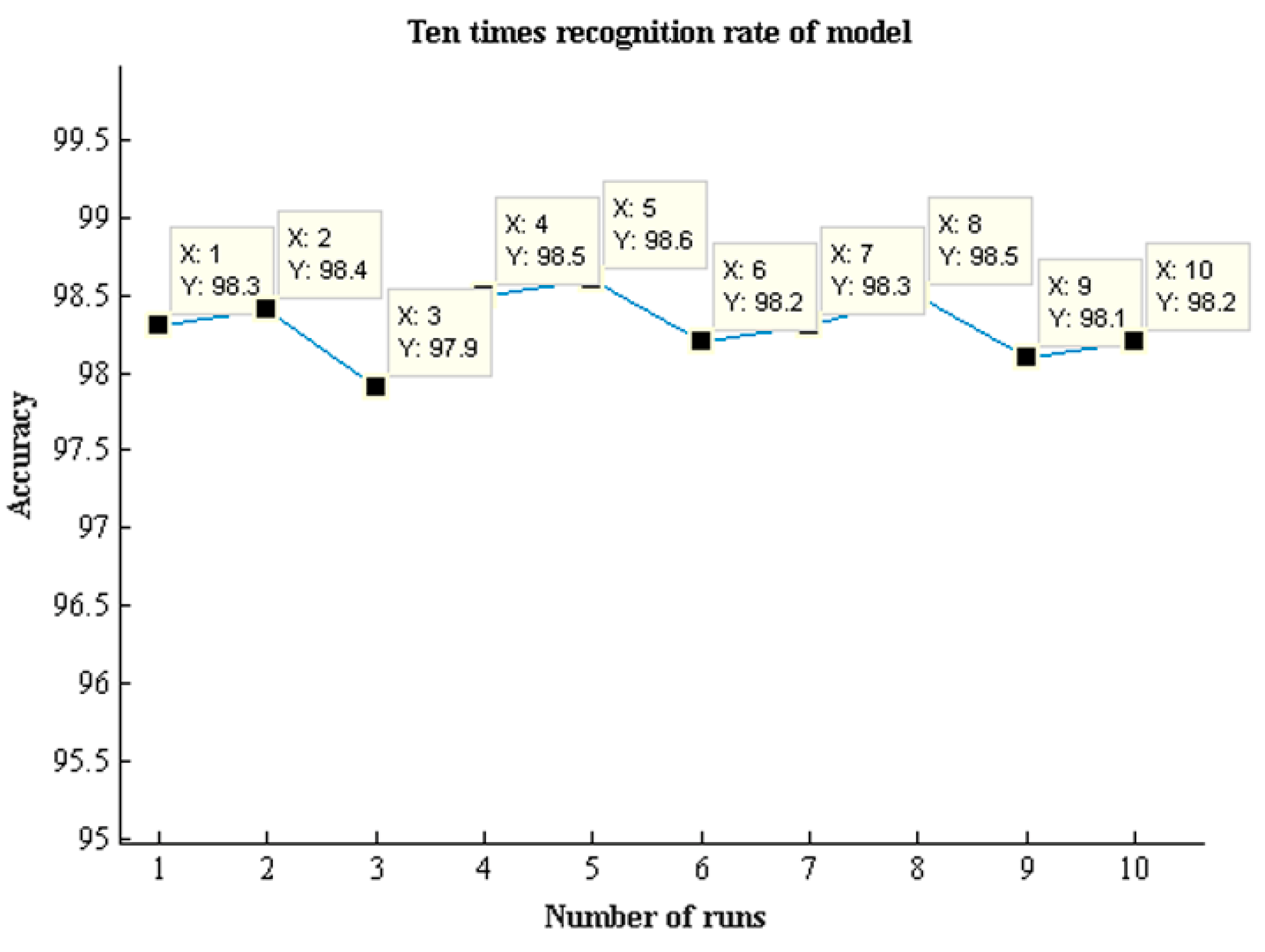
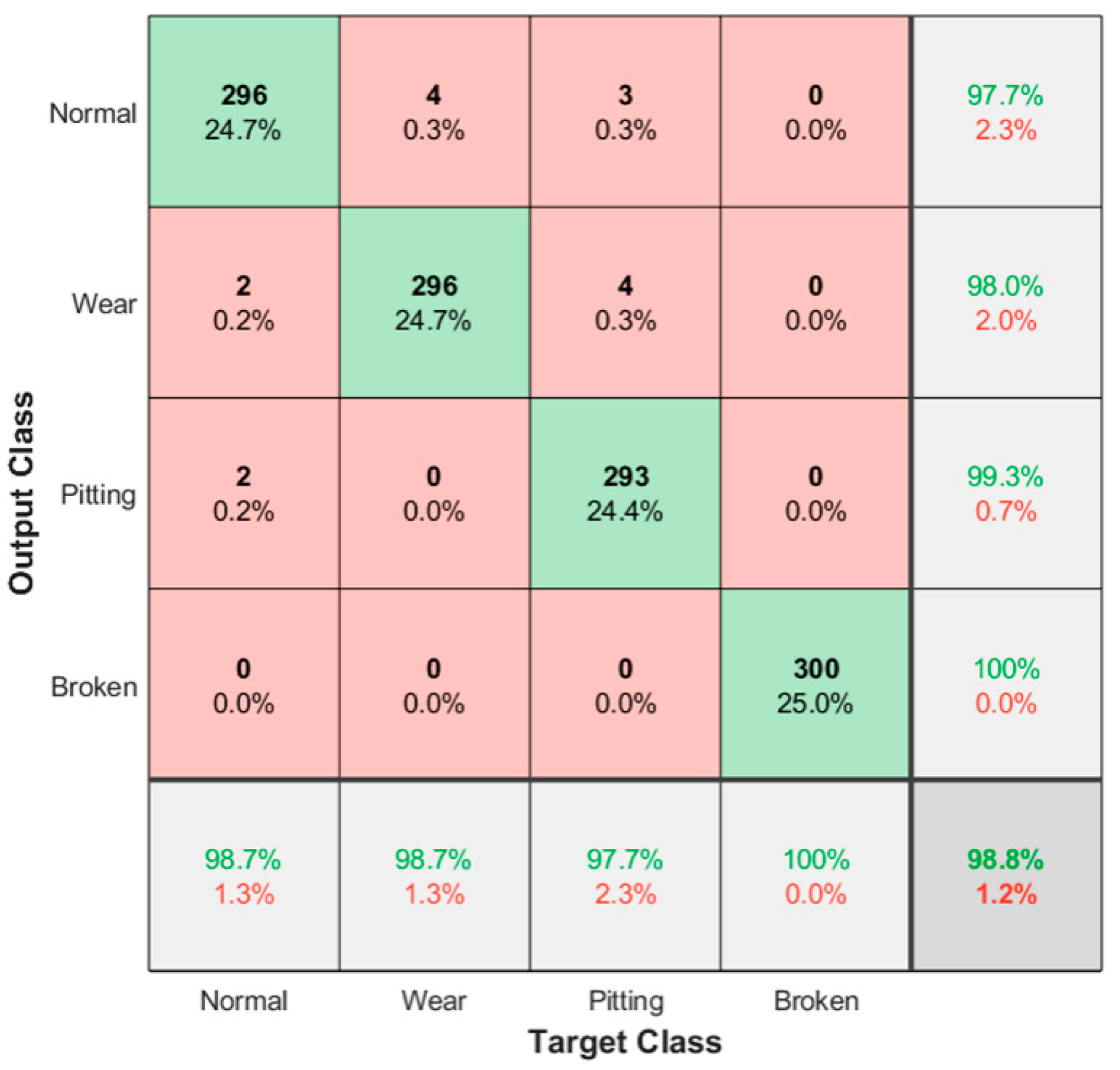
| Ten times average classification accuracy/% | 96.4 | 96.8 | 97.7 | 98.3 |
| standard deviation | 0.4190 | 0.4147 | 0.3553 | 0.2108 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, F.; Liu, H.; Dong, J.; Wang, G.; Wang, L.; Li, G. Research on the Gearbox Fault Diagnosis Method Based on Multi-Model Feature Fusion. Machines 2022, 10, 1186. https://doi.org/10.3390/machines10121186
Xie F, Liu H, Dong J, Wang G, Wang L, Li G. Research on the Gearbox Fault Diagnosis Method Based on Multi-Model Feature Fusion. Machines. 2022; 10(12):1186. https://doi.org/10.3390/machines10121186
Chicago/Turabian StyleXie, Fengyun, Hui Liu, Jiankun Dong, Gan Wang, Linglan Wang, and Gang Li. 2022. "Research on the Gearbox Fault Diagnosis Method Based on Multi-Model Feature Fusion" Machines 10, no. 12: 1186. https://doi.org/10.3390/machines10121186
APA StyleXie, F., Liu, H., Dong, J., Wang, G., Wang, L., & Li, G. (2022). Research on the Gearbox Fault Diagnosis Method Based on Multi-Model Feature Fusion. Machines, 10(12), 1186. https://doi.org/10.3390/machines10121186





