Reliable Design and Control Implementation of Parallel DC/DC Converter for High Power Charging System
Abstract
1. Introduction
2. Reliability Design and Control Method of the Charging System
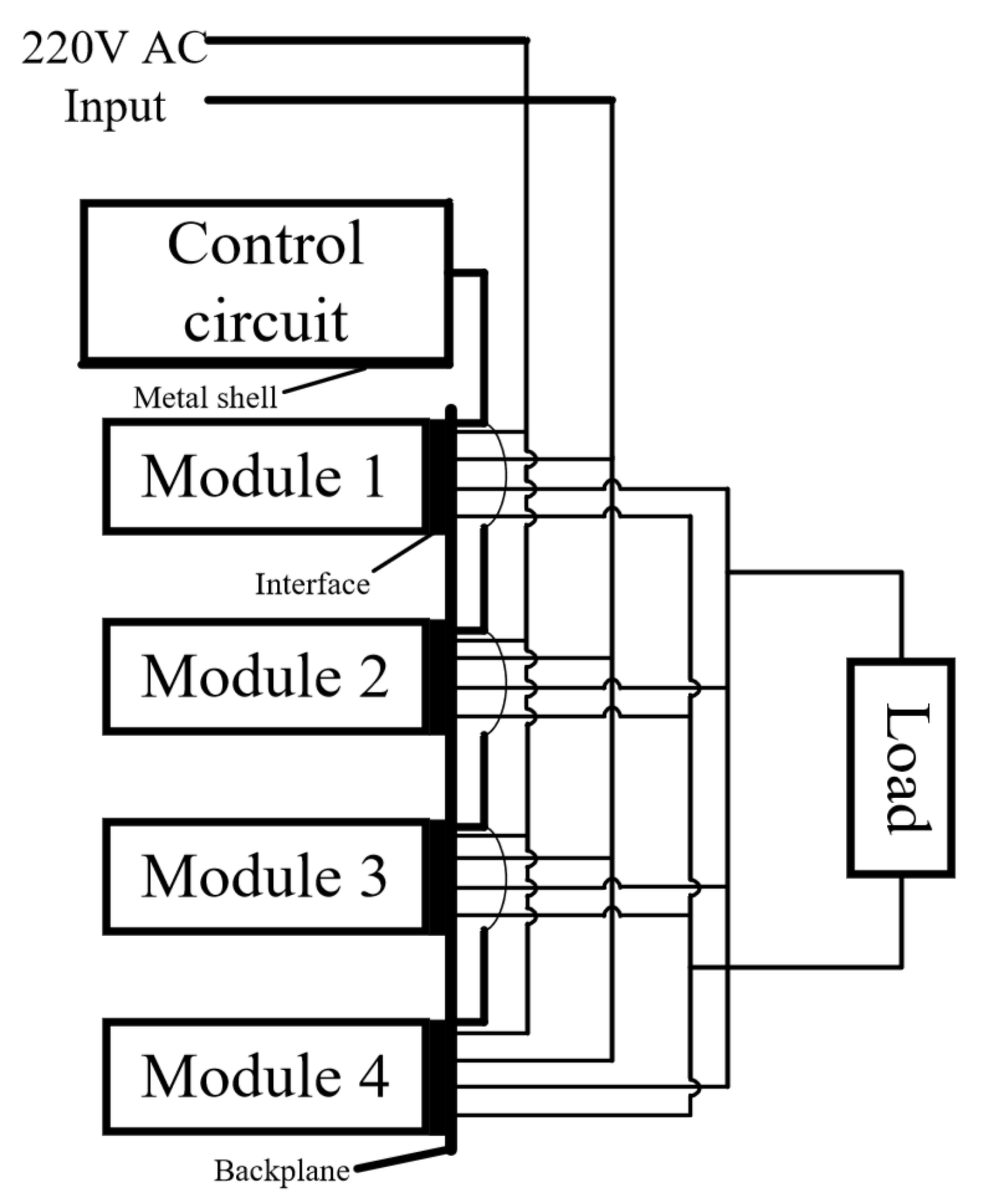
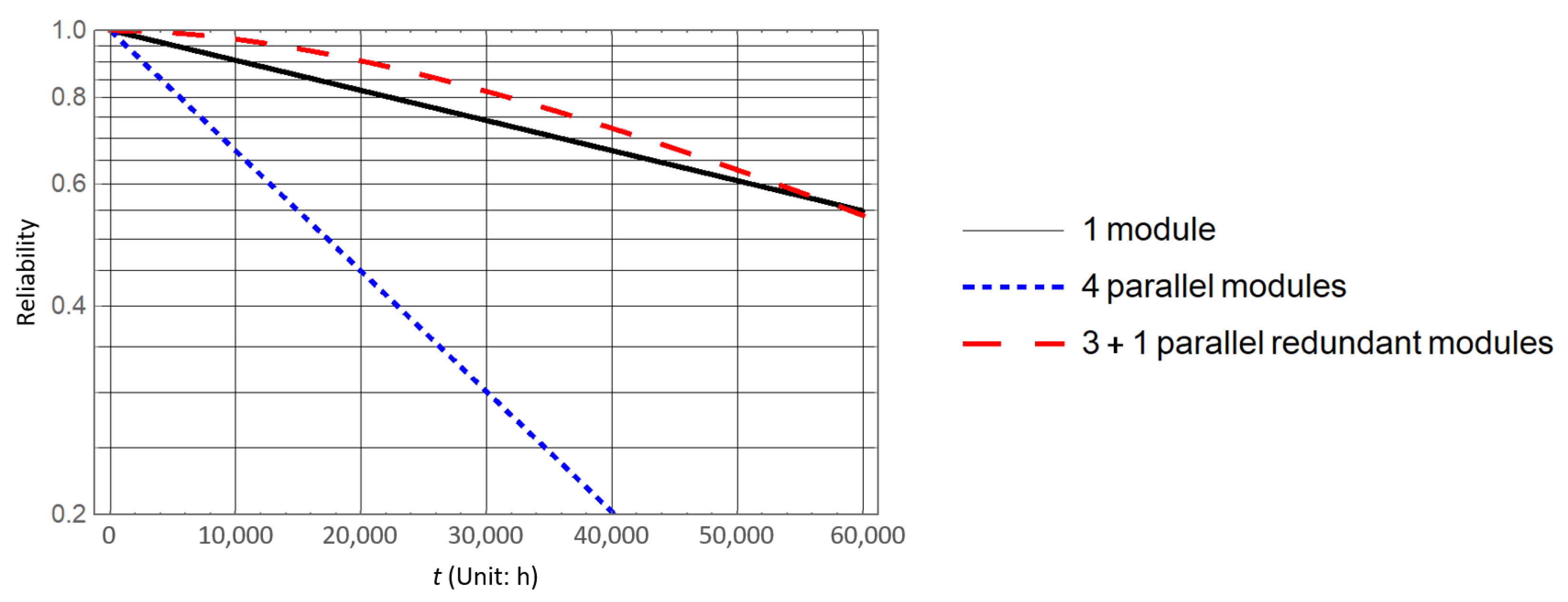
2.1. Reliability Design and Analysis of Charging System Structure
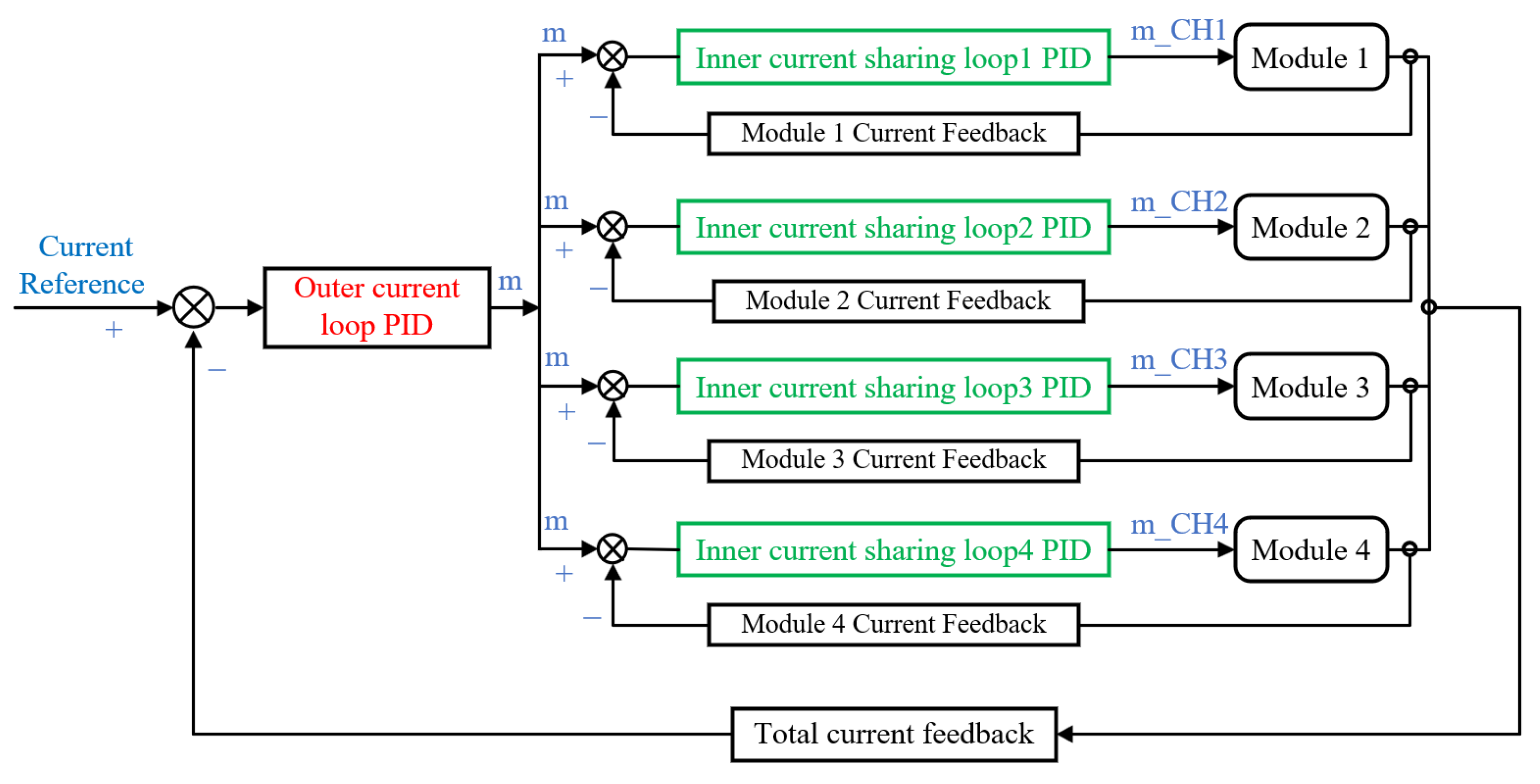
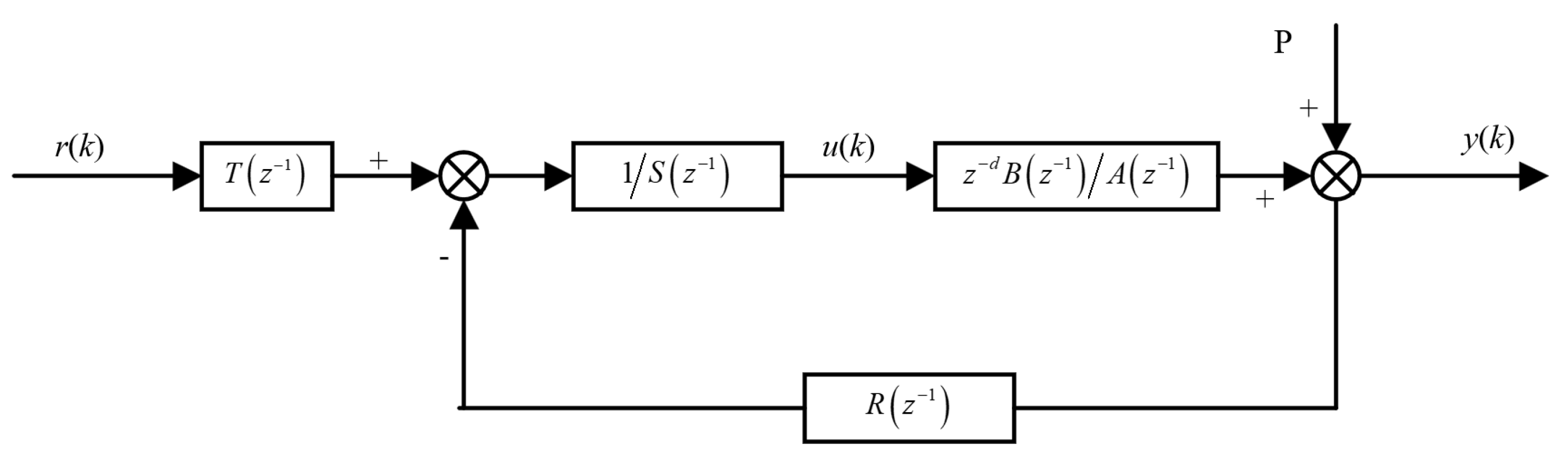
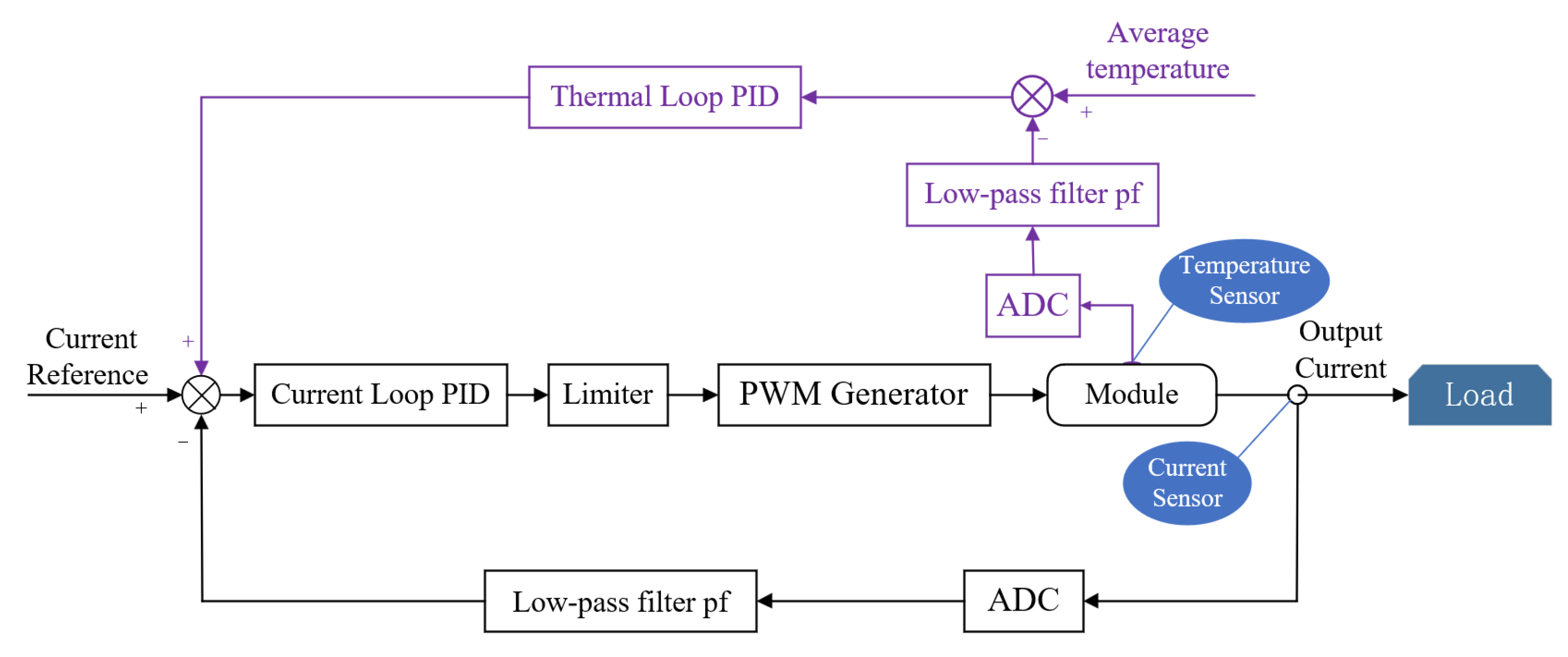
2.2. FPGA-Based Control Design for Redundancy and Fault Tolerance
3. Development of an FPGA-Based Control System
3.1. Introduction of the Control System
3.2. Implementation of the Main Control Logic
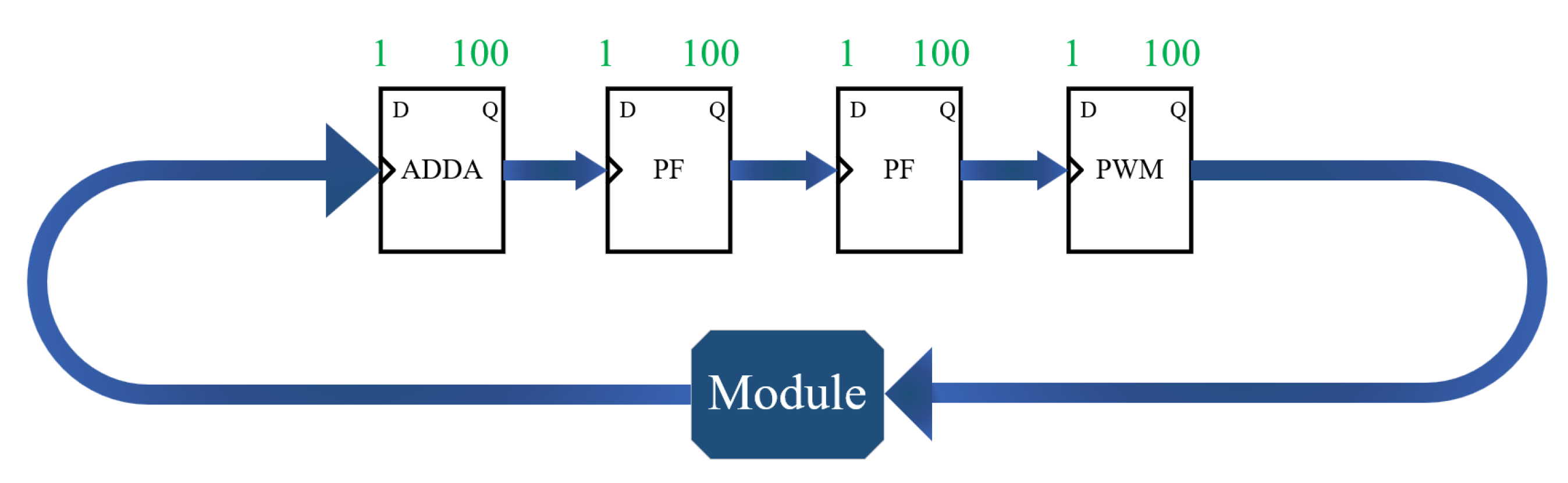
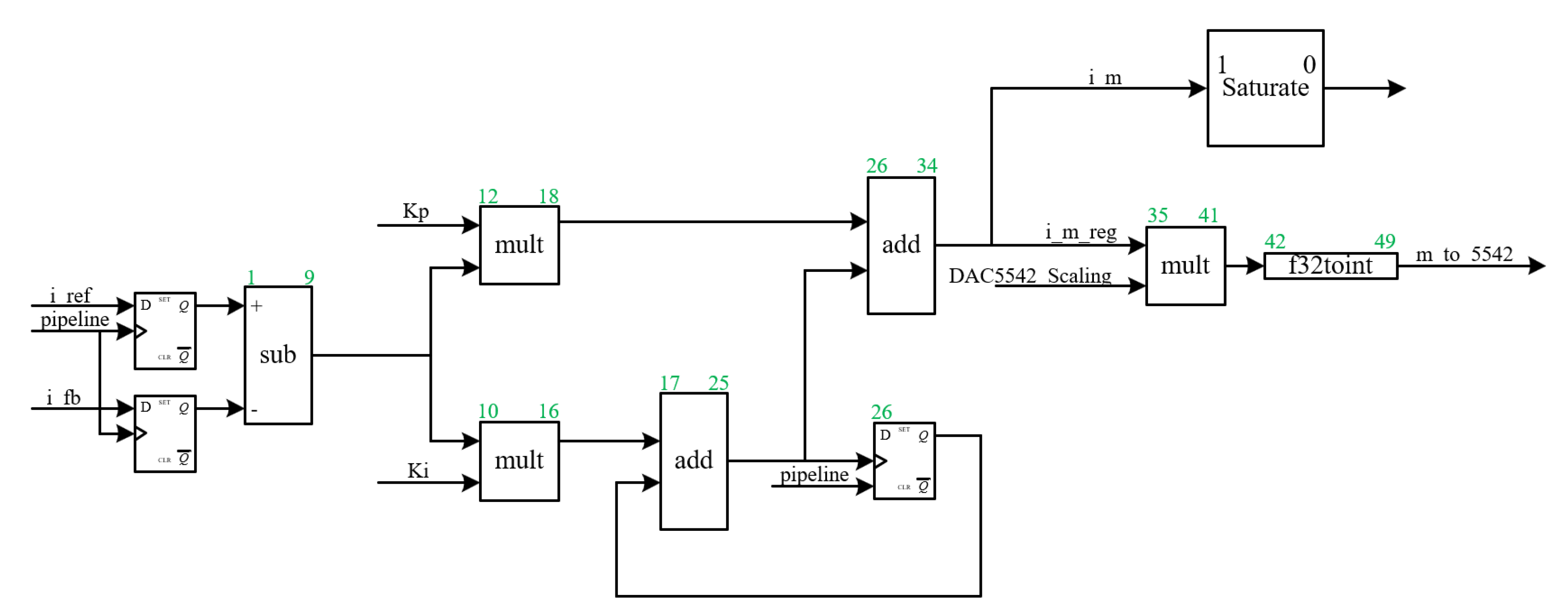
3.2.1. Main Parts of Control Logic and Pipeline Timing Processing
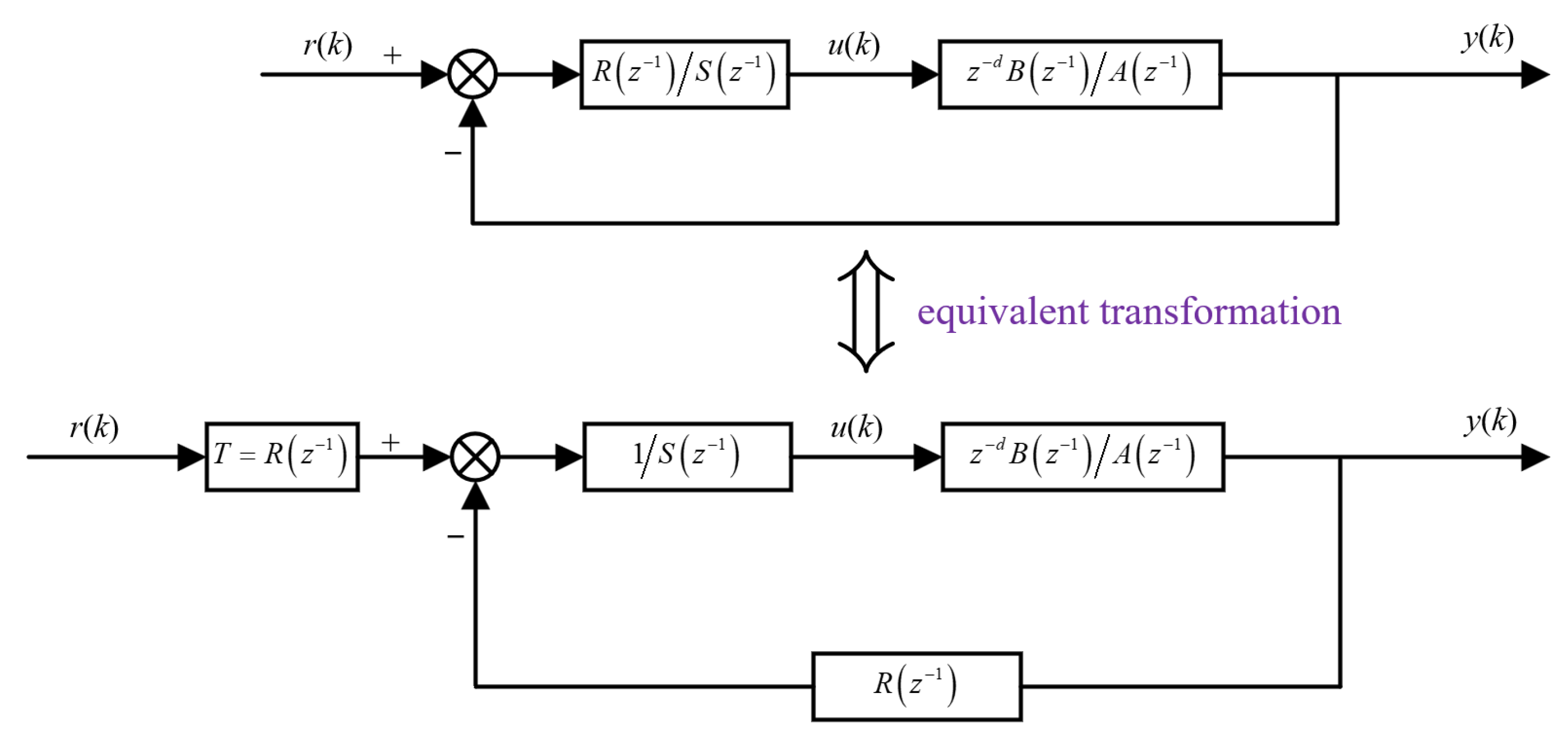
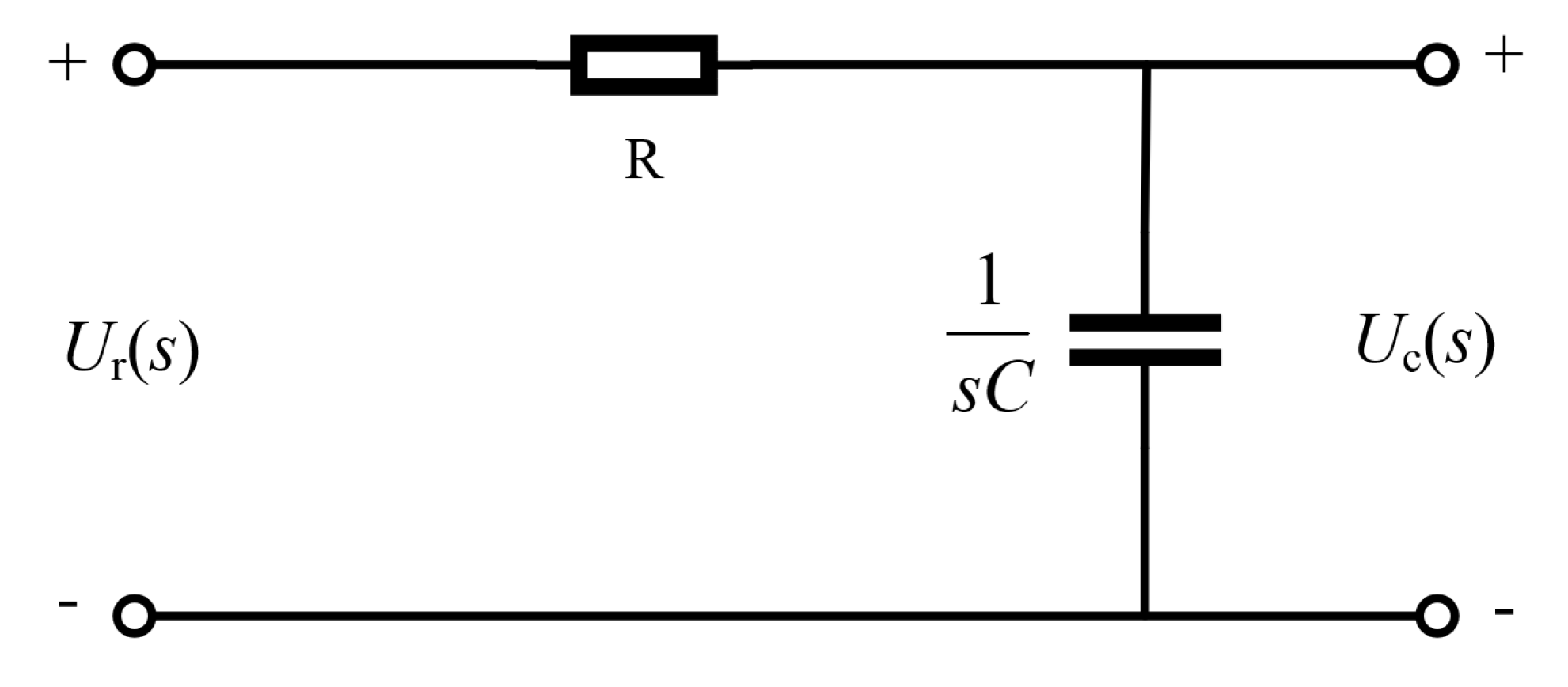
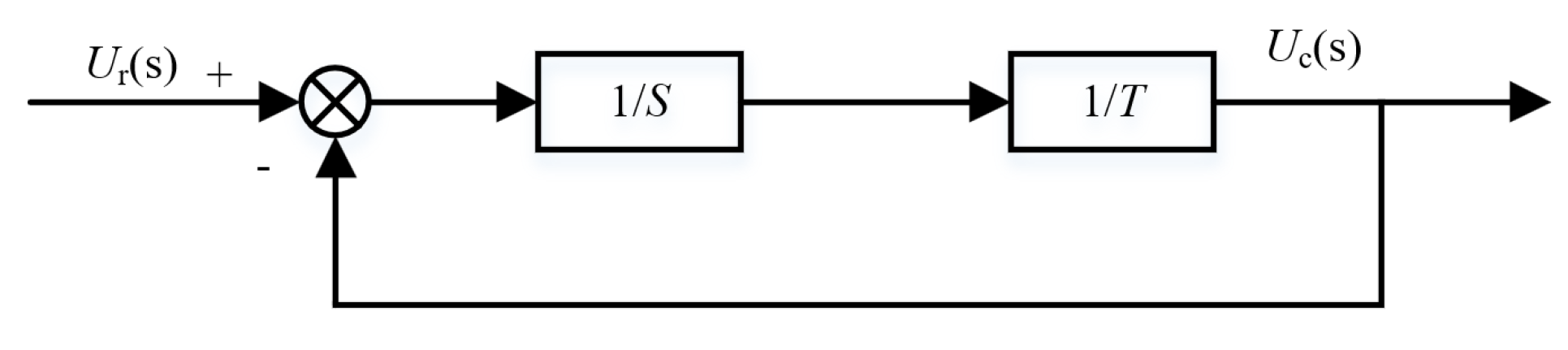
3.2.2. Logical Reasoning and Design of the Main Functions
4. Experimental Results
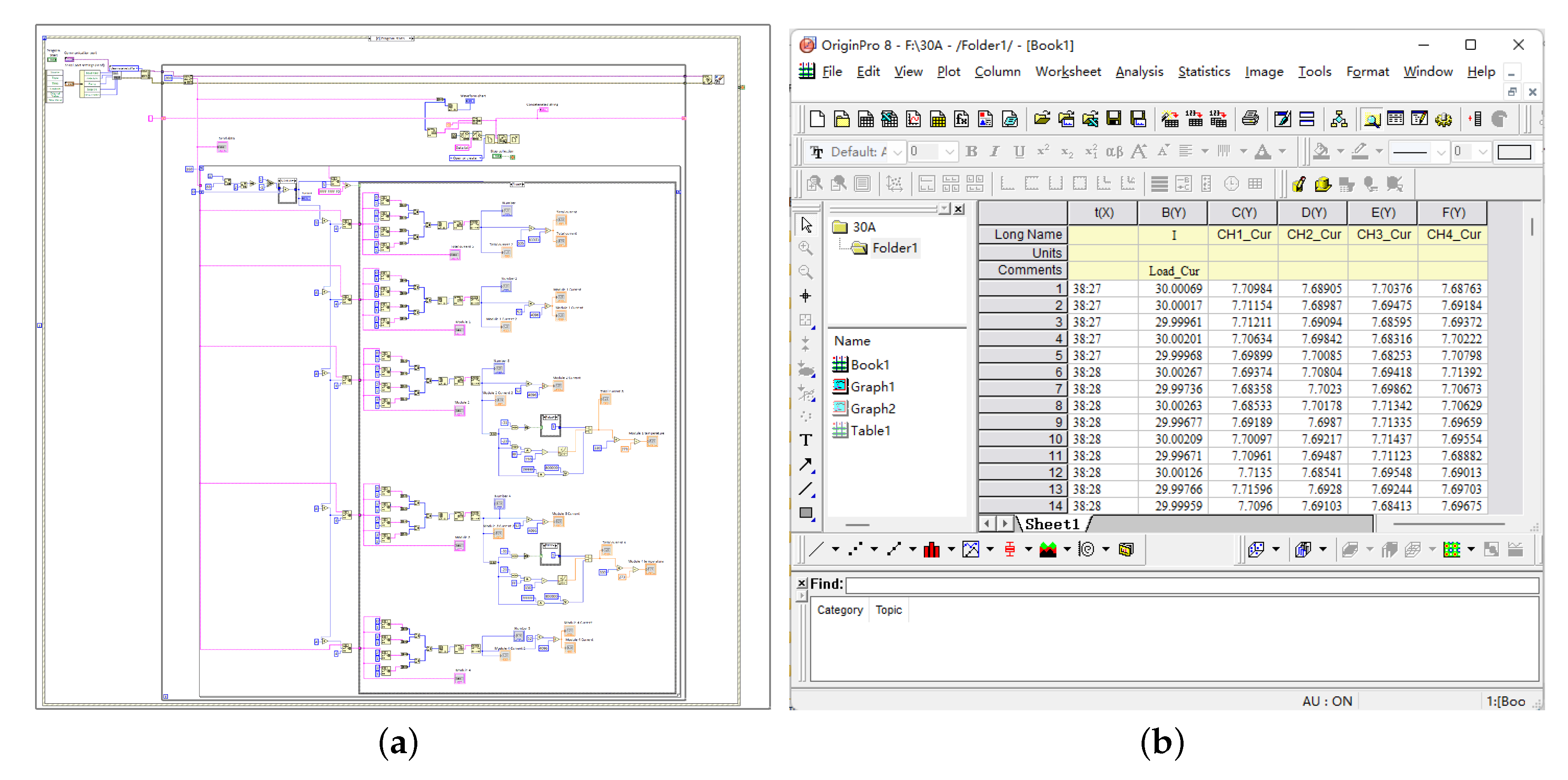
4.1. Introduction to the Experimental Platform
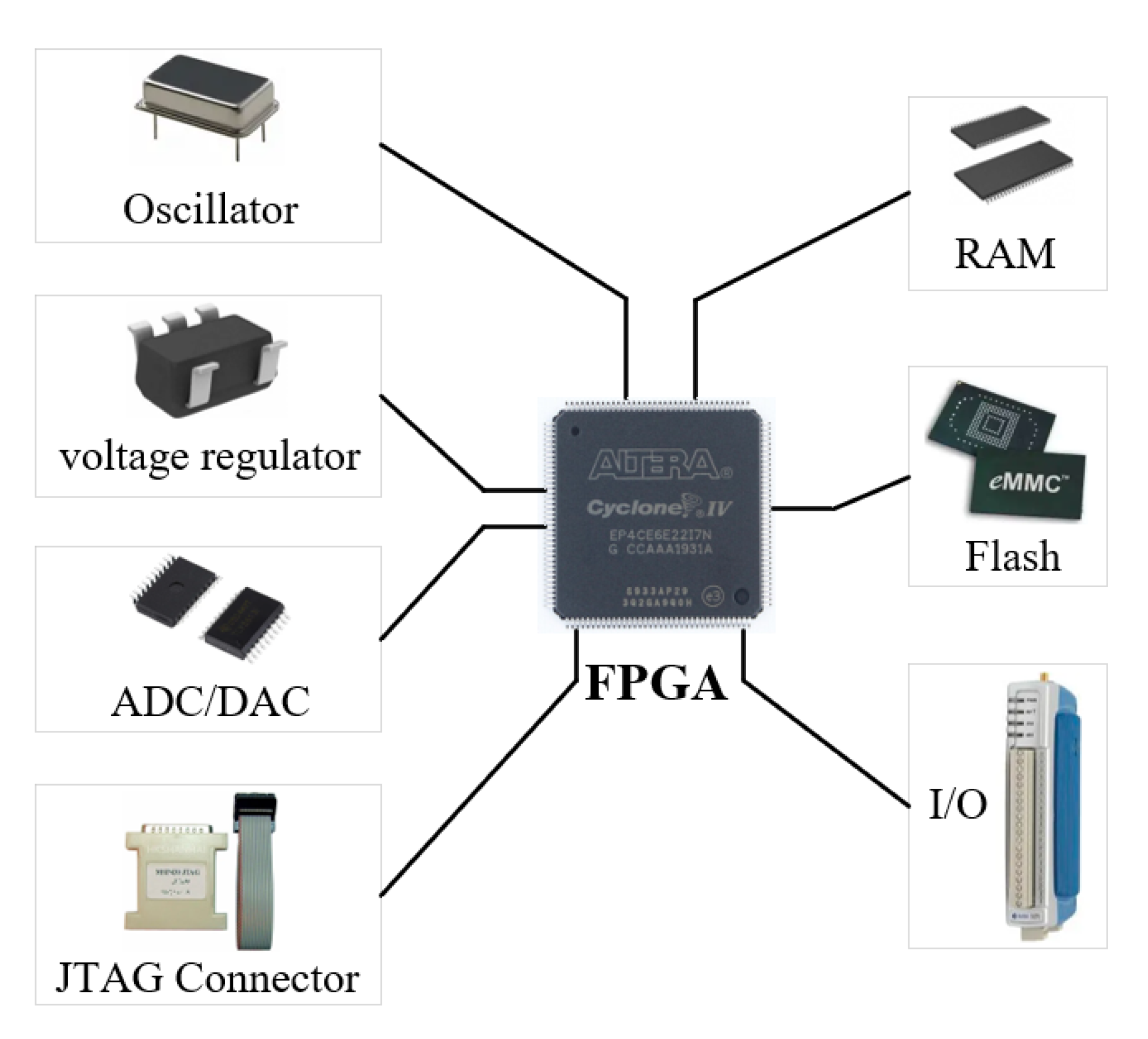
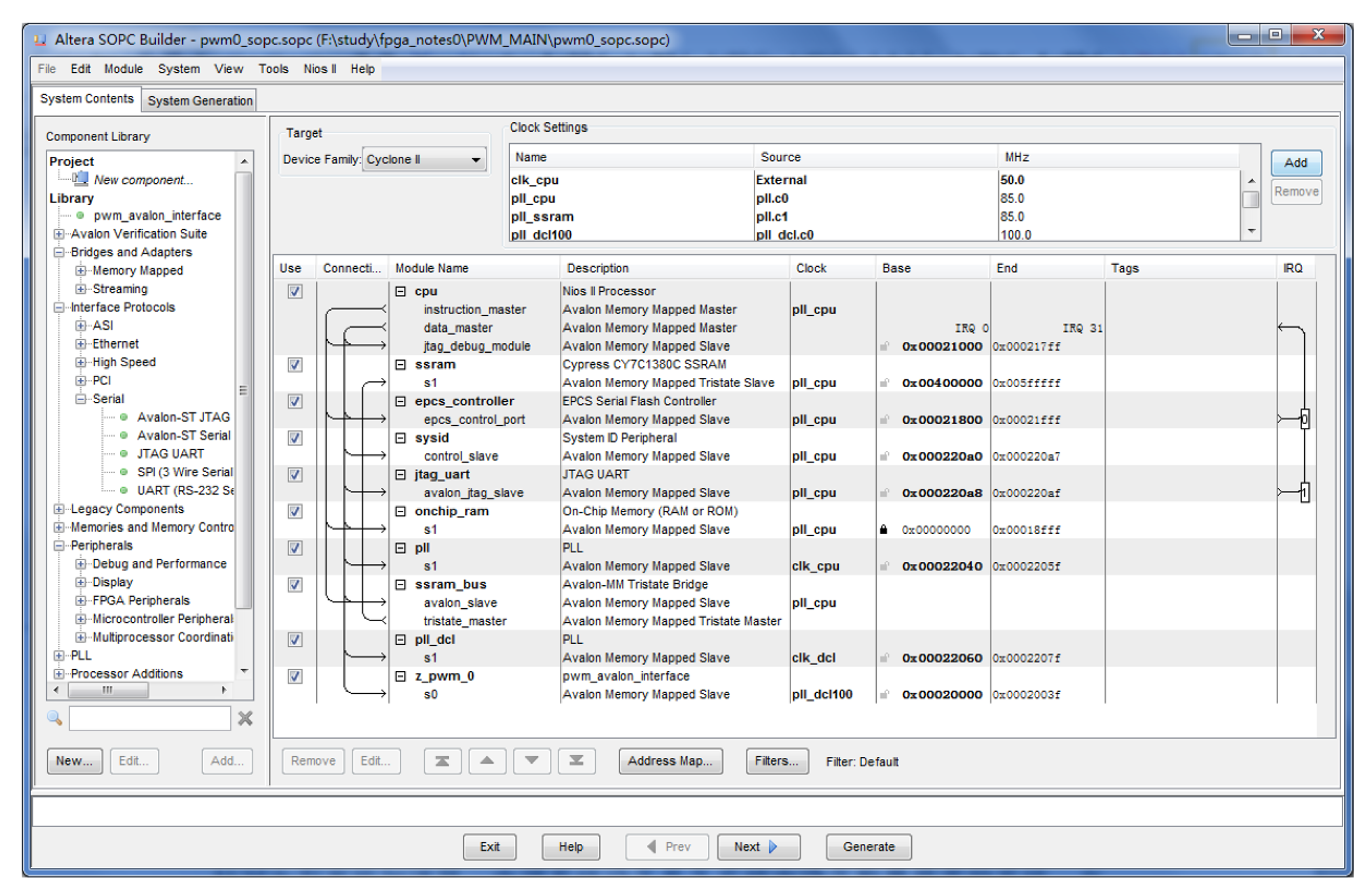
4.1.1. Hardware Platform
4.1.2. Software Platform
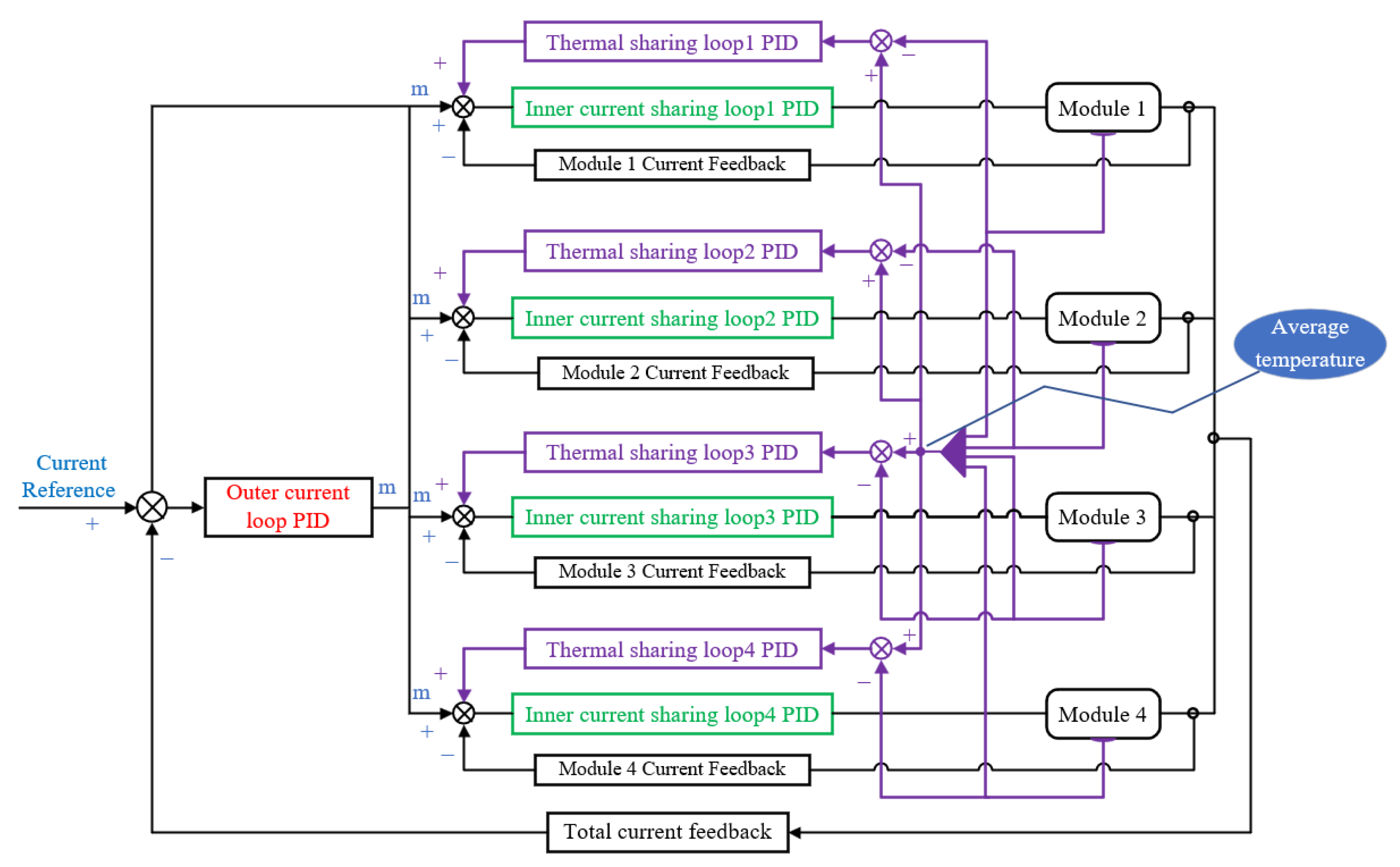
4.2. Current Sharing and Thermal Sharing Experiment
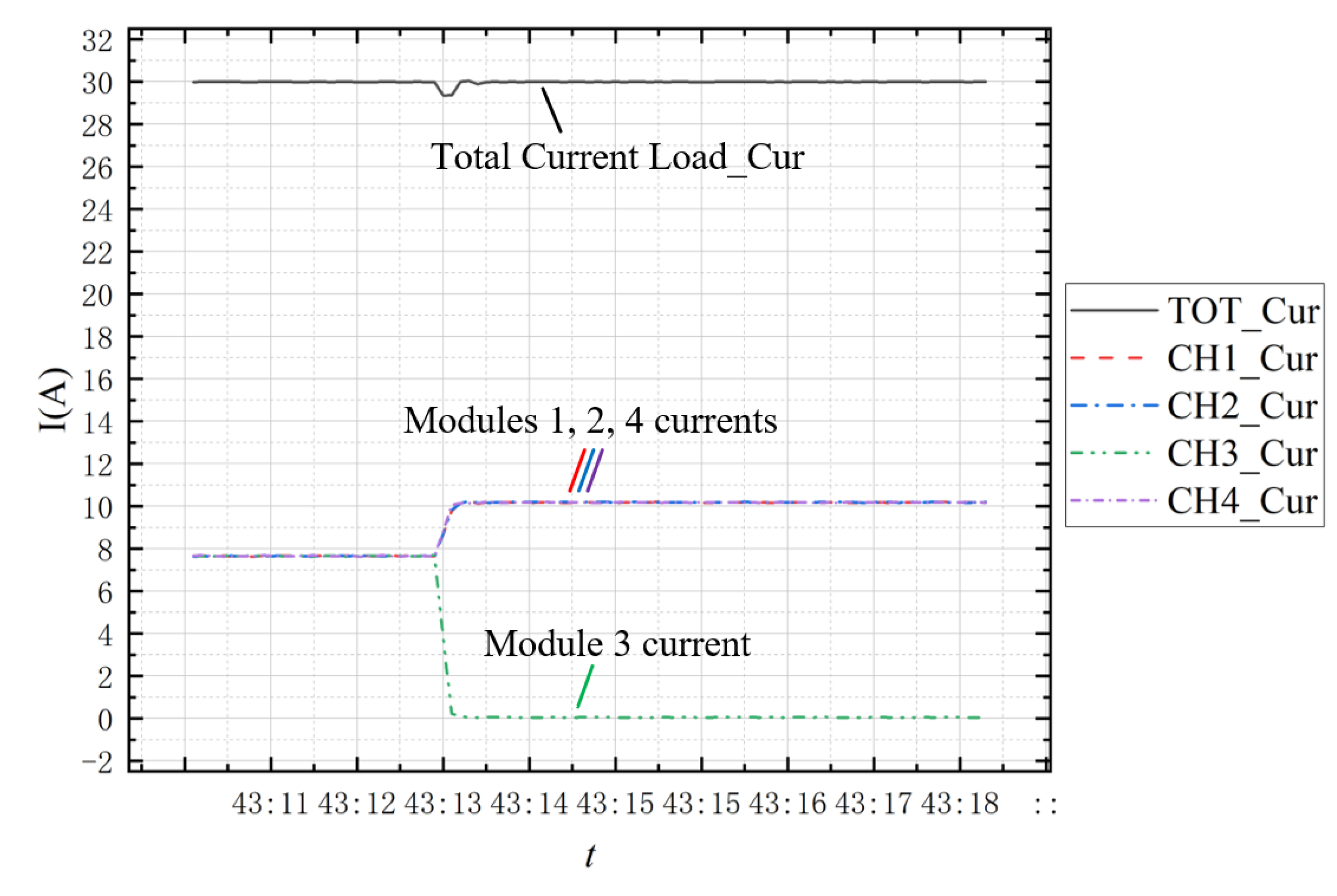
4.2.1. Current Sharing Mode
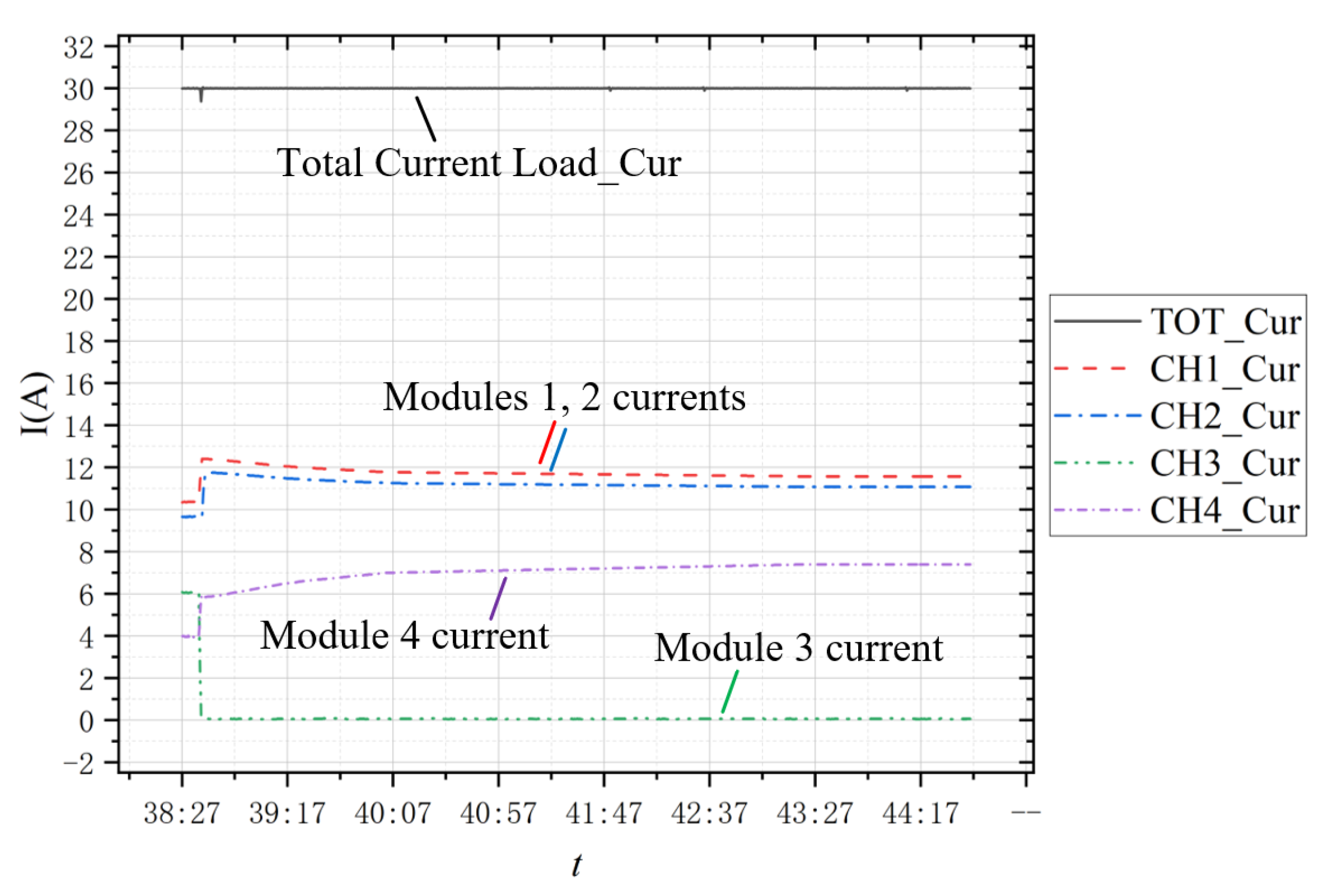
4.2.2. Thermal Sharing Mode
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Afshar, S.; Macedo, P.; Mohamed, F.; Disfani, V. Mobile charging stations for electric vehicles—A review. Renew. Sustain. Energy Rev. 2021, 152, 111654. [Google Scholar] [CrossRef]
- Haines, D.J. Practical Reliability Engineering - Fifth edition. Aeronaut. J. 2012, 116, 565–566. [Google Scholar] [CrossRef]
- Lüdeke, A. Accelerator Reliability Reporting at the Swiss Light Source. In Proceedings of the 5th International Particle Accelerator Conf. (IPAC’14), Dresden, Germany, 15–20 June 2014; pp. 3819–3821. [Google Scholar]
- Kalla, U.K.; Shukla, T. State of Art and Comprehensive Study on Charging Systems for Electric Vehicles. In Proceedings of the 2021 International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Virtual, 21–23 January 2021; pp. 1–6. [Google Scholar]
- Piasecki, S.; Zaleski, J.; Jasinski, M.; Bachman, S.; Turzyński, M. Analysis of AC/DC/DC Converter Modules for Direct Current Fast-Charging Applications. Energies 2021, 14, 6369. [Google Scholar] [CrossRef]
- Rahmani, F.; Niknejad, P.; Agarwal, T.; Barzegaran, M. Gallium nitride inverter design with compatible snubber circuits for implementing wireless charging of electric vehicle batteries. Machines 2020, 8, 56. [Google Scholar] [CrossRef]
- Wang, B.; Dehghanian, P.; Wang, S.; Mitolo, M. Electrical safety considerations in large-scale electric vehicle charging stations. IEEE Trans. Ind. Appl. 2019, 55, 6603–6612. [Google Scholar] [CrossRef]
- Kilic, E.; Akil, M.; Bayindir, R.; Sebati, A.; Malek, R. Electric Vehicles Charging Management with Monte Carlo Simulation. In Proceedings of the 2021 10th International Conference on Renewable Energy Research and Application (ICRERA), Ankara, Turkey, 26–29 September 2021; pp. 423–427. [Google Scholar]
- Bhatti, A.R.; Salam, Z. A rule-based energy management scheme for uninterrupted electric vehicles charging at constant price using photovoltaic-grid system. Renew. Energy 2018, 125, 384–400. [Google Scholar] [CrossRef]
- Qin, W.; Wu, X.; Zhang, J. A family of DC transformer (DCX) topologies based on new ZVZCS cells with DC resonant capacitance. IEEE Trans. Power Electron. 2016, 32, 2822–2834. [Google Scholar] [CrossRef]
- Qi, F.; Wang, Z.; Wu, Y.; Zuk, P. GaN FETs Enable High Frequency Dual Active Bridge Converters for Bi-directional Battery Chargers. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 1038–1043. [Google Scholar]
- Choi, H.-J.; Jung, S.-H.; Jung, J.-H. A Novel Switching Algorithm to improve Efficiency at light load conditions for Three-Phase DAB Converter in LVDC Application. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 383–387. [Google Scholar]
- Zhang, W.; Xu, D. Fault analysis and fault-tolerant design for parallel redundant inverter systems in case of IGBT short-circuit failures. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 2031–2041. [Google Scholar] [CrossRef]
- Kumar, G.K.; Elangovan, D. Review on fault-diagnosis and fault-tolerant for DC–DC converters. IET Power Electron. 2020, 13, 1–13. [Google Scholar] [CrossRef]
- Wang, H.; Pei, X.; Wu, Y.; Kang, Y. A general fault-tolerant operation strategy under switch fault for modular series–parallel DC–DC converter. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 872–884. [Google Scholar] [CrossRef]
- Bellomo, P.; Macnair, D.; Menlo, S. SLAC Next-Generation High Availability Power Supply; Accelerator Reliability Workshop: Menlo Park, CA, USA, 26–30 January 2009. [Google Scholar]
- Takahashi, T.; Onda, K.; Kanouda, A.; Sato, M.; Horie, H.; Hayashi, K. Power Supply System for Supplying Electric Power to a Load through Plural Converters. U.S. Patent 5,768,117, 16 June 1998. [Google Scholar]
- Choudhary, V.; Ledezma, E.; Ayyanar, R.; Button, R.M. Fault tolerant circuit topology and control method for input-series and output-parallel modular DC-DC converters. IEEE Trans. Power Electron. 2008, 23, 402–411. [Google Scholar] [CrossRef]
- Frivaldsky, M.; Spanik, P.; Morgos, J.; Pridala, M. Control strategy proposal for modular architecture of power supply utilizing LCCT converter. Energies 2018, 11, 3327. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, J.; Shi, Y.; Yang, J.; Zhang, J.; You, X. Mode analysis and fault-tolerant method of open-circuit fault for a dual active-bridge DC–DC converter. IEEE Trans. Ind. Electron. 2019, 67, 6916–6926. [Google Scholar] [CrossRef]
- Gosselin, C.; Schreiber, L.-T. Redundancy in parallel mechanisms: A review. Appl. Mech. Rev. 2018, 70, 010802. [Google Scholar] [CrossRef]
- Zhang, Z.; Meyer, E.; Liu, Y.-F.; Sen, P.C. A nonisolated ZVS self-driven current tripler topology for low-voltage and high-current applications. IEEE Trans. Power Electron. 2010, 26, 512–522. [Google Scholar] [CrossRef]
- Batarseh, I.; Siri, K.; Lee, H. Investigation of the output droop characteristics of parallel-connnected DC-DC converters. In Proceedings of the 1994 Power Electronics Specialist Conference-PESC’94, Taipei, Taiwan, 20–24 June 1994; pp. 1342–1351. [Google Scholar]
- Petruzziello, F.; Ziogas, P.; Joos, G. A novel approach to paralleling of power converter units with true redundancy. In Proceedings of the 21st Annual IEEE Conference on Power Electronics Specialists, San Antonio, TX, USA, 11–14 June 1990; pp. 808–813. [Google Scholar]
- Thottuvelil, V.J.; Verghese, G.C. Stability analysis of paralleled DC/DC converters with active current sharing. In Proceedings of the PESC Record, 27th Annual IEEE Power Electronics Specialists Conference, Baveno, Italy, 23–27 June 1996; pp. 1080–1086. [Google Scholar]
- Le Bolloch, M.; Cousineai, M.; Meynard, T. New masterless modular current-sharing technique for DC/DC parallel converters. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, Macedonia, 6–8 September 2010; pp. 73–80. [Google Scholar]
- Du, H.; Jiang, C.; Wen, G.; Zhu, W.; Cheng, Y. Current sharing control for parallel DC–DC buck converters based on finite-time control technique. IEEE Trans. Ind. Inform. 2018, 15, 2186–2198. [Google Scholar] [CrossRef]
- Effler, S.; Halton, M.; Rinne, K. Efficiency-based current distribution scheme for scalable digital power converters. IEEE Trans. Power Electron. 2010, 26, 1261–1269. [Google Scholar] [CrossRef]
- Fang, W.; Liu, X.-D.; Liu, S.-C.; Liu, Y.-F. A digital parallel current-mode control algorithm for DC–DC converters. IEEE Trans. Ind. Inform. 2014, 10, 2146–2153. [Google Scholar] [CrossRef]
- Khaligh, A.; D’Antonio, M. Global trends in high-power on-board chargers for electric vehicles. IEEE Trans. Veh. Technol. 2019, 68, 3306–3324. [Google Scholar] [CrossRef]
- ElMenshawy, M.; Massoud, A. Development of modular DC-DC converters for low-speed electric vehicles fast chargers. Alex. Eng. J. 2021, 60, 1067–1083. [Google Scholar] [CrossRef]
- Nesgaard, C.; Andersen, M.A. Efficiency improvement in redundant power systems by means of thermal load sharing. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, APEC’04, Anaheim, CA, USA, 22–26 February 2004; pp. 433–439. [Google Scholar]
- Blanks, H.S. Reliability prediction: A constructive critique of MIL-HDBK-217E. Qual. Reliab. Eng. Int. 1988, 4, 227–234. [Google Scholar] [CrossRef]
- Andresen, M.; Ma, K.; Buticchi, G.; Falck, J.; Blaabjerg, F.; Liserre, M. Junction temperature control for more reliable power electronics. IEEE Trans. Power Electron. 2017, 33, 765–776. [Google Scholar] [CrossRef]
- Birk, J.; Andresen, B. Parallel-connected converters for optimizing efficiency, reliability and grid harmonics in a wind turbine. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–7. [Google Scholar]
- Lee, S.W.; Lee, H.K. Reliability prediction system based on the failure rate model for electronic components. J. Mech. Sci. Technol. 2008, 22, 957–964. [Google Scholar] [CrossRef]
- Cu, P.X.; Bui, H.A. Methodologies for reliability prediction of electronic component in military vehicles. Adv. Mil. Technol. 2019, 14, 89–98. [Google Scholar] [CrossRef]
- Abdurraqeeb, A.M.; Al-Shamma’a, A.A.; Alkuhayli, A.; Noman, A.M.; Addoweesh, K.E. RST Digital Robust Control for DC/DC Buck Converter Feeding Constant Power Load. Mathematics 2022, 10, 1782. [Google Scholar] [CrossRef]
- Lam, B.; Bellomo, P.; De Lira, A.; MacNair, D. ILC-ATF2 dc-magnet power supplies. In Proceedings of the 2007 IEEE Particle Accelerator Conference (PAC), Albuquerque, NM, USA, 25–29 June 2007; pp. 569–571. [Google Scholar]
- Wang, B.-S.; Lin, K.-B. N+ 1 redundancy power supply system by paralleling current converter modules with digital regulation control. In Proceedings of the IPAC2011, San Sebastián, Spain, 4–9 September 2011. [Google Scholar]
- Siemaszko, D.; Pittet, S. Failure tolerant operation and trimming principle in the CLIC main linac. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–8. [Google Scholar]
- Nesgaard, C.; Andersen, M.A. Optimized load sharing control by means of thermal reliability management. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No. 04CH37551), Aachen, Germany, 20–25 June 2004; pp. 4901–4906. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Xu, Y.; Rasol, J.; Hui, T.; Yuan, C.; Li, F. Reliable Design and Control Implementation of Parallel DC/DC Converter for High Power Charging System. Machines 2022, 10, 1162. https://doi.org/10.3390/machines10121162
Zhou Q, Xu Y, Rasol J, Hui T, Yuan C, Li F. Reliable Design and Control Implementation of Parallel DC/DC Converter for High Power Charging System. Machines. 2022; 10(12):1162. https://doi.org/10.3390/machines10121162
Chicago/Turabian StyleZhou, Qing, Yuelei Xu, Jarhinbek Rasol, Tian Hui, Chaofeng Yuan, and Fan Li. 2022. "Reliable Design and Control Implementation of Parallel DC/DC Converter for High Power Charging System" Machines 10, no. 12: 1162. https://doi.org/10.3390/machines10121162
APA StyleZhou, Q., Xu, Y., Rasol, J., Hui, T., Yuan, C., & Li, F. (2022). Reliable Design and Control Implementation of Parallel DC/DC Converter for High Power Charging System. Machines, 10(12), 1162. https://doi.org/10.3390/machines10121162





