Disturbance Observer-Based Sliding Mode Controller for Underwater Electro-Hydrostatic Actuator Affected by Seawater Pressure
Abstract
1. Introduction
2. Principles and Modeling
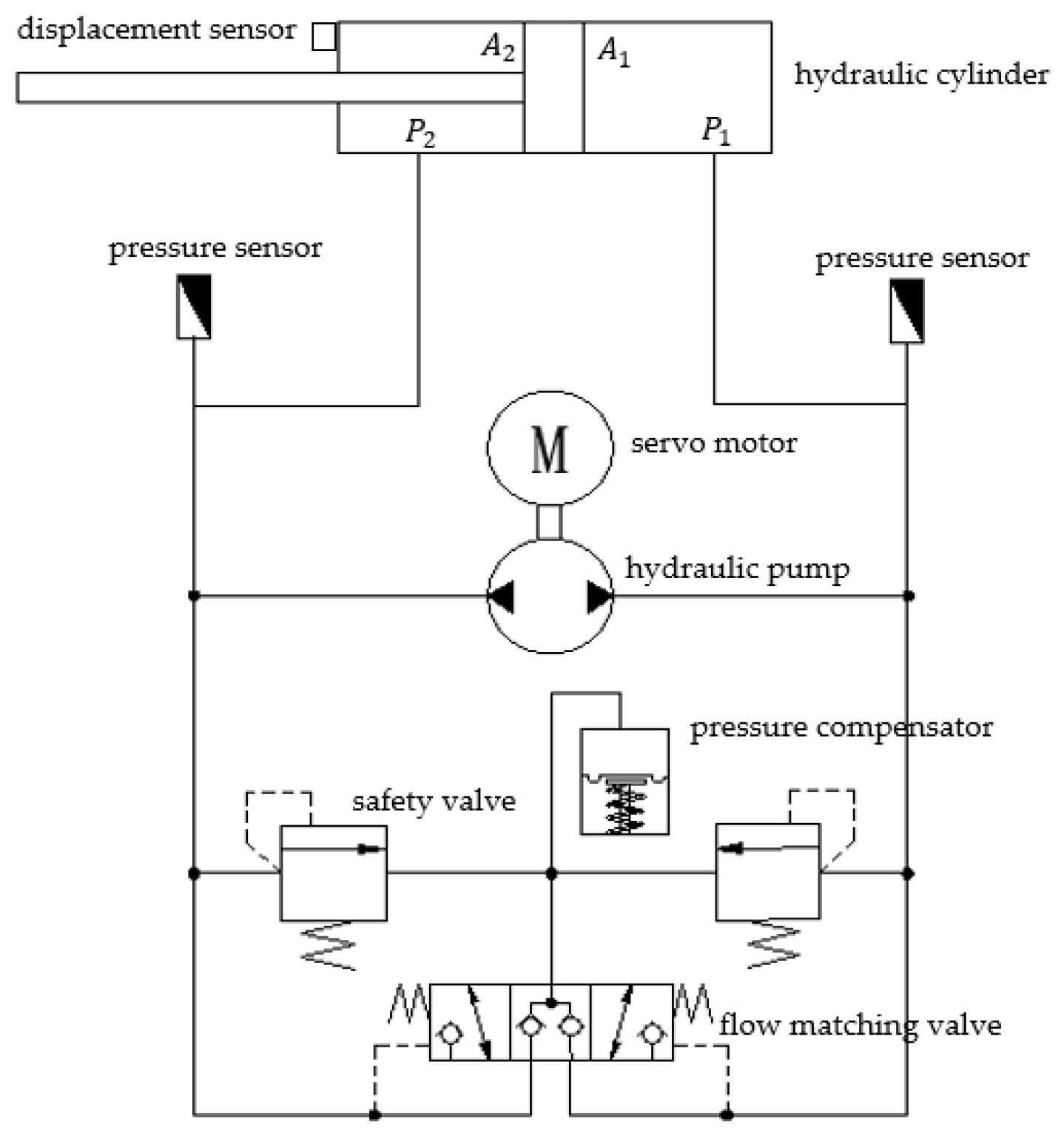
2.1. System Principles
2.2. System Modeling
2.3. System Formulation
3. Sliding Mode Control with Disturbance Observed
3.1. Disturbance Observer Design
3.2. Backstepping Sliding Mode Control (BSMC)
3.3. Backstepping Nonsingular Fast Terminal Sliding Mode Control Based on Hyperbolic Tangent Function (BNFTSM)
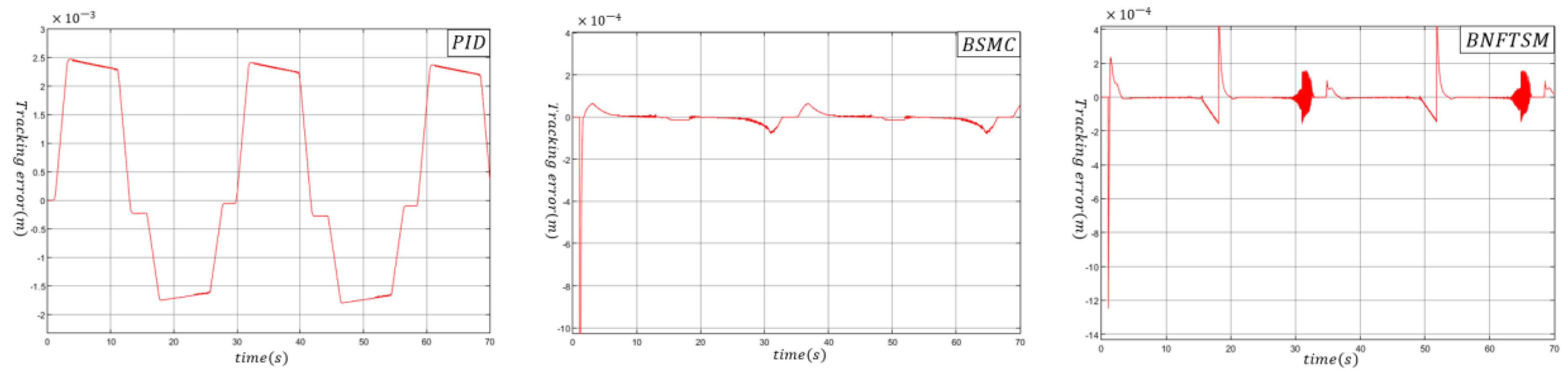
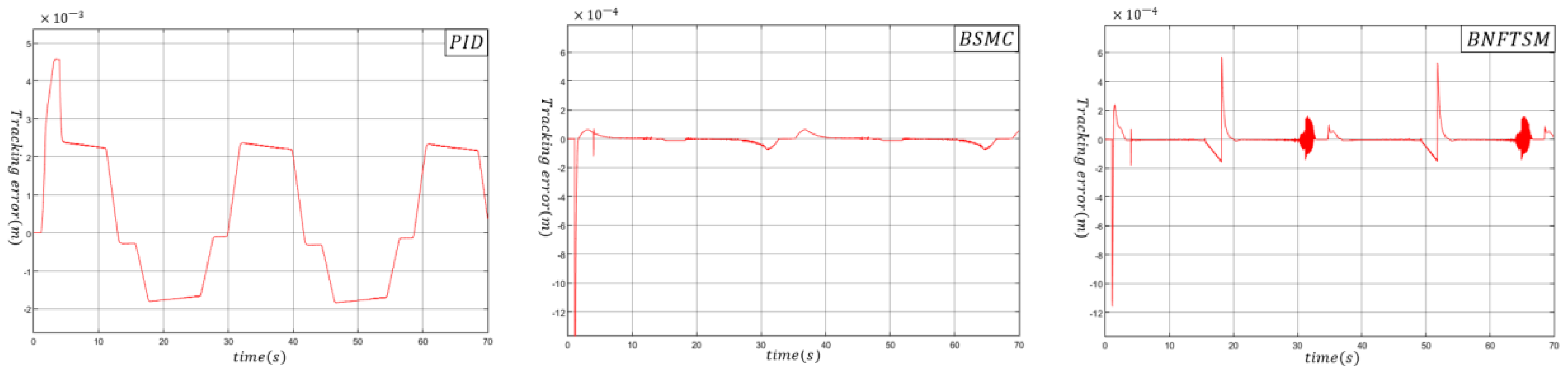
4. Simulation Results
4.1. Configuration of Simulations
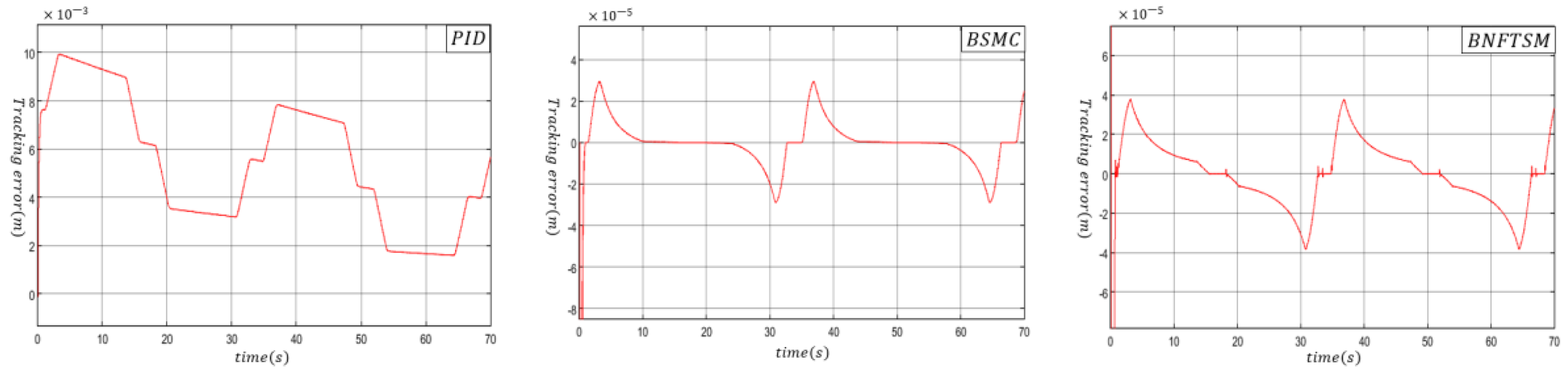
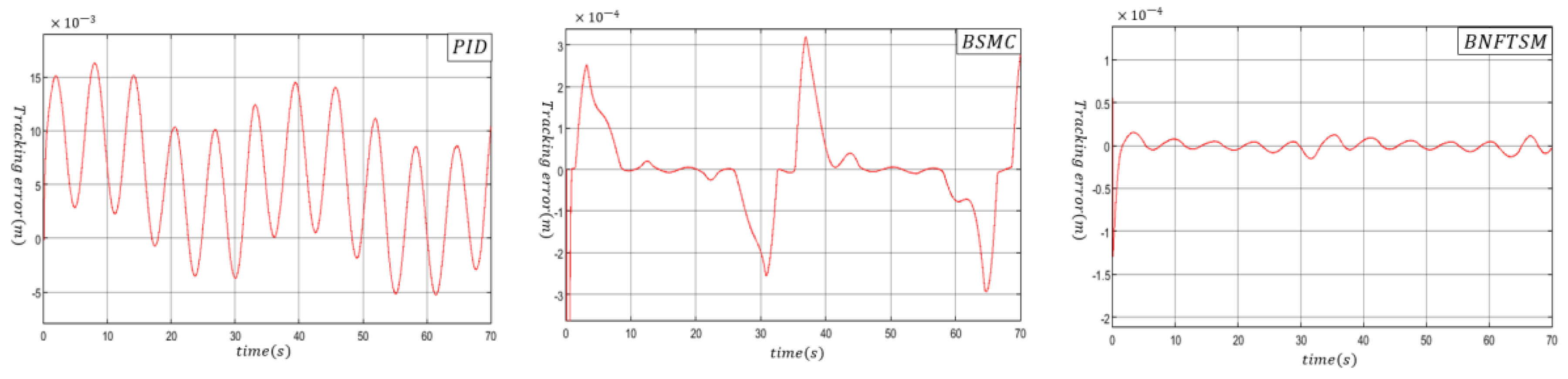
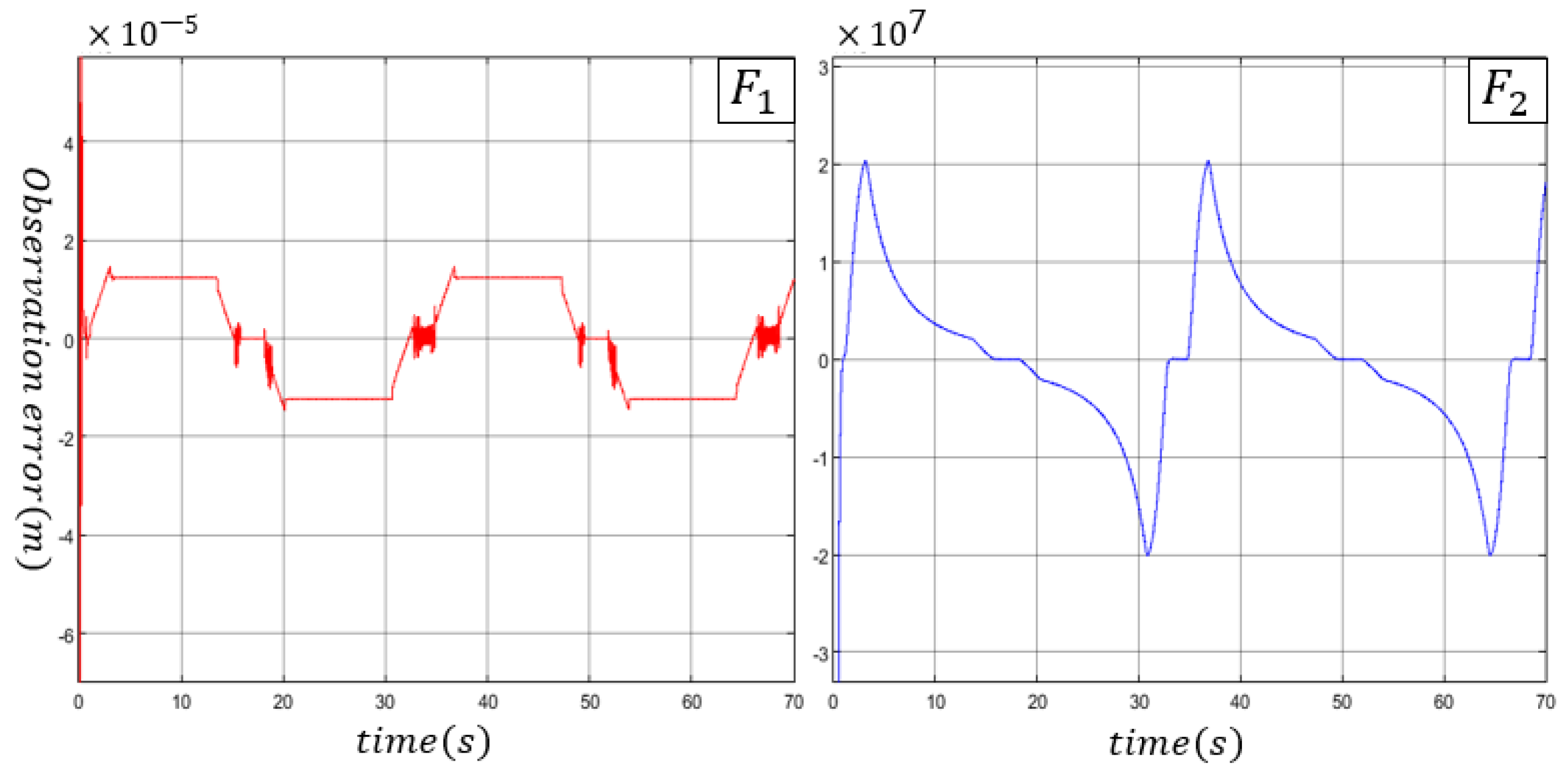
4.2. Comparative Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, S.; Shen, C.; Xia, Y.; Chen, Z.; Zhu, S. Adaptive Robust Control Design for Underwater Multi-DoF Hydraulic Manipulator. Ocean Eng. 2020, 15, 110822. [Google Scholar] [CrossRef]
- Lin, T.; Lin, Y.; Ren, H.; Chen, H.; Li, Z.; Chen, Q. A Double Variable Control Load Sensing System for Electric Hydraulic Excavator. Energy 2021, 15, 119999. [Google Scholar] [CrossRef]
- Nie, Y.; Liu, J.; Lao, Z.; Chen, Z. Modeling and Extended State Observer-Based Backstepping Control of Underwater Electro Hydrostatic Actuator with Pressure Compensator and External Load. Electronics 2022, 11, 1286. [Google Scholar] [CrossRef]
- Wang, S. Asymptotic Tracking Control for Nonaffine Systems with Disturbances. IEEE Trans. Circuits Syst. 2022, 69, 479–483. [Google Scholar] [CrossRef]
- Lyu, L.; Chen, Z.; Yao, B. Advanced Valves and Pump Coordinated Hydraulic Control Design to Simultaneously Achieve High Accuracy and High Efficiency. IEEE Trans. Control Syst. Technol. 2021, 29, 236–248. [Google Scholar] [CrossRef]
- Nie, Y.; Liu, J.; Liu, G.; Lyu, L.; Li, J.; Chen, Z. Force Tracking Impedance Control of Hydraulic Series Elastic Actuators Interacting with Unknown Environment. Mathematics 2022, 10, 3383. [Google Scholar] [CrossRef]
- Helian, B.; Chen, Z.; Yao, B. Precision Motion Control of a Servomotor-Pump Direct-Drive Electrohydraulic System with a Nonlinear Pump Flow Mapping. IEEE Trans. Ind. Electron. 2020, 67, 8638–8648. [Google Scholar] [CrossRef]
- Chen, Z.; Li, C.; Yao, B.; Yuan, M.; Yang, C. Integrated Coordinated/Synchronized Contouring Control of a Dual-Linear-Motor-Driven Gantry. IEEE Trans. Ind. Electron. 2020, 67, 3944–3954. [Google Scholar] [CrossRef]
- Chen, W.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Kürkçü, B.; Kasnakoğlu, C.; Efe, M.Ö. Disturbance/Uncertainty Estimator Based Integral Sliding-Mode Control. IEEE Trans. Autom. Control 2018, 11, 3940–3947. [Google Scholar] [CrossRef]
- Deng, W.; Yao, J. Asymptotic Tracking Control of Mechanical Servosystems with Mismatched Uncertainties. IEEE/ASME Trans. Mechatron. 2021, 26, 2204–2214. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D.; Yan, L. High-Accuracy Tracking Control of Hydraulic Rotary Actuators with Modeling Uncertainties. IEEE/ASME Trans. Mechatron. 2014, 19, 633–641. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J. High-Precision Motion Servo Control of Double-Rod Electro-Hydraulic Actuators with Exact Tracking Performance. ISA Trans. 2020, 103, 266–279. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.; Yao, J.; Gu, J. Extended-State-Observer-Based Output Feedback Adaptive Control of Hydraulic System with Con-tinuous Friction Compensation. J. Frankl. Inst. 2019, 356, 8414–8437. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, Y.; Celler, B.G.; Su, S.W. Backstepping Control of Electro-Hydraulic System Based on Extended-State-Observer with Plant Dynamics Largely Unknown. IEEE Trans. Ind. Electron. 2014, 19, 633–641. [Google Scholar] [CrossRef]
- Seo, I.; Shin, J.; Kim, H.; Kim, J. Adaptive Position Control Scheme with Neural Networks for Electro-Hydrostatic Actuator Systems. In Proceedings of the 2010 IEEE International Conference on Mechatronics and Automation, Xi’an, China, 4–7 August 2010; pp. 501–506. [Google Scholar]
- Chen, W.; Ballance, D.; Gawthrop, P.; O′Reilly, J. A Nonlinear Disturbance Observer for Robotic Manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]
- Chen, W. Disturbance Observer Based Control for Nonlinear Systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Chen, W. Harmonic Disturbance Observer for Nonlinear Systems. J. Dyn. Syst. Meas. Control 2003, 125, 114–117. [Google Scholar] [CrossRef]
- Kaddissi, C.; Kenne, J.; Saad, M. Indirect Adaptive Control of an Electrohydraulic Servo System Based on Nonlinear Backstepping. IEEE/ASME Trans. Mechatron. 2011, 16, 1171–1177. [Google Scholar] [CrossRef]
- Lin, H.; Li, E.; Liang, Z. Adaptive Backstepping Controllerfor Electro-Hydraulic Servo System with Nonlinear Uncertain Parameters. Control Theory Appl. 2016, 33, 181–188. [Google Scholar]
- Cho, S.H.; Burton, R. Position Control of High Performance Hydrostatic Actuation System Using a Simple Adaptive Control (SAC) Method. Mechatronics 2011, 21, 109–115. [Google Scholar] [CrossRef]
- Wang, S.; Habibi, S.; Burton, R. Sliding Mode Control for an Electrohydraulic Actuator System with Discontinuous Non-Linear Friction. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2008, 222, 799–815. [Google Scholar] [CrossRef]
- Chen, M.; Wu, Q.; Cui, R. Terminal Sliding Mode Tracking Control for a Class of SISO Uncertain Nonlinear Systems. ISA Trans. 2013, 52, 198–206. [Google Scholar] [CrossRef] [PubMed]
- Shen, W.; Wang, J. An Integral Terminal Sliding Mode Control Scheme for Speed Control System Using a Double-Variable Hydraulic Transformer. ISA Trans. 2022, 124, 386–394. [Google Scholar] [CrossRef] [PubMed]
- Helian, B.; Chen, Z.; Yao, B. Accurate Motion Control of a Direct-Drive Hydraulic System with an Adaptive Nonlinear Pump Flow Compensation. IEEE/ASME Trans. Mechatron. 2021, 26, 2593–2603. [Google Scholar] [CrossRef]
- Chen, Z.; Helian, B.; Zhou, Y.; Geimer, M. An Integrated Trajectory Planning and Motioicsn Control Strategy of a Variable Rotational Speed Pump-Controlled Electro-Hydraulic Actuator. IEEE/ASME Trans. Mechatron. 2022, 10, 1–10. [Google Scholar]
- Wang, K.; Paul, L. Modelling and Energy Efficiency Analysis of a Hybrid Pump-Controlled Asymmetric (Single-Rod) Cylinder Drive System. Int. J. Hydromechatron. 2020, 3, 1. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, Z.; Wei, H. Development of Pressure Compensator for Deep Water Hydraulic Power Station. Ship Eng. 2000, 2, 60–61. [Google Scholar]
- Tao, L.; Chen, Q.; Nan, Y. Disturbance-Observer Based Adaptive Control Forsecond-Order Nonlinear Systems Using Chattering-Free Reaching Law. Int. J. Control Autom. Syst. 2019, 17, 356–369. [Google Scholar] [CrossRef]
- Liu, X.; Huang, R.; Gao, Y. Adaptive Inversion Sliding Mode Control for Electro-Hydraulic Servo Motion System. Chin. Hydraul. Pneum. 2019, 7, 14–19. [Google Scholar]
- Zhao, P.; Yao, M.; Shen, X. Non Singular Fast Terminal Sliding Mode Liquid Level Tracking Control. J. Xi’an Jiaotong Univ. 2011, 45, 39–44. [Google Scholar]
- Du, X.; Fang, X.; Liu, F. Continuous Full-Order Nonsingular Terminal Sliding Mode Control for Systems with Matched and Mismatched Disturbances. IEEE Access 2019, 7, 130970–130976. [Google Scholar] [CrossRef]
- Hu, C.; Ou, T.; Zhu, Y.; Zhu, L. Deep GRU Neural-Network Prediction and Feedforward Compensation for Precision Multi-Axis Motion Control Systems. IEEE/ASME Trans. Mechatron. 2020, 25, 1377–1388. [Google Scholar] [CrossRef]
- Cheng, M.; Zhang, J.; Xu, B.; Ding, R.; Wei, J. Decoupling Compensation for Damping Improvement of the Electrohydraulic Control System with Multiple Actuators. IEEE/ASME Trans. Mechatron. 2018, 23, 1383–1392. [Google Scholar] [CrossRef]
- Ding, R.; Cheng, M.; Jiang, L. Active Fault-Tolerant Control for Electro-Hydraulic Systems with an Independent Metering Valve Against Valve Faults. IEEE Trans. Ind. Electron. 2020, 68, 7221–7232. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, Y.; Lao, Z.; Liu, J.; Huang, Y.; Sun, X.; Tang, J.; Chen, Z. Disturbance Observer-Based Sliding Mode Controller for Underwater Electro-Hydrostatic Actuator Affected by Seawater Pressure. Machines 2022, 10, 1115. https://doi.org/10.3390/machines10121115
Nie Y, Lao Z, Liu J, Huang Y, Sun X, Tang J, Chen Z. Disturbance Observer-Based Sliding Mode Controller for Underwater Electro-Hydrostatic Actuator Affected by Seawater Pressure. Machines. 2022; 10(12):1115. https://doi.org/10.3390/machines10121115
Chicago/Turabian StyleNie, Yong, Zhenhua Lao, Jiajia Liu, Yichi Huang, Xiangwei Sun, Jianzhong Tang, and Zheng Chen. 2022. "Disturbance Observer-Based Sliding Mode Controller for Underwater Electro-Hydrostatic Actuator Affected by Seawater Pressure" Machines 10, no. 12: 1115. https://doi.org/10.3390/machines10121115
APA StyleNie, Y., Lao, Z., Liu, J., Huang, Y., Sun, X., Tang, J., & Chen, Z. (2022). Disturbance Observer-Based Sliding Mode Controller for Underwater Electro-Hydrostatic Actuator Affected by Seawater Pressure. Machines, 10(12), 1115. https://doi.org/10.3390/machines10121115










