Fertilization Control System Research in Orchard Based on the PSO-BP-PID Control Algorithm
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Orchard Fertilization Process
2.1.2. Variable-Rate Fertilization Experiment Platform
2.2. Methods of Model Construction and Calibration Test
2.2.1. Mathematical Model of Rotating Speed and Fertilizer Discharge
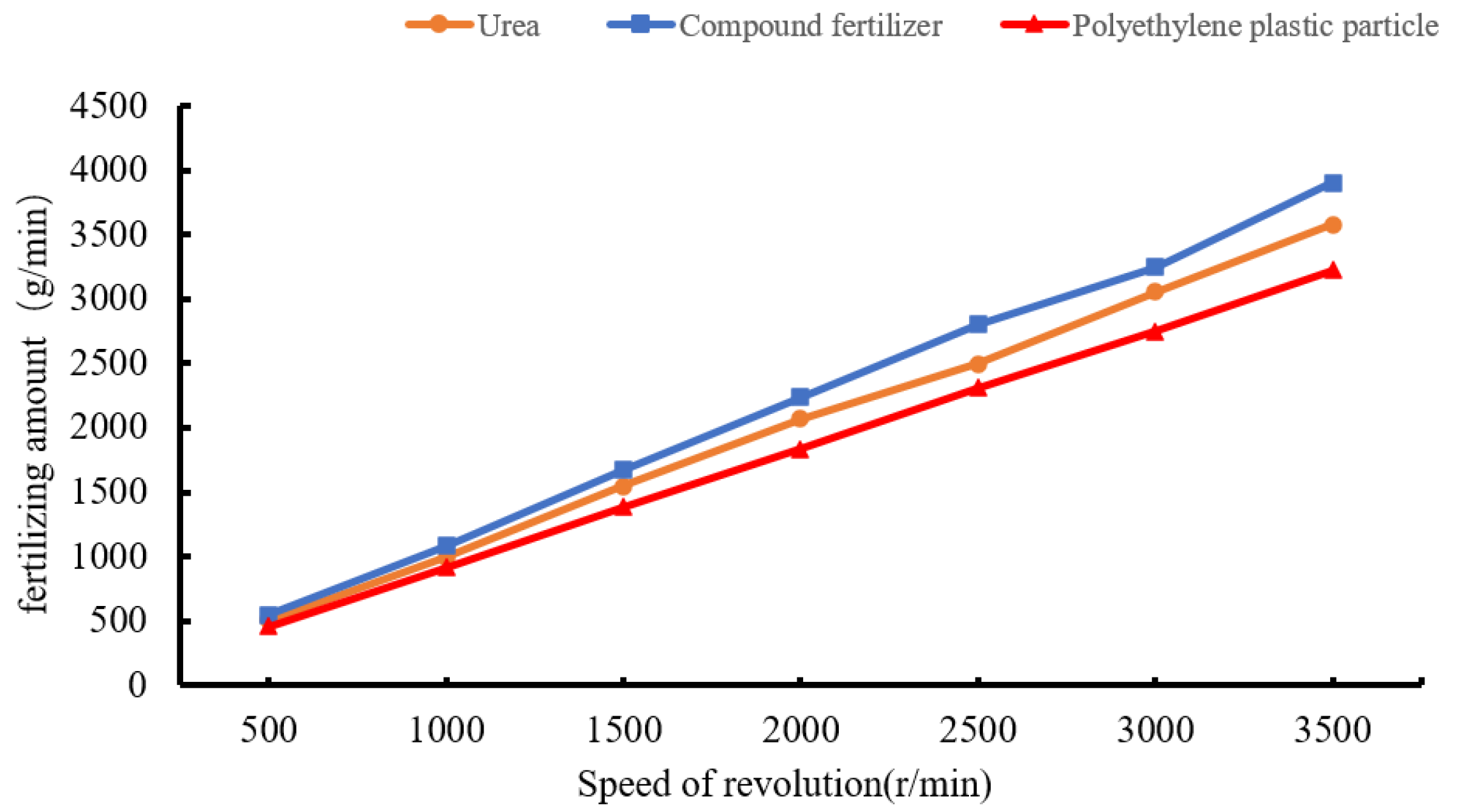
2.2.2. Calibration Method of Fertilization at Different Speeds
2.2.3. Rotating Speed Model of Fertilizer Discharging Motor
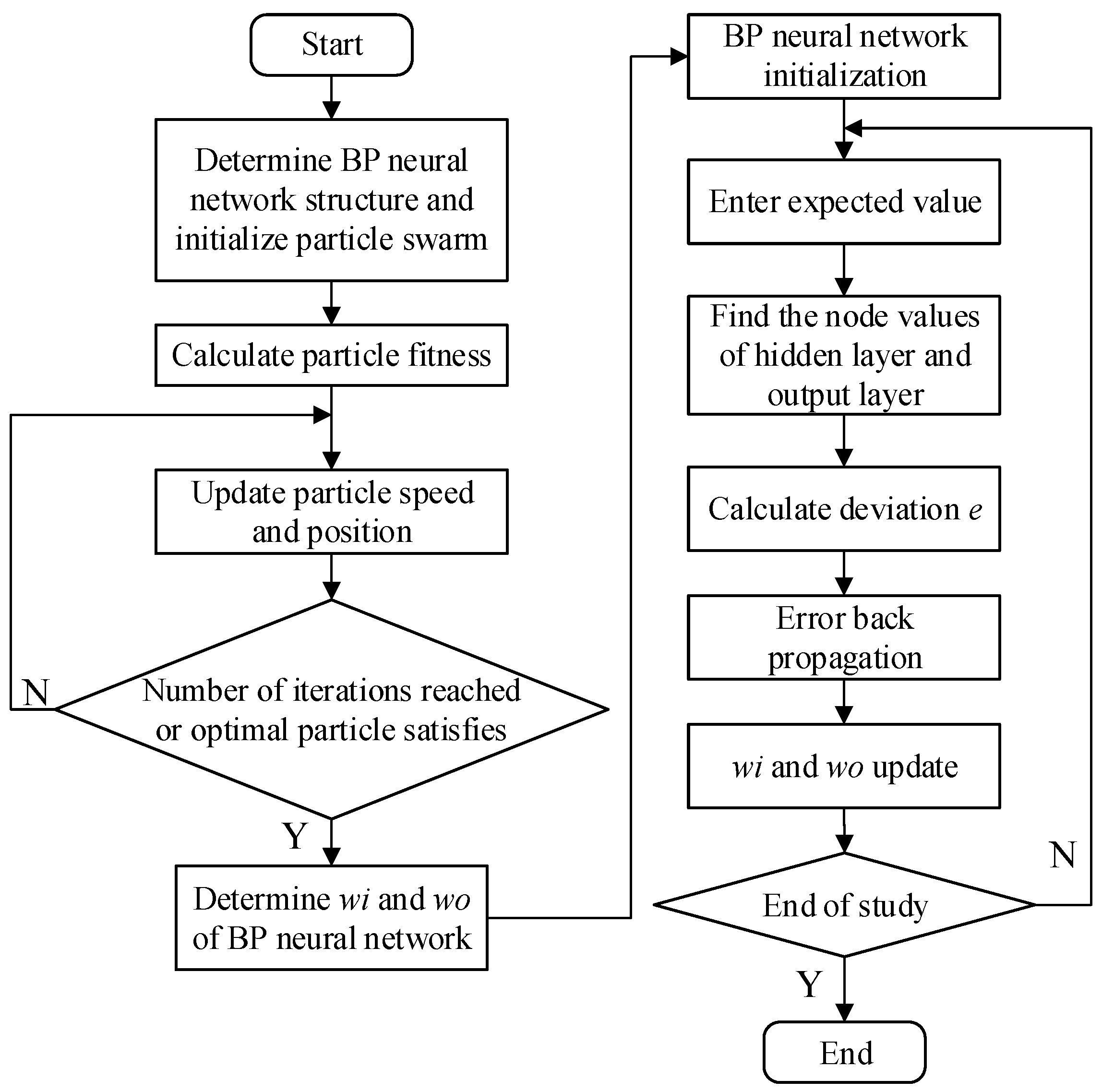
2.3. BP Neural Network PID Controller Design Based on Particle Swarm Optimization
2.3.1. Principle of Particle Swarm Optimization Algorithm
2.3.2. Design of the BP Neural Network PID Controller Based on PSO Optimization
2.4. Methods of Simulation Test and Variable Rate Fertilization Test
2.4.1. Methods of Simulation Test
2.4.2. Methods of the Variable-Rate Fertilization Test
- (1)
- Response test of fertilizer discharge motor speed.
- (2)
- Fertilizer discharge accuracy test of fertilizer discharger.
- Target fertilization as a variable.
- 2.
- Vehicle speed as a variable.
3. Results
3.1. Results of the Calibration Test
3.2. Results of Simulation Test
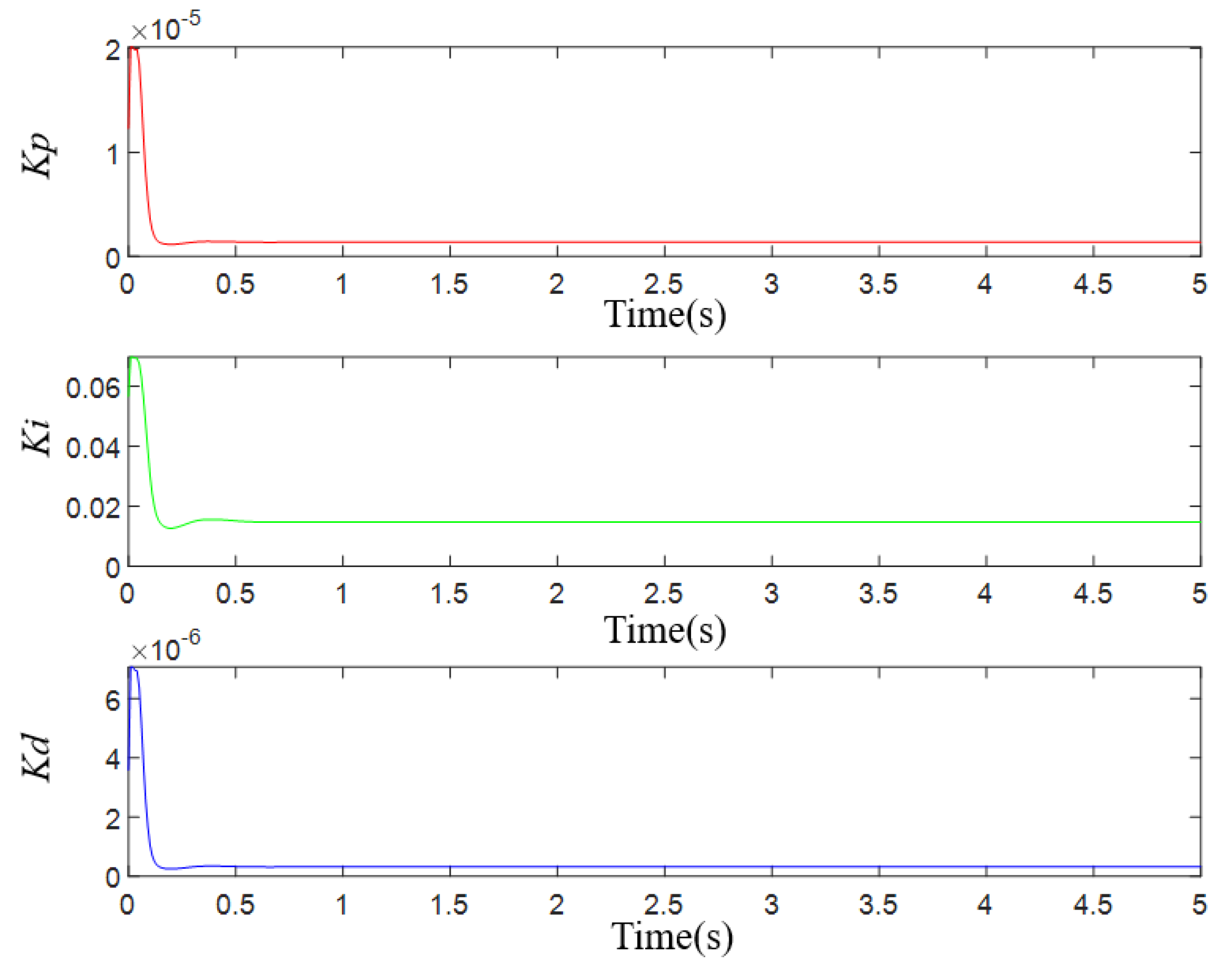
3.2.1. Results of the PSO-BP-PID Step Response Test
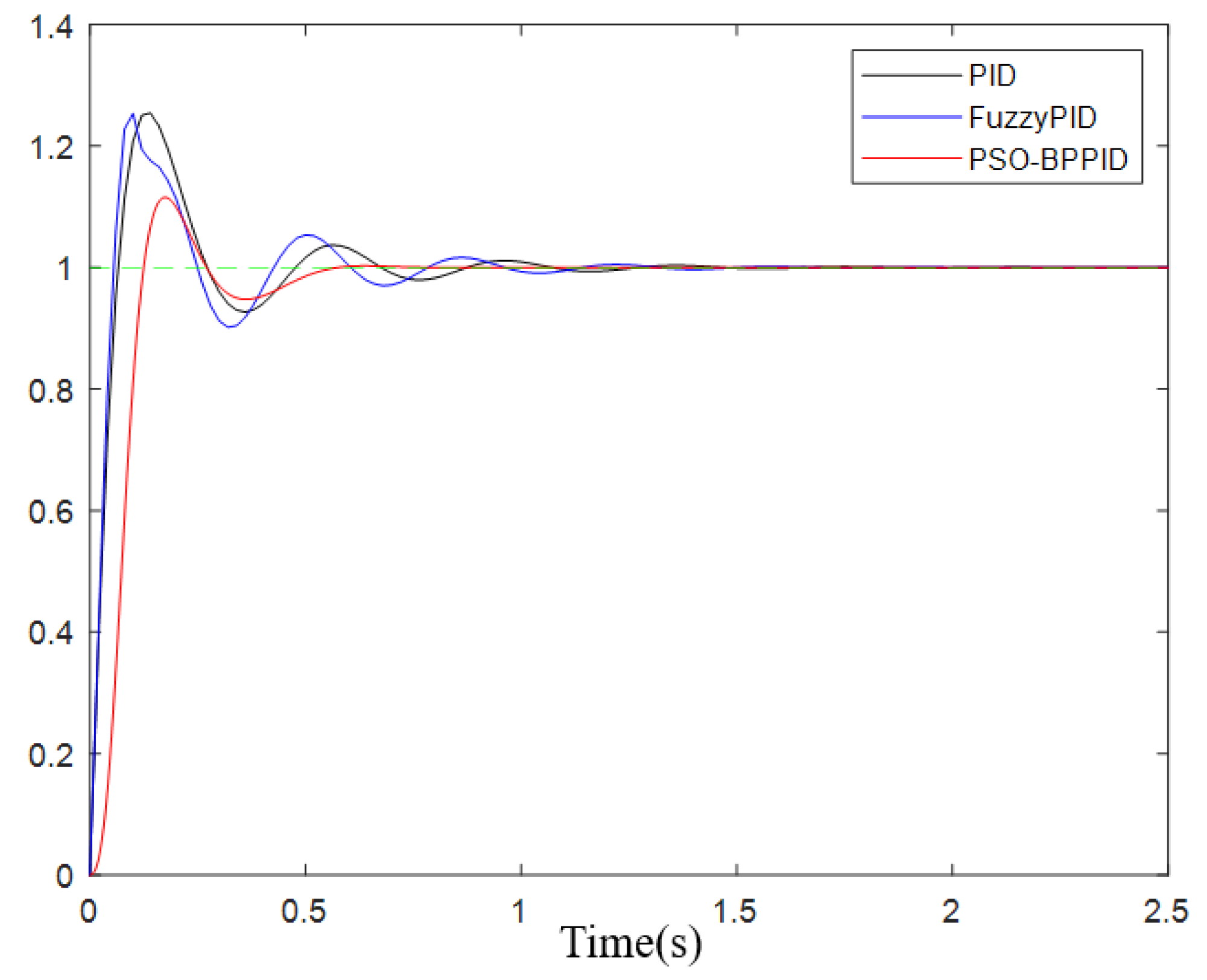
3.2.2. Results of Step Response Contrast Test
3.2.3. Results of Immunity Comparison Test
3.3. Results of the Variable-Rate Fertilization Test
3.3.1. Result of Response Test of Fertilizer Discharge Motor Speed
3.3.2. Result of Fertilizer Discharge Accuracy Test of Fertilizer Discharger
- (1)
- Result of target fertilization as a variable experiment
- (2)
- Result of vehicle speed as a variable experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meng, Z.J.; Zhao, C.J.; Fu, W.Q.; Ji, Y.X.; Wu, G.W. Prescription Map Identification and Position Lag Calibration Method for Variable Rate Application of Fertilizer. Trans. Chin. Soc. Agric. Mach. 2011, 42, 204–209. [Google Scholar]
- Bai, J.B.; Tian, M.; Li, J.Q. Control System of Liquid Fertilizer Variable-Rate Fertilization Based on Beetle Antennae Search Algorithm. Processes 2022, 10, 357. [Google Scholar] [CrossRef]
- Martins, R.N.; Pinto, F.A.; Moura, A.D.; Siqueira, W.C.; Villar, F.M. Nitrogen variable rate fertilization in corn crop prescribed by optical sensor. J. Plant Nutr. 2020, 43, 1681–1688. [Google Scholar] [CrossRef]
- Alameen, A.A.; Al-Gaadi, K.A.; Tola, E.K. Development and performance evaluation of a control system for variable rate granular fertilizer application. Comput. Electron. Agric. 2019, 160, 31–39. [Google Scholar] [CrossRef]
- An, X.F.; Fu, W.Q.; Wei, X.L.; Cong, Y.; Wang, P. Evaluation of Four-element Variable Rate Application of Fertilization Based on Maps. Trans. Chin. Soc. Agric. Mach. 2017, 48, 66–70. [Google Scholar]
- Meng, Z.J.; Zhao, C.J.; Liu, H.; Huang, W.Q.; Fu, W.Q.; Wang, X. Development and performance assessment of map-based variable rate granule application system. J. Jiangsu Univ. 2009, 30, 338–342. [Google Scholar]
- Yang, S.; Zhai, C.Y.; Long, J.; Zhang, B.; Li, H.Z. Wolfberry tree dual-model detection method and orchard target-oriented fertilization system based on photoelectric sensors. Int. J. Agric. Biol. Eng. 2018, 11, 65–73. [Google Scholar] [CrossRef]
- Huai, B.F.; Zhang, C.S.; Zhang, P.X.; Han, J.; Wang, X.; Zhuang, W.D. BP-PID Control Method in Control System of Variable Rate Fertilizer Application. J. Heilongjiang Bayi Agric. Univ. 2015, 27, 95–98. [Google Scholar]
- Wang, X.C.; Chen, M.; Sun, G.X.; Zhang, Y.; Zhang, Y.N. Design and test of control system on variable fertilizer applicator for winter wheat. Trans. Chin. Soc. Agric. Eng. 2015, 31, 88–92. [Google Scholar]
- Zhang, J.C.; Yan, S.C.; Ji, W.Y.; Song, B.G.; Zheng, P. Precision Fertilization Control System Research for Solid Fertilizers Based on Incremental PID Control Algorithm. Trans. Chin. Soc. Agric. Mach. 2021, 52, 99–106. [Google Scholar]
- Yuan, Q.C.; Xu, L.M.; Niu, C.; Ma, S.; Yan, C.G.; Zhao, S.J. Design and Test of Layered Variable Rate Fertilizer Discharge Control System for Organic Fertilizer Deep Applicator. Trans. Chin. Soc. Agric. Mach. 2020, 51, 195–202. [Google Scholar]
- Sun, Y.J.; Shen, J.X.; Dou, Q.Q.; Li, Q.L.; Chen, G.; Sun, Y.T. Design and Test of Monitoring System of Notillage Planter Based on Cortex-M3 Processor. Trans. Chin. Soc. Agric. Eng. 2018, 49, 50–58. [Google Scholar]
- An, X.F.; Fu, W.Q.; Wang, P.; Wei, X.L.; Li, L.W.; Meng, Z.J. Development of Variable Rate Fertilization Control System Based on Matching Fertilizer Line and Seed Line of Wheat. Trans. Chin. Soc. Agric. Eng. 2019, 50, 96–101. [Google Scholar]
- Zhang, J.Q.; Liu, G.; Hu, H.; Huang, J.Y. Development of bivariate fertilizer control system via independent control of fertilizing unit. Trans. Chin. Soc. Agric. Eng. 2021, 37, 38–45. [Google Scholar]
- Ren, H.J.; Hou, B.; Zhou, G.; Shen, L.; Wei, C.; Li, Q. Variable Pitch Active Disturbance Rejection Control of Wind Turbines Based on BP Neural Network PID. IEEE Access 2020, 8, 71782–71797. [Google Scholar] [CrossRef]
- Luo, Q.Y.; Li, J.X.; Zhang, H. Drag coefficient modeling of heterogeneous connected platooning vehicles via BP neural network and PSO algorithm. Neurocomputing 2022, 484, 117–127. [Google Scholar] [CrossRef]
- Ibrahim, B.; Abdelkader, H.; Patrice, W. Advanced Control of Doubly Fed Induction Generator for Wind Power Systems: Optimal Control of Power Using PSO Algorithm. Appl. Mech. Mater. 2022, 905, 29–42. [Google Scholar]
- Chavoshian, M.; Taghizadeh, M.; Mazare, M. Hybrid Dynamic Neural Network and PID Control of Pneumatic Artificial Muscle Using the PSO Algorithm. Int. J. Autom. Comput. 2020, 17, 428–438. [Google Scholar] [CrossRef]
- Chen, M.; Lu, W.; Wang, X.C.; Sun, G.X.; Zhang, Y.; Pan, F. Design and Experiment of Optimization Control System for Variable Fertilization in Winter Wheat Field Based on Fuzzy PID. Trans. Chin. Soc. Agric. Mach. 2016, 47, 71–76. [Google Scholar]
- Song, X.; Li, H.; Chen, C.; Xia, H.; Zhang, Z.; Tang, P. Design and Experimental Testing of a Control System for a Solid-Fertilizer-Dissolving Device Based on Fuzzy PID. Agriculture 2022, 12, 1382. [Google Scholar] [CrossRef]
- Yao, Y.F.; Chen, X.G.; Ji, C.; Chen, J.C.; Zhang, H.; Pan, F. Design and experiments of the single driver for maize precision seeders based on fuzzy PID control. Trans. Chin. Soc. Agric. Eng. 2022, 38, 12–21. [Google Scholar]
- Nuchkrua, T.; Leephakpreeda, T. Fuzzy Self-Tuning PID Control of Hydrogen-Driven Pneumatic Artificial Muscle Actuator. J. Bionic Eng. 2013, 10, 329–340. [Google Scholar] [CrossRef]
- Li, K.; Boonto, S.; Nuchkrua, T. On-line Self Tuning of Contouring Control for High Accuracy Robot Manipulators under Various Operations. Int. J. Control Autom. Syst. 2020, 18, 1818–1828. [Google Scholar] [CrossRef]
- Zhang, M.L.; Zhang, Y.J.; He, X.L.; Gao, Z.J. Adaptive PID Control and Its Application Based on a Double-Layer BP Neural Network. Processes 2021, 9, 1475. [Google Scholar] [CrossRef]
- Pei, G.J.; Yu, M.; Xu, Y.H.; Ma, C.; Lai, H.H.; Chen, F.K.; Lin, H. An Improved PID Controller for the Compliant Constant-Force Actuator Based on BP Neural Network and Smith Predictor. Appl. Sci. 2021, 11, 2685. [Google Scholar] [CrossRef]













| PID Controller | Kp | Ti | Td |
|---|---|---|---|
| P | 0.5Ku | / | / |
| PI | 0.45Ku | 0.85Tu | / |
| PID | 0.6Ku | 0.5Tu | 0.12Tu |
| Fertilizer Type | p-Value | R-Value |
|---|---|---|
| Urea | 3.4 × 10−9 | 0.99968 |
| Compound fertilizer | 1.08 × 10−8 | 0.99950 |
| Polyethylene plastic particles | 1 × 10−10 | 0.99997 |
| Controller | Overshoot | Rise Time | Adjustment Time |
|---|---|---|---|
| Traditional PID | 25.4% | 0.058 s | 1.555 s |
| Fuzzy PID | 25.4% | 0.053 s | 1.443 s |
| PSO-BP-PID | 12.7% | 0.105 s | 0.557 s |
| Controller | Disturbance Recovery Time | Maximum Fluctuation |
|---|---|---|
| Traditional PID | 3.654 s | 6.8% |
| Fuzzy PID | 3.923 s | 8.1% |
| PSO-BP-PID | 2.849 s | 3.2% |
| Rotating Speed (Increasing) r/min | 0 to 500 | 500 to 1000 | 1000 to 1500 | 1500 to 2000 | 2000 to 2500 | 2500 to 3000 | 3000 to 3500 |
|---|---|---|---|---|---|---|---|
| Response time s | 0.28 s | 0.24 s | 0.2 s | 0.14 s | 0.18 s | 0.22 s | 0.24 s |
| Rotating Speed (Decreasing) r/min | 3500 to 3000 | 3000 to 2500 | 2500 to 2000 | 2000 to 1500 | 1500 to 1000 | 1000 to 500 | 500 to 0 |
|---|---|---|---|---|---|---|---|
| Response time s | 0.22 s | 0.22 s | 0.18 s | 0.16 s | 0.18 s | 0.2 s | 0.26 s |
| Operating Speed m/s | Target Fertilization g/m | Actual Fertilization g/m | Coefficient of Variation % | Fertilizer Discharge Error % | Monitoring Fertilization g/m | Monitoring Error % |
|---|---|---|---|---|---|---|
| 1.0 | 24 | 23.472 | 2.83 | 2.20 | 24.52 | 4.47 |
| 36 | 35.784 | 1.34 | 0.60 | 36.448 | 1.86 | |
| 48 | 48.320 | 1.63 | 0.67 | 49.068 | 1.55 |
| Target Fertilization g/m | Operating Speed m/s | Actual Fertilization g/m | Coefficient of Variation % | Fertilizer Discharge Error % | Monitoring Fertilization g/m | Monitoring Error % |
|---|---|---|---|---|---|---|
| 48 | 0.6 | 47.432 | 1.06 | 1.18 | 48.252 | 1.69 |
| 0.8 | 47.396 | 1.22 | 1.25 | 48.344 | 1.96 | |
| 1.0 | 48.372 | 0.88 | 0.78 | 48.868 | 1.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, C.; Yang, J.; Zhou, L.; Wang, S.; Peng, J.; Tan, Y. Fertilization Control System Research in Orchard Based on the PSO-BP-PID Control Algorithm. Machines 2022, 10, 982. https://doi.org/10.3390/machines10110982
Wan C, Yang J, Zhou L, Wang S, Peng J, Tan Y. Fertilization Control System Research in Orchard Based on the PSO-BP-PID Control Algorithm. Machines. 2022; 10(11):982. https://doi.org/10.3390/machines10110982
Chicago/Turabian StyleWan, Chang, Jiawei Yang, Ling Zhou, Shuo Wang, Jie Peng, and Yu Tan. 2022. "Fertilization Control System Research in Orchard Based on the PSO-BP-PID Control Algorithm" Machines 10, no. 11: 982. https://doi.org/10.3390/machines10110982
APA StyleWan, C., Yang, J., Zhou, L., Wang, S., Peng, J., & Tan, Y. (2022). Fertilization Control System Research in Orchard Based on the PSO-BP-PID Control Algorithm. Machines, 10(11), 982. https://doi.org/10.3390/machines10110982






