A Digital Observer-Based Repetitive Learning Composite Control Method for Large Range Piezo-Driven Nanopositioning Systems
Abstract
1. Introduction
- A novel discrete compound control strategy, composed of a feedforward controller and a composite feedback controller, is proposed to guarantee the tracking performance of the large range PEA nanopositioning system;
- An efficient online discrete nonlinear observer is designed to implement a real-time estimation for the disturbance;
- A novel observer-based repetitive learning feedback control algorithm is designed, and the discrete Lyapunov-based stability analysis is provided to prove that the tracking error is globally uniformly ultimately bounded.
2. System Modeling and Parameter Identification
2.1. Dynamic Modeling
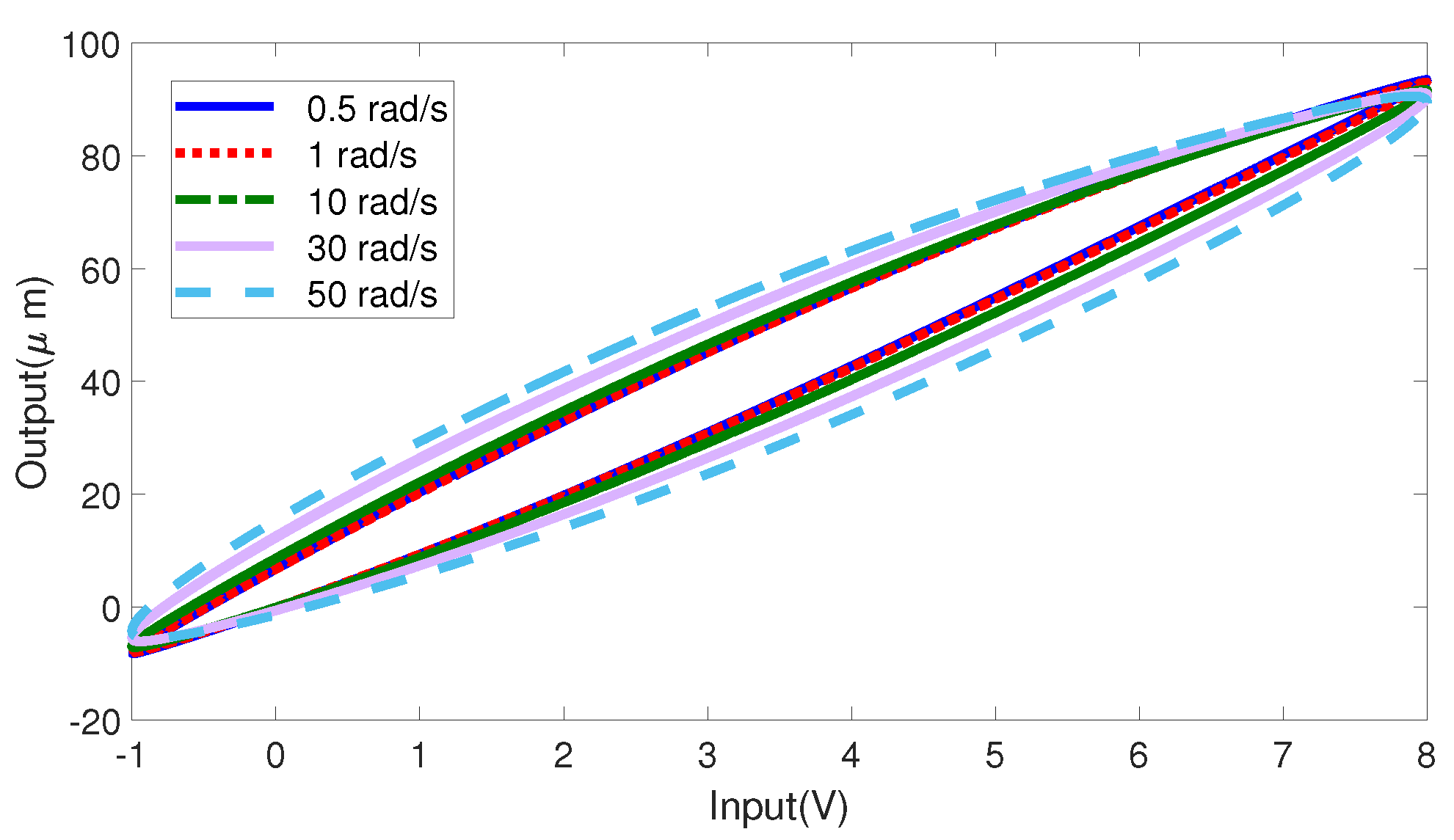
2.2. Static Hysteresis Calibration
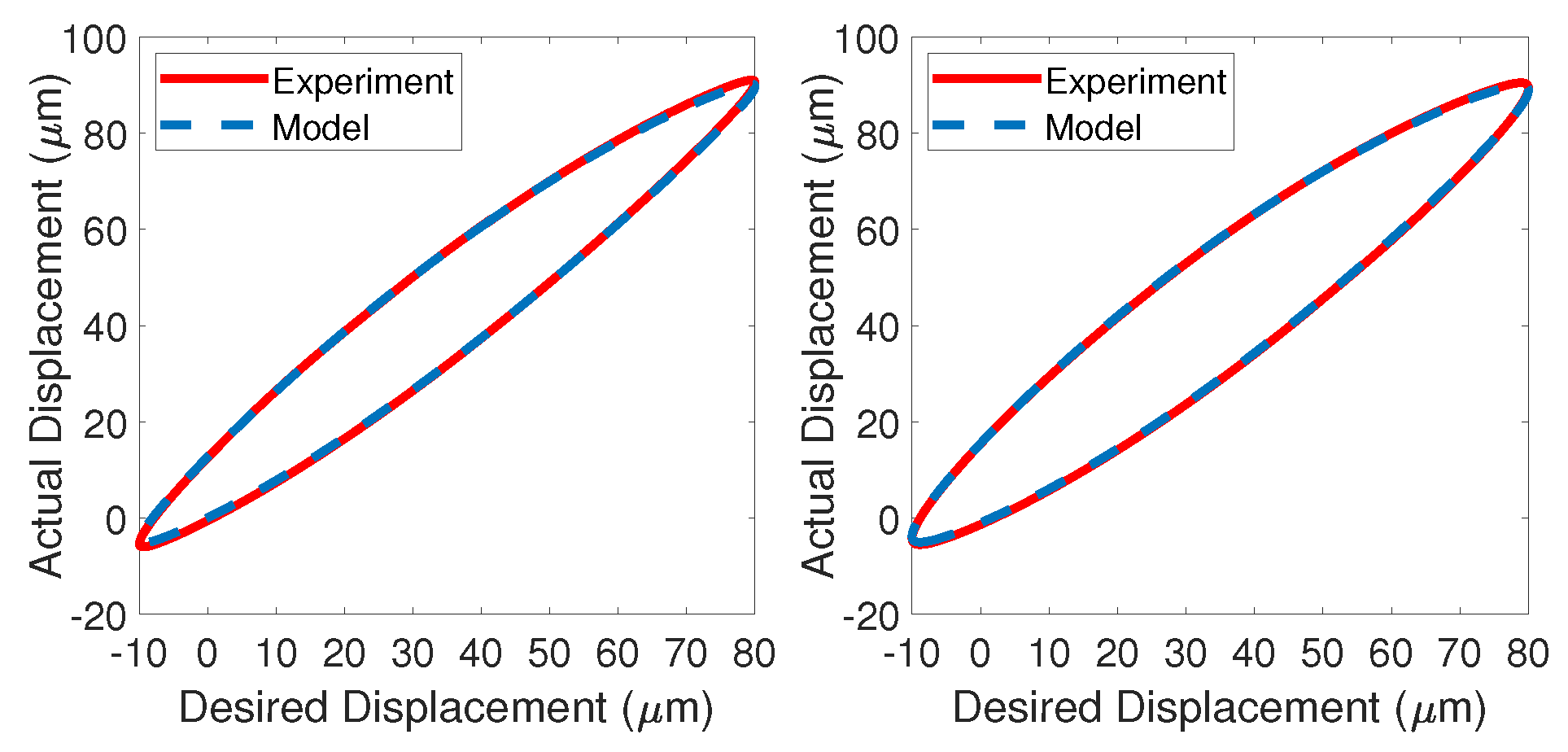
2.3. Modeling Accuracy Validation
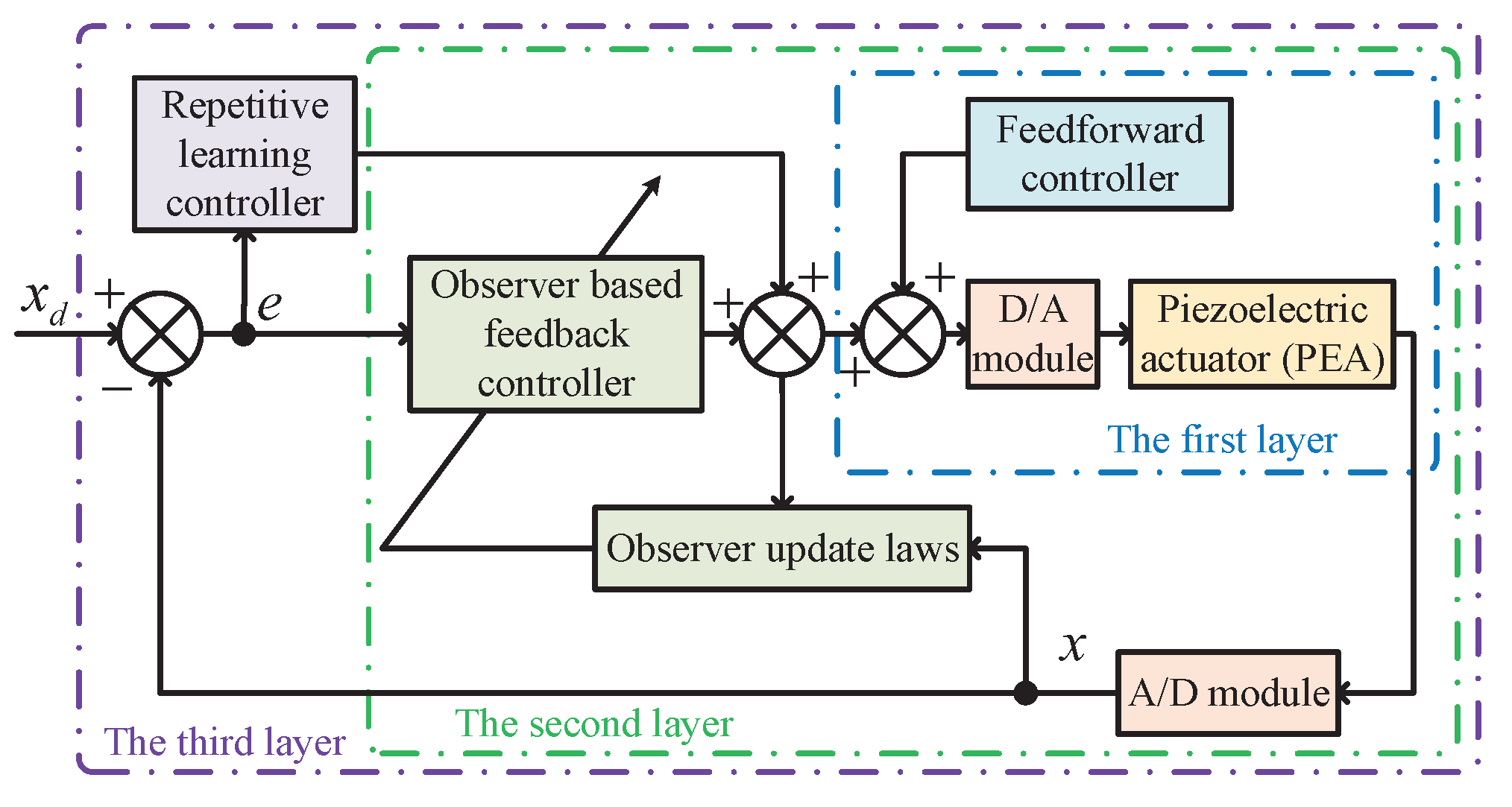
3. Closed-Loop System Control Method Design
3.1. Tracking Error System Formulation
3.2. Controller Design
4. Discrete Closed-Loop System Stability Analysis
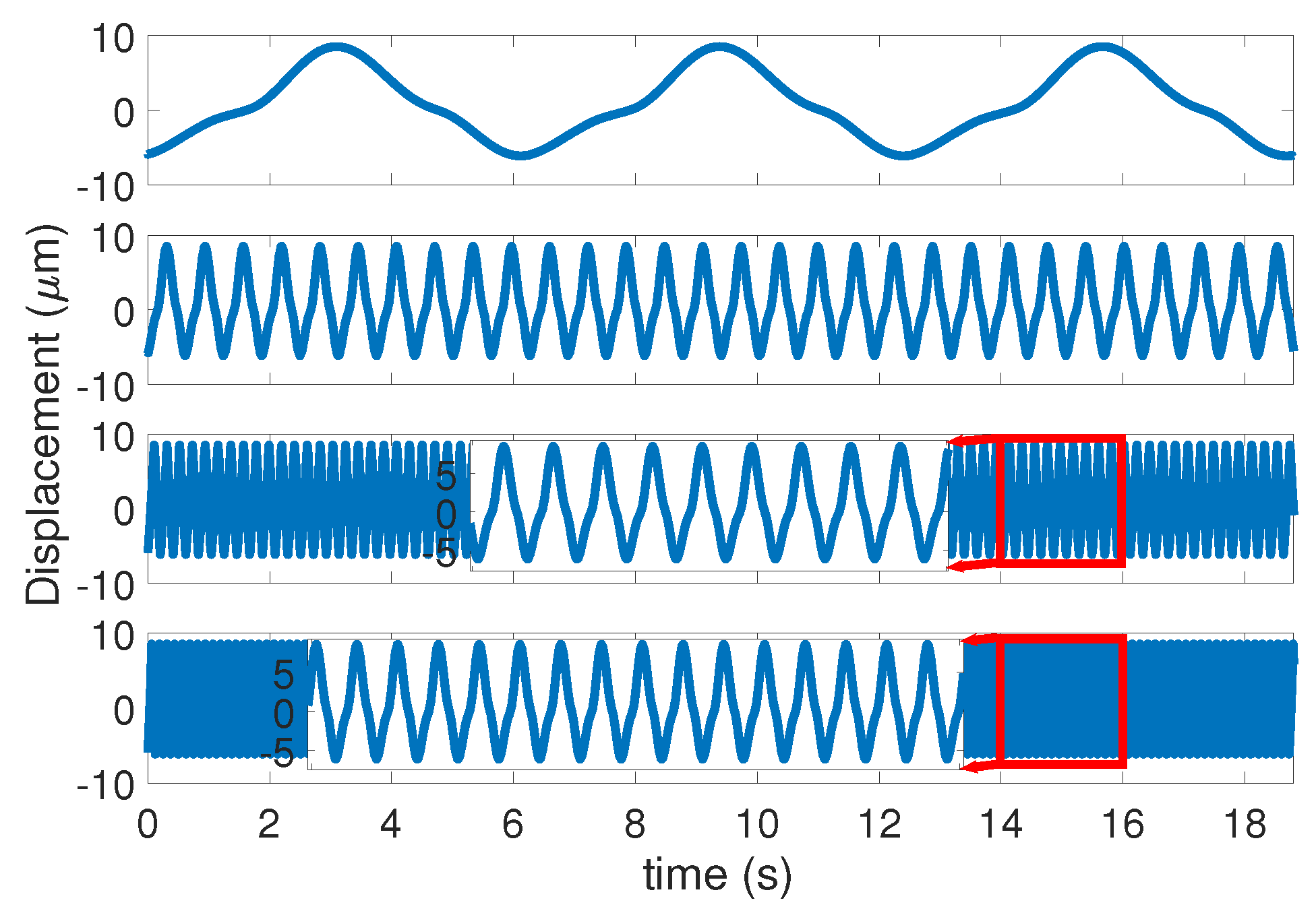
5. Simulation Analysis
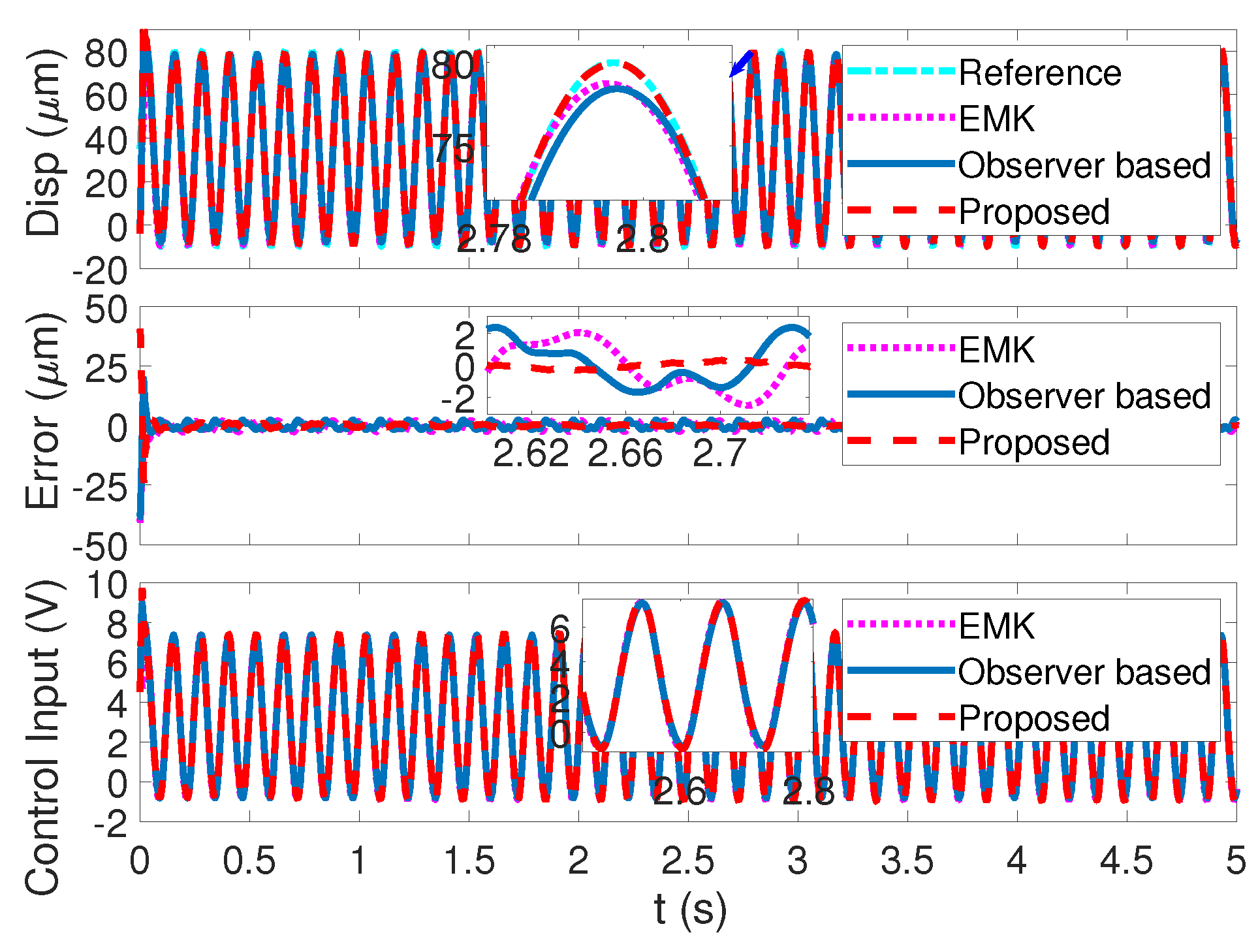
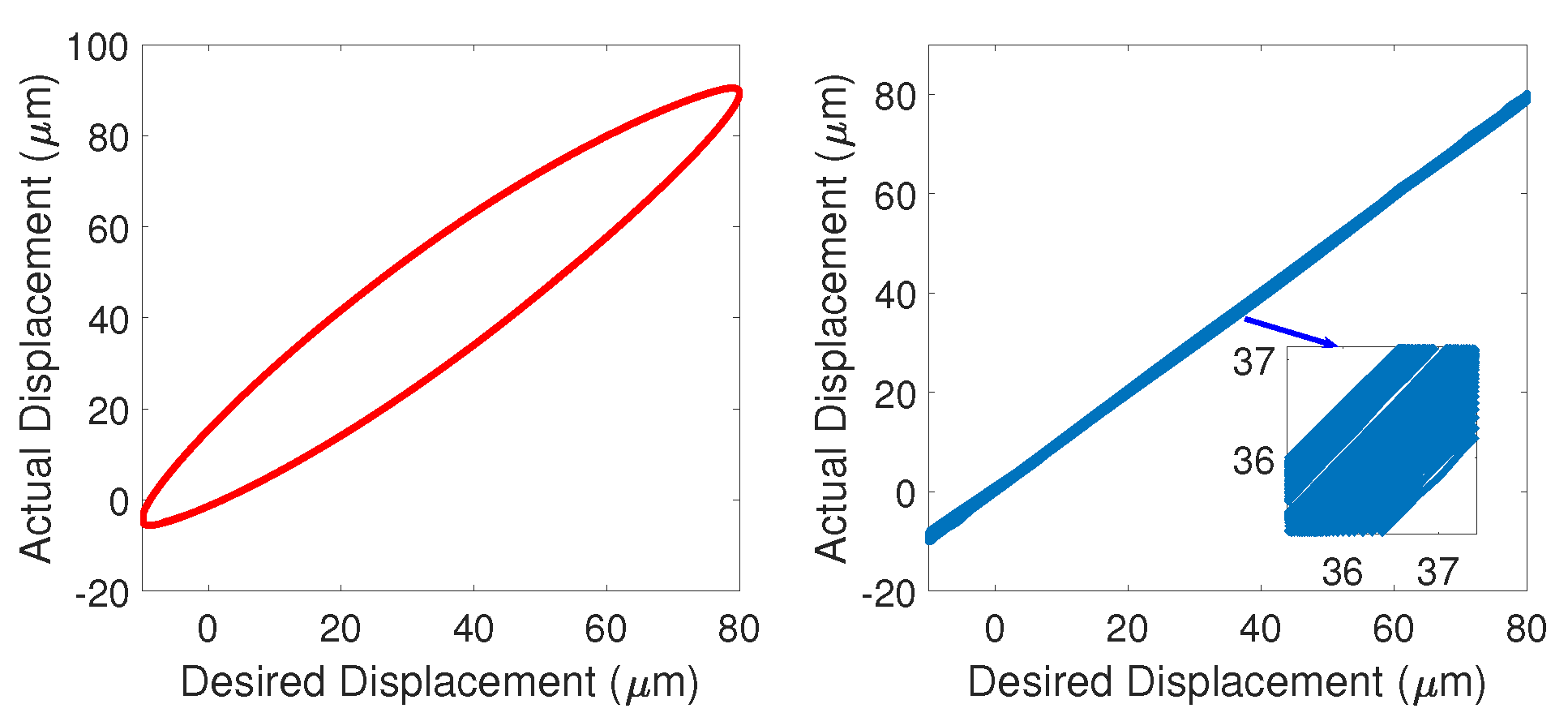
6. Hardware Experiment
6.1. Experiment Setup
6.2. Experiment Results Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic force microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Zhang, H.; Song, J.; Meng, X.; Wen, Y.; Sun, L. Highprecision automated micromanipulation and adhesive microbonding with cantilevered micropipette probes in the dynamic probing mode. IEEE/ASME Trans. Mechatron. 2018, 23, 1425–1435. [Google Scholar] [CrossRef]
- Brown, B.; Picco, L.; Miles, M.; Faul, C. Opportunities in high-speed atomic force microscopy. Small 2013, 9, 3201–3211. [Google Scholar] [CrossRef] [PubMed]
- Gu, G.; Zhu, L.; Su, C.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2016, 13, 313–332. [Google Scholar] [CrossRef]
- Qin, Y.; Tian, Y.; Zhang, D.; Shirinzadeh, B.; Fatikow, S. A novel direct inverse modeling approach for hysteresis compensation of piezoelectric actuator in feedforward applications. IEEE/ASME Trans. Mechatron. 2013, 18, 981–989. [Google Scholar] [CrossRef]
- Chen, X.; Su, C.; Li, Z.; Yang, F. Design of implementable adaptive control for micro/nano positioning system driven by piezoelectric actuator. IEEE Trans. Ind. Electron. 2016, 63, 6471–6481. [Google Scholar] [CrossRef]
- Gu, G.; Zhu, L. Motion control of piezoceramic actuators with creep, hysteresis and vibration compensation. Sens. Actuators A Phys. 2013, 197, 709–717. [Google Scholar] [CrossRef]
- Padthe, A.; Drincic, B.; Oh, J.; Rizos, D.; Fassois, S.; Bernstein, D. Duhem modeling of friction-induced hysteresis. IEEE Control Syst. Mag. 2008, 28, 90–107. [Google Scholar]
- Zhou, J.; Wen, C.; Zhang, C. Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlash-like hysteresis. Automatica 2004, 49, 1751–1759. [Google Scholar] [CrossRef]
- Ismail, M.M.; Ikhouane, F.; Rodellar, J. The hysteresis Bouc-Wen model, a survey. Arch. Comput. Methods Eng. 2009, 16, 161–188. [Google Scholar] [CrossRef]
- Ding, B.; Li, Y.; Xiao, X.; Tang, Y. Optimized PID tracking control for piezoelectric actuators based on the Bouc-Wen model. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Qingdao, China, 3–7 December 2017; p. 16709742. [Google Scholar]
- Mayergoyz, I. Mathematical Models of Hysteresis and Their Applications; Elsevier: New York, NY, USA, 2003. [Google Scholar]
- Wu, Y.; Fang, Y. Hysteresis modeling with deep learning network based on Preisach model. Control. Theory Appl. 2018, 35, 723–731. (In Chinese) [Google Scholar]
- Wu, Y.; Fang, Y.; Liu, C.; Fan, Z.; Wang, C. Gated recurrent unit based frequency-dependent hysteresis modeling and end-to-end compensation. Mech. Syst. Signal Process. 2020, 136, 106501. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Q.; Xiao, Y.; Li, Z. Hysteresis modeling of piezoelectric actuators based on a T-S fuzzy model. Electronics 2022, 11, 2786. [Google Scholar] [CrossRef]
- Liu, J.; Shan, Y.; Qi, N. Creep modeling and identification for piezoelectric actuators based on fractional-order system. Mechatronics 2013, 23, 840–847. [Google Scholar] [CrossRef]
- Mokaberi, B.; Requicha, A.A.G. Drift compensation for automatic nanomanipulation with scanning probe microscopes. IEEE Trans. Autom. Sci. Eng. 2006, 3, 199–207. [Google Scholar] [CrossRef]
- Li, G.; Wang, Y.; Liu, L. Drift compensation in AFM-based nanomanipulation by strategic local scan. IEEE Trans. Autom. Sci. Eng. 2012, 9, 755–762. [Google Scholar] [CrossRef]
- Wu, Y.; Zou, Q. Robust inversion-based 2-DOF control design for output tracking: Piezoelectric-actuator example. IEEE Trans. Control Syst. Technol. 2009, 17, 1069–1082. [Google Scholar]
- Ren, J.; Zou, Q. A control-based approach to accurate nanoindentation quantification in broadband nanomechanical measurement using scanning probe microscope. IEEE Trans. Nanotechnol. 2014, 13, 46–54. [Google Scholar] [CrossRef]
- Wang, J.; Zou, Q. Rapid probe engagement and withdrawal with force minimization in atomic force microscopy: A learning-based online-searching approach. IEEE/ASME Trans. Mechatron. 2020, 25, 581–593. [Google Scholar] [CrossRef]
- Nguyen, M.; Chen, X.; Yang, F. Discrete-time quasi-sliding-mode control with prescribed performance function and its application to piezo-actuated positioning systems. IEEE Trans. Ind. Electron. 2018, 65, 942–950. [Google Scholar] [CrossRef]
- Nguyen, M.; Chen, X. MPC inspired dynamical output feedback and adaptive feedforward control applied to piezo-actuated positioning systems. IEEE Trans. Ind. Electron. 2020, 67, 3921–3931. [Google Scholar] [CrossRef]
- Yong, Y.K.; Moheinami, S.O.R.; Kenton, B.J.; Leang, K.K. Invited review article: High-speed flexure-guided nanopositioning: Mechanical design and control issues. Rev. Sci. Instrum. 2012, 83, 121101. [Google Scholar] [CrossRef] [PubMed]
- Baziyad, A.; Ahmad, I.; Salamah, Y.; Alkuhayli, A. Robust tracking control of piezo-actuated nanopositioning stage using improved inverse LSSVM hysteresis model and RST controller. Actuators 2022, 11, 324. [Google Scholar] [CrossRef]
- Song, G.; Zhao, J.; Zhou, X.; Abreu-Garcia, J.A.D. Tracking control of a piezoceramic actuator with hysteresis compensation using inverse Preisach model. IEEE/ASME Trans. Mechatron. 2005, 10, 198–209. [Google Scholar] [CrossRef]
- Shan, Y.; Leang, K.K. Accounting for hysteresis in repetitive control design: Nanopositioning example. Automatica 2012, 48, 1751–1758. [Google Scholar] [CrossRef]
- Fang, Y.; Feemster, M.; Dawson, D.; Jalili, N. Nonlinear control techniques for an atomic force microscope system. Control. Theory Appl. 2005, 3, 85–92. [Google Scholar] [CrossRef]
- Gu, G.; Zhu, L.; Su, C. High-precision control of piezoelectric nanopositioning stages using hysteresis compensator and disturbance observer. Smart Mater. Struct. 2014, 23, 105007. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and outputfeedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Ding, B.; Li, Y. Hysteresis compensation and sliding mode control with perturbation estimation for piezoelectric actuators. Micromachines 2018, 9, 241. [Google Scholar] [CrossRef]
- Xu, Q. Continuous integral terminal third-order sliding mode motion control for piezoelectric nanopositioning system. IEEE/ASME Trans. Mechatron. 2017, 22, 1828–1838. [Google Scholar] [CrossRef]
- Dang, X.; Tan, Y. RBF neural networks hysteresis modelling for piezoceramic actuator using hybrid model. Mech. Syst. Signal Process. 2007, 21, 430–440. [Google Scholar] [CrossRef]
- Chen, W.; Ballance, D.; Gawthrop, P.; O’Reilly, J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]
- Feemster, M.; Fang, Y.; Dawson, D. Disturbance rejection for a magnetic levitation system. IEEE/ASME Trans. Mechatron. 2006, 11, 709–717. [Google Scholar] [CrossRef]

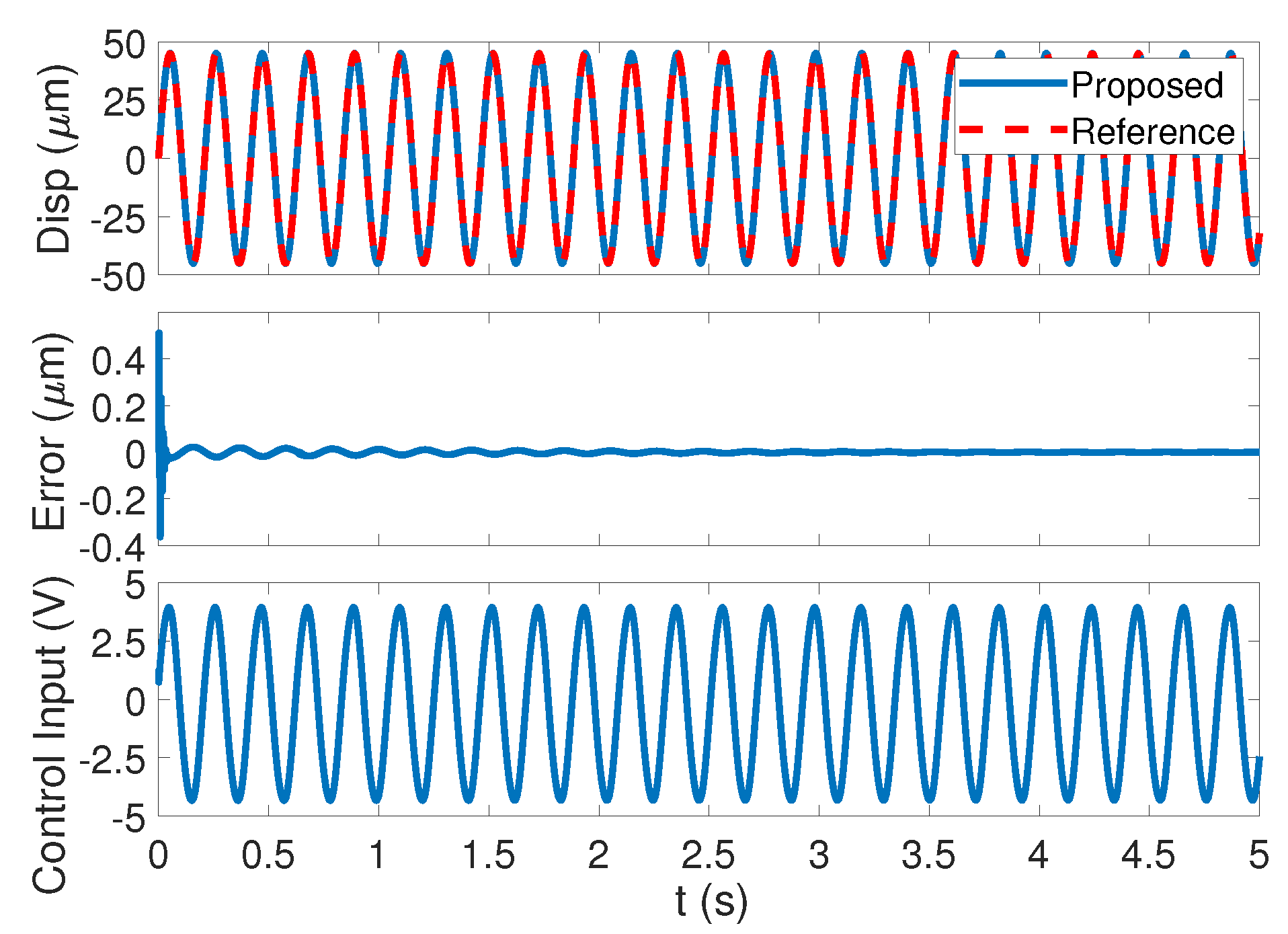
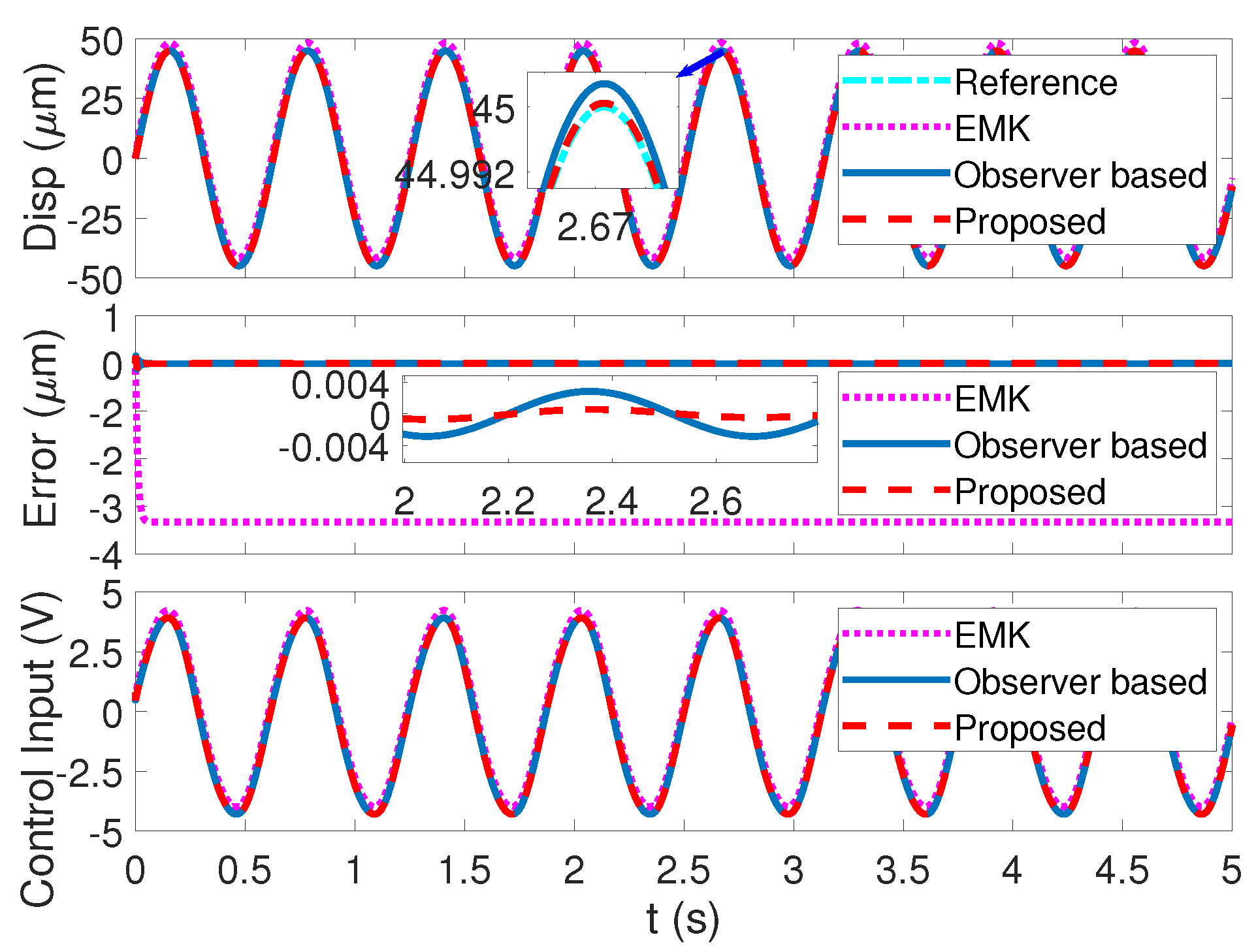




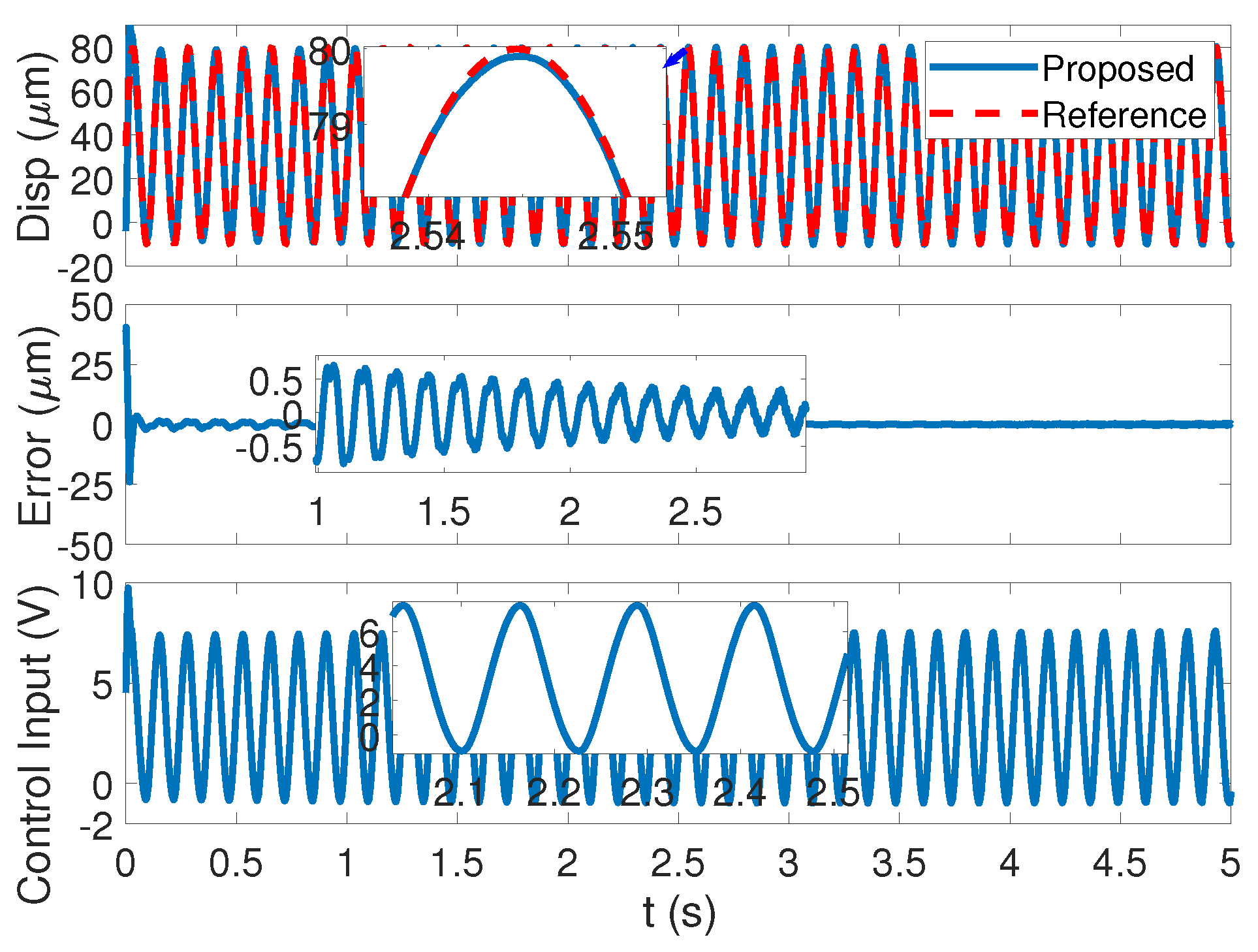

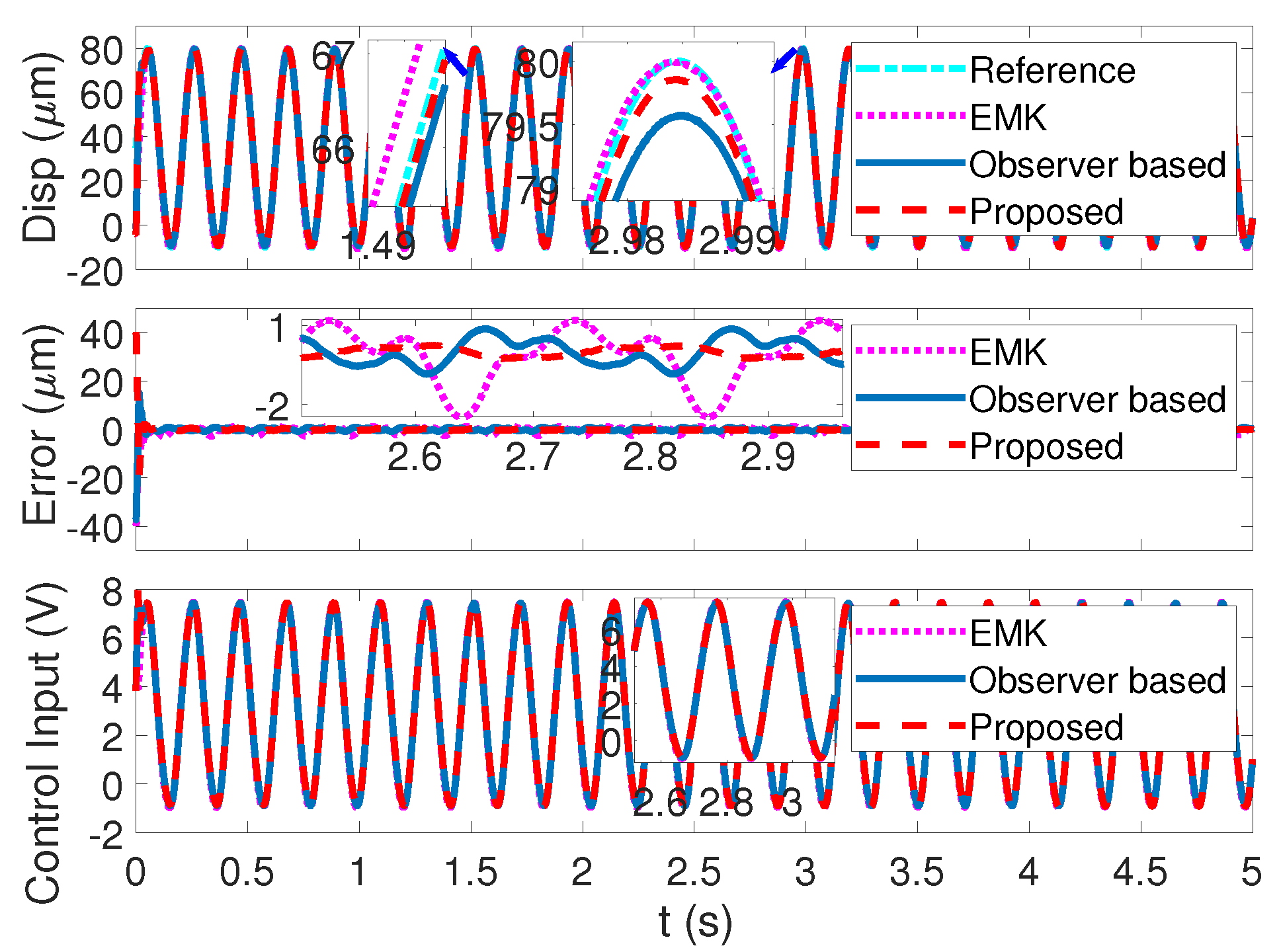


| Methods | Control Gains |
|---|---|
| EMK | |
| Observer-based | |
| Proposed |
| Methods | (MAE) | (MAE) | (MAE) |
|---|---|---|---|
| EMK | m | m | m |
| Observer-based | m | m | m |
| Proposed | m | m | m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Fang, Y.; Wu, Y.; Fan, Z. A Digital Observer-Based Repetitive Learning Composite Control Method for Large Range Piezo-Driven Nanopositioning Systems. Machines 2022, 10, 1092. https://doi.org/10.3390/machines10111092
Liu C, Fang Y, Wu Y, Fan Z. A Digital Observer-Based Repetitive Learning Composite Control Method for Large Range Piezo-Driven Nanopositioning Systems. Machines. 2022; 10(11):1092. https://doi.org/10.3390/machines10111092
Chicago/Turabian StyleLiu, Cunhuan, Yongchun Fang, Yinan Wu, and Zhi Fan. 2022. "A Digital Observer-Based Repetitive Learning Composite Control Method for Large Range Piezo-Driven Nanopositioning Systems" Machines 10, no. 11: 1092. https://doi.org/10.3390/machines10111092
APA StyleLiu, C., Fang, Y., Wu, Y., & Fan, Z. (2022). A Digital Observer-Based Repetitive Learning Composite Control Method for Large Range Piezo-Driven Nanopositioning Systems. Machines, 10(11), 1092. https://doi.org/10.3390/machines10111092






