Analysis of Hydrostatic Bearings Based on a Unstructured Meshing Scheme and Turbulence Model
Abstract
1. Introduction
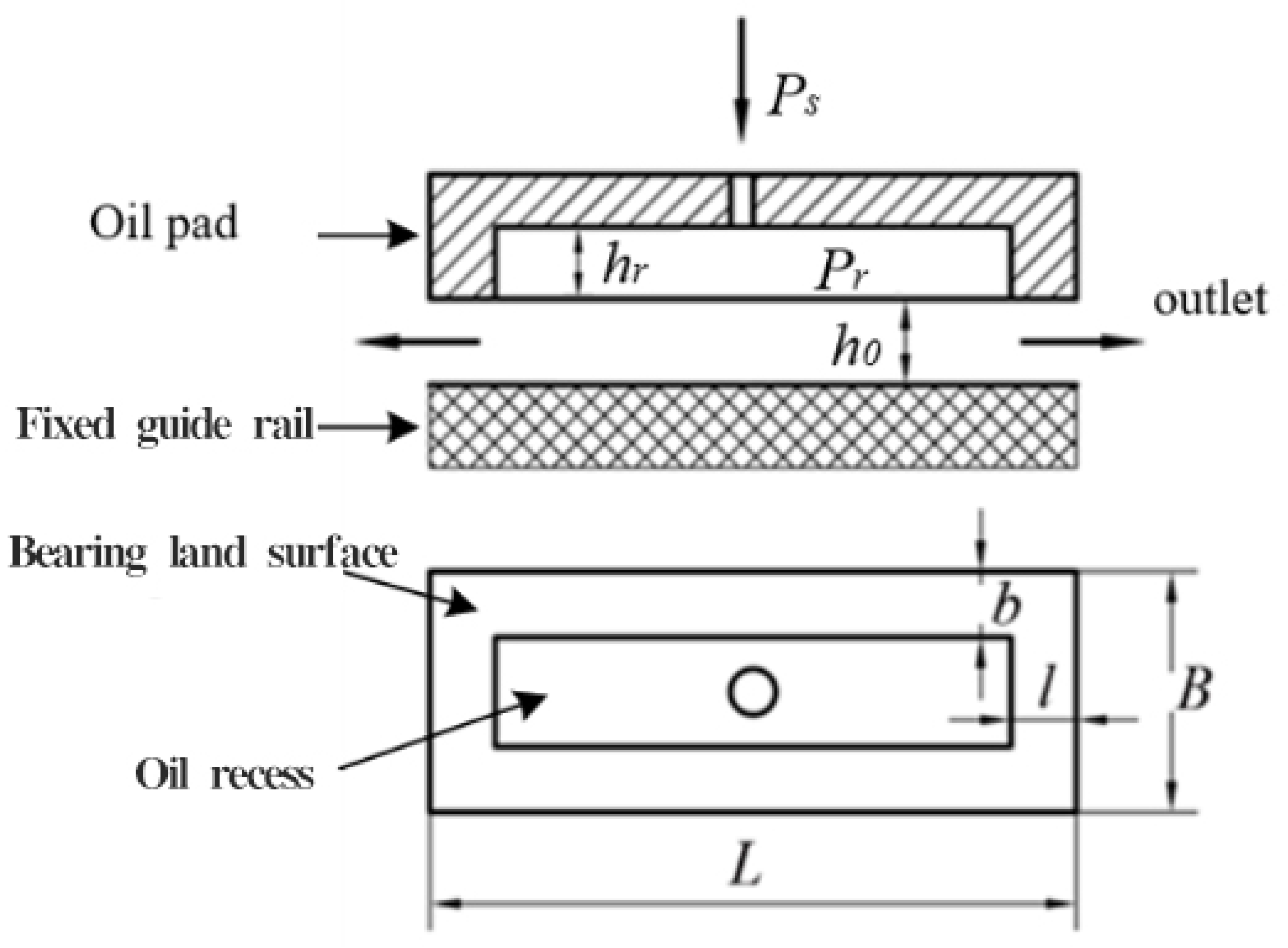
2. Prototype Design and Theoretical Performance Model
2.1. Supporting Capacity
2.2. Stiffness
2.3. Damping
3. Simulation Model
3.1. Flow Governing Equations
3.2. Dynamic Mesh Governing Equation
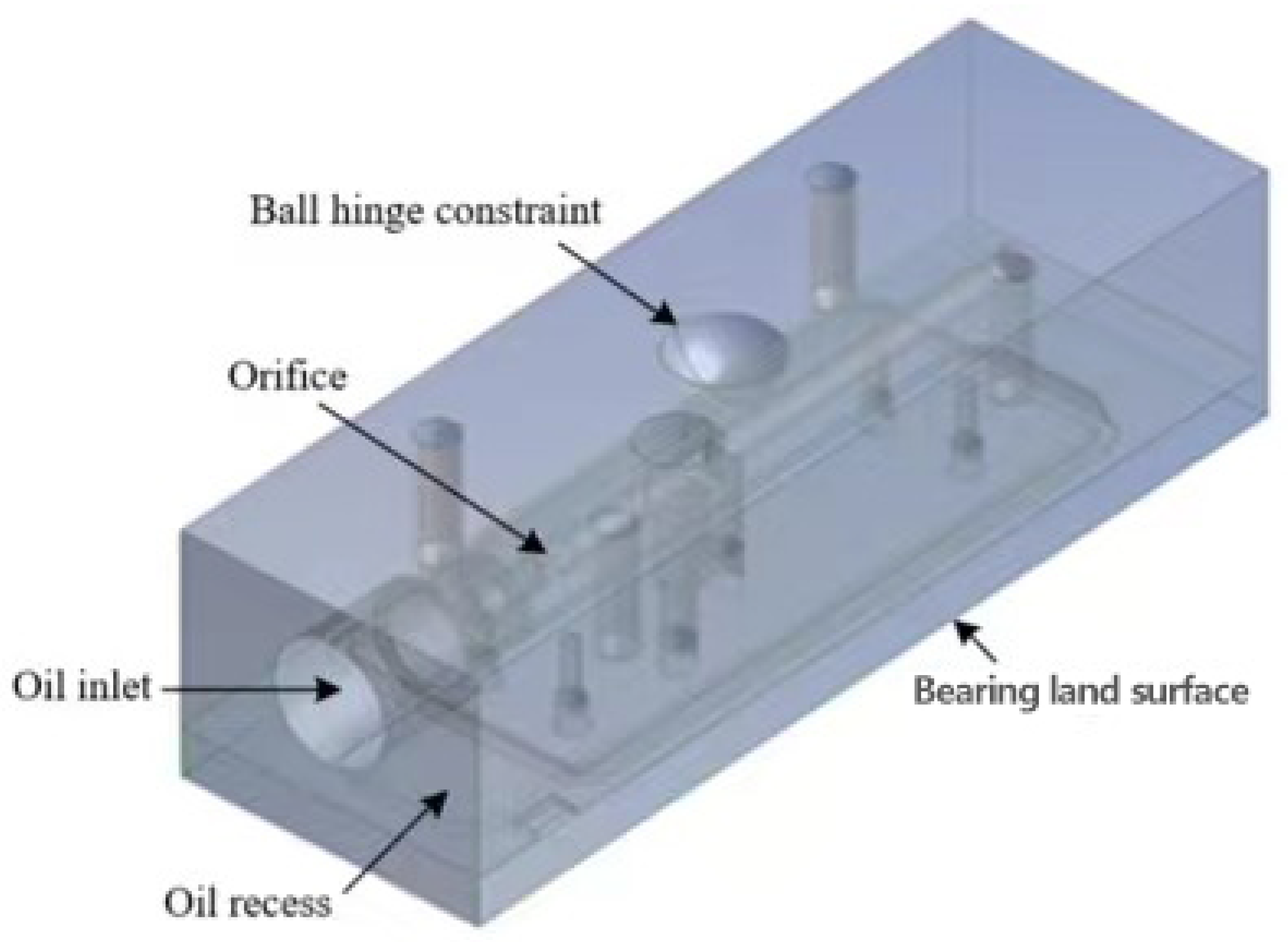
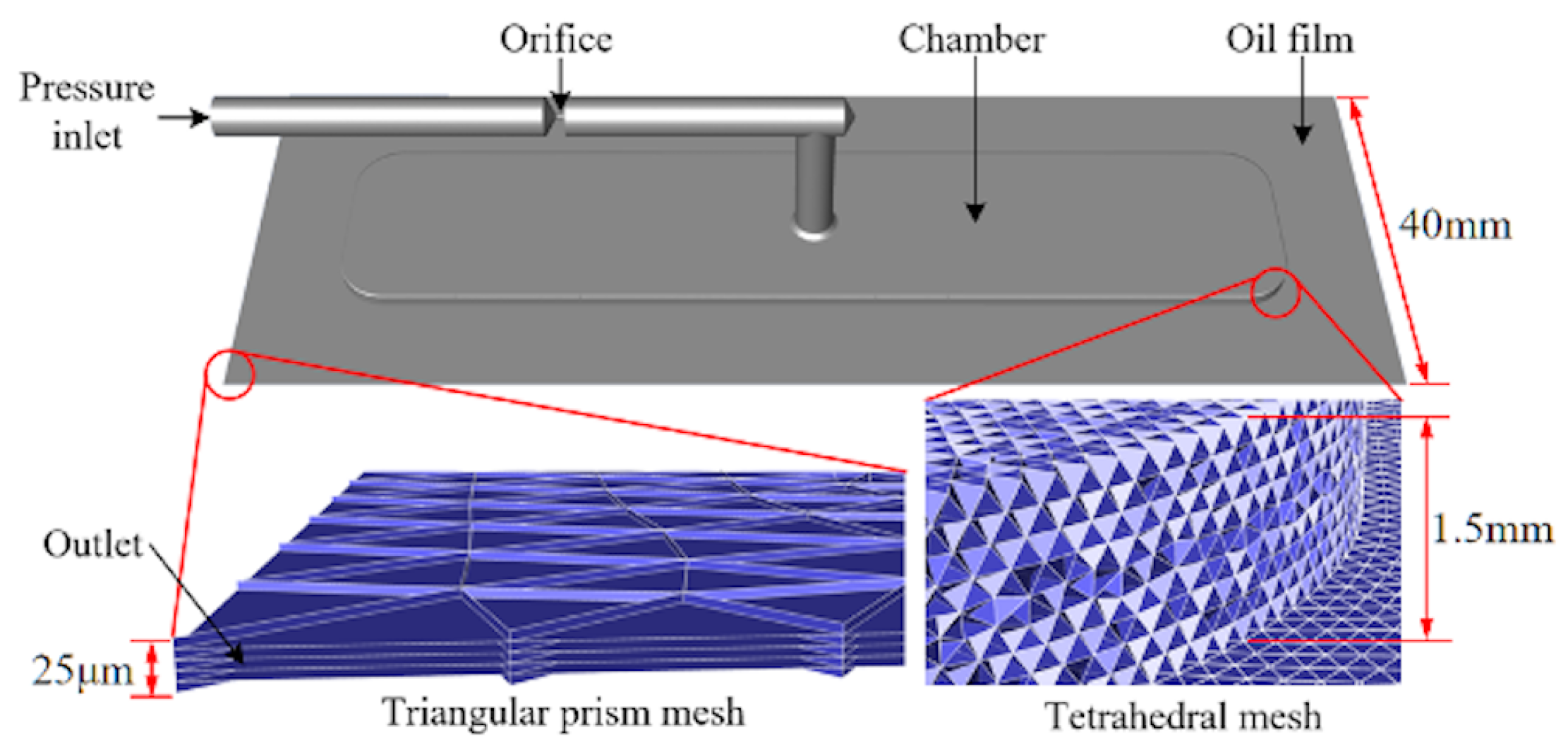
3.3. Generation of Mesh Model for Global Fluid Domain
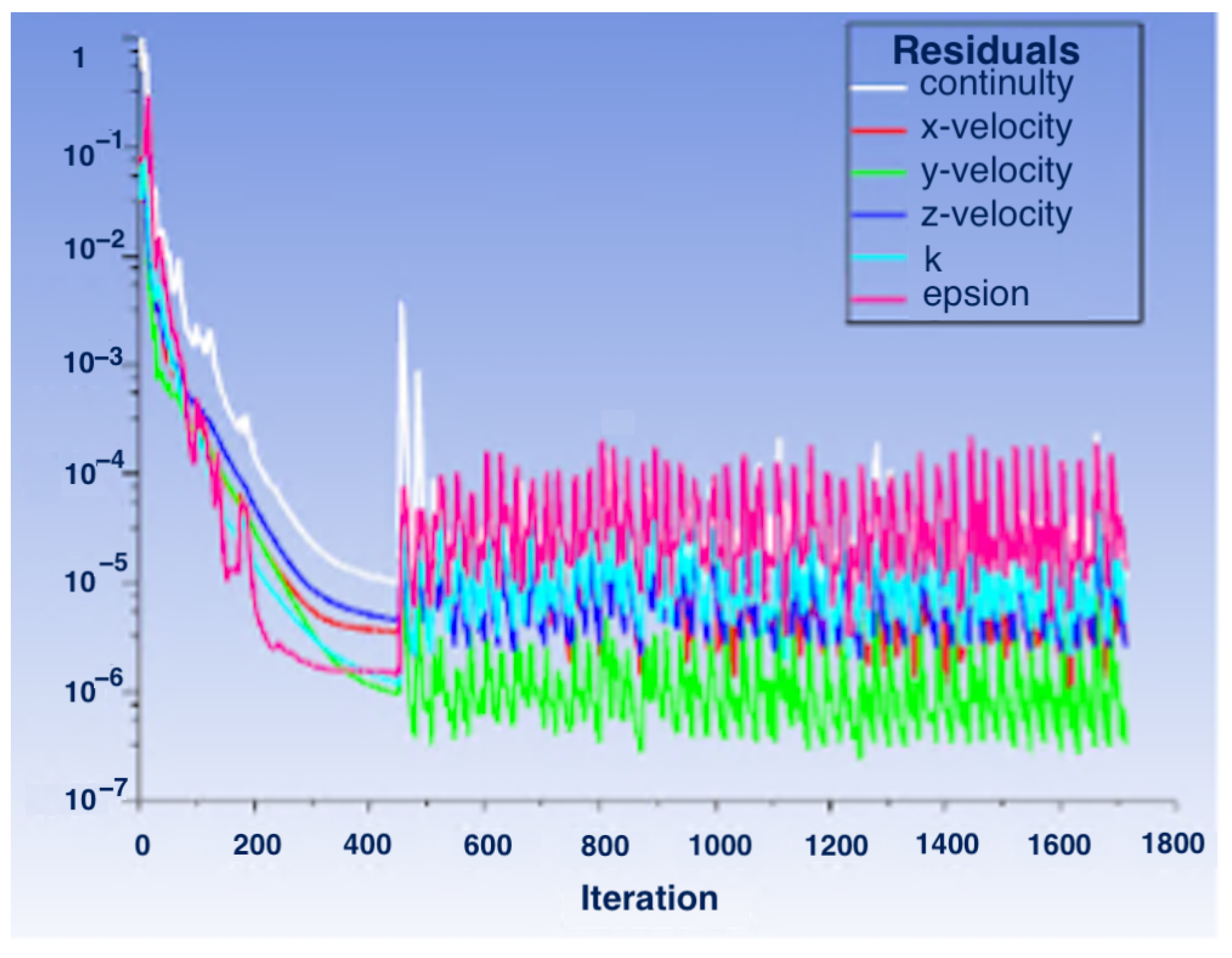
3.4. Boundary Conditions
4. Experimental Condition
5. Verification and Application
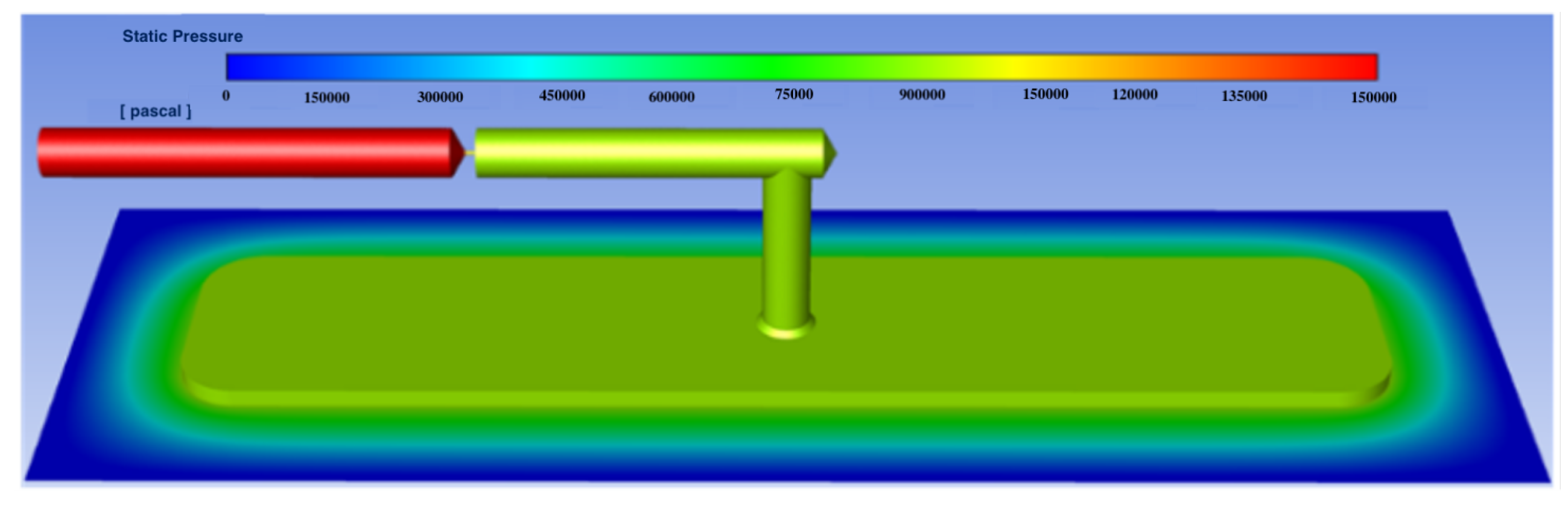
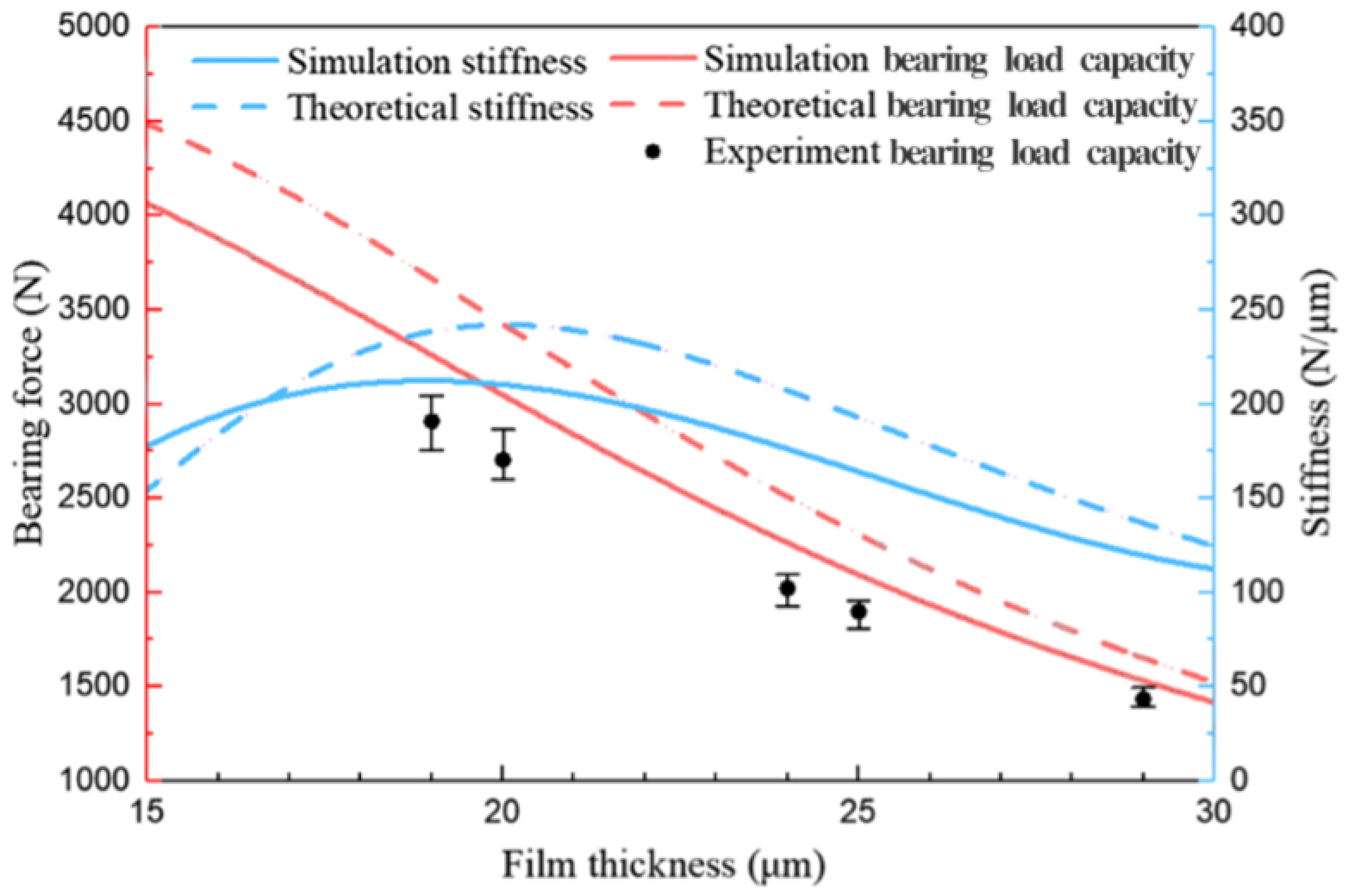
5.1. Compared Results
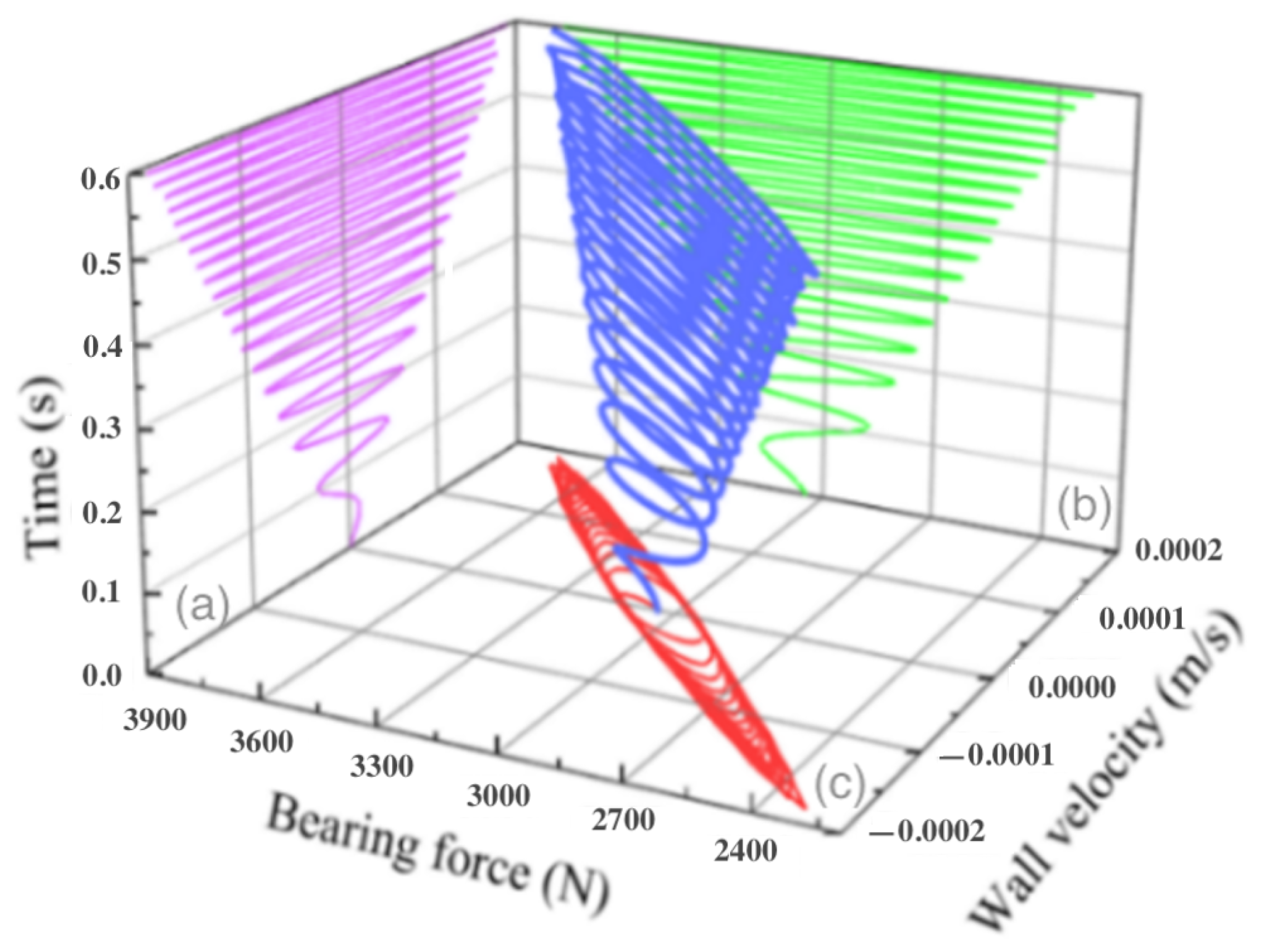
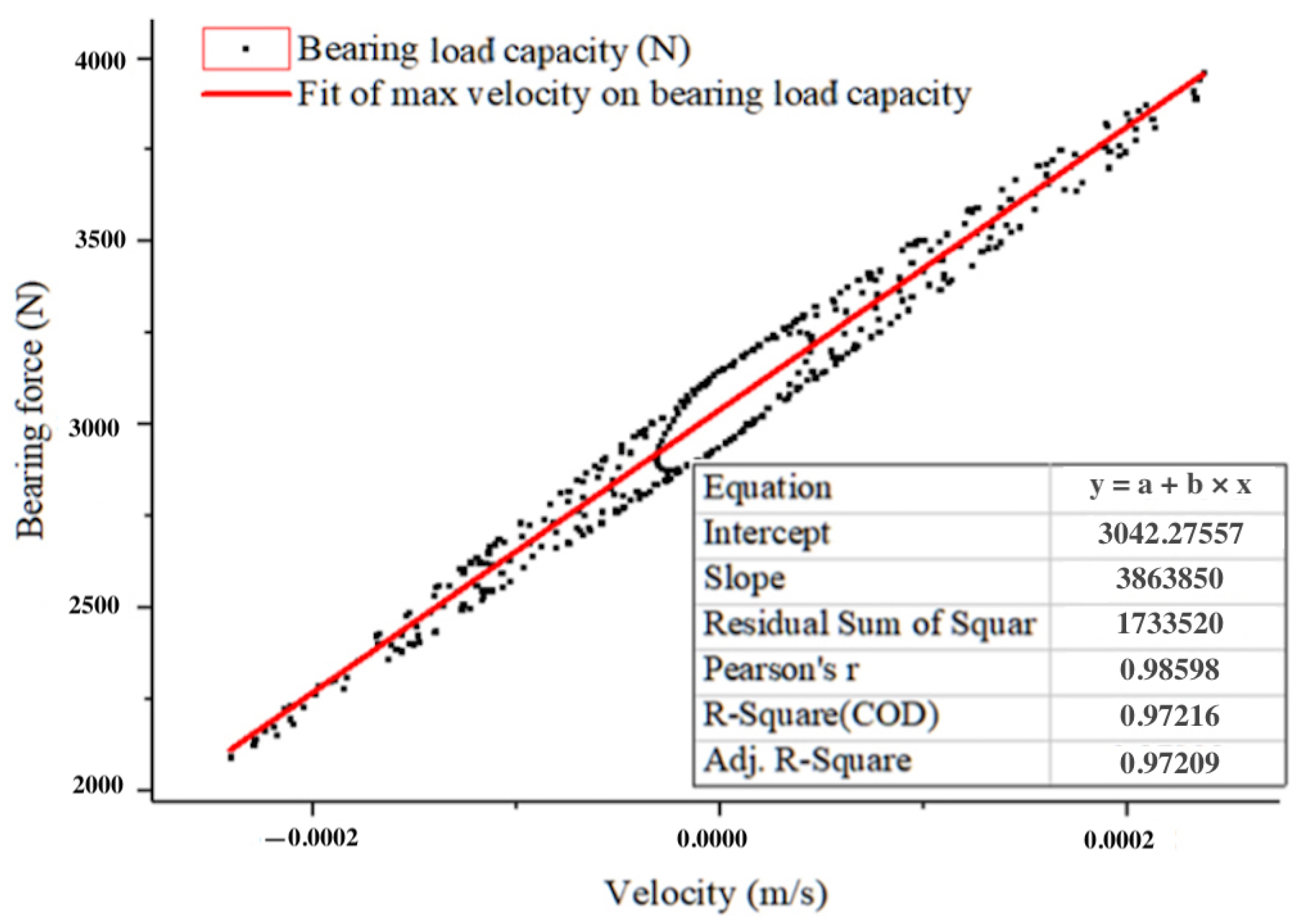
5.2. Frequency Sweep Analysis for Bearing Damping
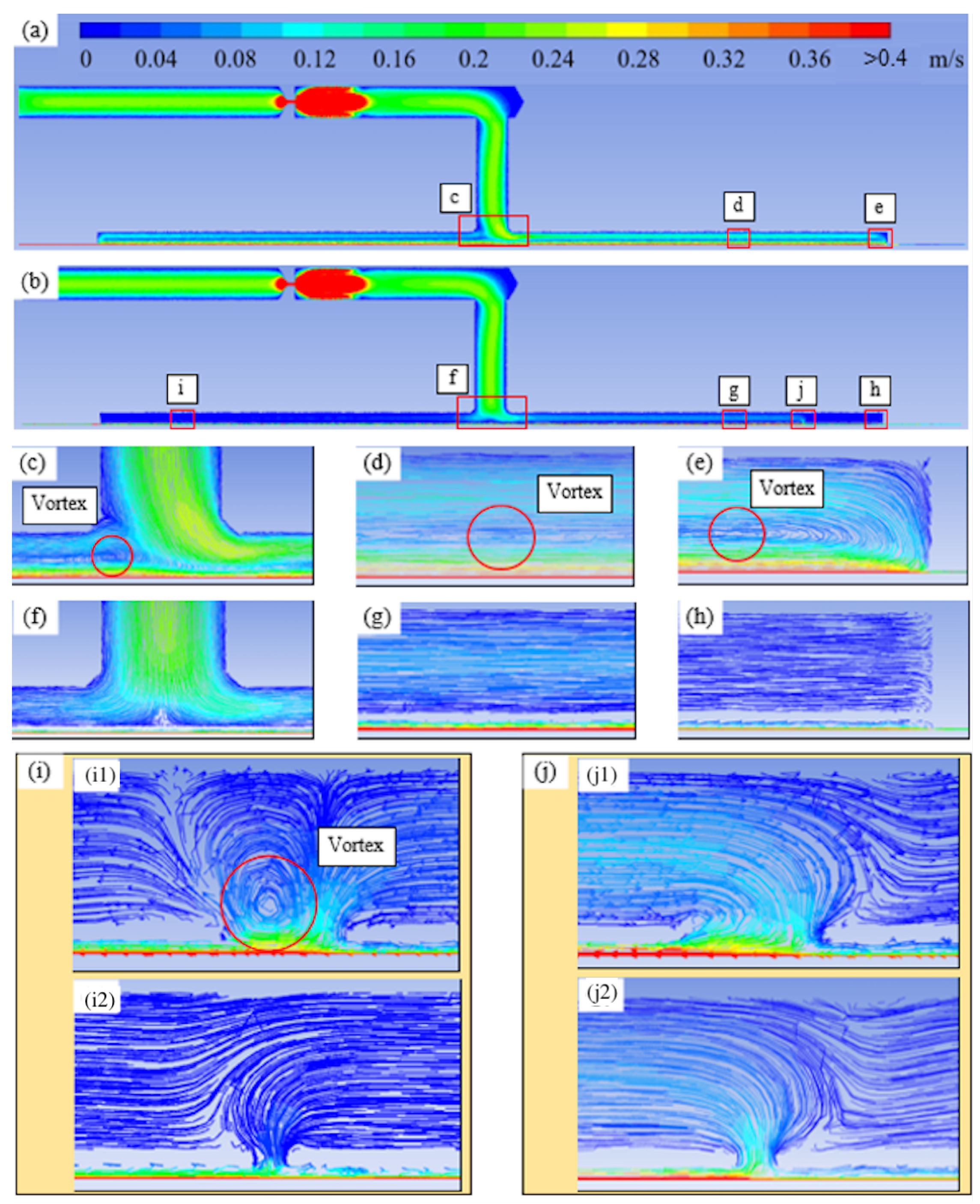
5.3. Vortex Analysis and Suppression
6. Conclusions
- The self-adaptive generation of the global fluid domain mesh model can solve the problem of mesh generation for the model with multi-scale geometric dimensions, and can also increase the efficiency of mesh model processing. Moreover, the maximum skewness of the grids is less than 0.8, which can make the calculation results accurate. Due to the low number of grids, the performance of current personal computers is sufficient to handle the numerical analysis of the mesh model with high efficiency;
- With the help of the above mesh model processing method, the supporting capacity, stiffness and damping were captured by the simulation and verified by the experiment, and were more accurate than the results of theoretical calculation. Thus, this method can make the optimization of the hydrostatic bearing structure more diverse and the analysis more convenient;
- In this study, the flow pattern of the global fluid domain inside the bearings was depicted based on the proposed mesh generation method, and vortices were discovered in the recess. A double-slit septum was installed between the recess and the oil film to suppress the visible vortices without bearing performance attenuation. The structure improvement, combining the advantages of deep and shallow recesses, is expected to make hydrostatic bearings more stable in high-speed conditions for ultra-precision machine tools.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rowe, W.B. Applications of the metacentre and of the general pressure equations, pressure of gases. In Hydrostatic, Aerostatic and Hybrid Bearing Design; Elsevier: Oxford, UK, 2012. [Google Scholar]
- Liu, Z.S.; Zhang, G.H.; Xu, H.J. Performance analysis of rotating externally pressurized air bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 653–663. [Google Scholar] [CrossRef]
- Khatri, C.B.; Sharma, S.C. Influence of textured surface on the performance of non-recessed hybrid journal bearing operating with non-Newtonian lubricant. Tribol. Int. 2016, 95, 221–235. [Google Scholar] [CrossRef]
- Zhang, G.J.; Li, J.; Tian, Z.X.; Huang, Y.; Chen, R.C. Film Shape Optimization for Two-Dimensional Rough Slider Bearings. Tribol. Trans. 2015, 59, 17–27. [Google Scholar] [CrossRef]
- Shen, F.; Chen, C.L.; Liu, Z.M. Effect of Pocket Geometry on the Performance of a Circular Thrust Pad Hydrostatic Bearing in Machine Tools. Tribol. Trans. 2014, 57, 700–714. [Google Scholar] [CrossRef]
- Liang, P.; Lu, C.H.; Pan, W.; Li, S.Y. A new method for calculating the static performance of hydrostatic journal bearing. Tribol. Int. 2014, 77, 72–77. [Google Scholar] [CrossRef]
- Shao, J.P.; Zhou, L.M.; Li, H.M.; Yang, X.D.; Zhang, Y.Q.; Chi, M.S. Influence of the oil Cavity Depth on Dynamic Pressure Effect of Hydrostatic Thrust Bearing. In Proceedings of the 2009 International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2009; pp. 11–14. [Google Scholar]
- Shao, J.P.; Liu, G.D.; Yu, X.D. Simulation and experiment on pressure field characteristics of hydrostatic hydrodynamic hybrid thrust bearings. Ind. Lubr. Tribol. 2018, 71, 102–108. [Google Scholar] [CrossRef]
- Xu, X.Q.; Shao, J.P.; Yang, X.D.; Zang, Y.Q.; Yu, X.D.; Gao, B.W. Simulation on Multi-oil-cavity and Multi-oil-pad Hydrostatic Bearings. Appl. Mech. Mater. 2013, 274, 274–277. [Google Scholar] [CrossRef]
- Gao, S.Y.; Cheng, K.; Chen, S.J.; Ding, H.; Fu, H.Y. CFD based investigation on influence of orifice chamber shapes for the design of aerostatic thrust bearings at ultra-high-speed spindles. Tribol. Int. 2015, 92, 211–221. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Fan, L.G.; Li, R.; Dai, C.X.; Yu, X.D. Simulation and experimental analysis of supporting characteristics of multiple oil pad hydrostatic bearing disk. J. Hydrodyn. 2013, 25, 236–241. [Google Scholar] [CrossRef]
- Horvat, F.E.; Braun, M.J. Comparative Experimental and Numerical Analysis of Flow and Pressure Fields Inside Deep and Shallow Pockets for a Hydrostatic Bearing. Tribol. Trans. 2011, 54, 548–567. [Google Scholar] [CrossRef]
- Tauviqirrahman, M.; Jamari, J.; Susilowati, S.; Pujiastuti, C.; Setiyana, B.; Pasaribu, A.H.; Ammarullah, M.I. Performance Comparison of Newtonian and Non-Newtonian Fluid on a Heterogeneous Slip/No-Slip Journal Bearing System Based on CFD-FSI Method. Fluids 2022, 7, 225. [Google Scholar] [CrossRef]
- Rasep, Z.; Yazid, M.N.; Samion, S. A study of cavitation effect in a journal bearing using CFD: A case study of engine oil, palm oil and water. J. Tribol. 2021, 28, 48–62. [Google Scholar]
- Tauviqirrahman, M.; Jamari, J.; Wicaksono, A.A.; Muchammad, M.; Susilowati, S.; Ngatilah, Y.; Pujiastuti, C. CFD Analysis of Journal Bearing with a Heterogeneous Rough/Smooth Surface. Lubricants 2021, 9, 88. [Google Scholar] [CrossRef]
- Shang, Y.; Cheng, K.; Ding, H.; Chen, S.; Samion, S. Design and Optimization of the Surface Texture at the Hydrostatic Bearing and the Spindle for High Precision Machining. Machines 2022, 10, 806. [Google Scholar] [CrossRef]
- Ghezali, F.; Bouzidane, A.; Thomas, M. 3D Numerical investigation of pressure field of an orifice compensated hydrostatic bearing. Mech. Ind. 2017, 18, 101. [Google Scholar] [CrossRef]
- Li, D.Y. Study on CFD solution method for static characteristics of hybrid oil film bearing. Appl. Mech. Mater. 2012, 155–156, 236–240. [Google Scholar] [CrossRef]
- Hou, Z.Q.; Xiong, W.L.; Yang, X.B.; Yuan, J.L. Study on Dynamic Characteristics of a Hydrostatic and Hydrodynamic Journal Bearings for Small Diameter Grinding Spindle. Adv. Mater. Res. 2012, 497, 99–104. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, S.; Ma, L.; Xu, W.W.; Zheng, S.Y. Stiffness and damping coefficients for journal bearing using the 3D transient flow calculation. J. Mech. Sci. Technol. 2017, 31, 2083–2091. [Google Scholar] [CrossRef]
- Liu, C.P.; Hu, J.P. A magnetorheological hydrostatic guideway system for machining vibration control. J. Braz. Soc. Mech. Sci. 2019, 41, 12. [Google Scholar] [CrossRef]
- Lin, Q.Y.; Wei, Z.Y.; Wang, N.; Chen, W. Analysis on the lubrication performances of journal bearing system using computational fluid dynamics and fluid-structure interaction considering thermal influence and cavitation. Tribol. Int. 2013, 10, 8–15. [Google Scholar] [CrossRef]
- Cui, C.; Guo, T.N.; Wang, Y.J.; Dai, Q. Research on Carrying Capacity of Hydrostatic Slideway on Heavy-duty Gantry CNC. AIP Conf. Proc. 2017, 1839, 020159. [Google Scholar]
- Wang, W.; Cheng, X.H.; Zhang, M.; Gong, W.W.; Cui, H.L. Effect of the deformation of porous materials on the performance of aerostatic bearings by fluid-solid interaction method. Tribol. Int. 2020, 150, 106391. [Google Scholar] [CrossRef]
- Wen, Z.P.; Wu, J.W.; Tan, J.B. An adaptive modeling method for multi-throttle aerostatic thrust bearing. Tribol. Int. 2020, 149, 105830. [Google Scholar] [CrossRef]
- Maamari, N.; Krebs, A.; Weikert, S.; Wild, H.; Wegener, K. Stability and dynamics of an orifice based aerostatic bearing with a compliant back plate. Tribol. Int. 2019, 138, 279–296. [Google Scholar] [CrossRef]
- Helene, M.; Arghir, M.; Frene, J. Numerical study of the pressure pattern in a two-dimensional hybrid journal bearing recess, laminar, and turbulent flow results. J. Tribol. 2003, 125, 283–290. [Google Scholar] [CrossRef]
- Wu, H.; Huang, Y.; Cui, H.; Rong, Y. A passive compensated method with hydraulic transmission for static infinite stiffness of thrust bearing. Tribol. Int. 2021, 163, 107193. [Google Scholar] [CrossRef]
- Hinze, J.O. Reference book for research of mechanics of turbulence. In Turbulence; McGraw-Hill Publishing Co.: New York, NY, USA, 1975. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Research of predictions of turbulent flow. In Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Berry, R.A.; Saurel, R.; LeMetayer, O. The discrete equation method (DEM) for fully compressible, two-phase flows in ducts of spatially varying cross-section. Nucl. Eng. Des. 2010, 240, 3797–3818. [Google Scholar] [CrossRef]
- Czaban, A. CFD analysis of hydrodynamic pressure distribution in non-Newtonian oil in journal bearing lubrication gap. Solid State Phenom. 2015, 220–221, 37–42. [Google Scholar] [CrossRef]
- Bharti, R.P.; Chhabra, R.P.; Eswaran, V. Steady flow of power law fluids across a circular cylinder. Can. J. Chem. Eng. 2006, 84, 406–421. [Google Scholar] [CrossRef]



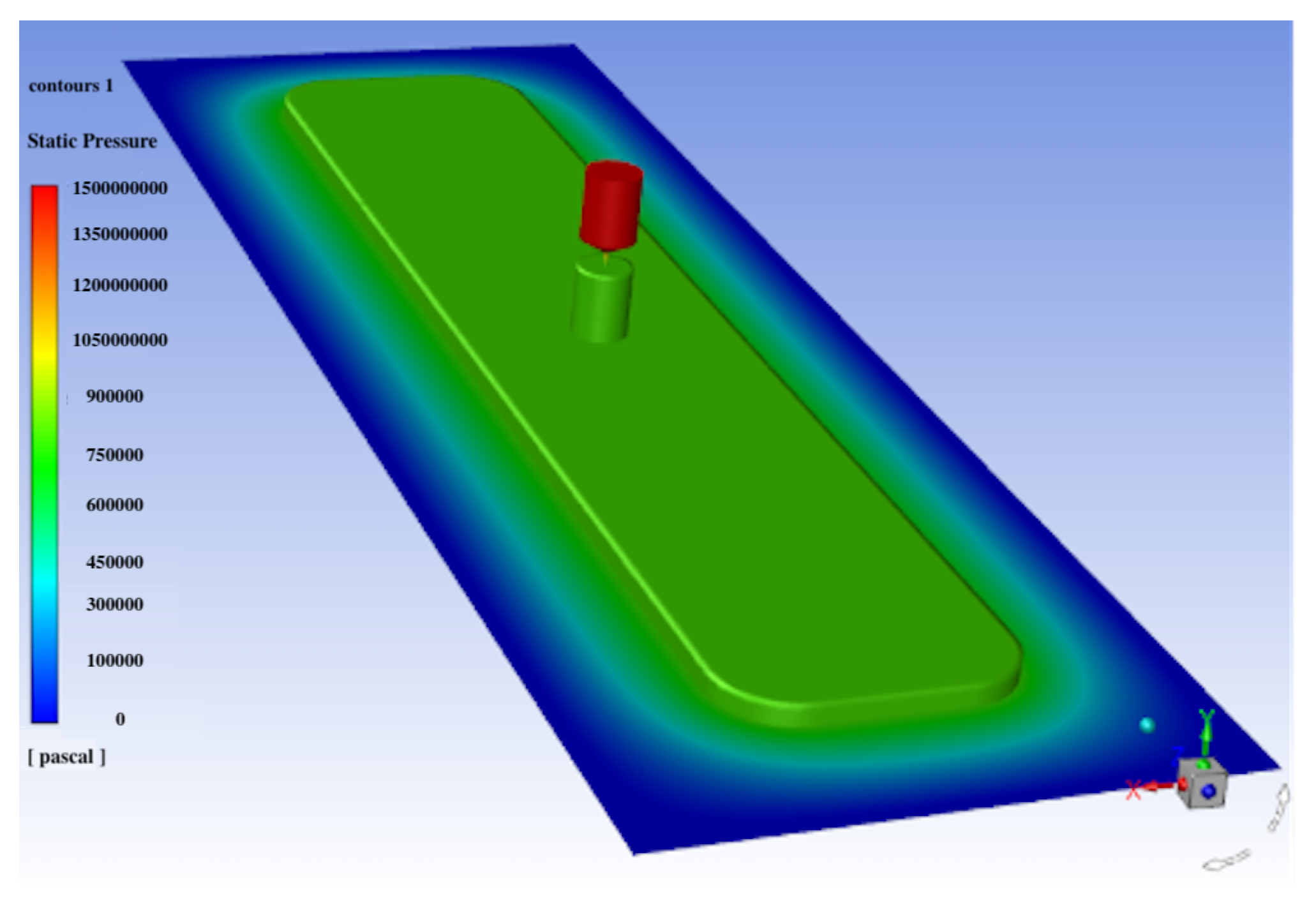
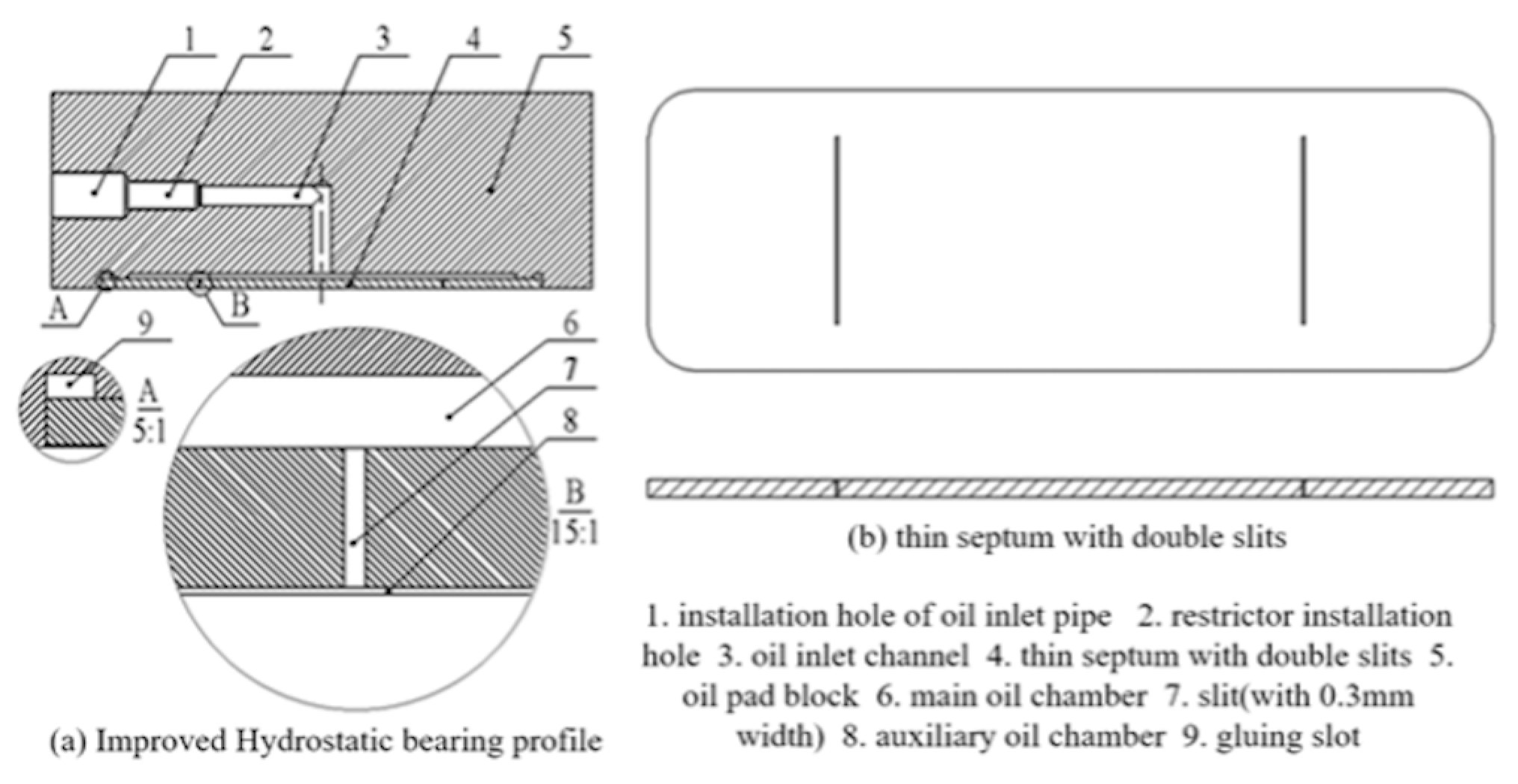

| Symbol | Quantity | Value |
|---|---|---|
| Supply pressure | 1.5 MPa | |
| B | Bearing width | 40 mm |
| L | Bearing length | 120 mm |
| b,l | Bearing land width | 10 mm |
| Measured film thickness | 19; 20; 24; 25; 29 m | |
| Recess depth | 1.5 mm | |
| Orifice flow coefficient | 0.6 | |
| Oil density | 844 kg/m | |
| Dynamic viscosity | 0.0175 Pa·s | |
| c | Specific heat | 2090 J/(kg·K) |
| Symbol | Quantity | Value |
|---|---|---|
| Solver | Absolute, Transient, Pressure-Based | |
| Viscous model | Standard k- | |
| Fluid density | 844 kg/m | |
| Viscosity type | Non-Newtonian-power-law | |
| Viscosity consistency index | 0.01403 Pa·s | |
| n | Viscosity power-law index | 0.99759 |
| Inlet gauge total pressure | 1,500,008 Pa | |
| Inlet initial gauge pressure | 1,500,000 Pa | |
| Outlet gauge pressure | 0 Pa | |
| Wall roughness height | 1.6 m | |
| Time step size | 1 s | |
| Number of time steps | 325 | |
| Dynamic mesh method | Smoothing | |
| Film bottom surface velocity | 0.1 m/s | |
| Initial film thickness | 30.1 m | |
| Terminational film thickness | 14.9 m | |
| Solution method | SIMPLE | |
| Residual absolute criteria | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wu, H.; Rong, Y. Analysis of Hydrostatic Bearings Based on a Unstructured Meshing Scheme and Turbulence Model. Machines 2022, 10, 1072. https://doi.org/10.3390/machines10111072
Wang Y, Wu H, Rong Y. Analysis of Hydrostatic Bearings Based on a Unstructured Meshing Scheme and Turbulence Model. Machines. 2022; 10(11):1072. https://doi.org/10.3390/machines10111072
Chicago/Turabian StyleWang, Yingjie, Hao Wu, and Youmin Rong. 2022. "Analysis of Hydrostatic Bearings Based on a Unstructured Meshing Scheme and Turbulence Model" Machines 10, no. 11: 1072. https://doi.org/10.3390/machines10111072
APA StyleWang, Y., Wu, H., & Rong, Y. (2022). Analysis of Hydrostatic Bearings Based on a Unstructured Meshing Scheme and Turbulence Model. Machines, 10(11), 1072. https://doi.org/10.3390/machines10111072








