Residual-Electrical-Endurance Prediction of AC Contactor Based on CNN-GRU
Abstract
1. Introduction
2. Principles
2.1. Neighbor Component Analysis
2.2. Maximal Information Coefficient
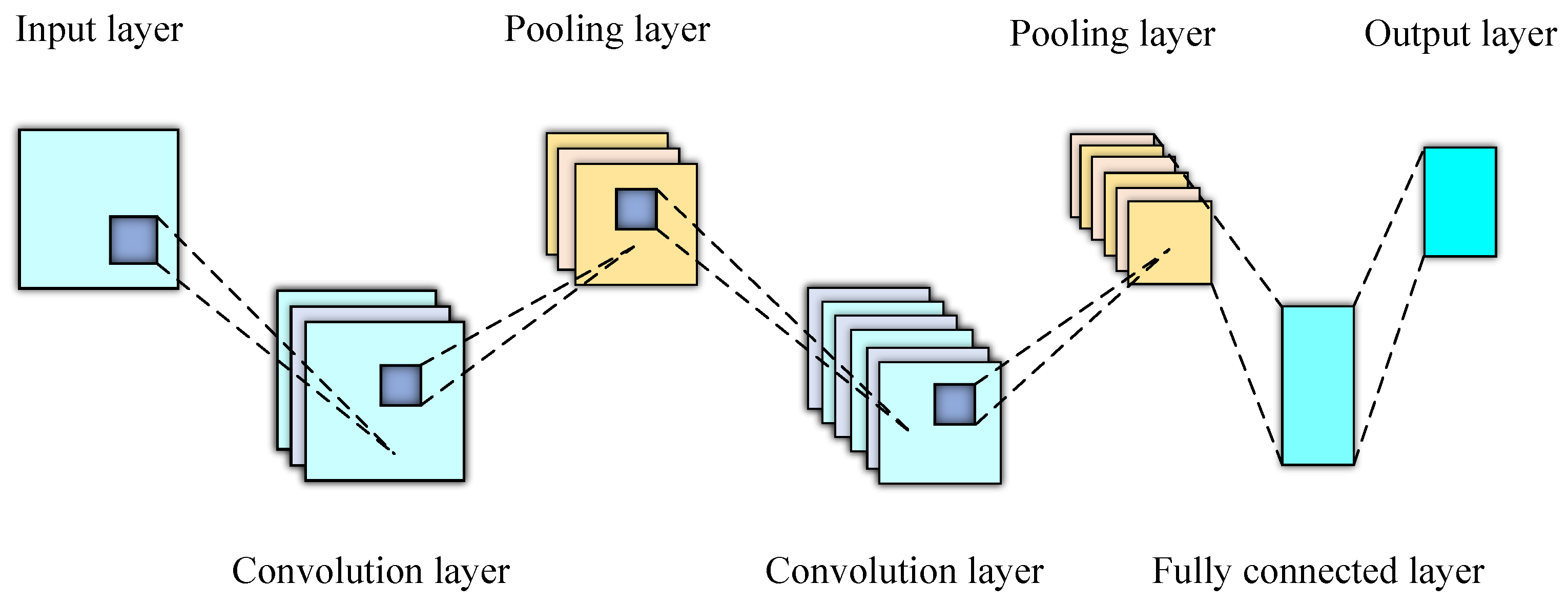
2.3. Convolutional Neural Network
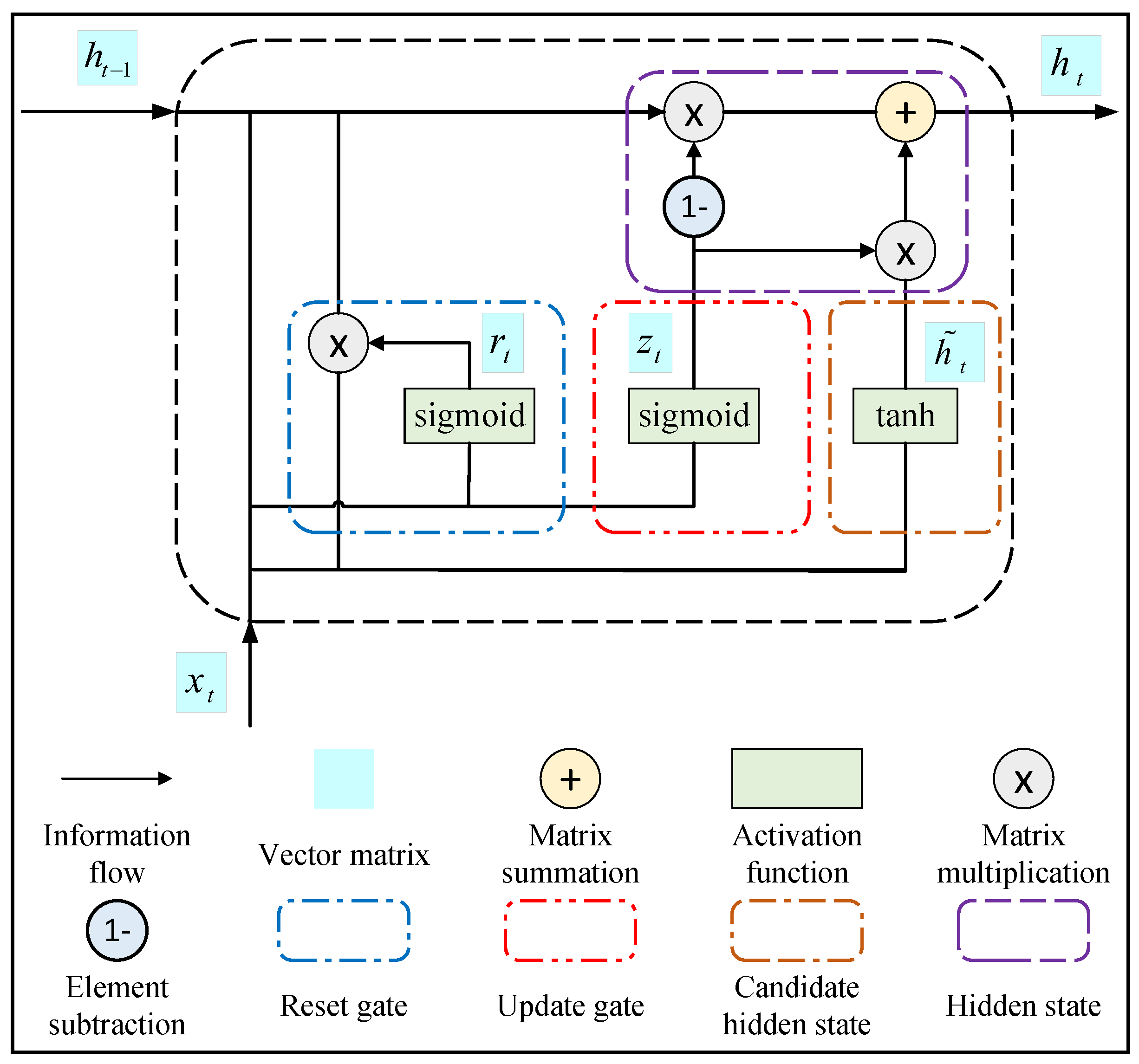
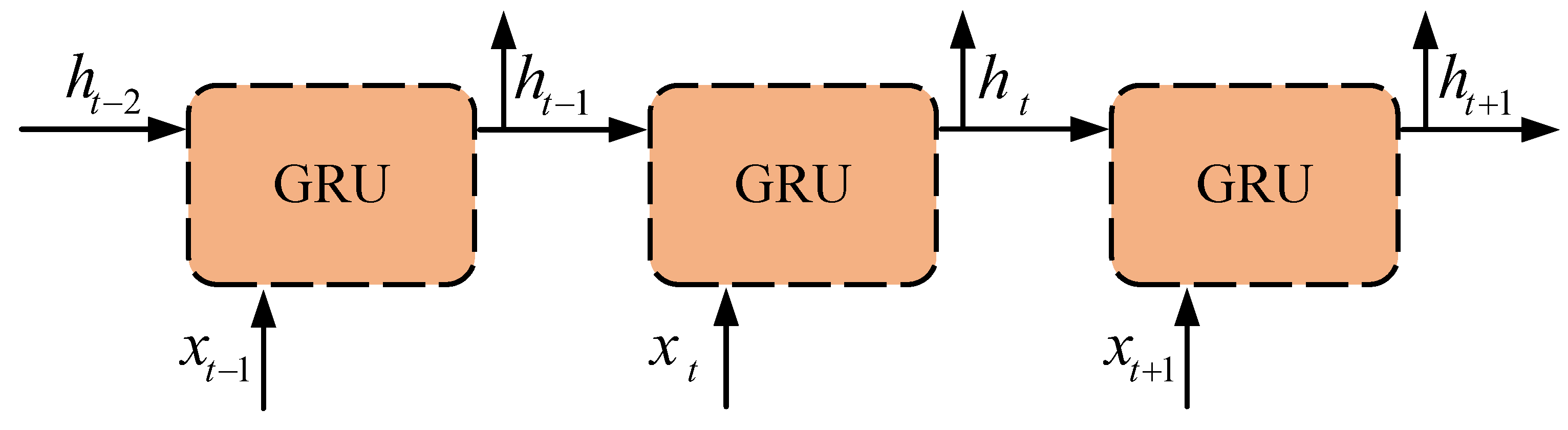
2.4. Gated Recurrent Unit
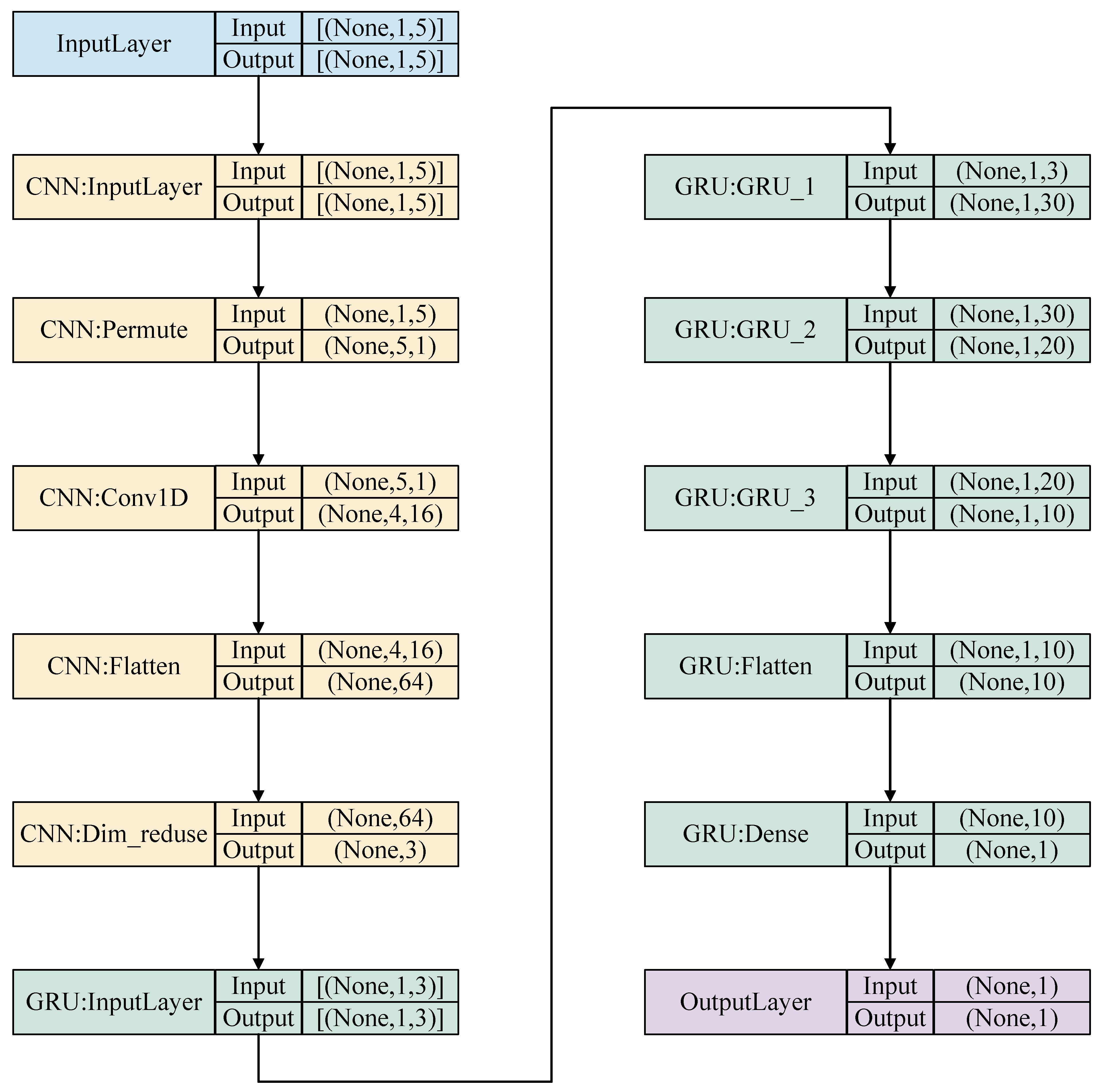
3. Prediction Model
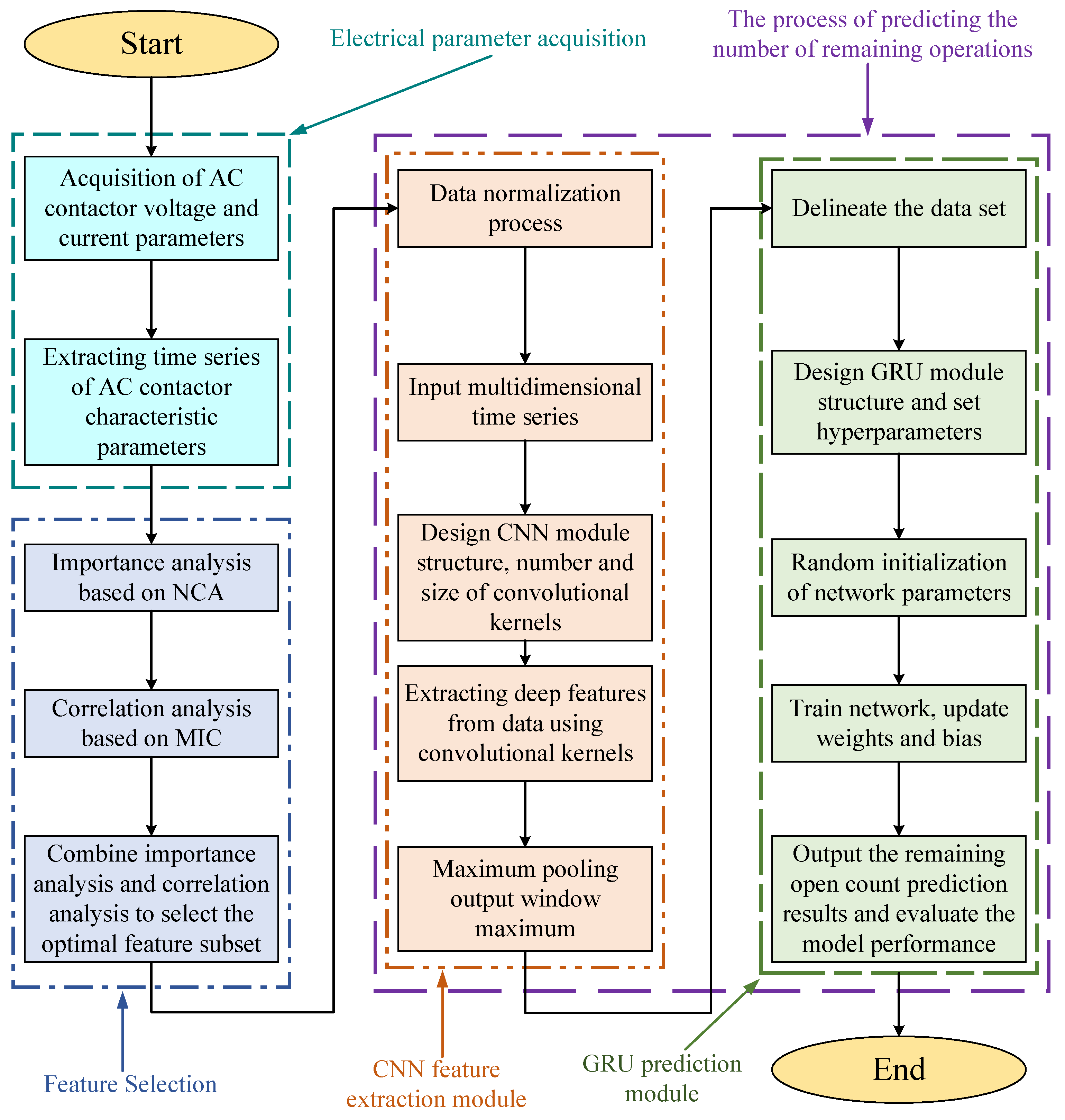
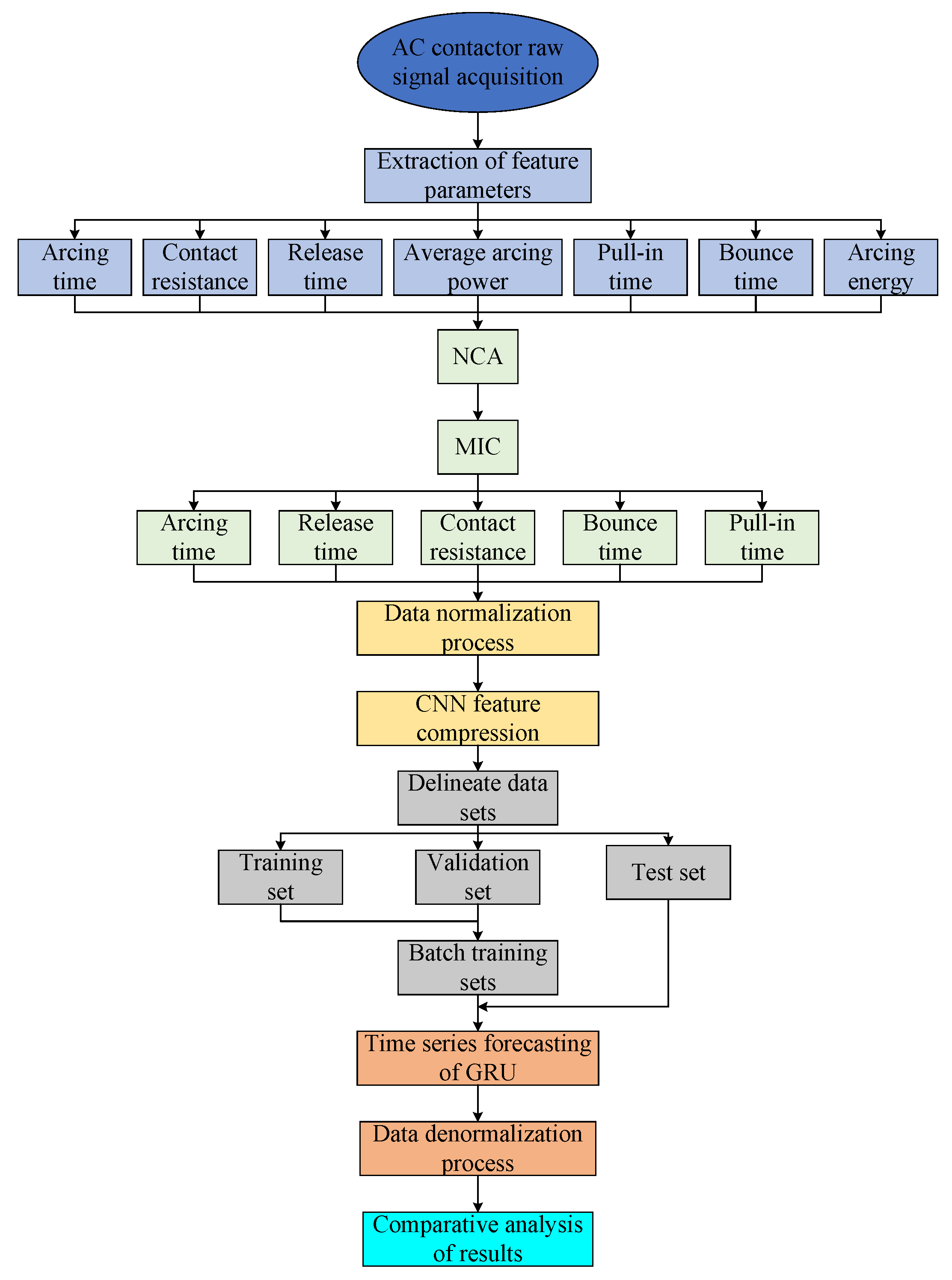
3.1. Overview of Prediction Model
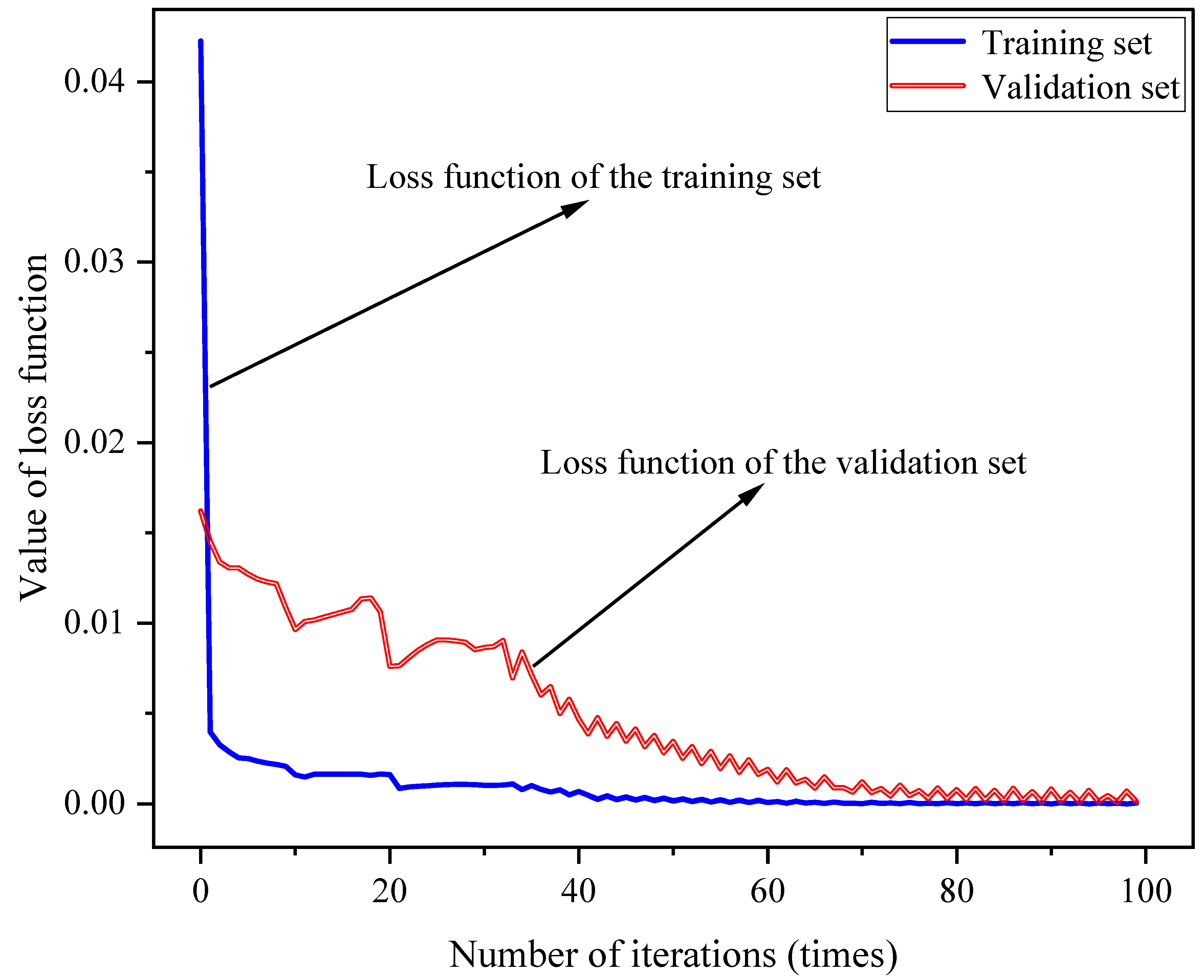
3.2. Model Loss-Function and Evaluation Index
4. Experimental Design and Feature Extraction
4.1. Construction of Test Platform
4.2. Extracting Feature Parameters
5. Case Analysis
5.1. Feature Parameter Extraction
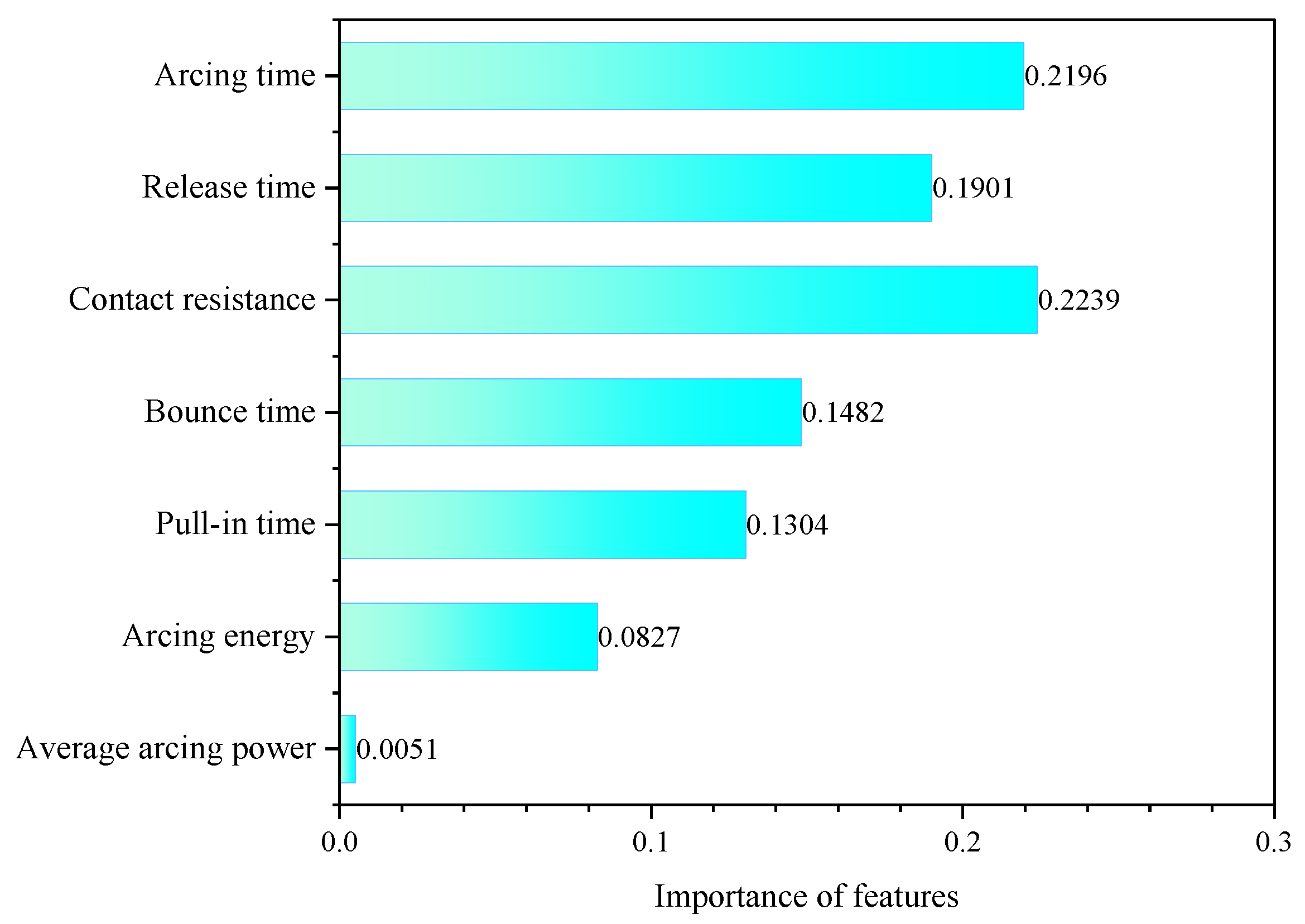
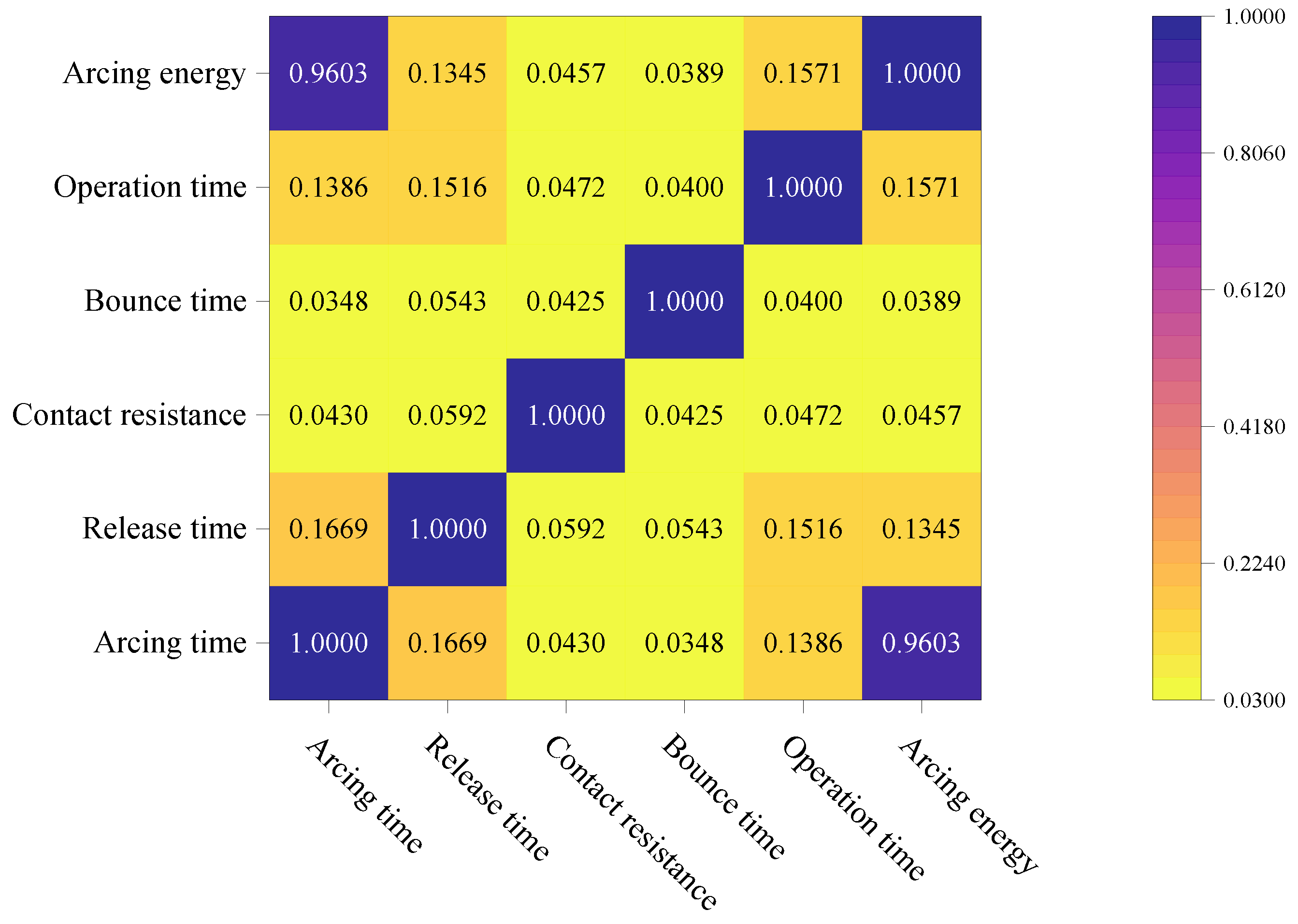
5.2. Feature Parameters Selection
5.3. Model Parameters Setting
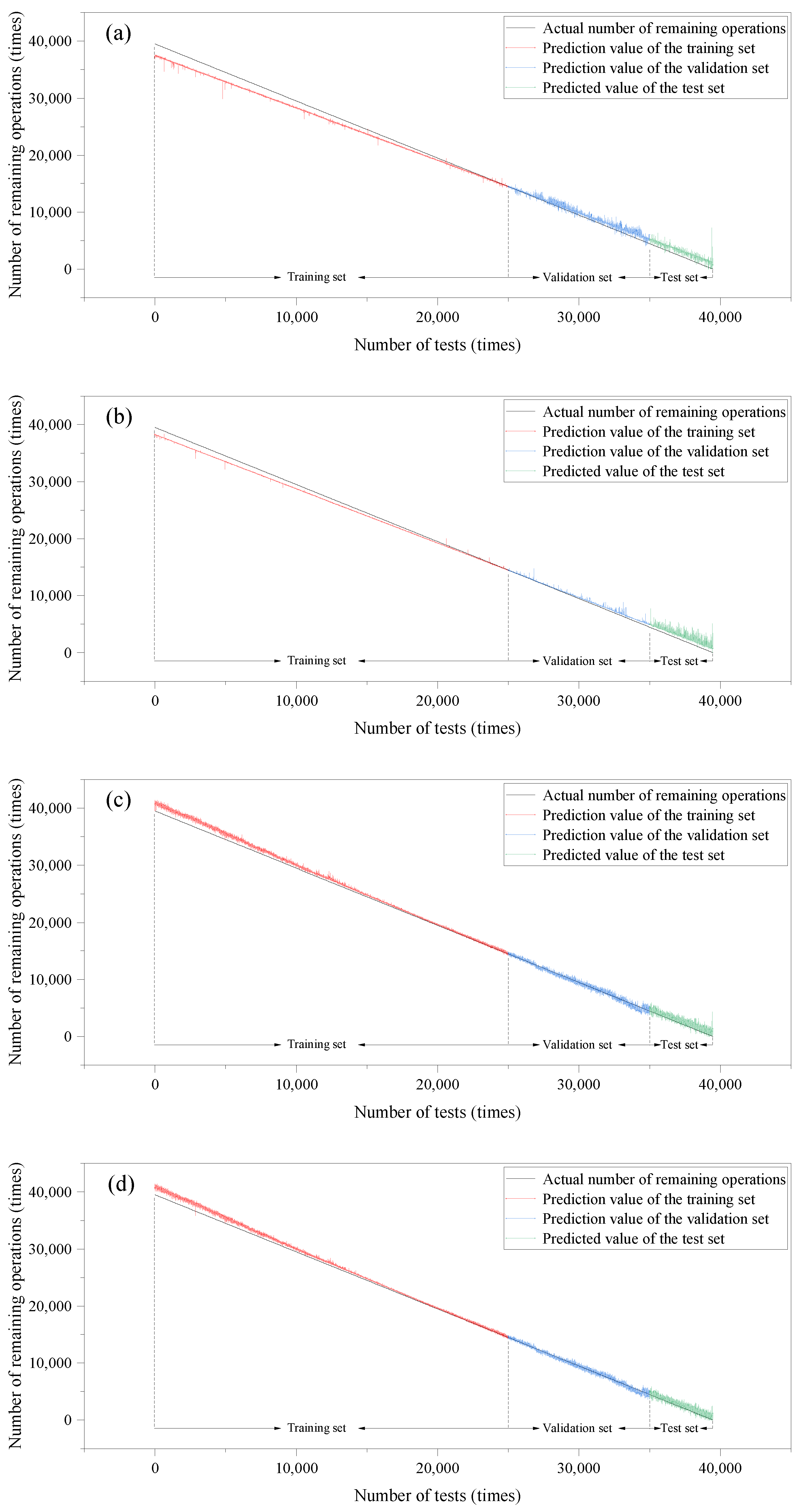
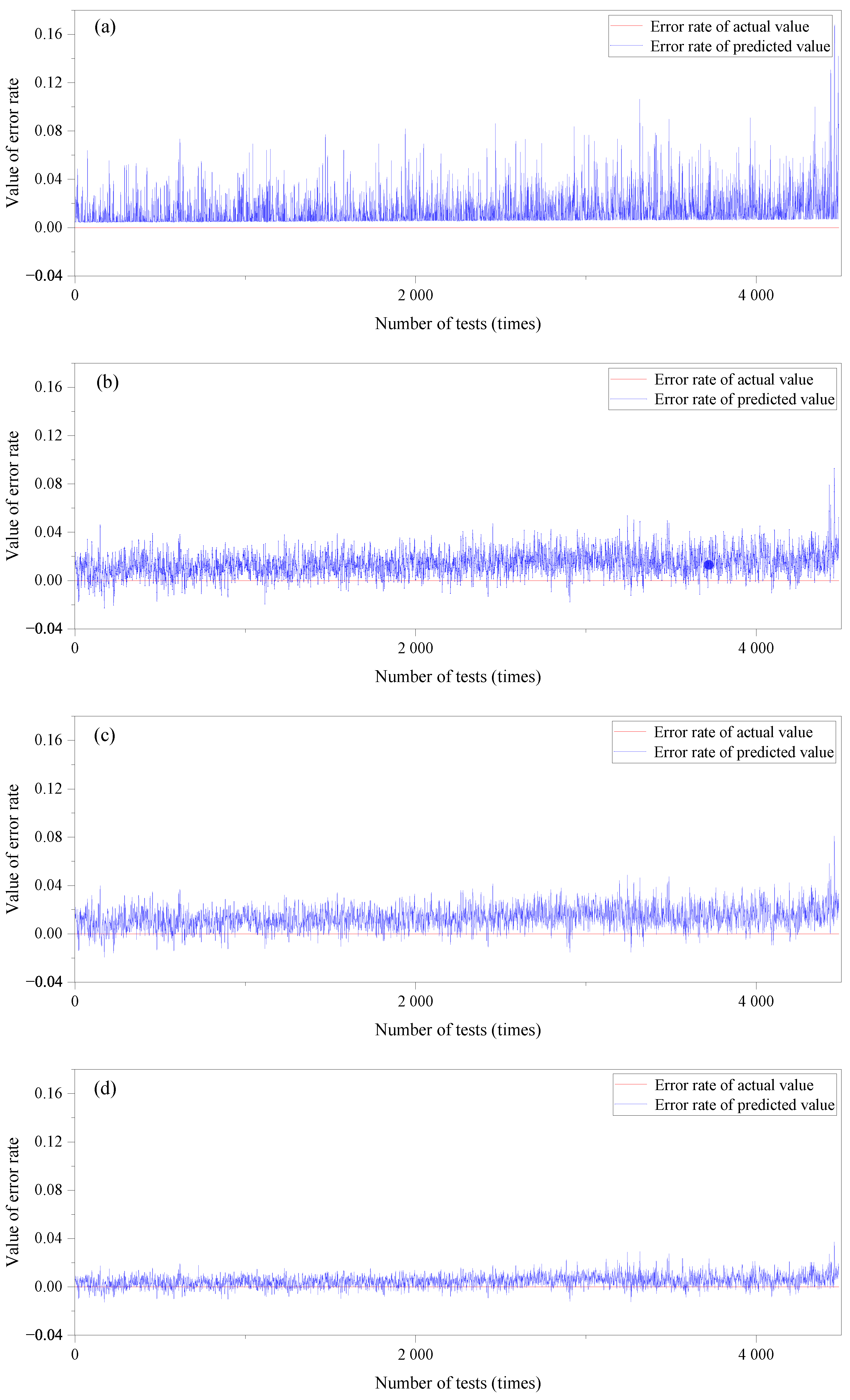
5.4. Comparison of Prediction Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, S.; Wang, Y.; Liu, Z.; Cao, Y.; Zhu, S. Condition evaluation of AC contactor based on the grey fuzzy theory. In Proceedings of the 2017 4th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Xi’an, China, 22–25 October 2017; pp. 238–242. [Google Scholar]
- Zhang, C.; Xu, Z. A Digital Controller for Series of AC Contactors. In Proceedings of the 2019 5th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Kitakyushu Japan, 13–16 October 2019; pp. 702–705. [Google Scholar]
- Yang, D.; Gao, X.; Ma, Z.; Cui, E.; Zhang, H. Novel voltage sag protection topology of contactors for uninterrupted switching capability. IEEE Trans. Ind. Appl. 2018, 54, 3170–3178. [Google Scholar] [CrossRef]
- Zong, M.; heng Li, Y. Researchon the key technology of contactor electrical life test. In Proceedings of the 2015 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 25–28 October 2015; pp. 312–315. [Google Scholar]
- Wu, Z.; Wu, G.; Huang, H.; You, Y. A novel residual electrical endurance prediction method for low-voltage electromagnetic alternating current contactors. IEEE Trans. Components Packag. Manuf. Technol. 2015, 5, 465–473. [Google Scholar]
- Kumari, S.; Kumar-M, P.; Muralidhar, M. Reliability estimation of distribution components-Contactors. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 2066–2070. [Google Scholar]
- Wu, Z.; Wu, G.; Chen, C.; Fang, Y.; Pan, L.; Huang, H. A novel breaking strategy for electrical endurance extension of electromagnetic alternating current contactors. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 6, 749–756. [Google Scholar] [CrossRef]
- Zheng, S.; Niu, F.; Li, K.; Huang, S.; Liu, Z.; Wu, Y. Analysis of electrical life distribution characteristics of AC contactor based on performance degradation. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 1604–1613. [Google Scholar] [CrossRef]
- Cui, H.; Wu, Z.; Wu, G.; Xu, X.; You, Y.; Fang, Y. Convolutional neural networks for electrical endurance prediction of alternating current contactors. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 1785–1793. [Google Scholar] [CrossRef]
- Sun, S.; Wang, Q.; Du, T.; Wang, J.; Li, S.; Zong, J. Quantitative evaluation of electrical life of AC contactor based on initial characteristic parameters. IEEE Trans. Instrum. Meas. 2020, 70, 1–10. [Google Scholar] [CrossRef]
- Li, K.; Zhao, C.; Niu, F.; Zheng, S.; Duan, Y.; Huang, S.; Wu, Y. Electrical performance degradation model and residual electrical life prediction for AC contactor. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 400–417. [Google Scholar] [CrossRef]
- Abirami, S.; Ruthvik, S.; Ali, M.S.; Kumar, R.S.; Kumar, J.S. AC Contactor Electrical Health Estimator Model. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1145, p. 012070. [Google Scholar]
- Kumbhar, A.; Dhawale, P.G.; Kumbhar, S.; Patil, U.; Magdum, P. A comprehensive review: Machine learning and its application in integrated power system. Energy Rep. 2021, 7, 5467–5474. [Google Scholar] [CrossRef]
- Wang, S.; Jin, S.; Bai, D.; Fan, Y.; Shi, H.; Fernandez, C. A critical review of improved deep learning methods for the remaining useful life prediction of lithium-ion batteries. Energy Rep. 2021, 7, 5562–5574. [Google Scholar] [CrossRef]
- Yang, B.; Liu, R.; Zio, E. Remaining useful life prediction based on a double-convolutional neural network architecture. IEEE Trans. Ind. Electron. 2019, 66, 9521–9530. [Google Scholar] [CrossRef]
- Kido, S.; Hirano, Y.; Hashimoto, N. Detection and classification of lung abnormalities by use of convolutional neural network (CNN) and regions with CNN features (R-CNN). In Proceedings of the 2018 International Workshop on Advanced Image Technology (IWAIT), Chiang Mai, Thailand, 7–9 January 2018; pp. 1–4. [Google Scholar]
- Bedi, J.; Toshniwal, D. Empirical mode decomposition based deep learning for electricity demand forecasting. IEEE Access 2018, 6, 49144–49156. [Google Scholar] [CrossRef]
- Shen, C. A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Yang, S.; Yu, X.; Zhou, Y. Lstm and gru neural network performance comparison study: Taking yelp review dataset as an example. In Proceedings of the 2020 International Workshop on Electronic Communication and Artificial Intelligence (IWECAI), Shanghai, China, 12–14 June 2020; pp. 98–101. [Google Scholar]
- Que, Z.; Jin, X.; Xu, Z. Remaining useful life prediction for bearings based on a gated recurrent unit. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Wei, M.; Gu, H.; Ye, M.; Wang, Q.; Xu, X.; Wu, C. Remaining useful life prediction of lithium-ion batteries based on Monte Carlo Dropout and gated recurrent unit. Energy Rep. 2021, 7, 2862–2871. [Google Scholar] [CrossRef]
- Roweis, S.; Hinton, G.; Salakhutdinov, R. Neighbourhood component analysis. Adv. Neural Inf. Process. Syst.(NIPS) 2004, 17, 4. [Google Scholar]
- Zhang, C.; Liu, L.; Zhang, S.; Huang, C. Microarray Data Classification Based on Neighbourhood Components Analysis Projection Method. In Proceedings of the 2021 IEEE 6th International Conference on Big Data Analytics (ICBDA), Xiamen, China, 5–8 March 2021; pp. 123–127. [Google Scholar]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Liang, T.; Zhang, Q.; Liu, X.; Lou, C.; Liu, X.; Wang, H. Time-frequency maximal information coefficient method and its application to functional corticomuscular coupling. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 2515–2524. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Zhao, Q.; Zheng, D.; Ning, Y.; Gao, Y. A short-term load forecasting model of multi-scale CNN-LSTM hybrid neural network considering the real-time electricity price. Energy Rep. 2020, 6, 1046–1053. [Google Scholar] [CrossRef]
- Zhai, N.; Yao, P.; Zhou, X. Multivariate Time Series Forecast in Industrial Process Based on XGBoost and GRU. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; Volume 9, pp. 1397–1400. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- GB14048.4-2020; Low-Voltage Switchgear and Control Equipment Part 4-1: Contactors and Motor Starters Electromechanical Contactors and Motor Starters. Standards Press of China: Beijing, China, 2011.
- Liu, Y.; Shuxin, L.; Cao, Y. Research on State Characterization of Switching Device Based on Modal Similarity Measurement. In Proceedings of the CSEE 2022, Lisbon, Portugal, 10–12 April 2022; pp. 173–176. [Google Scholar]
- Yang, Y.; Zhihong, X.; Fan, Y. An Indicator Reduction Method for Contactor’s Performance Evaluation. In Proceedings of the 2019 4th International Conference on Intelligent Green Building and Smart Grid (IGBSG), Yichang, China, 6–9 September 2019; pp. 173–176. [Google Scholar]

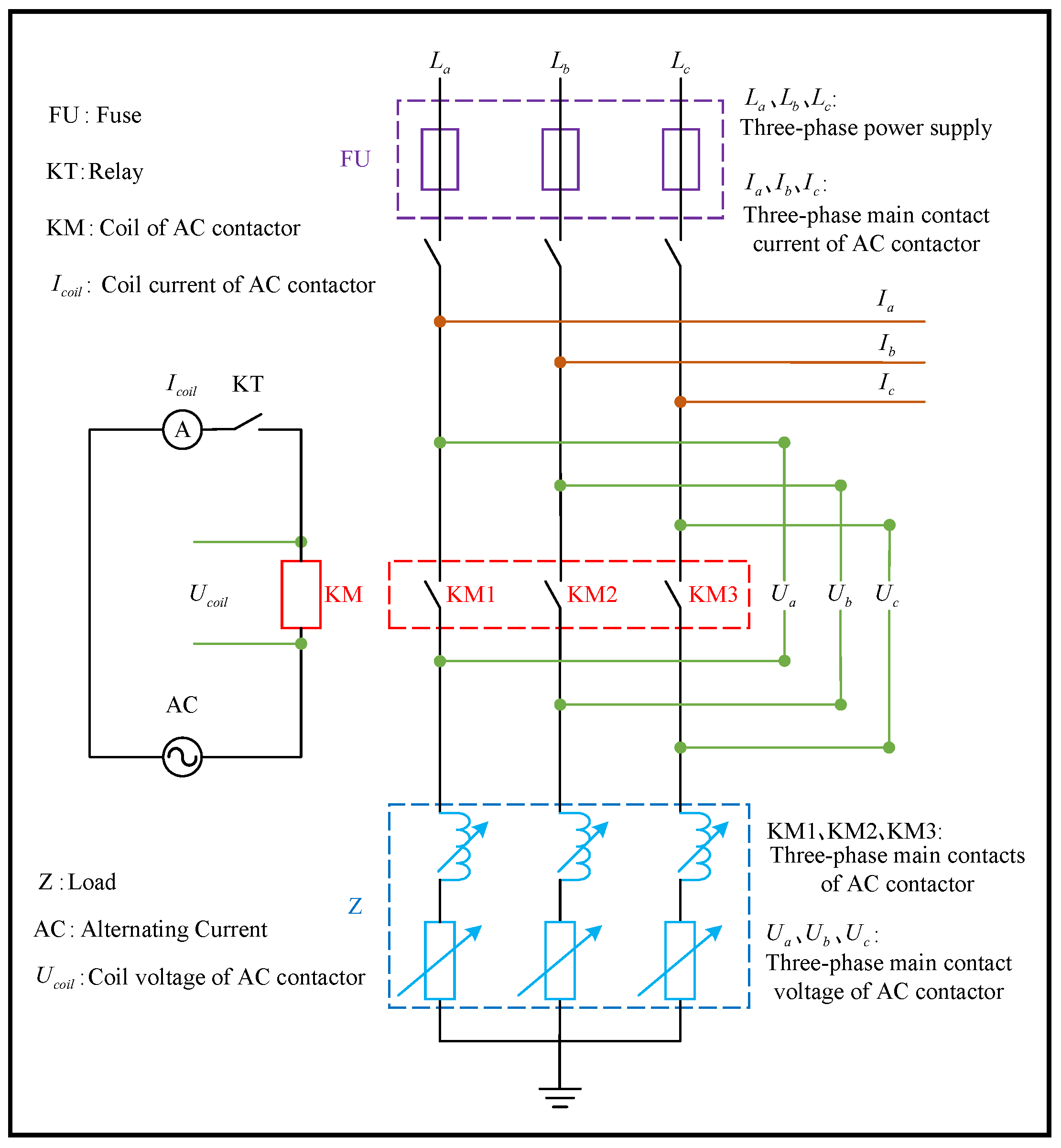

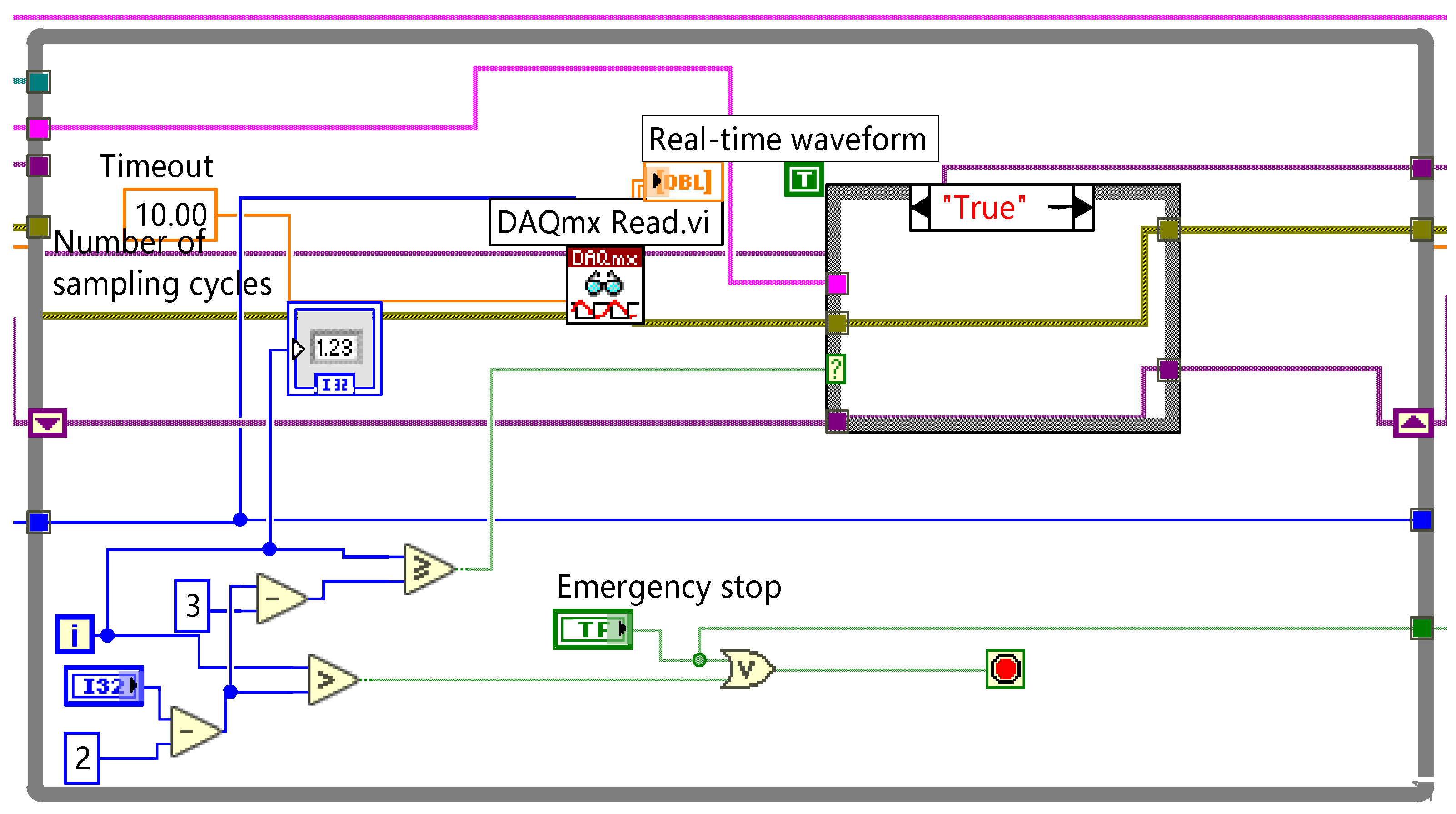
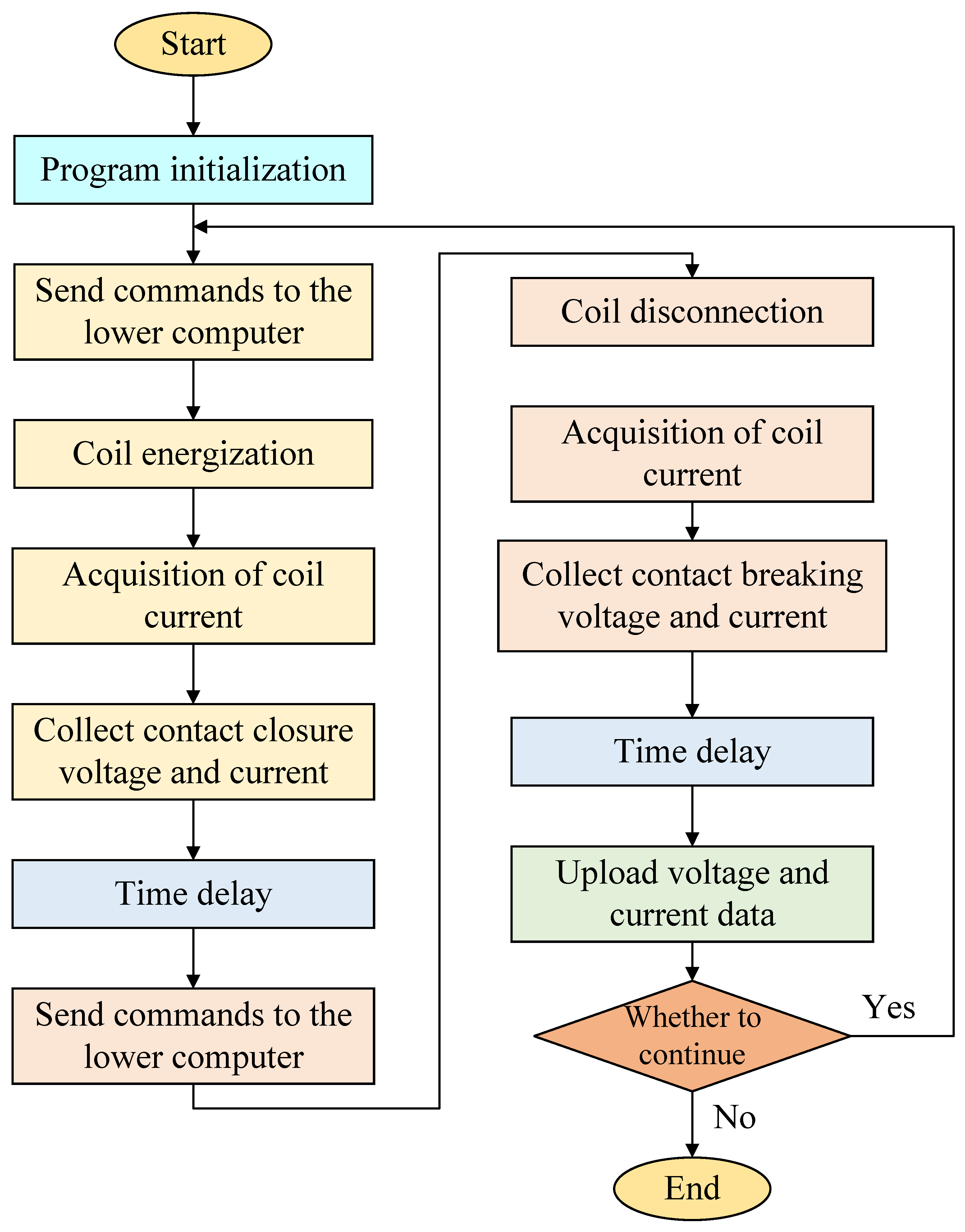

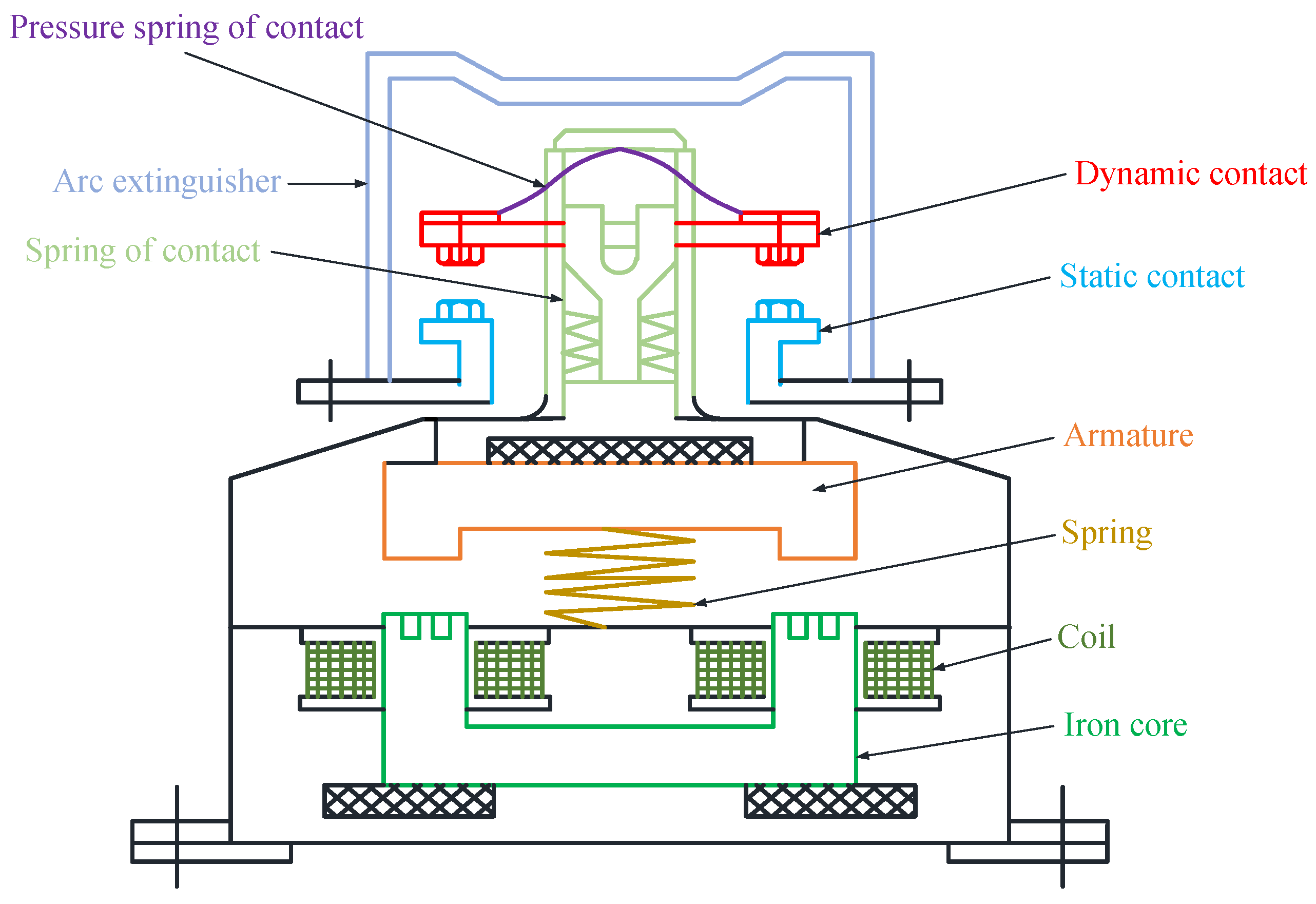




| Test Conditions | AC-4 |
|---|---|
| Load type | Resistance load |
| Load voltage | 400 (380) V |
| Load current | 222 A |
| Coil voltage | 220 V |
| Power factor | |
| Connection conditions | |
| Breaking conditions | |
| Operation frequency | |
| Sample frequency |
| LEM Sensor Types | LF310 | LV25-400 |
|---|---|---|
| Sensor Parameter | Current | Voltage |
| Rated measurement value | ||
| Maximum measurement value | ||
| Rated working voltage | ||
| Measurement accuracy | ||
| Sensor linearity |
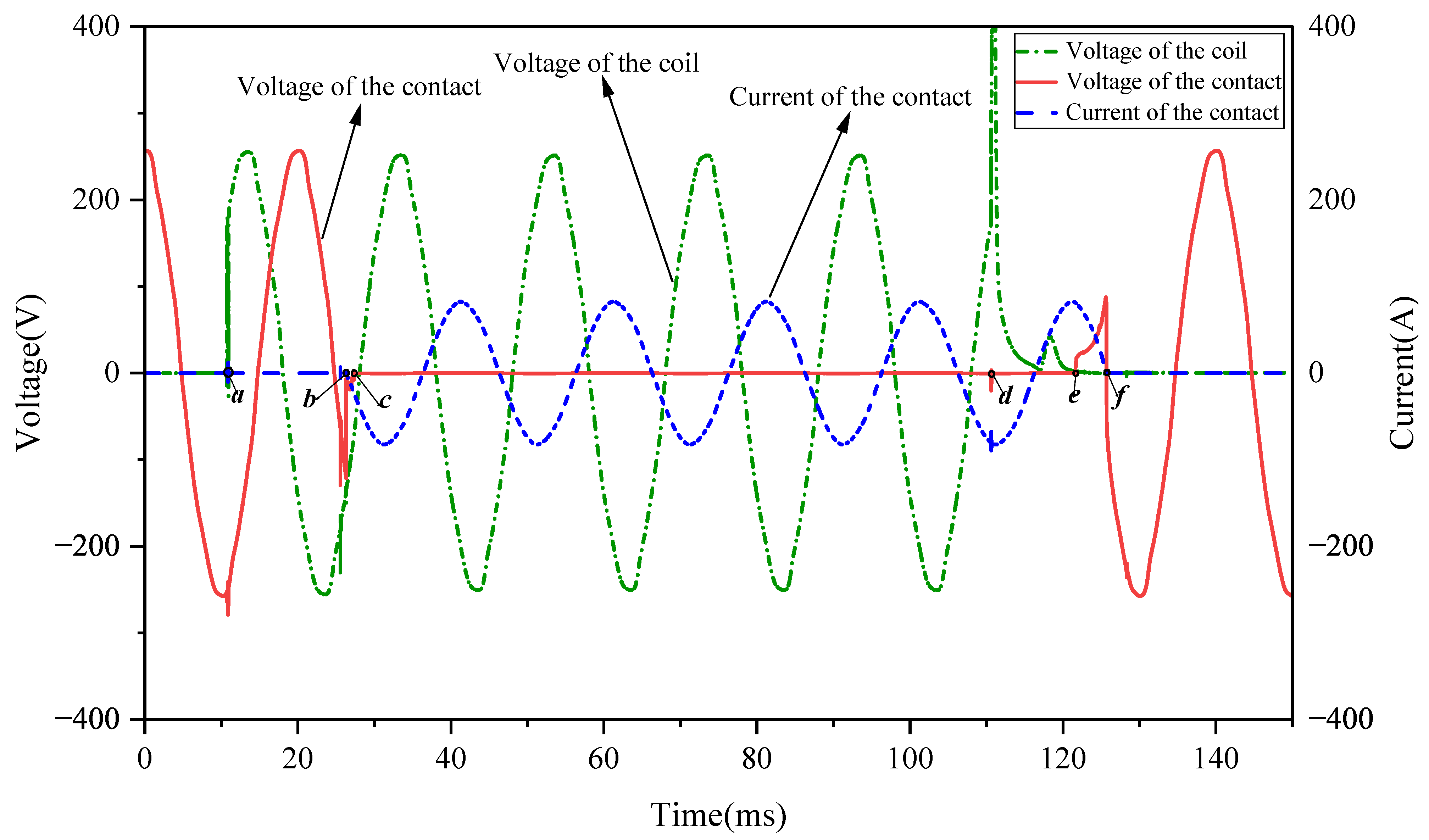
| Time | Status |
|---|---|
| When the coil is energized, the electromagnetic attraction force rises sharply, and the contacts act. | |
| When the contacts are closed for the first time, a current is generated between the contacts. | |
| The contact is stably closed, the contact voltage is stable, and the main circuit is connected. | |
| The coil loses power, the electromagnetic attraction drops sharply, and the contacts are separated. | |
| The voltage between the contacts rises and arc generates. | |
| The main circuit current crosses the zero point, and the arc is extinguished. |
| Serial Number | Feature Name | Computational Formulas |
|---|---|---|
| 1 | Contact resistance | |
| 2 | Pull-in time | |
| 3 | Bounce time | |
| 4 | Arcing time | |
| 5 | Arc energy E | |
| 6 | Average arcing power P | |
| 7 | Release time |
| Prediction Models | RNN | LSTM | GRU | CNN-GRU |
|---|---|---|---|---|
| RMSE | 3468.52 | 3218.61 | 3020.18 | 2914.98 |
| MAE | 1009.62 | 736.12 | 537.94 | 432.34 |
| 0.3665 | 0.6065 | 0.7519 | 0.8310 | |
| Max Error | 7255.93 | 5107.34 | 4329.07 | 2489.70 |
| Effective precision | 81.62% | 87.66% | 89.04% | 93.69% |
| Calculation time | 52.1 s | 49.6 s | 42.4 s | 35.6 s |
| Standard deviation of prediction accuracy | 1.2969% | 0.9761% | 1.0072% | 1.0466% |
| Prediction Models | RNN | LSTM | GRU | CNN-GRU |
|---|---|---|---|---|
| RMSE | 3072.97 | 3066.95 | 3042.85 | 2742.03 |
| MAE | 553.24 | 582.54 | 552.97 | 225.16 |
| 0.6368 | 0.7194 | 0.7529 | 0.9538 | |
| Max Error | 6633.20 | 3662.67 | 3203.21 | 1474.50 |
| Effective precision | 83.20% | 90.72% | 91.89% | 96.63% |
| Calculation time | 49.4 s | 45.9 s | 38.2 s | 31.8 s |
| Standard deviation of prediction accuracy | 1.3934% | 0.9994% | 0.9010% | 0.5006% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Gao, S.; Peng, S.; Liu, Y.; Li, J. Residual-Electrical-Endurance Prediction of AC Contactor Based on CNN-GRU. Machines 2022, 10, 1067. https://doi.org/10.3390/machines10111067
Liu S, Gao S, Peng S, Liu Y, Li J. Residual-Electrical-Endurance Prediction of AC Contactor Based on CNN-GRU. Machines. 2022; 10(11):1067. https://doi.org/10.3390/machines10111067
Chicago/Turabian StyleLiu, Shuxin, Shuyu Gao, Shidong Peng, Yang Liu, and Jing Li. 2022. "Residual-Electrical-Endurance Prediction of AC Contactor Based on CNN-GRU" Machines 10, no. 11: 1067. https://doi.org/10.3390/machines10111067
APA StyleLiu, S., Gao, S., Peng, S., Liu, Y., & Li, J. (2022). Residual-Electrical-Endurance Prediction of AC Contactor Based on CNN-GRU. Machines, 10(11), 1067. https://doi.org/10.3390/machines10111067






